1. Introduction
Quantum field theory in accelerated backgrounds has led to deep insights into the fundamental notions of
vacuum and
particles, forcing us to reconsider these basic concepts as observer-dependent notions. A prominent example of this feature is given by the Unruh effect [
1], affirming that an observer moving with constant acceleration in the Minkowski vacuum feels a
thermal bath at an Unruh temperature proportional to its proper acceleration,
a:
where
c is the speed of light,
the Planck constant, and
is the Boltzmann constant.
An analogous effect, in a curved space-time, is the Hawking radiation from a black hole: a free-falling observer outside a black hole should experience a bath of thermal radiation at the temperature
,
g being the local acceleration due to gravity at the event horizon [
2].
As paradoxical as the concept of thermal radiation from vacuum may appear, the Unruh effect is a clear manifestation of the
non-unicity of the notion of quantum vacuum (and of particles), as extensively discussed in the seminal paper by Fulling [
3] and in following papers on the subject [
4,
5]. This conceptually subtle effect, merging classical general relativity and quantum field theory, has been the object of intense investigations in the literature, with different and sometimes conflicting conclusions on its physical interpretation [
6,
7,
8,
9,
10,
11,
12]. Additionally, from Equation (
1) (cgs units), we have
and therefore extremely high accelerations, of the order of
, are necessary to obtain an Unruh thermal bath of a few kelvin, thus making the detection of this effect in the laboratory drastically difficult [
6,
8,
13,
14,
15,
16,
17,
18]. Whilst the absence of any experimental observation of the Unruh effect has led to question the reality of the effect [
12], it has been argued that the Unruh effect is a fundamental requirement to ensure the consistency of quantum field theory [
19]. In any case, a direct verification of the effect, and in general of acceleration-dependent effects, could allow us to solve some fundamental controversies about its physical interpretation.
Recently, the effects of an accelerated motion on the radiative properties of atoms/molecules in vacuum have been discussed in the literature [
20,
21,
22,
23,
24,
25,
26]. Changes in the spontaneous emission rate [
20,
27,
28,
29] or in the Lamb shift of single uniformly accelerating atoms [
21,
22], as well as the dispersion Casimir–Polder interaction between a uniformly accelerated atom and a reflecting plate [
30,
31,
32,
33,
34] or between two uniformly accelerated atoms [
35,
36], have been investigated, and their relation with the Unruh effect was discussed. The effect of non-equilibrium boundaries on radiative properties of atoms has been also considered [
37,
38].
Another, albeit related, problem, recently addressed in the literature, concerns the equivalence between acceleration and temperature. For example, it has been discussed that non-thermal features (related to a uniform acceleration) manifest in the dispersion (van der Waals/Casimir-Polder) and resonance interaction between non inertial atoms in the free-space [
25,
26,
36,
39]. These investigations reveal that the effects of a uniform acceleration are not always equivalent to Unruh thermal effects.
Motivated by these issues, in this paper, we investigate the effect of a non-inertial motion on the resonance interaction between two atoms, that accelerate with the same constant acceleration, parallel to a reflecting plate. The imposition of boundary conditions on the quantum field on the plate changes vacuum field fluctuations and the density of states of the quantized radiation field, and, thus, it can significantly influence radiative properties of atoms placed nearby [
40,
41,
42,
43,
44,
45]. Our aim is to investigate in detail physical manifestations of atomic acceleration in the radiation-mediated resonance interaction between the two atoms located in the proximity of a reflecting plate.
Resonance and dispersion Casimir–Polder interactions are long-range interactions involving neutral objects such as atoms or molecules [
46,
47], due to the zero-point fluctuations of the quantum electromagnetic field or to the source field [
47,
48,
49]. When one or more atoms are in their excited state, a resonance interaction between the atoms can occur, as a result of the exchange of real photons between them. If the two atoms are prepared in a factorized state, the resonance interaction is a fourth-order effect in the coupling and scales as
in the far-zone limit,
(
is the wavelength associated to the main atomic transition, and
R is the interatomic distance) [
50]. These interactions, for atoms in a factorized state, have been recently investigated in the literature, also in connection with some controversial results concerning the presence or not of space oscillating terms [
51,
52,
53,
54]. Recent results show that the force on the excited state is oscillatory in space, while that on the ground state is monotonic [
52,
53]. A different physical phenomenon occurs if two identical atoms are prepared in a superradiant (or subradiant) Dicke-state. In this case, the resonance interaction energy is obtained at the second-order in the coupling, and it shows space oscillations in the far-zone limit. Such interaction is usually stronger than dispersion interactions and scales as
, for very large separations (
). Resonance interactions, and the related Förster energy transfer [
55], have been extensively investigated in the literature [
56]. The possibility to manipulate (enhance or inhibit) the dispersion and resonance interactions through a structured environment has been also recently investigated [
57,
58,
59,
60,
61].
We consider two atoms moving with the same uniform proper acceleration in a direction parallel to a reflecting boundary and interacting with the quantum scalar and the electromagnetic field in the vacuum state. Following a procedure originally introduced by Dalibard, Dupont-Roc, and Cohen-Tannoudji [
62,
63], we identify the contribution of self reaction and vacuum fluctuations to the resonance energy shift of the two accelerated atoms [
25,
39,
44,
64]. This approach has been recently used to investigate radiative process of atoms at rest in the presence of a boundary [
44,
65] or in a cosmic string spacetime [
66], and it has been recently generalized to the fourth order to evaluate the dispersion Casimir–Polder interaction between two atoms accelerating in the vacuum space [
36]. We show that only the radiation reaction field (source field) contributes to the interatomic resonance interaction energy, while vacuum field fluctuations do not. Consequently, the resonance interaction does not show Unruh
thermal-like terms (which are related to vacuum field fluctuations). However, non-thermal effects of acceleration appear in the source field contribution, which significantly affect the resonance interaction energy between the two accelerated atoms. To explore these effects, we consider two distinct geometric configurations of the two-atom-plate system: atoms aligned perpendicular or parallel to the plane boundary. We show that the presence of the mirror significantly modifies the character of the resonance interaction energy between the two accelerated atoms. By an appropriate choice of the orientation of the two dipole moments, we show that new effects of atomic acceleration (not present for atoms at rest) appear, yielding a non-vanishing resonance interaction energy even for specific configurations in which the interaction for stationary atoms is zero. This result also suggests new possibilities of observing the effects of a uniform acceleration through a modification of the resonance interatomic interaction between two identical entangled atoms. Thus, our findings could have relevance for a possible detection of the effect of an accelerated motion in radiation-mediated interactions between non-inertial atoms.
The paper is structured as follows. In
Section 2, we briefly introduce the method used, and discuss the resonance interaction energy between two accelerating atoms interacting with a massless relativistic scalar field nearby a reflecting mirror. In
Section 3, we extend our investigation for atoms interacting with the vacuum electromagnetic field. Final remarks and conclusions are given in
Section 4.
Throughout the paper, we adopt units such that .
2. Resonance Interaction between Two Uniformly Accelerating Atoms: The Scalar Field Case
We consider two identical atoms,
A and
B, interacting with a massless relativistic scalar field in the vacuum state and in the presence of a perfectly reflecting plate satisfying Dirichlet boundary conditions. The two atoms are modeled as point-like systems with two internal energy levels,
, associated with the eigenstates
and
, respectively. We suppose that the mirror is located at
and that the two atoms move in a direction parallel to the mirror, with the same uniform proper acceleration, perpendicular to their (constant) separation. The atom-field Hamiltonian in the multipolar coupling scheme and within the dipole approximation, in the locally inertial frame of the two atoms (comoving frame), is as follows [
25,
36,
48,
67]:
where
and
are the pseudospin atomic operators,
and
are the creation and annihilation operators of the scalar field,
is the coupling constant, and
(
) is the trajectory of atom
(
is the proper time of the atoms);
is the scalar field operator, with Dirichlet boundary conditions at the surface of the plate. Equation (
3) is expressed in the comoving frame of the two atoms, and we use the Heisenberg representation.
We assume two identical atoms prepared in one of the two correlated, symmetrical (superradiant), or antisymmetrical (subradiant) states (
or
, respectively):
To investigate the interatomic resonance dipole–dipole interaction energy, we exploit the procedure originally introduced in Refs. [
62,
63], allowing to identify the contributions of the source field and vacuum fluctuations to the interaction energy. As discussed in [
25,
36,
62,
63], this leads to the introduction of an effective Hamiltonian that governs the time evolution of the atomic observables, pertaining to atom
A (
B), given by the sum of two terms (similar expressions are obtained for atom
B, by exchange of
A and
B):
where the functions
and
are the field statistical function (symmetric correlation function and the linear susceptibility), respectively:
To obtain the contributions of source field and vacuum fluctuations to the energy shift of the system, we take the average values of the effective Hamiltonians
and
on the correlated state (
4):
and
where
and
are the initial and final times (similar expressions are obtained for atom
B);
and
are respectively the antisymmetric and symmetric statistical functions of atom
A (
B), while
and
refer to the collective two-atom system:
From expressions above, it is clear that the resonance interaction is entirely due to the source field contribution [
25]. In fact, Equation (
9) does not depend on the interatomic distance; it only gives the vacuum fluctuations contribution to the Lamb shift of each atom (
A or
B). Hence, this term does not contribute to the resonance force between the atoms. Similar considerations apply to the first term on the right-hand side of Equation (
10). On the contrary, the second term on the right-hand side of Equation (
10), which depends on the distance between the two atoms, is the only contribution relevant at the second order to the interatomic interaction energy. Therefore, the interatomic resonant energy shift is obtained as
This conclusion is indeed expected on a physical ground, as the resonance interaction is due to the exchange of a (real and virtual) scalar quantum between the two correlated atoms. It is thus related to the field emitted by the two atoms (source field). This property has important consequences when we consider the interaction between accelerated atoms. In fact, as discussed in [
25,
26], this interaction energy does not show signatures of the Unruh thermal effect (which is exclusively related to the vacuum field correlations in the locally inertial frame). However, we find that the atomic acceleration can determine a qualitative change of the interaction between the two atoms, even if not equivalent to a thermal effect.
We now apply the procedure discussed above to evaluate the resonance interaction energy between two atoms moving with uniform acceleration, interacting with the vacuum scalar field nearby a reflecting plate. We first evaluate the field’s linear susceptibility. In the presence of a reflecting boundary, it can be expressed as the sum of two terms, a free term (
) that coincides with that obtained in free-space, and a boundary-dependent term (
), related to the presence of the reflecting plate [
68]:
with
where
,
,
, and
.
The atomic statistical function
can also be easily obtained [
25]:
where the ± sign respectively refers to the symmetric or antisymmetric states (Equation (
4)).
Equation (
14) has a general validity and can be applied to different situations, for example, two atoms at rest in the presence of a mirror or uniformly accelerating near a plane boundary, provided the appropriate atomic trajectories,
and
, are given.
We now specialize our considerations to two specific cases. We suppose a mirror located at and assume that the two atoms accelerate in the half-space , with the same uniform proper acceleration, parallel to the reflecting plate. The distance between the atoms is thus constant. We consider two different geometric configurations of the two-atom system relative to the plate: two atoms aligned along the z-axis, perpendicular to the boundary, and two atoms aligned in a direction parallel to the plate. This permits us to simplify our calculation and to discuss some relevant effects of the presence of the plate on the resonant interaction energy between the two accelerating atoms.
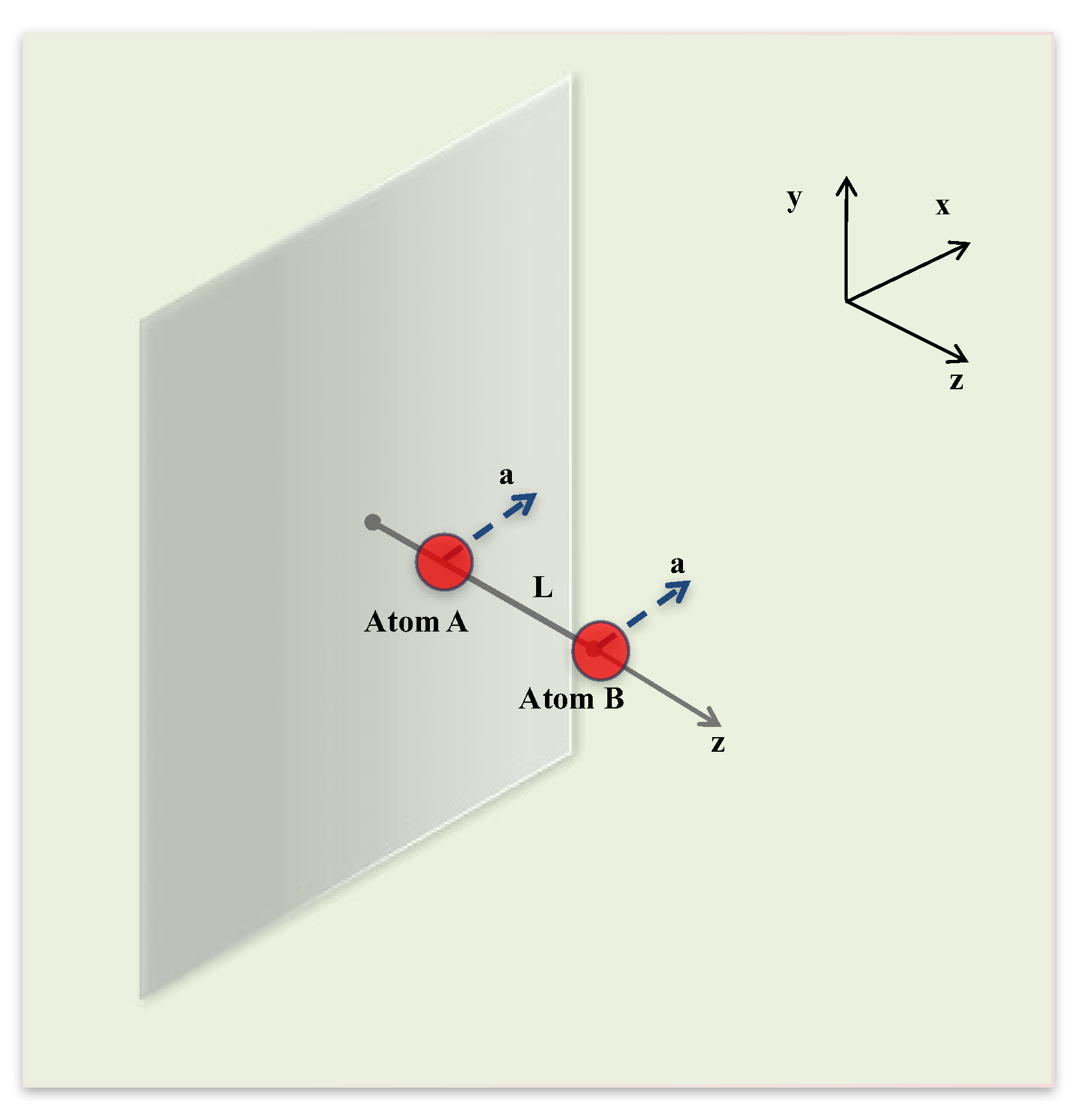
We first consider both atoms located along the
z-direction, perpendicular to the mirror, and uniformly accelerating along the
x-direction, perpendicular to their (constant) separation, as shown in
Figure 1.
In the locally inertial frame of the two-atom system, the atomic trajectories, as a function of the proper time
of both atoms, are
In order to obtain the distance-dependent energy shift of the two-atom system, we first give the linear susceptibility of the scalar field on the trajectories (Equation (
18)) of the two atoms. Substituting Equation (
18) into the expressions of the scalar-field linear susceptibility (Equations (
15) and (16)), we obtain
where
,
L is the interatomic distance, and
is the distance between one atom and the image of the second atom relative to the mirror.
The resonance dipole–dipole interaction energy is then obtained using Equations (
17) and (
19) in Equation (
13). We obtain
where the ∓ sign refers to the symmetric or antisymmetric superposition of the atomic states, respectively.
The expression above describes the resonance dipole–dipole interaction energy in terms of the proper acceleration of the two atoms and the atom-plate distances. In the limit
, it reduces to that for atoms at rest. It consists of two terms: a term coinciding with the resonance interaction energy for two accelerating atoms in the free-space, discussed in [
25], and a new term, depending on
, related to the presence of the mirror. The latter term, describing the effect of the boundary on the energy shift, originates from the interaction of one atom (e.g., atom
A) with the image of the other atom (
B). When both atoms are very distant from the reflecting boundary, the boundary-dependent term in Equation (
20) goes to zero, and we recover the resonance interaction between two atoms accelerating in free-space [
25]. On the other hand, when the atoms are very close to the mirror, we can approximate
, and the resonance interaction is strongly suppressed. Thus, in this limit, the interaction between the two entangled atoms can be strongly inhibited by means of the nearby plate, analogously to the case of atoms at rest discussed in [
44].
Most importantly, Equation (
20) shows that the effects of the atomic acceleration are not
thermal-like. Nevertheless, the relativistic acceleration significantly affects the interaction energy, giving a different scaling of it with the interatomic distance. In fact, similarly to the results in [
25,
36] for atoms accelerating in the unbounded space, we can identify a characteristic length scale related to the acceleration,
. For distances larger than
, the effects of relativistic acceleration can significantly change the interaction between the two non-inertial atoms; in fact, when
, we obtain
giving a different scaling law of the interaction compared to the case of inertial atoms. In the
near-zone limit,
, we recover the well-known result for inertial (static) atoms:
In the intermediate zone,
, when the distance between the two atoms is smaller than the characteristic length
but their distance from the mirror is such that
, we obtain
Thus the relativistic acceleration and the presence of the boundary affect the qualitative features of the resonance interaction, in particular, its power-law distance dependence, decreasing at large distances more rapidly than in the inertial case. Additionally, in the presence of a boundary, the non-inertial character of acceleration modifies the interatomic interaction energy, even when the separation between the two atoms is much smaller then . In fact, such a result can be expected on a physical ground: the boundary-dependent term, as mentioned, can be interpreted as the interaction of one atom with the image of the other atom with respect to the plate. When the atoms are accelerating, the distance traveled by the photon emitted by one atom to reach the other one, after reflection from the mirror, increases with time; if , this effect becomes relevant and causes an overall decrease of the interaction strength between the two atoms.
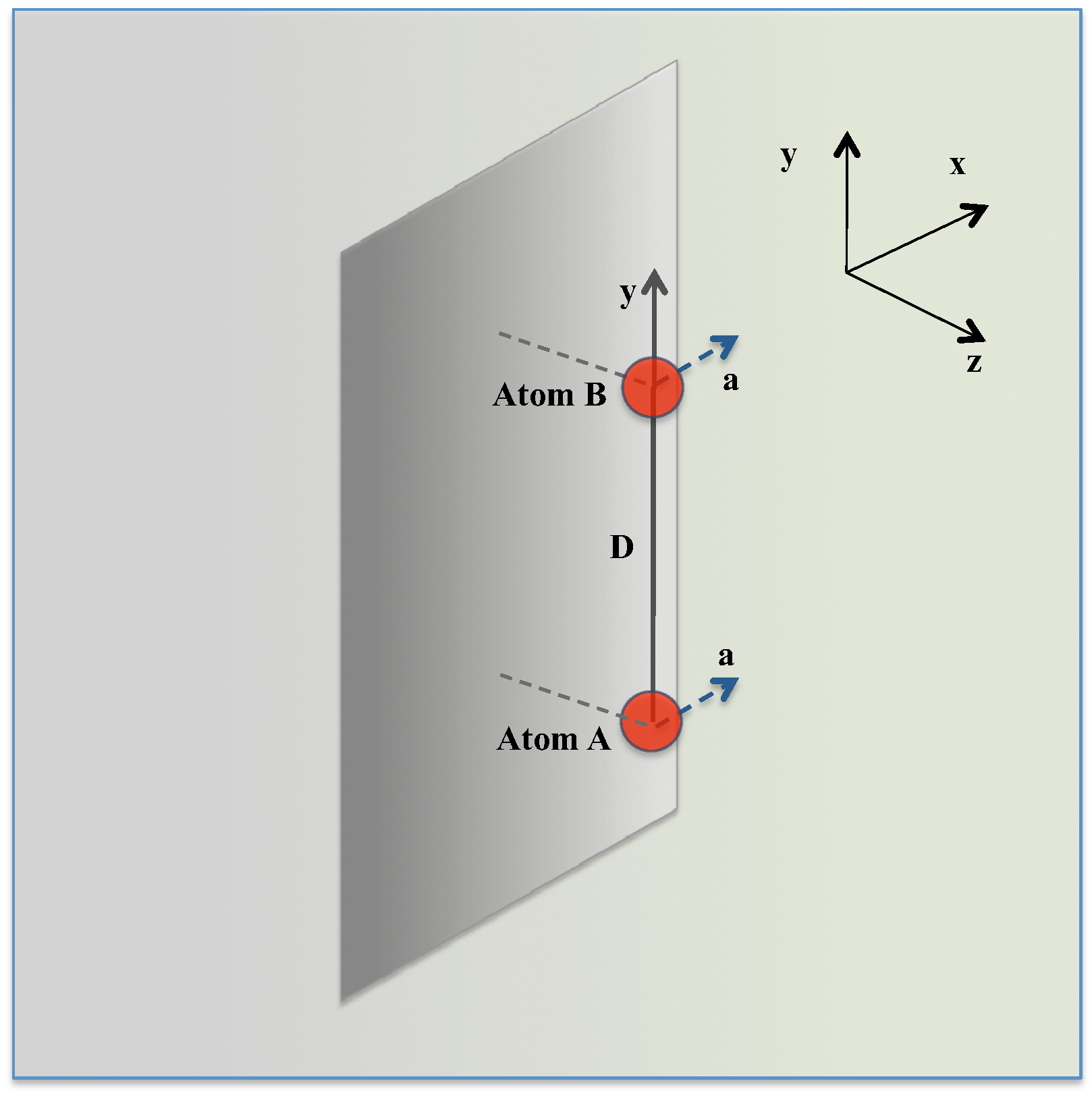
We now investigate whether similar effects manifest also for a different geometric configuration of the atom-plate system. Specifically, we consider two atoms aligned in the
y-direction, parallel to the mirror, as shown in
Figure 2, and uniformly accelerating in the
x-direction, perpendicular to their (constant) separation. In this case, the atomic trajectories are
with
.
Following the same procedure as before, we first obtain the scalar-field linear susceptibility:
where
D is the interatomic distance,
, and we have defined
.
The substitution of Equations (
25) and (
17) into Equation (
13) yields, after algebraic calculations, the resonance dipole–dipole interaction for accelerating atoms:
As before, we find that the resonance interaction energy consists of two terms. The first term on the right-hand side of Equation (
26) coincides with that for atoms uniformly accelerating in free-space [
25], while the second new term is related to the boundary. In the static (inertial) limit, we recover the expression of the resonance interaction for atoms at rest near the mirror for the configuration considered [
44]:
It is worth noting that the expression of
given by Equation (
26) is formally equal to that obtained for
in Equation (
20), provided
is replaced by
R. This is indeed expected, as the distance
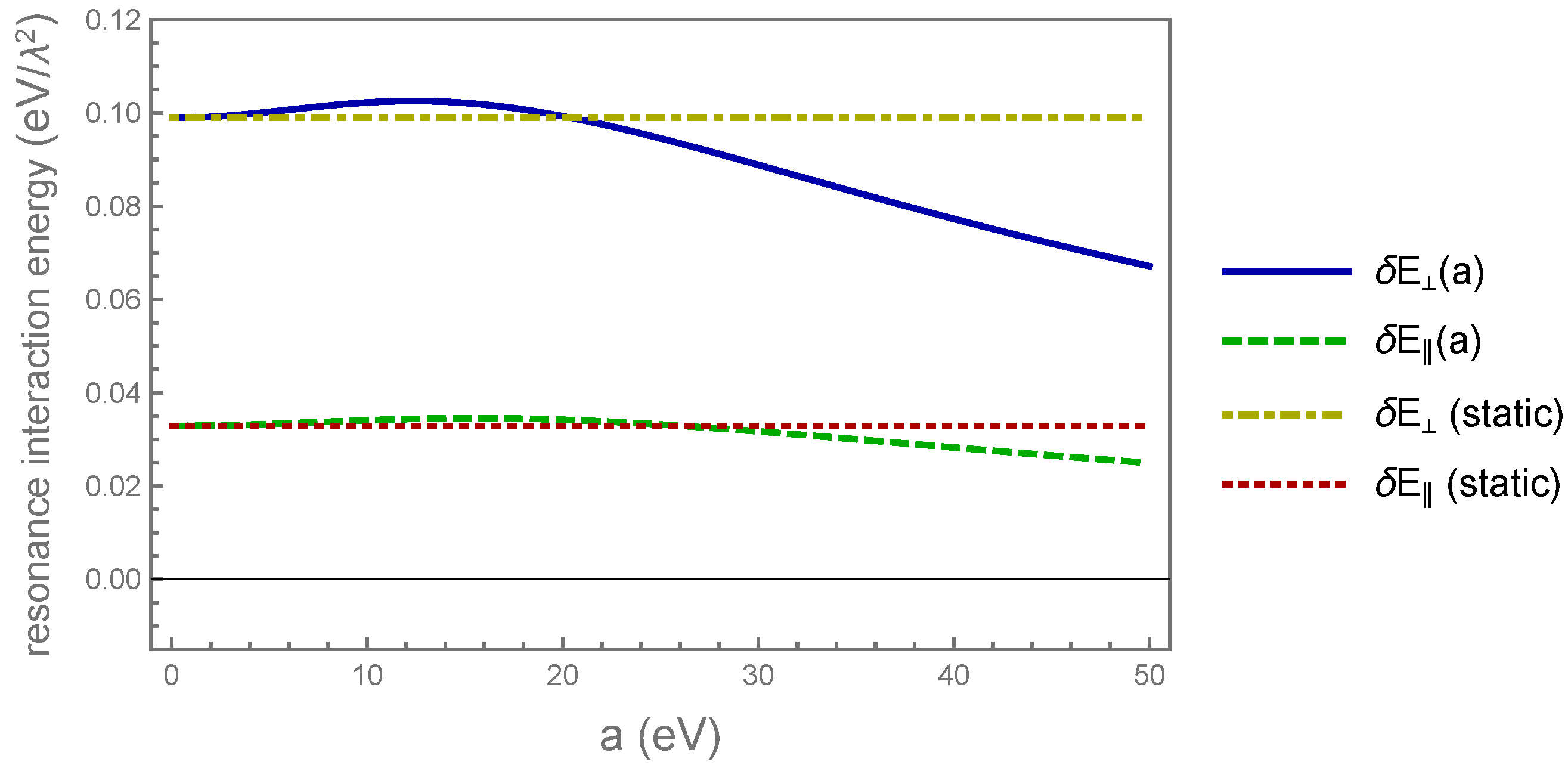
is the distance between one atom and the image of the other. In order to compare the results obtained in the two geometric configurations, in
Figure 3 are plotted Equations (
20) and (
26) of the resonance interaction energy (in units of eV/
λ2), as a function of the atomic acceleration. In the plots, the value used for
is the ionization energy of
87Rb, and the distances
and
z have been chosen in such a way that the plots cover near, intermediate, and far zones, for both perpendicular and parallel alignments of the atoms. The plots show that the resonance interaction energy depends on the acceleration and the geometric configuration of the two atoms with respect to the plate (perpendicular or parallel alignment) and that it can be enhanced or inhibited, depending on the atomic acceleration.
3. Resonance Interaction for Two Accelerating Atoms Interacting with the Electromagnetic Field
In this section, we extend our investigations to two uniformly accelerated identical atoms interacting with the vacuum electromagnetic field, placed nearby a perfectly reflecting plate. As before, the atoms move with a uniform proper acceleration a in a direction parallel to the plane, located at , and their distance is constant. Our aim is to discuss whether new and further effects of acceleration may manifest in their interaction, as a consequence of the vector nature of the electromagnetic field.
We adopt the Hamiltonian in the Coulomb gauge and in the multipolar coupling scheme, within dipole approximation. In the comoving reference frame of both atoms, this is
indicates the polarization ,
is the dipole moment operator of the atoms (restricted to the subspace of the two atomic levels considered), and
is the electric field operator, with the appropriate boundary conditions on the reflecting plate.
As shown in the previous section, the resonance interaction energy is due only to the radiation-reaction term and can be obtained through the effective Hamiltonian
(terms referring to atoms
A and
B, respectively) on the correlated state
(see Equations (
4)–(
6)), taking only terms depending on the interatomic distance:
where
. We first evaluate the electromagnetic field susceptibility
and the atomic symmetric correlation function
.
The field susceptibility in the comoving frame can be obtained from the two-point correlation function of the field [
68]. The two-point correlation function of the electric field operator in the presence of the reflecting boundary, is the following (for brevity, we omit the time-dependence in the following expressions):
It can be written as the sum of a free part,
, and a boundary-dependent term,
:
where
and
n is the unit vector along the line joining the two atoms.
We now specialize our considerations to the two specific configurations considered for the scalar-field case in
Section 2 and illustrated in
Figure 1 and
Figure 2, that is, atoms aligned in a direction perpendicular or parallel to the plate, respectively.
3.1. Atoms Aligned Perpendicularly to the Plate
We first consider two atoms aligned along the
z-direction, perpendicular to the boundary, and uniformly accelerating along the
x-direction, as shown in
Figure 1. Thus they move on the trajectory given by Equation (
18). Because of the vector structure of the electromagnetic field, the calculation of the field susceptibility turns out to be more complicated than for the scalar field [
68]. After lengthy algebraic calculations, involving a Lorentz transformation of the fields to the comoving frame, we obtain the following (in the locally inertial frame):
where
is the two-point correlation function of two atoms uniformly accelerated in vacuum [
25], and
is the contribution due to the presence of the boundary. In the equations above,
is a unit vector along the acceleration. As discussed in [
25], the function
is not isotropic, displaying a non-diagonal component. In fact, in the present case, we have two specific directions in space: the direction perpendicular to the plate and that of the acceleration. Similar anisotropies were already found for a single uniformly accelerated atom near a boundary [
31] or for two accelerated atoms in the free-space [
25]. They arise from the spatially extended structure of the two-atom-plate system here considered, as well as from the vector character of the electromagnetic field. This peculiarity, as we now show, has deep consequences for the interaction energy between the two atoms.
In order to evaluate the resonance energy, we first focus our attention on the boundary-dependent term and calculate the linear susceptibility of the electric field. Using Equation (
36), after lengthly algebraic calculations, involving a Fourier transform of the statistical function of the field, we finally obtain
where we have introduced the functions
and
given in
Appendix A (see Equations (A1) and (
A2)).
Substituting Equation (
37) and the atomic symmetric statistical function:
into Equation (
29), we finally obtain the boundary-dependent contribution to the resonant energy shift of the two accelerating atoms:
where we have introduced the function
:
modulating the interaction as a function of
and of the atomic acceleration.
With a similar procedure, evaluation of the boundary-independent contribution,
, to the resonance interaction energy yields the following [
25]:
where
and the functions
and
are given by Equations (
A3) and (
A4) of
Appendix A.
The complete resonance interaction energy of the accelerated two-atom system is then obtained by summing Equations (
39) and (
41):
The result (Equation (
43)) is valid for any value of the parameters
a,
L, and
. It is easy to show that in the
near-zone limit,
and
, the linear susceptibility is well described by its stationary counterpart, and we recover the expression of the resonance interaction for two atoms at rest [
25,
44]. However, at higher orders in
(and/or
), corrections related to the accelerated motion of the two atoms become relevant, yielding a different scaling of the interaction energy with the distance, in analogy to the scalar-field case discussed in the previous section. Interestingly, a comparison with the scalar-field case shows the emergence of new features in the resonance interaction, due to the boundary, and related to the anisotropic structure of the electromagnetic field susceptibility. Indeed, from Equation (
39), it follows that the effect of the acceleration on the interaction can be controlled by an appropriate choice of the dipoles’ orientations and of the distance of the two atoms from the plate. For example, when the dipole moments are orthogonal to each other, with one along
x and the other along
z, the diagonal term in Equation (
39) vanishes, and only the second (non-diagonal) term survives. The non-diagonal term is present only for
, and its contribution is a peculiar characteristic of the non inertial atomic motion, giving a non-vanishing interaction energy, in a configuration where that for static atoms is zero. This term is thus a sharp signature of an accelerated motion. To numerically estimate this energy shift, we can assume
m/s
2 (
eV, in our units),
m (
eV
−1),
m (
eV
−1), and
eV, obtaining
eV. This energy shift is about 4 orders of magnitude smaller than the Lamb shift for the
level of the hydrogen atom. Although quite small, we expect that such an energy shift should be measurable using high-resolution spectroscopy, provided the assumed constant acceleration could be reached.
The results above suggest investigation of whether analogous effects of acceleration manifest also for other geometric configurations of the two atoms system, for example, when both atoms are aligned parallel to the reflecting plane boundary. This configuration is considered in the next subsection.
3.2. Atoms Aligned Parallel to the Plate
We now consider the configuration of two atoms aligned along the
y-direction, parallel to the boundary, which move with uniform proper acceleration along the
x-direction, such that their trajectories are those given by Equation (
24). As before, the distance between the two atoms remains constant during their motion. This configuration is illustrated in
Figure 2.
The two-point correlation function of the field in the locally inertial frame of both atoms is
where
is the two-point correlation function in free-space [
25] and
is the boundary-dependent contribution, which consists of a diagonal term:
that is non-vanishing only for
, and a non-diagonal term:
that is different from zero only for
. We have here introduced the unit vector
and the distances
and
). The boundary-dependent contribution to the linear susceptibility of the field is then obtained as
re the functions
and
, given in Equations (
A5) and (
A6) of
Appendix A, modulate the resonance interaction energy with the distance
D and the atomic acceleration
a.
Substituting Equations (
47) and (
38) into Equation (
29), we find the boundary-dependent contribution to the resonant energy shift:
where
The resonance interaction energy between the accelerating atoms is finally obtained by adding Equation (
48) to the free-space interaction energy
, given by the following [
25]:
with
(the functions
and
can be obtained from Equations (
A3) and (
A4) in
Appendix A by exchanging subscripts
z and
y).
A comparison with the case of accelerated atoms aligned along the z-axis, considered in the previous subsection, shows the emergence of a new effect, related to the specific geometric configuration of the two-atom system with respect to the plane boundary. In fact, from the equations above, it follows that when the dipole moments are orthogonal to each other, one of them along y and the other in the plane , a new non-vanishing contribution to the interaction energy (not present for atoms located perpendicular to the boundary) arises. This contribution exists only when , and thus it is a peculiarity of an accelerated motion. This gives new additional possibilities to exploit the resonance interaction between accelerated atoms for detecting (non-thermal) effects of acceleration and, in general, physical effects of the accelerated motion on radiation-mediated interactions between atoms.