Neutrosophic Weighted Support Vector Machines for the Determination of School Administrators Who Attended an Action Learning Course Based on Their Conflict-Handling Styles

Abstract

In the recent years, school administrators often come across various problems while teaching, counseling, and promoting and providing other services which engender disagreements and interpersonal conflicts between students, the administrative staff, and others. Action learning is an effective way to train school administrators in order to improve their conflict-handling styles. In this paper, a novel approach is used to determine the effectiveness of training in school administrators who attended an action learning course based on their conflict-handling styles. To this end, a Rahim Organization Conflict Inventory II (ROCI-II) instrument is used that consists of both the demographic information and the conflict-handling styles of the school administrators. The proposed method uses the Neutrosophic Set (NS) and Support Vector Machines (SVMs) to construct an efficient classification scheme neutrosophic support vector machine (NS-SVM). The neutrosophic c-means (NCM) clustering algorithm is used to determine the neutrosophic memberships and then a weighting parameter is calculated from the neutrosophic memberships. The calculated weight value is then used in SVM as handled in the Fuzzy SVM (FSVM) approach. Various experimental works are carried in a computer environment out to validate the proposed idea. All experimental works are simulated in a MATLAB environment with a five-fold cross-validation technique. The classification performance is measured by accuracy criteria. The prediction experiments are conducted based on two scenarios. In the first one, all statements are used to predict if a school administrator is trained or not after attending an action learning program. In the second scenario, five independent dimensions are used individually to predict if a school administrator is trained or not after attending an action learning program. According to the obtained results, the proposed NS-SVM outperforms for all experimental works.

1. Introduction

Support Vector Machine (SVM) is a widely used supervised classifier, which has provided better achievements than traditional classifiers in many pattern recognition applications in the last two decades [1]. SVM is also known as a kernel-based learning algorithm where the input features are transformed into a high-dimensional feature space to increment the class separability of the input features. Then SVM seeks a separating optimal hyperplane that maximizes the margin between two classes in high-dimensional feature space [2]. Maximizing the margin is an optimization problem which can be solved using the Lagrangian multiplier [2]. In addition, some of the input features, which are called support vectors, can also be used to determine the optimal hyperplane [2].

Although SVM outperforms many classification applications, in some applications, some of the input data points may not be truly classified [3]. This misclassification may arise due to noises or other conditions. To handle such a problem, Lin et al. proposed Fuzzy SVMs (FSVMs), in which a fuzzy membership is assigned to each input data point [3]. Thus, a robust SVM architecture is constructed by combining the fuzzy memberships into the learning of the decision surface. Another fuzzy-based improved SVMs approach was proposed by Wang et al. The authors applied it to a credit risk analysis of consumer lending [4]. Ilhan et al. proposed a hybrid method where a genetic algorithm (GA) and SVM were used to predict Single Nucleotide Polymorphisms (SNP) [5]. In other words, GA was used to select the optimum C and γ parameters in order to predict the SNP. The authors also used a particle swarm optimization (PSO) algorithm to optimize C and $\gamma$ parameters of SVMs. Peng et al. proposed an improved SVM for heterogeneous datasets [6]. To do so, the authors used a mapping procedure to map nominal features to another space via the minimization of the predicted generalization errors. Ju et al. proposed neutrosophic logic to improve the efficiency of the SVMs classifier (N-SVM) [7]. More specifically, the proposed N-SVM approach was applied to image segmentation. The authors used the diverse density support vector machine (DD-SVM) to improve its efficiency with neutrosophic set theory [8]. Almasi et al. proposed a new fuzzy SVM method, which was based on an optimization method [9]. The proposed method simultaneously generated appropriate fuzzy memberships and solved the model selection problem for the SVM family in linear/nonlinear and separable/non-separable classification problems. In Reference [10], Tang et al. proposed a novel fuzzy membership function for linear and nonlinear FSVMs. The structural information of two classes in the input space and in the feature space was used for the calculation of the fuzzy memberships. Wu et al. used an artificial immune system (AIS) in the optimization of SVMs [11]. The authors used the AIS algorithm to optimize the C and γ parameters of SVMs and developed an efficient scheme called AISSVM. Chen et al. optimized the parameters of the SVM by using the artificial bee colony (ABC) approach [12]. Specifically, the authors used an enhanced ABC algorithm where cat chaotic mapping initialization and current optimum were used to improve the ABC approach. Zhao et al. used an ant colony algorithm (ACA) to improve the efficiency of SVMs [13]. The ACA optimization method was used to select the kernel function parameter and soft margin constant C penalty parameter. Guraksin et al. used particle swarm optimization (PSO) to tune SVM parameters to improve its efficiency [14]. The improved SVM approach was applied to a bone age determination system.

In this paper, a new approach is proposed: Neutrosophic SVM (NS-SVM). The neutrosophic set (NS) is defined as the generalization of the fuzzy set [15]. NS is quite effective in dealing with outliers and noises. The noises and outlier samples in a dataset can be treated as a kind of indeterminacy. NS has been successfully applied for indeterminate information processing, and demonstrates advantages to deal with the indeterminacy information of data [16,17,18]. NS employs three memberships to measure the degree of truth (T), indeterminacy (I), and falsity (F) of each dataset. The neutrosophic c-means (NCM) algorithm is used to produce T, I, and F memberships [16,17]. In recent years, school administrators often come across various problems while teaching, counseling, and promoting and providing other services which engender disagreements and interpersonal conflicts between students, the administrative staff, and others. Action learning is an effective way to train school administrators in order to improve their conflict-handling styles. To this end, the developed NS-SVM approach is applied to determine the effectiveness of training in school administrators who attended an action learning course based on their conflict-handling styles. A Rahim Organization Conflict Inventory II (ROCI-II) instrument is used that consists of both the demographic information and the conflict-handling styles of the school administrators. A five-fold cross-validation test is applied to evaluate the proposed method. The classification accuracy is calculated for performance measure. The proposed method is also compared with SVM and FSVM.

The paper is organized as follows. In the next section, a summarization of the present works on this topic is given. The proposed NS-SVM is introduced in Section 3. Section 4 gives the experimental work and results. We conclude the paper in Section 5.

2. Related Works

As mentioned earlier, there have been a number of presented works about the feature weighting for improving the efficiency of classifiers. To this end, Akbulut et al. proposed an NS-based Extreme Learning Machine (ELM) approach for imbalanced data classification [18]. They initially employed an NS-based clustering algorithm to assign a weight for each input data point and then the obtained weights were linked to the ELM formulation to improve its efficiency. In the experiments, the proposed scheme highly improved the classification accuracy. Ju et al. proposed a similar work and applied it to improve image segmentation performance [7]. The authors opted to construct the NS weights based on the formulations given in Reference [7]. The obtained weights were then used in SVM equations. In other words, the authors used the DD-SVM to improve its efficiency with neutrosophic logic. Guo et al. proposed an unsupervised approach for data clustering [16]. The authors combined NS theory in an unsupervised data clustering which can be seen as a weighting procedure. Thus, the indeterminate data points were also considered in the classification process more efficiently. An NS-based k-NN approach was proposed by Akbulut et al. [19]. The authors used the NS memberships to improve the classification performance of the k-NN classifier. The proposed scheme calculated the NS memberships based on a supervised neutrosophic c-means (NCM) algorithm. A final belonging membership U was calculated from the NS triples. A final voting scheme as given in fuzzy k-NN was considered for class label determination. Budak et al. proposed an NS-based efficient Hough transform [20]. The authors initially transferred the Hough space into the NS space by calculating the NS membership triples. An indeterminacy filtering was constructed where the neighborhood information was used to remove the indeterminacy in the spatial neighborhood of the neutrosophic Hough space. The potential peaks were detected based on thresholding on the neutrosophic Hough space, and these peak locations were then used to detect the lines in the image domain.

3. Proposed Neutrosophic Set Support Vector Machines (NS-SVM)

In this section, we briefly introduce the theories of SVM and NS. The readers may refer to related references for detailed information [1,3]. Then, the proposed neutrosophic set support vector machine is presented in detail below.

3.1. Support Vector Machine (SVM)

SVM is an important and efficient supervised classification algorithm [1,2]. Given a set of N training data points $\{{\left(x_i,y_i\right)}_{n=1}^N\}$ where x_i is a multidimensional feature vector and $y_i\in \left\{-1,1\right\}$ is the corresponding label, an SVM models a decision boundary between classes of training data as a separating hyperplane. SVM aims to find an optimal solution by maximizing the margin around the separating hyperplane, which is equivalent to minimizing $\left|\left|w\right|\right|$ with the constraint:

$$y_i\left(w.x_i+b\right)\ge 1$$

(1)

SVM employs non-linear mapping to transform the input data into a higher dimensional space. Thus, the hyperplane can be found in the higher dimensional space with a maximum margin as:

$$w.\phi \left(x\right)+b=0$$

(2)

such that for each data sample ($\phi \left(x_i\right),y_i$):

$$y_i\left(w.\phi \left(x_i\right)+b\right)\ge 1, i=1,\dots ,N.$$

(3)

when the input dataset is not linearly separable, then the soft margin is allowed by defining N non-negative variables, denoted by $\xi =\left({\xi }_1,{\xi }_2,\dots ,{\xi }_N\right)$, such that the constraint for each sample in Equation (3) is rewritten as:

$$y_i\left(w.\phi \left(x_i\right)+b\right)\ge 1-{\xi }_i, i=1,\dots ,N$$

(4)

where the optimal hyperplane is determined as;

$$\mathrm{minimum}\left(\frac{1}{2}{w}^2+C{\displaystyle \sum }_{i=1}^N{\xi }_i\right)$$

(5)

$$\mathrm{subjected}\mathrm{to}{y}_i\left(w.\phi \left(x_i\right)+b\right)\ge 1-{\xi }_i, i=1,\dots ,N$$

(6)

where C is a constant parameter that tunes the balance between the maximum margin and the minimum classification error.

3.2. Neutrosophic c-Means Clustering

In this section, a weighting function is defined by samples using the neutrosophic c-means (NCM) clustering. Let $\mathrm{A}=\left\{A_1,A_2,,\dots .,A_m\right\}$ be a set of alternatives in the neutrosophic set. A sample A_i is represented as $\left\{\mathrm{T}\left(A_i\right),\mathrm{I}\left(A_i\right),\mathrm{F}\left(A_i\right)\right\}/A_i$, where $\mathrm{T}\left(A_i\right)$, $\mathrm{I}\left(A_i\right)$ and $\mathrm{F}\left(A_i\right)$ are the membership values to the true, indeterminate, and false sets. $\mathrm{T}\left(A_i\right)$ is used to measure the belonging degree of the sample to the center of the labeled class, $\mathrm{I}\left(A_i\right)$ for indiscrimination degree between two classes, and $\mathrm{F}\left(A_i\right)$ for the belonging degree to the outliers.

The NCM clustering overcomes the disadvantages of handling indeterminate points in other algorithms [16]. Here we improve the NCM by only computing neutrosophic memberships to the true and indeterminate sets based on the samples’ distribution.

Using NCM, the truth and indeterminacy memberships are defined as:

$$K=\left[\frac{1}{{\varpi }_1}{\displaystyle \sum }_{j=1}^C{\left(x_i-c_j\right)}^{-\frac{2}{m-1}}+\frac{1}{{\varpi }_2}{\left(x_i-{\overline{c}}_{imax}\right)}^{-\left(\frac{2}{m-1}\right)}+\frac{1}{{\varpi }_3}{\delta }^{-\left(\frac{2}{m-1}\right)}\right]$$

(7)

$$T_{ij}=\frac{K}{{\varpi }_1}{(x_i-c_j)}^{-\left(\frac{2}{m-1}\right)}$$

(8)

$$I_i=\frac{K}{{\varpi }_2}{(x_i-{\overline{c}}_{imax})}^{-\left(\frac{2}{m-1}\right)}$$

(9)

where $T_{ij}$ and $I_i$ are the true and indeterminacy membership values of point i, and the cluster center is denoted as $c_j$. ${\overline{c}}_{i\max }$ is obtained from indexes of the largest and second largest value of T_ij. ${\varpi }_1$, ${\varpi }_2$, and ${\varpi }_3$ are constant weights. $T_{ij}$ and $I_i$ are updated at each iteration until $\left|T_{ij}^{\left(k+1\right)}-T_{ij}^{\left(k\right)}\right|<\epsilon$, where $\epsilon$ is a termination criterion.

3.3. Proposed Neutrosophic Set Support Vector Machine (NS-SVM)

In the fuzzy support vector machine (FSVM), a membership $g_i$ is assigned for each input data point $\{{\left(x_i,y_i\right)}_{n=1}^N\}$, where $0<g_i<1$ [3]. As $g_i\mathrm{and}{\xi }_i$ shows the membership and the error of SVM for input data point $x_i$, respectively, the term $g_i{\xi }_i$ shows the measure of error with different weighting. Thus, the optimal hyperplane problem can be re-solved as;

$$\mathrm{minimum}\left(\frac{1}{2}{w}^2+C{\displaystyle \sum }_{i=1}^N{g}_i{\xi }_i\right)$$

(10)

$$\mathrm{subjected}\mathrm{to}{y}_i\left(w.\phi \left(x_i\right)+b\right)\ge 1-{\xi }_i, i=1,\dots ,N$$

(11)

In the proposed method, a weighting function is defined in the NS based on the memberships to truth and indeterminacy and then used to remove the effect of indeterminacy information for classification.

$$g_{Ni}={\displaystyle \sum }_{j=1}^C{T}_{ij}·I_i$$

(12)

Then we use the newly defined weight function $g_{Ni}$ to replace the weight function in Equation (4), and an optimization procedure is employed to minimize the cost function as:

$$\mathrm{minimum}\left(\frac{1}{2}{w}^2+C{\displaystyle \sum }_{i=1}^N{g}_{Ni}·{\xi }_i\right)$$

(13)

$$\mathrm{subjected}\mathrm{to}{y}_i\left(w.\phi \left(x_i\right)+b\right)\ge 1-{\xi }_i, i=1,\dots ,N$$

(14)

Finally, the support vectors are identified and their weights are obtained for classification. The semantic algorithm of the proposed method is given as:

• Input: Labeled training dataset.
• Output: Predicted class labels.
• Step 1: Calculate the cluster centers according to the labeled dataset and employ NCM algorithm to determine NS memberships T and I for each data point.
• Step 2: Calculate $g_{Ni}$ by using T and I components according to Equation (8).
• Step 3: Optimize NS-SVM by minimizing the cost function according to Equation (9).
• Step 4: Calculate the labels of test data.

4. Experimental Work and Results

In this study, a new approach NS-SVM is proposed and applied to determine if an action learning experience resulted in school administrators being more productive in their conflict-management skills [21]. 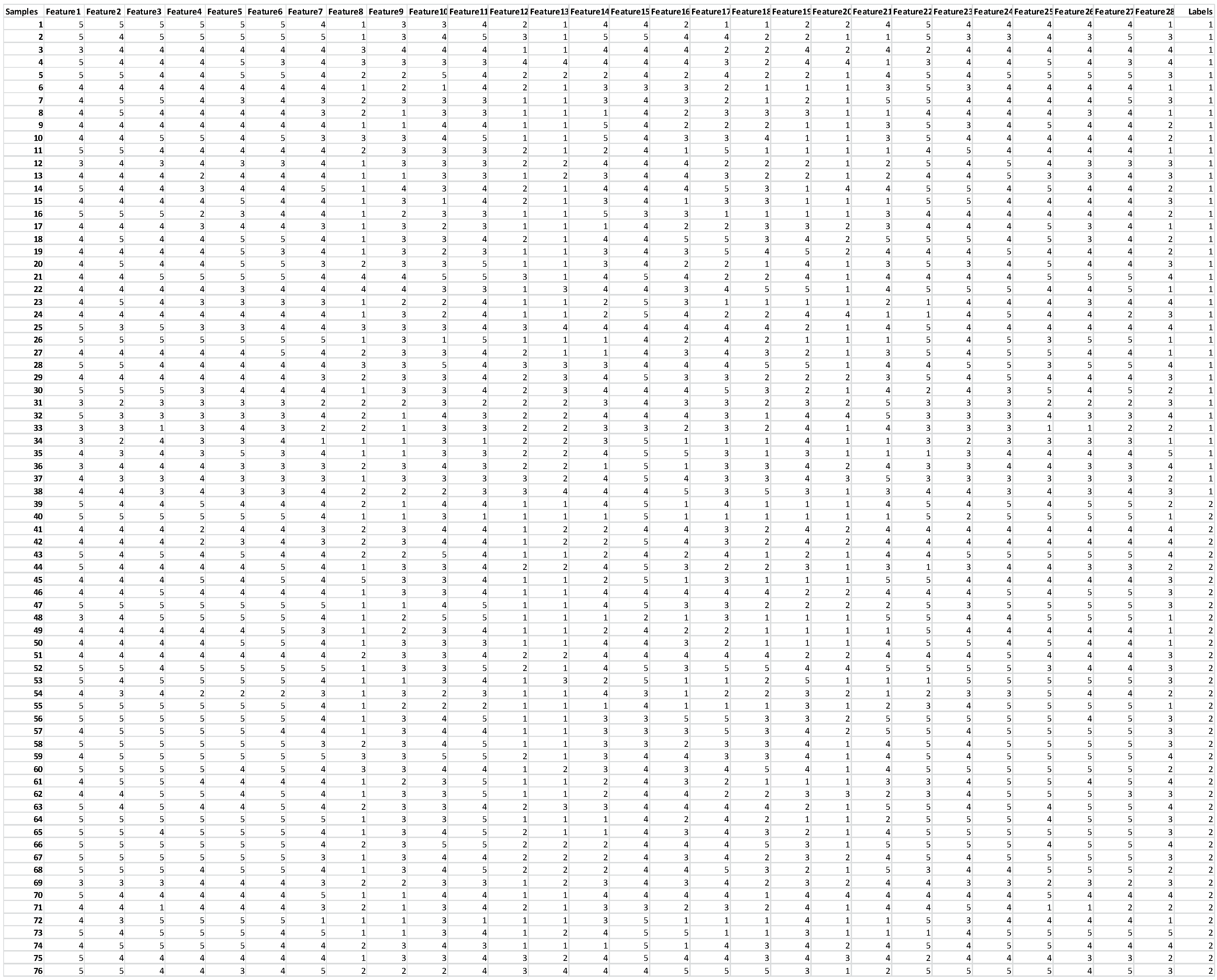To this end, an experimental organization was constructed where 38 administrators from various schools in Elazig/Turkey were administered a pre-test and a post-test of the Rahim Organization Conflict Inventory II (ROCI-II) [22]. The pre-test was applied to the administrators before the action learning experience and the post-test was applied after the action learning experience. The ROCI-II contains 28 scale items. These scale items are grouped into five dimensions: integrating, obliging, dominating, avoiding, and compromising. The dataset, which was used in this work, is given in Appendix A. The MATLAB software is used in construction of the NS-SVM approach. In the evaluation of the proposed method, a five-fold cross-validation test is used and the mean accuracy value is recorded. During the experimental work, two different scenarios are considered. In the first one, all 28 scale items are used to determine the trained and non-trained school administrators. In the second scenario, each dimension of ROCI-II is used to determine trained and non-trained administrators in order to determine the relationship between the dimensions and the trained and non-trained school administrators. The NS-SVM parameter C is searched in the range of [10⁻³, 10²] at a step size of 10⁻¹. In addition, for NCM the following parameters are chosen: ε= 10⁻³, ${\varpi }_1$= 0.75, ${\varpi }_2$= 0.125, ${\varpi }_3$= 0.125, which were obtained from trial and error. The $\delta$ parameter of NCM method is also searched in the range of $\left\{2^{-10},2^{-8},\dots ,2^8,2^{10}\right\}$. The dataset is normalized with zero mean and unit variance.

Table 1. Prediction accuracies for the first scenario. The bold case shows the highest accuracy. SVM: Support Vector Machines; FSVM: Fuzzy Support Vector Machines; NS-SVM: Neutrosophic Support Vector Machines.

Classifier Type	Accuracy (%)
Linear SVM	73.7
Quadratic SVM	68.4
Cubic SVM	68.4
Fine Gaussian SVM	48.7
Medium Gaussian SVM	73.7
Coarse Gaussian SVM	63.2
FSVM	76.9
NS-SVM	81.2

shows the obtained accuracy scores for the first scenario. The obtained results are further compared with FSVM and other SVM types such as Linear, Quadratic, Cubic, Fine Gaussian, Medium Gaussian, and Coarse Gaussian SVMs.

As seen in Table 1, 81.2% accuracy is obtained with the proposed NS-SVM method, which is the highest among all compared classifier types. The second highest accuracy, 76.9%, is obtained by the FSVM method. An accuracy score of 73.7% is produced by both linear and medium Gaussian SVM methods. In addition, quadratic and cubic SVM techniques produce 68.4% accuracy scores. An accuracy score of 63.2% is obtained by the coarse Gaussian SVM method and finally, the worst accuracy score, 48.7%, is obtained by the fine Gaussian SVM method. Generally speaking, contributing memberships as weighting to SVM highly increases the efficiency. Both FSVM and NS-SVM produce better results than traditional SVM methods. The experimental results that cover the second scenario are given in

Table 2. Prediction accuracies for the second scenario. The integrating dimension is used as input. The bold case shows the highest accuracy.

Classifier Type	Accuracy (%)
Linear SVM	73.7
Quadratic SVM	57.9
Cubic SVM	53.9
Fine Gaussian SVM	60.5
Medium Gaussian SVM	73.7
Coarse Gaussian SVM	67.1
FSVM	76.3
NS-SVM	80.3

,

Table 3. Prediction accuracies for the second scenario. The obliging dimension is used as input. The bold case shows the highest accuracy.

Classifier Type	Accuracy (%)
Linear SVM	61.8
Quadratic SVM	50.0
Cubic SVM	51.3
Fine Gaussian SVM	52.6
Medium Gaussian SVM	61.8
Coarse Gaussian SVM	55.3
FSVM	71.3
NS-SVM	73.8

,

Table 4. Prediction accuracies for the second scenario. The dominating dimension is used as input. The bold case shows the highest accuracy.

Classifier Type	Accuracy (%)
Linear SVM	59.2
Quadratic SVM	57.9
Cubic SVM	52.6
Fine Gaussian SVM	55.3
Medium Gaussian SVM	52.6
Coarse Gaussian SVM	55.3
FSVM	65.0
NS-SVM	70.0

,

Table 5. Prediction accuracies for the second scenario. The avoiding dimension is used as input. The bold case shows the highest accuracy.

Classifier Type	Accuracy (%)
Linear SVM	50.0
Quadratic SVM	43.4
Cubic SVM	53.9
Fine Gaussian SVM	48.7
Medium Gaussian SVM	44.7
Coarse Gaussian SVM	42.1
FSVM	63.8
NS-SVM	66.3

and

Table 6. Prediction accuracies for the second scenario. The compromising dimension is used as input. The bold case shows the highest accuracy.

Classifier Type	Accuracy (%)
Linear SVM	67.1
Quadratic SVM	67.1
Cubic SVM	57.9
Fine Gaussian SVM	65.8
Medium Gaussian SVM	71.1
Coarse Gaussian SVM	68.4
FSVM	73.8
NS-SVM	75.0

. Table 2 shows the obtained accuracy scores when the integrating dimension is used as input. The integrating dimension has six scale items.

As seen in Table 2, the highest accuracy score, 80.3%, is obtained by the proposed method. This score is 4% better than that achieved by FSVM. The FSVM method produces a 76.3% accuracy score, which is the second highest. Linear and medium Gaussian SVM methods produce 73.7% accuracy scores, which are the third highest. In addition, linear and medium Gaussian SVM methods achieve the best accuracy among the ordinary SVM techniques. It is worth mentioning that cubic SVM has the lowest accuracy score, with an achievement of 53.9%.

Table 3 shows the achievements obtained when the obliging dimension is used as input to the classifiers. The obliging dimension covers five scale items and 73.8% accuracy score, which is the highest, obtained by the NS-SVM method. FSVM also produces a 71.3% accuracy score, which is the second-best achievement. The worst accuracy score is obtained by quadratic SVM, for which the accuracy score is 50.0%. One important inference from Table 3 is that ordinary SVM techniques produce almost similar achievements, while weighting with memberships highly improves the accuracy.

The dominating dimension also covers five scale items and the produced results are shown in Table 4. As seen in Table 4, the highest accuracy, 70.0%, is produced by the proposed NS-SVM method. In addition, the second-best accuracy score, 65.0%, is obtained by the FSVM method. The linear SVM obtains 59.2% accuracy, which is the third highest accuracy score. When one considers the ordinary SVM’s achievements, an obvious improvement can be seen easily that is achieved by the NS-SVM method.

The avoiding dimension covers six scale items and the produced results are given in Table 5. As one evaluates the obtained results given in Table 5, it can be observed that the avoiding dimension is not efficient enough in discriminating trained and non-trained participants. In other words, the ordinary SVM techniques do not achieve better accuracy scores. Among them, the highest accuracy, 53.9%, is produced by the cubic SVM method. On the other hand, both FSVM and the proposed NS-SVM methods produce better accuracy scores, with achievements of 63.8% and 66.3%, respectively. Once more, the best accuracy is obtained by the proposed NS-SVM method.

Finally, the compromising dimension covers six scale items and the produced results are given in Table 6. As seen in Table 6, the compromising dimension is quite efficient in the determination of trained and non-trained participants, where better accuracy scores are visible when compared with the avoiding dimension’s accuracy scores. A 75.0% accuracy score, the highest among all methods, is obtained by NS-SVM. A 73.8% accuracy score is obtained by the FSVM method. The highest third accuracy score is produced by medium Gaussian SVM.

We further analyze the results obtained from the first scenario by considering a statistical measure and the running time. To this end, the f-measure metric was considered. The f-measure calculates the weighted harmonic mean of recall and precision [23]. The results are tabulated in

Table 7. Calculated f-measure and running times for the first scenario. The bold cases show the better achievements.

Classifier Type	f-Measure (%)	Time (s)
Linear SVM	73.50	0.314
Quadratic SVM	68.50	0.129
Cubic SVM	68.50	0.122
Fine Gaussian SVM	48.50	0.119
Medium Gaussian SVM	71.00	0.130
Coarse Gaussian SVM	61.00	0.129
FSVM	76.50	0.089
NS-SVM	80.00	0.065

.

In Table 7, the best f-measure achievement score, 80.00%, was achieved by the proposed NS-SVM method. The second-best f-measure score, 76.50%, was produced by FSVM. The other SVM techniques also produced reasonable f-measure scores when their accuracy achievements were considered (Table 1). In addition, the running time of the proposed method was less than those of the other SVM methods. The proposed method achieved its process at 0.065 s. In other words, this running time is almost half the running times of the non-weighted SVM methods. Thus, it is evident that the proposed NS-SVM performed more accurate results in a very short time, demonstrating its efficiency.

5. Conclusions

In this paper, neutrosophic set theory and SVM is used to construct an efficient classification approach called NS-SVM. It is then applied to an educational problem. More specifically, the determination of the effectiveness of training in school administrators who attended an action learning course based on their conflict-handling styles is achieved. To this end, a ROCI-II instrument is used that consists of both the demographic information and the conflict-handling styles of the school administrators. Six various SVM approaches and FSVM are used in performance comparison. The experimental works are carried out with a five-fold cross-validation technique and the classification accuracy is measured to evaluate the performance of the proposed NS-SVM approach. The experiments are conducted based on two scenarios. In the first one, all statements are used to predict if a school administrator is trained or not after attending an action learning program. In the second scenario, five independent dimensions are used individually to predict if a school administrator is educated or not after attending an action learning program. According to the obtained results, the first scenario achieves the best performance with the NS-SVM method, resulting in an accuracy score of 81.2%. In addition, for all experiments in the second scenario, the proposed NS-SVM achieves the highest accuracy scores as given in Table 2, Table 3, Table 4, Table 5 and Table 6. Furthermore, FSVM achieved the second highest accuracy scores for all experiments that are handled in scenarios 1 and 2. This situation shows that embedding the membership degrees into the SVM method highly improves its discriminatory ability. To further analyze the efficiency of the proposed method, we used the f-measure test and the running times of the methods. The proposed NS-SVM yielded the highest f-measure score. In addition, the running time of the proposed method was much less than those of the traditional SVM techniques.

This study revealed important results for both educational research and determining the effectiveness of educational practices. First, this research showed that the NS-SVM technique can be used in pre-test and post-test comparisons in experimental educational research. In addition, this study demonstrated that the effectiveness levels of training courses can be determined by examining the NS-SVM discrimination accuracy of individuals who attended training courses compared to those who did not.