Abstract
The proposed q-rung orthopair fuzzy set (q-ROFS) and picture fuzzy set (PIFS) are two powerful tools for depicting fuzziness and uncertainty. This paper proposes a new tool, called q-rung picture linguistic set (q-RPLS) to deal with vagueness and impreciseness in multi-attribute group decision-making (MAGDM). The proposed q-RPLS takes full advantages of q-ROFS and PIFS and reflects decision-makers’ quantitative and qualitative assessments. To effectively aggregate q-rung picture linguistic information, we extend the classic Heronian mean (HM) to q-RPLSs and propose a family of q-rung picture linguistic Heronian mean operators, such as the q-rung picture linguistic Heronian mean (q-RPLHM) operator, the q-rung picture linguistic weighted Heronian mean (q-RPLWHM) operator, the q-rung picture linguistic geometric Heronian mean (q-RPLGHM) operator, and the q-rung picture linguistic weighted geometric Heronian mean (q-RPLWGHM) operator. The prominent advantage of the proposed operators is that the interrelationship between q-rung picture linguistic numbers (q-RPLNs) can be considered. Further, we put forward a novel approach to MAGDM based on the proposed operators. We also provide a numerical example to demonstrate the validity and superiorities of the proposed method.
1. Introduction
Decision-making is a common activity in daily life, aiming to select the best alternative from several candidates. As one of the most important branches of modern decision-making theory, multi-attribute group decision-making (MAGDM) has been widely investigated and successfully applied to economics and management due to its high capacity to model the fuzziness and uncertainty of information [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15]. In actual decision-making problems, decision-makers usually rely on their intuition and prior expertise to make decisions. Owing to the complicacy of decision-making problems, the precondition is to represent the fuzzy and vague information appropriately in the process of MAGDM. Atanassov [16] originally proposed the concept of intuitionistic fuzzy set (IFS), characterized by a membership degree and a non-membership degree. Since its appearance, IFS has received substantial attention and has been studied by thousands of scientists worldwide in theoretical and practical aspects [17,18,19,20]. Thereafter, Yager [21] proposed the concept of Pythagorean fuzzy set (PYFS). The constraint of PYFS is that the square sum of membership and non-membership degrees is less than or equal to one, making PYFS more effective and powerful than IFS. Due to its merits and advantages, PYFS has been widely applied to decision-making [22,23,24,25].
PYFSs can effectively address some real MAGDM problems. However, there are quite a few cases that PYFSs cannot deal with. For instance, the membership and non-membership degrees provided by a decision-maker are 0.7 and 0.8 respectively. Evidently, the ordered pair (0.7, 0.8) cannot be represented by Pythagorean fuzzy numbers (PYFNs), as . In other words, PYFSs do not work for some circumstances in which the square sum of membership and non-membership degrees is greater than one. To effectively deal with these cases, Yager [26] proposed the concept of q-ROFS, whose constraint is the sum of qth power of membership degree and qth power of the degree of non-membership is less than or equal to one. Thus, q-ROFSs relax the constraint of PYFSs and widen the information range. In other words, all intuitionistic fuzzy membership degrees and Pythagorean fuzzy membership degrees are a part of q-rung orthopair fuzzy membership degrees. This characteristic makes q-ROFSs more powerful and general than IFSs and PYFSs. Subsequently, Liu and Wang [27] developed some simple weighted averaging operators to aggregate q-rung orthopair fuzzy numbers (q-ROFNs) and applied these operators to MAGDM. Considering these operators cannot capture the interrelationship among aggregated q-ROFNs, Liu P.D. and Liu J.L. [28] proposed a family of q-rung orthopair fuzzy Bonferroni mean operators.
As real decision-making problems are too complicated, we may face the following issues. The first issue is that although IFSs, PYFSs and q-ROFSs have been successfully applied in decision-making, there are situations that cannot be addressed by IFSs, PYFSs and q-ROFSs. For example, human voters may be divided into groups of those who: vote for, abstain, refusal of in a voting. In other words, in a voting we have to deal with more answers of the type: yes, abstain, no, refusal. Evidently, IFSs, PYFSs and q-ROFSs do not work in this case. Recently, Cuong [29] proposed the concept of PIFS, characterized by a positive membership degree, a neutral membership degree, and a negative membership degree. Since its introduction, PIFSs have drawn much scholars’ attention and have been widely investigated [30,31,32,33,34,35,36,37]. Therefore, motivated by the ideas of q-ROFS and PIFS, we propose the concept of q-rung picture fuzzy set (q-RPFS), which takes the advantages of both q-ROFS and PIFS. The proposed q-RPFS can not only express the degree of neutral membership, but also relax the constraint of PIFS that the sum of the three degrees must not exceed 1. The lax constraint of q-RPFS is that the sum of qth power of the positive membership, neutral membership and negative membership degrees is equal to or less than 1. In other words, the proposed q-RPFS enhances Yager’s [26] q-ROFS by taking the neutral membership degree into consideration. For instance, if a decision-maker provides the degrees of positive membership, neutral membership and negative membership as 0.6, 0.3, and 0.5 respectively. Then the ordered pair (0.6, 0.3, 0.5) is not valid for q-ROFSs or PIFSs, whereas valid for the proposed q-RPFSs. This instance reveals that q-RPFS has a higher capacity to model fuzziness than q-ROFSs and PIFSs. The second issue is that, in some situations, decision-makers prefer to make qualitative decisions instead of quantitative decisions due to time shortage and a lack of prior expertise. Zadeh’s [38] linguistic variables are powerful tools to model these circumstances. However, Wang and Li [39] pointed out that linguistic variables can only express decision-makers’ qualitative preference but cannot consider the membership and non-membership degrees of an element to a particular concept. And subsequently, they proposed the concept of intuitionistic linguistic set. Other extensions are interval-valued Pythagorean fuzzy linguistic set proposed by Du et al. [40] and picture fuzzy linguistic set proposed by Liu and Zhang [41]. Therefore, this paper proposes the concept of q-RPLS by combining linguistic variables with q-RPFSs. The third issue is that in most real MAGDM problems, attributes are dependent, meaning that the interrelationship among aggregated values should be considered. The Bonferroni mean (BM) [42] and Heronian mean (HM) [43] are two effective aggregation technologies which can capture the interrelationship among fused arguments. However, Yu and Wu [44] pointed out that HM has some advantages over BM. Therefore, we utilize HM to aggregate q-rung picture linguistic information.
The main contribution of this paper is that a novel decision-making model is proposed. In the proposed model, attribute values take the form q-RPLNs, and weights of attributes take the form of crisp numbers. The motivations and aims of this paper are: (1) to provide the definition of q-RPLS and operations for q-RPLNs; (2) to develop a family of q-rung picture linguistic Heronian mean operators; (3) to put forward a novel approach to MAGDM with q-rung picture linguistic information on the basis of the proposed operators. In order to do this, the rest of this paper is organized as follows. Section 2 briefly recalls some basic concepts. In Section 3, we develop some q-rung picture linguistic aggregation operators. In addition, we present and discuss some desirable properties of the proposed operators. In Section 4, we introduce a novel method to MAGDM problems based on the proposed operators. In Section 5, a numerical instance is provided to show the validity and superiority of the proposed method. The conclusions are given in Section 6.
2. Preliminaries
In this section, we briefly review concepts about q-ROFS, PIFS, linguistic term sets and HM. Meanwhile, we provide the definitions of q-PRFS and q-RPLS.
2.1. q-Rung Orthopair Fuzzy Set (q-ROFS) and q-Rung Picture Fuzzy Set (q-RPFS)
Definition 1 [26].
Let X be an ordinary fixed set, a q-ROFS A defined on X is given by
where and represent the membership degree and non-membership degree respectively, satisfying , and , . The indeterminacy degree is defined as . For convenience, is called a q-ROFN by Liu and Wang [27], which can be denoted by .
Liu and Wang [27] also proposed some operations for q-ROFNs.
Definition 2 [27].
Let , be two q-ROFNs, and be a positive real number, then
- ,
- ,
- ,
- .
To compare two q-ROFNs, Liu and Wang [27] proposed a comparison method for q-ROFNs.
Definition 3 [27].
Let be a q-ROFN, then the score of is defined as , the accuracy of is defined as . For any two q-ROFNs, and . Then
- If , then ;
- If , then
- (1)
- If , then ;
- (2)
- If , then .
The PIFS, constructed by a positive membership degree, a neutral membership degree as well as a negative membership degree, was originally proposed by Cuong [29].
Definition 4 [29].
Let X be an ordinary fixed set, a picture fuzzy set (PIFS) B defined on X is given as follows
where is called the degree of positive membership of B, is called the degree of neutral membership of B and is called the degree of negative membership of B, and satisfy the following condition: , . Then for , is called the degree of refusal membership of x in B.
Motivated by the concepts of q-ROFS and PIFS, we give the definition of q-RPFS.
Definition 5.
Let X be an ordinary fixed set, a q-rung picture fuzzy set (q-RPFS) C defined on X is given as follows
where and represent degree of positive membership, degree of neutral membership and degree of negative membership respectively, satisfying , , and , . Then for , is called the degree of refusal membership of x in C.
2.2. Linguistic Term Sets and q-Rung Picture Linguistic Set (q-RPLS)
Let be a linguistic term set with odd cardinality and t is the cardinality of S. The label represents a possible value for a linguistic variable. For instance, a possible linguistic term set can be defined as follows:
Motivated by the concept of picture linguistic set [41], we shall define the concept of q-RPLS by combining the linguistic term set with q-RPFS.
Definition 6.
Let X be an ordinary fixed set, be a continuous linguistic term set of , then a q-rung picture linguistic set (q-RPLS) D defined on X is given as follows
where , is called the degree of positive membership of D, is called the degree of neutral membership of D and is called the degree of negative membership of D, and satisfy the following condition: , . Then is called a q-RPLN, which can be simply denoted by . When q = 1, then D is reduced to the picture linguistic set (PFLS) proposed by Liu and Zhang [41].
In the following, we provide some operations for q-RPLNs.
Definition 7.
Let , and be three q-RPLNs and be a positive real number, then
- ,
- ,
- ,
- .
To compare two q-RPLNs, we first propose the concepts of score function and accuracy function of a q-RPLN and based on which we propose a comparison law for q-RPLNs.
Definition 8.
Let be a q-RPLN, then the score function of is defined as
Definition 9.
Let be a q-RPLN, then the accuracy function of is defined as
Definition 10.
Let and be two q-RPLNs, and be score functions of and respectively, and be the accuracy functions of and respectively, then
- if , then ;
- if , then
- (1)
- if , then ;
- (2)
- if , then .
2.3. Heronian Mean
Definition 11 [43,45].
Let be a collection of crisp numbers, and s, , then the Heronian mean (HM) is defined as follows:
Definition 12 [46].
Let be a collection of crisp numbers, and s, , then the geometric Heronian mean (GHM) is defined as follows:
3. The q-Rung Picture Linguistic Heronian Mean Operators
In this section, we extend the HM to q-rung picture linguistic environment and propose a family of q-rung picture linguistic Heronian mean operators. Moreover, some desirable properties of the proposed aggregation operators are presented and discussed.
3.1. The q-Rung Picture Linguistic Heronian Mean (q-RPLHM) Operator
Definition 13.
Let be a collection of q-RPLNs, and s, . If
then is called the q-rung picture linguistic Heronian mean (q-RPLHM) operator.
According to the operations for q-RPLNs, the following theorem can be obtained.
Theorem 1.
Let be a collection of q-RPLNs, then the aggregated value by using q-RPLHM operator is also a q-RPLN and
Proof.
According to the operations for q-RPLNs, we can obtain the followings
Therefore,
Further,
In addition,
Thus,
So,
□
In addition, the q-RPLHM operator has the following properties.
Theorem 2 (Monotonicity).
Let and be two collections of q-RPLNs, if for all , then
Proof.
As for all i, we can obtain
Since and for and , we have .
Then
So,
i.e.,
□
Theorem 3 (Idempotency).
Let be a collection of q-RPLNs, if , for all , then
Proof.
Since , for all i, we have
□
Theorem 4 (Boundedness).
The q-RPLHM operator lies between the max and min operators
Proof.
Let , according to Theorem 2, we have
Further, and .
So,
i.e.,
□
The parameters s and t play a very important role in the aggregated results. In the followings, we discuss some special cases of the q-RPLHM operator with respect to the parameters s and t.
Case 1: When , then the q-RPLHM operator reduces to the followings,
which is a q-rung picture linguistic generalized linear descending weighted mean operator. Evidently, it is equivalent to weight the information with .
Case 2: When , then the q-RPLHM operator reduces to the followings,
which is a q-rung picture linguistic generalized linear ascending weighted mean operator. Obviously, it is equivalent to weight the information with , i.e., when or , the q-RPLHM operator has the linear weighted function for input data.
Case 3: When , then the q-RPLHM operator reduces to the followings,
which is a q-rung picture linguistic line Heronian mean operator.
Case 4: When , then the q-RPLHM operator reduces to the followings
which is a q-rung picture linguistic basic Heronian mean operator.
Case 5: When , then the q-RPLHM operator reduces to the followings,
which is the Pythagorean picture linguistic Heronian mean operator.
Case 6: When , then the q-ROLHM operator reduces to the followings,
which is the picture linguistic Heronian mean operator.
3.2. The q-Rung Picture Linguistic Weighted Heronian Mean (q-RPLWHM) Operator
It is noted that the proposed q-RPLHM operator does not consider the self-importance of the aggregated arguments. Therefore, we put forward the weighted Heronian mean for q-RPLNs, which also considers the weights of aggregated arguments.
Definition 14.
Let be a collection of q-RPLNs, and , be the weight vector, satisfying and . If
then is called the q-RPLWHM.
According to the operations for q-RPLNs, the following theorems can be obtained.
Theorem 5.
Let be a collection of q-RPLNs, be the weight vector, satisfying and , then the aggregated value by using q-RPLWHM is also a q-RPLN and
The proof of Theorem 5 is similar to that of Theorem 1, which is omitted here.
Similarly, q-RPLWHM has the following properties.
Theorem 6 (Monotonicity).
Let and be two collections of q-RPLNs, if for all i, then
Theorem 7 (Boundedness).
The q-RPLWHM operator lies between the max and min operators
3.3. The q-Rung Picture Linguistic Geometric Heronian Mean (q-RPLGHM) Operator
Definition 15.
Let be a collection of q-RPLNs, and . If
then is called the q-rung picture linguistic geometric Heronian mean (q-RPLGHM) operator.
Similarly, the following theorem can be obtained according to Definition 7.
Theorem 8.
Let be a collection of q-RPLNs, then the aggregated value by using q-RPLGHM is also a q-RPLN and
The proof of Theorem 8 is similar to that of Theorem 1. In the following, we present some desirable properties of the q-RPLGHM operator.
Theorem 9 (Idempotency).
Let be a collection of q-RPLNs, if all the q-RPLNs are equal, i.e., for all i, then
The proof of Theorem 9 is similar to that of Theorem 2.
Theorem 10 (Monotonicity).
Let and be two collections of q-RPLNs, if for all i, then
The proof of Theorem 10 is similar to that of Theorem 3.
Theorem 11 (Boundedness).
Let be a collection of q-RPLNs, then
The proof of Theorem 11 is similar to that of Theorem 4. In the followings, we discuss some special cases of the q-RPLGHM operator.
Case 1: When , then the q-RPLGHM operator reduces to the followings,
which is a q-rung picture linguistic generalized geometric linear descending weighted mean operator.
Case 2: When , then the q-RPLGHM operator reduces to the followings,
which is a q-rung picture linguistic generalized geometric linear ascending weighted mean operator.
Case 3: When , then the q-RPLGHM operator reduces to the followings,
which is a q-rung picture linguistic geometric line Heronian mean operator.
Case 4: When , then the q-RPLGHM operator reduces to the followings,
which is a q-rung picture linguistic basic geometric Heronian mean operator.
Case 5: When , then the q-RPLGHM operator reduces to the followings
which is the Pythagorean picture linguistic geometric Heronian mean operator.
Case 6: When , then the q-RPLGHM operator reduces to the followings
which is the picture linguistic geometric Heronian mean operator.
3.4. The q-Rung Picture Linguistic Weighted Geometric Heronian Mean (q-RPLWGHM) Operator
Definition 16.
Let be a collection of q-RPLNs, and , be the weight vector, satisfying and . If
then is called the q-RPLWGHM.
Additionally, q- RPLWGHM has the following theorem.
Theorem 12.
Let be a collection of q-RPLNs, be the weight vector, satisfying and , then the aggregated value by using q-RPLWGHM is also a q-RPLN and
The proof of Theorem 12 is similar to that of Theorem 1, which is omitted here.
In addition, the q-RPLWGHM operator has the following properties.
Theorem 13 (Monotonicity).
Let and be two collections of q-RPLNs, if for all i, then
Theorem 14 (Boundedness).
The q-RPLWGHM operator lies between the max and min operators
4. A Novel Approach to MAGDM Based on the Proposed Operators
In this section, we shall apply the proposed aggregation operators to solving MAGDM problems in q-rung picture linguistic environment. Considering a MAGDM process in which the attribute value take the form of q-RPLNs.: let be a set of all alternatives, and be a set of attributes with the weight vector being , satisfying and . A set of decision-makers are organized to make the assessment for every attribute of all alternatives by q-RPLNs , and is the weight vector of decision-makers . Therefore, the q-rung picture linguistic decision matrices can be denoted by . The main steps to solve MAGDM problems based on the proposed operators are given as follows.
Step 1. Standardize the original decision matrices. There are two types of attributes, benefit and cost attributes. Therefore, the original decision matrix should be normalized by
where and represent the benefit attributes and cost attributes respectively.
Step 2. Utilize the q-RPLWHM operator
or the q-RPLWGHM operator
to aggregate all the decision matrices into a collective decision matrix .
Step 3. Utilize the q-RPLWHM operator
or the q-RPLWGHM operator
to aggregate the assessments for each so that the overall preference values of alternatives can be obtained.
Step 4. Calculate the score functions of the overall values .
Step 5. Rank all alternatives according to the score functions of the corresponding overall values and select the best one(s).
Step 6. End.
5. Numerical Instance
In this part, to validate the proposed method, we provide a numerical instance about choosing an Enterprise resource planning (ERP) system adopted from Liu and Zhang [41]. After primary evaluation, there are four possible systems provided by different companies remained on the candidates list and they are {A1, A2, A3, A4}. Four experts are invited to evaluate the candidates under four attributes, they are (1) technology C1; (2) strategic adaptability C2; (3) supplier’s ability C3; (4) supplier’s reputation C4. Weight vector of the four attributes is . The decision-makers are required to use picture fuzzy linguistic numbers (PFLNs) on the basic of the linguistic term set S = {s0 = terrible, s1 = bad, s2 = poor, s3 = neutral, s4 = good, s5 = well, s6 = excellent} to express their preference information. Decision-makers’ weight vector is . After evaluation, the individual picture fuzzy linguistic decision matrix can be obtained, which are shown in Table 1, Table 2, Table 3 and Table 4.

Table 1.
Decision matrix A1 provided by D1.

Table 2.
Decision matrix A2 provided by D2.

Table 3.
Decision matrix A3 provided by D3.

Table 4.
Decision matrix A4 provided by D4.
5.1. The Decision-Making Process
Step 1. As the four attributes are benefit types, the original decision matrices do not need normalization.
Step 2. Utilize Equation (40) to calculate the comprehensive value of each attribute for every alternative. The collective decision matrix is shown in Table 5 (suppose s = t = 1, q = 3):

Table 5.
Collective picture fuzzy linguistic decision matrix (by q-rung Picture Linguistic Weighted Geometric Heronian Mean (q-RPLWHM) operator).
Step 3. Utilize Equation (42) to obtain the overall values of each alternative, we can get
Step 4. Compute the score functions of the overall values, which are shown as follows:
Step 5. Then the rank of the four alternatives is obtained
Therefore, the optimal alternative is A1.
In step 2, if we utilize Equation (41) to aggregate the assessments, then we can derive the following collective decision matrix in Table 6 (suppose s = t = 1, q = 3).

Table 6.
Collective picture fuzzy linguistic decision matrix (by q-RPLWGHM operator).
Then we utilize Equation (43) to obtain the following overall values of alternatives:
In addition, we calculate the score functions of the overall assessments and we can get
Therefore, the rank of the four alternatives is and the best alternative is A1.
5.2. The Influence of the Parameters on the Results
The parameters q, s and t play significant roles in the final ranking results. In the following, we shall investigate the influence of the parameters on the overall assessments of alternatives and the final ranking results. First, we discuss the effects of the parameter q on the ranking results (suppose s = t = 1). Details are presented in Figure 1 and Figure 2.
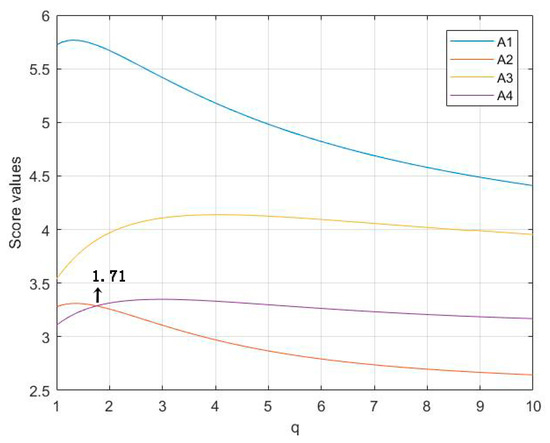
Figure 1.
Score values of the alternatives when based on q-RPLWHM operator.
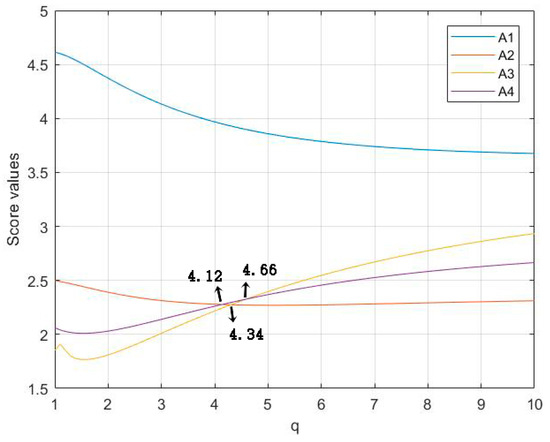
Figure 2.
Score values of the alternatives when using q-RPLWGHM operator.
As seen in Figure 1 and Figure 2, the score values of the overall assessments are different with different value of q, leading to different ranking results based the q-RFLWHM operator and the q-RFLWGHM operator. However, the best alternative is always A1. The decision-makers can choose the appropriate parameter value q according to their preferences. From Figure 1, we can find that when the ranking order is and when the ranking order is by the q-RFLWHM operator. In addition, from Figure 2 we know when the ranking order is ; when the ranking order is ; when the ranking order is , and when the ranking order is by the q-RFLWGHM operator.
In the followings, we investigate influence of the parameters s and t on the score functions and ranking orders respectively (suppose q = 3). Details are presented in Table 7 and Table 8.

Table 7.
Ranking orders by utilizing different values of s and t in the q-RPLWHM operator.

Table 8.
Ranking orders by utilizing different values of s and t in the q-RPLWGHM operator.
As seen in Table 7 and Table 8, when different values are assigned to the parameters s and t, different scores and corresponding ranking results can be obtained. However, the best alternative is always A1. Especially, in the q-RPLWHM operator, the increase of the parameters s and t leads to increase of the score functions, whereas a decrease of the score functions is witnessed using q-RPLWGHM operator. Furthermore, there is a difference in the ranking orders of A2, A3 and A4 when , or , for the linear weighting by q-RPLWHM or q-RPLWGHM operator. Therefore, the parameters s and t can be also viewed a decision-makers’ optimistic or pessimistic attitude to their assessments. This demonstrates the flexibility in the aggregation processes using the proposed operators.
5.3. Comparative Analysis
To further demonstrate the merits and superiorities of the proposed methods, we conduct the following comparative analysis.
5.3.1. Compared with the Method Proposed by Liu and Zhang [41]
We utilize Liu and Zhang’s [41] method to solve the above problem and results can be found in Table 9. From Table 9, we can find out that the results by using Liu and Zhang’s [41] method and the proposed method in this paper are quite different. The reasons can be explained as follows: (1) Our method is based on the HM, which considers the interrelationship among attribute values, whereas the method based Archimedean picture fuzzy linguistic weighted arithmetic averaging (A-PFLWAA) operator proposed by Liu and Zhang [41] can only provide the arithmetic weighting function. In other words, Liu and Zhang’s [41] method assumes that attributes are independent. In most real decision-making problems, attributes are correlated so that the interrelationship among attributes should be taken into consideration. Therefore, our proposed method is more reasonable than Liu and Zhang’s [41] method. (2) Liu and Zhang’s [41] method is based on PFLS, which is only a special case of q-RPLS (when q = 1). Therefore, our method is more general, flexible and reasonable than that proposed by Liu and Zhang [41].

Table 9.
Score values and ranking results using our methods and the method in Liu and Zhang [41].
5.3.2. Compared with the Methods Proposed by Wang et al. [47], Liu et al. [48], and Ju et al. [49]
To further demonstrate the effectiveness and validity of the proposed methods in this paper, we will deal with the problems in Wang et al. [47], Liu et al. [48], and Ju et al. [49] by using our methods respectively. Given that there is no method to aggregate q-rung picture linguistic information and there are various methods based on the intuitionistic linguistic numbers (ILNs), which are special cases of q-RPLNs when q equals to one and the neutral membership degree η equals to zero, we use the following three cases described by intuitionistic fuzzy numbers (ILNs) to verify our methods. For instance, when an ILN is ⟨s1, (0.6, 0.4)⟩, it can be transformed into a q-RPLN ⟨s1, (0.6, 0, 0.4)⟩. The score values and ranking results by different methods are shown in Table 10, Table 11 and Table 12.

Table 10.
Score values and ranking results using our method and the method in Wang et al. [47].

Table 11.
Score values and ranking results using our method and the method in Liu et al. [48].

Table 12.
Score values and ranking results using our method and the method in Ju et al. [49].
From Table 10, Table 11 and Table 12, it is obvious to find that the ranking results produced by our method are little different to those produced by other methods. However, their optimal selections are the same, which can prove the effectiveness of our methods very well. As mentioned above, the q-RPLN contains more information than ILN, and it is a generalization of the ILN. Thus, our method based on q-RPLNs can be utilized in a wider range of environments.
Wang et al.’s [47] method is based on intuitionistic linguistic hybrid averaging (ILHA) operator, which cannot consider the interrelationship among attribute values. Because our proposed method can make up for this disadvantage, our method is more reasonable than Wang et al.’s [47] method.
Liu et al.’s [48] method is based on intuitionistic linguistic weighted Bonferroni mean (ILWBM) operator. It can cope with the interrelationship between augments, which is same as our method. However, as Yu and Wu [44] pointed out that HM has some advantages over BM, our method is better than Liu et al.’s [48] method.
Ju et al.’s [49] method is based on weighted intuitionistic linguistic Maclaurin symmetric mean (WILMSM) operator and when k = 2, the interrelationship between any two arguments can be considered, which is the same as our proposed method. However, our methods are based on the q-RPLWHM and q-RPLWGHM operators, which have two parameters (s and t). The prominent advantage of our methods is that we can control the degree of the interactions of attribute values that are emphasized. The increase of values of the parameters means the interactions of attribute values are more emphasized. Therefore, the decision-making committee can properly select the desirable alternative according to their interests and the actual needs by determining the values of parameters. Moreover, in the WILMSM operator proposed by Ju et al. [49], the balancing coefficient n is not considered, leading to some unreasonable results. In our proposed operators, the coefficient n is considered so that our methods are more reliable and reasonable.
From above analysis, we can find out that our proposed methods can be successfully applied to actual decision-making problems. Compared with other methods, our methods are more flexible and suitable for addressing MAGDM problems. The advantages and merits of the proposed methods can be concluded as followings. Firstly, the proposed methods are based on q-RPLSs. The prominent characteristic of q-RPLS is that it allows the sum and square sum of positive membership degree, neutral membership degree, and negative membership degree to be greater than one, providing more freedom for decision-makers to express their evaluations, and further leading to less information loss in the process of MAGDM. Secondly, considering the fact that decision-makers prefer to make qualitative decisions due to lack of time and expertise, the proposed q-RPLSs not only express decision-makers’ qualitative assessments, but also reflect decision-makers’ quantitative ideas. Therefore, q-RPLSs are suitable and sufficient for modeling decision-makers’ evaluations on alternatives. Thirdly, in most real decision-making problems, attributes are correlated, so that the interrelationship between attribute values should be taken into account when fusing them. Our method to MAGDM is based on q-RPLWHM or q-RPLWGHM operators, which consider the interrelationship between arguments. Therefore, our method can effectively actual MAGDM problems. In a word, the proposed method not only provides a new tool for decision-makers to express their assessments, but also effectively model the process of real MAGDM problems. Therefore, our method is more general, powerful and flexible than other methods.
6. Conclusions
The main contribution of this paper is that a novel MAGDM model is proposed. In the proposed model, q-RPLNs are utilized to represent decision-makers’ assessments of alternatives and weights of attributes and decision-makers take the form of crisp numbers. In addition, q-RPLHM, q-RPLWHM, q-RPLGHM, and q-RPLWGHM operators are proposed to aggregate attribute values to obtain overall assessments of alternatives. In order to do this, we proposed the q-RPFS and q-RPLS, which are powerful and effective tools for coping with uncertainty and vagueness. Subsequently, the operations and comparison law for q-RPLNs were introduced. We also proposed some aggregation operators for fusing q-rung picture linguistic information. The prominent characteristic of these operators is that they can capture the interrelationship between q-RPLNs. Moreover, we have studied some desirable properties and special cases of the proposed operators. Thereafter, we utilized the proposed operators to establish a novel method to solve MAGDM problems. To illustrate the validity of the proposed method, we used the proposed method to solve an ERP system selection problem. In addition, we conducted comparative analysis to demonstrate the effectiveness and superiorities of the proposed method. Due to the high ability of q-RPLSs for describing fuzziness and expressing decision-makers’ assessments over alternatives, and the powerfulness of q-rung picture linguistic Heronian mean operators, the proposed method can be applied to solving real decision-making problems, such as supplier selection, low carbon supplier selection, hospital-based post-acute care, risk management, medical diagnosis, and resource evaluation, etc. In future works, considering the advantages of q-RPLSs, we should investigate more aggregation operators for fusing q-rung picture linguistic information such as the q-rung picture linguistic Bonferroni mean, q-rung picture linguistic Maclaurin symmetric mean, q-rung picture linguistic Hamy mean, and q-rung picture linguistic Muirhead mean. Additionally, we should investigate more methods of MAGDM with q-rung picture linguistic information.
Author Contributions
The idea of the whole thesis was put forward by L.L. She also wrote the paper. R.Z. analyzed the existing work and J.W. provided the numerical instance. The computation of the paper was conducted by X.S. and K.B.
Acknowledgments
This work was partially supported by National Natural Science Foundation of China (Grant number 71532002, 61702023), and the Fundamental Fund for Humanities and Social Sciences of Beijing Jiaotong University (Grant number 2016JBZD01).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Mardani, A.; Nilashi, M.; Zavadskas, E.K.; Awang, S.R.; Zare, H.; Jamal, N.M. Decision making methods based on fuzzy aggregation operators: Three decades review from 1986 to 2017. Int. J. Inf. Technol. Decis. Mak. 2018, 17, 391–466. [Google Scholar] [CrossRef]
- Liu, P.D.; Liu, J.L.; Merigó, J.M. Partitioned Heronian means based on linguistic intuitionistic fuzzy numbers for dealing with multi-attribute group decision making. Appl. Soft Comput. 2018, 62, 395–422. [Google Scholar] [CrossRef]
- Yu, D.J. Hesitant fuzzy multi-criteria decision making methods based on Heronian mean. Technol. Econ. Dev. Econ. 2017, 23, 296–315. [Google Scholar] [CrossRef]
- Liu, P.D.; Teng, F. Some Muirhead mean operators for probabilistic linguistic term sets and their applications to multiple attribute decision-making. Appl. Soft Comput. 2018, 68, 396–431. [Google Scholar] [CrossRef]
- Liang, X.; Jiang, Y.P.; Liu, P.D. Stochastic multiple-criteria decision making with 2-tuple aspirations: A method based on disappointment stochastic dominance. Int. Trans. Oper. Res. 2018, 25, 913–940. [Google Scholar] [CrossRef]
- Li, Y.; Liu, P.D. Some Heronian mean operators with 2-tuple linguistic information and their application to multiple attribute group decision making. Technol. Econ. Dev. Econ. 2015, 21, 797–814. [Google Scholar]
- Liu, W.H.; Liu, H.B.; Li, L.L. A multiple attribute group decision making method based on 2-D uncertain linguistic weighted Heronian mean aggregation operator. Int. J. Comput. Commun. 2017, 12, 254–264. [Google Scholar] [CrossRef]
- Geng, Y.S.; Wang, X.G.; Li, X.M.; Yu, K.; Liu, P.D. Some interval neutrosophic linguistic Maclaurin symmetric mean operators and their application in multiple attribute decision making. Symmetry 2018, 10, 127. [Google Scholar] [CrossRef]
- Garg, H. Some methods for strategic decision-making problems with immediate probabilities in Pythagorean fuzzy environment. Int. J. Intell. Syst. 2018, 33, 687–712. [Google Scholar] [CrossRef]
- Liu, P.D.; Chen, S.M. Multi-attribute group decision making based on intuitionistic 2-tuple linguistic information. Inf. Sci. 2018, 430, 599–619. [Google Scholar] [CrossRef]
- Liu, P.D.; Gao, H. Multicriteria decision making based on generalized Maclaurin symmetric means with multi-hesitant fuzzy linguistic information. Symmetry 2018, 10, 81. [Google Scholar] [CrossRef]
- Xing, Y.P.; Zhang, R.T.; Xia, M.M.; Wang, J. Generalized point aggregation operators for dual hesitant fuzzy information. J. Intell. Fuzzy Syst. 2017, 33, 515–527. [Google Scholar] [CrossRef]
- Liu, P.D.; Mahmood, T.; Khan, Q. Group decision making based on power Heronian aggregation operators under linguistic neutrosophic environment. Int. J. Fuzzy Syst. 2018, 20, 970–985. [Google Scholar] [CrossRef]
- Mahmood, T.; Liu, P.D.; Ye, J.; Khan, Q. Several hybrid aggregation operators for triangular intuitionistic fuzzy set and their application in multi-criteria decision making. Granul. Comput. 2018, 3, 153–168. [Google Scholar] [CrossRef]
- Liu, P.D.; Teng, F. Multiple attribute decision making method based on normal neutrosophic generalized weighted power averaging operator. Int. J. Mach. Learn. Cybern. 2018, 9, 281–293. [Google Scholar] [CrossRef]
- Atanassov, K.T. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Liu, P.D. Multiple attribute decision-making methods based on normal intuitionistic fuzzy interaction aggregation operators. Symmetry 2017, 9, 261. [Google Scholar] [CrossRef]
- Liu, P.D.; Mahmood, T.; Khan, Q. Multi-attribute decision-making based on prioritized aggregation operator under hesitant intuitionistic fuzzy linguistic environment. Symmetry 2017, 9, 270. [Google Scholar] [CrossRef]
- Zhao, J.; You, X.Y.; Liu, H.C.; Wu, S.M. An extended VIKOR method using intuitionistic fuzzy sets and combination weights for supplier selection. Symmetry 2017, 9, 169. [Google Scholar] [CrossRef]
- Wang, S.W.; Liu, J. Extension of the TODIM Method to Intuitionistic Linguistic Multiple Attribute Decision Making. Symmetry 2017, 9, 95. [Google Scholar] [CrossRef]
- Yager, R.R. Pythagorean membership grades in multicriteria decision making. IEEE Trans. Fuzzy Syst. 2014, 22, 958–965. [Google Scholar] [CrossRef]
- Wei, G.W.; Lu, M.; Tang, X.Y.; Wei, Y. Pythagorean hesitant fuzzy Hamacher aggregation operators and their application to multiple attribute decision making. Int. J. Intell. Syst. 2018, 33, 1197–1233. [Google Scholar] [CrossRef]
- Liang, D.; Xu, Z.S. The new extension of TOPSIS method for multiple criteria decision making with hesitant Pythagorean fuzzy sets. Appl. Soft Comput. 2017, 60, 167–179. [Google Scholar] [CrossRef]
- Zhang, R.T.; Wang, J.; Zhu, X.M.; Xia, M.M.; Yu, M. Some generalized Pythagorean fuzzy Bonferroni mean aggregation operators with their application to multi-attribute group decision-making. Complexity 2017, 2017, 5937376. [Google Scholar] [CrossRef]
- Ren, P.J.; Xu, Z.S.; Gou, X.J. Pythagorean fuzzy TODIM approach to multi-criteria decision making. Appl. Soft Comput. 2016, 42, 246–259. [Google Scholar] [CrossRef]
- Yager, R.R. Generalized orthopair fuzzy sets. IEEE Trans. Fuzzy Syst. 2017, 25, 1222–1230. [Google Scholar] [CrossRef]
- Liu, P.D.; Wang, P. Some q-rung orthopair fuzzy aggregation operators and their applications to multiple-attribute decision making. Int. J. Intell. Syst. 2018, 33, 259–280. [Google Scholar] [CrossRef]
- Liu, P.D.; Liu, J.L. Some q-rung orthopair fuzzy Bonferroni mean operators and their application to multi-attribute group decision making. Int. J. Intell. Syst. 2018, 33, 315–347. [Google Scholar] [CrossRef]
- Cuong, B.C. Picture fuzzy sets-first results. part 1. Semin. Neuro-Fuzzy Syst. Appl. 2013, 4, 2013. [Google Scholar]
- Wei, G.W. Picture uncertain linguistic Bonferroni mean operators and their application to multiple attribute decision making. Kybernetes 2017, 46, 1777–1800. [Google Scholar] [CrossRef]
- Son, L.H. Measuring analogousness in picture fuzzy sets: From picture distance measures to picture association measures. Fuzzy Optim. Decis. Mak. 2017, 16, 359–378. [Google Scholar] [CrossRef]
- Wei, G.W. Picture fuzzy aggregation operators and their application to multiple attribute decision making. J. Intell. Fuzzy Syst. 2017, 33, 713–724. [Google Scholar] [CrossRef]
- Wei, G.W. Picture fuzzy cross-entropy for multiple attribute decision making problems. J. Bus. Econ. Manag. 2016, 17, 491–502. [Google Scholar] [CrossRef]
- Garg, H. Some picture fuzzy aggregation operators and their applications to multicriteria decision-making. Arab. J. Sci. Eng. 2017, 42, 5275–5290. [Google Scholar] [CrossRef]
- Wei, G.W. Picture fuzzy Hamacher aggregation operators and their application to multiple attribute decision making. Fund. Inform. 2018, 157, 271–320. [Google Scholar] [CrossRef]
- Li, D.X.; Dong, H.; Jin, X. Model for evaluating the enterprise marketing capability with picture fuzzy information. J. Intell. Fuzzy Syst. 2017, 33, 3255–3263. [Google Scholar] [CrossRef]
- Thong, P.H. Picture fuzzy clustering: A new computational intelligence method. Soft Comput. 2016, 20, 3549–3562. [Google Scholar] [CrossRef]
- Zadeh, L.A. The concept of a linguistic variable and its application to approximate reasoning-Part II. Inf. Sci. 1965, 8, 301–357. [Google Scholar] [CrossRef]
- Wang, J.Q.; Li, J.J. The multi-criteria group decision making method based on multi-granularity intuitionistic two semantics. Sci. Technol. Inf. 2009, 33, 8–9. [Google Scholar]
- Du, Y.Q.; Hou, F.J.; Zafar, W.; Yu, Q.; Zhai, Y.B. A novel method for multi-attribute decision making with interval-valued Pythagorean fuzzy linguistic information. Int. J. Intell. Syst. 2017, 32, 1085–1112. [Google Scholar] [CrossRef]
- Liu, P.D.; Zhang, X.H. A novel picture fuzzy linguistic aggregation operator and its application to group decision-making. Cognit. Comput. 2018, 10, 242–259. [Google Scholar] [CrossRef]
- Bonferroni, C. Sulle medie multiple di potenze. Boll. Unione Mat. Ital. 1950, 5, 267–270. [Google Scholar]
- Sykora, S. Mathematical Means and Averages: Generalized Heronian Means; Stan’s Library: Italy, 2009; Available online: http://www.ebyte.it/library/docs/math09/Means_Heronian.html (accessed on 16 May 2018).
- Yu, D.J.; Wu, Y.Y. Interval-valued intuitionistic fuzzy Heronian mean operators and their application in multi-criteria decision making. Afr. J. Bus. Manag. 2012, 6, 4158. [Google Scholar] [CrossRef]
- Liu, P.D.; Shi, L.L. Some neutrosophic uncertain linguistic number Heronian mean operators and their application to multi-attribute group decision making. Neural Comput. Appl. 2017, 28, 1079–1093. [Google Scholar] [CrossRef]
- Yu, D.J. Intuitionistic fuzzy geometric Heronian mean aggregation operators. Appl. Soft Comput. 2013, 13, 1235–1246. [Google Scholar] [CrossRef]
- Wang, X.F.; Wang, J.Q.; Yang, W.E. Multi-criteria group decision making method based on intuitionistic linguistic aggregation operators. J. Intell. Fuzzy Syst. 2014, 26, 115–125. [Google Scholar]
- Liu, P.D.; Rong, L.L.; Chu, Y.C.; Li, Y.W. Intuitionistic linguistic weighted Bonferroni mean operator and its application to multiple attribute decision making. Sci. World J. 2014, 2014, 545049. [Google Scholar] [CrossRef] [PubMed]
- Ju, Y.B.; Liu, X.Y.; Ju, D.W. Some new intuitionistic linguistic aggregation operators based on Maclaurin symmetric mean and their applications to multiple attribute group decision making. Soft Comput. 2016, 22, 4521–4548. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).