Abstract
Cloud computing is intensifying the necessity for searchable encryption (SE) for data protection in cloud storage. SE encrypts data to preserve its confidentiality while offering a secure search facility on the encrypted data. Typical index-based SEs in data sharing scenarios can effectively search secure keyword indexes. However, due to the smaller size of the keyword space, SEs using a public key are susceptible to a Keyword Guessing Attack (KGA) and other statistical information leakage. In this paper, for secure search in a data sharing scenario, we propose Random Searchable enCryption (RanSCrypt) that adds randomness to a transformed keyword to increase its space and aspires to make it irreversible. At the core of the mechanism, two keywords are garbled with randomness, still enabling another party to determine if the two garbled keywords (RanSCrypt’s terms REST and Trapdoor) are the same or not without knowing the actual keywords. As SE in a public key setting suffers from vulnerability to KGA, RanSCrypt transfers into a symmetric key setting with minimum overhead and without losing the features of a data sharing scenario. RanSCrypt also adulterates the search result to add perplexity and provides full control of access only to the data receiver. The receiver can cull out the erroneous results from the search result locally. Finally, we introduce a new type of attack on SE, namely, the Keyword Luring Attack (KLA), and show that RanSCrypt is safe from KLA attack due to adulteration of the result. Our security analysis proves RanSCrypt is invulnerable against KGA and leaks no information.
1. Introduction
Cloud computing is emerging as a buzzword in the computing arena [1]. On-demand and scalable infrastructure resources, low-cost computing, and convenient payment policies invite both individuals and enterprises to switch to cloud computing. Individual users can use cloud facilities irrespective of time and location. Business users can avail themselves of these facilities at a cheaper price, exempting them from maintaining computing or storage infrastructures [2,3]. However, cloud security is not at the desired level [4], especially for cloud storage, in which privacy has become a challenging issue due to the concept of secure provenance [5]. While outsourcing data to the cloud, the user loses control of their data because they are unable to physically protect it in the cloud server [6,7]. In order to prevent data from any unauthorized access, the user encrypts the data before outsourcing it to the cloud [8]. In data sharing scenarios, when a sender sends data to a receiver, the sender encrypts data publicly using the receiver’s public key for data confidentiality. In either scenario, encryption transforms data into random text and does not allow the user (or receiver) to search through for a specific chunk of data. One wide-eyed solution to this dilemma may be to bring back all the encrypted data from the cloud (causing communication overhead), decrypting them locally (causing computation overhead) and then searching the plaintext for a particular portion of data. However, this is not feasible in terms of computation and communication costs. To remedy the situation, researchers have proposed Oblivious RAM [9] or Homomorphic Encryption [10]. However, searchable encryption (SE) is a more desired solution and is of increasing interest for secure cloud storage [6]. Searchable encryption (SE) is a cryptosystem in which the ciphertext is searchable with minimum—if any—data leakage [11]. Encryption preserves the confidentiality of data yet provides a search facility with data drainage tending to zero.
The email system is a good example of a data sharing environment, although there are other data sharing domains, too. We take the email system as in example because benchmark schemes have also discussed the email system as an example. In this work, we demonstrate searchable encryption in the emailing system. For such scenario, Boneh et al. proposed a scheme of searchable encryption (SE), namely, Public key Encryption with Keyword Search (PEKS) [12]. In PEKS, the sender encrypts the email using the receiver’s public key and sends it through the email server, i.e., the cloud. The sender encrypts the email using standard public key encryption (such as RSA, ECC) and generates PEKS ciphertext for each of the extracted keywords. While searching for a specific keyword, the receiver computes a trapdoor of that keyword and sends it to the email server (i.e., cloud server). The email server tests the trapdoor with all the PEKS keywords using an algorithmic approach to find any similarity between the keyword residing in the trapdoor and that of the PEKS ciphertext. Once the server finds the similarity, it sends the interrelated emails back to the receiver. Boneh et al. achieved the security of a PEKS ciphertext in the sense of semantic security, which implies “PEKS ciphertext indistinguishability”. PEKS ciphertext indistinguishability confirms that an attacker—even with the ability to obtain a trapdoor for any keyword chosen by himself—will be unable to separate the PEKS ciphertext of a keyword, , from that of another keyword, , if the trapdoors of and are unavailable to him. Nonetheless, PEKS ciphertext does not guarantee the security of a keyword after the trapdoor of a keyword is known.
Several variants of standard PEKS have since been proposed in the literature with different features and security definitions [13,14,15,16,17]. Recently, Byun et al. showed that PEKS schemes are vulnerable to Keyword Guessing Attacks (KGAs) [18] because of a smaller keyword space in comparison with the password space. For example, the latest edition of the Merriam–Webster dictionary has 225,000 () word definitions [19]. Low keyword entropy (i.e., keyword is chosen from a small keyword space) makes searchable encryption (SE) vulnerable to brute force attack. To make things worse, the sender selects representative words (as searching keywords) for emails to enable the receiver’s better understanding of the content (using only keywords). Usage of representative words further reduces the keyword space. Thus, when an attacker gets a trapdoor, he can easily compile a set of guessed keywords. Then, for each guessed keywords, he generates PEKS ciphertext and tests it against the trapdoor. Once the similarity between a PEKS ciphertext and a trapdoor is found, the attacker can conclude that the keyword residing in the PEKS ciphertext and that of the trapdoor are the same. A Keyword Guessing Attack (KGA) works in this fashion [18]. At the same time, Jeong et al. observed that constructing a PEKS scheme to secure against KGA is difficult when the number of keywords is bounded by some polynomial [20]. They showed that consistency in PEKS implies insecurity and this insecurity is attributed to the polynomial size of the keyword space. Equivalently, Shen et al. mentioned that predicate privacy (or trapdoor security) is inherently impossible to achieve in a public key setting [21]. Similarly, we detect that the seed of KGA lies in the fact that anyone can generate PEKS ciphertext of a keyword with only the public key (of the receiver) and the keyword itself. One way to resist this attack is to revoke this public ability so that an attacker cannot take advantage of it.
Furthermore, any consistent searchable encryption is subject to statistical information leakage [20]. Specially, the search pattern, which is number of (encrypted query) keywords searched in the history, and the access pattern, which is number of different document IDs retrieved in response to search operations in the history, are leaked naturally by virtue of a consistent searchable encryption [13]. Such drainage may be minimal but over time, as more search operations take place, the leaked information becomes enough to infer the content of the encrypted documents. Statistical information leakage turns into a serious issue for searchable encryption and the authors refer to this issue as Statistical Attack. Adding noise/randomness into inherently exposed information (i.e., encrypted query keywords or retrieved document IDs) may help to resist Statistical Attack.
Observing findings from [18,20,21], we focus on the construction of typical SE in a data sharing scenario, its workflow, security risk, and potential data breaches. SE has been studied both in public key and symmetric key settings. In data sharing scenarios, symmetric-key-centric solutions suffer from complicated key distribution. Public-key-based solutions have the upper hand in this sense, but they are vulnerable to KGA. We define the necessary requirements of an SE in a data sharing environment, then propose a secure searchable scheme titled Random Searchable enCryption (RanSCrypt) that complies with those requirements. We exploit the public key system for better management of keys in a data sharing scenario and incorporate a symmetric key system to avert KGA (from taking place) while ensuring secure and efficient transformation from public key to symmetric key contexts with minimal overhead. To ensure the irreversibility of the transformed keyword, we rely on integer factorization and the discrete logarithmic problem. Our construction introduces arbitrary randomness in each transformed keyword to enhance its space and to resist statistical attack. Moreover, to baffle an attacker from collecting the statistics of searched results, we add some faulty results (i.e., randomness) along with the correct one. The receiver/searcher can amend the erroneous result locally. Randomness scatters the actual information and prevents the attacker from gathering statistics.
Contribution: RanSCrypt obscures two keywords with randomness, ensures their irretrievability, and still provides the ability to determine their similarity without revealing the original keywords. It simulates a data sharing scenario using a public key cryptosystem and prevents KGA by tactfully transforming it into a symmetric key setting with minimal overhead. The contribution of this work is threefold.
- We detect the core reason behind keyword guessing attacks and statistical attacks and list the necessary requirements of searchable encryption in a data sharing scenario so that it bypasses the keyword guessing attacks and prevents statistical information leakage.
- We present a searchable encryption called random searchable encryption (RanSCrypt) using randomized algorithms for both PEKS ciphertext and trapdoors. To confuse the attacker, even if he gets the result of a search, we introduce a false positive result in RanSCrypt.
- Finally, we introduce a new type of attack on SE called the Keyword Luring Attack (KLA) and show that RanSCrypt is free from KLA while many other PEKS schemes are susceptible to it.
Organization: Section 2 reviews some related works. Section 3 discusses typical searchable encryption construction and the requirements of SE in a data sharing context (i.e., RanSCrypt). In Section 4, we present the proposed Random Searchable enCryption (RanSCrypt) and analyze its security. Section 5 discusses the performance analysis of RanSCrypt with other similar schemes. We introduce a new type of social engineering attack—the Keyword Luring Attack (KLA)—on SE in a data sharing scenario and prove that RanSCrypt is free from KLA in Section 6. We conclude the paper and highlight future research directions in Section 7.
2. Related Work
Searchable encryption (SE) is of increasing interest in cloud computing. SE can be divided into two main categories based on the application scenario. The first is data outsourcing, where the user outsources their data to an honest-but-curious cloud server and the user searches the data in future using keywords of their choice. Song et al. described the initial issue of searching encrypted data and provided proof of the resulting cryptosystem [22]. Their scheme is secure in the sense that the server learns nothing about the plaintext when only given the ciphertext. However, the scheme requires O(n) stream and block cipher operations to search encrypted data, which can be very time-consuming. Goh proposed an index-based solution by utilizing pseudo-random numbers and bloom filters to build a secure index [23]. However, the server can deduce a relationship among relevant documents in their scheme. Curtmola et al. proposed two schemes, namely, SSE-1 and SSE-2 [24]. SSE-1 is secure against chosen keyword attack (CKA1) and SSE-2 is secure against adaptively chosen keyword attack (CKA2). Chang et al. used a bit array for each document where each bit represents the existence of a keyword in that document. Then, they used pseudo-random bits to mask the array. Later, they incorporated a short simple seed to search a keyword while keeping the server blind about other keywords [25]. All these schemes [22,23,24,25] are early works in the symmetric setting and lack many of the security and other features of modern SE like multikeyword search, ranked search, fuzzy search, and so on. One of the latest works for data outsourcing in the cloud among multiple users is described in SeDaSC [26] but it lacks a search facility and requires an additional server (i.e., Cryptographic Server) for maintaining confidentiality.
Ranking search results such as by single-keyword ranked search, multikeyword ranked search, and fuzzy keyword search is a prominent feature in SE [27,28,29]. In single-keyword ranked search, a ranking based on the relevance score between keyword and document is generated for every search query with a single keyword [30,31]. Then, the score is encrypted to protect and hide it from the server [32]. For multikeyword ranked search [33,34,35], the relevance scores between keywords and the document are arranged as elements of an array. Then, scores are protected by incorporating a secure k nearest neighbor (kNN) algorithm [36] and randomizing a trapdoor. The trapdoor is randomized by mixing phantom terms or noises with the exact trapdoor. However, the randomized trapdoor is highly similar to the exact trapdoor and, consequently, the attacker can easily associate them. Another prominent feature in SE is fuzzy keyword search. Fu et al. broke a keyword into monograms and then resorted to a bloom filter and locality sensitive hashing for fuzzy matching. The sNN algorithm is incorporated into the work to secure the relevance scores [37].
The second type of searchable encryption scenario is data sharing where a sender sends data to a receiver via a cloud server, encrypting data using the receiver’s public key, and the receiver later searches the publicly encrypted ciphertext from the cloud. Early work on searchable encryption scenarios integrated the public key encryption with keyword search (PEKS) scheme [12]. Later, the scheme was improved with new features and security definitions [13,14,15,16]. In data sharing scenarios, searchable encryption is best suited to asymmetric-key- (public key) compared to symmetric-key-based solutions. This is because the symmetric-key-based solution [22,23,24,25] suffers from complex key distribution or key management, i.e., the sender requires the information about the secret key of a particular receiver to encrypt the data before sending it to the receiver via the cloud server. Conversely, the PEKS scheme is convenient and allows the sender to encrypt the data using the receiver’s public key. In our work, we concentrate on searchable encryption in a data sharing context which is relevant to Boneh et al.’s PEKS scheme [12]. Researchers has exerted much effort to combat the Keyword Guessing Attack (KGA) on PEKS. Among them, Xu et al. proposed to generate fuzzy keyword trapdoors in which a single (fuzzy keyword) trapdoor represents more than one query keyword and the server returns all documents related to all keywords related to that trapdoor [17]. This approach (PEFKS) helps to mitigate KGA at the cost of communication overhead, but is still subject to KGA to a certain extent. A recent work reported by Huang et al. suggested a scheme called Public-key-Authenticated Encryption with Keyword Search (PAEKS) where a sender not only encrypts the extracted keyword but also authenticates it [38]. This is helpful to eliminate KGA; however, in this method, the receiver has to generate sender-specific trapdoors (i.e., one trapdoor for each sender) for a single query keyword and the server has to know which trapdoor is intended for which sender.
3. Necessary Requirements of RanSCrypt
During the search process, the server learns and retrieves information about the data. Therefore, our proposed RanSCrypt maintains a stringent privacy policy to prevent the server from learning and retrieving anything but the noisy search result. Based on this strict privacy plan, RanSCrypt sets different requirements for different components of SE.
In a typical searchable encryption (SE) scheme in a data sharing context, the sender sends an encrypted document along with the transformed keyword (or PEKS ciphertext or PEKS in short) for each extracted keyword to the server (i.e., email server). The sender encrypts the document or transforms the keywords using the receiver’s public key. The server stores each encrypted document followed by its PEKS keywords in a secure index (SI) form, as shown in Figure 1. While searching, the receiver generates a trapdoor with a query keyword using his private key and sends it to the server (or email server). The server tests the trapdoor by associating it with each of the PEKSs. Once the similarity is found, the server sends the corresponding documents (or emails) back to the receiver. Figure 2 depicts an overview of searchable encryption in a data sharing model.
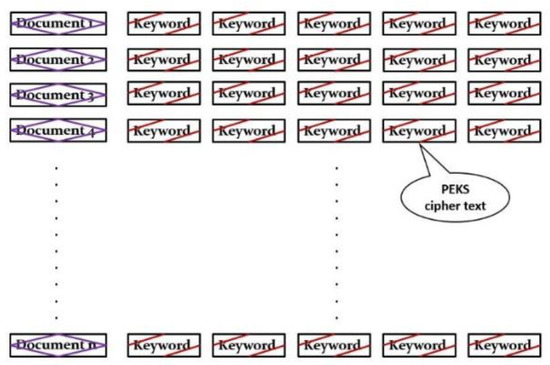
Figure 1.
Secure index.
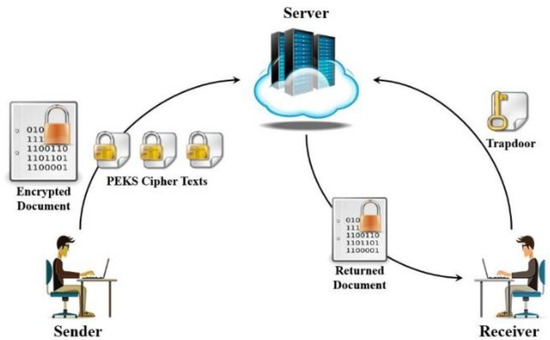
Figure 2.
Searchable encryption in a data sharing model.
SE comprises four main algorithms [11] as follows:
- KeyGen(λ) → K: The KeyGen algorithm takes security parameter λ as input and generates the public/private key pair (PK, SK) for the receiver based on difficulty/complexity level proportional to parameter λ.
- PEKS(PublicKey PK, Keyword w) → PEKS ciphertext: The PEKS algorithm takes the public key PK of the receiver along with an extracted keyword w as inputs and generates the PEKS ciphertext (or PEKS in short) of w. This algorithm runs on the sender side.
- Trapdoor(PrivateKey SK, Keyword w) → : The trapdoor algorithm takes the private key of the receiver and query keyword w as inputs and returns the trapdoor of w, . The receiver runs this algorithm.
- Test(, PEKS) → [0,1]: The test algorithm takes a trapdoor and a PEKS as inputs and returns 1 if the keyword residing in and that of PEKS are similar, or 0 otherwise. This algorithm runs on the server side.
A thorough investigation reveals that the root of KGA lies in the construction of the PEKS ciphertext. In a typical PEKS scheme, the PEKS ciphertext of a keyword w can be generated using the algorithm. The inputs to this algorithm are the receiver’s public key, which is readily available, and the keyword, which can be guessed or even be exhaustively checked from all possible keywords (from a dictionary). Consequently, the PEKS ciphertext of any keyword can easily be generated by anyone. Therefore, one way to avert KGA is to revoke public ability to generate PEKS ciphertext. Again, the ciphertext should not be reversible to the original keyword. Simultaneously, to increase keyword space, randomness should be incorporated with it; this is helpful to resisting statistical attack. Another issue of a typical searchable encryption scheme is that when the same keyword exists in different emails, the server can match those keywords and decide without decrypting the PEKS. This attack is known as association attack. To prevent association attack, the construction of a PEKS keyword needs to be randomized so that the same keyword will have different PEKS ciphertexts.
As a matter of fact, revoking public ability for PEKS ciphertext generation builds a scheme that is no longer like PEKS. However, RanSCrypt helps only to construct a searchable encryption scheme to facilitate secure search on encrypted data in a data sharing scenario. It utilizes a public key cryptosystem for better key management and switches to symmetric key settings to bypass KGA, assuring concealment of other statistical information.
The trapdoor is computed using the receiver’s private key but after multiple runs of the same trapdoor, some frequency information of the underlying keyword may be revealed. The search pattern is the number of times a keyword is searched over a period of time [13]. Henceforth, the trapdoor also needs to be indistinguishable—preferably random—to resist any statistical attack. Like PEKS, a trapdoor should be irreversible so that no one can retrieve the original keyword. Despite being random and irreversible, both PEKS and trapdoor should support the search facility. Furthermore, a search result (document list) can contain crucial information such as access pattern or search pattern [13]. To protect the privacy of the search pattern or access pattern, the search result should contain an erroneous result along with the accurate result. Mixing the erroneous and accurate results will help to perplex the attacker and thwart the gathering of any statistical information.
From the observations in [18,20,21], RanSCrypt adopts a construction of an index keyword that needs the receiver’s secret key for generation. At the same time, index keywords will be roaming on the network or residing on the server without leaking any information. Based on the above discussion, we list three properties as requirements for a secure searchable encryption (SE) in a data sharing context: (1) index keyword indistinguishability, (2) trapdoor indistinguishability, and (3) result perplexity. Table 1 shows the requirements of SE for different attacks.

Table 1.
Requirements of searchable encryption (SE). KGA: Keyword Guessing Attack.
- Index Keyword Indistinguishability: PEKS generates ciphertext using the following algorithm: PEKS(public_key, keyword).
PEKS takes a receiver’s public key and a keyword as inputs. As mentioned earlier, the receiver’s public key is readily available and keyword can be guessed even through exhaustive search due to its low entropy. Index keyword indistinguishability involves sending a randomly encrypted keyword with the receiver’s public key and then converting it into a searchably encrypted keyword with the receiver’s secret key. The index keyword should be encrypted randomly before sending it from sender to receiver. The exact index keyword can be retrieved and transformed into a searchable format by the receiver with minimum overhead. However, if the same keyword exists in multiple documents (or emails) then the same index keyword will exist multiple times in the secure index (Figure 1). This will help an attacker to correlate the similar emails and provides nontrivial information (association attack). Again, as the keyword has low entropy, a searchable index keyword should be randomized yet support search facility. Lastly, the index keyword should be irreversible to baffle an attacker from getting the original keyword. Thus, the index keyword should be indistinguishable (i.e., random), irreversible, and support the search facility.
- 2.
- Trapdoor Indistinguishability: A trapdoor, along with its result, will expose the search pattern [13]. In order to counteract an attacker, the trapdoor should be randomized and should not be linkable (i.e., it needs to be irreversible) to its originating keyword. Similar to index keywords, the trapdoor also needs to be indistinguishable, irreversible, and support the search facility.
- 3.
- Result Perplexity: RanSCrypt provides the server with noisy search results wherein the results contain an erroneous result along with the accurate result. While the receiver searches with a trapdoor of a keyword, documents (or emails) containing that keyword should be accompanied by some documents not containing the keyword. That means that the result should include some false positive results. The receiver can amend the result by decrypting the documents so it will not affect the final result of a query. This will cost extra communication and computation overhead. Noise in the result is necessary to thwart the revealing of an access pattern [13].
There are two ways to add the false positive result:
Add the same set of false positive results for a specific trapdoor each time.
Add a randomized false positive result for a specific trapdoor each time.
However, adding a randomized false positive result has a pitfall. Let, for a keyword, an accurate result be =.
For the first run, false positive result is =.
For the second run, false positive result is =.
For the third run, false positive result is =.
Then, for the first, second, and third runs, the results are
= ∪ = ,
= ∪ = ,
= ∪ = , respectively.
Now, if an attacker computes the intersection between , , and , he will obtain a very close approximation to the accurate result: ∩ ∩ =.
Consequently, RanSCrypt adopts the addition of a fixed set of false positive results each time for the same trapdoor. This can be done simply by adding noise in the index.
4. RanSCrypt: Random Searchable enCryption
RanSCrypt comprises five algorithms: Setup(Parameter λ), OPAC(PublicKey, keyword), REST(keyword), Trapdoor(keyword), and Test(REST, Trapdoor). OPAC, REST, and Trapdoor algorithms generate a transformed keyword to achieve different functionalities. These transformations contain randomness to increase the keyword space in order to frustrate a statistical attacker.
- Setup(Parameter λ): This algorithm takes a security parameter λ and generates a public/private key pair for the receiver (, ), base number b of the receiver, two large primes p, q to generate the modulus n = p * q, a secret key k, and a hash key . All of these parameters are chosen based on the complexity level defined by the input parameter λ.
- OPAC(, keyword): One Plaintext Assorted Ciphertexts (OPAC) is a randomized algorithm in an asymmetric key setting that returns different ciphertexts in different runs for the same plaintext. OPAC introduces opacity in the extracted keyword while the sender sends an email to a receiver but provides the receiver a way to retrieve the exact keyword. The OPAC algorithm takes the receiver’s public key and a keyword as input and returns indistinguishable OPAC ciphertext. To generate an OPAC of a keyword, the algorithm encrypts the keyword prepending a fixed-length random string with it. Thus, different ciphertexts result for different runs with the same keyword. To retrieve the original keyword, we decrypt the OPAC ciphertext and then remove the (prepended) fixed-length random string from it.
For example, we can generate OPAC ciphertexts two times for the word “secure”, where the length of the random string is twelve:
- = (“wpOuFrvb87hn” || “secure”),
- = (“xc5mb9rhpZBi” || “secure”).
Here, the symbol ‘||’ means concatenation between two strings. and will result in two different ciphertexts for the same keyword—“secure”. To retrieve the exact keyword, we decrypt the OPAC ciphertext and then remove the first (fixed-length characters; here, the first 12 characters) twelve characters from it:
- () = “wpOuFrvb87hn” || “secure”,
- Remove_First_12_Characters (“wpOuFrvb87hn” || “secure”) = “secure”.
OPAC can be used to encrypt a keyword while the keyword space is small enough and vulnerable to Ciphertext Only Attack (COA). OPAC does not provide a search facility on ciphertext. Nonetheless, it enables the sender to send a keyword securely to a receiver who can generate a searchable encrypted keyword (REST) later on.
- 3.
- REST(keyword w): REST stands for Randomly Encrypted and Searchable Text. It is a randomized algorithm that allows the user to transform a keyword randomly but provides a way to match with a trapdoor of the same keyword. REST makes it difficult to revert back to the original keyword. To construct REST for a keyword w,
- Generate a random number R.
- Compute hash digest of the keyword w (i.e., = (w)).
- Multiply the random number (R) and a secret key (k) with the square of the hash digest of w (i.e., R).
- Raise the power of base number b to the multiplication of , secret key (k), and the random number R (i.e., ).
- All computations are conducted as operations modulo n.
- The REST of the keyword w is [R, ].
The REST of a keyword has two features. First, it is a randomized algorithm that is difficult to revert to the exact keyword if the modulus n is large enough. Second, it offers a way to find similarity with a trapdoor of the same keyword. Thus, it is suitable for searching on hidden text.
- 4.
- Trapdoor(keyword w): The trapdoor algorithm takes a keyword and generates a randomized trapdoor. The trapdoor algorithm is similar to the REST of a keyword but with a slight difference in construction. Like REST, Trapdoor is also a randomized algorithm that hides its original keyword while supporting finding similarity with a REST of the same keyword. To generate a trapdoor, we use the same base number b as in REST. Trapdoor construction of a keyword w is as follows:
- Generate a random number R.
- Compute hash digest of the keyword w (i.e., = (w)).
- Multiply the random number (R), secret key (k) and the hash digest of keyword w (i.e., kR).
- Raise the power of b to the random number R (i.e., ).
- All computations are computed in modular operations.
- The trapdoor of the keyword w is [kR, ].
Similar with REST, Trapdoor has two characteristics. First, it is computationally laborious to redeem the original keyword if the modulus n is large enough. Second, it provides a way to find a REST keyword that originates from the same keyword as the Trapdoor. Thus, Trapdoor facilitates searching on the concealed text.
- 5.
- Test(REST, Trapdoor): The Test algorithm takes the REST of a keyword and the Trapdoor of another keyword as input and returns whether two keywords are the same. Suppose that the REST of a keyword is [A, B] and that the Trapdoor of a keyword is [C, D]. Then Test algorithm returns “true” ifor “false” otherwise.
Correctness:
The REST of a keyword is [, ] ≡ [A, B] for a random number and hash digest .
The Trapdoor of a keyword is [, ] ≡ [C, D] for a random number and hash digest .
L.H.S. = = =
R.H.S. = = =
Now, L.H.S. = R.H.S. if or, alternatively, if .
4.1. RanSCrypt Workflow
Before describing the workflow of the RanSCrypt scheme, we demonstrate the index data structure of the searchable encrypted data residing in the server, as depicted in Figure 3. Each email consists of an encrypted body, OPAC ciphertext for each extracted keyword, and a status that indicates whether this email can be searched using extracted keywords or not. In the data structure of Figure 3, where an email has OPAC ciphertexts for extracted keywords, that email has searchable status sets to “NO”, and for which emails there exist REST keywords, that email has searchable status sets to “YES”. This signifies that emails with OPAC ciphertexts cannot be searched through as OPAC ciphertexts are not searchable. On the other hand, emails’ REST keywords enable them to be searched through.
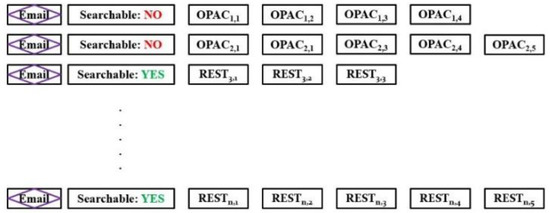
Figure 3.
Secure index for Random Searchable enCryption (RanSCrypt).
The workflow of the RanSCrypt scheme is shown in Figure 4.
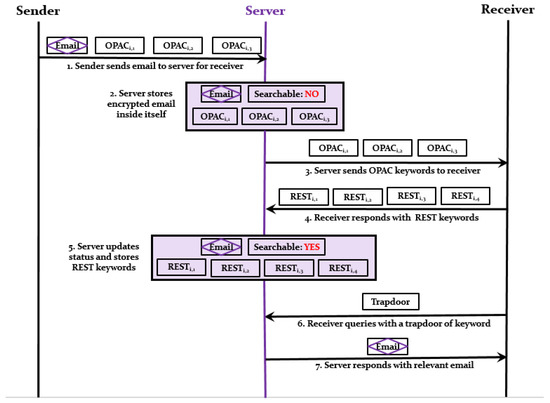
Figure 4.
RanSCrypt Workflow.
- When a sender sends an email to a receiver, the sender extracts keywords which the receiver can use to search the email. Then, the sender encrypts the body of the email using a regular cryptosystem (i.e., RSA, AES, etc.) and generates OPAC ciphertext for each keyword. After that, the sender sends the email along with OPAC ciphertexts to the server for the receiver.
- The server stores the email with its OPAC ciphertexts and sets the “Searchable” status to “NO” as the email with OPAC ciphertext is no longer searchable.
- The server sends the OPAC ciphertexts to the receiver to get the searchable REST keyword for each OPAC ciphertext. The server can send the OPAC ciphertexts immediately or later in some feasible moments as per policy.
- For each OPAC ciphertext, the receiver decrypts it and retrieves the original keyword. After that, the receiver computes the REST keyword for each of the original keywords. The receiver generates extra REST keywords and sends back all the REST keywords (including extra REST keywords) back to the server. Extra REST keywords are added for a false positive result, ensuring result perplexity. If the server sends -many OPAC keywords, then the receiver should return -many REST keywords where < and ( − ) will be defined by some predefined error percentage.
- The server stores all the REST keywords in place of the OPAC ciphertexts and updates the “Searchable” status to “YES” for that particular mail. This time, the corresponding email is searchable using these REST keywords. Each time the receiver searches for email, he can only search those emails which have “Searchable” status set to “YES”.
- The receiver can search anytime with the keyword of his choice. For this purpose, the receiver generates a Trapdoor of the keyword and sends to the server for the relevant email(s).
- Once the server gets a Trapdoor from the receiver, it searches all the REST keywords of emails for which the “Searchable” status is “YES”. The similarity between a REST keyword and trapdoor is obtained using the Test algorithm. Finally, the server sends the relevant email(s) back to the receiver.
- Getting a result, the receiver decrypts and removes false positive results from the result locally.
4.2. Security Analysis
RanSCrypt deals with three different components: data, keyword, and search result. The privacy of the data is protected by a modern cryptosystem that prevents an attacker from prying into the actual data. As RanSCrypt is a searchable encryption scheme, it must reveal the search result (i.e., encrypted document list corresponding to a trapdoor). To scatter statistics of the access pattern, RanSCrypt introduces noise into the result data, which adds the overhead of extra communication and computation cost. The current version of RanSCrypt only suggests adding noise rather than adding the noise to diffuse statistical data. Finally, RanSCrypt never uses a bare keyword either through network or in storage. Instead, RanSCrypt uses OPAC, REST, or Trapdoor with different functionalities. The following theorem shows the relation between these three constructions of keywords and RanSCrypt as a secure searchable encryption.
Theorem 1.
RanSCrypt is secure if OPAC, REST, and Trapdoor reveal no information about the underlying keyword.
Proof.
If we use secure(message) to indicate that “message” is secure, then we may rewrite Theorem 1 as the following:
secure(OPAC) ∧ secure(REST) ∧ secure(Trapdoor) ⟹ secure(RanSCrypt).
RanSCrypt transforms the index keyword into OPAC and REST. On the other hand, Trapdoor is a transformed query keyword that hides the query keyword inside it. There exists no other way to hide an isolated keyword (either index or query) in RanSCrypt.
So, as the attacker gets no information about the keyword either from the index keyword or from the trapdoor, then he cannot launch an attack; this necessarily makes RanSCrypt secure. Therefore,
secure(OPAC) ∧ secure(REST) ∧ secure(Trapdoor) ⟹ secure(RanSCrypt). The proof is completed here.□
Index keywords of RanSCrypt appear in two formats: OPAC and REST. The trapdoor appears in the Trapdoor format. The constructions of REST and Trapdoor are almost similar but the construction of OPAC is somewhat different than those of the other two. In the following theorems, we claim and prove that OPAC, REST, and Trapdoor do not leak any information about the underlying keyword.
Theorem 2.
OPAC does not reveal any information of the residing keyword.
Proof.
= (L_length_random_number || message)
From the construction of OPAC, we see that OPAC is a public key cryptosystem that holds semantic security. However, for a smaller keyword space, an attacker can easily launch a chosen plaintext attack (COA). To make it indistinguishable to chosen plaintext attack (IND-CPA), it prepends a fixed-length (L bits) random number before encryption and removes the first L-many bits after decryption. Thus, in a typical semantic security game, even each time an attacker asks for ciphertext of the same keyword, he receives different ciphertexts. Hence, he fails to get any insight about the keyword during the challenge phase which makes the OPAC transformation IND-CPA. Moreover, L (which is supposed to increase with increasing computation power) length random number baffles any attempted brute force attack hence, secure(OPAC) is proved. □
Theorem 3.
REST (or Trapdoor) does not reveal any information about the underlying keyword.
Proof.
REST (or Trapdoor) consists of two parts. The first part is a multiplication of several terms and the second is a base raised to the product of several terms. Both parts involve modular arithmetic with a modulus that is chosen similar to the RSA cryptosystem.
To break the REST, the attacker needs to factorize first part and to find the exponent of the second part.
| REST: [] Trapdoor: [] | Here, w = keyword, k = secret key, R = random number, b = base number. |
In the worst-case scenario, the attacker reveals the keyed hash digest of a keyword (). However, a collision-resistant one-way (keyed) hash function generates the hash digest. Thus, the actual keyword remains unknown to the attacker. All that an attacker can do with the hash digest is to collect some statistical information about keywords. However, RanSCrypt wants to prevent the attacker getting any clue of the underlying keyword, even from exposure of the hash digest of the keyword.
First, we assume that REST (or trapdoor) is breakable; that is, a polynomial time attacker easily finds the hash digest of a keyword ().
To break REST, the attacker needs to factorize the first part to get the hash digest (), secret key (k), and one-time random number (R). The attacker can confirm if the factorization is accurate by raising the power of base (b) to R and checking its equality with the second part. However, factorization (modulo n) is computationally infeasible if the number is reasonably large [39,40,41]. Therefore, a polynomial time attacker will find it difficult to retrieve R due to the integer factorization problem.
Alternatively, the attacker can search for the exponent of the second part of REST (R). This will give the attacker some insight about from the first portion. However, for large numbers, a polynomial time attacker will face the discrete logarithmic problem in extracting the exponent [42].
Obtaining is computationally intensive (because of integer factorization and the discrete logarithmic problem) for an attacker with limited resources, particularly when the secret key, modulus, base number, and random number space are chosen large enough to combat information leakage. However, RanSCrypt does not make recommendations about the length of any of these numbers; instead, they should be chosen in proportion to computing power during the implementation to withstand against any information leakage.
Consequently, the attacker must exert effort equivalent to resolving the integer factorization problem and the discrete logarithmic problem to retrieve the keyword. To date, no efficient algorithm has been found to solve the two problems, which makes our assumption of breakable REST obsolete and ensures secure(REST) (and, similarly, secure(Trapdoor)).
This completes the proof. □
Finally, from Theorems 2 and 3, we get
secure(OPAC),
secure(REST),
secure(Trapdoor),
and, from Theorem 1,
secure(OPAC) ∧ secure(REST) ∧ secure(Trapdoor) ⟹ secure(RanSCrypt).
Theorem 4.
RanSCrypt frustrates a Keyword Guessing Attack.
Proof.
KGA relies on the fact that an attacker can compile a guessed keyword set and can generate an index keyword (i.e., the PEKS ciphertext) to match with a trapdoor. As the attacker knows the original keyword inside an index keyword, the keyword inside a trapdoor can be obtained once a similarity is found.
RanSCrypt removes the public ability to generate PEKS ciphertext for a keyword of choice. Instead, it generates an OPAC keyword publicly and later transforms it into REST keyword with the help of the receiver (using the receiver’s private key) in a data sharing environment. Hence, there is no scope of KGA inside RanSCrypt’s context. This completes the proof. □
Revoking public ability for PEKS ciphertext generation does not build a PEKS-like scheme. Nonetheless, RanSCrypt intends to be a reliable searchable encryption in a data sharing plot. It utilizes a public key setting for efficient key distribution and shifts to a symmetric key setting in order to repel KGA, ensuring no statistical information leakage.
Theorem 5.
RanSCrypt withstands Statistical Attack.
Proof.
Statistical information, e.g., search pattern, access pattern, gets exposed inherently in Searchable Encryption. Apart from that, if the index or query keywords use deterministic transformation then they also leak other statistical information (such as association attack). However, RanSCrypt adds randomness in each transformation of keywords (Theorems 2 and 3) which baffles an attacker collecting statistics of different components. Similarly, RanSCrypt suggests to add noise while transforming from an OPAC keyword to a REST keyword (Step 4 of the RanSCrypt workflow) which prevents access pattern exposure. Thus, RanSCrypt withstands Statistical Attack. This completes the proof. □
5. Performance Analysis
In this section, we analyze the performance of RanSCrypt by implementing it using the Java language on a Windows10 machine with a Core2 CPU running at 3.33 GHz. We used Request for Comments database (RFC) similar to Fu et al.’s scheme [37]. Despite its applicability in a symmetric key setting, it serves the purpose of comparison of RanSCrypt with other PEKS schemes. We compare the performance of RanSCrypt with the first PEKS scheme by Boneh et al. [12] and other two schemes (PEFKS [17] and PAEKS [38]) that attempted to solve KGA.
5.1. Efficiency
The performance of the algorithms used in RanSCrypt, PEKS, PEFKS, and PAEKS depends on the size of keys and/or amount of randomness. Therefore, it is tough to analyze and compare their performance with empirical data. Instead, this research counts the number of operations taken by these algorithms and considers the same keys and random numbers to execute the operations. Again, ignoring the less resource-hungry operations, this work only inspects resource-intensive operations (i.e., modular exponentiation, hash digest computation).
PEKS-like schemes (e.g., RanSCrypt, PEKS, PEFSK, PAEKS) consist of four algorithms: (a) key generation, (b) secure index generation, (c) trapdoor generation, and (d) test. Among them, the secure index, trapdoor generation, and test algorithms define the nature of a scheme and this work compares different schemes in terms of the three algorithms.
As for memory usage, different PEKS schemes use the same order of memory space, given a fixed key size. However, PEKS schemes significantly differ in execution time due to the difference in algorithmic approaches. For illustration, in secure index keyword generation, RanSCrypt, PEKS, PEFKS, and PAEKS need 1, 3, 6, and 3 modular exponentiation operations, respectively, and 1, 2, 4, and 1 hash digest computation operations, respectively. In each case, we ignore the multiplication operation as it has logarithmic execution time in comparison with the modular exponentiation operation. We also ignore the operation of random number generation from the comparison since all the secure index keyword generation algorithms in each scheme require a random number. Based on this piece of information, the execution time of secure index keyword generation is shown in Figure 5 where the RSA key size is 1024 bits and the RanSCrypt modulus is chosen the same as the RSA modulus for ease of comparison.
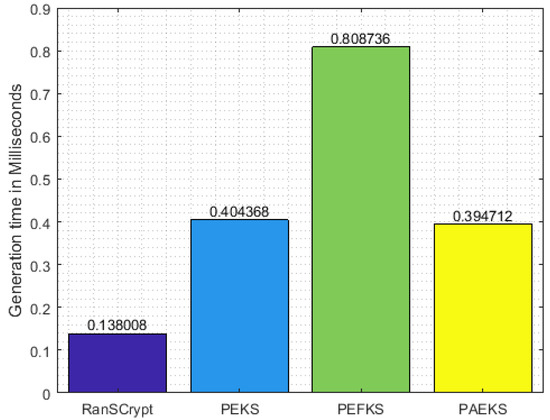
Figure 5.
Secure Index keyword generation.
Table 2 lists the number of resource-intensive operations for each algorithm of each scheme. On the basis of the information provided in the table, Figure 5, Figure 6 and Figure 7 demonstrate the execution time of the secure index keyword, trapdoor generation, and test algorithms, respectively. Since RanSCrypt requires a smaller number of operations, RanSCrypt has the upper hand in execution time compared to the other schemes. In trapdoor generation, RanSCrypt takes a significantly longer time than PEKS. However, PEKS is vulnerable to KGA; hence, we can ignore this for the sake of security. PEFKS tries to resolve KGA by masking the secure index/trapdoor/result with (approximately) twofold data. Hence, it needs almost double the amount of execution time in each algorithm. PAEKS, on the other hand, tries to combat KGA by encrypting the secure index/trapdoor with the sender’s public key. Thus, it requires the receiver to generate a sender-specific trapdoor for each query keyword. Consequently, it increases the trapdoor generation and testing time in proportion to the number of senders.

Table 2.
Number of operations required for different algorithms of different schemes. PEKS: Public key Encryption with Keyword Search; PAEKS: Public-key-Authenticated Encryption with Keyword Search.
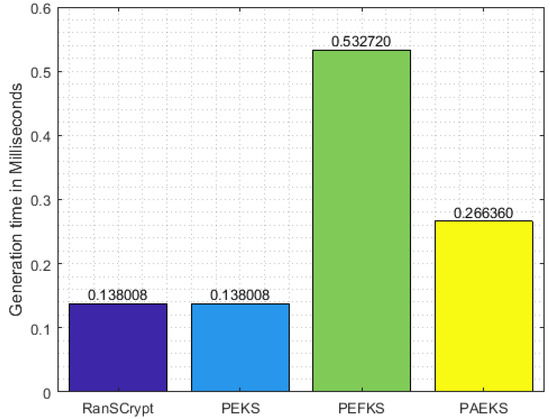
Figure 6.
Trapdoor generation.
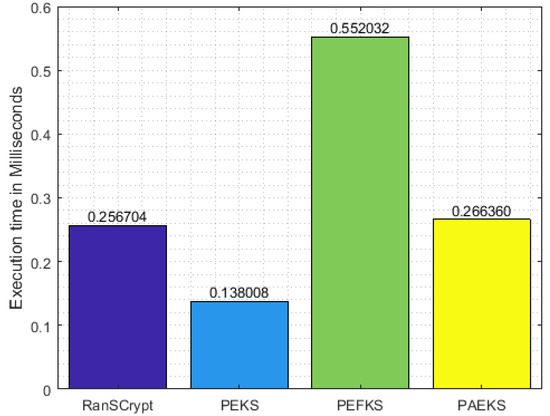
Figure 7.
Test algorithm computation.
Last, but not least, with a view to preventing an attacker from collecting statistical information, RanSCrypt prefers to add deterministic noise (Section 3). Noise helps to prevent statistical information leakage (like in PEFKS) and subsequently adds some (communication and computation) overhead. However, in RanSCrypt, the percentage of noise to be added for the resulting perplexity is totally at the receiver’s discretion and the receiver even can go without any noise at the risk of statistical information leakage.
5.2. Overhead to Transform from Public Key to Symmetric Key
Due to inherent nature of PEKS, it is not resistant to KGA. So, for better key management in a data sharing scenario, RanSCrypt starts with a public key cryptosystem and changes to a symmetric key setting for KGA protection with minimal communication and computation costs. In RanSCrypt’s workflow, Steps 3 and 4 play a role in shifting from the public key setting to the symmetric key setting. During this process, the receiver receives OPAC keywords for an email from the server, retrieves the original keywords, computes REST keywords, and finally sends them back to the server. It is noteworthy that the number of REST keywords is not necessarily equal to the number of OPAC keywords. This transformation cost involved here is in four parts. Firstly, the communication cost of OPAC keywords from the server to the receiver. Secondly, the retrieval cost of the keywords from the OPACs. Thirdly, the transformation of keywords into their RESTs. Lastly, the communication cost of the REST keywords back to the server.
Transmission of OPAC and REST keywords depends on their size, which is supposed be extremely small compared with that of the original encrypted documents (i.e., the email). Thus, it is very convenient, especially for the cloud’s pay-as-you-go payment policy. Figure 8 displays the public key size versus the size of OPAC ciphertext using the Java Crypto library. Similarly, the size of REST keywords depends on the modulus n. The size of a REST keyword is no greater than bits.
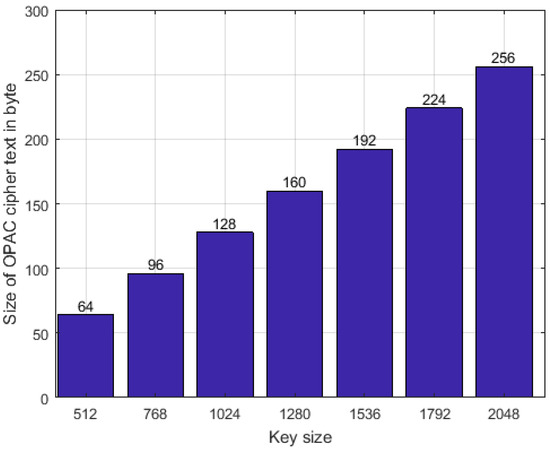
Figure 8.
Size of OPAC keywords vs. size of public key.
In case of computation, conversion from an OPAC keyword to a REST keyword via the original keyword depends on the size of the cryptographic key and number of keywords to be converted. The exact operations required for this computation are public key decryption, removal of the prepended random number from the decrypted text, and generation of the REST for the retrieved keyword. Figure 9 illustrates the empirical execution time for this computation (considering that the REST modulus and RSA modulus are the same) with different key sizes and a different number of keywords. Even though it depends on the amount of randomness mixed with the transformed keywords, Figure 9 shows that the curve of the execution time with a larger (cryptographic) key is much steeper than that with a smaller (cryptographic) key.
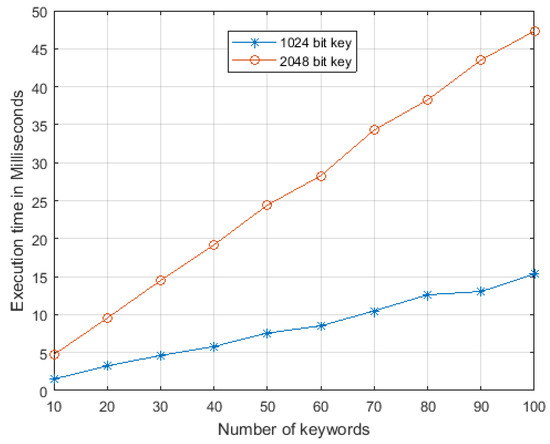
Figure 9.
Execution time for converting an OPAC keyword to a REST keyword via the original keyword.
Apparently, it seems to be cost-effective to preserve the secure index in the local device or local workstation. It saves costly cloud storage and half of the communication cost required in RanSCrypt as overhead (i.e., communication of REST keywords from local to server). Nonetheless, the size of the secure index is smaller compared with the size of the encrypted documents, so it does not add much storage cost over the total cost. Similarly, preserving the secure index locally prevents the receiver from searching on the fly (the receiver must have access to the secure index before getting the desired encrypted documents). Thus, the overhead incurred by transfer from OPAC to REST helps to prevent KGA and enables ease of searching.
6. Keyword Luring Attack (KLA)
Suppose that it is possible to construct a highly sophisticated searchable scheme in a data sharing scenario such that it reveals no information from ciphertext, trapdoor, or from the result. The searchable scheme is still vulnerable to a special type of social engineering attack referred to as a Keyword Luring Attack (KLA). KLA assists an attacker (who has collaboration with the server) to know all the documents (or emails) related to a specific keyword of his choice. Let us consider the following storyline which is depicted in Figure 10:
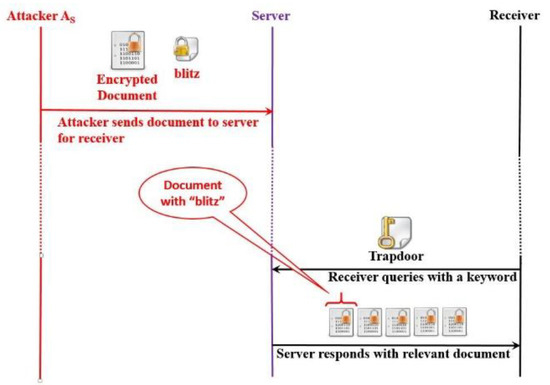
Figure 10.
Keyword Luring Attack.
An attacker, who has a collaboration with the server or who is a server itself, is symbolized as . He needs to know all the documents of a receiver containing a single word “blitz” as a keyword. With this intention in mind, he sends a document to the receiver with keyword “blitz” and starts observing the receiver’s interaction with the server. Whenever the receiver receives the document in the resulting document list, the attacker can figure out that the receiver queried with keyword “blitz” and that the resulting documents contain this keyword.
Probable solution: Inconsistency in a search result or a false positive result along with an accurate result can make SE secure against KLA.
Theorem 6.
RanSCrypt is secure against Keyword Luring Attack.
Proof.
Jeong et al. introduced and proved a theorem that consistency implies insecurity to keyword guessing in PESK when the number of possible keywords is bounded by some polynomial [20]. KLA is related to KGA. In KGA, the attacker can find out the underlying keyword of any trapdoor, whereas in KLA, the attacker can find out the underlying keyword of a (limited) trapdoor (and brute force attack is not possible using KLA). However, in both cases, consistency implies insecurity, or
Consistency → Insecurity
⇒ Consistency → ¬Security
⇒ ¬(¬Security) → ¬Consistency
⇒ Security → Inconsistency.
So, to ensure security, there must exist some inconsistency (false positive) in the result. In RanSCrypt, we propose to add some false positive result (in Step 4 of RanSCrypt workflow). Hence, RanSCrypt is secure from KLA.
Suppose that a RanSCrypt attacker sends an email with the keyword “blitz”. The attacker encrypts the email () and generates the OPAC of the keyword “blitz” (). Then the attacker sends and to the receiver.
[, ]: Attacker → Server
The receiver gets the from the server and generates the REST of “blitz” (). The receiver also generates the REST of another keyword () to confuse the attacker. The receiver sends both and to the server. If the REST keyword is irreversible, then the attacker/server will not learn which one is for “blitz”.
[]: Server → Receiver
[, ]: Receiver → Server
While searching, the receiver sends a trapdoor of a keyword in response; suppose the server sends along with other emails , .
[]: Receiver → Server
[, , ]: Server → Receiver
Now, observing email in the resulted email list, the attacker is not sure
if matches with or ,
or if the resulting emails contain or ,
or if the resulting emails contain keyword “blitz” or “other”.
The attacker can be sure with a certain probability but not with absolute certainty.
The proof completes here. □
7. Concluding Remark
In this paper, we explore the problem of searchable encryption in a data sharing context and its susceptibility to keyword guessing attacks and statistical attacks. We proposed a novel searchable encryption scheme called RanSCrypt that introduces randomness in a transformed keyword. At the core of the proposed scheme, we define two constructions of keywords with randomness and allow public verification of their similarity without revealing anything about the two keywords. This mechanism helps to prevent statistical information breaches. RanSCrypt incorporates secret keys to generate an index for the transformed keyword. To increase the keyword space, it uses random numbers for transformations, which dramatically increases keyword entropy. Resorting to the integer factorization and discrete logarithmic problems, RanSCrypt ensures that the transformed keyword reveals no information about the original keyword. Despite randomness and irreversibility, RanSCrypt supports matching between index and query keywords efficiently.
In our future work we will address the following issues:
- Multikeyword search: To enable RanSCrypt to support multiple query keyword search.
- Ranked result: Ranked resulting document list according to relevance score between query keyword and document.
- Fuzzy keyword search: To simulate real-life search capability, RanSCrypt needs to support fuzzy keyword search.
- Efficient searchable encryption: More efficient index and query keyword transformation and searching algorithms need to be investigated.
- Prioritizing encrypted data: Data searcher needs to be equipped with comparison capability among encrypted data, i.e., a doctor should be able to find emergency patients from many patients’ data based on severity of diseases.
Author Contributions
As a graduate candidate, M A Manazir Ahsan proposed and implemented the main idea under the supervision of Mohd Yamani Idna Bin Idris, Ainuddin Wahid Bin Abdul Wahab, and Ihsan Ali organized the flow of the manuscript. Nawsher Khan, Mohammed Ali Al-Garawi and Atiq Ur Rahman refined the manuscript and responses to the reviews.
Acknowledgments
This research work has been supported by University of Malaya Research Grant (UMRG) scheme (RP036 (A, B, C)-15AET) and Postgraduate Research Grant (PG035-2016A)
Conflicts of Interest
The authors declare no conflict of interest.
References
- Mell, P.; Grance, T. The NIST Definition of Cloud Computing; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2011. [Google Scholar]
- Armbrust, M.; Fox, A.; Griffith, R.; Joseph, A.D.; Katz, R.; Konwinski, A.; Lee, G.; Patterson, D.; Rabkin, A.; Stoica, I. A view of cloud computing. Commun. ACM 2010, 53, 50–58. [Google Scholar] [CrossRef]
- Feng, D.-G.; Zhang, M.; Zhang, Y.; Xu, Z. Study on cloud computing security. J. Softw. 2011, 22, 71–83. [Google Scholar] [CrossRef]
- Takabi, H.; Joshi, J.B.; Ahn, G.-J. Security and privacy challenges in cloud computing environments. IEEE Secur. Priv. 2010, 8, 24–31. [Google Scholar] [CrossRef]
- Ali, M.; Khan, S.U.; Vasilakos, A.V. Security in cloud computing: Opportunities and challenges. Inf. Sci. 2015, 305, 357–383. [Google Scholar] [CrossRef]
- Kamara, S.; Lauter, K. Cryptographic cloud storage. In Proceedings of the International Conference on Financial Cryptography and Data Security, Tenerife, Spain, 25–28 January 2010; Springer: Berlin/Heidelberg, Germany, 2010; pp. 136–149. [Google Scholar]
- Wei, L.; Zhu, H.; Cao, Z.; Dong, X.; Jia, W.; Chen, Y.; Vasilakos, A.V. Security and privacy for storage and computation in cloud computing. Inf. Sci. 2014, 258, 371–386. [Google Scholar] [CrossRef]
- Yan, Z.; Li, X.; Wang, M.; Vasilakos, A. Flexible data access control based on trust and reputation in cloud computing. IEEE Trans. Cloud Comput. 2017, 5, 485–498. [Google Scholar] [CrossRef]
- Goldreich, O.; Ostrovsky, R. Software protection and simulation on oblivious RAMs. J. ACM (JACM) 1996, 43, 431–473. [Google Scholar] [CrossRef]
- Ding, W.; Yan, Z.; Deng, R.H. Encrypted data processing with homomorphic re-encryption. Inf. Sci. 2017, 409, 35–55. [Google Scholar] [CrossRef]
- Han, F.; Qin, J.; Hu, J. Secure searches in the cloud: A survey. Future Gener. Comput. Syst. 2016, 62, 66–75. [Google Scholar] [CrossRef]
- Boneh, D.; Di Crescenzo, G.; Ostrovsky, R.; Persiano, G. Public key encryption with keyword search. In Proceedings of the International Conference on the Theory and Applications of Cryptographic Techniques, Interlaken, Switzerland, 2–6 May 2004; Springer: Berlin/Heidelberg, Germany, 2004; pp. 506–522. [Google Scholar]
- Abdalla, M.; Bellare, M.; Catalano, D.; Kiltz, E.; Kohno, T.; Lange, T.; Malone-Lee, J.; Neven, G.; Paillier, P.; Shi, H. Searchable encryption revisited: Consistency properties, relation to anonymous IBE, and extensions. J. Cryptol. 2008, 21, 350–391. [Google Scholar] [CrossRef]
- Baek, J.; Safavi-Naini, R.; Susilo, W. Public key encryption with keyword search revisited. In Proceedings of the International Conference on Computational Science and Its Applications (ICCSA 2008), Perugia, Italy, 30 June–3 July 2008; pp. 1249–1259. [Google Scholar]
- Park, D.J.; Kim, K.; Lee, P.J. Public key encryption with conjunctive field keyword search. In Proceedings of the International Workshop on Information Security Applications, Jeju Island, Korea, 23–25 August 2004; Springer: Berlin/Heidelberg, Germany, 2004; pp. 73–86. [Google Scholar]
- Rhee, H.S.; Park, J.H.; Susilo, W.; Lee, D.H. Trapdoor security in a searchable public-key encryption scheme with a designated tester. J. Syst. Softw. 2010, 83, 763–771. [Google Scholar] [CrossRef]
- Xu, P.; Jin, H.; Wu, Q.; Wang, W. Public-key encryption with fuzzy keyword search: A provably secure scheme under keyword guessing attack. IEEE Trans. Comput. 2013, 62, 2266–2277. [Google Scholar] [CrossRef]
- Byun, J.W.; Rhee, H.S.; Park, H.-A.; Lee, D.H. Off-line keyword guessing attacks on recent keyword search schemes over encrypted data. In Proceedings of the Workshop on Secure Data Management, Seoul, Korea, 10–11 September 2006; Springer: Berlin/Heidelberg, Germany, 2006; pp. 75–83. [Google Scholar]
- Mish, F. Merriam-Webster’s Collegiate Dictionary, 11th ed.; Merriam-Webster. Inc.: Springfield, MA, USA, 2003. [Google Scholar]
- Jeong, I.R.; Kwon, J.O.; Hong, D.; Lee, D.H. Constructing PEKS schemes secure against keyword guessing attacks is possible? Comput. Commun. 2009, 32, 394–396. [Google Scholar] [CrossRef]
- Shen, E.; Shi, E.; Waters, B. Predicate privacy in encryption systems. In Proceedings of the Theory of Cryptography Conference, San Francisco, CA, USA, 15–17 March 2009; Springer: Berlin/Heidelberg, Germany, 2009; pp. 457–473. [Google Scholar]
- Song, D.X.; Wagner, D.; Perrig, A. Practical techniques for searches on encrypted data. In Proceedings of the 2000 IEEE Symposium on Security and Privacy (S&P 2000), Berkeley, CA, USA, 14–17 May 2000; pp. 44–55. [Google Scholar]
- Goh, E.-J. Secure indexes. IACR Cryptol. ePrint Arch. 2003, 2003, 216. [Google Scholar]
- Curtmola, R.; Garay, J.; Kamara, S.; Ostrovsky, R. Searchable symmetric encryption: Improved definitions and efficient constructions. J. Comput. Secur. 2011, 19, 895–934. [Google Scholar] [CrossRef]
- Chang, Y.-C.; Mitzenmacher, M. Privacy preserving keyword searches on remote encrypted data. In Proceedings of the International Conference on Applied Cryptography and Network Security, New York, NY, USA, 7–10 June 2005; Springer: Berlin/Heidelberg, Germany, 2005; pp. 442–455. [Google Scholar]
- Ali, M.; Dhamotharan, R.; Khan, E.; Khan, S.U.; Vasilakos, A.V.; Li, K.; Zomaya, A.Y. SeDaSC: Secure data sharing in clouds. IEEE Syst. J. 2017, 11, 395–404. [Google Scholar] [CrossRef]
- Swaminathan, A.; Mao, Y.; Su, G.-M.; Gou, H.; Varna, A.L.; He, S.; Wu, M.; Oard, D.W. Confidentiality-preserving rank-ordered search. In Proceedings of the 2007 ACM Workshop on Storage Security and Survivability, Alexandria, VA, USA, 29 October 2007; ACM: New York, NY, USA, 2007; pp. 7–12. [Google Scholar]
- Wang, C.; Cao, N.; Ren, K.; Lou, W. Enabling secure and efficient ranked keyword search over outsourced cloud data. IEEE Trans. Parallel Distrib. Syst. 2012, 23, 1467–1479. [Google Scholar] [CrossRef]
- Zerr, S.; Olmedilla, D.; Nejdl, W.; Siberski, W. Zerber+R: Top-k retrieval from a confidential index. In Proceedings of the 12th International Conference on Extending Database Technology: Advances in Database Technology, Saint Petersburg, Russia, 24–26 March 2009; ACM: New York, NY, USA, 2009; pp. 439–449. [Google Scholar]
- Intille, S.; Jones, K.S. Simple, Proven Approaches to Text Retrieval; Technical Report UCAM-CL-TR-356; University of Cambridge, Computer Laboratory, CiteSeerX: Cambridge, UK, 1997. [Google Scholar]
- Witten, I.H.; Moffat, A.; Bell, T.C. Managing Gigabytes: Compressing and Indexing Documents and Images; Morgan Kaufmann: Burlington, MA, USA, 1999. [Google Scholar]
- Boldyreva, A.; Chenette, N.; Lee, Y.; O’neill, A. Order-preserving symmetric encryption. In Proceedings of the 28th Annual International Conference on the Theory and Applications of Cryptographic Techniques (EUROCRYPT), Cologne, Germany, 26–30 April 2009; Springer: Berlin/Heidelberg, Germany, 2009; pp. 224–241. [Google Scholar]
- Cao, N.; Wang, C.; Li, M.; Ren, K.; Lou, W. Privacy-preserving multi-keyword ranked search over encrypted cloud data. IEEE Trans. Parallel Distrib. Syst. 2014, 25, 222–233. [Google Scholar] [CrossRef]
- Sun, W.; Wang, B.; Cao, N.; Li, M.; Lou, W.; Hou, Y.T.; Li, H. Verifiable privacy-preserving multi-keyword text search in the cloud supporting similarity-based ranking. IEEE Trans. Parallel Distrib. Syst. 2014, 25, 3025–3035. [Google Scholar] [CrossRef]
- Xia, Z.; Wang, X.; Sun, X.; Wang, Q. A secure and dynamic multi-keyword ranked search scheme over encrypted cloud data. IEEE Trans. Parallel Distrib. Syst. 2016, 27, 340–352. [Google Scholar] [CrossRef]
- Wong, W.K.; Cheung, D.W.-L.; Kao, B.; Mamoulis, N. Secure kNN computation on encrypted databases. In Proceedings of the 2009 ACM SIGMOD International Conference on Management of Data, Providence, RI, USA, 29 June–2 July 2009; ACM: New York, NY, USA, 2009; pp. 139–152. [Google Scholar]
- Fu, Z.; Wu, X.; Guan, C.; Sun, X.; Ren, K. Toward efficient multi-keyword fuzzy search over encrypted outsourced data with accuracy improvement. IEEE Trans. Inf. Forensics Secur. 2016, 11, 2706–2716. [Google Scholar] [CrossRef]
- Huang, Q.; Li, H. An efficient public-key searchable encryption scheme secure against inside keyword guessing attacks. Inf. Sci. 2017, 403, 1–14. [Google Scholar] [CrossRef]
- Borg, C.W.; Dackebro, E. A Comparison of Performance between a CPU and a GPU on Prime Factorization Using Eratosthene’s Sieve and Trial Division. Bachelor’s Thesis, School of Computer Science and Communication (CSC), Stockholm, Sweden, 2017. [Google Scholar]
- Kleinjung, T.; Aoki, K.; Franke, J.; Lenstra, A.; Thomé, E.; Bos, J.; Gaudry, P.; Kruppa, A.; Montgomery, P.; Osvik, D.A. Factorization of a 768-bit RSA modulus. In Proceedings of the 30th Annual Cryptology Conference (CRYPTO), Santa Barbara, CA, USA, 15–19 August 2010; Springer: Berlin/Heidelberg, Germany, 2010; pp. 333–350. [Google Scholar]
- Kiviharju, M. On the fog of RSA key lengths: Verifying public key cryptography strength recommendations. In Proceedings of the 2017 International Conference on Military Communications and Information Systems (ICMCIS), Oulu, Finland, 15–16 May 2017; pp. 1–8. [Google Scholar]
- Koblitz, N.; Menezes, A.J. A survey of public-key cryptosystems. SIAM Rev. 2004, 46, 599–634. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).