Abstract
We introduce a dual-core system with double symmetry, one between the cores, and one along each core, imposed by the spatial modulation of local nonlinearity in the form of two tightly localized spots, which may be approximated by a pair of ideal delta-functions. The analysis aims to investigate effects of spontaneous symmetry breaking in such systems. Stationary one-dimensional modes are constructed in an implicit analytical form. These solutions include symmetric ones, as well as modes with spontaneously broken inter-core and along-the-cores symmetries. Solutions featuring the simultaneous (double) breaking of both symmetries are produced too. In the model with the ideal delta-functions, all species of the asymmetric modes are found to be unstable. However, numerical consideration of a two-dimensional extension of the system, which includes symmetric cores with a nonzero transverse thickness, and the nonlinearity-localization spots of a small finite size, produces stable asymmetric modes of all the types, realizing the separate breaking of each symmetry, and states featuring simultaneous (double) breaking of both symmetries.
1. Introduction
Dual-core couplers represent one of the basic types of optical waveguides [1]. In most cases, the couplers are realized as twin-core optical fibers [2,3] (i.e., in the temporal domain), as well as in double-layer planar waveguides (see, e.g., Reference [4]), i.e., in the spatial domain. Similar to two-core fiber waveguides for optical waves are dual-core cigar-shaped (strongly elongated) traps for matter waves in atomic Bose-Einstein condensates (BECs) [5]. Transmission of matter waves in the latter setting have been studied theoretically [6,7,8], making use of the fact that the Gross-Pitaevskii equation (GPE) for the mean-field wave function of the matter waves in BEC [9] is identical to the propagation equation for the complex amplitude electromagnetic waves in optical waveguides.
If the intrinsic nonlinearity in the parallel-coupled cores is strong enough, the field exchange between them is affected by the intensity of the guided waves [10,11]. This effect may be used as a basis for the design of switching devices [12,13,14,15,16,17,18] and other applications. Further, a fundamental property of nonlinear couplers with mutually symmetric cores is the symmetry-breaking bifurcation, which destabilizes obvious symmetric modes in the dual-core system, and gives rise to asymmetric states. The symmetry breaking was analyzed for temporally uniform states (continuous waves) in dual-core nonlinear optical fibers [19], as well as for solitons in the same system [20,21,22,23,24,25,26,27,28,29]. Some results obtained in this area were summarized in early reviews [30,31], and in a recent review article [32].
The Kerr nonlinearity in the dual-core system gives rise to the symmetry-breaking bifurcation for solitons of the subcritical type, with emerging unstable branches of asymmetric modes going backward (in the direction of decreasing nonlinearity strength), and then turning forward [33]. The branches stabilize themselves at the turning points. On the other hand, the bifurcation for continuous waves, in the same system, is of the supercritical type. It creates stable branches of asymmetric states, which immediately go forward (in the direction of strengthening nonlinearity).
The objective of the present paper is to report a new result for the ordinary and double symmetry breakings in dual-core systems, in which the additional symmetry in each core is introduced by assuming that its intrinsic nonlinearity is subject to the spatial modulation, being concentrated at two mutually symmetric spatially separated points. Such a setting may be implemented in optics, by means of spatially inhomogeneous distribution of a nonlinearity-enhancing dopant in the waveguiding cores [34], as well as in BEC, using Feshbach resonance controlled by laser beams focused at the nonlinearity-concentration spots [35]. In particular, as concerns this phenomenology in quantum gases, spontaneous symmetry breaking between degenerate ground states is an important feature of quantum phase transitions in bosonic systems. The understanding and control of symmetries of quantum systems may lead to realization of new quantum phases, which are subjects of great interest to fundamental and applied studies alike. It is relevant to mention that, while ordinary spontaneous symmetry breaking was considered in various settings [36], effects of double symmetry breaking were previously addressed only in a few cases, see, e.g., Reference [37].
The rest of the paper is organized as follows. The model is introduced in Section 2, where its general analytical solution, available (in an implicit form of coupled cubic equations for four constituent amplitudes, see Equation (11) below) in the case when the nonlinearity in each core is represented by a symmetric pair of ideal delta-functions (as suggested by Reference [38], in terms of the single-core model), is given too. Novel results are reported in Section 3, for states which maintain the spatial symmetry between the two delta-functional spots in each core, while breaking the inter-core symmetry via a subcritical bifurcation. In addition, a simplified model with the nonlinearity-modulation profile represented by a single delta-function is considered in Section 3 too. In Section 4, we address the breaking of the spatial symmetry (between the two nonlinearity-concentration spots) in the case when the symmetry between the cores is kept unbroken, hence the system is reduced to the single-core one. A similar setting was considered before in Reference [38], therefore in Section IV we briefly recapitulate results for this case.
While in all the versions of the model considered in Section 3 and Section 4 broken-symmetry states are unstable, essentially new results are reported in Section 5 for the two-dimensional version of the two-core system, with a small but finite transverse thickness of the channels (cores), and a small but finite width of the two nonlinearity spots. In this case, the system supports stable modes with broken inter-core symmetry, or the intra-core one symmetry between the two nonlinearity spots, as well as stable states which feature double symmetry breaking.
The paper is concluded by Section 6.
2. Model
The purpose of our study is to investigate the interplay of inter- and intra-channel symmetry breaking of soliton modes in a pair of linearly-coupled planar nonlinear optical waveguides, as well as in a Bose-Einstein condensate (BEC) loaded into a dual-cigar-shaped potential trap, with two parallel cores coupled by tunneling of atoms. In either case, the intra-channel symmetry breaking is considered with respect to a symmetric pair of spots at which the local nonlinearity is concentrated. The model of this setting is based on a system of linearly-coupled nonlinear Schrödinger equations, alias Gross-Pitaevskii equations (GPEs), in terms of the BEC realization [9]. In particular, the coupled GPEs can be derived, as usual, from the underlying 3D GPE by means of dimensional reduction to the effective 1D form, under the action of tight transverse confinement [39,40]. The result, written in the scaled form, is the following system of equations for wave functions and in the two tunnel-coupled cores:
where x is the longitudinal coordinate, is the local nonlinearity coefficient, and is the coupling strength. In terms of a dual-core planar optical waveguide, and are amplitudes of the electromagnetic waves in two cores, x is the transverse coordinate, while time t is replaced by the propagation distance (z). Equations (1) conserves the total norm,
(alias the total power, in terms of the optical waveguides) and the Hamiltonian,
where the asterisk stands for the complex conjugate wave function.
As mentioned above, our aim is to consider the setting in which the self-focusing nonlinearity is concentrated, in each core, at two tightly localized spots. To the first approximation, following References [38,41,42,43], this situation may be modelled by introducing the local nonlinearity coefficient taken in the form of a sum of two delta-functions:
with the separation between them fixed to be 2 by means of the remaining scaling invariance of Equation (1). This model, as well as its numerical implementation with -functions replaced by the standard approximation in the form of narrow Gaussians, makes it easier to analyze the double symmetry breaking, between the two cores (represented by and ), and between vicinities of points and .
Stationary solutions with real chemical potential ( is the propagation constant in the model of the optical waveguide) are looked for in the usual form,
and substitute it in Equation (1) to obtain a system of coupled equations for real functions and :
Everywhere except for infinitesimal vicinities of points , Equation (6) is linear, and it may be diagonalized for symmetric and antisymmetric solutions and :
where . Restricting the consideration to localized modes, with , and following the lines of Reference [38], where the analysis was developed for the single-component model, one can write respective solutions to Equation (7) as
The effect of localized nonlinear terms is introduced through the continuity and jump relations for the wave functions and their first derivatives, respectively, at . The former condition allows one to express amplitudes , , and in terms of A, B, C and D, in Equation (8):
Expressions for the jumps of the derivatives, , are obtained by integration of Equation (6) in infinitesimal vicinities of :
The solutions of the system of nonlinear Equation (6), in the form defined by Equations (9) and (11), are the main analytical result of the present work. They are analyzed through the rest of the paper in the context of the twofold spontaneous symmetry breaking in the system’s ground state, between the areas of and , and between components u and v. We show that, depending on parameters of the system, and , solutions of different kinds (co)exist, viz., completely symmetric ones, or solutions which break the symmetry between the channels, or break the parity (symmetry with respect to the origin) in each channel, or, finally, solutions breaking both symmetries (cf. functions presented in Figure 1).
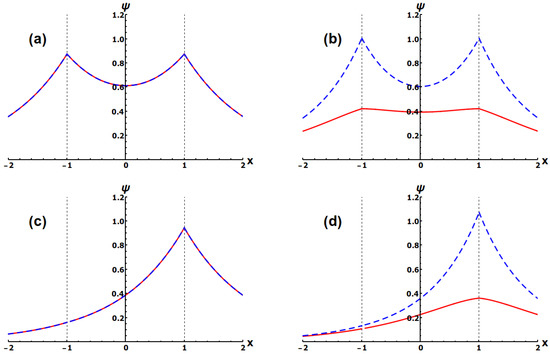
Figure 1.
Possible solutions of (11) plotted as the wavefunctions (red, solid) as well as (blue, dashed) corresponding to the cases when: (a) both symmetries are conserved; (b) the symmetry between both cores is broken; (c) only intra-core-symmetry is broken and (d) both symmetries are broken. These wavefunctions are numerical solutions of (11) for and .
Coupled algebraic Equation (11), to which the use of the ideal delta-functions makes it possible to reduce the solution of Equation (6), cannot be solved analytically (unlike the explicitly solution which is possible in the single-component model [38]). It is, nevertheless, relatively easy to find all physically relevant solutions of Equation (11) numerically, and thus classify all the solutions according to their symmetry.
In general, there are solutions, but many of them are highly degenerate. We summarize the results in the schematic form in Figure 2, in the parameter plane of linear coupling and shifted chemical potential . Ground-state solutions with both symmetries broken were found only in the region painted in pink. Next, as shown below, only above the horizontal line of one can find stationary solutions with the broken symmetry, and only above the slanted nearly straight line, originating from the origin, there exist solutions with the symmetry broken between components u and v. Below we derive conditions that predict these borders, and illustrate specific cases for selected values of , realizing scenarios of the spontaneous breaking of both symmetries. Note, however, that in Figure 2 there is also a region where only the solutions with preserving full symmetry or with both symmetries broken exist. In this region there are no solutions with only one symmetry broken.
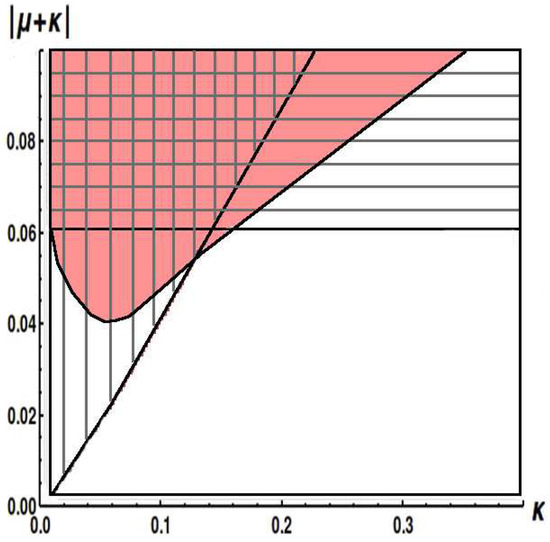
Figure 2.
The phase diagram, in the plane, illustrating regions where solutions of different types exist. Solutions with unbroken symmetry exist everywhere. Above horizontal line , in the horizontally shaded region, one additionally finds solutions with broken intra-channel symmetry. In the vertically shaded region, one observes solutions with broken symmetry between the channels (u and v). In the pink region, there exists solutions with both symmetries simultaneously broken. Note that there is a small triangular region where only fully symmetric solutions and ones with both symmetries broken can be found (the unshaded pink area).
In the following we fixed the value of , and by varying the chemical potential, we sampled solutions along vertical lines in Figure 2. Our results are outlined in Figure 3 and Figure 4, for and , respectively. In order to describe these figures we introduce asymmetry parameters and . The asymmetry between the u and v components is characterized by parameter
and asymmetry with respect to the parity transformation, , is quantified by
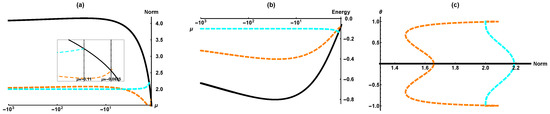
Figure 3.
Stationary states for a fixed value of the inter-core coupling constant, . Panels (a) and (b): the energy and norm of the fully symmetric states (black), ones with broken inter-core symmetry (orange), and states with broken symmetry in each channel (blue), as functions of the chemical potential. The inset in (a) displays details of the emergence of the asymmetric states from the symmetric one. Panel (c) displays the corresponding symmetry-breaking bifurcations by means of asymmetry parameters and (the orange and blue curves, respectively, see Equations (12) and (13), plotted versus the total norm.
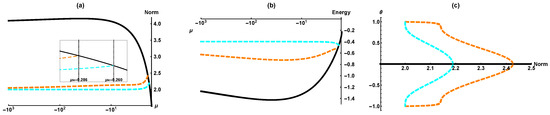
Figure 4.
Stationary states for fixed value of . Panels (a) and (b): energy and norm of the symmetric state (black), states with broken inter-core symmetry (orange), and states with broken symmetry in each channel (blue), vs. the chemical potential. The inset in (a) displays details of the emergence of the asymmetric states from the symmetric one. In panel (c), the corresponding symmetry-breaking bifurcations are shown by means of asymmetry parameters and (the orange and blue curves, respectively, see Equations (12) and (13), plotted versus the total norm.
In Figure 3, we vary to the point of crossing the slanted line in Figure 2, at . This is the border line above which (unstable) states featuring the asymmetry between the cores appear, only symmetric and antisymmetric states existing below this border. These asymmetric solutions are shown by the dashed orange line. Upon further decreasing the chemical potential, we eventually enter the region where new solutions appear, with parity symmetries broken, which are represented by the blue dashed line in Figure 3. Panels (a) and (b) show the norm and energy of these states as functions of the chemical potential, while panel (c) shows the asymmetry parameters and (see Equations (12) and (13) as functions of the norm, revealing that both symmetry-breaking bifurcations are of the subcritical [33] type.
In Figure 4 the black curve of symmetric states traverses the horizontal line into the region where (unstable) solutions, asymmetric with respect to , appear (the blue dashed lines), and the second symmetry is broken at , to produce the states with inter-core symmetry broken (orange lines). Again, both bifurcations have the subcritical character.
In the next two sections we investigate asymmetry solutions, to identify the respective bifurcations. First we restrict the analysis to the class of solutions that remain symmetric (or antisymmetric) with respect to in each core. Within this class, we consider the possibility of the symmetry breaking between the cores. Next, we summarize findings obtained in previous works for the single-component model, which corresponds to the setting which maintains the symmetry or antisymmetry between the cores (). In the case of the spatial symmetry breaking (), the model predicts a subcritical type of the spontaneous symmetry breaking. In that context, it is interesting to investigate to what extent the structure of the model affects the transition to the asymmetric states. To this end, we consider various forms of the nonlinearity modulation patterns, including an additional linear potential. Before addressing the model with the double delta function, as defined by Equation (4), we first consider the profile of with a single delta function.
3. Solutions Preserving the Spatial Symmetry in the Cores
3.1. The Basic Model
The first type of symmetry breaking, which was not studied in previous works, occurs under the assumption that the wave function remains spatially symmetric (even) or antisymmetric (odd), with respect to , in each core, while the wave functions in the two cores may become different, . As concerns coefficients in expression (8) for the solutions, this type of localized state is ensured by setting and . To obtain fully symmetric states, we choose ; then, it is straightforward to obtain from Equation (11) a previously known solution [38],
Likewise, for antisymmetric states we assume to obtain
Searching for states asymmetric between the parallel-coupled cores, we assume that all coefficients and are different from zero. In this case, solutions of Equation (11) are
To find the symmetry-breaking bifurcation point, we inspect the second expression in Equation (16), equating the numerator under the square root to zero. This leads to
which is the main result of this section. It corresponds to the almost straight slanted border line in Figure 2. We stress that, in the present model, all states besides totally symmetric ones are unstable. In particular, the states that exist above the line defined by Equation (17), which are asymmetric with respect to the two cores (), are unstable. Actually, this is the property of this particular model. In Section 5 we introduce a two-dimensional model, in which broken-symmetry solutions are stable.
We supplement this section by the following subsection, revealing the type of the symmetry-breaking bifurcation that one may expect dealing with models consisting of two identical cores and various nonlinearity-modulation patterns or linear potentials.
3.2. Review of Related Models
We first consider the case of the simplified spatial modulation with
representing one singularity instead of two. In this case, exact solution (8) is replaced by
The conditions for the derivative jump at are and , cf. Equation (10). This leads to the system of coupled cubic equations
cf. Equation (11), which can be easily solved. For the asymmetric solution, with and , the amplitudes are
The symmetry-breaking bifurcation point is derived by setting in Equation (21), which yields
Note that when the inter-core coupling is negligible, i.e. , the asymmetric states have , hence they exist everywhere in the trapped-mode regime. On the other hand, the symmetry breaking does not take place for , the solution keeping the form of .
Amplitudes of the symmetric and antisymmetric states ( and ) can be easily found too. In particular, amplitudes of the symmetric state amount to and , and norm (2) of symmetric and antisymmetric states is . The norm of the asymmetric state is
with limit value . The norms of the symmetric and asymmetric modes are plotted, as functions of , in Figure 5a.

Figure 5.
Norm (a) and energy (b) of the symmetric, antisymmetric and asymmetric states as a function of the chemical potential in the model with the nonlinearity modulation in the form of the single delta-function, as defined by Equation (18). Solid and dashed lines denote stable and unstable states, respectively.
The value of the energy (Hamiltonian), defined in Equation (3), can also be calculated for all the states under the consideration, a general expression being
In the special cases of the symmetric, antisymmetric and asymmetric states the corresponding energies are and , and
Finally, asymmetry coefficient (12), which measures the norm imbalance between the cores, is calculated for solution (21) as
It is plotted versus the chemical potential and norm in Figure 6. Note that in the limit of All the asymmetric states are unstable, in the model based on the single-delta modulation format (18).
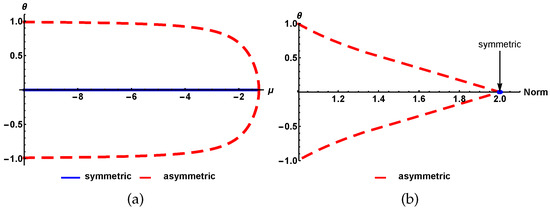
Figure 6.
Asymmetry parameter , defined as per Equation (24), as a function of the chemical potential (a) and total norm (b). Solid and dashed lines correspond to stable and unstable states, respectively.
Numerical investigation was also performed for similar models with the single delta function replaced by a finite-width Gaussian. In this case, the symmetry-breaking bifurcation keeps the subcritical form even in the case of a broad Gaussian, cf. Figure 6b. This finding is in agreement with the fact that, in various models of dual-core couplers with the uniform self-focusing nonlinearity, symmetry-breaking bifurcations for solitons are subcritical too [21,22,23,24,25,26,33,44]. Additionally, we have investigated the model of the coupled cores with the uniform self-focusing nonlinearity, combined with a local defect represented by a linear-potential well (not shown here in detail). In this case, we have found the subcritical transition in shallow wells, regardless of their width, which carry over into a supercritical transition when the well’s depth exceeds a certain critical value.
4. The Case of the Symmetry Maintained between the Cores
Here we present a short summary of results obtained when we impose the condition of the symmetry between the cores, i.e. , comparing this case to the study presented in Reference [38], where the spontaneous symmetry breaking in was due to the action of the nonlinear potential with two symmetric minima. When the respective modulation pattern was taken as per Equation (4), a fully analytical solution was obtained for symmetric, antisymmetric, and asymmetric states, the respective symmetry-breaking bifurcation was ultimately subcritical, with the branches of asymmetric localized states never turning in the forward direction.
In terms of Equation (11), the cases of and correspond, respectively, to setting and . In the former (symmetric) case the remaining equations for amplitudes A and B rare
To treat the antisymmetric, one may replace , and . The respective solutions are
and an antisymmetric form (i.e. antisymmetry in each channel)
The norm of these solutions is
where + and − correspond to the symmetric and antisymmetric ones, respectively. Both solutions are characterized by the same asymptotic limit, . The chemical potential at the bifurcation point is evaluated, for the symmetric solution, (in agreement with [38]) as
while the antisymmetric one undergoes no bifurcation. Likewise, the amplitudes for asymmetric states can be found analytically,
and the bifurcation point derived from this solution is identical to one given by Equation (29).
In the case when symmetry is imposed, we can compare our results with the more realistic model of with the Gaussian modulation format [38],
where the modulated nonlinearity coefficient is subject to the normalization condition It is found that, at a certain value of width a of the Gaussian pattern (31), a transition to the supercritical type of the symmetry-breaking bifurcation takes place. On the other hand, if we consider systems with uniform self-focusing nonlinearity in the presence of a linear potential representing a double potential well [8,45,46], spontaneous symmetry breaking occurs too, but it always has the supercritical character.
5. Double Symmetry Breaking in Two Dimensions
In the previous sections we considered solutions of coupled one-dimensional systems with the nonlinearity concentrated at two narrow spots, finding stationary states with one of the symmetries broken (either between the parallel-coupled cores, or between the two nonlinear spots in the cores), or even the situation when both underlying symmetries are broken in the stationary state. In most cases, however, and in all cases when the nonlinearity modulations is based on the pair of delta-functions (Equation (4)), states with broken symmetry were unstable. One can argue that the model with the ideal delta-functions is degenerate, which is reflected in the character of the stationary states. In this section, we do not consider bifurcations and spontaneous symmetry breaking for settings with the Gaussian nonlinearity-modulation profiles, replacing the two delta-functions. Instead of that, in this section we focus on a two-dimensional model with localized nonlinearity, showing that in this case states with broken symmetries may be stable. The setting that we address is based on the following GPE,
As displayed in Figure 7, potential creates the double-well (double-trough) trapping potential acting in the x direction, while nonlinearity coefficient is concentrated at four localized spots (striped in the figure). This model may be considered as a two-dimensional extension of the one-dimensional model introduced above.
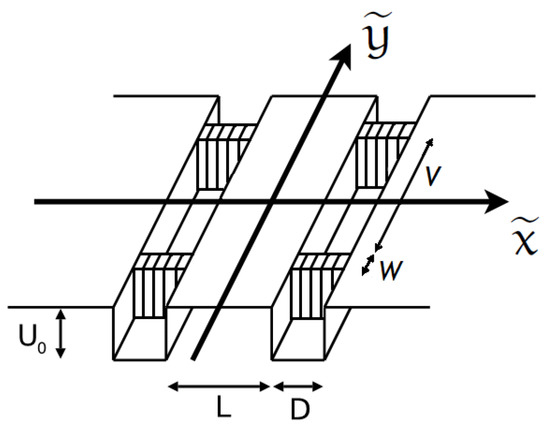
Figure 7.
The combination of the linear-potential double-trough trapping acting along the x direction, and the localized nonlinearity pattern shown by the striped structure. We address double symmetry breaking of two-dimensional solitons in this setting.
We used the imaginary-time method [47] to find ground states of the system. Their stability was then confirmed by simulating the real time evolution (using the split-step Fourier method). We have observed four types of stable solitons, which are shown in Figure 8. The figure confirms that, depending on the value of the norm, stable states with all possible combinations of the asymmetry can be produced. A general conclusion, suggested by the systematic simulations, is that, in the model with weaker coupling between the cores, it is easier to find stable states with the broken symmetry between the cores. With the increase of the norm, states with both symmetries broken are found too. On the other hand, the symmetry between the nonlinearity-concentration spots in both cores in broken first (in the setting with the nonlinearity spots) is set closer to each other. In particular, values of parameters in Figure 8 are: in Figure 8a,c,e, , , , , and the norm in the increasing order, , , and , respectively. Similarly, in Figure 8b,d,f, the parameters are , , , , and norms are, respectively, , 4, and . The depth of linear potential and the (constant) value of the nonlinear coupling can be rescaled. The strength of the interaction is now contained in the norm of the wavefunction.
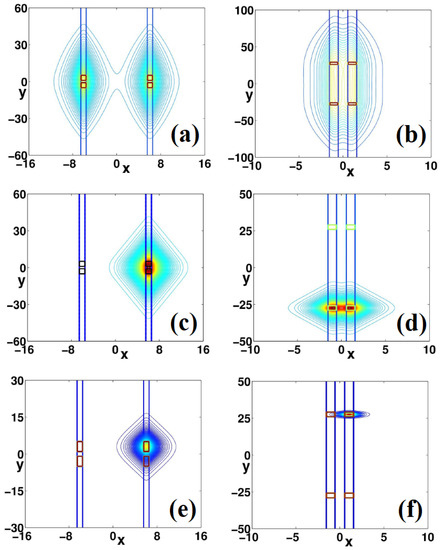
Figure 8.
Contour plots of the local density illustrating stable two-dimensional self-trapped states. Panels (a) and (b): fully symmetric ones. (c) and (d): States with broken symmetry between the two cores, and between the two nonlinear spots, respectively. States featuring the breaking of both symmetries are displayed in panels (e) and (f).
In the real-time simulations, we added small perturbations to check if the input states maintain their initial shapes after long evolution. All of the above states still survive, at least up to .
Our two-dimensional model surely deserves further investigation, including the identification of bifurcation diagrams, regions of stability of various types of solutions, and studies of dynamical behavior, including collisions between solitons. Detailed results addressing these issues will be reported elsewhere.
6. Conclusions
The objective of this work is to investigate the phenomenology of spontaneous symmetry breaking in the class of dual-core systems featuring the additional spatial symmetry in each core, induced by the nonlinearity-modulation pattern in the form of two tightly localized spots, which may be approximated, in some cases, by ideal delta-functions. In this case, solutions for stationary one-dimensional states can be obtained in the implicit analytical form, represented by coupled cubic equations for constituent amplitudes. The analysis makes it possible to construct modes with broken inter-core and intra-core symmetries, as well as ones featuring the double breaking of both symmetries. While all such asymmetric modes turn out to be unstable, the consideration of the most interesting two-dimensional version of the system, with a small transverse thickness of each core, and a small finite size of the nonlinearity-localization spots, reveals stable asymmetric states of all the types, including ones realizing the double symmetry breaking.
As an extension of the analysis, it may be interesting to construct stationary patterns in which the complex wave function, peaked at the nonlinearity-localization spots, features a phase structure which corresponds to trapped vorticity, following the pattern of Reference [48]. The existence and stability of such vortex modes, with unbroken or broken symmetries, is a challenging issue.
Author Contributions
M.T. and B.A.M. have introduced the model, and performed the analytical investigation. A.R., N.V.H. and K.B.Z. have performed numerical calculations. All the authors took part in formulating the results and drafting the paper.
Acknowledgments
The work was supported by the Polish National Science Centre 2016/22/M/ST2/00261 (A. Ramaniuk and M. Trippenbach.) K.B.Z. acknowledges support from the National Science Center of Poland through Project FUGA No. 2016/20/S/ST2/00366. N.V.H. was supported by Vietnam National Foundation for Science and Technology Development (NAFOSTED) under grant number 103.01-2017.55.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Huang, W.P. Coupled-mode theory for optical waveguides: An overview. J. Opt. Soc. Am. A 1994, 11, 963–983. [Google Scholar] [CrossRef]
- Digonnet, M.J.F.; Shaw, H.J. Analysis of a tunable single-mode optical fiber coupler. IEEE J. Quant. Electr. 1982, 18, 746–754. [Google Scholar] [CrossRef]
- Trillo, S.; Wabnitz, S.; Wright, E.M.; Stegeman, G.I. Soliton switching in fiber nonlinear directional couplers. Opt. Lett. 1988, 13, 672–674. [Google Scholar] [CrossRef] [PubMed]
- Harsoyono, H.; Siregar, R.E.; Tjia, M.O. A study of nonlinear coupling between two identical planar waveguides. J. Nonlinear Opt. Phys. Mater. 2001, 10, 233–247. [Google Scholar] [CrossRef]
- Strecker, K.E.; Partridge, G.B.; Truscott, A.G.; Hulet, R.G. Bright matter wave solitons in Bose-Einstein condensates. New J. Phys. 2003, 5, 73.1. [Google Scholar] [CrossRef]
- Gubeskys, A.; Malomed, B.A. Symmetric and asymmetric solitons in linearly coupled Bose-Einstein condensates trapped in optical lattices. Phys. Rev. A 2007, 75, 063602. [Google Scholar] [CrossRef]
- Salasnich, L.; Malomed, B.A.; Toigo, F. Competition between the symmetry breaking and onset of collapse in weakly coupled atomic condensates. Phys. Rev. A 2010, 81, 045603. [Google Scholar] [CrossRef]
- Matuszewski, M.; Malomed, B.A.; Trippenbach, M. Spontaneous symmetry breaking of solitons trapped in a double-channel potential. Phys. Rev. A 2007, 75, 063621. [Google Scholar] [CrossRef]
- Pitaevskii, L.; Stringari, S. Bose-Einstein Condensation; Clarendon: Oxford, UK, 2003. [Google Scholar]
- Jensen, S.M. The nonlinear coherent coupler. IEEE J. Quant. Electr. 1982, 18, 1580–1583. [Google Scholar] [CrossRef]
- Maier, A.A. Optical transistors and bistable devices utilizing nonlinear transmission of light in systems with unidirectional coupled waves. Sov. J. Quant. Electron. 1982, 12, 1490–1494. [Google Scholar] [CrossRef]
- Friberg, S.R.; Silberberg, Y.; Oliver, M.K.; Andrejco, M.J.; Saifi, M.A.; Smith, P.W. Ultrafast all-optical switching in dual-core fiber nonlinear coupler. Appl. Phys. Lett. 1987, 51, 1135–1137. [Google Scholar] [CrossRef]
- Friberg, S.R.; Weiner, A.M.; Silberberg, Y.; Sfez, B.G.; Smith, P.S. Femtosecond switching in dual-core-fiber nonlinear coupler. Opt. Lett. 1988, 13, 904–906. [Google Scholar] [CrossRef] [PubMed]
- Heatley, D.R.; Wright, E.M.; Stegeman, G.I. Soliton coupler. Appl. Phys. Lett. 1988, 53, 172–174. [Google Scholar] [CrossRef]
- Królikowski, W.; Kivshar, Y.S. Soliton-based optical switching in waveguide arrays. J. Opt. Soc. Am. B 1996, 13, 876–887. [Google Scholar] [CrossRef]
- Tsang, S.C.; Chiang, K.S.; Chow, K.W. Soliton interaction in a two-core optical fiber. Opt. Commun. 2004, 229, 431–439. [Google Scholar] [CrossRef]
- Uzunov, I.M.; Muschall, R.; Gölles, M.; Kivshar, Y.S.; Malomed, A.; Lederer, F. Pulse switching in nonlinear fiber directional couplers. Phys. Rev. E 1995, 51, 2527–2537. [Google Scholar] [CrossRef]
- Lederer, F.; Stegeman, G.I.; Christodoulides, D.N.; Assanto, G.; Segev, M.; Silberberg, Y. Discrete solitons in optics. Phys. Rep. 2008, 463, 1–126. [Google Scholar] [CrossRef]
- Snyder, A.W.; Mitchell, D.J.; Poladian, L.; Rowland, D.R.; Chen, Y. Physics of nonlinear fiber couplers. J. Opt. Soc. Am. B 1991, 8, 2102–2112. [Google Scholar] [CrossRef]
- Wright, E.M.; Stegeman, G.I.; Wabnitz, S. Solitary-wave decay and symmetry-breaking instabilities in two-mode fibers. Phys. Rev. A 1989, 40, 4455. [Google Scholar] [CrossRef]
- Paré, C.; Florjańczyk, M. Approximate model of soliton dynamics in all-optical fibers. Phys. Rev. A 1990, 41, 6287–6295. [Google Scholar] [CrossRef] [PubMed]
- Maimistov, A.I. Propagation of a light pulse in nonlinear tunnel-coupled optical waveguides. Kvantovaya Elektron. (Moscow) 1991, 18, 758–761. [Google Scholar] [CrossRef]
- Chu, P.L.; Malomed, B.A.; Peng, G.D. Soliton switching and propagation in nonlinear fiber couplers: Analytical results. J. Opt. Soc. Am. B 1993, 10, 1379–1385. [Google Scholar] [CrossRef]
- Akhmediev, N.; Ankiewicz, A. Novel soliton states and bifurcation phenomena in nonlinear fiber couplers. Phys. Rev. Lett. 1993, 70, 2395–2398. [Google Scholar] [CrossRef] [PubMed]
- Soto-Crespo, J.M.; Akhmediev, N. Stability of the soliton states in a nonlinear fiber coupler. Phys. Rev. E 1993, 48, 4710–4715. [Google Scholar] [CrossRef]
- Malomed, B.A.; Skinner, I.M.; Chu, P.L.; Peng, G.D. Symmetric and asymmetric solitons in twin-core nonlinear optical fibers. Phys. Rev. E 1996, 53, 4084–4091. [Google Scholar] [CrossRef]
- Trillo, S.; Stegeman, G.; Wright, E.; Wabnitz, S. Parametric amplification and modulational instabilities in dispersive nonlinear directional couplers with relaxing nonlinearity. J. Opt. Soc. Am. B 1989, 6, 889–900. [Google Scholar] [CrossRef]
- Tasgal, R.S.; Malomed, B.A. Modulational instabilities in the dual-core nonlinear optical fiber. Phys. Scr. 1999, 60, 418–422. [Google Scholar] [CrossRef]
- Chiang, K.S. Intermodal dispersion in two-core optical fibers. Opt. Lett. 1995, 20, 997–999. [Google Scholar] [CrossRef] [PubMed]
- Romagnoli, M.; Trillo, S.; Wabnitz, S. Soliton switching in nonlinear couplers. Opt. Quant. Electron. 1992, 24, S1237–S1267. [Google Scholar] [CrossRef]
- Malomed, B.A. Variational methods in fiber optics and related fields. Progr. Opt. 2002, 43, 71–193. [Google Scholar]
- Malomed, B.A. Solitons and nonlinear dynamics in dual-core optical fibers. In Handbook of Optical Fibers; Peng, G.-D., Ed.; Springer: Berlin, Germany, 2018. [Google Scholar]
- Iooss, G.; Joseph, D.D. Elementary Stability and Bifurcation Theory; Springer: Berlin, Germany, 1990. [Google Scholar]
- Hukriede, J.; Runde, D.; Kip, D. Fabrication and application of holographic Bragg gratings in lithium niobate channel waveguides. J. Phys. D 2003, 36, R1. [Google Scholar] [CrossRef]
- Clark, L.W.; Ha, L.; Xu, C.; Chin, C. Quantum dynamics with spatiotemporal control of interactions in a stable Bose-Einstein condensate. Phys. Rev. Lett. 2015, 115, 155301. [Google Scholar] [CrossRef] [PubMed]
- Malomed, B.A. (Ed.) Spontaneous Symmetry Breaking, Self-Trapping, and Josephson Oscillations; Springer: Berlin/Heildelberg, Germany, 2013; ISBN 978-3-642-21206-2. [Google Scholar]
- Li, Y.; Malomed, B.A.; Feng, M.; Zhou, J. Double symmetry breaking of solitons in one-dimensional virtual photonic crystals. Phys. Rev. A 2011, 83, 053832. [Google Scholar] [CrossRef]
- Mayteevarunyoo, T.; Malomed, B.A.; Dong, G. Spontaneous symmetry breaking in a nonlinear double-well structure. Phys. Rev. A 2008, 78, 053601. [Google Scholar] [CrossRef]
- Salasnich, L.; Parola, A.; Reatto, L. Effective wave equations for the dynamics of cigar-shaped and disk-shaped Bose condensates. Phys. Rev. A 2002, 65, 043614. [Google Scholar] [CrossRef]
- Mateo, A.M.; Delgado, V. Effective mean-field equations for cigar-shaped and disk-shaped Bose-Einstein condensates. Phys. Rev. A 2008, 77, 013617. [Google Scholar] [CrossRef]
- Sakaguchi, H.; Malomed, B.A. Symmetry breaking of solitons in two-component Gross-Pitaevskii equations. Phys. Rev. E 2011, 83, 036608. [Google Scholar] [CrossRef] [PubMed]
- Acus, A.; Malomed, B.A.; Shnir, Y. Spontaneous symmetry breaking of binary fields in a nonlinear double-well structure. Physica D 2012, 241, 9872. [Google Scholar] [CrossRef]
- Zhou, X.; Zhang, S.; Zhou, Z.; Malomed, B.A.; Pu, H. Bose-Einstein condensation on a ring-shaped trap with nonlinear double-well potential. Phys. Rev. A 2012, 85, 023603. [Google Scholar] [CrossRef]
- Hung, N.V.; Zin, P.; Trippenbach, M.; Malomed, B.A. Two-dimensional solitons in media with stripe-shaped nonlinearity Modulation. Phys. Rev. E 2010, 82, 046602. [Google Scholar] [CrossRef] [PubMed]
- Milburn, G.J.; Corney, J.; Wright, E.M.; Walls, D.F. Quantum dynamics of an atomic Bose-Einstein condensate in a double-well potential. Phys. Rev. A 1997, 55, 4318–4324. [Google Scholar] [CrossRef]
- Smerzi, A.; Fantoni, S.; Giovanazzi, S.; Shenoy, S.R. Quantum coherent atomic tunneling between two trapped Bose-Einstein condensates. Phys. Rev. Lett. 1997, 79, 4950–4953. [Google Scholar] [CrossRef]
- Chiofalo, M.L.; Succi, S.; Tosi, M.P. Ground state of trapped interacting Bose-Einstein condensates by an explicit imaginary-time algorithm. Phys. Rev. E 2000, 62, 7438–7444. [Google Scholar] [CrossRef]
- Malomed, B.A.; Kevrekidis, P.G. Discrete vortex solitons. Phys. Rev. E 2001, 64, 026601. [Google Scholar] [CrossRef] [PubMed]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).