Abstract
In this article, a nonlinear adaptive fuzzy backstepping controller combined with an adaptive backstepping controller and an adaptive fuzzy controller is proposed for real-time tracking control of an electro-hydraulic force loading system. Firstly, a nonlinear dynamic model for the electro-hydraulic force loading system is built with consideration of parameter uncertainties and external disturbances. Then, the adaptive backstepping controller is employed to obtain desired control output for the force loading control system considering parameter uncertainties and external disturbances. Furthermore, an adaptive fuzzy control scheme is designed to adjust uncertain control parameters based on adaptive fuzzy system to cope with the chattering condition that results from the overwhelming external disturbances. The stability of the overall system with the proposed control algorithm can be proved by Lyapunov stability theory. Finally, an electro-hydraulic force loading experimental system with xPC rapid prototyping technology is carried out to verify the effectiveness of the proposed nonlinear adaptive fuzzy backstepping controller. Experimental results verify that the proposed control method exhibit excellent performances on force loading tracking control of the electro-hydraulic force loading experimental system compared with a conventional proportional-integral-derivative (PID) controller with velocity feedforward and adaptive backstepping control schemes.
1. Introduction
An electro-hydraulic force loading system (EHFLS) is widely utilized to artificially simulate the force loading exerted on a test specimen to evaluate original performances and potential problems of the test specimen owing to its superiorities, including fast response, large force loading, high precision, and high power-to-weight ratio [1,2,3]. Therefore, the EHFLS is extensively employed in civil engineering structures [4], automobile industry [5], seismic testing [6], and structural fatigue testing [7].
The construction of the EHFLS is illustrated in Figure 1. The EHFLS is composed of a platform with a specimen moving on two linear rails in horizontal direction, which connects a force loading generate electro-hydraulic actuator and a disturbance generate electro-hydraulic actuator by four spherical hinges with low friction. The objective of the EHFLS is to ensure that the uniaxial force loading generate electro-hydraulic actuator can track the desired force loading instruction accurately. However, inherent nonlinearities and parameters uncertainties in the EHFLS make the traditional control algorithms inaccessible simultaneously, such as servo-valve flow-pressure nonlinearity, actuator frictions, and spherical joint clearances [8]. Furthermore, external disturbances have extremely negative impacts on the force loading tracking accuracy.
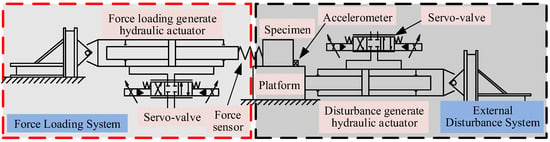
Figure 1.
Structure of the EHFLS.
The force loading tracking performance of the EHFLS, in the presence of parameter uncertainties and external disturbances, has been extensively studied by scholars and various methods are presented. Alleyne and Liu [9] evaluated a common Proportional-Integral-Derivative (PID) controller for a particular force tracking control, which showed that this simple solution method is deficient for force tracking resulting from fundamental limitations of the control parameters. Aiming at overcoming the drawback of the traditional PID controller, Truong and Ahn [10] designed a fuzzy PID controller, which was composed of a grey prediction model and a tuning algorithm. Kim [11] applied the quantitative feedback theory algorithm to improve force loading tracking performance of a dynamic road simulator, which was applicable to an uncertain hydraulic plant system. An inverse model controller with a damping compensator and an inverse-model-observer based on a velocity feedforward compensator was presented for the force loading system of a flight simulator by Zhao and Shen [12,13].
Although above-mentioned control algorithms are able to improve the force loading tracking performance of the EHFLS, they have a limitation on coping with parameter uncertainties of nonlinear dynamic model of the EHFLS and external disturbances in working condition, which have extremely negative impacts on the force loading tracking performance, especially as the run time increases. In order to reduce the negative influences of parameter uncertainties and external disturbances in nonlinear systems, many control approaches are presented. In order to decrease a surplus force, a feedforward force control algorithm combined with a modified inverse model compensator and a velocity feedforward compensator is employed by Shen [14]. An offline designed feedback controller and an online adaptive compensator was designed for an electro-hydraulic force servo system in literature [15] to improve the force tracking performance with consideration of varying dynamics. Backstepping technology is one of the most popular control schemes for nonlinear systems, which has been widely employed to ensure the global stability, tracking performances, and transient characteristics [16] based on Lyapunov function. Prut and Suwat [17] designed a nonlinear controller to guarantee the force tracking performance of an electro-hydraulic servo system by employing the backstepping approach. Yao [18] proposed a high dynamic feedback linearization controller with the help of the backstepping technology to ensure an excellent tracking performance even with high-frequency tracking demand. Park [19] proposed a backstepping controller for synchronization of Genesio chaotic systems. In literature [20], a nonlinear robust controller combined with an extended state observer using the backstepping method was presented for a hydraulic system with a position tracking controller.
However, system uncertainties and particularly parameters uncertainties cannot be solved only with the backstepping controller, thus, an adaptive controller was employed to improve the system tracking performance with the common backstepping controller. In order to effectively cope with various nonlinearity effects, an adaptive model compensator with an accurate online parameter estimation was presented by Chen [21]. Su [22] proposed a constrained adaptive robust controller to stabilize the system amplitude with consideration of parameter uncertainties and external disturbances. Wang [23] proposed a nonlinear adaptive control method for force loading tracking control of an electro-hydraulic load simulator in the presence of an actuator’s motion destabilization and dynamic model nonlinearity due to parameter uncertainties. A nonlinear adaptive robust controller based on a discontinuous projection technology for a hydraulic load system was proposed in literature [24], in which the controller simplification process was also discussed for easier engineering application purposes. An adaptive robust backstepping force control algorithm was developed by Chen et al. [25] to cope with the negative influences of parameter uncertainties of a human–machine interaction system to minimize the interaction force external disturbance was given. Wang [26] proposed a robust adaptive backstepping controller (ABC) combined with a two-loops controller, which was designed by the backstepping technology to eliminate dynamic model nonlinearities, system coupling, fast time-varying characteristics, and great parameter uncertainties in atmospheric density. In order to ensure the asymptotic tracking performance of a hydraulic rotary actuator, Yao [27] combined a robust integral of the sign of the error controller and an adaptive controller by employing the backstepping method with consideration of system uncertainties, such as parametric uncertainties and nonlinear frictions. An output feedback signal based on a nonlinear adaptive robust controller was presented in literature [28] to cope with adaptive robust control problem of an aircraft load emulator with high performance requirements in the presence of modeling errors, parameter uncertainties, and system nonlinearities.
Fuzzy control has achieved great practical successes in nonlinear systems. A sliding mode backstepping controller based on a fuzzy integral controller was designed in literature [29], in which a fuzzy control scheme is employed to ensure the displacement tracking performance. Wei et al. [30] used an extended fuzzy disturbance observer combined with a nonlinear cascade controller to achieve motion control with the high-performance of a hydraulic press. Fuzzy control research has been investigating an adaptive controller. A high-performance nonlinear adaptive controller combined with an adaptive fuzzy self-recurrent wavelet neural network controller with variable structure and a complementary controller was presented by Wang et al. [31] in order to perfect the torque tracking performance of the electric load simulator. A direct tracking control algorithm via the backstepping and fuzzy logic system was proposed in literature [32] for a nonlinear strict-feedback system in the presence of parameter uncertainties and dynamic disturbances. Rong et al. [33] introduced a new meta-cognitive fuzzy-neural mode to construct the uncertain system dynamics, based on which an adaptive backstepping controller was proposed. Paolo Mercorelli [34,35] dealt with an adaptive control strategy based on the resonance concept to minimize the regulation energy of a new generation of actuators for intake valves of the camless engines. Magdi [36] explained the principles of fuzzy systems in some depth together with information useful in realizing them within computational processes.
In this article, in order to realize force loading tracking accuracy of the EHFLS, a nonlinear dynamic model of the EHFLS is established with consideration of both parameter uncertainties and external disturbances. Then, an adaptive backstepping controller is employed to acquire the control output for the force loading tracking. Taking the overwhelming external disturbances into consideration, an adaptive fuzzy controller is applied to improve the chattering condition caused by the overwhelming external disturbances to strengthen the robustness of the EHFLS.
The contributions are organized as follows: Section 2 shows the experimental setup of the utilized electro-hydraulic force loading experimental system and dynamic model of the EHFLS and its hydraulic cylinder are firstly described. Section 3 presents the designed controller in this work for the EHFLS in detail. Section 4 presents a series of experimental results that are carried out on the electro-hydraulic force loading control experimental system to verify the availability of the proposed controller. Section 5 depicts the main points and contributions.
2. Experimental Set Up and Dynamic Model
2.1. Experimental Setup of the EHFLS
Figure 2 depicts an electro-hydraulic force loading control experimental system, which is utilized to implement the proposed nonlinear adaptive fuzzy backstepping controller designed in this paper and experiments on the EHFLS. The experimental system is composed of a 0.8 m × 0.8 m platform installed on the base that can move in a horizontal direction owing to two linear guides, a specimen fixed on the platform, two electro-hydraulic actuators consisting of 70 mm cylinder bores and 50 mm piston rods that are driven by two Moog, Inc. (East Aurora, NY, USA) manufactured servo-valves (G761-3004), and a hydraulic oil supply system for the two electro-hydraulic actuators. In order to measure feedback signals for force loading control of the EHFLS, a series of sensors are employed. To measure displacements of the two electro-hydraulic actuators, two linear variable differential transformers (LVDTs) are attached to piston rods and shell structures of the two electro-hydraulic actuators. In order to obtain real-time force loading inflicted on the specimen, a force sensor is fixed between the force loading generate hydraulic cylinder and a spherical hinge. An accelerometer attached to the platform is employed to measure the real-time acceleration output response signal.
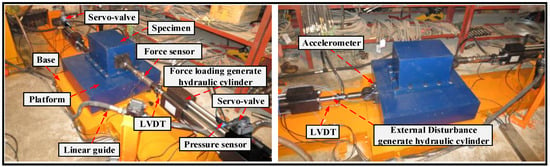
Figure 2.
Electro-hydraulic force loading control experimental system.
The control schematic diagram of the electro-hydraulic force loading experimental system exploiting xPC rapid prototyping technology is illustrated in Figure 3. The control hardware for the electro-hydraulic force loading control experimental system includes an ADVANTECH IPC-610 controller to realize the proposed controller, a digital to analog (D/A) board ACL-6126, an analog to digital (A/D) board PCI-1716, and a host computer for real-time monitoring and other auxiliary accessories. The real-time analog control output signals that are produced by the 12-bit D/A board ACL-6126 and processed by signal modular are sent to the two servo-valves to control the two electro-hydraulic actuators. The 16-bit A/D board PCI-1716 transforms feedback analog signals measured by sensors to digital signals and then sends the acquired digital signals to the controller after converting in signal modular. The procedure of the proposed control algorithm is programmed in MATLAB/Simulink (version, Manufacturer, Mathworks, Natick, MA, USA) and then compiled by the Microsoft Visual C++ 6.0 (Redmond, WA, USA) on the host computer. Finally, the compiled program is downloaded to the xPC target in the ADVANTECH IPC-610 controller by the Ethernet for real-time control. The sample time of the controller for the EHFLS is set to 1 ms.
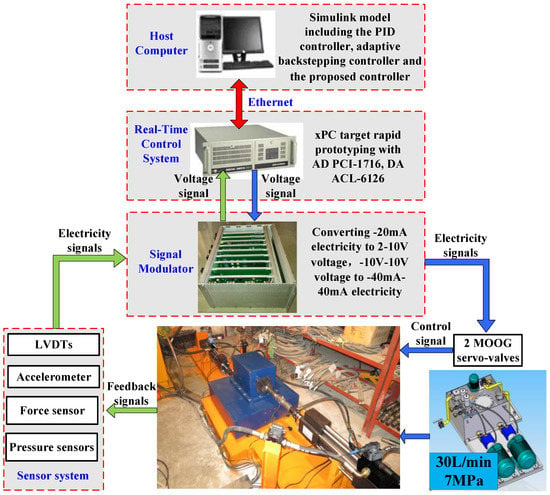
Figure 3.
Schematic diagram of the electro-hydraulic force loading experimental system.
2.2. Dynamic Model of the EHFLS
As shown in Figure 1, the left part presents the force loading generate hydraulic cylinder equipped with a servo-valve to exert force loading on the specimen and the right part denotes a disturbance generate hydraulic cylinder to simulate the external disturbances on the force loading control. The purpose of this work is to control the displacement of the force loading generate hydraulic cylinder to track the reference force loading as closely as possible. The electro-hydraulic cylinder used to generate force loading is shown in Figure 4. The nonlinear dynamic model of the EHFLS is given as follows [24].
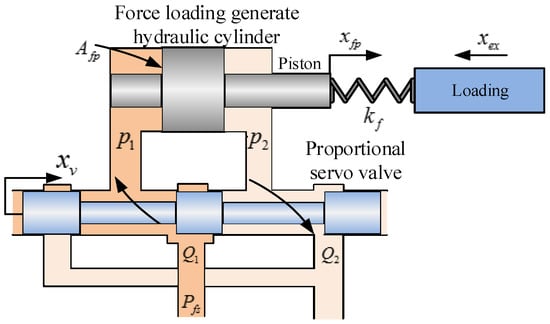
Figure 4.
Configuration of an electro-hydraulic cylinder.
Applying Newton’s second law, the force balance equation of an electro-hydraulic cylinder can be obtained:
where is mass of the platform and specimen, is effective action area of the electro-hydraulic cylinder, is displacement of the piston, is differential pressure between the two chambers of the electro-hydraulic cylinder, is viscosity coefficient, and is force loading.
The load flow of the servo-vale is given as:
where is flow coefficient of the servo-valve, is area gradient of the servo-valve, is oil density, is supplied system oil pressure, is spool displacement of the servo-valve, and sgn is a sign function that is defined as:
Since the servo-valve dynamics are significantly faster than that of the desired closed loop, the model accuracy would not reduce extremely even though the servo-valve dynamics is neglected. Therefore, the following approximation can be obtained:
where is the control voltage and is a positive constant.
The load flow from the valve to the chambers of the electro-hydraulic cylinder can be expressed as follows by applying the flow continuity equation:
where is the total leakage coefficient that can be written as , where is internal leakage coefficient and is external leakage coefficient, is effective bulk modulus, and is total volume of the electro-hydraulic cylinder.
The force loading obtained by the force sensor fixed between the force loading generate hydraulic cylinder and a spherical hinge can be further expressed as follows referring to Hooke’s law:
where is the stiffness of the force sensor, and is the displacement of the disturbances generate hydraulic cylinder.
Based on the dynamic model of the EHFLS, the state variables can be defined by . The nonlinear control system, which regards as the control input, can be presented in a state space form as follows:
where . and are external disturbances. Moreover, since and are time varying, the EHFLS have parameter uncertainties.
3. Controller Design
The framework of the nonlinear adaptive fuzzy backstepping controller (NAFBC) for the EHFLS is shown in Figure 5, in which it depicts that an adaptive backstepping controller and an adaptive fuzzy controller constitute the proposed controller. The adaptive backstepping controller is employed to design control output value to ensure the force loading tracking performance. However, the buffeting condition will come up when the value of external disturbances is too large. Then, the adaptive fuzzy controller is utilized to approach the external disturbances suppress object to improve the control output value designed by the adaptive backstepping controller. The stability of the overall system with the proposed control algorithm can be proved using Lyapunov analysis. Owing to the NAFBC, the load flow of the force loading generate hydraulic cylinder is obtained; then, the practical voltage output can be acquired by a Flow–Voltage converter.
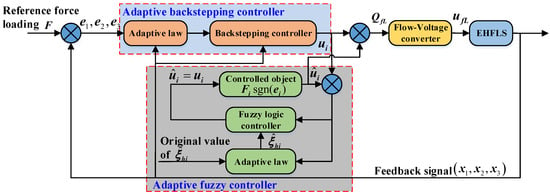
Figure 5.
Block diagram of the NAFBC.
3.1. Adaptive Backstepping Controller
The purpose of this section is intended to obtain the value of control input to track the reference force loading with an adaptive backstepping controller. The stability of the closed-loop system utilized the adaptive backstepping controller, which is ensured via Lyapunov analysis. The proposed design procedure can be given as the following three steps:
Step 1 Define the force loading tracking error as:
where is the value of the referential force loading.
Therefore, the time derivative of Equation (8) along Equation (7) can be given as:
Then, define the virtual control variable of as , and the deviation of from its virtual control variable can be expressed as:
Then, Equation (10) can be rewritten as:
Define Lyapunov function for Equation (8) as:
The time derivative of can be given as follows considering Equation (7):
Therefore, if , where , then . However, cannot contain and , so the virtual control variable can be obtained as:
Then, the time derivative of can be formulated as:
Remark 1.
As can be observed in Equation (14), the virtual control variable contains three parts. The first term is the force loading error feedback, which is used to stabilize the force loading error dynamics and govern the converge rate of tracking error. The second and third terms are in charge of the displacement of disturbances’ generate hydraulic cylinder and reference force loading, respectively. In addition, it can be seen that Equation (15) will be negative semi-definite if and are zero. Thus, the purpose of next control step is to compensate and .
Step 2 Referring to Equation (14), the time derivative of is given as:
Then, combining Equations (7) and (10), the time derivative of is given by:
In order to cope with the unknown parameter , the estimated value is defined and the parametric error of unknown parameters can be defined as , where . Then, Equation (17) can be rewritten as:
Define the Lyapunov function as:
where is gain for the parameter update law, respectively. Similarly, the unknown parameter is also regarded as variables slowly changed. Thus, the time derivative of is given as:
Define the virtual control variable of as , and the deviation of from its virtual control variable can be expressed as:
Then, combining Equations (7) and (22), the virtual control variable is designed as:
where .
Then, the time derivative of can be formulated as:
Remark 2.
As can be seen from Equation (23), the virtual control variable contains three parts. The first term is the force loading error feedback, which is used to stabilize the force loading error dynamics and govern the converge rate of tracking error. The second and third terms are responsible for the displacement of disturbances’ generate hydraulic cylinder and referential force loading, respectively. In addition, it can be seen that Equation (23) will be negative semi-definite if and are zero. Thus, the purpose of next control step is to compensate and .
Step 3 Because the final controlled variable is visualized, it is not necessary to imagine another virtual control variable at this step.
Referring to Equations (7) and (22), the time derivative of is given by:
where
Then, combining Equations (21) and (24), the time derivative of is given by:
Due to acting as a gain for the actual controlled variable, it only impacts the “size” rather than the “composition” of the desired anticlockwise rotation angle. For simplicity, is regarded as a constant. To cope with the unknown parameters and , the estimated values and are defined. Therefore, the parametric error of unknown parameters can be defined as and , where , . Then, Equation (25) can be rewritten as:
Define the Lyapunov function as:
where and are the gains for parameters’ update law, respectively. Similarly, the unknown parameters , are also regarded as variables slowly changed. Thus, the time derivative of the can be formulated as:
Then, the actual controlled variable can be chosen as:
where , , .
Under this situation, Equation (48) can be rewritten as:
Obviously, the values of , , and can be chosen as follows to eliminate the influence of estimation erroring for system stability:
Finally, the time derivative of the can be given as:
Therefore, it is obvious that the proposed control scheme combined with an adaptive backstepping controller and an adaptive fuzzy controller can ensure the stability of the EHFLS.
3.2. Adaptive Fuzzy Controller
Remark 3.
The gains , and are employed to compensate the external disturbances, however, whose value will be too large to cause chattering of the EHFLS if external disturbances is biggish. To restrain the chattering, the fuzzy systems are designed to approach , respectively. Then, Equation (29) can be rewritten as:
where are the set of the adjustable parameters. The following two steps are employed to construct fuzzy systems :
- Step 1
- Define fuzzy set to state variables (in this work, the order of the state space form of is 1, so ).
- Step 2
- The control output of fuzzy system can be expressed as by employing the strategy of product inference engine, singleton fuzzifier, and center average defuzzifier:where is the membership function of the state variable, and is a free parameter in the fuzzy set.
By defining the fuzzy basis function vector , Equation (36) can be written as:
where is designed by an adaptive law. is the fuzzy basis function vector with dimension, which can be expressed as:
The ideal and the adaptive law are respectively described as:
where .
Proof.
Define the optimal parameters of fuzzy systems:
where is a constraint set for ; then, define the Lyapunov function as:
where .
Then,
Therefore, the adaptive backstepping control with fuzzy law can stabilize the whole system.
Referring to Equations (2) and (4), the desired load flow of servo-valve can be given as:
where is the controlled voltage to obtain the desired load flow.
From Equation (44), it can be found that, in order to obtain the real control voltage , the values of and need to be given. In general, the rated flow and pressure drop of a certain servo-valve are known. Therefore, the following formulation can be obtained:
where is the saturated input of servo-valve, is the rated flow of servo-valve, and is the certain valve pressure drop.
Combing Equations (44) and (45), the controlled voltage is given by:
Since the value of the area gradient of servo-valve , the flow coefficient of servo-valve , , and are all positive, and the following formulation considering Equation (3) can be expressed:
Thus, Equation (46) can be expressed as:
Therefore, the controlled voltage can be obtained by the designed load flow .
4. Experimental Results and Analysis
To demonstrate effectiveness of the proposed control scheme for the EHFLS, experiments were carried out based on Matlab/Simulink for the electro-hydraulic force loading experimental system using the conventional PID controller with a velocity feedforward (PID + VF), a backstepping controller, an adaptive backstepping controller, and the proposed NAFBC to make a comparison. The parameters of the PID controller () were tuned by step loading condition and then velocity feedforward , which was used to suppress the external disturbances. Table 1 shows the main parameters of the electro-hydraulic force loading experimental system. The control parameters of four different controllers utilized in this work are shown in Table 2.

Table 1.
Parameters of the electro-hydraulic force loading control experimental system.

Table 2.
Control parameters of four different controllers.
The four control algorithms are compared under the same operation condition. The external disturbances were set as random position reference of amplitude 1 mm and frequency 10 Hz, and step position reference of amplitude 0.5 mm and frequency 2 Hz. The EHFLS was carried out for tracking sinusoidal random force loading reference of amplitude 5000 N and frequency 15 Hz.
Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13 present the force loading tracking performance and tracking errors with four controllers in the presence of a random position and a step position external disturbance. It can be seen from Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13 that the force loading tracking error with the conventional PID + VF is much bigger than that with the backstepping controller, the adaptive backstepping controller, and the proposed NAFBC. Owing to the adaptive law, the tracking performance with the ABC is better than that only with the common backstepping controller. Moreover, it can be noticed from Figure 7, Figure 8, Figure 9, Figure 11, Figure 12 and Figure 13 that the proposed NAFBC can further improve the force loading tracking performance, especially with consideration of the buffeting condition resulting from the extreme external disturbances, shown as the partially enlarged view of Figure 7, Figure 8, Figure 9, Figure 11, Figure 12 and Figure 13.
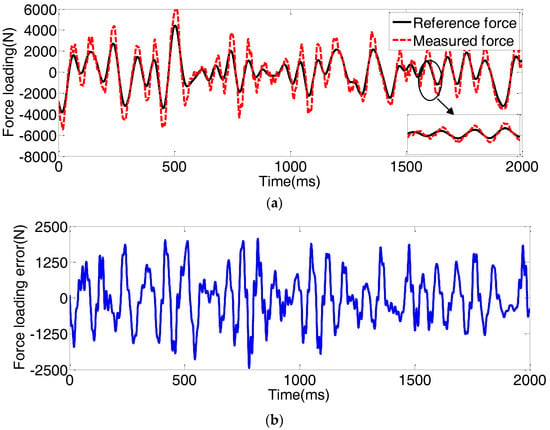
Figure 6.
Force loading tracking performance with the PID + VF subjected to the random position disturbances. (a) force loading tracking performance; (b) force loading tracking error.
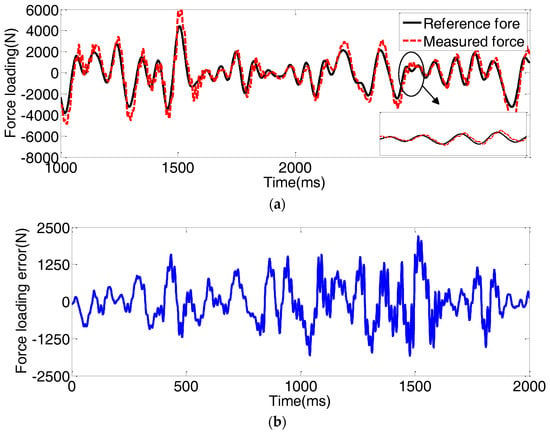
Figure 7.
Force loading tracking performance with the backstepping controller subjected to the random position disturbances. (a) force loading tracking performance; (b) force loading tracking error.
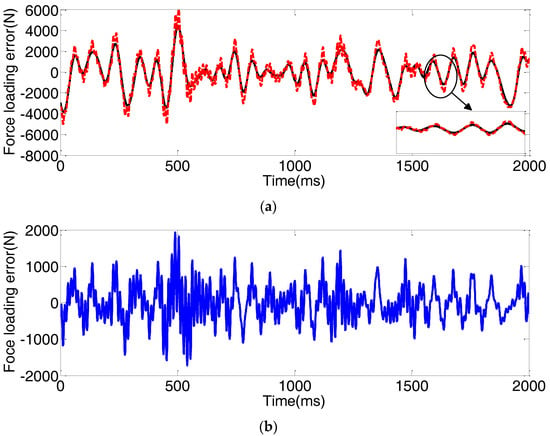
Figure 8.
Force loading tracking performance with the ABC subjected to the random position disturbances. (a) force loading tracking performance; (b) force loading tracking error.
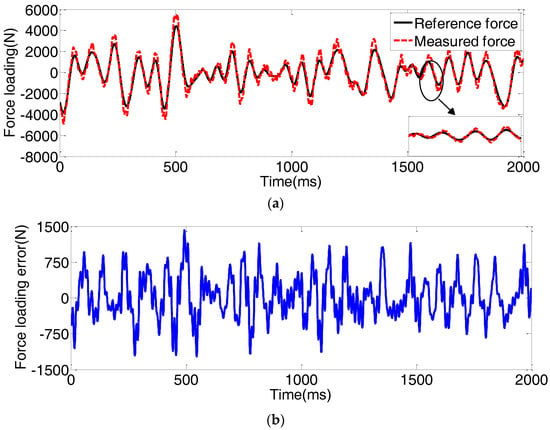
Figure 9.
Force loading tracking performance with the NAFBC subjected to the random position disturbances. (a) force loading tracking performance; (b) force loading tracking error.
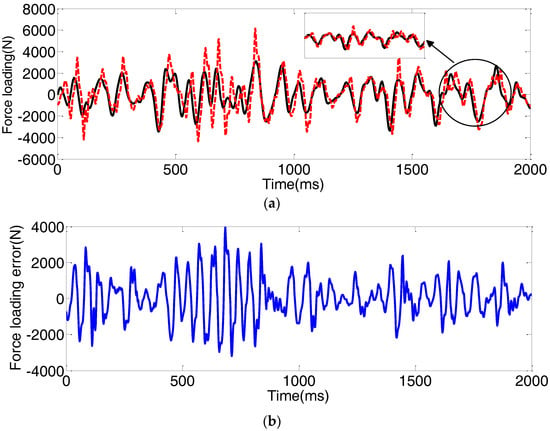
Figure 10.
Force loading tracking performance with the PID + VF subjected to the step position disturbances. (a) force loading tracking performance; (b) force loading tracking error.
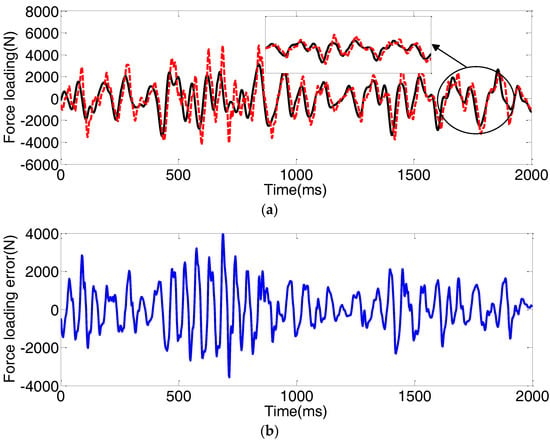
Figure 11.
Force loading tracking performance with the backstepping controller subjected to the step position disturbances. (a) force loading tracking performance; (b) force loading tracking error.
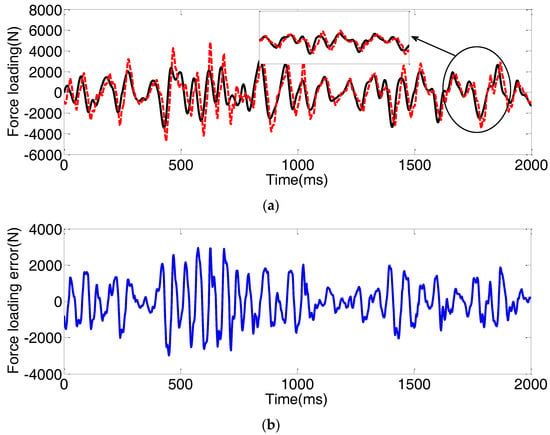
Figure 12.
Force loading tracking performance with the ABC subjected to the step position disturbances. (a) force loading tracking performance; (b) force loading tracking error.
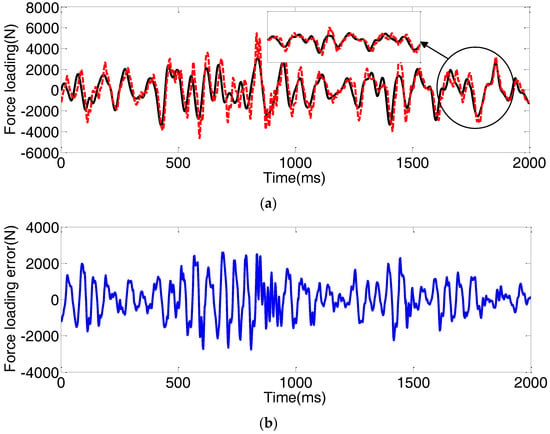
Figure 13.
Force loading tracking performance with the NAFBC subjected to the step position disturbances. (a) force loading tracking performance; (b) force loading tracking error.
The comparison of force loading tracking accuracy can be further appraised by several metrics, such as root mean square error (RMSE), which can be given by:
where in the value of the reference signal, is the value of the output signal, and is the length of reference and output signals. Table 3 and Table 4 list the RMSE and peak errors of the force loading tracking with the four different control methods under the random position and the step position external disturbances, respectively. As can be seen, the force loading tracking error based on four metrics can be perfected gradually.

Table 3.
Peak errors and the RMSE of four control algorithms with random position external disturbances.

Table 4.
Peak errors and the RMSE of four control algorithms with step position external disturbances.
5. Conclusions
In this work, a nonlinear force loading model is built for an electro-hydraulic force loading system. Then, a nonlinear adaptive fuzzy backstepping controller consists of an adaptive backstepping controller and an adaptive fuzzy controller is designed for force loading tracking control with consideration of the parameters uncertainties and external disturbances, of which the adaptive backstepping controller is employed to obtain the essential control output value and the adaptive fuzzy controller is utilized to suppress chattering. The stability of the overall system with the proposed controller can be proved with the help of Lyapunov theory. To verify the effectiveness of the proposed NAFBC, an electro-hydraulic force loading experimental system with xPC rapid prototyping technology is established. Experimental results conducted on the electro-hydraulic force loading experimental system prove that the NAFBC can yield more satisfactory force loading tracking performance, such as the tracking precision and chattering condition, on the electro-hydraulic force loading system than the conventional PID controller with velocity feedforward, a backstepping controller, and an adaptive backstepping controller. The adaptive parameters in this article are chosen by adjusting online incessantly, which lacks an optimization of mechanism to obtain the optimal parameters automatically. Thus, this issue should be considered in future work.
Author Contributions
For research articles with several authors, a short paragraph specifying their individual contributions must be provided. The following statements should be used “X.L. and Z.-C.Z. conceived and designed the experiments; X.L. performed the experiments; X.L., S.G., and Y.T. analyzed the data; G.-C.R. contributed reagents/materials/analysis tools; X.L., and D.C. wrote the paper.” Authorship must be limited to those who have contributed substantially to the work reported.
Acknowledgments
This research was supported by the National Basic Research and Development (973) Program of China (No. 2014CB049404), the National Natural Science Foundation of China (No. 51575511), the Program for Changjiang Scholars and Innovative Research Team in University (No. IRT_16R68), the Priority Academic Program Development of Jiangsu Higher Education Institutions (PAPD), and the Qing Lan Project in Jiangsu province.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Guan, C.; Pan, S.X. Nonlinear adaptive robust control of single-rod electro-hydraulic actuator with unknown nonlinear parameters. IEEE Trans. Control. Syst. Technol. 2008, 16, 434–445. [Google Scholar] [CrossRef]
- Shao, X.; Enyart, G. Development of a versatile hybrid testing system for seismic experimentation. Exp. Tech. 2014, 38, 44–60. [Google Scholar] [CrossRef]
- Shen, G.; Zhu, Z.C.; Zhang, L.; Tang, Y.; Yang, C.; Zhao, J.; Liu, G.; Han, J. Adaptive feed-forward compensation for hybrid control with acceleration time waveform replication on electro-hydraulic shaking table. Control Eng. Pract. 2013, 21, 1128–1142. [Google Scholar]
- Nakata, N. Effective force testing using a robust loop shaping controller. Earthq. Eng. Struct. D 2013, 42, 261–275. [Google Scholar] [CrossRef]
- Plummer, A.R. Robust electrohydraulic force control. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2007, 221, 717–731. [Google Scholar] [CrossRef]
- Aknouche, H.; Bechtoula, H.; Airouche, A. Investigation on the performance of the six DOF CGS, Algeria, shaking table. Earthq. Struct. 2014, 6, 539–560. [Google Scholar] [CrossRef]
- Han, J.W.; Kim, J.D.; Song, S.Y. Fatigue strength evaluation of a bogie frame for urban maglev train with fatigue test on full-scale test rig. Eng. Fail. Anal. 2013, 31, 412–420. [Google Scholar] [CrossRef]
- Tang, Y.; Zhu, Z.C.; Shen, G. Design and experimental evaluation of feedforward controller integrating filtered-x LMS algorithm with applications to electro-hydraulic force control systems. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2015, 230, 1951–1967. [Google Scholar] [CrossRef]
- Alleyne, A.; Rui, L.; Wright, H. On the limitations of force tracking control for hydraulic active suspensions. In Proceedings of the American Control Conference, Philadelphia, PA, USA, 21–26 June 1998; pp. 43–47. [Google Scholar]
- Truong, D.Q.; Ahn, K.K. Force control for hydraulic load simulator using self-tuning grey predictor—Fuzzy PID. Mechatronics 2009, 19, 233–246. [Google Scholar] [CrossRef]
- Kim, J.W.; Xuan, D.J.; Kim, Y.B. Design of a forced control system for a dynamic road simulator using QFT. Int. J. Automot. Technol. 2008, 9, 37–43. [Google Scholar] [CrossRef]
- Zhao, J.S.; Shen, G.; Yang, C.F.; Liu, G.; Yin, L.; Han, J. Feel force control incorporating velocity feedforward and inverse model observer for control loading system of flight simulator. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2013, 227, 161–175. [Google Scholar] [CrossRef]
- Zhao, J.S.; Shen, G.; Zhu, W.D.; Yang, C.; Agrawal, S.K. Force tracking control of an electro-hydraulic control loading system on a flight simulator using inverse model control and a damping compensator. Trans. Inst. Meas. Control 2016, 40, 135–147. [Google Scholar] [CrossRef]
- Shen, G.; Zhu, Z.C.; Li, X. Real-time electro-hydraulic hybrid system for structural testing subjected to vibration and force loading. Mechatronics 2015, 33, 49–70. [Google Scholar] [CrossRef]
- Shen, G.; Zhu, Z.C.; Zhao, J.S. Real-time tracking control of electro-hydraulic force servo systems using offline feedback control and adaptive control. ISA Tran. 2016, 11, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Li, H.Y.; Hu, Y.A. Robust sliding-mode backstepping design for synchronization control of cross-strict feedback hyperchaotic systems with unmatched uncertainties. Commun. Nonlinear Sci. 2011, 16, 3904–3913. [Google Scholar] [CrossRef]
- Prut, N.; Suwat, K. Observer-based backstepping force control of an electro hydraulic actuator. Control Eng. Pract. 2009, 17, 895–902. [Google Scholar]
- Yao, J.Y.; Yang, G.H.; Jiao, Z.X. High dynamic feedback linearization control of hydraulic actuators with backstepping. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2015, 229, 728–737. [Google Scholar] [CrossRef]
- Park, J.H. Synchronization of Genesio chaotic system via backstepping approach. Chaos Solitons Fractals 2006, 27, 1369–1375. [Google Scholar] [CrossRef]
- Yao, J.Y.; Jiao, Z.X.; Ma, D. Extended-State-Observer-Based Output Feedback Nonlinear Robust Control of Hydraulic Systems with Backstepping. IEEE Trans. Ind. Electron. 2014, 61, 6285–6293. [Google Scholar] [CrossRef]
- Chen, Z.; Yao, B.; Wang, Q. μ-synthesis based adaptive robust control of linear motor driven stages with high-frequency dynamics: A case study with comparative experiments. IEEE-ASME Trans. Mechatron. 2015, 20, 1482–1490. [Google Scholar] [CrossRef]
- Sun, W.C.; Gao, H.J.; Okyay, K. Vibration Isolation for Active Suspensions with Performance Constraints and Actuator Saturation. IEEE-ASME Trans. Mechatron. 2015, 20, 675–683. [Google Scholar] [CrossRef]
- Wang, C.W.; Jiao, Z.X.; Wu, S.; Shang, Y. Nonlinear adaptive torque control of electro-hydraulic load system with external active motion disturbance. Mechatronics 2014, 24, 32–40. [Google Scholar] [CrossRef]
- Yao, J.Y.; Jiao, Z.X.; Yao, B. Nonlinear adaptive robust backstepping force control of hydraulic load simulator: Theory and experiments. J. Mech. Sci. Technol. 2014, 28, 1499–1507. [Google Scholar] [CrossRef]
- Chen, S.; Yao, B.; Zhu, X.C.; Chen, Z.; Wang, Q.; Zhu, S.; Song, Y. Adaptive Robust Backstepping Force Control of 1-DOF Joint Exoskeleton for Human Performance Augmentation. IFAC-PapersOnLine 2016, 48, 142–147. [Google Scholar] [CrossRef]
- Wang, Z.; Wu, Z.; Du, Y.J. Robust adaptive backstepping control for reentry reusable launch vehicles. Acta Astronaut. 2016, 126, 258–264. [Google Scholar] [CrossRef]
- Yao, J.Y.; Jiao, Z.X.; Ma, D.W.; Yan, L. High-accuracy tracking control of hydraulic rotary actuators with modelling uncertainties. IEEE-ASME Trans. Mechatron. 2014, 19, 633–641. [Google Scholar] [CrossRef]
- Yao, J.Y.; Jiao, Z.X.; Ma, D.W. High dynamic adaptive robust control of load emulator with output feedback signal. J. Frankl. Inst. 2014, 351, 4415–4433. [Google Scholar] [CrossRef]
- Kadda, Z.M.; Tahar, M.; Benhadria, M.R.; Bestaoui, Y. Fuzzy integral sliding mode based on backstepping control synthesis for an autonomous helicopter. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2012, 227, 751–765. [Google Scholar]
- Wei, J.H.; Zhang, Q.; Li, M.J.; Shi, W. High-performance motion control of the hydraulic press based on an extended fuzzy disturbance observer. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2016, 230, 1044–1061. [Google Scholar] [CrossRef]
- Wang, C.; Gao, Q.; Hou, Y.L.; Hou, R.; Min, H. Adaptive complementary fuzzy self-recurrent wavelet neural network controller for the electric load simulator system. Adv. Mech. Eng. 2016, 8, 1–12. [Google Scholar]
- Zhang, X.M.; Liu, X.K.; Li, Y. Adaptive fuzzy tracking control for nonlinear strict-feedback systems with unmodeled dynamics via backstepping technique. Neurocomputing 2017, 235, 182–191. [Google Scholar] [CrossRef]
- Rong, H.J.; Yang, Z.X.; Wong, P.K.; Vong, C.M.; Zhao, G.S. A novel meta-cognitive fuzzy-neural model with backstepping strategy for adaptive control of uncertain nonlinear systems. Neurocomputing 2017, 230, 332–344. [Google Scholar] [CrossRef]
- Mercorelli, P.; Werner, N. An Adaptive Resonance Regulator for an Actuator using Periodic Signals in Camless Engine Systems. IFAC-PapersOnLine 2016, 49, 176–181. [Google Scholar] [CrossRef]
- Mercorelli, P.; Werner, N. An Adaptive Resonance Regulator Design for Motion Control of Intake Valves in Camless Engine Systems. IEEE Trans. Ind. Electron. 2017, 64, 3413–3422. [Google Scholar] [CrossRef]
- Magdi, S. Mahmoud, Fuzzy Control, Estimation and Diagnosis; Springer International Publishing: Berlin, Germany, 2018. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).