Ephemeral-Secret-Leakage Secure ID-Based Three-Party Authenticated Key Agreement Protocol for Mobile Distributed Computing Environments

Abstract

A three-party Authenticated Key Agreement (AKA) protocol in the distributed computing environment is a client that requests services from an application server through an authentication server. The authentication server is responsible for authenticating the participating entities and helping them to construct a common session key. Adopting the Key Transfer Authentication Protocol (KTAP) in such an environment, the authentication server is able to monitor the communication messages to prevent and trace network crime. However, the session key in the KTAP setting is created only by the authentication server and is vulnerable to the resilience of key control. On the other hand, with the rapid growth of network technologies, mobile devices are widely used by people to access servers in the Internet. Many AKA protocols for mobile devices have been proposed, however, most protocols are vulnerable to Ephemeral Secret Leakage (ESL) attacks which compromise the private keys of clients and the session key by an adversary from eavesdropped messages. This paper proposes a novel ESL-secure ID-based three-party AKA protocol for mobile distributed computing environments based on ESL-secure ID-based Authenticated Key Exchange (ID-AKE) protocol. The proposed protocol solves the key control problem in KTAP while retaining the advantages of preventing and tracing network crime in KTAP and also resists ESL attacks. The AVISPA tool simulation results confirm the correctness of the protocol security analysis. Furthermore, we present a parallel version of the proposed ESL-secure ID-based three-party AKA protocol that is communication-efficient.

1. Introduction

With the rapid growth of network technologies, portable mobile devices (e.g., mobile phone, notebook and tablet) are widely used by people to access remote servers on the Internet. Due to the limited computing capability and power energy of mobile devices, many Authenticated Key Agreement (AKA) protocols are based on the traditional public key cryptography system [1,2,3] and the ID-based AKA (ID-AKA) protocols [4,5,6] for mobile devices. Imbalanced computation is used to shift the computational burden to a powerful server using an online/offline computation technique to further reduce the mobile device computational load. If an AKA protocol adopted an online/offline computation technique, the ephemeral secrets are generally generated by an external source that may be controlled by an adversary. The ephemeral secrets are also involved in the offline pre-computation and stored in the insecure memory of mobile devices. If ephemeral secrets are compromised, an adversary can reveal the private keys of clients and the session key would turn out to be known from the eavesdropped messages. This phenomenon is called Ephemeral Secret Leakage (ESL) attacks [7]. To solve this security vulnerability, Tseng et al. [7] proposed the first ESL-secure ID-based Authenticated Key Exchange (ID-AKE) protocol for mobile client-server environments.

In 1976, Diffie and Hellman [8] proposed the first Public Key Cryptography (PKC) concept, and proposed the first key agreement protocol that allows two participants to construct a common session key over a public network. Unfortunately, Diffie and Hellman’s protocol does not authenticate the communication participants and is vulnerable to the man-in-the-middle attacks. Different approaches have been proposed by cryptographic researchers to defeat the weakness in terms of improving protocol security and efficiency. An AKA protocol should provide implicit key authentication for participants. Each participant is ensured that no other participants or adversaries can learn or determine the value of a common session key in a protocol run. The common session key is used to ensure information integrity, confidentiality and availability between participants using symmetric encryptions.

In traditional public key cryptography systems, the users have to access and verify other user’s certificate before using its public key through the Certificate Authority (CA). The CA requires high computational cost and storage efforts to manage the certificates and also increases the computational cost for the client side [9]. Shamir [10] proposed the first ID-based cryptosystem to simplify the certificate management procedures. In Shamir’s ID-based cryptosystem setting, the user’s public key is an easy calculated function of the user’s known identity information such as identity numbers, E-mail address and so forth. The corresponding private key can be calculated and issued to the user via a secure channel by a trusted party referred to as Private Key Generator (PKG). In this way, the users do not need to verify other user’s certificates before using the public key and thus can substantially reduce the computational burden of the CA. However, Shamir’s ID-based cryptosystem is not easy to be realized in practice due to lack of efficient encryption and decryption algorithms and thus restricts its development. Boneh and Franklin [11] proposed the first secure and efficient practical ID-based encryption scheme based on the Weil pairing defined on elliptic curves. Subsequently, the ID-based cryptographic schemes based on bilinear pairings have received much attention from cryptographic researchers and a large number of ID-based cryptographic systems using bilinear pairings have been published in the literatures [12,13,14].

Joux [15] proposed the first three-party key agreement protocol based on bilinear pairings. Joux’s key agreement protocol is the first key agreement protocol based on bilinear pairings and also the first one-round three-party key agreement protocol. However, like the basic Diffie-Hellman key agreement protocol, Joux’s protocol without authentication is also insecure against the man-in-the-middle attacks. To solve this problem, Al-Riyami and Paterson [16] proposed several three-party AKA protocols that use bilinear pairings. Al-Riyami and Paterson’s protocols overcome the security flaw in Joux’s protocol. However, Al-Riyami and Paterson’s protocols still need certificates issued by the CA to ensure the authenticity and a user also needs to verify the certificates before using other users’ public keys. Afterwards, many ID-based three-party AKA protocols using bilinear pairings have rapidly emerged and been well-studied as well [17,18,19].

Up to now, most of the literature on ID-based three-party AKA protocols using bilinear pairings focused on the environment in which PKG computes the public key and corresponding private key from a user’s identity information, and issuing the public/private key pair to the user via a secure channel. The participants can authenticate each other using the public/private key pair and construct a common session key. In 2004, Yeh et al. [20] pointed out that another common communication environment exists, referred to as the distributed computing environment, discussed in Kerberos [21]. In this open distributed computing environment, if the users would like to access services on application servers distributed throughout the network, a centralized authentication server is provided rather than building an elaborate authentication protocol at each server. The authentication server is responsible for participating entities’ authentication and helps the user and the application server construct a common session key. In the centralized authentication server model an inspection mechanism is provided to prevent and trace network crime, permitting users to access the services provided by the application servers legally. The Key Transfer Authentication Protocol (KTAP) is adopted in this system [22]. In a KTAP setting the session key is created by the authentication server and secretly transmitted to the user and the application server. The authentication server can therefore monitor the transferred messages [23,24,25,26]. However, the disadvantage of KTAP is that the session key is only created by the authentication server and the client and the application servers are unable to participate in constructing the common session key. KTAP is therefore vulnerable to key control resilience attacks [27].

With the rapid growth of network technologies, portable mobile devices (e.g., mobile phone, notebook and tablet) are widely used by people to access remote servers on the Internet. Due to the limited computing capability and power energy of mobile devices, many AKA protocols are based on the traditional public key cryptography system [1,2,3] and the ID-based AKA (ID-AKA) protocols [4,5,6] for mobile devices. Imbalanced computation is used to shift the computational burden to a powerful server using an online/offline computation technique to further reduce the mobile device computational load. If an AKA protocol adopted an online/offline computation technique, the ephemeral secrets are generally generated by an external source that may be controlled by an adversary. The ephemeral secrets are also involved in the offline pre-computation and stored in the insecure memory of mobile devices. If ephemeral secrets are compromised, an adversary can reveal the private keys of clients and the session key would turn out to be known from the eavesdropped messages. This phenomenon is called Ephemeral Secret Leakage (ESL) attacks. To solve this security vulnerability, Tseng et al. [7] proposed the first ESL-secure ID-based Authenticated Key Exchange (ID-AKE) protocol for mobile client-server environments.

Most KTAPs [20,23,24,25] are password-based authentication protocols. In these protocols the users need to share their own passwords with the authentication server and employ the authentication server public keys to ensure the identities of the participants. These protocols also use symmetric cryptosystems to encrypt the transferred messages. For password-based authentication protocol security a strong password should consist of letters (uppercase letters, lowercase letters), numbers and special punctuations to resist various attacks, such as password guessing attacks and dictionary attacks, etc. However, most mobile devices do not employ standard QWERTY keyboards for users to conveniently enter strong passwords. Instead, these mobile devices often use numeric passwords for user authentication, which is called Personal Identification Number based (PIN-based) authentication. The PIN-based authentication provides a small password space size and thus is vulnerable to various attacks [28]. Otherwise, using the authentication server public keys and the symmetric cryptosystems for the user authentication requires expensive computation, which is not applicable to mobile devices with limited computing capability.

This paper improved Tseng et al.’s scheme [7], to propose an ESL-secure ID-based three-party AKA protocol which is more suitable for mobile distributed computing environments. The proposed protocol adopts imbalanced computation to shift the computational burden to the powerful server and an online/offline computation technique to further reduce the computational cost required for mobile devices. The offline pre-computation is executed prior to protocol execution to achieve better performance. The proposed protocol keeps all of the merits of KTAP regarding security including the authentication server is able to monitor the communication messages to prevent and trace network crime and solves the session key problem, which is only created by the authentication server. All participants can contribute information to derive the common session key. In the security analysis, the proposed protocol resists ESL attacks and also satisfies the security attributes required for AKA protocols: known-key security, partial forward secrecy, key-compromise impersonation resilience, unknown key-share resilience and key control resilience [29]. Furthermore, the proposed protocol is validated by Automated Validation of Internet Security Protocols and Applications (AVISPA) [30] formal validation tool to show its security against various active and passive attacks. In addition, a parallel version of the proposed protocol is proposed to enhance the protocol run performance.

This paper is organized as follows. Section 2 gives a brief review of the basic bilinear pairing concept, the related mathematical assumptions and the security attributes required for AKA protocols and notions used in the proposed protocol. The proposed ESL-secure ID-based three-party AKA protocol is presented in Section 3. In Section 4 the proposed protocol security and performance analyses are conducted. Conclusions are given in Section 5.

2. Preliminaries

In this Section the basic bilinear pairings concept, the related mathematical assumptions, the security attributes required for AKA protocols, and the notations used in the proposed protocol are briefly introduced.

2.1. Bilinear Pairings

Let $P$ denote a generator of $G_1$, where $G_1$ is an additive cyclic group of large prime order $q$ and let $G_2$ be a multiplicative group of the same large prime order $q$. $G_1$ is a subgroup of the group of points on an elliptic curve $E$ defined over a finite field. $G_2$ is a subgroup of the group of the multiplicative cyclic group defined over a finite field. A bilinear pairing is defined as a map: $\widehat{e}: G_1\times G_1\to G_2$. The map $\widehat{e}$ is called an admissible bilinear map if it satisfies the following properties.

• Bilinearity: Let $P, Q, R\in G_1$, we have:

  (1)

  $\widehat{e}\left(P+Q, R\right)=\widehat{e}\left(P, R\right)\cdot \widehat{e}\left(Q, R\right)$.

  (2)

  $\widehat{e}\left(P, Q+R\right)=\widehat{e}\left(P, Q\right)\cdot \widehat{e}\left(P, R\right)$.

  (3)

  $\widehat{e}\left(aP, bP\right)=\widehat{e}\left(bP, aP\right)=\widehat{e}{\left(P, P\right)}^{ab}$.

• Non-degeneracy: There exist $P\in G_1$ such that $\widehat{e}\left(P, P\right)\ne 1$.
• Computable: For $P, Q\in G_1$, there exists an efficient algorithm to compute $\widehat{e}\left(P, Q\right)$.

2.2. Computational Problems

The security of the proposed protocol is based on the following two computational problems. There is no polynomial time algorithm to solve these computational problems with non-negligible probability:

• Discrete Logarithm Problem (DLP): Give $P, Q\in G_1$; find an integer $a$ such that $Q=aP$ whenever such integer exists.
• Computational Diffie-Hellman Problem (CDHP): Given $P, aP, bP\in G_1$ for unknown $a, b\in Z_q^{*}$, the CDHP is to compute the value $abP\in G_1$.

2.3. Security Attributes

Here, $A$, $B$ and $S$ are going to agree upon a common session key and communicate to each other securely. An AKA protocol should provide implicit key authentication for $A$, $B$ and $S$, so there are additional security attributes defined for AKA protocols.

• Known-Key Security. A unique session key should be constructed in each round of an AKA protocol. An adversary cannot derive other previous session keys if knowledge of the previous session keys has been compromised. The main purpose of known-key security is to ensure that the compromising of one session key will not compromise other or future session keys.
• Forward Secrecy. If the long-term private keys of one or more of the participants are compromised, the secrecy of previously established session keys will not be obtained by an adversary. The main purpose of forward secrecy is to provide complete protection for the previous transferred messages. If all long-term private keys of the participants are compromised without compromising previous established session keys, that means an AKA protocol still provides protection for the previously transferred messages. We say that the AKA protocol offers perfect forward secrecy.
• Key-Compromise Impersonation Resilience. Suppose that $A$’s private key has been revealed to an adversary. The adversary only can impersonate $A$ to cheat $S$ and $B$. It is desired that the compromise of $A$’s private key does not allow the adversary to impersonate $S$ or $B$ to cheat $A$.
• Unknown Key-Share Resilience. After the session key has been established, $A$ believes the session key is shared with $S$ and $B$, while $S$ and $B$ mistakenly believe that the session key is instead shared with an adversary. Therefore, a desirable AKA protocol should be resistant to unknown key-share attacks. None of the participants can force $A$ to establish a session key with a participant that he does not know but $A$ believes he is sharing the session key with the participants that he knows.
• Key Control Resilience. The session key should be determined jointly by all participants (e.g., $A$, $S$ and $B$). None of the participants can control the session key construction procedure alone. The main purpose of key control resilience is to ensure session key construction fairness and security. It should not be possible for any participants or adversaries to predict or predetermine the session key value.

Constructing a desirable AKA protocol must conform to these desirable security attributes: known-key security, forward secrecy, key-compromise impersonation resilience, unknown key-share resilience, key control resilience. Thus, an AKA protocol is able to resist various active and passive attacks.

2.4. Notations

The system parameters, notations and functions used in the whole proposed protocol are defined as follows:

• $G_1$: an additive cyclic group.
• $G_2$: a multiplicative cyclic group.
• $\widehat{e}$: a bilinear map, $\widehat{e}: G_1\times G_1\to G_2$.
• $P$: a generator of the group $G_1$.
• $s$: the private key of the authentication server, $s\in Z_q^{*}$.
• $P_{pub}$: the public key of the authentication server, $P_{pub}=s\cdot P$.
• $I{D}_S$: the identity of the authentication server.
• $I{D}_A$: the identity of the client.
• $I{D}_B$: the identity of the application server.
• $DI{D}_{A/B}$: the private key of $I{D}_A$/the private key of $I{D}_B$.
• $f_1(),f_2(), f_3(), f_4(), f_5(), f_6()$: six one-way hash functions, $f_1,f_2, f_3, f_4, f_5, f_6: {\left\{0, 1\right\}}^{*}\to {\left\{0, 1\right\}}^n$, where $n$ is a fixed length and $2^n<q$.
• $H_1(), H_2()$: two map-to-point hash functions, $H_1, H_2: {\left\{0, 1\right\}}^{*}\to G_1$.

3. The Proposed Protocol

We present the proposed ESL-secure ID-based three-party AKA protocol for mobile distributed computing environments in this section. The proposed protocol consists of three phases: the system setup phase, the key extract phase and the mutual authentication and key agreement phases. We also present a parallel version of the proposed protocol to enhance the protocol run performance.

3.1. System Setup Phase

The proposed protocol system consists of an authentication server $S$, an application server $B$ and a mobile client $A$. The client $A$ refers to a user with handheld device and communicates with the authentication server $S$ and the application server $B$ through open channels such as wireless networks. The application server $B$ provides services or applications to the client $A$. The authentication server $S$ is responsible for computing private keys according to the application server $B$ and the client $A$’ identities and distribute the private keys to them via a secure channel. The authentication server $S$ is also responsible to generate the systems parameters.

In the system setup phase the authentication server $S$ first generates two cyclic groups $G_1$ and $G_2$ of a large prime order $q$, an admissible bilinear map $\widehat{e}: G_1\times G_1\to G_2$, and a random generator $P$ of $G_1$, where $G_1$ and $G_2$ are additive and multiplicative cyclic groups of large prime order $q$, respectively. The authentication server $S$ then performs the following tasks:

• Randomly select a system private key $s\in Z_q^{*}$.
• Compute the system public key $P_{pub}=s\cdot P$.
• Choose two map-to-point hash functions $H_1, H_2: {\left\{0, 1\right\}}^{*}\to G_1$.
• Choose six one-way hash functions $f_1,f_2, f_3, f_4, f_5, f_6: {\left\{0, 1\right\}}^{*}\to {\left\{0, 1\right\}}^n$, where $n$ is a fixed length and $2^n<q$.
• Publish public parameters and functions $Params=<G_1, G_2, q, P, \widehat{e}, P_{Pub}, H_1, H_2, f_1,f_2, f_3, f_4, f_5, f_6>$.

3.2. Key Extract Phase

In the key extract phase client $A$ and the application server $B$ separately submit their identities $I{D}_A$ and $I{D}_B$ to the authentication server $S$ and receive their corresponding private keys $DI{D}_A$ and $DI{D}_B$, respectively. The key extract phase is depicted in Figure 1. To the client $A$ as an example, the detailed procedures are presented as follows:

Figure 1. The key extract phase.

• The client $A$ submits its identity $I{D}_A$ to the authentication server $S$.
• Upon receiving the client $A$ with identity $I{D}_A$, the authentication server $S$ chooses an ephemeral secret value $l_A\in Z_q^{*}$, and compute $QI{D}_{A1}=l_A\cdot P$, $h_A=f_1\left(I{D}_A,QI{D}_{A1}\right)$, $DI{D}_{A1}=l_A+h_A\cdot s$, $QI{D}_{A2}=H_1\left(I{D}_A\right)$, $QI{D}_S=H_1\left(I{D}_S\right)$ and $DI{D}_{A2}=s\cdot QI{D}_{A2}$.
• Set $DI{D}_A=\left(DI{D}_{A1},DI{D}_{A2},QI{D}_{A1},QI{D}_S\right)$ as the client $A$’s private key and send it to the client $A$ via a secure channel.

The authentication server $S$ also set $DI{D}_B=\left(DI{D}_{B1},DI{D}_{B2},QI{D}_{B1},QI{D}_S\right)$ as the application server $B$’s private key in the same procedures.

3.3. Mutual Authentication and Key Agreement Phase

Suppose that the client $A$ would like to communicate with the authentication server $S$ and request services or applications from the application server $B$. As depicted in Figure 2, the detailed interactions between the three participants are presented as below:

Figure 2. The mutual authentication and key agreement phase.

Step 1. $A\to S$: $<I{D}_A,I{D}_B,U_{A1},U_{A2},V_A,QI{D}_{A1}>$

The client $A$ with identity $I{D}_A$ performs the following off-line computations in advance:

(1)

Random select an ephemeral secret $r_A\in Z_q^{*}$.

(2)

Compute $U_{A1}=r_A\cdot P$ and $U_{A2}=r_A\cdot QI{D}_{A2}$.

(3)

Compute $W_A=H_2\left(U_{A1},U_{A2}\right)$ and $V_A=\left(r_A+DI{D}_{A1}\right)\cdot W_A+DI{D}_{A2}$.

(4)

Send $<I{D}_A,I{D}_B,U_{A1},U_{A2},V_A,QI{D}_{A1}>$ to the authentication server $S$.

Step 2. $S\to B$: $<I{D}_A,U_S,U_{SB1},U_{SB2},V_{SB}>$

Upon receiving $<I{D}_A,I{D}_B,U_{A1},U_{A2},V_A,QI{D}_{A1}>$, the authentication server $S$ authenticates the client $A$ by performing the following tasks:

(1)

Compute $W_A=H_2\left(U_{A1},U_{A2}\right)$, $h_A=f_1\left(I{D}_A,QI{D}_{A1}\right)$ and $QI{D}_{A2}=H_1\left(I{D}_A\right)$.

(2)

Check whether $\widehat{e}\left(P,V_A\right)=\widehat{e}\left(U_{A1}+QI{D}_{A1}, W_A\right)\cdot \widehat{e}\left(P_{pub}, h_A\cdot W_A+QI{D}_{A2}\right)$ or not. If the equation holds, then the authentication server $S$ accepts the request. Otherwise, the authentication server $S$ terminates it.

(3)

Random select an ephemeral secret $r_S\in Z_q^{*}$.

(4)

Compute $U_S=r_S\cdot P$, $U_{SB1}=r_S\cdot U_{A1}$ and $U_{SB2}=r_S\cdot U_{A2}$.

(5)

Compute $DI{D}_S=s\cdot QI{D}_S$, $h_{SB}=f_2\left(I{D}_A,I{D}_B,U_S,U_{SB1},U_{SB2}\right)$ and $V_{SB}=r_S\cdot P_{pub}+h_{SB}\cdot DI{D}_S$.

(6)

Send $<I{D}_A,U_S,U_{SB1},U_{SB2},V_{SB}>$ to the application server $B$.

Step 3. $B\to S$: $<I{D}_B,U_{B1},U_{B2},V_B,QI{D}_{B1}>$

Upon receiving $<I{D}_A,U_S,U_{SB1},U_{SB2},V_{SB}>$, the application server $B$ authenticates the authentication server $S$ by performing the following tasks:

(1)

Compute $h_{SB}=f_2\left(I{D}_A,I{D}_B,U_S,U_{SB1},U_{SB2}\right)$.

(2)

Check whether $\widehat{e}\left(V_{SB},P\right)=\widehat{e}\left(U_S+h_{SB}\cdot QI{D}_S, P_{pub}\right)$ or not. If the equation holds, then the application server $B$ accepts the request. Otherwise, the application server $B$ terminates it.

(3)

Random select an ephemeral secret $r_B\in Z_q^{*}$.

(4)

Compute $U_{B1}=r_B\cdot P$ and $U_{B2}=r_B\cdot QI{D}_{B2}$.

(5)

Compute $W_B=H_2\left(U_{B1},U_{B2}\right)$ and $V_B=\left(r_B+DI{D}_{B1}\right)\cdot W_B+DI{D}_{B2}$.

(6)

Send $<I{D}_B,U_{B1},U_{B2},V_B,QI{D}_{B1}>$ to the authentication server $S$.

Step 4. $S\to A$: $<N_A,Aut{h}_{SA},I{D}_B,U_S,U_{SA1},U_{SA2}>$, $<N_B,Aut{h}_{SB}>$

Upon receiving $<I{D}_B,U_{B1},U_{B2},V_B,QI{D}_{B1}>$, the authentication server $S$ authenticates the application server $B$ by performing the following tasks:

(1)

Compute $W_B=H_2\left(U_{B1},U_{B2}\right)$, $h_B=f_1\left(I{D}_B,QI{D}_{B1}\right)$ and $QI{D}_{B2}=H_1\left(I{D}_B\right)$.

(2)

Check whether $\widehat{e}\left(P,V_B\right)=\widehat{e}\left(U_{B1}+QI{D}_{B1}, W_B\right)\cdot \widehat{e}\left(P_{pub}, h_B\cdot W_B+QI{D}_{B2}\right)$ or not. If the equation holds, then the authentication server $S$ accepts the application server $B$. Otherwise, the authentication server $S$ terminates it.

(3)

Compute $U_{SA1}=r_S\cdot U_{B1}$ and $U_{SA2}=r_S\cdot U_{B2}$.

(4)

Acquire two nonce $N_A$, $N_B$.

(5)

Compute $K_{SA}=s\cdot U_{A2}$ and $Aut{h}_{SA}=f_3\left(I{D}_A,I{D}_B,U_{A1},U_{A2},V_A,N_A,K_{SA},U_S,U_{SA1},U_{SA2}\right)$.

(6)

Compute $K_{SB}=s\cdot U_{B2}$ and $Aut{h}_{SB}=f_3\left(I{D}_A,I{D}_B,U_{B1},U_{B2},V_B,N_B,K_{SB},U_S,U_{SB1},U_{SB2}\right)$.

(7)

Send $<N_A,Aut{h}_{SA},I{D}_B,U_S,U_{SA1},U_{SA2}>$ and $<N_B,Aut{h}_{SB}>$ to the client $A$.

Step 5. $A\to B$: $<N_B,Aut{h}_{SB},Aut{h}_{AB}>$

Upon receiving $<N_A,Aut{h}_{SA},I{D}_B,U_S,U_{SA1},U_{SA2}>$ and $<N_B,Aut{h}_{SB}>$, the client $A$ authenticates the authentication server $S$ by performing the following tasks:

(1)

Compute $K_{AS}=r_A\cdot DI{D}_{A2}$.

(2)

Check whether $Aut{h}_{SA}=f_3\left(I{D}_A,I{D}_B,U_{A1},U_{A2},V_A,N_A,K_{AS},U_S,U_{SA1},U_{SA2}\right)$ or not. If the equation holds, then the client $A$ accepts the authentication server $S$. Otherwise, the client $A$ terminates it.

(3)

Compute $K_{AB}=\widehat{e}\left(r_A\cdot P_{pub}+K_{AS}, U_{SA1}+U_{SA2}\right)$ and $Aut{h}_{AB}=f_4\left(I{D}_A,I{D}_B,U_S,K_{AB}\right)$.

(4)

Send $<N_B,Aut{h}_{SB},Aut{h}_{AB}>$ to the application server $B$.

Step 6. $B\to A$: $<Aut{h}_{BA}>$

Upon receiving $<N_B,Aut{h}_{SB},Aut{h}_{AB}>$, the application server $B$ authenticates the client $A$ and the authentication server $S$ by performing the following tasks:

(1)

Compute $K_{BS}=r_B\cdot DI{D}_{B2}$.

(2)

Check whether $Aut{h}_{SB}=f_3\left(I{D}_A,I{D}_B,U_{B1},U_{B2},V_B,N_B,K_{BS},U_S,U_{SB1},U_{SB2}\right)$ or not. If the equation holds, then the application server $B$ accepts the authentication server $S$. Otherwise, the application server $B$ terminates it.

(3)

Compute $K_{BA}=\widehat{e}\left(U_{SB1}+U_{SB2}, r_B\cdot P_{pub}+K_{BS}\right)$.

(4)

Check whether $Aut{h}_{AB}=f_4\left(I{D}_A,I{D}_B,U_S,K_{BA}\right)$ or not. If the equation holds, then the application server $B$ can be sure that the client $A$ has the ability to compute the session key. Otherwise, the application server $B$ notifies the authentication server $S$ that the authentication has been failed and terminates it.

(5)

Compute $Aut{h}_{BA}=f_5\left(I{D}_A,I{D}_B,U_S,K_{BA},Aut{h}_{AB}\right)$.

(6)

Compute the session key $S{K}_{AB}=f_6\left(I{D}_A,I{D}_B,U_S,K_{BA},Aut{h}_{AB},Aut{h}_{BA}\right)$.

(7)

Send $<Aut{h}_{BA}>$ to the client $A$.

On the other side, upon receiving $<Aut{h}_{BA}>$, the client $A$ checks whether $Aut{h}_{BA}=f_5\left(I{D}_A,I{D}_B,U_S,K_{AB},Aut{h}_{AB}\right)$ or not. If the equation holds, the client $A$ can be sure that the application server $B$ has the ability to compute the session key, then the client $A$ computes the session key $S{K}_{AB}=f_6\left(I{D}_A,I{D}_B,U_S,K_{AB},Aut{h}_{AB},Aut{h}_{BA}\right)$. Otherwise, the client $A$ notifies the authentication server $S$ that the authentication has been failed and terminates it. After transferring the messages in the above six steps, the client $A$ and the application server $B$ can authenticate each other via the authentication server $S$ and agree upon the session key. The authentication server $S$ also can compute $K_{AB}=\widehat{e}\left(s\cdot U_{A1}+K_{SA},U_{SA1}+U_{SA2}\right)$ or $K_{BA}=\widehat{e}\left(U_{SB1}+U_{SB2},s\cdot U_{B1}+K_{SB}\right)$ to compute the session key $S{K}_{AB}=f_6\left(I{D}_A,I{D}_B,U_S,K_{AB},Aut{h}_{AB},Aut{h}_{BA}\right)$ which is shared with the client $A$ and the application server $B$. The session key is created by the three participants and not created by the authentication server $S$ alone. Therefore, the proposed protocol can solve the problem in the resilience of key control of the KTAP while the authentication server $S$ still can monitor the communication messages to prevent and trace network crime.

In Steps 2 and 4, the correctness of the equations that the authentication server $S$ uses to authenticate the client $A$ and the application server $B$ can be proved by the bilinear pairings feature operation. To the client $A$ as an example, the correctness of $\widehat{e}\left(P,V_A\right)=\widehat{e}\left(U_{A1}+QI{D}_{A1}, W_A\right)\cdot \widehat{e}\left(P_{pub}, h_A\cdot W_A+QI{D}_{A2}\right)$ in Step 2 is presented as follows:

$$\begin{array}{cc}\hfill \widehat{e}\left(P, V_A\right)& =\widehat{e}\left(P, \left(r_A+DI{D}_{A1}\right)\cdot W_A+DI{D}_{A2}\right)\hfill \\ \hfill & =\widehat{e}\left(P, \left(r_A+l_A+h_A\cdot s\right)\cdot W_A+s\cdot QI{D}_{A2}\right)\hfill \\ \hfill & =\widehat{e}\left(P, \left(r_A+l_A\right)\cdot W_A+h_A\cdot s\cdot W_A+s\cdot QI{D}_{A2}\right)\hfill \\ \hfill & =\widehat{e}\left(P, \left(r_A+l_A\right)\cdot W_A+s\cdot \left(h_A\cdot W_A+QI{D}_{A2}\right)\right)\hfill \\ \hfill & =\widehat{e}\left(P, \left(r_A+l_A\right)\cdot W_A\right)\cdot \widehat{e}\left(P, s\cdot \left(h_A\cdot W_A+QI{D}_{A2}\right)\right)\hfill \\ \hfill & =\widehat{e}\left(\left(r_A+l_A\right)\cdot P, W_A\right)\cdot \widehat{e}\left(s\cdot P, h_A\cdot W_A+QI{D}_{A2}\right)\hfill \\ \hfill & =\widehat{e}\left(U_{A1}+QI{D}_{A1}, W_A\right)\cdot \widehat{e}\left(P_{pub}, h_A\cdot W_A+QI{D}_{A2}\right)\hfill \end{array}$$

In Step 3, the correctness of the equation that the application server $B$ uses to verify the message sent from the authentication server $S$. The correctness of $\widehat{e}\left(V_{SB}, P\right)=\widehat{e}\left(U_S+h_{SB}\cdot QI{D}_S, P_{pub}\right)$ is presented as follows:

$$\begin{array}{cc}\hfill \widehat{e}\left(V_{SB}, P\right)& =\widehat{e}\left(r_S\cdot P_{pub}+h_{SB}\cdot DI{D}_S,P \right)\hfill \\ \hfill & =\widehat{e}\left(r_S\cdot s\cdot P+h_{SB}\cdot s\cdot QI{D}_S, P\right)\hfill \\ \hfill & =\widehat{e}\left(r_S\cdot P+h_{SB}\cdot QI{D}_S,s\cdot P\right)\hfill \\ \hfill & =\widehat{e}\left(U_S+h_{SB}\cdot QI{D}_S, P_{pub}\right)\hfill \end{array}$$

In Steps 5 and 6, the equations $Aut{h}_{SA}$ and $Aut{h}_{SB}$ that the client $A$ and the application server $B$ use to authenticate the authentication server $S$, respectively. If $K_{SA}=K_{AS}$ and $K_{SB}=K_{BS}$, we say that $Aut{h}_{SA}$ and $Aut{h}_{SB}$ are valid, the equations hold because of $K_{SA}=s\cdot U_{A2}=s\cdot r_A\cdot QI{D}_{A2}=r_A\cdot DI{D}_{A2}=K_{AS}$ and $K_{SB}=s\cdot U_{B2}=s\cdot r_B\cdot QI{D}_{B2}=r_B\cdot DI{D}_{B2}=K_{BS}$.

In Step 6, if $K_{AB}=K_{BA}$, we say that $Aut{h}_{AB}$ and $Aut{h}_{BA}$ are valid. The client $A$, the application server $B$ and the authentication server $S$ have established a common session key $S{K}_{AB}$. The correctness of $K_{AB}=K_{BA}$ is presented as follows:

$$\begin{array}{cc}\hfill K_{AB}& =\widehat{e}\left(r_A\cdot P_{pub}+K_{AS},U_{SA1}+U_{SA2}\right)\hfill \\ \hfill & =\widehat{e}\left(r_A\cdot s\cdot P+r_A\cdot s\cdot QI{D}_{A2}, r_S\cdot r_B\cdot P+r_S\cdot r_B\cdot QI{D}_{B2}\right)\hfill \\ \hfill & =\widehat{e}{\left(r_A\cdot P+r_A\cdot QI{D}_{A2},r_B\cdot P+r_B\cdot QI{D}_{B2}\right)}^{s\cdot r_S}\hfill \\ \hfill & =\widehat{e}\left(r_S\cdot r_A\cdot P+r_S\cdot r_A\cdot QI{D}_{A2},s\cdot r_B\cdot P+s\cdot r_B\cdot QI{D}_{B2}\right)\hfill \\ \hfill & =\widehat{e}\left(r_S\cdot U_{A1}+r_S\cdot U_{A2},r_B\cdot s\cdot P+r_B\cdot DI{D}_{B2}\right)\hfill \\ \hfill & =\widehat{e}\left(U_{SB1}+U_{SB2}, r_B\cdot P_{pub}+K_{BS}\right)\hfill \\ \hfill & =K_{BA}\hfill \end{array}$$

3.4. The Parallel Version

Chen et al. [31] pointed out that to enhance the performance and reduce latency of an AKA protocol, the communication steps in the protocol should be as parallel as possible. To enhance the proposed protocol performance, a parallel version of the protocol is presented. We reordered the steps in the proposed protocol as shown in Figure 3. It can be obviously seen that the steps are reordered but the message exchange contents are the same as those in the preceding protocol. In the parallel version of the proposed protocol, the protocol can be executed in four rounds.

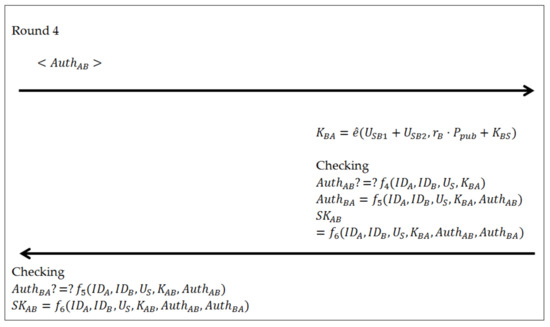
Figure 3. The parallel version of Ephemeral Secret Leakage (ESL)-secure ID-based three-party Authenticated Key Agreement (AKA) protocol.

3.5. Preventing and Tracing Network Crime

In a distributed computing environment preventing and tracing network crime often consists of mechanisms to prevent, detect and deter security violations that involve the transmission of messages. Authentication, Authorization, Accounting (AAA) services are the commonly used mechanisms to protect the security of networks in distributed computing environments [32,33,34]. The authentication service is the first inspection mechanism that prevents and traces network crime. The authorization service is based on the security primitives of the authentication service. The authentication service and the authorization service are usually performed together to ensure that a client requesting access to the services is in fact the client to whom entry is authorized. It is able to prevent services access by a client that is not authorized and trace which services were accessed by which client. After authentication and authorization, a common session key is constructed using symmetric encryptions. These are most effective techniques to protect transferred messages from being intercepted, disclosed and forged by an adversary. The AAA services also provide accounting services that are used to collect resources usage information for billing. In the generic AAA services, the authentication, authorization and accounting services are provided by an authentication server referred to as AAA server.

The proposed protocol is an ID-based three-party AKA protocol that provides mutual authentication and establishes a common session key between three participants. The authentication server in the proposed protocol is responsible for the authentication of participating entities and restricts access to authorized clients. Both clients and the application servers must send their identities to the authentication server and retrieve the private keys computed by the authentication server in the key extract phase. A client or an adversary without the private key is unable to request and access the services provided by an application server. An application server without the private key is unable to be accepted by the authentication server and the clients. The authentication server needs to authenticate the clients and the application servers but also needs to be authenticated by the clients and the application servers. The proposed protocol is able to prevent unauthorized access and detect, deter an adversary who constructs a forged identity as the real authentication server or application server to acquire useful information from the clients.

The proposed protocol allows three participants to establish a common session key to protect the transferred messages and also ensures the authenticity. The common session key of the proposed protocol is derived from the authentication server, the client and the application server’s private keys and their ephemeral secrets in the mutual authentication and key agreement phase. The three participants are able to ensure that no other participants or adversaries can learn or determine the value of the common session key and the authentication server could use the common session key to monitor the transferred messages. The common session key of the proposed protocol is able to protect and guarantee the authenticity of the transferred messages and also trace which client has accessed the services provided by which application server. None of the clients are able to deny that the client has requested and accessed the services provided by the application server.

In the proposed protocol the authentication server provides authentication service, authorization service and uses the common session key to prevent and trace network crime. However, the authentication server does not provide accounting services. The most important aspect in the AAA services is the authentication service and the purpose of the accounting service is to collect information on resource usage for billing, auditing and trend analysis [35,36,37,38]. Hence, the proposed protocol is suitable for various communication systems in the distributed computing environments in terms of protecting the security of network, preventing and tracing network crime.

4. Security and Performance Analysis

In this Section we discuss the security analysis of the proposed protocol. The simulation results were performed using the AVISPA tool. The methodology used in our performance analysis and the metrics utilized to evaluate the results of the proposed protocol.

4.1. Security Analysis

In this Section we present the security analysis of the proposed protocol to show the security attributes required for AKA protocols are satisfied and the simulation results by the AVISPA tool.

• Mutual authentication and Ephemeral-Secret-Leakage Resistance. The proposed protocol adopted Tseng et al.’s ESL-secure ID-AKE protocol [7] to achieve the client-to-server authentication. The authentication server $S$ authenticates the client $A$ and the application server $B$ by checking whether $\widehat{e}\left(P,V_A\right)=\widehat{e}\left(U_{A1}+QI{D}_{A1}, W_A\right)\cdot \widehat{e}\left(P_{pub}, h_A\cdot W_A+QI{D}_{A2}\right)$ and $\widehat{e}\left(P,V_B\right)=\widehat{e}\left(U_{B1}+QI{D}_{B1}, W_B\right)\cdot \widehat{e}\left(P_{pub}, h_B\cdot W_B+QI{D}_{B2}\right)$ or not. To the client $A$ as an example, the message $<I{D}_A,I{D}_B,U_{A1},U_{A2},V_A,QI{D}_{A1}>$, where $W_A=H_2\left(U_{A1},U_{A2}\right)$, $h_A=f_1\left(I{D}_A,QI{D}_{A1}\right)$ and $QI{D}_{A2}=H_1\left(I{D}_A\right)$ can be viewed as a signature on a message $U_{A2}$ in Tseng et al.’s ESL-secure ID-AKE protocol. According to the security analysis by Tseng et al., if an adversary could have obtained the ephemeral secret $r_A$ using ESL attacks, the adversary still needs to solve the computational Diffie-Hellman problem to violate the client-to-server authentication.
  The application server $B$ authenticates the authentication server $S$ by checking whether $\widehat{e}\left(V_{SB},P\right)=\widehat{e}\left(U_S+h_{SB}\cdot QI{D}_S, P_{pub}\right)$ or not. The message $V_{SB}$, where $V_{SB}=r_S\cdot P_{pub}+h_{SB}\cdot DI{D}_S$, $h_{SB}=f_2\left(I{D}_A,I{D}_B,U_S,U_{SB1},U_{SB2}\right)$ and $DI{D}_S=s\cdot QI{D}_S$, can be viewed as a signature on a message $<I{D}_A,U_S, U_{SB1},U_{SB2}>$. Without knowledge of the authentication server $S$’s private key $s$, none of the participants or adversaries can forge the message and compute a valid signature. To forge a valid message $<I{D}_A,U_S, U_{SB1},U_{SB2},V_{SB}>$, an adversary must have obtained the authentication server $S$’s private key $s$ from $P_{pub}$, where $P_{pub}=s\cdot P$. It is a discrete logarithm problem to the adversary.
  The proposed protocol provides the server-to-client authentication that is also based on Tseng et al.’s ESL-secure ID-AKE protocol. The client $A$ and the application server $B$ authenticate the authentication server $S$ by checking whether $Aut{h}_{SA}=f_3\left(I{D}_A,I{D}_B,U_{A1},U_{A2},V_A,N_A,K_{AS},U_S,U_{SA1},U_{SA2}\right)$ and $Aut{h}_{SB}=f_3\left(I{D}_A,I{D}_B,U_{B1},U_{B2},V_B,N_B,K_{BS},U_S,U_{SB1},U_{SB2}\right)$ or not. Even though an adversary could obtain the client $A$’s ephemeral secret $r_A$ by the ESL attacks. Since $<Aut{h}_{SA}>$ and $<Aut{h}_{SB}>$ are derived from $K_{SA}=s\cdot U_{A2}=r_A\cdot DI{D}_{A2}=K_{AS}$ and $K_{SB}=s\cdot U_{B2}=r_B\cdot DI{D}_{B2}=K_{BS},$ respectively. To violate the server-to-client authentication, the adversary has to solve the computational Diffie-Hellman problem to obtain $DI{D}_{A2}$ and the discrete logarithm problem to compute the application server $B$’s ephemeral secret $r_B$ and the computational Diffie-Hellman problem to obtain $DI{D}_{B2}$ from the transferred messages. Otherwise, the adversary only can compute the authentication server $S$’s private key $s$ from $P_{pub}$, in which the adversary needs to solve the discrete logarithm problem.
  The application server $B$ can be sure that the client $A$ has obtained the session key by checking whether $Aut{h}_{AB}=f_4\left(I{D}_A,I{D}_B,U_S,K_{BA}\right)$ or not. The client $A$ checks whether $Aut{h}_{BA}=f_5\left(I{D}_A,I{D}_B,U_S,K_{AB},Aut{h}_{AB}\right)$ or not to be sure that the application server $B$ also has obtained the session key and both of them with the authentication server $S$ can agree upon the common session key $S{K}_{AB}=f_6\left(I{D}_A,I{D}_B,U_S,K_{AB},Aut{h}_{AB},Aut{h}_{BA}\right)$. For computing a valid message $<Aut{h}_{AB}>$ or $<Aut{h}_{BA}>$, we assume that the client $A$’s ephemeral secret $r_A$ has been compromised by an adversary. Since the messages $<Aut{h}_{AB}>$ and $<Aut{h}_{BA}>$ are derived from $K_{AB}=\widehat{e}\left(r_A\cdot P_{pub}+K_{AS},U_{SA1}+U_{SA2}\right)=\widehat{e}\left(U_{SB1}+U_{SB2},r_B\cdot P_{pub}+K_{BS}\right)=K_{BA}$, where $K_{AS}=r_A\cdot DI{D}_{A2}$ and $K_{BS}=r_B\cdot DI{D}_{B2}$, the adversary must solve the computational Diffie-Hellman problem to compute $DI{D}_{A2}$ or the discrete logarithm problem to compute $r_B$ and the computational Diffie-Hellman problem to compute $DI{D}_{B2}$ from transferred messages. Otherwise, the adversary only can compute the authentication server $S$’s private key $s$ from $P_{pub}$, in which the adversary needs to solve the discrete logarithm problem.
  Without knowledge of the private key of a participant (e.g., the client $A$’s private key $DI{D}_A$). An adversary cannot impersonate the participant since the adversary is unable to forge a valid signature. The proposed protocol employs the signature to authenticate the participants’ identities and one way hash function to protect the integrity of the transferred messages. Even though the ephemeral secret of the client has been compromised, each participant can be sure that none of the adversaries can impersonate other participants to violate the verification procedures and corrupt the participants’ private keys and the session key.
• Known Key Security. Suppose that an adversary can eavesdrop on the transmitted messages to learn the previous session keys. However, the session key of the proposed protocol is unique and dependent of each participant’s ephemeral secrets $r_A$, $r_B$ and $r_S$ and private keys $DI{D}_{A2}$, $DI{D}_{B2}$ and $s$. Therefore, knowledge of the previous session keys does not enable the adversary to derive other session keys and does not give the adversary any information that the adversary could use to derive other session keys. Even though the client $A$’s ephemeral secret $r_A$ has been compromised. If an adversary would like to compute $K_{AB}=\widehat{e}\left(r_A\cdot P_{pub}+K_{AS},U_{SA1}+U_{SA2}\right)$, where $K_{AS}=r_A\cdot DI{D}_{A2}$ from the transferred messages, the adversary needs to solve the computational Diffie-Hellman problem to compute the client $A$’s private key $DI{D}_{A2}$ or the discrete logarithm problem from $P_{pub}$, where $P_{pub}=s\cdot P$ to obtain the authentication server $S$’s private key $s$. Otherwise, the adversary only can solve the discrete logarithm problem and the computational Diffie-Hellman problem to compute the application server $B$’s corresponding ephemeral secret $r_B$ and private key $DI{D}_{B2}$. In the proposed protocol, even if one of the session key has been compromised, the security of the other or future session keys is not endangered.
• Partial Forward Secrecy. The proposed protocol session key is dependent on each participant’s private key and corresponding ephemeral secret. In the proposed protocol, if the private key of client $A$ or the application server $B$ has been compromised, an adversary also needs to obtain the corresponding ephemeral secrets to compute the session key. Suppose that the adversary would like to compute the corresponding ephemeral secrets from the transferred messages, the adversary needs to solve the discrete logarithm problem. However, if the adversary corrupts the private key $s$ of the authentication server $S$, it is obvious that all of the previous session keys can be recovered from the transferred messages. Since the adversary is indeed able to compute $K_{SA}=s\cdot U_{A2}$, $K_{AB}=\widehat{e}\left(s\cdot U_{A1}+K_{SA},U_{SA1}+U_{SA2}\right)$ or $K_{SB}=s\cdot U_{B2}$, $K_{BA}=\widehat{e}\left(U_{SB1}+U_{SB2},s\cdot U_{B1}+K_{SB}\right)$ and $S{K}_{AB}=f_6\left(I{D}_A,I{D}_B,U_S,K_{AB},Aut{h}_{AB},Aut{h}_{BA}\right)$. The proposed protocol offers partial forward secrecy.
• Key-Compromise Impersonation Resilience. To discuss the key-compromise impersonation resilience property, we assume that client $A$’s private key $DI{D}_A$ is compromised to an adversary who tries to impersonate the application server $B$ to cheat the client $A$ and the authentication server $S$. When the client $A$ requests service from the application server $B$, the adversary only can choose $<I{D}_B,U_{B1},U_{B2},V_B,QI{D}_{B1}>$ and $<Aut{h}_{BA}>$ from the previous sessions and send them to the authentication server $S$ and the client $A$, respectively. Since the adversary cannot derive the application server $B$’s private key $DI{D}_{B2}$ and the corresponding ephemeral secret $r_B$ from the transferred messages to compute $K_{BA}=\widehat{e}\left(U_{SB1}+U_{SB2},r_B\cdot P_{pub}+K_{BS}\right)$, where $K_{BS}=r_B\cdot DI{D}_{B2}$. The adversary only can violate the verification procedures of the authentication server $S$. If the adversary tries to derive the ephemeral secret $r_B$ and the private key $DI{D}_{B2}$ from the transferred messages to compute $Aut{h}_{BA}=f_5\left(I{D}_A,I{D}_B,U_S,K_{BA},Aut{h}_{AB}\right)$ and construct the session key, the adversary needs to solve the discrete logarithm problem and the computational Diffie-Hellman problem.
• Unknown Key-Share Resilience. To implement such an attack, the adversary is required to obtain the private key of client $A$ or the application server $B$. In the proposed protocol, both of the client $A$ and the application server $B$ have to be authenticated by the authentication server $S$. Only the participant that has the private key distributed from the authentication server $S$ could compute the valid signature and thus pass the verification procedures and compute the session key. To the client $A$ as an example, the client $A$ with its private key $DI{D}_A$ and the ephemeral secret $r_A$ can compute $V_A=\left(r_A+DI{D}_{A1}\right)\cdot W_A+DI{D}_{A2}$ and $K_{AB}=\widehat{e}\left(r_A\cdot P_{pub}+K_{AS},U_{SA1}+U_{SA2}\right)$ to pass the verification procedures of the authentication server $S$ and the application server $B$. The ephemeral secret $r_A$ with $DI{D}_{A2}$ are able to compute the session key $S{K}_{AB}=f_6\left(I{D}_A,I{D}_B,U_S,K_{AB},Aut{h}_{AB},Aut{h}_{BA}\right)$. Hence, the proposed protocol can withstand an unknown key-shared attack.
• Key control Resilience. In the proposed protocol, the session key $S{K}_{AB}=f_6\left(I{D}_A,I{D}_B,U_S,K_{AB},Aut{h}_{AB},Aut{h}_{BA}\right)$, where $K_{AB}=\widehat{e}\left(r_A\cdot P_{pub}+K_{AS},U_{SA1}+U_{SA2}\right)=\widehat{e}\left(U_{SB1}+U_{SB2},r_B\cdot P_{pub}+K_{BS}\right)=K_{BA}$ is determined by all participants’ private keys and corresponding ephemeral secrets. None of the participants can force a session key to be predetermined or predict the value and control the outcome of the session key. Hence, the proposed protocol ability to prevent the session key is created only by the authentication server $S$ or other two participants.

4.2. Formal Analysis Using AVISPA

Besides the above analysis we also provide a formal analysis of the proposed protocol using AVISPA. AVISPA is a push-button tool which is one of the commonly used automated security validation tools for Internet security-sensitive protocols and applications [19]. AVISPA was developed based on the Dolev-Yao intruder model [35]. In this model, the intruder has full control over the network and the intruder can intercept, inject, analyze and modify messages in transit. In addition, the intruder can play the role of a legitimate participant and gain knowledge of the compromised participant, but he is not allowed to crack the underlying cryptography. The first step in using AVISPA is to implement the analyzed protocol in High-Level Protocol Specification Language (HLPSL) that is an expressive, modular, role-based formal language for security protocol description and specifying their security properties. The HLPSL presentation of the analyzed protocol is translated into a lower level language called Intermediate Format (IF) using HLPSL2IF. IF the analyzed protocol is used as an input to different back-ends, the current version of AVISPA tool comprises four back-ends that implement a variety of automatic analysis techniques, namely, On-the-fly Model-Checker (OFMC), Constraint-Logic-based Attack Searcher (CL-AtSe), SAT-based Model-Checker (SATMC), and Tree Automata based on Automatic Approximations for the Analysis of Security Protocols (TA4SP) [30]. The four back-ends perform the analysis and output the results in precisely defined output format stating whether problems exist in the protocol or not. Thus, AVISPA is appropriate for the analysis of large-scale security protocols and applications.

To evaluate the proposed protocol security using AVISPA, we implemented the proposed protocol using the HLPSL and the role specifications of the client, the application server and the authentication server are given in Appendix A. We simulated the proposed protocol using the AVISPA web tool [36]. The proposed protocol is analyzed in the OFMC and CL-AtSe back-ends. Both of the two back-ends are helpful for the verification of the proposed protocol and detection of attacks. Note that intruder knowledge of the proposed protocol comprises the ephemeral secret $r_A$ of the client. After executing the code in AVISPA web tool, both OFMC and CL-AtSe back-ends outputs were generated and shown in Figure 4 and Figure 5. From the simulated results, there are no major attacks to the protocol and the simulated results also confirm the correctness of the protocol security analysis. The security goals of the proposed protocol are achieved and thus the proposed protocol confirms security against various active and passive attacks.

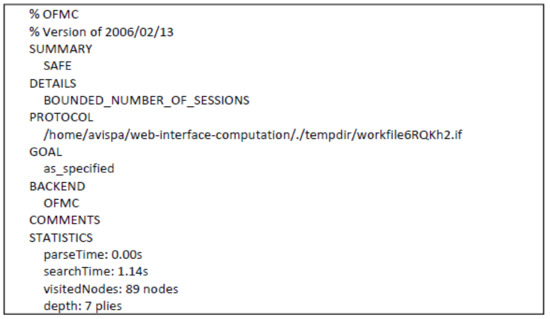
Figure 4. Simulation result of the proposed protocol on On-the-fly Model-Checker (OFMC) model checker.

Figure 5. Simulation result of the proposed protocol on Constraint-Logic-based Attack Searcher (CL-AsSe) model checker.

4.3. Performance Analysis

In this section, the performance and the simulation results of the proposed protocol are analyzed. For convenience, the following notations are used to analyze the computational cost:

• $T{G}_e$: the execution time for a bilinear pairing operation $\widehat{e}: G_1\times G_1\to G_2$.
• $T{G}_{mul}$: the execution time for points in $G_1$ multiplication operation.
• $T_{exp}$: the execution time for a modular exponential operation in $G_2$.
• $T{G}_H$: the execution time for a map-to-point hash function in $G_1$.
• $T{G}_{add}$: the execution time for an addition operation of points in $G_1$ or a multiplication operation in $G_2$.
• $T_H$: the execution time for a one-way hash function.

The total computational cost for the client side in this proposed protocol is $T{G}_e+5T{G}_{mul}+T{G}_H+3T{G}_{add}+4T_H$. However, the computation in Step 1 of the mutual authentication and key agreement phase for the client side can be pre-computed using offline computation. The total cost for on-line computation on the client side is $T{G}_e+2T{G}_{mul}+2T{G}_{add}+4T_H$. The total computational cost for the application server side is $3T{G}_e+6T{G}_{mul}+T{G}_H+4T{G}_{add}+5T_H$. On the other hand, the authentication server side performs Steps 2 and 4 to authenticate the client, the application server and constructs the session key. The total computational cost for the authentication server side is $7T{G}_e+13T{G}_{mul}+4T{G}_H+7T{G}_{add}+8T_H$.

Note that compared with $T{G}_{add}$ and $T_H$, $T{G}_e$, $T{G}_{mul}$, $T_{exp}$ and $T{G}_H$ are more time-consuming [31]. The proposed protocol adopts an imbalanced computation technique and an online/offline computation technique to reduce the computational load for the client side. From the analysis result mentioned above, the computational burdens are major on the authentication server and the application server which are powerful servers and the offline pre-computation reduces the computational cost required for the client side. Although, bilinear pairing operations are still required for the client side, the proposed protocol captures all basic desirable security attributes including the ESL resistance and the authentication server is able to monitor the transferred messages to prevent and trace network crime. The required computation cost of the proposed protocol is also reasonable.

4.4. Software Performance

Scott et al. [37] and Oliveira et al. [38] implemented the related pairing-based operations for low-power computing devices (i.e., smartcards and sensor nodes) in 2006 and 2011, respectively. Scott et al. used the processor on the Philips HiPersmart card offers the maximum clock speed of 36 MHz for related pairing-based operations. Scott et al. pointed out that for the security level of the Ate pairing system, a popular and valid choice would be to use a supersingular curve or non-supersingular curve over a finite field $E\left(F_p\right)$, with $p=512$ bits and a large prime order $q=160$ bits. The simulations are performed with a simulator implemented in Android system. We used the Jpair library to execute the simulations, which is a Java implementation of bilinear pairings to implement the software and a mobile device (Android 5.0 and 2.3 GHz Intel Atom with 4 GB of RAM) for the client side. Since the Weil pairing evaluation is more time-consuming than the Tate pairing [39], simulations are provided based on the Tate pairing on a supersingular elliptic curve. In the proposed protocol security level, the parameters will be the same as Scott et al.’s experimental data mentioned above. Table 1 lists the simulations data for related pairing-based operations on the client side. The execution time results for the client side have an average of 1000 simulations. Table 2 lists the computational cost and the execution time (in seconds) on the client side, where the execution time is measured using Table 1. The proposed protocol adopts an online/offline computation technique in which the online execution time on the client side requires 0.553 s. Although, the bilinear pairing operations are still required for the client side, the proposed protocol is still efficient and suitable for mobile distributed computing environments.

Table 1. Computational cost on the client side.

	$\mathit{T}{\mathit{G}}_{\mathit{e}}$	$\mathit{T}{\mathit{G}}_{\mathit{m}\mathit{u}\mathit{l}}$	${\mathit{T}}_{\mathit{e}\mathit{x}\mathit{p}}$	$\mathit{T}{\mathit{G}}_{\mathit{H}}$	$\mathit{T}{\mathit{G}}_{\mathit{a}\mathit{d}\mathit{d}}$	${\mathit{T}}_{\mathit{H}}$
Android 5.0 and 2.3 $G{H}_z$ Intel Atom with 4 GB of RAM	0.251 s	0.148 s	0.076 s	0.002 s	0.001 s	0.001 s

Table 2. Execution time on the client side.

	Computational Cost (Total)	Computational Cost (Online)	Execution Time (Total)	Execution Time (Online)
Client Side	$T{G}_e+5T{G}_{mul}+T{G}_H+3T{G}_{add}+4T_H$	$T{G}_e+2T{G}_{mul}+2T{G}_{add}+4T_H$	$\fallingdotseq 1.0$s	$\fallingdotseq 0.553$s

5. Conclusions

We proposed an ESL-secure ID-based three-party AKA protocol for mobile distributed computing environments. The proposed protocol employs Tseng et al.’s ESL-secure ID-AKE protocol [7] against ESL attacks. The proposed protocol keeps all of the merits of KTAP regarding security including the authentication server is able to monitor the communication messages to prevent and trace network crime and solves the problems of KTAP in which the session key is only created by the authentication server. Each participant can contribute information to derive the common session key. In the security analysis, the proposed protocol resists ESL attacks and also satisfies the security attributes required for AKA protocols: known-key security, partial forward secrecy, key-compromise impersonation resilience, unknown key-share resilience and key control resilience. In addition, the formal validation of the proposed protocol is performed using an automated validation tool AVISPA. The simulations results show that the proposed protocol is secure against active and passive adversaries. In the performance analysis, the proposed protocol adopted an imbalanced computation technique to shift the computational burden to the powerful servers. The software performance simulation result shows that the mobile client could perform offline pre-computation to reduce the online computation cost. Furthermore, a parallel version of the proposed protocol is proposed to enhance the protocol run performance.

In the future, we will implement the proposed in the “To Say” APP. The “To Say” APP allows users store the last words (text, image, audio, and video) in the application server and send the last words to the designated receivers in a secure channel. The authentication server is responsible for authenticate the users and helps them to construct a common session key with the receivers. When the APP detects the users are not active, the server will automatically send the last words to the designated receivers.