Abstract
Virtual network embedding (VNE) is a key technology in network virtualization. Advantages of network symmetry are well known in the design of load-balanced routing algorithms and in network performance analysis. Our work in this paper shows that benefits of graph symmetry also extend to the domain of network embedding. Specifically, we propose an efficient VNE method based on modular and structured agency guidance, a regular graph function. The proposed method, which is based on symmetric intermediate graphs, offers two main advantages. Firstly, characteristics of the intermediate structures enhance the computational efficiency of the VNE process. Secondly, the static agency network modeled with such intermediate structures improves the quality of the resulting embedding. These two advantages of our method are elaborated upon and verified by examples and simulations, respectively. In addition, we present a theoretical analysis explaining the reasons behind the benefits offered by such middleware.
Keywords:
resource provisioning; network assignment; graph algorithms; network optimization; network simulations; overlay and other logical network structures MSC:
68M10
1. Introduction
1.1. Research Advances in Virtual Network Embedding
Network virtualization (NV) technology [1] represents a promising way of overcoming the network ossification problem, via providing an efficient solution to the mismatch between various Internet applications and rigid substrate physical network (SPN) architecture. Success in applying NV to allocation of computational resources in cloud data centers [1] encourages researchers to explore more efficient solutions and reliable schemes for realizing NV.
The main objects in NV are called virtual networks, which will be provided by Internet Service Provider (ISP) in next-generation network architecture. One virtual network consists of virtual nodes connected by virtual links. In essence, the virtual nodes are logical function entries that are constructed by allocating computational or communication resources from ISPs to provide user-expected services. This function of resource allocation is known as virtual network embedding (VNE). The term embedding is sometimes equivalent to mapping, provisioning or assignment. The process of virtual network embedding maps virtual nodes in VN to the resource nodes in SPN, and virtual links to the physical paths in SPN.
As key parts of NV technology, VN embedding and scheduling have received a great deal of attention from researchers since 2008. At first, static VNE algorithms, running in an offline mode, were considered [2]. In this approach, after the user VN is embedded into SPN by a mapping , the mapping need not be reconstructed when the property and status of SPN are changed.
Generally, the virtual network request (VNR) always arrives and leaves dynamically (almost randomly), and it is not known a priori. Thus, the VNE algorithm must process the continuously arriving VNRs in real time, along with the current status of the SPN, and needs to implement VNE in an online scheme. Even though the static VNE has a relatively simple algorithmic design, it is still difficult to apply practically, since its model relies on assumptions that do not hold in practice. Thus, online VNE has been pursued by Marquezan et al. [3], who begin by presenting a distributed way of solving dynamic type VNE. They then reorganize SPN to renew the embedding of VN when the original VNR changes, but the connection between VN nodes and links is not coordinated. Houidi [4] has proposed a fault-tolerant VNE scheme to tackle the node and link failures in SPN.
Currently, the main research focus is still on mathematical optimization and heuristics. Optimization approaches still derive by linear or integer programming, but with added objects reflecting varied user demands, changed SPN structure and performance, and relaxed optimization limitation to mitigate the computational complexity of solving VNE. Heuristic algorithms usually try to achieve a near-optimal solution, and contributions focus on improving the quality of VNE solution, i.e., closing the gap between approximate and optimal solutions. The various works in two approaches can be characterized as survivable/dependable VNE; multiple InPs [5], and topology-aware VNE [6,7]. Furthermore, VNE for special SPN has also garnered some attention, as in the case of datacenters, optical networks, and wireless networks. For example, Beck et al. [8] proposes a distributed and parallel framework called DPVNE to implement VNE, in which several VNE algorithms are run to map VNR into SPN so that the single point pressure in SPN is reduced and overall efficiency is improved. Zhang et al. [9] provide opportunistic resource sharing VNE scheme called ORS to deal with time-dependent VNRs, with time-slot allocation expressed as an optimization problem.
The online VNE with multiple InPs has also been discussed by Shen et al. [5], who employ a broker-like entity to make centralized decisions, with an information-sharing scheme providing part of InP’s information, while keeping its privacy. Their scheme uses integer programming to settle VNE in polynomial time. Their VNE scheme achieves 80–90% efficacy over other methods under the assumption of all SPN information being known.
Distributed and parallel algorithms are preferred for realizing VNE among multiple InPs. Houidi et al. [10] proposed a distributed method to solve the cross-domain (multiple InPs) VNE, regardless of network scale. Generally, parallel and distributed algorithms become desirable, if not necessary, when dealing with large-scale input objects, which requires the work to be extended to more SPN locations. Beck et al. [8] introduced an algorithmic framework named DPVNE to implement VNE in a parallel and distributed fashion. In their scheme, the SPN is clustered as levels, via a multi-level recursive bisection algorithm. Next, they determine the delegate nodes in each cluster to receive VNR and select the most appropriate to process it, setting the deadlock tree for each cluster to deal with parallel embedding of many VNRs to avoid conflicts in utilizing the resources of the SPN. Although experiments show that DPVNE can simultaneously process many VNRs with a low communication overhead and comparable embedding cost compared to centralized algorithms, the computational complexity of dynamic real-time embedding is unknown. Moreover, selecting the delegate nodes and embedding VNE in all clusters, usually with irregular topologies, also present difficult challenges. Houidi et al. [4] reconfigured the VNE in a distributed real-time scheme. However, the influence of existing VNE on the reconfiguration necessitates a formal approach, and the scheme usually entails a large overhead in message communication.
The main drawback of optimization type VNE methods is that they have a high computational complexity. Actually, when connecting the VNE to the multi-way separator problem, solving it is NP-hard [1]. Accordingly, Xue et al. [11] has aimed to implement VNE with a partition, using concurrency. The method called NC-DSBA utilizes a dynamically balanced service to improve the efficiency of VNE.
There are also other innovative approaches in the VNE field. Zhang et al. [9] postulate the application of an opportunistic mechanism to resource sharing in VNE. Cheng and Su [7] focus on the topology of SPN, coordinating the mapping of nodes and links. In the node-mapping stage, the topological properties of nodes in the physical network are considered as the most significant parameter of the VNE. They then emulate PageRank, Google’s method of ranking web pages, to rank the nodes for associating VN nodes with SPN nodes. Ultimately, the relations of node association are merged into the VNE algorithm to improve efficiency and acceptance ratio. Ref. [5] formulates VNE across-domain physical networks. Zhang and Gao [6] rank the nodes of SPN by topological properties to embed the users’ VN.
1.2. The Role of Network Symmetry
Readers of this journal hardly need to be reminded of the theoretical and practical importance of symmetry in nature and various technical domains. We thus focus in this section on the benefits of network symmetry in the design, analysis, management, and applications of computer and communications networks [12], factors that motivated us to pursue the line of research described in this paper. Sometimes, complete symmetry can be troublesome, and we must resort to symmetry-breaking methods to make progress by preventing or removing deadlocks and other points of indecision [13]. In a vast majority of instances, however, symmetry is an ally of network designer, evaluator, manager, and user because it leads to simplifications and efficiencies, advantages that we demonstrate for solving the VNE problem in this paper.
Symmetric networks lack a weakest point that might lead to service disruptions as a result of random malfunctions or deliberate attacks, and they lend themselves better to the use of distributed diagnostic methods [14]. They lead to simpler routing and load-balancing algorithms [15,16] because all nodes have the same view of the system and thus execute identical component tasks as part of the overall algorithm. The interchangeable parts of a symmetric network allow the system to more easily recover from the effects of node and link failures [17]. It has been proven that the ratio of network diameter to the average internode distance is upper-bounded by 2 in symmetric networks [18], thus making the diameter, which is an easily derived quantity, a good predictor of network performance. The average internode distance, which is a better predictor of actual network performance, is, by comparion, much harder to compute and much more sensitive to assumptions about link and node capacities, especially under failure scenarios.
Wide-area and local-area computer networks grow in an ad hoc manner, based on communications needs and geographic considerations. They are thus often irregular. However, given that such networks tend to contain a large number of nodes and links, lack of symmetry isn’t a major drawback. Such networks are often characterized as small-world or scale-free networks [19] that exhibit strong advantages in the face of failures, congestions, and other routing difficulties. Distributed decision-making reduces the complexity burden for many applications. However, for global resource management and mapping of user computations to such a network, topological irregularity creates immense computational burdens. Interconnection networks for parallel processing are more controllable in terms of topology, be they implemented by cables within equipment racks or by etched/printed paths on microchips or printed circuit-boards. It would be nice if the benefits of symmetry could be extended to all domains, including those in which topological symmetry is non-existent. Our work reported here represents a step in this direction.
1.3. Application of Symmetry to Our Scheme
Mainly, our VNE scheme employs the graph symmetry for two purposes: raising efficiency of VNE via symmetric graph auxiliary, and stabilizing VNE process via symmetric graph inducement.
To reduce the complexity of embedding a virtual network H into an irregular substrate network G, one can select a static topology model K to assist the embedding. The main advance of using an auxiliary K is that some good algorithm properties can be induced from K to H and G such that the related algorithms are probably simplified and enhanced after VNE is implemented, like routing and load balancing. As shown in Figure 1, we obtain a generalized subgraph homomorphism in (a) and isomorphism in (b) to model the abstract embedding H into G relying on a regular hypercube topology Cube(3). As aforementioned, a static model K with symmetry properties may reduce the complexity of embedding H to G. From the viewpoints of mathematics, one can solve to map K to G, and to map H to K so as to obtain the final to embed H to G. It should be noticed that the two structures related to are relatively static, and of the other two ones related to , the larger one generally keeps static. The total time complexity to solve and is reduced apparently than to solve independently.
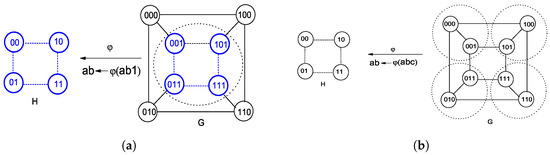
Figure 1.
Using the static Cube(3) as a substrate network model to reduce virtual network embedding problem into the generalized subgraph homomorphism in (a) and isomorphism in (b).
2. Defining and Modeling of VNE
In general, network virtualization represents the user demand as a virtual network in which the nodes and links indicate the resource and communication demands, respectively. Then, the virtual network embedding (VNE) algorithm, designed by SPN, embeds VN into SPN by way of resource allocation. The performance and impact of the NV system are influenced by its VNE scheme. Thus, efficient VNE solution is a key element in NV. Theoretically, VNE can be modeled as a generalized subgraph homomorphism from VN to SPN, which is a map keeping the adjacency relation along SPN nodes. The graph H abstracting VN is embedded into graph G representing SPN. This embedding should satisfy some constraints over the requested and provided resources, and it should optimize some parameters of interest to user and virtual network providers (VNP), such as maximal provider revenue and accepted ratio, and minimal embedding cost. To gain an intuition for grasping these notions, consider a two-level architectural model for virtual network embedding depicted in Figure 2.
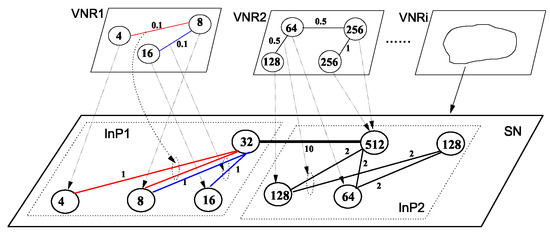
Figure 2.
A two-level architectural model for virtual network embedding, with the correspondence between virtual edge and physical edge for InP2 omitted. The numbers in circles indicate the switching capacity of the routing and switching devices, and the ones near the links represent the transmission bandwidth, in Gbps. Virtual-to-physical edge correspondence is marked by distinct colors.
Finding the optimal solution to a general graph embedding with constraints is an NP-hard problem. Thus, much research has dealt with designing heuristic algorithms to solve it [2,7,11,20,21], an area which has received much attention in recent years with the spread of network virtualization.
Let represent the SPN provided by the Infrastructure Provider (InP), where denotes the set of physical nodes and the set of physical links. Assume the existence of n types of physical resources and m types of physical links, and let be the vector space consisting of the available resource vector, namely,
, and be the vector space consisting of the available bandwidth vector, namely, . Likewise, let represent a virtual network request (VNR) from user, where denotes the set of virtual nodes and the set of virtual links. Let and be two functions representing the available resources of the nodes and links of SPN. Let and be two functions representing the allocated resources of the nodes and links of SPN. Then, the problem of embedding H into G can be modeled as finding two functions and , which are subject to and . If we merge these two functions as a pair of maps and the objective is to minimize the cost of embedding operation, then the current known methods to find can be characterized as solving following optimization problem:
where denotes the cost of the variable x. This problem is NP-hard [1].
3. Presentation and Analysis of Our Scheme
3.1. Overall Description of Scheme
Many relevant optimization problems are known to be NP-Hard. Heuristic algorithms exhibit multiple representation forms without a common framework, which makes their evaluation non-trivial. Thus, more precise models and efficient solution methods are called for. Additionally, structural features should be considered to improve the quality of algorithm with regard to practical applications. Techniques incorporating structural properties are expected to lead to more accurate and efficient solutions. The fundamental reason behind this situation is that real-time embeddings among highly random networks are usually hard to implement.
In order to increase the determinism of embedding the virtual network H into an irregular physical network, it is reasonable to create a static intermediate network, which we call agency network (AN), represented as graph K, as an auxiliary model between VN and SN. Theoretically, K should induce some desirable algorithmic properties to H and G such that simplified embedding can be discovered through it. Firstly, K should hold a low complexity in embedding VN and SN to it. Furthermore, some common algorithms such as routing should have a tendency to be easier in K than in SN. There are a few symmetric networks, including the well-known hypercube, swapped networks [22], as well as their biswapped [23] derivatives, which meet these two characteristics, and can be considered as suitable candidates for the intermediate network K.
From a mathematical viewpoint, one can find to embed K to G, and to embed H to K, so as to obtain the final to embed H to G, by merging and as . It should be noted that the two structures related to are relatively changeless and of the other ones related to , generally, the larger one remains static. Thus, the total time complexity of deriving and maybe less than that of deriving directly. As shown in Figure 3, we obtain a generalized subgraph homomorphism in Figure 3a and isomorphism in Figure 3b to model the abstract embedding of H into G, relying on the regular static hypercube topology.

Figure 3.
Performance and quality comparisons of our scheme with three representative VNE schemes for embedding a random VN into a random SN. (a) Runtime; (b) VNR acceptance ratio; (c) Cost/revenue ratio; (d) Node utilization ratio.
We now describe the concrete procedure of our proposed algorithm, called virtual network embedding through symmetric agency graph (SAG). To assist in understanding the critical steps, description of the algorithm is intertwined with a simple example.
3.2. Details of our Scheme
In this section, we first describe the fundamental principle of our proposed algorithm SAG. Then, we introduce three procedures of the algorithm, accompanied by a simple example. The presentation of each procedure is composed of the general description, pseudo-code elaboration, and figure explanation. A performance analysis of SAG at the end of this section provides the needed theoretical support.
Observe that almost all the substrate networks commonly exhibit a structural characteristic in which they have modular communication links (twisted-pair, optical fiber, and wireless transmission media) and processing nodes (router, switch node, and sever), though they are geographically scattered in different locations in the world. In essence, our scheme is to construct a symmetric graph agency to enhance the efficiency of virtual network embedding and accuracy of mapping. Putting it another way, this scheme decomposes the node and link mappings of VNE into two steps. Initially, we utilize the modular feature of VN and SN to re arrange the links and nodes of the seemingly unstructured VN and SN such that they are statically registered to a modular intermediate network AN. Then, relying on the guidance of AN, the substrate resources of optimal matching of the virtual demands will be discovered. Next, we explain the critical steps of this scheme, supplemented with its execution details. The pseudo-code for Algorithm 1 can be interpreted as follows.
| Algorithm 1 SAG-SP |
Input: virtual network VN= and substrate network SN = ; Output: virtual network mapping f which embeds and onto and , respectively;
|
3.2.1. Create a Symmetric Graph Agency, Based on Splitting the Substrate Network
The nodes and links of substrate network are split into groups. A modular and structured agency network is built for redistributing these grouped nodes and edges. The modularity of AN guarantees that each node group is correlated to a module that can induce the node mapping efficiently. Simultaneously, the structured module of the redistributed nodes and links can share precise and efficient routing algorithm such that discovering a link-balanced path required by a VNR is less complex. As listed in the pseudo code, Algorithm 2 partitions the nodes of VN and SN in terms of node weights. The weight of a node is assigned as the ratio between its performance and its cost. A majority of previous VNE algorithms pay more attention to minimizing the cost of embedding, and maximizing the SNP revenue. However, a VNE scheme is truly promising if and only if it can meet the performance requirement of customers at an attractive price. Although price and cost are two different notions, they are often linked, in that a low cost usually implies an acceptable price to users. Given a well partitioned SN, algorithm SAG selects a symmetric graph topology architecture as an agency network model for rearranging the nodes and links of SN.
| Algorithm 2 Pseudocode: partitionSNodes |
|
Figure 4a illustrates a substrate network G and a virtual network H that has been embedded, where the weights and the labels of SN nodes are expressed together as nonnegative integers . All nodes were split into two groups and , and a 2-modular structured network hypercube has been selected to act as the agency network.
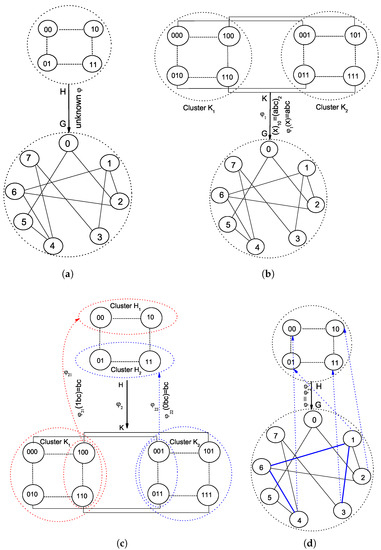
Figure 4.
As an example of implementing the SAG algorithm, (a) the virtual network H to be embedded into the substrate network G by mapping ; (b) initially, the substrate network G is registered to a 2-module cube network K by mapping ; (c) then, the virtual network H is embedded into K by mapping with a decomposition of embedding into two subsets corresponding to the two modules of H and K, respectively; (d) the mapping embedding H into G is found by merging mappings and .
3.2.2. Register the Resources of SN to AN
Subsequently, each node of SN is registered into that of symmetric agency graph with the closest node weight, and a link of SN is registered into an edge if there is an edge between two endpoints of this link in AN. Otherwise, an optimal path between two endpoints will be registered. Algorithm 3 (see the pseudo code) maps all nodes of SN to AN. It starts by discovering the closest node group matching each SN node, and registering an exact position in a real interval that is maintained by a node in the found AN module. The range of interval accommodating in k-th SAG node is , with a mechanism familiar with an efficient P2P lookup structure Chord [24]. In order to map links of SN to AN, the function executes the weighted Dijkstra algorithm for determining the optimal path connecting two AN nodes x and y. Then, the SN link whose two endpoints were mapped to x and y is embedded to this derived optimal path. Note that the bandwidth and delay of links are taken into consideration in calculating their weights.
| Algorithm 3 Pseudocode: registerSNnodes |
|
To give the reader a feel for the statement above, Figure 4a depicts a scenario that SN nodes have been registered to two well-structured modules and through a mapping . In particular, the mapping has been ideally simplified for clarifying the description.
3.2.3. Embed VN to SN via AN
Algorithm 4 performs mapping , integrates it with , and deduces the overall mapping . This process initializes with a preprocessing step, which ranks the nodes of VN according to their weighs. When mapping a VN node, directly locate its lower goal module in AN, and map this VN node to a node in located AN module with optimally matched weight. Finally, by integrating this mapping with the one derived in the stage of registering SN nodes, we have derived a mapping from VN to SN through AN as an intermediary. In order to assess how well our scheme functions for solving a VNE problem, its efficiency will be analyzed later.
At first sight, it seems that decomposing into two independent mappings and instead of exploring a direct embedding may lead to redundant work. However, there are theoretical and experimental indications that such a two-stage method is indeed beneficial for solving VNE problem under multiple practical circumstances. Actually, compared with the dynamically varied virtual network requests, the structure and state of the substrate network keep fairly static. Empirically, this will reduce the complexity of finding and maintaining the mapping between K and G. Additionally, obtaining the mapping between H and K generally holds a lower complexity since the ordered VN nodes are able to rapidly match a goal in a set of ordered nodes located at a well-structured network. Simultaneously, the link spanning them will be mapped more simply because the routing related algorithms, such as the one of Dijkstra’s shortest path, can be implemented more efficiently. For example, as illustrated in Figure 4c, all nodes of H and K are partitioned into two groups, and the node with label of K is mapped into one with label by a mapping made possible by the property of being symmetric. Finally, the overall embedding is derived after merging with in Figure 4d.
| Algorithm 4 Pseudocode: embedding |
|
3.3. Efficiency Analysis
As already stated, resolving the problem formulated by Equation (1) is NP-hard. Recent research therefore focuses on exploring approximate algorithms that generally treat VNE as an issue analogous to the node assignment or matching between a graph and its subgraphs or other graphs. The problem of assigning or matching nodes of a graph to its subgraphs or other graphs has received broad attention in machine learning and related fields, where graph-based data are used. The problem has emerged as subgraph isomorphism detection, that is, discovering a hidden goal usually expressed as subgraphs in a given graph pattern. The same problem has emerged in molecular biology, where it was equivalently defined as network alignment for identifying possible mappings between the nodes representing the proteins of protein networks to understand how proteins in the cell interact with others [25]. The essence of network alignment is to find an isomorphic subgraph between the two networks, a problem that is known in graph theory as the problem of maximum common subgraph. A majority of combinatorial optimization problems alluded to in the discussion above are NP-complete. Graph isomorphism or (maximum) subgraph isomorphism are both challenging problems in theoretical computer science. Though virtual network mapping has also been treated as subgraph isomorphism detection [26], it is perhaps more complicated than subgraph isomorphism because one node or link in SN can accommodate multiple VN nodes or links, and one link in VN can be mapped into a path in SN. Generally speaking, this means an explosive growth in number of combinatorial enumerations. It is slightly more accurate to formulate virtual network mapping as seeking a p-homomorphism between a graph H and a subgraph of other graph G, where p-homomorphism is formally defined by Fan et al. [27] as follows.
Definition [27] (p-homomorphism): Graph is said to be p-homomorphic to , denoted by , if there exists a mapping from to such that, for each edge in , there exists a nonempty path in such that and , i.e., each edge from is mapped to a path emanating from . The mapping is referred to as a p-hom mapping from to . In particular, if mapping is a one to one(injective) p-hom mapping, then graph is further said to be 1-1 p-hom to . □
In order to understand the NP-completeness degree of a general VNE, let us estimate the time complexity devoted to this task. Determining whether graph is p-hom or 1-1 p-hom to its subgraph cannot be accomplished in polynomial time. This suggests that no matter how we embed a virtual node to a substrate node, that is, one-to-one or multiple-to-one, VNE is intractable in polynomial time. Theorem 1 ([27]) confirms this conclusion via a formal generalization. For more details of its proof, please refer to Appendix A of [27].
Theorem 1.
Given graphs and , it is NP-complete to decide whether is p-hom or 1-1 p-hom to .
In order to get around the intractability of VNE problem, much recent research has focused on devising efficient heuristic algorithms (e.g., [2,6,7,9]). Unfortunately, no algorithm can find the p-hom mappings within of its optimal runtime. This means that, if guaranteeing embedding quality is desired, VNE is hard to approximate. This fact has been referred to as the approximation hardness of p-hom related problems, and formalized as Theorem 2 ([27]).
Theorem 2.
The p-hom related problems are not approximable within for any constant ϵ, where n is the maximal number of nodes in graphs and .
We now proceed with Theorem 3 that demonstrates our SAG algorithm to be capable of approaching this lower bound, thus providing a performance guarantee on embedding quality. In the SAG algorithm, assume that the substrate network with n nodes has been registered to a AN with a number of modules r such that the i-th module contains nodes, and all m nodes of the virtual network are associated with these modules, such that there are nodes that are embedded into module i. Theorem 3 shows that SAG reaches complexity under the condition .
Theorem 3.
Let n and m be the number of SN and VN nodes and denote by and be the number of SN and VN nodes corresponding to the ith module of r AN modules, respectively. Assume that the weights of SN and VN nodes conform to the uniform probability distribution. If , then SAG can find a p-hom mapping from graph H to a subgraph of G within time .
Proof.
Denote by and the groups of SN and VN nodes that have been registered to the ith AN module. Let be a set of random variables whose values are set to if the ith SN or VN node is associated with the node group with probability , where represents the probability that a randomly selected node lies in . Then, and , where denotes the binomial distribution. Likewise, and . The complexity of algorithm SAG can be expressed as according to the embedding procedure. By the precondition of node weights being uniform, it can be deduced from the mathematical expectation properties of binomial distribution that
☐
In essence, this theorem establishes that, for a symmetric graph AN, our algorithm can embed an VN with limited size to an SN in a time linearly growing with the scale of networks. Experimental results support this theoretical argument, where SAG runtime exhibits nearly linear growth upon increasing the size of the substrate network with uniform increments.
4. Simulation Results
In this section, we report on the results of a number of simulations conducted to experimentally validate performance and quality of algorithm SAG. The experimental platform is facilitated with software IDE Eclipse (Neon, Eclipse Foundation, Ottawa, ON, Canada) under the 32-bit Windows 7 operating system (Microsoft Corporation, Redmond, Washington, D.C., USA), and hardware CPU Intel(R) Core(TM) i7 5600-U @2.6 GHz with 8.0 GB RAM (Intel Corporation, Santa Clara, CA, USA). All simulations generate the results with Alevin 2.1, developed by Beck et al. [28], which has successfully functioned as a significant simulation framework for examining virtual network embedding algorithms.
We encoded algorithm SAG with programming language Java to generate subclass extending the class GenericMappingAlgorithm that has been realized as an algorithmic framework of generic VNE algorithms, and implemented all simulations under multiple experimental circumstances under various associated scenarios. In addition, we enriched the java package vnreal.generators of Alevin to allow more network topologies to be derived from it, including the well-structured hypercube network, and the highly-modular swapped networks. The latter class is established by an approach of selecting a graph from the list of network generator as the basic graph, then connecting n copies of this basic graph by edges called swapped links. The process of each experiment can be decomposed into network generation, algorithm configuration and execution, and algorithm evaluation, with various experimental configurations.
The experimental steps and corresponding configurations are further detailed in Table 1. In addition, a comparison of SAG with a couple of representative VNE algorithms, that have been cited as the focus of considerable VNE research, has been conducted in terms of runtime, VNR acceptance ratio, cost revenue ratio (C/R), and node utilization ratio (NU), factors that have been recognized as effective means of assessing VNE algorithms. Eventually, the results of comparison have been figured to perceive the effect of varied topologies and scale of VN and SN on VNE performance and quality.

Table 1.
Experimental parameters of network generation, a and b being constant factors.
4.1. Scenario Generation
The step of network generation goes through establishing network topology, adding resources to SN, as well as adding demands to VN. Two network topologies, the Fat-tree topology suggested in [29], and the randomly constructed network, which have been recognized as practical topologies modelling datacenters and the Internet, respectively, are selected as the SN models. The random topologies are generated with a probability 0.5 of connecting a pair of nodes. The number n and m of SN and VN nodes increase linearly with the iteration i of experiment and , where a and b are constant factors controlling the growth of SN and VN, respectively. For the topology of agency network, a swapped network is chosen, in which the swapped approach is used to construct an expanded network based on the factor graph being an node ring. Refer to [22] for more details regarding how to build a swapped network. The configuration parameters of network generation are listed in Table 1.
4.2. Algorithm Configuration
Algorithms chosen for our experimental evaluation involve three representative VNE algorithms, which have been proposed in [7,20,30] described in Table 2. These algorithms along with our proposed SAG are executed on identical scenarios and parameter configurations. In order to observe the performance of SAG, all algorithms chosen for evaluation were run 40–50 times under identical scenario set-ups, but increasing size of SN and VN, as reflected in Table 1. In the stage of mapping nodes, the weights of CPU nodes are set to 1, and the candidates of a VN node are limited within a distance of 20 hops away from it. The situation of node overload has not yet been considered. In the stage of mapping links, the parameter k of mapping a VN link to a length-k shortest path is set to , and the weights on link bandwidth conform to the uniform distribution in interval (see Table 1).

Table 2.
Representative VNE approaches chosen for evaluation.
4.3. Evaluation Results
The simulation proceeds with a set of widely applied network topologies, as listed in Table 1. In addition, the evaluation focuses on a collection of well-recognized VNE evaluation metrics, such as runtime, VNR acceptance ratio, cost revenue ratio (C/R), and node utilization ratio (NU), for assessing the competitiveness of our proposal. We expected that our algorithm would outperform its counterparts at least with respect to runtime, without guarantee of benefits in other metrics. Note that an intermediate network is perhaps capable of deducing the complexity of matching an objective resource to a request node, but we cannot be sure that this matching is accurate and low-cost. The results of performing all algorithms 40–50 times confirm that our strategy behaves with the expected runtime. Likewise, it generates a high-quality approximate solution in terms of other evaluation metrics. This means that SAG’s gains in efficiency come without loss of quality. Because we are primarily interested in the type of shortest path that VNE approaches, experiments regarding the kinds of path splitting have not yet been performed.
The results of comparisons with other algorithms in multiple metrics listed above are depicted in Figure 3 and Figure 5. We analyze these results by producing curves, and start the evaluation of each metric with a brief introduction to this that metric. We address the evaluation of SAG in three domains: efficiency, quality, and extensibility.
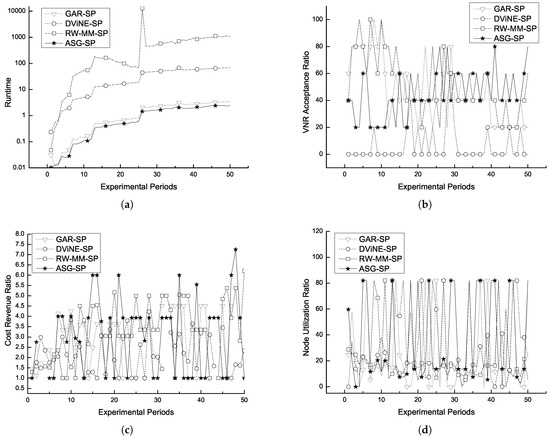
Figure 5.
Comparisons in performance and quality of SAG with three representative VNE schemes for embedding random VN into fat-tree SN. (a) runtime; (b) VNR acceptance ratio; (c) cost/revenue ratio; (d) node utilization ratio.
● Embedding efficiency
In the past, efficiency has not been widely considered as a criterion for assessing algorithms. Most previous VNE approaches [1,7,11,20,21,30] focus on quality-related metrics such as cost, revenue, node/link utilization, and node/link stress. However, the runtime of a VNE algorithm has a substantial effect on deployment in real applications, as pointed out in [8], where a distributed and parallel mechanism is proposed to improve efficiency. Actually, when our experiment reached the 46th iteration on randomly generated SN with 230 nodes, as shown in Figure 5, the optimization package GLPK 4.7 reached its time limit and stopped searching for solutions. This is why we were forced to reduce the originally scheduled 50 iterations in our experiment to 40 (Figure 3).
With respect to runtime, our algorithm exhibits an apparent improvement over DViNE-SP and RW-MM-SP, and also performs better than GAR-SP, as depicted in Figure 3a and Figure 5a. The simulation producing Figure 3a was conducted on a pair of randomly generated VN and SN. Through a 40-iteration test, SAG-SP embedded 71 percent of virtual network requests (VNR acceptance ratio) within average runtime , amounting to a less than half of GAR-SP’s . Unfortunately, the other two tested algorithms, DViNE-SP and RW-MM-SP, exhibited poor efficiency with average runtimes of and . As depicted in Figure 5a, an analogous trend in runtime can be observed from other experimental scenarios of embedding a random VN into a fat tree SN. In the case of fat tree SN, SAG-SP has a lower VNR acceptance ratio than in the case of random SN, and a moderate VNR acceptance ratio compared to other algorithms. This motivates us to strive for improved results in follow-up research.
● Embedding quality
The acceptance ratio is the ratio of successfully embedded virtual networks, which also reflects the number of VNRs that could not be embedded (rejected)by a VNE algorithm. The cost metric ratio reflects the amount of resources used by an embedding. As in previous approaches, cost is defined as the sum of the substrate resources allocated to the VNR. The revenue sums the revenue of the VNRs that were successfully mapped and the revenue of those that were not mapped. The cost-revenue ratio (C/R) measures the proportion of cost spent in the substrate network, taking into account the revenue that has been mapped. The lower the cost-revenue, the better the mapping quality. The node utilization (NU) of SN is calculated as the ratio of used CPU cycles to the number of nodes in it. It reflects the proportion of resources being utilized to meet the currently accepted VNRs.
On the randomly generated SN, SAG-SP generates a highest average VNR acceptance ratio , lowest average cost/revenue ratio , and the second largest average node utilization ratio compared with the other three algorithms, as listed in Table 3 and Table 4. More broadly, Figure 3a,c,d demonstrates that SAG-SP produces more competitive values with regard to three VNE evaluation metrics than the other three approaches. The only exception being that SAG-SP lags behind DViNE-SP in node utilization ratio. This anomaly is probably due to the fact that DViNE-SP, as the exclusively optimization-based VNE approach being tested achieves an exact solution from its objective function that assigns SN resources to VN more precisely. On the other hand, we also notice that sometimes the experimental results yield unstable distributions in terms of cost/revenue ratio and node utilization ratio in the case of the Fat-tree SN. In this regard, our future research plans include attempts at understanding how topological features of SN affect stability in our algorithm, so that we can fine-tune it to behave more stably on fat-tree class networks. Overall, our algorithm is capable of trading off performance and quality better than other approaches, including for fat-tree SN.

Table 3.
Comparison of the average values of the evaluation metrics from 40 test iterations executed on randomly generated VN and SN.

Table 4.
A comparison in performance and quality of VNE algorithms when the VN and SN networks are enlarged to maximal sizes of 200 and 80 (reached in the 40th iteration of our experiment), respectively, to demonstrate the scalability of our strategy.
● Scalability
To assess the scalability of presented method, our experimental setup handles increasingly various VN and SN sizes, with a more extensive VN range, varying from 2 to 100. Note that the number of VN nodes ranges from 2 to 20 in [20], 20 to 40 in [26], and 20 to 100 in [7]. It can be observed from Figure 3 and Figure 5 that our approach exhibits greater advantages as the network sizes grow. It exhibits a nearly linearly increasing runtime with the growth of VN and SN sizes. In the 40th iteration of our experiment, when the VN and SN networks reach the maximal sizes of 200 and 80, SAG-SP’s runtime is , compared with , , and for its counterparts GAR-SP, RW-MM-SP, and DViNE-SP, respectively, with a nearly equal mapping quality.
As stated earlier, it is an extremely challenging goal to achieve optimal or nearly optimal solutions for addressing a general VNE problem. Besides runtime, the rest of the parameters reflecting VNE quality appear to fluctuate in the process of increasing VN and SN nodes. This implies that stability should also be a concern in assessing our method and competing approaches. In fact, a higher VNR acceptance ratio only reflects to what extent a VNR can be fulfilled technically. A holistic concept termed “acceptance” may be required to gauge the extent to which users and providers achieve an agreement, regardless of technical or business factors. In this regard, efficiency and stability are most essential standards to affect user’s decision in current user-centered environment.
5. Conclusions
Virtual network embedding is a fairly substantial part in network virtualization technology, and the latter may be qualified as a promising approach to overcoming the ossification problem arising in future network architectures. The computational intractability of optimization-based approaches, and the uncertain quality of heuristic algorithms have triggered vast amounts of research.
Our work brings forth the notion of using the structural characteristics of an intermediate network to facilitate the process of virtual network embedding. We have conducted a theoretical analysis and a series of simulation studies on multiple scenarios to validate that our strategy of using an appropriate agency network can accelerate the algorithm’s runtime, while maintaining the quality for a general VNE task.
An important observation arising from our experimental work is that current VNE algorithms lack stability. Theoretically, we are also interested in exploring the potential correlation of network topology with the quality of VNE. Our future research will cover these two problems, which will no doubt come with many challenges.
Acknowledgments
Chenggui Zhao’s work was supported by the National Science Foundation of China, Grant No. 61562089.
Author Contributions
Chenggui Zhao performed the theoretical derivation, experiments, and wrote the paper; Behrooz Parhami checked the derivation, and revised the paper.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| InP | Infrastructure Provider |
| ISP | Internet Service Provider |
| SN | Substrate Network |
| VN | Virtual Network |
| VNE | Virtual Network Embedding |
| VNP | Virtual Network Provider |
| VNR | Virtual Network Request |
References
- Fischer, A.; Botero, J.F.; Beck, M.T.; De Meer, H.; Hesselbach, X. Virtual network embedding: A survey. IEEE Commun. Surv. Tutor. 2013, 15, 1888–1906. [Google Scholar] [CrossRef]
- Lee, T.H.; Tursunova, S.; Choi, T.S. Graph clustering based provisioning algorithm for virtual network embedding. In Proceedings of the 2012 IEEE Network Operations and Management Symposium (NOMS), Maui, HI, USA, 16–20 April 2012. [Google Scholar]
- Marquezan, C.C.; Granville, L.Z.; Nunzi, G.; Brunner, M. Distributed autonomic resource management for network virtualization. In Proceedings of the 2010 IEEE Network operations and management symposium (NOMS), Osaka, Japan, 19–23 April 2010; pp. 463–470. [Google Scholar]
- Houidi, I.; Louati, W.; Ameur, W.B.; Zeghlache, D. Virtual network provisioning across multiple substrate networks. Comput. Netw. 2011, 55, 1011–1023. [Google Scholar] [CrossRef]
- Shen, M.; Xu, K.; Yang, K.; Chen, H.H. Towards efficient virtual network embedding across multiple network domains. In Proceedings of the 2014 IEEE 22nd International Symposium of Quality of Service (IWQoS), Hong Kong, China, 2 October 2014; pp. 61–70. [Google Scholar]
- Zhang, D.; Gao, L. Virtual network mapping through locality-aware topological potential and Influence node ranking. Chin. J. Electron. 2014, 23, 61–64. [Google Scholar]
- Cheng, X.; Su, S.; Zhang, Z.; Wang, H.; Yang, F.; Luo, Y.; Wang, J. Virtual network embedding through topology-aware node ranking. ACM SIGCOMM Comput. Commun. Rev. 2011, 41, 38–47. [Google Scholar] [CrossRef]
- Beck, M.T.; Fischer, A.; Botero, J.F.; Linnhoff-Popien, C.; de Meer, H. Distributed and scalable embedding of virtual networks. J. Netw. Comput. Appl. 2015, 56, 124–136. [Google Scholar] [CrossRef]
- Zhang, S.; Qian, Z.; Wu, J.; Lu, S.; Epstein, L. Virtual network embedding with opportunistic resource sharing. IEEE Trans. Parallel Distrib. Syst. 2014, 25, 816–827. [Google Scholar] [CrossRef]
- Houidi, I.; Louati, W.; Zeghlache, D. A distributed virtual network mapping algorithm. In Proceedings of the IEEE International Conference on Communications, ICC’08, Beijing, China, 19–23 May 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 5634–5640. [Google Scholar]
- Xue, J.; You, J.; Wang, J.; Deng, F. Nodes clustering and dynamic service balance awareness based virtual network embedding. In Proceedings of the TENCON 2013–2013 IEEE Region 10 Conference (31194), Xi’an, China, 22–25 October 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 1–4. [Google Scholar]
- Lakshmivarahan, S.; Jwo, J.S.; Dhall, S.K. Symmetry in interconnection networks based on Cayley graphs of permutation groups: A survey. Parallel Comput. 1993, 19, 361–407. [Google Scholar] [CrossRef]
- Itai, A.; Rodeh, M. Symmetry Breaking in Distributed Networks; Academic Press, Inc.: Cambridge, MA, USA, 1990; pp. 60–87. [Google Scholar]
- Parhami, B.; Tao, S. Taxonomy and Overview of Distributed Malfunction Diagnosis in Networks of Intelligent Nodes. J. Comput. Sci. Eng. 2016, 13, 23–31. [Google Scholar]
- Wang, N.C.; Hung, Y.P. Multicast Communication in Wormhole-Routed 2D Torus Networks with Hamiltonian Cycle Model; Elsevier: North-Holland, The Netherlands, 2009; pp. 70–78. [Google Scholar]
- Zhao, C.; Xiao, W.; Parhami, B. Load-balancing on swapped or OTIS networks. J. Parallel Distrib. Comput. 2009, 69, 389–399. [Google Scholar] [CrossRef]
- Dekker, A.H.; Colbert, B.D. Network robustness and graph topology. In Proceedings of the Australasian Conference on Computer Science, Dunedin, New Zealand, 18–22 January 2004; pp. 359–368. [Google Scholar]
- Parhami, B.; Yeh, C.H. Why Network Diameter is Still Important. In Proceedings of the International Conference on Communications in Computing, Las Vegas, NV, USA, 26–29 June 2000. [Google Scholar]
- Wang, X.F.; Chen, G. Complex networks: Small-world, scale-free and beyond. IEEE Circuits Syst. Mag. 2003, 3, 6–20. [Google Scholar] [CrossRef]
- Yu, M.; Yi, Y.; Rexford, J.; Chiang, M. Rethinking virtual network embedding: Substrate support for path splitting and migration. ACM Sigcomm Comput. Commun. Rev. 2008, 38, 17–29. [Google Scholar] [CrossRef]
- Aron, M.; Druschel, P.; Zwaenepoel, W. Cluster reserves: A mechanism for resource management in cluster-based network servers. ACM SIGMETRICS Perform. Evaluation Rev. 2000, 28, 90–101. [Google Scholar] [CrossRef]
- Parhami, B. Swapped interconnection networks: Topological, performance, and robustness attributes. J. Parallel Distrib. Comput. 2005, 65, 1443–1452. [Google Scholar] [CrossRef]
- Xiao, W.; Parhami, B.; Chen, W.; He, M.; Wei, W. Biswapped networks: A family of interconnection architectures with advantages over swapped or OTIS networks. Int. J. Comput. Math. 2011, 88, 2669–2684. [Google Scholar] [CrossRef][Green Version]
- Stoica, I.; Morris, R.; Karger, D.; Kaashoek, M.F.; Balakrishnan, H. Chord: A Scalable Peer-to-Peer Lookup Service for Internet Applications; ACM: New York, NY, USA, 2001; pp. 149–160. [Google Scholar]
- Singh, R.; Xu, J.; Berger, B. Pairwise global alignment of protein interaction networks by matching neighborhood topology. In Research in Computational Molecular Biology; Springer: Berlin/Heidelberg, Germany, 2007; pp. 16–31. [Google Scholar]
- Lischka, J.; Karl, H. A virtual network mapping algorithm based on subgraph isomorphism detection. In Proceedings of the 1st ACM Workshop on Virtualized Infrastructure Systems and Architectures, Barcelona, Spain, 17 August 2009; ACM: New York, NY, USA, 2009; pp. 81–88. [Google Scholar]
- Fan, W.; Li, J.; Ma, S.; Wang, H.; Wu, Y. Graph homomorphism revisited for graph matching. Proc. VLDB Endow. 2010, 3, 1161–1172. [Google Scholar] [CrossRef]
- Beck, M.T.; Linnhoff-Popien, C.; Fischer, A.; Kokot, F.; de Meer, H. A simulation framework for Virtual Network Embedding algorithms. In Proceedings of the 2014 16th International Telecommunications Network Strategy and Planning Symposium (Networks), Funchal, Portugal, 17–19 September 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 1–6. [Google Scholar]
- Leiserson, C.E. Fat-trees: Universal networks for hardware-efficient supercomputing. IEEE Trans. Comput. 2012, C-34, 892–901. [Google Scholar] [CrossRef]
- Chowdhury, M.; Rahman, M.R.; Boutaba, R. Vineyard: Virtual network embedding algorithms with coordinated node and link mapping. IEEE/ACM Trans. Netw. (TON) 2012, 20, 206–219. [Google Scholar] [CrossRef]
- Google. Available online: https://scholar.google.com (accessed on 1 April 2017).
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).