The LHC Higgs Boson Discovery: Updated Implications for Finite Unified Theories and the SUSY Breaking Scale

Abstract

Finite Unified Theories (FUTs) are $N=1$ supersymmetric Grand Unified Theories, which can be made finite to all orders in perturbation theory, based on the principle of the reduction of couplings. The latter consists of searching for renormalization group invariant relations among parameters of a renormalizable theory holding to all orders in perturbation theory. FUTs have proven very successful so far. In particular, they predicted the top quark mass one and half years before its experimental discovery, while around five years before the Higgs boson discovery, a particular FUT was predicting the light Higgs boson in the mass range ∼121–126 GeV, in striking agreement with the discovery at LHC. Here, we review the basic properties of the supersymmetric theories and in particular finite theories resulting from the application of the method of reduction of couplings in their dimensionless and dimensionful sectors. Then, we analyze the phenomenologically-favored FUT, based on SU(5). This particular FUT leads to a finiteness constrained version of the Minimal SUSY Standard Model (MSSM), which naturally predicts a relatively heavy spectrum with colored supersymmetric particles above 2.7 TeV, consistent with the non-observation of those particles at the LHC. The electroweak supersymmetric spectrum starts below 1 TeV, and large parts of the allowed spectrum of the lighter might be accessible at CLIC. The FCC-hhwill be able to fully test the predicted spectrum.

1. Introduction

In 2012, the discovery of a new particle at the LHC was announced [1,2]. Within theoretical and experimental uncertainties, the new particle is compatible with predictions for the Higgs boson of the Standard Model (SM) [3,4], constituting a milestone in the quest for understanding the physics of Electroweak Symmetry Breaking (EWSB). However, taking the experimental results and the respective uncertainties into account, also many models beyond the SM can accommodate the data. Furthermore, the hierarchy problem, the neutrino masses, the dark matter, the over twenty free parameters of the model, just to name some questions, ask for a more fundamental theory to answer some, if not all, of those.

Therefore, one of the main aims of this fundamental theory is to relate these free parameters, or rephrasing it, to achieve a reduction of these parameters in favor of a smaller number (or ideally only one). This reduction is usually based on the introduction of a larger symmetry, rendering the theory more predictive. Very good examples are the Grand Unified Theories (GUTs) [5,6,7,8,9] and their supersymmetric extensions [10,11]. The case of minimal $SU\left(5\right)$ is one example, where the number of couplings is reduced to one due to the corresponding unification. Data from LEP [12] suggested that a $N=1$ global Supersymmetry (SUSY) [10,11] is required in order for the prediction to be viable. Relations among the Yukawa couplings are also suggested in GUTs. For example, the $SU\left(5\right)$ predicts the ratio of the tau to the bottom mass $M_{\tau }/M_b$ [13] in the SM. GUTs introduce, however, new complications such as the different ways of breaking this larger symmetry, as well as new degrees of freedom.

A way to relate the Yukawa and the gauge sector, in other words achieving Gauge-Yukawa Unification (GYU) [14,15,16], seems to be a natural extension of the GUTs. The possibility that $N=2$ SUSY [17] plays such a role is highly limited due to the prediction of light mirror fermions. Other phenomenological drawbacks appear in composite models and superstring theories.

A complementary approach is to search for all-loop Renormalization Group Invariant (RGI) relations [18,19], which hold below the Planck scale and are preserved down to the unification scale [14,15,16,20,21,22,23,24,25]. With this approach, Gauge-Yukawa Unification (GYU) is possible. A remarkable point is that, assuming finiteness at one-loop in $N=1$ gauge theories, RGIrelations that guarantee finiteness to all orders in perturbation theory can be found [26,27,28].

The above approach seems to need SUSY as an essential ingredient. However, the breaking of SUSY has to be understood as well, since it provides the SM with several predictions for its free parameters. Actually, the RGI relation searches have been extended to the Soft SUSY Breaking (SSB) sector [25,29,30,31] relating parameters of mass dimension one and two. This is indeed possible to be done on the RGI surface, which is defined by the solution of the reduction equations.

Applying the reduction of couplings method to $N=1$ SUSY theories has led to very interesting phenomenological developments. Previously, an appealing “universal” set of soft scalar masses was assumed in the SSB sector of SUSY theories, given that, apart from economy and simplicity: (1) they are part of the constraints that preserve finiteness up to two loops [32,33]; (2) they are RGI up to two loops in more general SUSY gauge theories, subject to the condition known as $P=1/3Q$ [29]; and (3) they appear in the attractive dilaton-dominated SUSY breaking superstring scenarios [34,35,36]. However, further studies exhibited problems all due to the restrictive nature of the “universality” assumption for the scalar masses. For instance: (a) in Finite Unified Theories (FUTs) the universality predicts that the lightest SUSY particle is a charged particle, namely the superpartner of the $\tau$ lepton $\tilde{\tau }$; (b) the Minimal SUSY Standard Model (MSSM) with universal soft scalar masses is inconsistent with the attractive radiative electroweak symmetry breaking; and worst of all, (c) the universal soft scalar masses lead to charge and/or color breaking minima deeper than the standard vacuum [37]. Therefore, there have been attempts to relax this constraint without loosing its attractive features. First, an interesting observation was made that in $N=1$ GYU theories, there exists an RGI sum rule for the soft scalar masses at lower orders; at one loop for the non-finite case [38] and at two loops for the finite case [39]. The sum rule manages to overcome the above unpleasant phenomenological consequences. Moreover, it was proven [40] that the sum rule for the soft scalar masses is RGI to all orders for both the general and the finite case. Finally, the exact $\beta$-function for the soft scalar masses in the Novikov–Shifman–Vainshtein–Zakharov (NSVZ) scheme [41,42,43] for the softly-broken SUSY QCDhas been obtained [40]. the use of RGI both in the dimensionful and dimensionless sector, together with the above-mentioned sum rule, allows for the construction of realistic and predictive $N=1$ all-loop finite $SU\left(5\right)$ SUSY GUTs, also with interesting predictions, as was shown in [14,20,22,31,44,45,46,47,48].

This paper is organized as follows. In Section 2, we review the theoretical basis of the method of the reduction of couplings, which is extended in Section 2 to the dimensionful parameters. Section 3 is devoted to finiteness in the dimensionless sector of a SUSY theory in some detail. In Section 4, we discuss the implications of the method of reduction of couplings in the SUSY breaking sector of an $N=1$ SUSY theory including the finite case. Then, in Section 5, we review the best Finite Unified Modelselected previously on the basis of agreement with the known experimental data at the time [45]. the current setup of experimental constraints and predictions is briefly reviewed in Section 6 and applied to our best Finite Unified Model in Section 7, including in particular the latest improvements in the prediction of the light Higgs boson mass (as implemented in FeynHiggs). Our conclusions can be found in Section 8.

2. Theoretical Basis

In this section, we outline the idea of the reduction of couplings. Any RGI relation among couplings (which does not depend on the renormalization scale $\mu$ explicitly) can be expressed, in the implicit form $\mathrm{\Phi }(g_1,\cdots ,g_A)=const.$, which has to satisfy the Partial Differential Equation (PDE):

$$\mu \frac{d\mathrm{\Phi }}{d\mu }=\overrightarrow{\nabla }·\overrightarrow{\beta }=\sum _{a=1}^A{\beta }_a\frac{\partial \mathrm{\Phi }}{\partial g_a}=0,$$

(1)

where ${\beta }_a$ is the $\beta$-function of $g_a$. This PDE is equivalent to a set of ordinary differential equations, the so-called Reduction Equations (REs) [18,19,49],

$${\beta }_g\frac{d{g}_a}{dg}={\beta }_a,a=1,\cdots ,A,$$

(2)

where g and ${\beta }_g$ are the primary coupling and its $\beta$-function, and the counting on a does not include g. Since maximally ($A-1$) independent RGI “constraints” in the A-dimensional space of couplings can be imposed by the ${\mathrm{\Phi }}_a$’s, one could in principle express all the couplings in terms of a single coupling g. However, a closer look at the set of Equation (2) reveals that their general solutions contain as many integration constants as the number of equations themselves. Thus, using such integration constants, we have just traded an integration constant for each ordinary renormalized coupling, and consequently, these general solutions cannot be considered as reduced ones. The crucial requirement in the search for RGE relations is to demand power series solutions to the REs,

$$g_a=\sum _n{\rho }_a^{\left(n\right)}{g}^{2n+1},$$

(3)

which preserve perturbative renormalizability. Such an ansatz fixes the corresponding integration constant in each of the REs and picks up a special solution out of the general one. Remarkably, the uniqueness of such power series solutions can be decided already at the one-loop level [18,19,49]. To illustrate this, let us assume that the $\beta$-functions have the form:

$$\begin{array}{cc}\hfill {\beta }_a& =\frac{1}{16{\pi }^2}[\sum _{b,c,d\ne g}{\beta }_a^{\left(1\right)bcd}{g}_b{g}_c{g}_d+\sum _{b\ne g}{\beta }_a^{\left(1\right)b}{g}_b{g}^2]+\cdots ,\hfill \\ \hfill {\beta }_g& =\frac{1}{16{\pi }^2}{\beta }_g^{\left(1\right)}{g}^3+\cdots ,\hfill \end{array}$$

(4)

where ⋯ stands for higher order terms and ${\beta }_a^{\left(1\right)bcd}$’s are symmetric in $b,c,d$. We then assume that the ${\rho }_a^{\left(n\right)}$’s with $n\le r$ have been uniquely determined. To obtain ${\rho }_a^{(r+1)}$’s, we insert the power series (3) into the REs (2) and collect terms of $\mathcal{O}\left(g^{2r+3}\right)$ and find:

$$\sum _{d\ne g}M{\left(r\right)}_a^d{\rho }_d^{(r+1)}=\mathrm{lower} \mathrm{order} \mathrm{quantities},$$

where the r.h.s. is known by assumption, and:

$$\begin{array}{cc}\hfill M{\left(r\right)}_a^d& =3\sum _{b,c\ne g}{\beta }_a^{\left(1\right)bcd}{\rho }_b^{\left(1\right)}{\rho }_c^{\left(1\right)}+{\beta }_a^{\left(1\right)d}-(2r+1){\beta }_g^{\left(1\right)}{\delta }_a^d,\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill 0& =\sum _{b,c,d\ne g}{\beta }_a^{\left(1\right)bcd}{\rho }_b^{\left(1\right)}{\rho }_c^{\left(1\right)}{\rho }_d^{\left(1\right)}+\sum _{d\ne g}{\beta }_a^{\left(1\right)d}{\rho }_d^{\left(1\right)}-{\beta }_g^{\left(1\right)}{\rho }_a^{\left(1\right)},\hfill \end{array}$$

(6)

Therefore, the ${\rho }_a^{\left(n\right)}$’s for all $n>1$ for a given set of ${\rho }_a^{\left(1\right)}$’s can be uniquely determined if $\det M{\left(n\right)}_a^d\ne 0$ for all $n\ge 0$.

As will be clear later by examining specific examples, the various couplings in SUSY theories have the same asymptotic behavior. Therefore, searching for a power series solution of the form (3) to the REs (2) is justified. This is not the case in non-SUSY theories, although the deeper reason for this fact is not fully understood.

The possibility of coupling unification described in this section is without any doubt attractive, because the “completely reduced” theory contains only one independent coupling, but it can be unrealistic. Therefore, one often would like to impose fewer RGI constraints, and this is the idea of partial reduction [50,51].

Reduction of Dimension One and Two Parameters

The reduction of couplings was originally formulated for massless theories on the basis of the Callan–Symanzik equation [18,19]. The extension to theories with massive parameters is not straightforward if one wants to keep the generality and the rigor on the same level as for the massless case; one has to fulfill a set of requirements coming from the renormalization group equations, the Callan–Symanzik equations, etc. along with the normalization conditions imposed on irreducible Green’s functions [52]. There has been much progress in this direction starting from [25], where it was assumed that a mass-independent renormalization scheme could be employed so that all the RGfunctions have only trivial dependencies on dimensional parameters, and then, the mass parameters were introduced similarly to couplings (i.e., as a power series in the couplings). This choice was justified later in [30,53], where the scheme independence of the reduction principle has been proven generally, i.e., it was shown that apart from dimensionless couplings, pole masses and gauge parameters, the model may also involve coupling parameters carrying a dimension and masses. Therefore, here, to simplify the analysis, we follow [25], and we also use a mass-independent renormalization scheme.

We start by considering a renormalizable theory that contains a set of $(N+1)$ dimension zero couplings, $\left({\widehat{g}}_0,{\widehat{g}}_1,\dots ,{\widehat{g}}_N\right)$, a set of L parameters with mass-dimension one, $\left({\widehat{h}}_1,\dots ,{\widehat{h}}_L\right)$, and a set of M parameters with mass-dimension two, $({\widehat{m}}_1^2,\dots ,{\widehat{m}}_M^2)$. The renormalized irreducible vertex function $\mathrm{\Gamma }$ satisfies the RG equation:

$$\mathcal{D}\mathrm{\Gamma }\left[{\mathrm{\Phi }}^{\prime }s;{\widehat{g}}_0,{\widehat{g}}_1,\dots ,{\widehat{g}}_N;{\widehat{h}}_1,\dots ,{\widehat{h}}_L;{\widehat{m}}_1^2,\dots ,{\widehat{m}}_M^2;\mu \right]=0,$$

(7)

where:

$$\mathcal{D}=\mu \frac{\partial }{\partial \mu }+\sum _{i=0}^N{\beta }_i\frac{\partial }{\partial {\widehat{g}}_i}+\sum _{a=1}^L{\gamma }_a^h\frac{\partial }{\partial {\widehat{h}}_a}+\sum _{\alpha =1}^M{\gamma }_{\alpha }^{m^2}\frac{\partial }{\partial {\widehat{m}}_{\alpha }^2}+\sum _J{\mathrm{\Phi }}_I{\gamma }_J^{\varphi I}\frac{\delta }{\delta {\mathrm{\Phi }}_J},$$

(8)

where $\mu$ is the energy scale, while ${\beta }_i$ are the $\beta$-functions of the various dimensionless couplings $g_i$, ${\mathrm{\Phi }}_I$ are the various matter fields and ${\gamma }_{\alpha }^{m^2}$, ${\gamma }_a^h$ and ${\gamma }_J^{\varphi I}$ are the mass, trilinear coupling and wave function anomalous dimensions, respectively (where I enumerates the matter fields). In a mass independent renormalization scheme, the $\gamma$’s are given by:

$$\begin{array}{cc}\hfill {\gamma }_a^h& =\sum _{b=1}^L{\gamma }_a^{h,b}(g_0,g_1,\dots ,g_N){\widehat{h}}_b,\hfill \\ \hfill {\gamma }_{\alpha }^{m^2}& =\sum _{\beta =1}^M{\gamma }_{\alpha }^{m^2,\beta }(g_0,g_1,\dots ,g_N){\widehat{m}}_{\beta }^2+\sum _{a,b=1}^L{\gamma }_{\alpha }^{m^2,ab}(g_0,g_1,\dots ,g_N){\widehat{h}}_a{\widehat{h}}_b,\hfill \end{array}$$

(9)

where ${\gamma }_a^{h,b}$, ${\gamma }_{\alpha }^{m^2,\beta }$ and ${\gamma }_{\alpha }^{m^2,ab}$ are power series of the g’s (which are dimensionless) in perturbation theory.

We look for a reduced theory where:

$$g\equiv g_0,h_a\equiv {\widehat{h}}_a\mathrm{for} 1\le a\le P,m_{\alpha }^2\equiv {\widehat{m}}_{\alpha }^2\mathrm{for} 1\le \alpha \le Q$$

are independent parameters and the reduction of the parameters left:

$$\begin{array}{cc}\hfill {\widehat{g}}_i& ={\widehat{g}}_i\left(g\right),(i=1,\dots ,N),\hfill \\ \hfill {\widehat{h}}_a& =\sum _{b=1}^P{f}_a^b\left(g\right)h_b,(a=P+1,\dots ,L),\hfill \\ \hfill {\widehat{m}}_{\alpha }^2& =\sum _{\beta =1}^Q{e}_{\alpha }^{\beta }\left(g\right)m_{\beta }^2+\sum _{a,b=1}^P{k}_{\alpha }^{ab}\left(g\right)h_a{h}_b,(\alpha =Q+1,\dots ,M)\hfill \end{array}$$

(10)

is consistent with the RG Equations (7) and (8). It turns out that the following relations should be satisfied:

$$\begin{array}{cc}\hfill {\beta }_g\frac{\partial {\widehat{g}}_i}{\partial g}& ={\beta }_i,(i=1,\dots ,N),\hfill \\ \hfill {\beta }_g\frac{\partial {\widehat{h}}_a}{\partial g}+\sum _{b=1}^P{\gamma }_b^h\frac{\partial {\widehat{h}}_a}{\partial h_b}& ={\gamma }_a^h,(a=P+1,\dots ,L),\hfill \\ \hfill {\beta }_g\frac{\partial {\widehat{m}}_{\alpha }^2}{\partial g}+\sum _{a=1}^P{\gamma }_a^h\frac{\partial {\widehat{m}}_{\alpha }^2}{\partial h_a}+\sum _{\beta =1}^Q{\gamma }_{\beta }^{m^2}\frac{\partial {\widehat{m}}_{\alpha }^2}{\partial m_{\beta }^2}& ={\gamma }_{\alpha }^{m^2},(\alpha =Q+1,\dots ,M).\hfill \end{array}$$

(11)

Using Equations (9) and (10), the bove relations reduce to:

$$\begin{array}{c}{\beta }_g\frac{d{f}_a^b}{dg}+\sum _{c=1}^P{f}_a^c\left[{\gamma }_c^{h,b}+\sum _{d=P+1}^L{\gamma }_c^{h,d}{f}_d^b\right]-{\gamma }_a^{h,b}-\sum _{d=P+1}^L{\gamma }_a^{h,d}{f}_d^b=0,\hfill \\ (a=P+1,\dots ,L;b=1,\dots ,P),\hfill \\ {\beta }_g\frac{d{e}_{\alpha }^{\beta }}{dg}+\sum _{\gamma =1}^Q{e}_{\alpha }^{\gamma }\left[{\gamma }_{\gamma }^{m^2,\beta }+\sum _{\delta =Q+1}^M{\gamma }_{\gamma }^{m^2,\delta }{e}_{\delta }^{\beta }\right]-{\gamma }_{\alpha }^{m^2,\beta }-\sum _{\delta =Q+1}^M{\gamma }_{\alpha }^{m^2,d}{e}_{\delta }^{\beta }=0,\hfill \\ (\alpha =Q+1,\dots ,Mq\beta =1,\dots ,Q),\hfill \\ {\beta }_g\frac{d{k}_{\alpha }^{ab}}{dg}+2\sum _{c=1}^P\left({\gamma }_c^{h,a}+\sum _{d=P+1}^L{\gamma }_c^{h,d}{f}_d^a\right)k_{\alpha }^{cb}+\sum _{\beta =1}^Q{e}_{\alpha }^{\beta }\left[{\gamma }_{\beta }^{m^2,ab}+\sum _{c,d=P+1}^L{\gamma }_{\beta }^{m^2,cd}{f}_c^a{f}_d^b\right.\hfill \\ \left.+2\sum _{c=P+1}^L{\gamma }_{\beta }^{m^2,cb}{f}_c^a+\sum _{\delta =Q+1}^M{\gamma }_{\beta }^{m^2,d}{k}_{\delta }^{ab}\right]-\left[{\gamma }_{\alpha }^{m^2,ab}+\sum _{c,d=P+1}^L{\gamma }_{\alpha }^{m^2,cd}{f}_c^a{f}_d^b\right.\hfill \\ \left.+2\sum _{c=P+1}^L{\gamma }_{\alpha }^{m^2,cb}{f}_c^a+\sum _{\delta =Q+1}^M{\gamma }_{\alpha }^{m^2,\delta }{k}_{\delta }^{ab}\right]=0,\hfill \\ (\alpha =Q+1,\dots ,M;a,b=1,\dots ,P).\hfill \end{array}$$

(12)

The above relations ensure that the irreducible vertex function of the reduced theory:

$$\begin{array}{cc}\hfill {\mathrm{\Gamma }}_R& \left[\mathrm{\Phi }{}^{\prime }\mathrm{s};g;h_1,\dots ,h_P;m_1^2,\dots ,m_Q^2;\mu \right]\equiv \hfill \\ & \mathrm{\Gamma }\left[\mathrm{\Phi }{}^{\prime }\mathrm{s};g,{\widehat{g}}_1\left(g\right)\dots ,{\widehat{g}}_N\left(g\right);h_1,\dots ,h_P,{\widehat{h}}_{P+1}(g,h),\dots ,{\widehat{h}}_L(g,h);\right.\hfill \\ & \left.m_1^2,\dots ,m_Q^2,{\widehat{m}}_{Q+1}^2(g,h,m^2),\dots ,{\widehat{m}}_M^2(g,h,m^2);\mu \right]\hfill \end{array}$$

(13)

has the same renormalization group flow as the original one.

The assumptions that the reduced theory is perturbatively renormalizable means that the functions ${\widehat{g}}_i$, $f_a^b$, $e_{\alpha }^{\beta }$ and $k_{\alpha }^{ab}$, defined in (10), should be expressed as a power series in the primary coupling g:

$$\begin{array}{cc}\hfill {\widehat{g}}_i& =g\sum _{n=0}^{\infty }{\rho }_i^{\left(n\right)}{g}^n,f_a^b=g\sum _{n=0}^{\infty }{\eta }_a^{b\left(n\right)}{g}^n\hfill \\ \hfill e_{\alpha }^{\beta }& =\sum _{n=0}^{\infty }{\xi }_{\alpha }^{\beta \left(n\right)}{g}^n,k_{\alpha }^{ab}=\sum _{n=0}^{\infty }{\chi }_{\alpha }^{ab\left(n\right)}{g}^n.\hfill \end{array}$$

(14)

The above expansion coefficients can be found by inserting these power series into Equations (11) and (12) and requiring the equations to be satisfied at each order of g. It should be noted that the existence of a unique power series solution is a non-trivial matter: it depends on the theory, as well as on the choice of the set of independent parameters.

It should also be noted that in the case that there are no independent mass-dimension one parameters ($\widehat{h}$), the reduction of these terms takes naturally the form:

$${\widehat{h}}_a=\sum _{b=1}^L{f}_a^b\left(g\right)M,$$

where M is a mass-dimension one parameter, which could be a gaugino mass, which corresponds to the independent (gauge) coupling. In case, on top of that, there are no independent mass-dimension two parameters (${\widehat{m}}^2$), the corresponding reduction takes the analogous form:

$${\widehat{m}}_a^2=\sum _{b=1}^M{e}_a^b\left(g\right)M^2.$$

3. Finiteness in N = 1 Supersymmetric Gauge Theories

Let us consider a chiral, anomaly-free, $N=1$ globally SUSY gauge theory based on a group Gwith gauge coupling constant g. The superpotential of the theory is given by:

$$W=\frac{1}{2}{m}_{ij}{\varphi }_i{\varphi }_j+\frac{1}{6}{C}_{ijk}{\varphi }_i{\varphi }_j{\varphi }_k,$$

(15)

where $m_{ij}$ and $C_{ijk}$ are gauge invariant tensors and the matter field ${\varphi }_i$ transforms according to the irreducible representation $R_i$ of the gauge group G. The renormalization constants associated with the superpotential (15), assuming that SUSY is preserved, are:

$$\begin{array}{cc}\hfill {\varphi }_i^0& ={(Z_i^j)}^{(1/2)}{\varphi }_j,\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill m_{ij}^0& =Z_{ij}^{i^{\prime }{j}^{\prime }}{m}_{i^{\prime }{j}^{\prime }},\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill C_{ijk}^0& =Z_{ijk}^{i^{\prime }{j}^{\prime }{k}^{\prime }}{C}_{i^{\prime }{j}^{\prime }{k}^{\prime }}.\hfill \end{array}$$

(18)

The $N=1$ non-renormalization theorem [54,55,56] ensures that there are no mass and cubic-interaction-term infinities, and therefore:

$$\begin{array}{cc}\hfill Z_{ijk}^{i^{\prime }{j}^{\prime }{k}^{\prime }}{Z}_{i^{\prime }}^{1/2i^{″}}{Z}_{j^{\prime }}^{1/2j^{″}}{Z}_{k^{\prime }}^{1/2k^{″}}& ={\delta }_{(i}^{i^{″}}{\delta }_j^{j^{″}}{\delta }_{k)}^{k^{″}},\hfill \\ \hfill Z_{ij}^{i^{\prime }{j}^{\prime }}{Z}_{i^{\prime }}^{1/2i^{″}}{Z}_{j^{\prime }}^{1/2j^{″}}& ={\delta }_{(i}^{i^{″}}{\delta }_{j)}^{j^{″}}.\hfill \end{array}$$

(19)

As a result, the only surviving possible infinities are the wave-function renormalization constants $Z_i^j$, i.e., one infinity for each field. the one-loop $\beta$-function of the gauge coupling g is given by [57]:

$${\beta }_g^{\left(1\right)}=\frac{dg}{dt}=\frac{g^3}{16{\pi }^2}[\sum _{i}l\left(R_i\right)-3C_2\left(G\right)],$$

(20)

where $l\left(R_i\right)$ is the Dynkin index of $R_i$ and $C_2\left(G\right)$ is the quadratic Casimir invariant of the adjoint representation of the gauge group G. The $\beta$-functions of $C_{ijk}$, by virtue of the non-renormalization theorem, are related to the anomalous dimension matrix ${\gamma }_{ij}$ of the matter fields ${\varphi }_i$ as:

$${\beta }_{ijk}=\frac{d{C}_{ijk}}{dt}=C_{ijl}{\gamma }_k^l+C_{ikl}{\gamma }_j^l+C_{jkl}{\gamma }_i^l.$$

(21)

At one-loop level, ${\gamma }_{ij}$ is [57]:

$${\gamma }_j^{i\left(1\right)}=\frac{1}{32{\pi }^2}[C^{ikl}{C}_{jkl}-2g^2{C}_2\left(R\right){\delta }_j^i],$$

(22)

where $C_2\left(R\right)$ is the quadratic Casimir invariant of the representation $R_i$, and $C^{ijk}=C_{ijk}^{\ast }$. Since dimensional coupling parameters such as masses and couplings of cubic scalar field terms do not influence the asymptotic properties of a theory that we are interested in here, it is sufficient to take into account only the dimensionless SUSY couplings such as g and $C_{ijk}$. Therefore, we neglect the existence of dimensional parameters and assume furthermore that $C_{ijk}$ are real so that $C_{ijk}^2$ are always positive numbers.

As one can see from Equations (20) and (22), all the one-loop $\beta$-functions of the theory vanish if ${\beta }_g^{\left(1\right)}$ and ${\gamma }_{ij}^{\left(1\right)}$ vanish, i.e.,

$$\sum _i\ell \left(R_i\right)=3C_2\left(G\right),$$

(23)

$$C^{ikl}{C}_{jkl}=2{\delta }_j^i{g}^2{C}_2\left(R_i\right),$$

(24)

The conditions for finiteness for $N=1$ field theories with $SU\left(N\right)$ gauge symmetry are discussed in [58], and the analysis of the anomaly-free and no-charge renormalization requirements for these theories can be found in [59]. A very interesting result is that Conditions (23) and (24) are necessary and sufficient for finiteness at the two-loop level [57,60,61,62,63].

In the case that SUSY is broken by soft terms, the requirement of finiteness in the one-loop soft breaking terms imposes further constraints among themselves [32]. In addition, the same set of conditions that are sufficient for one-loop finiteness of the soft breaking terms renders the soft sector of the theory two-loop finite [33].

The one- and two-loop finiteness Conditions (23) and (24) restrict considerably the possible choices of the irreducible representations (irreps) $R_i$ for a given group G, as well as the Yukawa couplings in the superpotential (15). Note in particular that the finiteness conditions cannot be applied to the Minimal SUSY Standard Model (MSSM), since the presence of a $U\left(1\right)$ gauge group is incompatible with the condition (23), due to $C_2\left[U\left(1\right)\right]=0$. This naturally leads to the expectation that finiteness should be attained at the grand unified level only, the MSSM being just the corresponding, low-energy, effective theory.

Another important consequence of one- and two-loop finiteness is that SUSY (most probably) can only be broken due to the soft breaking terms. Indeed, due to the unacceptability of gauge singlets, F-type spontaneous symmetry breaking [64] terms are incompatible with finiteness, as well as D-type [65] spontaneous breaking, which requires the existence of a $U\left(1\right)$ gauge group.

A natural question to ask is what happens at higher-loop orders. The answer is contained in a theorem [27,66] that states the necessary and sufficient conditions to achieve finiteness at all orders. Before we discuss the theorem, let us make some introductory remarks. The finiteness conditions impose relations between gauge and Yukawa couplings. To require such relations that render the couplings mutually dependent at a given renormalization point is trivial. What is not trivial is to guarantee that relations leading to a reduction of the couplings hold at any renormalization point. As we have seen, the necessary and also sufficient condition for this to happen is to require that such relations are solutions to the REs:

$${\beta }_g\frac{d{C}_{ijk}}{dg}={\beta }_{ijk}$$

(25)

and hold at all orders. Remarkably, the existence of all-order power series solutions to (25) can be decided at the one-loop level, as already mentioned.

Let us now turn to the all-order finiteness theorem [27,66], which states the conditions under which an $N=1$ SUSY gauge theory can become finite to all orders in the sense of vanishing $\beta$-functions, that is of physical scale invariance. It is based on (a) the structure of the supercurrent in $N=1$ SUSY gauge theory [67,68,69] and on (b) the non-renormalization properties of $N=1$ chiral anomalies [26,27,66,70,71]. Details on the proof can be found in [27,66] and further discussion in [26,28,70,71,72]. Here, following mostly [72], we present a comprehensible sketch of the proof.

Consider an $N=1$ SUSY gauge theory, with simple Lie group G. The content of this theory is given at the classical level by the matter supermultiplets $S_i$, which contain a scalar field ${\varphi }_i$ and a Weyl spinor ${\psi }_{ia}$, and the vector supermultiplet $V_a$, which contains a gauge vector field $A_{\mu }^a$ and a gaugino Weyl spinor ${\lambda }_{\alpha }^a$.

Let us first recall certain facts about the theory:

(1) A massless $N=1$ SUSY theory is invariant under a $U\left(1\right)$ chiral transformation R under which the various fields transform as follows:

$$\begin{array}{cc}\hfill A_{\mu }^{\prime }& =A_{\mu },{\lambda }_{\alpha }^{\prime }=\exp \left(-i\theta \right){\lambda }_{\alpha }\hfill \\ \hfill {\varphi }^{\prime }& =\exp (-i\frac{2}{3}\theta )\varphi ,{\psi }_{\alpha }^{\prime }=\exp (-i\frac{1}{3}\theta ){\psi }_{\alpha },\cdots \hfill \end{array}$$

(26)

The corresponding axial Noether current $J_R^{\mu }\left(x\right)$:

$$J_R^{\mu }\left(x\right)=\overline{\lambda }{\gamma }^{\mu }{\gamma }^5\lambda +\cdots$$

(27)

is conserved classically, while in the quantum case, it is violated by the axial anomaly:

$${\partial }_{\mu }{J}_R^{\mu }=r({ϵ}^{\mu \nu \sigma \rho }{F}_{\mu \nu }{F}_{\sigma \rho }+\cdots ).$$

(28)

From its known topological origin in ordinary gauge theories [73,74,75], one would expect the axial vector current $J_R^{\mu }$ to satisfy the Adler–Bardeen theorem and receive corrections only at the one-loop level. Indeed, it has been shown that the same non-renormalization theorem holds also in SUSY theories [26,70,71]. Therefore:

$$r=\hslash {\beta }_g^{\left(1\right)}.$$

(29)

(2) The massless theory we consider is scale invariant at the classical level, and in general, there is a scale anomaly due to radiative corrections. The scale anomaly appears in the trace of the energy momentum tensor $T_{\mu \nu }$, which is traceless classically. It has the form

$$T_{\mu }^{\mu }={\beta }_g{F}^{\mu \nu }{F}_{\mu \nu }+\cdots$$

(30)

(3) Massless, $N=1$ SUSY gauge theories are classically invariant under the SUSY extension of the conformal group: the superconformal group. Examining the superconformal algebra, it can be seen that the subset of superconformal transformations consisting of translations, SUSY transformations and axial R transformations is closed under SUSY, i.e., these transformations form a representation of SUSY. It follows that the conserved currents corresponding to these transformations make up a supermultiplet represented by an axial vector superfield called the supercurrent J,

$$J\equiv \{J_R^{{}^{\prime }\mu },Q_{\alpha }^{\mu },T_{\nu }^{\mu },\dots \},$$

(31)

where $J_R^{{}^{\prime }\mu }$ is the current associated with Rinvariance, $Q_{\alpha }^{\mu }$ is the one associated with SUSY invariance and $T_{\nu }^{\mu }$ the one associated with translational invariance (energy-momentum tensor).

The anomalies of the R current $J_R^{{}^{\prime }\mu }$, the trace anomalies of the SUSY current and the energy-momentum tensor form also a second supermultiplet, called the supertrace anomaly:

$$\begin{array}{cc}\hfill S& =\{ReS,ImS,S_{\alpha }\}=\hfill \\ & \{T_{\mu }^{\mu },{\partial }_{\mu }{J}_R^{{}^{\prime }\mu },{\sigma }_{\alpha \dot{\beta }}^{\mu }{\overline{Q}}_{\mu }^{\dot{\beta }}+\cdots \}\hfill \end{array}$$

where $T_{\mu }^{\mu }$ is given in Equation (30) and:

$$\begin{array}{cc}\hfill {\partial }_{\mu }{J}_R^{{}^{\prime }\mu }& ={\beta }_g{ϵ}^{\mu \nu \sigma \rho }{F}_{\mu \nu }{F}_{\sigma \rho }+\cdots \hfill \end{array}$$

(32)

$$\begin{array}{cc}\hfill {\sigma }_{\alpha \dot{\beta }}^{\mu }{\overline{Q}}_{\mu }^{\dot{\beta }}& ={\beta }_g{\lambda }^{\beta }{\sigma }_{\alpha \beta }^{\mu \nu }{F}_{\mu \nu }+\cdots \hfill \end{array}$$

(33)

(4) It is very important to note that the Noether current defined in (27) is not the same as the current associated with R invariance that appears in the supercurrent J in (31), but they coincide in the tree approximation. Therefore, starting from a unique classical Noether current $J_{R\left(class\right)}^{\mu }$, the Noether current $J_R^{\mu }$ is defined as the quantum extension of $J_{R\left(class\right)}^{\mu }$, which allows for the validity of the non-renormalization theorem. On the other hand, $J_R^{{}^{\prime }\mu }$, is defined to belong to the supercurrent J, together with the energy-momentum tensor. The two requirements cannot be fulfilled by a single current operator at the same time.

Although the Noether current $J_R^{\mu }$, which obeys (28), and the current $J_R^{{}^{\prime }\mu }$ belonging to the supercurrent multiplet J are not the same, there is a relation [27,66] between quantities associated with them:

$$r={\beta }_g(1+x_g)+{\beta }_{ijk}{x}^{ijk}-{\gamma }_A{r}^A$$

(34)

where r was given in Equation (29). The $r^A$ are the non-renormalized coefficients of the anomalies of the Noether currents associated with the chiral invariances of the superpotential and (like r) are strictly one-loop quantities. The ${\gamma }_A$’s are linear combinations of the anomalous dimensions of the matter fields, and $x_g$ and $x^{ijk}$ are radiative correction quantities. The structure of Equality (34) is independent of the renormalization scheme.

One-loop finiteness, i.e., vanishing of the $\beta$-functions at one loop, implies that the Yukawa couplings $C_{ijk}$ must be functions of the gauge coupling g. To find a similar condition to all orders, it is necessary and sufficient for the Yukawa couplings to be a formal power series in g, which is the solution of the REs (25).

We can now state the theorem for all-order vanishing $\beta$-functions [26,27,72].

Theorem 1.

Consider an $N=1$ SUSY Yang–Mills theory, with the simple gauge group. If the following conditions are satisfied:

1.

There is no gauge anomaly.

2.

The gauge β-function vanishes at one loop:

$${\beta }_g^{\left(1\right)}=0=\sum _{i}l\left(R_i\right)-3C_2\left(G\right).$$

(35)

3.

There exist solutions of the form:

$$C_{ijk}={\rho }_{ijk}g,{\rho }_{ijk}\in \mathrm{I}\mathrm{C}$$

(36)

to the conditions of vanishing one-loop matter fields’ anomalous dimensions:

$$\begin{array}{c}{\gamma }_j^{i\left(1\right)}=0\hfill \\ =\frac{1}{32{\pi }^2}[C^{ikl}{C}_{jkl}-2g^2{C}_2\left(R\right){\delta }_j^i].\hfill \end{array}$$

(37)

4.

These solutions are isolated and non-degenerate when considered as solutions of vanishing one-loop Yukawa β-functions:

$${\beta }_{ijk}=0.$$

(38)

Then, each of the solutions (36) can be uniquely extended to a formal power series in g, and the associated super Yang–Mills models depend on the single coupling constant g with a $\beta$ function, which vanishes at all orders.

It is important to note a few things: The requirement of isolated and non-degenerate solutions guarantees the existence of a unique formal power series solution to the reduction equations. the vanishing of the gauge $\beta$ function at one loop, ${\beta }_g^{\left(1\right)}$, is equivalent to the vanishing of the R current anomaly (28). The vanishing of the anomalous dimensions at one loop implies the vanishing of the Yukawa coupling $\beta$ functions at that order. It also implies the vanishing of the chiral anomaly coefficients $r^A$. This last property is a necessary condition for having $\beta$ functions vanishing at all orders. For an alternative way to find finite theories see ref. [76].

Proof. 

Insert ${\beta }_{ijk}$ as given by the REs into the relationship (34) between the axial anomalies coefficients and the $\beta$-functions. Since these chiral anomalies vanish, we get for ${\beta }_g$ a homogeneous equation of the form:

$$0={\beta }_g(1+O\left(\hslash \right)).$$

(39)

The solution of this equation in the sense of a formal power series in ℏ is ${\beta }_g=0$, order by order. Therefore, due to the REs (25), ${\beta }_{ijk}=0$, as well.

Thus, we see that finiteness and reduction of couplings are intimately related. Since an equation like Equation (34) is lacking in non-SUSY theories, one cannot extend the validity of a similar theorem in such theories. ☐

4. The SSB Sector of Reduced N = 1 SUSY and Finite Theories

As we have seen in Section 2, the method of reducing the dimensionless couplings has been extended [25], to the Soft SUSY Breaking (SSB) dimensionful parameters of $N=1$ SUSY theories. In addition, it was found [38] that RGI SSB scalar masses in GYU models satisfy a universal sum rule.

Consider the superpotential given by (15) along with the Lagrangian for SSB terms:

$$\begin{array}{cc}\hfill -{\mathcal{L}}_{\mathrm{SSB}}& =\frac{1}{6}{h}^{ijk}{\varphi }_i{\varphi }_j{\varphi }_k+\frac{1}{2}{b}^{ij}{\varphi }_i{\varphi }_j\hfill \\ & +\frac{1}{2}{\left(m^2\right)}_i^j{\varphi }^{\ast i}{\varphi }_j+\frac{1}{2}M\lambda \lambda +h.c.,\hfill \end{array}$$

where the ${\varphi }_i$ are the scalar parts of the chiral superfields ${\mathrm{\Phi }}_i$, $\lambda$ are the gauginos and M their unified mass.

We assume that the reduction equations admit power series solutions of the form:

$$C^{ijk}=g\sum _n{\rho }_{\left(n\right)}^{ijk}{g}^{2n}.$$

(40)

If we knew higher-loop $\beta$-functions explicitly, we could follow the same procedure and find higher-loop RGI relations among SSB terms. However, the $\beta$-functions of the soft scalar masses are explicitly known only up to two loops. In order to obtain higher-loop results, some relations among $\beta$-functions are needed.

In the case of finite theories, we assume that the gauge group is a simple group, and the one-loop $\beta$-function of the gauge coupling g vanishes. According to the finiteness theorem of [27,66] and the assumption given in (40), the theory is then finite to all orders in perturbation theory, if, among others, the one-loop anomalous dimensions ${\gamma }_i^{j\left(1\right)}$ vanish. The one- and two-loop finiteness for $h^{ijk}$ can be achieved by [33]:

$$h^{ijk}=-M{C}^{ijk}+\cdots =-M{\rho }_{\left(0\right)}^{ijk}g+O\left(g^5\right),$$

(41)

where … stand for higher order terms.

Now, to obtain the two-loop sum rule for soft scalar masses, we assume that the lowest order coefficients ${\rho }_{\left(0\right)}^{ijk}$ and also ${(m^2)}_j^i$ satisfy the diagonality relations:

$${\rho }_{ipq\left(0\right)}{\rho }_{\left(0\right)}^{jpq}\propto {\delta }_i^j\mathrm{for} \mathrm{all}p\mathrm{and}q\mathrm{and}{\left(m^2\right)}_j^i=m_j^2{\delta }_j^i,$$

(42)

respectively. Then, we find the following soft scalar-mass sum rule [16,39,77]:

$$(m_i^2+m_j^2+m_k^2)/M{M}^{†}=1+\frac{g^2}{16{\pi }^2}{\Delta }^{\left(2\right)}+O\left(g^4\right)$$

(43)

for i, j, k with ${\rho }_{\left(0\right)}^{ijk}\ne 0$, where ${\Delta }^{\left(2\right)}$ is the two-loop correction:

$${\Delta }^{\left(2\right)}=-2\sum _l[(m_l^2/M{M}^{†})-(1/3)]T\left(R_l\right),$$

(44)

which vanishes for the universal choice in accordance with the previous findings of [33] (in the above relation, $T\left(R_l\right)$ is the Dynkin index of the $R_l$ irrep).

Making use of the spurion technique [56,78,79,80,81], it is possible to find the following all-loop relations among SSB $\beta$-functions [82,83,84,85,86,87]:

$$\begin{array}{cc}\hfill {\beta }_M& =2\mathcal{O}\left(\frac{{\beta }_g}{g}\right),\hfill \end{array}$$

(45)

$$\begin{array}{cc}\hfill {\beta }_h^{ijk}& ={\gamma }^i{}_l{h}^{ljk}+{\gamma }^j{}_l{h}^{ilk}+{\gamma }^k{}_l{h}^{ijl}\hfill \\ & -2{\gamma }_1^i{}_l{C}^{ljk}-2{\gamma }_1^j{}_l{C}^{ilk}-2{\gamma }_1^k{}_l{C}^{ijl},\hfill \end{array}$$

(46)

$$\begin{array}{cc}\hfill {\left({\beta }_{m^2}\right)}^i{}_j& =\left[\Delta +X\frac{\partial }{\partial g}\right]{\gamma }^i{}_j,\hfill \end{array}$$

(47)

$$\begin{array}{cc}\hfill \mathcal{O}& =\left(M{g}^2\frac{\partial }{\partial g^2}-h^{lmn}\frac{\partial }{\partial C^{lmn}}\right),\hfill \end{array}$$

(48)

$$\begin{array}{cc}\hfill \Delta & =2\mathcal{O}{\mathcal{O}}^{\ast }+2{\left|M\right|}^2{g}^2\frac{\partial }{\partial g^2}+{\tilde{C}}_{lmn}\frac{\partial }{\partial C_{lmn}}+{\tilde{C}}^{lmn}\frac{\partial }{\partial C^{lmn}},\hfill \end{array}$$

(49)

where ${\left({\gamma }_1\right)}^i{}_j=\mathcal{O}{\gamma }^i{}_j$, $C_{lmn}={\left(C^{lmn}\right)}^{\ast }$, and:

$${\tilde{C}}^{ijk}={\left(m^2\right)}^i{}_l{C}^{ljk}+{\left(m^2\right)}^j{}_l{C}^{ilk}+{\left(m^2\right)}^k{}_l{C}^{ijl}.$$

(50)

Assuming, following [83], that the relation:

$$h^{ijk}=-M{\left(C^{ijk}\right)}^{\prime }\equiv -M\frac{d{C}^{ijk}\left(g\right)}{d\ln g},$$

(51)

among couplings is all-loop RGI and using the all-loop gauge $\beta$-function of Novikov et al. [41,42,43] given by:

$${\beta }_g^{\mathrm{NSVZ}}=\frac{g^3}{16{\pi }^2}\left[\frac{{\sum }_{l}T\left(R_l\right)(1-{\gamma }_l/2)-3C\left(G\right)}{1-g^{2}C\left(G\right)/8{\pi }^2}\right],$$

(52)

the all-loop RGI sum rule [40] was found:

$$\begin{array}{cc}\hfill m_i^2+m_j^2+m_k^2& ={\left|M\right|}^2\{\frac{1}{1-g^{2}C\left(G\right)/\left(8{\pi }^2\right)}\frac{d\ln C^{ijk}}{d\ln g}+\frac{1}{2}\frac{d^2\ln C^{ijk}}{d{\left(\ln g\right)}^2}\}\hfill \\ & +\sum _l\frac{m_l^{2}T\left(R_l\right)}{C\left(G\right)-8{\pi }^2/g^2}\frac{d\ln C^{ijk}}{d\ln g}.\hfill \end{array}$$

(53)

In addition, the exact-$\beta$-function for $m^2$ in the NSVZ scheme has been obtained [40] for the first time and is given by:

$$\begin{array}{cc}\hfill {\beta }_{m_i^2}^{\mathrm{NSVZ}}& =\left[{\left|M\right|}^2\{\frac{1}{1-g^{2}C\left(G\right)/\left(8{\pi }^2\right)}\frac{d}{d\ln g}+\frac{1}{2}\frac{d^2}{d{\left(\ln g\right)}^2}\}\right.\hfill \\ & \left.+\sum _l\frac{m_l^{2}T\left(R_l\right)}{C\left(G\right)-8{\pi }^2/g^2}\frac{d}{d\ln g}\right]{\gamma }_i^{\mathrm{NSVZ}}.\hfill \end{array}$$

(54)

Surprisingly enough, the all-loop result (53) coincides with the superstring result for the finite case in a certain class of orbifold models [39] if $d\ln C^{ijk}/d\ln g=1$.

All-Loop RGI Relations in the SSB Sector

Let us now see how the all-loop results on the SSB $\beta$-functions, Equations (45)–(50) lead to all-loop RGI relations. We make two assumptions:

(a) the existence of an RGI surface on which $C=C\left(g\right)$, or equivalently that:

$$\frac{d{C}^{ijk}}{dg}=\frac{{\beta }_C^{ijk}}{{\beta }_g}$$

(55)

holds, i.e., the reduction of couplings is possible, and

(b) the existence of an RGI surface on which:

$$h^{ijk}=-M\frac{dC{\left(g\right)}^{ijk}}{d\ln g}$$

(56)

holds, as well, in all orders.

Then, one can prove [88,89] that the following relations are RGI to all loops (note that in both Assumptions (a) and (b) above, we do not rely on specific solutions of these equations):

$$\begin{array}{cc}\hfill M& =M_0\frac{{\beta }_g}{g},\hfill \end{array}$$

(57)

$$\begin{array}{cc}\hfill h^{ijk}& =-M_0{\beta }_C^{ijk},\hfill \end{array}$$

(58)

$$\begin{array}{cc}\hfill b^{ij}& =-M_0{\beta }_{\mu }^{ij},\hfill \end{array}$$

(59)

$$\begin{array}{cc}\hfill {\left(m^2\right)}_{\phantom{a}j}^i& =\frac{1}{2}{\left|M_0\right|}^2\mu \frac{d{\gamma }_{\phantom{a}j}^i}{d\mu }\hfill \end{array}$$

(60)

where $M_0$ is an arbitrary reference mass scale to be specified shortly. the assumption that:

$$C_{\alpha }\frac{\partial }{\partial C_{\alpha }}=C_{\alpha }^{\ast }\frac{\partial }{\partial C_{\alpha }}$$

(61)

for an RGI surface $F(g,C^{ijk},C^{\ast ijk})$ leads to:

$$\frac{d}{dg}=\left(\frac{\partial }{\partial g}+2\frac{\partial }{\partial C}\frac{dC}{dg}\right)=\left(\frac{\partial }{\partial g}+2\frac{{\beta }_C}{{\beta }_g}\frac{\partial }{\partial C}\right),$$

(62)

where Equation (55) has been used. Now, let us consider the partial differential operator $\mathcal{O}$ in Equation (48), which assuming Equation (51), becomes:

$$\mathcal{O}=\frac{1}{2}M\frac{d}{d\ln g}.$$

(63)

In turn, ${\beta }_M$ given in Equation (45) becomes:

$${\beta }_M=M\frac{d}{d\ln g}(\frac{{\beta }_g}{g}),$$

(64)

which by integration provides us [88,90] with the generalized, i.e., including Yukawa couplings, all-loop RGI Hisano–Shifman relation [82]:

$$M=\frac{{\beta }_g}{g}{M}_0,$$

(65)

where $M_0$ is the integration constant and can be associated with the unification scale $M_U$ in GUTs or to the gravitino mass $m_{3/2}$ in a supergravity framework. Therefore, Equation (65) becomes the all-loop RGE Equation (57). Note that ${\beta }_M$ using Equations (64) and (65) can be written as:

$${\beta }_M=M_0\frac{d}{dt}({\beta }_g/g).$$

(66)

Similarly:

$${\left({\gamma }_1\right)}_{\phantom{a}j}^i=\mathcal{O}{\gamma }_{\phantom{a}j}^i=\frac{1}{2}{M}_0\frac{d{\gamma }_{\phantom{a}j}^i}{dt}.$$

(67)

Next, from Equations (51) and (65), we obtain:

$$h^{ijk}=-M_0{\beta }_C^{ijk},$$

(68)

while ${\beta }_h^{ijk}$, given in Equation (46) and using Equation (67), becomes [88]:

$${\beta }_h^{ijk}=M_0\frac{d}{dt}{\beta }_C^{ijk}$$

(69)

which shows that Equation (68) is all-loop RGI. In a similar way, Equation (59) can be shown to be all-loop RGI.

Finally, we would like to emphasize that under the same Assumptions (a) and (b), the sum rule given in Equation (53) has been proven [40] to be all-loop RGI, which (using Equation (65)) gives us a generalization of Equation (60) to be applied in considerations of non-universal soft scalar masses, which are necessary in many cases. Moreover, the sum rule holds also in the more general cases, discussed in Section 2, according to which exact relations among the squared scalar and gaugino masses can be found.

5. A Successful Finite Unified Theory

We review an all-loop FUT with $SU\left(5\right)$ as the gauge group, where the reduction of couplings has been applied to the third generation of quarks and leptons. This FUT was selected previously on the basis of agreement with the known experimental data at the time [45] and was predicting the Higgs mass to be in the range 121–126 GeV almost five years before the discovery. The particle content of the model we will study, which we denote $\mathit{SU}\left(\mathbf{5}\right)$-FUT  consists of the following supermultiplets: three ($\overline{\mathbf{5}}+\mathbf{10}$), needed for each of the three generations of quarks and leptons, four ($\overline{\mathbf{5}}+\mathbf{5}$) and one $\mathbf{24}$ considered as Higgs supermultiplets. When the gauge group of the finite GUT is broken, the theory is no longer finite, and we will assume that we are left with the MSSM [15,20,21,22,23,24].

A predictive GYU $SU\left(5\right)$ model, which is finite to all orders, in addition to the requirements mentioned already, should also have the following properties:

• One-loop anomalous dimensions are diagonal, i.e., ${\gamma }_i^{\left(1\right)j}\propto {\delta }_i^j$.
• Three fermion generations in the irreducible representations ${\overline{\mathbf{5}}}_i,{\mathbf{10}}_i(i=1,2,3)$, which obviously should not couple to the adjoint $\mathbf{24}$.
• The two Higgs doublets of the MSSM should mostly be made out of a pair of Higgs quintet and anti-quintet, which couple to the third generation.

After the reduction of couplings, the symmetry is enhanced, leading to the following superpotential [39,91]:

$$\begin{array}{cc}\hfill W& =\sum _{i=1}^3[\frac{1}{2}{g}_i^u{\mathbf{10}}_i{\mathbf{10}}_i{H}_i+g_i^d{\mathbf{10}}_i{\overline{\mathbf{5}}}_i{\overline{H}}_i]+g_{23}^u{\mathbf{10}}_2{\mathbf{10}}_3{H}_4\hfill \\ & +g_{23}^d{\mathbf{10}}_2{\overline{\mathbf{5}}}_3{\overline{H}}_4+g_{32}^d{\mathbf{10}}_3{\overline{\mathbf{5}}}_2{\overline{H}}_4+g_2^f{H}_2\mathbf{24}{\overline{H}}_2+g_3^f{H}_3\mathbf{24}{\overline{H}}_3+\frac{g^{\lambda }}{3}{\left(\mathbf{24}\right)}^3.\hfill \end{array}$$

(70)

The non-degenerate and isolated solutions to ${\gamma }_i^{\left(1\right)}=0$ give us:

$$\begin{array}{c}{\left(g_1^u\right)}^2=\frac{8}{5}{g}^2,{\left(g_1^d\right)}^2=\frac{6}{5}{g}^2,{\left(g_2^u\right)}^2={\left(g_3^u\right)}^2=\frac{4}{5}{g}^2,\hfill \\ {\left(g_2^d\right)}^2={\left(g_3^d\right)}^2=\frac{3}{5}{g}^2,{\left(g_{23}^u\right)}^2=\frac{4}{5}{g}^2,{\left(g_{23}^d\right)}^2={\left(g_{32}^d\right)}^2=\frac{3}{5}{g}^2,\hfill \\ {(g^{\lambda })}^2=\frac{15}{7}{g}^2,{(g_2^f)}^2={(g_3^f)}^2=\frac{1}{2}{g}^2,{(g_1^f)}^2=0,{(g_4^f)}^2=0,\hfill \end{array}$$

(71)

and from the sum rule, we obtain:

$$m_{H_u}^2+2m_{\mathbf{10}}^2=M^2,m_{H_d}^2-2m_{\mathbf{10}}^2=-\frac{M^2}{3},m_{\overline{\mathbf{5}}}^2+3m_{\mathbf{10}}^2=\frac{4M^2}{3},$$

(72)

i.e., in this case, we have only two free parameters $m_{\mathbf{10}}$ and M for the dimensionful sector.

As already mentioned, after the $SU\left(5\right)$ gauge symmetry breaking, we assume we have the MSSM, i.e., only two Higgs doublets. This can be achieved by introducing appropriate mass terms that allow one to perform a rotation of the Higgs sector [20,24,92,93,94], in such a way that only one pair of Higgs doublets, coupled mostly to the third family, remains light and acquires vacuum expectation values. To avoid fast proton decay the usual fine tuning to achieve doublet-triplet splitting is performed, although the mechanism is not identical to minimal $SU\left(5\right)$, since we have an extended Higgs sector.

Thus, after the gauge symmetry of the GUT theory is broken, we are left with the MSSM, with the boundary conditions for the third family given by the finiteness conditions, while the other two families are not restricted.

6. Phenomenological Constraints

In this section, we briefly review the relevant experimental constraints that we apply in our phenomenological analysis.

6.1. Flavor Constraints

We consider four types of flavor constraints to apply to the SU(5)-FUT, where SUSY is known to have significant impact. More specifically, we consider the flavor observables $\mathrm{BR}(b\to s\gamma )$, $\mathrm{BR}(B_s\to {\mu }^{+}{\mu }^{-})$, $\mathrm{BR}(B_u\to \tau \nu )$ and $\Delta M_{B_s}$.We do not use the latest experimental and theoretical values here. However, this has a minor impact on the general form of our results. The uncertainties are the linear combination of the experimental error and twice the theoretical uncertainty in the MSSM. We include the MSSM uncertainty also in the ratios of exp. data and SM prediction, to apply it readily to our prediction of the ratio of our MSSM and SM calculation. In the case that no specific estimate is available, we use the SM uncertainty.

For the branching ratio $\mathrm{BR}(b\to s\gamma )$, we take a value from the Heavy Flavor Averaging Group (HFAG) [95,96,97,98,99,100]:

$$\frac{\mathrm{BR}{(b\to s\gamma )}^{\exp }}{\mathrm{BR}{(b\to s\gamma )}^{\mathrm{SM}}}=1.089\pm 0.27.$$

(73)

For the branching ratio $\mathrm{BR}(B_s\to {\mu }^{+}{\mu }^{-})$, a combination of CMS and LHCb data [101,102,103,104,105,106,107,108] is used:

$$\mathrm{BR}(B_s\to {\mu }^{+}{\mu }^{-})=(2.9\pm 1.4)\times {10}^{-9}.$$

(74)

For the $B_u$ decay to $\tau \nu$, we use the limit [100,109,110,111]:

$$\frac{\mathrm{BR}{(B_u\to \tau \nu )}^{\exp }}{\mathrm{BR}{(B_u\to \tau \nu )}^{\mathrm{SM}}}=1.39\pm 0.69,$$

(75)

while for $\Delta M_{B_s}$ [112,113]:

$$\frac{\Delta M_{B_s}^{\exp }}{\Delta M_{B_s}^{\mathrm{SM}}}=0.97\pm 0.2$$

(76)

At the end of the phenomenological discussion, we also comment on the Cold Dark Matter (CDM) density. It is well known that the lightest neutralino, being the Lightest SUSY Particle (LSP), is an excellent candidate for CDM [114,115]. Consequently, one can in principle demand that the lightest neutralino is indeed the LSP, and parameters leading to a different LSP could be discarded.

The current bound, favored by a joint analysis of WMAP/Planck and other astrophysical and cosmological data, is at the $2\sigma$ level given by the range [116,117],

$${\mathrm{\Omega }}_{\mathrm{CDM}}{h}^2=0.1120\pm 0.0112.$$

(77)

6.2. The Light Higgs Boson Mass

The quartic couplings in the Higgs potential are given by the SM gauge couplings. As a consequence, the lightest Higgs mass is not a free parameter, but rather predicted in terms of the other parameters of the model. Higher order corrections are crucial for a precise prediction of $M_h$; see [118,119,120] for reviews.

The discovery of a Higgs boson at ATLAS and CMS in July 2012 [1,2] can be interpreted as the discovery of the light $\mathcal{CP}$-even Higgs boson of the MSSM Higgs spectrum [121,122,123]. The experimental average for the (SM) Higgs boson mass is taken to be: [124]

$$M_H^{\exp }=125.1\pm 0.3\mathrm{GeV},$$

(78)

and adding in quadrature a 3 (2) GeV theory uncertainty [125,126,127] for the Higgs mass calculation in the MSSM, we arrive at an allowing range of:

$$M_h=125.1\pm 3.1\left(2.1\right)\mathrm{GeV}.$$

(79)

We used the code FeynHiggs [125,127,128,129,130,131,132,133] (Version 2.14.0 beta) to predict the lightest Higgs boson mass. the evaluation of the Higgs masses with FeynHiggs is based on the combination of a Feynman-diagrammatic calculation and a resummation of the (sub)leading and logarithms contributions of the (general) type of $\log (m_{\tilde{t}}/m_t)$ in all orders of perturbation theory. This combination ensures a reliable evaluation of $M_h$ also for large SUSY scales. Several refinements in the combination of the fixed order log resummed calculation have been included w.r.t. previous versions; see [127]. They resulted not only in a more precise $M_h$ evaluation for high SUSY mass scales, but in particular in a downward shift of $M_h$ at the level of $\mathcal{O}\left(2\mathrm{GeV}\right)$ for large SUSY masses.

7. Numerical Analysis

In this section, we will analyze the particle spectrum predicted in the $\mathit{SU}\left(\mathbf{5}\right)$-FUT . Since the gauge symmetry is spontaneously broken below $M_{\mathrm{GUT}}$, the finiteness conditions do not restrict the renormalization properties at low energies, and all that remains are boundary conditions on the gauge and Yukawa couplings (71), the $h=-MC$ (41) relation and the soft scalar-mass sum rule at $M_{\mathrm{GUT}}$.

In Figure 1, we show the $\mathit{SU}\left(\mathbf{5}\right)$-FUT predictions for $m_t$ and $m_b\left(M_Z\right)$ as a function of the unified gaugino mass M, for the two cases $\mu <0$ and $\mu >0$. We use the experimental value of the top quark pole mass as [111]. We did not include the latest LHC/Tevatron combination, leading to $m_t^{\exp }=(173.34\pm 0.76)\mathrm{GeV}$ [134], which would have a negligible impact on our analysis.

$$m_t^{\exp }=(173.2\pm 0.9)\mathrm{GeV}.$$

(80)

The bottom mass is calculated at $M_Z$ to avoid uncertainties that come from running down to the pole mass; the leading SUSY radiative corrections to the bottom and tau masses have been taken into account [135]. We use the following value for the bottom mass at $M_Z$ [111],

$$m_b\left(M_Z\right)=(2.83\pm 0.10)\mathrm{GeV}.$$

(81)

The bounds on the $m_b\left(M_Z\right)$ and the $m_t$ mass clearly single out $\mu <0$, as the solution most compatible with these experimental constraints.

As was already mentioned, for the lightest Higgs boson mass, we used the code FeynHiggs (2.14.0 beta). the prediction for $M_h$ of $\mathit{SU}\left(\mathbf{5}\right)$-FUT with $\mu <0$ is shown in Figure 2, in a range where the unified gaugino mass varies from 0.5 TeV ≲M≲ 9 TeV. The green points include the B-physics constraints. One should keep in mind that these predictions are subject to a theory uncertainty of 3 (2) GeV [125]. Older analysis, including in particular less refined evaluations of the light Higgs boson mass, are given in [46,136,137].

The allowed values of the Higgs mass put a limit on the allowed values of the SUSY masses, as can be seen in Figure 3. In the left (right) plot, we impose $M_h=125.1\pm 3.1\left(2.1\right)\mathrm{GeV}$ as discussed above. In particular, very heavy colored SUSY particles are favored (nearly independent of the $M_h$ uncertainty), in agreement with the non-observation of those particles at the LHC [138,139]. Overall, the allowed colored SUSY masses would remain unobservable at the (HL-)LHC, the ILC or CLIC. However, the colored spectrum would be accessible at the FCC-hh [140], as could the full heavy Higgs boson spectrum. On the other hand, the Lightest Observable SUSY Particle (LSOP) is the scalar tau. Some parts of the allowed spectrum of the lighter scalar tau or the lighter charginos/neutralinos might be accessible at CLIC with $\sqrt{s}=3\mathrm{TeV}$.

In

Table 1. Two example spectra of the $\mathit{SU}\left(\mathbf{5}\right)$-FUT (with $\mu <0$) . All masses are in GeV and rounded to 1 (0.1) GeV (for the light Higgs mass).

$\mathit{\delta }{\mathit{M}}_{\mathit{h}}=2.1$	${\mathit{M}}_{\mathit{h}}$	${\mathit{M}}_{\mathit{H}}$	${\mathit{M}}_{\mathit{A}}$	${\mathit{M}}_{{\mathit{H}}^{\pm }}$	${\mathit{m}}_{{\tilde{\mathit{t}}}_1}$	${\mathit{m}}_{{\tilde{\mathit{t}}}_2}$	${\mathit{m}}_{{\tilde{\mathit{b}}}_1}$	${\mathit{m}}_{{\tilde{\mathit{b}}}_2}$	${\mathit{m}}_{\tilde{\mathit{g}}}$
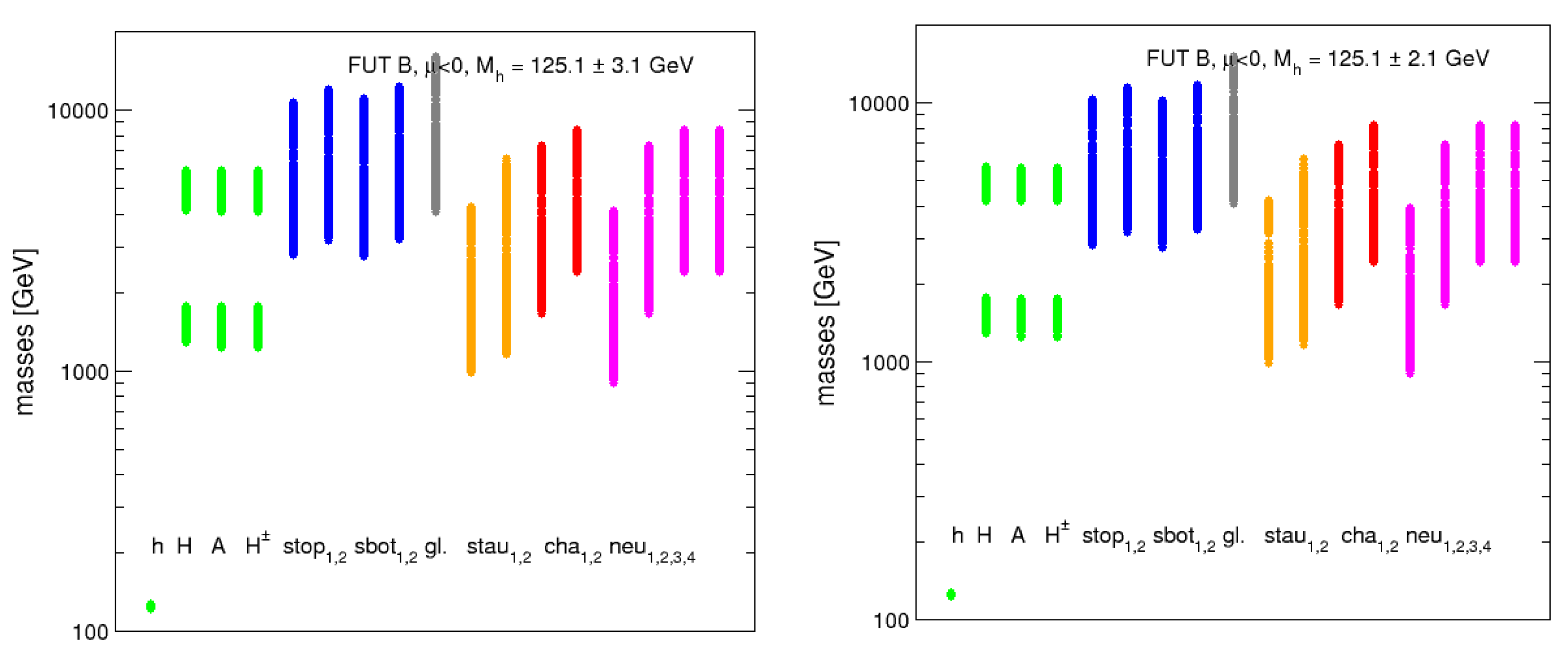
lightest	123.1	1533	1528	1527	2800	3161	2745	3219	4077
heaviest	127.2	4765	4737	4726	10,328	11,569	10,243	11,808	15,268
	$m_{{\tilde{\tau }}_1}$	$m_{{\tilde{\tau }}_2}$	$m_{{\tilde{\chi }}_1^{\pm }}$	$m_{{\tilde{\chi }}_2^{\pm }}$	$m_{{\tilde{\chi }}_1^0}$	$m_{{\tilde{\chi }}_2^0}$	$m_{{\tilde{\chi }}_3^0}$	$m_{{\tilde{\chi }}_4^0}$	$\tan \beta$
lightest	983	1163	1650	2414	900	1650	2410	2414	45
heaviest	4070	5141	6927	8237	3920	6927	8235	8237	46
$\mathit{\delta }{\mathit{M}}_{\mathit{h}}=\mathbf{3.1}$	${\mathit{M}}_{\mathit{h}}$	${\mathit{M}}_{\mathit{H}}$	${\mathit{M}}_{\mathit{A}}$	${\mathit{M}}_{{\mathit{H}}^{\pm }}$	${\mathit{m}}_{{\tilde{\mathit{t}}}_{\mathbf{1}}}$	${\mathit{m}}_{{\tilde{\mathit{t}}}_{\mathbf{2}}}$	${\mathit{m}}_{{\tilde{\mathit{b}}}_{\mathbf{1}}}$	${\mathit{m}}_{{\tilde{\mathit{b}}}_{\mathbf{2}}}$	${\mathit{m}}_{\tilde{\mathit{g}}}$
lightest	122.8	1497	1491	1490	2795	3153	2747	3211	4070
heaviest	127.9	4147	4113	4103	10,734	12,049	11,077	12,296	16,046
	$m_{{\tilde{\tau }}_1}$	$m_{{\tilde{\tau }}_2}$	$m_{{\tilde{\chi }}_1^{\pm }}$	$m_{{\tilde{\chi }}_2^{\pm }}$	$m_{{\tilde{\chi }}_1^0}$	$m_{{\tilde{\chi }}_2^0}$	$m_{{\tilde{\chi }}_3^0}$	$m_{{\tilde{\chi }}_4^0}$	$\tan \beta$
lightest	1001	1172	1647	2399	899	647	2395	2399	44
heaviest	4039	6085	7300	8409	4136	7300	8406	8409	45

, we show two example spectra of the $\mathit{SU}\left(\mathbf{5}\right)$-FUT (with $\mu <0$)  which span the mass range of the parameter space that is in agreement with the B-physics observables and the Higgs-boson mass measurement. We give the lightest and the heaviest spectrum for $\delta M_h=2.1$ and $\delta M_h=3.1$, respectively. The four Higgs boson masses are denoted as $M_h$, $M_H$, $M_A$ and $M_{H^{\pm }}$. $m_{{\tilde{t}}_{1,2}}$, $m_{{\tilde{t}}_{1,2}}$, $m_{\tilde{g}}$ and $m_{{\tilde{\tau }}_{1,2}}$, are the scalar top, scalar bottom, gluino and scalar tau masses, respectively. $m_{{\tilde{\chi }}_{1,2}^{\pm }}$ and $m_{{\tilde{\chi }}_{1,2,3,4}^0}$ denote the chargino and neutralino masses.

We find that no point of $\mathit{SU}\left(\mathbf{5}\right)$-FUT (with $\mu <0$) fulfills the strict bound of Equation (77) (for our evaluation, we have used the code MicroMegas [141,142,143]). Consequently, on a more general basis, a mechanism is needed in our model to reduce the CDM abundance in the early universe. This issue could, for instance, be related to another problem, that of neutrino masses. This type of mass cannot be generated naturally within the class of Finite Unified Theories that we are considering in this paper, although a non-zero value for neutrino masses has clearly been established [111]. However, the class of FUTs discussed here can, in principle, be easily extended by introducing bilinear R-parity violating terms that preserve finiteness and introduce the desired neutrino masses [144,145]. R-parity violation [146,147,148,149] would have a small impact on the collider phenomenology presented here (apart from the fact that SUSY search strategies could not rely on a ‘missing energy’ signature), but remove the CDM bound of Equation (77) completely. The details of such a possibility in the present framework attempting to provide the models with realistic neutrino masses will be discussed elsewhere. Other mechanisms, not involving R-parity violation (and keeping the ‘missing energy’ signature), that could be invoked if the amount of CDM appears to be too large, concern the cosmology of the early universe. For instance, “thermal inflation” [150] or “late time entropy injection” [151] could bring the CDM density into agreement with the WMAP measurements. This kind of modification of the physics scenario neither concerns the theory basis nor the collider phenomenology, but could have a strong impact on the CDM bounds (lower values than those permitted by Equation (77) are naturally allowed if a particle other than the lightest neutralino constitutes CDM).

8. Conclusions

The MSSM is considered a very attractive candidate for describing physics beyond the SM. However, the serious problem of the SM having too many free parameters is further proliferated in the MSSM. Assuming a GUT beyond the scale of gauge coupling unification, based on the idea that a Particle Physics Theoryshould be more symmetric at higher scales, seems to fit the MSSM. On the other hand, the unification scenario seems to be unable to further reduce the number of free parameters.

Attempting to reduce the free parameters of a theory, a new approach was proposed in [18,19] based on the possible existence of RGI relations among couplings. Although this approach could uncover further symmetries, its application opens new horizons, as well. At least the Finite Unified Theories seem to comprise a very promising field for applying the reduction approach. In the FUT case, the discovery of RGI relations among couplings above the unification scale ensures at the same time finiteness to all orders.

The discussion in the previous sections of this paper shows that the predictions of the particular FUT discussed here are impressive. In addition, one could add some comments on a successful FUT from the theoretical side, as well. The developments on treating the problem of divergencies include string and non-commutative theories, as well as $N=4$ SUSY theories [152,153], $N=8$ supergravity [154,155,156,157,158] and the AdS/CFT correspondence [159]. It is very interesting that the $N=1$ FUT discussed here includes many ideas that have survived phenomenological and theoretical tests, as well as the ultraviolet divergence problem. It is actually solving that problem in a minimal way.

We concentrated our examination on the predictions of one particular $SU\left(5\right)$ Finite Unified Theory, including the restrictions of third generation quark masses and B-physics observables. The model, $\mathit{SU}\left(\mathbf{5}\right)$-FUT (with $\mu <0$), is consistent with all the phenomenological constraints. Compared to our previous analyses [46,47,136,137], the improved evaluation of $M_h$ prefers a heavier (Higgs) spectrum and thus in general allows only a very heavy SUSY spectrum. The colored spectrum could easily escapes the (HL-)LHC searches, but can likely be tested at the FCC-hh. The lower part of the electroweak spectrum could be accessible at CLIC.