Social Group Optimization Supported Segmentation and Evaluation of Skin Melanoma Images
Abstract
1. Introduction
2. Materials and Methods
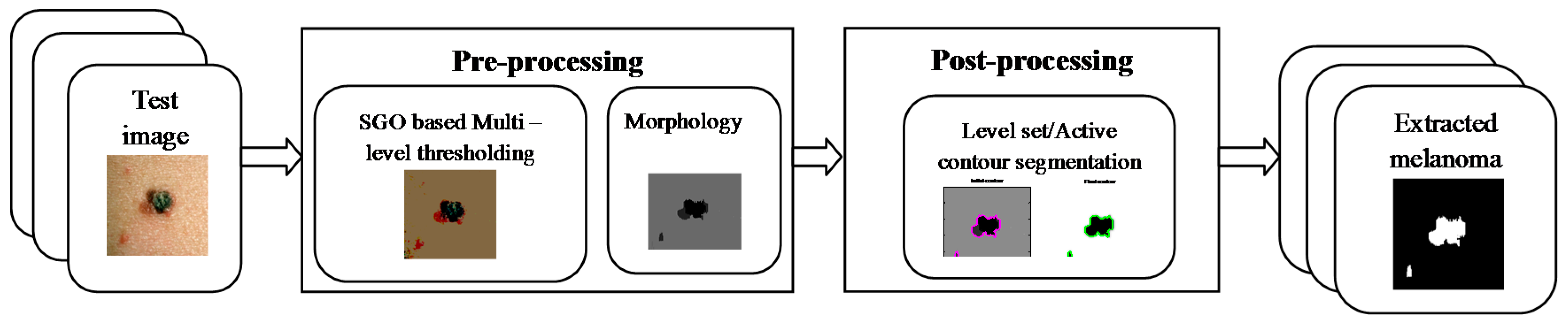
2.1. Pre-Processing
2.1.1. Multi-Level Thresholding
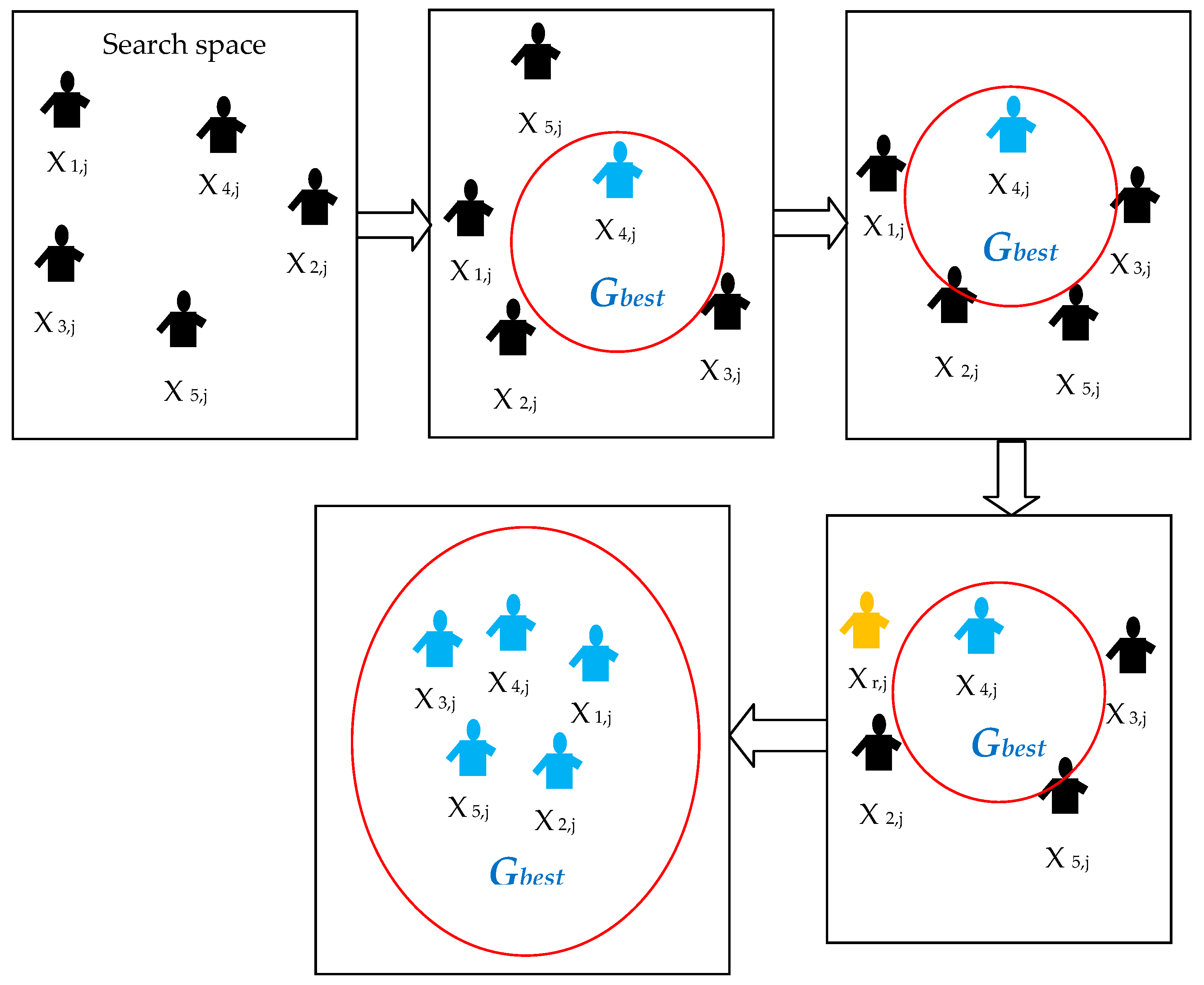
2.1.2. Social Group Optimization
| Algorithm 1: Standard Social Group Optimization Algorithm |
| Start Assume five agents (i = 1,2,3,4,5) Assign these agents to find the Gbestj in a D-dimensional search space Randomly distribute the entire agents in the group throughout the search space during initialization process Computethe fitness value based on the problem under concern Updatethe orientation of agents using Gbestj = max {f(Xi)} Initiatethe improving phase to update the knowledge of other agents in order to reach the Gbestj Initiatethe acquiring phase to further update the knowledge of agents by randomly choosing the agents with best fitness value Repeatthe procedure till the entire agents move toward the best possible position in the D-dimensional search space If all the agents have approximately similar fitness values (Gbestj) Then Terminate the search and display the optimized result for the chosen problem Else Repeat the previous steps End Stop |
2.1.3. Otsu Based Thresholding
2.1.4. Kapur Based Thresholding
2.1.5. Image Morphology
2.2. Post-Processing
2.2.1. Level Set
2.2.2. Active Contour
2.3. Implementation of the Proposed Tool
2.4. Image Quality Assessment
2.5. Proposed Tool
3. Results and Discussion
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Premaladha, J.; Sujitha, S.; Priya, M.L.; Rajichandran, K.S. A survey on melanoma diagnosis using image processing and soft computing techniques. Res. J. Inf. Tech. 2014, 6, 65–80. [Google Scholar] [CrossRef][Green Version]
- Celebi, M.E.; Zornberg, A. Automated quantification of clinically significant colors in dermoscopy images and its application to skin lesion classification. IEEE Syst. J. 2014, 8, 980–984. [Google Scholar] [CrossRef]
- Celebi, M.E.; Iyatomi, H.; Schaefer, G.; Stoecker, W.V. Lesion border detection in dermoscopy images. Comput. Med. Imag. Graph. 2009, 33, 148–153. [Google Scholar] [CrossRef] [PubMed]
- Celebi, M.E.; Kingravi, H.; Uddin, B.; Iyatomi, H.; Aslandogan, A.; Stoecker, W.V.; Moss, R.H. A methodological approach to the classification of dermoscopy images. Comput. Med. Imag. Graph. 2007, 31, 362–373. [Google Scholar] [CrossRef] [PubMed]
- Amelard, R.; Glaister, J.; Wong, A.; Clausi, D.A. Melanoma decision support using lighting-corrected intuitive feature models. Comput. Vis. Tech. Diagn. Skin Cancer 2013, 193–219. [Google Scholar]
- Nachbar, F.; Stolz, W.; Merckle, T.; Cognetta, A.B.; Vogt, T.; Landthaler, M.; Bilek, P.; Braun-Falco, O.; Plewig, G. The ABCD rule of dermatoscopy: High prospective value in the diagnosis of doubtful melanocytic skin lesions. J. Am. Acad. Dermatol. 1994, 30, 551–559. [Google Scholar] [CrossRef]
- Barata, C.; Celebi, M.E.; Marques, J.S. Improving dermoscopy image classification using color constancy. IEEE J. Biomed. Health. Inform. 2015, 19, 1146–1152. [Google Scholar] [PubMed]
- Rajinikanth, V.; Raja, N.S.M.; Satapathy, S.C.; Fernandes, S.L. Otsu’s multi-thresholding and active contour snake model to segment dermoscopy images. J. Med. Imag. Health Inf. 2017, 7, 1837–1840. [Google Scholar] [CrossRef]
- Amelard, R.; Glaister, J.; Wong, A.; Clausi, D.A. High-level intuitive features (HLIFs) for intuitive skin lesion description. IEEE Trans. Biomed. Eng. 2015, 62, 820–831. [Google Scholar] [CrossRef] [PubMed]
- Glaister, J.; Wong, A.; Clausi, D.A. Segmentation of skin lesions from digital images using joint statistical texture distinctiveness. IEEE Trans. Biomed. Eng. 2014, 61, 1220–1230. [Google Scholar] [CrossRef] [PubMed]
- Glaister, J.; Amelard, R.; Wong, A.; Clausi, D.A. MSIM: Multistage illumination modeling of dermatological photographs for illumination-corrected skin lesion analysis. IEEE Trans. Biomed. Eng. 2013, 60, 1873–1883. [Google Scholar] [CrossRef] [PubMed]
- Oliveira, R.B.; Filho, M.E.; Ma, Z.; Papa, J.P.; Pereira, A.S.; Tavares, J.M.R.S. Computational methods for the image segmentation of pigmented skin lesions: A review. Comput. Method. Progr. Biomed. 2016, 131, 127–141. [Google Scholar] [CrossRef] [PubMed]
- Mercedes Filho, M.; Ma, Z.; Tavares, J.M.R.S. A Review of the quantification and classification of pigmented skin lesions: From dedicated to hand-held devices. J. Med. Syst. 2015, 39. [Google Scholar] [CrossRef]
- Ma, Z.; Tavares, J.M.R.S. Novel approach to segment skin lesions in dermoscopic images based on a deformable model. IEEE J. Biomed. Health 2016, 20, 615–623. [Google Scholar] [CrossRef] [PubMed]
- Oliveira, R.B.; Marranghello, N.; Pereira, A.S.; Tavares, J.M.R.S. A computational approach for detecting pigmented skin lesions in macroscopic images. Expert. Syst. Appl. 2016, 61, 53–63. [Google Scholar] [CrossRef]
- Pennisi, A.; Bloisi, D.D.; Nardi, D.; Giampetruzzi, A.R.; Mondino, C.; Facchianoc, A. Skin lesion computational diagnosis of dermoscopic images: Ensemble models based on input feature manipulation. Comput. Meth. Prog. Bio. 2017, 149, 43–53. [Google Scholar]
- Rosado, L.; Vasconcelos, M.J.V.; Castro, R.; Tavares, J.M.R.S. From Dermoscopy to Mobile Teledermatology. Dermoscopy Image Analysis; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Xu, L.; Jackowski, M.; Goshtasby, A.; Roseman, D.; Bines, S.; Yu, C.; Dhawan, A.; Huntley, A. Segmentation of skin cancer images. Image Vis. Comput. 1999, 17, 65–74. [Google Scholar] [CrossRef]
- Silveira, M.; Nascimento, J.C.; Marques, J.S.; Marcal, A.R.S.; Mendonca, T.; Yamauchi, S.; Maeda, J.; Rozeira, J. Comparison of segmentation methods for melanoma diagnosis in dermoscopy images. IEEE J. Sel. Top. Signal Process 2009, 3, 35–45. [Google Scholar] [CrossRef]
- Lee, T.; Ng, V.; Gallagher, R.; Coldman, A.; McLean, D. DullRazor: A software approach to hair removal from images. Comput. Biol. Med. 1997, 27, 533–543. [Google Scholar] [CrossRef]
- Available online: http://www.dermweb.com/dull_razor (accessed on 1 December 2017).
- Wighton, P.; Lee, T.K.; Atkinsa, M.S. Dermoscopic hair disocclusion using inpainting. Proc. SPIE Med. Imaging 2008, 1–8. [Google Scholar] [CrossRef]
- Mirzaalian, H.; Lee, T.K.; Hamarneh, G. Hair enhancement in dermoscopic images using dual-channel quaternion tubularness filters and MRF-based multilabel optimization. IEEE Trans. Image Process. 2014, 23, 5486–5496. [Google Scholar] [CrossRef] [PubMed]
- Satheesha, T.Y.; Satyanarayana, D.; Giriprasad, M.N. A pixel interpolation technique for curved hair removal in skin images to support melanoma detection. J. Theor. App. Infor. Tech. 2014, 70, 559–565. [Google Scholar]
- Abbas, Q.; Celebi, M.E.; Garcia, I.F. Hair removal methods: A comparative study for dermoscopy images. Biomed. Signal Proces. 2011, 6, 395–404. [Google Scholar] [CrossRef]
- Available online: https://uwaterloo.ca/vision-image-processing-lab/research-demos/skin-cancer-detection (accessed on 1 December 2017).
- Available online: https://challenge.kitware.com/#challenge/560d7856cad3a57cfde481ba (accessed on 1 December 2017).
- Chang, W.-Y.; Huang, A.; Yang, C.-Y.; Lee, C.-H.; Chen, Y.-C.; Wu, T.-Y.; Chen, G.-S. Computer-aided diagnosis of skin lesions using conventional digital photography: A reliability and feasibility study. PLoS ONE 2013, 8, e76212. [Google Scholar] [CrossRef] [PubMed]
- Tuba, M. Multilevel image thresholding by nature-inspired algorithms: A short review. Comput. Sci. J. Mold. 2014, 22, 318–338. [Google Scholar]
- Satapathy, S.C.; Raja, N.S.M.; Rajinikanth, V.; Ashour, A.S.; Dey, N. Multi-level image thresholding using Otsu and chaotic bat algorithm. Neural Comput. Applic. 2016. [Google Scholar] [CrossRef]
- Rajinikanth, V.; Couceiro, M.S. RGB histogram based color image segmentation using firefly algorithm. Proced. Com. Sci. 2015, 46, 1449–1457. [Google Scholar] [CrossRef]
- Samanta, S.; Acharjee, S.; Mukherjee, A.; Das, D.; Dey, N. Ant Weight lifting algorithm for image segmentation. In Proceedings of the IEEE International Conference on Computational Intelligence and Computing Research (ICCIC), Madurai, India, 26–28 December 2013; pp. 1–5. [Google Scholar] [CrossRef]
- Rajinikanth, V.; Raja, N.S.M.; Satapathy, S.C. Robust color image multi-thresholding using between-class variance and cuckoo search algorithm. Adv. Intell. Syst. Comput. 2016, 433, 379–386. [Google Scholar]
- Balan, N.S.; Kumar, A.S.; Raja, N.S.M.; Rajinikanth, V. Optimal multilevel image thresholding to improve the visibility of Plasmodium sp. in blood smear images. Adv. Intell. Syst. Comput. 2016, 397, 563–571. [Google Scholar]
- Rajinikanth, V.; Raja, N.S.M.; Latha, K. Optimal multilevel image thresholding: An analysis with PSO and BFO algorithms. Aust. J. Basic Appl. Sci. 2014, 8, 443–454. [Google Scholar]
- Raja, N.S.M.; Rajinikanth, V.; Latha, K. Otsu based optimal multilevel image thresholding using firefly algorithm. Model. Sim. Engg. 2014, 2014, 794574. [Google Scholar] [CrossRef]
- Otsu, N. A threshold selection method from gray-level histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Satapathy, S.; Naik, A. Social group optimization (SGO): A new population evolutionary optimization technique. Complex Intell. Sys. 2016, 2, 173–203. [Google Scholar] [CrossRef]
- Naik, A.; Satapathy, S.C.; Ashour, A.S.; Dey, N. Social group optimization for global optimization of multimodal functions and data clustering problems. Neural Comput. Applic. 2016. [Google Scholar] [CrossRef]
- Dey, N.; Ashour, A.S.; Althoupety, A.S. Thermal Imaging in Medical Science. In Recent Advances in Applied Thermal Imaging for Industrial Applications; IGI: New Delhi, India, 2017; pp. 87–117. [Google Scholar] [CrossRef]
- Moraru, L.; Moldovanu, S.; Culea-Florescu, A.-L.; Bibicu, D.; Ashour, A.S.; Dey, N. Texture analysis of parasitological liver fibrosis images. Microsc. Res. Tech. 2017. [Google Scholar] [CrossRef] [PubMed]
- Dey, N.; Ahmed, S.S.; Chakraborty, S.; Maji, P.; Das, A.; Chaudhuri, S.S. Effect of trigonometric functions-based watermarking on blood vessel extraction: An application in ophthalmology imaging. Int. J. Embed. Sys. 2017, 9, 90–100. [Google Scholar] [CrossRef]
- Ahmed, S.S.; Dey, N.; Ashour, A.S.; Sifaki-Pistolla, D.; Bălas-Timar, D.; Balas, V.E.; Tavares, J.M.R.S. Effect of fuzzy partitioning in Crohn’s disease classification: A neuro-fuzzy-based approach. Med. Biol. Eng. Comput. 2017, 55, 101–115. [Google Scholar] [CrossRef] [PubMed]
- Ngan, T.T.; Tuan, T.M.; Minh, N.H.; Dey, N. Decision making based on fuzzy aggregation operators for medical diagnosis from dental x-ray images. J. Med. Syst. 2016, 40, 280. [Google Scholar] [CrossRef] [PubMed]
- Dey, N.; Ashour, A.S.; Chakraborty, S.; Samanta, S.; Sifaki-Pistolla, D.; Ashour, A.S.; Le, D.-N.; Nguyen, G.N. Healthy and unhealthy rat hippocampus cells classification: A neural based automated system for alzheimer disease classification. J. Adv. Microsc. Res. 2016, 11, 1–10. [Google Scholar] [CrossRef]
- Kotyk, T.; Dey, N.; Ashour, A.S.; Balas-Timar, D.; Chakraborty, S.; Ashour, A.S.; Tavares, J.M.R.S. Measurement of glomerulus diameter and Bowman’s space width of renal albino rats. Comput. Meth. Prog. Bio. 2016, 126, 143–153. [Google Scholar] [CrossRef] [PubMed]
- Kausar, N.; Abdullah, A.; Samir, B.B.; Palaniappan, S.; Al Ghamdi, B.S.; Dey, N. Ensemble Clustering Algorithm with Supervised Classification of Clinical Data for Early Diagnosis of Coronary Artery Disease. J. Med. Imaging Health Inf. 2016, 6, 78–87. [Google Scholar] [CrossRef]
- Araki, T.; Ikeda, N.; Molinari, F.; Dey, N.; Acharjee, S.; Saba, L.; Nicolaides, A. Automated Identification of Calcium Coronary Lesion Frames From Intravascular Ultrasound Videos. J. Ultrasound Med. 2014, 33, S1–S124. [Google Scholar]
- Kapur, J.N.; Sahoo, P.K.; Wong, A.K.C. A new method for gray-level picture thresholding using the entropy of the histogram. Comput. Vis. Graph. Image Process. 1985, 29, 273–285. [Google Scholar] [CrossRef]
- Lakshmi, V.S.; Tebby, S.G.; Shriranjani, D.; Rajinikanth, V. Chaotic cuckoo search and Kapur/Tsallis approach in segmentation of T. cruzi from blood smear images. Int. J. Comp. Sci. Infor. Sec. (IJCSIS) 2016, 14, 51–56. [Google Scholar]
- Manic, K.S.; Priya, R.K.; Rajinikanth, V. Image multithresholding based on Kapur/Tsallis entropy and firefly algorithm. Ind. J. Sci. Technol. 2016, 9. [Google Scholar] [CrossRef]
- Akay, B. A study on particle swarm optimization and artificial bee colony algorithms for multilevel thresholding. Appl. Soft Comput. 2013, 13, 3066–3091. [Google Scholar] [CrossRef]
- Bhandari, A.K.; Kumar, A.; Singh, G.K. Modified artificial bee colony based computationally efficient multilevel thresholding for satellite image segmentation using Kapur’s, Otsu and Tsallis functions. Expert Syst. Appl. 2015, 42, 1573–1601. [Google Scholar] [CrossRef]
- Caselles, V.; Catte, F.; Coll, T.; Dibos, F. A geometric model for active contours in image processing. Numer. Math. 1993, 66, 1–31. [Google Scholar] [CrossRef]
- Malladi, R.; Sethian, J.A.; Vemuri, B.C. Shape modeling with front propagation: A level set approach. IEEE Trans. Pattern Anal. Mac. Int. 1995, 17, 158–175. [Google Scholar] [CrossRef]
- Li, C.; Xu, C.; Gui, C.; Fox, M.D. Distance regularized level set evolution and its application to image segmentation. IEEE T. Image Process. 2010, 19, 3243–3254. [Google Scholar]
- Vaishnavi, G.K.; Jeevananthan, K.; Begum, S.R.; Kamalanand, K. Geometrical analysis of schistosome egg images using distance regularized level set method forautomated species identification. J. Bioinform. Intell. Cont. 2014, 3, 147–152. [Google Scholar] [CrossRef]
- Bresson, X.; Esedoglu, S.; Vandergheynst, P.; Thiran, J.-P.; Osher, S. Fast global minimization of the active contour/snake model. J. Math. Imaging Vis. 2007, 28, 151–167. [Google Scholar] [CrossRef]
- Chan, T.F.; Vese, L.A. Active contours without edges. IEEE Trans. Image Process. 2001, 10, 266–277. [Google Scholar] [CrossRef] [PubMed]
- Lankton, S.; Tannenbaum, A. Localizing region-based active contours. IEEE Trans. Image Process. 2008, 17, 2029–2039. [Google Scholar] [CrossRef] [PubMed]
- Chaddad, A.; Tanougast, C. Quantitative evaluation of robust skull stripping and tumor detection applied to axial MR images. Brain Infor. 2016, 3, 53–61. [Google Scholar] [CrossRef] [PubMed]
- Lu, H.; Kot, A.C.; Shi, Y.Q. Distance-reciprocal distortion measurefor binary document images. IEEE Signal Process. Lett. 2004, 11, 228–231. [Google Scholar] [CrossRef]
- Moghaddam, R.F.; Cheriet, M. A multi-scale framework for adaptive binarization of degraded document images. Pat. Recognit. 2010, 43, 2186–2198. [Google Scholar] [CrossRef]
- Mostafa, A.; Hassanien, A.E.; Houseni, M.; Hefny, H. Liver segmentation in MRI images based on whale optimization algorithm. Multimed. Tools Appl. 2017. [Google Scholar] [CrossRef]
- Sokolova, M.; Lapalme, G. A systematic analysis of performance measures for classification tasks. Inf. Process. Manag. 2009, 45, 427–437. [Google Scholar] [CrossRef]
- Demsar, J. Statistical comparisons of classifiers over multiple data sets. J. Mach. Learn. Res. 2006, 7, 1–30. [Google Scholar]
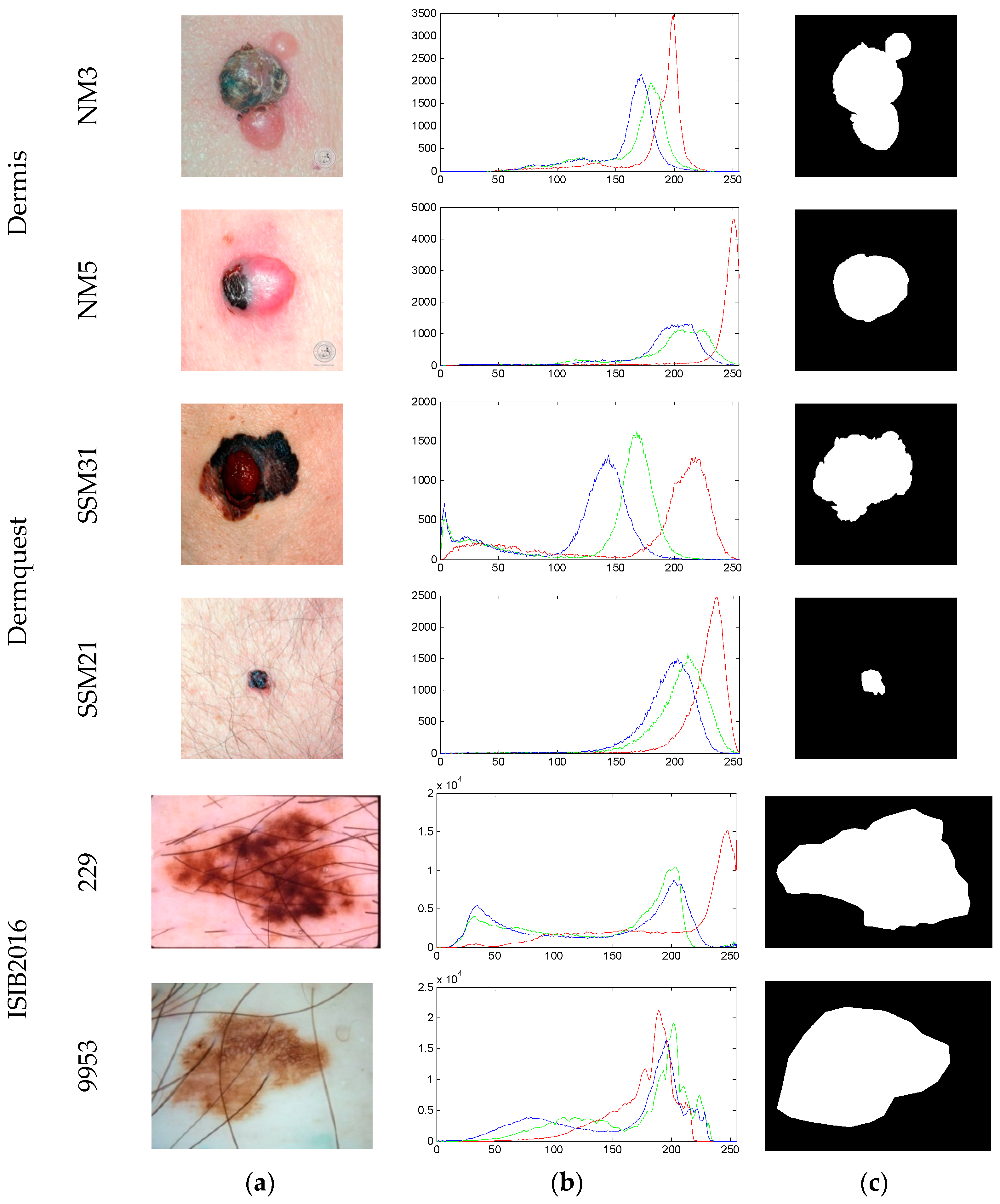




| Image | Segmentation Approach | JI | DC | FPR | FNR |
|---|---|---|---|---|---|
| NM3 | LS | 0.8794 | 0.9305 | 0.1285 | 0.0101 |
| GAC | 0.8728 | 0.9310 | 0.1004 | 0.0073 | |
| LAC | 0.8744 | 0.9311 | 0.1026 | 0.0193 | |
| NM5 | LS | 0.8395 | 0.9004 | 0.0885 | 0.0064 |
| GAC | 0.8226 | 0.8917 | 0.1743 | 0.0110 | |
| LAC | 0.8106 | 0.8853 | 0.1006 | 0.0097 | |
| SSM31 | LS | 0.8652 | 0.9106 | 0.0713 | 0.0093 |
| GAC | 0.8408 | 0.9274 | 0.0945 | 0.0115 | |
| LAC | 0.8511 | 0.9037 | 0.0836 | 0.0284 | |
| SSM21 | LS | 0.8316 | 0.8925 | 0.0814 | 0.0377 |
| GAC | 0.8014 | 0.8818 | 0.1004 | 0.0604 | |
| LAC | 0.8028 | 0.8674 | 0.0560 | 0.0840 | |
| 229 | LS | 0.8284 | 0.8911 | 0.0106 | 0.0947 |
| GAC | 0.8004 | 0.8972 | 0.0219 | 0.0956 | |
| LAC | 0.8084 | 0.8779 | 0.0724 | 0.0821 | |
| 9953 | LS | 0.7827 | 0.8922 | 0.0084 | 0.0726 |
| GAC | 0.8173 | 0.9105 | 0.0202 | 0.0622 | |
| LAC | 0.8091 | 0.9007 | 0.0115 | 0.0519 |
| Image | Approach | PRE | FM | SEN | SPE | BCR | BER% | ACC |
|---|---|---|---|---|---|---|---|---|
| NM3 | LS | 0.9981 | 0.9813 | 0.9652 | 0.9939 | 0.9793 | 2.0606 | 0.9792 |
| GAC | 0.9941 | 0.9852 | 0.9765 | 0.9799 | 0.9782 | 2.1781 | 0.9782 | |
| LAC | 0.9930 | 0.9843 | 0.9758 | 0.9759 | 0.9759 | 2.4114 | 0.9759 | |
| NM5 | LS | 0.9980 | 0.9911 | 0.9844 | 0.9888 | 0.9866 | 1.3403 | 0.9866 |
| GAC | 0.9998 | 0.9774 | 0.9561 | 0.9990 | 0.9775 | 2.2420 | 0.9773 | |
| LAC | 0.9998 | 0.9789 | 0.9589 | 0.9992 | 0.9791 | 2.0882 | 0.9789 | |
| SSM31 | LS | 0.9988 | 0.9847 | 0.9709 | 0.9964 | 0.9837 | 1.6268 | 0.9836 |
| GAC | 0.9986 | 0.9822 | 0.9663 | 0.9957 | 0.9810 | 1.8980 | 0.9809 | |
| LAC | 0.9993 | 0.9825 | 0.9662 | 0.9980 | 0.9821 | 1.7858 | 0.9820 | |
| SSM21 | LS | 0.9975 | 0.9983 | 0.9990 | 0.8585 | 0.9288 | 7.1187 | 0.9261 |
| GAC | 0.9966 | 0.9978 | 0.9990 | 0.8087 | 0.9038 | 9.6129 | 0.8988 | |
| LAC | 0.9968 | 0.9979 | 0.9991 | 0.8194 | 0.9092 | 9.0752 | 0.9048 | |
| 229 | LS | 0.8629 | 0.9261 | 0.9993 | 0.7867 | 0.8930 | 10.6964 | 0.8866 |
| GAC | 0.9641 | 0.9703 | 0.9767 | 0.9511 | 0.9639 | 3.6049 | 0.9638 | |
| LAC | 0.9646 | 0.9723 | 0.9802 | 0.9517 | 0.9659 | 3.4019 | 0.9658 | |
| 9953 | LS | 0.8465 | 0.8967 | 0.9531 | 0.7139 | 0.8335 | 16.6418 | 0.8249 |
| GAC | 0.8946 | 0.9436 | 0.9982 | 0.8053 | 0.9018 | 9.8166 | 0.8966 | |
| LAC | 0.8919 | 0.9424 | 0.9990 | 0.7996 | 0.8993 | 10.0619 | 0.8938 |
| Image | Segmentation Approach | JI | DC | FPR | FNR |
|---|---|---|---|---|---|
| NM3 | LS | 0.8852 | 0.9391 | 0.1225 | 0.0064 |
| GAC | 0.8669 | 0.9287 | 0.1174 | 0.0312 | |
| LAC | 0.8401 | 0.9131 | 0.1079 | 0.0692 | |
| NM5 | LS | 0.8111 | 0.8957 | 0.2320 | 7.10 × 10−4 |
| GAC | 0.8004 | 0.8891 | 0.2482 | 9.13 × 10−4 | |
| LAC | 0.6695 | 0.8020 | 0.2226 | 0.1815 | |
| SSM31 | LS | 0.9102 | 0.9530 | 0.0948 | 0.0035 |
| GAC | 0.8971 | 0.9458 | 0.1099 | 0.0043 | |
| LAC | 0.8989 | 0.9468 | 0.1102 | 0.0020 | |
| SSM21 | LS | 0.8157 | 0.8985 | 0.0525 | 0.1415 |
| GAC | 0.7792 | 0.8759 | 0.0516 | 0.1806 | |
| LAC | 0.7658 | 0.8674 | 0.0560 | 0.1913 | |
| 229 | LS | 0.8031 | 0.8908 | 0.0029 | 0.1946 |
| GAC | 0.7985 | 0.8879 | 0.0015 | 0.2003 | |
| LAC | 0.7355 | 0.8476 | 0.0908 | 0.1977 | |
| 9953 | LS | 0.7253 | 0.8408 | 0.0000 | 0.2747 |
| GAC | 0.9271 | 0.9622 | 0.0266 | 0.0483 | |
| LAC | 0.9223 | 0.9596 | 0.0313 | 0.0488 |
| Approach | Value | JI | DC | FPR | FNR | |
|---|---|---|---|---|---|---|
| Otsu based threshold | LS | Min | 0.6924 | 0.7216 | 0.0048 | 0.0035 |
| Max | 0.8917 | 0.9506 | 0.1281 | 0.1016 | ||
| Average | 0.8217 | 0.8812 | 0.0725 | 0.0883 | ||
| GAC | Min | 0.5729 | 0.7104 | 0.0051 | 0.0052 | |
| Max | 0.8611 | 0.9422 | 0.1316 | 0.1218 | ||
| Average | 0.8016 | 0.8961 | 0.0857 | 0.0829 | ||
| LAC | Min | 0.5748 | 0.7048 | 0.0033 | 0.0029 | |
| Max | 0.8573 | 0.9518 | 0.1725 | 0.1314 | ||
| Average | 0.8005 | 0.8873 | 0.0815 | 0.0528 | ||
| Kapur based threshold | LS | Min | 0.6284 | 0.6826 | 0.0051 | 3.41 × 10−4 |
| Max | 0.9165 | 0.9517 | 0.1177 | 0.2818 | ||
| Average | 0.8296 | 0.8832 | 0.0615 | 0.0726 | ||
| GAC | Min | 0.5477 | 0.7062 | 0.0038 | 5.72 × 10−4 | |
| Max | 0.8917 | 0.9415 | 0.1226 | 0.2661 | ||
| Average | 0.8188 | 0.9004 | 0.0744 | 0.0779 | ||
| LAC | Min | 0.5385 | 0.6863 | 0.0028 | 4.08 × 10−4 | |
| Max | 0.8618 | 0.9571 | 0.1534 | 0.2514 | ||
| Average | 0.8192 | 0.8916 | 0.0795 | 0.0528 | ||
| Approach | PRE | FM | SEN | SPE | BCR | BER% | ACC | |
|---|---|---|---|---|---|---|---|---|
| Otsu based threshold | LS | 0.9812 | 0.9795 | 0.9827 | 0.9014 | 0.9331 | 5.7715 | 0.9517 |
| GAC | 0.9796 | 0.9727 | 0.9803 | 0.8958 | 0.9186 | 6.0843 | 0.9416 | |
| LAC | 0.9685 | 0.9736 | 0.9774 | 0.8971 | 0.9158 | 5.8025 | 0.9481 | |
| Kapur based threshold | LS | 0.9826 | 0.9805 | 0.9841 | 0.9116 | 0.9284 | 4.9963 | 0.9619 |
| GAC | 0.9803 | 0.9772 | 0.9825 | 0.9028 | 0.9188 | 5.8670 | 0.9571 | |
| LAC | 0.9715 | 0.9758 | 0.9781 | 0.8987 | 0.9172 | 5.7016 | 0.9486 | |
| Image | Segmentation Approach | Lesion Malignancy | |||
|---|---|---|---|---|---|
| Otsu | Kapur | ||||
| Probability | Risk | Probability | Risk | ||
| NM3 | LS | 0.8363 | High | 0.8784 | High |
| GAC | 0.7947 | 0.8216 | |||
| LAC | 0.8144 | 0.8027 | |||
| NM5 | LS | 0.8153 | 0.8639 | ||
| GAC | 0.8271 | 0.8406 | |||
| LAC | 0.8026 | 0.8013 | |||
| SSM31 | LS | 0.8246 | 0.8815 | ||
| GAC | 0.8116 | 0.8217 | |||
| LAC | 0.8075 | 0.8015 | |||
| SSM21 | LS | 0.7260 | 0.8037 | ||
| GAC | 0.7826 | 0.8110 | |||
| LAC | 0.7624 | 0.8046 | |||
| 229 | LS | 0.8016 | 0.8218 | ||
| GAC | 0.8261 | 0.8639 | |||
| LAC | 0.8136 | 0.7915 | |||
| 9953 | LS | 0.7940 | 0.8125 | ||
| GAC | 0.8003 | 0.8016 | |||
| LAC | 0.8117 | 0.7918 | |||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dey, N.; Rajinikanth, V.; Ashour, A.S.; Tavares, J.M.R.S. Social Group Optimization Supported Segmentation and Evaluation of Skin Melanoma Images. Symmetry 2018, 10, 51. https://doi.org/10.3390/sym10020051
Dey N, Rajinikanth V, Ashour AS, Tavares JMRS. Social Group Optimization Supported Segmentation and Evaluation of Skin Melanoma Images. Symmetry. 2018; 10(2):51. https://doi.org/10.3390/sym10020051
Chicago/Turabian StyleDey, Nilanjan, Venkatesan Rajinikanth, Amira S. Ashour, and João Manuel R. S. Tavares. 2018. "Social Group Optimization Supported Segmentation and Evaluation of Skin Melanoma Images" Symmetry 10, no. 2: 51. https://doi.org/10.3390/sym10020051
APA StyleDey, N., Rajinikanth, V., Ashour, A. S., & Tavares, J. M. R. S. (2018). Social Group Optimization Supported Segmentation and Evaluation of Skin Melanoma Images. Symmetry, 10(2), 51. https://doi.org/10.3390/sym10020051







