Three Classes of Fractional Oscillators

Abstract

This article addresses three classes of fractional oscillators named Class I, II and III. It is known that the solutions to fractional oscillators of Class I type are represented by the Mittag-Leffler functions. However, closed form solutions to fractional oscillators in Classes II and III are unknown. In this article, we present a theory of equivalent systems with respect to three classes of fractional oscillators. In methodology, we first transform fractional oscillators with constant coefficients to be linear 2-order oscillators with variable coefficients (variable mass and damping). Then, we derive the closed form solutions to three classes of fractional oscillators using elementary functions. The present theory of equivalent oscillators consists of the main highlights as follows. (1) Proposing three equivalent 2-order oscillation equations corresponding to three classes of fractional oscillators; (2) Presenting the closed form expressions of equivalent mass, equivalent damping, equivalent natural frequencies, equivalent damping ratio for each class of fractional oscillators; (3) Putting forward the closed form formulas of responses (free, impulse, unit step, frequency, sinusoidal) to each class of fractional oscillators; (4) Revealing the power laws of equivalent mass and equivalent damping for each class of fractional oscillators in terms of oscillation frequency; (5) Giving analytic expressions of the logarithmic decrements of three classes of fractional oscillators; (6) Representing the closed form representations of some of the generalized Mittag-Leffler functions with elementary functions. The present results suggest a novel theory of fractional oscillators. This may facilitate the application of the theory of fractional oscillators to practice.

1. Introduction

Any systems that consist of three elements, namely, inertia, restoration, and damping, may oscillate. Therefore, oscillations are common phenomena encountered in various fields, ranging from physics to mechanical engineering, see, e.g., [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17].

Fractional oscillators and their processes attract the interests of researchers, see, e.g., [18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53]. There are problems worth studying with respect to fractional oscillators. On the one hand, the analytical expressions in the closed forms of responses to certain fractional oscillators, e.g., those described by (42) and (43) in Section 2, remain unknown. In addition, closed form representations of some physical quantities in fractional oscillators, such as mass, damping, natural frequencies, in the intrinsic sense, are lacking. On the other hand, technology and analysis methods, based on 2-order linear oscillations, almost dominate the preference of engineers although nonlinear oscillations have been paid attention to. Therefore, from a view of engineering, it is meaningful to establish a theory to deal with fractional oscillators with equivalent linear oscillation systems of order 2. This article contributes my results in this aspect.

This research studies three classes of fractional oscillators.

Class I: The first class contains oscillators with fractional inertia force $m\frac{d^{\alpha }x(t)}{d{t}^{\alpha }}(1<\alpha \le 2)$ only. Its oscillation equation is in the form of (31), see, e.g., Duan ([24], Equation (3)), Mainardi ([25], Equation (27)), Zurigat ([26], Equation (16)), Blaszczyk and Ciesielski ([27], Equation (1)), Blaszczyk et al. ([28], Equation (10)), Al-rabtah et al. ([29], Equation (3.1)), Drozdov ([30], Equation (9)), Stanislavsky [31], Achar et al. ([32], Equation (1), [33], Equation (9), [34], Equation (2)), Tofighi ([35], Equation (2)), Ryabov and Puzenko ([36], Equation (1)), Ahmad and Elwakil ([37], Equation (1)), Uchaikin ([38], Chapter 7), Duan et al. ([39], Equation (4.2)).

Class II: The second consists of oscillators only with fractional damping term $c\frac{d^{\beta }x(t)}{d{t}^{\beta }}(0<\beta \le 1),$ see, e.g., Lin et al. ([40], Equation (2)), Duan ([41], Equation (31)), Alkhaldi et al. ([42], Equation (1a)), Dai et al. ([43], Equation (1)], Ren et al. ([44], Equation (1)), Xu et al. ([45], Equation (1)), He et al. ([46], Equation (4)), Leung et al. ([47], Equation (2)), Chen et al. ([48], Equation (1)), Deü and Matignon ([49], Equation (1)), Drăgănescu et al. ([50], Equation (4)), Rossikhin and Shitikova ([51], Equation (3)), Xie and Lin ([52], Equation (1)), Chung and Jung [53]. That takes the form of (42) in the next Section.

Class III: The third includes the oscillators with both fractional inertia force $m\frac{d^{\alpha }x(t)}{d{t}^{\alpha }}(1<\alpha \le 2)$ and fractional friction $c\frac{d^{\beta }x(t)}{d{t}^{\beta }}(0<\beta \le 1),$ see, e.g., Liu et al. ([54], Equation (1)), Gomez-Aguilar ([53], Equation (10)), Leung et al. ([50], Equation (3)). This class of oscillators is expressed by (43).

By fractional oscillating in this research, we mean that either the inertia term (31) or the damping (42) or both (43) are described by fractional derivative. Thus, this article studies all described above from Class I to III except those fractional nonlinear ones, such as fractional van der Pol oscillators (Leung et al. [47,55], Xie and Lin [52], Kavyanpoor and Shokrollahi [56], Xiao et al. [57]), fractional Duffing ones (Xu et al. [45], Liu et al. [54], Chen et al. [58], Wen et al. [59], Liao [60]). Besides, the meaning of fractional oscillation in this research neither implies those with fractional displacement such as Abu-Gurra et al. [61] discussed nor those in the sense of subharmonic oscillations as stated by Den Hartog ([3], Sections 8–10, Chapter 4), Ikeda [62], Fudan Univ. ([63], pp. 96–97), Andronov et al. ([64], Section 5.1).

Fractional differential equations represented by (31), (42), and (43) are designated as fractional oscillators in Class I, II, and III, respectively, in what follows. Note that closed form analytic expressions for the responses (free, impulse, step, frequency, and sinusoidal) to fractional oscillators in Class II and III are rarely reported. For oscillators in Class I, analytic expressions for the responses (free, impulse, step) are only represented by a type of special functions called the Mittag-Leffler functions but lack in representing the intrinsic properties, such as damping. This article aims at presenting a unified approach to deal with three classes of fractional oscillators.

The present highlights are as follows.

• Establishing three equivalent 2-order differential equations respectively corresponding to three classes of fractional oscillators.
• Presenting the analytical representations, in the closed form, of equivalent masses, equivalent dampings, equivalent damping ratios, equivalent natural frequencies, and equivalent frequency ratios, for each class of fractional oscillators.
• Proposing the analytic expressions, in the closed form by using elementary functions, of the free, impulse, step, frequency, and sinusoidal responses to three classes of fractional oscillators.
• Revealing the power laws of equivalent mass and equivalent damping for each class of fractional oscillators.
• Representing some of the generalized Mittag-Leffler functions by using elementary functions.

Note that this article studies fractional oscillators by the way of dealing with fractional inertia force and or fractional friction equivalently using inertia force and or fractional friction of integer order. In doing so, methodologically speaking, the key point is about three equivalent oscillation models, which transform fractional inertia force and or fractional friction equivalently into inertia force and or fractional friction of integer order, which we establish with Theorems 1–7. Though they may yet imply a novel way to study fractional derivatives from the point of view of mathematics, my focus in this research is on treating fractional oscillators from a view of physical or engineering oscillations (vibrations).

The rest of the article is organized as follows. Section 2 is about preliminaries. The problem statement and research thoughts are described in Section 3. We establish three equivalent 2-order oscillation equations respectively corresponding to three classes of fractional oscillators in Section 4. The analytical representations of equivalent masses, equivalent dampings, equivalent damping ratios, equivalent natural frequencies for three classes of fractional oscillators are proposed in Section 5. We present the analytic expressions of the free responses to three classes of fractional oscillators in Section 6, the impulse responses to three classes of fractional oscillators in Section 7, the step responses in Section 8, the frequency responses in Section 9, and the sinusoidal ones in Section 10. Discussions are in Section 11, which is followed by conclusions.

2. Preliminaries

This Section consists of two parts. One is to describe the basic of linear oscillations and fractional ones related to the next sections. The other the solutions to fractional oscillators in Class I based on the generalized Mittag-Leffler functions.

2.1. Brief of Linear Oscillations of Order 2

2.1.1. Simple Oscillation Model

The simplest model of an oscillator of order 2 is with single degree of freedom (SDOF). It consists of a constant mass m and a massless damper with a linear viscous damping constant c. The stiffness of spring is denoted by spring constant k. That SDOF mass-spring system is described by

$$\{\begin{array}{l}m\frac{d^{2}q(t)}{d{t}^2}+c\frac{dq(t)}{dt}+kq(t)=e(t)\\ q(0)=q_0,q^{\prime }(0)=v_0,\end{array}$$

(1)

where e(t) is the forcing function. The solution q(t) may be the displacement in mechanical engineering [1,2,3,4,5,6,7] or current in electronics engineering [8].

In physics and engineering, for facilitating the analysis, one usually rewrites (1) by

$$\{\begin{array}{l}\frac{d^{2}q(t)}{d{t}^2}+\frac{c}{m}\frac{dq(t)}{dt}+\frac{k}{m}q(t)=\frac{e(t)}{m}\\ q(0)=q_0,q^{\prime }(0)=v_0,\end{array}$$

(2)

and further rewrites it by

$$\{\begin{array}{l}\frac{d^{2}q(t)}{d{t}^2}+2\varsigma {\omega }_n\frac{dq(t)}{dt}+{\omega }_n^{2}q(t)=\frac{e(t)}{m}\\ q(0)=q_0,q^{\prime }(0)=v_0,\end{array}$$

(3)

where ${\omega }_n$ is called the natural angular frequency (natural frequency for short) with damping free given by

$${\omega }_n=\sqrt{\frac{k}{m}},$$

(4)

and the parameter ς is the damping ratio expressed by

$$\varsigma =\frac{c}{2\sqrt{mk}}.$$

(5)

The characteristic equation of (3) is in the form

$$p^2+2\varsigma {\omega }_{n}p+{\omega }_n^2=0,$$

(6)

which is usually called the frequency equation in engineering [1,2,3,4,5,6,7]. The solution to the above is given by

$$p_{1,2}=-\varsigma {\omega }_n\pm i{\omega }_n\sqrt{1-{\varsigma }^2},$$

(7)

where $i=\sqrt{-1}.$ Taking into account damping, one uses the term damped natural frequency denoted by ${\omega }_d.$ It is given by

$${\omega }_d={\omega }_n\sqrt{1-{\varsigma }^2}.$$

(8)

Note 2.1: All parameters above, namely, m, c, k, ζ, ${\omega }_n,$ and ${\omega }_d,$ are constants.

2.1.2. Responses

The free response, meaning that the response with e(t) = 0, is driven by initial conditions only. It is given by

$$q(t)=e^{-\varsigma {\omega }_{n}t}\left(q_0\cos {\omega }_{d}t+\frac{v_0+\varsigma {\omega }_n{q}_0}{{\omega }_d}\sin {\omega }_{d}t\right),\hspace{1em}t\ge 0.$$

(9)

If e(t) = δ(t), where δ(t) is the Dirac-delta function, the response with zero initial conditions is called the impulse response. In the theory of linear systems (Gabel and Roberts [65], Zheng et al. [66]), the symbol h(t) is used for the impulse response. Thus, consider the equation

$$\frac{d^{2}h(t)}{d{t}^2}+2\varsigma {\omega }_n\frac{dh(t)}{dt}+{\omega }_n^{2}h(t)=\frac{\delta (t)}{m}.$$

(10)

One has

$$h(t)=\frac{e^{-\varsigma {\omega }_{n}t}}{m{\omega }_d}\sin {\omega }_{d}t,\hspace{1em}t\ge 0.$$

(11)

Let u(t) be the Heaviside unit step (unit step for short) function. Then, the response to (3) with zero initial conditions is called the unit step response. As usual, it is denoted by g(t) in practice. Thus, consider

$$\frac{d^{2}g(t)}{d{t}^2}+2\varsigma {\omega }_n\frac{dg(t)}{dt}+{\omega }_n^{2}g(t)=\frac{u(t)}{m}.$$

(12)

One has

$$g(t)={\displaystyle \underset{0}{\overset{t}{\int }}h(\tau )d\tau }=\frac{1}{k}\left[1-\frac{e^{-\varsigma {\omega }_{n}t}}{\sqrt{1-{\varsigma }_{}^2}}\cos \left({\omega }_{d}t-\varphi \right)\right],$$

(13)

where

$$\varphi ={\tan }^{-1}\frac{\varsigma }{\sqrt{1-{\varsigma }_{}^2}}.$$

(14)

Denote by H(ω) the Fourier transform of h(t). Then, H(ω) is usually called the frequency response to the oscillator described by (3). It is in the form

$$H(\omega )=\frac{1}{m\left({\omega }_n^2-{\omega }^2+i2\varsigma {\omega }_n\omega \right)}=\frac{1}{m{\omega }_n^2\left(1-\frac{{\omega }^2}{{\omega }_n^2}+i2\varsigma \frac{\omega }{{\omega }_n}\right)}.$$

(15)

With the parameter γ defined by

$$\gamma =\frac{\omega }{{\omega }_n},$$

(16)

which is called frequency ratio, H(ω) may be rewritten by

$$H(\omega )=\frac{1}{m{\omega }_n^2\left(1-{\gamma }^2+i2\varsigma \gamma \right)}.$$

(17)

The amplitude of H(ω) is called the amplitude frequency response. It is in the form

$$\left|H(\omega )\right|=\frac{1}{m{\omega }_n^2\sqrt{{\left(1-{\gamma }^2\right)}^2+{\left(2\varsigma \gamma \right)}^2}}.$$

(18)

Its phase is termed the phase frequency response given by

$$\phi (\omega )={\tan }^{-1}\frac{2\varsigma \gamma }{1-{\gamma }_{}^2}.$$

(19)

When the oscillator is excited by a sinusoidal function, the solution to (3) is termed the sinusoidal or simple harmonic response. Suppose the sinusoidal excitation function is Acosωt, where A is a constant. Then, the solution to

$$\{\begin{array}{l}\frac{d^{2}q(t)}{d{t}^2}+2\varsigma {\omega }_n\frac{dq(t)}{dt}+{\omega }_n^{2}q(t)=\frac{A\cos \omega t}{m}\\ q(0)=q_0,q^{\prime }(0)=v_0,\end{array}$$

(20)

is the sinusoidal response in the form

$$q(t)=\frac{\frac{A}{m{\omega }_d}}{{\left({\omega }_n^2-{\omega }^2\right)}^2+{\left(2\varsigma {\omega }_n\omega \right)}^2}\left\{\begin{array}{l}\left({\omega }_n^2-{\omega }^2\right)\cos \omega t+2\varsigma {\omega }_n\omega \sin \omega t\\ +e^{-\varsigma {\omega }_{n}t}\left[\left({\omega }_n^2-{\omega }^2\right)\cos {\omega }_{d}t-\frac{\varsigma }{\sqrt{1-{\varsigma }_{}^2}}\left({\omega }_n^2+{\omega }^2\right)\sin {\omega }_{d}t\right]\end{array}\right\}.$$

(21)

The responses mentioned above are essential to linear oscillators. We shall give our results for three classes of fractional oscillators with respect to those responses in this research.

2.1.3. Spectra of Three Excitations

The spectrum of δ(t) below means that δ(t) contains the equal frequency components for ω ∈ (0, ∞).

$${\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\delta (t)e^{-i\omega t}dt}=1.$$

(22)

The spectrum of u(t) is in the form

$${\displaystyle \underset{-\infty }{\overset{\infty }{\int }}u(t)e^{-i\omega t}dt}=\pi \delta (\omega )+\frac{1}{i\omega }.$$

(23)

The Fourier transform of $\cos {\omega }_{1}t$ is given by

$${\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\cos {\omega }_{1}t{e}^{-i\omega t}dt}=\pi \left[\delta (\omega +{\omega }_1)+\delta (\omega -{\omega }_1)\right].$$

(24)

Three functions or signals above, namely, δ(t), u(t), and sinusoidal functions, are essential to the excitation forms in oscillations. However, their spectra do not exist in the domain of ordinary functions but they exist in the domain of generalized functions. Due to the importance of generalized functions in oscillations, for example, δ(t) and u(t), either theory or technology of oscillations nowadays is in the domain of generalized functions. In the domain of generalized functions, any function is differentiable of any times. The Fourier transform of any function exists (Gelfand and Vilenkin [67], Griffel [68]).

2.1.4. Generalization of Linear Oscillators

Let us be beyond the scope of the conventionally physical quantities, such as displacement, velocity, acceleration in mechanics, or current, voltage in electronics. Then, we consider the response of the quantity $q^{(n)}(t),$ where n is a positive integer. Precisely, we consider the following oscillation equation

$$\{\begin{array}{l}\frac{d^2}{d{t}^2}\left[\frac{d^{n}q(t)}{d{t}^n}\right]+2\varsigma {\omega }_n\frac{d}{dt}\left[\frac{d^{n}q(t)}{d{t}^n}\right]+{\omega }_n^2\frac{d^{n}q(t)}{d{t}^n}=\frac{e(t)}{m}\\ q^{(n)}(0)=q_0,q^{(n+1)}(0)=v_0.\end{array}$$

(25)

The above may be taken as a generalization of the conventional oscillator described by (3). Another expression of the above may be given by

$$\{\begin{array}{l}\frac{d^n}{d{t}^n}\left[\frac{d^{2}q(t)}{d{t}^2}\right]+2\varsigma {\omega }_n\frac{d^n}{d{t}^n}\left[\frac{dq(t)}{dt}\right]+{\omega }_n^2\frac{d^{n}q(t)}{d{t}^n}=\frac{e(t)}{m}\\ q^{(n)}(0)=q_0,q^{(n+1)}(0)=v_0.\end{array}$$

(26)

Alternatively, we have a linear oscillation system described by

$$\{\begin{array}{l}\frac{d^{n+2}q(t)}{d{t}^{n+2}}+2\varsigma {\omega }_n\frac{d^{n+1}q(t)}{d{t}^{n+1}}+{\omega }_n^2\frac{d^{n}q(t)}{d{t}^n}=\frac{e(t)}{m}\\ q^{(n)}(0)=q_0,q^{(n+1)}(0)=v_0.\end{array}$$

(27)

Physically, the above item with $q^{(n+2)}(t)$ corresponds to inertia, the one with $q^{(n)}(t)$ to restoration, and the one with $q^{(n+1)}(t)$ damping.

Note that (27) remains a linear oscillator after all. Nevertheless, when generalizing n to be fractions, for instance, considering −1 < ${\epsilon }_1$ ≤ 0 and −1 < ${\epsilon }_2$ ≤ 0, we may generalize (27) to be

$$\{\begin{array}{l}m\frac{d^{{\epsilon }_1+2}q(t)}{d{t}^{{\epsilon }_1+2}}+c\frac{d^{{\epsilon }_2+1}q(t)}{d{t}^{{\epsilon }_2+1}}+kq(t)=e(t)\\ q(0)=q_0,q^{\prime }(0)=v_0.\end{array}$$

(28)

Then, we go into the scope of fractional oscillations.

2.2. Three Classes of Fractional Oscillators

Denote by $\frac{d^{\nu }}{d{t}^{\nu }}={}_{-\infty }D_t^{\nu }$ the Weyl fractional derivative of order ν > 0. Then (Uchaikin [38], Miller and Ross [69], Klafter et al. [70]),

$${}_{-\infty }D_t^{\nu }f(t)=\frac{1}{\mathsf{\Gamma }(-\nu )}{\displaystyle \underset{-\infty }{\overset{t}{\int }}\frac{f(u)du}{{(t-u)}^{1+\nu }}},$$

(29)

where Γ(ν) is the Gamma function. The Weyl fractional derivative is used in this research because it is suitable for the Fourier transform in the domain of fractional calculus (Lavoie et al. ([71], p. 247)).

The Fourier transform of $\frac{d^{\nu }f(t)}{d{t}^{\nu }},$ following Uchaikin ([72], Section 4.5.3), is given by

$${\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\frac{d^{\nu }f(t)}{d{t}^{\nu }}{e}^{-i\omega t}dt}={\left(i\omega \right)}^{\nu }F(\omega ),$$

(30)

where F(ω) is the Fourier transform of f(t).

This article relates to three classes of fractional oscillators as follow. We denote the following oscillation equation as a fractional oscillator in Class I.

$$\{\begin{array}{c}m\frac{d^{\alpha }{y}_1(t)}{d{t}^{\alpha }}+k{y}_1(t)=e(t)\\ y_1(0)=y_1{}_0,{y^{\prime }}_1(0)={y^{\prime }}_1{}_0\end{array},\hspace{1em}1<\alpha \le 2.$$

(31)

The free response to (31) is in the form (Mainardi [25], Achar et al. [33], Uchaikin ([38], Chapter 7))

$$y_1(t)=y_{10}{E}_{\alpha ,1}\left[-{\left({\omega }_{n}t\right)}^{\alpha }\right]+{y^{\prime }}_{10}t{E}_{\alpha ,2}\left[-{\left({\omega }_{n}t\right)}^{\alpha }\right],\hspace{1em}1<\alpha \le 2,t\ge 0,$$

(32)

where $E_{a,b}(z)$ is the generalized Mittag-Leffler function given by

$$E_{a,b}(z)={\displaystyle \sum _{k=0}^{\infty }\frac{z^k}{\mathsf{\Gamma }(ak+b)}},\hspace{1em}a,b\in C,\mathrm{Re}(a)>0,\mathrm{Re}(b)>0.$$

(33)

The Mittag-Leffler function denoted by E_a(t) is in the form

$$E_a(z)={\displaystyle \sum _{k=0}^{\infty }\frac{z^k}{\mathsf{\Gamma }(ak+1)}},\hspace{1em}a\in C,\mathrm{Re}(a)>0,$$

(34)

referring Mathai and Haubold [73], or Gorenflo et al. [74], or Erdelyi et al. [75] for the Mittag-Leffler functions.

Denote by $h_y{}_1(t)$ the impulse response to a fractional oscillator in Class I. Then (Uchaikin ([38], Chapter 7)),

$$h_y{}_1(t)=t^{\alpha -1}{E}_{\alpha ,\alpha }\left[-{\left({\omega }_{n}t\right)}^{\alpha }\right],\hspace{1em}1<\alpha \le 2,t\ge 0.$$

(35)

Let $g_{y1}(t)$ be the step response to a fractional oscillator of Class I type. Then,

$$g_{y1}(t)=t^{\alpha }{E}_{\alpha ,\alpha +1}\left[-{\left({\omega }_{n}t\right)}^{\alpha }\right],\hspace{1em}1<\alpha \le 2,t\ge 0.$$

(36)

For a fractional oscillator in Class I, its sinusoidal response driven by sinωt is expressed by

$$y_1(t)=A_1\sin (\omega t-{\theta }_1)+A_2{e}^{-\beta t}\cos \left[{\omega }_{n}t\sin \frac{\pi }{\alpha }-{\theta }_2\right]+{\displaystyle \underset{0}{\overset{\infty }{\int }}{e}^{-st}{K}_{\alpha }(s)ds},$$

(37)

where

$$\begin{gathered} A_1=\frac{1}{\sqrt{{\omega }_n^{2\alpha }+{\omega }^{2\alpha }+2{\omega }_n^{\alpha }{\omega }^{\alpha }\cos \frac{\alpha \pi }{2}}}, \\ {A}_2=\frac{2\omega }{\alpha {\omega }_n^{\alpha -1}\sqrt{{\omega }_n^4+{\omega }^4+2{\omega }_n^2{\omega }^2\cos \frac{2\pi }{\alpha }}}, \end{gathered}$$

(38)

$$\beta =-{\omega }_n\cos \frac{\pi }{\alpha },$$

(39)

$$\begin{gathered} {\theta }_1={\tan }^{-1}\frac{{\omega }^{\alpha }\sin \frac{\alpha \pi }{2}}{{\omega }_n^{\alpha }+{\omega }^{\alpha }\cos \frac{\alpha \pi }{2}}, \\ {\theta }_2={\tan }^{-1}\left[\frac{{\omega }_n^2\sin \frac{(1+\alpha )\pi }{\alpha }-{\omega }^2\sin \frac{(1-\alpha )\pi }{\alpha }}{{\omega }_n^2\cos \frac{(1+\alpha )\pi }{\alpha }+{\omega }^2\cos \frac{(1-\alpha )\pi }{\alpha }}\right], \end{gathered}$$

(40)

$$K_{\alpha }(s)=\frac{\omega \sin (\pi \alpha )}{\pi \left(s^2+{\omega }^2\right)\left(s^{2\alpha }+2s^{\alpha }{\omega }_n^2\cos (\pi \alpha )+{\omega }_n^{2\alpha }\right)}.$$

(41)

An oscillator that follows the oscillation equation below is called a fractional oscillator in Class II.

$$m\frac{d^2{y}_2(t)}{d{t}^2}+c\frac{d^{\beta }{y}_2(t)}{d{t}^{\beta }}+k{y}_2(t)=0,\hspace{1em}0<\beta \le 1.$$

(42)

The equation below is called an oscillation equation of a fractional oscillator in Class III.

$$m\frac{d^{\alpha }{y}_3(t)}{d{t}^{\alpha }}+c\frac{d^{\beta }{y}_3(t)}{d{t}^{\beta }}+k{y}_3(t)=0,\hspace{1em}1<\alpha \le 2,0<\beta \le 1.$$

(43)

2.3. Equivalence of Functions in the Sense of Fourier Transform

Denote by $F_1(\omega )$ and $F_2(\omega )$ the Fourier transforms of $f_1(t)$ and $f_2(t),$ respectively. Then, if

$$F_1(\omega )=F_2(\omega ),$$

(44)

one says that

$$f_1(t)=f_2(t),$$

(45)

in the sense of Fourier transform (Gelfand and Vilenkin [67], Papoulis [76]), implying

$${\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\left[f_1(t)-f_2(t)\right]e^{-i\omega t}dt}=0.$$

(46)

The above implies that a null function as a difference between $f_1(t)$ and $f_2(t)$ is allowed for (45). An example relating to oscillation theory is the unit step function.

Denote by $u_1(t)$ in the form

$$u_1(t)=\{\begin{array}{c}1,t\ge 0\\ 0,t<0\end{array}.$$

(47)

Let $u_2(t)$ be

$$u_2(t)=\{\begin{array}{c}1,t>0\\ 0,t\le 0\end{array}.$$

(48)

Clearly, either $u_1(t)$ or $u_2(t)$ is a unit step function. The difference between two is a null function given by

$$u_1(t)-u_2(t)=\{\begin{array}{cc}1,\hfill & \hfill t=1\\ 0,\hfill & \hfill \mathrm{elsewhere}\end{array}.$$

(49)

Thus, $u_1(t)=u_2(t).$ In fact, the Fourier transform of either $u_1(t)$ or $u_2(t)$ equals to the right side on (23).

Similarly, if $f_1(t)=f_2(t),$ we say that (44) holds in the sense of

$${\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\left[F_1(\omega )-F_2(\omega )\right]e^{i\omega t}d\omega }=0.$$

(50)

3. Problem Statement and Research Thoughts

We have mentioned three classes of fractional oscillators in Section 2. This section contains two parts. One is the problem statement and the other research thoughts.

3.1. Problem Statement

We first take fractional oscillators in Class I as a case to state the problems this research concerns with.

The analytical expressions with respect to the responses of free, impulse, step, to the oscillators of Class I are mathematically obtained (Mainardi [25], Achar et al. [33], Uchaikin ([38], Chapter 7)), also see Section 2.2 in this article. All noticed that a fractional oscillator of Class I is damping free in form but it is damped in nature due to fractional if 1 < α < 2. However, there are problems unsolved in this regard.

Problem 1.

How to analytically represent the damping of Class I oscillators?

In this article, we call the damping of fractional oscillators in Class I equivalent damping denoted by $c_{eq1}.$

It is known that damping relates to mass. Therefore, if we find $c_{eq1}$ in a fractional oscillator in Class I, its intrinsic mass must be different from the primary one m unless α = 2. We call it equivalent mass and denote it by $m_{eq1}.$

Problem 2.

How to analytically represent $m_{eq1}?$

Because a fractional oscillator in Class I is damped in nature for α ≠ 2, there must exist a damped natural frequency. We call it equivalent damped natural frequency, denoted by ${\omega }_{eqd,1}.$ Then, comes the problem below.

Problem 3.

What is the representation of ${\omega }_{eqd,1}?$

As there exists $m_{eq1}$ that differs from m if α ≠ 2, the equivalent damping free natural frequency, we denote it by ${\omega }_{eqn,1},$ is different from the primary damping free natural frequency ${\omega }_n=\sqrt{\frac{k}{m}}.$ Consequently, the following problem appears.

Problem 4.

What is the expression of ${\omega }_{eqn,1}?$

If we find the solutions to the above four, a consequent problem is as follows.

Problem 5.

How to represent response (free, or impulse, or step, or sinusoidal) with $m_{eq1},$ $c_{eq1},$ ${\omega }_{eqn,1},$ and ${\omega }_{eqd,1}$ to a fractional oscillator in Class I?

If we solve the above problems, the solution to the following problem is ready.

Problem 6.

What is the physical mechanism of a fractional oscillator in Class I?

Note that the intrinsic damping for a Class II fractional oscillator must differ from its primary damping c owing to the fractional friction $c\frac{d^{\beta }{y}_2(t)}{d{t}^{\beta }}$ for β ≠ 1. We call it the equivalent damping denoted by $c_{eq2}.$ Because $c_{eq2}$≠ c if β ≠ 1, the equivalent mass of a fractional oscillator in Class II, denoted by $m_{eq2},$ is not equal to the primary m for β ≠ 1. Thus, the six stated above are also unsolved problems for fractional oscillators in Class II. They are, consequently, the problems unsolved for Class III fractional oscillators.

Note that there are other problems regarding with three classes of fractional oscillators. For example, the explicit expression of the sinusoidal response (37) in closed form needs investigation because of the difficulty in finding the solution to ${\displaystyle \underset{0}{\overset{\infty }{\int }}{e}^{-st}{K}_{\alpha }(s)ds}.$ We shall deal with them in separate sections. The solutions to the problems described above constitute main highlights of this research.

We note that the damping nature of a fractional oscillator in Class I was also observed by other researchers, not explicitly stated though, as can be seen from, e.g., Zurigat ([26], Figure 1), Blaszczyk et al. ([28], Figure 2), Al-rabtah et al. ([29], Figure 2), Ryabov and Puzenko ([36], Equation (5)), Uchaikin ([38], Chapter 7), Duan et al. ([39], Equation (4.3), Figure 2), Gomez-Aguilar et al. ([53], Equation (15), Figures 2 and 3), Chung and Jung ([77], Figure 1). One thing remarkable is by Tofighi, who explored the intrinsic damping of an oscillator in Class I, see ([35], pp. 32–33). That was an advance regarding with the damping implied in (31) but it may be unsatisfactory if one desires its closed form of analytic expression.

3.2. Research Thoughts

Let us qualitatively consider possible performances of equivalent mass and damping. In engineering, people may purposely connect an auxiliary mass $m_a$ to the primary mass m so that the equivalent mass of the total system is related to the oscillation frequency ω (Harris ([4], p. 6.4)). In the field of ship hull vibrations, added mass has to be taken into account in the equivalent mass (i.e., total mass) of a ship hull (Korotkin [78]) so that the equivalent mass is ω-varying. In fact, the three dimensional fluid coefficient with respect to the added mass to a ship hull relates to the oscillation frequency, see, e.g., Jin and Xia ([79], pp. 135–136), Nakagawa et al. [80].

In addition, damping may be also ω-varying. A well-known case of ω-varying damping is the Coulomb damping (Timoshenko ([2], Chapter 1), Harris ([4], Equation (30.4))). Frequency varying damping is a technique used in damping treatments, see, e.g., Harris ([4], Equation (37.8)). Besides, commonly used damping assumptions in ship hull vibrations, such as the Copoknh’s, the Voigt’s, the Rayleigh’s, are all ω-varying (Jin and Xia ([79], pp. 157–158)). Therefore, with the concept of ω-varying mass and damping, I purposely generalize the simple oscillation model expressed by (1) in the form

$$\{\begin{array}{l}{m}_{eq}(\omega )\frac{d^{2}q(t)}{d{t}^2}+c_{eq}(\omega )\frac{dq(t)}{dt}+kq(t)=e(t)\\ q(0)=q_0,q^{\prime }(0)=v_0.\end{array}$$

(51)

The above second-order equation may not be equivalent to a fractional oscillator unless $m_{eq}$ and or $c_{eq}$ are appropriately expressed and properly related to the fractional order α for Class I oscillators, or β for Class II oscillators, or (α, β) for oscillators in Class III. For those reasons, we further generalize (51) by

$$\{\begin{array}{l}{m}_{eq1}(\omega ,\alpha )\frac{d^2{x}_1(t)}{d{t}^2}+c_{eq1}(\omega ,\alpha )\frac{d{x}_1(t)}{dt}+k{x}_1(t)=e(t)\\ x_1(0)=x_{10},{\dot{x}}_1(0)=v_{10},\end{array}$$

(52)

for Class I oscillators. As for Class II oscillators, (51) should be generalized by

$$\{\begin{array}{l}{m}_{eq2}(\omega ,\beta )\frac{d^2{x}_2(t)}{d{t}^2}+c_{eq2}(\omega ,\beta )\frac{d{x}_2(t)}{dt}+k{x}_2(t)=e(t)\\ x_2(0)=x_{10},{\dot{x}}_2(0)=v_{20}.\end{array}$$

(53)

Similarly, for Class III oscillators, we generalize (51) to be the form

$$\{\begin{array}{l}{m}_{eq3}(\omega ,\alpha ,\beta )\frac{d^2{x}_3(t)}{d{t}^2}+c_{eq3}(\omega ,\alpha ,\beta )\frac{d{x}_2(t)}{dt}+k{x}_3(t)=e(t)\\ x_3(0)=x_{30},{\dot{x}}_3(0)=v_{30}.\end{array}$$

(54)

Three generalized oscillation Equations (52)–(54), can be unified in the form

$$\{\begin{array}{l}{m}_{eqj}\frac{d^2{x}_j(t)}{d{t}^2}+c_{eqj}\frac{d{x}_j(t)}{dt}+k{x}_j(t)=e(t)\\ x_j(0)=x_{j0},{\dot{x}}_j(0)=v_{30}\end{array},\hspace{1em}j=1,2,3.$$

(55)

By introducing the symbols ${\omega }_{eqn,j}=\sqrt{\frac{k}{m_{eqj}}}$ and ${\varsigma }_{eqj}=\frac{c_{eqj}}{2\sqrt{m_{eqj}k}}$ for j = 1, 2, 3, we rewrite the above by

$$\{\begin{array}{l}\frac{d^2{x}_j(t)}{d{t}^2}+2{\varsigma }_{eqj}{\omega }_{eqn,j}\frac{d{x}_j(t)}{dt}+{\omega }_{eqn,j}^2{x}_j(t)=\frac{e(t)}{m_{eqj}}\\ x_j(0)=x_{j0},{\dot{x}}_j(0)=v_{30}\end{array}, j=1,2,3.$$

(56)

Let $Y_j(\omega )$ be the Fourier transform of $y_j(t),$ where $y_j(t)$(j = 1, 2, 3) respectively corresponds to the one in (31), (42), and (43). Denote by $X_j(\omega )$ the Fourier transform of $x_j(t).$ Then, if we find proper $m_{eqj}$ and $c_{eqj}$ such that

$$Y_j(\omega )=X_j(\omega ), j = 1, 2, 3,$$

(57)

the second-order equation (52), or (53), or (54) is equal to the fractional oscillation Equation (31), or (42), or (43), respectively.

Obviously, once we discover the equivalent equations of the fractional oscillation Equations (52), or (53), and (54), all problems stated previously can be readily solved.

4. Equivalent Systems of Three Classes of Fractional Oscillators

In this section, we first present an equivalent system and then its equivalent mass and damping in Section 4.1, Section 4.2 and Section 4.3, respectively for each class of fractional oscillators.

4.1. Equivalent System for Fractional Oscillators in Class I

4.1.1. Equivalent Oscillation Equation of Fractional Oscillators in Class I

Theorem 1 gives the equivalent oscillator with the integer order for the fractional oscillators in Class I.

Theorem 1 (Equivalent oscillator I).

Denote a fractional oscillator in Class I by

$$m\frac{d^{\alpha }{y}_1(t)}{d{t}^{\alpha }}+k{y}_1(t)=0,\hspace{1em}1<\alpha \le 2.$$

(58)

Then, its equivalent oscillator with the equation of order 2 is in the form

$$-m{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}\frac{d^2{x}_1(t)}{d{t}^2}+m{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}\frac{d{x}_1(t)}{dt}+k{x}_1(t)=0,\hspace{1em}1<\alpha \le 2.$$

(59)

Proof. 

Consider the frequency response of (58) with the excitation of the Dirac-delta function δ(t). In doing so, we study

$$m\frac{d^{\alpha }{h}_{y1}(t)}{d{t}^{\alpha }}+k{h}_{y1}(t)=\delta (t),\hspace{1em}1<\alpha \le 2.$$

(60)

Doing the Fourier transform on the both sides of (60) produces

$$\left[m{\left(i\omega \right)}^{\alpha }+k\right]H_{y1}(\omega )=1,\hspace{1em}1<\alpha \le 2,$$

(61)

where $H_{y1}(\omega )$ is the Fourier transform of $h_{y1}(t).$ Using the principal value of i, we have

$$i^{\alpha }=\cos \frac{\alpha \pi }{2}+i\sin \frac{\alpha \pi }{2}.$$

(62)

Thus, (61) implies

$$\begin{array}{l}\left[m{\left(i\omega \right)}^{\alpha }+k\right]H_{y1}(\omega )=\left\{m\left(\cos \frac{\alpha \pi }{2}+i\sin \frac{\alpha \pi }{2}\right){\omega }^{\alpha }+k\right\}{H}_{y1}(\omega )\\ =\left(m{\omega }^{\alpha }\cos \frac{\alpha \pi }{2}+im{\omega }^{\alpha }\sin \frac{\alpha \pi }{2}+k\right)H_{y1}(\omega )=1.\end{array}$$

(63)

Therefore, we have the frequency response of (60) in the form

$$H_{y1}(\omega )=\frac{1}{m{\omega }^{\alpha }\cos \frac{\alpha \pi }{2}+im{\omega }^{\alpha }\sin \frac{\alpha \pi }{2}+k}.$$

(64)

On the other hand, for 1 < α ≤ 2, we consider (59) by

$$-m{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}\frac{d^2{h}_{x1}(t)}{d{t}^2}+m{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}\frac{d{h}_{x1}(t)}{dt}+k{h}_{x1}(t)=\delta (t).$$

(65)

Performing the Fourier transform on the both sides of (65) yields

$$\begin{array}{l}\left[-m{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}\left(-{\omega }^2\right)+m{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}\left(i\omega \right)+k\right]H_{x1}(\omega )\\ =\left(m{\omega }^{\alpha }\cos \frac{\alpha \pi }{2}+im{\omega }^{\alpha }\sin \frac{\alpha \pi }{2}+k\right)H_{x1}(\omega )=1,\end{array}$$

(66)

where $H_{x1}(\omega )$ is the Fourier transform of $h_{x1}(t).$ Therefore, we have

$$H_{x1}(\omega )=\frac{1}{m{\omega }^{\alpha }\cos \frac{\alpha \pi }{2}+im{\omega }^{\alpha }\sin \frac{\alpha \pi }{2}+k}.$$

(67)

By comparing (64) with (67), we see that

$$H_{y1}(\omega )=H_{x1}(\omega ).$$

(68)

Thus, (59) is the equivalent equation of (58). The proof completes. □

4.1.2. Equivalent Mass of Fractional Oscillators in Class I

From the first item on the left side of (59), we obtain the equivalent mass for the fractional oscillators of Class I type.

Theorem 2 (Equivalent mass I).

The equivalent mass of the fractional generators in Class I, denoted by $m_{eq1},$ is expressed by

$$m_{eq1}=m_{eq1}(\omega ,\alpha )=-\left({\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}\right)m,\hspace{1em}1<\alpha \le 2.$$

(69)

Proof. 

According to the Newton’s second law, the inertia force in the system of the fractional oscillator (58) corresponds to the first item on the left side of its equivalent system (59). That is, $-m{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}\frac{d^2{x}_1(t)}{d{t}^2}.$ Thus, the coefficient of $\frac{d^2{x}_1(t)}{d{t}^2}$ is an equivalent mass expressed by (69). Hence, the proof finishes. □

From Theorem 2, we reveal a power law phenomenon with respect to $m_{eq1}$ in terms of ω.

Remark 1.

The equivalent mass I, $m_{eq1},$ follows the power law in terms of oscillation frequency ω in the form

$$m_{eq1}(\omega ,\alpha )~{\omega }^{\alpha -2}m,\hspace{1em}1<\alpha \le 2.$$

(70)

The equivalent mass $m_{eq1}$ relates to the oscillation frequency ω, the fractional order α, and the primary mass m. Denote by

$$R_{m1}(\omega ,\alpha )=-{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2},\hspace{1em}1<\alpha \le 2.$$

(71)

Then, we have

$$m_{eq1}=m_{eq1}(\omega ,\alpha )=R_{m1}(\omega ,\alpha )m,\hspace{1em}1<\alpha \le 2.$$

(72)

Note 4.1: Since

$$R_{m1}(\omega ,2)=1,$$

(73)

$m_{eq1}(\omega ,\alpha )$ reduces to the primary mass m when α = 2. That is,

$$m_{eq1}(\omega ,2)=m.$$

(74)

In the case of α = 2, therefore, both (58) and (59) reach the conventional harmonic oscillation with damping free in the form

$$m\frac{d^2{x}_1(t)}{d{t}^2}+k{x}_1(t)=0.$$

Note 4.2: If α → 1, we have

$$\underset{\alpha \to 1}{\lim }{m}_{eq1}(\omega ,\alpha )=0 \mathrm{for} \omega \ne 0.$$

(75)

The above implies that $m_{eq1}$ vanishes if α → 1. Consequently, any oscillation disappears in that case.

Note 4.3: When 1 < α ≤ 2, we attain

$$0<R_{m1}(\omega ,\alpha )\le 1 \mathrm{for} \omega > 1.$$

(76)

Thus, we reveal an interesting phenomenon expressed by

$$m_{eq1}(\omega ,\alpha )\le m \mathrm{for} 1 < \alpha \le 2, \omega > 1.$$

(77)

The coefficient $R_{m1}(\omega ,\alpha )$ is plotted in Figure 1.

Figure 1. Plots of $R_{m1}(\omega ,\alpha ).$ Solid line: α = 1.2. Dot line: α = 1.5. Dash line: α = 1.8.

Remark 2.

For α ∈ (0, 2), we have

$$\underset{\omega \to \infty }{\lim }{m}_{eq1}(\omega ,\alpha )=0.$$

(78)

The interesting and novel behavior, described above, implies that a fractional oscillator in Class I does not oscillate for ω → ∞ because it is equivalently massless in that case.

Remark 3.

For α ∈ (0, 2), we have

$$\underset{\omega \to 0}{\lim }{m}_{eq1}(\omega ,\alpha )=\infty .$$

(79)

The interesting behavior, revealed above, says that a fractional oscillator of Class I type does not oscillate at ω = 0 because its mass is equivalently infinity in addition to the explanation of static status conventionally described by ω = 0.

4.1.3. Equivalent Damping of Fractional Oscillators of Class I

We now propose the equivalent damping.

Theorem 3 (Equivalent damping I).

The equivalent damping of a fractional oscillator in Class I, denoted by $c_{eq1},$ is expressed by

$$c_{eq1}=c_{eq1}(\omega ,\alpha )=\left({\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}\right)m,\hspace{1em}1<\alpha \le 2.$$

(80)

Proof. 

The second term on the left side of (59) is the friction with the linear viscous damping coefficient denoted by (80). The proof completes. □

Denote

$$R_{c1}(\omega ,\alpha )={\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2},\hspace{1em}1<\alpha \le 2.$$

(81)

Then, we have

$$c_{eq1}(\omega ,\alpha )=R_{c1}(\omega ,\alpha )m.$$

(82)

The coefficient $R_{c1}(\omega ,\alpha )$ is indicated in Figure 2.

Figure 2. $R_{c1}(\omega ,\alpha ).$ Solid line: α = 1.2. Dot line: α = 1.5. Dash line: α = 1.8.

Remark 4.

The equivalent damping I relies on ω, m, and α. It obeys the power law in terms of ω in the form

$$c_{eq1}(\omega ,\alpha )~{\omega }^{\alpha -1}m,\hspace{1em}1<\alpha \le 2.$$

(83)

Note 4.4: Because

$${c_{eq1}(\omega ,\alpha )|}_{\alpha =2}=0,$$

(84)

we see again that a fractional oscillator of Class I type reduces to the conventional harmonic one when α = 2.

Remark 5.

An interesting behavior of $c_{eq1},$ we found, is expressed by

$$\underset{\omega \to \infty }{\lim }{c}_{eq1}(\omega ,\alpha )=\infty ,\hspace{1em}1<\alpha <2.$$

(85)

The above says that the equivalent oscillator (59), as well as the fractional oscillator (58), never oscillates at ω → ∞ for 1 < α < 2 because its damping is infinitely large in that case. Due to

$$\underset{\omega \to 0}{\lim }{c}_{eq1}(\omega ,\alpha )=0,\hspace{1em}1<\alpha <2,$$

(86)

we reveal a new damping behavior of a fractional oscillator in Class I in that it is equivalently dampingless for 1 < α < 2 at ω = 0.

4.2. Equivalent Oscillation System for Fractional Oscillators of Class II Type

4.2.1. Equivalent Oscillation Equation of Fractional Oscillators in Class II

Theorem 4 below describes the equivalent oscillator for the fractional oscillators of Class II type.

Theorem 4 (Equivalent oscillator II).

Denote a fractional oscillator in Class II by

$$m\frac{d^2{y}_2(t)}{d{t}^2}+c\frac{d^{\beta }{y}_2(t)}{d{t}^{\beta }}+k{y}_2(t)=0,\hspace{1em}0<\beta \le 1.$$

(87)

Then, its equivalent 2-order oscillation equation is given by

$$\left(m-c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)\frac{d^2{x}_2(t)}{d{t}^2}+\left(c{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}\right)\frac{d{x}_2(t)}{dt}+k{x}_2(t)=0,\hspace{1em}0<\beta \le 1.$$

(88)

Proof. 

Consider the following equation:

$$m\frac{d^2{h}_y{}_2(t)}{d{t}^2}+c\frac{d^{\beta }{h}_y{}_2(t)}{d{t}^{\beta }}+k{h}_y{}_2(t)=\delta (t),\hspace{1em}0<\beta \le 1.$$

(89)

Denote by $H_{y2}(\omega )$ the Fourier transform of $h_y{}_2(t).$ Then, it is its frequency transfer function. Taking the Fourier transform on the both sides of (89) yields

$$\left[-m{\omega }^2+c{\left(i\omega \right)}^{\beta }+k\right]H_{y2}(\omega )=1,\hspace{1em}0<\beta \le 1.$$

(90)

With the principal value of $i^{\beta },$ (90) becomes

$$\begin{array}{l}\left[-m{\omega }^2+c{\left(i\omega \right)}^{\beta }+k\right]H_{y2}(\omega )=\left\{-m{\omega }^2+c\left(\cos \frac{\beta \pi }{2}+i\sin \frac{\beta \pi }{2}\right){\omega }^{\beta }+k\right\}{H}_{y2}(\omega )\\ =\left(-m{\omega }^2+c{\omega }^{\beta }\cos \frac{\beta \pi }{2}+k+ic{\omega }^{\beta }\sin \frac{\beta \pi }{2}\right)H_{y2}(\omega )=1.\end{array}$$

(91)

The above means

$$H_{y2}(\omega )=\frac{1}{-m{\omega }^2+c{\omega }^{\beta }\cos \frac{\beta \pi }{2}+k+ic{\omega }^{\beta }\sin \frac{\beta \pi }{2}}.$$

(92)

On the other hand, we consider the equivalent oscillation equation II with the Dirac-δ excitation by

$$\left(m-c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)\frac{d^2{h}_{x2}(t)}{d{t}^2}+\left(c{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}\right)\frac{d{h}_{x2}(t)}{dt}+k\frac{d^2{h}_{x2}(t)}{d{t}^2}=\delta (t),\hspace{1em}0<\beta \le 1.$$

(93)

Performing the Fourier transform on the both sides of the above produces

$$\begin{array}{l}\left[-m{\omega }^2+c{\omega }^{\beta }\cos \frac{\beta \pi }{2}+ic{\omega }^{\beta }\sin \frac{\beta \pi }{2}\left(i\omega \right)+k\right]H_{x2}(\omega )\\ =\left(-m{\omega }^2+c{\omega }^{\beta }\cos \frac{\beta \pi }{2}+k+ic{\omega }^{\beta }\sin \frac{\beta \pi }{2}\right)H_{x2}(\omega )=1,\end{array}$$

(94)

where $H_{x2}(\omega )$ the Fourier transform of $h_x{}_2(t).$ Thus, from the above, we have

$$H_{x2}(\omega )=\frac{1}{-m{\omega }^2+c{\omega }^{\beta }\cos \frac{\beta \pi }{2}+k+ic{\omega }^{\beta }\sin \frac{\beta \pi }{2}}.$$

(95)

Equations (92) and (95) imply

$$H_{y2}(\omega )=H_{x2}(\omega ).$$

(96)

Hence, (88) is the equivalent oscillation equation of the fractional oscillators of Class II. This completes the proof. ☐

4.2.2. Equivalent Mass of Fractional Oscillators of Class II

The equivalent mass of the fractional oscillators of Class II type is presented in Theorem 5.

Theorem 5 (Equivalent mass II).

Let $m_{eq2}$ be the equivalent mass of the fractional oscillators of Class II type. Then,

$$m_{eq2}=m_{eq2}(\omega ,\beta )=m-c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2},\hspace{1em}0<\beta \le 1.$$

(97)

Proof. 

Consider the Newton’s second law. Then, we see that the inertia force in the equivalent oscillator II is $\left(m-c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)\frac{d^2{x}_2}{d{t}^2}.$ Therefore, (97) holds. The proof completes. □

From Theorem 5, we reveal a power law phenomenon with respect to the equivalent mass II.

Remark 6.

The equivalent mass $m_{eq2}$ obeys the power law in terms of ω in the form

$$m_{eq2}~-c{\omega }^{\beta -2},\hspace{1em}0<\beta \le 1.$$

(98)

Note 4.5: Equation (97) exhibits that $m_{eq2}$ is related to the oscillation frequency ω, the fractional order β, the primary mass m, and the primary damping c.

Remark 7.

For 0 < β ≤ 1, we have

$$\underset{\omega \to \infty }{\lim }{m}_{eq2}(\omega ,\beta )=m.$$

(99)

Figure 3 shows its plots for m = c = 1 with the part of $m_{eq2}(\omega ,\beta )$> 0.

Figure 3. Plots of $m_{eq2}(\omega ,\beta )$ > 0 for m = c = 1.

Remark 8.

For 0 < β < 1, we have

$$\underset{\omega \to 0}{\lim }{m}_{eq2}(\omega ,\beta )=-\infty .$$

(100)

Note 4.6: The equivalent mass II is negative if ω is small enough.

Figure 4 exhibits the negative part of $m_{eq2}(\omega ,\beta ).$

Figure 4. Illustrating negative part of $m_{eq2}(\omega ,\beta )$ for m = c = 1. (a) β = 0.9. (b) β = 0.7. (c) β = 0.5. (d) β = 0.3.

Remark 9.

We restrict our research for $m_{eq2}(\omega ,\beta )$ > 0.

Note 4.7: The equivalent mass II reduces to the primary mass m for β = 1 as indicated below.

$${m_{eq2}(\omega ,\beta )|}_{\beta =1}=m.$$

(101)

In fact, a fractional oscillator in Class II reduces to the conventional oscillator below if β = 1

$$m\frac{d^2{x}_2}{d{t}^2}+c\frac{d{x}_2}{ct}+k{x}_2=0.$$

4.2.3. Equivalent Damping of Fractional Oscillators in Class II

Let $c_{eq2}$ be the equivalent damping of a fractional oscillator in Class II. Then, we put forward the expression of $c_{eq2}$ with Theorem 6.

Theorem 6 (Equivalent damping II).

The equivalent damping of the fractional oscillators in Class II is in the form

$$c_{eq2}=c_{eq2}(\omega ,\beta )=c{\omega }^{\beta -1}\sin \frac{\beta \pi }{2},\hspace{1em}0<\beta \le 1.$$

(102)

Proof. 

The second term on the left side of (88) is the friction force with the linear viscous damping coefficient denoted by (102). The proof completes. □

Denote by

$$R_{c2}(\omega ,\beta )={\omega }^{\beta -1}\sin \frac{\beta \pi }{2},\hspace{1em}0<\beta \le 1.$$

(103)

Then, we have

$$c_{eq2}(\omega ,\beta )=R_{c2}(\omega ,\beta )c.$$

(104)

Figure 5 indicates $R_{c2}(\omega ,\beta ).$

Figure 5. Indication of $R_{c2}(\omega ,\beta )$ Solid line: β = 0.9. Dot line: β = 0.6. Dash line: β = 0.3.

Remark 10.

The equivalent damping $c_{eq2}$ is associated with the oscillation frequency ω, the primary damping c, and the fractional order β. It follows the power law in terms of ω in the form

$$c_{eq2}(\omega ,\beta )~{\omega }^{\beta -1}c,\hspace{1em}0<\beta \le 1.$$

(105)

Note 4.8: The following says that $c_{eq2}$ reduces to the primary damping c if β = 1.

$${c_{eq2}(\omega ,\beta )|}_{\beta =1}=c.$$

(106)

Remark 11.

The equivalent damping $c_{eq2}$ has, for β ∈ (0, 1), the property given by

$$\underset{\omega \to \infty }{\lim }{c}_{eq2}(\omega ,\beta )=0.$$

(107)

Note 4.9: The equivalent oscillation equation of Class II fractional oscillators reduces to $m\frac{d^2{x}_2(t)}{d{t}^2}+k{x}_2(t)=0$ in the two cases. One is ω → ∞, see Remark 7 and Remark 12. The other is c = 0.

Note 4.10: Remark 5 for $\underset{\omega \to \infty }{\lim }{c}_{eq1}(\omega ,\beta )=\infty$ and Remark 11 just above suggest a substantial difference between two types of fractional oscillators from the point of view of the damping at ω → ∞.

Remark 12.

The equivalent damping $c_{eq2}$ has, for β∈ (0, 1), the asymptotic property for ω → 0 in the form

$$\underset{\omega \to 0}{\lim }{c}_{eq2}(\omega ,\beta )=\infty .$$

(108)

The above property implies that a fractional oscillator in Class II does not oscillate at ω → 0 because not only it is in static status but also its equivalent damping is infinitely large.

4.3. Equivalent Oscillation System for Fractional Oscillators of Class III

4.3.1. Equivalent Oscillation Equation of Fractional Oscillators in Class III

We present Theorem 7 below to explain the equivalent oscillation equation for the fractional oscillators of Class III.

Theorem 7 (Equivalent oscillator III).

Denote a fractional oscillation equation in Class III by

$$m\frac{d^{\alpha }{y}_3(t)}{d{t}^{\alpha }}+c\frac{d^{\beta }{y}_3(t)}{d{t}^{\beta }}+k{y}_3(t)=0,\hspace{1em}1<\alpha \le 2,0<\beta \le 1.$$

(109)

Then, its equivalent oscillator of order 2 for 1 < α ≤ 2 and 0 < β ≤ 1 is in the form

$$\begin{array}{l}-\left(m{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)\frac{d^2{x}_3(t)}{d{t}^2}\\ +\left(m{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+c{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}\right)\frac{d{x}_3(t)}{dt}+k{x}_3(t)=0.\end{array}$$

(110)

Proof. 

Let us consider the equation

$$m\frac{d^{\alpha }{h}_y{}_3(t)}{d{t}^{\alpha }}+c\frac{d^{\beta }{h}_y{}_3(t)}{d{t}^{\beta }}+k{h}_y{}_3(t)=\delta (t),\hspace{1em}1<\alpha \le 2,0<\beta \le 1.$$

(111)

Let $H_y{}_3(\omega )$ be the Fourier transform of $h_y{}_3(t).$ Doing the Fourier transform on the both sides of the above results in

$$\left[m{\left(i\omega \right)}^{\alpha }+c{\left(i\omega \right)}^{\beta }+k\right]H_y{}_3(\omega )=1,\hspace{1em}1<\alpha \le 2,0<\beta \le 1.$$

(112)

Taking into account the principal values of $i^{\alpha }$ and $i^{\beta },$ (112) becomes

$$\begin{array}{l}\left[m{\left(i\omega \right)}^{\alpha }+c{\left(i\omega \right)}^{\beta }+k\right]H_y{}_3(\omega )\\ =\left[m\left(\cos \frac{\alpha \pi }{2}+i\sin \frac{\alpha \pi }{2}\right){\omega }^{\alpha }+c\left(\cos \frac{\beta \pi }{2}+i\sin \frac{\beta \pi }{2}\right){\omega }^{\beta }+k\right]H_y{}_3(\omega )\\ =\left[m{\omega }^{\alpha }\cos \frac{\alpha \pi }{2}+c{\omega }^{\beta }\cos \frac{\beta \pi }{2}+k+i\left(m{\omega }^{\alpha }\sin \frac{\alpha \pi }{2}+c{\omega }^{\beta }\sin \frac{\beta \pi }{2}\right)\right]H_y{}_3(\omega )=1.\end{array}$$

(113)

Consequently, we have

$$H_y{}_3(\omega )=\frac{1}{m{\omega }^{\alpha }\cos \frac{\alpha \pi }{2}+c{\omega }^{\beta }\cos \frac{\beta \pi }{2}+k+i\left(m{\omega }^{\alpha }\sin \frac{\alpha \pi }{2}+c{\omega }^{\beta }\sin \frac{\beta \pi }{2}\right)}.$$

(114)

On the other hand, considering the equivalent oscillator III driven by the Dirac-δ function, we have

$$\begin{array}{l}-\left(m{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)\frac{d^2{h}_x{}_3(t)}{d{t}^2}+\left(m{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+c{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}\right)\frac{d{h}_x{}_3(t)}{dt}+k{h}_x{}_3(t)\\ =\delta (t).\end{array}$$

(115)

When doing the Fourier transform on the both sides of the above, we obtain

$$\begin{array}{l}\left(m{\omega }^{\alpha }\cos \frac{\alpha \pi }{2}+c{\omega }^{\beta }\cos \frac{\beta \pi }{2}\right)H_x{}_3(\omega )+i\left(m{\omega }^{\alpha }\sin \frac{\alpha \pi }{2}+c{\omega }^{\beta }\sin \frac{\beta \pi }{2}\right)H_x{}_3(\omega )+k{H}_x{}_3(\omega )\\ =1,\end{array}$$

(116)

where $H_x{}_3(\omega )$ is the Fourier transform of $h_x{}_3(t).$ Therefore, from the above, we get

$$H_x{}_3(\omega )=\frac{1}{m{\omega }^{\alpha }\cos \frac{\alpha \pi }{2}+c{\omega }^{\beta }\cos \frac{\beta \pi }{2}+k+i\left(m{\omega }^{\alpha }\sin \frac{\alpha \pi }{2}+c{\omega }^{\beta }\sin \frac{\beta \pi }{2}\right)}.$$

(117)

Two expressions, (114) and (117), imply that

$$H_x{}_3(\omega )=H_y{}_3(\omega ).$$

(118)

Thus, Theorem 7 holds. □

4.3.2. Equivalent Mass of Fractional Oscillators in Class III

From Section 4.3.1, we propose the equivalent mass of the fractional oscillators in Class III type by Theorem 8.

Theorem 8 (Equivalent mass III).

Let $m_{eq3}$ be the equivalent mass of the fractional oscillators in Class III. Then, for 1 < α ≤ 2 and 0 < β ≤ 1,

$$m_{eq3}=m_{eq3}(\omega ,\alpha ,\beta )=-\left(m{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right).$$

(119)

Proof. 

When considering the Newton’s second law in the equivalent oscillator III (110), we immediately see that Theorem 8 holds. □

Remark 13.

The equivalent mass $m_{eq3}$ obeys the power law in terms of ω.

Note 4.11: The equivalent mass $m_{eq3}$ is related to ω, m, and c, as well as a pair of fractional orders (α, β).

Note 4.12: If α = 2 and β = 1, $m_{eq3}$ reduces to the primary m, i.e.,

$${m_{eq3}(\omega ,\alpha ,\beta )|}_{\alpha =2,\beta =1}=m.$$

(120)

As a matter of fact, a fractional oscillator of Class III reduces to the ordinary oscillator when α = 2 and β = 1.

Remark 14.

In the case of ω → ∞, we obtain

$$\underset{\omega \to \infty }{\lim }{m}_{eq3}(\omega ,\alpha ,\beta )=0,\hspace{1em}1<\alpha <2,0<\beta <1.$$

(121)

Therefore, we suggest that a fractional oscillator in Class III does not oscillate for ω → ∞ because its equivalent mass disappears in that case. Figure 6 shows its positive part for α = 1.5, β = 0.9, m = c = 1.

Figure 6. Indicating the positive part of $m_{eq3}(\omega ,\alpha ,\beta )$ for α = 1.5, β = 0.9, m = c = 1.

Remark 15.

In the case of ω → 0, we obtain

$$\underset{\omega \to 0}{\lim }{m}_{eq3}(\omega ,\alpha ,\beta )=-\infty ,\hspace{1em}1<\alpha <2,0<\beta <1.$$

(122)

In fact, if ω is small enough, $m_{eq3}(\omega ,\alpha ,\beta )$ will be negative, see Figure 7.

Figure 7. Negative part of $m_{eq3}(\omega ,\alpha ,\beta )$ for m = c = 1 and β = 0.9. Solid line: α = 1.9. Dot line: α = 1.6. Dash line: α = 1.3.

Remark 16.

This research restricts $m_{eq3}(\omega ,\alpha ,\beta )$ ∈ (0, ∞).

4.3.3. Equivalent Damping of Fractional Oscillators in Class III

Let $c_{eq3}$ be the equivalent damping of a fractional oscillator of Class III type. Then, we propose its expression with Theorem 9.

Theorem 9 (Equivalent damping III).

The equivalent damping of the fractional oscillators in Class III is given by, for 1 < α ≤ 2 and 0 < β ≤ 1,

$$c_{eq3}=c_{eq3}(\omega ,\alpha ,\beta )=m{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+c{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}.$$

(123)

Proof. 

The second term on the left side of the equivalent oscillator III is the friction force with the linear viscous damping coefficient denoted by (123). Thus, the proof completes. □

Remark 17.

The equivalent damping $c_{eq3}$ relates to ω, m, c, and a pair of fractional orders (α, β). It obeys the power law in terms of ω. It contains two terms. The first term is hyperbolically increasing in ${\omega }^{\alpha -1}$ as α > 1 and the second hyperbolically decayed with ${\omega }^{\beta -1}$ since β < 1.

Note 4.13: From (123), we see that $c_{eq3}$ reduces to the primary damping c for α = 2 and β = 1. That is,

$${c_{eq3}(\omega ,\alpha ,\beta )|}_{\alpha =2,\beta =1}=c.$$

(124)

Remark 18.

One asymptotic property of $c_{eq3}$ for ω → ∞, due to $\underset{\omega \to \infty }{\lim }{\omega }^{\alpha -1}=\infty$ for 1 < α ≤ 2, is given by

$$\underset{\omega \to \infty }{\lim }{c}_{eq3}(\omega ,\alpha ,\beta )=\infty .$$

(125)

The above says that a fractional oscillator of Class III does not vibrate for ω → ∞.

Remark 19.

Another asymptotic property of $c_{eq3}$ in terms of ω for ω → 0, owing to $\underset{\omega \to 0}{\lim }{\omega }^{\beta -1}=\infty$ for 0 < β < 1, is expressed by

$$\underset{\omega \to 0}{\lim }{c}_{eq3}(\omega ,\alpha ,\beta )=\infty .$$

(126)

A system does not vibrate obviously in the case of ω → 0 but Remark 19 suggests a new view about that. Precisely, its equivalent damping is infinitely large at ω → 0. Figure 8 and Figure 9 illustrate $c_{eq3}(\omega ,\alpha ,\beta )$ for m = c = 1.

Figure 8. Plots of equivalent damping III for m = c = 1. Solid line: α = 1.9. Dot line: α = 1.6. Dash line: α = 1.3. (a) For β = 0.9. (b) For β = 0.7. (c) For β = 0.5. (d) For β = 0.3.

Figure 9. Plots of $c_{eq3}(\omega ,\alpha ,\beta )$ for m = c = 1. Solid line: β = 0.8. Dot line: β = 0.5. Dash line: β = 0.3. (a) For α = 1.8. (b) For α = 1.3.

Note 4.14: The equivalent damping $c_{eq3}$= 0 if both α = 2 and c = 0:

$${c_{eq3}(\omega ,\alpha ,\beta )|}_{\alpha =2,c=0}=0.$$

(127)

4.4. Summary

We have proposed three equivalent oscillation equations with order 2 to equivalently characterize three classes of fractional oscillators, opening a novel way of studying fractional oscillators. The analytic expressions of equivalent mass $m_{eqj}$ and damping $c_{eqj}$ (j = 1, 2, 3) for each equivalent oscillator have been presented. One general thing regarding $m_{eqj}$ and damping $c_{eqj}$ is that they follow power laws. Another thing in common is that they are dependent on oscillation frequency ω and fractional order.

5. Equivalent Natural Frequencies and Damping Ratio of Three Classes of Fractional Oscillators

We have presented three equivalent oscillation equations corresponding to three classes of fractional oscillators in the last section. Functionally, they are abstracted in a unified form

$$m_{eqj}\frac{d^2{x}_j(t)}{d{t}^2}+c_{eqj}\frac{d{x}_j(t)}{dt}+k{x}_j(t)=f(t),\hspace{1em}j=1,2,3.$$

(128)

In each equivalent oscillator, either $m_{eqj}$ or $c_{eqj}$ is not a constant in general. Instead, either is a function of the oscillation frequency ω and the fractional order α for $m_{eq1}$ and $c_{eq1},$ β for $m_{eq2}$ and $c_{eq2},$ (α, β) for $m_{eq3}$ and $c_{eq3}.$ Consequently, natural frequencies and damping ratios of fractional oscillators should rely on ω and fractional order. We shall propose their analytic expressions in this section.

5.1. Equivalent Natural Frequency I

Definition 1.

Denote by ${\omega }_{eqn,j}$ a natural frequency of a fractional oscillator in the jth class (j = 1, 2, 3). It takes the form

$${\omega }_{eqn,j}=\sqrt{\frac{k}{m_{eqj}}},\hspace{1em}j=1,2,3,$$

(129)

where $m_{eqj}$ is the equivalent mass of the fractional oscillator in the jth class.

With the above definition, we write (128) by

$$\frac{d^2{x}_j(t)}{d{t}^2}+\frac{c_{eqj}}{m_{eqj}}\frac{d{x}_j(t)}{dt}+\frac{k}{m_{eqj}}{x}_j(t)=\frac{d^2{x}_j(t)}{d{t}^2}+\frac{c_{eqj}}{m_{eqj}}\frac{d{x}_j(t)}{dt}+{\omega }_{eqn,j}^2{x}_j(t)=\frac{f(t)}{m_{eqj}},\hspace{1em}j=1,2,3.$$

(130)

Note 5.1: ${\omega }_{eqn,j}$ may take the conventional natural frequency, denoted by

$${\omega }_n=\sqrt{\frac{k}{m}},$$

(131)

as a special case.

Corollary 1 (Equivalent natural frequency I1).

The equivalent natural frequency I1, which we denote it by ${\omega }_{eqn,1},$ of a fractional oscillator in Class I is given by

$${\omega }_{eqn,1}=\frac{{\omega }_n}{\sqrt{-{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}}},\hspace{1em}1<\alpha \le 2.$$

(132)

Proof. 

According to (129), we have, for 1 < α ≤ 2,

$${\omega }_{eqn,1}=\sqrt{\frac{k}{m_{eq1}}}=\sqrt{\frac{k}{-m{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}}}=\sqrt{\frac{1}{-{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}}}\sqrt{\frac{k}{m}}=\frac{{\omega }_n}{\sqrt{-{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}}}.$$

(133)

The proof finishes. □

Figure 10 shows the plots of ${\omega }_{eqn,1}$.

Figure 10. Natural frequency ${\omega }_{eqn,1}.$ Solid line: α = 1.8. Dot line: α = 1.5. Dash line: α = 1.2. (a) ${\omega }_n$ = 1. (b) ${\omega }_n$ = 2.

Note 5.2: From Figure 10, we see that ${\omega }_{eqn,1}$ is an increasing function with ω. Besides, the greater the value of α the smaller the ω_eqn,1.

Note 5.3: ${\omega }_{eqn,1}$ becomes ${\omega }_n$ if α = 2. In fact,

$${{\omega }_{eqn,1}|}_{\alpha =2}={\sqrt{\frac{k}{m_{eq1}}}|}_{\alpha =2}={\frac{{\omega }_n}{\sqrt{-{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}}}|}_{\alpha =2}={\omega }_n.$$

(134)

Corollary 2 (Equivalent natural frequency I2).

The natural frequency I2, ${\omega }_{eqn,2},$ of a fractional oscillator in Class II is given by

$${\omega }_{eqn,2}=\frac{{\omega }_n}{\sqrt{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}}.$$

(135)

Proof. 

Following (129), we have

$${\omega }_{eqn,2}=\sqrt{\frac{k}{m_{eq2}}}=\sqrt{\frac{k}{m-c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}}=\sqrt{\frac{k}{m\left(1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}}=\frac{{\omega }_n}{\sqrt{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}}.$$

Hence, the proof completes. □

Figure 11 indicates the curves of ${\omega }_{eqn,2}.$

Figure 11. Curves of ${\omega }_{eqn,2}$ for m = c = 1. Solid line: β = 0.8. Dot line: β = 0.5. Dash line: β = 0.3. (a) ${\omega }_n$ = 1. (b) ${\omega }_n$ = 2.

Note 5.4: Figure 11 shows that ${\omega }_{eqn,2}$ is a decreasing function with ω. The greater the value of β the smaller the ${\omega }_{eqn,2}.$

Note 5.5: ${\omega }_{eqn,2}$ takes ${\omega }_n$ as a special case for β = 1. As a matter of fact,

$${{\omega }_{eqn,2}|}_{\beta =1}={\frac{{\omega }_n}{\sqrt{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}}|}_{\beta =1}={\omega }_n.$$

(136)

Corollary 3 (Equivalent natural frequency I3).

The natural frequency I3, denoted by ${\omega }_{eqn,3},$ of a fractional oscillator in Class III is given by

$${\omega }_{eqn,3}=\frac{{\omega }_n}{\sqrt{-\left({\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}}.$$

(137)

Proof. 

With (129), we write

$${\omega }_{eqn,3}=\sqrt{\frac{k}{m_{eq3}}}=\sqrt{\frac{k}{-\left(m{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}}=\frac{{\omega }_n}{\sqrt{-\left({\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}}.$$

(138)

The above completes the proof. □

Figure 12 gives the illustrations of ${\omega }_{eqn,3}.$

Figure 12. Illustrations of ${\omega }_{eqn,3}$ for m = c = 1. Solid line: α = 1.8, β = 0.9. Dot line: α = 1.5, β = 0.9. Dash line: α = 1.2, β = 0.9. (a) ${\omega }_n$ = 1. (b) ${\omega }_n$ = 2.

Note 5.6: Figure 12 exhibits that ${\omega }_{eqn,3}$ is an increasing function in terms of ω.

Note 5.7: ${\omega }_{eqn,3}$ takes ${\omega }_n$ as a special case for α = 2 and β = 1. Indeed,

$${{\omega }_{eqn,3}|}_{\alpha =2,\beta =0}={\sqrt{\frac{k}{-\left(m{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}}|}_{\alpha =2,\beta =1}=\sqrt{\frac{k}{m}}={\omega }_n.$$

(139)

5.2. Equivalent Damping Ratio

Definition 2.

Let ${\varsigma }_{eqj}$ be the equivalent damping ratio of the equivalent system of a fractional oscillator in Class j. It is defined by

$${\varsigma }_{eqj}=\frac{c_{eqj}}{2\sqrt{m_{eqj}k}},\hspace{1em}j=1,2,3.$$

(140)

Corollary 4 (Equivalent damping ratio I).

The equivalent damping ratio of a fractional oscillator in Class I is expressed by

$${\varsigma }_{eq1}={\varsigma }_{eq1}(\omega ,\alpha )=\frac{{\omega }^{\frac{\alpha }{2}}\sin \frac{\alpha \pi }{2}}{2{\omega }_n\sqrt{-\cos \frac{\alpha \pi }{2}}},\hspace{1em}1<\alpha \le 2.$$

(141)

Proof. 

Replacing $m_{eq1}$ and $c_{eq1}$ in the expression below with the equivalent mass I and the equivalent damping I described in Section 4

$${\varsigma }_{eq1}=\frac{c_{eq1}}{2\sqrt{m_{eq1}k}}$$

(142)

yields

$${\varsigma }_{eq1}=\frac{m{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}}{2\sqrt{\left(-m{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}\right)k}}=\frac{{\omega }^{\frac{\alpha }{2}}\sin \frac{\alpha \pi }{2}}{2\sqrt{-\cos \frac{\alpha \pi }{2}}}\sqrt{\frac{m}{k}}=\frac{{\omega }^{\frac{\alpha }{2}}\sin \frac{\alpha \pi }{2}}{2{\omega }_n\sqrt{-\cos \frac{\alpha \pi }{2}}},\hspace{1em}1<\alpha \le 2.$$

(143)

The proof finishes. □

Remark 20.

The damping ratio ${\varsigma }_{eq1}$ follows the power law in terms of ω.

Remark 21.

The damping ratio of fractional oscillators in Class I relates to the oscillation frequency ω and the fractional order α. It is increasing with respect to ω.

$${\varsigma }_{eq1}(0,\alpha ) =0\mathrm{and}{\varsigma }_{eq1}(\infty ,\alpha )=\infty .$$

(144)

Figure 13 shows the curves of ${\varsigma }_{eq1}(\omega ,\alpha ).$

Figure 13. Illustrations of ${\varsigma }_{eq1}(\omega ,\alpha ).$ Solid line: α = 1.3. Dot line: α = 1.6. Dash line: α = 1.9. (a) For ${\omega }_n$ = 1. (b) For ${\omega }_n$ = 3.

Note 5.8: Figure 13 indicates that the smaller the α the greater the ${\varsigma }_{eq1}.$

Corollary 5 (Equivalent damping ratio II).

The damping ratio of a fractional oscillator in Class II is given by

$${\varsigma }_{eq2}={\varsigma }_{eq2}(\omega ,\beta )=\frac{\varsigma {\omega }^{\beta -1}\sin \frac{\beta \pi }{2}}{\sqrt{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}},\hspace{1em}0<\beta \le 1,$$

(145)

where $\varsigma =\frac{c}{2\sqrt{mk}}.$

Proof. 

When replacing the $m_{eq2}$ and $c_{eq2}$ in the following expression by the equivalent mass II and the equivalent damping II proposed in Section 4, we attain

$$\begin{array}{l}{\varsigma }_{eq2}=\frac{c_{eq2}}{2\sqrt{m_{eq2}k}}=\frac{c{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}}{2\sqrt{\left(m-c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)k}}=\frac{c{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}}{2\sqrt{\left(1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)mk}}\\ =\frac{c{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}}{2\sqrt{mk}\sqrt{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}}=\frac{\varsigma {\omega }^{\beta -1}\sin \frac{\beta \pi }{2}}{\sqrt{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}},\hspace{1em}0<\beta \le 1.\end{array}$$

This finishes the proof. □

Remark 22.

The damping ratio ${\varsigma }_{eq2}$ obeys the power law in terms of ω.

Remark 23.

The damping ratio ${\varsigma }_{eq2}$ is associated with ω and the fractional order β. It is decreasing in terms of ω.

Note 5.9: ${\varsigma }_{eq2}$ takes ζ as a special case for β = 1. In fact,

$${{\varsigma }_{eq2}(\omega ,\beta )|}_{\beta =1}={\frac{\varsigma {\omega }^{\beta -1}\sin \frac{\beta \pi }{2}}{\sqrt{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}}|}_{\beta =1}=\varsigma .$$

(146)

Figure 14 indicates the plots of ${\varsigma }_{eq2}(\omega ,\beta )$ in the case of m = 1, c = 1, and k = 1.

Figure 14. Plots of ${\varsigma }_{eq2}(\omega ,\beta )$ for m = c = k = 1. Solid line: β = 0.9. Dot line: β = 0.6. Dash line: β = 0.3.

Corollary 6 (Equivalent damping ratio III).

Let ${\varsigma }_{eq3}$ be the damping ratio of a fractional oscillator in Class III. Then, for 1 < α ≤ 2, 0 < β ≤ 1,

$${\varsigma }_{eq3}={\varsigma }_{eq3}(\omega ,\alpha ,\beta )=\frac{{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+2\varsigma {\omega }_n{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}}{2{\omega }_n\sqrt{-\left({\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+2\varsigma {\omega }_n{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}}.$$

(147)

Proof. 

If replacing the $m_{eq3}$ and $c_{eq3}$ below with the equivalent mass III and the equivalent damping III presented in Section 4, we obtain

$$\begin{array}{l}{\varsigma }_{eq3}=\frac{c_{eq3}}{2\sqrt{m_{eq3}k}}=\frac{m{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+c{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}}{2\sqrt{-\left(m{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)k}}\\ =\frac{m\left({\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+\frac{c}{m}{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}\right)}{2\sqrt{-\left({\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)mk}}=\frac{m\left({\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+2\varsigma {\omega }_n{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}\right)}{2\sqrt{mk}\sqrt{-\left({\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+2\varsigma {\omega }_n{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}}\\ =\frac{{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+2\varsigma {\omega }_n{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}}{2{\omega }_n\sqrt{-\left({\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+2\varsigma {\omega }_n{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}}.\end{array}$$

Thus, we finish the proof. □

Remark 24.

The damping ratio ${\varsigma }_{eq3}$ follows the power law in terms of ω.

Remark 25.

${\varsigma }_{eq3}$ relates to ω and a pair of fractional orders (α, β).

Note 5.10: ${\varsigma }_{eq3}$ regards ζ as a special case for α = 2 and β = 1. As a matter of fact,

$${\varsigma }_{eq3}(\omega ,2,1)={\frac{{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+2\varsigma {\omega }_n{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}}{2{\omega }_n\sqrt{-\left({\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+2\varsigma {\omega }_n{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}}|}_{\alpha =2,\beta =1}=\varsigma .$$

(148)

Figure 15 demonstrates the figures of ${\varsigma }_{eq3}(\omega ,\alpha ,\beta )$ in the case of m = 1, c = 1, and k = 1.

Figure 15. Demonstrations of ${\varsigma }_{eq3}(\omega ,\alpha ,\beta )$ in m = c = k = 1. Solid line: α = 1.9. Dot line: α = 1.8. Dash line: α = 1.7. (a) For β = 0.8. (b) For β = 0.5. (c) For β = 0.2. (d) For β = 1.

5.3. Equivalent Natural Frequency II

Now, with two parameters ${\omega }_{eqn,j}$ and ${\varsigma }_{eqj}$ presented above, we rewrite the equivalent oscillator (130) by

$$\frac{d^2{x}_j(t)}{d{t}^2}+2{\varsigma }_{eqj}{\omega }_{eqn,j}\frac{d{x}_j(t)}{dt}+{\omega }_{eqn,j}^2{x}_j(t)=\frac{f(t)}{m_{eqj}},\hspace{1em}j=1,2,3.$$

(149)

The characteristic equation of (149) is given by

$$s_j^2+2{\varsigma }_{eqj}{\omega }_{eqn,j}{s}_j+{\omega }_{eqn,j}^2=0,\hspace{1em}j=1,2,3.$$

(150)

The characteristic roots are in the form

$$s_{j,1,2}=-{\varsigma }_{eqj}{\omega }_{eqn,j}\pm \sqrt{{\varsigma }_{eqj}^2{\omega }_{eqn,j}^2-{\omega }_{eqn,j}^2}=-{\varsigma }_{eqj}{\omega }_{eqn,j}\pm i{\omega }_{eqn,j}\sqrt{1-{\varsigma }_{eqj}^2},\hspace{1em}j=1,2,3.$$

(151)

Functionally, we utilize the symbol ${\omega }_{eqd,j}$ for

$${\omega }_{eqd,j}={\omega }_{eqn,j}\sqrt{1-{\varsigma }_{eqj}^2},\hspace{1em}j=1,2,3.$$

(152)

Thus, the characteristic roots are

$$s_{j,1,2}=-{\varsigma }_{eqj}{\omega }_{eqn,j}\pm i{\omega }_{eqd,j},\hspace{1em}j=1,2,3.$$

(153)

Note that, in practice, 0 ≤ ${\varsigma }_{eqj}$ < 1 because 1 ≤ ${\varsigma }_{eqj}$ means no oscillation at all.

We write those above for the sake of applying the theory of linear oscillations to fractional ones. Now, we discuss ${\omega }_{eqd,j}.$

Corollary 7 (Equivalent natural frequency II1).

Let ${\omega }_{eqd,1}$ be the functional damped natural frequency of a fractional oscillator in Class I. It may be termed the equivalent natural frequency II1. Then,

$${\omega }_{eqd,1}={\omega }_{eqd,1}(\omega ,\alpha )=\frac{{\omega }_n}{\sqrt{-{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}}}\sqrt{1-\frac{{\omega }^{\alpha }{\sin }^2\frac{\alpha \pi }{2}}{4{\omega }_n^2\left|\cos \frac{\alpha \pi }{2}\right|}},\hspace{1em}1<\alpha \le 2.$$

(154)

Proof. 

Note that

$${\omega }_{eqd,1}={\omega }_{eqn,1}\sqrt{1-{\varsigma }_{ed1}^2}.$$

(155)

Using the above ${\varsigma }_{ed1},$ we have

$${\omega }_{eqd,1}={\omega }_{eqn,1}\sqrt{1-{\varsigma }_{ed1}^2}=\frac{{\omega }_n}{\sqrt{-{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}}}\sqrt{1-{\left(\frac{{\omega }^{\frac{\alpha }{2}}\sin \frac{\alpha \pi }{2}}{2{\omega }_n\sqrt{\left|\cos \frac{\alpha \pi }{2}\right|}}\right)}^2}.$$

This finishes the proof. □

The parameter ${\omega }_{eqd,1}$ functionally takes the form of damped natural frequency as in the conventional linear oscillation theory. In this research, we do not distinguish the natural frequencies with damped or damping free. At most, we just say that it is a functional damped one. It relates to the oscillation frequency ω and the fractional order α.

Remark 26.

${\omega }_{eqd,1}$ is not a monotonic function of ω.

Note 5.11: ${\omega }_n$ is a special case of ${\omega }_{eqd,1}$ when α = 2:

$${\omega }_{eqd,1}(\omega ,2)={\frac{{\omega }_n}{\sqrt{-{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}}}\sqrt{1-\frac{{\omega }^{\alpha }{\sin }^2\frac{\alpha \pi }{2}}{4{\omega }_n^2\left|\cos \frac{\alpha \pi }{2}\right|}}|}_{\alpha =2}={\omega }_n.$$

(156)

As a matter of fact, fractional oscillators of Class I are damping free for α = 2. Figure 16 illustrates the plots of ${\omega }_{eqd,1}(\omega ,\alpha ).$

Figure 16. Plots of ${\omega }_{eqd,1}(\omega ,\alpha ).$ Solid line: α = 1.8. Dot line: α = 1.5. Dash line: α = 1.2. (a) For ${\omega }_n$ = 1. (b) For ${\omega }_n$ = 2.

Corollary 8 (Equivalent natural frequency II2).

Let ${\omega }_{eqd,2}$ be the functional damped natural frequency of a fractional oscillator in Class II. Term it with the equivalent natural frequency II2. Then, for 0 < β ≤ 1,

$${\omega }_{eqd,2}={\omega }_{eqd,2}(\omega ,\beta )=\frac{{\omega }_n}{\sqrt{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}}\sqrt{1-\frac{{\varsigma }^2{\omega }^{2(\beta -1)}{\sin }^2\frac{\beta \pi }{2}}{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}}.$$

(157)

Proof. 

Consider

$${\omega }_{eqd,2}={\omega }_{eqn,2}\sqrt{1-{\varsigma }_{ed2}^2}.$$

(158)

Replacing ${\omega }_{eqn,2}$ and ${\varsigma }_{ed2}$ in the above yields

$$\begin{array}{l}{\omega }_{eqd,2}={\omega }_{eqn,2}\sqrt{1-{\varsigma }_{ed2}^2}=\frac{{\omega }_n}{\sqrt{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}}\sqrt{1-{\left(\frac{\varsigma {\omega }^{\beta -1}\sin \frac{\beta \pi }{2}}{2\sqrt{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}}\right)}^2}\\ =\frac{{\omega }_n}{\sqrt{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}}\sqrt{1-\frac{{\varsigma }^2{\omega }^{2(\beta -1)}{\sin }^2\frac{\beta \pi }{2}}{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}}.\end{array}$$

Thus, Corollary 8 holds. □

Remark 27.

${\omega }_{eqd,2}$ is related to ω and the fractional order β.

Note 5.12: The conventional damped natural frequency, say,

$${\omega }_d={\omega }_n\sqrt{1-{\varsigma }^2}$$

(159)

is a special case of ${\omega }_{eqd,2}(\omega ,\beta )$ for β = 1.

Figure 17 gives the plots of ${\omega }_{eqd,2}(\omega ,\beta ).$

Figure 17. Illustrating ${\omega }_{eqd,2}(\omega ,\beta )$ for m = c = 1. Solid line: β = 0.8. Dot line: β = 0.5. Dash line: β = 0.2. (a) For ${\omega }_n$ = 1. (b) For ${\omega }_n$ = 0.3. (c) For ${\omega }_n$ = 10.

Corollary 9 (Equivalent natural frequency II3).

Let ${\omega }_{eqd,3}={\omega }_{eqd,3}(\omega ,\alpha ,\beta )$ be the functional damped natural frequency of a fractional oscillator in Class III. Call it the equivalent natural frequency II3. Then, for 1 < α ≤ 2 and 0 < β ≤ 1, we have

$${\omega }_{eqd,3}=\frac{{\omega }_n\sqrt{1-{\left[\frac{{\left({\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+2\varsigma {\omega }_n{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}\right)}^2}{4{\omega }_n^2\left[-\left({\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+2\varsigma {\omega }_n{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)\right]}\right]}^2}}{\sqrt{-\left({\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}}.$$

(160)

Proof. 

In the expression below

$${\omega }_{eqd,3}={\omega }_{eqn,3}\sqrt{1-{\varsigma }_{ed3}^2},$$

(161)

we replace ${\omega }_{eqd,3}$ and ${\varsigma }_{eq3}$ by those expressed above. Then, we have

$$\begin{array}{l}{\omega }_{eqd,3}={\omega }_{eqn,3}\sqrt{1-{\varsigma }_{ed3}^2}=\sqrt{\frac{k}{m_{eq3}}}\sqrt{1-{\varsigma }_{ed3}^2}\\ =\frac{{\omega }_n\sqrt{1-{\left[\frac{{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+2\varsigma {\omega }_n{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}}{2{\omega }_n\sqrt{-\left({\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+2\varsigma {\omega }_n{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}}\right]}^2}}{\sqrt{-\left({\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}}\\ =\frac{{\omega }_n\sqrt{1-{\left[\frac{{\left({\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+2\varsigma {\omega }_n{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}\right)}^2}{4{\omega }_n^2\left[-\left({\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+2\varsigma {\omega }_n{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)\right]}\right]}^2}}{\sqrt{-\left({\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}}.\end{array}$$

Therefore, the corollary holds. □

Note 5.13: The conventional damped natural frequency ${\omega }_d$ is a special case of ${\omega }_{eqd,3}$ for (α, β) = (2, 1). Indeed,

$${\omega }_{eqd,3}(\omega ,2,1)={\frac{{\omega }_n\sqrt{1-{\left[\frac{{\left({\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+2\varsigma {\omega }_n{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}\right)}^2}{4{\omega }_n^2\left[-\left({\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+2\varsigma {\omega }_n{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)\right]}\right]}^2}}{\sqrt{-\left({\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}}|}_{\alpha =1,\beta =1}={\omega }_n\sqrt{1-{\varsigma }^2}.$$

(162)

Remark 28.

The natural frequency ${\omega }_{eqd,3}$ is associated with ω and a pair of fractional orders (α, β).

Figure 18 and Figure 19 indicate its plots.

Figure 18. Demonstrations of ${\omega }_{eqd,3}(\omega ,\alpha ,\beta )$ for m = c = k = 1. Solid line: α = 1.9. Dot line: α = 1.6. Dash line: α = 1.3. (a) For β = 0.9. (b) For β = 0.8. (c) For β = 0.3. (d) For β = 0.2.

Figure 19. ${\omega }_{eqd,3}(\omega ,\alpha ,\beta )$ for m = c = 1, β = 0.9. Solid line: α = 1.9. Dot line: α = 1.6. Dash line: α = 1.3. (a) For ${\omega }_n$ = 3. (b) For ${\omega }_n$ = 5.

5.4. There Exists Infinity of Natural Frequencies of a Fractional Oscillator

The previous discussions imply that there exists infinity of natural frequencies, for either ${\omega }_{eqn,j}$ or ${\omega }_{eqd,j},$ because each is dependent on ω ∈ (0, ∞). We functionally derived the two characteristic roots of the frequency equation (151), namely, $s_{j,1,2},$ actually stand for infinity of roots owing to ω ∈ (0, ∞).

Taking a fractional oscillator in Class I into account, its frequency equation is given by

$$s^{\alpha }+{\omega }_n^2=0,\hspace{1em}1<\alpha \le 2.$$

(163)

Then, it is easy to see that there exists infinitely many characteristic roots in the above, also see Li et al. [18].

A contribution in this work in representing characteristic roots of three classes of fractional oscillators is that they are expressed analytically. Moreover, functionally, they take the form as that in the theory of conventional linear oscillations, making it possible to represent solutions to three classes of fractional oscillators by using elementary functions, which are easier for use in both engineering applications and theoretic analysis of fractional oscillators.

6. Free Responses to Three Classes of Fractional Oscillators

We put forward the free responses in this section to three classes of fractional oscillators based on their equivalent oscillators presented in Section 4. Since the equivalent oscillators are expressed by using second-order differential equations in form, in methodology, therefore, it is easy for us to find the responses we concern with. Note that the equivalence explained in Section 4 says that

$$Y_j(\omega )=X_j(\omega ),j=1,2,3,$$

(164)

where the subscript j stands for the Class I to III. Consequently,

$$y_j(t)=x_j(t),j=1,2,3.$$

(165)

Therefore, our research implies three advances.

• First, proposing the free responses to three classes of fractional oscillators using the way of solving conventional oscillators.
• Then, since the responses to conventional oscillators are represented by elementary functions while those to fractional ones are expressed by special functions, such as the Mittag-Leffler function and its generalizations, we shall present novel representation to a certain special functions by elementary ones.
• Finally, analytic expressions of the logarithmic decrements, which are useful in practice, of three classes of fractional oscillators are proposed.

6.1. General Form of Free Responses

Consider the free response to the functional equivalent oscillator in Class j in the form

$$\{\begin{array}{c}{m}_{eqj}\frac{d^2{x}_j(t)}{d{t}^2}+c_{eqj}\frac{d{x}_j(t)}{dt}+k{x}_j(t)=0\\ x_j(0)=x_{j0},{\frac{d{x}_j(t)}{dt}|}_{t=0}=v_{j0}\end{array},\hspace{1em}j=1,2,3.$$

(166)

Following the representation style in engineering, we rewrite it by

$$\{\begin{array}{c}\frac{d^2{x}_j(t)}{d{t}^2}+2{\varsigma }_{eqj}{\omega }_{eqn,j}\frac{d{x}_j(t)}{dt}+{\omega }_{eqn,j}^2{x}_j(t)=0\\ x_j(0)=x_{j0},{\frac{d{x}_j(t)}{dt}|}_{t=0}=v_{j0}\end{array},\hspace{1em}j=1,2,3.$$

(167)

Therefore (Timoshenko ([1], p. 34), Jin and Xia ([79], p. 11)), we have, for t ≥ 0,

$$x_j(t)=e^{-{\varsigma }_{eqj}{\omega }_{eqn,j}t}\left(x_{j0}\cos {\omega }_{eqd,j}t+\frac{v_{j0}+{\varsigma }_{eqj}{\omega }_{eqn,j}{x}_{j0}}{{\omega }_{eqd,j}}\sin {\omega }_{eqd,j}t\right).$$

(168)

The above may be rewritten in the form

$$x_j(t)=A_{eqj}{e}^{-{\varsigma }_{eqj}{\omega }_{eqn,j}t}\cos \left({\omega }_{eqd,j}t-{\theta }_{eqj}\right),\hspace{1em}t\ge 0,$$

(169)

where the equivalent amplitude $A_{eqj}$ is given by

$$A_{eqj}=\sqrt{x_{j0}^2+{\left[\frac{v_{j0}+{\varsigma }_{eqj}{\omega }_{eqn,j}{x}_{j0}}{{\omega }_{eqd,j}}\right]}^2},$$

(170)

and the equivalent phase ${\theta }_{eqj}$ is

$${\theta }_{eqj}={\tan }^{-1}\frac{v_{j0}+{\varsigma }_{eqj}{\omega }_{eqn,j}{x}_{j0}}{{\omega }_{eqd,j}{x}_{j0}}.$$

(171)

Note that, for ${\omega }_{eqn,j},$ ${\varsigma }_{eqj},$ $A_{eqj},$ and ${\theta }_{eqj},$ each is not constant for fractional oscillators. Instead, each is generally a function of oscillation frequency ω and fractional order.

6.2. Free Response to Fractional Oscillators in Class I

We state the free response to a fractional oscillator in Class I by Theorem 10.

Theorem 10 (Free response I).

Let $x_1(t)$ be the free response to a fractional oscillator in Class I. Then, for 1 < α ≤ 2, $x_1(t)$ is given by

$$x_1(t)=e^{-\frac{\omega \sin \frac{\alpha \pi }{2}}{2\left|\cos \frac{\alpha \pi }{2}\right|}t}\left[\begin{array}{l}{x}_{10}\cos \left(\frac{{\omega }_n}{\sqrt{{\omega }^{\alpha -2}\left|\cos \frac{\alpha \pi }{2}\right|}}\sqrt{1-\frac{{\omega }^{\alpha }{\sin }^2\frac{\alpha \pi }{2}}{4{\omega }_n^2\left|\cos \frac{\alpha \pi }{2}\right|}}t\right)\\ +\frac{v_{10}+\frac{{\omega }^{\frac{\alpha }{2}}\sin \frac{\alpha \pi }{2}}{2{\omega }_n\sqrt{\left|\cos \frac{\alpha \pi }{2}\right|}}{x}_{10}}{\sqrt{1-\frac{{\omega }^{\alpha }{\sin }^2\frac{\alpha \pi }{2}}{4{\omega }_n^2\left|\cos \frac{\alpha \pi }{2}\right|}}}\sin \left(\frac{{\omega }_n}{\sqrt{{\omega }^{\alpha -2}\left|\cos \frac{\alpha \pi }{2}\right|}}\sqrt{1-\frac{{\omega }^{\alpha }{\sin }^2\frac{\alpha \pi }{2}}{4{\omega }_n^2\left|\cos \frac{\alpha \pi }{2}\right|}}t\right)\end{array}\right].$$

(172)

Proof. 

For t ≥ 0, consider

$$x_1(t)=e^{-{\varsigma }_{eq1}{\omega }_{eqn,1}t}\left(x_{10}\cos {\omega }_{eqd,1}t+\frac{v_{10}+{\varsigma }_{eq1}{\omega }_{eqn,1}{x}_{10}}{{\omega }_{eqd,1}}\sin {\omega }_{eqd,1}t\right).$$

(173)

In the above, replacing ${\omega }_{eqn,1}$ by the one in (132), ${\varsigma }_{eq1}$ with that in (141), and ${\omega }_{eqd,1}$ by the one in (154) yields

$$\begin{gathered} x_1(t)=e^{-\frac{{\omega }^{\frac{\alpha }{2}}\sin \frac{\alpha \pi }{2}}{2{\omega }_n\sqrt{\left|\cos \frac{\alpha \pi }{2}\right|}}\frac{{\omega }_n}{\sqrt{{\omega }^{\alpha -2}\left|\cos \frac{\alpha \pi }{2}\right|}}t}\left[\begin{array}{l}{x}_{10}\cos \left(\frac{{\omega }_n\sqrt{1-\frac{{\omega }^{\alpha }{\sin }^2\frac{\alpha \pi }{2}}{4{\omega }_n^2\left|\cos \frac{\alpha \pi }{2}\right|}}}{\sqrt{{\omega }^{\alpha -2}\left|\cos \frac{\alpha \pi }{2}\right|}}t\right)\\ +\frac{v_{10}+\frac{{\omega }^{\frac{\alpha }{2}}\sin \frac{\alpha \pi }{2}}{2{\omega }_n\sqrt{\left|\cos \frac{\alpha \pi }{2}\right|}}\frac{{\omega }_n}{\sqrt{{\omega }^{\alpha -2}\left|\cos \frac{\alpha \pi }{2}\right|}}{x}_{10}}{\frac{{\omega }_n}{\sqrt{{\omega }^{\alpha -2}\left|\cos \frac{\alpha \pi }{2}\right|}}\sqrt{1-\frac{{\omega }^{\alpha }{\sin }^2\frac{\alpha \pi }{2}}{4{\omega }_n^2\left|\cos \frac{\alpha \pi }{2}\right|}}}\sin \left(\frac{{\omega }_n\sqrt{1-\frac{{\omega }^{\alpha }{\sin }^2\frac{\alpha \pi }{2}}{4{\omega }_n^2\left|\cos \frac{\alpha \pi }{2}\right|}}}{\sqrt{{\omega }^{\alpha -2}\left|\cos \frac{\alpha \pi }{2}\right|}}t\right)\end{array}\right] \\ =e^{-\frac{\omega \sin \frac{\alpha \pi }{2}}{2\left|\cos \frac{\alpha \pi }{2}\right|}t}\left[x_{10}\cos \left(\frac{{\omega }_n\sqrt{1-\frac{{\omega }^{\alpha }{\sin }^2\frac{\alpha \pi }{2}}{4{\omega }_n^2\left|\cos \frac{\alpha \pi }{2}\right|}}t}{\sqrt{{\omega }^{\alpha -2}\left|\cos \frac{\alpha \pi }{2}\right|}}\right)+\frac{v_{10}+\frac{{\omega }^{\frac{\alpha }{2}}\sin \frac{\alpha \pi }{2}}{2{\omega }_n\sqrt{\left|\cos \frac{\alpha \pi }{2}\right|}}{x}_{10}}{\sqrt{1-\frac{{\omega }^{\alpha }{\sin }^2\frac{\alpha \pi }{2}}{4{\omega }_n^2\left|\cos \frac{\alpha \pi }{2}\right|}}}\sin \left(\frac{{\omega }_n\sqrt{1-\frac{{\omega }^{\alpha }{\sin }^2\frac{\alpha \pi }{2}}{4{\omega }_n^2\left|\cos \frac{\alpha \pi }{2}\right|}}}{\sqrt{{\omega }^{\alpha -2}\left|\cos \frac{\alpha \pi }{2}\right|}}t\right)\right]. \end{gathered}$$

This completes the proof. □

Figure 20 indicates $x_1(t)$ with fixed ω.

Figure 20. Indicating free response $x_1(t)$ for $x_{10}=v_{10}={\omega }_n$ = 1. (a) α = 1.9. Solid line: ω = 1 (${\varsigma }_{eq1}$ = 0.08). Dot line: ω = 0.7 (${\varsigma }_{eq1}$ = 0.04). (b) α = 1.6. Solid line: ω = 1 (${\varsigma }_{eq1}$ = 0.33). Dot line: ω = 0.7 (${\varsigma }_{eq1}$ = 0.16). (c) α = 1.3. Solid line: ω = 1 (${\varsigma }_{eq1}$ = 0.66). Dot line: ω = 0.7 (${\varsigma }_{eq1}$ = 0.42). (d) α = 2. Solid line: ω = 1 (${\varsigma }_{eq1}$ = 0). Dot line: ω = 0.7 (${\varsigma }_{eq1}$ = 0).

Note 6.1: As indicated in Figure 20, both oscillation frequency ω and the fractional order α have affects on the damping ${\varsigma }_{eq1}(\omega ,\alpha ),$ also see Figure 10. When α = 2, $x_1(t)$ reduces to the free response to the ordinary harmonic oscillation with damping free in the form (also see Figure 20d)

$$x_1(t)=\left(x_{10}\cos {\omega }_{n}t+\frac{v_{10}}{{\omega }_n}\sin {\omega }_{n}t\right),\hspace{1em}t\ge 0.$$

The free response to a fractional oscillator in Class I is presented in (172). It uses elementary functions instead of special functions.

Since there exists infinity of natural frequencies for a fractional oscillator, as we explained in Section 5, $x_1(t)$ is actually a function of both t and ω as can be seen from (172). In Figure 20, plots are only specifically with fixed ω. Its plots with varying ω are viewed by Figure 21.

Figure 21. Illustrating free response $x_1(t)$ with variable ω ( = 0, 0.2, 0.4, ..., 10) for $x_{10}=v_{10}=1.$ (a) For ${\omega }_n$ = 1 and α = 1.9 (0 ≤ ${\varsigma }_{eq1}$ ≤ 0.64). (b) For ${\omega }_n$ = 3 and α = 1.6 (0 ≤ ${\varsigma }_{eq1}$ ≤ 0.63).

When emphasizing the point of time-frequency behavior, we view it in t-ω plane as Figure 22 shows.

Figure 22. Indicating free response $x_1(t)$ in t-ω plane for t = 0, 1, ..., 30 and ω = 1, 2, ..., 5, with $x_{10}=v_{10}=1,$ ${\omega }_n$ = 6. (a) α = 1.9 (0.01 ≤ ${\varsigma }_{eq1}$ ≤ 0.28). (b) α = 1.6 (0.05 ≤ ${\varsigma }_{eq1}$ ≤ 0.72). (c) α = 1.3 (0.11 ≤ ${\varsigma }_{eq1}$ ≤ 0.89). (d) α = 2 (${\varsigma }_{eq1}$ = 0).

Let t_i and t_{i + 1} be two time points where $x_j(t_i)$ reaches its successive peak values of $x_j(t_i)$ and $x_j(t_{i+1}),$ respectively. Let ${\Delta }_{eqj}$ be the logarithmic decrement of $x_j(t_i).$ Then, from (178), we immediately obtain

$${\Delta }_{eqj}=\ln \frac{x_j(t_i)}{x_j(t_{i+1})}=\frac{2\pi {\varsigma }_{eqj}}{\sqrt{1-{\varsigma }_{eqj}^2}}.$$

(174)

Corollary 10 (Decrement I).

Let $x_1(t)$ be the free response of a fractional oscillator in Class I. Then, its logarithmic decrement is given in the form

$${\Delta }_{eq1}=\frac{\pi }{\sqrt{1-{\left(\frac{{\omega }^{\frac{\alpha }{2}}\sin \frac{\alpha \pi }{2}}{2{\omega }_n\sqrt{-\cos \frac{\alpha \pi }{2}}}\right)}^2}}\frac{{\omega }^{\frac{\alpha }{2}}\sin \frac{\alpha \pi }{2}}{{\omega }_n\sqrt{-\cos \frac{\alpha \pi }{2}}},\hspace{1em}1<\alpha \le 2.$$

(175)

Proof. 

According to (174), we have

$${\Delta }_{eq1}=\ln \frac{x_1(t_i)}{x_1(t_{i+1})}=\frac{2\pi {\varsigma }_{eq1}}{\sqrt{1-{\varsigma }_{eq1}^2}}=\frac{\pi }{\sqrt{1-{\left(\frac{{\omega }^{\frac{\alpha }{2}}\sin \frac{\alpha \pi }{2}}{2{\omega }_n\sqrt{-\cos \frac{\alpha \pi }{2}}}\right)}^2}}\frac{{\omega }^{\frac{\alpha }{2}}\sin \frac{\alpha \pi }{2}}{{\omega }_n\sqrt{-\cos \frac{\alpha \pi }{2}}},\hspace{1em}1<\alpha \le 2.$$

The proof finishes. □

Since ${\Delta }_{eq1}$ is a function of ω and α, we may write it with ${\Delta }_{eq1}(\omega ,\alpha ).$ Figure 23 indicates ${\Delta }_{eq1}.$

Figure 23. Plots of ${\Delta }_{eq1}.$ Solid line: α = 1.9. Dot line: α = 1.6. (a) For ${\omega }_n$ = 1. (b) For ${\omega }_n$ = 5. (c) For ${\omega }_n$ = 10.

Note 6.2: ${\Delta }_{eq1}$= 0 for α = 2. As a matter of fact, a fractional oscillator in Class I reduces to a harmonic one if α = 2. Accordingly, ${\Delta }_{eq1}$= 0 in that case.

6.3. Free Response to Fractional Oscillators in Class II

We state the free response to a fractional oscillator in Class II by Theorem 11.

Theorem 11 (Free response II).

Denote by $x_2(t)$ the free response to a fractional oscillator of Class II type. Then, it is, for t ≥ 0 and 1 < β ≤ 2, in the form

$$x_2(t)=e^{-\frac{\varsigma {\omega }_n{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}}{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}t}\left[\begin{array}{l}{x}_{20}\cos \left(\frac{{\omega }_n\sqrt{1-\frac{c^2{\omega }^{2(\beta -1)}{\sin }^2\frac{\beta \pi }{2}}{4\left(m-c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)k}}t}{\sqrt{\left(1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}}\right)\\ +\frac{v_{20}+\frac{c{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}}{2\left(m-c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}{x}_{20}}{{\omega }_n\sqrt{1-\frac{c^2{\omega }^{2(\beta -1)}{\sin }^2\frac{\beta \pi }{2}}{4\left(m-c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)k}}}\\ \sin \left(\frac{{\omega }_n\sqrt{1-\frac{c^2{\omega }^{2(\beta -1)}{\sin }^2\frac{\beta \pi }{2}}{4\left(m-c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)k}}t}{\sqrt{\left(1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}}\right)\end{array}\right].$$

(176)

Proof. 

Note that, for t ≥ 0,

$$x_2(t)=e^{-{\varsigma }_{eq2}{\omega }_{eqn,2}t}\left(x_{20}\cos {\omega }_{eqd,2}t+\frac{v_{20}+{\varsigma }_{eq2}{\omega }_{eqn,2}{x}_{20}}{{\omega }_{eqd,2}}\sin {\omega }_{eqd,2}t\right).$$

(177)

In the above expression, we replace ${\varsigma }_{eq2},$ ${\omega }_{eqd,2},$ and ${\omega }_{eqn,2}$ by those expressed in Section 5. Then, we have (176). Thus, Theorem 11 holds. □

Note 6.3: If β = 1, $x_2(t)$ degenerates to the ordinary free response to an oscillator with the viscous damper c. In fact,

$$\begin{array}{l}{x_2(t)|}_{\beta =1}=e^{-\frac{\varsigma {\omega }_n{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}}{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}t}{\left[\begin{array}{l}{x}_{20}\cos \left(\frac{{\omega }_n\sqrt{1-\frac{c^2{\omega }^{2(\beta -1)}{\sin }^2\frac{\beta \pi }{2}}{4\left(m-c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)k}}t}{\sqrt{\left(1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}}\right)\\ +\frac{v_{20}+\frac{c{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}}{2\left(m-c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}{x}_{20}}{{\omega }_n\sqrt{1-\frac{c^2{\omega }^{2(\beta -1)}{\sin }^2\frac{\beta \pi }{2}}{4\left(m-c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)k}}}\\ \sin \left(\frac{{\omega }_n\sqrt{1-\frac{c^2{\omega }^{2(\beta -1)}{\sin }^2\frac{\beta \pi }{2}}{4\left(m-c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)k}}t}{\sqrt{\left(1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}}\right)\end{array}\right]}_{\beta =1}\\ =e^{-\varsigma {\omega }_{n}t}\left[x_{20}\cos \left({\omega }_n\sqrt{1-\frac{c^2}{4mk}}t\right)+\frac{v_{20}+\frac{c}{2m}{x}_{20}}{{\omega }_n\sqrt{1-\frac{c^2}{4mk}}}\sin \left({\omega }_n\sqrt{1-\frac{c^2}{4mk}}t\right)\right]\\ =e^{-\varsigma {\omega }_{n}t}\left[x_{20}\cos \left({\omega }_n\sqrt{1-{\varsigma }^2}t\right)+\frac{v_{20}+\varsigma {\omega }_n{x}_{20}}{{\omega }_n\sqrt{1-{\varsigma }^2}}\sin \left({\omega }_n\sqrt{1-{\varsigma }^2}t\right)\right].\end{array}$$

Note 6.4: As far as a fractional oscillator in Class II was concerned, its free response in the closed form is rarely reported. Theorem 11 gives it by using elementary functions.

Let m = c = k = $x_{10}=v_{10}=1,$ and ω = 30. We use Figure 24 to illustrate $x_2(t).$

Figure 24. Illustrating free response $x_2(t)$ with fixed ω when m = c = k = $x_{10}=v_{10}=1.$ (a) β = 0.3. Solid line: ω = 30 (${\varsigma }_{eq2}$ = 0.02). Dot line: ω = 10 (${\varsigma }_{eq2}$ = 0.05). (b) β = 0.6. Solid line: ω = 30 (${\varsigma }_{eq2}$ = 0.10). Dot line: ω = 10 (${\varsigma }_{eq2}$ = 0.16). (c) β = 0.9 Solid line: ω = 30 (${\varsigma }_{eq2}$ = 0.35). Dot line: ω = 10 (${\varsigma }_{eq2}$ = 0.40). (d) β = 1. Solid line: ω = 30 (${\varsigma }_{eq2}$ = 0.50). Dot line: ω = 10 (${\varsigma }_{eq2}$ = 0.50).

Similar to $x_1(t),$ $x_2(t)$ is also with the argument ω. Its plots with variable ω are demonstrated in Figure 25. Figure 26 shows its plots in t-ω plane.

Figure 25. Plots of free response $x_2(t)$ with ω (= 1, 2, ..., 5), m = c = k = 1 = $x_{10}=v_{10}=1.$ (a) For β = 0.2 (0.04 ≤ ${\varsigma }_{eq2}$ ≤ 0.70). (b) For β = 0.4 (0.12 ≤ ${\varsigma }_{eq2}$ ≤ 0.67). (c) For β = 0.6 (0.22 ≤ ${\varsigma }_{eq2}$ ≤ 0.63). (d) For β = 0.8 (0.35 ≤ ${\varsigma }_{eq2}$ ≤ 0.57).

Figure 26. Plots of free response $x_2(t)$ in t-ω plane with m = k = $x_{10}=v_{10}=1,$ c = 0.5, for t = 0, 1, ..., 30; ω = 1, 2, ..., 5. (a) β = 0.3 (0.04 ≤ ${\varsigma }_{eq2}$ ≤ 0.15). (b) β = 0.6 (0.11 ≤ ${\varsigma }_{eq2}$ ≤ 0.24). (c) β = 0.9 (0.21 ≤ ${\varsigma }_{eq2}$ ≤ 0.26). (d) β = 1 (${\varsigma }_{eq2}$ = 0.25).

Corollary 11 (Decrement II).

Denote by $x_2(t)$ the free response to a fractional oscillator in Class II. Then, for 0 < β ≤ 1, its logarithmic decrement ${\Delta }_{eq2},$ is in the form

$${\Delta }_{eq2}=\frac{2\pi }{\sqrt{1-{\left(\frac{\varsigma {\omega }^{\beta -1}\sin \frac{\beta \pi }{2}}{\sqrt{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}}\right)}^2}}\frac{\varsigma {\omega }^{\beta -1}\sin \frac{\beta \pi }{2}}{\sqrt{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}}.$$

(178)

Proof. 

According to (174), we have

$${\Delta }_{eq2}=\ln \frac{x_2(t_i)}{x_2(t_{i+1})}=\frac{2\pi {\varsigma }_{eq2}}{\sqrt{1-{\varsigma }_{eq2}^2}}.$$

(179)

Replacing the above ${\varsigma }_{eq2}$ with that in (145) produces

$${\Delta }_{eq2}=\frac{2\pi {\varsigma }_{eq2}}{\sqrt{1-{\varsigma }_{eq2}^2}}=\frac{2\pi }{\sqrt{1-{\left(\frac{\varsigma {\omega }^{\beta -1}\sin \frac{\beta \pi }{2}}{\sqrt{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}}\right)}^2}}\frac{\varsigma {\omega }^{\beta -1}\sin \frac{\beta \pi }{2}}{\sqrt{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}}.$$

This finishes the proof. □

Similar to ${\Delta }_{eq1},$ we may write ${\Delta }_{eq2}$ with ${\Delta }_{eq2}(\omega ,\beta ).$ Figure 27 indicates its plots.

Figure 27. Logarithmic decrement ${\Delta }_{eq2}$ of fractional oscillator in Class II for m = c = 1. Solid line: β = 0.9. Dot line: β = 0.6. (a) For ${\omega }_n$ = 1. (b) For ${\omega }_n$ = 5. (c) For ${\omega }_n$ = 10.

Note 6.5: ${\Delta }_{eq2}$ reduces to the conventional logarithmic decrement if β = 1, because

$${{\Delta }_{eq2}|}_{\beta =1}={\left[\frac{\frac{2\pi \varsigma {\omega }^{\beta -1}\sin \frac{\beta \pi }{2}}{\sqrt{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}}}{\sqrt{1-{\left(\frac{\varsigma {\omega }^{\beta -1}\sin \frac{\beta \pi }{2}}{\sqrt{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}}\right)}^2}}\right]}_{{}_{\beta =1}}=\frac{2\pi \varsigma }{\sqrt{1-{\varsigma }^2}}.$$

(180)

6.4. Free Response to Fractional Oscillators in Class III

We now present the free response to a fractional oscillator in Class III by Theorem 12.

Theorem 12 (Free response III).

Let $x_3(t)$ be the free response to a fractional oscillator in Class III. Then, for t ≥ 0, 1< α ≤ 2, 0 < β ≤ 1, it is given by

$$x_3(t)=e^{-\frac{m{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+c{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}}{2\left(m{\omega }^{\alpha -2}\left|\cos \frac{\alpha \pi }{2}\right|-c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}t}\left[\begin{array}{l}{x}_{30}\cos \left(\frac{{\omega }_n\sqrt{1-\frac{{\left(m{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+c{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}\right)}^2}{4\left[-\left(m{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)k\right]}}t}{\sqrt{-\left({\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}}\right)\\ +\left\{\frac{v_{30}+\frac{m{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+c{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}}{2\left(m{\omega }^{\alpha -2}\left|\cos \frac{\alpha \pi }{2}\right|-c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}{x}_{30}}{\left\{\begin{array}{l}\frac{{\omega }_n}{\sqrt{\left({\omega }^{\alpha -2}\left|\cos \frac{\alpha \pi }{2}\right|-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}}\\ \sqrt{1-\frac{{\left(m{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+c{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}\right)}^2}{4\left[-\left(m{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)k\right]}}\end{array}\right\}}\right\}\\ \sin \left(\frac{{\omega }_n\sqrt{1-\frac{{\left(m{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+c{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}\right)}^2}{4\left[-\left(m{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)k\right]}}t}{\sqrt{-\left({\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}}\right)\end{array}\right].$$

(181)

Proof. 

Note that, for t ≥ 0,

$$x_3(t)=e^{-{\varsigma }_{eq3}{\omega }_{eqn,3}t}\left(x_{30}\cos {\omega }_{eqd,3}t+\frac{v_{30}+{\varsigma }_{eq3}{\omega }_{eqn,3}{x}_{30}}{{\omega }_{eqd,3}}\sin {\omega }_{eqd,3}t\right).$$

(182)

In (182), when substituting ${\varsigma }_{eq3},$ ω_eqd,3, and ω_eqn,3 with those explained in Section 5, we have (181). The proof finishes. □

Note 6.6: If (α, β) = (2, 1), $x_3(t)$ returns to be the free response to an ordinary oscillator with the viscous damping. As a matter of fact,

$${x_3(t)|}_{\alpha =2,\beta =1}=e^{-\varsigma {\omega }_{n}t}\left(x_{30}\cos {\omega }_{d}t+\frac{v_{30}+\varsigma {\omega }_n{x}_{30}}{{\omega }_d}\sin {\omega }_{d}t\right),$$

(183)

where ${\omega }_d={\omega }_n\sqrt{1-{\varsigma }^2}.$

Figure 28 indicates $x_3(t)$ for m = c = k = $x_{10}=v_{10}=1.$

Figure 28. Plots of free response $x_3(t)$ for m = c = k = $x_{10}=v_{10}=1.$ Solid line: ω = 1.1. Dot line: ω = 1.5. (a) α = 1.8, β = 0.8 (${\varsigma }_{eq3}$ = 0.78). (b) α = 1.5, β = 0.8 (${\varsigma }_{eq3}$ = 1.33). (c) α = 1.8, β = 0.3 (${\varsigma }_{eq3}$ = 0.91). (d) α = 2, β = 1 (${\varsigma }_{eq3}$ = 0.50).

Note that the plots regarding with $x_3(t)$ in Figure 28 are with fixed ω. However, actual $x_3(t)$ is frequency varying. Figure 29 shows its frequency varying pictures in time domain and Figure 30 in t-ω plane.

Figure 29. Free response $x_3(t)$ with variable ω (=1, 2, ..., 10) for m = c = k = 1. (a) α = 1.9, β = 0.8 (${\varsigma }_{eq3}$ = 0.66). (b) α = 1.5, β = 0.8 (${\varsigma }_{eq3}$ = 1.33). (c) α = 1.8, β = 0.3 (${\varsigma }_{eq3}$ = 0.91). (d) α = 2, β = 1 (${\varsigma }_{eq3}$ = 0.50).

Figure 30. Free response $x_3(t)$ in t-ω plane with m = k = $x_{10}=v_{10}=1$ and c = 0.1 for t = 0, 1, ..., 30; ω = 1, 2, ..., 5. (a) α = 1.8, β = 0.8 (0.21 ≤ ${\varsigma }_{eq3}$ ≤ 0.72). (b) α = 1.8, β = 0.5 (0.20 ≤ ${\varsigma }_{eq3}$ ≤ 0.70). (c) α = 1.5, β = 0.8 (0.49 ≤ ${\varsigma }_{eq3}$ ≤ 1.49). (d) α = 2, β = 1 (${\varsigma }_{eq3}$ = 0.05).

Corollary 12 (Decrement III).

Denote by $x_3(t)$ the free response to a fractional oscillator in Class III. Then, for 1 < α ≤ 2 and 0 < β ≤ 1, its logarithmic decrement, denoted by ${\Delta }_{eq3},$ is given by

$${\Delta }_{eq3}=\frac{\frac{\pi \left({\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+2\varsigma {\omega }_n{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}\right)}{{\omega }_n\sqrt{-\left({\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+2\varsigma {\omega }_n{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}}}{\sqrt{1-{\left(\frac{{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+2\varsigma {\omega }_n{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}}{2{\omega }_n\sqrt{-\left({\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+2\varsigma {\omega }_n{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}}\right)}^2}}.$$

(184)

Proof. 

Note that

$${\Delta }_{eq3}=\ln \frac{x_3(t_i)}{x_3(t_{i+1})}=\frac{2\pi {\varsigma }_{eq3}}{\sqrt{1-{\varsigma }_{eq3}^2}}.$$

(185)

Replacing the above ${\varsigma }_{eq3}$ with that in (147) yields (184). This completes the proof. □

When α = 2 and β = 1, ${\Delta }_{eq3}={\Delta }_{eq3}(\omega ,\alpha ,\beta )$ becomes the conventional logarithmic decrement. In fact,

$${{\Delta }_{eq3}|}_{\alpha =1,\beta =1}={\frac{\frac{\pi \left({\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+2\varsigma {\omega }_n{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}\right)}{{\omega }_n\sqrt{-\left({\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+2\varsigma {\omega }_n{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}}}{\sqrt{1-{\left(\frac{{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+2\varsigma {\omega }_n{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}}{2{\omega }_n\sqrt{-\left({\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+2\varsigma {\omega }_n{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}}\right)}^2}}|}_{\alpha =1,\beta =1}=\frac{2\pi \varsigma }{\sqrt{1-{\varsigma }^2}}.$$

(186)

As ${\Delta }_{eq3}$ is a function of ω and (α, β), we write it by ${\Delta }_{eq3}(\omega ,\alpha ,\beta ).$ Figure 31 and Figure 32 show its plots.

Figure 31. ${\Delta }_{eq3}(\omega ,\alpha ,\beta ):$ Logarithmic decrement of fractional oscillator in Class III for m = c = k = 1. (a) Solid line: α = 1.7, β = 0.8. Dot line: α = 1.7, β = 0.5. (b) Solid line: α = 1.8, β = 0.8. Dot line: α = 1.8, β = 0.5.

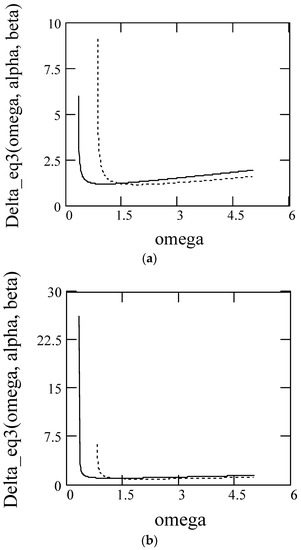
Figure 32. ${\Delta }_{eq3}(\omega ,\alpha ,\beta )$ for m = c = 1, k = 25. (a) Solid line: α = 1.7, β = 0.8. Dot line: α = 1.7, β = 0.5. (b) Solid line: α = 1.8, β = 0.8. Dot line: α = 1.8, β = 0.5.

6.5. Application to Representing Generalized Mittag-Leffler Function (1)

The previous research (Mainardi [25], Achar et al. [33], Uchaikin ([38], Chapter 7)) presented the free response to fractional oscillators of Class I type by using a kind of special function, called the generalized Mittag-Leffler function, see (32). The novelty of our result presented in Theorem 10 is in that Equation (172) or (173) is consistent with the representation style in engineering by using elementary functions. Thus, we obtain novel representations of the generalized Mittag-Leffler functions as follows.

Corollary 13.

The generalized Mittag-Leffler function in the form

$$x_1(t)=x_{10}{E}_{\alpha ,1}\left[-{\left({\omega }_{n}t\right)}^{\alpha }\right]+v_{10}t{E}_{\alpha ,2}\left[-{\left({\omega }_{n}t\right)}^{\alpha }\right],\hspace{1em}1<\alpha \le 2,t\ge 0,$$

(187)

is the solution to fractional oscillators in Class I (Mainardi [25], Achar et al. [33], Uchaikin ([38], Chapter 7)). It can be expressed by the one in (172). That is, for 1 < α ≤ 2, t ≥ 0,

$$\begin{array}{l}{x}_1(t)=x_{10}{E}_{\alpha ,1}\left[-{\left({\omega }_{n}t\right)}^{\alpha }\right]+v_{10}t{E}_{\alpha ,2}\left[-{\left({\omega }_{n}t\right)}^{\alpha }\right]\\ =e^{-\frac{\omega \sin \frac{\alpha \pi }{2}}{2\left|\cos \frac{\alpha \pi }{2}\right|}t}\left[\begin{array}{l}{x}_{10}\cos \left(\frac{{\omega }_n\sqrt{1-\frac{{\omega }^{\alpha }{\sin }^2\frac{\alpha \pi }{2}}{4{\omega }_n^2\left|\cos \frac{\alpha \pi }{2}\right|}}t}{\sqrt{{\omega }^{\alpha -2}\left|\cos \frac{\alpha \pi }{2}\right|}}\right)\\ +\left[\frac{v_{10}+\frac{{\omega }^{\frac{\alpha }{2}}\sin \frac{\alpha \pi }{2}}{2{\omega }_n\sqrt{\left|\cos \frac{\alpha \pi }{2}\right|}}{x}_{10}}{\sqrt{1-\frac{{\omega }^{\alpha }{\sin }^2\frac{\alpha \pi }{2}}{4{\omega }_n^2\left|\cos \frac{\alpha \pi }{2}\right|}}}\right]\sin \left(\frac{{\omega }_n\sqrt{1-\frac{{\omega }^{\alpha }{\sin }^2\frac{\alpha \pi }{2}}{4{\omega }_n^2\left|\cos \frac{\alpha \pi }{2}\right|}}t}{\sqrt{{\omega }^{\alpha -2}\left|\cos \frac{\alpha \pi }{2}\right|}}\right)\end{array}\right].\end{array}$$

(188)

The proof of Corollary 13 is straightforward from (172).

When $v_{10}$= 0 in (187), we obtain a corollary below.

Corollary 14.

The generalized Mittag-Leffler function given by

$$x_1(t)=x_{10}{E}_{\alpha ,1}\left[-{\left({\omega }_{n}t\right)}^{\alpha }\right],\hspace{1em}1<\alpha \le 2,t\ge 0,$$

(189)

can be expressed by the elementary functions, for 1 < α ≤ 2, t ≥ 0, in the form

$$x_1(t)=x_{10}{E}_{\alpha ,1}\left[-{\left({\omega }_{n}t\right)}^{\alpha }\right]=e^{-\frac{\omega \sin \frac{\alpha \pi }{2}}{2\left|\cos \frac{\alpha \pi }{2}\right|}t}\left[\begin{array}{l}{x}_{10}\cos \left(\frac{{\omega }_n}{\sqrt{{\omega }^{\alpha -2}\left|\cos \frac{\alpha \pi }{2}\right|}}\sqrt{1-\frac{{\omega }^{\alpha }{\sin }^2\frac{\alpha \pi }{2}}{4{\omega }_n^2\left|\cos \frac{\alpha \pi }{2}\right|}}t\right)\\ +\left(\frac{\frac{{\omega }^{\frac{\alpha }{2}}\sin \frac{\alpha \pi }{2}}{2{\omega }_n\sqrt{\left|\cos \frac{\alpha \pi }{2}\right|}}{x}_{10}}{\sqrt{1-\frac{{\omega }^{\alpha }{\sin }^2\frac{\alpha \pi }{2}}{4{\omega }_n^2\left|\cos \frac{\alpha \pi }{2}\right|}}}\right)\sin \left(\frac{{\omega }_n\sqrt{1-\frac{{\omega }^{\alpha }{\sin }^2\frac{\alpha \pi }{2}}{4{\omega }_n^2\left|\cos \frac{\alpha \pi }{2}\right|}}t}{\sqrt{{\omega }^{\alpha -2}\left|\cos \frac{\alpha \pi }{2}\right|}}\right)\end{array}\right].$$

(190)

Proof. 

If $v_{10}$ = 0 in (187), (188) becomes (189). The proof completes. □

If $x_{10}$= 0 in (187), we obtain another corollary as follows.

Corollary 15.

The generalized Mittag-Leffler function expressed by

$$x_1(t)=v_{10}t{E}_{\alpha ,2}\left[-{\left({\omega }_{n}t\right)}^{\alpha }\right],\hspace{1em}1<\alpha \le 2,t\ge 0,$$

(191)

can be represented, for 1 < α ≤ 2, t ≥ 0, by the elementary functions in the form

$$x_1(t)=v_{10}t{E}_{\alpha ,2}\left[-{\left({\omega }_{n}t\right)}^{\alpha }\right]=e^{-\frac{\omega \sin \frac{\alpha \pi }{2}}{2\left|\cos \frac{\alpha \pi }{2}\right|}t}\left[\left(\frac{v_{10}}{\sqrt{1-\frac{{\omega }^{\alpha }{\sin }^2\frac{\alpha \pi }{2}}{4{\omega }_n^2\left|\cos \frac{\alpha \pi }{2}\right|}}}\right)\sin \left(\frac{{\omega }_n\sqrt{1-\frac{{\omega }^{\alpha }{\sin }^2\frac{\alpha \pi }{2}}{4{\omega }_n^2\left|\cos \frac{\alpha \pi }{2}\right|}}}{\sqrt{{\omega }^{\alpha -2}\left|\cos \frac{\alpha \pi }{2}\right|}}t\right)\right].$$

(192)

Proof. 

When $x_{10}$ = 0 in (187), (188) becomes (192). The proof finishes. □

7. Impulse Responses to Three Classes of Fractional Oscillators

In this section, we shall present the impulse responses to three classes of fractional oscillators using elementary functions.

In Section 4, we have proved that

$$H_{yj}(\omega )=H_{xj}(\omega ),j=1,2,3,$$

where $H_{yj}(\omega )$ is the frequency response function solved directly from a jth fractional oscillator while $H_{xj}(\omega )$ is the one derived from its equivalent oscillator. Doing the inverse Fourier transform on the both sides above, therefore, we have

$$h_{yj}(t)=h_{xj}(t),j=1,2,3,$$

where $h_{yj}(t)$ is the impulse response obtained directly from the jth fractional oscillator but $h_{xj}(t)$ is the one solved from its equivalent one. In that way, therefore, we may establish the theoretic foundation for representing the impulse responses to three classes of fractional oscillators by using elementary functions.

The main highlight presented in this section is to propose the impulse responses to three classes of fractional oscillators in the closed analytic form expressed by elementary functions. As a by product, we shall represent a certain generalized Mittag-Leffler functions using elementary functions.

7.1. General Form of Impulse Responses

Given a following functional form of equivalent oscillators for finding their impulse responses, we denote by $h_j(t)$ the impulse response to the equivalent oscillator in Class j in the form

$$m_{eqj}\frac{d^2{h}_j(t)}{d{t}^2}+c_{eqj}\frac{d{h}_j(t)}{dt}+k{h}_j(t)=\delta (t),\hspace{1em}j=1,2,3.$$

(193)

Rewrite the above in the form

$$\frac{d^2{h}_j(t)}{d{t}^2}+\frac{c_{eqj}}{m_{eqj}}\frac{d{h}_j(t)}{dt}+\frac{k}{m_{eqj}}{h}_j(t)=\frac{\delta (t)}{m_{eqj}},\hspace{1em}j=1,2,3.$$

(194)

According to the results in the previous sections, we have

$$\frac{d^2{h}_j(t)}{d{t}^2}+2{\varsigma }_{eqj}{\omega }_{eqn,j}\frac{d{h}_j(t)}{dt}+{\omega }_{eqn,j}^2{h}_j(t)=\frac{\delta (t)}{m_{eqj}},\hspace{1em}j=1,2,3.$$

(195)

Therefore, functionally, we have

$$h_j(t)=\frac{e^{-{\varsigma }_{eqj}{\omega }_{eqn,j}t}}{m_{eqj}{\omega }_{eqd,j}}\sin {\omega }_{eqd,j}t,\hspace{1em}t\ge 0.$$

(196)

Equation (196) is a general form of the impulse response to fractional oscillators for Class j (j = 1, 2, 3). Its specific form for each Class is discussed as follows.

7.2. Impulse Response to Fractional Oscillators in Class I

Theorem 13 (Impulse response I).

Let $h_1(t)$ be the impulse response to a fractional oscillator in Class I. Then, for t ≥ 0 and 1 < α ≤ 2, we have

$$h_1(t)=\frac{e^{-\frac{\omega \sin \frac{\alpha \pi }{2}}{2\left|\cos \frac{\alpha \pi }{2}\right|}t}\sin \left(\frac{{\omega }_n}{\sqrt{{\omega }^{\alpha -2}\left|\cos \frac{\alpha \pi }{2}\right|}}\sqrt{1-\frac{{\omega }^{2\alpha }{\sin }^2\frac{\alpha \pi }{2}}{4{\omega }_n^2\left|\cos \frac{\alpha \pi }{2}\right|}}t\right)}{m{\omega }_n\sqrt{{\omega }^{\alpha -2}\left|\cos \frac{\alpha \pi }{2}\right|}\sqrt{1-\frac{{\omega }^{2\alpha }{\sin }^2\frac{\alpha \pi }{2}}{4{\omega }_n^2\left|\cos \frac{\alpha \pi }{2}\right|}}}.$$

(197)

Proof. 

From (196), we have

$$h_1(t)=\frac{e^{-{\varsigma }_{eq1}{\omega }_{eqn,1}t}}{m_{eq1}{\omega }_{eqd,1}}\sin {\omega }_{eqd,1}t,\hspace{1em}t\ge 0.$$

(198)

When replacing $m_{eq1}$ by that in Section 4, ${\varsigma }_{eq1}$ and ${\omega }_{eqd,1}$ as well as ${\omega }_{eqn,1}$ with those in Section 5, respectively, we obtain

$$\begin{array}{l}{h}_1(t)=\frac{e^{-{\varsigma }_{eq1}{\omega }_{eqn,1}t}}{m_{eq1}{\omega }_{eqd,1}}\sin {\omega }_{eqd,1}t=\frac{e^{-\frac{{\omega }^{\frac{\alpha }{2}}\sin \frac{\alpha \pi }{2}}{2{\omega }_n\sqrt{\left|\cos \frac{\alpha \pi }{2}\right|}}\frac{{\omega }_n}{\sqrt{{\omega }^{\alpha -2}\left|\cos \frac{\alpha \pi }{2}\right|}}t}\sin \frac{{\omega }_n\sqrt{1-\frac{{\omega }^{2\alpha }{\sin }^2\frac{\alpha \pi }{2}}{4{\omega }_n^2\left|\cos \frac{\alpha \pi }{2}\right|}}t}{\sqrt{{\omega }^{\alpha -2}\left|\cos \frac{\alpha \pi }{2}\right|}}}{{\omega }^{\alpha -2}\left|\cos \frac{\alpha \pi }{2}\right|m\frac{{\omega }_n}{\sqrt{{\omega }^{\alpha -2}\left|\cos \frac{\alpha \pi }{2}\right|}}\sqrt{1-\frac{{\omega }^{2\alpha }{\sin }^2\frac{\alpha \pi }{2}}{4{\omega }_n^2\left|\cos \frac{\alpha \pi }{2}\right|}}}\\ =\frac{e^{-\frac{\omega \sin \frac{\alpha \pi }{2}}{2\left|\cos \frac{\alpha \pi }{2}\right|}t\sin \frac{{\omega }_n\sqrt{1-\frac{{\omega }^{2\alpha }{\sin }^2\frac{\alpha \pi }{2}}{4{\omega }_n^2\left|\cos \frac{\alpha \pi }{2}\right|}}t}{\sqrt{{\omega }^{\alpha -2}\left|\cos \frac{\alpha \pi }{2}\right|}}}}{m{\omega }_n\sqrt{{\omega }^{\alpha -2}\left|\cos \frac{\alpha \pi }{2}\right|}\sqrt{1-\frac{{\omega }^{2\alpha }{\sin }^2\frac{\alpha \pi }{2}}{4{\omega }_n^2\left|\cos \frac{\alpha \pi }{2}\right|}}}.\end{array}$$

This finishes the proof. □

Figure 33 shows the plots of h₁(t), where the oscillation frequency ω is fixed. Note that ω is an argument of h₁(t). Therefore, its pictures in time domain are indicated in Figure 34. Figure 35 indicates its figures in t-ω plane.

Figure 33. Plots of impulse response $h_1(t)$ with ${\omega }_n$ = 1. (a) α = 1.9, solid line: ω = 1 (${\varsigma }_{eq1}$ = 0.08); dot line: ω = 0.7 (${\varsigma }_{eq1}$ = 0.04). (b) α = 1.6, solid line: ω = 1 (${\varsigma }_{eq1}$ = 0.33); dot line: ω = 0.7 (${\varsigma }_{eq1}$ = 0.19). (c) α = 1.3, solid line: ω = 1 (${\varsigma }_{eq1}$ = 0.66); dot line: ω = 0.7 (${\varsigma }_{eq1}$ = 0.42). (d) α = 2, solid line: ω = 1 (${\varsigma }_{eq1}$ = 0); dot line: ω = 0.7 (${\varsigma }_{eq1}$ = 0).

Figure 34. Plots of impulse response $h_1(t)$ for ${\omega }_n$ = 5, ω = 0, 1, ..., 5. (a) For α = 1.8 (0 ≤ ${\varsigma }_{eq1}$ ≤ 0.57). (b) For α = 1.5 (0 ≤ ${\varsigma }_{eq1}$ ≤ 0.94). (c) For α = 1.3 (0 ≤ ${\varsigma }_{eq1}$ ≤ 1.07). (d) For α = 2 (${\varsigma }_{eq1}$ = 0).

Figure 35. Impulse response $h_1(t)$ in t-ω plane with m = 1, ${\omega }_n$ = 0.3 for t = 0, 1, ..., 30; ω = 1, 2, ..., 5. (a) α = 1.9 (0.26 ≤ ${\varsigma }_{eq1}$ ≤ 5.58). (b) α = 2 (${\varsigma }_{eq1}$ = 0).

Note 7.1: The impulse response $h_1(t)$ reduces to the conventional one if α = 2. In fact,

$${h_1(t)|}_{\alpha =2}={\left(\frac{e^{-\frac{\omega \sin \frac{\alpha \pi }{2}}{2\left|\cos \frac{\alpha \pi }{2}\right|}t}\sin \frac{{\omega }_n}{\sqrt{{\omega }^{\alpha -2}\left|\cos \frac{\alpha \pi }{2}\right|}}\sqrt{1-\frac{{\omega }^{2\alpha }{\sin }^2\frac{\alpha \pi }{2}}{4{\omega }_n^2\left|\cos \frac{\alpha \pi }{2}\right|}}t}{m{\omega }_n\sqrt{{\omega }^{\alpha -2}\left|\cos \frac{\alpha \pi }{2}\right|}\sqrt{1-\frac{{\omega }^{2\alpha }{\sin }^2\frac{\alpha \pi }{2}}{4{\omega }_n^2\left|\cos \frac{\alpha \pi }{2}\right|}}}\right)}_{\alpha =2}=\frac{1}{m{\omega }_n}\sin {\omega }_{n}t.$$

(199)

7.3. Impulse Response to Fractional Oscillators in Class II

Theorem 14 (Impulse response II).

Denote by $h_2(t)$ the impulse response to a fractional oscillator in Class II. For t ≥ 0 and 1 < β ≤ 2, therefore, it is given by

$$h_2(t)=\frac{e^{-\frac{\varsigma {\omega }_n{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}}{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}t}\sin \frac{{\omega }_n\sqrt{1-\frac{{\varsigma }^2{\omega }^{2(\beta -1)}{\sin }^2\frac{\beta \pi }{2}}{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}}}{\sqrt{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}}t}{{\omega }_{n}m\sqrt{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}\sqrt{1-\frac{{\varsigma }^2{\omega }^{2(\beta -1)}{\sin }^2\frac{\beta \pi }{2}}{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}}}.$$

(200)

Proof. 

From (196), we have

$$h_2(t)=e^{-{\varsigma }_{eq2}{\omega }_{eqn,2}t}\frac{1}{m_{eq2}{\omega }_{eqd,2}}\sin {\omega }_{eqd,2}t,\hspace{1em}t\ge 0.$$

(201)

By replacing $m_{eq2}$ with that in Section 4, ${\varsigma }_{eq2},$ ${\omega }_{eqn,2},$ and ${\omega }_{eqd,2}$ by those in Section 5, we obtain

$$\begin{array}{l}{h}_2(t)=\frac{e^{-{\varsigma }_{eq2}{\omega }_{eqn,2}t}\sin {\omega }_{eqd,2}t}{m_{eq2}{\omega }_{eqd,2}}=\frac{e^{-\frac{\varsigma {\omega }^{\beta -1}\sin \frac{\beta \pi }{2}}{\sqrt{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}}\frac{{\omega }_n}{\sqrt{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}}t}\sin {\omega }_{eqd,2}t}{\left(m-c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right){\omega }_{eqd,2}}\\ =e^{-\frac{\varsigma {\omega }_n{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}}{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}t}\frac{\sin \frac{{\omega }_n\sqrt{1-\frac{{\varsigma }^2{\omega }^{2(\beta -1)}{\sin }^2\frac{\beta \pi }{2}}{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}}}{\sqrt{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}}t}{\frac{\left(m-c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right){\omega }_n}{\sqrt{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}}\sqrt{1-\frac{{\varsigma }^2{\omega }^{2(\beta -1)}{\sin }^2\frac{\beta \pi }{2}}{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}}}\\ =e^{-\frac{\varsigma {\omega }_n{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}}{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}t}\frac{\sin \frac{{\omega }_n}{\sqrt{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}}\sqrt{1-\frac{{\varsigma }^2{\omega }^{2(\beta -1)}{\sin }^2\frac{\beta \pi }{2}}{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}}t}{{\omega }_{n}m\sqrt{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}\sqrt{1-\frac{{\varsigma }^2{\omega }^{2(\beta -1)}{\sin }^2\frac{\beta \pi }{2}}{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}}}.\end{array}$$

This is (200). Hence, the proof completes. □

Figure 36 illustrates $h_2(t)$ with fixed ω. Its plots with variable ω are shown in Figure 37. Its pictures in t-ω plane are indicated in Figure 38.

Figure 36. Illustrating impulse response $h_2(t)$ for m = c = k = 1. Solid line: ω = 30. Dot line: ω = 10. (a) β = 0.3, solid line: ω = 30 (${\varsigma }_{eq2}$ = 0.02); dot line: ω = 10 (${\varsigma }_{eq2}$ = 0.05). (b) β = 0.6, solid line: ω = 30 (${\varsigma }_{eq2}$ = 0.10); dot line: ω = 10 (${\varsigma }_{eq2}$ = 0.16). (c) β = 0.9, solid line: ω = 30 (${\varsigma }_{eq2}$ = 0.35); dot line: ω = 10 (${\varsigma }_{eq2}$ = 0.40). (d) β = 1, solid line: ω = 30 (${\varsigma }_{eq2}$ = 0.50); dot line: ω = 10 (${\varsigma }_{eq2}$ = 0.50).

Figure 37. Plots of impulse response $h_2(t)$ with variable ω for m = c = k = 1 in time domain. (a) For β = 0.63, ω = 1, 2, ..., 5 (0.24 ≤ ${\varsigma }_{eq2}$ ≤ 0.62). (b) For β = 0.63, ω = 1, 2, ..., 10 (0.18 ≤ ${\varsigma }_{eq2}$ ≤ 0.62). (c) For β = 0.83, ω = 1, 2, ..., 5 (0.37 ≤ ${\varsigma }_{eq2}$ ≤ 0.56). (d) For β = 0.83, ω = 1, 2, ..., 10 (0.33 ≤ ${\varsigma }_{eq2}$ ≤ 0.56).

Figure 38. Illustrating impulse response $h_2(t)$ in t-ω plane for m = c = k = 1 with t = 0, 1, ..., 50; ω = 1, 2, ..., 5. (a) β = 0.3 (0.08 ≤ ${\varsigma }_{eq2}$ ≤ 0.69). (b) β = 0.6 (0.22 ≤ ${\varsigma }_{eq2}$ ≤ 0.63). (c) β = 0.9 (0.43 ≤ ${\varsigma }_{eq2}$ ≤ 0.54). (d) β = 1 (${\varsigma }_{eq2}$ = 0.50).

Note 7.2: The impulse response $h_2(t)$ reduces to the conventional one if β = 1. As a matter of fact,

$$\begin{array}{l}{h_2(t)|}_{\beta =1}={\left[\frac{e^{-\frac{\varsigma {\omega }_n{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}}{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}t}\sin {\omega }_n\sqrt{1-\frac{{\varsigma }^2{\omega }^{2(\beta -1)}{\sin }^2\frac{\beta \pi }{2}}{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}}t}{{\omega }_{n}m\sqrt{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}\sqrt{1-\frac{{\varsigma }^2{\omega }^{2(\beta -1)}{\sin }^2\frac{\beta \pi }{2}}{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}}}\right]}_{\beta =1}\\ =\frac{e^{-\varsigma {\omega }_{n}t}}{m{\omega }_n\sqrt{1-{\varsigma }^2}}\sin {\omega }_n\sqrt{1-{\varsigma }^2}t.\end{array}$$

(202)

7.4. Impulse Response to Fractional Oscillators in Class III

We present the impulse response to fractional oscillators in Class III with Theorem 15.

Theorem 15 (Impulse response III).

Let $h_3(t)$ be the impulse response to a fractional oscillator in Class III. For t ≥ 0, 1 < α ≤ 2, 0 < β ≤ 1, it is in the form

$$h_3(t)=\frac{e^{-\frac{m{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+c{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}}{2\sqrt{-\left(m{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)k}}{\omega }_{eqn,3}t}\sin {\omega }_{eqd,3}t}{-\left(m{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right){\omega }_{eqd,3}},$$

(203)

where

$${\omega }_{eqn,3}=\frac{{\omega }_n}{\sqrt{-\left({\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}},$$

and

$${\omega }_{eqd,3}=\frac{{\omega }_n\sqrt{1-\frac{{\left(m{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+c{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}\right)}^2}{4\left[-\left(m{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)k\right]}}}{\sqrt{-\left({\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}}.$$

Proof. 

With (196), we get

$$h_3(t)=e^{-{\varsigma }_{eq3}{\omega }_{eqn,3}t}\frac{1}{m_{eq3}{\omega }_{eqd,3}}\sin {\omega }_{eqd,3}t,\hspace{1em}t\ge 0.$$

(204)

In the above expression, substitute $m_{eq3}$ with the one in Section 4, ${\varsigma }_{eq3},$ ${\omega }_{eqd,3},{\omega }_{eqn,3}$ by those in Section 5, respectively, we have, for t ≥ 0,

$$h_3(t)=\frac{e^{-\frac{m{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+c{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}}{2\sqrt{-\left(m{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)k}}{\omega }_{eqn,3}t}\sin {\omega }_{eqd,3}t}{-\left(m{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right){\omega }_{eqd,3}}.$$

The right side on the above is (203). Thus, the proof completes. □

The plots of $h_3(t)$ with fixed ω are shown in Figure 39, with variable ω in Figure 40, and in t-ω plane by Figure 41.

Figure 39. Impulse response $h_3(t)$ for m = c = 1, k = 25 (${\omega }_n$ = 5). (a) (α, β) = (1.8, 0.3), solid line: ω = 2 (${\varsigma }_{eq3}$ = 0.03); dot line: ω = 1 (${\varsigma }_{eq3}$ = 0.02). (b) (α, β) = (1.5, 0.8), solid line: ω = 2 (${\varsigma }_{eq3}$ = 0.20); dot line: ω = 1 (${\varsigma }_{eq3}$ = 0.10). (c) (α, β) = (1.8, 0.5), solid line: ω = 2 (${\varsigma }_{eq3}$ = 0.05); dot line: ω = 1 (${\varsigma }_{eq3}$ = 0.02). (d) (α, β) = (2, 1), solid line: ω = 2 (${\varsigma }_{eq3}$ = 0); dot line: ω = 1 (${\varsigma }_{eq3}$ = 0).

Figure 40. Impulse response $h_3(t)$ to a fractional oscillator in Class III for m = c = 1, k = 25 (${\omega }_n$ = 5). (a) (α, β) = (1.8, 0.8), ω = 1, 2, ..., 5 (0.09 ≤ ${\varsigma }_{eq3}$ ≤ 0.45). (b) (α, β) = (1.5, 0.8), ω = 1, 2, ..., 5 (0.09 ≤ ${\varsigma }_{eq3}$ ≤ 0.20). (c) (α, β) = (1.3, 0.8), ω = 1, 2, ..., 5 (0.48 ≤ ${\varsigma }_{eq3}$ ≤ 0.67).

Figure 41. Impulse response to a fractional oscillator in Class III in t-ω plane for m = c = 1, k = 25 (${\omega }_n$= 5) with t = 0, 1, ..., 30; ω = 1, 2, ..., 5. (a) α = 1.8, β = 0.8 (0.09 ≤ ${\varsigma }_{eq3}$ ≤ 0.45). (b) α = 1.8, β = 0.4 (0.07 ≤ ${\varsigma }_{eq3}$ ≤ 0.15). (c) α = 1.5, β = 0.8 (0.33 ≤ ${\varsigma }_{eq3}$ ≤ 0.91). (d) α = 2, β = 1 (${\varsigma }_{eq3}$ = 0).

Note 7.3: The impulse response $h_3(t)$ degenerates to the conventional one when α = 2 and β = 1. Indeed,

$${h_3(t)|}_{\alpha =2,\beta =1}={\left[\frac{e^{-\frac{m{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+c{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}}{2\sqrt{-\left(m{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)k}}{\omega }_{eqn,3}t}\sin {\omega }_{eqd,3}t}{-\left(m{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right){\omega }_{eqd,3}}\right]}_{\alpha =2,\beta =1}=\frac{e^{-\varsigma {\omega }_{n}t}}{m{\omega }_d}\sin {\omega }_{d}t.$$

(205)

7.5. Application to Represetenting Generalized Mittag-Leffler Function (2)

The impulse response to fractional oscillators in Class I by using the generalized Mittag-Leffler function is in the form (Uchaikin ([38], Chapter 7))

$$h_1(t)=t^{\alpha -1}{E}_{\alpha ,\alpha }\left[-{\left({\omega }_{n}t\right)}^{\alpha }\right],\hspace{1em}1<\alpha \le 2,t\ge 0.$$

(206)

In this section, we propose the representation of (206) by elementary functions.

Corollary 16.

The generalized Mittag-Leffler function in the form (206) can be expressed by the elementary functions in Theorem 13, for 1 < α ≤ 2 and t ≥ 0, in the form

$$t^{\alpha -1}{E}_{\alpha ,\alpha }\left[-{\left({\omega }_{n}t\right)}^{\alpha }\right]=\frac{e^{-\frac{\omega \sin \frac{\alpha \pi }{2}}{2\left|\cos \frac{\alpha \pi }{2}\right|}t}\sin \frac{{\omega }_n\sqrt{1-\frac{{\omega }^{2\alpha }{\sin }^2\frac{\alpha \pi }{2}}{4{\omega }_n^2\left|\cos \frac{\alpha \pi }{2}\right|}}}{\sqrt{{\omega }^{\alpha -2}\left|\cos \frac{\alpha \pi }{2}\right|}}t}{m{\omega }_n\sqrt{{\omega }^{\alpha -2}\left|\cos \frac{\alpha \pi }{2}\right|}\sqrt{1-\frac{{\omega }^{2\alpha }{\sin }^2\frac{\alpha \pi }{2}}{4{\omega }_n^2\left|\cos \frac{\alpha \pi }{2}\right|}}}.$$

(207)

The proof is straightforward from Theorem 13 and (206).

8. Step Responses to Three Classes of Fractional Oscillators

In this section, we shall put forward the unit step responses to three classes of fractional oscillators in the analytic closed forms with elementary functions. Besides, we shall suggest a novel expression of a certain generalized Mittag-Leffler function by using elementary functions.

8.1. General Form of Step Responses

Denote by $g_j(t)$ (j = 1, 2, 3) the step response to a fractional oscillator in the jth Class. Then, it is also the step response to the jth equivalent oscillator. Precisely, $g_j(t)$ is the solution to the jth equivalent oscillator expressed by

$$\{\begin{array}{c}{m}_{eqj}{\ddot{g}}_j(t)+c_{eqj}{\dot{g}}_j(t)+k{g}_j(t)=u(t)\\ g_j(0)=0,{\dot{g}}_j(0)=0\end{array},\hspace{1em}j=1,2,3.$$

(208)

The solution to the above equation is given by

$$g_j(t)={\displaystyle \underset{0}{\overset{t}{\int }}{h}_j(\tau )d\tau }=\frac{1}{k}\left[1-\frac{e^{-{\varsigma }_{eqj}{\omega }_{eqn,j}t}}{\sqrt{1-{\varsigma }_{eqj}^2}}\cos \left({\omega }_{eqd,j}t-{\varphi }_j\right)\right],\hspace{1em}j=1,2,3,$$

(209)

where

$${\varphi }_j={\tan }^{-1}\frac{{\varsigma }_{eqj}}{\sqrt{1-{\varsigma }_{eqj}^2}},\hspace{1em}j=1,2,3.$$

(210)

8.2. Step Response to a Fractional Oscillator in Class I

Theorem 16 (Step response I).

Let $g_1(t)$ be the unit step response to a fractional oscillator in Class I. For t ≥ 0 and 1 < α ≤ 2, it is given by

$$g_1(t)=\frac{1}{k}\left[1-\frac{e^{-\frac{\omega \sin \frac{\alpha \pi }{2}}{2\left|\cos \frac{\alpha \pi }{2}\right|}t}\cos \left(\frac{{\omega }_n\sqrt{1-\frac{{\omega }^{\alpha }{\sin }^2\frac{\alpha \pi }{2}}{4{\omega }_n^2\left|\cos \frac{\alpha \pi }{2}\right|}}}{\sqrt{-{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}}}t-{\varphi }_1\right)}{\sqrt{1-{\left(\frac{{\omega }^{\frac{\alpha }{2}}\sin \frac{\alpha \pi }{2}}{2{\omega }_n\sqrt{-\cos \frac{\alpha \pi }{2}}}\right)}^2}}\right],$$

(211)

where

$${\varphi }_1={\tan }^{-1}\frac{{\varsigma }_{eq1}}{\sqrt{1-{\varsigma }_{eq1}^2}}={\tan }^{-1}\frac{\frac{{\omega }^{\frac{\alpha }{2}}\sin \frac{\alpha \pi }{2}}{2{\omega }_n\sqrt{\left|\cos \frac{\alpha \pi }{2}\right|}}}{\sqrt{1-{\left(\frac{{\omega }^{\frac{\alpha }{2}}\sin \frac{\alpha \pi }{2}}{2{\omega }_n\sqrt{\left|\cos \frac{\alpha \pi }{2}\right|}}\right)}^2}}.$$

(212)

Proof. 

Note that

$$g_1(t)=\frac{1}{k}\left[1-\frac{e^{-{\varsigma }_{eq1}{\omega }_{eqn,1}t}}{\sqrt{1-{\varsigma }_{eq1}^2}}\cos \left({\omega }_{eqd,1}t-{\varphi }_1\right)\right].$$

(213)

Substituting ${\varsigma }_{eq1}$ with the one in (141) into the above produces

$$g_1(t)=\frac{1}{k}\left[1-\frac{e^{-{\varsigma }_{eq1}{\omega }_{eqn,1}t}\cos \left({\omega }_{eqd,1}t-{\varphi }_1\right)}{\sqrt{1-{\varsigma }_{eq1}^2}}\right]=\frac{1}{k}\left[1-\frac{e^{-\frac{{\omega }^{\frac{\alpha }{2}}\sin \frac{\alpha \pi }{2}}{2{\omega }_n\sqrt{-\cos \frac{\alpha \pi }{2}}}{\omega }_{eqn,1}t}\cos \left({\omega }_{eqd,1}t-{\varphi }_1\right)}{\sqrt{1-{\left(\frac{{\omega }^{\frac{\alpha }{2}}\sin \frac{\alpha \pi }{2}}{2{\omega }_n\sqrt{-\cos \frac{\alpha \pi }{2}}}\right)}^2}}\right].$$

(214)

Replacing ${\omega }_{eqn,1}$ and ${\omega }_{eqd,1}$ with those in Section 5 in the above yields (211) and (212). The proof finishes. □

Figure 42 shows the unit step response $g_1(t)$ with fixed oscillation frequency ω. Note that $g_1(t)$ takes ω as an argument. Thus, we use Figure 43 to indicate $g_1(t)$ with variable ω in time domain. Its plots in t-ω plane are shown in Figure 44.

Figure 42. Unit step response $g_1(t)$ to a fractional oscillator in Class I with fixed ω for m = k = 1. (a) α = 1.3, solid line: ω = 1 (${\varsigma }_{eq1}$ = 0.66); dot line: ω = 0.7 (${\varsigma }_{eq1}$ = 0.52). (b) α = 1.6, solid line: ω = 1 (${\varsigma }_{eq1}$ = 0.33); dot line: ω = 0.7 (${\varsigma }_{eq1}$ = 0.25). (c) α = 1.9, solid line: ω = 1 (${\varsigma }_{eq1}$ = 0.08); dot line: ω = 0.7 (${\varsigma }_{eq1}$ = 0.06). (d) α = 2 (${\varsigma }_{eq1}$ = 0).

Figure 43. Step response $g_1(t)$ to a fractional oscillator in Class I with variable ω for m = k = 1. (a) α = 1.3, ω = 1, 1.2, 1.4, ..., 5 (0.66 ≤ ${\varsigma }_{eq1}$ ≤ 1.88). (b) α = 1.5, ω = 1, 1.2, 1.4, ..., 10 (0.66 ≤ ${\varsigma }_{eq1}$ ≤ 2.95). (c) α = 1.7, ω = 1, 1.2, 1.4, ..., 10 (0.08 ≤ ${\varsigma }_{eq1}$ ≤ 0.36). (d) α = 1.9, ω = 1, 1.12, 1.14, ..., 10 (0.08 ≤ ${\varsigma }_{eq1}$ ≤ 0.70).

Figure 44. Step response $g_1(t)$ to a fractional oscillator in Class I in t-ω plane for m = k = 1, ω = 0, 1, ..., 5. (a) α = 1.9 (0 ≤ ${\varsigma }_{eq1}$ ≤ 0.36). (b) α = 1.6 (0 ≤ ${\varsigma }_{eq1}$ ≤ 1.18).

Note 8.1: If α = 2, $g_1(t)$ reduces to the conventional step response with damping free. In fact,

$${g_1(t)|}_{\alpha =2}=\frac{1}{k}{\left[1-\frac{e^{-\frac{\omega \sin \frac{\alpha \pi }{2}}{2\left|\cos \frac{\alpha \pi }{2}\right|}t}\cos \left(\frac{{\omega }_n\sqrt{1-\frac{{\omega }^{\alpha }{\sin }^2\frac{\alpha \pi }{2}}{4{\omega }_n^2\left|\cos \frac{\alpha \pi }{2}\right|}}}{\sqrt{-{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}}}t-{\varphi }_1\right)}{\sqrt{1-{\left(\frac{{\omega }^{\frac{\alpha }{2}}\sin \frac{\alpha \pi }{2}}{2{\omega }_n\sqrt{-\cos \frac{\alpha \pi }{2}}}\right)}^2}}\right]}_{\alpha =2}=\frac{1}{k}\left(1-\cos {\omega }_{n}t\right),$$

(215)

and

$${{\varphi }_1|}_{\alpha =1}={{\tan }^{-1}\frac{\frac{{\omega }^{\frac{\alpha }{2}}\sin \frac{\alpha \pi }{2}}{2{\omega }_n\sqrt{\left|\cos \frac{\alpha \pi }{2}\right|}}}{\sqrt{1-{\left(\frac{{\omega }^{\frac{\alpha }{2}}\sin \frac{\alpha \pi }{2}}{2{\omega }_n\sqrt{\left|\cos \frac{\alpha \pi }{2}\right|}}\right)}^2}}|}_{\alpha =2}=0.$$

(216)

8.3. Step Response to a Fractional Oscillator in Class II

Theorem 17 (Step response II).

Denote by $g_2(t)$ the unit step response to a fractional oscillator in Class II. It is in the form, for t ≥ 0 and 0 < β ≤ 1,

$$g_2(t)=\frac{1}{k}\left[1-\frac{e^{-\frac{\varsigma {\omega }_n{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}}{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}t}\cos \left(\frac{{\omega }_n\sqrt{1-\frac{{\varsigma }^2{\omega }^{2(\beta -1)}{\sin }^2\frac{\beta \pi }{2}}{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}}}{\sqrt{\left(1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}}t-{\varphi }_2\right)}{\sqrt{1-\frac{{\varsigma }^2{\omega }^{2(\beta -1)}{\sin }^2\frac{\beta \pi }{2}}{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}}}\right],$$

(217)

where

$${\varphi }_2={\tan }^{-1}\frac{{\varsigma }_{eq2}}{\sqrt{1-{\varsigma }_{eq2}^2}}={\tan }^{-1}\frac{\frac{\varsigma {\omega }^{\beta -1}\sin \frac{\beta \pi }{2}}{\sqrt{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}}}{\sqrt{1-\frac{{\varsigma }^2{\omega }^{2(\beta -1)}{\sin }^2\frac{\beta \pi }{2}}{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}}}.$$

(218)

Proof. ;

Substituting ${\varsigma }_{eq2}$ with that in Section 5 into the following expression

$$g_2(t)=\frac{1}{k}\left[1-\frac{e^{-{\varsigma }_{eq2}{\omega }_{eqn,2}t}}{\sqrt{1-{\varsigma }_{eq2}^2}}\cos \left({\omega }_{eqd,2}t-{\varphi }_2\right)\right]$$

(219)

yields

$$g_2(t)=\frac{1}{k}\left[1-\frac{e^{-\frac{\varsigma {\omega }^{\beta -1}\sin \frac{\beta \pi }{2}}{\sqrt{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}}{\omega }_{eqn,2}t}}{\sqrt{1-\frac{{\varsigma }^2{\omega }^{2(\beta -1)}{\sin }^2\frac{\beta \pi }{2}}{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}}}\cos \left({\omega }_{eqd,2}t-{\varphi }_2\right)\right].$$

(220)

On the other side, replacing ${\omega }_{eqn,2}$ by the one in (135) in the above results in

$$g_2(t)=\frac{1}{k}\left[1-\frac{e^{-\frac{\varsigma {\omega }^{\beta -1}\sin \frac{\beta \pi }{2}}{\sqrt{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}}{\omega }_{eqn,2}t}\cos \left({\omega }_{eqd,2}t-{\varphi }_2\right)}{\sqrt{1-\frac{{\varsigma }^2{\omega }^{2(\beta -1)}{\sin }^2\frac{\beta \pi }{2}}{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}}}\right]=\frac{1}{k}\left[1-\frac{e^{-\frac{\varsigma {\omega }_n{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}}{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}t}\cos \left({\omega }_{eqd,2}t-{\varphi }_2\right)}{\sqrt{1-\frac{{\varsigma }^2{\omega }^{2(\beta -1)}{\sin }^2\frac{\beta \pi }{2}}{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}}}\right].$$

Finally, substituting ${\omega }_{eqd,2}$ by that in (157) in the above produces (217) and (218). Hence, we finish the proof. □

We use Figure 45 to indicate $g_2(t)$ with fixed ω. When considering variable ω, we show $g_2(t)$ in Figure 46 in time domain and Figure 47 in t-ω plane.

Figure 45. Step response $g_2(t)$ to a fractional oscillator in Class II with fixed ω for m = c = k = 1. (a) β = 0.3, solid line: ω = 20 (${\varsigma }_{eq2}$ = 0.03); dot line: ω = 5 (${\varsigma }_{eq2}$ = 0.08). (b) β = 0.6, solid line: ω = 20 (${\varsigma }_{eq2}$ = 0.12); dot line: ω = 5 (${\varsigma }_{eq2}$ = 0.22). (c) β = 0.9, solid line: ω = 20 (${\varsigma }_{eq2}$ = 0.37); dot line: ω = 5 (${\varsigma }_{eq2}$ = 0.43). (d) β = 1, solid line: ω = 20 (${\varsigma }_{eq2}$ = 0.50); dot line: ω = 5 (${\varsigma }_{eq2}$ = 0.50).

Figure 46. Step response $g_2(t)$ to a fractional oscillator in Class II with variable ω for m = c = k = 1. (a) β = 0.3, ω = 1, 2, ..., 5 (0.08 ≤ ${\varsigma }_{eq2}$ ≤ 0.69). (b) β = 0.3, ω = 1, 2, ..., 10 (0.22 ≤ ${\varsigma }_{eq2}$ ≤ 0.63). (c) β = 0.9, ω = 1, 2, ..., 5 (0.43 ≤ ${\varsigma }_{eq2}$ ≤ 0.54). (d) β = 0.9, ω = 1, 2, ..., 10 (0.40 ≤ ${\varsigma }_{eq2}$ ≤ 0.54).

Figure 47. Step response $g_2(t)$ in t-ω plane for m = c = 1 and ${\omega }_n$ = 0.3 (k = 0.09), with t = 0, 1, ..., 30, ω = 1, 2, 3, 4. (a) β = 0.3 (0.09 ≤ ${\varsigma }_{eq2}$ ≤ 0.69). (b) β = 0.6 (0.24 ≤ ${\varsigma }_{eq2}$ ≤ 0.63). (c) β = 0.9 (0.44 ≤ ${\varsigma }_{eq2}$ ≤ 0.54). (d) β = 1 (${\varsigma }_{eq2}$ = 0.50).

Note 8.2: When β = 1, $g_2(t)$ turns to be the ordinary step response. As a matter of fact,

$${g_2(t)|}_{\beta =1}=\frac{1}{k}\left[1-\frac{e^{-\varsigma {\omega }_{eqn,2}t}}{\sqrt{1-{\varsigma }^2}}\cos \left({\omega }_n\sqrt{1-{\varsigma }^2}t-{\varphi }_2\right)\right],$$

(221)

where

$${{\varphi }_2|}_{\beta =1}{={\tan }^{-1}\frac{\frac{\varsigma {\omega }^{\beta -1}\sin \frac{\beta \pi }{2}}{\sqrt{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}}}{\sqrt{1-\frac{{\varsigma }^2{\omega }^{2(\beta -1)}{\sin }^2\frac{\beta \pi }{2}}{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}}}|}_{{}_{\beta =1}}={\tan }^{-1}\frac{\varsigma }{\sqrt{1-{\varsigma }^2}}.$$

(222)

8.4. Step Response to a Fractional Oscillator in Class III

Theorem 18 (Step response III).

Let $g_3(t)$ be the unit step response to a fractional oscillator in Class III. It is in the form, for t ≥ 0, 1 < α ≤ 2, and 0 < β ≤ 1,

$$g_3(t)=\frac{1}{k}\left\{1-\frac{\left[\begin{array}{l}{e}^{-\frac{m{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+c{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}}{2\left(m{\omega }^{\alpha -2}\left|\cos \frac{\alpha \pi }{2}\right|-c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}t}\\ \cos \left(\frac{{\omega }_n\sqrt{1-\frac{{\left(m{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+c{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}\right)}^2}{4\left[-\left(m{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)k\right]}}}{\sqrt{-\left({\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}}t-{\varphi }_3\right)\end{array}\right]}{\sqrt{1-{\left[\frac{m{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+c{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}}{2\sqrt{-\left(m{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)k}}\right]}^2}}\right\},$$

(223)

where

$${\varphi }_3={\tan }^{-1}\frac{{\varsigma }_{eq3}}{\sqrt{1-{\varsigma }_{eq3}^2}}={\tan }^{-1}\frac{\frac{c{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}}{2\sqrt{\left(m-c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)k}}}{\sqrt{1-\left(\frac{c^2{\omega }^{2(\beta -1)}{\sin }^2\frac{\beta \pi }{2}}{4\left(m-c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)k}\right)}}.$$

(224)

Proof. 

Replacing ${\varsigma }_{eq3}$ by that in (147) on the left side of the following produces the right side in the form

$$\begin{array}{l}{g}_3(t)=\frac{1}{k}\left[1-\frac{e^{-{\varsigma }_{eq3}{\omega }_{eqn,3}t}}{\sqrt{1-{\varsigma }_{eq3}^2}}\cos \left({\omega }_{eqd,3}t-{\varphi }_3\right)\right]\\ =\frac{1}{k}\left[1-\frac{e^{-\frac{m{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+c{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}}{2\sqrt{-\left(m{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)k}}{\omega }_{eqn,3}t}\cos \left({\omega }_{eqd,3}t-{\varphi }_3\right)}{\sqrt{1-{\left[\frac{m{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+c{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}}{2\sqrt{-\left(m{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)k}}\right]}^2}}\right].\end{array}$$

(225)

Further, replacing ${\omega }_{eqn,3}$ with the one in (137) in the above yields

$$\begin{array}{l}{g}_3(t)=\frac{1}{k}\left[1-\frac{e^{-\frac{\frac{{\omega }_n\left(m{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+c{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}\right)}{\sqrt{-\left({\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}}}{2\sqrt{-\left(m{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)k}}t}\cos \left({\omega }_{eqd,3}t-{\varphi }_3\right)}{\sqrt{1-{\left[\frac{m{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+c{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}}{2\sqrt{-\left(m{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)k}}\right]}^2}}\right]\\ =\frac{1}{k}\left[1-\frac{e^{-\frac{m{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+c{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}}{2\left(m{\omega }^{\alpha -2}\left|\cos \frac{\alpha \pi }{2}\right|-c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}t}\cos \left({\omega }_{eqd,3}t-{\varphi }_3\right)}{\sqrt{1-{\left[\frac{m{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+c{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}}{2\sqrt{-\left(m{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)k}}\right]}^2}}\right].\end{array}$$

(226)

Finally, considering ${\omega }_{eqd,3}$ expressed by (160), we have (223) and (224). Hence, the proof finishes. □

Figure 48 illustrates $g_3(t)$ in time with fixed ω while Figure 49 is with variable ω. Its illustrations in t-ω plane are shown in Figure 50.

Figure 48. Illustrating step response $g_3(t)$ with fixed ω for m = c = 1, k = 25 (${\omega }_n$ = 5). (a) (α, β) = (1.8, 0.8), solid line: ω = 1 (${\varsigma }_{eq3}$ = 0.13), dot line: ω = 2 (${\varsigma }_{eq3}$ = 0.05). (b) (α, β) = (1.5, 0.8), solid line: ω = 1 (${\varsigma }_{eq3}$ = 0.33), dot line: ω = 2 (${\varsigma }_{eq3}$ = 0.15). (c) (α, β) = (1.3, 0.8), solid line: ω = 1 (${\varsigma }_{eq3}$ = 0.49), dot line: ω = 2 (${\varsigma }_{eq3}$ = 0.24). (d) (α, β) = (1.8, 0.5), solid line: ω = 1 (${\varsigma }_{eq3}$ = 0.09), dot line: ω = 2 (${\varsigma }_{eq3}$ = 0.03). (e) (α, β) = (2, 1), solid line: ω = 1 (${\varsigma }_{eq3}$ = 0), dot line: ω = 2 (${\varsigma }_{eq3}$ = 0).

Figure 49. Demonstrating step response $g_3(t)$ with variable ω ( = 1, 2, ..., 5) for m = c = 1, k = 25 (${\omega }_n$ = 5). (a) (α, β) = (1.8, 0.8) (0.13 ≤ ${\varsigma }_{eq3}$ ≤ 1.22). (b) (α, β) = (1.5, 0.8) (0.34 ≤ ${\varsigma }_{eq3}$ ≤ 0.91). (c) (α, β) = (1.3, 0.8) (0.49 ≤ ${\varsigma }_{eq3}$ ≤ 1.14).

Figure 50. Illustrating step response $g_3(t)$ in t-ω plane for m = c = k = 1, with t = 0, 1, ..., 30, ω = 1, 2, ..., 5. (a) (α, β) = (1.8, 0.3) (0.05 ≤ ${\varsigma }_{eq3}$ ≤ 0.10). (b) (α, β) = (1.8, 0.5) (0.09 ≤ ${\varsigma }_{eq3}$ ≤ 0.20). (c) (α, β) = (1.5, 0.6) (0.25 ≤ ${\varsigma }_{eq3}$ ≤ 0.55). (d) (α, β) = (2, 1) (0.49 ≤ ${\varsigma }_{eq3}$ ≤ 0.96).

Note 8.3: For (α, β) = (2, 1), $g_3(t)$ reduces to the conventional step response. Indeed,

$${g_3(t)|}_{\alpha =2,\beta =1}=\frac{1}{k}\left[1-\frac{e^{-\varsigma {\omega }_{n}t}}{\sqrt{1-{\varsigma }^2}}\cos \left({\omega }_n\sqrt{1-{\varsigma }^2}t-{{\varphi }_3|}_{\alpha =2,\beta =1}\right)\right],$$

(227)

where

$${{\varphi }_3|}_{\alpha =2,\beta =1}={{\tan }^{-1}\frac{\frac{m{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+c{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}}{2\sqrt{-\left(m{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)k}}}{\sqrt{1-{\left[\frac{m{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+c{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}}{2\sqrt{-\left(m{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)k}}\right]}^2}}|}_{\alpha =2,\beta =1}={\tan }^{-1}\frac{\varsigma }{\sqrt{1-{\varsigma }^2}}.$$

(228)

8.5. Application to Represetenting Mittag-Leffler Function (3)

The step response to fractional oscillators in Class I by using the generalized Mittag-Leffler function is in the form (Uchaikin ([38], Chapter 7))

$$g_1(t)=t^{\alpha }{E}_{\alpha ,\alpha +1}\left[-{\left({\omega }_{n}t\right)}^{\alpha }\right],\hspace{1em}1<\alpha \le 2,t\ge 0.$$

(229)

In the following corollary, we propose the representation of (229) by elementary functions.

Corollary 17.

The generalized Mittag-Leffler function expressed by (229) can be represented by using the elementary functions described in Theorem 16. Precisely, for t ≥ 0 and 1 < α ≤ 2, we have

$$t^{\alpha }{E}_{\alpha ,\alpha +1}\left[-{\left({\omega }_{n}t\right)}^{\alpha }\right]=\frac{1}{k}\left[1-\frac{e^{-\frac{\omega \sin \frac{\alpha \pi }{2}}{2\left|\cos \frac{\alpha \pi }{2}\right|}t}\cos \left(\frac{{\omega }_n\sqrt{1-\frac{{\omega }^{\alpha }{\sin }^2\frac{\alpha \pi }{2}}{4{\omega }_n^2\left|\cos \frac{\alpha \pi }{2}\right|}}}{\sqrt{-{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}}}t-{\varphi }_1\right)}{\sqrt{1-{\left(\frac{{\omega }^{\frac{\alpha }{2}}\sin \frac{\alpha \pi }{2}}{2{\omega }_n\sqrt{-\cos \frac{\alpha \pi }{2}}}\right)}^2}}\right],$$

(230)

where ${\varphi }_1$ is given by (212).

Proof. 

The left side of (230) equals to $g_1(t)$ following Theorem 16. According to (229), therefore, (230) holds. This completes the proof. □

9. Frequency Responses to Three Classes of Fractional Oscillators

We put forward frequency responses to three classes of fractional oscillators in this section. They are expressed by elementary functions based on the theory of three equivalent oscillators addressed in Section 4.

9.1. General Form of Frequency Responses to Three Classes of Fractional Oscillators

Denote by $H_j(\omega )$ the Fourier transform of the impulse response $h_j(t)$ to a fractional oscillator in Class j (j = 1, 2, 3), where $h_j(t)$ is given by (196). Then, it is the frequency response function to a fractional oscillator in Class j (j = 1, 2, 3).

In fact, doing the Fourier transform on the both sides of (195) produces

$$\left(-{\omega }^2+i2{\varsigma }_{eqj}{\omega }_{eqn,j}\omega +{\omega }_{eqn,j}^2\right)H_j(\omega )=\frac{1}{m_{eqj}}.$$

(231)

Thus, we have

$$H_j(\omega )=\frac{1}{m_{eqj}\left({\omega }_{eqn,j}^2-{\omega }^2+i2{\varsigma }_{eqj}{\omega }_{eqn,j}\omega \right)}=\frac{1}{m_{eqj}{\omega }_{eqn,j}^2\left(1-\frac{{\omega }^2}{{\omega }_{eqn,j}^2}+i2{\varsigma }_{eqj}\frac{\omega }{{\omega }_{eqn,j}}\right)}.$$

(232)

Note that

$$m_{eqj}{\omega }_{eqn,j}^2=m_{eqj}\frac{k}{m_{eqj}}=k.$$

(233)

Therefore, by letting ${\gamma }_{eqj}$ be the equivalent frequency ratio of a fractional oscillator in Class j, $H_j(\omega )$ may be expressed by

$$H_j(\omega )=\frac{1}{k\left(1-{\gamma }_{eqj}^2+i2{\varsigma }_{eqj}{\gamma }_{eqj}\right)},\hspace{1em}j=1,2,3.$$

(234)

The amplitude of $H_j(\omega )$ is

$$\left|H_j(\omega )\right|=\frac{1}{k}\frac{1}{\sqrt{{\left(1-{\gamma }_{eqj}^2\right)}^2+{\left(2{\varsigma }_{eqj}{\gamma }_{eqj}\right)}^2}},\hspace{1em}j=1,2,3.$$

(235)

Its phase frequency response is given by

$${\phi }_j(\omega )={\tan }^{-1}\frac{2{\varsigma }_{eqj}{\gamma }_{eqj}}{1-{\gamma }_{eqj}^2},\hspace{1em}j=1,2,3.$$

(236)

9.2. Frequency Response to a Fractional Oscillator in Class I

Theorem 19 (Frequency response I).

Let $H_1(\omega )$ be the frequency response to a fractional oscillator in Class I. Then, for 1 < α ≤ 2, it is in the form

$$H_1(\omega )=\frac{1}{k\left(1-\frac{{\omega }^{\alpha }\left|\cos \frac{\alpha \pi }{2}\right|}{{\omega }_n^2}+i\frac{{\omega }^{\alpha }\sin \frac{\alpha \pi }{2}}{{\omega }_n^2}\right)}.$$

(237)

Proof. 

In the equation below,

$$H_1(\omega )=\frac{1}{k\left(1-{\gamma }_{eq1}^2+i2{\varsigma }_{eq1}{\gamma }_{eq1}\right)},$$

(238)

when replacing ${\gamma }_{eq1}$ by

$${\gamma }_{eq1}={\gamma }_{eq1}(\omega ,\alpha )=\frac{\omega }{{\omega }_{eqn,1}}=\frac{\omega \sqrt{{\omega }^{\alpha -2}\left|\cos \frac{\alpha \pi }{2}\right|}}{{\omega }_n},$$

(239)

and $2{\varsigma }_{eq1}{\gamma }_{eq1}$ by

$$2{\varsigma }_{eq1}{\gamma }_{eq1}=2\frac{{\omega }^{\frac{\alpha }{2}}\sin \frac{\alpha \pi }{2}}{2{\omega }_n\sqrt{\left|\cos \frac{\alpha \pi }{2}\right|}}\frac{\omega \sqrt{{\omega }^{\alpha -2}\left|\cos \frac{\alpha \pi }{2}\right|}}{{\omega }_n}=\frac{{\omega }^{\alpha }\sin \frac{\alpha \pi }{2}}{{\omega }_n^2},$$

(240)

we have (237). This completes the proof. □

From Theorem 19, we have the amplitude of $H_1(\omega )$ given by

$$\left|H_1(\omega )\right|=\frac{1/k}{\sqrt{{\left(1-\frac{{\omega }^{\alpha }\left|\cos \frac{\alpha \pi }{2}\right|}{{\omega }_n^2}\right)}^2+{\left(\frac{{\omega }^{\alpha }\sin \frac{\alpha \pi }{2}}{{\omega }_n^2}\right)}^2}},$$

(241)

and the phase in the form

$${\phi }_1(\omega )={\tan }^{-1}\frac{\frac{{\omega }^{\alpha }\sin \frac{\alpha \pi }{2}}{{\omega }_n^2}}{1-\frac{{\omega }^{\alpha }\left|\cos \frac{\alpha \pi }{2}\right|}{{\omega }_n^2}}={\tan }^{-1}\frac{{\omega }^{\alpha }\sin \frac{\alpha \pi }{2}}{{\omega }_n^2-{\omega }^{\alpha }\left|\cos \frac{\alpha \pi }{2}\right|}.$$

(242)

Note 9.1 (Equivalent frequency ratio I): The equivalent frequency ratio ${\gamma }_{eq1}$ is a function of oscillation frequency ω and the fractional order α. It may be denoted by ${\gamma }_{eq1}(\omega ,\alpha ).$

Figure 51 shows the plot of ${\gamma }_{eq1}.$ Figure 52 indicates the illustrations of $H_1(\omega ).$

Figure 51. Equivalent frequency ratio ${\gamma }_{eq1}(\omega ,\alpha )$ for fractional oscillators in Class I with m = k = 1. Solid line: α = 1.8. Dot line: α = 1.5. Dash line: α = 1.2.

Figure 52. Frequency response $H_1(\omega )$ to fractional oscillators in Class I with m = k = 1. Solid line: α = 1.8 (0.04 ≤ ${\varsigma }_{eq1}$ ≤ 0.06). Dot line: α = 1.5 (0.13 ≤ ${\varsigma }_{eq1}$ ≤ 0.19). Dash line: α = 1.2 (0.33 ≤ ${\varsigma }_{eq1}$ ≤ 0.46). (a) Amplitude $\left|H_1(\omega )\right|$ in ordinary coordinate. (b) $\left|H_1(\omega )\right|$ in log-log. (c) Phase ${\phi }_1(\omega )$ in ordinary coordinate. (d) ${\phi }_1(\omega )$ in log-log.

Note 9.2: If α = 2, $H_1(\omega )$ → ∞ at ω = ${\omega }_n.$ In that case, $H_1(\omega )$ turns to be the ordinary frequency response with damping free in the form

$${H_1(\omega )|}_{\alpha =2}={\frac{1/k}{1-\frac{{\omega }^{\alpha }\left|\cos \frac{\alpha \pi }{2}\right|}{{\omega }_n^2}+i\frac{{\omega }^{\alpha }\sin \frac{\alpha \pi }{2}}{{\omega }_n^2}}|}_{\alpha =2}=\frac{1/k}{1-\frac{{\omega }^2}{{\omega }_n^2}}=\frac{1/k}{1-{\gamma }^2}.$$

(243)

9.3. Frequency Response to a Fractional Oscillator in Class II

Theorem 20 (Frequency response II).

Denote by $H_2(\omega )$ the frequency response to a fractional oscillator in Class II. Then, for 0 < β ≤ 1, it is given by

$$H_2(\omega )=\frac{1/k}{1-{\gamma }^2\left(1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)+i\frac{2\varsigma {\omega }^{\beta }\sin \frac{\beta \pi }{2}}{{\omega }_n}},$$

(244)

where $\gamma =\frac{\omega }{{\omega }_n}$ is the ordinary frequency ratio.

Proof. 

Consider

$$H_2(\omega )=\frac{1}{k\left(1-{\gamma }_{eq2}^2+i2{\varsigma }_{eq2}{\gamma }_{eq2}\right)}.$$

(245)

Note that

$${\gamma }_{eq2}={\gamma }_{eq2}(\omega ,\beta )=\frac{\omega }{{\omega }_{eqn,2}}=\frac{\omega }{{\omega }_n}\sqrt{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}=\gamma \sqrt{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}.$$

(246)

Besides,

$$2{\varsigma }_{eq}{\gamma }_{eq2}=\frac{2\varsigma {\omega }^{\beta -1}\sin \frac{\beta \pi }{2}}{\sqrt{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}}\left(\frac{\omega }{{\omega }_n}\sqrt{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}\right)=\frac{2\varsigma {\omega }^{\beta }\sin \frac{\beta \pi }{2}}{{\omega }_n}.$$

(247)

Therefore, (245) becomes

$$\begin{array}{l}{H}_2(\omega )=\frac{1}{k\left(1-{\gamma }_{eq2}^2+i2{\varsigma }_{eq2}{\gamma }_{eq2}\right)}\\ =\frac{1/k}{1-{\left(\frac{\omega }{{\omega }_n}\sqrt{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}\right)}^2+i\frac{2\varsigma {\omega }^{\beta }\sin \frac{\beta \pi }{2}}{{\omega }_n}}\\ =\frac{1/k}{1-{\gamma }^2\left(1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)+i\frac{2\varsigma {\omega }^{\beta }\sin \frac{\beta \pi }{2}}{{\omega }_n}}.\end{array}$$

This finishes the proof. □

From Theorem 20, we have the amplitude of $H_2(\omega )$ in the form

$$\left|H_2(\omega )\right|=\frac{1/k}{\sqrt{{\left[1-{\gamma }^2\left(1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)\right]}^2+{\left(\frac{2\varsigma {\omega }^{\beta }\sin \frac{\beta \pi }{2}}{{\omega }_n}\right)}^2}},$$

(248)

and its phase given by

$${\phi }_2(\omega )={\tan }^{-1}\frac{\frac{2\varsigma {\omega }^{\beta }\sin \frac{\beta \pi }{2}}{{\omega }_n}}{1-{\gamma }^2\left(1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}.$$

(249)

Note 9.3 (Equivalent frequency ratio II): The equivalent frequency ratio ${\gamma }_{eq2}$ is dependent on oscillation frequency ω and the fractional order β as can be seen from (9.16). We denote it by ${\gamma }_{eq2}(\omega ,\beta ).$

Figure 53 indicates the plot of ${\gamma }_{eq2}(\omega ,\beta ).$ $H_2(\omega )$ is shown in Figure 54.

Figure 53. Equivalent frequency ratio ${\gamma }_{eq2}(\omega ,\beta )$ of fractional oscillators in Class II with m = c = k = 1. Solid line: β = 0.8. Dot line: β = 0.5. Dash line: β = 0.2.

Figure 54. Frequency response $H_2(\omega )$ to fractional oscillators of Class II type with m = c = 1 and k = 4. Solid line: β = 0.8 (0.15 ≤ ${\varsigma }_{eq2}$ ≤ 0.29). Dot line: β = 0.5 (0.06 ≤ ${\varsigma }_{eq2}$ ≤ 0.33). Dash line: β = 0.2 (0.01 ≤ ${\varsigma }_{eq2}$ ≤ 0.35). (a) Amplitude $\left|H_2(\omega )\right|$ in ordinary coordinate. (b) $\left|H_2(\omega )\right|$ in log-log. (c) Phase ${\phi }_2(\omega )$ in ordinary coordinate. (d) ${\phi }_2(\omega )$ in log-log.

Note 9.4: When β = 1, $H_2(\omega )$ reduces to that of an ordinary oscillator’s in the form (also see Figure 55).

$$\begin{array}{l}{H_2(\omega )|}_{\beta =1}={\frac{1/k}{1-{\gamma }^2\left(1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)+i\frac{2\varsigma {\omega }^{\beta }\sin \frac{\beta \pi }{2}}{{\omega }_n}}|}_{\beta =1}\\ =\frac{1/k}{1-{\gamma }^2+i2\varsigma \frac{\omega }{{\omega }_n}}=\frac{1/k}{1-{\gamma }^2+i2\varsigma \gamma }.\end{array}$$

(250)

Figure 55. $H_2(\omega )$ for β = 1 with m = c = 1 and k = 4 (ζ_eq2 = 0.25). (a) $\left|H_2(\omega )\right|$ in ordinary coordinate. (b) $\left|H_2(\omega )\right|$ in log-log. (c) Phase ${\phi }_2(\omega )$ in log-log.

9.4. Frequency Response to a Fractional Oscillator in Class III

Theorem 21 (Frequency response III).

Let $H_3(\omega )$ be the frequency response to a fractional oscillator of Class III type. Then, for 1 < α ≤ 2 and 0 < β ≤ 1, $H_3(\omega )$ is in the form

$$H_3(\omega )=\frac{1/k}{1-{\gamma }^2\left({\omega }^{\alpha -2}\left|\cos \frac{\alpha \pi }{2}\right|-\frac{c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}{m}\right)+i\frac{\gamma \left({\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+2\varsigma {\omega }_n{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}\right)}{{\omega }_n\left({\omega }^{\alpha -2}\left|\cos \frac{\alpha \pi }{2}\right|-2\varsigma {\omega }_n{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}}.$$

(251)

Proof. 

In the equation below

$$H_3(\omega )=\frac{1}{k\left(1-{\gamma }_{eq3}^2+i2{\varsigma }_{eq3}{\gamma }_{eq3}\right)},$$

(252)

we notice

$$\begin{array}{l}{\gamma }_{eq3}={\gamma }_{eq3}(\omega ,\alpha ,\beta )=\frac{\omega }{{\omega }_{eqn,3}}=\frac{\omega }{{\omega }_n}\sqrt{-\left({\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}\\ =\gamma \sqrt{-\left({\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}.\end{array}$$

(253)

In addition,

$$\begin{array}{l}2{\varsigma }_{eq3}{\gamma }_{eq3}=2\frac{\left[\begin{array}{l}\left({\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+2\varsigma {\omega }_n{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}\right)\\ \gamma \sqrt{-\left({\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}\end{array}\right]}{2{\omega }_n\sqrt{-\left({\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+2\varsigma {\omega }_n{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}}\\ =\frac{\gamma \left({\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+2\varsigma {\omega }_n{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}\right)}{{\omega }_n\left({\omega }^{\alpha -2}\left|\cos \frac{\alpha \pi }{2}\right|-2\varsigma {\omega }_n{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}.\end{array}$$

(254)

Thus, (252) becomes

$$H_3(\omega )=\frac{1/k}{1-{\gamma }^2\left({\omega }^{\alpha -2}\left|\cos \frac{\alpha \pi }{2}\right|-\frac{c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}{m}\right)+i\frac{\gamma \left({\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+2\varsigma {\omega }_n{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}\right)}{{\omega }_n\left({\omega }^{\alpha -2}\left|\cos \frac{\alpha \pi }{2}\right|-2\varsigma {\omega }_n{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}}.$$

Therefore, the proof completes. □

From Theorem 21, we obtain $\left|H_3(\omega )\right|$ in the form

$$\left|H_3(\omega )\right|=\frac{1/k}{\sqrt{\left\{\begin{array}{l}{\left[1-{\gamma }^2\left({\omega }^{\alpha -2}\left|\cos \frac{\alpha \pi }{2}\right|-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)\right]}^2\\ +{\left[\frac{\gamma \left({\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+2\varsigma {\omega }_n{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}\right)}{{\omega }_n\left({\omega }^{\alpha -2}\left|\cos \frac{\alpha \pi }{2}\right|-2\varsigma {\omega }_n{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}\right]}^2\end{array}\right\}}}.$$

(255)

The phase ${\phi }_3(\omega )$ is given by

$${\phi }_3(\omega )={\tan }^{-1}\frac{\frac{\gamma \left({\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+2\varsigma {\omega }_n{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}\right)}{{\omega }_n\left({\omega }^{\alpha -2}\left|\cos \frac{\alpha \pi }{2}\right|-2\varsigma {\omega }_n{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}}{1-{\gamma }^2\left({\omega }^{\alpha -2}\left|\cos \frac{\alpha \pi }{2}\right|-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}.$$

(256)

Note 9.5 (Equivalent frequency ratio III): ${\gamma }_{eq3}$ relates to ω and a pair of fractional orders (α, β).

Figure 56 indicates its plots. Figure 57 demonstrates $H_3(\omega ).$

Figure 56. Plots of equivalent frequency ratio ${\gamma }_{eq3}(\omega ,\alpha ,\beta )$ for m = c = k = 1. (a) Solid line: (α, β) = (1.8, 0.8). Dot line: (α, β) = (1.5, 0.8). (b) Solid line: (α, β) = (1.5, 0.8). Dot line: (α, β) = (1.5, 0.6).

Figure 57. Illustrations of frequency response $H_3(\omega )$ to fractional oscillators of Class III with m = c = 1, k = 25. (a) $\left|H_3(\omega )\right|$ and ${\phi }_3(\omega ).$ Solid line: (α, β) = (1.8, 0.9) (0.23 ≤ ${\varsigma }_{eq3}$ ≤ 0.54). Dot line: (α, β) = (1.5, 0.9) (0.36 ≤ ${\varsigma }_{eq3}$ ≤ 1.04). (b) $\left|H_3(\omega )\right|$ and ${\phi }_3(\omega ).$ Solid line: (α, β) = (1.8, 0.7) (0.27 ≤ ${\varsigma }_{eq3}$ ≤ 0.50). Dot line: (α, β) = (1.5, 0.7) (0.50 ≤ ${\varsigma }_{eq3}$ ≤ 0.95). (c) $\left|H_3(\omega )\right|$ and ${\phi }_3(\omega ).$ Solid line: (α, β) = (1.8, 0.55) (0.31 ≤ ${\varsigma }_{eq3}$ ≤ 0.46). Dot line: (α, β) = (1.5, 0.55) (0.86 ≤ ${\varsigma }_{eq3}$ ≤ 0.97).

Note 9.6: If (α, β) = (2, 1), $H_3(\omega )$ reduces to the ordinary one given by

$${H_3(\omega )|}_{(\alpha ,\beta )=(2,1)}=\frac{1/k}{1-{\gamma }^2+i2\varsigma \gamma }.$$

(257)

10. Sinusoidal Responses of Three Classes of Fractional Oscillators

When the excitation force takes the sinusoidal one in the form of cosωt or sinωt, the response is termed sinusoidal response, which plays a role in the field of oscillations.

10.1. Stating Problem

Note that the sinusoidal response to fractional oscillators attracts research interests but it is yet a problem that has not been solved satisfactorily. In fact, the existence of the sinusoidal response to fractional oscillators remains a problem. In mathematics, it is regarded as a problem of periodic solution to fractional oscillators. Kaslik and Sivasundaram stated that the exact periodic solution does not exist ([81], p. 1495, Remark 5). The view of Kaslik and Sivasundaram’s in [81] is also implied in other works of researchers. Taking fractional oscillators in Class I as an example, Mainardi noticed that the solution to fractional oscillators for 1 < α < 2, when driven by sinusoidal function, does not exhibit permanent oscillations but asymptotically algebraic decayed ([25], p. 1469), also see Achar et al. ([33], lines above Equation (14)), Duan et al. ([39], p. 49).

As a matter of fact, when considering a fractional oscillator of Class I type for 1 < α < 2 without the case of α = 2 in the form

$$m\frac{d^{\alpha }{y}_1(t)}{d{t}^{\alpha }}+k{y}_1(t)=\cos \omega t,\hspace{1em}1<\alpha <2,$$

(258)

it is obvious that $y_1(t)$ must contain steady-state component that is not equal to 0 for t → ∞ no matter what value of α ∈ (1, 2) is. Otherwise, the conservation law of energy would be violated. The problem is what the complete solution of y₁(t) should be.

The actual solution $y_1(t)$ should, in reality, consist of two parts. One is the steady-state part, denoted by $y_{1s}(t),$ where the subscript s stands for steady-state, which is not equal to 0 for t → ∞ and for any value of α ∈ (1, 2). The other is the transient part, denoted by $y_{1tr}(t),$ where the subscript tr means transient. Thus, the complete solution should, qualitatively, be in the form

$$y_1(t)=y_{1tr}(t)+y_{1s}(t).$$

(259)

We contribute the complete solutions to three classes of fractional oscillators regarding their sinusoidal responses in this section. Our results will show that there exist steady-state components for fractional oscillators in either class with any value of α ∈ (1, 2) for those in Class I, or β ∈ (0, 1) in Class II, or any combination of α ∈ (1, 2) with β ∈ (0, 1) for those in Class III.

10.2. Stating Research Thought

Consider the sinusoidal responses to three classes fractional oscillators based on the equivalent oscillation equation in the form

$$\{\begin{array}{c}{m}_{eqj}\frac{d^2{x}_j(t)}{d{t}^2}+c_{eqj}\frac{d{x}_j(t)}{dt}+k{x}_j(t)=A\cos \omega t\\ x_j(0)=x_{j0},{\frac{d{x}_j(t)}{dt}|}_{t=0}=v_{j0}\end{array},\hspace{1em}j=1,2,3.$$

(260)

The complete response $x_j(t)$ consists of the zero state response, denoted by $x_{jzs}(t),$ and zero input response denoted by $x_{jzi}(t),$ according to the theory of differential equations. Therefore,

$$x_j(t)=x_{jzs}(t)+x_{jzi}(t),$$

(261)

where $x_{jzi}(t)$ is solved from

$$\{\begin{array}{c}{m}_{eqj}\frac{d^2{x}_{jzi}(t)}{d{t}^2}+c_{eqj}\frac{d{x}_{jzi}(t)}{dt}+k{x}_{jzi}(t)=0\\ x_j(0)=x_{j0},{\frac{d{x}_j(t)}{dt}|}_{t=0}=v_{j0}\end{array},\hspace{1em}j=1,2,3.$$

(262)

On the other hand, $x_{jzs}(t)$ is the solution to

$$\{\begin{array}{c}{m}_{eqj}\frac{d^2{x}_{jzs}(t)}{d{t}^2}+c_{eqj}\frac{d{x}_{jzs}(t)}{dt}+k{x}_{jzs}(t)=A\cos \omega t\\ x_j(0)=0,{\frac{d{x}_j(t)}{dt}|}_{t=0}=0\end{array},\hspace{1em}j=1,2,3.$$

(263)

Note that $x_{jzi}(t)$ is actually the free response to the fractional oscillators in Class j. It has been solved in Section 6. Thus, the focus of this section is on (263).

10.3. General Form of Sinusoidal Responses to Three Classes of Fractional Oscillators

The solution to (263) in the general form, for t > 0, j = 1, 2, 3, is given by

$$x_{jzs}(t)=\frac{1}{m_{eqj}{\omega }_{eqd,j}}\frac{A\left\{\begin{array}{l}\left({\omega }_{eqn,j}^2-{\omega }^2\right)\cos \omega t+2{\varsigma }_{eqj}{\omega }_{eqn,j}\omega \sin \omega t\\ +e^{-{\varsigma }_{eqj}{\omega }_{eqn,j}t}\left[\left({\omega }_{eqn,j}^2-{\omega }^2\right)\cos {\omega }_{eqd,j}t-\frac{{\varsigma }_{eqj}\left({\omega }_{eqn,j}^2+{\omega }^2\right)\sin {\omega }_{eqd,j}t}{\sqrt{1-{\varsigma }_{eqj}^2}}\right]\end{array}\right\}}{{\left({\omega }_{eqn,j}^2-{\omega }^2\right)}^2+{\left(2{\varsigma }_{eqj}{\omega }_{eqn,j}\omega \right)}^2}.$$

(264)

10.4. Sinusoidal Response to Fractional Oscillators in Class I

Theorem 22 (Sinusoidal response I).

Let $x_{1zs}(t)$ be the zero state sinusoidal response to a fractional oscillator in Class I. Then, for t > 0 and 1 < α ≤ 2, it is in the form

$$\begin{array}{l}{x}_{1zs}(t)=\frac{1}{\left(\begin{array}{l}m{\omega }_n\sqrt{-{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}}\\ \sqrt{1-\frac{{\omega }^{\alpha }{\sin }^2\frac{\alpha \pi }{2}}{4{\omega }_n^2\left|\cos \frac{\alpha \pi }{2}\right|}}\end{array}\right)}\frac{A}{\left[{\omega }^4{\left(\frac{{\omega }_n^2}{-{\omega }^{\alpha }\cos \frac{\alpha \pi }{2}}-1\right)}^2+\frac{{\omega }^4{\sin }^2\frac{\alpha \pi }{2}}{{\left|\cos \frac{\alpha \pi }{2}\right|}^2}\right]}\\ \left\{\begin{array}{l}{\omega }^4{\left(\frac{{\omega }_n^2}{-{\omega }^{\alpha }\cos \frac{\alpha \pi }{2}}-1\right)}^2\cos \omega t+\frac{{\omega }^2\sin \frac{\alpha \pi }{2}}{\left|\cos \frac{\alpha \pi }{2}\right|}\sin \omega t\\ +e^{-\frac{\omega \sin \frac{\alpha \pi }{2}}{2\left|\cos \frac{\alpha \pi }{2}\right|}t}\left[\begin{array}{l}{\omega }^4{\left(\frac{{\omega }_n^2}{-{\omega }^{\alpha }\cos \frac{\alpha \pi }{2}}-1\right)}^2\cos \frac{{\omega }_n\sqrt{1-\frac{{\omega }^{\alpha }{\sin }^2\frac{\alpha \pi }{2}}{4{\omega }_n^2\left|\cos \frac{\alpha \pi }{2}\right|}}t}{\sqrt{-{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}}}\\ -\frac{\frac{{\omega }^{\frac{\alpha }{2}}\sin \frac{\alpha \pi }{2}}{2{\omega }_n\sqrt{-\cos \frac{\alpha \pi }{2}}}{\omega }^4{\left(\frac{{\omega }_n^2}{-{\omega }^{\alpha }\cos \frac{\alpha \pi }{2}}+1\right)}^2\sin \frac{{\omega }_n\sqrt{1-\frac{{\omega }^{\alpha }{\sin }^2\frac{\alpha \pi }{2}}{4{\omega }_n^2\left|\cos \frac{\alpha \pi }{2}\right|}}t}{\sqrt{-{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}}}}{\sqrt{1-{\left(\frac{{\omega }^{\frac{\alpha }{2}}\sin \frac{\alpha \pi }{2}}{2{\omega }_n\sqrt{-\cos \frac{\alpha \pi }{2}}}\right)}^2}}\end{array}\right]\end{array}\right\}.\end{array}$$

(265)

Proof. 

Consider the expression below

$$x_{1zs}(t)=\frac{1}{m_{eq1}{\omega }_{eqd,1}}\frac{A\left\{\begin{array}{l}\left({\omega }_{eqn,1}^2-{\omega }^2\right)\cos \omega t+2{\varsigma }_{eq1}{\omega }_{eqn,1}\omega \sin \omega t\\ +e^{-{\varsigma }_{eq1}{\omega }_{eqn,1}t}\left[\left({\omega }_{eqn,1}^2-{\omega }^2\right)\cos {\omega }_{eqd,1}t-\frac{{\varsigma }_{eq1}}{\sqrt{1-{\varsigma }_{eq1}^2}}\left({\omega }_{eqn,1}^2+{\omega }^2\right)\sin {\omega }_{eqd,1}t\right]\end{array}\right\}}{{\left({\omega }_{eqn,1}^2-{\omega }^2\right)}^2+{\left(2{\varsigma }_{eq1}{\omega }_{eqn,1}\omega \right)}^2}.$$

(266)

In the above, replacing $m_{eq1}$ by the one in Section 4, ${\varsigma }_{eq1},$ ${\omega }_{eqd,1}$ and ${\omega }_{eqn,1}$ by those in Section 5, respectively, produces (265). This finishes the proof. □

Denote by $x_{1zs,s}(t)$ and $x_{1zs,tr}(t)$ the steady component and the instantaneous one, respectively. Then, we have

$$\begin{array}{l}{x}_{1zs,s}(t)=\left[\frac{1}{m{\omega }_n\sqrt{-{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}}\sqrt{1-\frac{{\omega }^{\alpha }{\sin }^2\frac{\alpha \pi }{2}}{4{\omega }_n^2\left|\cos \frac{\alpha \pi }{2}\right|}}}\frac{A}{{\omega }^4{\left(\frac{{\omega }_n^2}{-{\omega }^{\alpha }\cos \frac{\alpha \pi }{2}}-1\right)}^2+\frac{{\omega }^4{\sin }^2\frac{\alpha \pi }{2}}{{\left|\cos \frac{\alpha \pi }{2}\right|}^2}}\right]\\ \left[{\omega }^4{\left(\frac{{\omega }_n^2}{-{\omega }^{\alpha }\cos \frac{\alpha \pi }{2}}-1\right)}^2\cos \omega t+\frac{{\omega }^2\sin \frac{\alpha \pi }{2}}{\left|\cos \frac{\alpha \pi }{2}\right|}\sin \omega t\right].\end{array}$$

(267)

and

$$\begin{array}{l}{x}_{1zs,tr}(t)=\left[\frac{1}{m{\omega }_n\sqrt{-{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}}\sqrt{1-\frac{{\omega }^{\alpha }{\sin }^2\frac{\alpha \pi }{2}}{4{\omega }_n^2\left|\cos \frac{\alpha \pi }{2}\right|}}}\frac{A}{{\omega }^4{\left(\frac{{\omega }_n^2}{-{\omega }^{\alpha }\cos \frac{\alpha \pi }{2}}-1\right)}^2+\frac{{\omega }^4{\sin }^2\frac{\alpha \pi }{2}}{{\left|\cos \frac{\alpha \pi }{2}\right|}^2}}\right]\\ \left\{e^{-\frac{\omega \sin \frac{\alpha \pi }{2}}{2\left|\cos \frac{\alpha \pi }{2}\right|}t}\left[\begin{array}{l}{\omega }^4{\left(\frac{{\omega }_n^2}{-{\omega }^{\alpha }\cos \frac{\alpha \pi }{2}}-1\right)}^2\cos \frac{{\omega }_n\sqrt{1-\frac{{\omega }^{\alpha }{\sin }^2\frac{\alpha \pi }{2}}{4{\omega }_n^2\left|\cos \frac{\alpha \pi }{2}\right|}}t}{\sqrt{-{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}}}\\ -\frac{\frac{{\omega }^{\frac{\alpha }{2}}\sin \frac{\alpha \pi }{2}}{2{\omega }_n\sqrt{-\cos \frac{\alpha \pi }{2}}}}{\sqrt{1-{\left(\frac{{\omega }^{\frac{\alpha }{2}}\sin \frac{\alpha \pi }{2}}{2{\omega }_n\sqrt{-\cos \frac{\alpha \pi }{2}}}\right)}^2}}{\omega }^4{\left(\frac{{\omega }_n^2}{-{\omega }^{\alpha }\cos \frac{\alpha \pi }{2}}+1\right)}^2\sin \frac{{\omega }_n\sqrt{1-\frac{{\omega }^{\alpha }{\sin }^2\frac{\alpha \pi }{2}}{4{\omega }_n^2\left|\cos \frac{\alpha \pi }{2}\right|}}t}{\sqrt{-{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}}}\end{array}\right]\right\}.\end{array}$$

(268)

Figure 58 shows the plots of $x_{1zs}(t).$

Figure 58. Illustrating $x_{1zs}(t)$ for m = 1, k = 9 (${\omega }_n$ = 3), ω = 1. Solid line: α = 1.9 (${\varsigma }_{eq1}$ = 0.03). Dot line: α = 1.6 (${\varsigma }_{eq1}$ = 0.11). (a) t = 0, 1, ..., 20. (b) t = 0, 1, ..., 100.

Note 10.1: x_1zs(t) is not a pure harmonic function as can be seen from Figure 58.

Remark 29.

We found that the sinusoidal response to fractional oscillators in Class I for any value of α ∈ (1, 2) does have steady-state component $x_{1zs,s}(t)$ expressed by (267), also see Figure 59.

Figure 59. Steady-state component, $x_{1zs,s}(t),$ of sinusoidal response to a fractional oscillator in Class I for m = 1, k = 9 (${\omega }_n$ = 3), ω = 1. Solid line: α = 1.9 (${\varsigma }_{eq1}$ = 0.03). Dot line: α = 1.6 (${\varsigma }_{eq1}$ = 0.11). Dash dot line: α = 1.3 (${\varsigma }_{eq1}$ = 0.22).

The illustration of $x_{1zs,tr}(t)$ is indicated in Figure 60.

Figure 60. Instantaneous component $x_{1zs,tr}(t)$ for m = 1, k = 9 (${\omega }_n$ = 3), ω = 1. Solid line: α = 1.9 (${\varsigma }_{eq1}$ = 0.03). Dot line: α = 1.6 (${\varsigma }_{eq1}$ = 0.11). Dash dot line: α = 1.3 (${\varsigma }_{eq1}$ = 0.22).

Note 10.2: For α = 2, we have

$$\begin{array}{l}{x}_{1zs}(t)=\frac{1}{m{\omega }_n}\frac{A}{{\omega }^4{\left(\frac{{\omega }_n^2}{{\omega }^2}-1\right)}^2}\left[{\omega }^4{\left(\frac{{\omega }_n^2}{{\omega }^2}-1\right)}^2\cos \omega t+{\omega }^4{\left(\frac{{\omega }_n^2}{{\omega }^2}-1\right)}^2\cos {\omega }_{n}t\right]\\ =\frac{A}{m{\omega }_n}\left(\cos \omega t+\cos {\omega }_{n}t\right).\end{array}$$

(269)

10.5. Sinusoidal Response to Fractional Oscillators in Class II

Theorem 23 (Sinusoidal response II).

Denote by $x_{2zs}(t)$ the zero state sinusoidal response to a fractional oscillator in Class II. Then, for t > 0 and 0 < β ≤ 1, it is expressed by

$$\begin{array}{l}{x}_{2zs}(t)=\frac{1}{m{\omega }_n\sqrt{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}\sqrt{1-{\left(\frac{{\varsigma }^2{\omega }^{2(\beta -1)}{\sin }^2\frac{\beta \pi }{2}}{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}\right)}^2}}\\ \frac{A}{{\left(\frac{{\omega }_n^2}{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}-{\omega }^2\right)}^2+{\left(\frac{2\varsigma {\omega }_n{\omega }^{\beta }\sin \frac{\beta \pi }{2}}{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}\right)}^2}\\ \left\{\begin{array}{l}\left(\frac{{\omega }_n^2}{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}-{\omega }^2\right)\cos \omega t+\frac{2\varsigma {\omega }_n{\omega }^{\beta }\sin \frac{\beta \pi }{2}}{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}\sin \omega t\\ +e^{-\frac{\varsigma {\omega }_n{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}}{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}t}\left[\begin{array}{l}\left[\left(\frac{{\omega }_n^2}{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}-{\omega }^2\right)\cos \frac{{\omega }_n\sqrt{1-{\left(\frac{{\varsigma }^2{\omega }^{2(\beta -1)}{\sin }^2\frac{\beta \pi }{2}}{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}\right)}^2}t}{\sqrt{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}}\right]\\ -\frac{\frac{\varsigma {\omega }^{\beta -1}\sin \frac{\beta \pi }{2}}{\sqrt{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}}\left(\frac{{\omega }_n^2}{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}+{\omega }^2\right)}{\sqrt{1-{\left(\frac{\varsigma {\omega }^{\beta -1}\sin \frac{\beta \pi }{2}}{\sqrt{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}}\right)}^2}}\\ \sin \frac{{\omega }_n\sqrt{1-{\left(\frac{{\varsigma }^2{\omega }^{2(\beta -1)}{\sin }^2\frac{\beta \pi }{2}}{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}\right)}^2}t}{\sqrt{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}}\end{array}\right]\end{array}\right\}.\end{array}$$

(270)

Proof. 

In the following expression,

$$\begin{array}{l}{x}_{2zs}(t)=\frac{1}{m_{eq2}{\omega }_{eqd,2}}\frac{A}{{\left({\omega }_{eqn,2}^2-{\omega }^2\right)}^2+{\left(2{\varsigma }_{eq2}{\omega }_{eqn,2}\omega \right)}^2}\\ \left\{\begin{array}{l}\left({\omega }_{eqn,2}^2-{\omega }^2\right)\cos \omega t+2{\varsigma }_{eq2}{\omega }_{eqn,2}\omega \sin \omega t\\ +e^{-{\varsigma }_{eq2}{\omega }_{eqn,2}t}\left[\left({\omega }_{eqn,2}^2-{\omega }^2\right)\cos {\omega }_{eqd,2}t-\frac{{\varsigma }_{eq2}}{\sqrt{1-{\varsigma }_{eq2}^2}}\left({\omega }_{eqn,2}^2+{\omega }^2\right)\sin {\omega }_{eqd,2}t\right]\end{array}\right\},\end{array}$$

(271)

replacing $m_{eq2}$ with the one in Section 4, ${\varsigma }_{eq2},$ ${\omega }_{eqd,2}$ and ${\omega }_{eqn,2}$ by those in Section 5, results in (270). The proof completes. □

The stead-state part of $x_{2zs,s}(t)$ is represented by

$$\begin{array}{l}{x}_{2zs,s}(t)=\frac{1}{m{\omega }_n\sqrt{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}\sqrt{1-\frac{{\varsigma }^2{\omega }^{2(\beta -1)}{\sin }^2\frac{\beta \pi }{2}}{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}}}\\ \frac{A}{{\left(\frac{{\omega }_n^2}{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}-{\omega }^2\right)}^2+{\left(\frac{2\varsigma {\omega }_n{\omega }^{\beta }\sin \frac{\beta \pi }{2}}{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}\right)}^2}\\ \left[\left(\frac{{\omega }_n^2}{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}-{\omega }^2\right)\cos \omega t+\frac{2\varsigma {\omega }_n{\omega }^{\beta }\sin \frac{\beta \pi }{2}}{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}\sin \omega t\right].\end{array}$$

(272)

On the other side, the transient part $x_{2zs,tr}(t)$ is given by

$$\begin{array}{l}{x}_{2zs,tr}(t)=\frac{1}{m{\omega }_n\sqrt{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}\sqrt{1-\left(\frac{{\varsigma }^2{\omega }^{2(\beta -1)}{\sin }^2\frac{\beta \pi }{2}}{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}\right)}}\\ \frac{A}{{\left(\frac{{\omega }_n^2}{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}-{\omega }^2\right)}^2+{\left(\frac{2\varsigma {\omega }_n{\omega }^{\beta }\sin \frac{\beta \pi }{2}}{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}\right)}^2}\\ \left\{e^{-\frac{\varsigma {\omega }_n{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}}{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}t}\left[\begin{array}{l}\left[\left(\frac{{\omega }_n^2}{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}-{\omega }^2\right)\cos \frac{{\omega }_n\sqrt{1-\left(\frac{{\varsigma }^2{\omega }^{2(\beta -1)}{\sin }^2\frac{\beta \pi }{2}}{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}\right)}t}{\sqrt{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}}\right]\\ -\frac{\frac{\varsigma {\omega }^{\beta -1}\sin \frac{\beta \pi }{2}}{\sqrt{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}}\left(\frac{{\omega }_n^2}{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}+{\omega }^2\right)}{\sqrt{1-{\left(\frac{\varsigma {\omega }^{\beta -1}\sin \frac{\beta \pi }{2}}{\sqrt{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}}\right)}^2}}\\ \sin \frac{{\omega }_n\sqrt{1-\left(\frac{{\varsigma }^2{\omega }^{2(\beta -1)}{\sin }^2\frac{\beta \pi }{2}}{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}\right)}t}{\sqrt{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}}\end{array}\right]\right\}.\end{array}$$

(273)

Figure 61, Figure 62 and Figure 63 show the plots of $x_{2zs}(t),$ $x_{2zs,s}(t),$ and $x_{2zs,tr}(t).$

Figure 61. Sinusoidal response $x_{2zs}(t)$ to a fractional oscillator in Class II with β = 0.9 (solid line) (${\varsigma }_{eq2}$ = 0.14), β = 0.6 (dot line) (${\varsigma }_{eq2}$ = 0.07), β = 0.3 (dash dot line) (${\varsigma }_{eq2}$ = 0.03) with m = c = 1, ${\omega }_n$ = 3 and ω = 1.

Figure 62. Steady-state sinusoidal part of $x_{2zs}(t)$ with β = 0.9 (solid line) (${\varsigma }_{eq2}$ = 0.14), β = 0.6 (dot line) (${\varsigma }_{eq2}$ = 0.07), β = 0.3 (dash dot line) (${\varsigma }_{eq2}$ = 0.03) with m = c = 1, ${\omega }_n$ = 3 and ω = 1.

Figure 63. Transient part of $x_{2zs}(t)$ with β = 0.9 (solid line) (${\varsigma }_{eq2}$ = 0.14), β = 0.6 (dot line) (${\varsigma }_{eq2}$ = 0.07), β = 0.3 (dash dot line) (${\varsigma }_{eq2}$ = 0.03) with m = c = 1, ${\omega }_n$ = 3 and ω = 1.

Note 10.3: If β = 1, we obtain the zero-state response of the conventional sinusoidal response to a 2-order oscillator in the form

$${x_{2zs}(t)|}_{\beta =1}=\frac{1}{m{\omega }_n\sqrt{1-{\varsigma }^2}}\frac{A{e}^{-\varsigma {\omega }_{n}t}\left[\left({\omega }_n^2-{\omega }^2\right)\cos {\omega }_n\sqrt{1-{\varsigma }^2}t-\frac{\varsigma \left({\omega }_n^2+{\omega }^2\right)\sin {\omega }_n\sqrt{1-{\varsigma }^2}t}{\sqrt{1-{\varsigma }^2}}\right]}{{\left({\omega }_n^2-{\omega }^2\right)}^2+{\left(2\varsigma {\omega }_n\omega \right)}^2}.$$

(274)

Remark 30.

We discovered that the sinusoidal response to fractional oscillators in Class II for any value of β ∈ (0, 1) does have steady-state component $x_{2zs,s}(t)$ described by (272), also see Figure 62.

10.6. Sinusoidal Response to Fractional Oscillators in Class III

Theorem 24 (Sinusoidal response III).

Let $x_{3zs}(t)$ be the zero state sinusoidal response to a fractional oscillator of Class III type. Then, for t > 0, 1 < α ≤ 2, and 0 < β ≤ 1, it is written in the form

$$\begin{array}{l}{x}_{3zs}(t)=\left\{\begin{array}{l}\frac{\sqrt{-\left({\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}}{{\omega }_n{m}_{eq3}\sqrt{1-\frac{{\left(m{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+c{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}\right)}^2}{4\left[-\left(m{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)k\right]}}}\\ \frac{A}{\left\{\begin{array}{l}{\left[\frac{{\omega }_n^2}{-\left({\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}-{\omega }^2\right]}^2\\ +{\left(\frac{{\omega }^{\alpha }\sin \frac{\alpha \pi }{2}+2\varsigma {\omega }_n{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}}{{\omega }^{\alpha -2}\left|\cos \frac{\alpha \pi }{2}\right|-2\varsigma {\omega }_n{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}\right)}^2\end{array}\right\}}\end{array}\right\}\\ \left\{\begin{array}{l}\left\{\begin{array}{l}\left[\frac{{\omega }_n^2}{-\left({\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}-{\omega }^2\right]\cos \omega t\\ +\frac{{\omega }^{\alpha }\sin \frac{\alpha \pi }{2}+2\varsigma {\omega }_n{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}}{{\omega }^{\alpha -2}\left|\cos \frac{\alpha \pi }{2}\right|-2\varsigma {\omega }_n{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}\sin \omega t\end{array}\right\}\\ +e^{-\frac{{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+2\varsigma {\omega }_n{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}}{2\left({\omega }^{\alpha -2}\left|\cos \frac{\alpha \pi }{2}\right|-2\varsigma {\omega }_n{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}t}\left[\begin{array}{l}\left[\frac{{\omega }_n^2}{-\left({\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}-{\omega }^2\right]\cos {\omega }_{eqd,3}t\\ -\left\{\begin{array}{l}\frac{\frac{{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+2\varsigma {\omega }_n{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}}{2{\omega }_n\sqrt{-\left({\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+2\varsigma {\omega }_n{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}}}{\sqrt{1-{\left[\frac{{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+2\varsigma {\omega }_n{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}}{2{\omega }_n\sqrt{-\left({\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+2\varsigma {\omega }_n{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}}\right]}^2}}\\ \left(\frac{{\omega }_n^2}{-\left({\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}+{\omega }^2\right)\end{array}\right\}\\ \sin {\omega }_{eqd,3}t\end{array}\right]\end{array}\right\},\end{array}$$

(275)

where m_eq3 and ω_{eqd, 3} are given by (119) and (160), respectively.

Proof. 

In the following expression,

$$x_{3zs}(t)=\frac{1}{m_{eq3}{\omega }_{eqd,3}}\frac{A\left\{\begin{array}{l}\left({\omega }_{eqn,3}^2-{\omega }^2\right)\cos \omega t+2{\varsigma }_{eq3}{\omega }_{eqn,3}\omega \sin \omega t\\ +e^{-{\varsigma }_{eq3}{\omega }_{eqn,3}t}\left[\begin{array}{l}\left({\omega }_{eqn,3}^2-{\omega }^2\right)\cos {\omega }_{eqd,3}t\\ -\frac{{\varsigma }_{eq3}}{\sqrt{1-{\varsigma }_{eq3}^2}}\left({\omega }_{eqn,3}^2+{\omega }^2\right)\sin {\omega }_{eqd,3}t\end{array}\right]\end{array}\right\}}{{\left({\omega }_{eqn,3}^2-{\omega }^2\right)}^2+{\left(2{\varsigma }_{eq3}{\omega }_{eqn,3}\omega \right)}^2},$$

(276)

Substituting ${\varsigma }_{eq3},$ ${\omega }_{eqn,3}$ and ${\omega }_{eqd,3}$ with those in Section 5 yields the Theorem 24. That completes the proof. □

Figure 64 illustrates $x_{3zs}(t).$

Figure 64. Indicating the sinusoidal response $x_{3zs}(t)$ to a fractional oscillator in Class III with (α, β) = (1.8, 0.8) (solid line) (${\varsigma }_{eq3}$ = 0.13), (α, β) = (1.5, 0.8) (dot line) (${\varsigma }_{eq3}$ = 0.22), (α, β) = (1.3, 0.8) (dash dot line) (${\varsigma }_{eq3}$ = 0.40) with m = c = 1, k = 36 (ω_n = 6) and ω = 1.

The steady-state part of $x_{3zs}(t)$ is in the form

$$\begin{array}{l}{x}_{3zs,s}(t)=\left\{\begin{array}{l}\frac{\sqrt{-\left({\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}}{{\omega }_n{m}_{eq3}\sqrt{1-\frac{{\left(m{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+c{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}\right)}^2}{4\left[-\left(m{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)k\right]}}}\\ \frac{A}{\left\{\begin{array}{l}{\left[\frac{{\omega }_n^2}{-\left({\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}-{\omega }^2\right]}^2\\ +{\left(\frac{{\omega }^{\alpha }\sin \frac{\alpha \pi }{2}+2\varsigma {\omega }_n{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}}{{\omega }^{\alpha -2}\left|\cos \frac{\alpha \pi }{2}\right|-2\varsigma {\omega }_n{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}\right)}^2\end{array}\right\}}\end{array}\right\}\\ \left\{\begin{array}{l}\left[\frac{{\omega }_n^2}{-\left({\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}-{\omega }^2\right]\cos \omega t\\ +\frac{\left({\omega }^{\alpha }\sin \frac{\alpha \pi }{2}+2\varsigma {\omega }_n{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}\right)\sin \omega t}{{\omega }^{\alpha -2}\left|\cos \frac{\alpha \pi }{2}\right|-2\varsigma {\omega }_n{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}\end{array}\right\}.\end{array}$$

(277)

Its transient part, taking into account (160), is given by

$$\begin{array}{l}{x}_{3zs,tr}(t)=\left\{\begin{array}{l}\frac{\sqrt{-\left({\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}}{{\omega }_n{m}_{eq3}\sqrt{1-\frac{{\left(m{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+c{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}\right)}^2}{4\left[-\left(m{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)k\right]}}}\\ \frac{A}{\left\{\begin{array}{l}{\left[\frac{{\omega }_n^2}{-\left({\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}-{\omega }^2\right]}^2\\ +{\left(\frac{{\omega }^{\alpha }\sin \frac{\alpha \pi }{2}+2\varsigma {\omega }_n{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}}{{\omega }^{\alpha -2}\left|\cos \frac{\alpha \pi }{2}\right|-2\varsigma {\omega }_n{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}\right)}^2\end{array}\right\}}\end{array}\right\}\\ \left\{e^{-\frac{{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+2\varsigma {\omega }_n{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}}{2\left({\omega }^{\alpha -2}\left|\cos \frac{\alpha \pi }{2}\right|-2\varsigma {\omega }_n{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}t}\left[\begin{array}{l}\left[\frac{{\omega }_n^2}{-\left({\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}-{\omega }^2\right]\\ \cos \left\{\begin{array}{l}\frac{{\omega }_n}{\sqrt{-\left({\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}}\\ \sqrt{1-\frac{{\left(m{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+c{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}\right)}^2}{4\left[-\left(m{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)k\right]}}t\end{array}\right\}\\ -\left\{\begin{array}{l}\frac{\frac{{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+2\varsigma {\omega }_n{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}}{2{\omega }_n\sqrt{-\left({\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+2\varsigma {\omega }_n{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}}}{\sqrt{1-{\left[\frac{{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+2\varsigma {\omega }_n{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}}{2{\omega }_n\sqrt{-\left({\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+2\varsigma {\omega }_n{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}}\right]}^2}}\\ \left(\frac{{\omega }_n^2}{-\left({\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}+{\omega }^2\right)\end{array}\right\}\\ \sin \left\{\frac{{\omega }_n\sqrt{1-\frac{{\left(m{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+c{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}\right)}^2}{4\left[-\left(m{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)k\right]}}t}{\sqrt{-\left({\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}}\right\}\end{array}\right]\right\}.\end{array}$$

(278)

The steady-state component and the transient one of $x_{3zs}(t)$ are shown in Figure 65 and Figure 66, respectively.

Figure 65. Indicating the steady-state component of $x_{3zs}(t)$ with (α, β) = (1.8, 0.8) (solid line) (${\varsigma }_{eq3}$ = 0.13), (α, β) = (1.5, 0.8) (dot line) (${\varsigma }_{eq3}$ = 0.22), (α, β) = (1.3, 0.8) (dash dot line) (${\varsigma }_{eq3}$ = 0.40) with m = c = 1, k = 36 (${\omega }_n$ = 6) and ω = 1.

Figure 66. Transient component of $x_{3zs}(t)$ with (α, β) = (1.8, 0.8) (solid line) (${\varsigma }_{eq3}$ = 0.13), (α, β) = (1.5, 0.8) (dot line) (${\varsigma }_{eq3}$ = 0.22), (α, β) = (1.3, 0.8) (dash dot line) (${\varsigma }_{eq3}$ = 0.40) with m = c = 1, k = 36 (${\omega }_n$ = 6) and ω = 1.

Note 10.4: When (α, β) = (2, 1), $x_{3zs}(t)$ reduces to the ordinary zero-state sinusoidal response to a 2-order oscillator in the form

$$\begin{array}{l}{x_{3zs}(t)|}_{\alpha =2,\beta =1}=\frac{\frac{A}{m{\omega }_n\sqrt{1-{\varsigma }^2}}{e}^{-\varsigma {\omega }_{n}t}\left[\left({\omega }_n^2-{\omega }^2\right)\cos {\omega }_n\sqrt{1-{\varsigma }^2}t-\frac{\varsigma \left({\omega }_n^2+{\omega }^2\right)\sin {\omega }_n\sqrt{1-{\varsigma }^2}t}{\sqrt{1-{\varsigma }^2}}\right]}{{\left({\omega }_n^2-{\omega }^2\right)}^2+{\left(2\varsigma {\omega }_n\omega \right)}^2}\\ =\frac{1}{m{\omega }_d}\frac{A{e}^{-\varsigma {\omega }_{n}t}\left[\left({\omega }_n^2-{\omega }^2\right)\cos {\omega }_{d}t-\frac{\varsigma \left({\omega }_n^2+{\omega }^2\right)\sin {\omega }_{d}t}{\sqrt{1-{\varsigma }^2}}\right]}{{\left({\omega }_n^2-{\omega }^2\right)}^2+{\left(2\varsigma {\omega }_n\omega \right)}^2}.\end{array}$$

(279)

Remark 31.

We revealed that the sinusoidal response to fractional oscillators in Class III for any value of α ∈ (1, 2) and β ∈ (0, 1) does have steady-state component $x_{3zs,s}(t)$ described by (277), also see Figure 65.

Remark 32.

The results presented above show that the exact periodic solutions to three classes of fractional oscillators exist.

11. Discussion

Three classes of fractional oscillators previously studied are usually characterized by constant-coefficient fractional differential equations. The basic theory and key point I presented in Section 4 is to equivalently represent them by the second-order differential equations with variable-coefficients. In this way, three classes of fractional oscillators, which are nonlinear in nature, all reduce to linear oscillators with variable-coefficients. In methodology, that may open a new way of the linearization to describe and research fractional oscillators.

In addition to keep fractional properties of fractional oscillators with its equivalences, for instance, the characteristic roots of a fractional oscillator being infinitely large as explained by Li et al. [18] and Duan et al. [39], based on the proposed equivalent oscillators, we also reveal other properties of fractional oscillators, which may be very difficult, if not impossible, to be described directly from the point of view of fractional differential equations, such as the equivalent, i.e., intrinsic, masses $m_{eqj},$ equivalent dampings $c_{eqj},$ equivalent natural frequencies ${\omega }_{eqn,j}$ and ${\omega }_{eqd,j}$ (j = 1, 2, 3) of fractional oscillators, which are nonlinear with the power laws in terms of oscillation frequency ω as stated in Section 4 and Section 5.

The significance of the presented theory with respect to three classes of fractional oscillators in both theory and practice is about the closed form analytic formulas of the responses to fractional oscillators explained in Section 6, Section 7, Section 8, Section 9 and Section 10 by using elementary functions, making the matters much better in engineering.

Note that power laws plays a role in understanding the nature in general, see, e.g., Gabaix et al. [82], Stanley [83]. As a matter of fact, the fractional order α relates to the fractal dimension, see Lim et al. [20,21,22]. Thus, my study of the power laws previously stated is quite beginning in the aspect of fractional oscillations. Further research is needed in future. In addition to that, our future work will consider the applications of the present equivalent theory of the fractional oscillators to fractional noise in communication systems (Levy and Pinchas [84], Pinchas [85]), partial differential equations, such as transient phenomena of complex systems or fractional diffusion equations (Toma [86], Bakhoum and Toma [87], Cattani [88], Mardani et al. [89]).

12. Conclusions

We have established a theory of equivalent oscillators with respect to three classes of fractional oscillation systems. Its principle is to represent a fractional oscillator with constant coefficients (mass and damping) by a 2-order oscillator equivalently with variable mass and damping. The analytic expressions of equivalent masses, equivalent dampings, equivalent damping ratios, equivalent natural frequencies, and equivalent frequency ratios have been presented. We have revealed that the equivalent masses and dampings of three classes of fractional oscillators follow power laws in terms of oscillation frequency. By using elementary functions, we have put forward the closed form representations of responses (free, impulse, step, frequency, sinusoidal) to three classes of fractional oscillators. Additionally, analytic expressions of the logarithmic decrements of three classes of fractional oscillators have been proposed. As by products, we have stated the representations of four types of the generalized Mittag-Leffler functions in the closed form with elementary functions.