Edge-Version Atom-Bond Connectivity and Geometric Arithmetic Indices of Generalized Bridge Molecular Graphs
Abstract
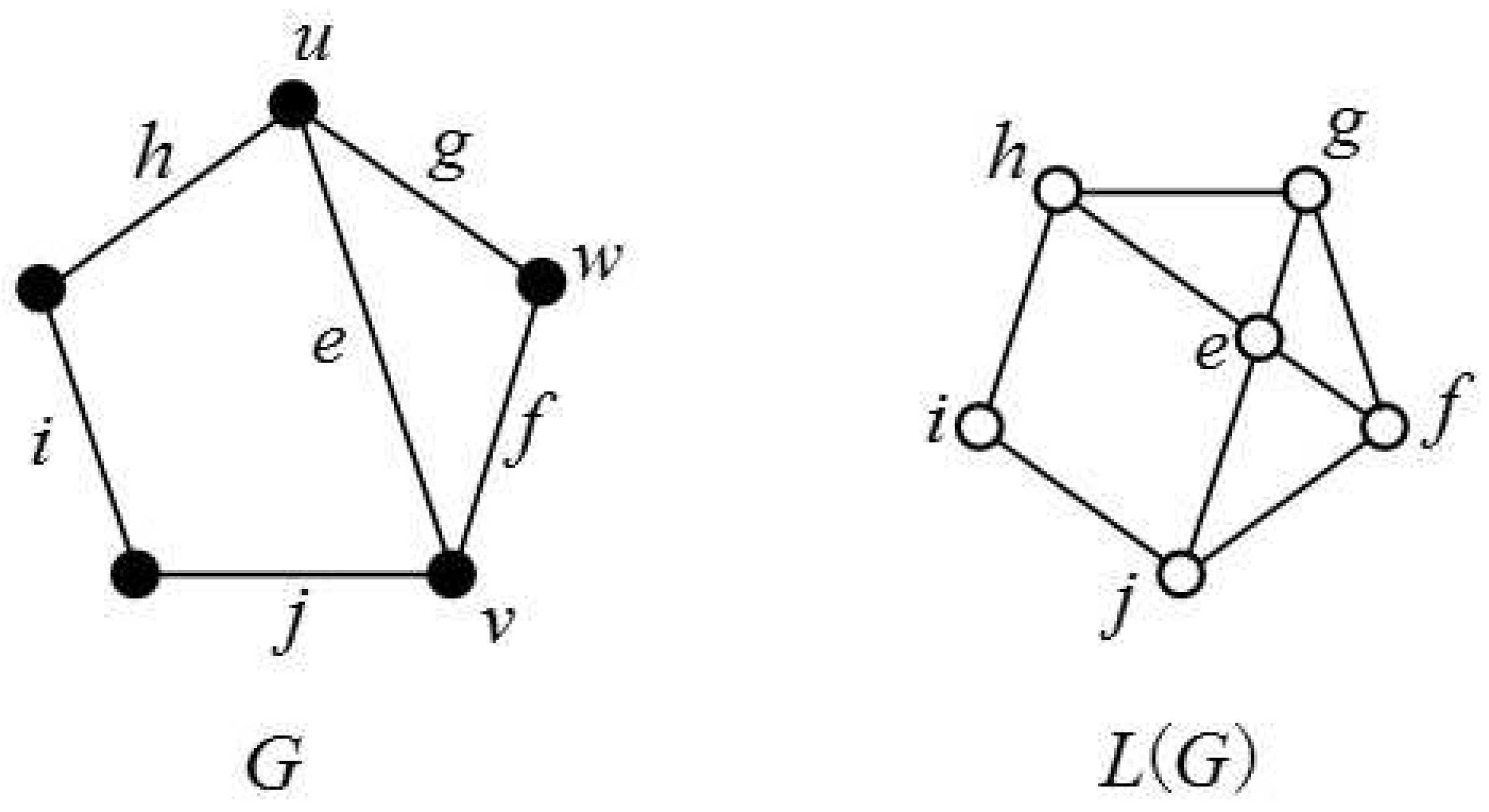
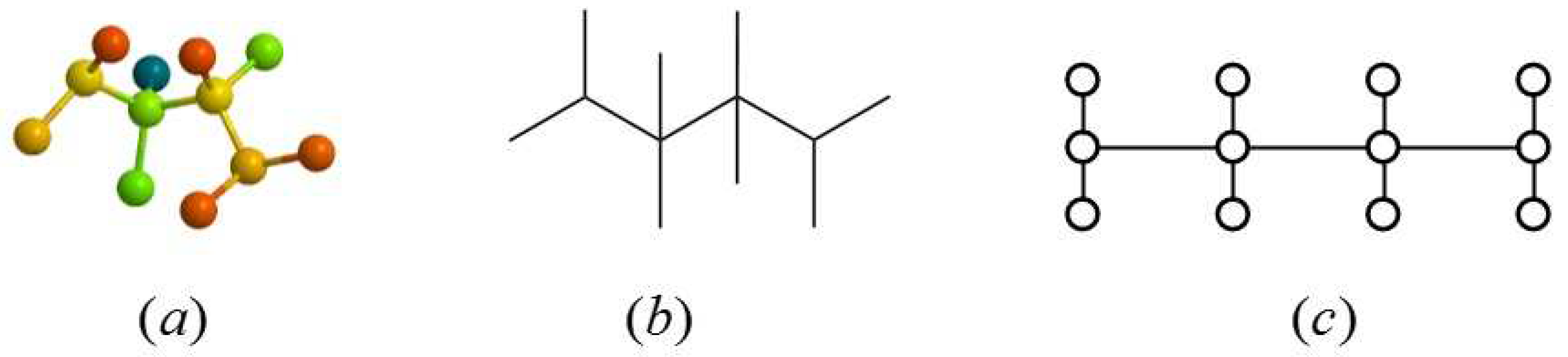
:1. Introduction
2. Main Results and Proofs
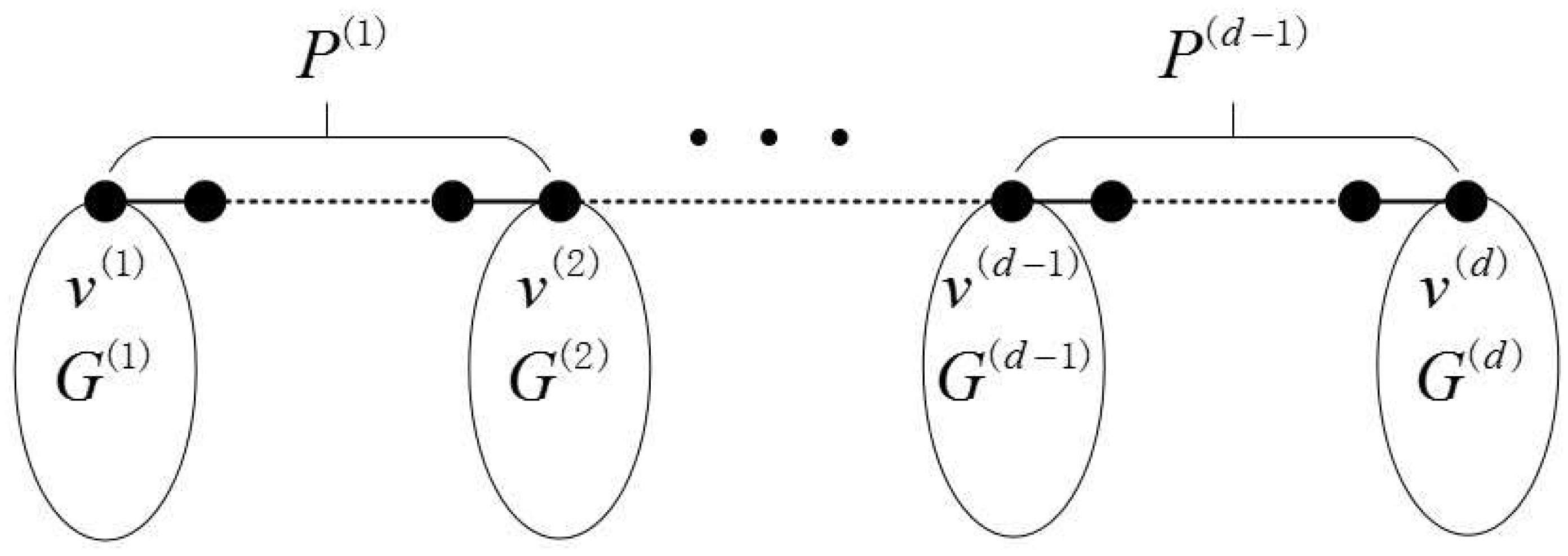
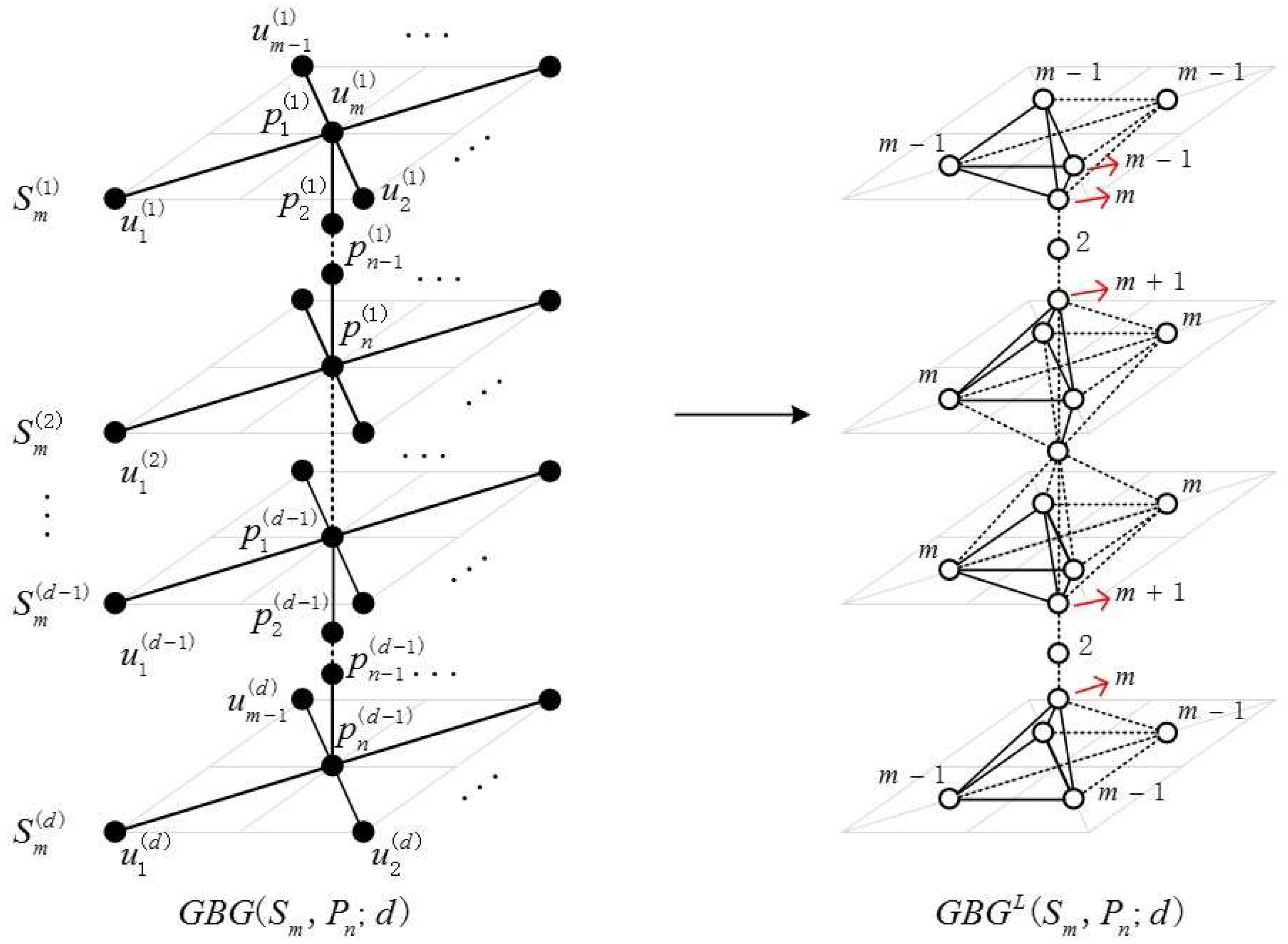
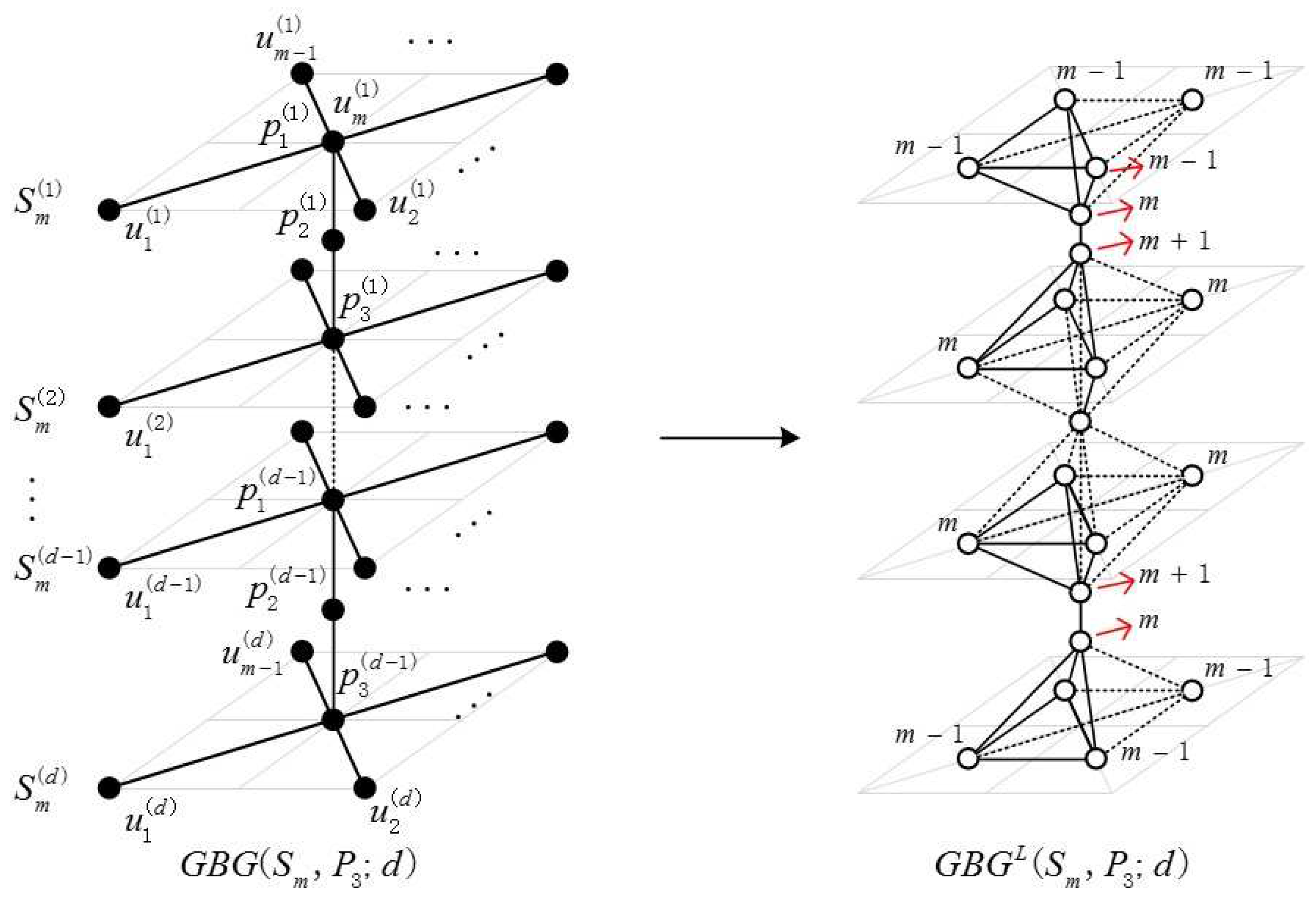
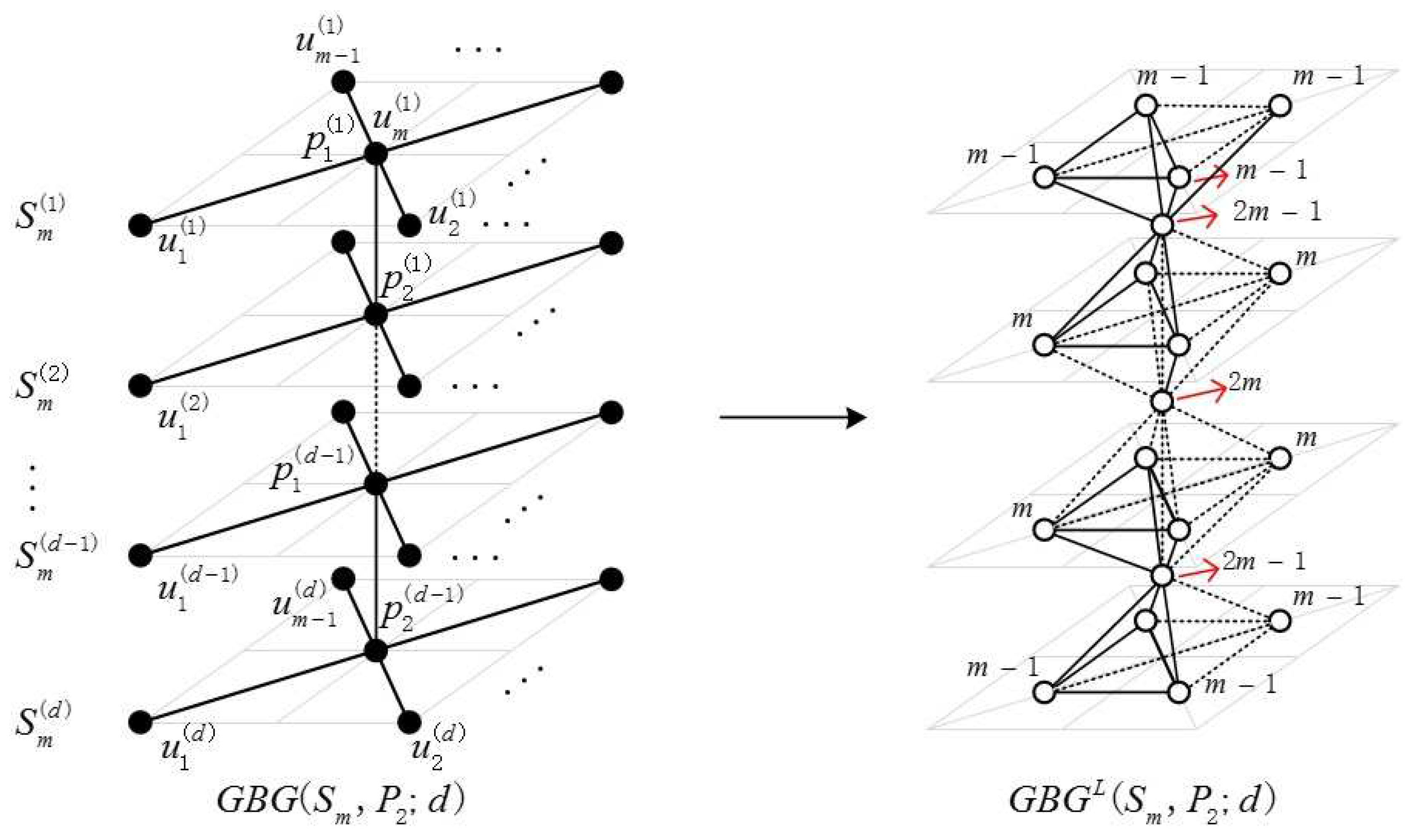
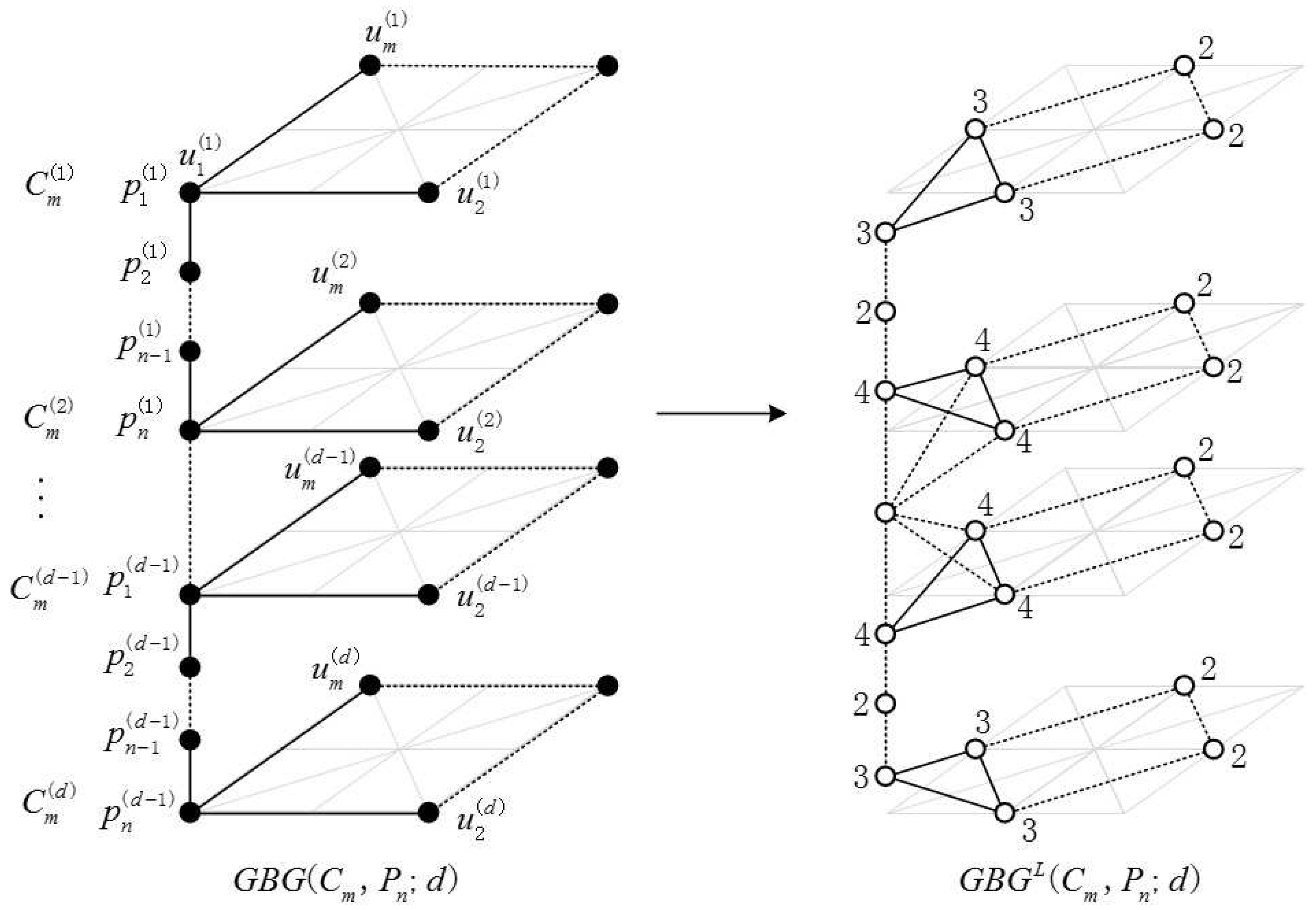
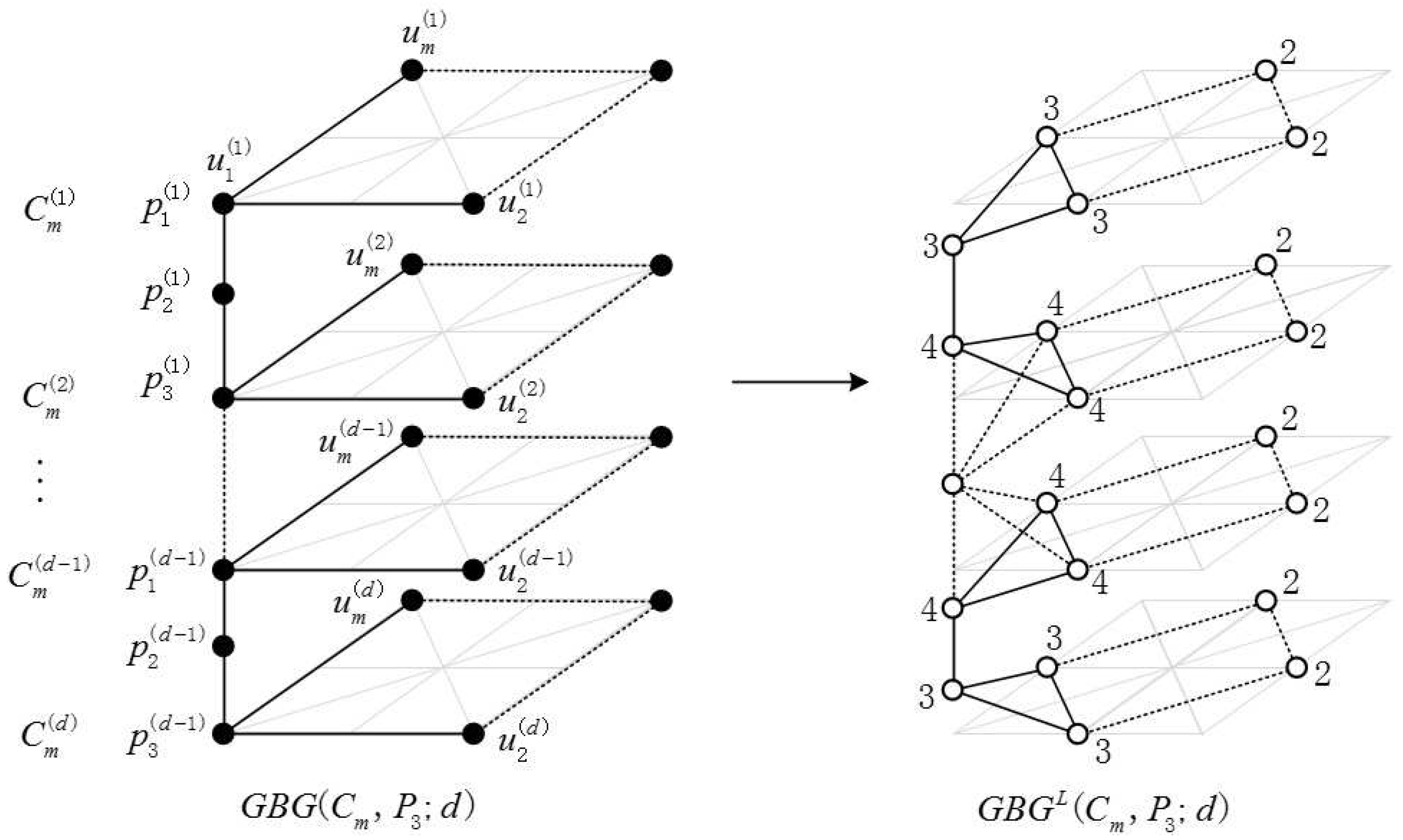
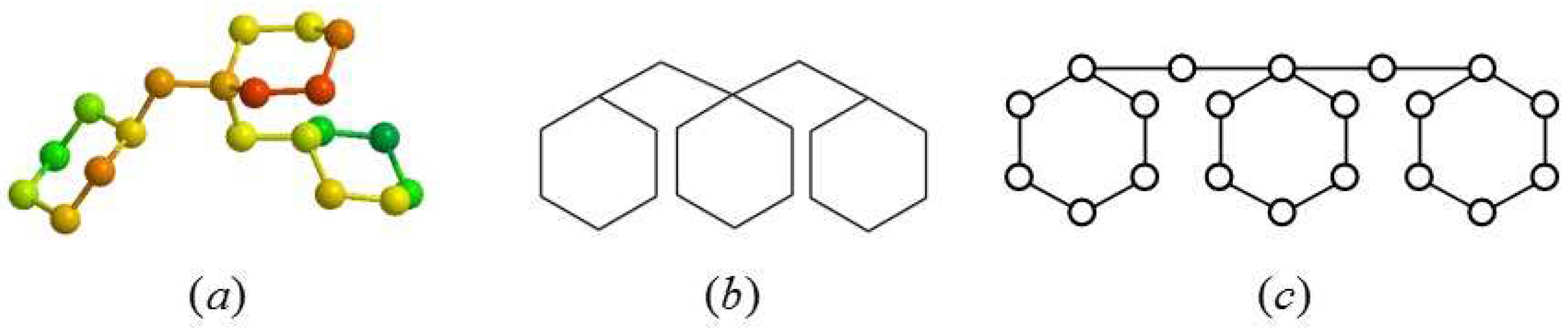
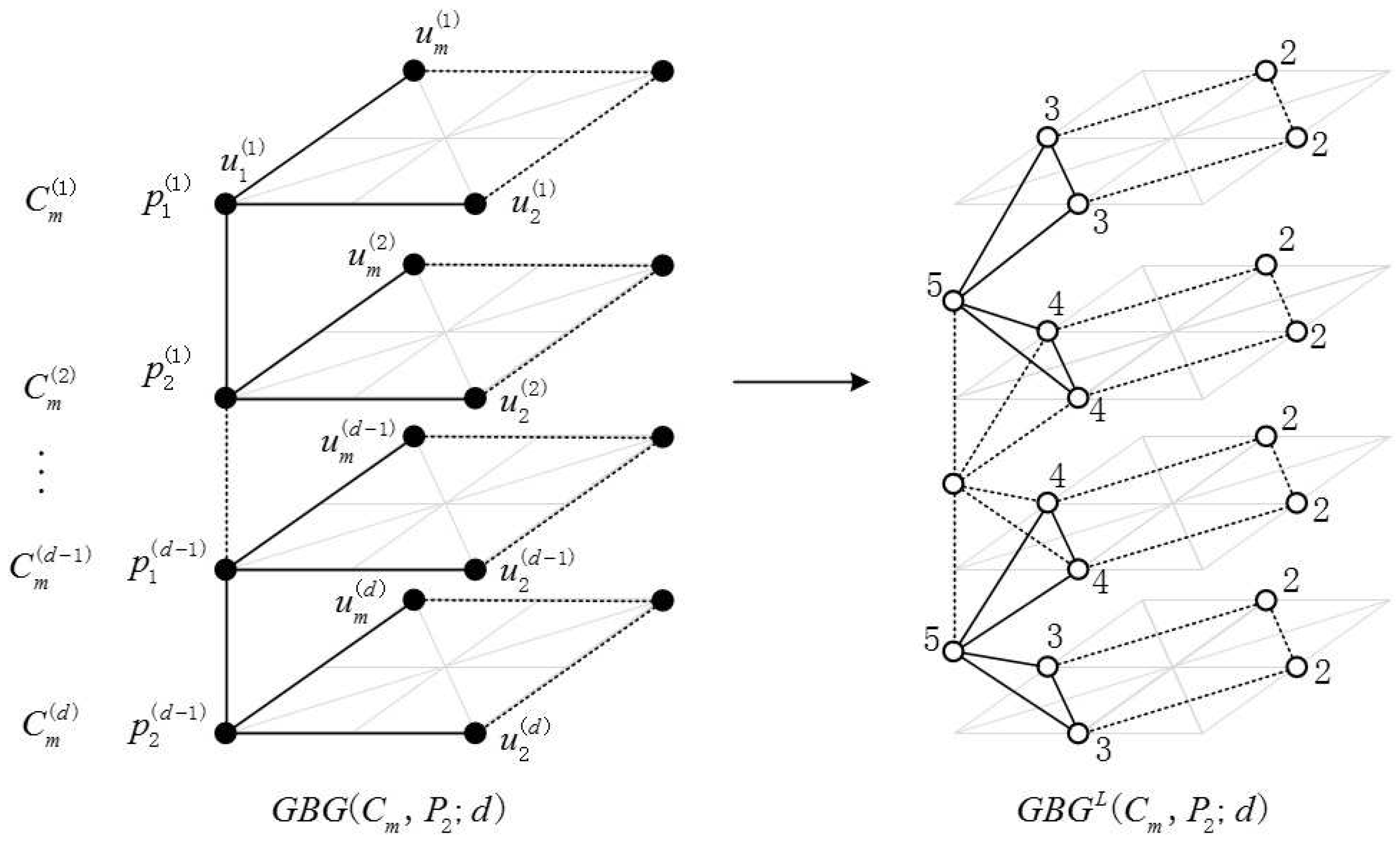
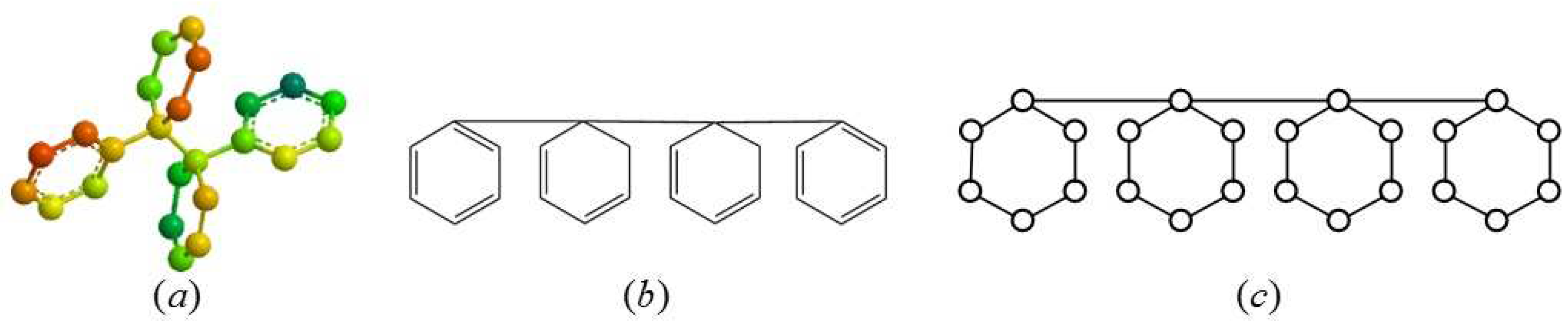
2.1. Definition of the Generalized Bridge Molecular Graph
2.2. Results and Discussion
3. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Harary, F.; Norman, R.Z. Some properties of line digraphs. Rendiconti del Circolo Matematico di Palermo 1960, 9, 161–169. [Google Scholar] [CrossRef]
- Wiener, H. Structural determination of paraffin boiling points. J. Am. Chem. Soc. 1947, 69, 7–20. [Google Scholar] [CrossRef]
- Iranmanesh, A.; Gutman, I.; Khormali, O.; Mahmiani, A. The edge versions of the wiener index. MATCH Commun. Math. Comput. Chem. 2009, 61, 663–672. [Google Scholar]
- Devillers, J.; Balaban, A.T. Topological Indices and Related Descriptors in QSAR and QSPR; CRC Press: Boca Raton, FL, USA, 1999. [Google Scholar]
- Gao, W.; Farahani, M.R.; Wang, S.H.; Husin, M.N. On the edge-version atom-bond connectivity and geometric arithmetic indices of certain graph operations. Appl. Math. Comput. 2017, 308, 11–17. [Google Scholar] [CrossRef]
- Gao, W.; Siddiqui, M.K.; Imran, M.; Jamil, M.K.; Farahani, M.R. Forgotten topological index of chemical structure in drugs. Saudi Pharm. J. 2016, 24, 258. [Google Scholar] [CrossRef] [PubMed]
- Nikolić, S.; Kovačević, G.; Miličević, A.; Trinajstić, N. The Zagreb indices 30 years after. Croat. Chem. Acta 2003, 76, 113–124. [Google Scholar]
- Estrada, E.; Torres, L.; Rodriguez, L.; Gutman, I. An atom-bond connectivity index: Modelling the enthalpy of formation of Alkanes. Indian J. Chem. 1998, 37A, 849–855. [Google Scholar]
- Dimitrov, D. Efficient computation of trees with minimal atom–bond connectivity index. Appl. Math. Comput. 2013, 224, 663–670. [Google Scholar] [CrossRef]
- Shao, Z.; Wu, P.; Gao, Y.; Gutman, I.; Zhang, X.J. On the maximum ABC index of graphs without pendent vertices. Appl. Math. Comput. 2017, 315, 298–312. [Google Scholar] [CrossRef]
- Shao, Z.; Wu, P.; Zhang, X.; Dimitrov, D.; Liu, J.B. On the maximum ABC index of graphs with prescribed size and without pendent vertices. IEEE Access 2018, 6, 27604–27616. [Google Scholar] [CrossRef]
- Farahani, M.R. The edge version of atom bond connectivity index of connected graph. Acta Univ. Apul. 2012, 36, 277–284. [Google Scholar]
- Gao, W.; Husin, M.N.; Farahani, M.R.; Imran, M. On the Edges Version of Atom-Bond Connectivity Index of Nanotubes. J. Comput. Theor. Nanosci. 2017, 13, 6733–6740. [Google Scholar] [CrossRef]
- Farahani, M.R. The Edge Version of Geometric-Arithmetic Index of Benzenoid Graph. Proc. Romanian Acad. Ser. B 2013, 15, 95–98. [Google Scholar]
- Vukicevic, D.; Furtula, B. Topological index based on the ratios of geometric and arithmetical means of end-vertex degrees of edges. J. Math. Chem. 2009, 46, 1369–1376. [Google Scholar] [CrossRef]
- Martińez–Peŕez, A.; Rodriǵuez, J.M.; Sigarreta, J.M. CMMSE: A new approximation to the geometric–arithmetic index. J. Math. Chem. 2017, 4, 1–19. [Google Scholar]
- Baig, A.Q.; Imran, M.; Khalid, W.; Naeem, M. Molecular description of carbon graphite and crystal cubic carbon structures. Can. J. Chem. 2017, 95, 674–686. [Google Scholar] [CrossRef]
- Gutman, I.; Furtula, B.; Das, K.C. Extended energy and its dependence on molecular structure. Can. J. Chem. 2017, 95, 526–529. [Google Scholar] [CrossRef]
- Mahmiani, A.; Khormali, O.; Iranmanesh, A. On the edge version of geometric-arithmetic index. Dig. J. Nanomater. Biostruct. 2012, 7, 411–414. [Google Scholar]
- Zafar, S.; Nadeem, M.F.; Zahid, Z. On the edge version of geometric-arithmetic index of nanocones. Stud. Univ. Babes-Bolyai Chem. 2016, 61, 273–282. [Google Scholar]
- Gao, W.; Husin, M.N.; Farahani, M.R.; Imran, M. On the Edges Version of Atom-Bond Connectivity and Geometric Arithmetic Indices of Nanocones CNCk. J. Comput. Theor. Nanosci. 2016, 13, 6741–6746. [Google Scholar] [CrossRef]



© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Wu, X.; Akhter, S.; Jamil, M.K.; Liu, J.-B.; Farahani, M.R. Edge-Version Atom-Bond Connectivity and Geometric Arithmetic Indices of Generalized Bridge Molecular Graphs. Symmetry 2018, 10, 751. https://doi.org/10.3390/sym10120751
Zhang X, Wu X, Akhter S, Jamil MK, Liu J-B, Farahani MR. Edge-Version Atom-Bond Connectivity and Geometric Arithmetic Indices of Generalized Bridge Molecular Graphs. Symmetry. 2018; 10(12):751. https://doi.org/10.3390/sym10120751
Chicago/Turabian StyleZhang, Xiujun, Xinling Wu, Shehnaz Akhter, Muhammad Kamran Jamil, Jia-Bao Liu, and Mohammad Reza Farahani. 2018. "Edge-Version Atom-Bond Connectivity and Geometric Arithmetic Indices of Generalized Bridge Molecular Graphs" Symmetry 10, no. 12: 751. https://doi.org/10.3390/sym10120751
APA StyleZhang, X., Wu, X., Akhter, S., Jamil, M. K., Liu, J.-B., & Farahani, M. R. (2018). Edge-Version Atom-Bond Connectivity and Geometric Arithmetic Indices of Generalized Bridge Molecular Graphs. Symmetry, 10(12), 751. https://doi.org/10.3390/sym10120751







