Abstract
Hyperspectral imaging technology with sufficiently discriminative spectral and spatial information brings new opportunities for robust facial image recognition. However, hyperspectral imaging poses several challenges including a low signal-to-noise ratio (SNR), intra-person misalignment of wavelength bands, and a high data dimensionality. Many studies have proven that both global and local facial features play an important role in face recognition. This research proposed a novel local features extraction algorithm for hyperspectral facial images using local patch based low-rank tensor decomposition that also preserves the neighborhood relationship and spectral dimension information. Additionally, global contour features were extracted using the polar discrete fast Fourier transform (PFFT) algorithm, which addresses many challenges relevant to human face recognition such as illumination, expression, asymmetrical (orientation), and aging changes. Furthermore, an ensemble classifier was developed by combining the obtained local and global features. The proposed method was evaluated by using the Poly-U Database and was compared with other existing hyperspectral face recognition algorithms. The illustrative numerical results demonstrate that the proposed algorithm is competitive with the best CRC_RLS and PLS methods.
1. Introduction
Intra-person differences in terms of emotions, view point, illumination variations, and occlusion effects are still a challenging problem for face recognition tasks. It is necessary to research and develop an effective method for exploring the unexposed information rather than the structure and texture in a facial spatial domain. From this point of view, hyperspectral imaging (HSI) technology is considered as a technical solution since it provides the information beyond the human visible spectrum. The other reason is that the cost of hyperspectral cameras has been significantly reduced due to the rapid development of relevant technology. Therefore, hyperspectral imaging has become a popular tool for object detection and recognition.
The structure of a hyperspectral image is in a 3D data cube format that comprises of two spatial dimensions and one spectral dimension. As shown in Figure 1a, a hyperspectral image consists of tens to hundreds of bands, which increases the intra-face discrimination. As shown in Figure 1b, each pixel point of a facial image is represented as a spectrum or a vector which indicates the reflectance as a function of wavelength that is able to enhance spatial heterogeneities. The cause of the difference in spectral reflectance between the same points of inter-person (as an example of Figure 1) or intra-person skin are chromophores such as melanin, water, oxygenated or deoxygenated hemoglobin, and other chemicals [1,2]. On the other hand, the processing of hyperspectral images has a number of challenges. For example, a high dimension hyperspectral facial image increases the computational complexity of the process. Low-SNR information in hyperspectral facial images has an impact on the experimental performance. The phenomenon of intra-person misalignment variation that should be avoided also affects hyperspectral image processing. Furthermore, the hyperspectral reflectance feature of facial skin can be affected by environmental factors such as blood vessel pattern and pigmentation variation over time; these features—including blood vessel patterns and pigmentation variation—may exist throughout an individual’s lifetime. Apart from the above challenges, there are few publicly available hyperspectral face libraries for researchers to use, so the related research have been fewer in number.
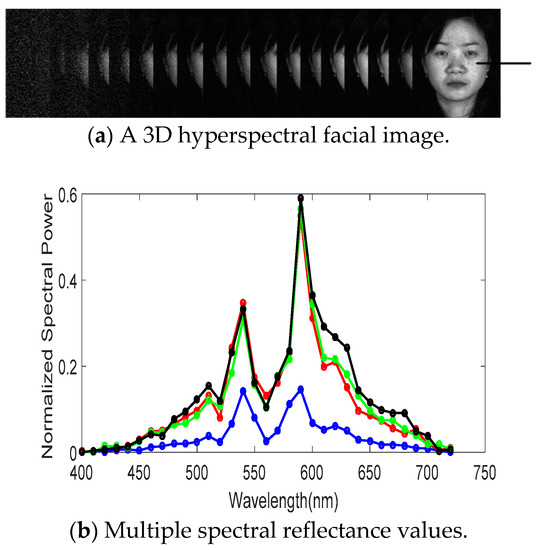
Figure 1.
Spectral reflectance values of a hyperspectral facial image at the check of the same area of interest in four different periods.
Pan et al. [3] demonstrated that the spectral-only algorithm performed better than the spatial-based face recognition approach. In [3], the experimental tests were based on the hyperspectral face database with 31 spectral bands ranging from 700 nm to 1000 nm at hand-picked locations. Unfortunately, such experiments could not be duplicated on other public hyperspectral facial image databases [4]; Uzair et al. [5] proved that the spectral-only algorithm was unsatisfied for face classification based on either their own established face database or two public hyperspectral facial image databases. Di et al. [6] proposed a feature band selection algorithm and three recognition methods for hyperspectral facial image processing including a whole band principal component analysis (PCA), a single band PCA with decision level fusion, and a band subset fusion based PCA. Uzair et al. [7] proposed a spatial-spectral feature extraction method based on the 3D discrete cosine transform and formulated a PLS regression for accurate classification. They [8] further put forward a band fusion method using spatial-spectral covariance to solve the problem of misalignment bands for a hyperspectral facial image. Shen et al. [9] proposed a 3D Gabor wavelet, which incorporated both spatial and spectral information. Zhu et al. [10] improved the 3D Gabor feature extraction algorithm using the memetic method to optimize parameters for accurate classification. Pan et al. [11] generated a spectral-face that preserved high-spatial and high-spectral resolution to achieve better classification results than that of eigenfaces [12] using single and multiple bands.
Fortunately, technology for grayscale or RGB based facial image processing has been explored and matured in the past few years, and these algorithms can be extended to hyperspectral facial image processing. Feature representation plays an important role in the processing of large-scale, complex datasets or high-dimensional structure data with low intrinsic dimension. The sparse representation [13,14,15] concept from neurobiology transforms the visual natural images into appropriate sparse expressions quickly and accurately. It is a low cost technology with suitable dictionaries and sparse coefficients to simplify learning tasks as well as reduce the modeling complexity. Sparse representation is a linear data analysis method based on vectors and matrices. In contrast, tensor decomposition [16,17,18] is a multi-linear data analysis with three or more dimension input data. Vasilescu et al. [16] introduced the ‘TensorFaces’ method using the higher order singular value decomposition (HOSVD) to naturally analyze the multifactor structure of image ensembles such as scene geometry, viewpoint, and illumination conditions. However, its weakness lay in the difficulty in obtaining a large number of the required coefficients of facial images in the texting phase. Savas et al. [17] adopted the factor coefficients learning algorithm, which created respective subspaces for each individual facial image in order to reduce factor coefficients. Furthermore, Fourier transform based algorithms play an important role in image feature extraction [19,20,21,22,23,24]. Lai et al. [19] proposed a holistic facial representation method that combined wavelet transform and Fourier transform which had the advantage of remaining invariant in translation, scale, and on-the-plane rotation. Sao et al. [20] proposed a facial imaging representation method based on the phase spectrum of 2D Fourier transform, which preserved the edges locations for a given facial image and reduced the adverse effect of illumination. Jing et al. [21] applied the fractional Fourier transform (FrFT) into the discrimination analysis technique for robust face recognition. Zhang et al. [22] proposed a facial expression recognition algorithm based on Fast Fourier Transform (FFT) which combined the amplitude spectrum and the phase spectrum with two different images, respectively, to generate a hybrid image. Likewise, Angadi et al. [23] proposed a robust face recognition model using Polar FFT features as symbolic data.
Ensemble classifier, as a very efficient technique, has good classification performance by combining of multiple classifiers. That is, the classification performance of the ensemble classifier is better than that of the best single classifier [25,26,27,28]. Yan et al. [25] designed a set of multiple correlation filters matching different face sub-regions to optimize the overall correlation outputs. Li et al. [26] trained an ensemble model able to minimize the empirical risk for the patch-representation features. Cheng et al. [29] gathered several classification results obtained from different algorithms to generate a regional voting framework embedded by a holistic algorithm and then conducted a final decision. In the present study, the above-mentioned methods were given attention and were introduced into hyperspectral face recognition processing. This paper presents a novel ensemble classifier algorithm that combined both the local classifiers using the tensor decomposition feature extraction method and global classifiers using the pseudo-polar fast Fourier transform feature extraction method for hyperspectral facial image (HFI) processing. The first research focus was to apply the Trucker decomposition [30,31] and a tensor network contractor (NCON) algorithm [32,33] to achieve dimensionality reduction and local feature extraction simultaneously Then, a local ensemble classifier (LEC) could be obtained by combination multiply local Naive Bayesian (NB) classifiers [34] using particle swarm optimization (PSO) [35]. The second research focus was to apply polar discrete fast Fourier transform (PFFT) to describe holistic face contour features, which focused on several challenging problems such as illumination, expression, orientation, and aging changes. Finally, we combined the global classifier and the LEC to obtain a satisfied decision using the PSO method. The flow chart of the proposed algorithm is shown in Figure 2.
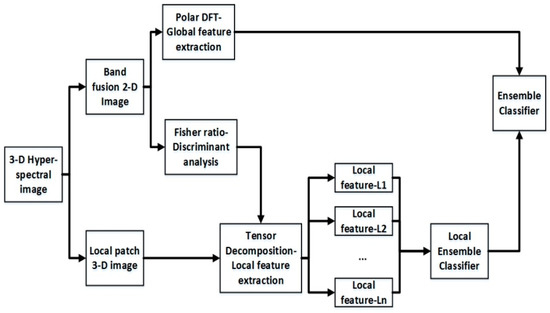
Figure 2.
Flow chart of the proposed algorithm.
Note that several feature extracting methods for hyperspectral 3D image are based on a fused 2D image as illustrated in Figure 3. Since the Fourier transform based global feature extraction module and weight learning modules are based on the fusion of the 2D hyperspectral facial image, in this case, Uzair’s algorithm [8] was employed to incorporate the local spatial information as well as efficiently remove the noise by averaging the spectral and spatial dimensions; in addition, it effectively dealt with inter-band alignment errors such as eye blinks or small expression variations.

Figure 3.
Band fusion process of a hyperspectral facial image. The images (left) represent a 3D hyperspectral image, and the (right) image is the fused 2D image.
The remainder of this study is organized as follows. Section 2 reviews the related work of the tensor algorithm. Section 3 introduces the proposed ensemble classifier model. Section 4 discusses the experimental results obtained from two hyperspectral facial image databases. This study is summarized in Section 5.
2. Related Work
In fact, tensors have two distinct features including exchange rules and multidimensional properties for the coordinate system. It also provides a powerful mathematical framework tool for analyzing the multifactor structured high-dimensional data, especially in the field of pattern recognition and machine vision; this section provides some notions and basic definitions about the tensor used in the present research work. High-order tensor data distinguished from a vector (first-order tensor) and a matrix (second-order tensor) should be compressed into a smaller size or factorized into an easy-to-interpret component. The Tucker decomposition (TKD) and canonical polyadic decomposition (CPD) [31,32] are mainly introduced in the following.
Tensors can be considered as a set of multidimensional data arrays, denoted by underlined capital letters A; matrices are denoted by uppercase letters A, and vectors are denoted by lower-case letters y. The first notion of a tensor related to this research is Mode-d vectors, which are a process of unfolding a P-order tensor into a matrix like form in which by keeping a fixed index Ld and varying the other indices. Next, we discuss several different tensor products as follows. The mode-d product of a tensor and a matrix is expressed as , which is equivalent to . An outer product of a tensor is defined as , where and yields . Since CPD decomposes a high-order tensor into a multiple tensor sum of rank-1, it is typically used for factorizing data into easy-to-interpret components. For example, considering rank-1 decomposition for a diagonal tensor , it can be expressed as an outer product sum of N vectors under a special case:
where sum equals to 1. The rank of the Pth order tensor represents the minimum number of a rank-1 tensor that is in a linear combination, denoted as . The rank-k of the Pth order tensor is the dimension of k-mode vector unfolding vector space, denoted as .
In general, the Tucker core cannot be diagonalized, so unconstrained Tucker decomposition (TKD) mostly achieves the goal of dimensionality reduction. Some constraints containing orthogonality, sparsity, and nonnegativity are often imposed on basis vectors or core tensors for a TKD to obtain meaningful and unique factors or component matrices. In this study, we adopted a model integrated orthogonality constraint into basis tensors called higher order singular value decomposition (HOSVD), which is similar to the SVD decomposition of matrix. The SVD intends to orthogonalize two spaces and decomposes a matrix T as , but this product can be given as for a tensor decomposition. Likewise, HOSVD orthogonalizes P spaces and expresses a tensor as a mode-p product in P-orthogonal spaces:
Unfold vector equivalent form of Equation (2) as a series of mode-k product (Kronecker product):
3. Extraction Features for Hyperspectral Facial Image
This subsection describes the proposed algorithms including a path-based low rank local features extraction method and a PFFT-based global features extraction method.
3.1. Local Feature Extraction
3.1.1. Discriminative Patch Selection
Before local features extraction processing, we first selected the discriminative local feature spaces (eyebrows, eyes, nose, etc.) called patches using the classic algorithm of the Fisher ratio. The candidate patches with different sizes generated from an image are employed to construct multiple local classifiers, which have different discriminating capacities. However, these patches usually contribute differently to the classification result. Therefore, the selection of patches is based on the largest discriminating capacities as well as the smallest correlation. In this paper, the Fisher ratio was exploited to measure the class separation of different patches using local binary patterns (LBP) [36,37] and Gabor [38,39] features; these features are considered as the best operators to describe facial images. The selection process is clearly shown in Figure 4. Note that LBP is a powerful tool for coding facial appearance and texture fine details while Gabor features encode facial shape and appearance information on a series of coarser scales. It is clear that their rich complementarity information makes the fused features more discriminatory. The original LBP proposed by Ojiala et al. [40] as a texture feature extraction operator was defined within a window of 3 × 3 pixels.
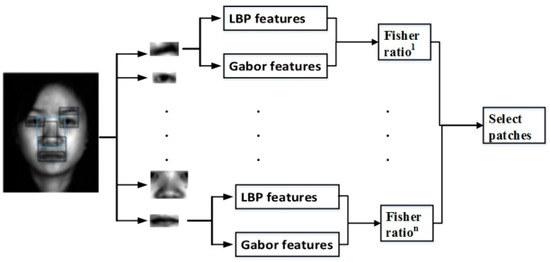
Figure 4.
Discriminative patch selection by the Fisher ratio.
It is clear that a small area within a fixed radius is clearly not sufficient for variable dimensions and frequency textures. Furthermore, the LBP operator is grayscale invariant, but it is not rotationally invariant. Ojala et al. [41] improved a LBP operator by extending a 3 × 3 pixels neighborhood to a circular neighborhood with any radius R and any number of sampling points P. Hence, it generated P2 patterns, which raised a large number of data processing problems. In order to overcome this weakness, a uniform pattern LBP was employed to solve this problem. The uniform pattern, as defined as the cyclic binary number corresponding to an LBP, has two hops from 0 to 1 or from 1 to 0. In the present research, we used the uniform pattern LBP method to extract features.
On the other hand, the use of Gabor wavelets in extracting the local space and frequency domain information of the target object is very similar to the visual stimuli response of simple cells in the human visual system. Gabor wavelets are also sensitive to the image edges, which provide better directional and scale characteristics. Moreover, Gabor wavelets are insensitive to illumination changes that can provide good adaptability to illumination change. Therefore, Gabor wavelets have been widely used in visual information understanding, especially in the face recognition domain [38,39]. Gabor filters are obtained by multiplying Gaussian filters and a complex wave. A commonly used form of Gabor filters is illustrated as follows:
where µ, v defines the direction and length for the Gabor kernel z, respectively. The parameter σ represents the standard deviation.
The evaluation of the class separation capacity for local feature spaces βk is presented by the Fisher ratio criterion, which is the simplest criterion [42]. A large βk value indicates better class separation capacity, where a multi-category case is explained as follows:
where Fij is a two-category case between the ith and the jth class, that is
where is the between-class scatter matrix, and is the within-class scatter matrix.
3.1.2. Discriminant Local Feature Extraction
The tensor tool for processing the hyperspectral data considers the neighborhood correlation across the spatial dimension and the global relationship among the spectral dimension unlike the HFI traditional re-arrangement as band interleaved by pixel (BIP) and band sequential (BSQ). Related studies have been applied by Li et al. [18], who utilized a robust low-rank tensor recovery algorithm to realize the dimensionality reduction for hyperspectral images which simultaneously preserved the global structure. Du et al. [43] proposed another application of this study that learned basis factors and components based on similarly grouped tensor patches to reconstruct the hyperspectral image. In addition, comparing the low-rank decomposition of higher-order tensors with low-rank decomposition of matrices (second-order tensors), a most significant advantage of the former is essentially unique under mild conditions, whereas the latter is never essentially unique, except in cases where the rank is equal to one, or where we impose additional constraints on the factor matrices [30]. However, a uniqueness condition provides a theoretical boundary for an accurate tensor or matrices decomposition.
A novel local feature extraction method using the tensor decomposition method included the following three steps. A number of patches with M different features (m = 1, 2, …, M) are extracted from an original (can be seen as a third-order tensor), where represents the spatial size and LS represents the spectral band number (lW < LW, lH < LH). The second step aims to integrate patches with the same features into a fourth-order tensor to extract discriminative features, as illustrated in Figure 5a. As the fourth-order tensors are redundant in both spatial and spectral modes, the third step is to establish a block-sparsity coefficient tensor and three dictionaries matrix to solve the problem of low SNR and high data dimensionality, as illustrated in Figure 5b.
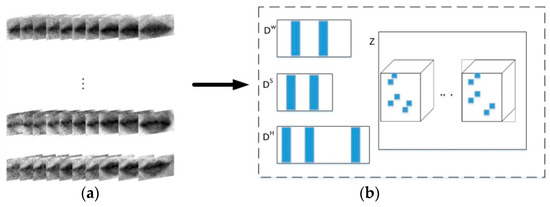
Figure 5.
(a) Local samples of mouth with fourth-order tensor form. (b) Sparse representation for a 4D tensor with a block-sparsity coefficient tensor and three dictionaries matrix.
Matrix dictionary learning represents all of the training samples as a sparse linear combination, expressed as A = DZ. Therefore, a dictionary optimization and enough sparsity of the coefficient can be performed simultaneously in the signal reconstruction process by the following optimization model:
where is a redundant dictionary composed of m atoms, and indicates a sparse coefficient vector. A sparse restriction operator can also be a l1 norm. Note that matrix dictionary learning can be expanded into 3D space tensor by:
where are the fourth-order grouped patches of the kth local feature for all examples; nk indicates the total number of kth patch features; and n is the total number of local features. In addition, , , and (lW × dW, lH × dH, lS × dS), are the redundant coefficient tensor of patch .
Since the tensor sparsity value is equal to the number of non-zero entries for a given tensor T, therefore, a origin redundant dictionary with a sparse limit is expressed as , where , , [44]. It is clear that for a grouped 4D tensor, Equation (8) can be rewritten as:
where , , and , and , , and represent the number of sparsity values that occurred in the kth local feature along the width, height, and spectral models, respectively. This function is much simpler than Equation (8) because there is no need to consider the tensor sparsity constraints. Meanwhile, the spectral bands lead to the dimensionality reduction. The rank parameters , , can be solved by the minimum description length (MDL) method based on the mode-i (i = 1, 2, 3) flattening of each input tensor [45].
A common task of a tensor network contractor (NCON) algorithm is the need to evaluate the product of multiple tensors sharing one or more summed indices. As illustrated in Figure 6, when the orthogonal basis factor and core features from the training data are obtained, discerning features (called LFT features) with tag information of training data are generated using a tensor network contractor (NCON) [33] algorithm, and discerning features are extracted for the test data using the basis factors obtained from the training data.
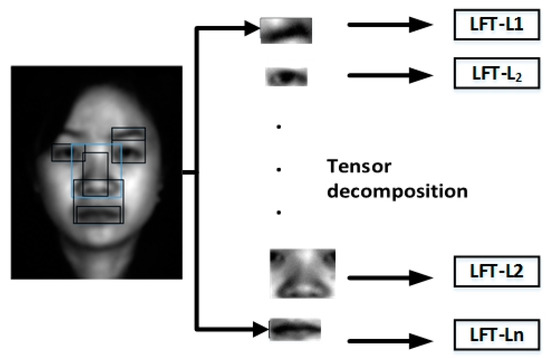
Figure 6.
Local patch features extraction by tensor decomposition.
3.2. Global Feature Extraction
Cartesian coordinates are not robust to rotated and scaled images such as a side facial image, but polar Fourier transform is a powerful tool for organizing the understanding of such rotated and scaled images. The pseudo-polar FFT provides a polar-like frequency coordinate system, which conducts exact rapid FT evaluation. Therefore, this paper adopted an algorithm called the polar discrete fast Fourier transform (PFFT) [46] for the hyperspectral facial images classification task. Considering a special case with variables u and v equal to 0, that is , which indicates that the zero-frequency term is proportional to the average value of [47]. Therefore,
where the is an average value of an input image f. As the coefficient of MN is usually large, so is the largest component, which is called the dc component. The dc component is the dominate value, so the dynamic range of an image spectrum are compressed, that is to say, the detailed features of an image are totally lost. In this case, the low frequency components of Fourier transform reflect the holistic attribute and the contour of a facial image. Thus, these low frequency features are robust to the local variations including facial expressions, noise, and so on.
In the proposed method, only the Fourier coefficients in low frequency of pseudo-polar fast Fourier transform are reserved as global features. More specifically, a single feature vector is formed by concatenating real and imaginary components in the low frequency, as shown in Figure 7.
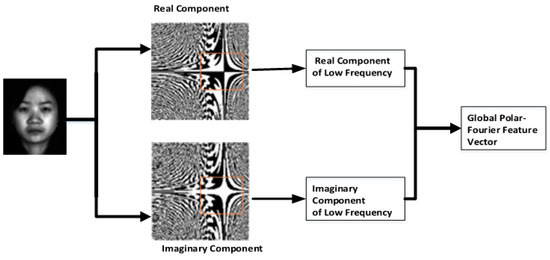
Figure 7.
Global feature extraction by PFFT.
4. Ensemble Classification for Hyperspectral Facial Images
A classification ensemble algorithm has been developed as a more robust and stable solution [48] compared to individual classification algorithm in the area of pattern recognition. As shown in [49], global and local features play a different role in face recognition, respectively. The global extraction algorithm describes the global contour features from whole face images. Local extraction algorithm reflects more detailed features from spatially partitioned image patches. For combining the advantages of global and local-based facial features, the ensemble classifier algorithm has become an important research topic. From this point of view, the weight learning related to the ensemble classifier is formulated as the feature classification ability problem of a single classifier. This proposed method improves the accuracy in robust facial image classification.
4.1. Construction of Ensemble Classifier
Discriminative features extraction can obtain the local and global features by tensor decomposition and the polar discrete fast Fourier transform (PFFT) algorithm, respectively. As a local feature embodies discriminatory information for a given facial image, its low dimensionality characteristic can facilitate the operation while the holistic features attributed by the facial organs and facial contour become robust to unconstrained conditions [49]. Obviously, global and local facial features play different roles in the classification process, respectively, thus single classifiers may make different decisions on test images. In this case, an ensemble classifier presents its superiority to single classifiers. A minimum reconstruction error is required for the weight learning of single classifiers.
The proposed ensemble method is divided into two parts: the ensemble of local patch classifiers (ELPC), and ensemble of local and global classifiers (ELGC) [50]. First, ELPC, denoted as , can be obtained by the selected single LPC, expressed as:
where dk is the kth LPC’s properly classified probability obtained by Native Bayes (NB) and wk represents the weight of kth LPC. Second, the is combined with the global classifier to form an ELGC, denoted as C,
where wc is the weight of LPC.
4.2. Combination of Multiple Classifiers
As explained in [48], different single classifiers offer complementary information regarding the instances to be classified. Hence, ensemble learning integrates the multiple discriminative decisions made by classifiers to improve the performance in terms of accuracy. Therefore, the proposed algorithm treats the weight learning as a function optimization problem, and the merits of the PSO introduced by Eberhart et al. [51] are simple and easily implemented without gradient information, few parameters; in particular, its natural real coding features are especially suitable for dealing with real optimization problems. It is also based on group iterations, but the particles search in the solution space to follow the optimal particles.
5. Results and Discussion
The following is a discussion on the influence of parameter on both the global and local classifier as well as a comparison between our algorithm with other fusion algorithms and classifications algorithms.
5.1. Hyperspectral Face Database
The experiments were based on the Hong Kong Polytechnic University Hyperspectral Face Database (PolyU–HSFD) gathered by Di et al. [6]. As shown in Figure 8, the database was acquired with the CRI’s VariSpec liquid crystal tunable filter (LCTF) and a halogen light indoor acquisition system, respectively. The database consisted of 25 data subjects of Asian descent including eight females and 17 males between 21–38 years of age. The varying poses included frontal, right, and left view of a subject, and two different time spans of 3–10 months as well as hairstyle changes and skin condition diversification. In data collection processing, positions of the camera, light, and subject were fixed. Each hyperspectral image data cube was 220 × 180 × 33 pixels, with 33 bands ranging from a 400–720 nm spectrum of a step size 10 nm. In this study, we randomly selected 16 out of 24 people including four front faces, three left faces, and three right faces. Therefore, each individual person had 10 hyperspectral image examples, and samples were randomly divided into gallery and probe groups with six and four examples per group, respectively.

Figure 8.
One person from the Polytechnic University Hyperspectral Face Database (PolyU–HSFD).
For all databases, we performed a ten-fold cross-validation experiment, randomly selecting the gallery/probe combination from the samples each time, and selecting average values of the 10 experimental results as the recognition rate of the evaluation algorithm.
5.2. Experiments on Global and Local Classifiers
For the LPF extraction process, an input facial image with 220 × 180 × 33 pixels was cropped into different sizes. In contrast, for a global feature extraction process, a fused facial image was scaled to 117 × 97 pixels in order to reduce the computational burden, however, the down scale does not affect the classification accuracy.
5.2.1. Experiments on the Global Classifier
The global classifier focuses on the low frequency Fourier coefficients including amplitude and phase for further classification. The experiment selected the approximate position with low frequency based on the Fourier diagram illustrated in Figure 6. As illustrated in Figure 9, FFT coefficients with a size of 40 × 40 pixels were identified after several attempts where the amplitude value and phase value were concatenated into a global Fourier feature vector with dimensions of 40 × 40 × 2 = 3200, and these feature vectors were processed by NB to obtain a global classifier.
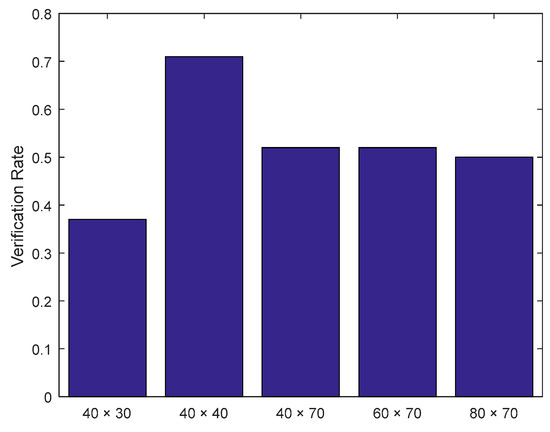
Figure 9.
Performance of different sizes of low frequency feature.
5.2.2. Experiments on the Local Classifier
This subsection presents the results of the selected discriminate patches and the rank parameters of each patch feature group, followed by the occlusion detection process and the experiment of local classifiers and their ensemble.
Rank Parameters Learning and Patch Selection
The candidate patches used for the experiment were in the range of [22, 67] × [27, 75]. In the patch selection process, the training sets are randomly divided into two subsets without any overlapping for prediction learning and evaluation learning, respectively. As shown in Figure 10, the first four discriminative patches learned by the Fisher ratio are presented. In addition, rank parameters were learned by the MDL algorithm as illustrated in Table 1, and the first two dimensions represent the spatial information and the third dimension represents the spectral information. For example, the spatial information for Mouth were 36 and 15; in contrast, its spectral information is two.

Figure 10.
The top four most discriminative patches learned by the Fisher ratio.

Table 1.
The most appropriate number of atoms for different local features.
Local Patch Classifiers and Their Ensemble
Local discriminative features were extracted using the tensor decomposition algorithm; as shown in Figure 11, the first nine histograms represent local patch classifiers (LPC). Since each individual LPC only exploits partial discriminating information for a certain facial region, hence, the ensemble of LPCs is required and this can be validated by the last histogram experimental results called ELPC, as shown in Figure 11. In addition, we also observed that a single LPC with low verification rate could not provide a satisfied classification performance.
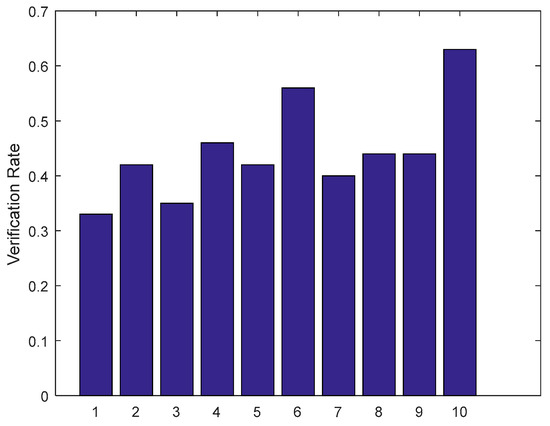
Figure 11.
Performance comparison of local patch classifiers and local ensemble classifier.
5.3. Experiments on the Ensemble Classifier
In order to make full use of the global and the local discriminative information to further improve the classification performance, the global classifier and ELPC were integrated to generate an ELGC. As each single classifier plays a different role in the ensemble process, the weight learning for them is important. Here, a variety of different ensemble methods and classifiers methods are presented in the following subsection.
5.3.1. Comparison of Different Ensemble Methods
In addition to the above mentioned particle swarm optimization (PSO) algorithm, the performance of weighted-majority vote, Fisher’s linear discriminant, and SWENC are also presented, as illustrated in Table 2. Mao et al. [52] proposed an ensemble method of weighted individual classifiers by singular value decomposition (SVD) for the 0–1 matrix (SWENC) based on linear mapping. As can be seen from Table 2, the performance of PSO was better than that of the other comparison methods.

Table 2.
Average recognition rates of different ensemble methods.
5.3.2. Comparison of Different Classification Methods
We compared our method with the best known classification methods based on the fused 2D facial images achieved by the band fusion algorithm [8]. In Table 3, the well-known classification methods include the PCA method, where 99% energy is preserved for classification; the LIBSVM method [53], which consists of principal component analysis (PCA); Fisher’s linear discriminant (FLD) analysis; and support vector machines (SVM). Note that the aim of FLD combined with PCA is to reduce dimensionality and extract relevant features. In contrast, the collaborative representation based classification with regularized least square (CRC_RLS) proposed by Zhang et al. [54] is a simple and efficient face classification scheme. As shown in Table 3, it can be seen that the proposed method was able to achieve better classification accuracy than that of the other existing classification methods. For example, the CRC_RLS and PLS achieved an accuracy of 0.71 and 0.75, respectively, in contrast, the proposed method was 0.79. From the ROC curve shown in Figure 12, we can also see the robustness of our algorithm. Such numerical results demonstrate that the method proposed in this paper is a highly competitive classification method.

Table 3.
Average recognition rates of different methods.
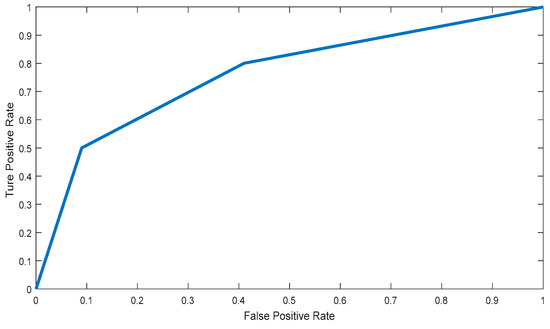
Figure 12.
ROC curve of the proposed method.
6. Conclusions
This paper presented a hyperspectral face recognition algorithm using the ensemble method by exploiting both global and local facial features. The numerical results obtained from the experiments illustrated that the global and local facial features had complementary information that could be combined to improve the classification accuracy rate. The proposed algorithm was tested on a standard hyperspectral database and compared with several existing well known algorithms. On the other hand, the fused facial image comprised the spectral information, not just the spatial information comprised in a grayscale/RGB image, which are efficient for face recognition processing. This is a significant advantage of the proposed method when compared to other existing methods such as CRC_RLS and PLS. In our experiment, it was found that the locally ensemble classifier did not present the deserved advantage when compared to a global classifier. From this point of view, future work needs to increase more discriminative information by selecting more local patches or learning a better ensemble method.
Author Contributions
M.W. conceived of the presented idea and verified the analytical methods; L.Z. participated in the revision and correction of the article; Y.Z. discussed the findings and monitored the results; D.W. monitored the results.
Funding
The research leading to these results has received funding from the Shandong Province Science Key Research and Development Project (2016GGX101016).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Lu, G.; Fei, B. Medical hyperspectral imaging: A review. J. Biomed. Opt. 2014, 19, 10901. [Google Scholar] [CrossRef] [PubMed]
- Zonios, G.; Bykowski, J.; Kollias, N. Skin Melanin, Hemoglobin, and Light Scattering Properties Can Be Quantitatively Assessed In Vivo Using Diffuse Reflectance Spectroscopy. J. Investig. Dermatol. 2001, 117, 1452–1457. [Google Scholar] [CrossRef] [PubMed]
- Pan, Z.; Healey, G.E.; Prasad, M.; Tromberg, B.J. Face recognition in hyperspectral images. IEEE Trans. Pattern Anal. Mach. Intell. 2003, 25, 1552–1560. [Google Scholar]
- Ryer, D.M.; Bihl, T.J.; Bauer, K.W.; Rogers, S.K. QUEST hierarchy for hyperspectral face recognition. Adv. Artif. Intell. 2012, 2012, 1. [Google Scholar] [CrossRef]
- Uzair, M.; Mahmood, A.; Shafait, F.; Nansen, C.; Mian, A. Is spectral reflectance of the face a reliable biometric? Opt. Express 2015, 23, 15160–15173. [Google Scholar] [CrossRef] [PubMed]
- Di, W.; Zhang, L.; Zhang, D.; Pan, Q. Studies on Hyperspectral Face Recognition in Visible Spectrum with Feature Band Selection. IEEE Trans. Syst. Man Cybern. Part A Syst. Hum. 2010, 40, 1354–1361. [Google Scholar] [CrossRef]
- Uzair, M.; Mahmood, A.; Mian, A. Hyperspectral Face Recognition using 3D-DCT and Partial Least Squares. In Proceedings of the BMVC, Bristol, UK, 9–13 September 2013. [Google Scholar]
- Uzair, M.; Mahmood, A.; Mian, A. Hyperspectral Face Recognition with Spatiospectral Information Fusion and PLS Regression. Image Process. IEEE Trans. 2015, 24, 1127–1137. [Google Scholar] [CrossRef]
- Shen, L.; Zheng, S. Hyperspectral face recognition using 3D Gabor wavelets. In Proceedings of the International Conference on Pattern Recognition, Tsukuba, Japan, 11–15 November 2012; pp. 1574–1577. [Google Scholar]
- Zhu, Z.; Jia, S.; He, S.; Sun, Y.; Ji, Z.; Shen, L. Three-dimensional Gabor feature extraction for hyperspectral imagery classification using a memetic framework. Inf. Sci. 2015, 298, 274–287. [Google Scholar] [CrossRef]
- Pan, Z.; Healey, G.; Tromberg, B. Comparison of Spectral-Only and Spectral/Spatial Face Recognition for Personal Identity Verification. Eurasip J. Adv. Signal Process. 2009, 2009, 8. [Google Scholar] [CrossRef]
- Turk, M.A.; Pentland, A.P. Face recognition using eigenfaces. J. Cogn. Neurosci. 2012, 3, 71–86. [Google Scholar] [CrossRef]
- Mairal, J.; Elad, M.; Sapiro, G. Sparse Representation for Color Image Restoration. IEEE Trans. Image Process. 2007, 17, 53–69. [Google Scholar] [CrossRef]
- Wright, J.; Ma, Y.; Mairal, J.; Sapiro, G.; Huang, T.S.; Yan, S. Sparse Representation for Computer Vision and Pattern Recognition. Proc. IEEE 2010, 98, 1031–1044. [Google Scholar] [CrossRef]
- Yang, M.; Zhang, L.; Yang, J.; Zhang, D. Robust sparse coding for face recognition. In Proceedings of the Computer Vision and Pattern Recognition, Colorado Springs, CO, USA, 20–25 June 2011; pp. 625–632. [Google Scholar]
- Vasilescu, M.A.O.; Terzopoulos, D. Multilinear Analysis of Image Ensembles: TensorFaces. In Proceedings of the European Conference on Computer Vision, Copenhagen, Denmark, 28–31 May 2002; pp. 447–460. [Google Scholar]
- Savas, B.; Eldén, L. Handwritten digit classification using higher order singular value decomposition. Pattern Recognit. 2007, 40, 993–1003. [Google Scholar] [CrossRef]
- Li, C.; Ma, Y.; Huang, J.; Mei, X.; Ma, J. Hyperspectral image denoising using the robust low-rank tensor recovery. J. Opt. Soc. Am. A Opt. Image Sci. Vis. 2015, 32, 1604–1612. [Google Scholar] [CrossRef] [PubMed]
- Lai, J.H.; Yuen, P.C.; Feng, G.C. Face recognition using holistic Fourier invariant features. Pattern Recognit. 2001, 34, 95–109. [Google Scholar] [CrossRef]
- Sao, A.K.; Yegnanarayana, B. On the use of phase of the Fourier transform for face recognition under variations in illumination. Signal Image Video Process. 2010, 4, 353–358. [Google Scholar] [CrossRef]
- Jing, X.Y.; Wong, H.S.; Zhang, D. Face recognition based on discriminant fractional Fourier feature extraction. Pattern Recognit. Lett. 2006, 27, 1465–1471. [Google Scholar] [CrossRef]
- Zhang, D.; Ding, D.; Li, J.; Liu, Q. A novel way to improve facial expression recognition by applying Fast Fourier Transform. In Proceedings of the International MultiConference of Engineers and Computer Scientists, Hong Kong, China, 12–14 March 2014. [Google Scholar]
- Angadi, S.A.; Kagawade, V.C. A Robust Face Recognition Approach through Symbolic Modeling of Polar FFT features. Pattern Recognit. 2017, 71, 235–248. [Google Scholar] [CrossRef]
- Zhao, R.; Li, X.; Sun, P. An improved windowed Fourier transform filter algorithm. Opt. Laser Technol. 2015, 74, 103–107. [Google Scholar] [CrossRef]
- Yan, Y.; Wang, H.; Suter, D. Multi-subregion based correlation filter bank for robust face recognition. Pattern Recognit. 2014, 47, 3487–3501. [Google Scholar] [CrossRef]
- Li, H.; Shen, F.; Shen, C.; Yang, Y.; Gao, Y. Face recognition using linear representation ensembles. Pattern Recognit. 2016, 59, 72–87. [Google Scholar] [CrossRef]
- Zhang, L.; Zhou, W.D.; Li, F.Z. Kernel sparse representation-based classifier ensemble for face recognition. Multimed. Tools Appl. 2015, 74, 123–137. [Google Scholar] [CrossRef]
- Zhu, P.; Zhang, L.; Hu, Q.; Shiu, S.C.K. Multi-scale patch based collaborative representation for face recognition with margin distribution optimization. In Proceedings of the European Conference on Computer Vision, Florence, Italy, 7–13 October 2012; pp. 822–835. [Google Scholar]
- Cheng, J.; Chen, L. A Weighted Regional Voting Based Ensemble of Multiple Classifiers for Face Recognition. In Proceedings of the International Symposium on Visual Computing, Las Vegas, NV, USA, 8–10 December 2014; pp. 482–491. [Google Scholar]
- Sidiropoulos, N.D.; Lathauwer, L.D.; Fu, X.; Huang, K.; Papalexakis, E.E.; Faloutsos, C. Tensor Decomposition for Signal Processing and Machine Learning. IEEE Trans. Signal Process. 2017, 65, 3551–3582. [Google Scholar] [CrossRef]
- Phan, A.H.; Cichocki, A. Tensor decompositions for feature extraction and classification of high dimensional datasets. Nonlinear Theory Its Appl. Ieice 2010, 1, 37–68. [Google Scholar] [CrossRef]
- Pfeifer, R.N.C.; Evenbly, G.; Singh, S.; Vidal, G. NCON: A tensor network contractor for MATLAB. arXiv, 2014; arXiv:1402.0939. [Google Scholar]
- Cichocki, A.; Mandic, D.; Lathauwer, L.D.; Zhou, G.; Zhao, Q.; Caiafa, C.; Phan, H.A. Tensor Decompositions for Signal Processing Applications: From two-way to multiway component analysis. IEEE Signal Process. Mag. 2014, 32, 145–163. [Google Scholar] [CrossRef]
- Russell, S.J.; Norvig, P.N. Artificial Intelligence: A Modern Approach. Prentice Hall. Appl. Mech. Mater. 2003, 263, 2829–2833. [Google Scholar]
- Shi, Y.; Eberhart, R.C. Empirical study of particle swarm optimization. In Proceedings of the 1999 Congress on Evolutionary Computation-CEC99, Washington, DC, USA, 6–9 July 1999; Volume 321, pp. 320–324. [Google Scholar]
- Wang, X.; Han, T.X.; Yan, S. An HOG-LBP human detector with partial occlusion handling. In Proceedings of the 2009 IEEE International Conference on Computer Vision, Kyoto, Japan, 29 September–2 October 2009; pp. 32–39. [Google Scholar]
- Ameur, B.; Masmoudi, S.; Derbel, A.G.; Hamida, A.B. Fusing Gabor and LBP feature sets for KNN and SRC-based face recognition. In Proceedings of the 2016 International Conference on Advanced Technologies for Signal and Image Processing, Monastir, Tunisia, 21–23 March 2016; pp. 453–458. [Google Scholar]
- Lyons, M.; Akamatsu, S.; Kamachi, M.; Gyoba, J. Coding facial expressions with Gabor wavelets. In Proceedings of the IEEE International Conference on Automatic Face and Gesture Recognition, Nara, Japan, 14–16 April 1998; pp. 200–205. [Google Scholar]
- Yang, M.; Zhang, L.; Shiu, S.C.K.; Zhang, D. Gabor feature based robust representation and classification for face recognition with Gabor occlusion dictionary. Pattern Recognit. 2013, 46, 1865–1878. [Google Scholar] [CrossRef]
- Ojala, T.; Harwood, I. A Comparative Study of Texture Measures with Classification Based on Feature Distributions. Pattern Recognit. 1996, 29, 51–59. [Google Scholar] [CrossRef]
- Ojala, T.; Pietikainen, M.; Maenpaa, T. Multiresolution gray-scale and rotation invariant texture classification with local binary patterns. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 971–987. [Google Scholar] [CrossRef]
- Duda, R.O.; Hart, P.E. Pattern Classification and Scene Analysis; Wiley: Hoboken, NJ, USA, 1973; pp. 119–131. [Google Scholar]
- Du, B.; Zhang, M.; Zhang, L.; Hu, R.; Tao, D. PLTD: Patch-Based Low-Rank Tensor Decomposition for Hyperspectral Images. IEEE Trans. Multimed. 2017, 19, 67–79. [Google Scholar] [CrossRef]
- Peng, Y.; Meng, D.; Xu, Z.; Gao, C.; Yang, Y.; Zhang, B. Decomposable Nonlocal Tensor Dictionary Learning for Multispectral Image Denoising. In Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 2949–2956. [Google Scholar]
- Saito, N. Simultaneous Noise Suppression and Signal Compression Using a Library of Orthonormal Bases and the Minimum-Description-Length Criterion; Academic Press: Cambridge, MA, USA, 1994; pp. 299–324. [Google Scholar]
- Averbuch, A.; Coifman, R.R.; Donoho, D.L.; Elad, M.; Israeli, M. Fast and accurate Polar Fourier transform. Appl. Comput. Harmon. Anal. 2006, 21, 145–167. [Google Scholar] [CrossRef]
- Gonzalez, R.C.; Woods, R.E. Digital Image Processing; Prentice Hall International: Upper Saddle River, NJ, USA, 1992; Volume 28, pp. 484–486. [Google Scholar]
- Kittler, J.; Hatef, M.; Duin, R.P.W.; Matas, J. On Combining Classifiers. In Proceedings of the International Conference on Pattern Recognition, Vienna, Austria, 25–29 August 1996. [Google Scholar]
- Ellis, H.D.; Frse, M.A.J.; Newcombe, F.; Young, A. Aspects of Face Processing; Springer Science & Business Media: Berlin, Germany, 1986. [Google Scholar]
- Su, Y.; Shan, S.; Chen, X.; Gao, W. Hierarchical Ensemble of Global and Local Classifiers for Face Recognition. IEEE Trans. Image Process. 2009, 18, 1885–1896. [Google Scholar] [CrossRef] [PubMed]
- Eberhart, R.; Kennedy, J. A new optimizer using particle swarm theory. In Proceedings of the Sixth International Symposium on Micro Machine and Human Science, Nagoya, Japan, 4–6 October 1995; pp. 39–43. [Google Scholar]
- Mao, S.; Xiong, L.; Jiao, L.C.; Zhang, S.; Chen, B. Weighted ensemble based on 0–1 matrix decomposition. Electron. Lett. 2013, 49, 116–118. [Google Scholar] [CrossRef]
- Robila, S.A. Toward hyperspectral face recognition. Proc. SPIE 2008, 6812, 68120. [Google Scholar]
- Chang, C.C.; Lin, C.J. A Library for Support Vector Machines. ACM Trans. Intell. Syst. Technol. 2011, 2. [Google Scholar] [CrossRef]
- Zhang, L.; Yang, M. Sparse representation or collaborative representation: Which helps face recognition? In Proceedings of the 2011 International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; pp. 471–478. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).