1. Introduction
Key derivation functions are employed to obtain one or more keys from a master secret. This is especially useful in the case of user passwords, which can be of arbitrary length and are unsuitable to be used directly as fixed-size cipher keys, so, there must be a process for converting passwords into secret keys. This process is performed by password-based key derivation functions (PBKDFs). PBKDFs are also called password hashing functions, and they are commonly employed in user authentication since they have certain advantages over other password processing methods: they are capable of accepting a salt, preventing precalculated table attacks; they are one-way functions (much as ordinary cryptographic hash functions), so the hashed password database cannot be reversed if it is stolen; and they can usually be parameterized in terms of temporal and memory cost to prevent attacks based on massively parallel hardware, like general-purpose graphical processing units (GPGPU) or custom hardware. Password hashing is a field of active research (see [
1,
2]), with several recent publications [
3,
4,
5,
6,
7,
8,
9,
10] that improve the current industry standard (PBKDF2, see [
11]). Besides password hashing and key derivation, PBKDFs have found applications in the field of cryptocurrencies and blockchain algorithms, where they are used as proof-of-work functions for such designs (see [
12]).
Symmetric encryption (see [
13]) is a type of cryptography that employs the same (or easily derivable from one another) keys for encryption and decryption, hence the establishment of a symmetric process from
cleartext to
ciphertext and, back again, from
ciphertext to
cleartext. There are two basic kinds of symmetric cryptosystems: block ciphers and stream ciphers; they differ in that block ciphers have no internal state and usually process data in blocks, while stream ciphers do have an internal state and process data element by element (an element is usually a bit or a byte of data). Nevertheless, most block ciphers can be run in operation modes that make them work as stream ciphers; such is the case in our proposal, where we employ the current advanced encryption standard (AES, [
14]) in counter (CTR) mode to work as a stream cipher in the role of a pseudo-random number generator (PRNG); the use of AES as a PRNG has been proposed by the United States National Institute of Standards and Technology (NIST, see [
15]). Besides having been independently tested for almost two decades and considered secure by the community, AES has the advantage of being accelerated in hardware on most common modern processors, like those found on laptop, desktop or server machines we use nowadays.
The main contributions of this paper are two different optimizations of a previously proposed PBKDF (see [
3]) that favorably compare in performance to the original version and widely employed PBKDFs, such as Scrypt [
7] and Argon2 [
5]. This is significant for user authentication applications that are based on passwords, as well as in blockchain applications where a proof-of-work algorithm is required. Taking advantage of the fact that hardware acceleration support is available for AES, our proposed PBKDF design reduces the performance advantage of attackers employing GPGPU or custom hardware since its main core primitive is also run on hardware.
The rest of the paper is structured as follows: a short review on related work is included in
Section 2, the proposed optimized algorithms are described in
Section 3, the results obtained by our studies are presented in
Section 4, the significance of the results are discussed in
Section 5, while the testing methodology is detailed in
Section 6, followed by some conclusions and future lines of work in
Section 7.
2. Related Work
There is abundant recent literature on the connection between symmetry and cryptography. Chang et al. proposed a mobility network authentication scheme based on elliptic-curve cryptography (see [
16]) that ensures anonymity, security, and convenience. Hung et al. designed a lattice-based revocable certificateless signature scheme (see [
17]) that aims to resist cryptanalysis, even in the post-quantum era. Sakalauskas et al. improved upon an asymmetric cipher based on the matrix power function (see [
18]) to avoid a successful discrete logarithm attack against the original version. Ramadan et al. published a survey of public key infrastructure (PKI)-based security for mobile systems (see [
19]) covering aspects such as authentication, key agreement, and privacy.
Qiao et al. described a black-box traceable ciphertext-policy attribute-based encryption (CP-ABE, see [
20,
21]) that is scalable and efficient and, therefore, better suited for cryptographic cloud storage. Zhu et al. cryptanalyzed an image encryption algorithm based on a chaos s-box (see [
22]), proposing an improved version with better security and performance. Park et al. described the use cases, challenges, and solutions involved in the application of blockchain-based security technologies to cloud computing (see [
23]).
Chang et al. proposed password-authenticated key exchange and protected password change protocols that do not involve symmetric or asymmetric cryptosystems (see [
24]), basing the security on the computational Diffie–Hellman assumption in the random oracle model. Nam et al. presented a provably secure three-party password-only authenticated key exchange protocol (see [
25]) that can run in only two rounds of communication.
Regarding PBKDF and password hashing functions, the finalists to the Password Hashing Competition (
Argon2 [
5],
Catena [
6],
Makwa [
8],
Lyra2 [
9], and
Yescrypt [
10]) are highly relevant functions related to our proposed optimized PBKDF. Also, there is previous work by the authors in this field, including the original version of the proposal [
3] and others (see [
4,
26]).
3. Description
In the following, we describe the parameters and elements, as well as the design, of the original PBKDF function and the proposed optimized versions. There are three variants of our proposal: the original version (
AESCTR-o, published in [
3]); the intermediate optimization step (
AESCTR-i); and the final optimization (
AESCTR-f). We use a pseudocode notation loosely based on the Go language to describe the initialization and output stages of the proposal.
3.1. Parameters
Our proposal and most PBKDF designs share a very similar set of parameters, mainly including the user password (
pass[]) and random salt (
salt[]) byte strings to be hashed, the length of the output hash to be generated (
plen), and some kinds of cost parameters. Those PBKDFs that have been designed to slow down attackers employing GPGPU or specialized hardware usually involve two cost parameters: a time cost (
ptime) and a memory cost (
pmem) that, due to its nature, tends to influence the time cost as well. These parameters are the same as in the original version (see [
3] for more details).
Most of the variables of the algorithm are unchanged as well; M[] is the main memory buffer that is parameterized by plen and pmem, while out[] constitutes the output hash of the function. Also, M64[] and out64[] are employed in the final optimization (AESCTR-f) to perform 64-bit native operations for performance reasons.
The algorithm employs SHA3-256 as a secure cryptographic hash function (see [
27]) during the initial seeding phase, and AES-128 (see [
14]) is used in CTR mode as a pseudo-random generator; both of these could be swapped for different, equivalent primitives were it necessary in the future.
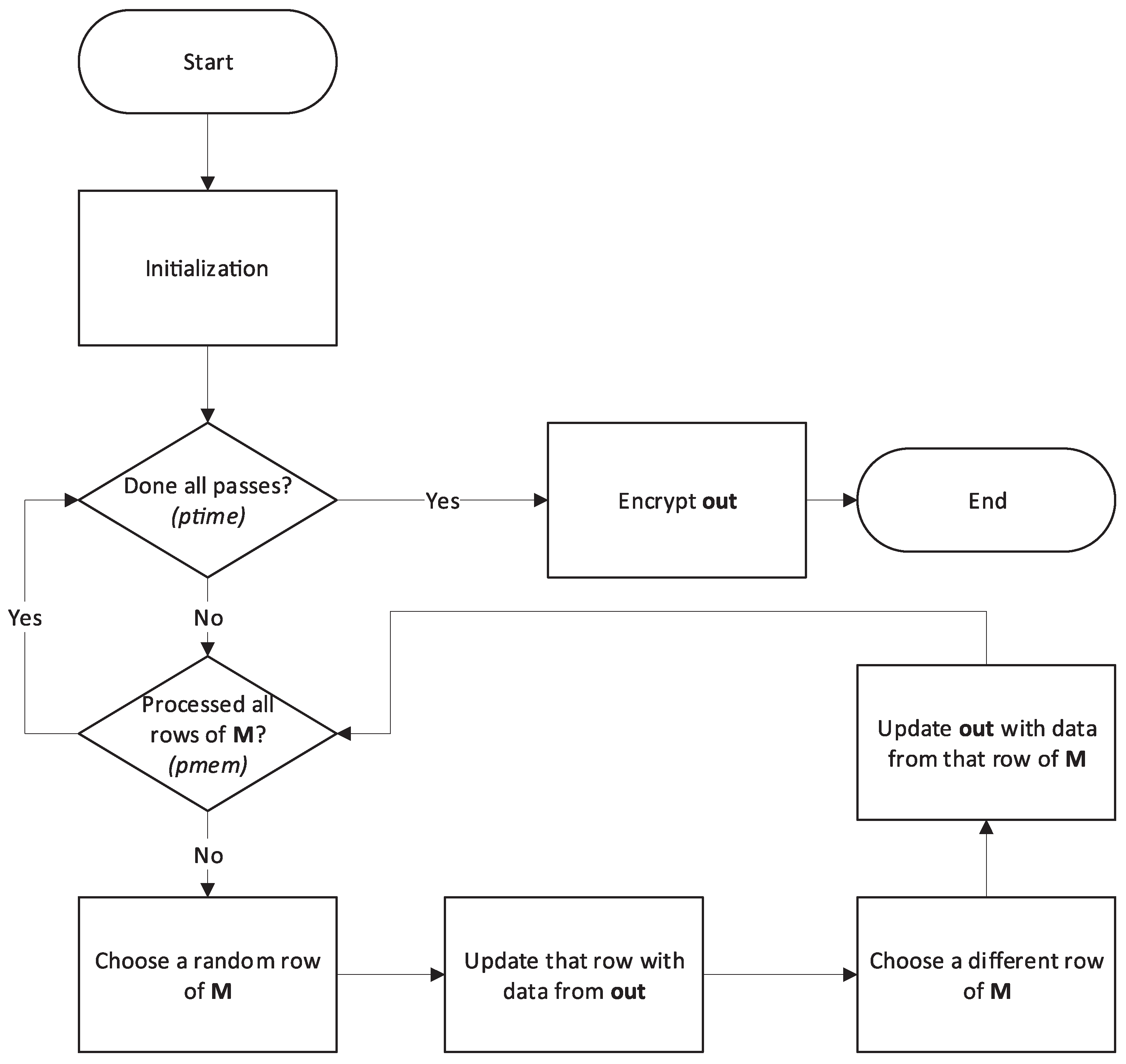
3.2. Initialization
The initialization stage is unchanged from the original version of the algorithm (see [
3]) and is reproduced here in
Figure 1. We have added comments to detail the seeding and buffer initialization steps.
3.3. Output
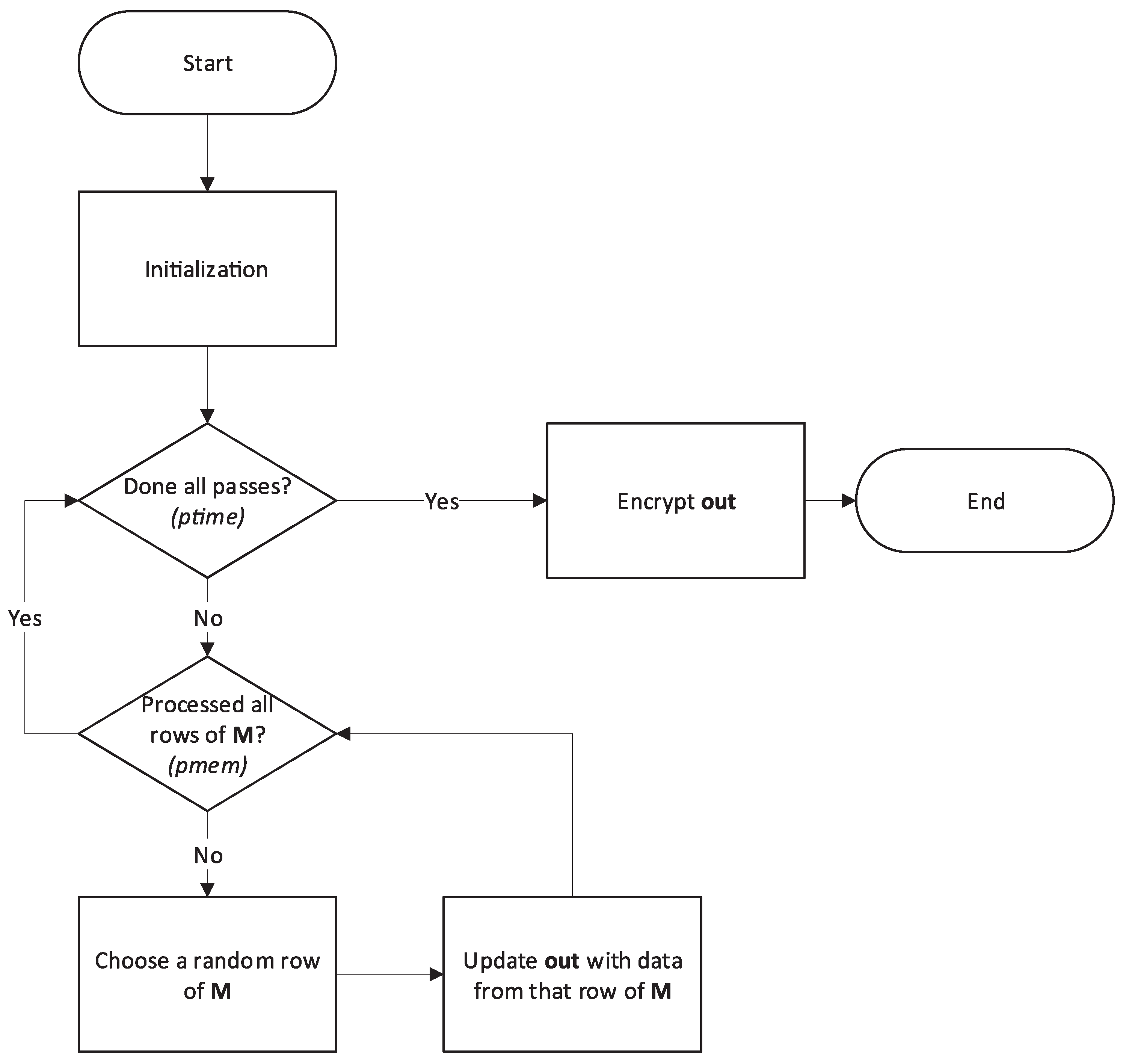
The intermediate optimization attempts to improve the performance of the original version (see [
3]) by avoiding AES encryption steps inside the loops and just encrypting the
out[] buffer as the last step. For this reason, there is a second inner loop that generates a new index so that a different row from
M[] can be processed into
out[]. These modifications are shown in
Figure 2 (pseudocode) and in
Figure 3 (flow diagram).
The final optimization further improves the performance by avoiding writing back to
M[] and having a second inner loop. Also, memory access and operations are performed in 64-bit. The differences between the final and intermediate optimizations are shown in
Figure 4 (pseudocode) and in
Figure 5 (flow diagram).
4. Results
Regarding performance, we benchmarked in the following the optimized proposals, together with the original version [
3], when modulating the time (
ptime) and space (
pmem) complexity parameters. The testing methodology is detailed in
Section 6.
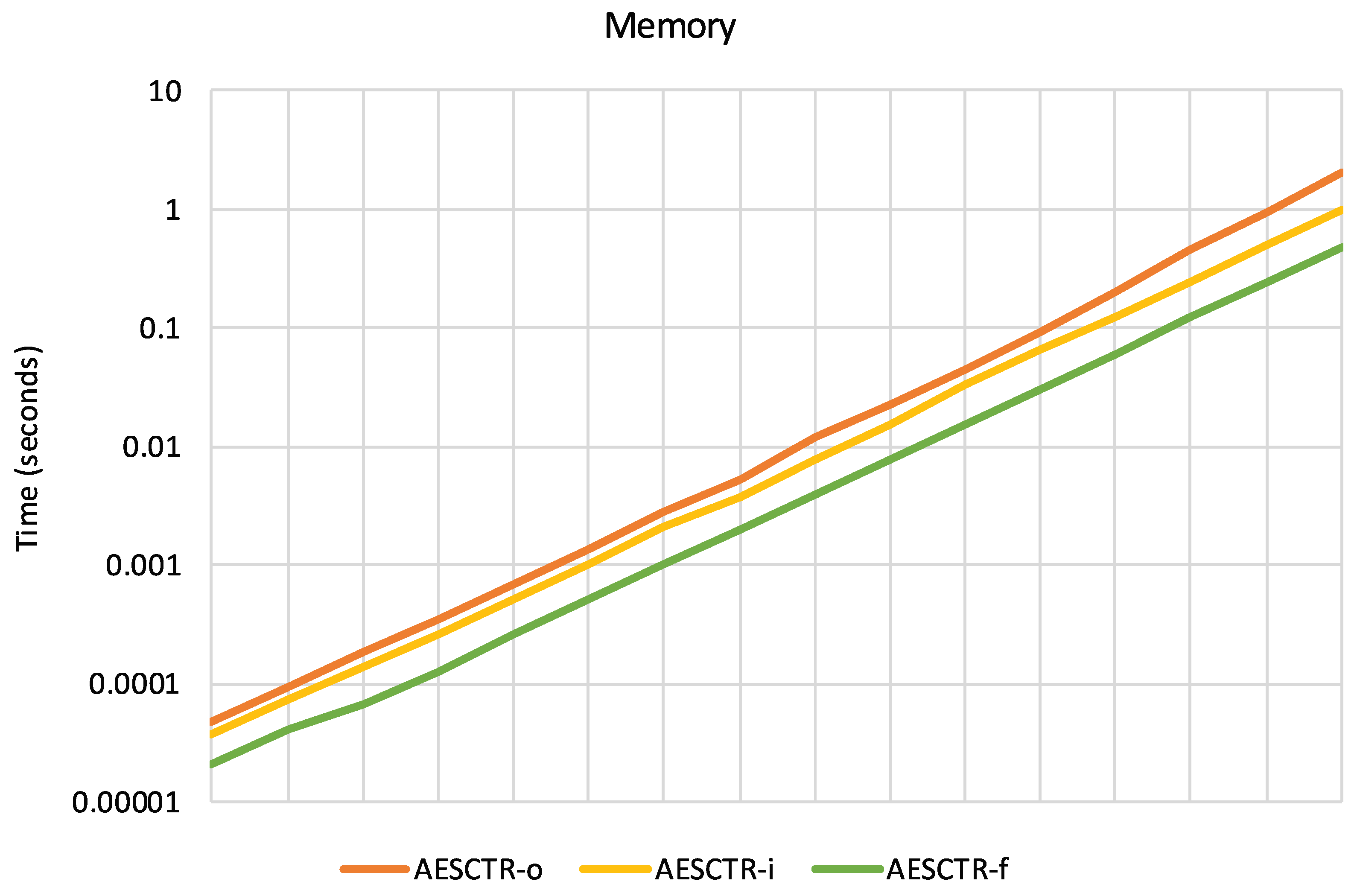
In
Figure 6, we present the computational cost (execution time in logarithmic scale) of all three variants of the proposal as the
pmem parameter modulation ranges from
to
entries of 32 bytes (a memory usage varying from 8 KB to 256 MB) and with
ptime = 1. We can see that the intermediate optimization is a significant improvement over the original function, but it is clearly overtaken by the final optimization, which is about 5 times faster than the original version.
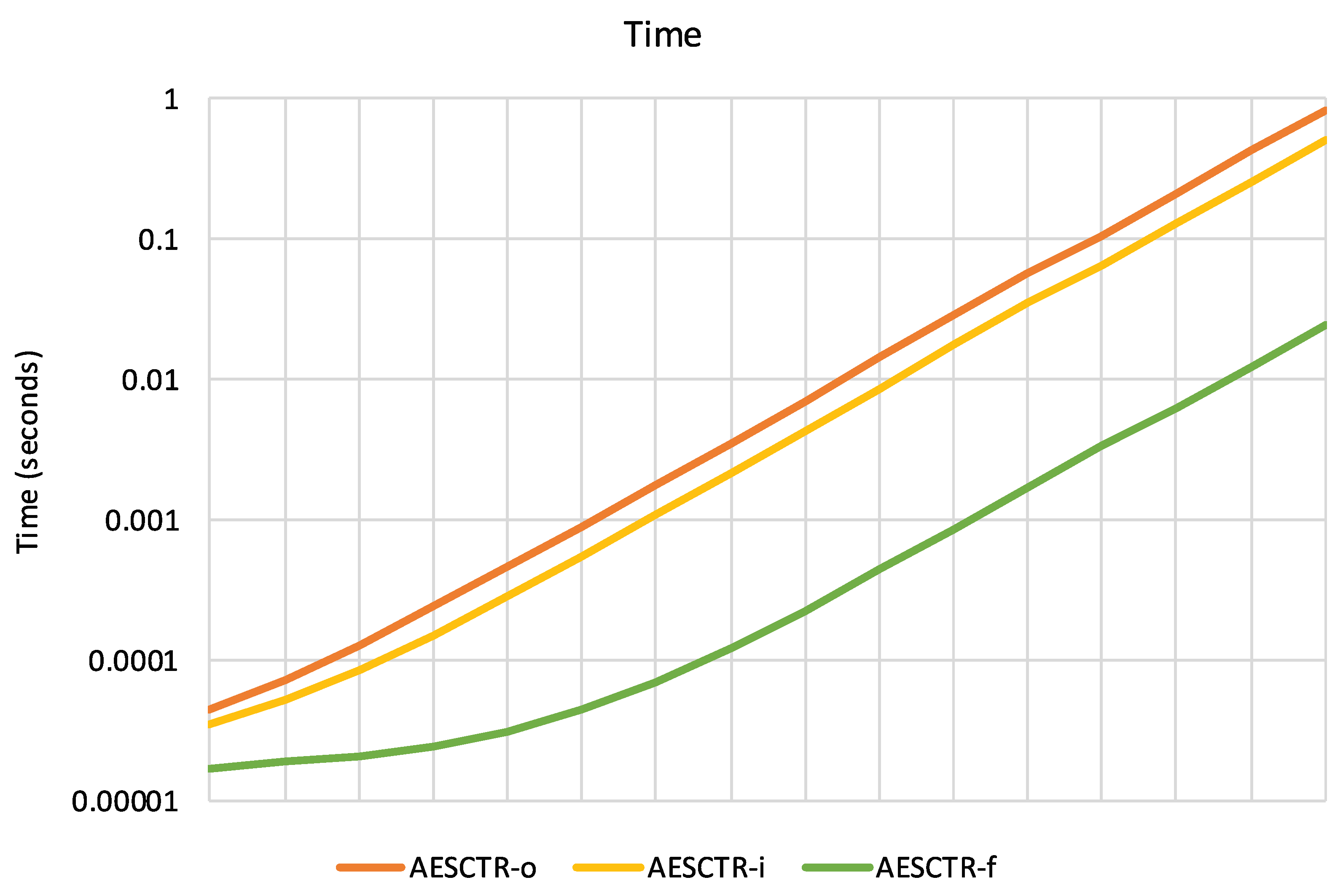
Figure 7 shows the behavior of the proposed optimizations when the time parameter is modulated. In this test,
ptime values range from 1 to
passes and memory usage (
pmem) is kept constant at
entries of
plen bytes (8 KB of memory). In this case, the difference in performance of the final optimization (
AESCTR-f) is more pronounced than in the case of the memory parameter.
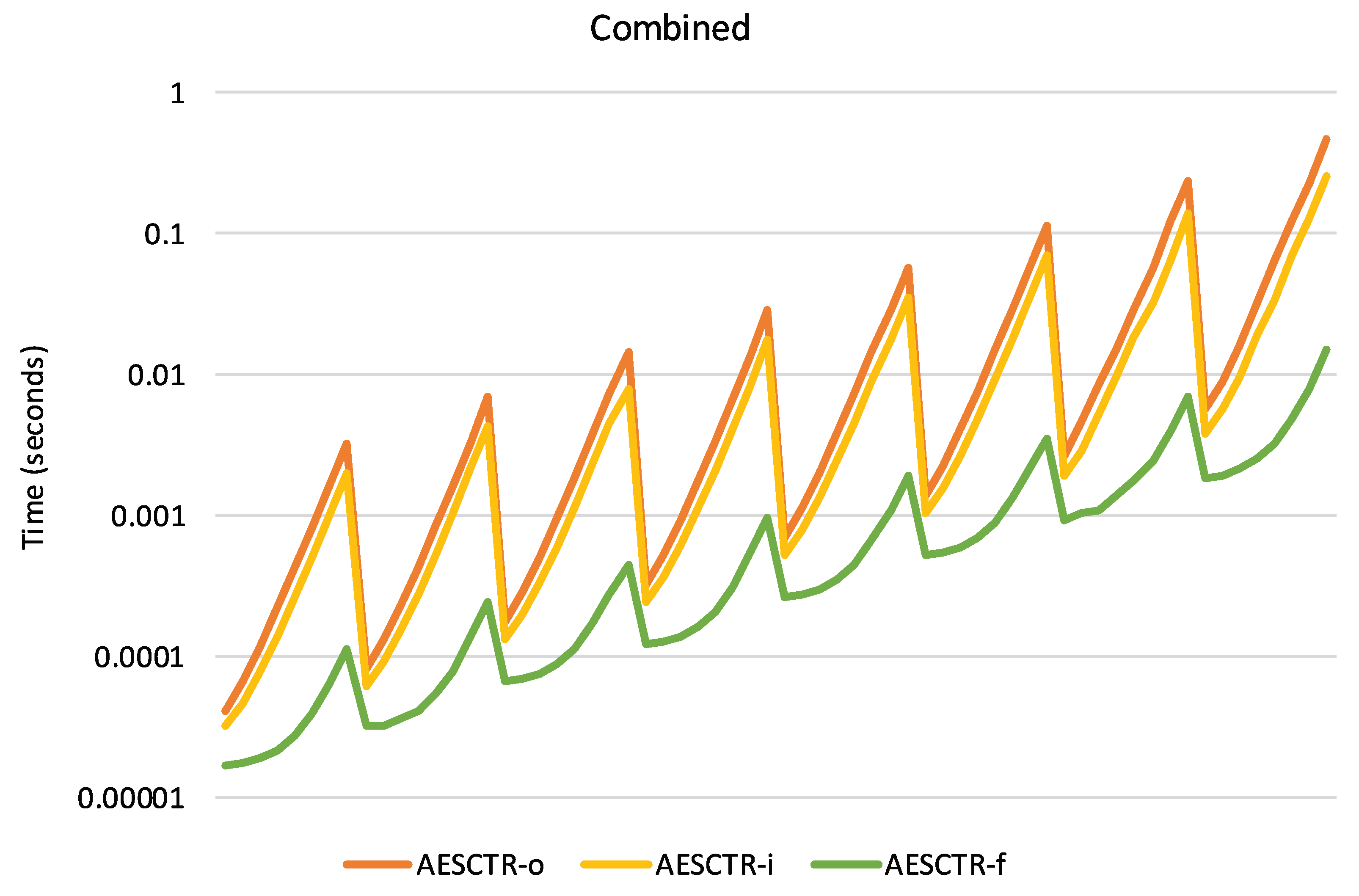
Figure 8 represents the execution time (in logarithmic scale) when both parameters,
pmem and
ptime, are simultaneously modulated in a double
for loop. The outer loop is
pmem, corresponding to the number of entries in the main memory buffer,
M[], going from
to
, and the inner loop corresponds to
ptime, ranging from 1 to
; the maximum amount of memory usage is 128 MB and occurs when pmem =
and ptime =
. The sawtooth shapes are expected in a double-loop arrangement. In this combined benchmark, the performance gain achieved with the final optimization is readily apparent.
5. Discussion
In the following, we discuss the security characteristics of our proposal and compare all three variants to Scrypt and Argon2 in terms of performance.
5.1. Comparison with Scrypt and Argon2
Scrypt (see [
7]) is a PBKDF that was designed by Colin Percival in 2009. It has been employed for many services and applications, acting as a de facto standard in recent years. It has also been employed as a proof-of-work algorithm in some blockchain implementations.
Argon2 (see [
5]) became the Password Hashing Competition (PHC) winner in 2015, overcoming finalists such as Catena [
6], Lyra2 [
9], Yescrypt [
10], and Makwa [
8]. It provides very interesting options, such as data-dependent or data-independent memory access, and is gaining traction in many new secure authentication implementations.
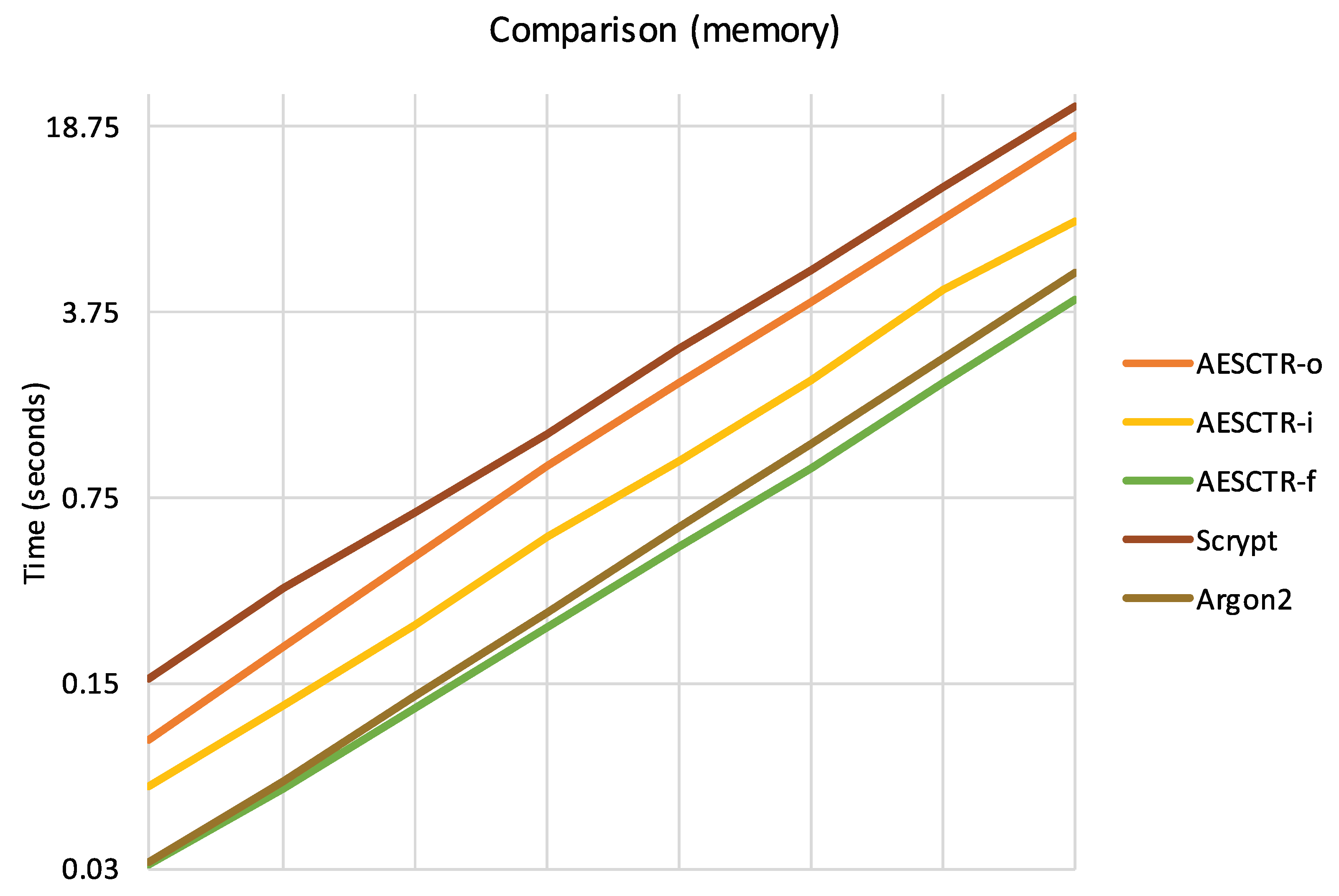
As shown in
Figure 9, for an equal amount of memory, Scrypt is slower than all three variants of the proposed AES-CTR algorithm, while Argon2 is a very efficient algorithm, but the final optimization (
AESCTR-f) is slightly faster than Argon2. Moreover, the
speedup between our proposal and Argon2 increases with memory usage, as shown in
Table 1.
It is interesting to note that while Argon2 has been implemented using Intel’s SSE4 instruction set and our proposal takes advantage of the native AES instructions, Scrypt does not benefit directly from the hardware acceleration available in modern processors. More details regarding the testing methodology are included in
Section 6.
5.2. Security
This design is based on two different cryptographic primitives: a pseudo-random generator that provides the initial contents of the memory and output buffers, and a hash function that processes the user password and salt and produces a seed for this pseudo-random generator. We employed a symmetric cipher, AES-128 [
14] in CTR mode, as the pseudo-random generator and SHA3-256 [
27] as the hash function that provides the seed (128-bit key and initialization vector) for AES.
Both of these cryptographic primitives are well-known, independently tested current standards. Nevertheless, if they were to be deemed insecure in the future, they could be replaced by different, size-compatible, secure alternatives.
The proposed optimized design should be on par with the original version and these primitives at a minimum-security level of 128 bits against brute force attacks since the output of the PBKDF (in all three variants) comes directly from the output of the AES-128 symmetric cipher.
6. Methods
We employed the Go programming language (version 1.11.1, see [
28]) for the implementation of all tested algorithms; Go is an excellent choice for cryptography testing since it is a very efficient, compiled language and includes most security standards and algorithms in its standard library. All benchmarks were run on the same computer, a desktop PC with an Intel i7 CPU (6950X, 3.5 GHz and with AES Native Instructions support) and 32 GB of RAM, running Microsoft Windows 10 (1803 release). The length for passwords, salts, and output was chosen as 32 bytes (256 bits), and all tests were run 100 times to avoid the interference from external processes as much as possible.
In the case of the comparison benchmarks, the official implementations available in the golang.org/x/crypto packages were used for Scrypt and Argon2 testing. It should be noted that this implementation of Argon2 supports hardware acceleration via SSE4 instructions and that the recommended parameters (three passes) and a single thread were used. To ensure fair testing, an equal amount of RAM usage was chosen for each algorithm in all comparison tests.
7. Conclusions
We optimized a previously published password-based key derivation function that employs the Advanced Encryption Standard (AES) in counter mode as a core primitive, proposing two new algorithms based on the original design: a more conservative optimization and a fully optimized one. The design philosophy is based on taking advantage of the custom AES instructions available on most modern processors that enable hardware support to defend against brute force password cracking attacks mounted on specialized hardware or general-purpose graphical processing units.
We have also analyzed the performance of all three variants in comparison with Scrypt and Argon2, which are the current industry standards in terms of password hashing functions. The final optimization version of the algorithm (AESCTR-f) is faster than Argon2 for an equal amount of memory usage, showing that AES can be an excellent candidate for the design of password hashing functions. Moreover, since the design is based primarily on AES in counter mode as a pseudo-random generator and the final output is directly encrypted with AES, we can establish that our proposal is equivalent, in terms of security, to this extensively analyzed encryption standard.
For future research, there are several possible interesting topics, such as server-side ROM, client-independent update, server relief, parallelism, or specialized implementations, among others.
Server-side ROM is an extra security measure that involves employing a very big random file on the server as part of the hashing process. In this way, an attacker would have to produce the same random file, and the large amount of memory required would further deter the use of specialized hardware. Our proposal can be adapted to accept such a file as part of the algorithm without compromising its performance or security.
Client-independent update is the capability of changing PBKDF parameters without the need for the user to reenter the password. This is a convenient feature in password authentication since the server can increase the security of the PBKDF as necessary but without any friction for the end users. This can be performed without modification to the proposed algorithm by multiple-step processing, but other optimized methods might be possible.
Server relief implies delegating part of the PBKDF computation to the end user so that the server is less impacted by computational requirements of password-authenticating a large number of users simultaneously. It is, in essence, a way of increasing the parallelism of the server and reducing the advantage that attackers might have by using general-purpose graphical processing units or other specialized hardware. This usually involves some kind of protocol in order to share the computational load between the server and the user node in a secure manner.
Multiple-thread parallelism can also be studied and incorporated by modifying the proposed final optimization (AESCTR-f). This can be useful in situations where server relief is not possible or when further parallelism is desired. Since Argon2 allows for multiple-thread parallelism, a comparison between the parallel performance scalability of the final optimization and Argon2 might be possible.
Specialized implementation on hardware platforms, such as general-purpose graphic processing units or field programmable gate arrays, could be very useful for further performance testing and optimization of the proposed PBKDF algorithm.