Abstract
The community shuttle system plays an important role in serving communities with a heavy travel demand for the metro service. Stop location and route design are the two main decisions of planning a community shuttle service. Those two decisions are interrelated and interact, and are strongly related to the user cost and operating cost. The optimal stop location and route can help to reduce the walking distance of passengers and the route length. To make a trade-off between the walking distance of passengers and route length, we propose a discrete optimization problem. A single integrated formulation is established to optimize stop location and route design. Planners can decide the stop location and route design of the community shuttle system simultaneously based on this formulation. Then, we present a non-dominated sorting genetic (NSGA-II) based algorithm to obtain the non-dominated solutions of the discrete optimization formulation. The numerical experiments and a case study based on real-world data are used to demonstrate that the proposed solution method can yield a set of plans of stop location and route in a reasonable time. We also find that when the maximum tolerable walking distance is set to 418 m, the trade-off between the total walking distance of passengers and route length can be obtained.
1. Introduction
A heavy demand for the metro service has arisen along with the continuous expansion of communities in China. In the urban public transport system, the community shuttle service plays an important role in transporting these ever-increasing passengers from their origins to metro stations or from metro stations to their destinations. Obviously, systematic and proper planning of the community shuttle system is necessary before this public transport system is in operation. The planning process of the public transport service includes four components: route and network design, timetabling, vehicle scheduling, and crew scheduling [1]. Among these components, route and network design is a basic one which can influence the overall operational efficiency of the public transport system. There have been many studies concentrating on this component [2,3,4,5,6]. However, most of them are carried out for conventional bus or feeder bus network design, and few scholars focus on community shuttle route optimization.
A distinctive feature of the community shuttle system is that it mainly provides feeder service for the travel demand for metro station access. The travel demand presents a many-to-one or one-to-many travel characteristic. This kind of community shuttle service has been commonly implemented in practice. For example, Figure 1 shows typical community shuttle route access to a metro station (Zhuxinzhuang subway station) in Beijing, China. Community shuttle routes have the following features: (1) there are a number of demand points (e.g., residential areas, schools, hospitals, commercial areas) to be served by community shuttle routes; (2) there are many candidate stops from which some stops can be selected; (3) among the candidate stops, there is a transfer stop located close to a metro station and passengers can transfer between the metro and community shuttle at this stop; and (4) in general, only one community shuttle route is available for metro station access in each community. These features are visually presented in Figure 2. Here, the stops and route of a community shuttle line are represented by circles and arrowed solid lines, respectively. Usually, a community shuttle route is circular. A transfer stop, denoted as a square, is usually located near a metro station. Hexagons represent demand points which are served by stops selected from candidate stops. Dash lines show the situation of matching demand points to stops.
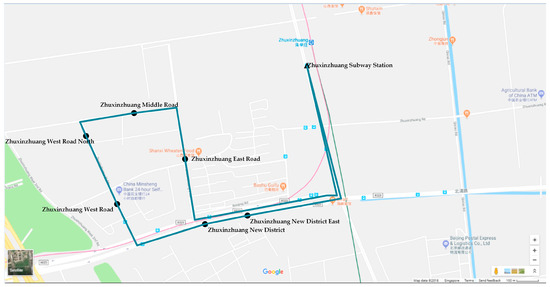
Figure 1.
A community shuttle route access to Zhuxinzhuang subway station.
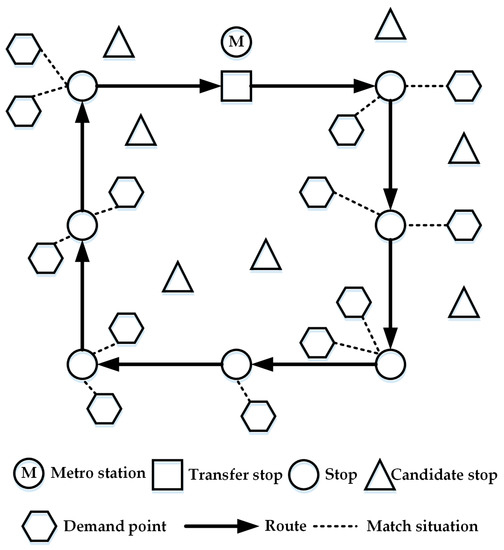
Figure 2.
Stops and route of a community shuttle line.
From Figure 2, it is clear that stop location and route design are the two main decisions in the first component of the community shuttle service planning process. Route design determines route length, which influences fleet size and vehicle travel cost. Moreover, route length is directly related to the in-vehicle time of passengers. Operators and passengers usually hope to reduce route length. However, the community shuttle system aims to improve the accessibility of the public transport system. Therefore, the walking distance of passengers, related to stop location, should be taken into account when the community shuttle system is designed, more than just the route length. The walking distance of passengers is expected to be as short as possible and should be within an acceptable range. Generally, reducing the walking distance of passengers often means more detours or stops, whereas reducing the route length generally increases the walking distance of passengers, as stops may not be allowed to be located near passengers’ origins or destinations. Hence, a balance or a trade-off between the two objectives is critical. To analyze this trade-off, a properly integrated method for stop location and route design is necessary for planners.
Considering the features of the community shuttle system, integrated optimization of stop location and route design for the community shuttle service is a multi-objective location-routing problem, which is different from the conventional bus network design problem. When planning conventional bus network, frequent transfers and complicated route plans require planners to consider passengers’ route choice behaviors [7].
Our goal is to define an approach to tackle the integration of community shuttle stop location and route design. A multi-objective integer programing formulation is proposed to minimize the total walking distance of passengers, as well as the route length. This formulation takes into account the route length constraints, the stop spacing constraints, and the maximum tolerable walking distance constraint. An algorithm based on the non-dominated sorting genetic algorithm II (NSGA-II) is designed to solve the formulation. The correctness and validity of the formulation and algorithm are verified by numerical examples and a real-world problem in Shanghai, China.
The remainder of this paper is organized as follows. Section 2 reviews the literature on route design, stop location, and the integrated problem of route design and stop location. In Section 3, the problem studied is described and a mathematical formulation for the integrated optimization of stop location and route design for the community shuttle service is proposed. Section 4 introduces the algorithm to solve our formulation. Section 5 presents numerical experiments. A case study is given in Section 6. Conclusions are presented in Section 7.
2. Literature Review
This section presents a review on three major problems of community shuttle service research: route design, stop location, and the integrated optimization of route design and stop location.
2.1. Route Design
Route design is one of the key steps of feeder bus network planning [8] and is a well-studied subject.
Many researchers consider route length or travel time associated with the feeder bus route in their works. Shrivastava and Dhingra [9], Verma and Dhingra [10], Shrivastava and O’Mahony [11,12], and Song and Liu [13] generate feeder bus routes using a heuristic algorithm and the route length limit is considered. Their approaches are based on an assumption, i.e., stop location is an input and bus stops are demand points in their works, which is reasonable if planners hope to design feeder bus routes based on existing bus stops or adjust existing feeder bus routes. When planners hope to make new feeder bus route plans, their approaches are not applicable [14]. A similar assumption is used by Szeto and Wu [15], and the travel time of buses is a part of the objective of a mathematical formulation in their work. Teng et al. [16] take into account the travel time constraint, but ignore stop locations based on the assumption that if residents live in the traffic zones passed by the feeder bus, they can be served. This assumption indicates that if a traffic zone is not passed by feeder bus routes, passengers there cannot be served, even if they are near by the bus routes. This may not be reasonable.
The access cost of passengers is not considered by all the above studies. Transit operators and passengers prefer short community shuttle or feeder bus routes to reduce travel time and in-vehicle time. Passengers also hope to easily access the community shuttle or feeder bus service. In addition, operators hope to decrease the access cost of passengers to attract more passengers. Therefore, it is necessary to consider the access cost of passengers. Access cost is considered by some scholars. Chien and Yang [17] and Jerby and Ceder [18] assumed that the travel demand is uniformly distributed along route links or within traffic zones. Hence, travel demand is related to bus routes and locations of bus stops are neglected. This assumption may be easily violated, because buses cannot enter gated communities in China. Instead, passengers will gather at some pick-up/drop-off points [19]. Xiong et al. [20] and Zhu et al. [21] regard access distance as the distance between the center point of each traffic zone and the corresponding road link. However, in fact, buses cannot stop anywhere on bus routes. In addition, Lin and Wong [22] present a multi-objective programming formulation and the maximum service distance of a feeder bus route is considered. They assume that stop spacing is commonly within a reasonable walking distance, thus stop location is not considered. Nevertheless, this assumption is not suitable for communities in the suburbs or large communities.
2.2. Stop Location
Few studies have concentrated on the stop location of a community shuttle or feeder bus service. Liu et al. [23] propose a stop planning method for an airport shuttle bus. Their objective is to improve the accessibility of airport shuttle bus stops. However, stop location can also influence travel time due to the extra detours, more than just the accessibility of feeder bus service. Realizing the above critical problem, Zhao and Chien [24] aim at minimizing user cost (access time, wait time, and in-vehicle travel time) and operator cost. However, they consider that travel demand is uniformly distributed along the bus route, which may be unreasonable in China for the same reason described in Section 2.1.
Some studies have been conducted on the stop location of a conventional bus system. Alonso et al. [25] and Moura et al. [26] use a bi-level optimization model to obtain optimal bus stop locations on a macroscopic scale. Their model considers user cost and operator cost; however, the maximum walking distance of passengers is ignored. We believe that it is significant for a public transport service, especially for a community shuttle service, to ensure that no passenger is connected to a bus stop further away than the maximum walking distance. Chen et al. [27] select the optimal stops from candidate stops along bus routes and the bus routes are given as inputs. This may not be valid if planners hope to make bus stop plans from scratch or radically different plans from the existing one. For stop location, the most similar to our model is Jahani et al. [28], who propose a multi-objective bus stop location model to determine the optimal stop locations and the match situation of demand points to stops. Their numerical cases show that the model can generate sensible stop results.
2.3. Integrated Optimization of Stop Location and Route Design
Some scholars concentrate on the optimization of stop location and route design in a successive way. Xiong et al. [29] develop a solution method for the optimization of a community shuttle route. A heuristic algorithm is proposed for locating stops on a community shuttle route. This community shuttle route is an input of the heuristic algorithm. Li and Chen [30] and Leksakul et al. [31] determine stop locations by clustering algorithms first, and then bus route are constructed based on bus stops. A successive approach optimizes stop location or route design first, while the results are the input of the other problem. According to its definition, a successive approach may result in sub-optimal solutions.
Other scholars solve the two problems in a completely integrated way. They propose a formulation or a solution methodology to determine the stop location and route design simultaneously. For example, Perugia et al. [14] propose a cluster routing approach to model both bus stop location and route design for a home-to-work bus service in a metropolitan area and the model is solved by a tabu search algorithm. The main difference between the method of Perugia and ours is that we simultaneously determine the number of bus stops to be served, which is considered as an input in their research. When decision makers hope to make a new plan from scratch or a radically different plan with respect to the existing one, considering the number of bus stops as an input may not be valid. Chen et al. [7] consider how to design a suburban bus route for airport access. Their approach can generate the bus route and stop location simultaneously. However, the number of stops to be served is also given as an input. In order to consider the access cost of passengers, we take into account the locations and travel demand of demand points, which is ignored by Chen et al. [7].
In summary, the access cost of passengers should be considered when optimizing the community shuttle service. In addition, to our knowledge, most of the existing community shuttle or feeder bus service studies ignore the relationship between stop location and route design, and few studies are known about the simultaneous optimization of stop location and route design. However, as a matter of fact, stop location is directly related to route design, thus the integrated optimization of the two problems will lead to a better understanding of the planning of the community shuttle service.
In this paper, we propose a multi-objective integrated formulation to simultaneously decide the stop location and route design of the community shuttle, which is characterized by two aspects that make our problem different from other similar problems in the literature. First, considering that gated communities are common in China, we believe that travel demand is related to demand points. Our approach can decide the community shuttle route, stop location, and the match situation of demand points to stops simultaneously. Second, we can simultaneously decide the number of stops to be served and stop locations. To the best of our knowledge, these features cannot be found in other works (e.g., Perugia et al. [14], Chen et al. [7]) in which the number of stops to be served is an input and the situation of matching demand points to stops is ignored.
3. Mathematical Formulation
3.1. Problem Description and Assumptions
The problem considered in this paper can be described as follows. A metro station is located near a community and connects this community with other areas in the same city. There are a set of demand points in the community. The travel demand for the community shuttle service is an input. There is also a set of candidate stops to be considered. Some candidate stops will be chosen as stops and passengers can only be picked up and dropped off at stops which are located within the maximum tolerable walking distance of their demand points. The problem is deciding where stops are located and which demand points can be served by each stop. Furthermore, the shortest loop route based on these stops is determined simultaneously. The objectives are to minimize the total walking distance of passengers and the community shuttle route length.
In order to simplify the problem and make the formulation reflect the practical situation, the following assumptions are made.
- The locations of all demand points and candidate stops are known.
- The travel demand for the community shuttle service of each demand point is given.
- The distances between different candidate stops and the distances between demand points and candidate stops are known.
3.2. Mathematical Formulation
To describe the formulation, the following notations are introduced in Table 1.

Table 1.
List of notations.
The integer programing formulation is given below.
subject to
The objectives (1) and (2) minimize the total walking distance of passengers and the route length, respectively. Constraint (3) defines the degree of the transfer stop vertex. Constraint (4) ensures flow conservation at the candidate stop vertices. Constraints (5) and (6) mean that a candidate stop can serve demand points under the condition that the candidate stop is visited by the community shuttle route. Constraint (7), in conjunction with constraint (8), indicates that if a candidate stop is selected as a stop, the candidate stop must serve at least one demand point. Constraint (9) ensures that each demand point is served by a stop. Constraint (10) ensures that the route length is within a range. Constraint (11) ensures that stop spacing lies within the maximum and minimum values. The maximum tolerable walking distance of passengers is enforced by constraint (12). Constraint (13) indicates that there is only one loop route. Constraints (14) and (15) restrict the feasible domains of decision variables.
4. Solution Method
The formulation presented in Section 3 is a bi-objective programing formulation which aims to minimize the total walking distance of passengers depending on stop location and, at the same time, to minimize the route length based on route design. Assigning weight to each objective function is a classical solution method of the multi-objective optimization problem. Multiple objectives are converted into a single one with this method. However, we believe that it is of great practical significance to provide decision makers with trade-off curves between values of different objective functions (i.e., the Pareto optimal front). Furthermore, it is difficult for decision makers to determine the weight of each objective reasonably. Therefore, we plan to search for the Pareto optimal front and each Pareto optimal solution is a plan of community shuttle stop location and route design. To this end, an algorithm based on the non-dominated sorting genetic algorithm II (NSGA-II) is designed to find the Pareto optimal front. As one of the most effective multi-objective evolutionary algorithms (MOEAs), NSGA-II has been used in urban public transport planning and operation problems successfully, including the public transport network design problem [32], timetabling problem [33], and vehicle scheduling problem [34]. Deb et al. [35] introduce details about NSGA-II and indicate that solutions obtained by NSGA-II are closer to the true Pareto optimal front compared to two other MOEAs, i.e., PAES and SPEA.
A brief description of NSGA-II is as follows. Firstly, an initial population P0 of size Z is created. Then, all solutions in the initial population P0 are sorted into different non-dominated levels by the fast non-dominated sorting procedure. Each non-dominated front is assigned a rank which is equal to its non-dominated level and represents the fitness of solutions in this non-dominated front. Thereafter, the selection operator, crossover operator, and mutation operator are applied to obtain a child population Q0 of the same size Z. After the child population Q0 is generated, P0 and Q0 are associated to create a new population R0 of size 2Z. The best Z solutions are chosen from R0 to fill a new population P1. Then, the procedure continues, iterating until the number of iterations I is reached. Finally, the Pareto optimal front is obtained.
Based on the general framework of NSGA-II, we modify chromosome coding and an infeasible solution processing method to better suit our problem. The algorithm based on NSGA-II in this paper is described in detail below.
4.1. Chromosome Coding
An integer coding method is used for the chromosome. The length of the chromosome is |D|, which is the number of demand points. Each gene presents which candidate stop serves the corresponding demand point. For example, a gene “5” means that the corresponding demand point is served by the fifth candidate stop. Logically, this candidate stop is chosen as a stop.
4.2. Solution Evaluation
The fitness of each solution is calculated based on its values of the two objective functions (i.e., the total walking distance of passengers and the route length). Each solution shows a plan of stop location and the situation of matching demand points to stops. Based on the stop location, the length of the optimal community shuttle route can be solved by formulation M1, shown as follows.
subject to (3) and (4), (10) and (11), (13)–(15)
(M1) min C2
M1 is a linear programing formulation and can be solved by ILOG CPLEX.
The total walking distance of passengers can be solved based on the distance between demand points and candidate stops and the situation of matching demand points to stops presented by chromosome coding.
Then, the fitness of a solution is represented by the non-domination rank and crowding distance. If a solution’s non-domination rank is less than other solutions, or if its crowding distance is larger than other solutions with the same non-dominated rank, this solution is fitter than other solutions. For the calculating method of crowding distance, readers can refer to Deb et al. [23].
4.3. Infeasible Solution Processing Method
Crossover operator and mutation operator may result in a mass of infeasible solutions, which affects the efficiency and quality of the algorithm. Therefore, the following measures are adopted to solve this problem. Firstly, infeasible solutions are allowed to exist in crossover and mutation operators. If the passengers’ walking distance shown by a gene of an infeasible solution exceeds the maximum tolerable walking distance, the passengers’ total walking distance of the solution is set to a large constant. If model M1 has no solution, the route length of the infeasible solution is set to a large constant. Infeasible solutions of these two cases will be treated as feasible solutions in the algorithm. Then, the initial population is created under the premise that all solutions in the initial population are feasible. Algorithm 1 can be used to generate the initial population.
| Algorithm 1 |
| Step 1 For , set i = 0. P0 is the initial population whose size is Z. Step 2 For solution i, set j = 0 and . Step 3 Define a set Lj, and put each candidate stop whose distance to demand point j does not exceed the maximum tolerable walking distance into Lj. Step4 Choose a candidate stop from Lj randomly to serve demand point j. Set j = j + 1, go to Step 3, until j = |D|, then solution i can be created. Step 5 For solution i, solve model M1, if the optimal solution of M1 exists, set objective value of this optimal solution as the route length of solution i. Otherwise, go to Step 4 to create solution i again. Step 6 Calculate the total walking distance of passengers for solution i. Set i = i + 1, go to Step 2, until i = Z. Output the initial population. |
4.4. NSGA-II Based Algorithm
The NSGA-II-based algorithm designed in this paper works as Algorithm 2:
| Algorithm 2 |
| Step 1 Initialization. Set i = 0, and determine population size Z, crossover probability pc, mutation probability pm, and the number of iterations I. Create the initial population P0 using Algorithm 1. Step 2 Apply the fast non-dominated sorting procedure to Pi to obtain a series of non-dominated fronts. Step 3 Perform selection, crossover, and mutation operators for Pi, and then the child population Qi with size Z can be obtained. Calculate each solution’s route length and total walking distance of passengers in Qi. Step 4 Combine Pi and Qi to generate a new population with size 2Z. Implement the fast non-dominated sorting procedure for Ri. Then, a series of non-dominated fronts can be obtained and solutions whose non-dominated rank is r are in Pareto front Fr. Step 5 Elitism. Set , r = 1. Execute Step 5.1–5.3: Step 5.1 If the total number of solutions in Fr and Pi+1 does not exceed Z, put all solutions of Fr in Pi+1. Step 5.2 If the total number of solutions in Fr and Pi+1 exceeds Z, calculate crowding distances of solutions in Fr. Then, these solutions are put in Pi+1 according to the crowding distances from large to small, until the number of solutions in Pi+1 is Z. Step 5.3 If the number of solutions in Pi+1 does not exceed Z, r = r + 1, go to Step 5.1. Otherwise, go to Step 6. Step 6 Apply the fast non-dominated sorting procedure to Pi + 1 to obtain a set of non-dominated fronts. Step 7 Update the Pareto optimal front. Solutions in the first non-dominated front are the latest Pareto optimal front. Step 8 Judge whether stop. If i = I, output the Pareto optimal front and stop the algorithm. Otherwise, set i = i + 1, go to Step 3. |
5. Computational Experiments
In this section, numerical results solved by the NSGA-II-based algorithm are presented. A randomly generated network example is used to illustrate the efficiency of the algorithm. Moreover, the effects of the maximum tolerable walking distance on the total walking distance of passengers and route length are discussed.
5.1. Network Configuration
In the example network, a metro station is located near a community and connects the community with other areas in the same city. There are 20 demand points and 25 candidate stops (the first one is the transfer stop and near the metro station) in the community. The randomly generated distances between demand points and candidate stops and the randomly generated distances between candidate stops are presented as Table A1 and Table A2 in Appendix A. The travel demand for the community shuttle service of the demand points (as shown in Table 2) is also known. The minimum route length lmin is 3 km, and the maximum route length lmax is 12 km. The minimum and maximum stop spacing (i.e., smin and smax) values are 300 m and 840 m, respectively. The maximum tolerable walking distance dmax is 400 m.

Table 2.
Travel demand of demand points. (trip/day).
5.2. Parameters Setting
The key parameters used in the algorithm are given as follows. Crossover probability pc and mutation probability pm are 0.9 and 0.5, respectively. The number of iterations I is set to 500. The NSGA-II-based algorithm is implemented in C# language and ILOG CPLEX 12.4. All tests are executed on an Intel Core (TM) i5 processor at 2.27 GHz under Windows 7 using 4 GB of RAM.
5.3. Computational Results
For the example network shown in Section 5.1, the non-dominated solutions obtained by the NSGA-II-based algorithm are presented in Table 3. The computing time is 55.09 min. Considering that we are in the planning phase and this computational experiment is on an actual size, the amount of computing time is reasonable.

Table 3.
Non-dominated solutions generated by the NSGA-II-based algorithm.
As can be seen from Table 3, we can obtain more than one non-dominated solutions by running the NSGA-II algorithm once. Decision makers can choose a solution as the final plan of stop location and route design. The demand points served by each candidate stop are shown in Table 4. Figure 3 shows the non-dominated solutions for this sample network visually.

Table 4.
Demand points served by each candidate stop.
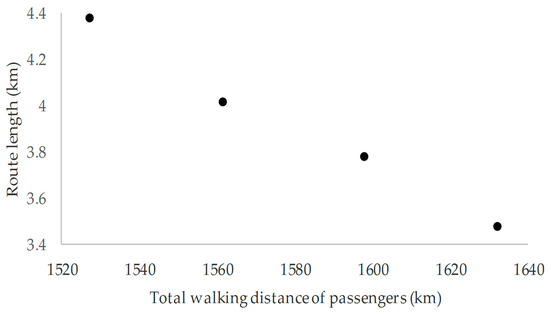
Figure 3.
Non-dominated solutions generated by the NSGA-II-based algorithm.
It is important to select optimization objectives reasonably for multi-objective optimization problems. If there is a positive correlation relationship between two minimized objectives, the two objectives are not conflicting, which means that only one objective is effective. It can be seen from Figure 3 that for the optimization objective values of these non-dominated solutions, the shorter the total walking distance of passengers, the longer the route length for the non-dominated solutions, which means that the two objectives are conflicting. Hence, the two objectives are reasonable in this paper.
5.4. Effect of the Maximum Tolerable Walking Distance
The main aim of the community shuttle service is to reduce the walking distance of passengers. Therefore, the maximum tolerable walking distance is an important parameter reflecting the service level of the community shuttle system. The total walking distance of passengers and route length are normalized according to Equations (17) and (18), respectively, so that the values of the two objectives are between 0 and 1. Therefore, the two objectives can be described uniformly.
where indexes i = 1, 2, 3, 4, and 5 correspond to cases that the maximum tolerable walking distances are 300 m, 350 m, 400 m, 450 m and 500 m, respectively; is the total walking distance of passengers of the ith case; and is the value of the total walking distance of passengers after normalization of the ith case.
where indexes i share the same meaning as that in Equation (17); is the route length of the ith case; and is the value of route length after normalization of the ith case.
We adjust the maximum tolerable walking distance between 300 m and 500 m for the example network represented in Section 5.1. The total walking distance of passengers and route length after normalization are presented in Figure 4.
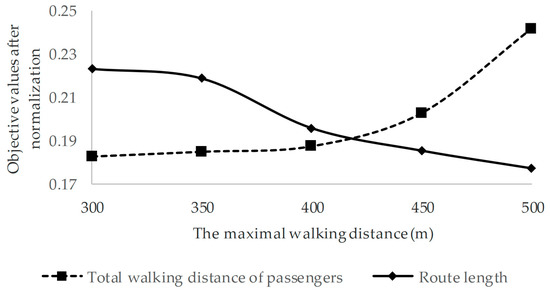
Figure 4.
Relation between the maximum tolerable walking distance, total walking distance of passengers, and route length.
As shown in Figure 4, when the maximum tolerable walking distance increases from 300 m to 500 m, the total walking distance of passengers increases and the route length decreases. When the maximum tolerable walking distance increases from 300 m to 400 m, the total walking distance grows slowly. When the maximum tolerable walking distance grows from 400 m to 500 m, the total walking distance of passengers increases significantly. When the maximum tolerable walking distance increases from 300 m to 500 m, the route length decreases continuously. If the maximum tolerable walking distance is set to 418 m, the trade-off between the total walking distance of passengers and the route length can be achieved. Therefore, the optimal maximum tolerable walking distance is 418 m. Decision makers can set this parameter to 400 m to make it convenient to be applied in practice. Decision makers can also measure the total walking distance of passengers and route length to determine the maximum tolerable walking distance.
6. Case Study
This section demonstrates the effectiveness of the formulation and algorithm by applying them to a community in Shanghai, China. As shown in Figure 5, there are nine demand points, one candidate stop (transfer stop, H1) near a metro station, and 12 other candidate stops in the community. The connection between the demand points and the candidate stops and the connection between the candidate stops are shown by the topological diagram in Figure 6. The travel demand for the community shuttle service of each demand point is shown in Table 5 (refer to Wu [36]). Actual data, including the distances between candidate stops and demand points and the distances between candidate stops, are shown as Table A3 and Table A4 in Appendix A. The minimum route length is 2 km and the maximum route length is 8 km. The minimum and maximum stop spacing values are 150 m and 1000 m, respectively. The maximum tolerable walking distance of passengers is 500 m. The key parameters used in the algorithm are the same as those in Section 5.2.
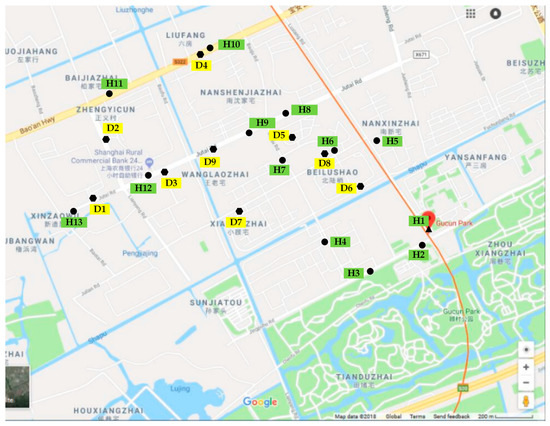
Figure 5.
Geographic distribution of demand points and candidate stops.
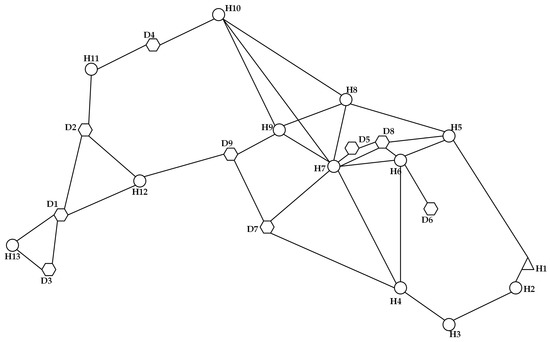
Figure 6.
Topological structure of demand points and candidate stops.

Table 5.
Travel demand of demand points for the community shuttle service (trip/day).
As shown in Table 6, there are two non-dominated solutions obtained by the NSGA-II-based algorithm. The demand points served by each candidate stop are shown in Table 7. The optimal route and stops of the community shuttle system in the topological graph and realistic network are presented in Figure 7, Figure 8, Figure 9 and Figure 10, respectively.

Table 6.
Results of the non-dominated solutions.

Table 7.
Demand points served by each candidate stop.
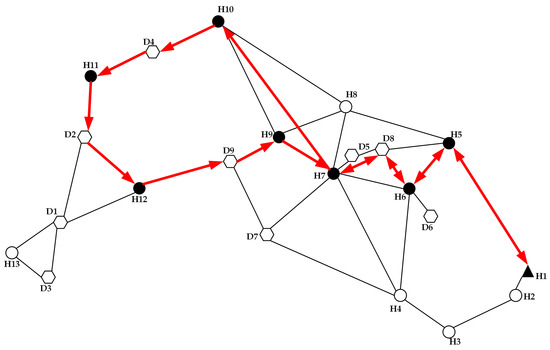
Figure 7.
The optimal route and stops of Solution 1 in the topological network.
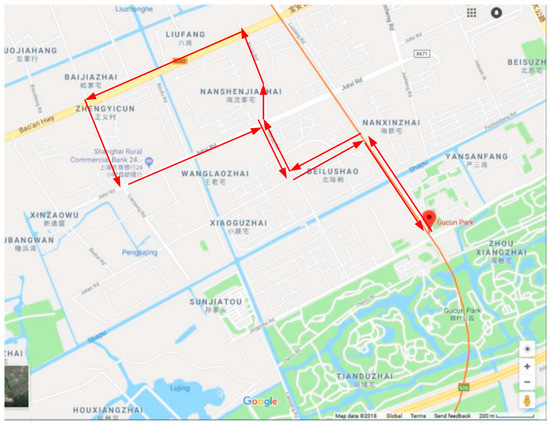
Figure 8.
The optimal route of Solution 1 in the realistic network.
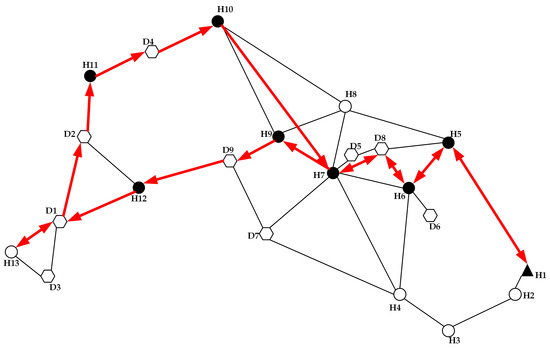
Figure 9.
The optimal route and stops of Solution 2 in the topological network.
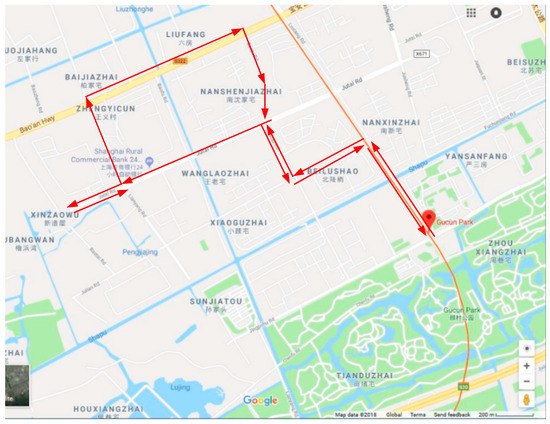
Figure 10.
The optimal route of Solution 2 in the realistic network.
There is a community shuttle line (i.e., Line 1604) through this community now. Residents in this community often take the section between Gucun Park and Jutai Road-Baotai Road of Line 1604. The route and stops of this section are shown in Figure 11. The length of this section is 4.8 km. If passengers choose the nearest stops, the total walking distance is 2597.75 km. As can be seen from Table 6, the proposed method generates a longer route than Line 1604. However, for the total walking distance of passengers, the solutions obtained by the proposed method are shorter than Line 1604. Therefore, compared with Line 1604, the solutions obtained by the proposed method are more convenient for passengers. Operators can make decisions by considering the trade-off between route length and the total walking distance of passengers.
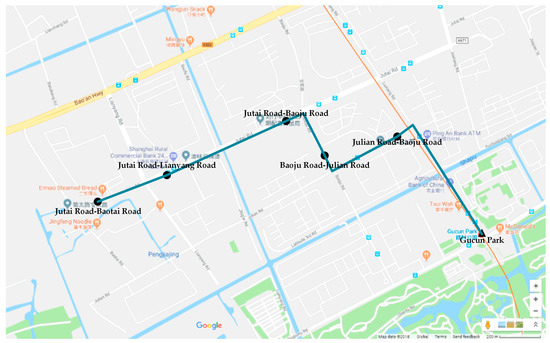
Figure 11.
Route and stops of Line 1604.
7. Conclusions
In a good community shuttle system, a proper compromise exists between the passengers’ walking distance and the route length. The passengers’ walking distance and the route length are closely related to stop location and route design, respectively. Nevertheless, stop location and route design, although directly related, have been rarely considered simultaneously in literature, which makes the relationship between them difficult to analyze. In this paper, a formulation aiming at minimizing the total walking distance of passengers and the route length is developed to determine the plans of stop location, route design, and the situation of matching demand points to stops simultaneously. The route length constraint, stop spacing constraint, maximum tolerable walking distance constraint, and situation of matching demand points to stops are taken into account. Based on the formulation, a NSGA-II-based algorithm is devised to obtain non-dominated solutions. Results of the computational experiment and the case study show that decision makers can obtain more than one solution through the formulation and algorithm within a reasonable time, which verifies the correctness and effectiveness of the formulation and algorithm. In addition, decision makers can find a compromise between the total walking distance of passengers and the route length and know how long the passengers’ walking distance will be reduced if buses travel a longer distance. Therefore, the proposed integrated approach is a significant method for obtaining plans of stop location and route design of a community shuttle service.
In conclusion, contributions of this paper are threefold. First, a multi-objective mathematical formulation is proposed to simultaneously determine the stop location, route design plans of a community shuttle service, and the situation of matching demand points to stops, which makes it possible to study the trade-off between the total walking distance of passengers and the route length. Second, we can know how many bus stops should be set up based on our approach. Third, an efficient NSGA-II-based algorithm is provided, which is suitable for our problem. This algorithm is capable of handling numerical examples of a realistic size.
One of the future research topics is to consider scheduling decisions, such as headway, while planning stop location and route design, for the reason that headway is important to the service level and operating cost. Another topic of future work is to design the stop location and route plan of a community shuttle system, considering more than one metro stations near a community.
Author Contributions
Conceptualization, X.G.; Methodology, X.G., R.S., S.H., M.B., and G.J.; Software, X.G. and M.B.; Supervision, R.S. and S.H.; Writing—original draft, X.G.; Writing—review & editing, X.G., R.S., S.H., M.B., and G.J.
Funding
This paper is supported by the National Key R&D Program of China (2018YFB1201402).
Acknowledgments
The authors would like to thank the editors and the anonymous referees for their valuable comments and suggestions which improve the quality of this paper.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Distances between demand points and candidate stops for the computational experiments (m).
Table A1.
Distances between demand points and candidate stops for the computational experiments (m).
| H1 | H2 | H3 | H4 | H5 | H6 | H7 | H8 | H9 | H10 | H11 | H12 | H13 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| D1 | 1140 | 1140 | 540 | 1140 | 540 | 1080 | 480 | 720 | 120 | 660 | 60 | 600 | 1140 |
| D2 | 900 | 900 | 300 | 600 | 1140 | 540 | 1080 | 480 | 1020 | 420 | 960 | 360 | 900 |
| D3 | 540 | 360 | 1140 | 540 | 1080 | 480 | 1020 | 480 | 1020 | 420 | 960 | 360 | 900 |
| D4 | 600 | 60 | 600 | 1140 | 540 | 1080 | 540 | 1080 | 480 | 1020 | 420 | 960 | 360 |
| D5 | 720 | 720 | 420 | 960 | 360 | 900 | 300 | 840 | 240 | 780 | 180 | 720 | 120 |
| D6 | 780 | 780 | 180 | 720 | 120 | 660 | 60 | 600 | 1140 | 300 | 840 | 240 | 780 |
| D7 | 600 | 60 | 840 | 240 | 540 | 1080 | 480 | 1020 | 420 | 960 | 600 | 1140 | 540 |
| D8 | 600 | 60 | 300 | 1140 | 540 | 1080 | 480 | 1020 | 420 | 960 | 360 | 900 | 300 |
| D9 | 540 | 420 | 60 | 600 | 1140 | 840 | 240 | 780 | 180 | 720 | 120 | 660 | 60 |
| D10 | 540 | 420 | 1020 | 120 | 660 | 60 | 600 | 1140 | 780 | 240 | 780 | 180 | 720 |
| D11 | 1080 | 1080 | 480 | 180 | 420 | 960 | 360 | 900 | 300 | 840 | 240 | 780 | 180 |
| D12 | 600 | 600 | 1140 | 780 | 180 | 720 | 1020 | 420 | 960 | 360 | 900 | 300 | 840 |
| D13 | 540 | 300 | 840 | 480 | 1080 | 480 | 1020 | 420 | 960 | 360 | 900 | 300 | 840 |
| D14 | 1140 | 1140 | 540 | 240 | 780 | 180 | 720 | 120 | 660 | 900 | 300 | 900 | 300 |
| D15 | 900 | 900 | 300 | 1080 | 480 | 1020 | 420 | 960 | 360 | 960 | 360 | 900 | 1140 |
| D16 | 900 | 900 | 300 | 540 | 1080 | 780 | 180 | 720 | 120 | 660 | 600 | 600 | 1140 |
| D17 | 1020 | 1020 | 420 | 660 | 1140 | 540 | 1080 | 660 | 60 | 600 | 480 | 1080 | 480 |
| D18 | 960 | 960 | 360 | 900 | 1140 | 540 | 1140 | 540 | 180 | 720 | 120 | 660 | 60 |
| D19 | 900 | 900 | 1140 | 780 | 180 | 720 | 120 | 660 | 60 | 660 | 60 | 600 | 1140 |
| D20 | 780 | 780 | 180 | 420 | 960 | 660 | 60 | 600 | 1140 | 540 | 1080 | 480 | 1020 |
| H14 | H15 | H16 | H17 | H18 | H19 | H20 | H21 | H22 | H23 | H24 | H25 | ||
| D1 | 540 | 1140 | 780 | 180 | 720 | 120 | 360 | 900 | 360 | 900 | 300 | 840 | |
| D2 | 300 | 840 | 540 | 1080 | 480 | 1020 | 420 | 960 | 360 | 900 | 300 | 840 | |
| D3 | 300 | 540 | 1080 | 480 | 1020 | 480 | 1020 | 420 | 960 | 360 | 900 | 300 | |
| D4 | 1140 | 540 | 1080 | 540 | 1080 | 480 | 1020 | 420 | 960 | 360 | 900 | 300 | |
| D5 | 660 | 120 | 660 | 60 | 600 | 840 | 240 | 780 | 180 | 720 | 120 | 660 | |
| D6 | 180 | 720 | 120 | 660 | 60 | 600 | 1140 | 840 | 240 | 780 | 180 | 720 | |
| D7 | 1080 | 540 | 1080 | 480 | 1020 | 420 | 960 | 360 | 900 | 1140 | 540 | 1080 | |
| D8 | 840 | 240 | 780 | 240 | 480 | 1020 | 420 | 960 | 360 | 900 | 300 | 840 | |
| D9 | 600 | 1140 | 540 | 1080 | 540 | 1080 | 480 | 1020 | 420 | 660 | 60 | 600 | |
| D10 | 120 | 660 | 60 | 600 | 1140 | 540 | 1080 | 480 | 1020 | 420 | 720 | 120 | |
| D11 | 720 | 180 | 720 | 120 | 660 | 60 | 600 | 1140 | 540 | 180 | 720 | 180 | |
| D12 | 240 | 780 | 180 | 720 | 120 | 660 | 60 | 660 | 60 | 840 | 240 | 780 | |
| D13 | 240 | 780 | 180 | 480 | 1020 | 420 | 960 | 360 | 900 | 300 | 840 | 240 | |
| D14 | 840 | 240 | 780 | 180 | 720 | 120 | 660 | 300 | 900 | 300 | 840 | 240 | |
| D15 | 540 | 1080 | 480 | 1020 | 420 | 960 | 360 | 960 | 360 | 900 | 300 | 840 | |
| D16 | 540 | 1080 | 480 | 1020 | 420 | 720 | 120 | 660 | 60 | 600 | 1140 | 540 | |
| D17 | 1020 | 420 | 960 | 60 | 600 | 1140 | 540 | 1080 | 480 | 1080 | 480 | 1020 | |
| D18 | 600 | 1140 | 540 | 1140 | 540 | 1080 | 480 | 1020 | 660 | 60 | 600 | 1140 | |
| D19 | 540 | 1080 | 480 | 720 | 120 | 660 | 60 | 660 | 60 | 600 | 1140 | 540 | |
| D20 | 420 | 960 | 420 | 960 | 360 | 600 | 1140 | 540 | 1080 | 480 | 1020 | 420 |

Table A2.
Distances between candidate stops for the computational experiments (m).
Table A2.
Distances between candidate stops for the computational experiments (m).
| H1 | H2 | H3 | H4 | H5 | H6 | H7 | H8 | H9 | H10 | H11 | H12 | H13 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| H1 | 0 | 420 | 960 | 660 | 60 | 600 | 1140 | 780 | 180 | 780 | 180 | 720 | 120 |
| H2 | 420 | 0 | 960 | 360 | 900 | 300 | 840 | 240 | 780 | 180 | 720 | 120 | 660 |
| H3 | 960 | 960 | 0 | 300 | 540 | 1140 | 540 | 1080 | 480 | 1020 | 420 | 960 | 360 |
| H4 | 660 | 360 | 300 | 0 | 300 | 840 | 300 | 1080 | 480 | 720 | 120 | 660 | 60 |
| H5 | 60 | 900 | 540 | 300 | 0 | 540 | 1080 | 480 | 1020 | 480 | 1020 | 420 | 960 |
| H6 | 600 | 300 | 1140 | 840 | 540 | 0 | 1080 | 480 | 1020 | 420 | 960 | 360 | 900 |
| H7 | 1140 | 840 | 540 | 300 | 1080 | 1080 | 0 | 1080 | 480 | 120 | 720 | 120 | 660 |
| H8 | 780 | 240 | 1080 | 1080 | 480 | 480 | 1080 | 0 | 480 | 1020 | 420 | 960 | 420 |
| H9 | 180 | 780 | 480 | 480 | 1020 | 1020 | 480 | 480 | 0 | 480 | 1020 | 480 | 1020 |
| H10 | 780 | 180 | 1020 | 720 | 480 | 420 | 120 | 1020 | 480 | 0 | 780 | 180 | 720 |
| H11 | 180 | 720 | 420 | 120 | 1020 | 960 | 720 | 420 | 1020 | 780 | 0 | 1080 | 480 |
| H12 | 720 | 120 | 960 | 660 | 420 | 360 | 120 | 960 | 480 | 180 | 1080 | 0 | 240 |
| H13 | 120 | 660 | 360 | 60 | 960 | 900 | 660 | 420 | 1020 | 720 | 480 | 240 | 0 |
| H14 | 660 | 60 | 900 | 600 | 360 | 300 | 60 | 960 | 420 | 120 | 1020 | 780 | 240 |
| H15 | 60 | 600 | 300 | 60 | 900 | 840 | 600 | 360 | 960 | 660 | 420 | 180 | 780 |
| H16 | 600 | 300 | 840 | 600 | 300 | 300 | 1140 | 600 | 360 | 60 | 960 | 720 | 180 |
| H17 | 1140 | 840 | 240 | 240 | 840 | 840 | 540 | 1140 | 900 | 600 | 360 | 120 | 960 |
| H18 | 240 | 240 | 1080 | 780 | 240 | 1080 | 1080 | 540 | 300 | 1140 | 900 | 660 | 360 |
| H19 | 780 | 780 | 480 | 180 | 780 | 480 | 480 | 1080 | 1080 | 540 | 600 | 60 | 900 |
| H20 | 180 | 180 | 1020 | 720 | 180 | 1020 | 1020 | 480 | 480 | 240 | 1140 | 300 | 360 |
| H21 | 780 | 720 | 420 | 120 | 720 | 420 | 420 | 1020 | 1020 | 780 | 540 | 840 | 900 |
| H22 | 180 | 120 | 960 | 660 | 420 | 960 | 720 | 420 | 480 | 180 | 1080 | 300 | 300 |
| H23 | 720 | 660 | 360 | 60 | 960 | 360 | 120 | 960 | 1020 | 720 | 480 | 840 | 840 |
| H24 | 120 | 60 | 900 | 600 | 360 | 900 | 660 | 420 | 420 | 120 | 1020 | 240 | 240 |
| H25 | 660 | 600 | 300 | 60 | 900 | 300 | 60 | 960 | 960 | 660 | 420 | 780 | 780 |
| H14 | H15 | H16 | H17 | H18 | H19 | H20 | H21 | H22 | H23 | H24 | H25 | ||
| H1 | 660 | 60 | 600 | 1140 | 240 | 780 | 180 | 780 | 180 | 720 | 120 | 660 | |
| H2 | 60 | 600 | 300 | 840 | 240 | 780 | 180 | 720 | 120 | 660 | 60 | 600 | |
| H3 | 900 | 300 | 840 | 240 | 1080 | 480 | 1020 | 420 | 960 | 360 | 900 | 300 | |
| H4 | 600 | 60 | 600 | 240 | 780 | 180 | 720 | 120 | 660 | 60 | 600 | 60 | |
| H5 | 360 | 900 | 300 | 840 | 240 | 780 | 180 | 720 | 420 | 960 | 360 | 900 | |
| H6 | 300 | 840 | 300 | 840 | 1080 | 480 | 1020 | 420 | 960 | 360 | 900 | 300 | |
| H7 | 60 | 600 | 1140 | 540 | 1080 | 480 | 1020 | 420 | 720 | 120 | 660 | 60 | |
| H8 | 960 | 360 | 600 | 1140 | 540 | 1080 | 480 | 1020 | 420 | 960 | 420 | 960 | |
| H9 | 420 | 960 | 360 | 900 | 300 | 1080 | 480 | 1020 | 480 | 1020 | 420 | 960 | |
| H10 | 120 | 660 | 60 | 600 | 1140 | 540 | 240 | 780 | 180 | 720 | 120 | 660 | |
| H11 | 1020 | 420 | 960 | 360 | 900 | 600 | 1140 | 540 | 1080 | 480 | 1020 | 420 | |
| H12 | 780 | 180 | 720 | 120 | 660 | 60 | 300 | 840 | 300 | 840 | 240 | 780 | |
| H13 | 240 | 780 | 180 | 960 | 360 | 900 | 360 | 900 | 300 | 840 | 240 | 780 | |
| H14 | 0 | 780 | 180 | 720 | 120 | 660 | 60 | 600 | 900 | 300 | 840 | 240 | |
| H15 | 780 | 0 | 1080 | 480 | 720 | 120 | 660 | 120 | 660 | 60 | 600 | 1140 | |
| H16 | 180 | 1080 | 0 | 840 | 240 | 780 | 180 | 720 | 120 | 960 | 360 | 900 | |
| H17 | 720 | 480 | 840 | 0 | 1080 | 480 | 1020 | 420 | 1020 | 420 | 960 | 360 | |
| H18 | 120 | 720 | 240 | 1080 | 0 | 240 | 780 | 480 | 1020 | 420 | 960 | 360 | |
| H19 | 660 | 120 | 780 | 480 | 240 | 0 | 540 | 1080 | 480 | 1020 | 660 | 60 | |
| H20 | 60 | 660 | 180 | 1020 | 780 | 540 | 0 | 1080 | 480 | 1020 | 420 | 960 | |
| H21 | 600 | 120 | 720 | 420 | 480 | 1080 | 1080 | 0 | 1080 | 480 | 1020 | 660 | |
| H22 | 900 | 660 | 120 | 1020 | 1020 | 480 | 480 | 1080 | 0 | 480 | 1020 | 420 | |
| H23 | 300 | 60 | 960 | 420 | 420 | 1020 | 1020 | 480 | 480 | 0 | 780 | 180 | |
| H24 | 840 | 600 | 360 | 960 | 960 | 660 | 420 | 1020 | 1020 | 780 | 0 | 780 | |
| H25 | 240 | 1140 | 900 | 360 | 360 | 60 | 960 | 660 | 420 | 180 | 780 | 0 |

Table A3.
Distances between demand points and candidate stops for the case study (m).
Table A3.
Distances between demand points and candidate stops for the case study (m).
| H1 | H2 | H3 | H4 | H5 | H6 | H7 | H8 | H9 | H10 | H11 | H12 | H13 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| D1 | 2370 | 2510 | 2250 | 1920 | 1800 | 1590 | 1270 | 1370 | 930 | 1730 | 830 | 330 | 150 |
| D2 | 2480 | 2620 | 2360 | 2030 | 1910 | 1700 | 1380 | 1480 | 1040 | 1260 | 360 | 440 | 620 |
| D3 | 1950 | 2090 | 1830 | 1500 | 1380 | 1170 | 850 | 950 | 510 | 1350 | 890 | 90 | 570 |
| D4 | 2390 | 2530 | 2270 | 1940 | 1820 | 1610 | 1290 | 1270 | 1310 | 470 | 430 | 1230 | 1410 |
| D5 | 1030 | 1170 | 1130 | 800 | 460 | 250 | 150 | 520 | 490 | 970 | 1870 | 1090 | 1570 |
| D6 | 1020 | 1160 | 1220 | 890 | 450 | 240 | 560 | 930 | 900 | 1380 | 2280 | 1500 | 1980 |
| D7 | 1530 | 1670 | 1070 | 740 | 960 | 750 | 430 | 800 | 770 | 1250 | 1890 | 1090 | 1570 |
| D8 | 880 | 1020 | 1080 | 750 | 310 | 100 | 220 | 590 | 560 | 1040 | 1940 | 1160 | 1640 |
| D9 | 1630 | 1770 | 1510 | 1180 | 1060 | 850 | 530 | 630 | 190 | 1030 | 1210 | 410 | 890 |

Table A4.
Distances between candidate stops for the case study (m).
Table A4.
Distances between candidate stops for the case study (m).
| H1 | H2 | H3 | H4 | H5 | H6 | H7 | H8 | H9 | H10 | H11 | H12 | H13 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| H1 | 0 | 140 | 1020 | 1350 | 570 | 780 | 1100 | 1120 | 1440 | 1920 | 2820 | 2040 | 2520 |
| H2 | 140 | 0 | 880 | 1210 | 710 | 920 | 1240 | 1260 | 1580 | 2060 | 2960 | 2180 | 2660 |
| H3 | 1020 | 880 | 0 | 330 | 1190 | 980 | 980 | 1350 | 1320 | 1800 | 2700 | 1920 | 2400 |
| H4 | 1350 | 1210 | 330 | 0 | 860 | 650 | 650 | 1020 | 990 | 1470 | 2370 | 1590 | 2070 |
| H5 | 570 | 710 | 1190 | 860 | 0 | 210 | 530 | 550 | 870 | 1350 | 2250 | 1470 | 1950 |
| H6 | 780 | 920 | 980 | 650 | 210 | 0 | 320 | 690 | 660 | 1140 | 2040 | 1260 | 1740 |
| H7 | 1100 | 1240 | 980 | 650 | 530 | 320 | 0 | 370 | 340 | 820 | 1720 | 940 | 1420 |
| H8 | 1120 | 1260 | 1350 | 1020 | 550 | 690 | 370 | 0 | 440 | 800 | 1700 | 1040 | 1520 |
| H9 | 1440 | 1580 | 1320 | 990 | 870 | 660 | 340 | 440 | 0 | 840 | 1400 | 600 | 1080 |
| H10 | 1920 | 2060 | 1800 | 1470 | 1350 | 1140 | 820 | 800 | 840 | 0 | 900 | 1440 | 1880 |
| H11 | 2820 | 2960 | 2700 | 2370 | 2250 | 2040 | 1720 | 1700 | 1400 | 900 | 0 | 800 | 980 |
| H12 | 2040 | 2180 | 1920 | 1590 | 1470 | 1260 | 940 | 1040 | 600 | 1440 | 800 | 0 | 480 |
| H13 | 2520 | 2660 | 2400 | 2070 | 1950 | 1740 | 1420 | 1520 | 1080 | 1880 | 980 | 480 | 0 |
References
- Ceder, A.; Wilson, N.H.M. Bus network design. Transp. Res. 1986, 20, 331–344. [Google Scholar] [CrossRef]
- Kuah, G.K.; Perl, J. Optimization of feeder bus routes and bus-stop spacing. J. Transp. Eng. 1988, 114, 341–354. [Google Scholar] [CrossRef]
- Shrivastava, P.; Dhingra, S.L. Operational integration of suburban railway and public buses—Case study of Mumbai. J. Transp. Eng. 2006, 132, 518–522. [Google Scholar] [CrossRef]
- Cipriani, E.; Gori, S.; Petrelli, M. Transit network design: A procedure and an application to a large urban area. Transp. Res. Part C Emerg. Technol. 2012, 20, 3–14. [Google Scholar] [CrossRef]
- Deng, L.B.; Gao, W.; Fu, Y.B.; Zhou, W.L. Optimal design of the feeder-bus network based on the transfer system. Discrete Dyn. Nat. Soc. 2013, 2013, 483682:1–483682:11. [Google Scholar] [CrossRef]
- Gulhan, G.; Ceylan, H.; Ceylan, H. Using accessibility measures in transit network design. Transport 2018, 33, 510–519. [Google Scholar] [CrossRef]
- Chen, J.X.; Wang, S.A.; Liu, Z.Y.; Wang, W. Design of suburban bus route for airport access. Transp. A 2017, 13, 568–589. [Google Scholar] [CrossRef]
- Jiang, B.L.; Sun, A.C. Urban rapid rail transit feeder buses routes planning. Syst. Eng. Theory Pract. 1998, 18, 130–139. [Google Scholar] [CrossRef]
- Shrivastava, P.; Dhingra, S.L. Development of feeder routes for suburban railway stations using heuristic approach. J. Transp. Eng. 2001, 127, 334–341. [Google Scholar] [CrossRef]
- Verma, A.; Dhingra, S.L. Feeder bus routes generation within integrated mass transit planning framework. J. Transp. Eng. 2005, 131, 822–834. [Google Scholar] [CrossRef]
- Shrivastava, P.; O’Mahony, M. A model for development of optimized feeder routes and coordinated schedules—A genetic algorithms approach. Transp. Policy 2006, 13, 413–425. [Google Scholar] [CrossRef]
- Shrivastava, P.; O’Mahony, M. Use of a hybrid algorithm for modeling coordinated feeder bus route network at suburban railway station. J. Transp. Eng. 2009, 135, 1–8. [Google Scholar] [CrossRef]
- Song, R.; Liu, Z.Q. Heuristic algorithm for feeder bus route generation in railway traffic system. J. Jilin. Univ. 2011, 41, 1234–1239. [Google Scholar] [CrossRef]
- Perugia, A.; Moccia, L.; Cordeau, J.F.; Laporte, G. Designing a home-to-work bus service in a metropolitan area. Transp. Res. B Meth. 2011, 45, 1710–1726. [Google Scholar] [CrossRef]
- Szeto, W.Y.; Wu, Y.Z. A simultaneous bus route design and frequency setting problem for Tin Shui Wai, Hong Kong. Eur. J. Oper. Res. 2011, 209, 141–155. [Google Scholar] [CrossRef]
- Teng, J.; Shen, B.; Fei, X.; Zhang, J.X.; Jiang, Z.B.; Ma, C. Designing feeder bus lines for high-speed railway terminals. Syst. Eng. Theory Pract. 2013, 33, 2937–2944. [Google Scholar] [CrossRef]
- Chien, S.; Yang, Z.W. Optimal feeder bus routes on irregular street networks. J. Adv. Transpt. 2000, 34, 213–248. [Google Scholar] [CrossRef]
- Jerby, S.; Ceder, A. Optimal routing design for shuttle bus service. In Proceedings of the 85th Annual Meeting of the Transportation-Research-Board, Transportation Research Board Natl Research Council, Washington, DC, USA, 22–26 January 2006. [Google Scholar]
- Pan, S.L.; Yu, J.; Yang, X.F.; Liu, Y.; Zou, N. Designing a flexible feeder transit system serving irregularly shaped and gated communities: Determining service area and feeder route planning. J. Urban Plan. Dev. 2014, 141, 04014028:1–04014028:9. [Google Scholar] [CrossRef]
- Xiong, J.; Guan, W.; Huang, A.L. Research on optimal routing of community shuttle connect rail transit line. J. Trans. Syst. Eng. Inf. Technol. 2014, 14, 166–173. [Google Scholar] [CrossRef]
- Zhu, Z.J.; Guo, X.C.; Zeng, J.; Zhang, S.R. Route design model of feeder bus service for urban rail transit stations. Math. Probl. Eng. 2017, 2017, 1090457:1–1090457:6. [Google Scholar] [CrossRef]
- Lin, J.J.; Wong, H.I. Optimization of a feeder-bus route design by using a multiobjective programming approach. Transpt. Plan. Technol. 2014, 37, 430–449. [Google Scholar] [CrossRef]
- Liu, Y.; Jia, G.C.; Tao, X.; Xu, X.L. A stop planning method over big traffic data for airport shuttle bus. In Proceedings of the IEEE Fourth International Conference on Big Data and Cloud Computing, Sydney, Australia, 3–5 December 2014. [Google Scholar]
- Zhao, L.H.; Chien, S.I. Investigating the impact of stochastic vehicle arrivals to optimal stop spacing and headway for a feeder bus route. J. Adv. Transp. 2015, 49, 341–357. [Google Scholar] [CrossRef]
- Alonso, B.; Moura, J.L.; dell’Olio, L.; Ibeas, A. Bus stop location under different levels of network congestion and elastic demand. Transport 2011, 26, 141–148. [Google Scholar] [CrossRef]
- Moura, J.L.; Alonso, B.; Ibeas, A.; Ruisánchez, F.J. A two-stage urban bus stop location model. Netw. Spat. Econ. 2012, 12, 403–420. [Google Scholar] [CrossRef]
- Chen, J.X.; Wang, S.A.; Liu, Z.Y.; Chen, X.W. Network-level optimization of bus stop placement in urban areas. KSCE J. Civ. Eng. 2018, 22, 1446–1453. [Google Scholar] [CrossRef]
- Jahani, M.; Hashemi, S.M.; Ghatee, M.; Jahanshahi, M. A novel model for bus stop location appropriate for public transit network design: The case of central business districts (CBD) of Tehran. Int. J. Smart Electr. Eng. 2013, 2, 133–141. [Google Scholar] [CrossRef]
- Xiong, J.; Guan, W.; Song, L.Y.; Huang, A.L.; Shao, C.F. Optimal routing design of a community shuttle for metro stations. J. Transp. Eng. 2013, 139, 1211–1223. [Google Scholar] [CrossRef]
- Li, H.G.; Chen, Y.S. Study on enterprise shuttle bus location and route optimization: An integrated approach. J. Univ. Electron. Sci. Technol. China 2016, 18, 68–73. [Google Scholar] [CrossRef]
- Leksakul, K.; Smutkupt, U.; Jintawiwat, R.; Phongmoo, S. Heuristic approach for solving employee bus routes in a large-scale industrial factory. Adv. Eng. Inf. 2017, 32, 176–187. [Google Scholar] [CrossRef]
- Shimamoto, H.; Schmöcker, J.D.; Kurauchi, F. Optimisation of a bus network configuration and frequency considering the common lines problem. J. Transp. Technol. 2012, 2, 49–56. [Google Scholar] [CrossRef]
- Wu, Y.H.; Yang, H.; Tang, J.F.; Yu, Y. Multi-objective re-synchronizing of bus timetable: Model, complexity and solution. Transp. Res. Part C Emerg. Technol. 2016, 67, 149–168. [Google Scholar] [CrossRef]
- Zhu, C.; Chen, X.H. Optimizing battery electric bus transit vehicle scheduling with battery exchanging: Model and case study. In Proceedings of the 13th COTA International Conference of Transportation Professionals, Shenzhen, China, 13–16 August 2013. [Google Scholar]
- Deb, K.; Agrawal, S.; Pratap, A.; Meyarivan, T. A fast elitist non-dominated sorting genetic algorithm for multi-objective optimization: NSGA-II. In Proceedings of the Sixth International Conference on Parallel Problem Solving From Nature, Paris, France, 18–20 September 2000. [Google Scholar]
- Wu, M.M. Study on Urban Microcirculation Public Transit—Analyze the Characteristic of Passengers’ Trip and Research on the Method of Planning the Bus Stops. Master’s Thesis, Chang’an University, Xi’an, Shanxi, China, 2014. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).