1. Introduction
Pawlak [
1,
2] proposed rough sets theory in 1982 as a method of dealing with inaccuracy and uncertainty, and it has been developed into a variety of theories [
3,
4,
5,
6]. For example, the multi-granulation rough sets (MRS) model is one of the important developments [
7,
8]. The MRS can also be regarded as a mathematical framework to handle granular computing, which is proposed by Qian et al. [
9]. Thereinto, the problem of granularity reduction is a vital research aspect of MRS. Considering the test cost problem of granularity structure selection in data mining and machine learning, Yang et al. constructed two reduction algorithms of cost-sensitive multi-granulation decision-making system based on the definition of approximate quality [
10]. Through introducing the concept of distribution reduction [
11] and taking the quality of approximate distribution as the measure in the multi-granulation decision rough sets model, Sang et al. proposed an α-lower approximate distribution reduction algorithm based on multi-granulation decision rough sets, however, the interactions among multiple granularities were not considered [
12]. In order to overcome the problem of updating reduction, when the large-scale data vary dynamically, Jing et al. developed an incremental attribute reduction approach based on knowledge granularity with a multi-granulation view [
13]. Then other multi-granulation reduction methods have been put forward one after another [
14,
15,
16,
17].
The notion of intuitionistic fuzzy sets (IFS), proposed by Atanassov [
18,
19], was initially developed in the framework of fuzzy sets [
20,
21]. Within the previous literature, how to get reasonable membership and non-membership functions is a key issue. In the interest of dealing with fuzzy information better, many experts and scholars have expanded the IFS model. Huang et al. combined IFS with MRS to obtain intuitionistic fuzzy MRS [
22]. On the basis of fuzzy rough sets, Liu et al. constructed covering-based multi-granulation fuzzy rough sets [
23]. Moreover, multi-granulation rough intuitionistic fuzzy cut sets model was structured by Xue et al. [
24]. In order to reduce the classification errors and the limitation of ordering by single theory, they further combined IFS with graded rough sets theory based on dominance relation and extended them to a multi-granulation perspective. [
25]. Under the optimistic multi-granulation intuitionistic fuzzy rough sets, Wang et al. proposed a novel method to solve multiple criteria group decision-making problems [
26]. However, the above studies rarely deal with the optimal granularity selection problem in intuitionistic fuzzy environments. The measure of similarity between intuitionistic fuzzy sets is also one of the hot areas of research for experts, and some similarity measures about IFS are summarized in references [
27,
28,
29], whereas these metric formulas cannot measure the importance degree of multiple granularities in the same IFS.
For further explaining the semantics of decision-theoretic rough sets (DTRS), Yao proposed a three-way decisions theory [
30,
31], which vastly pushed the development of rough sets. As a risk decision-making method, the key strategy of three-way decisions is to divide the domain into acceptance, rejection, and non-commitment. Up to now, researchers have accumulated a vast literature on its theory and application. For instance, in order to narrow the applications limits of three-way decisions model in uncertainty environment, Zhai et al. extended the three-way decisions models to tolerance rough fuzzy sets and rough fuzzy sets, respectively, the target concepts are relatively extended to tolerance rough fuzzy sets and rough fuzzy sets [
32,
33]. To accommodate the situation where the objects or attributes in a multi-scale decision table are sequentially updated, Hao et al. used sequential three-way decisions to investigate the optimal scale selection problem [
34]. Subsequently, Luo et al. applied three-way decisions theory to incomplete multi-scale information systems [
35]. With respect to multiple attribute decision-making, Zhang et al. study the inclusion relations of neutrosophic sets in their case in reference [
36]. For improving the classification correct rate of three-way decisions, Zhang et al. proposed a novel three-way decisions model with DTRS by considering the new risk measurement functions through the utility theory [
37]. Yang et al. combined three-way decisions theory with IFS to obtain novel three-way decision rules [
38]. At the same time, Liu et al. explored the intuitionistic fuzzy three-way decision theory based on intuitionistic fuzzy decision systems [
39]. Nevertheless, Yang et al. [
38] and Liu et al. [
39] only considered the case of a single granularity, and did not analyze the decision-making situation of multiple granularities in an intuitionistic fuzzy environment. The DTRS and three-way decisions theory are both used to deal with decision-making problems, so it is also enlightening for us to study three-way decisions theory through DTRS. An extension version that can be used to multi-periods scenarios has been introduced by Liang et al. using intuitionistic fuzzy decision- theoretic rough sets [
40]. Furthermore, they introduced the intuitionistic fuzzy point operator into DTRS [
41]. The three-way decisions are also applied in multiple attribute group decision making [
42], supplier selection problem [
43], clustering analysis [
44], cognitive computer [
45], and so on. However, they have not applied the three-way decisions theory to the optimal granularity selection problem. To solve this problem, we have expanded the three-way decisions models.
The main contributions of this paper include four points:
(1) The new granularity importance degree calculating methods among multiple granularities (i.e., and ) are given respectively, which can generate more discriminative granularities.
(2) Optimistic optimistic multi-granulation rough intuitionistic fuzzy sets (OOMRIFS) model, optimistic pessimistic multi-granulation rough intuitionistic fuzzy sets (OIMRIFS) model, pessimistic optimistic multi-granulation rough intuitionistic fuzzy sets (IOMRIFS) model and pessimistic pessimistic multi-granulation rough intuitionistic fuzzy sets (IIMRIFS) model are constructed by combining intuitionistic fuzzy sets with the reduction of the optimistic and pessimistic multi-granulation rough sets. These four models can reduce the subjective errors caused by a single intuitionistic fuzzy set.
(3) We put forward four kinds of three-way decisions models based on the proposed four multi-granulation rough intuitionistic fuzzy sets (MRIFS), which can further reduce the redundant objects in each granularity of reduction sets.
(4) Comprehensive score function and comprehensive accuracy function based on MRIFS are constructed. Based on this, we can obtain the optimal granularity selection results.
The rest of this paper is organized as follows. In
Section 2, some basic concepts of MRS, IFS, and three-way decisions are briefly reviewed. In
Section 3, we propose two new granularity importance degree calculating methods and a granularity reduction Algorithm 1. At the same time, a comparative example is given. Four novel MRIFS models are constructed in
Section 4, and the properties of the four models are verified by Example 2.
Section 5 proposes some novel three-way decisions models based on above four new MRIFS, and the comprehensive score function and comprehensive accuracy function based on MRIFS are built. At the same time, through Algorithm 2, we make the optimal granularity selection. In
Section 6, we use Example 3 to study and illustrate the three-way decisions models based on new MRIFS.
Section 7 concludes this paper.
3. Granularity Reduction Algorithm Derives from Granularity Importance Degree
Definition 5 ([
10,
12])
. Let be a decision information system, are m sub-attributes of condition attributes C. is the partition induced by the decision attributes D, then approximation quality of about granularity set A is defined as:where denotes the cardinal number of set X. represents two cases of optimistic and pessimistic multi-granulation rough sets, the same as the following. Definition 6 ([
12])
. Let be a decision information system, are m sub-attributes of C, , ,
(1) If , then is important in A for X;
(2) If , then is not important in A for X.
Definition 7 ([
10,
12])
. Suppose is a decision information system, are m sub-attributes of C, . , on the granularity sets , the internal importance degree of Ai for D can be defined as follows: Definition 8 ([
10,
12])
. Let be a decision information system, are m sub-attributes of C, . , on the granularity sets , the external importance degree of Ai for D can be defined as follows: Theorem 1. Letbe a decision information system,are m sub-attributes of C,.
(1)
For , on the basis of attribute subset family , the granularity importance degree of in with respect to D is expressed as follows:where ,
, the same as the following.(2)
For , on the basis of attribute subset family , the granularity importance degree of in with respect to D, we have: Proof. (1) According to Definition 7, then
(2) According to Definition 8, we can get:
□
In Definitions 7 and 8, only the direct effect of a single granularity on the whole granularity sets is given, without considering the indirect effect of the remaining granularities on decision-making. The following Definitions 9 and 10 synthetically analyze the interdependence between multiple granularities and present two new methods for calculating granularity importance degree.
Definition 9. Letbe a decision information system,are m sub-attributes of C,., on the attribute subset family, A, the new internal importance degree of Ai relative to D is defined as follows: andrespectively indicate the direct and indirect effects of granularity Ai on decision-making. Whenis satisfied, it is shown that the granularity importance degree of Ak is increased by the addition of Ai in attribute subset, so the granularity importance degree of Ak should be added to Ai. Therefore, when there are m sub-attributes, we should addto the granularity importance degree of Ai.
Ifand, then it shows that there is no interaction between granularity Ai and other granularities, which means
Definition 10. Letbe a decision information system,be m sub-attributes of C,., the new external importance degree of Ai relative to D is defined as follows: Similarly, the new external importance degree calculation formula has a similar effect.
Theorem 2. Letbe a decision information system,be m sub-attributes of C,,. The improved internal importance can be rewritten as: Theorem 3. Letbe a decision information system,are m sub-attributes of C,. The improved external importance can be expressed as follows: Theorems 2 and 3 show that when is satisfied, having . And each granularity importance degree is calculated on the basis of removing Ak from , which makes it more convenient for us to choose the required granularity.
According to [
10,
12], we can get optimistic and pessimistic multi-granulation lower approximations
and
. The granularity reduction algorithm based on improved granularity importance degree is derived from Theorems 2 and 3, as shown in Algorithm 1.
| Algorithm 1. Granularity reduction algorithm derives from granularity importance degree |
Input:, are m sub-attributes of C,, , ;
Output: A granularity reduction set of this information system.
1: set up , ;
2: compute , optimistic and pessimistic multi-granulation lower approximations ;
3: for
4: compute via Definition 9;
5: if then ;
6: end
7: for
8: if then compute via Definition 10;
9: end
10: if then ;
11: end
12: end
13: for ,
14: if then ;
15: end
16: end
17: return granularity reduction set ;
18: end |
Therefore, we can obtain two reductions by utilizing Algorithm 1.
Example 1. This paper calculates the granularity importance of 10 on-line investment schemes given in Reference [12]. After comparing and analyzing the obtained granularity importance degree, we can obtain the reduction results of 5 evaluation sites through Algorithm 1, and the detailed calculation steps are as follows. According to [
12], we can get
- (1)
Reduction set of OMRS
First of all, we can calculate the internal importance degree of OMRS by Theorem 2 as shown in
Table 2.
Then, according to Algorithm 1, we can deduce the initial granularity set is . Inspired by Definition 5, we obtain . So, the reduction set of the OMRS is .
As shown in
Table 2, when using the new method to calculate internal importance degree, more discriminative granularities can be generated, which are more convenient for screening out the required granularities. In literature [
12], the approximate quality of granularity
A2 in the reduction set is different from that of the whole granularity set, so it is necessary to calculate the external importance degree again. When calculating the internal and external importance degree, References [
10,
12] only considered the direct influence of the single granularity on the granularity
A2, so the influence of the granularity
A2 on the overall decision-making can’t be fully reflected.
- (2)
Reduction set of IMRS
Similarly, by using Theorem 2, we can get the internal importance degree of each site under IMRS, as shown in
Table 3.
According to Algorithm 1, the sites 2, 4, and 5 with internal importance degrees greater than 0, which are added to the granularity reduction set as the initial granularity set, and then the approximate quality of it can be calculated as follows:
Namely, the reduction set of IMRS is or without calculating the external importance degree.
In this paper, when calculating the internal and external importance degree of each granularity, the influence of removing other granularities on decision-making is also considered. According to Theorem 2, after calculating the internal importance degree of OMRS and IMRS, if the approximate quality of each granularity in the reduction sets are the same as the overall granularities, it is not necessary to calculate the external importance degree again, which can reduce the amount of computation.
6. Example Analysis 3 (Continued with Example 2)
In Example 1, only site 1 can be ignored under optimistic and pessimistic multi-granulation conditions, so it can be determined that site 1 does not need to be evaluated, while sites 2 and 3 need to be further investigated under the environment of optimistic multi-granulation. At the same time, with respect to the environment of pessimistic multi-granulation, comprehensive considera- tion site 3 can ignore the assessment and sites 2, 4 and 5 need to be further investigated.
According to Example 1, we can get that the reduction set of OMRS is , but in the case of IMRS, there are two reduction sets, which are contradictory. Therefore, two reduction sets should be reconsidered simultaneously, so the joint reduction set under IMRS is .
Where the corresponding granularity structures of sites 2, 3, 4 and 5 are divided as follows:
According to reference [
11], we can get:
;
The optimal site selection process under optimistic and IMRS is as follows:
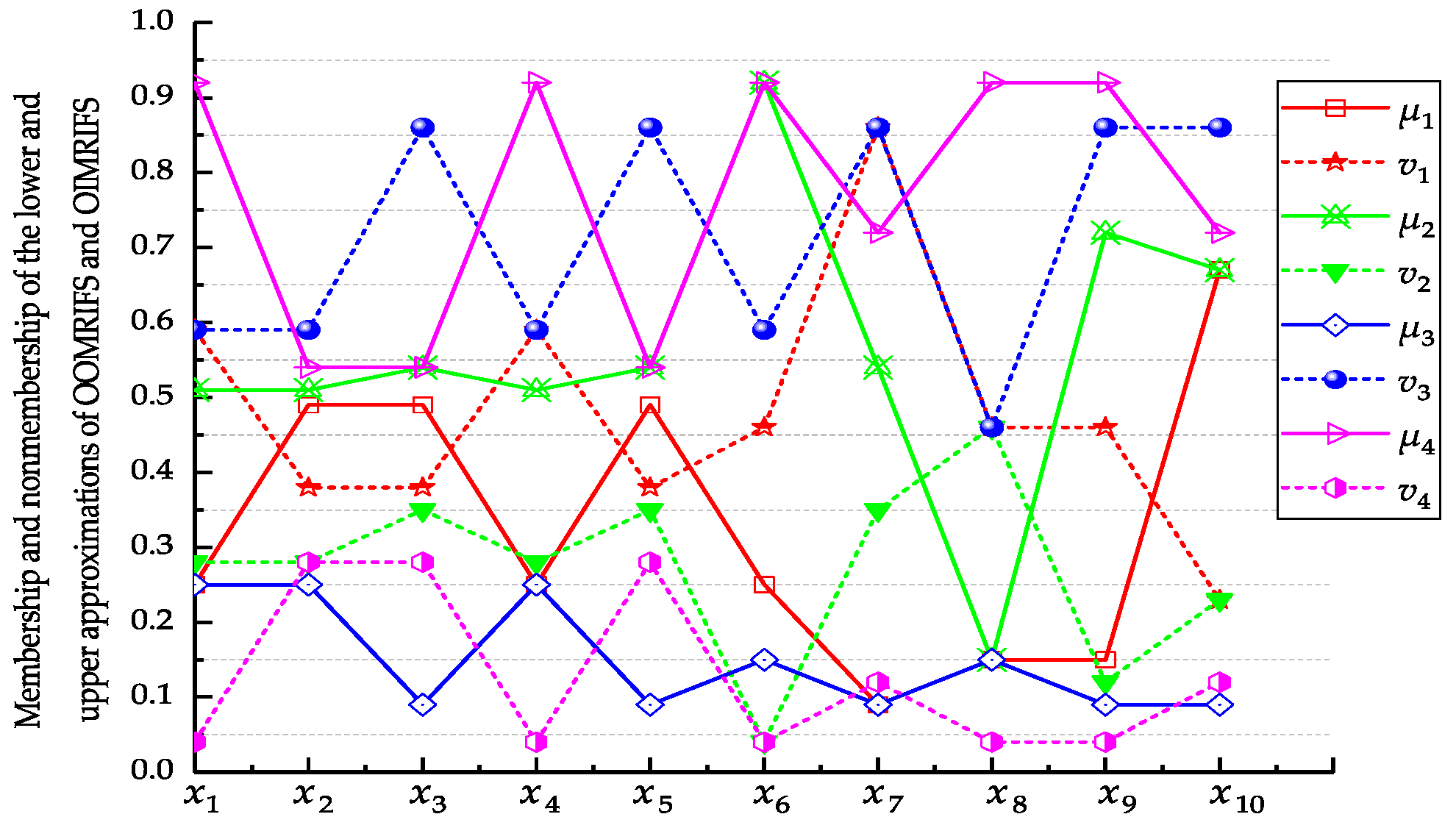
(1) Optimal site selection based on OOMRIFS
According to the Example 2, we can get the values of evaluation functions
,
,
,
,
and
of OOMRIFS, as shown in
Table 4.
We can get decision results of the lower and upper approximations of OOMRIFS by three-way decisions of the
Section 5.1, as follows:
In the light of three-way decisions rules based on OOMRIFS, after getting rid of the objects in the rejection domain, we choose to fuse the objects in the delay domain with those in the acceptance domain for the optimal granularity selection. Therefore, the new granularities A2, A3 are as follows:
Then, according to Definition 18, we can get:
Similarly, we have:
From the above results, in OOMRIFS, we can see that we can’t get the selection result of sites 2 and 3 only according to the comprehensive score function of granularities
A2 and
A3. Therefore, we need to further calculate the comprehensive accuracies to get the results as follows:
Analogously, we have:
Through calculation above, we know that the comprehensive accuracy of the granularity A3 is higher, so the site 3 is selected as the selection result.
(2) Optimal site selection based on OIMRIFS
The same as (1), we can get the values of evaluation functions
,
,
,
,
and
of OIMRIFS listed in
Table 5.
We can get decision results of the lower and upper approximations of OIMRIFS by three-way decisions in the
Section 5.2, as follows:
Hence, in the upper approximations of OIMRIFS, the new granularities A2, A3 are as follows:
According to Definition 18, we can calculate that
In OIMRIFS, the comprehensive score and comprehensive accuracy of the granularity A3 are both higher than the granularity A2. So, we choose site 3 as the evaluation site.
In reality, we are more inclined to select the optimal granularity in the case of more stringent requirements. According to (1) and (2), we can find that the granularity A3 is a better choice when the requirements are stricter in four cases of OMRS. Therefore, we choose site 3 as the optimal evaluation site.
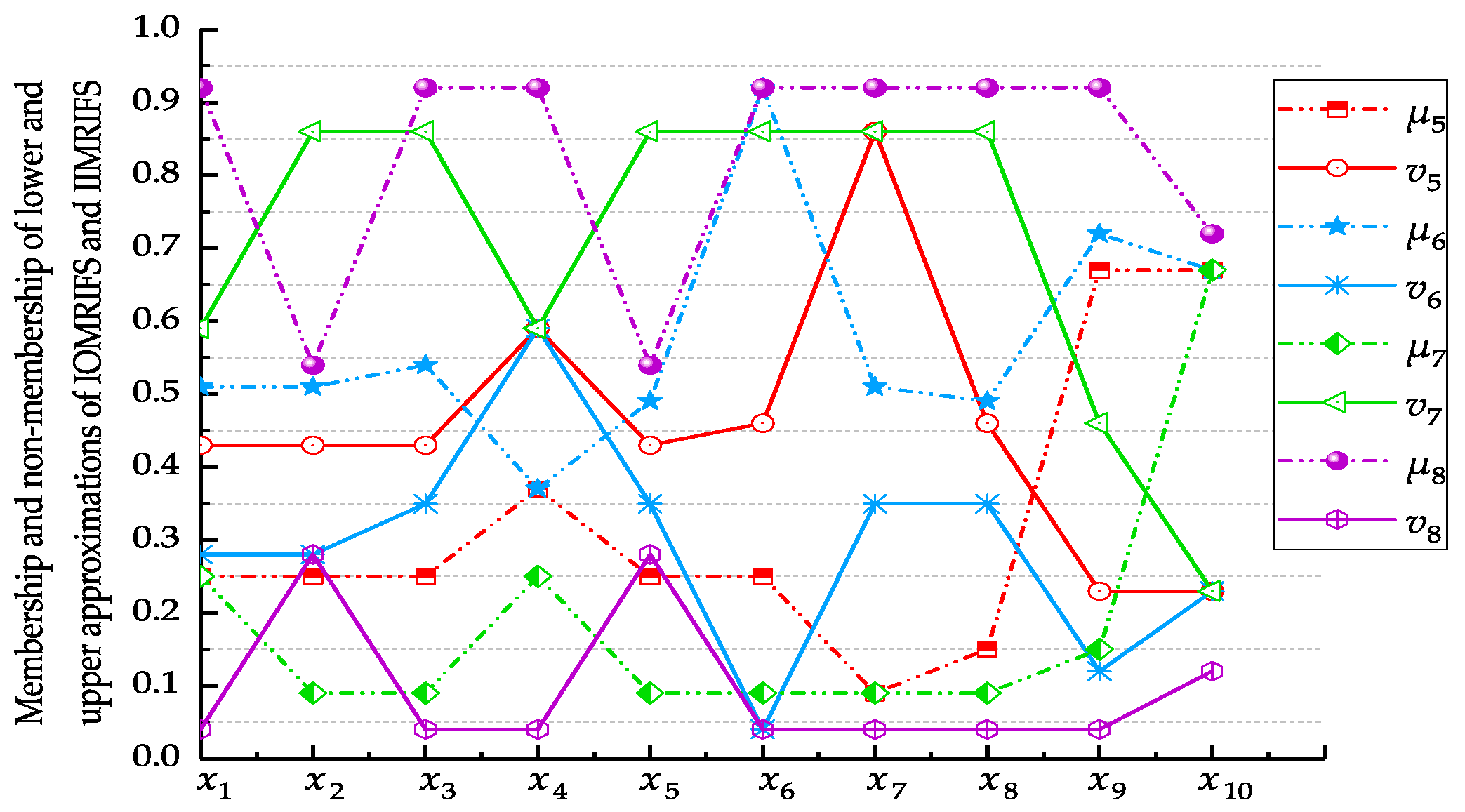
(3) Optimal site selection based on IOMRIFS
Similar to (1), we can obtain the values of evaluation functions
,
,
,
,
and
of IOMRIFS, as described in
Table 6.
We can get decision results of the lower and upper approximations of IOMRIFS by three-way decisions in the
Section 5.3, as follows:
Therefore, the granularities A2, A4, A5 can be rewritten as follows:
According to Definition 18, one can see that the results are captured as follows:
In summary, the comprehensive score function of the granularity A2 is higher than the granularity A3 in IOMRIFS, so we choose site 2 as the result of granularity selection.
(4) Optimal site selection based on IIMRIFS
In the same way as (1), we can get the values of evaluation functions
,
,
,
,
and
of IIMRIFS, as shown in
Table 7.
We can get decision results of the lower and upper approximations of IIMRIFS by three-way decisions in the
Section 5.4, as follows:
Therefore, the granularity structures of A2, A4, A5 can be rewritten as follows:
According to Definition 18, one can see that the results are captured as follows:
In IIMRIFS, the values of the comprehensive score and comprehensive accuracy of granularity A4 are higher than A2 and A5, so site 4 is chosen as the evaluation site.
Considering (3) and (4) synthetically, we find that the results of granularity selection in IOMRIFS and IIMRIFS are inconsistent, so we need to further compute the comprehensive accuracies of IIMRIFS.
Through the above calculation results, we can see that the comprehensive score and comprehensive accuracy of granularity A4 are higher than A2 and A5 in the case of pessimistic multi- granulation when the requirements are stricter. Therefore, the site 4 is eventually chosen as the optimal evaluation site.