Abstract
The Symmetric Traveling Salesman Problem (sTSP) is an intensively studied NP-hard problem. It has many important real-life applications such as logistics, planning, manufacturing of microchips and DNA sequencing. In this paper we propose a cluster level incremental tour construction method called Intra-cluster Refinement Heuristic (IntraClusTSP). The proposed method can be used both to extend the tour with a new node and to improve the existing tour. The refinement step generates a local optimal tour for a cluster of neighbouring nodes and this local optimal tour is then merged into the global optimal tour. Based on the performed evaluation tests the proposed IntraClusTSP method provides an efficient incremental tour generation and it can improve the tour efficiency for every tested state-of-the-art methods including the most efficient Chained Lin-Kernighan refinement algorithm. As an application example, we apply IntraClusTSP to automatically determine the optimal number of clusters in a cluster analysis problem. The standard methods like Silhouette index, Elbow method or Gap statistic method, to estimate the number of clusters support only partitional (single level) clustering, while in many application areas, the hierarchical (multi-level) clustering provides a better clustering model. Our proposed method can discover hierarchical clustering structure and provides an outstanding performance both in accuracy and execution time.
1. Introduction
Symmetric graphs have many real-life applications as vehicle routing, warehouse logistics, planning circuit boards, virtual networking [1,2,3,4]. The goal of the base Symmetric Traveling Salesman Problem (sTSP) is to find the shortest Hamiltonian cycle in a graph. The Hamiltonian cycle visits each vertex exactly once. The length of the path is calculated with the sum of the corresponding edge weights. The weight values of the graph edges, in general case, are given with a squared matrix of non-negative values. In this paper, we are focusing on Euclidean TSP (eTSP) problems where the graph nodes correspond to points in the Euclidean metric space and the weights are equal to the Euclidean distances between these points. In this case we get a symmetric distance matrix. The generation of the shortest Hamiltonian cycle is an NP-hard problem [5] usually formulated as an integer linear programming problem [6].
Regarding the complexity of the sTSP, two different problems are usually investigated: the Decision problem (DTSP) and the Optimization problem (OTSP). DTSP aims to determine whether a Hamiltonian cycle of length not greater than a given value exists. The goal of OTSP is to find the Hamiltonian cycle of minimal length.
In the brute-force solution method, all possible permutations of the nodes are tested to select the optimal route. This approach requires O(N!) execution cost. Regarding the other alternative exact solution methods, we can emphasize the integer linear programming approach and the Held-Karp algorithm. In the case of integer linear programming formulation [7], we have O(N2) variables and subtour elimination constraints. As a direct solution is unfeasible, the model is relaxed to find a solution. In the proposal [8] a novel representation form was introduced to reduce the number of subtour elimination constraints. In Reference [9], the related integer linear programming problem is based on the two-commodity network flow formulation of the TSP.
The Held-Karp method [10] uses the dynamic programming approach. The algorithm follows the idea of successive approximation; the global problem is decomposed into a set of related subproblems and the optimal solutions of the subproblems are composed into an optimal global solution. Although, this method provides a better time cost efficiency than the brute-force algorithm, it belongs to exponential complexity class, having a worst-case cost O(2NN2). Another drawback of the method is that it raises a significant space requirement too.
In Reference [11] the branch-and-bound approach was implemented to determine the exact optimal tour. The method builds up a state-tree that manages the paths already processed. Each node stores a path description together with its cost values involving a lower bound cost value too. The construction of the state tree requires O(N!) costs in the worst case. In the [12] a genetic node is assigned to an assignment problem. The related subtours are broken by creating subproblems in which all edges of the subtour are prohibited.
Due to high computational costs of the exact solution methods, the heuristic optimization of sTSP is one of the most widely investigated combinatorial optimization problem. One group of the heuristic methods use algorithms for direct route construction. As the main goal is to minimize the sum of a fixed number of edge weights, a sound heuristic is to minimize the components in the sum. Thus, the constructional heuristic methods are in general aimed for selecting the edges of minimal length. In the case of Nearest Neighbour method [13], the algorithm starts with a random selection of a vertex. In each iteration step, the nearest free vertex is selected and it will be connected to the current node. In the Greedy Edge Insertion heuristic method [14], the edges are ordered by their weight values. The algorithm inserts the shortest available edge into the route in every iteration step. During the construction process there are two constraints to be met: (a) any node is connected to exactly two other nodes; (b) no cycle can exist with less than N edges. The Greedy Vertex Insertion algorithm [15] extends the existing route with a vertex having the lowest cost increase. A similar approach was implemented in the Boruvka algorithm [16] where the edges are processed in length order. An edge with minimal length is inserted into the tour if it does not affect the integrity of the current route.
The Fast Recursive Partitioning method [17] performs a hierarchical clustering of the nodes corresponding to points in the Euclidean space. The points are structured into a hierarchical tree, similarly to the R-tree structure. The leaf nodes contain a smaller number of points, with a given capacity. In first phase, the algorithm performs a TSP route generation for each of the leaf buckets and in the second phase, the local routes are merged into a global tour. The Karp’s Partitioning Heuristic [18] is based on a similar hierarchical decomposition technique but it uses a more sophisticated patch-based method. The Double Minimum Spanning Tree algorithm [19] and its improved version, the Christofides Algorithm [20], generates first a minimal spanning tree for the input graph and adjusts this tree with a minimum-weight matching.
Another family of heuristic methods aims at the improvement of existing solutions found so far. Having one or more initial suggestions, the algorithm tries to find a better solution. The improvement heuristics can achieve significantly better results than the direct construction methods [6]. These algorithms use iterations and random search components; thus the execution time is here usually higher. The k-opt method [21] belongs to the family of local search heuristics. Similarly to the string edit distance, a tour distance is defined between two edge sequences. The tour t’ is considered in the k-neighbourhood of t if the distance between t and t’ is not greater than k. Having an initial tour, this method repeatedly replaces the current tour with a tour in its neighbourhood providing a smaller tour length. Due to the higher time cost of the neighbourhood construction process, the variants with lower k values (2-opt and 3-opt) are preferred in the practical implementations.
The Lin-Kernighan [22] algorithm improves the efficiency of the standard k-opt approaches by using a flexible neighbourhood construction. The method first determines the optimal k value for the k-opt method and performs the search operation in the dynamic k-neighbourhood environment, where each move is composed of special 2-opt and 3-opt moves. As the quality of the base Lin-Kernighan local optimization methods depends significantly on the quality of the initial route, a usual approach is to repeat the local search with different initial routes and return the best result. The approach presented by [23] uses a different idea to work harder on the current tours using kicks on the tour found by Lin-Kernighan. The resulting algorithm is known as Chained Lin-Kernighan method.
There are also approaches using generic Evolutionary Optimization [24] methods for the shortest tour problem. Such a method generates a set of initial tours and using the route length as a fitness function, the next generation is produced with the application of the reproduction, crossover and mutation operators. As the mutation and crossover has a random nature, the quality of the result is weak for large search space problems. In Reference [25], the predictability of TSP optimization is investigated analysing different bacterial evolutionary algorithms with local search.
In the Multi-level Approach [26], the tour is constructed with a hierarchy of increasingly coarse approximations. Having an initial problem on N nodes, the algorithm first fixes an edge at every level, thus the next level optimizes a problem of smaller size having only (N − 1) nodes. After generating an initial tour, a usual refinement phase is executed to improve the tour quality. The Tour-merging Method [27] is based on the observation that the routes of good quality usually share a large set of common edges. The algorithm uses specific heuristics to generate near-optimal tours and dynamic programming to unify the partial solutions into a common solution.
There is a rich literature on detailed analysis and performance comparison of the main heuristic methods (Nearest Neighbour, Nearest Insertion, Tabu Search, Lin-Kernighan, Greedy, Boruvka, Savings and Genetic Algorithm). Based on the results presented in Reference [16,19,28]: (a) the fastest algorithms are the Greedy and Savings method but they provide an average tour quality; (b) the Nearest Neighbour and Nearest Insertion algorithms are dominated by the Greedy and Savings methods both in time and tour quality factors; (c) the best route quality can be achieved by the application of 3-opt/5-opt methods (Lin-Kernighan and Helsgaun); (d) considering both the time and tour quality, the Chained Lin-Kernighan algorithm proves the best performance; (e) the Evolutionary and Swarm optimization methods are dominated by the k-opt methods both in time and tour quality factors; (f) the Tour-merging methods applied on the Chained Lin-Kernighan algorithm can improve the tour quality at some level but it requires a significantly higher time cost.
Most of the available heuristic methods work in a batch mode, where the full graph is presented as input. In this case the algorithm can get all information already at the start of the tour generation. An alternative approach is the incremental mode where the graph is initially empty and it is extended with new nodes incrementally. This can happen in some application areas as knowledge engineering or transportation problems where new concepts/locations can be added to the existing network. Having only a batch algorithm, after the insertion of a new node, we should rerun the full optimization process to get the new optimal tour. In these cases the incremental algorithms can provide a better solution than the standard batch methods.
Considering the main heuristic methods, only few can be adapted to the incremental construction approach. In the family of constructional heuristic methods, the methods usually process the edges in some selected order. For example, in Greedy Edge Insertion heuristic method [14] or in Boruvka algorithm [16], the edges are sorted by the length value. Greedy Vertex Insertion algorithm [15] extends the existing route with a vertex having the lowest cost increase. In the case of Nearest Neighbour method [13], the shortest free edge is selected related to the actual node. In all cases, if we extend the graph with a random new element and process this element with the mentioned methods, the resulted route will be usually suboptimal. In a batch mode, this element would be processed in an earlier step. The heuristics methods form the other groups use such operations (improvements, hierarchical decomposition) which are defined on the complete graph or on a complete subgraph.
In this paper, we propose a novel algorithm, called IntraClusTSP that can be used in Euclidean TSP for both incremental tour construction and tour refinement. The method first selects one or more clusters in the object graph and then it performs cluster-level route optimization for each cluster. In the final step, the optimized local routes are merged with the current global route yielding a new optimal route. This approach is based on the observation that adjacent nodes in the shortest Hamiltonian cycle in eTSP are usually nearest neighbour nodes. The IntraClusTSP refinement method provides a general framework for route optimization as it can use any current TSP methods to perform cluster level optimization. In our model, we use Chained Lin-Kernighan method for local optimization. The clusters selected for refinement may be overlapping clusters. Based on the performed tests, the proposed method provides superior efficiency for incremental route construction.
The rest of this paper is structured as follows. In the next section, a survey on TSP heuristics using incremental or cluster-based optimization is presented. Section 3 presents the motivation for the development of the proposed IntraClusTSP method, the formal model and the constructed algorithms. Section 4 focuses on its cost model and cost analysis. It presents the test results of the empirical efficiency comparison of the proposed method with the several TSP solution algorithms. Section 5 demonstrates the application of IntraClusTSP algorithm in solving of a data analysis problem.
2. Incremental and Segmentation-Based Approaches in Solving eTSP
In the TSP terminology, the term incremental insertion heuristic refers to methods where the optimal tour is constructed by extension steps where in each step, the route is extended with a single node. The most widely known methods of this group are Nearest point insertion [29], Furthest point insertion [30] or Random point insertion [31]. Based on the literature, the Furthest point insertion provides the best tour length. In this case, the point x as the solution of
is selected to be inserted. In the formula, T denotes the current route and T″ is its complement. In our problem domain, this method is not suitable, as in every insertion cycle, the T″ set contains only one node, the rest nodes are not known yet. Similarly, the Nearest point insertion method selects the nearest node from the points not linked into the tour yet. Thus, only the Random insertion heuristic can be used for our problem domain.
Considering the approximation efficiency of the insertion algorithms, Rosenkrantz et al. [32] has been proven that every insertion algorithm provides an approximation threshold O(log(N)). The Furthest insertion method that performs better than the other method has a constant lower bound [33] of 2.43 for eTSP problems. Regarding the efficiency of the Random insertion algorithm, Azar has proven in Reference [31] that the worst case approximation factor can be given with
The shape of the worst case factor function is given in Figure 1.
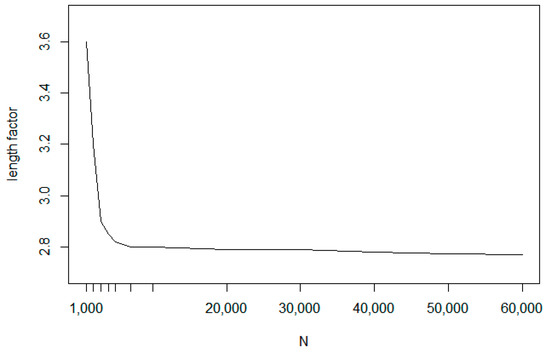
Figure 1.
Worst case approximation bound function.
As this theorem proves the Random insertion method provides in general about 15% weaker result than the Furthest insertion method. In the Random insertion approach, the position of the new node within the route is calculated with a local optimization step. One option is to minimize the tour length increase:
Another option is to connect the new node to the closest tour element:
and take the neighbour node with shortest distance as the second adjusted node.
One of the first publications on incremental tour generation [34] is made by T.M. Cronin in 1990. The algorithm ensures optimality as each city is inserted. The author has developed a dynamic programming algorithm which begins with a baseline tour consisting of the outer convex hull of cities and proceeds by adding a city at a time to the interior.
The proposed method is based on the following theoretical result: the shortest tour containing k cities is a quartic and hyperbolic function of the shortest tour containing (k − 1) cities. It can be proven that an optimal tour must preserve the order defined on the convex hull of nodes [35,36]. In this model, a perturbation is a sub-tour which leads into the interior of the hull through two adjacent hull vertices, to capture nodes which do not lie on the hull. Considering the insertion a new node into the tour, the tour is extended by inserting the new node between those two nodes for which the distance is smallest. The tests were executed on small examples containing only 127 nodes.
A generalization of the insertion method is presented in Reference [37] where during the insertion procedure the two neighbouring nodes of the new item are not necessarily consecutive.
As the practical experiences show [19] the most efficient methods use a mixed approach where a refinement phase is applied on the tour constructed initially. In our investigation, we focus on segment-level refinement optimization. The motivation on segmentation in eTSP is based on the experience that the optimal route usually connects near vertices in the plane. The segmentation generates a set of smaller optimization subproblems to be solved.
This TSP domain was introduced in 1975 by the research paper [38]. In CTSP (Clustered Traveling Salesman Problem), the salesman must not only visit each city once and only once but a subset (cluster) of these cities must be visited contiguously. The presented method first reduces the weights of every intra-cluster edges. Then, a standard branch and bound optimization is applied to the whole graph. The performed weight reduction ensures that the optimization algorithm will generate the required intra-cluster routes. Later, several new methods were proposed to solve the CTSP problem, like the Langrangian method using spanning tree constructions for the graph optimization [39].
The cluster-based segmentation can be considered as an integrity constraints but it can be used a tool for reduce the execution costs of the optimization algorithms. The segmentation as a divide and conquer approach was introduced among others in Reference [40], where the algorithm starts with the segmentation of the nodes into disjoint clusters using a K-means clustering algorithm. In the next phase of the proposed method, the local clusters are optimized using the Lin-Kernighan method yielding a set of optimal local tours. The local tours are merged into a global tour in the final step. In the merge phase, the cluster centroids are calculated first, then k-nearest elements in the global tour are determined. Next, each of the k nodes will be tested to determine the cost of inserting the cluster tour in place of the following edge. The given local tour will be inserted before the node with best cost value.
The idea of combining local clustering (segmentation) in generation of initial route is used in many current proposals. In the literature, we can find many variants of this segmentation approach, as Geometric Partitioning [41], Tour-Based Partitioning [42] and Karp’s Partitioning Heuristic (Karp) [43]. In more complex cases, like [44], the method constructs a hierarchy of segmentations in order to provide a cluster leaves with small amount of graph nodes. In Reference [17], the graph nodes are separated into four disjoint groups corresponding to the different sides of a rectangle. In Reference [45], the route generated by merging the cluster level clusters is refined with a genetic algorithm heuristic. In Reference [46], the genetic algorithm and the ant colony optimization are used to find the optimal local path for the clusters. In the final step, a simple method for choosing clusters and nodes is presented to connect all clusters in the TSP. The Tour-merging Method [27,35] is based on the observation that the routes of good quality usually share a large set of common edges. The algorithm uses specific heuristics to generate near optimal tours and specific dynamic programming techniques to unify the partial solutions into a common solution.
The extensive literature survey that we made shows that the targeted incremental graph and optimal route construction approach attracted little attention and no detailed analysis can be found. In contrary to the rich variety of optimization algorithms on general TSP, only the Random point insertion method can be used directly as an incremental TSP method. As the Random point insertion method is considered as a sub-optimal algorithm dominated by many other methods (like Furthest point insertion, Chained Lin-Kernighan), our motivation is to propose a novel incremental method having a better optimization efficiency than Random point insertion method has and having a better execution cost than the standard non-incremental TSP methods have.
3. IntraClusTSP: Intra-Cluster Refinement Method for Incremental sTSP
3.1. Motivations for the Development of a Novel Algorithm
Although, a variety of methods for the tour improvement heuristics have been proposed [36,47], the best methods are based on the following two main optimization approaches: (a) systematic exchange of edge tuples (the k-opt optimization methods use this approach); and, (b) hierarchical decomposition of the original problem into smaller problems.
Due to the complexity of the k-opt method, usually only a lower k value is used in optimization process. One refinement step relocates the current status vector to a neighbouring position, modifying arbitrary segments of the tour. In this sense, the k-opt method aims at a global optimization, there is no way to perform the optimization only on a predefined segment of the node set.
The main goal of our proposed method is to provide a different approach to the tour optimization that can focus on a cluster of edges in the tour reordering process. The algorithm is based on the idea of ‘divide and conquer’ concept, that is, it selects an arbitrary segment (a cluster of nodes with the corresponding edges among them) and then an efficient known TSP algorithm is used to solve this sub-problem. In the second phase of the iteration, the generated local tour is merged with the rest (unchanged) part of the initial tour. The proposed approach reuses some known concepts but it differs from the existing approaches in many aspects:
- -
- The proposed method performs a tour improvement and not an initial tour construction (unlike the Greedy, Nearest Neighbour or Savings methods).
- -
- The segments may be overlapping; the same segment can be processed several times.
- -
- The proposed model can be used as an incremental TSP construction method. The new item is inserted into the current route using the simple Random point insertion method and then a cluster level refinement phase is executed.
- -
- The link between a segment and the main route is very flexible, there may be any number of connection edges
- -
- It differs from the k-opt, Lin-Kernighan and Helsgaun methods because the size of the sub-graph to be improved may be arbitrary and the algorithm of the subgraph optimization can be considered as a black box optimization.
- -
- Unlike the multi-level approach, this method performs a single level edge fixing and not a hierarchic refinement.
- -
- Unlike the tour-merging method, the method generates only a sub-tour to be replaced in the original tour.
3.2. Formal Model and Algorithm of the Proposed Method
Let denote the set of N positions in a metric space with a distance function
The corresponding distance matrix is denoted by A Hamiltonian cycle of visiting each position only once is denoted by . The permutation related to Hamiltonian cycle t is given by . The tour length of t is defined as
where denotes the i-th element of the permutation. The set of all Hamiltonian cycles is given with
Having an initial approximation of the optimal Hamiltonian cycle for V, the intra-cluster reordering tour improvement method selects a subset and using an appropriate distance matrix, a local optimal tour is generated. The distance matrix is constructed from on the following way. First, we decompose into two parts: a set of internal nodes and a set of border nodes. A node is a border node if one of its adjacent nodes is an element of and the other adjacent node in not element of V’. Two border nodes are linked nodes if there exists a route in connecting these elements. The distance values are given with
If , then the new route is involved into the global tour. In the optimization phase, two linked border nodes are merged into a single virtual border node. Thus the tour sections in V\V′ remain hidden is this phase. It can be seen that the distances related to the virtual border nodes are not symmetric as these nodes have two physical positions.
In the merge phase, the generated cluster level route which contains both the internal and border nodes is merged into the global tour. In this phase, the tour sections hidden in the border nodes are uncovered again. Using a tour merge operation, the improved route is given with
Thus, the route sequence is an improvement sequence of the initial route .
As an example, let us take the tour given in Figure 2a. In the example, 17 nodes are given. The internal nodes (modes in the cluster) are given in white colour. There are 6 border nodes given in grey and there are 5 external nodes in black. For the local optimization phase, three virtual border nodes are generated, the related pairs are denoted with thick edges. The cluster-level local optimization process involves 10 nodes. The generated local optimal tour is shown in Figure 2b. After uncovering merging with the external, hidden section, we get the new, refined global tour (Figure 2c).
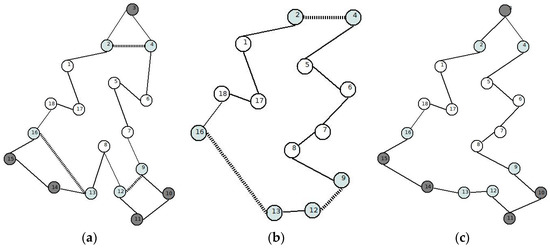
Figure 2.
(a–c) Sample cluster level tour optimization.
If the IntraClusTSP is used to general tour refinement, then we apply the Quality Threshold Clustering (QTC) to provide an appropriate segmentation. This method uses a partitioning clustering [48] proposed for analysis of co-expressed genes, generating clusters with a bounded intra-cluster diameter.
If the IntraClusTSP is used to add a new node in the incremental route construction task, then we should select a cluster where the new node is near to the cluster centre. We applied a minimum tour extension concept, where
is met. After this insertion phase, we determine a cluster around the new element and perform a cluster level refinement with the IntraClusTSP method.
An important motivation was in our investigation the fact that the search space of larger TSP problems are significantly more complex than the search space of smaller problems. A deep analysis of the corresponding search landscape can be found in Reference [49] where a statistical model was introduced to estimate the number of local optima in the search space for different problems sizes. In the proposed method, random sampling technology is used to determine the corresponding model parameters. A similar analysis was presented later in Reference [50] for a larger problem domain. An important empirical result of the investigation on Euclidean TSP problems was that the number of local optima () grows exponentially in the function of the problem size (N):
To demonstrate the complexity of the optimization landscape, we present an experiment in a low complexity permutation space. Figure 1a,b shows the space of all permutations (N = 6) positioned along a circle. The permutations are ordered by a lexicographic ordering, where means that there exists an index value such that for every , the node is on the same position in both permutations and for the element , the position in is less than in . The lines between two permutation nodes represent the neighborhood relationship. Two permutations are neighbored if they can be converted into each other by a single inversion transformation. The red ray lines from the centre represent the goal function (the route length) of the corresponding permutation. The largest route length has a zero ray length, while the longest ray segment denotes the minimum route length.
If we allow discovering the whole neighbourhood in the heuristic optimization process, then we get 16 local optima denoted by green points in the Figure 3. The number of neighbouring elements is , thus the processing of the elements in the neighborhood can be very time consuming for large problems.
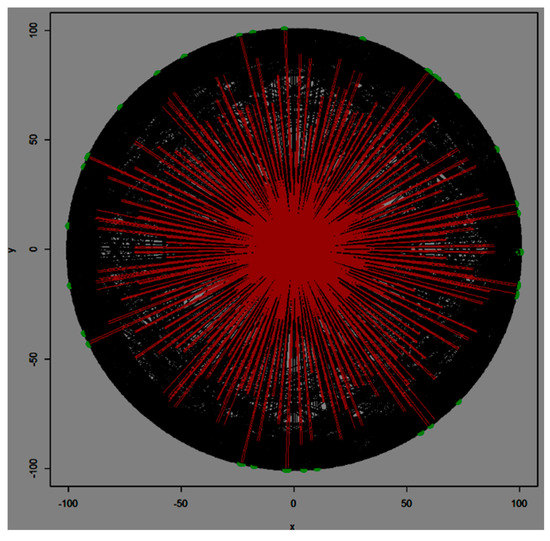
Figure 3.
TSP Optimization landscape (N = 6).
In the proposed method, the tour planning for a cluster is performed with the following algorithm. Having an initial tour and the vertex subset, the route can be segmented into inner-V′ and outer-V′ sections. The start and end vertexes of the outer-V′ sections are taken as border vertexes. For the local route optimization, the set of V′ vertexes are extended with the border vertexes. In the tour optimization of the local cluster, the link between two related border vertexes denotes an external section which cannot contain inner vertexes. Thus the related border vertexes must be adjacent in the winner optimal local Hamiltonian cycle. This constraint is ensured with the following adjustment of the distance matrix. The distance value between two related border vertexes is set to 0 (or very near to zero), thus this edge will be included into the optimal tour with high probability. The system always verifies this constraint explicitly and the proposed tour is rejected if the route is invalid.
After generating the local optimal tour, it will be extended with the corresponding outer sections. For every related border vertex pair, there exists a sub-tour from the global tour and the edge of the border vertex pair will be substituted with the corresponding sub-tour. In an extreme case, the sub-tour may be empty and the two border vertexes denote the same node, that is, the external section contains only one vertex.
The corresponding algorithm (see Algorithms 1 and 2) of the proposed cluster level refinement proceeds as follows:
| Algorithm 1: Ic_optim (V, T) |
| 1: // V: set of all vertexes |
| 2: // T: current optimal tour |
| 3: // l: length of current tour |
| 4: // W: set of clusters |
| 5: // Tc: candidate tour |
| 6: l : = d(T); // calculate tour length |
| 7: W := gen-clusters(V); // generate clusters |
| 8: for each VL in W do // loop on clusters |
| 9: // refinement of the local route |
| 10: Tc := Intra-cluster_reordering (V, VL, T); |
| 11: lc = d(Tc); // calculate tour length |
| 12: if lc < l then |
| 13: T := Tc; |
| 14: l : = lc; |
| 15: end if; |
| 16: end for; |
| Algorithm 2: Intra-cluster_reordering (V, VL, T) |
| 1: // V: set of all vertexes |
| 2: // VL: set of cluster vertexes |
| 3: // T: current optimal tour |
| 4: // B: set of border vertexes |
| 5: // ET: set of external tour segments of T |
| 6: // VLB: the extended local vertex set for local optimization |
| 7: // DL: adjusted distance matrix for the VLB set |
| 8: // TL: the local optimal tour |
| 9: (B, ET) : = partition_tour (T, VL); // determine inner and outer sections |
| 10: VLB := VL union B; // replace outer sections with port symbols |
| 11: DL := gen_dist(VLB); // generate distance matrix |
| 12: TL := Optim (VLB, DL); // generate optimal local route |
| 13: Tnew : = merge (T, TL, B); // update global route |
| 14: Return (Tnew); // the new global optimal tour |
4. Cost Analysis of the Cluster Level Refinement Method
In the cost analysis of the tour construction algorithm using cluster level refinement (intra-cluster_reordering), the cost factors depend on the following parameters:
- N: number of vertices in V;
- f: cost function of the local optimization algorithm;
- N′: number of vertices in local cluster V′;
In the partition_tour function, the tour T is segmented into V′ inner and V′ outer sections. Having a list representation of the tour and using a status field in the vertex descriptor, the cost of this step can be approximated with
Regarding the generation of the distance matrix, there are two main approaches to be applied. In the first version, there is a global distance matrix generated in the preparation phase of the optimization algorithm. This step requires
cost, while the other approach does not use a global distance matrix but it calculates the local distance matrix in each iteration step. The cost of this step is equal to
The generation of the local optimum route is performed with a cost value
In the last phase, the local optimum tour is merged with the current global optimum tour. The cost of this operation is equal to
In the case of application of global distance matrix, the total cost can be given with
where m denotes the total number of iterations. Considering a partitioning with M clusters, the approximation for the cluster size is
The value of M related to the optimum cost can be calculated with the following formula for the case of global distance matrix:
When using local distance matrix, the corresponding equation is
Using the approximation
where The optimal cluster number for the global distance matrix approach is given by
The optimal relative size of the clusters depends on both the α parameter and the N value. Taking the simplification assumption that all the cost coefficients are equal to 1 ( = 1, = 1, …), we can calculate the optimal values. The dependency between α and the optimal cluster size is shown in Figure 4, where the curve denoted with hollow circle is for N = 100, filled circle for N = 1000 and rectangle symbol is for N = 10,000.
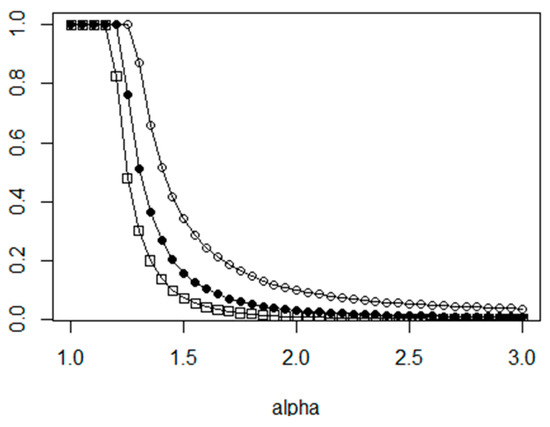
Figure 4.
Optimal relative cluster size in dependency of alpha using global distance matrix.
In the case of local distance matrices, the optimal value is calculated as the solution of the following equation:
In Figure 3, the optimal relative size of the clusters is shown for two N values, the line with hollow circle notation belongs to N = 100, the line with filled circles relates to N = 1000. As the figures show, in the case of local distance matrix management, the optimal cluster sizes are smaller than the optimal sizes of global distance matrix management.
Considering the time cost of a global optimization and of the optimization for the partitioning with optimal cluster size, we get the ratio function presented in Figure 5. The function shows the ratio value for different α values. Based on the test calculations, we can say that the partitioning method provides benefits especially for larger problems using base optimization method with higher execution costs.
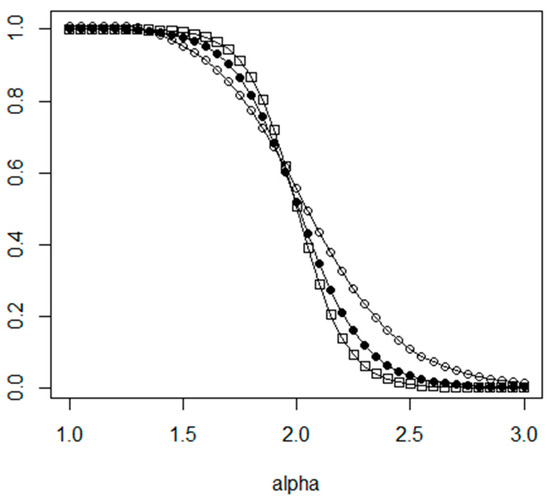
Figure 5.
Cost ratio in dependency of α.
Considering the construction of clusters, there are many different clustering approaches in the literature. In our algorithm, the quality threshold clustering method was implemented as it has many benefits from the viewpoint of the sTSP problem. Based on the obtained experimental results, we can say that the adjacent elements in the route are usually the nearest neighbours in the object space, too. We have investigated optimal tours and tested whether adjacent elements of the route are nearest neighbours in the node space or not. In Figure 6, the histogram of the adjacent element’s position in the corresponding neighbourhood is shown. The axis X denotes the position in the neighbourhood and axis Y denotes the corresponding frequency in the set of adjacent elements. In the test N is set to 4000. According to our test results, about 75% of the adjacent elements are the nearest neighbour elements, too. Thus the clusters must contain elements which are in the near neighbourhood of each other. The cliques generated by the QTC algorithm can provide this property as it contains such elements that for every pair, the distance is always less than a given threshold:
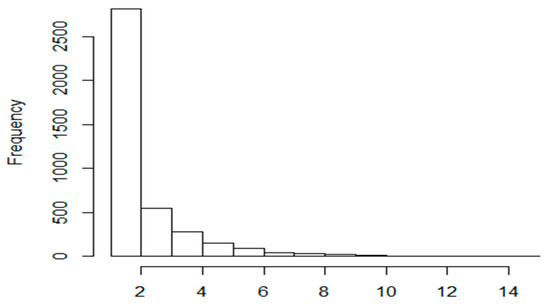
Figure 6.
The relative distance of the adjacent elements in the optimal tour.
5. Performance Evaluation Tests for Local Refinements
In the following, the efficiency of the proposed intra-cluster level route improvement approach is investigated. The main question is to what extend can the intra-cluster level reordering improve the shortest tour found so far. For the performance analysis, a series of tests were executed.
Our tests focused on the operations where the proposed cluster level refinement method may provide an improvement against the competitor methods. There are three main areas where IntraClusTSP can be applied to improve the optimization performance:
- (a)
- General refinement of initial tour using arbitrary internal/local TSP optimization method;
- (b)
- Application of refinement for a specific local area;
- (c)
- Incremental route generation.
In the case of incremental route generation, an existing node graph with optimal route is extended with a new node. The task is to generate a new optimal Hamiltonian cycle involving the new node. One solution is to consider the new graph as an independent new task and we use some existing batch TSP optimization method. This solution requires a lot of redundant calculations as most part of the tour remains unchanged. The incremental approach will perform only the required modifications on the initial route, thus its time cost is significantly lower. Among the known TSP optimization method, the NN algorithm is based on this incremental approach but it tests only a limited set of neighbours to find best position of the new node. From this point of view, the IntraClusTSP method can be considered as an improved version of the standard NN optimization method.
Based on the detailed analysis and performance comparison in Reference [21,28,51], the following methods were implemented for route generation in the performance tests: (a) Nearest Neighbour direct construction algorithm (NN); (b) GA-based refinement algorithm (GA); (c) Hierarchical GA-based refinement algorithm (HGA); (d) Nearest insertion algorithm with refinement (N2); and (e) Chained Lin-Kernighan refinement algorithm (LK).
5.1. Evaluation Methodology
We have selected two different node distributions to generate the input data set for the investigated eTSP problem. The first version is the usual uniform data set distribution in the two dimensional Euclidean space. Most of the benchmark data sets in the well-known TSPLIB library (https://www.iwr.uni-heidelberg.de/groups/comopt/software/TSPLIB95) have similar distribution characteristics. In this case, the point locations are distributed within a two-dimensional square uniformly. The only input parameter of the input set is the number of points (N). The second distribution model uses two level distribution, that is, there is cluster level containing the cluster centres and there is node level distribution for the point positions within the clusters. The elements of both levels are generated with uniform random distribution. Here, the generation algorithm involves the following parameters: number of the clusters (M), number of the points (N), radius of the clusters ().
In the tests, one execution step corresponds to a series of local refinement runs on all elements of a partitioning. For example, if the domain is partitioned into M clusters, the execution step contains M runs on all of the clusters. In the experiments, we have tested clustering with both non-overlapping and overlapping clusters. The cluster shapes considered were circular with a given centroid and radius. In the tests, a clustering is given with the following parameters. N: number of objects, positions; M: number of clusters; : relative radius of the cluster; L: number of iterations.
Regarding the cluster construction for the refinement runs, we have used a QTC algorithm to select a compact set of neighbouring positions. The mean value for the radius of the refinement clusters was set to 15% of the diameter of the base region.
All performance tests were performed in R environment. The Concorde TSP Solver package (http://www.math.uwaterloo.ca/tsp/concorde.html) was used to execute the Chained Lin-Kernighan algorithm. Using this optimization method, we The Nearest insertion algorithm with two_opt refinement was included from the TSP package. For execution of the GA optimization, the implementation of the GA package was invoked into our test program. In the tests, we have selected the method “linkern” for Chained Lin-Kernighan. Based on our experiments which are summarized in Table 1, this method provides the best optimization quality. In the table, TL denotes the tour length value, while T is the symbol for the execution time. Three Lin-Kerninghan variants were compared, beside linkern-variant, also the nearest insertion and the arbitrary insertion variants were tested. The Nearest Neighbour and the Hierarchical GA-based refinement algorithm were implemented directly.

Table 1.
Comparison of the different Lin-Kernighan variants.
5.2. Nearest Neighbour Direct Construction Algorithm
The goal of the first experiments was to evaluate the efficiency of IntraClusTSP refinement algorithm for routes generated by the Nearest Neighbour method. The Nearest Neighbour direct construction method has only one main algorithmic parameter, the distance matrix of the graph. In our case, we have constructed the distance matrix from a point distribution using the Euclidean distance. In the test, we have generated the initial route with the NN method, then we have applied a sequence of IntraClusTSP refinement steps. The results for the data set parameters M = 324, = 0.15 on a sample with N = 6000 are shown in Figure 7a,b. According to the test results, the proposed cluster route refinement algorithm improved the route length by 8%. As it is shown in the figure, the first refinement cycle provides the largest improvement (about 5%). Based on the literature, the tour length generated by the NN algorithm is about 25% above the theoretical optimum value, the result of the proposed refinement is about 14% above the theoretical optimum. Considering the comparisons performed in Reference [29], this result is a significant improvement of the original method. The optimal route length as a function of the iteration count is shown in Figure 4. Considering the number of generated clusters, M, we can see that the IntraClusTSP method provides a better improvement for partitioning with higher number of clusters.
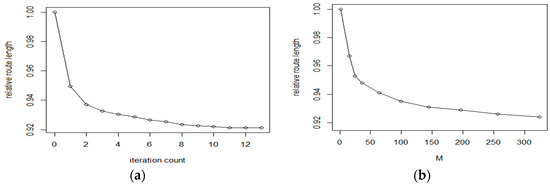
Figure 7.
(a,b) Efficiency of improvement iterations for the NN algorithm.
In Figure 8, two time cost functions are presented. The first function corresponds to the base NN method (denoted by hollow circles) while the second shows the execution cost of IntraClusTSP (filled circle). The second function corresponds to the case when M is equal to the calculated optimum value. As it is expected, the total cost of optimizing the whole node set is higher than the cost to perform a set of local optimizations for the covering cluster set.
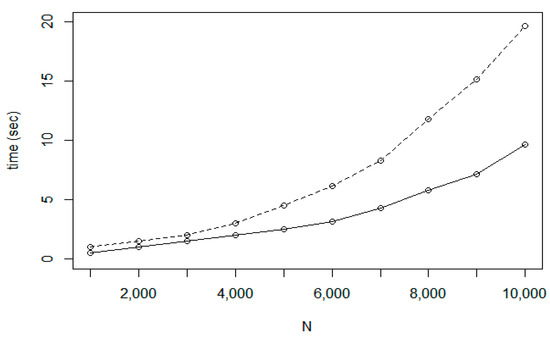
Figure 8.
Time cost of the base NN and of the IntraClusTSP refinement method (solid line).
5.3. GA and Hierarchical GA Refinement Algorithms
In the GA based refinement algorithm, an individual route corresponds to a permutation of the positions. The fitness of an individual is given with the corresponding tour length. The GA algorithm uses the crossover, mutation and selection operators on the population of selected individuals. Based on our experiences, if the number of population iterations is limited, the GA can provide only weaker results, especially for GA with random initialization. In order to improve the search space, the route of the NN direct optimization algorithm is taken as an element of the initial population. In the case of hierarchical GA, the algorithm first performs a partitioning of the original position set into disjoint clusters. In the next step, every cluster is considered as position represented by the centre point and the optimal route on the cluster level is calculated. Then, for every cluster, a local tour optimization is performed and finally the local optimal routes are merged into a global optimal route.
Based on the experiences, as it is shown in Figure 9, the random GA is significantly dominated by the NN-initialized GA method. In the figure, the values related to the random GA are given with hollow circles, while NN-initialized GA is denoted by filled circles. The GA algorithm is based on the following main parameters: population size, probability of crossover, probability of mutation, maximum number of iterations to run before the GA search is halted and number of consecutive generations without any improvement in the best fitness value before the GA is stopped. Based on our preparation test, the population size has the largest effect on optimization efficiency. For a wide range of N in our input, the optimal population size is near 40, we have used this parameter in our comparison tests. Regarding the other parameters, the following settings was used: probability of mutation: 0.2, probability of crossover: 0.7; maximal number of iterations: 500 and number of runs: 200.
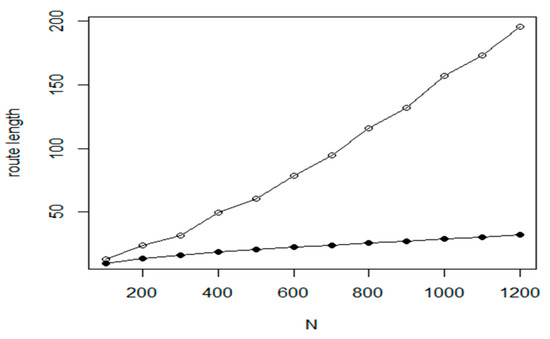
Figure 9.
Route length of the random GA and the NN-GA methods (filled circle).
The results of the NN_GA can be improved by some percent using the hierarchical GA approach. The corresponding results are given in Figure 10, where the filled circles denote the HGA method. The proposed refinement method can reduce the tour length by 5–10%, similar to the base NN approach (see Figure 11).
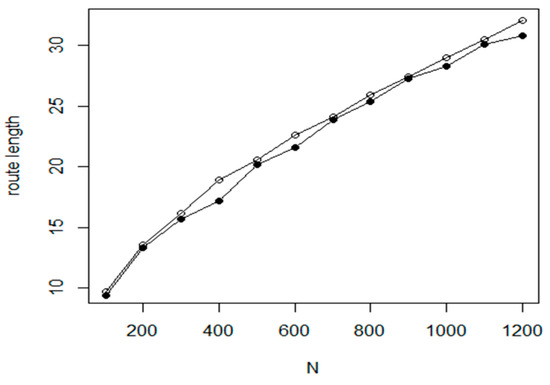
Figure 10.
Route length of the NN-GA and the HGA (filled circle) methods.
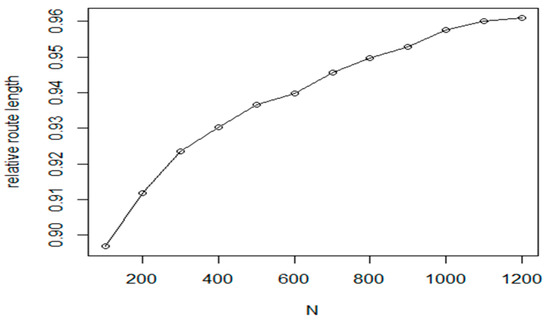
Figure 11.
Efficiency of improvement iterations for the HGA algorithm.
5.4. Nearest Insertion Algorithm with Two_Opt Refinement
The Nearest insertion algorithm with two_opt refinement is the default solver in the TSP package of R and it can provide a very good approximation of the optimal route. The Nearest insertion (NI) algorithm chooses city in each step as the city which is nearest to a city on the tour. The NI and two-opt algorithms does not require any special parameter to be set in our tests. Figure 12 shows the measured efficiency comparison of the Nearest Neighbour method and the Nearest insertion with two_opt refinement algorithm. In the figure, the following notations are used.
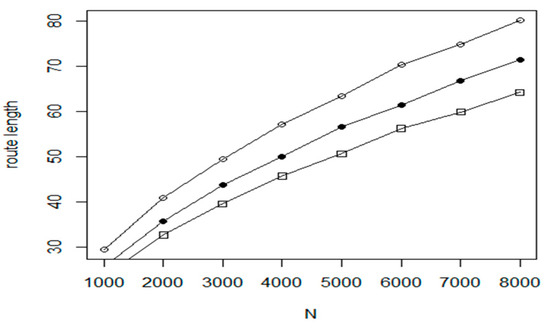
Figure 12.
Efficiency of the Nearest insertion algorithm with two_opt refinement.
The hollow circle denotes the Nearest Neighbour method, filled circle is for Nearest insertion algorithm with two_opt refinement and hollow rectangle is the symbol for the theoretical optimum. Although the efficiency is very good, we experienced a weakness of this algorithm too, the high execution time. As it is shown in Figure 13, the execution time for the problem with N = 8000, the required time is more than 200 times larger with = 10 s and = 2300 s.
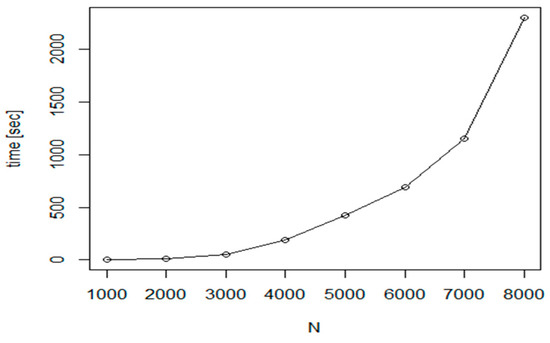
Figure 13.
Execution cost of the Nearest insertion algorithm with two_opt refinement.
Based on this experiment, the method is not suitable for larger problems. In order to reduce the execution costs, a hybrid approach was introduced in our tests. The proposed method first uses the fast NN algorithm to create an initial route. Then, in the refinement phase, the Nearest insertion algorithm with two_opt refinement is used for tour optimization at cluster level. Taking an iteration of cluster level execution steps, we have created a fast and efficient algorithm.
The experiments prove that the proposed method can improve the efficiency of base method by 2–3% (see Figure 14) while the required execution time is only a small fraction of the base execution time (Figure 15). In the experiments, the following parameter values were used: M is between 25 and 64; L: between 6 and 10 and is equal to 0.15.
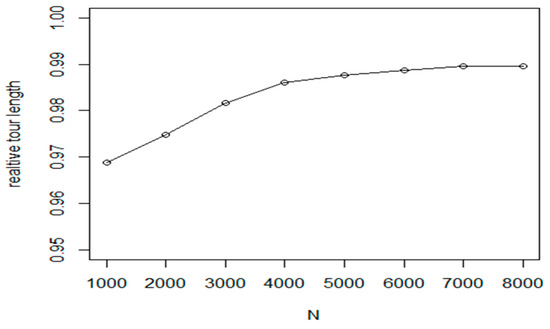
Figure 14.
Relative efficiency of the proposed NN-initialized NI-2opt cluster level refinement method.
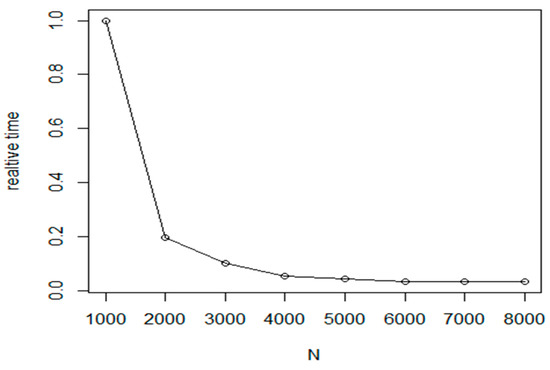
Figure 15.
Relative time cost of the NN-initialized NI-2opt cluster level refinement method.
5.5. Chained Lin-Kernighan Refinement Algorithm
According to the analyses [19,28], the Chained Lin-Kernighan refinement algorithm provides the best solution for the TSP optimization problems. Its tour length efficiency is very near to the theoretical optimum (the difference is only 1–2%). This superior efficiency is confirmed by our test experiments too. In our tests, the LINKERN package was used to run the Chained Lin-Kernighan refinement algorithm. The Chained Lin-Kernighan refinement method is an algorithm with many parameters. In our tests, we have used the standard settings [52] with the following values: Kick value: random walk; number of kicks: number of nodes; method to generate staring cycle: QBoruvka.
The cluster level refinement method can provide here only a tiny improvement. Based on our test experiments, the average improvement ratio is 0.2%, the best result is a one percent improvement for an input distribution with N = 60,000. Considering the fact that the result of the Chained Lin-Kernighan refinement method is very near (1–2%) to the theoretical optimum, the case with 1% improvement is an important achievement.
5.6. Convergence of the IntraClusTSP Refinement Method
In the tests to analyse the convergence of the proposed IntraClusTSP method, we have selected the GA method with random initialization to generate the initial route. Regarding the convergence efficiency of IntraClusTSP, the main determining factor is the applied algorithm for the cluster-level optimization. The Chained Lin-Kernighan method applied in our proposal, provides a very fast convergence. In Reference [53], the investigation of the route length—iteration step function has shown that in the first 20% of the total running time, the optimization process provides 80% improvement and the rest 80% of the time yields 20% improvement. In our cluster-level refinement approach, the convergence rate is influenced by the following factors:
- -
- size of the cluster (large clusters can provide larger improvements but they require larger execution time)
- -
- quality of the cluster-level route (the quality shows how far is the length of the current route from the optimal length)
As the average quality of the graph increases during the refinement process, the convergence rate will decrease as it is shown also in the referenced paper.
In our convergence tests, we have used random cluster selection. In every iteration step, only one cluster was processed. In the tests, the following parameter settings were used:
- N (number of nodes): 400, 800, 1200
- r (relative radius of the clusters): 0.1, 0.2, 0.3
- m (number of iteration steps): 25
Our test results can be summarized in the following points:
- -
- Similar to the convergence of the base LK method, the convergence ratio is significantly larger in the first few iteration steps. In Figure 16, a sample convergence example is presented as a route length—iteration count function for the input parameters (N = 400, r = 0.2)
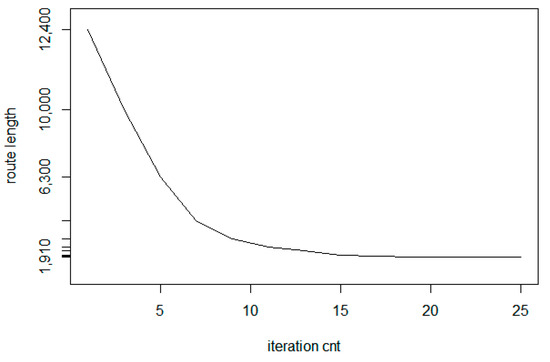 Figure 16. Convergence function of the IntraClusTSP algorithm.
Figure 16. Convergence function of the IntraClusTSP algorithm. - -
- The convergence ratio is larger for larger cluster sizes. Figure 17 shows the comparison run for three different cluster size values. The bottom (solid) line belongs to r = 0.3 (large clusters); the middle (dashed) line relates to r = 0.2 and the top (dotted) line belongs to r = 0.1. The reason of the fact that the curves may have local plateau is that the clusters are selected here randomly, thus there is a chance to select areas already processed before. In this case, only little improvement can be achieved.
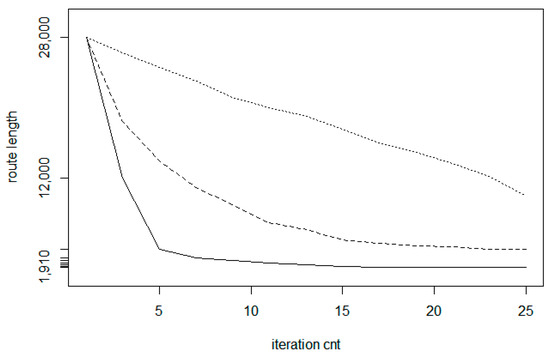 Figure 17. Comparison of the convergence for different cluster radius values (solid line: r = 0.3, dashed line: r = 0.2; dotted line: r = 0.1).
Figure 17. Comparison of the convergence for different cluster radius values (solid line: r = 0.3, dashed line: r = 0.2; dotted line: r = 0.1). - -
- The convergence as relative length reduction is not very sensitive to the graph size but as the experiments show, in larger graphs we can achieve larger length reduction and a better convergence. In Figure 18, the results for three different sizes are summarized. The bottom (solid) line belongs to N = 1200 (large graph); the middle (dashed) line relates to N = 800 and the top (dotted) line belongs to N = 400.
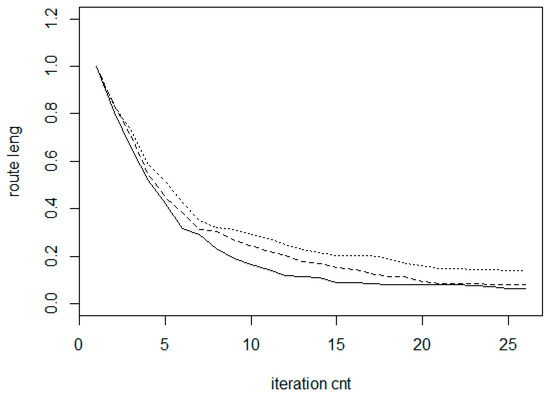 Figure 18. Comparison of the convergence for different graph size values (solid line: N = 1200, dashed line: N = 800; dotted line: N = 400).
Figure 18. Comparison of the convergence for different graph size values (solid line: N = 1200, dashed line: N = 800; dotted line: N = 400).
6. Performance Evaluation Tests for Incremental TSP
In the following, we compare IntraClusTSP with Chained Lin-Kernighan method and with the Random insertion methods from the viewpoint of both time cost and route length optimization efficiency. We have involved the following algorithms into the tests:
- -
- Random insertion with random position (RR);
- -
- Random insertion with smallest single distance (RS);
- -
- Random insertion with smallest route length increase (RI);
- -
- Random insertion with smallest single distance with IntraClusTSP refinement (RCI);
- -
- Chained Lin-Kernighan method on the whole graph (LK).
In the case of RR, the position of the new node in the route is selected randomly.
First, we investigate the insertion of a single new node into the current optimal route. Considering the route length optimization, we have experienced that in this simple case, all methods provided about the same result. Thus, there were no significant differences between the investigated methods, only the RR method had a worst time optimization value. In the tests, the method RR provided a very low efficiency as it is shown in Table 2 and Figure 19. The input node distribution was generated with uniform distribution within a rectangle area. The size of the graph was running from 1000 to 10,000. The proposed IntraClusTSP algorithm provided a better result than known insertion methods. In Figure 19 we present the cost difference between the new and old tour versions for the insertion algorithms and for the Chained Lin-Kernighan method. The presented values are the average values related to samples of size 10.

Table 2.
Average tour length increase.
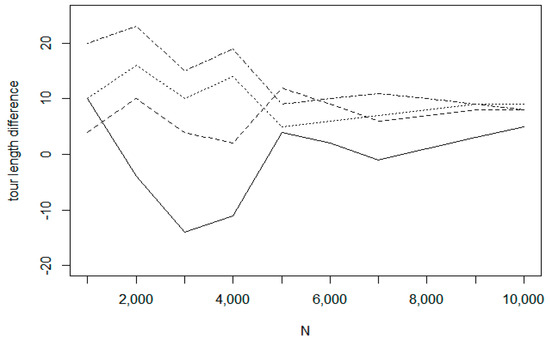
Figure 19.
Tour length increase functions. (LK: solid; RCI: dashed, RI: dotted, RS: dotdash).
In the next experiments, we investigated the efficiency for insertion sequences, when 200 new elements are inserted into the graph. For the case of single insertion, is proven that our algorithm provides a better result in general but the difference tends to decrease as the size of the initial tour increases. In the case of insertion sequences we may get a different result, as standard insertion methods (RS, RI) can modify only one edge in the original tour, while RCT can perform a larger scale modifications during the same amount of time.
In the tests on insertion sequences, we have selected three kinds of training set. The first is the uniform random distribution (UDT) while the two others (TSPLIB_fin10639 and TSPLIB_xql662) belong to the TSPLIB data repository. For the TSPLIB_fin10369 data set (http://www.math.uwaterloo.ca/tsp/world/countries.html) we performed two experiments with different initial tour sizes. The test results are shown in Figure 20, Figure 21, Figure 22 and Figure 23. In Figure 20 which relates to the uniform random distribution, the bottom dot-dashed line belongs to the Chained Lin-Kernighan method which is a batch method. For this method, the line is a linear approximation, only the values at the start and end positions are measured. For the incremental methods, all values are measurement results. The second solid line denotes the proposed IntraClusTSP method. The next line relates to the RI (Random insertion with smallest route length increase) algorithm and the weakest result is given by the RS (Random insertion with smallest single distance) method. Similar efficiency order can be observed by the other experiments too. Figure 21 relates to dataset fin10639 on the size interval 5000–5200. Figure 22 shows the tour length values for the size interval 10,000–10,200 of the same data set. In Figure 23, the measured tour length values are presented for the TSPLIB xql662 dataset (http://www.math.uwaterloo.ca/tsp/vlsi/).
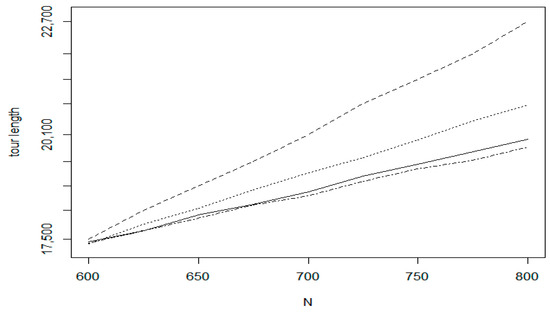
Figure 20.
Tour length functions (UDT).
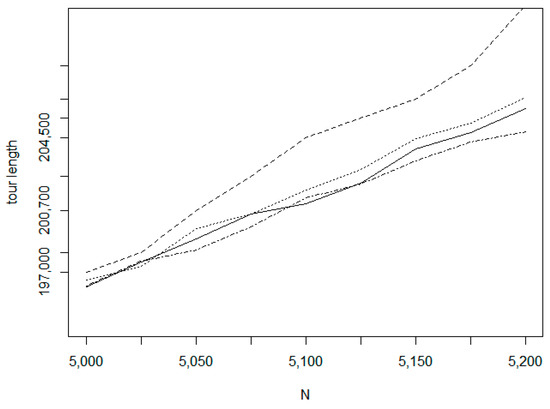
Figure 21.
Tour length functions (TSPLIB_fin10639).
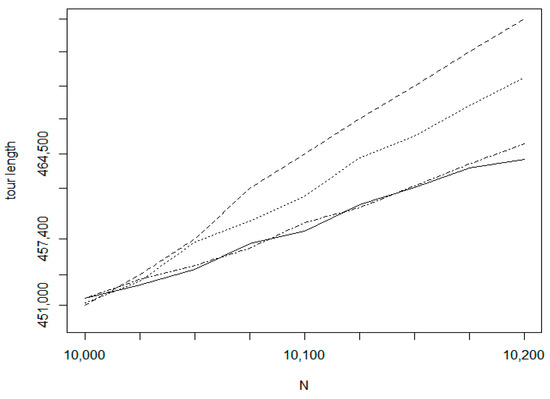
Figure 22.
Tour length functions (TSPLIB_fin10639).
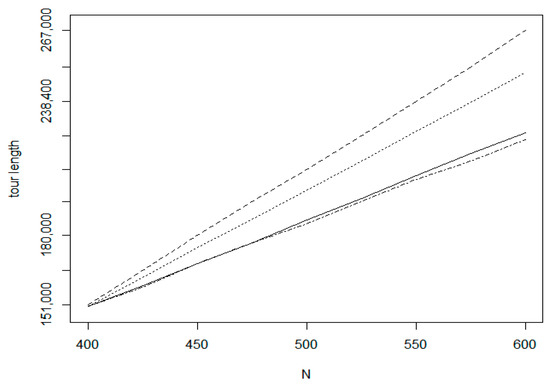
Figure 23.
Tour length functions (TSPLIB xql662).
In Figure 24, the time costs are compared. The largest cost belongs to the Lin-Kernighan method, the cost function of NN shows a very similar characteristics. The incremental route update using the IntraClusTSP algorithm requires only 0.5 s for the graph with N = 10,000. In case of Random insertion with smallest route length increase algorithm on the fin10369 dataset, required 10 s, which is a significant difference.
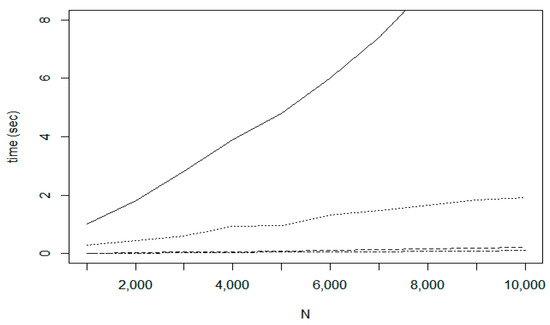
Figure 24.
Time cost functions (LK: solid; RCI: dashed, RI: dotted, RS: dotdash).
The test results proved that the proposed IntraClusTSP significantly dominates the random insertion algorithms on the field of incremental TSP construction, regarding both optimization efficiency and execution costs.
7. Application in Data Mining
The proposed IntraClusTSP algorithm can be used also in the context of data analysis to support clustering A cluster group consists of elements similar to each other. A key factor in clustering is the quality of the clustering (how similar are the objects within a cluster to each other) [54] and the number of the clusters. Usually, the users should set this number either directly or indirectly in advance as an input parameter of the clustering process. For example, in the case of k-means clustering, the number of required clusters is fixed in advance. The determination of the appropriate number of clusters, is considered as a fundamental and largely unsolved problem [50]. In the literature, we can find numerus approaches like Silhouette statistics [55], gap-statistics [56] or Gaussian-model based approach [57].
In this section, we present an algorithm based on TSP optimization to support the determination of the optimal number of clusters. The proposed method is based on the following considerations. As it was shown in Section 3, the shortest path usually connects the elements located in the neighbourhood. Thus, the distances between adjacent elements belonging to the same cluster, should be small. On the other hand, if the adjacent element belongs to different cluster, the distance should have a large value. Thus, a relatively large distance in the optimal route should mean a gap, a connection from a cluster to another cluster. Based on these considerations, we evaluate the distance function between two adjacent elements of the optimal route to determine the clustering structure.
The proposed method is based on the analysis of the corresponding edge length histogram. Having this histogram, we consider it as a mixture of normal distributions and we can perform a Gaussian Mixture Density Decomposition (GMDD) [58]. In GMDD, having the current density function, we first determine the location of the maximum density and we fit a Gaussian distribution with maximum overlap. This Gaussian is added to the components’ list and this component is removed from the current input distribution. If this reduced density is a not a zero function then it will be analysed in the same way. Figure 25 shows the result of a sample GMDD process.
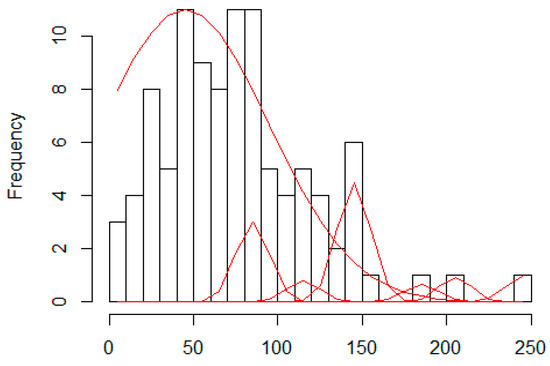
Figure 25.
Sample GMDD decomposition.
Having the GMDD spectrum, we have to determine those components which belong to different clustering levels. In our model, we consider an edge as cluster level connection if its length is significantly larger than the average length of the intra-cluster connections:
The parameter ∝ is considered as an input parameter of the algorithm. Based on our experiments with human observers, we take value 2 as default value of alpha. Our tests show that the point distribution in Figure 26a () is usually considered as single cluster while the points in Figure 26b () are considered to belong to two clusters.

Figure 26.
(a) single cluster; (b) two clusters.
Thus, if the length difference between two elements in the corresponding edge length histogram is significantly larger than the average length of the previous level, then the larger element will belong to a new clustering level. The algorithm to calculate the cluster counts for different levels can be summarized in the following steps.
| Algorithm 3: Histogram of edge length containing M bins |
| 1: CL := cluster level descriptors; |
| 2: g : = 0; // cluster level index |
| 3: for each i in (1 to M) do |
| 4: b := H[i]; // current bin |
| 5: b.count := count of edges in the bin |
| 6: b.length := average edge length in the bin |
| 7: bp := the previous not empty bin |
| 8: if b.count > 0 then |
| 9: L_g := the average edge length in the current cluster level CL[g]; |
| 10: L_a : = b.length – bp.length; |
| 11: if L_a > alpha * L_l then |
| 12: g = g + 1; //create a new cluster level |
| 13: add b to CL[g]; |
| 14: else |
| 15: add b to CL[g]; |
| 16: end if |
| 17: bp : = b; |
| 18: end if |
| 19: end for |
| 20: Calculate the GMDD distributions for the cluster levels |
In the following, we present the application of the algorithm on an example distribution.
Figure 27 denotes the initial distribution of the graph nodes. Can be detected two clustering levels. At the first level, there are 12 small clusters, while the second level contains three large clusters. The calculated shortest path is denoted by red line. The generated edge length histogram with the GMDD spectrum is presented in Figure 28, where the corresponding edge-length function is given in Figure 29. The first large peak belongs to the base level, here we have 120 elements in the distribution. The second peak denotes the first cluster level with the small clusters and the last component relates to the level of the large clusters. Table 3 summarizes the main parameters of the discovered clusters.
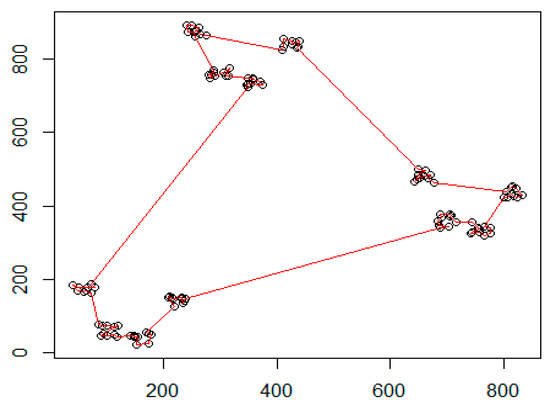
Figure 27.
Sample initial distribution in a two dimensional space.
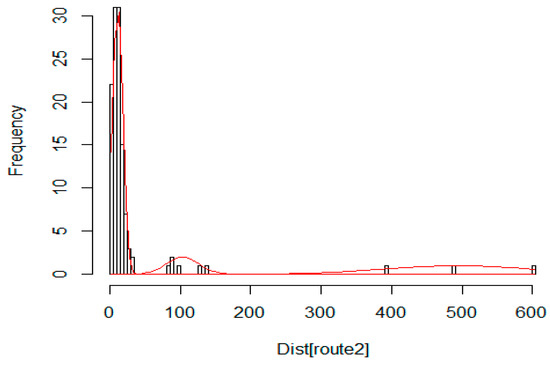
Figure 28.
GMDD components for the sample distribution.
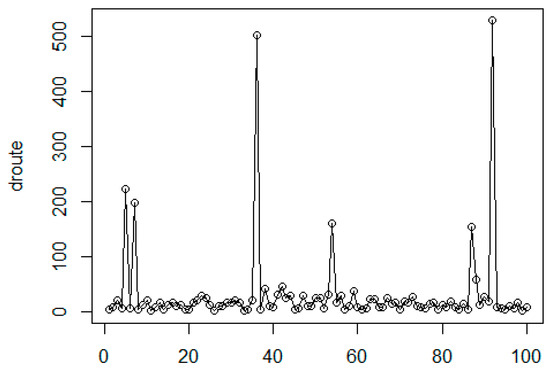
Figure 29.
The edge length function of the route.

Table 3.
Cluster level parameters.
As the results show the method discovered the multi-level clustering structure in the input distribution.
We have compared our algorithm with two widely used methods for determining cluster count. The first investigated method uses the Silhouette index [59] approach. This index prefers small intra-cluster distances and it is defined in the following way for a partitioning with clusters ():
The cluster count is the k value, where the value is maximum optimum:
The second investigated method is the gap statistic method [55] Estimating the number of clusters in a data set via the gap statistics. The method calculates the goodness of clustering measure by the “gap” statistic.
The value is calculated via bootstrapping, that is, simulating from a reference distribution. A sample calculated gap statistic value in dependency of cluster count k is shown in Figure 30. There are different approaches to determine the cluster count K from the gap function, like the first maximum or the global maximum.
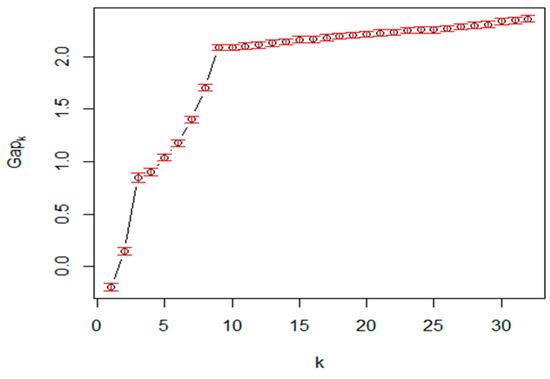
Figure 30.
The gap statistics function.
In the comparison tests, the factoextra and cluster packages of R were included to perform the silhouette and gap statistic calculations. In the generated data distributions for the evaluation test, the objects are arranged into either a single-level or a two-level clustering structure. For the comparisons, we have generated Table 4 describing the typical test results has the following structure:

Table 4.
Comparison of the calculated optimal number of clusters.
- column (observed): the real clustering structure observed by humans. The column contains one or two numbers. The first number denotes the number of clusters at the first clustering level, while the second value is the cluster counter of the second level.
- column (gap-A): cluster count proposed by gap analysis using the first maximum optimum criteria;
- column (gap-B): cluster count proposed by gap analysis using the Tibs2001Semax optimum criteria;
- column (silhouette): cluster count given by the Silhouette method;
- column (multi-level GMDD): cluster count calculated by our proposed multi-level GMDD-based method;
- column (time [silhouette]): the execution time of the Silhouette method in milliseconds;
- column (time [gap]): the execution time of the gap statistics method in milliseconds;
- column (time [ml GMDD]): the execution time of our proposed multi-level GMDD method in milliseconds.
The test results in the comparison of the alternative methods can be summarized in the following experiences:
- -
- Only our proposed method can discover the multi-level clustering structure, while the current standard methods are aimed at determining the cluster count of the first clustering level.
- -
- In most cases, the proposed method could discover the hidden clustering structure.
- -
- Our proposed method could provide the best accuracy in all test cases.
- -
- The proposed method requires significantly less execution time.
8. Conclusions
The proposed cluster level tour refinement method called IntraClusTSP provides a novel approach to improve the existing heuristic eTSP solution methods. IntraClusTSP takes an initial tour and then performs tour optimization for a selected set of node clusters. In the last phase, the local optimal tours are then merged into a global optimal tour. Based on the performed evaluation tests the proposed method can improve the tour efficiency for every tested base methods (Random insertion with random position; Random insertion with smallest single distance; Random insertion with smallest route length increase; Random insertion with smallest single distance with IntraClusTSP refinement; Chained Lin-Kernighan method on the whole graph). IntraClusTSP performs intermediate level optimizations requiring smaller execution costs than a global level optimization. The proposed IntraClusTSP method can be used to
- refinement of existing routes;
- extension of any existing TSP optimization methods;
- perform a region-level refinement in large graphs;
- implement an efficient incremental route construction method.
For these cases, the proposed method can improve not only the tour length but also the execution time. The generated shortest Hamiltonian path can be used also in data analysis to determine the optimal number of clusters. Our proposed method is based on a novel approach, an adjusted GMDD analysis to determine gaps in the corresponding edge length histogram. Unlike the standard methods, the proposed method can discover also multi-level clustering structure and provides an outstanding performance both in accuracy and execution time.
The proposed cluster level tour refinement method provided very good efficiency and execution time characteristics in our base level experiments. Our plan is to perform further analysis to
- investigate the application for real life TSP problems;
- adapt the proposed algorithm to specific TSP problems like multi-level vehicle routing problem in logistics;
- discover the deeper behaviour of the corresponding permutation space.
Author Contributions
L.K. proposed the research direction, participated in the conceptualization, conducted experiments and wrote the paper L.B.I. participated in conceptualization and wrote the paper; D.K.I. participated in conceptualization and wrote the paper.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Zhao, C.; Parhami, B. Symmetric Agency Graphs Facilitate and Improve the Quality of Virtual Network Embedding. Symmetry 2018, 10, 63. [Google Scholar] [CrossRef]
- Jiang, W.; Zhai, Y.; Zhuang, Z.; Martin, P.; Zhao, Z.; Liu, J.B. Vertex Labeling and Routing for Farey-Type Symmetrically-Structured Graphs. Symmetry 2018, 10, 407. [Google Scholar] [CrossRef]
- José, M.V.; Zamudio, G.S. Symmetrical Properties of Graph Representations of Genetic Codes: From Genotype to Phenotype. Symmetry 2018, 10, 388. [Google Scholar] [CrossRef]
- Ball, F.; Geyer-Schulz, A. How Symmetric Are Real-World Graphs? A Large-Scale Study. Symmetry 2018, 10, 29. [Google Scholar] [CrossRef]
- Akiyama, T.; Nishizeki, T.; Saito, N. NP-completeness of the Hamiltonian cycle problem for bipartite graphs. J. Inf. Process. 1980, 3, 73–76. [Google Scholar]
- Laporte, G. The Traveling Salesman Problem: An overview of exact and approximate algorithms. Eur. J. Oper. Res. 1992, 59, 231–247. [Google Scholar] [CrossRef]
- Dantzig, G.B.; Fulkerson, D.R.; Johnson, S.M. Solution of a large-scale traveling-salesman problem. Oper. Res. 1954, 2, 393–410. [Google Scholar] [CrossRef]
- Miller, C.E.; Tucker, A.W.; Zemlin, R.A. Integer programming formulations and traveling salesman problems. J. Assoc. Comput. Mach. 1960, 7, 326–329. [Google Scholar] [CrossRef]
- Baldacci, R.; Hadjiconstantinou, E.; Mingozzi, A. An exact algorithm for the traveling salesman problem with deliveries and collections. Netw. Int. J. 2003, 42, 26–41. [Google Scholar] [CrossRef]
- Held, M.; Karp, R.M. A dynamic programming approach to sequencing problems. J. Soc. Ind. Appl. Math. 1962, 10, 196–210. [Google Scholar] [CrossRef]
- Bomze, I.M.; Budinich, M.; Pardalos, P.M.; Pelillo, M. The maximum clique problem. In Handbook of Combinatorial Optimization; Springer: Boston, MA, USA, 1999; pp. 1–74. [Google Scholar]
- Carpaneto, G.; Toth, P. Some new branching and bounding criteria for the asymmetric travelling salesman problem. Manag. Sci. 1980, 26, 736–743. [Google Scholar] [CrossRef]
- Hougardy, S.; Wilde, M. On the nearest neighbor rule for the metric traveling salesman problem. Discret. Appl. Math. 2015, 195, 101–103. [Google Scholar] [CrossRef]
- Monnot, J. A note on the traveling salesman reoptimization problem under vertex insertion. Inf. Process. Lett. 2015, 115, 435–438. [Google Scholar] [CrossRef]
- Schuetz, P.; Caflisch, A. Efficient modularity optimization by multistep greedy algorithm and vertex mover refinement. Phys. Rev. 2008, 77, 046112. [Google Scholar] [CrossRef] [PubMed]
- Borůvka, O. “O jistémproblémuminimálním” [About a certain minimal problem]. Prácemor. Přírodověd. Spol. vBrně III 1926, 3, 37–58, (In Czech and German). [Google Scholar]
- Xiang, Z.; Chen, Z.; Gao, X.; Wang, X.; Di, F.; Li, L.; Zhang, Y. Solving large-scale TSP using a fast wedging insertion partitioning approach. Math. Probl. Eng. 2015, 2015, 854218. [Google Scholar] [CrossRef]
- Mosheiov, G. The travelling salesman problem with pick-up and delivery. Eur. J. Oper. Res. 1994, 79, 299–310. [Google Scholar] [CrossRef]
- Weise, T.; Chiong, R.; Lassig, J.; Tang, K.; Tsutsui, S.; Chen, W.; Yao, X. Benchmarking optimization algorithms: An open source framework for the traveling salesman problem. IEEE Comput. Intell. Mag. 2014, 9, 40–52. [Google Scholar] [CrossRef]
- Genova, K.; Williamson, D.P. An experimental evaluation of the best-of-many Christofides’ algorithm for the traveling salesman problem. Algorithmica 2017, 78, 1109–1130. [Google Scholar] [CrossRef]
- Ma, Z.; Liu, L.; Sukhatme, G.S. An adaptive k-opt method for solving traveling salesman problem. In Proceedings of the 2016 IEEE 55th Conference on Decision and Control (CDC), Las Vegas, NV, USA, 12–14 December 2016; Volume 1, pp. 6537–6543. [Google Scholar]
- Lin, S.; Kernighan, B.W. An effective heuristic algorithm for the traveling-salesman problem. Oper. Res. 1973, 21, 498–516. [Google Scholar] [CrossRef]
- Ismkhan, H. Effective three-phase evolutionary algorithm to handle the large-scale colorful traveling salesman problem. Expert Syst. Appl. 2017, 67, 148–162. [Google Scholar] [CrossRef]
- Valdez, F.; Melin, P.; Castillo, O. A survey on nature-inspired optimization algorithms with fuzzy logic for dynamic parameter adaptation. Expert Syst. Appl. 2014, 41, 6459–6466. [Google Scholar] [CrossRef]
- Kóczy, L.T.; Földesi, P.T.; Szabó, B. An effective Discrete Bacterial Memetic Evolutionary Algorithm for the Traveling Salesman Problem. Int. J. Intell. Syst. 2017, 32, 862–876. [Google Scholar] [CrossRef]
- Imran, A.; Salhi, S.; Wassan, N.A. A variable neighborhood-based heuristic for the heterogeneous fleet vehicle routing problem. Eur. J. Oper. Res. 2009, 197, 509–518. [Google Scholar] [CrossRef]
- Cook, W.; Seymour, P. Tour merging via branch-decomposition. INFORMS J. Comput. 2003, 15, 233–248. [Google Scholar] [CrossRef]
- Johnson, D.; McGeoch, L. Experimental Analysis of Heuristics for the STSP. In The Traveling Salesman Problem and Its Variations; Springer: Boston, MA, USA, 2007; pp. 369–443. [Google Scholar]
- Johnson, D.S.; McGeoch, L.A. The traveling salesman problem: A case study in local optimization. Local Search Comb. Optim. 1997, 1, 215–310. [Google Scholar]
- Golden, B.; Bodin, L.; Doyle, T.; Stewart, W., Jr. Approximate traveling salesman algorithms. Oper. Res. 1980, 28, 694–711. [Google Scholar] [CrossRef]
- Azar, Y. Lower bounds for insertion methods for TSP. Comb. Probab. Comput. 1994, 3, 285–292. [Google Scholar] [CrossRef]
- Rosenkrantz, D.J.; Stearns, R.E.; Lewis, P.M. An analysis of several heuristics for the traveling salesman problem. SIAM J. Comput. 1977, 6, 563–581. [Google Scholar] [CrossRef]
- Hurkens, C.A. Nasty TSP instances for farthest insertion. In Proceedings of the 2nd Integer Programming and Combinatorial Optimization Conference, Pittsburgh PA, USA, 25–27 May 1992; Carnegie Mellon University: Pittsburgh, PA, USA, 1992. [Google Scholar]
- Cronin, T.M. Maintaining Incremental Optimality When Building Shortest Euclidean Tours (No. CSWD-92-TRF-0042); Army Cecom Signals Warfare: Warrenton, VA, USA, 1990. [Google Scholar]
- Mladenović, N. An efficient general variable neighborhood search for large travelling salesman problem with time windows. Jugoslav J. Oper. Res. 2016, 23, 19–30. [Google Scholar] [CrossRef]
- Ariyasingha, I.D.; Fernando, T.G. Performance analysis of the multi-objective ant colony optimization algorithms for the traveling salesman problem. Swarm Evol. Comput. 2015, 23, 11–26. [Google Scholar] [CrossRef]
- Gendreau, M.; Hertz, A.; Laporte, G. New insertion and postoptimization procedures for the traveling salesman problem. Oper. Res. 1992, 40, 1086–1094. [Google Scholar] [CrossRef]
- Chisman, J.A. The clustered traveling salesman problem. Comput. Oper. Res. 1975, 2, 115–119. [Google Scholar] [CrossRef]
- Jongens, K.; Volgenant, T. The symmetric clustered traveling salesman problem. Eur. J. Oper. Res. 1985, 19, 68–75. [Google Scholar] [CrossRef]
- Mulder, S.; Wunsch, D., II. Million city traveling salesman problem solution by divide and conquer clustering with adaptive resonance neural networks. Neural Netw. 2003, 16, 827–832. [Google Scholar] [CrossRef]
- Applegate, D.; Cook, W. Solving large-scale matching problems. In Network Flows and Matching: First DIMACS Mathematical Problems in Engineering 7 Implementation Challenge; American Mathematical Society: Providence, RI, USA, 1993; pp. 557–576. [Google Scholar]
- Verhoeven, M.G.A.; Aarts, E.H.L.; Swinkels, P.C.J. A parallel 2-opt algorithm for the traveling salesman problem. Future Gener. Comput. Syst. 1995, 11, 175–182. [Google Scholar] [CrossRef]
- Karp, R.M. Probabilistic analysis of partitioning algorithms for the traveling-salesman problem in the plane. Math. Oper. Res. 1977, 2, 209–224. [Google Scholar] [CrossRef]
- Bentley, J.J. Fast algorithms for geometric traveling salesman problems. ORSA J. Comput. 1992, 4, 387–411. [Google Scholar] [CrossRef]
- El-Samak, A.F.; Ashour, W. Optimization of traveling salesman problem using affinity propagation clustering and genetic algorithm. J. Artif. Intell. Soft Comput. Res. 2015, 5, 239–245. [Google Scholar] [CrossRef]
- Phienthrakul, T. Clustering evolutionary computation for solving travelling salesman problems. Int. J. Adv. Comput. Sci. Inf. Technol. 2014, 3, 243–262. [Google Scholar]
- Psychas, I.D.; Delimpasi, E.; Marinaki, Y. Hybrid evolutionary algorithms for the multiobjective traveling salesman problem. Expert Syst. Appl. 2015, 42, 8956–8970. [Google Scholar] [CrossRef]
- Bednarik, L.; Kovács, L. Efficiency analysis of quality threshold clustering algorithms. Prod. Syst. Inf. Eng. 2012, 6, 1275–1285. [Google Scholar]
- Garnier, R.; Taylor, J. Discrete Matrhematics for New Technolology; IoP Publisher: Bristol, UK, 2001. [Google Scholar]
- Sugar, C.A.; James, G.M. Finding the number of clusters in a dataset: An information-theoretic approach. J. Am. Stat. Assoc. 2003, 98, 750–763. [Google Scholar] [CrossRef]
- Haroun, S.A.; Jamal, B.; Hicham, E.H. A Performance Comparison of GA and ACO Applied to TSP. Int. J. Comput. Appl. 2015, 117, 28–35. [Google Scholar] [CrossRef]
- Richter, D.; Goldengorin, B.; Jäger, G.; Molitor, P. Improving the efficiency of Helsgaun’s Lin-Kernighan heuristic for the symmetric TSP. In Proceedings of the Workshop on Combinatorial and Algorithmic Aspects of Networking, Halifax, NS, Canada, 14 August 2007; pp. 99–111. [Google Scholar]
- Walshaw, C. A Multilevel Lin-Kernighan-Helsgaun Algorithm for the Travelling Salesman Problem; CMS Press: London, UK, 2001. [Google Scholar]
- Ma, F.M.; Guo, Y.J.; Yi, P.T. Cluster-reliability-induced OWA operators. Int. J. Intell. Syst. 2017, 32, 823–836. [Google Scholar] [CrossRef]
- Rousseeuw, P.J.; Kaufman, L. Finding groups in data. Ser. Probab. Math. Stat. 2003, 34, 111–112. [Google Scholar]
- Tibshirani, R.; Walther, G.; Hastie, T. Estimating the number of clusters in a data set via the gap statistic. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 2001, 63, 411–423. [Google Scholar] [CrossRef]
- Kass, R.E.; Raftery, A.E. Bayes factors. J. Am. Stat. Assoc. 1995, 90, 773–795. [Google Scholar] [CrossRef]
- Yang, X.; Kong, F.; Xu, W.; Liu, B. Gaussian mixture density modeling and decomposition with weighted likelihood. J. Men’s Health 2004, 5, 4245–4249. [Google Scholar]
- Liu, Y.; Li, Z.; Xiong, H.; Gao, X.; Wu, J. Understanding of internal clustering validation measures. In Proceedings of the 2010 IEEE International Conference on Data Mining, Sydney, Australia, 13–17 December 2010; pp. 911–916. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).