Mean-Square Estimation of Nonlinear Functionals via Kalman Filtering
Abstract
1. Introduction
1.1. Background and Significance
1.2. Literature Review
1.3. Formulation of the Problem of Interest for this Investigation
1.4. Scope and Contributions of this Investigation
- (1)
- This paper studies the MMSE estimation problem of an NFS within the discrete-time Kalman filtering framework. Using the mean square estimation approach, an optimal two-stage nonlinear estimator is proposed.
- (2)
- The optimal MMSE estimator for polynomial functionals (such as quadratic, cubic and quartic) is derived. We establish that the polynomial estimator representing a compact closed-form formula depends only on the Kalman estimate and its error covariance.
- (3)
- An important class of quadratic estimators is comprehensively investigated, including derivation of novel matrix equations for the estimated and true mean square error.
- (4)
- Performance of the proposed estimators for real NFS illustrates their theoretical and practical usefulness.
1.5. Organization of the Paper
2. Motivating Examples
3. Theoretical Results: Optimal Mean Square Estimator for NFS
3.1. Main Idea and General Solution
3.2. Optimal Closed-Form MMSE Estimator for Quadratic Functional
3.2.1. Examples of Quadratic Functional as Energy and Work
3.2.2. Closed-Form Quadratic Estimator
3.2.3. True Mean Square Error for Quadratic Estimators
3.3. Optimal Closed-Form MMSE Estimator for Polynomial Functional
3.4. Application of Unscented Transformation for Estimation of General NFS
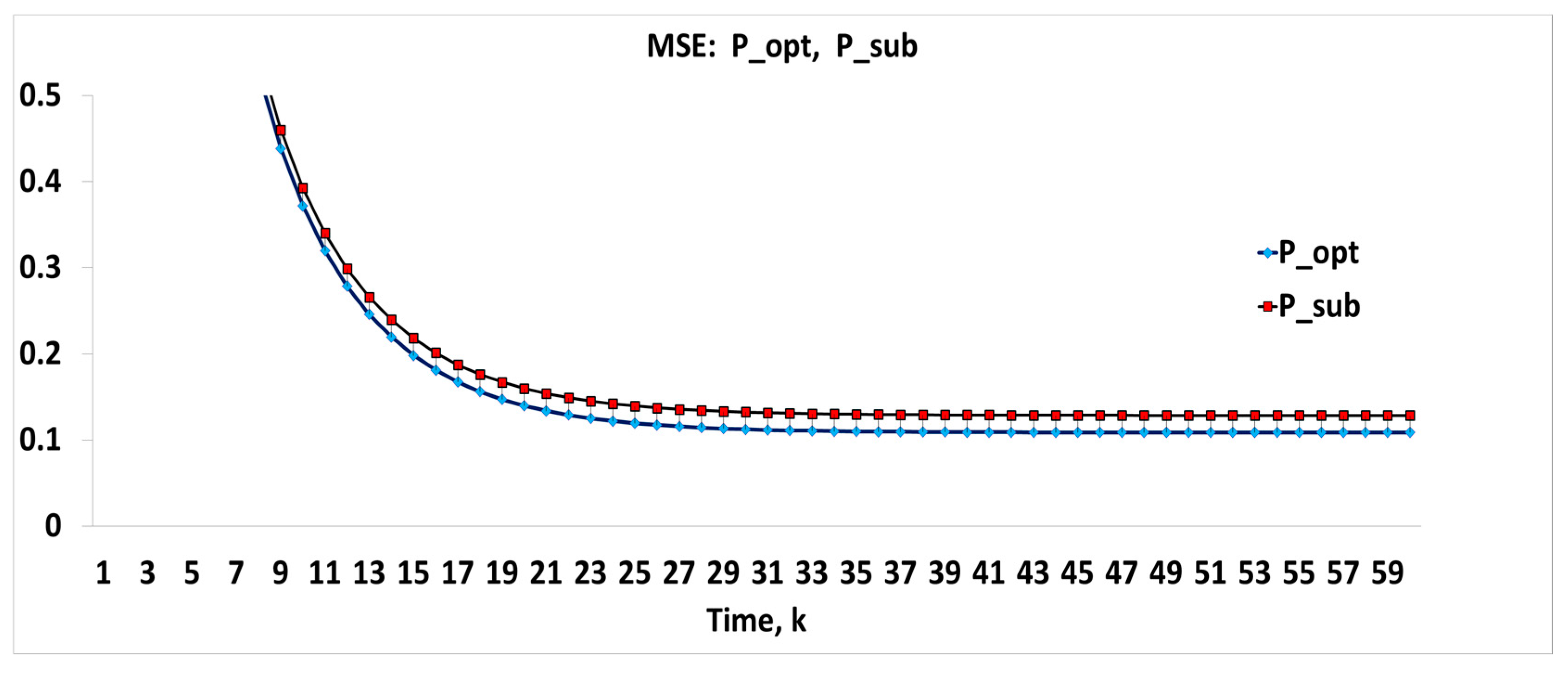
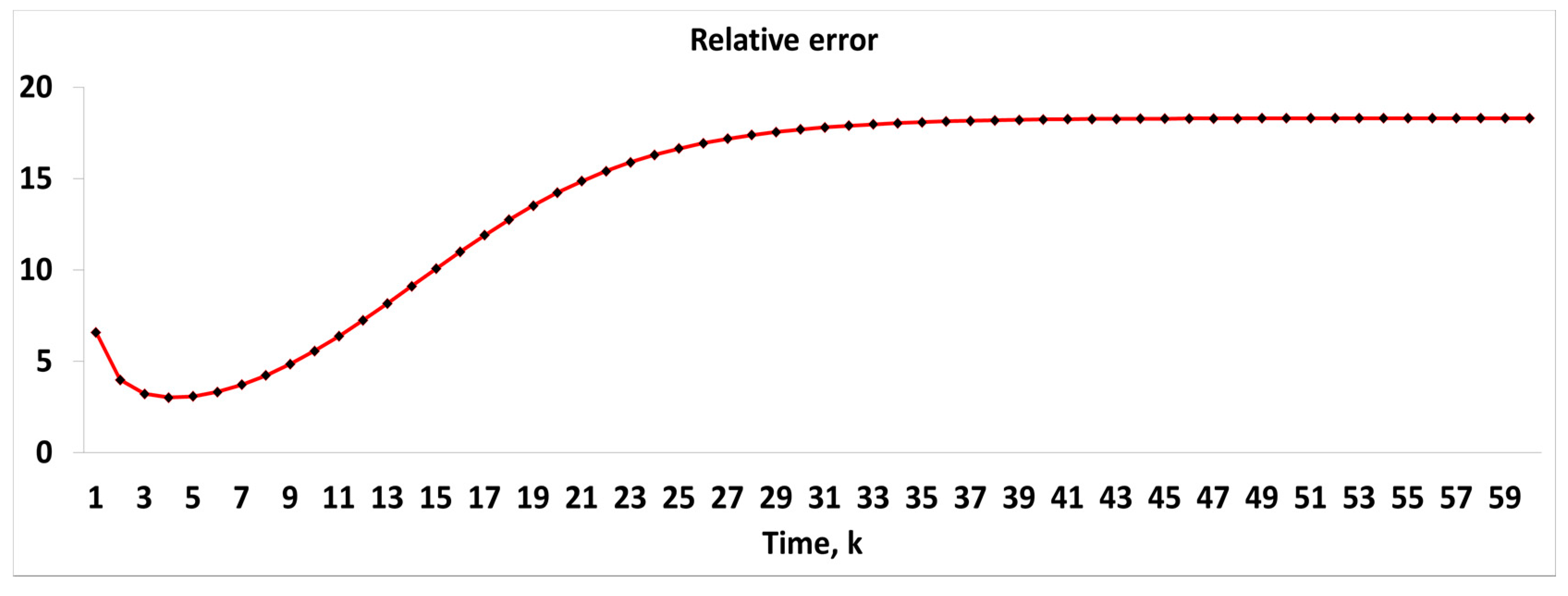
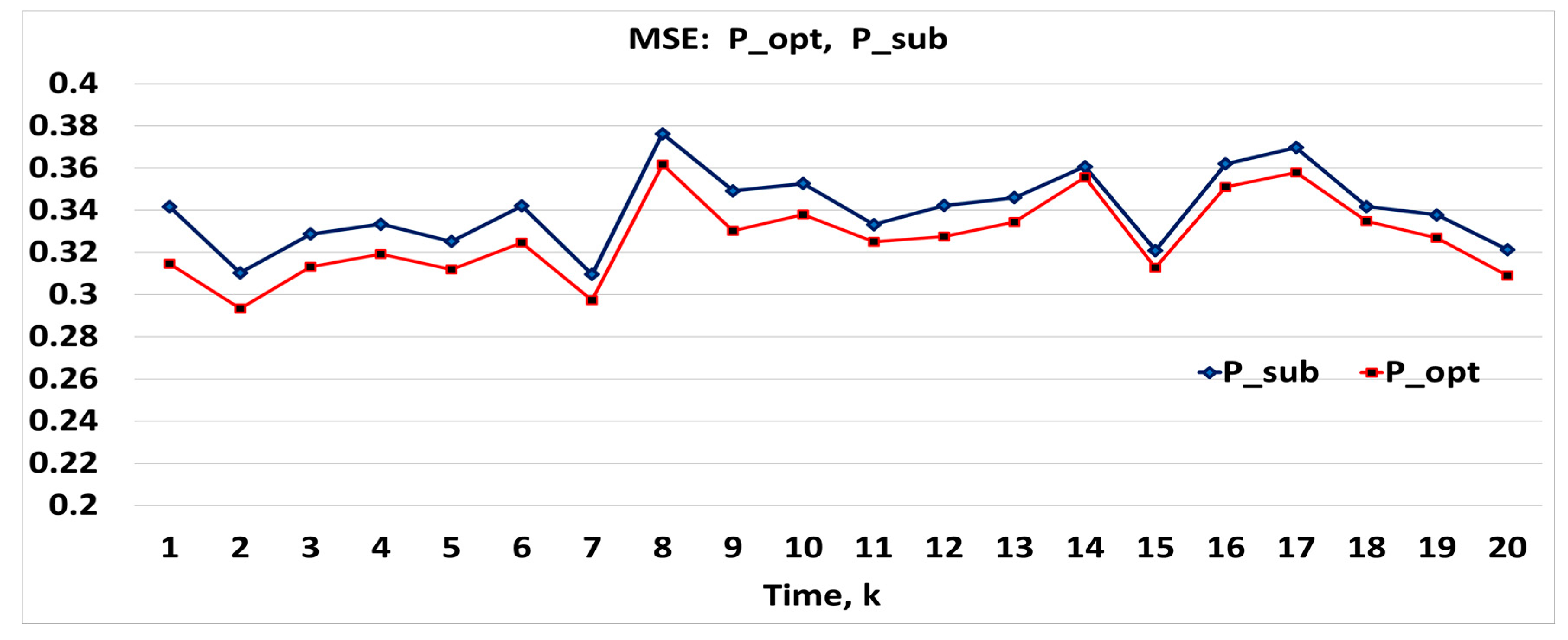
4. Numerical Verification
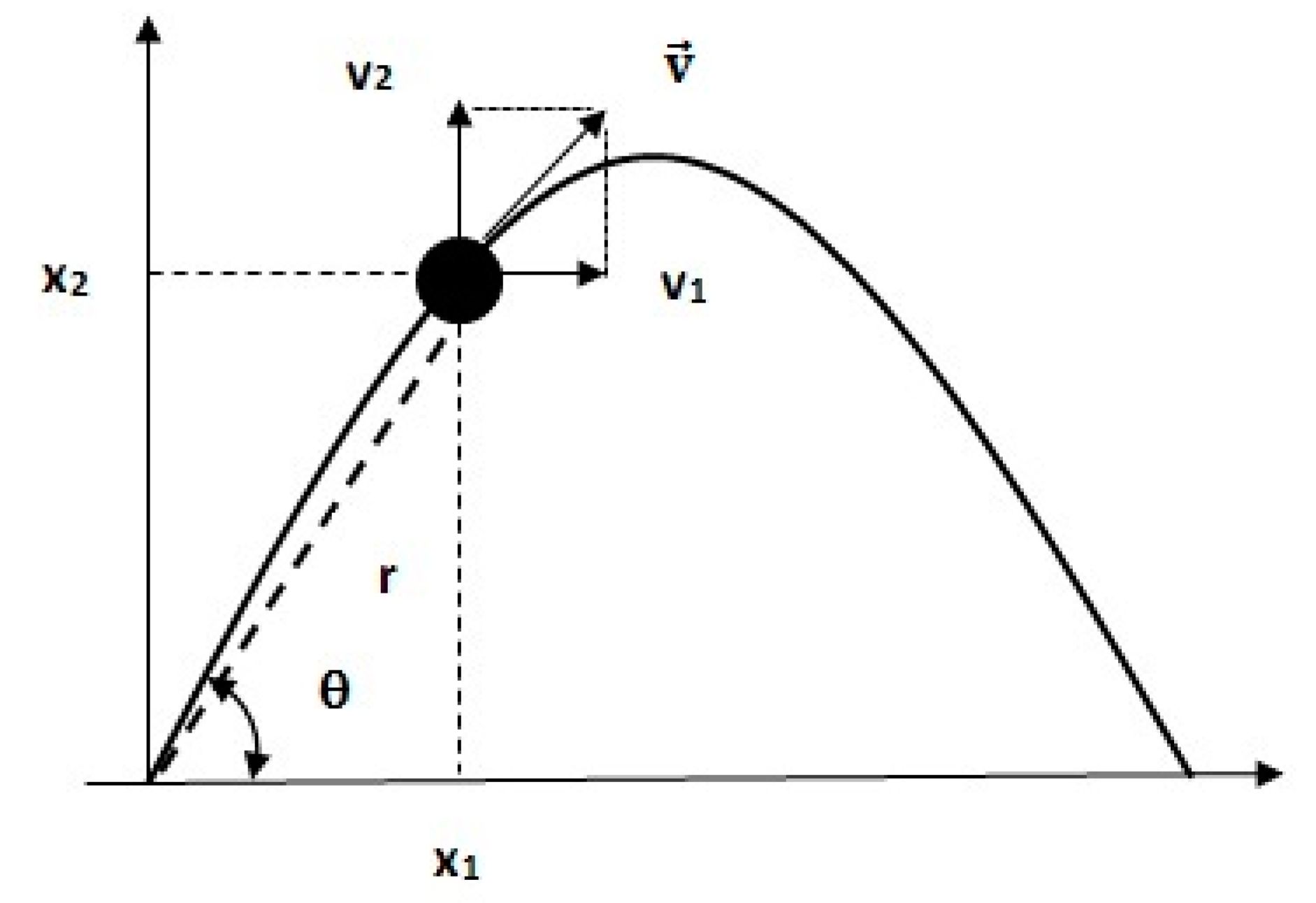
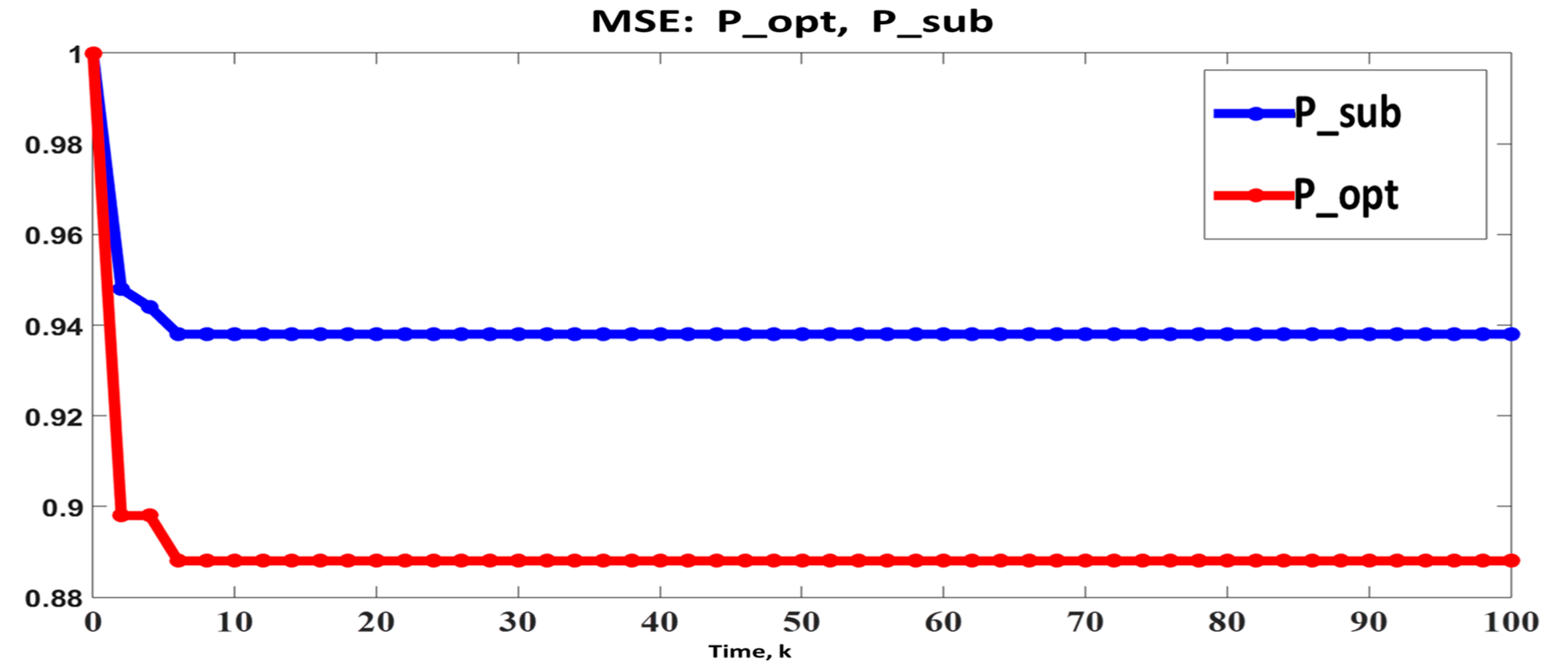
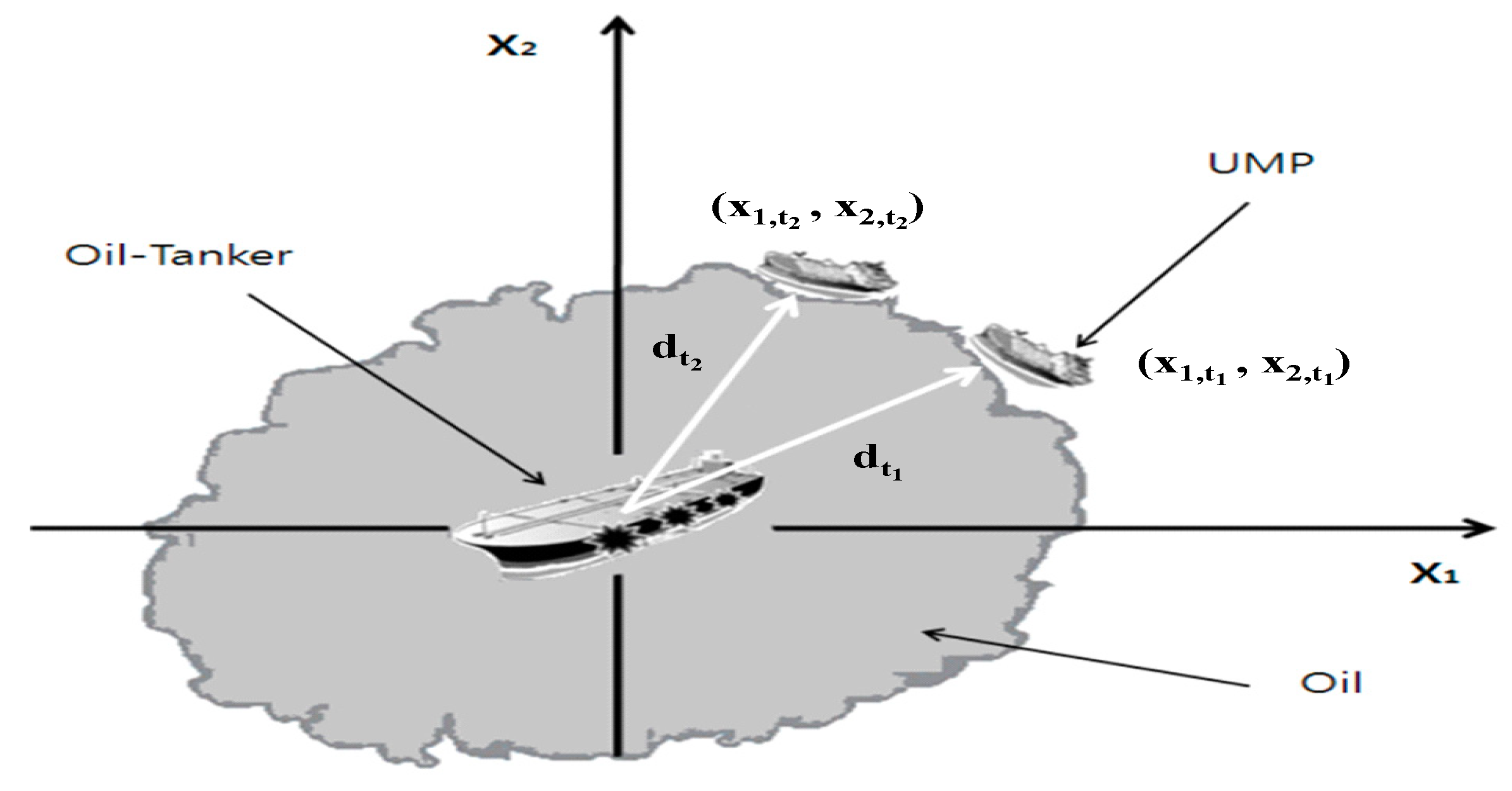
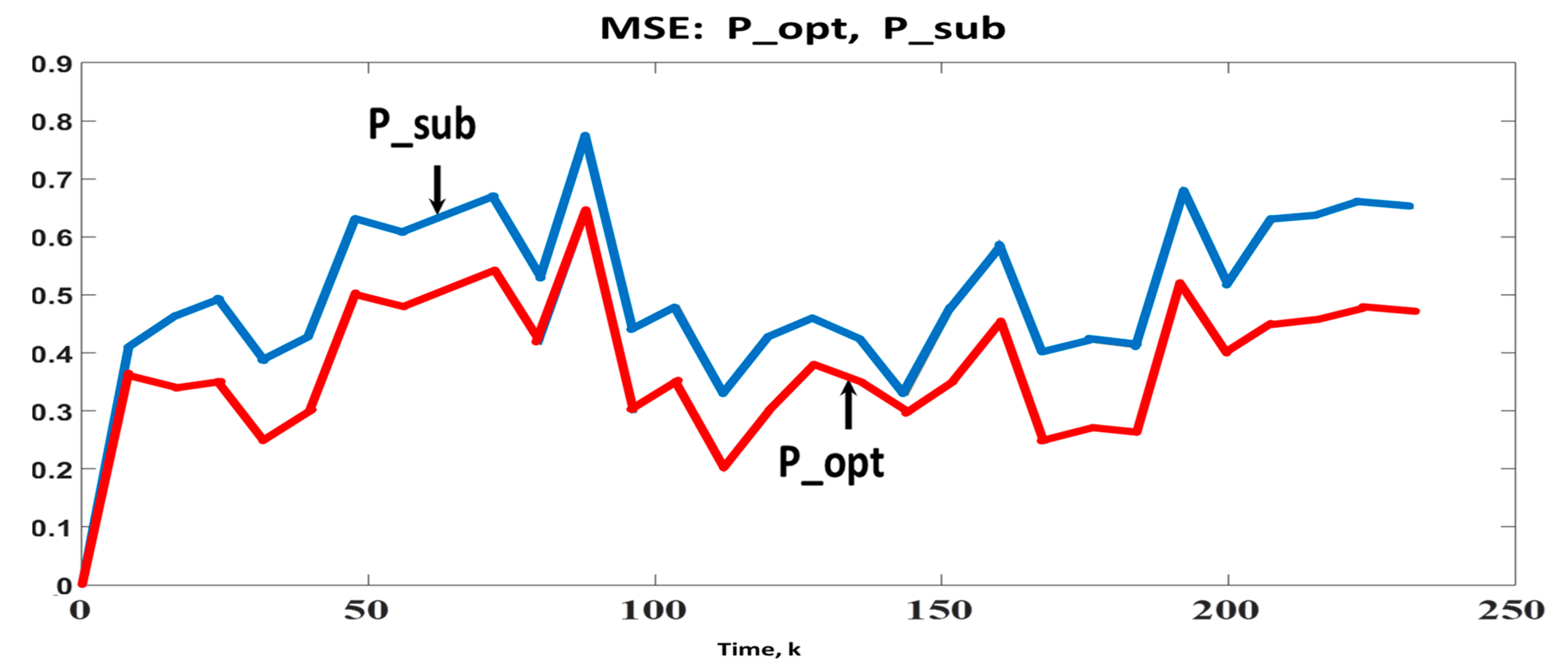
4.1. Estimation of Distance between Unknown and Moving Points
4.2. Estimation of Power and Modulus of Unknown Signal
4.2.1. Estimation of Power of Signal
4.2.2. Estimation of Modulus of Signal
4.3. Numerical Example of QF: Wind Tunnel System
4.4. Numerical Example of General NFS: Motion of Unmanned Marine Probe
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Pappalardo, C.M.; Guida, D. Use of the Adjoint Method for Controlling the Mechanical Vibrations of Nonlinear Systems. Machines 2018, 6, 19. [Google Scholar] [CrossRef]
- Bryson, A.E. Applied Optimal Control: Optimization, Estimation and Control; Routledge: London, UK, 2018. [Google Scholar]
- Davari, N.; Gholami, A. An Asynchronous Adaptive Direct Kalman Filter Algorithm to Improve Underwater Navigation System Performance. IEEE Sens. J. 2017, 17, 1061–1068. [Google Scholar] [CrossRef]
- Kulikova, M.V.; Tsyganova, J.V. Improved Discrete-Time Kalman Filtering within Singular Value Decomposition. IET Control Theory Appl. 2017, 11, 2412–2418. [Google Scholar] [CrossRef]
- Shmaliy, Y.; Zhao, S.; Ahn, C.K. Unbiased Finite Impulse Response Filtering: An Iterative Alternative to Kalman Filtering Ignoring Noise and Initial Conditions. IEEE Control Syst. 2017, 37, 70–89. [Google Scholar]
- Grewal, M.S.; Andrews, A.P.; Bartone, C.G. Global Navigation Satellite Systems, Inertial Navigation, and Integration, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Rigatos, G.G.; Siano, P. Sensorless Control of Electric Motors with Kalman Filters: Applications to Robotic and Industrial Systems. Int. J. Adv. Robot. Syst. 2011, 8, 62–80. [Google Scholar] [CrossRef]
- Simon, D. Optimal State Estimation. Kalman, H-Infinity, and Nonlinear Approaches; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Haykin, S. Kalman Filtering and Neural Networks; John Wiley & Sons: Hoboken, NJ, USA, 2004; Volume 47. [Google Scholar]
- Bar-Shalom, Y.; Li, Y.; Kirubarajan, T. Estimation with Applications to Tracking and Navigation; John Wiley & Sons: New York, NY, USA, 2001. [Google Scholar]
- Cai, T.T.; Low, M.G. Optimal Adaptive Estimation of a Quadratic Functional. Ann. Stat. 2006, 34, 2298–2325. [Google Scholar] [CrossRef]
- Robins, J.; Li, L.; Tchetgen, E.; Vaart, A. Higher Order Infuence Functions and Minimax Estimation of Nonlinear Functionals. Probab. Stat. 2008, 2, 335–421. [Google Scholar]
- Jiao, J.; Venkat, K.; Han, Y.; Weissman, T. Minimax Estimation of Functionals of Discrete Distributions. IEEE Trans. Inf. Theory 2015, 61, 2835–2885. [Google Scholar] [CrossRef] [PubMed]
- Jiao, J.; Venkat, K.; Han, Y.; Weissman, T. Maximum Likelihood Estimation of Functionals of Discrete Distributions. IEEE Trans. Inf. Theory 2017, 63, 6774–6798. [Google Scholar] [CrossRef]
- Amemiya, Y.; Fuller, W.A. Estimation for the Nonlinear Functional Relationship. Ann. Stat. 1988, 16, 147–160. [Google Scholar] [CrossRef]
- Donoho, D.L.; Nussbaum, M. Minimax Quadratic Estimation of a Quadratic Functional. J. Complex. 1990, 6, 290–323. [Google Scholar] [CrossRef]
- Grebenkov, D.S. Optimal and Suboptimal Quadratic Forms for Noncentered Gaussian Processes. Phys. Rev. 2013, E88, 032140. [Google Scholar] [CrossRef] [PubMed]
- Laurent, B.; Massart, P. Adaptive Estimation of a Quadratic Functional by Model Selection. Ann. Stat. 2000, 28, 1302–1338. [Google Scholar] [CrossRef]
- Vladimirov, I.G.; Petersen, I.R. Directly Coupled Observers for Quantum Harmonic Oscillators with Discounted Mean Square Cost Functionals and Penalized Back-Action. In Proceedings of the IEEE Conference on Norbert Wiener in the 21st Century, Melbourne, Australia, 13–15 July 2016; pp. 78–83. [Google Scholar]
- Sricharan, K.; Raich, R.; Hero, A.O. Estimation of Nonlinear Functionals of Densities with Confidence. IEEE Trans. Inf. Theory 2012, 58, 4135–4159. [Google Scholar] [CrossRef]
- Wisler, A.; Berisha, V.; Spanias, A.; Hero, A.O. Direct Estimation of Density Functionals Using a Polynomial Basis. IEEE Trans. Signal Process. 2018, 66, 558–588. [Google Scholar] [CrossRef]
- Taniguchi, M. On Estimation of Parameters of Gaussian Stationary Processes. J. Appl. Probab. 1979, 16, 575–591. [Google Scholar] [CrossRef]
- Zhao-Guo, C.; Hanman, E.J. The Distribution of Periodogram Ordinates. J. Time Ser. Anal. 1980, 1, 73–82. [Google Scholar] [CrossRef]
- Janas, D.; Sachs, R. Consistency for Nonlinear Functions of the Periodogram of Tapered Data. J. Time Ser. Anal. 1995, 16, 585–606. [Google Scholar] [CrossRef]
- Fay, G.; Moulines, E.; Soulier, P. Nonlinear Functionals of the Periodogram. J. Time Ser. Anal. 2002, 23, 523–553. [Google Scholar] [CrossRef]
- Noviello, C.; Fornaro, G.; Braca, P.; Martorella, M. Fast and Accurate ISAR Focusing Based on a Doppler Parameter Estimation Algorithm. IEEE Geosci. Remote Sens. Lett. 2017, 14, 349–353. [Google Scholar] [CrossRef]
- Wu, Y.; Yang, P. Minimax Rates of Entropy Estimation on Large Alphabets via Best Polynomial Approximation. IEEE Trans. Inf. Theory 2016, 62, 3702–3720. [Google Scholar] [CrossRef]
- Wu, Y.; Yang, P. Optimal Entropy Estimation on Large Alphabets via Best Polynomial Approximation. In Proceedings of the IEEE International Symposium on Information Theory, Hong Kong, China, 14–19 June 2015; pp. 824–828. [Google Scholar]
- Song, I.Y.; Shevlyakov, G.; Shin, V. Estimation of Nonlinear Functions of State Vector for Linear Systems with Time-Delays and Uncertainties. Math. Probl. Eng. 2015, 2015, 217253. [Google Scholar] [CrossRef]
- Pugachev, V.S.; Sinitsyn, I.N. Stochastic Differential Systems. Analysis and Filtering; Wiley& Sons: New York, NY, USA, 1987. [Google Scholar]
- Kan, R. From Moments of Sum to Moments of Product. J. Multivar. Anal. 2008, 99, 542–554. [Google Scholar] [CrossRef]
- Holmquist, B. Expectations of Products of Quadratic Forms in Normal Variables. Stoch. Anal. Appl. 1996, 14, 149–164. [Google Scholar] [CrossRef]
- Julier, S.J.; Uhlmann, J.K. Unscented Filtering and Nonlinear Estimation. Proc. IEEE 2004, 92, 401–422. [Google Scholar] [CrossRef]
- Chang, L.; Hu, B.; Li, A.; Qin, F. Transformed Unscented Kalman Filter. IEEE Trans. Autom. Control 2013, 58, 252–257. [Google Scholar] [CrossRef]
- Armstrong, E.S.; Tripp, J.S. An Application of Multivariable Design Techniques to the Control of the National Transonic Facility; NASA Tech. Paper 1887; NASA Langley Research Center: Hampton, VA, USA, 1981.
- Mutambara, A.G.O. Decentralized Estimation and Control for Multisensor Systems; CRC Press: Boca Raton, FL, USA, 1998. [Google Scholar]
- Chen, G. Approximate Kalman Filtering; World Scientific Publishing: Singapore, 1993. [Google Scholar]
- Jiang, C.; Zhang, S.B.; Zhang, Q.Z. Adaptive Estimation of Multiple Fading Factors for GPS/INS Integrated Navigation Systems. Sensors 2017, 17, 1254. [Google Scholar] [CrossRef] [PubMed]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choi, W.; Shin, V.; Song, I.Y. Mean-Square Estimation of Nonlinear Functionals via Kalman Filtering. Symmetry 2018, 10, 630. https://doi.org/10.3390/sym10110630
Choi W, Shin V, Song IY. Mean-Square Estimation of Nonlinear Functionals via Kalman Filtering. Symmetry. 2018; 10(11):630. https://doi.org/10.3390/sym10110630
Chicago/Turabian StyleChoi, Won, Vladimir Shin, and Il Young Song. 2018. "Mean-Square Estimation of Nonlinear Functionals via Kalman Filtering" Symmetry 10, no. 11: 630. https://doi.org/10.3390/sym10110630
APA StyleChoi, W., Shin, V., & Song, I. Y. (2018). Mean-Square Estimation of Nonlinear Functionals via Kalman Filtering. Symmetry, 10(11), 630. https://doi.org/10.3390/sym10110630




