Time-Varying Ultra-Wideband Channel Modeling and Prediction
Abstract
1. Introduction
2. UWB Channel Impulse Response
2.1. Channel Model
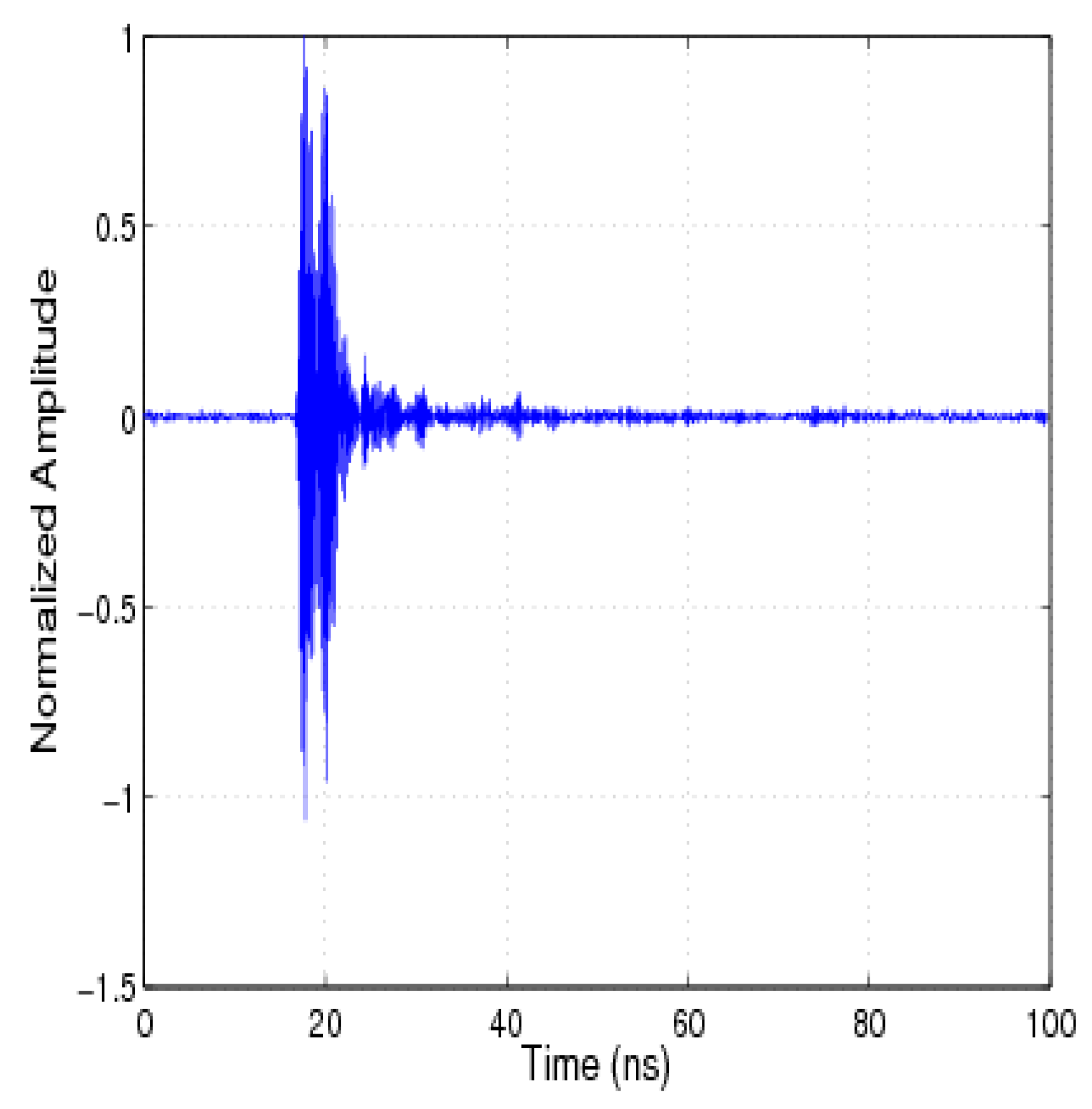
2.2. UWB Channel Measurement
2.3. UWB Channel Impulse Response Extraction
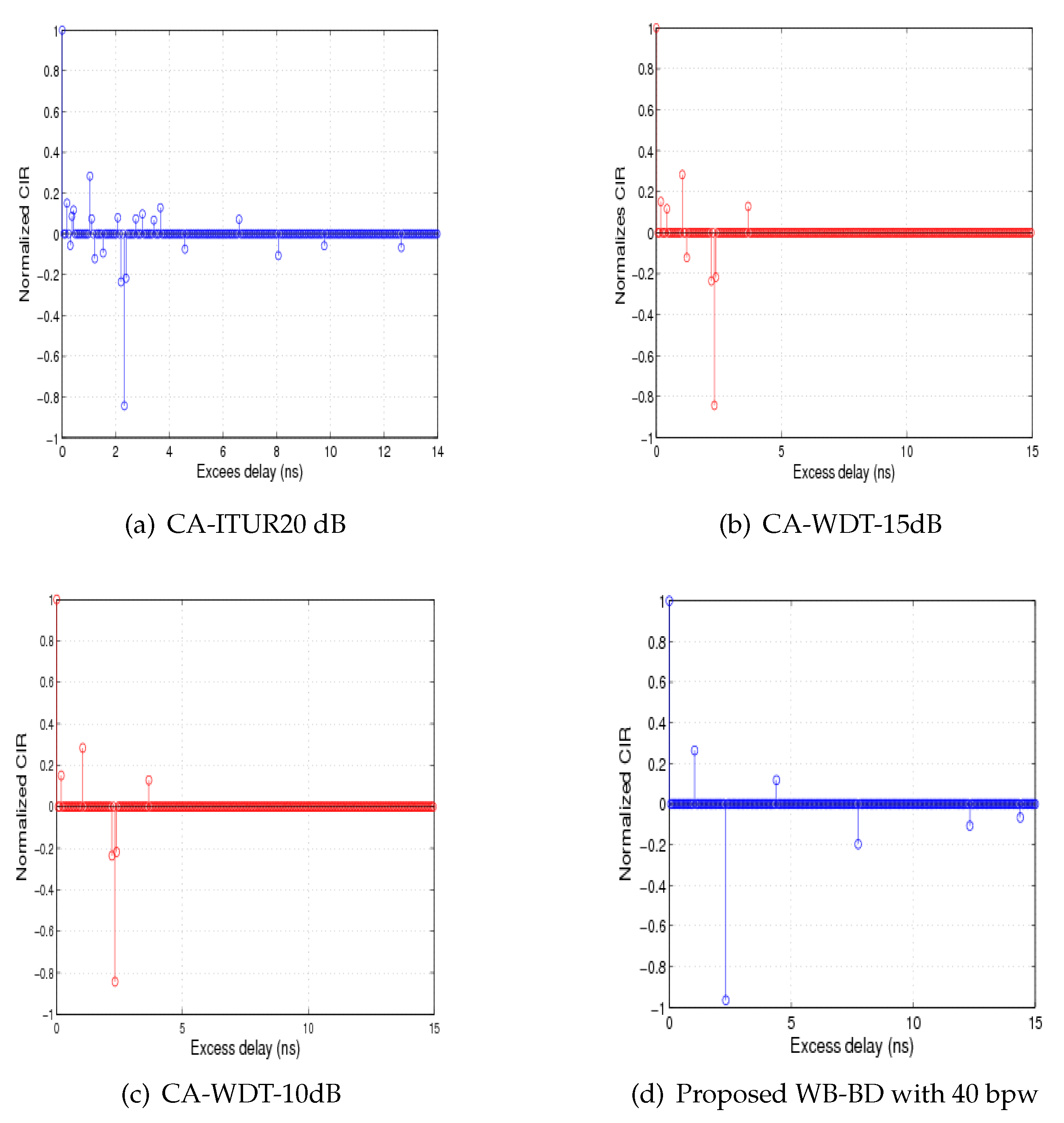
3. Window-Based UWB Channel Impulse Response Proposed Model
3.1. Window Selection
3.2. Channel Tap Selection
4. Channel Impulse Response Tap Prediction Algorithms
5. Evaluation Criterion
6. Complexity Analysis
7. Results and Discussion
7.1. Modeling Results
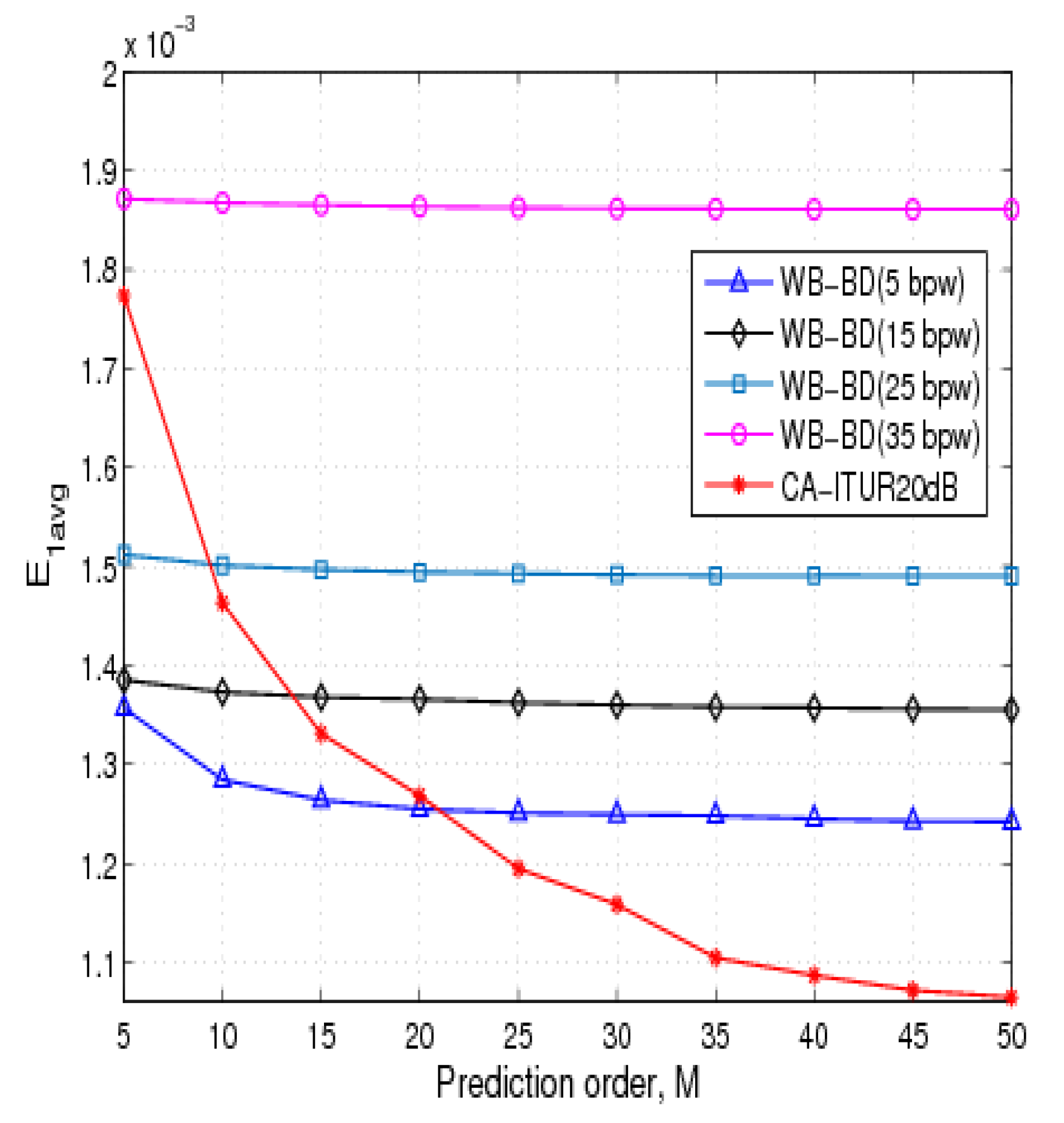
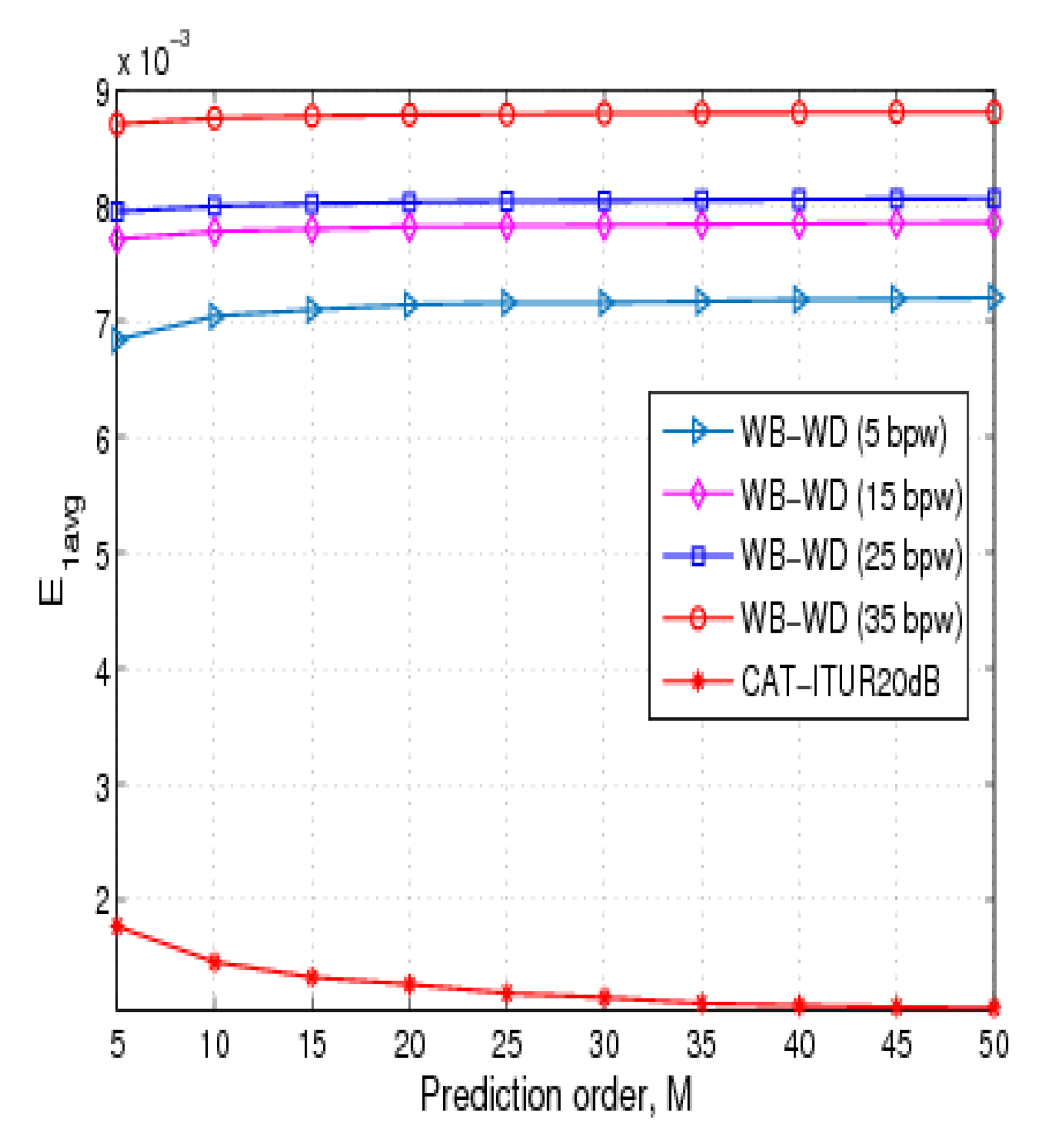
7.2. Prediction Results
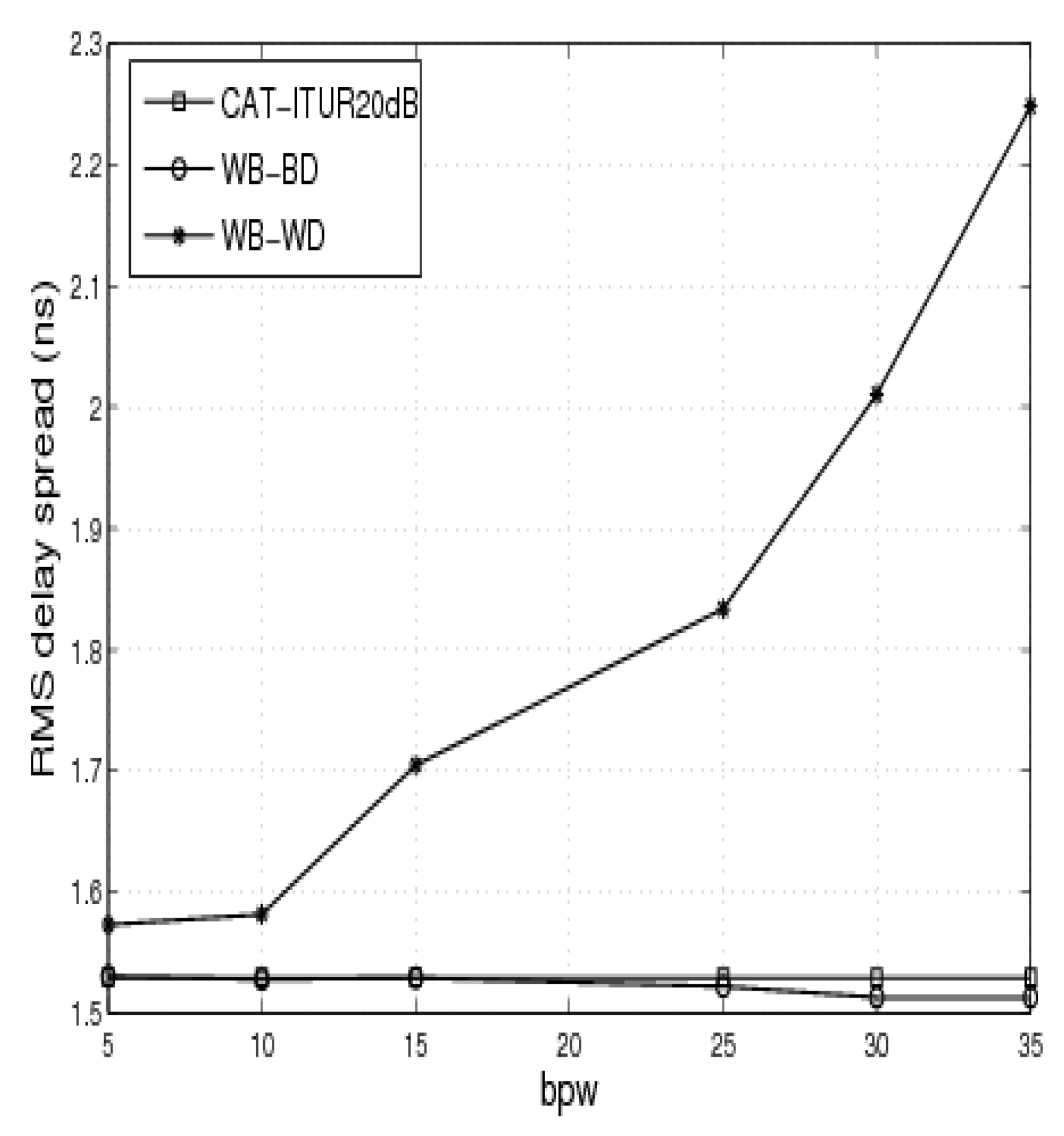
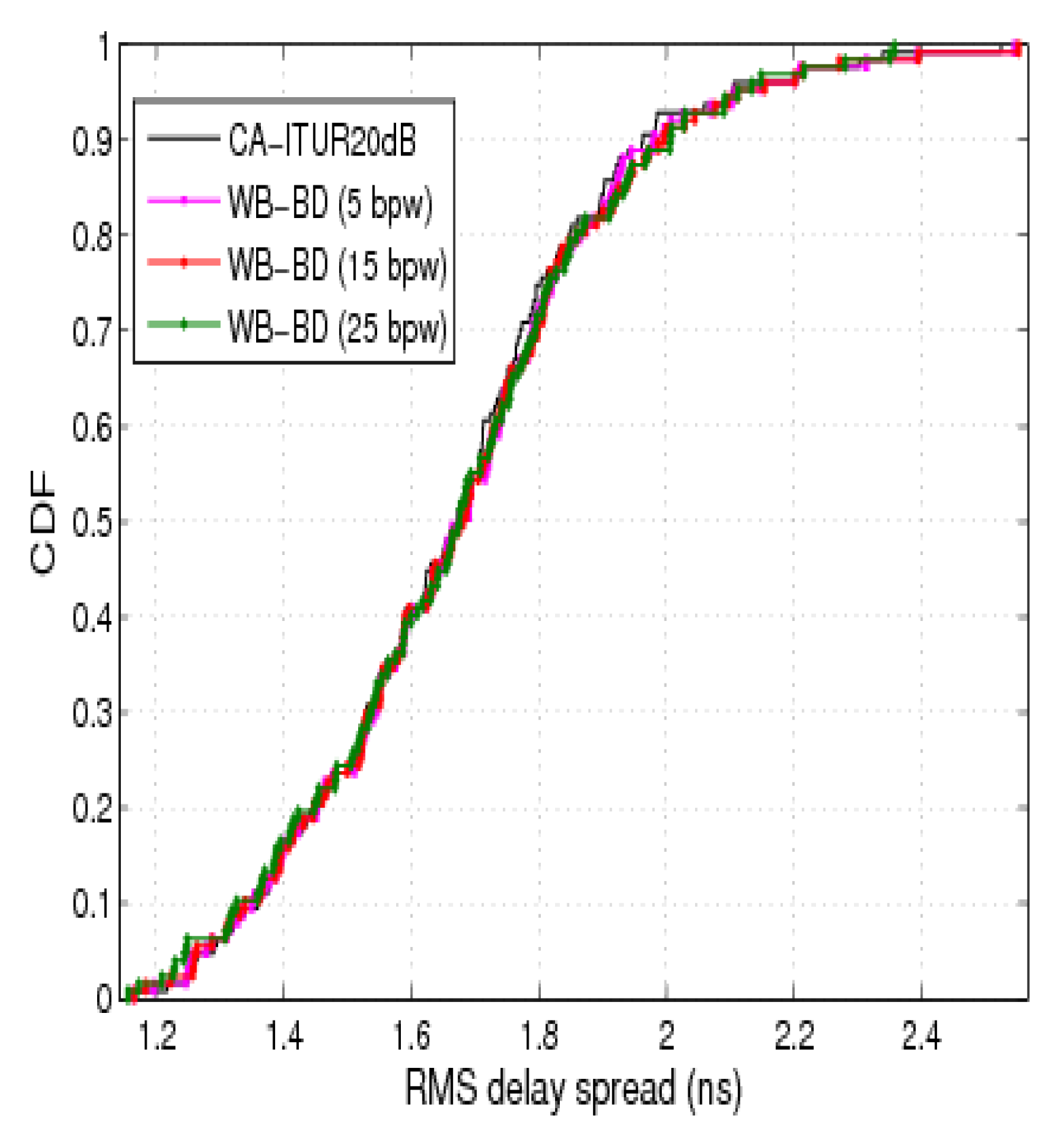
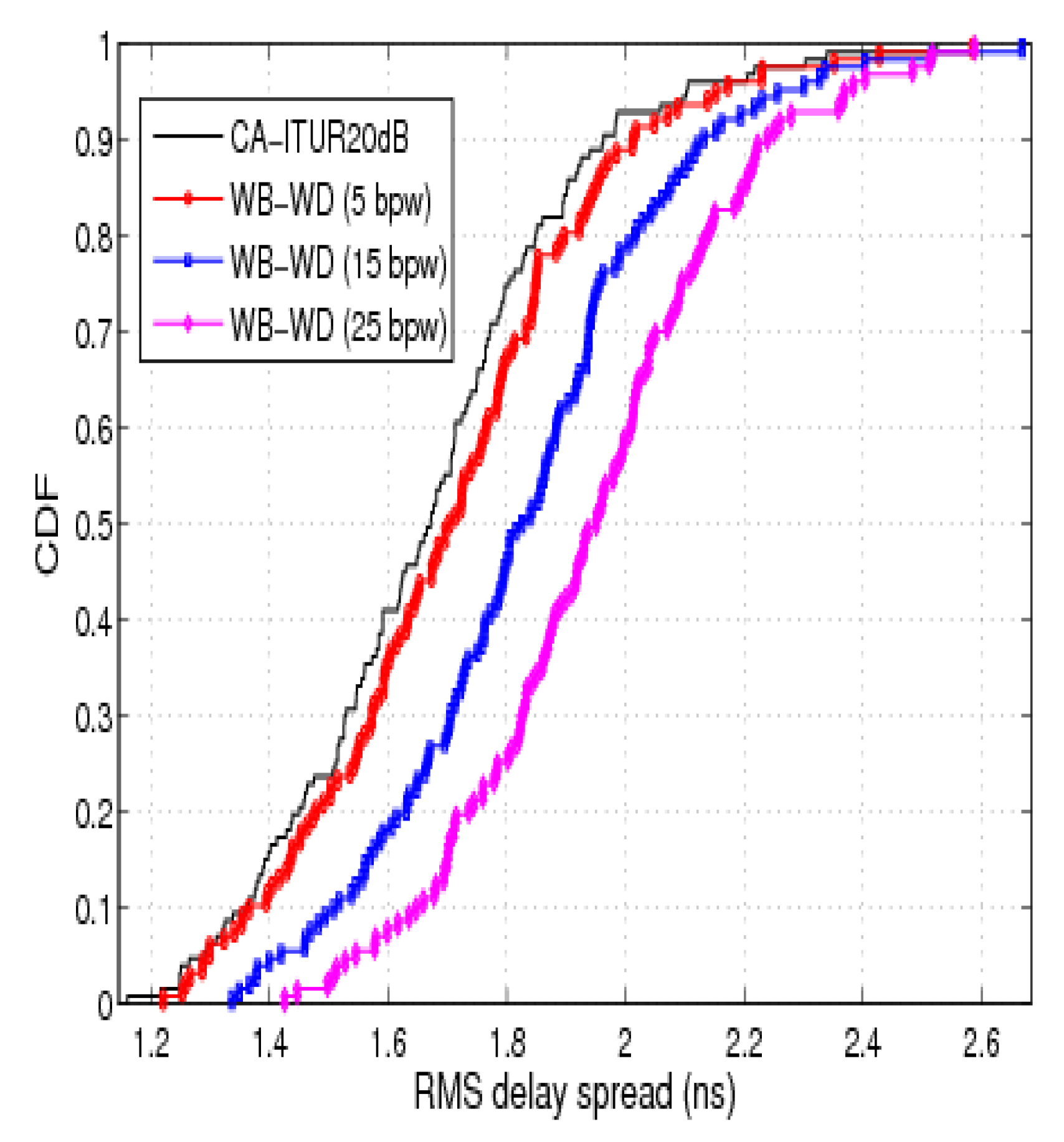
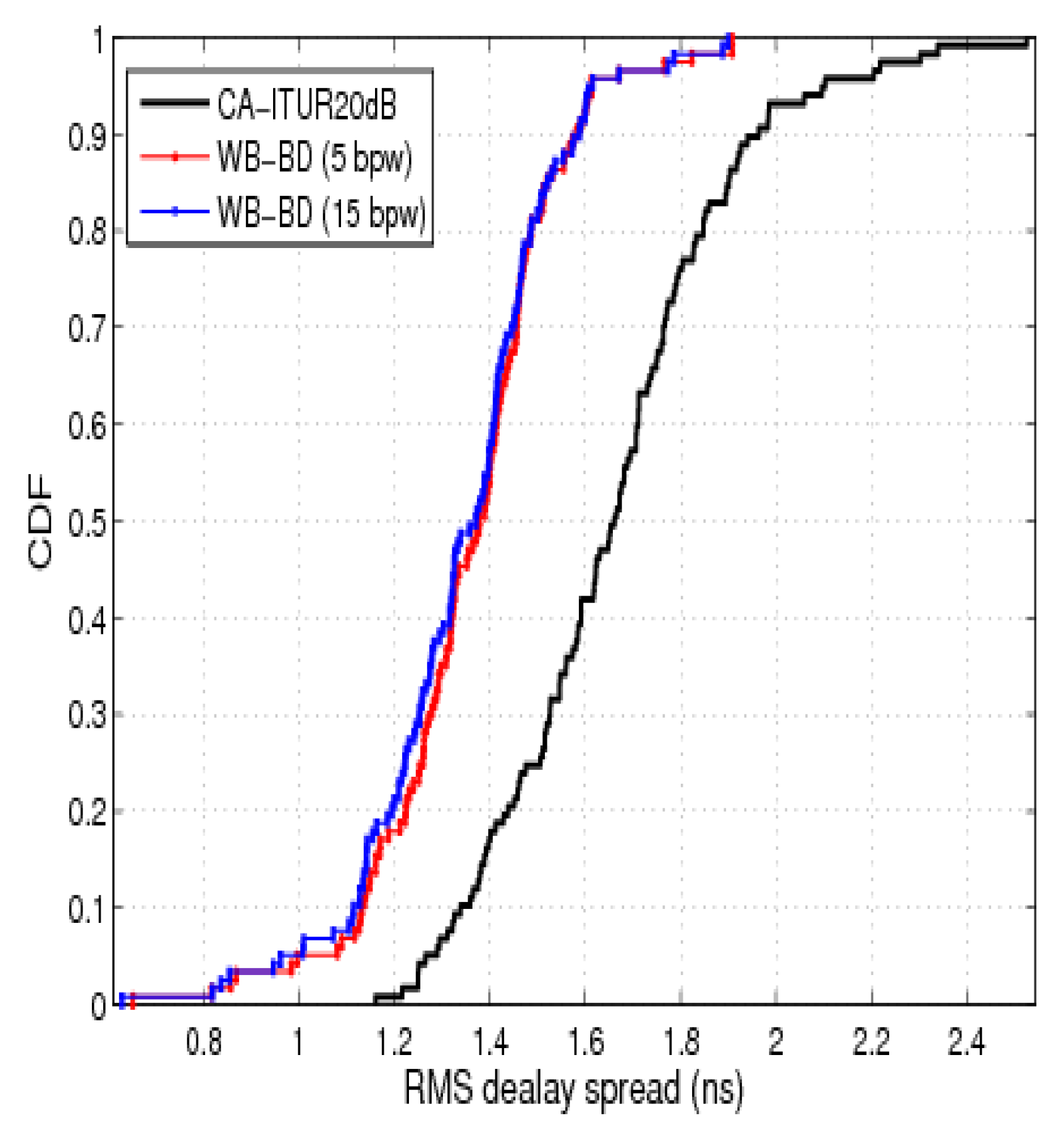
7.3. CDF of RMS Delay Spread
8. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Benedetto, M.G.D.; Kaiser, T.; Molisch, A.F.; Oppermann, I.; Politano, C.; Porcino, D. UWB Communications Systems: A Comprehensive Overview (EURASIP Book Series on Signal Processing and Communications); Hindawi Publishing Corporation: New York, NY, USA, 2006. [Google Scholar]
- Yang, L.; Giannakis, G. Ultra-wideband communications: An idea whose time has come. IEEE Signal Process. Mag. 2004, 21, 26–54. [Google Scholar] [CrossRef]
- Roy, S.; Foerster, J.; Somayazulu, V.; Leeper, D. Ultrawideband radio design: The promise of high-speed, short-range wireless connectivity. Proc. IEEE 2004, 92, 295–311. [Google Scholar] [CrossRef]
- Molisch, A. Ultrawideband propagation channels-theory, measurement, and modeling. IEEE Trans. Veh. Technol. 2005, 54, 1528–1545. [Google Scholar] [CrossRef]
- FCC Notice of Proposed Rule Making, Revision of Part 15 of the Commission’s Rules Regarding Ultra-Wideband Transmission Systems. ET-Docket; 2005; pp. 98–153. Available online: https://www.fcc.gov/document/revision-part-15-commissions-rules-regarding-ultra-wideband-transmission-systems-2 (accessed on 1 October 2018).
- Tsiropoulou, E.E.; Kapoukakis, A.; Papavassiliou, S. Uplink resource allocation in SC-FDMA wireless networks: A survey and taxonomy. Comput. Netw. 2016, 96, 1–28. [Google Scholar] [CrossRef]
- Myung, H.G.; Lim, J.; Goodman, D.J. Single carrier FDMA for uplink wireless transmission. IEEE Veh. Technol. Mag. 2006, 1, 30–38. [Google Scholar] [CrossRef]
- Tsiropoulou, E.E.; Kapoukakis, A.; Papavassiliou, S. Energy-efficient subcarrier allocation in SC-FDMA wireless networks based on multilateral model of bargaining. In Proceedings of the 2013 IFIP Networking Conference, Brooklyn, NY, USA, 22–24 May 2013; pp. 1–9. [Google Scholar]
- Myung, H.G. Introduction to single carrier FDMA. In Proceedings of the 15th European Signal Processing Conference, Poznan, Poland, 3–7 September 2007; pp. 2144–2148. [Google Scholar]
- Gustafson, C.; Haneda, K.; Wyne, S.; Tufvesson, F. On mm-Wave Multipath Clustering and Channel Modeling. IEEE Trans. Antennas Propag. 2014, 62, 1445–1455. [Google Scholar] [CrossRef]
- Sulyman, A.I.; Alwarafy, A.; Maccartney, G.; Rappaport, T.; Al-Sanie, A. Directional Radio Propagation Path Loss Models for Millimeter-Wave Wireless Networks in the 28, 60, and 73 GHz Bands. IEEE Trans. Wirel. Commun. 2016, 15, 6939–6947. [Google Scholar] [CrossRef]
- Andrews, J.; Buzzi, S.; Choi, W.; Hanly, S.; Lozano, A.; Soong, A.; Zhang, J. What Will 5G Be? IEEE J. Sel. Areas Commun. 2014, 32, 1065–1082. [Google Scholar] [CrossRef]
- Li, Y.; Jin, Z.; Wang, Y. Adaptive Channel Estimation Based on an Improved Norm-Constrained Set-Membership Normalized Least Mean Square Algorithm. Wirel. Commun. Mob. Comput. 2017, 2017, 8056126. [Google Scholar] [CrossRef]
- Molish, A.; Tufvesson, F. Propagation channel models for next-generation wireless communications systems. IEICE Trans. Commun. 2014, 97, 2022–2034. [Google Scholar] [CrossRef]
- METIS ICT-317669-METIS/D1.1, S. Scenarios, Requirements and KPIs for 5G Mobile and Wireless System. Available online: www.metis2020.com (accessed on 1 October 2018).
- Anderson, C.R.; Volos, H.I.; Buehrer, R.M. Characterization of Low-Antenna Ultrawideband Propagation in a Forest Environment. IEEE Trans. Veh. Technol. 2013, 62, 2878–2895. [Google Scholar] [CrossRef]
- Cramer, R.M.; Scholtz, R.; Win, M. Evaluation of an ultra-wide-band propagation channel. IEEE Trans. Antennas Propag. 2002, 50, 561–570. [Google Scholar] [CrossRef]
- Molisch, A.F. Ultra-Wide-Band Propagation Channels. Proc. IEEE 2009, 97, 353–371. [Google Scholar] [CrossRef]
- Athanasiadou, G.; Nix, A. A novel 3-D indoor ray-tracing propagation model: The path generator and evaluation of narrow-band and wide-band predictions. IEEE Trans. Veh. Technol. 2000, 49, 1152–1168. [Google Scholar] [CrossRef]
- Al-Samman, A.M.; Rahman, T.A.; Hadri, M.; Khan, I.; Chua, T.H. Experimental UWB Indoor Channel Characterization in Stationary and Mobility Scheme. Measurement 2017, 111, 333–339. [Google Scholar] [CrossRef]
- Al-Samman, A.M.; Rahman, T.A.; Azmi, M.H.; Hindia, M.N.; Khan, I.; Hanafi, E. Statistical Modelling and Characterization of Experimental mm-Wave Indoor Channels for Future 5G Wireless Communication Networks. PLoS ONE 2016, 11, e0163034. [Google Scholar] [CrossRef] [PubMed]
- Maccartney, G.R.; Rappaport, T.S.; Sun, S.; Deng, S. Indoor Office Wideband Millimeter-Wave Propagation Measurements and Channel Models at 28 and 73 GHz for Ultra-Dense 5G Wireless Networks. IEEE Access 2015, 3, 2388–2424. [Google Scholar] [CrossRef]
- Rappaport, T.S.; MacCartney, G.R.; Samimi, M.K.; Sun, S. Wideband Millimeter-Wave Propagation Measurements and Channel Models for Future Wireless Communication System Design. IEEE Trans. Commun. 2015, 63, 3029–3056. [Google Scholar] [CrossRef]
- Al-Samman, A.M.; Rahman, T.A.; Azmi, M.H.; Hindia, M. Large-scale path loss models and time dispersion in an outdoor line-of-sight environment for 5G wireless communications. AEU—Int. J. Electron. Commun. 2016, 70, 1515–1521. [Google Scholar] [CrossRef]
- Gupta, A.; Jha, R.K. A Survey of 5G Network: Architecture and Emerging Technologies. IEEE Access 2015, 3, 1206–1232. [Google Scholar] [CrossRef]
- Huo, Y.; Member, S.; Dong, X.; Member, S. 5G Cellular User Equipment: From Theory to Practical Hardware Design. IEEE Access 2017, 5, 13992–14010. [Google Scholar] [CrossRef]
- Duel-Hallen, A. Fading channel prediction for mobile radio adaptive transmission systems. Proc. IEEE 2007, 95, 2299–2313. [Google Scholar] [CrossRef]
- Al-Samman, A.M.; Nunoo, S.; Rahman, T.A.; Chude-Okonkwo, U.A.K.; Ngah, R. Hybrid Channel Estimation Technique with Reduced Complexity for LTE Downlink. Wirel. Pers. Commun. 2015, 82, 1147–1159. [Google Scholar] [CrossRef]
- Heo, J.; Wang, Y.P.; Chang, K.H. A novel two-step channel-prediction technique for supporting adaptive transmission in OFDM/FDD system. IEEE Trans. Veh. Technol. 2008, 57, 188–193. [Google Scholar] [CrossRef]
- Akhtman, J.; Hanzo, L. Channel Impulse Response Tap Prediction for Time-Varying Wireless Channels. IEEE Trans. Veh. Technol. 2007, 56, 2767–2769. [Google Scholar] [CrossRef]
- Malmirchegini, M.; Mostofi, Y. On the Spatial Predictability of Communication Channels. IEEE Trans. Wirel. Commun. 2012, 11, 964–978. [Google Scholar] [CrossRef]
- Jarinová, D. On autoregressive model order for long-range prediction of fast fading wireless channel. Telecommun. Syst. 2011, 52, 1533–1539. [Google Scholar] [CrossRef]
- Wang, Y.; Li, Y. Sparse Multipath Channel Estimation Using Norm Combination Constrained Set-Membership NLMS Algorithms. Wirel. Commun. Mob. Comput. 2017, 2017, 8140702. [Google Scholar] [CrossRef]
- Tsao, J.; Porrat, D.; Tse, D. Prediction and Modeling for the Time-Evolving Ultra-Wideband Channel. IEEE J. Sel. Top. Signal Process. 2007, 1, 340–356. [Google Scholar] [CrossRef]
- Tse, D. Fundamentals of Wireless Communication; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Saleh, A.; Valenzuela, R. A Statistical Model for Indoor Multipath Propagation. IEEE J. Sel. Areas Commun. 1987, 5, 128–137. [Google Scholar] [CrossRef]
- Santos, T.; Karedal, J.; Almers, P.; Tufvesson, F.; Molisch, A.F. Modeling the ultra-wideband outdoor channel: Measurements and parameter extraction method. IEEE Trans. Wirel. Commun. 2010, 9, 282–290. [Google Scholar] [CrossRef]
- Nunoo, S.; Chude-Okonkwo, U.A.K.; Ngah, R.; Al-Samman, A.; Onubogu, J. UWB channel measurement and data transfer analysis for multiuser Infostation applications. In Proceedings of the 2014 IEEE 10th International Colloquium on Signal Processing and its Applications, Kuala Lumpur, Malaysia, 7–9 March 2014. [Google Scholar] [CrossRef]
- Liu, T.K.; Kim, D.I.; Vaughan, R.G. A high-resolution, multi-template deconvolution algorithm for time-domain UWB channel characterization. Can. J. Electr. Comput. Eng. 2007, 32, 207–213. [Google Scholar] [CrossRef]
- Chandra, A.; Blumenstein, J.; Mikulasek, T.; Vychodil, J.; Pospisil, M.; Marsalek, R.; Prokes, A.; Zemen, T.; Mecklenbrauker, C. CLEAN Algorithms for Intra-vehicular Time-domain UWB Channel Sounding. In Proceedings of the 2015 International Conference on Pervasive and Embedded Computing and Communication Systems (PECCS), Angers, France, 11–13 February 2015. [Google Scholar]
- Propagation, M. Multipath Propagation and Parameterization of Its Characteristics; International Telecommunication Union: Geneva, Switzerland, 2017. [Google Scholar]
- Varela, M.; Sanchez, M. RMS delay and coherence bandwidth measurements in indoor radio channels in the UHF band. IEEE Trans. Veh. Technol. 2001, 50, 515–525. [Google Scholar] [CrossRef]
- Sayed, A.H. Adaptive Filters; John Wiley & Sons: New York, NY, USA, 2011. [Google Scholar]



| Operation | × | + | / |
|---|---|---|---|
| M | M | ||
| M | |||
| 1 | |||
| M | |||
| M | |||
| 1 | 1 | ||
| . | M | ||
| M | |||
| Total cost per iteration | 1 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
M. Al-Sammna, A.; Hadri Azmi, M.; Abd Rahman, T. Time-Varying Ultra-Wideband Channel Modeling and Prediction. Symmetry 2018, 10, 631. https://doi.org/10.3390/sym10110631
M. Al-Sammna A, Hadri Azmi M, Abd Rahman T. Time-Varying Ultra-Wideband Channel Modeling and Prediction. Symmetry. 2018; 10(11):631. https://doi.org/10.3390/sym10110631
Chicago/Turabian StyleM. Al-Sammna, Ahmed, Marwan Hadri Azmi, and Tharek Abd Rahman. 2018. "Time-Varying Ultra-Wideband Channel Modeling and Prediction" Symmetry 10, no. 11: 631. https://doi.org/10.3390/sym10110631
APA StyleM. Al-Sammna, A., Hadri Azmi, M., & Abd Rahman, T. (2018). Time-Varying Ultra-Wideband Channel Modeling and Prediction. Symmetry, 10(11), 631. https://doi.org/10.3390/sym10110631






