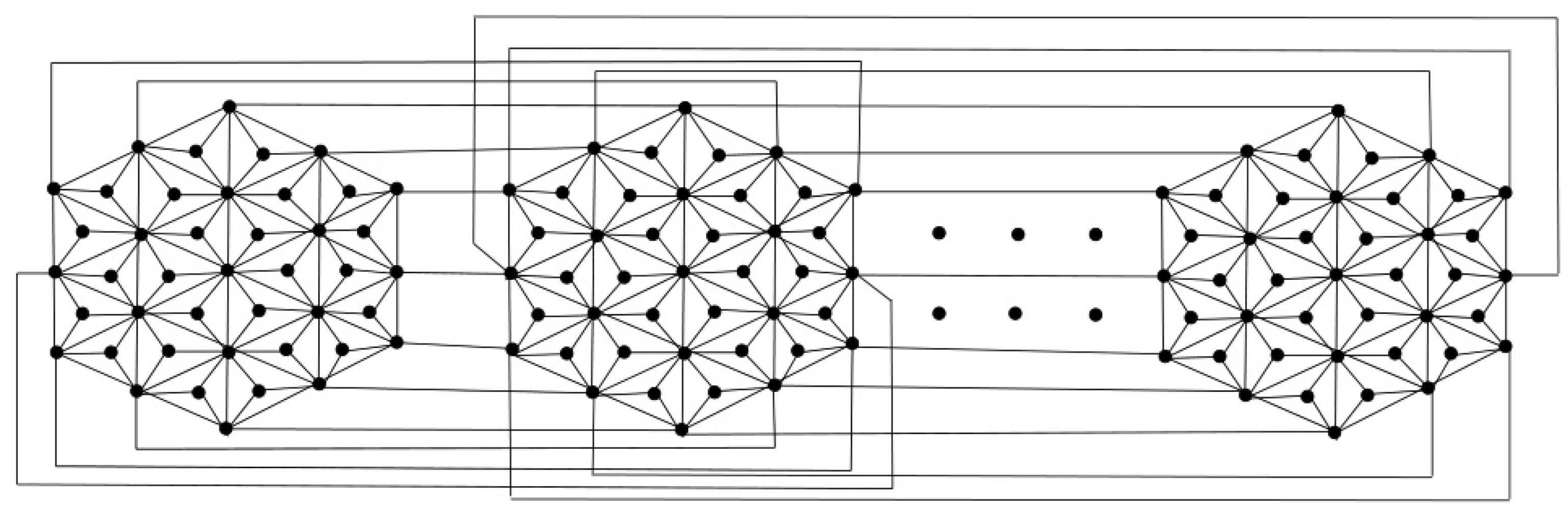
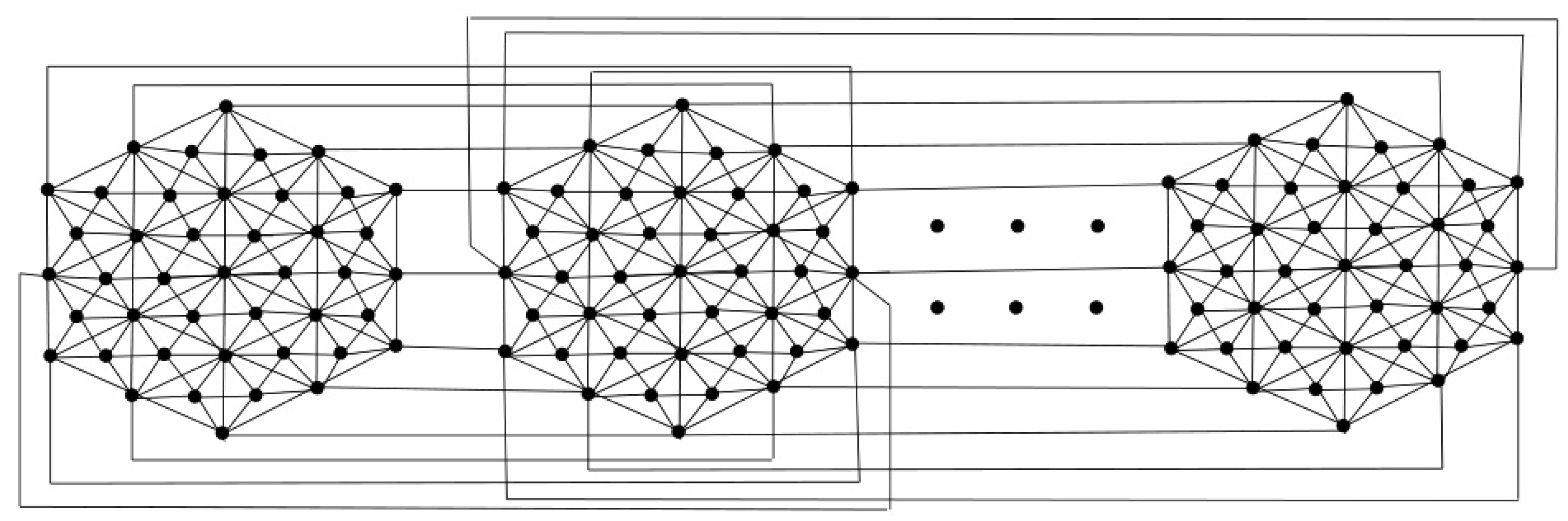
Hex-Derived Cage networks
(show in
Figure 1) and
(show in
Figure 2) give closed formulas of that indices, we study the general Randić, first Zagreb, ABC, GA,
and
indices of certain graphs in [
10]. These days there is a broad research activity on
and
indices and their variants, for additionally investigation of topological indices of different families see, [
1,
11,
12,
13,
14,
15,
16,
17,
18,
19,
20,
21,
22,
23].
2.1. Results for Hex-Derived Cage Networks
We compute specific degree-based topological indices of Hex-Derived Cage networks. In this paper, we calculate Randić index with , , ABC, GA, and for Hex-Derived Cage networks and .
Theorem 1. Let be the Hex-Derived Cage network, then its general Randić index is equal to Proof. Let
be the Hex-Derived Cage network
where
m =
n. The edge set of
are divided into seventeen partitions based on the degree of end vertices shows in
Table 1. Thus from Equation
, is follows that
For By using the edge partition given in
Table 1, we have
After simplification, we have
For Using the edge partition from
Table 1, we have
After simplification, we have
For After simplification, we have
For After simplification, we have □
In the below theorem, we calculate the Zagreb index of (m,n).
Theorem 2. The first Zagreb index of hex-derived cage network is equal to Proof. With the help of
Table 1, we calculate the Zagreb index as
After some calculations, we get
□
In the next theorem, we calculate the , , and indices of Hex-Derived Cage network .
Theorem 3. Let HDCN1(m,n) be Hex-Derived Cage network, then we have
.
.
.
Proof. From
Table 1 we calculate the
as
.
After simplification, we have .
Now we calculate
from Equation (
6) as
From
Table 1 calculate
as
.
After simplification, we have
If we consider an edge partition based on degree sum of neighbors of end vertices; then the edge set
are divided into sixtynine edge partition
shows in
Table 2.
From Equation (
7), we have
From
Table 2 we use edge partition, we get
.
After simplification, we get
Now we find
as
Using the edge partition from
Table 2, we get
.
After simplification, we get
□
2.2. Results for Hex-Derived Cage Network (HDCN2(m,n))
In this portion, we find some degree-based topological indices for Hex-Derived Cage network . We calculate the general Randić index with , , , and in the the below theorems for .
Theorem 4. Let be the Hex-Derived Cage network, then its general index is equal to Proof. Let
be the Hex-Derived Cage network
where
. The edge set of
is divided into twenty partitions based on the degree of end vertices.
Table 3 shows these edge partition of
.
For Using the edge partition from
Table 3, we get
After simplification, we get
For Using edge partition from
Table 3, we get
After simplification, we get
For After simplification, we get
For After simplification, we get
□
In this theorem, we find the first Zagreb index for hex-derived cage network .
Theorem 5. For Hex-Derived Cage Network (), the first Zagreb index is equal to Proof. Let
be the Hex-Derived Cage Network (
). Using the edge partition from
Table 3, we have
.
After simplification, we get
□
In below theorem, we calculate the , , and indices of Hex-Derived Cage Network .
Theorem 6. Let be the Hex-Derived Cage Network for every positive integer ; then we have
.
.
.
Proof. Using the edge partition from
Table 3, we find
as
.
After simplification, we get
Using the edge partition from
Table 3, we find
as
.
After simplification, we get
.
If we suppose an edge partition based on degree sum of neighbors of end vertices, then the edge set
can be divided into seventy six edge partition
,
.
Table 4 shows these edge partitions.
From Equation (
7), we get
Using the edge partition from
Table 3, we get
.
After simplification, we have
From Equation (
8), we get
Using the edge partition from
Table 4, we get
.
After simplification, we get
. □
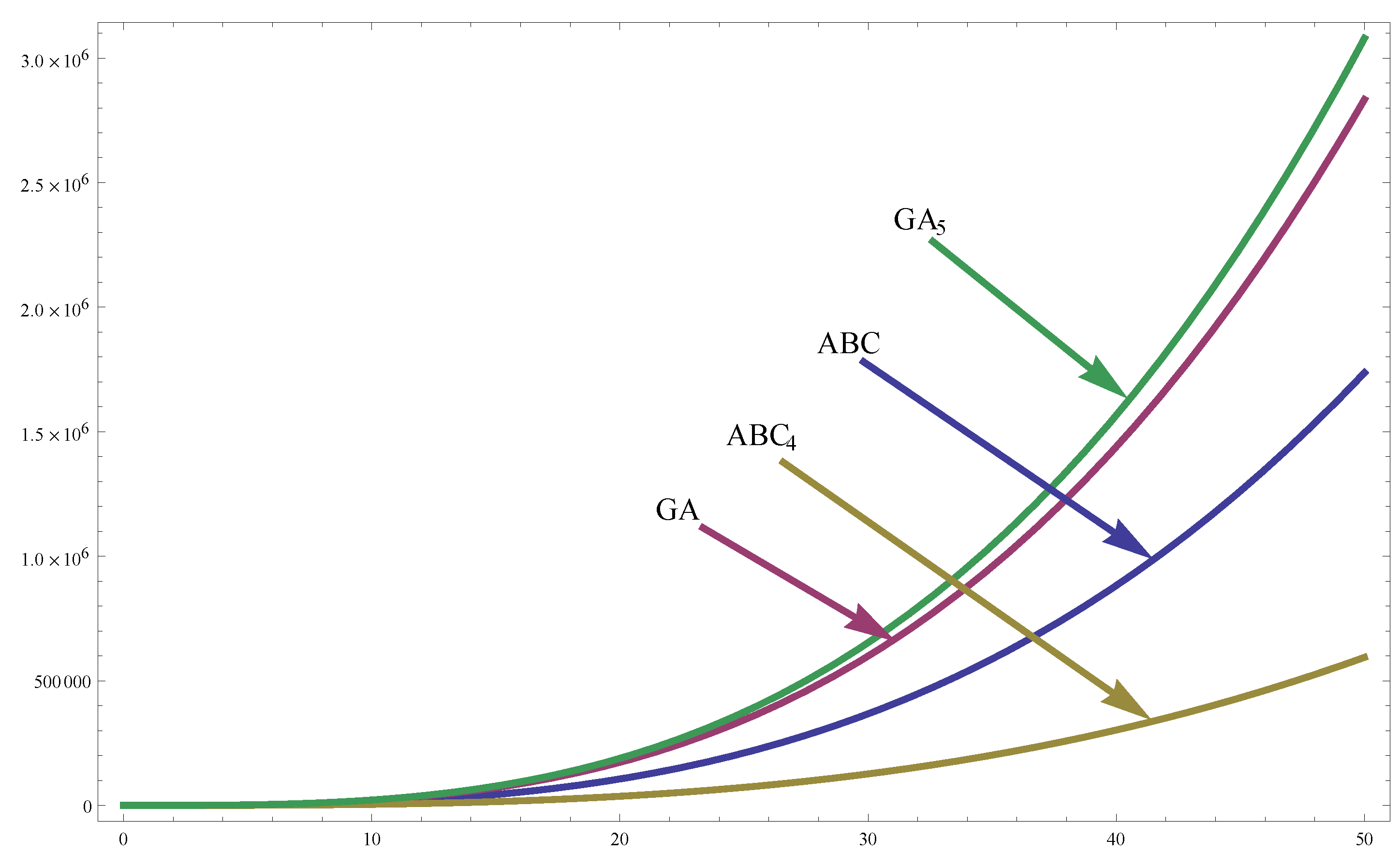
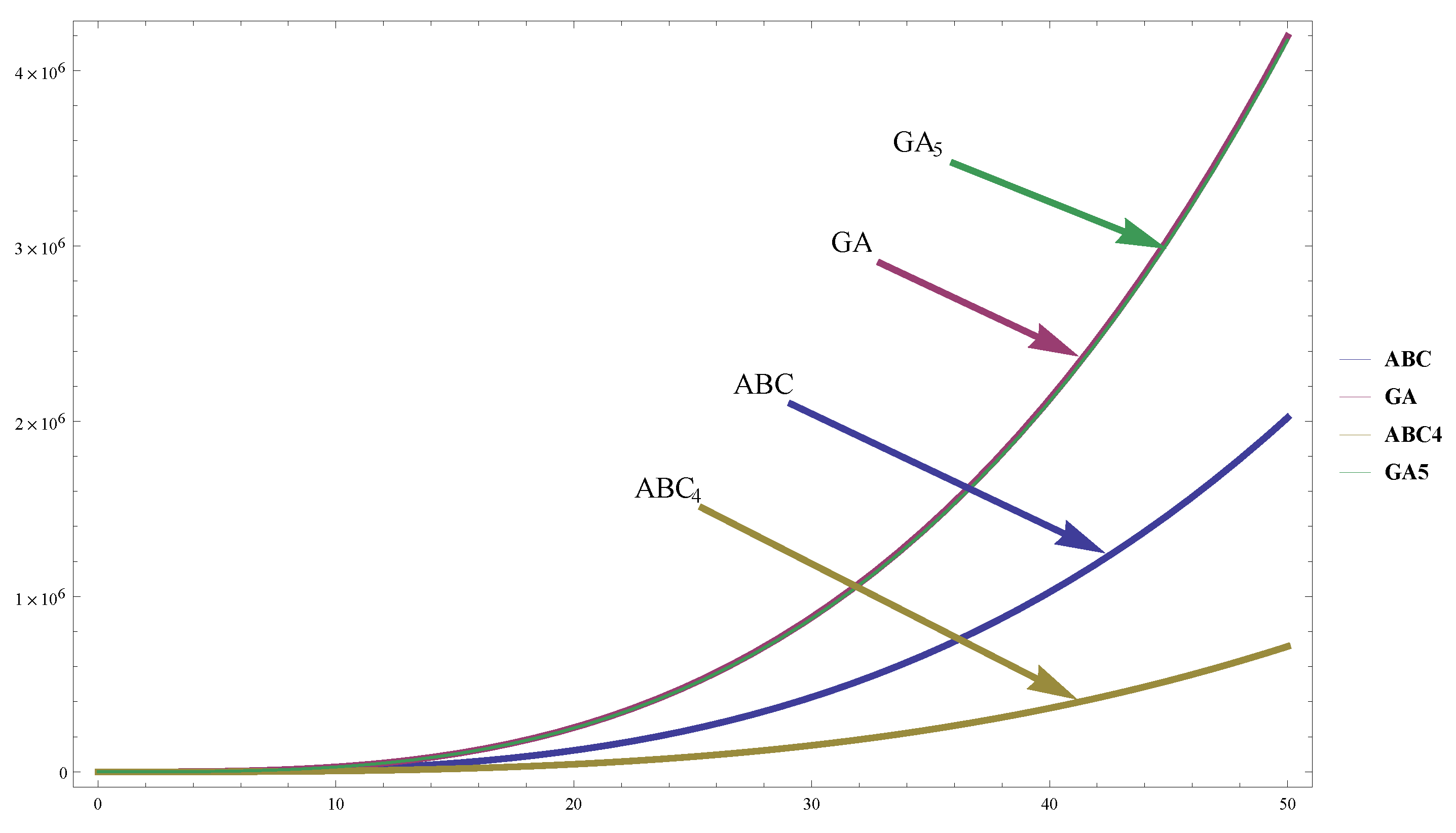
The Comparison graphs for ABC, GA,
and
in case of a Hex Derived Cage networks
and
of dimension
m and
n are shown in
Figure 3 and
Figure 4 respectively.