A Fuzzy Classifier with Feature Selection Based on the Gravitational Search Algorithm

Abstract

This paper concerns several important topics of the Symmetry journal, namely, pattern recognition, computer-aided design, diversity and similarity. We also take advantage of the symmetric and asymmetric structure of a transfer function, which is responsible to map a continuous search space to a binary search space. A new method for design of a fuzzy-rule-based classifier using metaheuristics called Gravitational Search Algorithm (GSA) is discussed. The paper identifies three basic stages of the classifier construction: feature selection, creating of a fuzzy rule base and optimization of the antecedent parameters of rules. At the first stage, several feature subsets are obtained by using the wrapper scheme on the basis of the binary GSA. Creating fuzzy rules is a serious challenge in designing the fuzzy-rule-based classifier in the presence of high-dimensional data. The classifier structure is formed by the rule base generation algorithm by using minimum and maximum feature values. The optimal fuzzy-rule-based parameters are extracted from the training data using the continuous GSA. The classifier performance is tested on real-world KEEL (Knowledge Extraction based on Evolutionary Learning) datasets. The results demonstrate that highly accurate classifiers could be constructed with relatively few fuzzy rules and features.

1. Introduction

Data classification is one of the most productive fields of study within the scope of data mining and machine learning. Classification can be applied to scientific and industrial data, handwritten text and multimedia content, biomedical data and social network data. Such a broad scope is due to the fact that the aim of classification is to identify the interrelation among the set of pre-defined input variables (features) and the desired output variable (class label). Some of the most common data classification methods are decision trees, rule-based methods, probabilistic methods, support vector machines and neural networks [1].

Fuzzy classifiers, which are rule-based classifiers, offer a significant advantage both in terms of their functionality and in terms of subsequent analysis and design. A unique advantage of fuzzy classifiers is associated with the interpretability of classification rules. The key measure of efficiency is classification accuracy that is frequently used in comparative analysis of fuzzy classifiers versus classifiers based on other principles [2,3].

Design of any classifier is based on the assumption that the class labels for each instance in the training dataset are known. Class labels in a test dataset are predicted using a classifier designed with a training set. The relation of accurately classified instances to the overall test data is indicative of classification accuracy. However, the large number of features found in datasets results in an increased calculation time and decreased accuracy of prediction. Selection of features makes it possible to reduce the dimensions of the feature input space by identifying and eliminating noise and irrelevant features [4].

The process of fuzzy classifier design includes the following principal stages: feature selection, structure formation (rule base), optimization of fuzzy rule parameters. Feature selection methods are conventionally grouped into two categories: filters and wrappers [5], the difference between the two being whether or not a classifier is designed during feature selection. The structure of the classifier is most often formed with the use of clustering methods designed to identify the data structure and build information granules that may be related to linguistic terms [2]. Parameters of fuzzy rules can be optimized using conventional approaches based on calculation of derivatives or with the help of metaheuristics methods [6].

No Free Lunch Theorem [7,8] tells us that there are no context- or problem-independent reasons to favour one learning or classification method over another. The performance of all the metaheuristics is by and large problem-dependent. The superiority of a classification method depends on dataset properties. If a classifier generalizes better to a certain data set, then it is a result of its better match for a specific problem rather than its supremacy over other classifiers [9].

A swarm optimization algorithm from the physical field was introduced in [10]. An algorithm was called Gravitational Search Algorithm (GSA). Its agents represent particles that have masses with different sizes that follow the Newtonian gravity law. GSA was compared with some known metaheuristic search methods.

To solve different kinds of optimization problems, modified versions of GSA have been introduced, including continuous, binary-valued, discrete, multimodal and multi-objective versions of GSA. The efficiency of GSA has been improved using enhanced operators, hybridization of GSA with other metaheuristic algorithms, designing the adaptive algorithms and intelligent techniques [11]. An adaptive GSA that switches between synchronous and asynchronous update is presented in Reference [12]. The proposed algorithm combines both synchronous and asynchronous updates. The integration of these iterative strategies changes the behaviour of the particles. In Reference [13] the authors propose a fuzzy gravitational search algorithm for the design of optimal 8th order IIR filters. The proposed algorithm is a combination between fuzzy techniques and gravitational search. Two Mamdani inference systems tune parameters of GSA, finding a good trade-off between exploration and exploitation of the search process. In Reference [14], to find trade-off between exploration and exploitation, it was proposed to use an approach, which combines neural network and fuzzy system for the tuning of GSA parameters. In Reference [15] the authors propose to tune a suitable parameter of GSA through a fuzzy controller whose membership functions are optimized by Genetic Algorithms, Particle Swarm Optimization and Differential Evolution.

The results which were obtained confirmed the high performance of the proposed method in solving various nonlinear functions. It has been demonstrated that the Gravitational Search Algorithm has the ability to find the optimum solution for many benchmarks [10,12,16,17,18,19]. For this reason, this algorithm was chosen to solve the problem of designing a fuzzy-rule-based classifier.

This paper aims at developing the fuzzy-rule-based classifier using Gravitational Search Algorithm.

The main contributions of this work are the following:

• A new technique for generating a fuzzy-rule-based classifier.
• A method that selects a compact and efficient subset of features.
• A new method of tuning fuzzy-rule-based classifier parameters.
• A statistical comparison among the results achieved by the fuzzy-rule-based classifiers generated by our technique and by two state-of-the-art learning algorithms.

2. Related Work

This section gives a brief overview of work in two related research fields, namely fuzzy classifier design using metaheuristics and approaches to feature selection for classification.

2.1. Fuzzy Classifier Design Using Metaheuristics

Several approaches using metaheuristics related to fuzzy classifier design can be found in the literature. Kumar and Devaraj [20] propose a modified genetic algorithm approach to obtain the optimal set of rules and a membership function for a fuzzy classifier. A modified form of representation is used to encode the rule base and membership functions. In the proposed approach, genetic operators were also modified to improve convergence and solution quality.

Chang and Lilly [21] propose to construct a fuzzy classifier directly from the data, without using a priori knowledge or assumptions about the distribution of data. Membership functions and fuzzy rules are created automatically and optimized during execution.

Olivas et al. [22] propose to design fuzzy classifiers using methods such as simple particle swarm optimization and methods with dynamically adapted parameters. Dynamical adjustment of the optimization method parameters can improve the quality of results and increase the diversity of solutions to a problem. Chen et al. [23] proposes an alternative approach using Particle Swarm Optimisation (PSO) in the search of a set of optimal rule weights, entailing high classification accuracy. This approach works for situations where an initial fuzzy rule-base has been built with predefined fuzzy sets, which must be maintained for the purpose of consistent interpretability, both in the learned models and in the inference results using such models. In Reference [24], the application of chaotic particle swarm optimization to fuzzy system parameter estimation is presented. Unlike traditional PSO, chaotic PSO uses chaotic coordinate transformations to improve the search capabilities of particles. Various mapping functions have been investigated to generate sequences of chaotic transformations.

Pulkkinen and Koivisto [25] use hybridization methods to find a compromise between accuracy and interpretability in the construction of fuzzy classifiers.

In order to solve the problem of high dimensional classification in linguistic fuzzy-rule-based classification systems Aydogan et al. [26] propose a hybrid heuristic approach based on a genetic algorithm and integer-programming formulation. In this algorithm, each chromosome represents a rule for the specified class, whereupon a genetic algorithm is used for producing several rules for each class, whilst an integer-programming formulation is utilized for selecting the rules from within a pool of rules obtained via the genetic algorithm.

In Reference [27], the construction of fuzzy classifiers using the algorithm of the classifier structure generation and 14 differential evolution algorithms are presented. The algorithm of structure generation is aimed at obtaining a compact classifier (the compactness depends on the number of rules). The differential evolution algorithms optimize the parameters to obtain an accurate classifier.

Alcala-Fdez et al. [28] propose a fuzzy association rule-based classification method for high-dimensional problems (FARC-HD). The method is based upon three stages in order to obtain an accurate and compact fuzzy-rule-based classifier whilst keeping computational costs low. This method is based on an improved weighted relative accuracy measure, which preselects the most interesting rules prior to a genetic post processing procedure for rule selection and parameter tuning.

In Reference [29], the authors present a multi-objective evolutionary method, which performs two processes in concurrence: a process of tuning as well as a rule-selection process performed upon an initial knowledge base of fuzzy-rule-based classifiers. A fuzzy discretization algorithm was designed in order to extract suitable granularities from data and also to generate fuzzy partitions that constitute the initial database. To generate an associative knowledge base, the FARC-HD methods described in Reference [28] were used.

2.2. Feature Selection

Feature selection is a procedure where such a subset of features is isolated from the initial set that entirely satisfies the current task or the training objective. The goals of feature selection are to: (1) avoid overtraining, (2) reduce the volume of data for analysis, (3) enhance classification efficiency, (4) eliminate irrelevant and noise features, (5) improve interpretability of the result [30].

Feature selection methods can be grouped into two categories: filter and wrapper [5,31,32]. Filter methods are based on certain metrics, such as entropy, probability distribution, or mutual information [33] and do not use a classifying algorithm during the process. Wrapper methods use the classifier to evaluate the feature subset and the classifier itself is “wrapped” in the feature selection cycle. Both filter and wrapper methods have their strengths and weaknesses. The advantage of the filter-based methods lies in their higher scalability and speed of execution. Its general disadvantage is that the lack of interaction with the classifier and disregard of the relationship between features result in a lower classification accuracy that varies for different classifiers. The advantage of the wrapper methods is that they work together with the specific classification algorithm and account for the synergy of the joint usage of selected features. The disadvantages of the wrapper methods are the higher risk of overtraining and long time required to calculate classification accuracy [34].

Let us consider the use of metaheuristics for the problem of feature selection. Yusta [35] considers three metaheuristic strategies to address the problem of feature selection—GRASP, Tabu Search and Memetic Algorithm. These three strategies are compared to a genetic algorithm, which is a metaheuristic strategy that is most often used to address this problem [36] and to other typical feature selection methods examples of which include Sequential Forward Floating Selection and Sequential Backward Floating Selection. The results demonstrate that in general GRASP and Tabu Search attain markedly better results than the other methods.

Aladeemy et al. [37] propose a variation of the cohort intelligence algorithm for feature selection. The efficiency of the proposed algorithm was compared to the well-known metaheuristics: Genetic Algorithm, Particle Swarm Optimization, Differential Evolution and Artificial Bee Colony. A comparative analysis shows that the proposed algorithm offers classification accuracy and a number of features selected that are comparable to the results obtained by the above algorithms.

Hodashinsky and Mekh [38] propose feature selection based on harmony search. Several feature subsets on the basis of discrete harmonic search are generated by using the wrapper scheme. The Akaike information criterion is deployed to identify the best performing classifiers. Experimental results show efficiency of the proposed approach and demonstrate that highly accurate classifiers can be constructed by using relatively few features.

Vieira et al. [39] propose an ant colony optimization algorithm for the feature selection problem and compare it with tree search methods for feature selection. To construct a fuzzy classifier of the Takagi–Sugeno type, all the above algorithms were used.

Gurav et al. [40] propose a hybrid filter-wrapper algorithm, named GSO-Infogain, for simultaneous feature selection, which improves the accuracy of classification. GSO-Infogain employs the Glowworm-Swarm Optimization (GSO) algorithm with the Support Vector Machine as its internal learning algorithm and utilizes feature ranking based on information gain as a heuristic. GSO-Infogain also performs well in this experiment. It gives similar prediction accuracies on the training and test datasets. This is a good indicator of its robustness.

Marinaki et al. [41] propose using the Honey Bees Mating Optimization algorithm for at the feature selection stage and the Nearest Neighbour based classifiers at the classification stage. The proposed method is tested in a financial classification task.

3. Materials and Methods

A fuzzy classifier is designed in three stages: feature selection, generation of a fuzzy-rule base and optimization of the antecedent parameters of rules. Features are selected with the Binary Gravitational Search Algorithm. The classifier structure is formed by the rule base generation algorithm, using extreme feature values. In the proposed learning method, the related parameters of the proposed classifier are tuned by using the continuous GSA. The performance of the classifier is tested on real-world KEEL datasets. At the final stage, classifiers designed with the proposed method are compared to similar classifiers using the Mann-Whitney-Wilcoxon test as the criterion.

3.1. Fuzzy Classifier

Classification consists in finding such a class label in a set of class labels that would correspond to the vector of the object’s feature values [38]. In universe U = (A, C), where A = {$x_1$,$x_2$, …, $x_n$} is a set of input features, C = {$c_1$, $c_2$, …, $c_m$} is a set of class labels, the object is characterized by its vector of feature values. Let x = ${\mathrm{x}}_1$ × ${\mathrm{x}}_2$ × … × ${\mathrm{x}}_n$ ∈ ℜⁿ be an n-dimensional feature space.

A fuzzy classifier can be represented as a function that assigns a class label to a point x in the input feature space with a calculable degree of confidence:

$$f:{\mathsf{\Re }}^n\to {[0,g]}^m.$$

(1)

The fuzzy classifier is based on a production rule base that appears as follows:

$$R_j:\mathrm{IF}{s}_1˄x_1=A_{1j}\mathrm{AND}{s}_2˄x_2=A{}_{2j}\mathrm{AND}\dots \mathrm{AND}{s}_n˄x_n=A_{\mathit{nj}}\mathrm{THEN}\mathrm{class}=c_j,j=1,\dots ,R,$$

where j is the rule index; R is the number of rules; A_kj is a fuzzy term that characterizes the k-th feature in the j-th rule (k = 1, …, n); $c_j$ is the consequent class; S = ($s_1$, $s_2$, …, $s_n$) is the binary vector of features: line $s_1˄x_k$ indicates presence ($s_k$ = 1) or absence ($s_k$ = 0) of a feature in the classifier.

The class label is defined in the observation table {($x_p$; $c_p$), $p=\overline{1,z}$} as follows:

$$\begin{array}{l}\mathrm{class}=c_t,t=\arg \underset{1\le j\le m}{\max }\{{\beta }_j\}\\ {\mu }_j(x_p)={\mu }_{A_{j1}}(x_{p1})\dots {\mu }_{A_{jn}}(x_{pn})={\displaystyle \prod _{k=1}^n{\mu }_{A_{jk}}(x_{pk})}\\ {\beta }_t(x_p)={\displaystyle \sum _{\begin{array}{l}{R}_j\\ C_j=\mathrm{class}t\end{array}}{\mu }_j(x_p)}={\displaystyle \sum _{\begin{array}{l}{R}_j\\ C_j=\mathrm{class}t\end{array}}{\displaystyle \prod _{k=1}^n{\mu }_{A_{jk}}(x_{pk})}}\end{array}$$

(2)

where ${\mu }_{A_{jk}}(x_{pk})$ is the membership function value of fuzzy term A_jk at point $x_{pk}$.

3.2. Performance Measures

The classification accuracy measure is defined as a ratio between accurately determined class labels and the number of objects:

$$E(\mathsf{\theta },S)=\frac{{\displaystyle \sum _{p=1}^z\{\begin{array}{l}1,\mathrm{IF}{c}_p=\arg \underset{1\le j\le m}{\max }{f}_j\left({\mathbf{x}}_p;\mathsf{\theta },\mathbf{S}\right)\\ 0,\mathrm{OTHERWISE}\end{array}}}{z},$$

(3)

where f($x_p$; θ, S) is the fuzzy classifier output with parameters of fuzzy terms θ and features S at point $x_p$.

The problem of fuzzy classifier design is confined to finding the maximum of the function in space S and θ = (θ¹, θ², …, θ^D):

$$\{\begin{array}{l}E\left(\mathsf{\theta },S\right)\to \max \\ {\theta }_{\min }^i\le {\theta }^i\le {\theta }_{\max }^i,i=\overline{1,D}\\ s_j\in \{0,1\},j=\overline{1,n}\end{array},$$

(4)

where θⁱ_min, θⁱ_max are the upper and lower boundaries of the domain of each parameter, correspondingly. This problem is NP-hard; in this paper, we propose to solve it by splitting it into two tasks: feature selection and tuning fuzzy term parameters.

3.3. Binary Gravitational Search Algorithm

The feature selection problem consists in searching for such a subset of the predetermined set of features x that would not cause a decrease in classification accuracy as the number of features is reduced; the solution is represented as a binary vector S = ($s_1$, $s_2$, …, $s_n$)^T, where $s_i$= 0 means that the i-th feature does not participate in classification, $s_i$ = 1 means that the i-th feature is used by the classifier. This problem can be solved with the Binary Gravitational Search Algorithm.

The idea of gravitational search is that the input vector population is presented as a system of elementary particles with gravity forces acting between them [10]. The higher the accuracy of a vector-based classifier, the higher the mass of a particle corresponding to that vector and the stronger it attracts other particles. But since the particle is affected by gravity forces as well, it will be moving while searching in its local domain.

The binary version of the algorithm is used to find the binary vector of features S_best that makes it possible to achieve the highest level of classification accuracy.

The input data for gravitational search is the following: vectors of system parameters θ, number of vectors P, maximum number of iterations T, initial value of gravitational constant G₀, coefficients α and small constant ε. The initial population S = {S₁, S₂, …, S_P} is randomly generated. Before the start, a classifier is built based on each vector and fitness function is evaluated:

$$fi{t}_i=E(S_i,\mathsf{\theta }).$$

(5)

The mass, acceleration, velocity and movement of particles are measured at each iteration of the algorithm. The mass of the i-th particle is calculated with due regard to classification accuracy:

$$m_i(t)=\frac{(1-fi{t}_i(t)-worst(t))}{(best(t)-worst(t))},$$

(6)

where m is the mass of the particle, t is the iteration number, best(t) and worst(t) are the values of fitness function of the least and the most accurate vectors at the current iteration, correspondingly.

According to Newton’s second law, the total force acting on a particle imparts acceleration to it:

$$a_i^d[t]={\displaystyle \sum _{j=1,j\ne i}^{P}rand(0;1)\cdot G[t]\cdot \frac{M_j[t]\cdot (S_j^d[t]-S_i^d[t])}{(\Vert {\mathbf{S}}_j[t]-{\mathbf{S}}_i[t]\Vert +\epsilon )}},$$

(7)

where $d=\overline{1,\left|S_i\right|}$ is the ordinal number of the vector element; rand(0; 1) is a random number within the interval [0; 1];

$$M_j(t)=m_j(t)/{\displaystyle {\sum }_{k=1}^P{m}_k}(t)$$

(8)

is the normalized mass value of the j-th particle; $i=\overline{1,P}$;

$$G(t)=G_0\cdot {(t/T)}^{\alpha }$$

(9)

is the value of the gravitational constant. The denominator uses the distance and not the distance squared, which, as the authors of the algorithm [10] believe, makes it possible to achieve better results.

The particle velocity is determined as follows:

$$V_i^d(t+1)=rand(0;1)\cdot V_i^d(t)+a_i^d(t).$$

(10)

Then each particle is updated with the help of the transfer function; a detailed description of the functions is given in Section 3.4 of this paper. An iteration of the algorithm is deemed to have ended after the vectors are updated and the value of the population classification accuracy is calculated. When the population counter reaches value T, the algorithm stops and feeds the vector with the highest accuracy value S_best to the output.

3.4. The Transfer Functions

In the Binary Gravitational Search Algorithm, the velocity gained by the vector element shows how much the element needs to change to reach the best solution available in the population. If the velocity is high, it can be assumed that the element is far removed from the best solution element and the mass of the particle is rather low. Therefore, the element must be replaced with an inverse element or excluded from the vector by assigning a zero to it. Thus, the vector is updated with a certain probability that is calculated based on velocity [42] with the help of the transfer function, which is responsible to map a continuous search space to a discrete search space [43]. The study used four such functions.

The first function S1 belongs to the class of S-shaped asymmetric functions and represents the probability of 0:

$$\{\begin{array}{c}\mathrm{IF}(rand(0;1)<\frac{1}{1+e^{-V_i^d(t+1)}}),\mathrm{THEN}{S}_i^d(t+1)=0\\ \mathrm{OTHERWISE}{S}_i^d(t+1)=1\end{array}.$$

(11)

The second function S2 makes use of an additional coefficient:

$$\{\begin{array}{c}\mathrm{IF}\left(rand(0;1)<\frac{1}{1+e^{-\mathsf{\beta }\cdot V_i^d(t+1)}}\right),\mathrm{THEN}{S}_i^d(t+1)=0\\ \mathrm{OTHERWISE}{S}_i^d(t+1)=1\end{array},$$

(12)

where $\beta =\frac{T-t}{T}.$

The third function V1 belongs to the class of V-shaped symmetric functions:

$$\{\begin{array}{c}\mathrm{IF}\left(rand(0;1)<\left|\frac{2}{\mathsf{\pi }}\arctan \left(\frac{\mathsf{\pi }}{2}{V}_i^d(t+1)\right)\right|\right),\mathrm{THEN}{S}_i^d(t+1)=0\\ \mathrm{OTHERWISE}{S}_i^d(t+1)=1\end{array}.$$

(13)

The last function used, V2, is also a V-shaped function that represents the probability that the vector element value will change to the opposite:

$$\{\begin{array}{c}\mathrm{IF}\left(rand(0;1)<\left|\frac{2}{\mathsf{\pi }}\arctan \left(\frac{\mathsf{\pi }}{2}{V}_i^d(t+1)\right)\right|\right),\mathrm{THEN}p=1\\ \mathrm{OTHERWISE}p=0\\ S_i^d(t+1)=S_i^d(t)\oplus p\end{array},$$

(14)

where ⨁ means the logical OR operator.

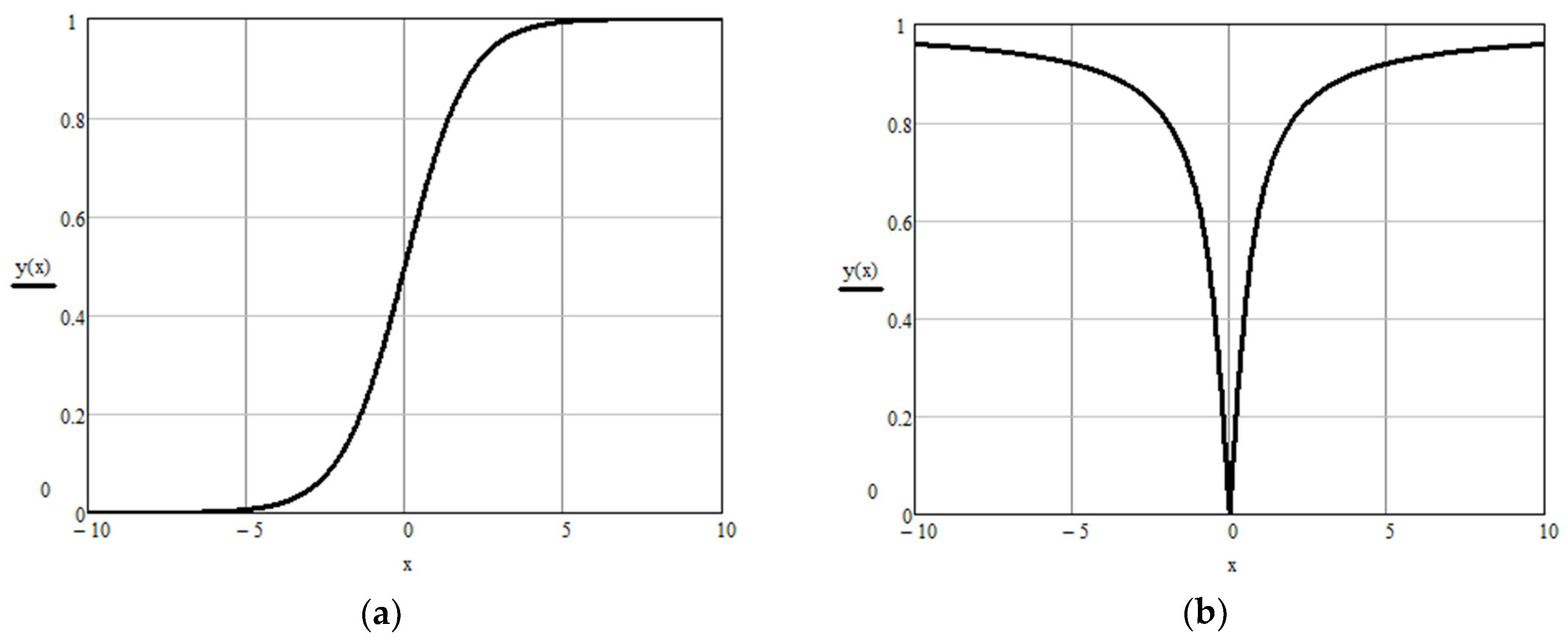
Figure 1 shows typical graphs produced by the functions used, where the S-shaped function is defined as follows:

$$Y=\frac{1}{1+e^{-x}},$$

(15)

V-shaped function:

$$Y=\left|\frac{2}{\pi }\arctan \left(\frac{\pi x}{2}\right)\right|.$$

(16)

Velocity that is used to calculate the value of the transfer function is a numerical value. One disadvantage of S-shaped transfer functions for the Binary Gravitational Algorithm is that the particle elements that have gained a high negative velocity will with a high probability remain in the vector. V-shaped functions are symmetrical with respect to the axis of ordinates and therefore are free of that disadvantage.

A pseudo code of the Binary Gravitational Search Algorithm is shown in Algorithm 1.

Algorithm 1. Binary Gravitational Search Algorithm.

Input: θ, P, T, G0, α, ε.

Output: Sbest.

begin

Initialize the population S = {S1, S2, …, SP};

while (t < T)

$\mathrm{estimate}\mathrm{the}\mathrm{fitness}\mathrm{function}fi{t}_i$ by Equation (5) for i = 1, 2, ..., P;

find best(t) and worst(t);

update G(t) by Equation (9);

$\mathrm{calculate}\mathrm{the}\mathrm{mass}{M}_i$$\left(t\right)\mathrm{by}\mathrm{Equation}\left(6\right),\mathrm{acceleration}{a}_i$$\left(t\right)\mathrm{by}\mathrm{Equation}\left(7\right)\mathrm{and}\mathrm{velocity}{V}_i$(t) by Equation (10) for i = 1, 2, ..., P;

update the position of particles with one of the Equations (11)–(14);

end while

output the particle with the best fitness value Sbest;

end

3.5. Algorithm for Generating Rule Base by Extreme Feature Values

The algorithm is designed to form an initial base of rules of a fuzzy classifier containing one rule for each class. The rules are formed based on extreme values of the training sample Tr = {(x_p; $t_p$), p = 1 ,..., |Tr|}. Let us introduce the following notation: m is the number of classes, n is the number of features, Ω* is the classifier rule base. A pseudo code of the generating algorithm is demonstrated in Algorithm 2.

Algorithm 2. Algorithm for generating rule base by extreme feature values.

Input: m, n, Tr.

Output: classifier rule base Ω*.

begin

Ω:= ∅;

do loop j from 1 till m

do loop k from 1 till n

$\mathrm{search}\min clas{s}_{jk}:=\underset{p}{\min }(x_{pk})$;

$\mathrm{search}\max clas{s}_{jk}:=\underset{p}{\max }(x_{pk})$;

$\mathrm{formation}\mathrm{of}\mathrm{fuzzy}\mathrm{term}{A}_{\mathrm{jk}},\mathrm{covering}\mathrm{the}\mathrm{interval}[\min clas{s}_{jk}$$,\max clas{s}_{jk}$];

end of loop

creation of rule R1j on the basis of terms Ajk that refers observation to the class

$\mathrm{with}\mathrm{identifier}{c}_j$;

Ω*:= Ω ∪ {R1j}

end of loop

output Ω*.

end

3.6. Continuous Gravitational Search Algorithm

Fuzzy term parameters obtained during the classifier structure generation will not always ensure that the classification is efficient. In order to improve its accuracy, the parameters must be adjusted. This can be achieved by optimizing the vector of fuzzy terms parameters θ using continuous gravitational search.

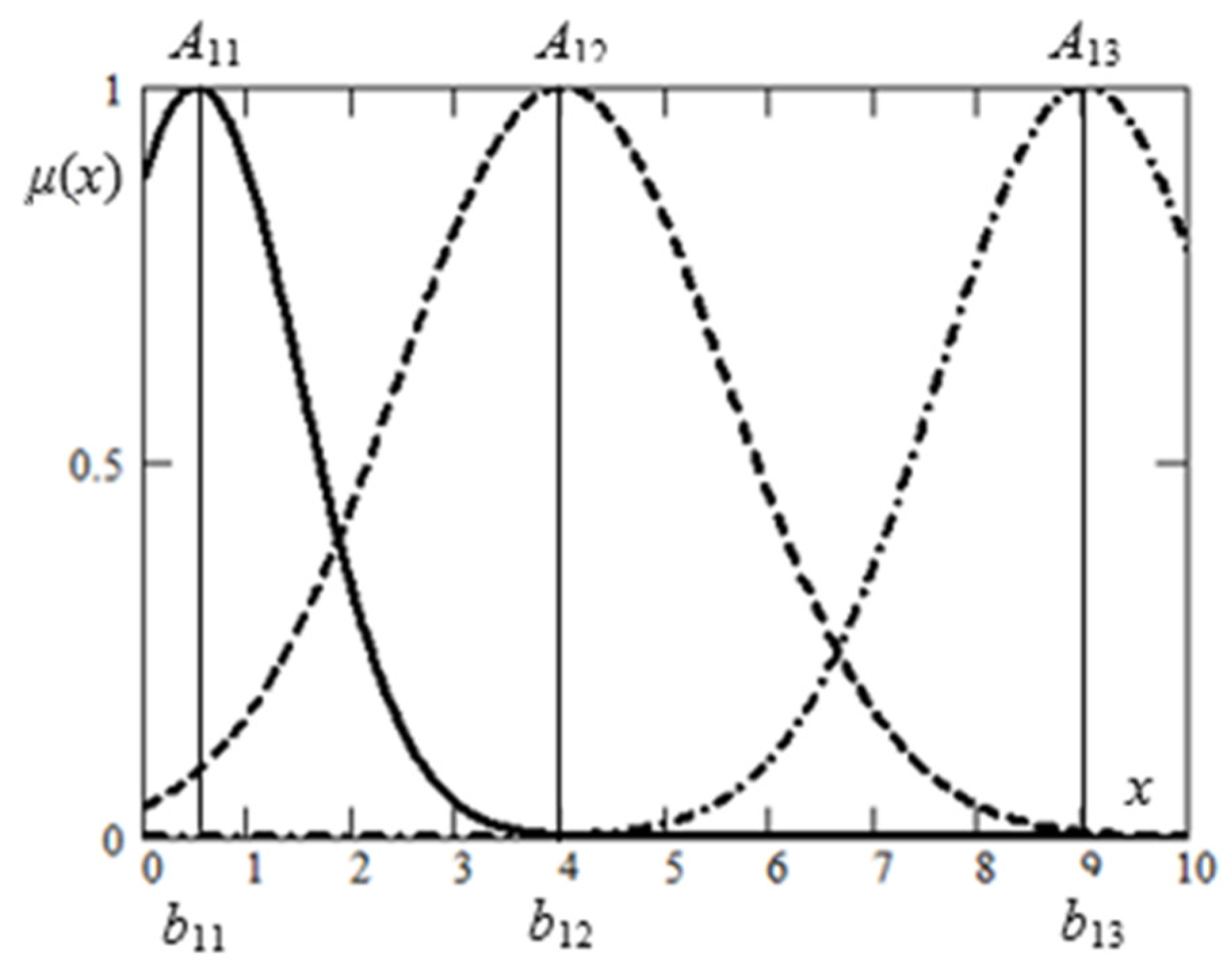
Figure 2 shows an example demonstrating the formation of vector θ. Feature a here is represented by three symmetric Gaussian terms, each of them determined by two parameters (b—the coordinate of the peak on the abscissa, c—scatter) included in vector θ = ($b_{11}$, $c_{11}$, $b_{12}$, $c_{12}$, $b_{13}$, $c_{13}$, $b_{21}$, $c_{21}$, …). The use of symmetric membership functions is preferable because of their better interpretability.

Dimensions of the vector θ are determined by the number of input features used in classification and by the number and type of terms describing each feature. For some datasets, asymmetrical types of terms, such as triangular membership functions, can be a better choice.

Population Θ = {θ₁, θ₂, …, θ_P} for the Continuous Gravitational Search Algorithm is created by copying the input vector θ₁, generated by the classifier structure generation algorithm, with normal deviation. The input data for the algorithm is: vector of features S, number of term parameter vectors P, maximum number of iterations T, initial value of gravitational constant G₀, coefficients α and small constant ε. Before the start, a classifier is built based on each vector and classification accuracy is evaluated:

$$fi{t}_i=E(S,{\mathsf{\theta }}_i).$$

(17)

The mass, acceleration, velocity and movement of particles are measured in each iteration as well as in the binary algorithm. According to Newton’s second law, the total force acting on a particle imparts acceleration to it:

$$a_i^d[t]={\displaystyle \sum _{j=1,j\ne i}^{P}rand(0;1)\cdot G[t]\cdot \frac{M_j[t]\cdot ({\theta }_j^d[t]-{\theta }_i^d[t])}{(\Vert {\mathsf{\theta }}_j[t]-{\mathsf{\theta }}_i[t]\Vert +\epsilon )}},$$

(18)

where $d=\overline{1,\left|{\mathsf{\theta }}_i\right|}$ is the ordinal number of the vector element; rand(0; 1) is a random number within the interval [0; 1]; $M_j(t)=m_j(t)/{\displaystyle {\sum }_{k=1}^P{m}_k}(t)$ is the normalized value of the mass of the j-th particle; $i=\overline{1,P}$; $G(t)=G_0\cdot {(t/T)}^{\alpha }$ is the value of the gravitational constant.

Vector elements are updated as follows:

$${\theta }_i^d(t+1):={\theta }_i^d(t)+V_i^d(t+1),$$

(19)

where $V_i^d(t+1)=rand(0;1)\cdot V_i^d(t)+a_i^d(t)$. After the entire population is updated, classification accuracy is recalculated and the iteration ends.

The algorithm ends when the number of iterations (t = T) is exhausted, or if all vectors are equal. The output data produced by the algorithm is the vector of system parameters θ_best that possess the highest level of classification accuracy.

A pseudo code of the Binary Gravitational Search Algorithm is shown in Algorithm 3.

Algorithm 3. Continuous Gravitational Search Algorithm.

Input: S, P, T, G0, α, ε.

Output: θbest.

begin

Initialize the population Θ = {θ1, θ2, …, θP};

while (t < T)

$\mathrm{estimate}\mathrm{the}\mathrm{fitness}\mathrm{function}fi{t}_i$ by Equation (17) for i = 1, 2, ..., P;

find best(t) and worst(t);

update G(t) by Equation (9);

$\mathrm{calculate}\mathrm{the}\mathrm{mass}{M}_i$$\left(t\right)\mathrm{by}\mathrm{Equation}\left(6\right),\mathrm{acceleration}{a}_i$$\left(t\right)\mathrm{by}\mathrm{Equation}\left(18\right)\mathrm{and}\mathrm{velocity}{V}_i$(t) by Equation (10) for i = 1, 2, ..., P;

update the position of particles with the Equation (19);

end while

output the particle with the best fitness value θbest;

end

3.7. Datasets

The algorithms described above have been validated using real-world datasets from the dataset repository KEEL (http://keel.es).

Table 1. Dataset characteristics.

Name	Abbreviation	Features	Instances	Classes
banana	bnn	2	5300	2
haberman	hbm	3	306	2
titanic	tit	3	2201	2
iris	irs	4	150	3
balance	bln	4	625	3
newthyroid	nth	5	215	3
phoneme	phn	5	5404	2
bupa	bup	6	345	2
pima	pim	8	768	2
glass	gls	9	214	7
wisconsin	wis	9	683	2
page-blocks	pbl	10	5472	5
magic	mag	10	19,020	2
wine	win	13	178	3
cleveland	clv	13	297	5
heart	hrt	13	270	2
penbased	pbs	16	10,992	10
vehicle	veh	18	846	4
hepatitis	hep	19	80	2
segment	seg	19	2310	7
ring	rin	20	7400	2
twonorm	twn	20	7400	2
thyroid	thr	21	7200	3
satimage	sat	36	6435	7
spambase	spb	57	4597	2
coil2000	coil	85	9822	2

shows a description of the datasets used.

3.8. Test Phase

Two experiments have been conducted within the framework of the study. The first experiment focused on validation of the Binary Gravitational Search Algorithm in the wrapper mode for a fuzzy classifier while using various transfer functions. The feature selection experiment was designed as follows. Datasets with the number of features exceeding four were grouped into ten training and test sets in accordance with the cross-validation scheme. For each sample, the Binary Gravitational Search Algorithm was started with each of the four transfer functions, one at a time. Then, the resulting feature sets were used to design a fuzzy classifier with the help of a class extremum-based algorithm for all ten samples. The experiment has produced averages of classification accuracy and of the number of features for each transfer function.

The second experiment focused on designing fuzzy classifiers using the Binary and Continuous Gravitational Search Algorithms. Out of the feature set found in the first experiment, the best set in terms of its training accuracy was selected. The selected feature set was used to design a classifier with the help of a class extremum-based algorithm. Then the Continuous Gravitational Search Algorithm was used to optimize parameters of membership functions for the resultant classifier. The results were averaged over five independent runs of the Continuous Gravitational Search Algorithm.

The number of particles in gravitational search populations P is ten, the initial value of the gravitational constant is G₀ = 10, coefficient α = 10, small constant ε = 0.01. The maximum number of iterations for the Continuous Binary Search Algorithm is T = 1000. The number of iterations for the Binary Algorithm varied depending on the number of features in the dataset (100 to 1000 iterations). The value of the parameters is determined empirically.

4. Experimental Results

The present study aims to identify different classifiers, which would encounter the performance for the data that was selected.

4.1. Comparison of Feature Selection Results Using the Binary Gravitational Algorithm with Various Transfer Functions

The first experiment focused on validation of the Binary Gravitational Algorithm in the wrapper mode for a fuzzy classifier.

The test accuracy obtained while designing a fuzzy system based on a full set of features (without feature selection) is compared to the test accuracy obtained after selecting features by the Binary Gravitational Search Algorithm for each of the transfer functions described in Section 3.3.

Table 2. Results of feature selection using the Binary Gravitational Algorithm.

Dataset	Full Set		S1		S2		V1		V2
	#F	#T	#F	#T	#F	#T	#F	#T	#F	#T
newthyroid	5	96.3	3.5	96.5	3.7	96.5	3.3	96.5	3.4	96.4
phoneme	5	70.7	4	76.2	4	76.2	2.3	75.3	3.7	76.1
bupa	6	49.0	2.7	60.0	2.8	59.8	2.7	60.0	2.8	57.1
pima	8	70.2	3.9	71.0	3.9	71.0	2.6	70.8	4.1	70.6
glass	9	49.1	5.2	55.9	5.1	56.0	5.9	53.2	5.5	53.9
wisconsin	9	90.0	5.8	94.0	5.7	94.0	3.5	93.6	5.9	93.8
page-blocks	10	6.1	2	80.5	2	80.5	2	80.5	2	80.5
magic	10	56.1	4.1	70.7	4.1	70.7	4.1	70.7	4.1	70.7
wine	13	88.2	5.9	92.6	5.8	94.8	6.8	92.2	6.2	94.5
cleveland	13	53.5	7.4	53.1	7.3	52.5	2.8	54.4	5.6	48.8
heart	13	57.4	3.1	67.1	2.8	67.0	3	67.7	4.1	67.7
penbased	16	31.9	8.2	49.7	8.1	49.7	9.3	46.8	9	48.5
vehicle	18	29.9	7.9	45.5	7.8	45.6	4.8	40.0	7.4	45.6
hepatitis	19	61.0	7.7	87.4	7.9	87.2	5.3	82.5	6.7	85.1
segment	19	78.2	10.2	85.4	9.1	85.7	8.8	84.1	8.5	85.7
ring	20	49.5	1.0	58.6	1.0	58.6	1.0	57.9	2.5	55.5
twonorm	20	96.8	19.7	96.8	19.9	96.8	17.8	96.1	17.1	95.8
thyroid	21	99.3	19.9	99.3	20	99.3	16.9	99.3	14.6	99.3
satimage	36	58.4	15.4	62.5	15.9	62.3	9.9	61.1	13.2	60.8
spambase	57	56.3	29.7	65.9	27.0	65.4	2.7	70.0	27.9	64.2
coil2000	85	16.4	38.2	90.1	38.5	90.6	1	94.0	37.6	86.4

shows the results of the experiment for datasets with the number of features exceeding four. Here, #F is the number of features, #T is the classification accuracy percentage for the test data. The best results are in bold.

In all of the datasets used, at least one transfer function makes it possible to achieve an accuracy equal or superior to the classification accuracy obtained on the full dataset. The Wilcoxon signed rank test was used to evaluate the statistical significance of the difference between the resulting accuracy values.

Table 3. Wilcoxon test for comparison of prediction accuracy.

Transfer Function	All	S1	S2	V1	V2
All	-	0.064	0.064	0.087	0.159
S1	0.064	-	1.0	0.940	0.792
S2	0.064	1.0	-	0.910	0.734
V1	0.087	0.940	0.910	-	0.940
V2	0.159	0.792	0.734	0.940	-

shows the values calculated based on pairwise algorithm comparison.

The resulting values of the Wilcoxon test exceed the significance level of 0.05; therefore, there is no statistically significant difference between the test accuracy obtained with full dataset-based fuzzy classifiers and the accuracy values obtained after feature selection using the Binary Gravitational Algorithm. A conclusion can be made that there is no statistically significant difference between the accuracy values obtained on different transfer functions.

Table 4. Wilcoxon test for comparison of the numbers of features.

Transfer Function	All	S1	S2	V1	V2
All	-	0.004	0.004	0.00001	0.002
S1	0.004	-	1.0	0.082	0.960
S2	0.004	1.0	-	0.092	0.990
V1	0.00001	0.082	0.092	-	0.078
V2	0.002	0.960	0.990	0.078	-

shows the calculated values of the Wilcoxon test for evaluation of the statistical significance of difference in the number of features in the resulting classifiers.

The above test values show that there is a statistically significant difference between the initial number of features and the number of features selected by any of the transfer functions. There is no statistically significant difference between the number of features selected with the help of different transfer functions.

GSA has the same computational complexity O(nd), where n is the number of agents and d is the search space dimension [14]. GSA in our work has not been modified, so it has complexity O(Pd), where P is the number of particles and d is the size of the dataset.

4.2. Comparison to Similar Solutions

Table 5. Results of fuzzy classifier design.

Dataset	Type of Membership Function	GSb + GSc				GSc		D-MOFARC			FARC-HD
		#R	#F	#L	#T	#L	#T	#R	#L	#T	#R	#L	#T
bnn	triangle	2	2	72.3	72.8	72.3	72.8	8.7	90.3	89.0	12.9	86.0	85.5
hbm	triangle	2	3	75.6	74.4	75.6	74.4	9.2	81.7	69.4	5.7	79.2	73.5
tit	gaussoid	2	3	77.8	78.6	77.8	78.6	10.4	78.9	78.7	4.1	79.1	78.8
irs	triangle	3	4	98.3	97.3	98.3	97.3	5.6	98.1	96.0	4.4	98.6	95.3
bln	gaussoid	3	4	83.7	81.8	83.7	81.8	20.1	89.4	85.6	18.8	92.2	91.2
nth	gaussoid	3	3	98.2	99.0	98.3	98.1	9.5	99.8	95.5	9.6	99.2	94.4
phn	gaussoid	2	4	78.4	78.5	77.3	77.5	9.3	84.8	83.5	17.2	83.9	82.4
bup	triangle	2	4	71.6	68.7	68.9	69	7.7	82.8	70.1	10.6	78.2	66.4
pim	triangle	2	2	75.4	77.9	76.9	74	10.4	82.3	75.5	20.2	82.3	76.2
gls	gaussoid	7	4	66	70.7	63.4	57.5	27.4	95.2	70.6	18.2	79.0	69.0
wis	triangle	2	4	97.3	97.2	96	96.3	9.0	98.6	96.8	13.6	98.3	96.2
pbl	gaussoid	5	2	89.7	89.7	90.8	90.8	21.5	97.8	97.0	18.4	95.5	95.0
mag	gaussoid	2	4	71.1	70.9	79.9	79.5	32.2	86.3	85.4	43.8	85.4	84.8
win	gaussoid	3	7	99.9	97.4	99.3	97.1	8.6	100.0	95.8	8.3	100.0	95.5
clv	gaussoid	5	2	58.1	58.3	63.4	62.6	45.6	90.9	52.9	42.1	82.2	58.3
hrt	gaussoid	2	6	76.2	70.7	86.5	84.1	18.7	94.4	84.4	27.8	93.1	83.7
pbs	gaussoid	10	8	68.0	67.8	55.1	55.0	119.2	97.4	96.2	152.7	97.0	96.0
veh	triangle	4	7	50.4	51.1	53.4	50	22.4	84.5	70.6	31.6	77.2	68.0
hep	gaussoid	2	7	91.5	93.3	94.1	89.9	11.4	100.0	90.0	10.4	99.4	88.7
seg	triangle	7	9	88.3	89.1	84.4	82.8	26.2	98.0	96.6	41.1	94.8	93.3
rin	gaussoid	2	3	74.9	74.3	82.1	82.5	15.3	94.2	93.3	24.9	95.1	94.0
twn	gaussoid	2	14	96.9	96.8	94.4	94.4	10.2	94.5	93.1	60.4	96.6	95.1
thr	triangle	3	12	99.1	98.6	99.5	99.3	5.9	99.3	99.1	4.9	94.3	94.1
sat	gaussoid	7	8	85.5	84.6	84.6	83.7	56.0	90.8	87.5	30.2	84.4	83.8
spb	gaussoid	2	3	73.7	74.0	70.5	69.7	24.3	91.7	90.5	30.5	92.4	91.6
coil	triangle	2	1	94.0	94.0	92.2	92.1	89.0	94.0	94.0	2.6	94.0	94.0

shows the experiment results. Here, #R is the number of rules, #F is the number of features when using selection, #L is the classification accuracy percentage on training data, #T is the classification accuracy percentage on test data. As a comparison, Table 5 also shows the results for the D-MOFARC and FARC-HD algorithms [28,29]. The best results are in bold.

The Wilcoxon signed-rank test was used to assess the statistical significance of differences in the accuracy of fuzzy classifiers formed using the Gravitational Algorithm and using D-MOFARC and FARC-HD.

Table 6. Wilcoxon test for comparison of prediction accuracy.

Method	GSAB + GSAC	GSAC
D-MOFARC	0.297	0.161
FARC-HD	0.346	0.241

shows the values calculated based on pairwise algorithm comparison.

The resulting values of the Wilcoxon test exceed the significance level of 0.05; therefore, there is no statistically significant difference between the test accuracy obtained with fuzzy classifiers using Gravitational Search Algorithms and accuracy values obtained using D-MOFARC and FARC-HD.

Pairwise comparison of the rule numbers shows that there exists a statistically significant difference between the number of rules in the resulting classifiers and the D-MOFARC algorithm (the test value is 2.47 × 10⁻⁹) and the number of rules in the resulting classifiers and the FARC-HD algorithm (the test value is 2.48 × 10⁻⁸).

Since the algorithms D-MOFARC and FARC-HD are based on full datasets, it is necessary to compare the number of features in full datasets and the number of features selected by the Binary Gravitational Algorithm. A check with the Wilcoxon signed-rank test produces the value of 1.13 × 10⁻⁴, making it possible to conclude that the Binary Gravitational Algorithm demonstrates a high level of performance.

To compare the proposed method with other non-fuzzy classifiers, basic methods and ensemble methods were selected. Basic methods are a logistic regression method (LR), Gaussian Naive Bayes, a k-nearest-neighbour method (kNN), a Support Vector Machine (SVC), a Multi-Layer Perceptron (MLP), a WiSARD Classifier (WNN). Ensemble methods are a Random Forest (RF), Adaboost (AB), a Gradient Tree Boosting (GTB) [44].

Table 7. Average accuracy of methods.

Dataset	Methods
	LR	GNB	kNN	SVC	RF	AB	GTB	MLP	WNN	GSA
bln	0.8607	0.8381	0.8369	0.8881	0.712	0.8417	0.8083	0.9729	0.7808	0.818
bnn	0.5709	0.614	0.9036	0.6504	0.897	0.7168	0.8989	0.8949	0.903	0.728
bup	0.6463	0.5622	0.5911	0.5943	0.7363	0.7361	0.7334	0.7448	0.6781	0.687
clv	0.5892	0.5345	0.5534	0.5656	0.5697	0.5623	0.5426	0.5023	0.5892	0.583
coil	0.9402	0.1355	0.9405	0.9403	0.929	0.9403	0.9394	0.9371	0.9403	0.94
gls	0.5802	0.469	0.6695	0.5906	0.7926	0.5146	0.7249	0.6893	0.7243	0.707
hbm	0.7485	0.7424	0.7354	0.7353	0.6862	0.7355	0.7133	0.7389	0.732	0.744
hrt	0.8444	0.8407	0.8259	0.8111	0.8222	0.8259	0.8111	0.8444	0.8333	0.707
hep	0.8405	0.5919	0.8181	0.8405	0.8891	0.8827	0.8323	0.8038	0.875	0.933
irs	0.9	0.9533	0.9533	0.9667	0.96	0.9467	0.96	0.96	0.9467	0.973
nth	0.8885	0.9677	0.9437	0.9208	0.9582	0.9537	0.9487	0.9626	0.9721	0.99
pbl	0.9445	0.8864	0.9519	0.9361	0.9686	0.9541	0.9698	0.9636	0.9567	0.897
pbs	0.9306	0.8559	0.9931	0.9953	0.9915	0.6912	0.9915	0.9922	0.9916	0.678
phn	0.7496	0.7605	0.8901	0.797	0.913	0.8231	0.9099	0.8458	0.899	0.785
pim	0.7707	0.7629	0.759	0.7837	0.7524	0.7564	0.7564	0.7746	0.776	0.779
sat	0.8236	0.7932	0.8925	0.8909	0.904	0.7748	0.9001	0.8814	0.892	0.846
seg	0.9108	0.7987	0.961	0.9437	0.9784	0.8065	0.9818	0.9662	0.9714	0.891
thr	0.9455	0.1235	0.9404	0.9385	0.9956	0.9894	0.9962	0.9843	0.9425	0.986
tit	0.776	0.7733	0.7287	0.7819	0.7878	0.7783	0.7905	0.7892	0.7878	0.786
twn	0.9778	0.9786	0.9749	0.9785	0.9736	0.9673	0.9734	0.9773	0.9759	0.968
veh	0.7533	0.4611	0.6915	0.7567	0.7483	0.6089	0.7745	0.8181	0.7435	0.511
win	0.9666	0.9663	0.9712	0.9826	0.9774	0.9215	0.9329	0.9826	0.9888	0.974
wis	0.9693	0.962	0.9723	0.9693	0.965	0.9562	0.9634	0.965	0.9722	0.972

lists the benchmarking methods we have compared to fuzzy classifier using GSA.

Classification accuracies compared by means of a statistical analysis based on Wilcoxon test with a significance level of 0.05 to prove how the fuzzy classifiers using Gravitational Search Algorithms is very close in performance to the best methods of machine learning. The null hypothesis is the following:

H₀: 

The distribution of classification accuracy for the GSA and another method is the same over N datasets; where N = 23.

Pairwise comparisons of methods conducted in the statistical analysis proved that fuzzy classifiers using Gravitational Search Algorithms is very close to Support Vector Machines, while it outperforms Gaussian Naive Bayes (

Table 8. p-Values of Wilcoxon test for comparison of 9 algorithms.

Method	LR	GNB	kNN	SVC	RF	AB	GTB	MLP	WNN
FC+GSA	0.543	0.008 *	0.503	0.808	0.114	0.429	0.144	0.094	0.107

* Indicates that the null hypothesis is rejected, using α = 0.05.

).

The numerical experimentations were performed on a personal computer equipped with a 2.40 GHz Intel(R) Core™ i5-2430M with NVIDEA GeForce GT 520MX Graphics processor and 4 GB of RAM. The described method was implemented using C# programming language under Microsoft Windows operating system environment.

5. Conclusions

This paper discusses methods for fuzzy classifier design with feature selection. Features were selected using the Binary Gravitational Algorithm. The classifier structure was formed by the rule base generation algorithm by using extreme feature values. Parameter classifier optimization was achieved by using the Continuous Gravitational Algorithm.

The performance of the fuzzy classifiers adjusted by the algorithms described above is tested on 26 real-world KEEL datasets. The resulting classifiers possess good trainability, which is confirmed by the high percentage of accurate classification on training samples and equally good predictive capability, which is supported by the high percentage of accurate classification on test samples.

The number of features used by the classifiers designed with the help of the algorithms is significantly smaller than the total number of features in datasets.

As can be seen from the above, the classifier design algorithms based on combinations of the algorithms proposed in this paper make it possible to design fuzzy classifiers that use a smaller number of features while offering an accuracy on the reduced number of features that is statistically equivalent to the accuracy of classifiers designed based on a full set of features.

In the future, the authors expect to study other ways to binarize the Gravitational Search Algorithm and increase the number of test datasets. Based on [45], in our future research a strict computational complexity analysis of GSA_B + GSA_C will be carried out.