Maximum Detour–Harary Index for Some Graph Classes
Abstract
1. Introduction
2. Preliminaries
2.1. Edge-Lifting Transformation
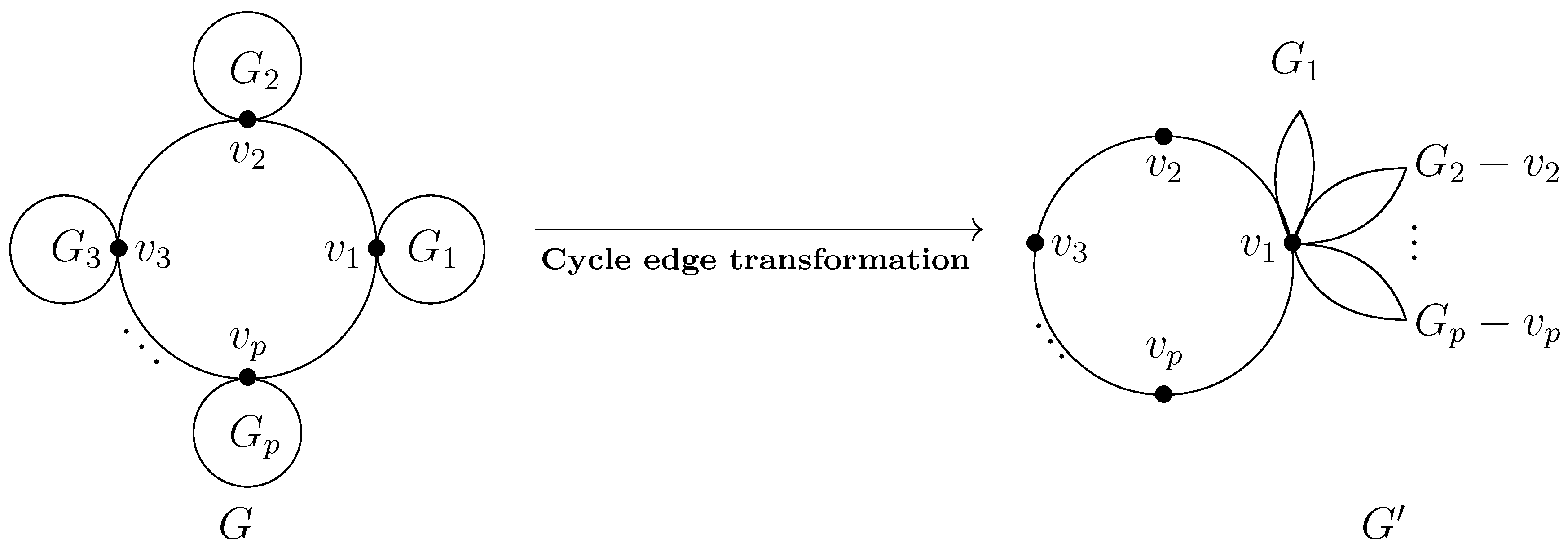
2.2. Cycle-Edge Transformation
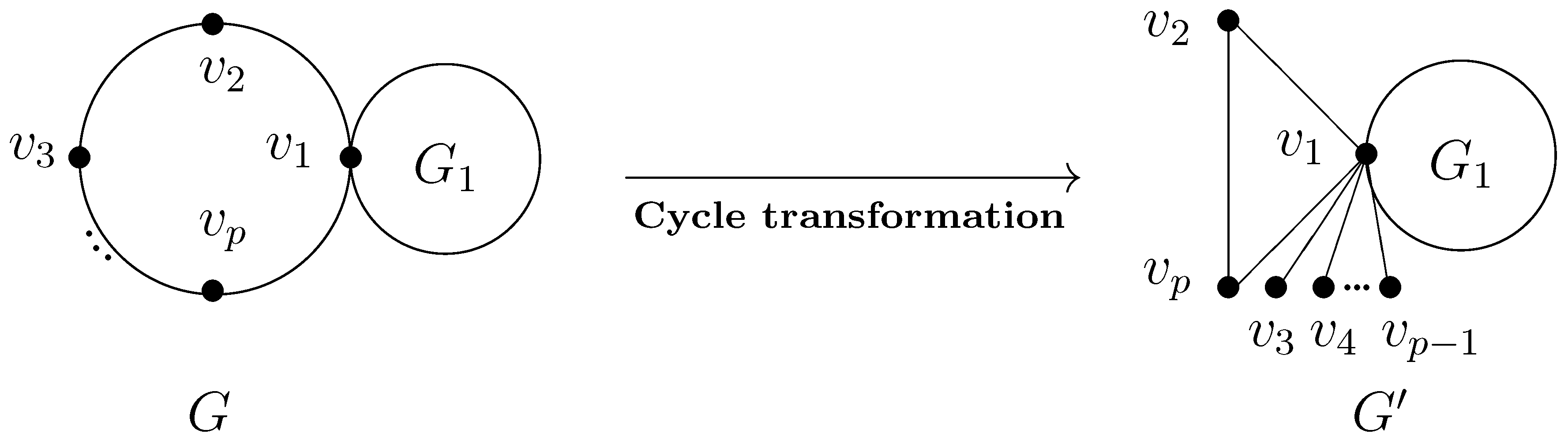
2.3. Cycle Transformation
3. Maximum Detour–Harary Index of Unicyclic Graphs
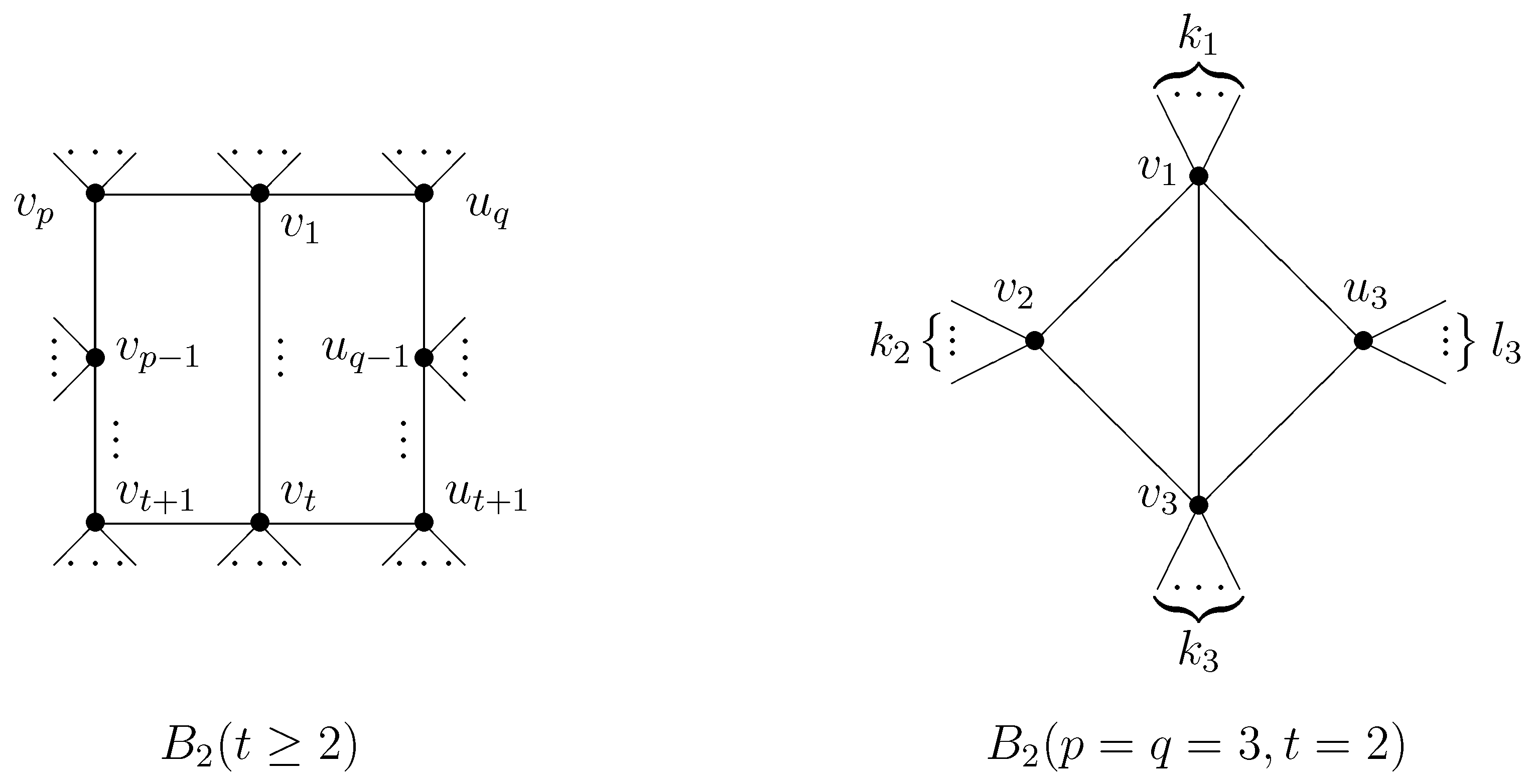
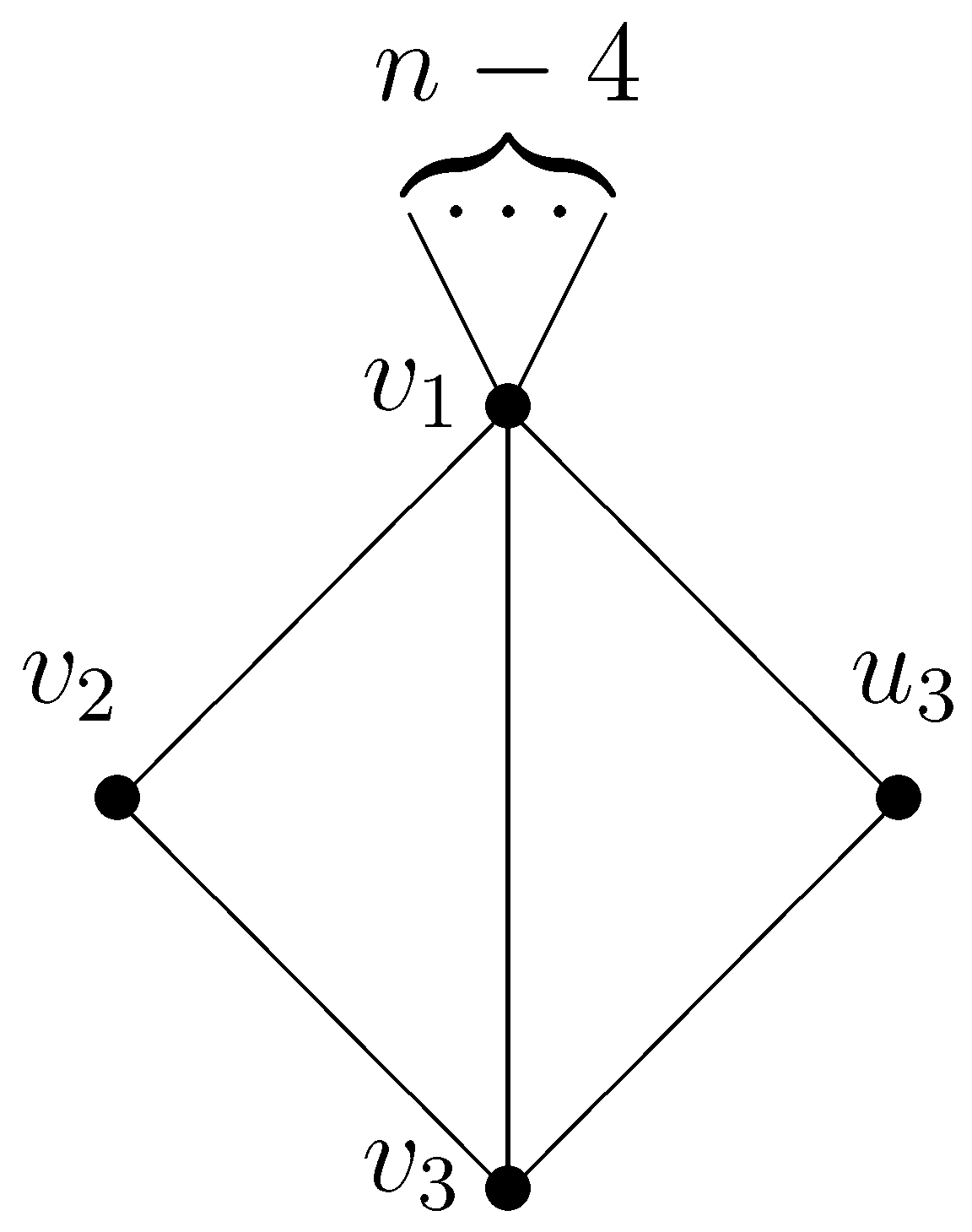
4. Maximum Detour–Harary Index of Bicyclic Graphs
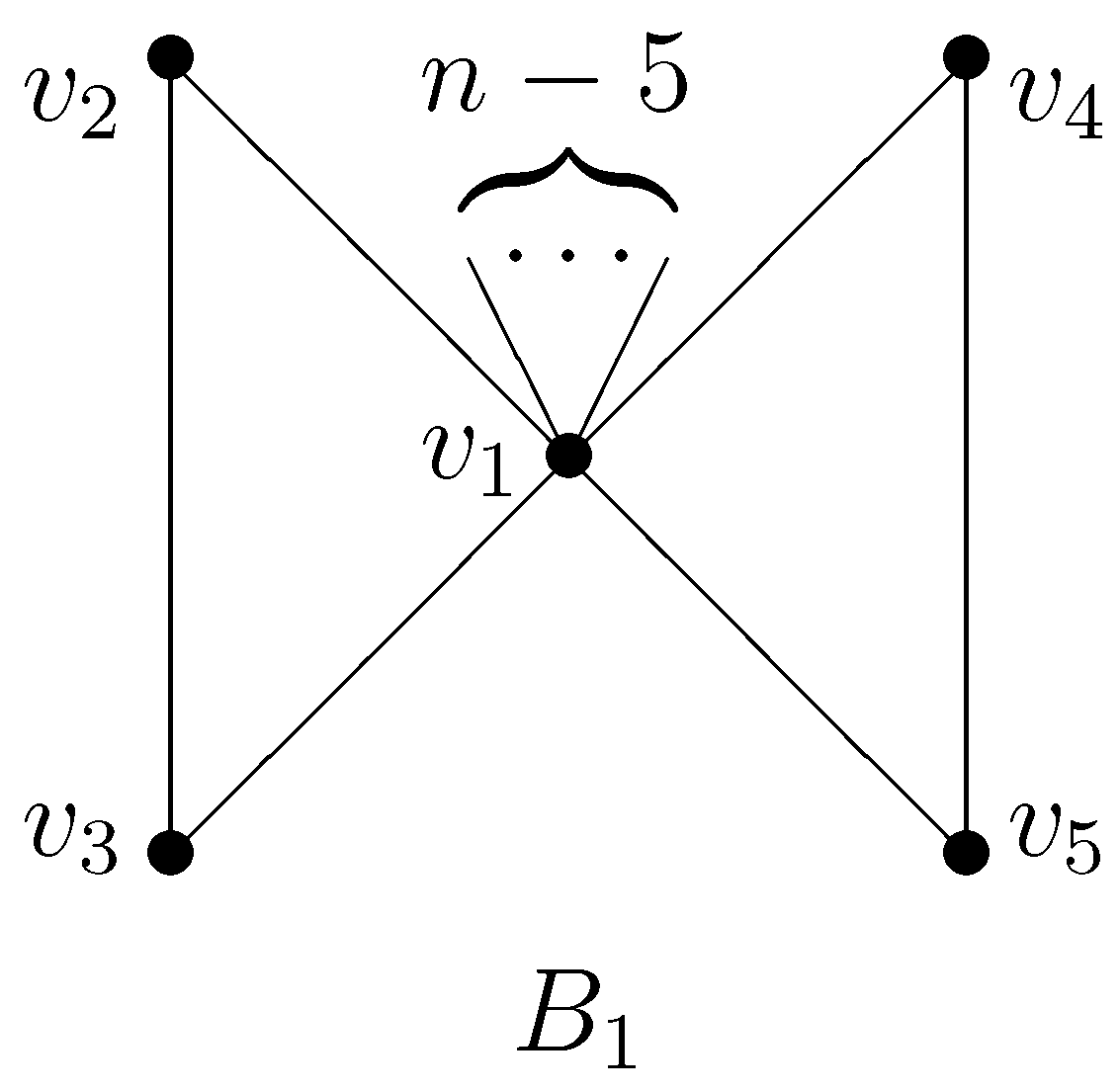
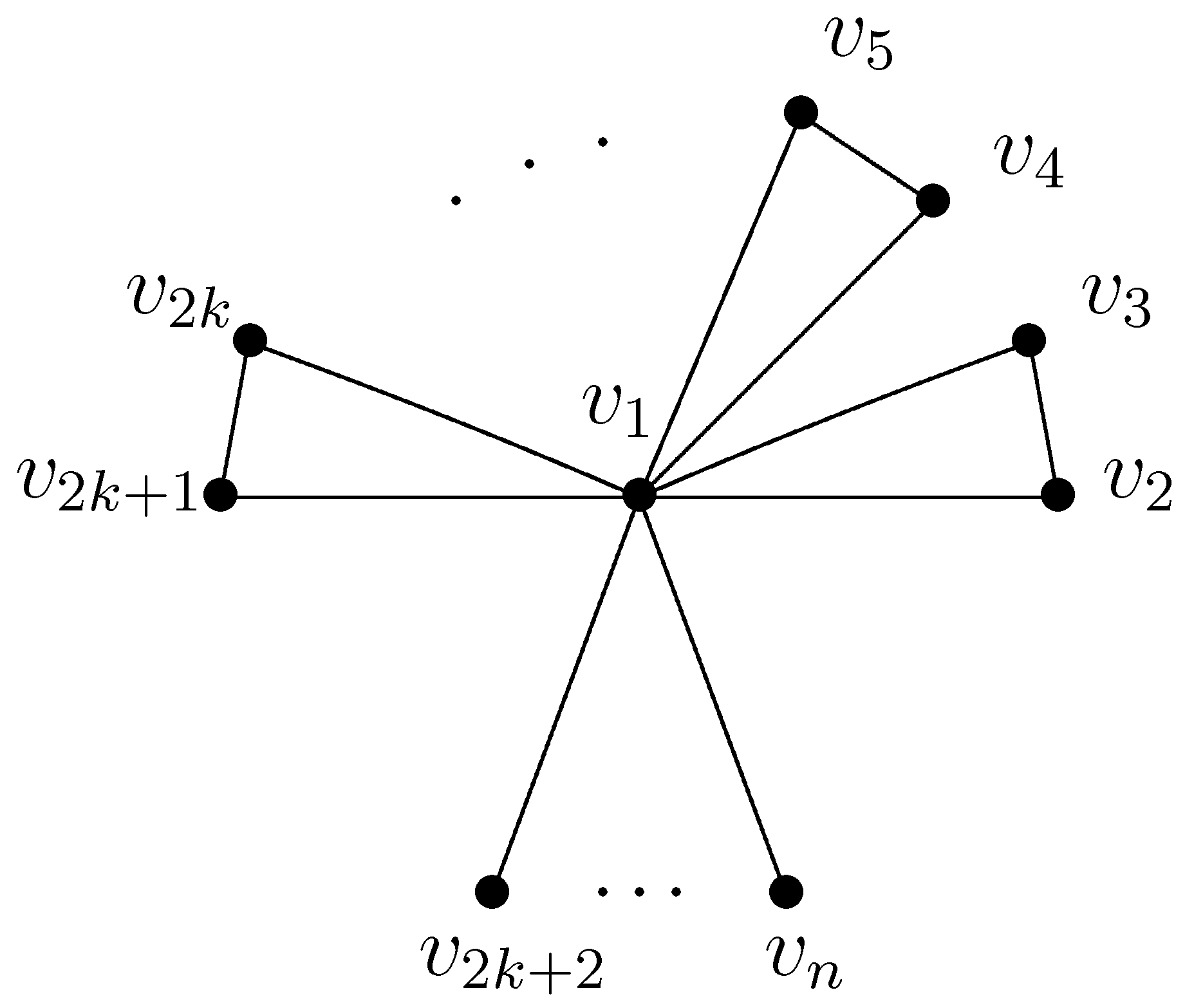
5. Maximum Detour–Harary Index of Cacti
Author Contributions
Funding
Conflicts of Interest
References
- Imran, M.; Ali, M.A.; Ahmad, S.; Siddiqui, M.K.; Baig, A.Q. Topological sharacterization of the symmetrical structure of bismuth tri-iodide. Symmetry 2018, 10, 201. [Google Scholar] [CrossRef]
- Liu, J.; Siddiqui, M.K.; Zahid, M.A.; Naeem, M.; Baig, A.Q. Topological Properties of Crystallographic Structure of Molecules. Symmetry 2018, 10, 265. [Google Scholar] [CrossRef]
- Shao, Z.; Siddiqui, M.K.; Muhammad, M.H. Computing zagreb indices and zagreb polynomials for symmetrical nanotubes. Symmetry 2018, 10, 244. [Google Scholar] [CrossRef]
- Dobrynin, A.; Entringer, R.; Gutman, I. Wiener Index of Trees: Theory and Applications. Acta Appl. Math. 2001, 66, 211–249. [Google Scholar] [CrossRef]
- Alizadeh, Y.; Andova, V.; Zar, S.K.; Skrekovski, R.V. Wiener dimension: Fundamental properties and (5,0)-nanotubical fullerenes. MATCH Commun. Math. Comput. Chem. 2014, 72, 279–294. [Google Scholar]
- Needham, D.E.; Wei, I.C.; Seybold, P.G. Molecular modeling of the physical properties of alkanes. J. Am. Chem. Soc. 1988, 110, 4186–4194. [Google Scholar] [CrossRef]
- Vijayabarathi, A.; Anjaneyulu, G.S.G.N. Wiener index of a graph and chemical applications. Int. J. ChemTech Res. 2013, 5, 1847–1853. [Google Scholar]
- Gutman, I.; Cruz, R.; Rada, J. Wiener index of Eulerian graphs. Discret. Appl. Math. 2014, 162, 247–250. [Google Scholar] [CrossRef]
- Lin, H. Extremal Wiener index of trees with given number of vertices of even degree. MATCH Commun. Math. Comput. Chem. 2014, 72, 311–320. [Google Scholar]
- Lin, H. Note on the maximum Wiener index of trees with given number of vertices of maximum degree. MATCH Commun. Math. Comput. Chem. 2014, 72, 783–790. [Google Scholar]
- Wiener, H. Structural determination of paraffin boiling points. Am. Chem. Soc. 1947, 69, 17–20. [Google Scholar] [CrossRef]
- Plavšić, D.; Nikolić, S.; Trinajstić, N.; Mihalić, Z. On the Harary index for the characterization of chemical graphs. J. Math. Chem. 1993, 12, 235–250. [Google Scholar] [CrossRef]
- Ivanciuc, O.; Balaban, T.S.; Balaban, A.T. Reciprocal distance matrix, related local vertex invariants and topological indices. J. Math. Chem. 1993, 12, 309–318. [Google Scholar] [CrossRef]
- Lukovits, I. The Detour index. Croat. Chem. Acta 1996, 69, 873–882. [Google Scholar]
- Trinajstić, N.; Nikolić, S.; Lučić, B.; Amić, D.; Mihalić, Z. The Detour matrix in chemistry. J. Chem. Inf. Comput. Sci. 1997, 37, 631–638. [Google Scholar] [CrossRef]
- Chen, S. Cacti with the smallest, second smallest, and third smallest Gutman index. J. Comb. Optim. 2016, 31, 327–332. [Google Scholar] [CrossRef]
- Chen, Z.; Dehmer, M.; Shi, Y.; Yang, H. Sharp upper bounds for the Balaban index of bicyclic graphs. MATCH Commun. Math. Comput. Chem. 2016, 75, 105–128. [Google Scholar]
- Fang, W.; Gao, Y.; Shao, Y.; Gao, W.; Jing, G.; Li, Z. Maximum Balaban index and sum-Balaban index of bicyclic graphs. MATCH Commun. Math. Comput. Chem. 2016, 75, 129–156. [Google Scholar]
- Fang, W.; Wang, Y.; Liu, J.-B.; Jing, G. Maximum Resistance-Harary index of cacti. Discret. Appl. Math. 2018. [Google Scholar] [CrossRef]
- Gutman, I.; Li, S.; Wei, W. Cacti with n-vertices and t-cycles having extremal Wiener index. Discret. Appl. Math. 2017, 232, 189–200. [Google Scholar] [CrossRef]
- Ji, S.; Li, X.; Shi, Y. Extremal matching energy of bicyclic graphs. MATCH Commun. Math. Comput. Chem. 2013, 70, 697–706. [Google Scholar]
- Liu, J.; Pan, X.; Yu, L.; Li, D. Complete characterization of bicyclic graphs with minimal Kirchhoff index. Discret. Appl. Math. 2016, 200, 95–107. [Google Scholar] [CrossRef]
- Wang, H.; Hua, H.; Wang, D. Cacti with minimum, second-minimum, and third-minimum Kirchhoff indices. Math. Commun. 2010, 15, 347–358. [Google Scholar]
- Wang, L.; Fan, Y.; Wang, Y. Maximum Estrada index of bicyclic graphs. Discret. Appl. Math. 2015, 180, 194–199. [Google Scholar] [CrossRef]
- Lu, Y.; Wang, L.; Xiao, P. Complex Unit Gain Bicyclic Graphs with Rank 2,3 or 4. Linear Algebra Appl. 2017, 523, 169–186. [Google Scholar] [CrossRef]
- Furtula, B.; Gutman, I.; Katanić, V. Three-center Harary index and its applications. Iran. J. Math. Chem. 2016, 7, 61–68. [Google Scholar]
- Feng, L.; Lan, Y.; Liu, W.; Wang, X. Minimal Harary index of graphs with small parameters. MATCH Commun. Math. Comput. Chem. 2016, 76, 23–42. [Google Scholar]
- Hua, H.; Ning, B. Wiener index, Harary index and hamiltonicity of graphs. MATCH Commun. Math. Comput. Chem. 2017, 78, 153–162. [Google Scholar]
- Li, X.; Fan, Y. The connectivity and the Harary index of a graph. Discret. Appl. Math. 2015, 181, 167–173. [Google Scholar] [CrossRef]
- Xu, K.; Das, K.C. On Harary index of graphs. Discret. Appl. Math. 2011, 159, 1631–1640. [Google Scholar] [CrossRef]
- Xu, K. Trees with the seven smallest and eight greatest Harary indices. Discret. Appl. Math. 2012, 160, 321–331. [Google Scholar] [CrossRef]
- Xu, K.; Das, K.C. Extremal unicyclic and bicyclic graphs with respect to Harary Index. Bull. Malaysian Math. Sci. Soc. 2013, 36, 373–383. [Google Scholar]
- Xu, K.; Wang, J.; Das, K.C.; Klavžar, S. Weighted Harary indices of apex trees and k-apex trees. Discret. Appl. Math. 2015, 189, 30–40. [Google Scholar] [CrossRef]
- Zhou, B.; Cai, X.; Trinajstić, N. On Harary index. J. Math. Chem. 2008, 44, 611–618. [Google Scholar] [CrossRef]
- Fang, W.; Yu, H.; Gao, Y.; Jing, G.; Li, Z.; Li, X. Minimum Detour index of cactus graphs. Ars Comb. 2019, in press. [Google Scholar]
- Qi, X.; Zhou, B. Detour index of a class of unicyclic graphs. Filomat 2010, 24, 29–40. [Google Scholar]
- Qi, X.; Zhou, B. Hyper-Detour index of unicyclic graphs. MATCH Commun. Math. Comput. Chem. 2011, 66, 329–342. [Google Scholar]
- Rücker, G.; Rücker, C. Symmetry-aided computation of the Detour matrix and the Detour index. J. Chem. Inf. Comput. Sci. 1998, 38, 710–714. [Google Scholar] [CrossRef]
- Zhou, B.; Cai, X. On Detour index. MATCH Commun. Math. Comput. Chem. 2010, 44, 199–210. [Google Scholar]
- Qi, X. Detour index of bicyclic graphs. Util. Math. 2013, 90, 101–113. [Google Scholar]
- Deng, H. On the Balaban index of trees. MATCH Commun. Math. Comput. Chem. 2011, 66, 253–260. [Google Scholar]
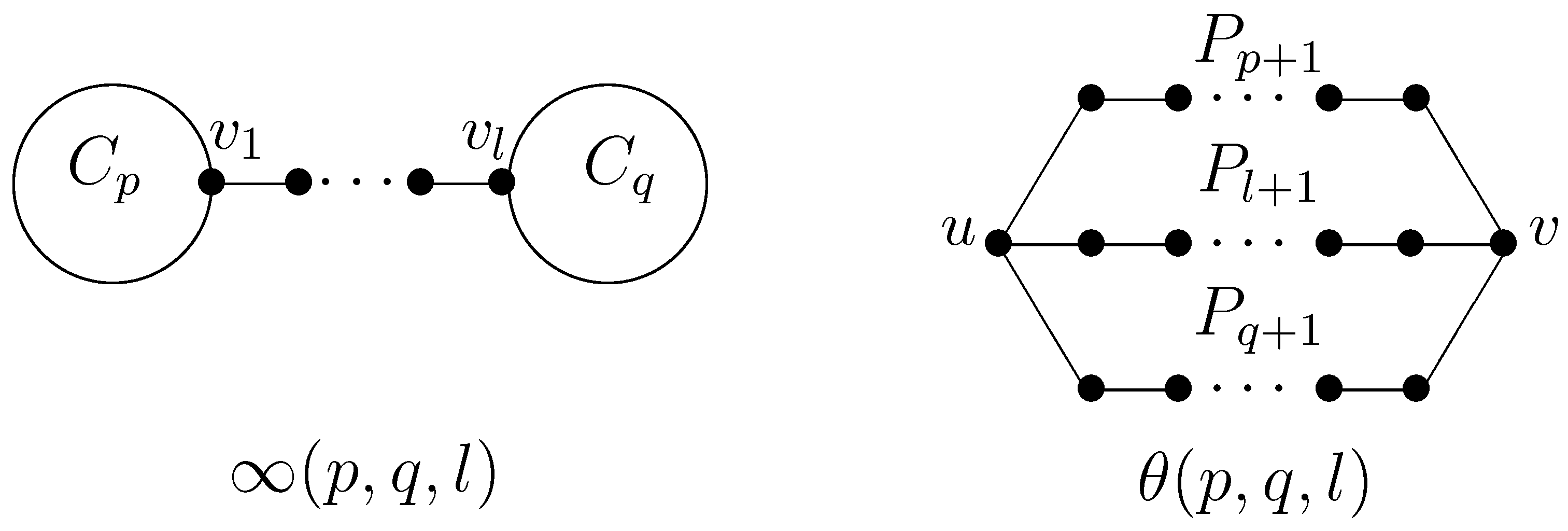

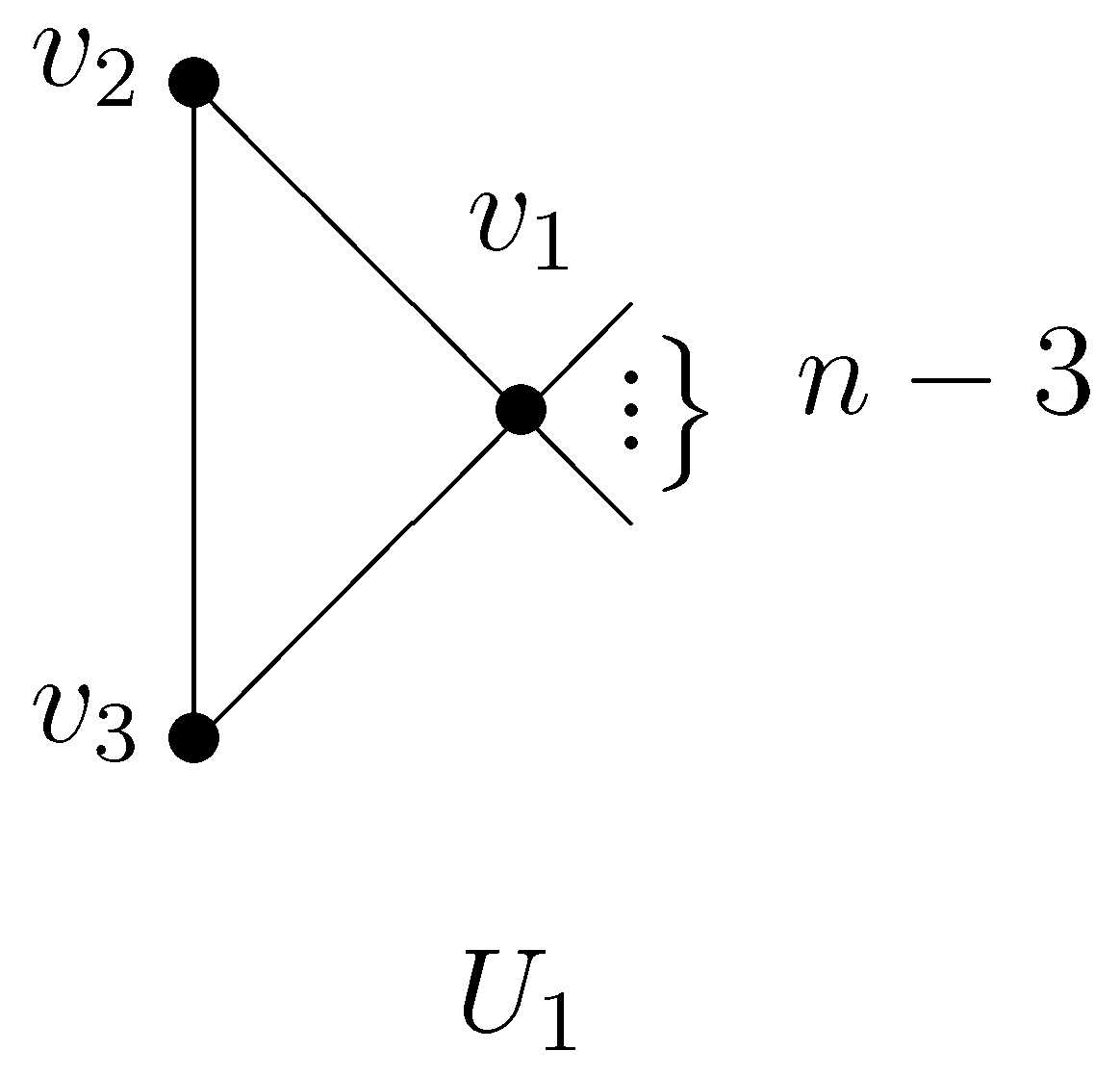
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, W.; Liu, W.-H.; Liu, J.-B.; Chen, F.-Y.; Hong, Z.-M.; Xia, Z.-J. Maximum Detour–Harary Index for Some Graph Classes. Symmetry 2018, 10, 608. https://doi.org/10.3390/sym10110608
Fang W, Liu W-H, Liu J-B, Chen F-Y, Hong Z-M, Xia Z-J. Maximum Detour–Harary Index for Some Graph Classes. Symmetry. 2018; 10(11):608. https://doi.org/10.3390/sym10110608
Chicago/Turabian StyleFang, Wei, Wei-Hua Liu, Jia-Bao Liu, Fu-Yuan Chen, Zhen-Mu Hong, and Zheng-Jiang Xia. 2018. "Maximum Detour–Harary Index for Some Graph Classes" Symmetry 10, no. 11: 608. https://doi.org/10.3390/sym10110608
APA StyleFang, W., Liu, W.-H., Liu, J.-B., Chen, F.-Y., Hong, Z.-M., & Xia, Z.-J. (2018). Maximum Detour–Harary Index for Some Graph Classes. Symmetry, 10(11), 608. https://doi.org/10.3390/sym10110608





