Maximum Detour–Harary Index for Some Graph Classes

Abstract

The definition of a Detour–Harary index is $\omega H(G)=\frac{1}{2}{\sum }_{u,v\in V(G)}$$\frac{1}{l(u,v|G)}$, where G is a simple and connected graph, and $l(u,v|G)$ is equal to the length of the longest path between vertices u and v. In this paper, we obtained the maximum Detour–Harary index about unicyclic graphs, bicyclic graphs, and cacti, respectively.

1. Introduction

In recent years, chemical graph theory (CGT) has been fast-growing. It helps researchers to understand the structural properties of a molecular graph, for example, References [1,2,3].

A simple graph is an undirected graph without multiple edges and loops. Let G be a simple and connected graph, and $V(G)$ and $E(G)$ be the vertex set and edge set of G, respectively. For vertices $u,v$ of G, $d_G(v_1,v_2)$ (or $d(v_1,v_2)$ for short) is the distance between $v_1$ and $v_2$, which equals to the length of the shortest path between $v_1$ and $v_2$ in G; $l(v_1,v_2|G)$ (or $l(v_1,v_2)$ for short) is the detour distance between $v_1$ and $v_2$, which equals to the longest path of a shortest path between $v_1$ and $v_2$ in G.

$G[S]$ is an induced subgraph of G, the vertex set is S, and the edge set is the set of edges of G and both ends in S. $G-S$ is the induced subgraph $G[V(G)\setminus S]$; when $S=\{w\}$, we write $G-w$ for short.

In 1947, Wiener introduced the first molecular topological index–Wiener index. The Wiener index has applications in many fields, such as chemistry, communication, and cryptology [4,5,6,7]. Moreover, the Wiener index was studied from a purely graph-theoretical point of view [8,9,10]. In Reference [11], Wiener gave the definition of the Wiener index:

$$W(G)=\frac{1}{2}{\displaystyle \sum _{u,v\in V(G)}}d(u,v).$$

The Harary index was independently introduced by Plavšić et al. [12] and by Ivanciuc et al. [13] in 1993. In References [12,13], they gave the definition of the Harary index:

$$H(G)=\frac{1}{2}{\displaystyle \sum _{u,v\in V(G)}}\frac{1}{d(u,v)}.$$

In Reference [13], Ivanciuc gave the definition of the Detour index:

$$\omega (G)=\frac{1}{2}{\displaystyle \sum _{u,v\in V(G)}}l(u,v|G).$$

Lukovits [14] investigated the use of the Detour index in quantitative structure–activity relationship (QSAR) studies. Trinajstić and his collaborators [15] analyzed the use of the Detour index, and compared its application with Wiener index. They found that the Detour index in combination with the Wiener index is very efficient in the structure-boiling point modeling of acyclic and cyclic saturated hydrocarbons.

In this paper, we introduce a new graph invariant reciprocal to the Detour index, namely, the Detour–Harary index, as

$$\omega H(G)=\frac{1}{2}{\displaystyle \sum _{u,v\in V(G)}}\frac{1}{l(u,v|G)}.$$

Let G be a simple and connected graph, $V(G)=n$ and $E(G)=m$. If $m=n-1$, then G is a tree; if $m=n$, then G is a unicyclic graph; if $m=n+1$, then G is a bicyclic graph.

Suppose ${\mathcal{U}}_n({\mathcal{B}}_n,\mathrm{respectively})$ is the set of unicyclic (bicyclic, respectively) graphs set with n vertices. Any bicyclic graph G can be obtained from $\theta (p,q,l)$-graph or $\theta (p,q,l)$-graph $G_0$ by attaching trees to the vertices, where $p,q,l\ge 1$, and at most one of them is equal to 1. We denote $G_0$ be the kernel of G (Figure 1).

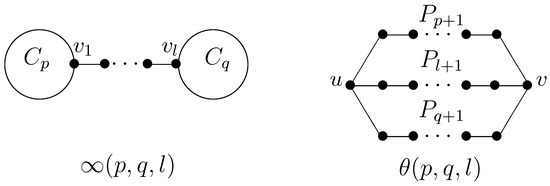
Figure 1. ∞-graph and $\theta$-graph.

If each block of G is either a cycle or an edge, then we called graph G a cactus graph. Suppose ${\mathcal{C}}_n^k$ be the set of all cacti with n-vertices and k cycles. Obviously, ${\mathcal{C}}_n^0$ are trees, ${\mathcal{C}}_n^1$ are unicyclic graphs, and ${\mathcal{C}}_n^2$ are bicyclic graphs with exactly two cycles.

There are more results about cacti and bicyclic graphs [16,17,18,19,20,21,22,23,24,25]. More results about Harary index can be found in References [26,27,28,29,30,31,32,33,34], and more results about Detour index can be found in References [14,35,36,37,38,39].

Note that the Detour–Harary index is the same as Harary index for a tree graph; we study the Detour–Harary index of topological structures containing cycles. In this paper, we gave the maximum Detour–Harary index among ${\mathcal{U}}_n$,${\mathcal{B}}_n$ and ${\mathcal{C}}_n^k(k\ge 3)$, respectively.

2. Preliminaries

In this section, we introduce useful lemmas and graph transformations.

Lemma 1.

[40] Let G be a connected graph, x be a cut-vertex of G, and u and v be vertices occurring in different components that arise upon the deletion of vertex x. Then

$$l(u,v|G)=l(u,x|G)+l(x,v|G).$$

2.1. Edge-Lifting Transformation

The edge-lifting transformation [41]. Let $G_1$ and $G_2$ be two graphs with $n_1\ge 2$ and $n_2\ge 2$ vertices. $u_0\in V(G_1)$ and $v_0\in V(G_2)$, G is the graph obtained from $G_1$ and $G_2$ by adding an edge between $u_0$ and $v_0$. $G^{\prime }$ is the graph obtained by identifying $u_0$ to $v_0$ and adding a pendent edge to $u_0(v_0)$. We called graph $G^{\prime }$ the edge-lifting transformation of graph G (see Figure 2).

Figure 2. Edge-lifting transformation.

Lemma 2.

Let graph $G^{\prime }$ be the edge-lifting transformation of graph G. Then $\omega H(G)<\omega H(G^{\prime })$.

Proof. 

By the definition of $\omega H(G)$ and Lemma 1,

$$\begin{array}{cc}\hfill \omega H(G)=& \omega H(G_1)+\omega H(G_2)+{\displaystyle \sum _{x\in V(G_1)\setminus \{u_0\}}}\frac{1}{l(v_0,x|G)}+{\displaystyle \sum _{y\in V(G_2)\setminus \{v_0\}}}\frac{1}{l(u_0,y|G)}\hfill \\ & +\frac{1}{l(u_0,v_0|G)}+{\displaystyle \sum _{\begin{array}{c}x\in V(G_1)\setminus \{u_0\}\\ y\in V(G_2)\setminus \{v_0\}\end{array}}}\frac{1}{l(x,y|G)}\hfill \\ \hfill =& \omega H(G_1)+\omega H(G_2)+{\displaystyle \sum _{x\in V(G_1)\setminus \{u_0\}}}\frac{1}{1+l(u_0,x|G)}+{\displaystyle \sum _{y\in V(G_2)\setminus \{v_0\}}}\frac{1}{1+l(v_0,y|G)}\hfill \\ & +1+{\displaystyle \sum _{\begin{array}{c}x\in V(G_1)\setminus \{u_0\}\\ y\in V(G_2)\setminus \{v_0\}\end{array}}}\frac{1}{l(u_0,x|G)+1+l(v_0,y|G)},\hfill \\ \hfill \omega H(G^{\prime })=& \omega H(G_1^{\prime })+\omega H(G_2^{\prime })+{\displaystyle \sum _{x^{\prime }\in V(G_1^{\prime })\setminus \{u_0\}}}\frac{1}{l(w_0,x^{\prime }|G^{\prime })}+{\displaystyle \sum _{y^{\prime }\in V(G_2^{\prime })\setminus \{u_0\}}}\frac{1}{l(w_0,y^{\prime }|G^{\prime })}\hfill \\ & +\frac{1}{l(u_0,w_0|G^{\prime })}+{\displaystyle \sum _{\begin{array}{c}{x}^{\prime }\in V(G_1^{\prime })\setminus \{u_0\}\\ y^{\prime }\in V(G_2^{\prime })\setminus \{u_0\}\end{array}}}\frac{1}{l(x^{\prime },y^{\prime }|G^{\prime })}\hfill \\ \hfill =& \omega H(G_1^{\prime })+\omega H(G_2^{\prime })+{\displaystyle \sum _{x^{\prime }\in V(G_1^{\prime })\setminus \{u_0\}}}\frac{1}{1+l(u_0,x^{\prime }|G^{\prime })}+{\displaystyle \sum _{y^{\prime }\in V(G_2^{\prime })\setminus \{u_0\}}}\frac{1}{1+l(u_0,y^{\prime }|G^{\prime })}\hfill \\ & +1+{\displaystyle \sum _{\begin{array}{c}{x}^{\prime }\in V(G_1^{\prime })\setminus \{u_0\}\\ y^{\prime }\in V(G_2^{\prime })\setminus \{u_0\}\end{array}}}\frac{1}{l(u_0,x^{\prime }|G^{\prime })+l(u_0,y^{\prime }|G^{\prime })}.\hfill \end{array}$$

Obviously,

$$\begin{array}{cc}\hfill \omega H(G_1)=& \omega H(G_1^{\prime });\hfill \\ \hfill \omega H(G_2)=& \omega H(G_2^{\prime });\hfill \\ \hfill l(u_0,x|G)=& l(u_0,x^{\prime }|G^{\prime }),\mathrm{where}x\in V(G_1)\setminus \{u_0\}\mathrm{and}{x}^{\prime }\in V(G_1^{\prime })\setminus \{u_0\};\hfill \\ \hfill l(v_0,y|G)=& l(u_0,y^{\prime }|G^{\prime }),\mathrm{where}y\in V(G_2)\setminus \{v_0\}\mathrm{and}{y}^{\prime }\in V(G_2^{\prime })\setminus \{u_0\}.\hfill \end{array}$$

Then

$$\begin{array}{cc}\hfill \omega H(G)-\omega H(G^{\prime })=& {\displaystyle \sum _{\begin{array}{c}x\in V(G_1)\setminus \{u_0\}\\ y\in V(G_2)\setminus \{v_0\}\end{array}}}\frac{1}{l(x,u_0|G)+1+l(v_0,y|G)}\hfill \\ & -{\displaystyle \sum _{\begin{array}{c}{x}^{\prime }\in V(G_1^{\prime })\setminus \{u_0\}\\ y^{\prime }\in V(G_2^{\prime })\setminus \{u_0\}\end{array}}}\frac{1}{l(x^{\prime },u_0|G^{\prime })+l(u_0,y^{\prime }|G^{\prime })}<0.\hfill \end{array}$$

 □

2.2. Cycle-Edge Transformation

Suppose $G\in {\mathcal{C}}_n^l$ is a cactus as shown in Figure 3. $C_p=v_1{v}_2\cdots v_p{v}_1$ is a cycle of G; $G_i$ is a cactus, and $v_i\in V(G_i)$, $1\le i\le p$; $W_{v_i}=N_G(v_i)\cap V(G_i)$, $1\le i\le p$. $G^{\prime }$ is the graph obtained from G by deleting the edges from $v_i$ to $W_{v_i}(2\le i\le p)$, while adding the edges from $v_1$ to $W_{v_i}(2\le i\le p)$.

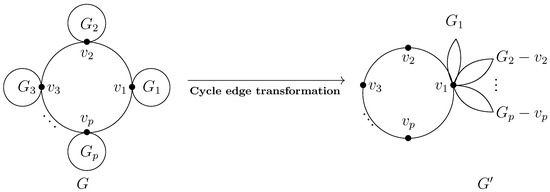
Figure 3. Cycle-edge transformation.

We called graph $G^{\prime }$ the cycle-edge transformation of graph G (see Figure 3).

Lemma 3.

Suppose $G\in {\mathcal{C}}_n^l$ is a cactus, $p\ge 3$, and $G^{\prime }$ is the cycle-edge transformation of G (see Figure 3). Then, $\omega H(G)\le \omega H(G^{\prime })$, and the equality holds if and only if $G\cong G^{\prime }$.

Proof. 

Let $V_i=V(G_i-v_i)$, $1\le i\le p$. By the definition of $\omega H(G)$ and Lemma 1,

$$\begin{array}{cc}\hfill \omega H(G)=& \omega H(C_p)+\frac{1}{2}{\displaystyle \sum _{i=1}^p}{\displaystyle \sum _{x,y\in V_i}}\frac{1}{l(x,y|G)}+\frac{1}{2}{\displaystyle \sum _{i=1}^p}{\displaystyle \sum _{j=1}^p}{\displaystyle \sum _{\begin{array}{c}x\in V_i\\ y\in V_j\\ i\ne j\end{array}}}\frac{1}{l(x,y|G)}+{\displaystyle \sum _{i=1}^p}{\displaystyle \sum _{\begin{array}{c}x\in V_i\\ y\in V(C_p)\end{array}}}\frac{1}{l(x,y|G)}\hfill \\ \hfill =& \omega H(C_p)+\frac{1}{2}{\displaystyle \sum _{i=1}^p}{\displaystyle \sum _{x,y\in V_i}}\frac{1}{l(x,y|G)}+\frac{1}{2}{\displaystyle \sum _{i=1}^p}{\displaystyle \sum _{j=1}^p}{\displaystyle \sum _{\begin{array}{c}x\in V_i\\ y\in V_j\\ i\ne j\end{array}}}\frac{1}{l(x,v_i|G)+l(v_i,v_j|G)+l(v_j,y|G)}\hfill \\ & +{\displaystyle \sum _{i=1}^p}{\displaystyle \sum _{\begin{array}{c}x\in V_i\\ y\in V(C_p)\end{array}}}\frac{1}{l(x,v_i|G)+l(v_i,y|G)},\hfill \end{array}$$

$$\begin{array}{cc}\hfill \omega H(G^{\prime })=& \omega H(C_p)+\frac{1}{2}{\displaystyle \sum _{i=1}^p}{\displaystyle \sum _{x,y\in V_i}}\frac{1}{l(x,y|G^{\prime })}+\frac{1}{2}{\displaystyle \sum _{i=1}^p}{\displaystyle \sum _{j=1}^p}{\displaystyle \sum _{\begin{array}{c}x\in V_i\\ y\in V_j\\ i\ne j\end{array}}}\frac{1}{l(x,y|G^{\prime })}+{\displaystyle \sum _{i=1}^p}{\displaystyle \sum _{\begin{array}{c}x\in V_i\\ y\in V(C_p)\end{array}}}\frac{1}{l(x,y|G^{\prime })}\hfill \\ \hfill =& \omega H(C_p)+\frac{1}{2}{\displaystyle \sum _{i=1}^p}{\displaystyle \sum _{x,y\in V_i}}\frac{1}{l(x,y|G^{\prime })}+\frac{1}{2}{\displaystyle \sum _{i=1}^p}{\displaystyle \sum _{j=1}^p}{\displaystyle \sum _{\begin{array}{c}x\in V_i\\ y\in V_j\\ i\ne j\end{array}}}\frac{1}{l(x,v_1|G^{\prime })+l(v_1,y|G^{\prime })}\hfill \\ & +{\displaystyle \sum _{i=1}^p}{\displaystyle \sum _{\begin{array}{c}x\in V_i\\ y\in V(C_p)\end{array}}}\frac{1}{l(x,v_1|G^{\prime })+l(v_1,y|G^{\prime })}.\hfill \end{array}$$

Obviously,

$$\begin{array}{cc}\hfill {\displaystyle \sum _{i=1}^p}{\displaystyle \sum _{x,y\in V_i}}\frac{1}{l(x,y|G)}=& {\displaystyle \sum _{i=1}^p}{\displaystyle \sum _{x,y\in V_i}}\frac{1}{l(x,y|G^{\prime })};\hfill \\ \hfill l(x,v_i|G)=& l(x,v_1|G^{\prime }),\mathrm{where}x\in V_i;\hfill \\ \hfill l(v_j,y|G)=& l(v_1,y|G^{\prime }),\mathrm{where}y\in V_j;\hfill \\ \hfill {\displaystyle \sum _{i=1}^p}{\displaystyle \sum _{\begin{array}{c}x\in V_i\\ y\in V(C_p)\end{array}}}\frac{1}{l(x,v_i|G)+l(v_i,y|G)}=& {\displaystyle \sum _{i=1}^p}{\displaystyle \sum _{\begin{array}{c}x\in V_i\\ y\in V(C_p)\end{array}}}\frac{1}{l(x,v_1|G^{\prime })+l(v_1,y|G^{\prime })}.\hfill \end{array}$$

Then

$$\begin{array}{cc}\hfill \omega H(G)-\omega H(G^{\prime })=& \frac{1}{2}{\displaystyle \sum _{i=1}^p}{\displaystyle \sum _{j=1}^p}{\displaystyle \sum _{\begin{array}{c}x\in V_i\\ y\in V_j\\ i\ne j\end{array}}}\frac{1}{l(x,v_i|G)+l(v_i,v_j|G)+l(v_j,y|G)}\hfill \\ & -\frac{1}{2}{\displaystyle \sum _{i=1}^p}{\displaystyle \sum _{j=1}^p}{\displaystyle \sum _{\begin{array}{c}x\in V_i\\ y\in V_j\\ i\ne j\end{array}}}\frac{1}{l(x,v_1|G^{\prime })+l(v_1,y|G^{\prime })}<0.\hfill \end{array}$$

The proof is completed. □

2.3. Cycle Transformation

Suppose $G\in {\mathcal{C}}_n^l$ is a cactus, as shown in Figure 4. $C_p=v_1{v}_2\cdots v_p{v}_1$ is a cycle of G, and $G_1$ is a simple and connected graph, $v_1\in V(G_1)$. $G^{\prime }$ is the graph obtained from G by deleting the edges from $v_i$ to $v_{i+1}(2\le i\le p-1)$, meanwhile, adding the edges from $v_1$ to $v_i(3\le i\le p-1)$.

Figure 4. Cycle transformation.

We called graph $G^{\prime }$ is the cycle transformation of G (see Figure 4).

Lemma 4.

Suppose graph G is a simple and connected graph with $p\ge 4$, and $G^{\prime }$ is the cycle transformation of G(see Figure 4). Then, $\omega H(G)<\omega H(G^{\prime })$.

Proof. 

Let $V(C_p)=\{v_1,v_2,\cdots ,v_p\}$, $V_1=V(C_p-v_1)$, $V_2=V(G_1-v_1)$. By the definition of $\omega H(G)$,

$$\begin{array}{cc}\hfill \omega H(G)=& \omega H(G_1)+{\displaystyle \sum _{x,y\in V(C_p)}}\frac{1}{l(x,y|G)}+{\displaystyle \sum _{\begin{array}{c}x\in V_1\\ y\in V_2\end{array}}}\frac{1}{l(x,y|G)}\hfill \\ \hfill =& \omega H(G_1)+{\displaystyle \sum _{x,y\in V(C_p)}}\frac{1}{l(x,y|G)}+{\displaystyle \sum _{\begin{array}{c}x\in V_1,\\ y\in V_2\end{array}}}\frac{1}{l(x,v_1|G)+l(v_1,y|G)},\hfill \\ \hfill \omega H(G^{\prime })=& \omega H(G_1)+{\displaystyle \sum _{x,y\in V(C_p)}}\frac{1}{l(x,y|G^{\prime })}+{\displaystyle \sum _{\begin{array}{c}x\in V_1,\\ y\in V_2\end{array}}}\frac{1}{l(x,y|G^{\prime })}\hfill \\ \hfill =& \omega H(G_1)+{\displaystyle \sum _{x,y\in V(C_p)}}\frac{1}{l(x,y|G^{\prime })}+{\displaystyle \sum _{\begin{array}{c}x\in V_1,\\ y\in V_2\end{array}}}\frac{1}{l(x,v_1|G^{\prime })+l(v_1,y|G^{\prime })},\hfill \end{array}$$

Obviously,

$$\begin{array}{cc}\hfill l(x,y|G)\ge & l(x,y|G^{\prime }),\mathrm{where}x,y\in V_1;\hfill \\ \hfill l(x,v_1|G)>& 2\ge l(x,v_1|G^{\prime }),\mathrm{where}x\in V_1;\hfill \\ \hfill l(v_1,y|G)=& l(v_1,y|G^{\prime }),\mathrm{where}y\in V_2.\hfill \end{array}$$

Then

$$\begin{array}{cc}\hfill \omega H(G)-\omega H(G^{\prime })=& ({\displaystyle \sum _{x,y\in V(C_p)}}\frac{1}{l(x,y|G)}-{\displaystyle \sum _{x,y\in V(C_p)}}\frac{1}{l(x,y|G^{\prime })})\hfill \\ & +({\displaystyle \sum _{\begin{array}{c}x\in V_1,\\ y\in V_2\end{array}}}\frac{1}{l(x,v_1|G)+l(v_1,y|G)}-{\displaystyle \sum _{\begin{array}{c}x\in V_1,\\ y\in V_2\end{array}}}\frac{1}{l(x,v_1|G^{\prime })+l(v_1,y|G^{\prime })})<0.\hfill \end{array}$$

 □

3. Maximum Detour–Harary Index of Unicyclic Graphs

For any unicyclic graph $G\in {\mathcal{U}}_n$, by repeating edge-lifting transformations, cycle-edge transformations, cycle transformations, or any combination of these on G, we get $U_1$ from G, where graph $U_1$ is defined in Figure 5.

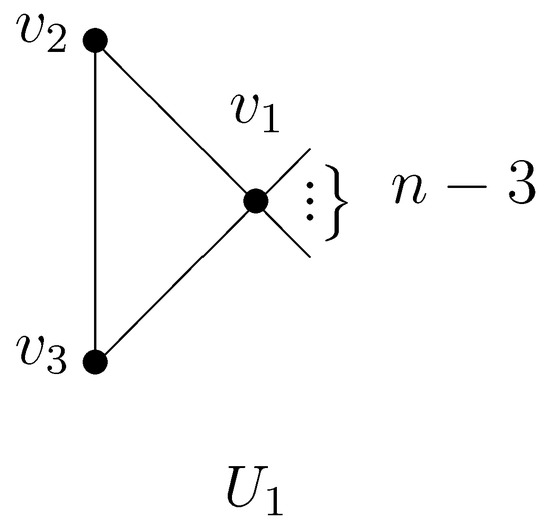
Figure 5. Unicyclic graph $U_1$.

Theorem 1.

Let $U_1$ be defined as Figure 5. Then, $U_1$ is the unique graph that attains the maximum Detour–Harary index among all graphs in ${\mathcal{U}}_n(n\ge 3)$, and $\omega H(U_1)=\frac{3n^2-n-6}{12}.$

Proof. 

By Lemmas 2–4, $U_1$ is the unique graph which attains the maximum Detour–Harary index of all graphs in ${\mathcal{U}}_n$. We then calculate the value $\omega H(U_1)$.

Let $V(U_1)=\{v_1,v_2,\cdots ,v_n\}.$ It can be checked directly that

$$\begin{array}{cc}\hfill {\displaystyle \sum _{i=2}^n}\frac{1}{l(v_1,v_i|U_1)}=& n-2;\hfill \\ \hfill {\displaystyle \sum _{1\le i\le n,i\ne 2}}\frac{1}{l(v_2,v_i|U_1)}=& {\displaystyle \sum _{1\le j\le n,j\ne 3}}\frac{1}{l(v_3,v_j|U_1)}=\frac{1}{2}+\frac{1}{2}+\frac{n-3}{3}=\frac{n}{3};\hfill \\ \hfill {\displaystyle \sum _{1\le i\le n,i\ne 4}}\frac{1}{l(v_4,v_i|U_1)}=& 1+\frac{n-4}{2}+\frac{2}{3}=\frac{3n-2}{6}.\hfill \end{array}$$

Then

$$\begin{array}{cc}\hfill \omega H(U_1)=& \frac{1}{2}[{\displaystyle \sum _{i=2}^n}\frac{1}{l(v_1,v_i|U_1)}+2{\displaystyle \sum _{1\le i\le n,i\ne 2}}\frac{1}{l(v_2,v_i|U_1)}+(n-3){\displaystyle \sum _{i=1}^n}\frac{1}{l(v_4,v_i|U_1)}]\hfill \\ \hfill =& \frac{3n^2-n-6}{12}.\hfill \end{array}$$

The proof is completed. □

4. Maximum Detour–Harary Index of Bicyclic Graphs

For any bicyclic graph $G\in \infty (p,q,l)$ with exactly two cycles, by repeating edge-lifting transformations, cycle-edge transformations, cycle transformations, or any combination of these on G, we get $B_1$ from G, where graph $B_1$ is defined in Figure 6.

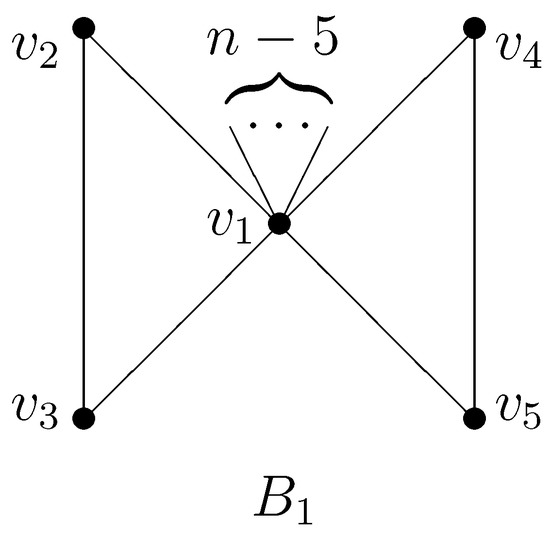
Figure 6. Bicyclic graph $B_1$.

For any bicyclic graph $G\in \theta (p,q,l)$ with n vertices, by repeating edge-lifting transformations on G, we get $B_2$ from G, where graph $B_2$ is defined in Figure 7.

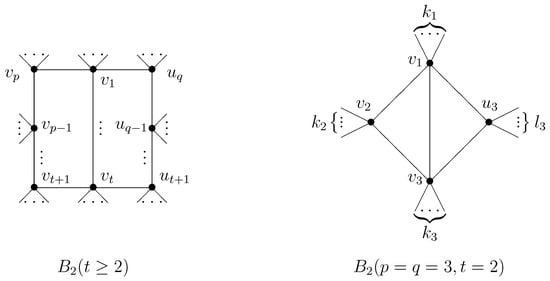
Figure 7. Bicyclic graph $B_2$($t\ge 2$).

Theorem 2.

Let $B_2,B_3$ be defined as Figure 7 and Figure 8. Then, $\omega H(B_2)\le \omega H(B_3),$ and the equality holds if and only if $B_2\cong B_3$.

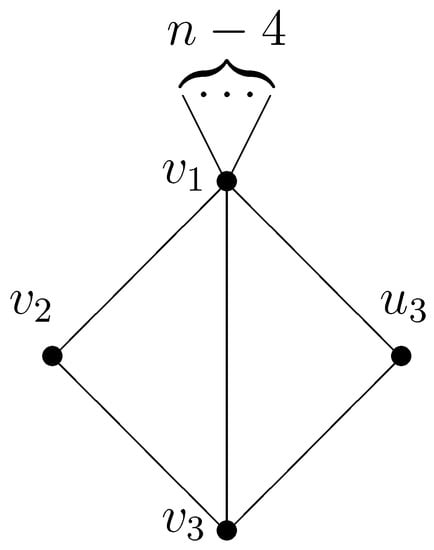
Figure 8. Bicyclic graph $B_2$($t\ge 2$).

Proof. 

Case 1. $B_2=B_3$. Obviously, $\omega H(B_2)=\omega H(B_3).$

Case 2. $B_2\ne B_3$ and $p=q=3,t=2$(see Figure 7 and Figure 8).

Let $V_1=\{v_1,v_2,v_3,u_3\}$, $W_{v_i}=\{w\mid w{v}_i\in E(B_2)$ and $d_{B_2}(w)=1\}$ and $|W_{v_i}|=k_i$, $W_{u_3}=\{w\mid w{u}_3\in E(B_2)$ and $d_{B_2}(w)=1\}$ and $|W_{u_3}|=l_3,k_i+l_3=n-4$ for $1\le i\le 3$.

$$\begin{array}{cc}\hfill \omega H(B_2)=& {\displaystyle \sum _{x,y\in V_1}}\frac{1}{l(x,y|B_2)}+{\displaystyle \sum _{\begin{array}{c}x\in V_1,\\ y\in V(B_2)-V_1\end{array}}}\frac{1}{l(x,y|B_2)}+{\displaystyle \sum _{x,y\in V(B_2)-V_1}}\frac{1}{l(x,y|B_2)},\hfill \\ \hfill \omega H(B_3)=& {\displaystyle \sum _{x,y\in V_1}}\frac{1}{l(x,y|B_3)}+{\displaystyle \sum _{\begin{array}{c}x\in V_1,\\ y\in V(B_3)-V_1\end{array}}}\frac{1}{l(x,y|B_3)}+{\displaystyle \sum _{x,y\in V(B_3)-V_1}}\frac{1}{l(x,y|B_3)}.\hfill \end{array}$$

Easily,

$${\displaystyle \sum _{x,y\in V_1}}\frac{1}{l(x,y|B_2)}={\displaystyle \sum _{x,y\in V_1}}\frac{1}{l(x,y|B_3)}$$

(1)

$$\begin{array}{cc}\hfill {\displaystyle \sum _{\begin{array}{c}x\in V_1,\\ y\in V(B_2)-V_1\end{array}}}\frac{1}{l(x,y|B_2)}=& {\displaystyle \sum _{\begin{array}{c}w\in V(B_2)-V_1\end{array}}}\frac{1}{l(v_1,w|B_2)}+{\displaystyle \sum _{\begin{array}{c}w\in V(B_2)-V_1\end{array}}}\frac{1}{l(v_2,w|B_2)}\hfill \\ & +{\displaystyle \sum _{\begin{array}{c}w\in V(B_2)-V_1\end{array}}}\frac{1}{l(v_3,w|B_2)}+{\displaystyle \sum _{\begin{array}{c}w\in V(B_2)-V_1\end{array}}}\frac{1}{l(u_3,w|B_2)}\hfill \\ \hfill =& (1·k_1+\frac{1}{4}·k_2+\frac{1}{3}·k_3+\frac{1}{4}·l_3)+(\frac{1}{4}·k_1+1·k_2+\frac{1}{4}·k_3+\frac{1}{4}·l_3)\hfill \\ & +(\frac{1}{3}·k_1+\frac{1}{4}·k_2+1·k_3+\frac{1}{4}·l_3)+(\frac{1}{4}·k_1+\frac{1}{4}·k_2+\frac{1}{4}·k_3+1·l_3)\hfill \\ \hfill =& \frac{11(k_1+k_3)}{6}+\frac{7(k_2+l_3)}{4},\hfill \end{array}$$

$$\begin{array}{cc}\hfill {\displaystyle \sum _{\begin{array}{c}x\in V_1,\\ y\in V(B_3)-V_1\end{array}}}\frac{1}{l(x,y|B_3)}=& {\displaystyle \sum _{\begin{array}{c}w\in V(B_3)-V_1\end{array}}}\frac{1}{l(v_1,w|B_3)}+{\displaystyle \sum _{\begin{array}{c}w\in V(B_3)-V_1\end{array}}}\frac{1}{l(v_2,w|B_3)}\hfill \\ & +{\displaystyle \sum _{\begin{array}{c}w\in V(B_3)-V_1\end{array}}}\frac{1}{l(v_3,w|B_3)}+{\displaystyle \sum _{\begin{array}{c}w\in V(B_3)-V_1\end{array}}}\frac{1}{l(u_3,w|B_3)}\hfill \\ \hfill =& 1·(n-4)+\frac{1}{4}·(n-4)+\frac{1}{3}·(n-4)+\frac{1}{4}·(n-4)\hfill \\ \hfill =& \frac{11(n-4)}{6}\hfill \\ \hfill =& \frac{11(k_1+k_2+k_3+l_3)}{6},(\sin \mathrm{ce}{k}_i+l_3=n-4\mathrm{for}1\le i\le 3)\hfill \end{array}$$

Then,

$${\displaystyle \sum _{\begin{array}{c}x\in V_1,\\ y\in V(B_2)-V_1\end{array}}}\frac{1}{l(x,y|B_2)}-{\displaystyle \sum _{\begin{array}{c}x\in V_1,\\ y\in V(B_3)-V_1\end{array}}}\frac{1}{l(x,y|B_3)}=\frac{1}{12}(k_2+l_3)\ge 0,$$

(2)

the equality holds if and only if $k_2=l_3=0$.

On the other hand $\frac{1}{l(x,y|B_2)}\le \frac{1}{l(x,y|B_3)}=\frac{1}{2}$, where $x,y\in V(B_2)-V_1$, then

$${\displaystyle \sum _{x,y\in V(B_3)-V_1}}\frac{1}{l(x,y|B_2)}\le {\displaystyle \sum _{x,y\in V(B_3)-V_1}}\frac{1}{l(x,y|B_3)},$$

(3)

the equality holds if $k_1=n-4$ or $k_2=n-4$ or $k_3=n-4$ or $l_3=n-4$.

By (1)–(3) and $B_2\ne B_3$, we have $\omega H(B_2)<\omega H(B_3)$.

Case 3. $B_2\ne B_3$ and $p+q-t>4$.

It can be checked directly that

$$\omega H(B_2)\le \underset{n-p-q+t}{\underbrace{(1+1+\cdots +1)}}+\frac{1}{2}\left(\genfrac{}{}{0pt}{}{n-p-q+t}{2}\right)+\frac{1}{4}\left[\left(\genfrac{}{}{0pt}{}{n}{2}\right)-(n-p-q+t)-\left(\genfrac{}{}{0pt}{}{n-p-q+t}{2}\right)\right],$$

$$\omega H(B_3)=\underset{n-4}{\underbrace{(1+1+\cdots +1)}}+\frac{1}{2}[1+\left(\genfrac{}{}{0pt}{}{n-4}{2}\right)]+\frac{1}{3}[5+(n-4)]+\frac{1}{4}[2(n-4)].$$

$B_2,B_3$ are bicyclic graphs and $\mid V(B_2)\mid =\mid V(B_3)\mid =n$. Since $p+q-t>4,$ then $n-p-q+t\le n-5$ and $\left(\genfrac{}{}{0pt}{}{n-p-q+t}{2}\right)<\left(\genfrac{}{}{0pt}{}{n-4}{2}\right)$, we have $\omega H(B_2)<\omega H(B_3).$

The proof is completed. □

Theorem 3.

Let $B_1,B_3$ be defined as Figure 6 and Figure 8. Then,

$$\begin{array}{c}max\{\omega H({\mathcal{B}}_n)\}=\left\{\begin{array}{cc}\omega H(B_3)=\frac{13}{6},\hfill & ifn=4,\hfill \\ \omega H(B_1)=\omega H(B_3)=\frac{3n^2-5n-2}{12},\hfill & ifn\ge 5.\hfill \end{array}\right.\hfill \end{array}$$

Proof. 

Let $G\in \infty (p,q,l)$, by Lemmas 2–4, we have $\omega H(G)\le \omega H(B_1)$, and the equality holds if and only if $G\cong B_1.$

For any bicyclic graph with $G\in \theta (p,q,l)$, by Lemmas 2–4 and Theorem 2, we have $\omega H(G)\le \omega H(B_3)$, and the equality holds if and only if $G\cong B_3.$ Thus, $max\{\omega H({\mathcal{B}}_n)\}=max\{\omega H(B_1),\omega H(B_3)\}$.

It can be checked directly that

$$\omega H(B_1)=(n-5)+\frac{1}{2}[\left(\genfrac{}{}{0pt}{}{n-5}{2}\right)+6]+\frac{1}{3}[4(n-5)]+\frac{1}{4}·4=\frac{3n^2-5n-2}{12},n\ge 5;$$

$$\omega H(B_3)=(n-4)+\frac{1}{2}\left(\genfrac{}{}{0pt}{}{n-4}{2}\right)+\frac{1}{3}(n-4)+\frac{1}{4}[2(n-4)]=\frac{3n^2-5n-2}{12},n\ge 4.$$

Therefore

$$\begin{array}{c}max\{\omega H({\mathcal{B}}_n)\}=\left\{\begin{array}{cc}\omega H(B_3)=\frac{13}{6},\hfill & \mathrm{if}n=4,\hfill \\ \omega H(B_1)=\omega H(B_3)=\frac{3n^2-5n-2}{12},\hfill & \mathrm{if}n\ge 5.\hfill \end{array}\right.\hfill \end{array}$$

The proof is completed. □

5. Maximum Detour–Harary Index of Cacti

For any cactus graph $G\in {\mathcal{C}}_n^k(k\ge 3)$, by repeating edge-lifting transformations, cycle-edge transformations, cycle transformations, or any combination of these on G, we get ${\mathcal{C}}_1$ from G, where graph ${\mathcal{C}}_1$ is defined in Figure 9.

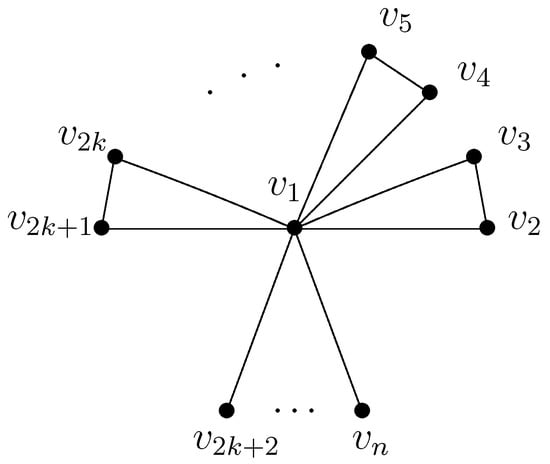
Figure 9. Cactus graph ${\mathcal{C}}_1(k\ge 3)$.

Theorem 4.

Let ${\mathcal{C}}_1$ be defined as Figure 9. Then, ${\mathcal{C}}_1$ is the unique cactus graph in ${\mathcal{C}}_n^k(k\ge 3)$ that attains the maximum Detour–Harary index, and $\omega H({\mathcal{C}}_1)=\frac{3n^2+2k^2-4nk+3n-2k-6}{12}.$

Proof. 

By Lemmas 2–4, ${\mathcal{C}}_1$ is the unique graph that attains the maximum Detour–Harary index of all graphs in ${\mathcal{C}}_n^k(k\ge 3)$.

Let $V({\mathcal{C}}_1)=\{v_1,v_2,\cdots ,v_n\}$, and it can be checked directly that

$$\begin{array}{cc}\hfill {\displaystyle \sum _{i=2}^n}\frac{1}{l(v_1,v_i|{\mathcal{C}}_1)}=& 1·(n-2k-1)+\frac{1}{2}·2k=n-k-1;\hfill \\ \hfill {\displaystyle \sum _{1\le i\le n,i\ne 2}}\frac{1}{l(v_2,v_i|{\mathcal{C}}_1)}=& \frac{1}{2}·2+\frac{1}{3}·(n-2k-1)+\frac{1}{4}·(2k-2)=\frac{1}{3}n-\frac{1}{6}k+\frac{1}{6};\hfill \\ \hfill {\displaystyle \sum _{j=1}^{n-1}}\frac{1}{l(v_n,v_j|{\mathcal{C}}_1)}=& 1+\frac{1}{2}·(n-2k-2)+\frac{1}{3}·2k=\frac{1}{2}n-\frac{1}{3}k.\hfill \end{array}$$

Then,

$$\begin{array}{cc}\hfill \omega H({\mathcal{C}}_1)=& \frac{1}{2}[(n-k-1)+2k·(\frac{1}{3}n-\frac{1}{6}k+\frac{1}{6})+(n-2k-1)·(\frac{1}{2}n-\frac{1}{3}k)]\hfill \\ \hfill =& \frac{3n^2+2k^2-4nk+3n-2k-6}{12}.\hfill \end{array}$$

The proof is completed. □