A Symmetry Motivated Link Table
Abstract
1. Introduction
Importance of Link Symmetries in DNA Topology
2. Writhe and Linking Number
3. Link Symmetries and Nomenclature
3.1. Isotopy Classes
3.2. Doll and Hoste Notation
3.3. Link Symmetries
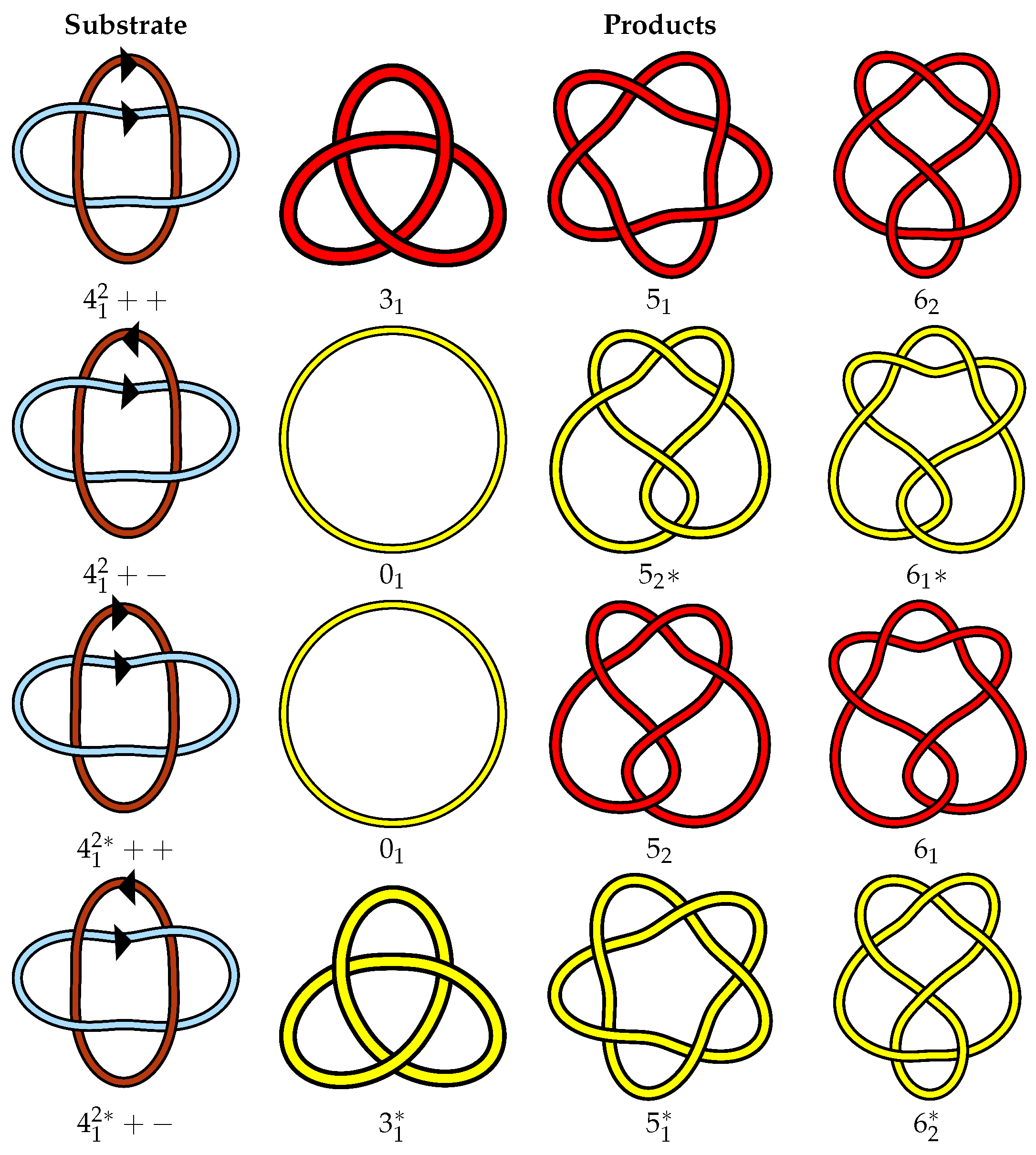
- L is purely invertible if it is isotopic to the link found by simultaneously reversing both components (L++ = L−−).
- L is fully invertible if it is isotopic to L with every other choice of orientation.
- L has even operations symmetry if it is isotopic to links obtained by an even number of reflections and/or component reversals.
- L has pure exchange symmetry if it is isotopic to L with the component labels exchanged (L++ = L++).
- L has a non-pure exchange symmetry if it is isotopic to L with a combination of exchanged labels with a reflection and/or with component reversals, but L++ ≠ L++.
- L has no exchange symmetry, if it is not isotopic to L with the component labels exchanged regardless of any reversals or reflections.
- L has full symmetry if it is isotopic to every link obtained by component relabeling, component reversal, and reflection.
- L has no symmetry if it is not isotopic to any link obtained by component relabeling, component reversal, or reflection.
3.4. Symmetries, Writhe and Linking Number
3.5. Previous Classification Schemes
4. Defining a Canonical Isotopy Class for Links
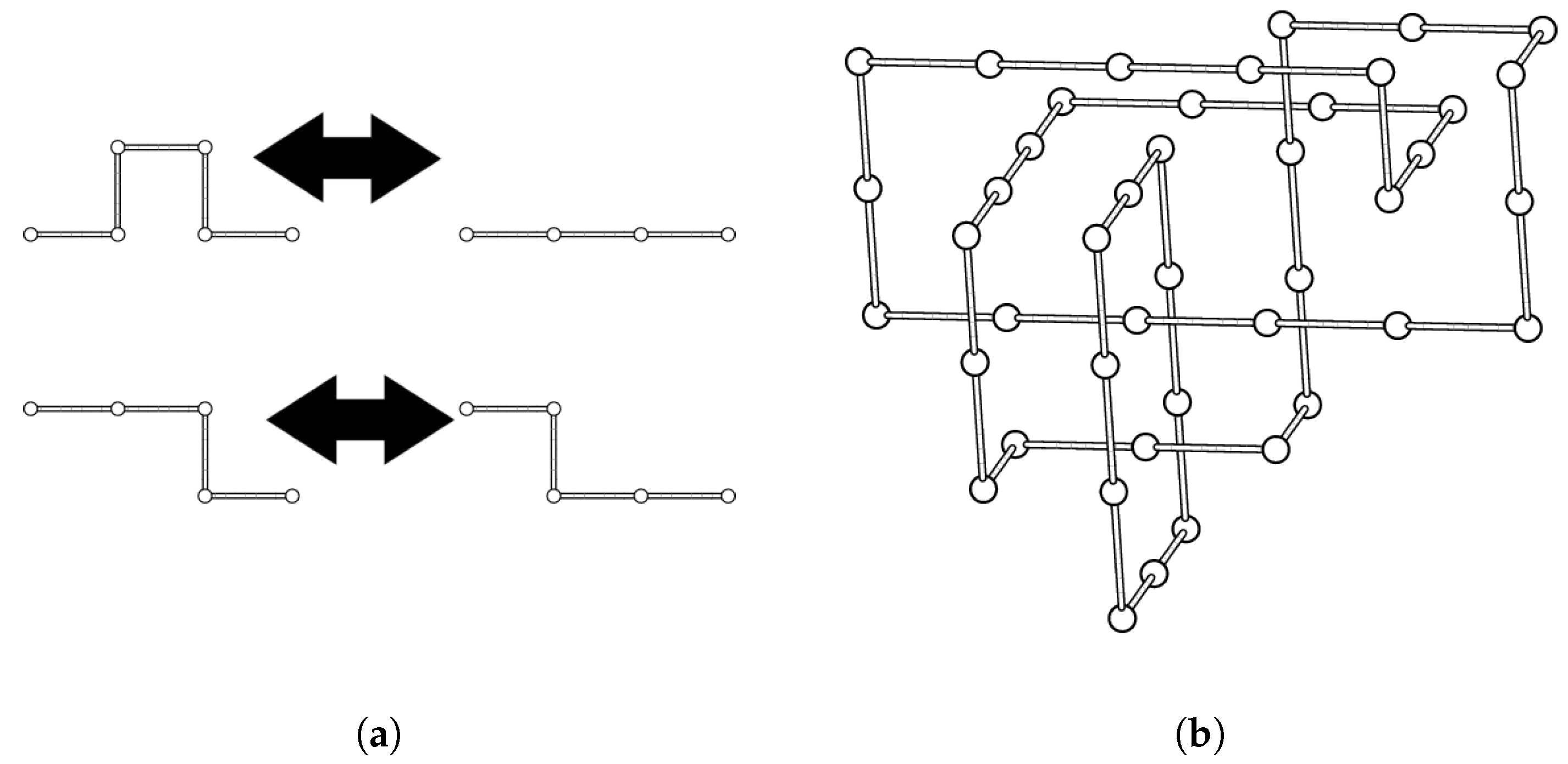
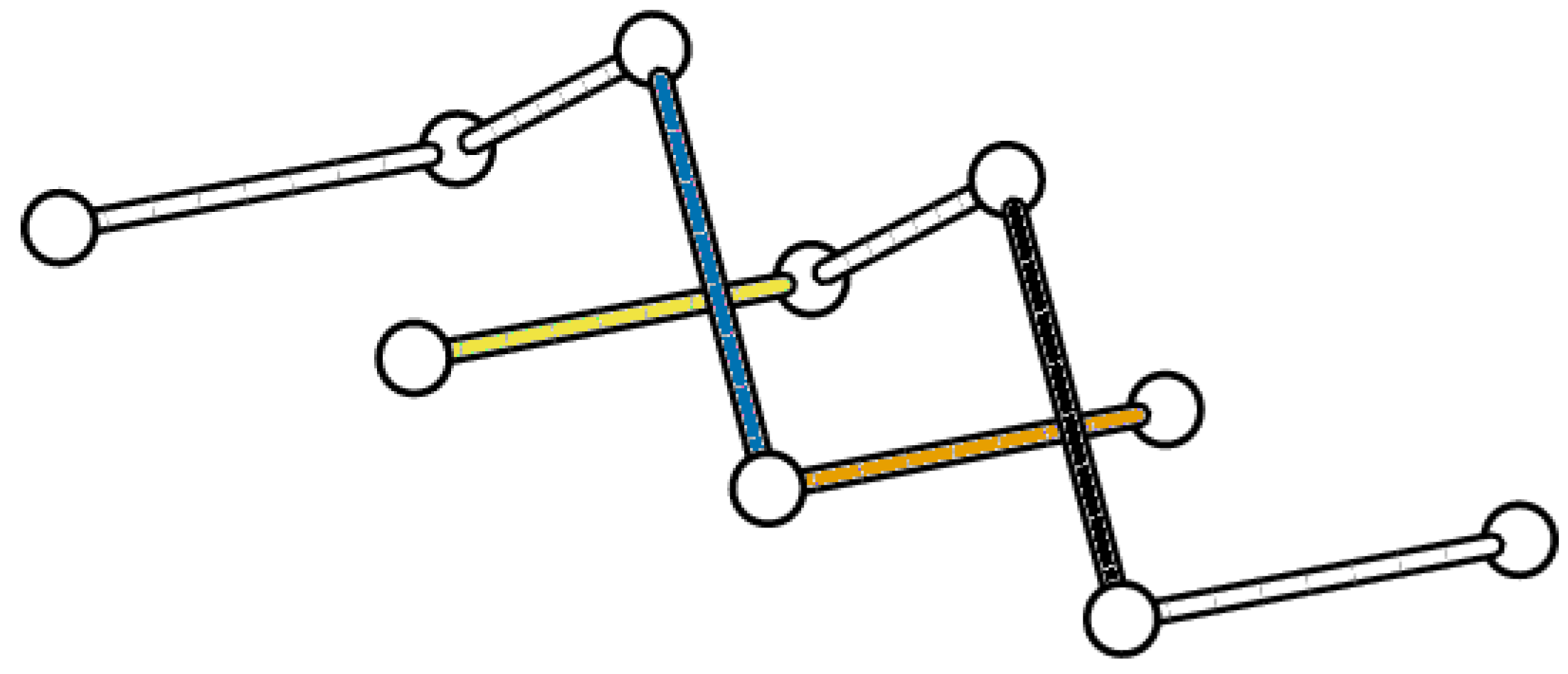
4.1. Cubic Lattice Links and the BFACF Algorithm
4.2. Canonical Isotopy Class
4.3. Proposed Link Table
4.4. Note on Minimum Lattice Links
5. Results and Discussion
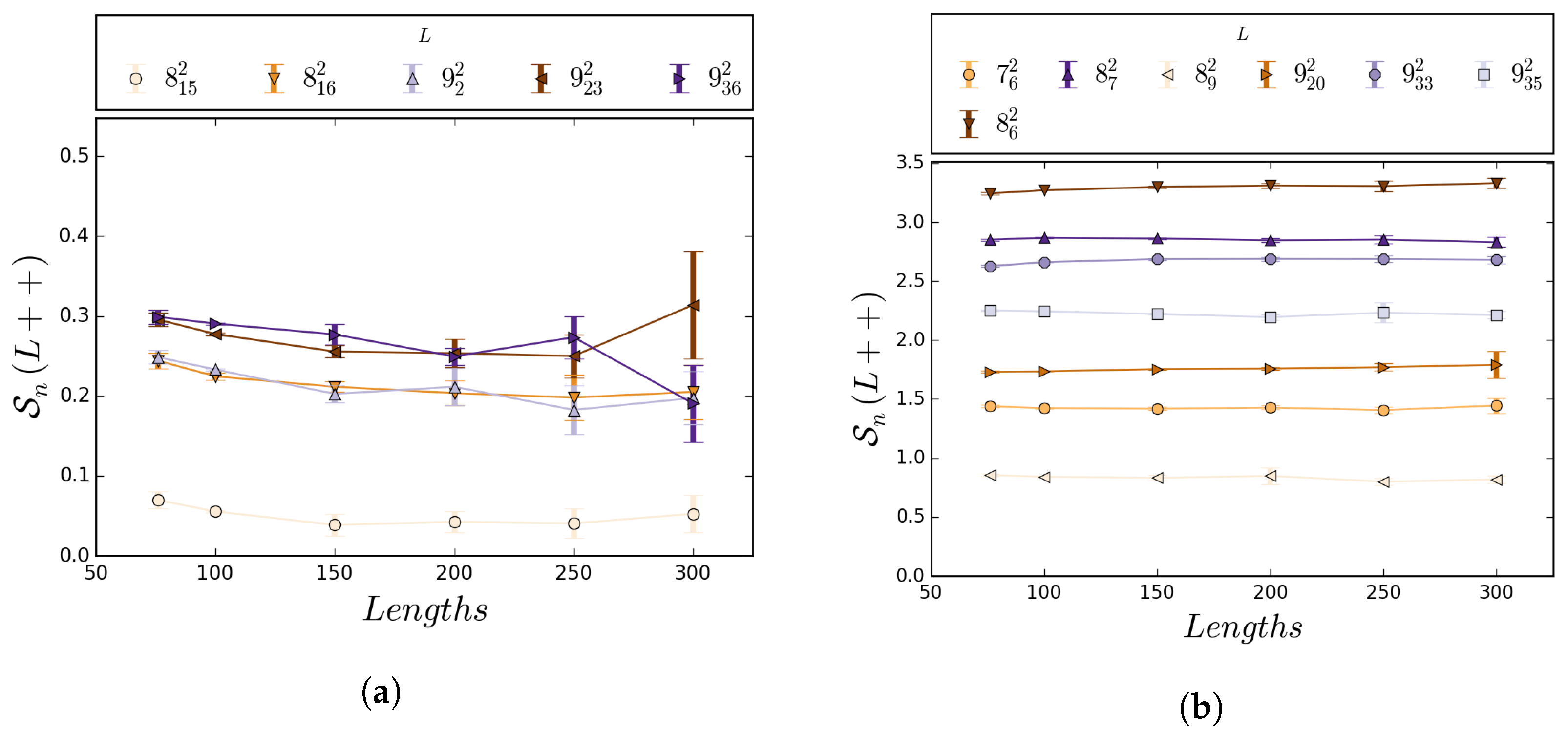
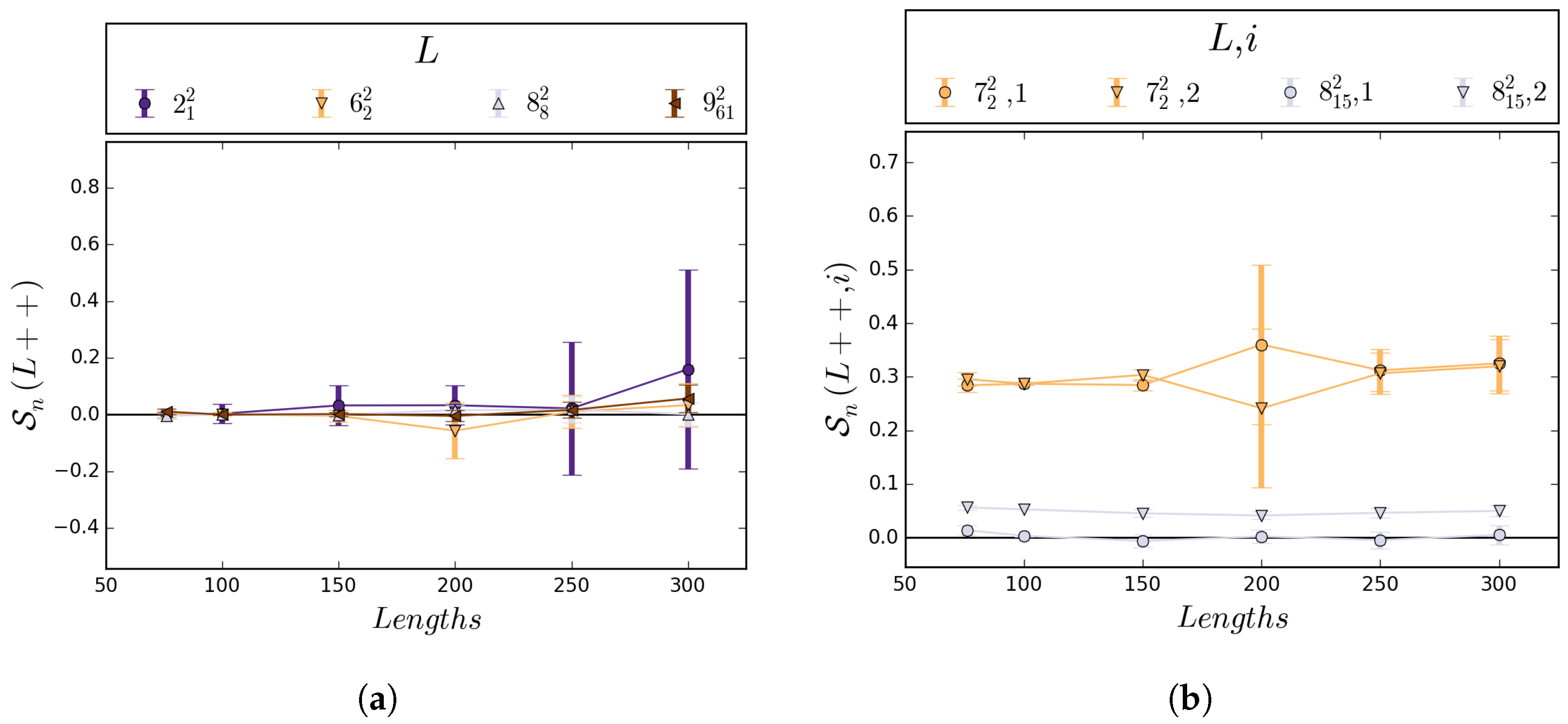
5.1. Numerical Results
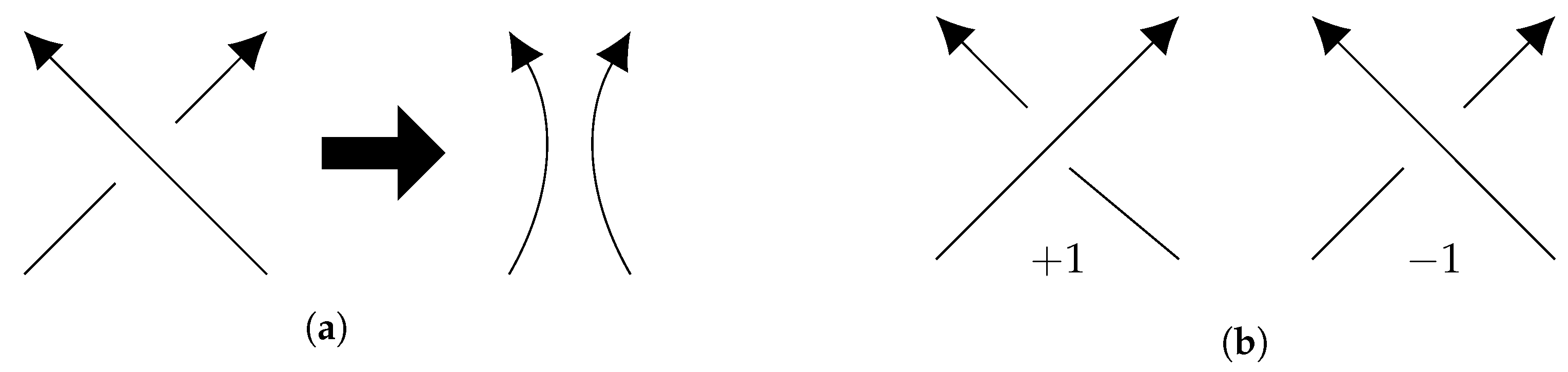
5.2. Boundedness of Writhe under BFACF Moves
- the BFACF edge runs from to ), and
- the result of the BFACF move will push the BFACF edge to an edge from to .
6. Numerical Methods
6.1. BFACF Simulations
6.2. Minimum Length Links
7. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Link Table
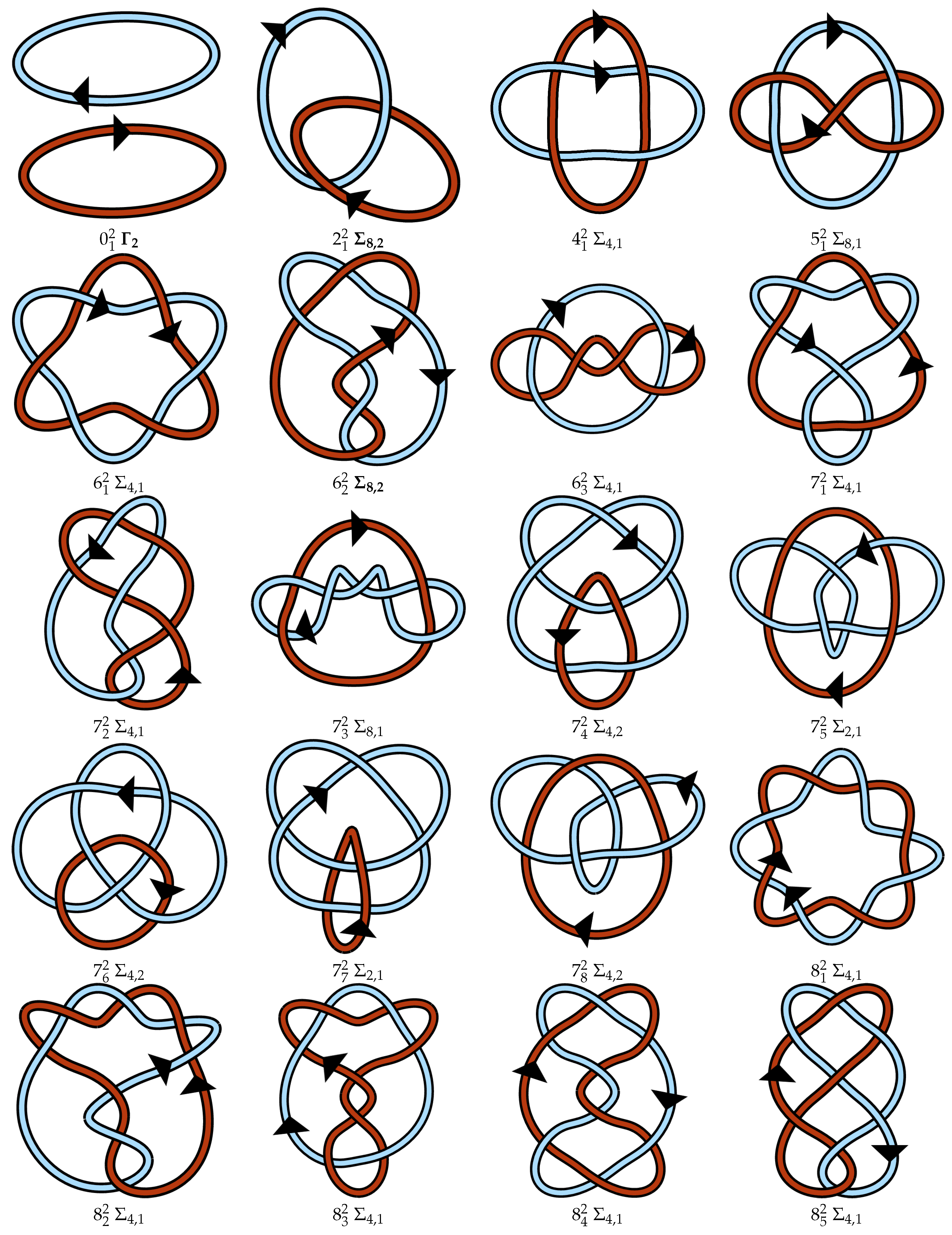
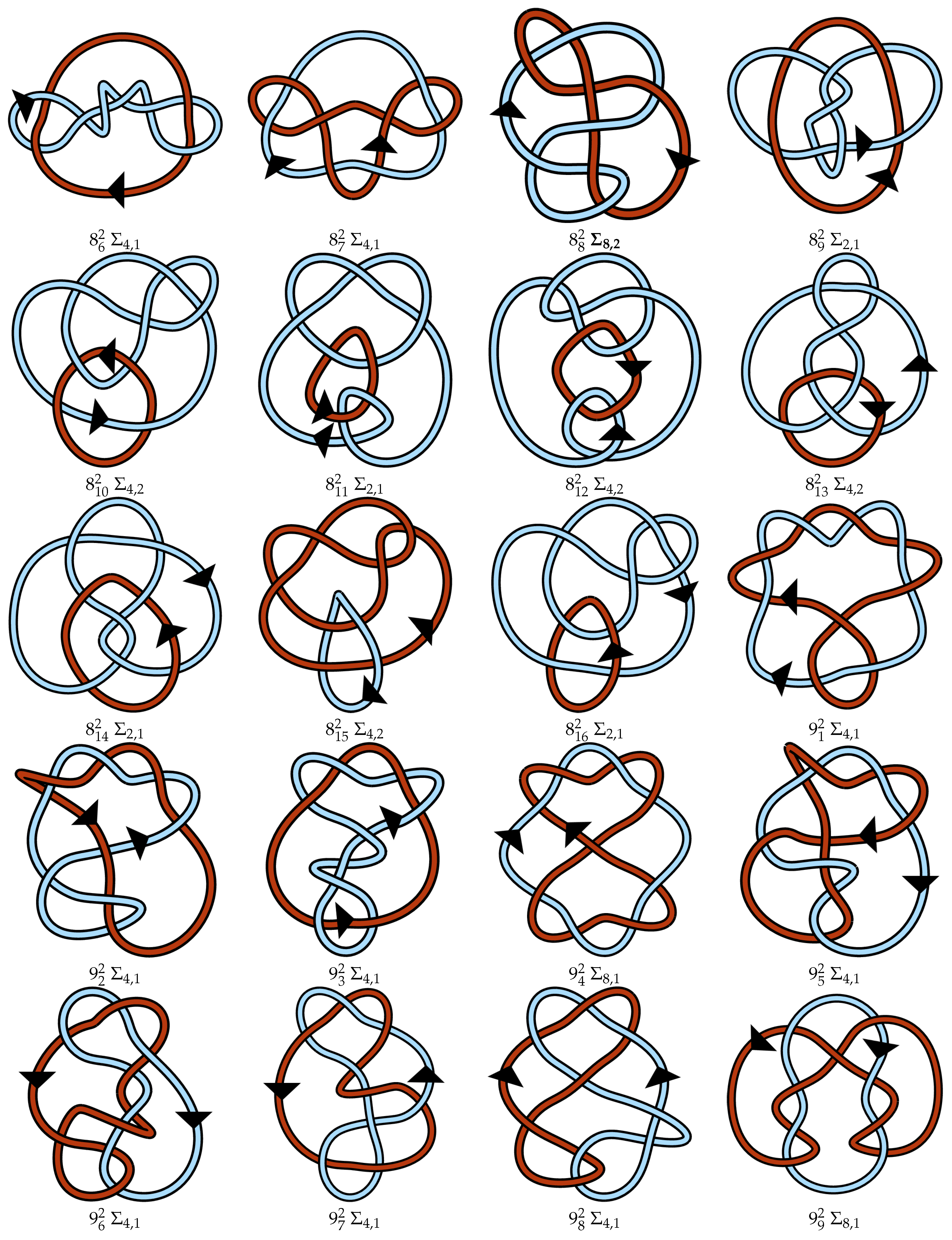
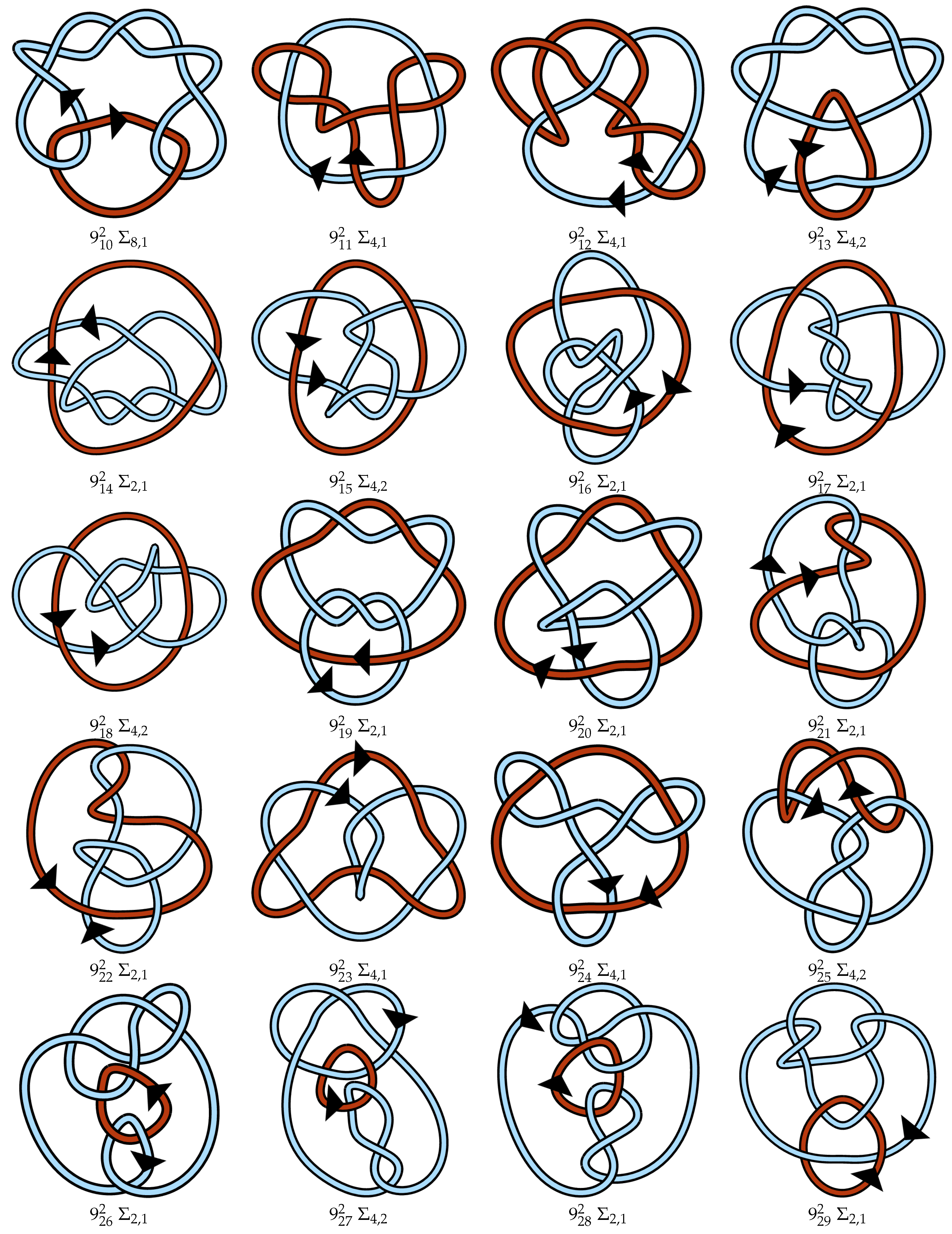
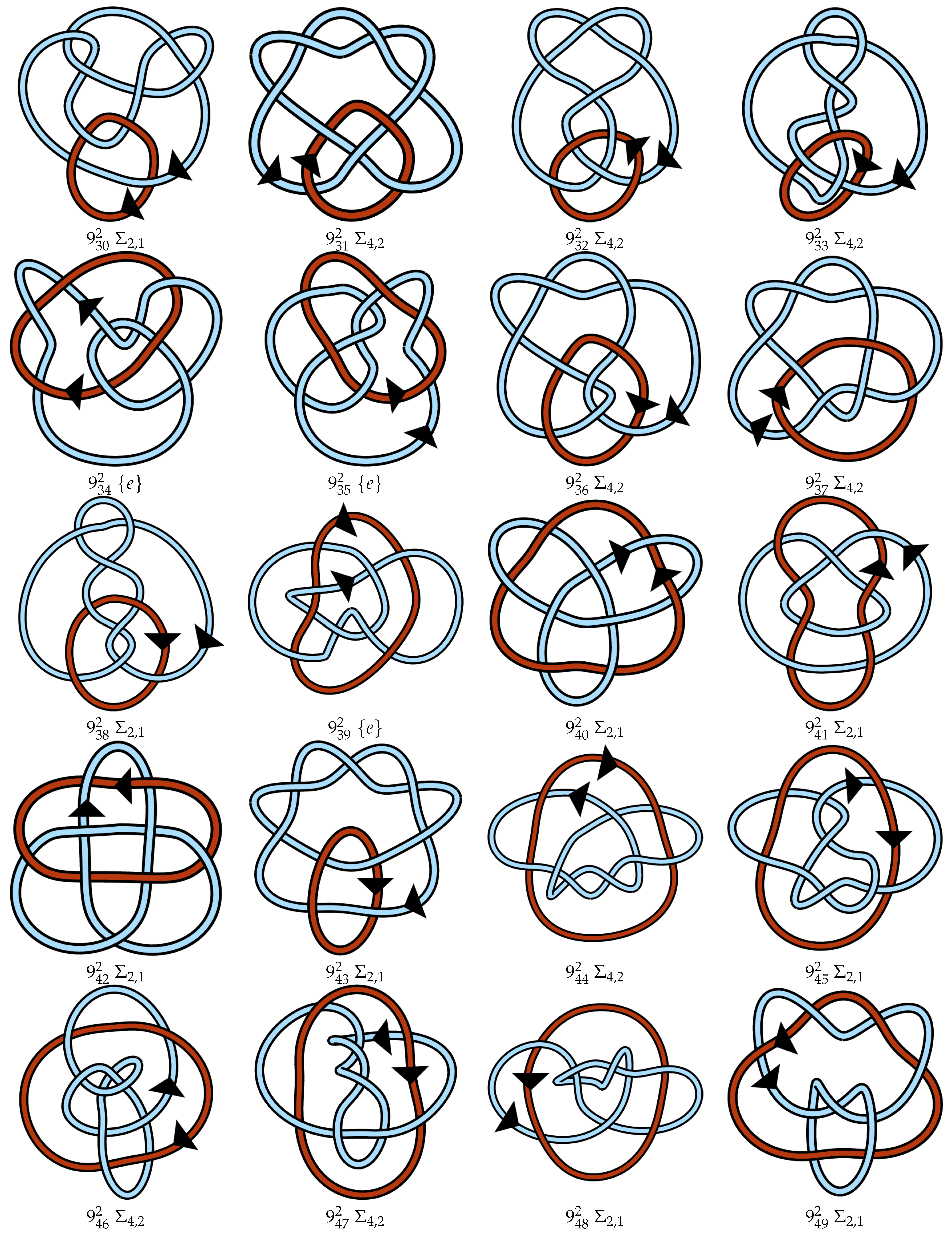
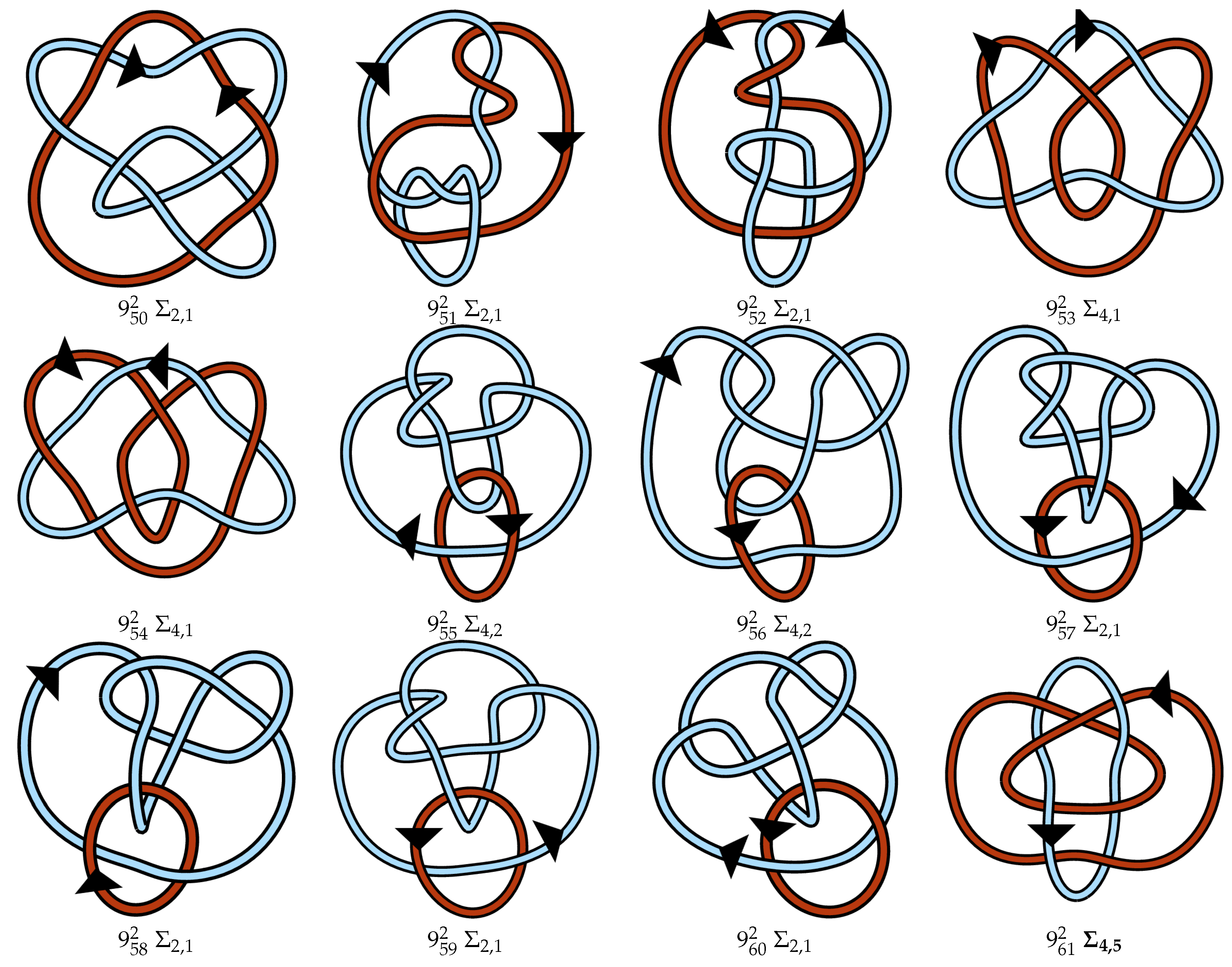
References
- Briggs, G. On types of knotted curves. Ann. Math. 1927, 28, 562–586. [Google Scholar]
- Rolfsen, D. Knots and Links; AMS/Chelsea Publication Series; AMS Chelsea Pub.: Providence, RI, USA, 1976. [Google Scholar]
- Conway, J.H. An enumeration of knots and links, and some of their algebraic properties. In Computational Problems in Abstract Algebra; Elsevier: Amsterdam, The Netherlands, 1970; pp. 329–358. [Google Scholar]
- Portillo, J.; Diao, Y.; Scharein, R.; Arsuaga, J.; Vazquez, M. On the mean and variance of the writhe of random polygons. J. Phys. A Math. Theor. 2011, 44, 275004. [Google Scholar] [CrossRef] [PubMed]
- Brasher, R.; Scharein, R.G.; Vazquez, M. New biologically motivated knot table. Biochem. Soc. Trans. 2013, 41, 606–611. [Google Scholar] [CrossRef] [PubMed]
- Janse Van Rensburg, E.; Whittington, S. The BFACF algorithm and knotted polygons. J. Phys. A Math. Gen. 1991, 24, 5553. [Google Scholar] [CrossRef]
- Janse Van Rensburg, E.J.; Orlandini, E.; Sumners, D.W.; Tesi, M.C.; Whittington, S.G. The Writhe of Knots in the Cubic Lattice. J. Knot Theory Its Ramif. 1997, 6, 31–44. [Google Scholar] [CrossRef]
- Stolz, R.; Yoshida, M.; Brasher, R.; Flanner, M.; Ishihara, K.; Sherratt, D.J.; Shimokawa, K.; Vazquez, M. Pathways of DNA unlinking: A story of stepwise simplification. Sci. Rep. 2017, 7, 12420. [Google Scholar] [CrossRef] [PubMed]
- Adams, D.E.; Shekhtman, E.M.; Zechiedrich, E.L.; Schmid, M.B.; Cozzarelli, N.R. The role of topoisomerase IV in partitioning bacterial replicons and the structure of catenated intermediates in DNA replication. Cell 1992, 71, 277–288. [Google Scholar] [CrossRef]
- Grainge, I.; Bregu, M.; Vazquez, M.; Sivanathan, V.; Ip, S.C.; Sherratt, D.J. Unlinking chromosome catenanes in vivo by site-specific recombination. EMBO J. 2007, 26, 4228–4238. [Google Scholar] [CrossRef] [PubMed]
- Shimokawa, K.; Ishihara, K.; Grainge, I.; Sherratt, D.J.; Vazquez, M. FtsK-dependent XerCD-dif recombination unlinks replication catenanes in a stepwise manner. Proc. Natl. Acad. Sci. USA 2013, 110, 20906–20911. [Google Scholar] [CrossRef] [PubMed]
- Klenin, K.; Langowski, J. Computation of writhe in modeling of supercoiled DNA. Biopolymers 2000, 54, 307–317. [Google Scholar] [CrossRef]
- Doll, H.; Hoste, J. A tabulation of oriented links. Math. Comp. 1991, 57, 747–761. [Google Scholar] [CrossRef]
- Berglund, M.; Cantarella, J.; Casey, M.P.; Dannenberg, E.; George, W.; Johnson, A.; Kelley, A.; LaPointe, A.; Mastin, M.; Parsley, J.; et al. Intrinsic Symmetry Groups of Links with 8 and Fewer Crossings. Symmetry 2012, 4, 143–207. [Google Scholar] [CrossRef]
- Cantarella, J.; Cornish, J.; Mastin, M.; Parsley, J. The 27 Possible Intrinsic Symmetry Groups of Two-Component Links. Symmetry 2012, 4, 129–142. [Google Scholar] [CrossRef]
- Henry, S.R.; Weeks, J.R. Symmetry Groups of Hyperbolic Knots and Links. J. Knot Theory Its Ramif. 1992, 1, 185–201. [Google Scholar] [CrossRef]
- Liang, C.; Cerf, C.; Mislow, K. Specification of chirality for links and knots. J. Math. Chem. 1996, 19, 241–263. [Google Scholar] [CrossRef]
- Berg, B.; Foerster, D. Random paths and random surfaces on a digital computer. Phys. Lett. B 1981, 106, 323–326. [Google Scholar] [CrossRef]
- De Carvalho, C.A.; Caracciolo, S. A new Monte-Carlo approach to the critical properties of self-avoiding random walks. J. Phys. 1983, 44, 323–331. [Google Scholar] [CrossRef]
- De Carvalho, C.A.; Caracciolo, S.; Fröhlich, J. Polymers and g| φ| 4 theory in four dimensions. Nucl. Phys. B 1983, 215, 209–248. [Google Scholar] [CrossRef]
- Madras, N.; Slade, G. The Self-Avoiding Walk; Probability and Its Applications; Birkhäuser: Basel, Switzerland, 1993. [Google Scholar]
- Culler, M.; Dunfield, N.M.; Goerner, M.; Weeks, J.R. SnapPy, a Computer Program for Studying the Geometry and Topology of 3-Manifolds. Available online: http://snappy.computop.org (accessed on 3 March 2017).
- Hypnagogic Software. KnotPlot. Available online: http://www.knotplot.com/ (accessed on 24 October 2014).
- Laing, C.; Sumners, D.W. Computing the writhe on lattices. J. Phys. A 2006, 39, 3535–3543. [Google Scholar] [CrossRef]
- Freund, G.; Witte, S.; Vazquez, M. Bounds for the Minimum Step Number for 2-Component Links in the Simple Cubic Lattice. 2018. in progress. [Google Scholar]
- Lacher, R.; Sumners, D. Data Structures and Algorithms for Computation of Topological Invariants of Entanglements: Link, Twist and Writhe; Prentice-Hall: New York, NY, USA, 1991. [Google Scholar]
- Fishman, G. Monte Carlo: Concepts, Algorithms, and Applications; Springer Series in Operations Research and Financial Engineering; Springer: New York, NY, USA, 2013. [Google Scholar]

| Symmetry Name | Occurences for | Subgroup of | Generators of Subgroup | Equivalence Class of |
|---|---|---|---|---|
| Full Symmetry | 1 | ++, L+−, L−+, L−−, ++,+−, −+, −−, L++, L+−,L−+, L−−, ++, +−,−+, −−} | ||
| Purely Inv. (Pure Ex.) | 25 | ++−−, L++, L−−} | ||
| Purely Inv. (No Ex.) | 32 | ++−−} | ||
| Fully Inv. (Pure Ex.) | 5 | +++−−+−−,L++, L+−, L−+, L−−} | ||
| Fully Inv. (no Ex.) | 22 | +++−−+−−} | ||
| Even Op. (Pure Ex.) | 3 | ++, L−−, +−, −+, L++,L−−, +−, −+} | ||
| Even Op. (Non-Pure Ex.) | 1 | ++−−+−−+} | ||
| No Symmetry | 3 | ++} |
| L | Rolfsen | KP | lk | Sym | |||
|---|---|---|---|---|---|---|---|
| [] | [] | [] | ++ | 0 | |||
| [] | [] | [] | ++ | 1 | |||
| [] | [] | [] | +− | 2 | |||
| [] | [] | [] | ++ | 0 | |||
| [] | [] | [] | ++ | 3 | |||
| [] | [] | [] | ++ | 3 | |||
| [] | [] | [] | +− | 2 | |||
| [] | [] | [] | ++ | 1 | |||
| [] | [] | [] | +− | 1 | |||
| [] | [] | [] | ++ | 0 | |||
| [] | [] | [] | + | 0 | |||
| [] | [] | [] | ++ | 2 | |||
| [] | [] | [] | ++ | 0 | |||
| [] | [] | [] | + | 2 | |||
| [] | [] | [] | ++ | 0 | |||
| [] | [] | [] | +− | 4 | |||
| [] | [] | [] | + | 4 | |||
| [] | [] | [] | ++ | 3 | |||
| [] | [] | [] | +− | 4 | |||
| [] | [] | [] | ++ | 3 | |||
| [] | [] | [] | ++ | 2 | |||
| [] | [] | [] | +− | 1 | |||
| [] | [] | [] | ++ | 1 | |||
| [] | [] | [] | + | 2 | |||
| [] | [] | [] | + | 0 | |||
| [] | [] | [] | + | 2 | |||
| [] | [] | [] | ++ | 0 | |||
| [] | [] | [] | ++ | 0 | |||
| [] | [] | [] | + | 2 | |||
| [] | [] | [] | + | 0 | |||
| [] | [] | [] | + | 2 |
| Link | |||
|---|---|---|---|
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Witte, S.; Flanner, M.; Vazquez, M. A Symmetry Motivated Link Table. Symmetry 2018, 10, 604. https://doi.org/10.3390/sym10110604
Witte S, Flanner M, Vazquez M. A Symmetry Motivated Link Table. Symmetry. 2018; 10(11):604. https://doi.org/10.3390/sym10110604
Chicago/Turabian StyleWitte, Shawn, Michelle Flanner, and Mariel Vazquez. 2018. "A Symmetry Motivated Link Table" Symmetry 10, no. 11: 604. https://doi.org/10.3390/sym10110604
APA StyleWitte, S., Flanner, M., & Vazquez, M. (2018). A Symmetry Motivated Link Table. Symmetry, 10(11), 604. https://doi.org/10.3390/sym10110604





