Exactly Solvable One-Qubit Driving Fields Generated via Nonlinear Equations

Abstract

Using the Hubbard representation for $SU\left(2\right),$ we write the time-evolution operator of a two-level system in the disentangled form. This allows us to map the corresponding dynamical law into a set of nonlinear coupled equations. In order to find exact solutions, we use an inverse approach and find families of time-dependent Hamiltonians whose off-diagonal elements are connected with the Ermakov equation. A physical model with the so-obtained Hamiltonians is discussed in the context of the nuclear magnetic resonance phenomenon.

1. Introduction

The dynamical manipulation of two-level systems has been a long-standing issue in quantum mechanics [1,2,3]. In recent times, the problem has acquired more relevance due to its potential applications in quantum computing and quantum information [4,5,6], where the design of robust and precise control protocols is essential. To this end, the analytically solvable, time-dependent problems in quantum mechanics are of great importance. However, it is well known that the solution of the Schrödinger equation with time-dependent Hamiltonians represents, in general, a difficult task and the number of exactly solvable cases is very limited. These include rotating fields [6,7], nonlinear modulated Rabi fields [8], periodic driving fields [9,10], and pulse shaped fields [11]. Another method that has been widely used to generate exact solutions of the evolution equation concerns the inverse technique approach, where some aspects on the dynamics are prescribed and then the interactions are found. In [12], for instance, some families of exactly solvable driving fields for spin-1/2 systems are obtained by requiring the spin to accomplish particular trajectories in the projective space. In [9,13,14], on the other hand, this approach has been used to find analytical solutions for a two-level system driven by a single-axis control field.

Of particular interest in the solution of the evolution equation and in the generation of exactly solvable models is the Lie algebraic technique, which takes advantage of the fact that the Hamiltonian can be written as a linear combination of the generators of a Lie algebra [15,16,17,18,19,20,21,22]. In this scheme, the Wei Norman theorem establishes that the corresponding evolution operator can be factorized (or disentangled) into independent exponential factors involving only one generator of the algebra [23]. This technique has deserved a lot of interest as it is closely related to the group theoretical approach to the time evolution of quantum systems and has found a number of applications in the disentangling of exponential operators for the study of the dynamics of systems with $SU\left(2\right)$ and $SU(1,1)$ symmetries [15,16,17,18], as, e.g., the interaction of two-level atoms with electromagnetic radiation [20], the field modulation in nuclear magnetic resonance [19], the propagation and perfect transmission in three-waveguide axially varying structures [24], the time-evolution of harmonic oscillators with time-dependent, both mass and frequency [25,26], the description of coherent and squeezed states [27] and the optical coupling in nonlinear crystals [28], among others. In a previous work, we show that the disentangling of the $SU\left(2\right)$ evolution operator is reduced to the solution of a scalar parametric oscillator-type equation, whose time-dependent frequency is given in terms of the driving field in a non trivial form [22]. Hence, the core difficulty in solving the problem lies in the fact that the solutions to the parametric oscillator-like equation can be explicitly written only in a restricted number of cases.

The aim of the present work is to obtain new families of analytically solvable driving fields in the framework of the Wei–Norman Lie algebraic approach and the inverse problem technique. Once the evolution operator is expressed in its disentangled form, the driving fields will be obtained by considering well known solutions to the corresponding parametric oscillator-type equation for a real-valued time-dependent frequency. It will be shown that, in this approach, the construction of the driving fields is accomplished by solving an Ermakov equation whose solutions can be readily expressed in terms of that of a parametric oscillator-like equation. In the statement of the direct approach, we consider the realization of the group $SU\left(2\right)$ constituted by the Hubbard operators (also called X-operators). These operators were introduced by Hubbard in [29,30,31] and are useful to describe models of strongly correlated electrons. In addition, the algebraic properties of such operators allow for dealing with the observables of quantum systems in a suitable way [32,33]. For instance, a d-level system Hamiltonian can be diagonalized through a sequence of unitary transformations properly written in terms of Hubbard operators [34]. This method has been extended to the multipartite case by taking advantage of the Kronnecker product of the X-operators. The geometric measure of entanglement of a symmetric n-qubit is easily calculated in this approach [33].

The paper is organized as follows. In Section 2, the statement of the problem and the direct approach are reviewed. The inverse problem and the main result of this work are reported in Section 3. In addition, a physical model concerning a spin 1/2-particle in a time-dependent external magnetic field is discussed in Section 4. Some concrete examples are analyzed in Section 5 where we show that our results generalize the case of a circularly polarized field and discuss some aspects of the dynamics such as the time-evolution of population inversion. Finally, the conclusions and perspectives of our work are presented in Section 6.

2. The Direct Approach

We are interested in the dynamics of systems whose Hamiltonians can be written in the form

$$H\left(t\right)=\mathsf{\Delta }{J}_0+V\left(t\right)J_{+}+\overline{V}\left(t\right)J_{-},$$

(1)

where the operators $\{J_0,J_{\pm }\}$ are the generators of the $su\left(2\right)$ algebra and $\mathsf{\Delta }\in \mathbb{R}$, so that $H\left(t\right)$ is Hermitian. For the two-dimensional representation, one obtains the Hamiltonian of a driven two-level system (or qubit). In this case, the constant $\mathsf{\Delta }$ is interpreted as the splitting between the two energy eigenvalues, while the complex-valued function V is the driving field that rules the transitions between the two energy states. A convenient realization of the group $SU\left(2\right)$ is constituted by the Hubbard operators as they provide a useful mathematical framework to deal with some calculations in a simpler way [22,32,33], as well as to extend our formalism to the cases of qudits and multipartite systems.

In an n-dimensional vector space, the Hubbard or X-operators are defined as a set of $n^2$ two-labeled operators ${\left\{X^{i,j}\right\}}_{i,j=1}^n$ fulfilling the properties [32]

• $X^{i,j}{X}^{k,m}={\delta }_{j,k}{X}^{i,m}$ (multiplication rule),
• ${\displaystyle \sum _{k=1}^n{X}^{k,k}=\mathbb{I}}$ (completeness),
• ${\left(X^{i,j}\right)}^{†}=X^{j,i}$ (non-hermiticity),
• $[X^{i,j},X^{k,m}]={\delta }_{j,k}{X}^{i,m}-{\delta }_{m,i}{X}^{k,j}$ (commutation rule),

where $[·,·]$ stands for the conventional commutator. The most elementary case arises for $n=2$, for which it is possible to construct a representation of the Hubbard operators in the space of states of a two-level system. Indeed, if $|p\rangle$ and $|q\rangle$ are two orthonormal qubit states corresponding to the eigenvalues ${ϵ}_p$, ${ϵ}_q$, respectively, the four operators defined as

$$X_2^{k,\ell }:=|k\rangle \langle \ell |,k,\ell =p,q$$

(2)

conforms a representation of the set of Hubbard operators in the space ${\mathcal{H}}_2=\mathrm{span}\left\{\right|p\rangle ,|q\rangle \}$. Here, the subindex 2 is related to the dimension of the corresponding representation. Additionally, a simple calculation shows that the action of the operator (2) on the basis vectors reads

$$X_2^{k,\ell }|n\rangle ={\delta }_{\ell ,n}|k\rangle ,k,\ell ,n=p,q.$$

(3)

On the other hand, it is not difficult to verify that the three operators

$$J_0:=\frac{1}{2}(X_2^{p,p}-X_2^{q,q}),J_{-}=X_2^{q,p},J_{+}={\left(J_{-}\right)}^{†}:=X_2^{p,q}$$

(4)

constitute a representation of the $su\left(2\right)$ algebra. Remark that, even though we are restricting ourselves to the representation of this algebra corresponding to $j=1/2$, our results are equivalent for any value of j once the generators are written in the proper realization (see [32] for details). The Hamiltonian (1) in terms of the X-operators reads

$$H_2\left(t\right)=\frac{\mathsf{\Delta }}{2}(X_2^{p,p}-X_2^{q,q})+V\left(t\right)X_2^{p,q}+\overline{V}\left(t\right)X_2^{q,p}.$$

(5)

A discussion on a physical model associated to this operator is given in Section 4.

In the direct approach, once the driving field $V\left(t\right)$ and the initial state $\left|\psi \right(0)\rangle$ are given, one must determine the state of the system $\left|\psi \right(t)\rangle$ at an arbitrary time according to

$$\left|\psi \right(t)\rangle =U(t\left)\right|\psi \left(0\right)\rangle ,$$

where $U\left(t\right)$ is the time evolution operator associated to the Hamiltonian (5) fulfilling the dynamical law

$$i\frac{dU\left(t\right)}{dt}=H_2\left(t\right)·U\left(t\right),$$

(6)

with the initial condition $U\left(0\right)=\mathbb{I}$. This operator can be cast in a factorized or disentangled form using the Wei–Norman theorem [23], yet

$$U\left(t\right)=exp\left[\alpha \left(t\right)X_2^{p,q}\right]exp[\mathsf{\Delta }f\left(t\right)J_0]exp\left[\beta \left(t\right)X_2^{q,p}\right],$$

(7)

where $\alpha$, f and $\beta$ are three factorizing complex-valued functions to be determined in such a way that $\alpha \left(0\right)=f\left(0\right)=\beta \left(0\right)=0$. The action of the time-evolution operator (7) on the basis vectors can be straightforwardly computed by using the following relations [22]

$$\begin{array}{c}exp\left[\alpha \left(t\right)X_2^{p,q}\right]=1+\alpha \left(t\right)X_2^{p,q},exp\left[\beta \left(t\right)X_2^{q,p}\right]=1+\beta \left(t\right)X_2^{q,p},\hfill \\ exp\left[\frac{\mathsf{\Delta }f\left(t\right)}{2}{X}_2^{p,p}\right]=X_2^{q,q}+e^{\mathsf{\Delta }f\left(t\right)/2}{X}_2^{p,p},exp\left[\frac{-\mathsf{\Delta }f\left(t\right)}{2}{X}_2^{q,q}\right]=X_2^{p,p}+e^{-\mathsf{\Delta }f\left(t\right)/2}{X}_2^{q,q},\hfill \\ exp\left[\mathsf{\Delta }f\left(t\right)J_0\right]=e^{\mathsf{\Delta }f\left(t\right)/2}{X}_2^{p,p}+e^{-\mathsf{\Delta }f\left(t\right)/2}{X}_2^{q,q}.\hfill \end{array}$$

(8)

Thus, if the qubit is initially, for instance, in the state $|p\rangle$, the state of the system at an arbitrary time reads

$$|\psi \left(t\right)\rangle =e^{-\mathsf{\Delta }f\left(t\right)/2}[e^{\mathsf{\Delta }f\left(t\right)}+\alpha \left(t\right)\beta \left(t\right)]|p\rangle +e^{-\mathsf{\Delta }f\left(t\right)/2}\beta \left(t\right)|q\rangle .$$

(9)

In Ref. [22], it is shown that the solutions to the evolution problem (5)–(7) is given by

$${\displaystyle \alpha \left(t\right)=i\frac{e^{-i\mathsf{\Delta }t}}{R\left(t\right)}\left[\frac{{\phi }^{\prime }\left(t\right)}{\phi \left(t\right)}+\frac{1}{2}\frac{R^{\prime }\left(t\right)}{R\left(t\right)}\right],}$$

(10)

$$\mathsf{\Delta }f\left(t\right)=-2ln\left[\frac{\phi \left(t\right)}{{\phi }_0}\right]-ln\left[\frac{R\left(t\right)}{R_0}\right]-i\mathsf{\Delta }t,{\phi }_0=\phi \left(0\right),R_0=R\left(0\right),$$

(11)

and

$$\beta \left(t\right)=-i{R}_0{\phi }_0^2{\int }_0^t\frac{ds}{{\phi }^2\left(s\right)},$$

(12)

where the function $R\left(t\right)=e^{-i\mathsf{\Delta }t}\overline{V}\left(t\right)$, which will be also referred to as the driving field, has been introduced to shorten the notation. The function $\phi$ turns out to fulfill the parametric oscillator-like equation

$${\phi }^{″}\left(t\right)+{\mathsf{\Omega }}^2\left(t\right)\phi \left(t\right)=0,$$

(13)

with time-dependent frequency given by

$${\mathsf{\Omega }}^2\left(t\right)=-\frac{1}{4}{\left[\frac{d}{dt}lnR\left(t\right)\right]}^2+\frac{1}{2}\frac{d^2}{d{t}^2}lnR\left(t\right)+{\left|R\left(t\right)\right|}^2.$$

(14)

Without having a loss of generality we may set ${\phi }_0=1$, as the predictions will not depend on this initial value. In addition, the initial condition $\alpha \left(0\right)=0$ will fix the initial condition for the first derivative of $\phi$ in terms of $R_0$ and $R_0^{\prime }=R^{\prime }\left(0\right)$ through

$$\underset{t\to 0}{lim}\frac{1}{R\left(t\right)}\left[\frac{{\phi }^{\prime }\left(t\right)}{\phi \left(t\right)}+\frac{1}{2}\frac{R^{\prime }\left(t\right)}{R\left(t\right)}\right]=0.$$

(15)

We emphasize that, given a particular driving field $V\left(t\right)$ (or equivalently $R\left(t\right)$), the problem of finding the time-evolution operator $U\left(t\right)$ for the Hamiltonian (5) is turned into solving Equation (13). As it was mentioned before, the number of exactly solvable cases is limited as the form of the frequency (14) is in general non-trivial. Some exactly solvable cases are $V\left(t\right)=\mathrm{constant}$ [15], the circularly polarized field: $V\left(t\right)\propto e^{-i\delta t}$ [22] and the hyperbolic secant pulse: $V\left(t\right)\propto \mathrm{sech}\left(\sigma t\right)$ [19], just to mention some.

The aim of the next section is to explore the possibility of constructing new analytical solutions from the framework of the inverse approach.

3. The Inverse Approach

From the inverse problem technique point of view, a natural question at this point is what would be the form of a driving field $R\left(t\right)$ giving rise to a particular well known solution of (13) fulfilling the proper initial conditions? In order to answer this question, we have to consider the expression (14) as a differential equation for the driving field, rather than a definition for the time-dependent frequency. First note that this equation is not of the Riccati-type in the function $lnR\left(t\right)$ because of the term ${\left|R\left(t\right)\right|}^2$. Therefore, in order to transform this equation into a known one, let us consider the function $\gamma$ defined by

$$\gamma \left(t\right)=\frac{d}{dt}lnR\left(t\right).$$

(16)

It follows immediately that

$$R\left(t\right)=R_{0}exp\left[{\int }_0^t\gamma \left(s\right)ds\right].$$

(17)

In general, $\gamma$ is a complex-valued function that can be split into its real and imaginary parts as $\gamma \left(s\right)={\gamma }_1\left(s\right)+i{\gamma }_2\left(s\right)$. We will restrict ourselves to the case in which the function ${\mathsf{\Omega }}^2$ is real-valued. Under this assumption, the substitution of expression (17) into the Equation (14) leads to the set of equations

$$-\frac{1}{4}{\gamma }_1^2+\frac{1}{4}{\gamma }_2^2+\frac{1}{2}{\gamma }_1^{\prime }+{\left|R_0\right|}^{2}exp\left(2{\int }_0^t{\gamma }_{1}ds\right)={\mathsf{\Omega }}^2,$$

(18)

$${\gamma }_1=\frac{{\gamma }_2^{\prime }}{{\gamma }_2}=\frac{d}{dt}ln{\gamma }_2.$$

(19)

This last equation suggest that the function ${\gamma }_1$ can be written in the form [35]

$${\gamma }_1\left(t\right)=k\frac{d}{dt}ln\mu \left(t\right),$$

with k a real constant and $\mu$ a real-valued function. Indeed, it can be shown that Equation (18) can be reduced to an Ermakov equation choosing $k=-2$. In this case,

$${\gamma }_1=-\frac{d}{dt}ln{\mu }^2,{\gamma }_2=\frac{\lambda }{{\mu }^2},$$

(20)

where $\lambda$ is an integration constant and $\mu$ satisfies the Ermakov equation

$${\mu }^{″}\left(t\right)+{\mathsf{\Omega }}^2\left(t\right)\mu \left(t\right)=\frac{{\mathsf{\Omega }}_0^2}{{\mu }^3\left(t\right)},\mathrm{with}{\mathsf{\Omega }}_0^2={\lambda }^2\left[\frac{|R_0{|}^2}{{\gamma }_2^2\left(0\right)}+\frac{1}{4}\right].$$

(21)

The corresponding initial conditions for $\mu$ define the initial conditions on the driving field R as

$${\gamma }_1\left(0\right)=-2\frac{{\mu }_0^{\prime }}{{\mu }_0}=\mathrm{Re}\left[\frac{R_0^{\prime }}{R_0}\right],{\gamma }_2\left(0\right)=\frac{\lambda }{{\mu }_0}=\mathrm{Im}\left[\frac{R_0^{\prime }}{R_0}\right],$$

(22)

where ${\mu }_0=\mu \left(0\right)$ and ${\mu }_0^{\prime }={\mu }^{\prime }\left(0\right)$. However, without loss of generality, we may fix ${\mu }_0=1$. In this case, ${\gamma }_2\left(0\right)=\lambda$ and

$${\mathsf{\Omega }}_0={\left[|R_0{|}^2+\frac{{\lambda }^2}{4}\right]}^{1/2}.$$

(23)

For reasons that will be clarified in the sequel, we call this quantity the generalized Rabi-like frequency.

Finally, inserting the functions ${\gamma }_1$ and ${\gamma }_2$ into the expression (17), we obtain the driving field in terms of the solutions of the Ermakov Equation (21)

$$R\left(t\right)=\frac{R_0}{{\mu }^2\left(t\right)}exp\left[i\lambda {\int }_0^t\frac{ds}{{\mu }^2\left(s\right)}\right].$$

(24)

This function defines a two-parametric family of exactly solvable time-dependent Hamiltonians of the form (5) with $V\left(t\right)=e^{-i\mathsf{\Delta }t}\overline{R}\left(t\right)$.

It is worthwhile to stress that the solutions to Equation (21) can be constructed provided that the solutions of (13) are known. Indeed, it can be shown that, if ${\phi }_1$ is a particular solution of such equation, then the function $\mu$ is given by [35,36]:

$${\mu }^2\left(t\right)=\frac{{\mathsf{\Omega }}_0^2{\phi }_1^2\left(t\right)}{c_1}+c_1{\phi }_1^2\left(t\right){\left[c_2+{\int }^t\frac{ds}{{\phi }_1^2\left(s\right)}\right]}^2.$$

(25)

Here, $c_1$ and $c_2$ are integration constants [36,37] that can be determined from the initial conditions imposed on $\mu$. Moreover, for the so-obtained Hamiltonians, the time-evolution operator $U\left(t\right)$ is readily written from Equation (7) with the factorization functions $\alpha ,f$ and $\beta$ given by

$$\alpha \left(t\right)=\frac{i}{R_0}{\mu }^2\left(t\right)exp\left[-i\mathsf{\Delta }t-i\lambda \eta \left(t\right)\right]\left[\frac{{\phi }^{\prime }\left(t\right)}{\phi \left(t\right)}-\frac{{\mu }^{\prime }\left(t\right)}{\mu \left(t\right)}+\frac{i\lambda }{2{\mu }^2\left(t\right)}\right],$$

(26)

$$\mathsf{\Delta }f\left(t\right)=ln\left[\frac{{\mu }^2\left(t\right)}{{\phi }^2\left(t\right)}\right]+i\lambda \eta \left(t\right)-i\mathsf{\Delta }t,\beta \left(t\right)=-i{R}_0{\int }_0^t\frac{ds}{{\phi }^2\left(s\right)},$$

(27)

where the real-valued function

$$\eta \left(t\right)={\int }_0^t\frac{ds}{{\mu }^2\left(s\right)}$$

(28)

has been introduced to shorten the notation.

Periodic Interactions

Of particular interest are the driving fields fulfilling the condition $V\left(t\right)=V(t+{\tau }_p)$ leading to the Floquet Hamiltonians or quasi-energy operators. Remark that a periodic function $\mu$ does not assure the periodicity of V. Indeed, if the period of the function $\mu$ is $\tau$, it can be shown that

$$V(t+\tau )=exp\left[-i\left(\lambda \eta \left(\tau \right)+\mathsf{\Delta }\tau \right)\right]V\left(t\right).$$

(29)

From this last expression, it is clear that, for V to be a periodic function, we should adjust $\lambda$ and the parameters involved in the function $\mu$ in a very restrictive form. However, note that, for a natural number p, the following expression holds

$$V\left(p\tau \right)=exp\left[-i\left(p\lambda \eta \left(\tau \right)+\mathsf{\Delta }\tau \right)\right]V\left(0\right).$$

(30)

This parameter p gives versatility to manipulate the period of the function V. Indeed, by requiring that

$$p\lambda \eta \left(\tau \right)+\mathsf{\Delta }\tau =p\lambda {\int }_0^{\tau }\frac{ds}{{\mu }^2\left(s\right)}+\mathsf{\Delta }\tau \equiv 0\left(\mathrm{mod}2\pi \right),$$

(31)

it is assured that V is a periodic function with period ${\tau }_p=p\tau$.

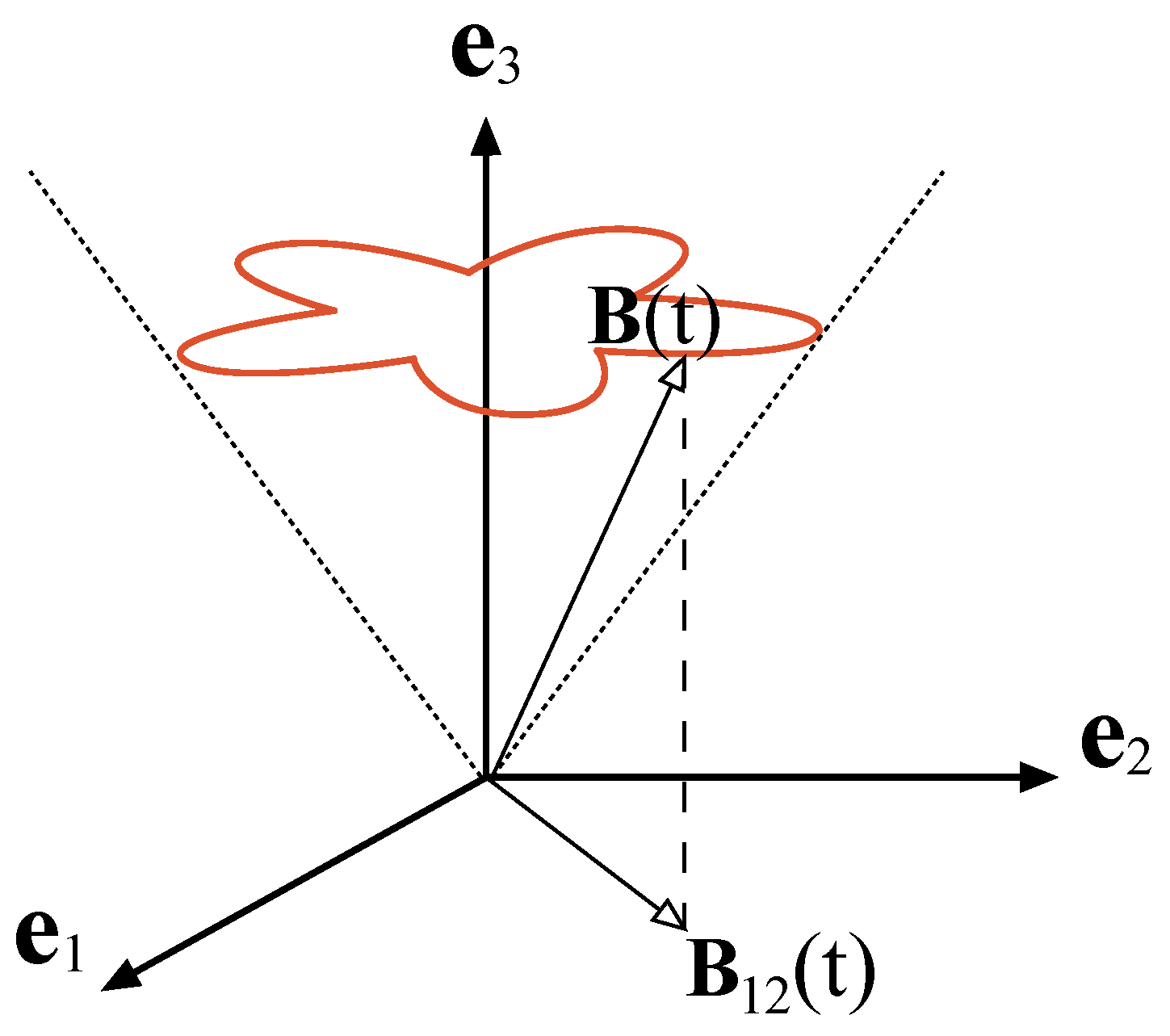
4. A Physical Model

In this section, we consider a quantum system whose Hamiltonian has the form (5) in terms of the Hubbard operators. Consider a spin-1/2 particle with magnetic moment $\mathbf{m}={\mu }_B{g}_{\ell }\overrightarrow{\sigma }$ in an external magnetic field $\mathbf{B}\left(t\right)$, where ${\mu }_B$ and $g_{\ell }$ stand for the Bohr magneton and the Landé factor, respectively, and $\overrightarrow{\sigma }=({\sigma }_1,{\sigma }_2,{\sigma }_3)$ with ${\sigma }_i$, $i=1,2,3$ the Pauli matrices. The corresponding Hamiltonian reads

$$H=-\mathbf{m}·\mathbf{B}=\frac{b}{2}\overrightarrow{\sigma }·\mathbf{B},$$

(32)

where $b=-2g_{\ell }{\mu }_B$ is constant. We pay attention to the case where the field precesses around a fixed axis, say, the axis defined by ${\mathbf{e}}_3$. Thus, the magnetic field is written as $\mathbf{B}={\mathbf{B}}_{12}\left(t\right)+B_3{\mathbf{e}}_3$, where $B_3$ is a constant and the driving field ${\mathbf{B}}_{12}\left(t\right)=B_1\left(t\right){\mathbf{e}}_1+B_2\left(t\right){\mathbf{e}}_2$ is used to manipulate the spin states of the particle. This field is represented schematically in Figure 1. In Hubbard notation, the Hamiltonian (32) is expressed as

$$H=\frac{b{B}_3}{2}\left(X_2^{p,p}-X_2^{q,q}\right)+\frac{b}{2}[B_1\left(t\right)-i{B}_2\left(t\right)]X_2^{p,q}+\frac{b}{2}[B_1\left(t\right)+i{B}_2\left(t\right)]X_2^{q,p}.$$

(33)

Thus, with the identification $V\left(t\right)=b[B_1\left(t\right)-i{B}_2\left(t\right)]/2$ and $\mathsf{\Delta }=b{B}_3$, the Hamiltonian (33) takes the form (1). Note that the real and imaginary parts of the function V are proportional to the components 1 and 2 of the field, respectively. This justifies the name given to the function V. Although this model is valid in general, a particularly interesting exactly solvable problem arises whenever the transverse field has a constant amplitude $B_0$. In addition, if we take $B_1\left(t\right)=B_{0}cos\omega t$ and $B_2\left(t\right)=B_{0}sin\omega t$, $\omega$ being the oscillation frequency, then the transverse vector ${\mathbf{B}}_{12}$ describes a circle in a plane transverse to ${\mathbf{e}}_3$ and thus $\mathbf{B}\left(t\right)$ becomes a circularly polarized field. Hence $V\left(t\right)=\frac{b}{2}{B}_0{e}^{-i\omega t}$ and the solutions to the factorization problem (7) are easily constructed. We obtain $R\left(t\right)=g{e}^{i\delta t}$ where $g=\frac{b}{2}{B}_0$ is a real constant, and the detuning $\delta =\omega -\mathsf{\Delta }$. The factorization functions are (compare to [22]):

$$\begin{array}{c}{\displaystyle \alpha \left(t\right)=\frac{-2ig{e}^{-i\omega t}sin\left({\mathsf{\Omega }}_{0}t\right)}{2{\mathsf{\Omega }}_{0}cos\left({\mathsf{\Omega }}_{0}t\right)-i\delta sin\left({\mathsf{\Omega }}_{0}t\right)},}\\ {\displaystyle \mathsf{\Delta }f\left(t\right)=-2ln\left[cos\left({\mathsf{\Omega }}_{0}t\right)-\frac{i\delta }{2{\mathsf{\Omega }}_0}sin\left({\mathsf{\Omega }}_{0}t\right)\right]-i\omega t,}\\ {\displaystyle \beta \left(t\right)=\frac{-2igsin\left({\mathsf{\Omega }}_{0}t\right)}{2{\mathsf{\Omega }}_{0}cos\left({\mathsf{\Omega }}_{0}t\right)-i\delta sin\left({\mathsf{\Omega }}_{0}t\right)},}\end{array}$$

(34)

where ${\mathsf{\Omega }}_0={\left(g^2+{\delta }^2/4\right)}^{1/2}$ is the Rabi frequency. If it is assumed that the system is initially in the state $\left|\psi \right(0)\rangle =|p\rangle$, then, according to expression (9), the state of the system at an arbitrary time can be computed to yield

$$|\psi \left(t\right)\rangle =e^{-i\omega t/2}\left[cos\left({\mathsf{\Omega }}_{0}t\right)+\frac{i\delta }{2{\mathsf{\Omega }}_0}sin\left({\mathsf{\Omega }}_{0}t\right)\right]|p\rangle -\frac{ig}{{\mathsf{\Omega }}_0}{e}^{i\omega t/2}sin\left({\mathsf{\Omega }}_{0}t\right)|q\rangle .$$

(35)

In addition, the population inversion $P=|c_p{|}^2-{\left|c_q\right|}^2$ is also computed:

$$P\left(t\right)=\frac{g^2}{{\mathsf{\Omega }}_0^2}cos\left(2{\mathsf{\Omega }}_{0}t\right)+\frac{{\delta }^2}{4{\mathsf{\Omega }}_0^2}.$$

(36)

5. Some Simple Applications

In this section, we explicitly obtain some families of exactly solvable one-qubit time-dependent Hamilitonians for a given function $\mathsf{\Omega }$. This function is chosen in such a way that the solutions to the parametric oscillator Equation (13) are known. The construction of the driving field $R\left(t\right)$ through Equation (14) involves two arbitrary parameters, namely ${\mu }_0^{\prime }$ and $\lambda$ (or equivalently $c_1$ and $c_2$ from Equation (25)) that fix the corresponding parameters $R_0$ and $R_0^{\prime }$. We will discuss the case for which ${[lnR\left(0\right)]}^{\prime }=i\delta$, with $\delta \in \mathbb{R}$, analogous to the case of a circularly polarized field of the previous section. This choice leads to the simple conditions ${[ln\mu \left(0\right)]}^{\prime }=0$, and $\lambda =\delta$. We may also write $R_0=-i\overline{g}$, where g may be, in general, a complex constant. Thus, the driving field will be given in terms of the parameters $\delta$ and g.

We will consider that the frequency $\mathsf{\Omega }$ is a constant. In this case, two important limits are of interest. In the first one, the frequency $\mathsf{\Omega }={\mathsf{\Omega }}_1=0$, which leads to a decaying driving field. The second one arises as $\mathsf{\Omega }={\mathsf{\Omega }}_1\to {\mathsf{\Omega }}_0$ and corresponds to the problem of one qubit interacting with a single mode circularly polarized field.

5.1. Case $\mathsf{\Omega }\left(t\right)=0$: A Decaying Driving Field

On one hand, note that, when the frequency $\mathsf{\Omega }\left(t\right)$ vanishes, the parametric oscillator Equation (13) becomes ${\phi }^{″}\left(t\right)=0,$ whose solution meeting the initial conditions (15) is $\phi \left(t\right)=-i\delta t/2+1$. Next, the function $\mu$ can be found by taking ${\phi }_1\left(t\right)=t$ in (25). The initial conditions $\mu \left(0\right)=1$ and ${[ln\mu \left(0\right)]}^{\prime }=0$ lead to ${\mu }^2\left(t\right)={\mathsf{\Omega }}_0^2{t}^2+1$ and to the corresponding driving field

$$R\left(t\right)=\frac{-i\overline{g}}{{\mathsf{\Omega }}_0^2{t}^2+1}exp\left[i\frac{\delta }{{\mathsf{\Omega }}_0}arctan\left({\mathsf{\Omega }}_{0}t\right)\right],{\mathsf{\Omega }}_0^2={\left|g\right|}^2+\frac{{\delta }^2}{4}.$$

(37)

The factorizing functions $\alpha ,\beta$ and f can be explicitly constructed to yield

$$\alpha \left(t\right)=\frac{-2igt}{-i\delta t+2}exp\left[-i\mathsf{\Delta }t-i\frac{\delta }{{\mathsf{\Omega }}_0}arctan\left({\mathsf{\Omega }}_{0}t\right)\right],\beta \left(t\right)=\frac{-2i\overline{g}t}{-i\delta t+2},$$

(38)

and

$$\mathsf{\Delta }f\left(t\right)=ln\left[\frac{4{\mathsf{\Omega }}_0^2{t}^2+4}{{(-i\delta t+2)}^2}\right]+i\frac{\delta }{{\mathsf{\Omega }}_0}arctan\left({\mathsf{\Omega }}_{0}t\right)-i\mathsf{\Delta }t.$$

(39)

According to Equation (9), the time-evolution of the state $\left|\psi \right(t)\rangle$ can be computed in terms of the factorization functions as

$$\begin{array}{cc}\hfill |\psi \left(t\right)\rangle =& \frac{(i\delta t+2)e^{-i\mathsf{\Delta }t/2}}{2\mu \left(t\right)}exp\left[-i\frac{\delta }{2{\mathsf{\Omega }}_0}arctan\left({\mathsf{\Omega }}_{0}t\right)\right]|p\rangle \hfill \\ & -i\frac{\overline{g}t{e}^{i\mathsf{\Delta }t/2}}{\mu \left(t\right)}exp\left[i\frac{\delta }{2{\mathsf{\Omega }}_0}arctan\left({\mathsf{\Omega }}_{0}t\right)\right]|q\rangle .\hfill \end{array}$$

(40)

Hence, the population inversion P is calculated as function of time

$$P\left(t\right)=\frac{({\delta }^2/4-{\left|g\right|}^2)t^2+1}{{\mathsf{\Omega }}_0^2{t}^2+1}.$$

(41)

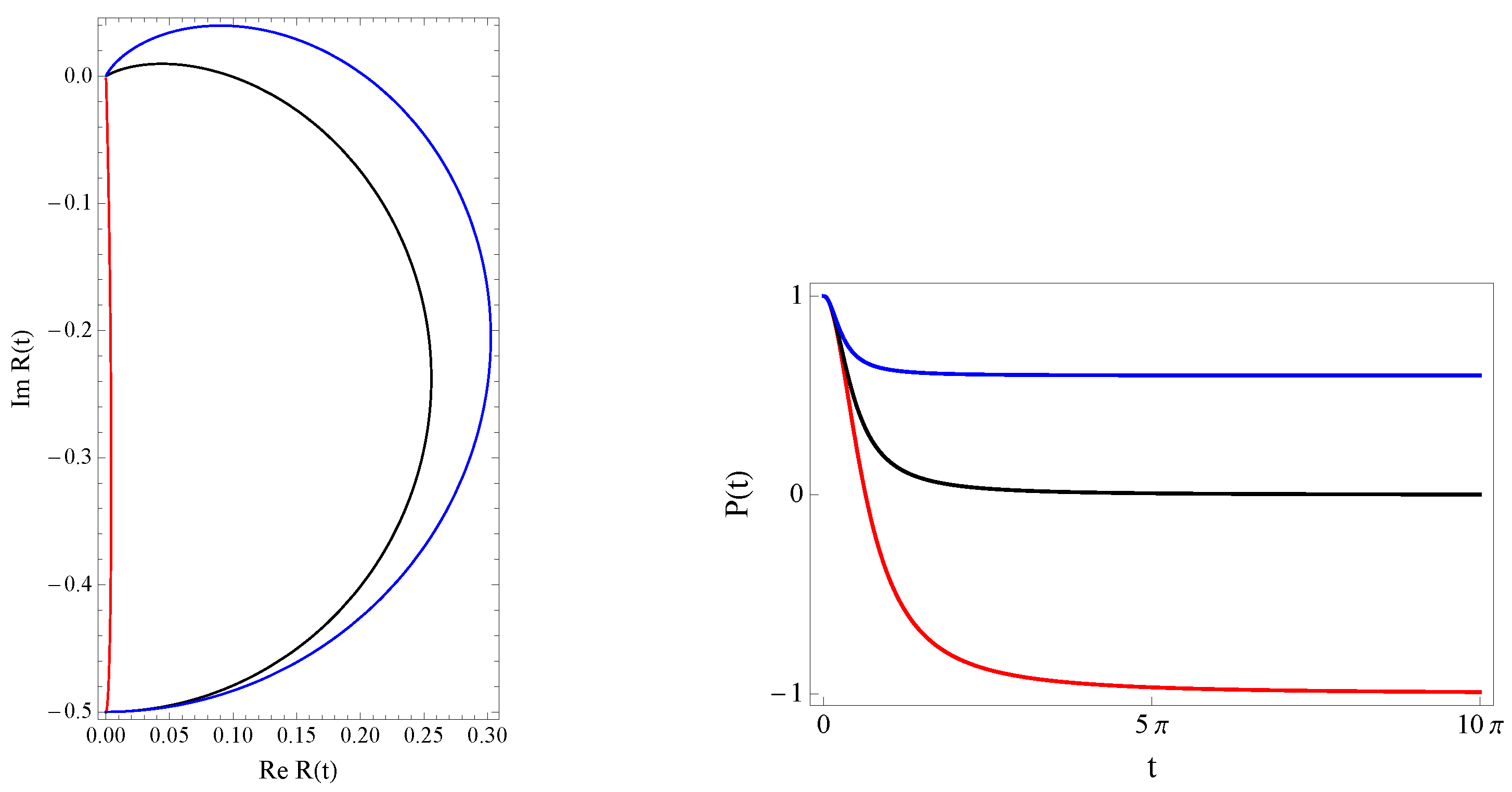
Figure 2 shows the function R in the complex plane for several values of the parameters g and $\delta$. Remark that the real and imaginary parts can be considered as the transversal components of a control magnetic field. It can be seen from the driving field (37) that as $t\to \infty$, we have $R\left(t\right)\to 0$. This fact is noted in the population inversion P, which tends to a fixed value as time increases (see Figure 2)

$$P(t\to \infty )=\frac{{\delta }^2-4{\left|g\right|}^2}{{\delta }^2+4{\left|g\right|}^2}.$$

(42)

5.2. Case $\mathsf{\Omega }\left(t\right)={\mathsf{\Omega }}_1$: A Precessing Field with Oscillating Amplitude

A more general instance arises if the frequency is a real constant ${\mathsf{\Omega }}_1\ne 0$. With this choice, the parametric oscillator-like equation reduces to the conventional Newtonian harmonic oscillator equation

$${\phi }^{″}\left(t\right)+{\mathsf{\Omega }}_1^2\phi \left(t\right)=0.$$

(43)

The solution that meets the initial conditions (15) reads

$$\phi \left(t\right)=cos\left({\mathsf{\Omega }}_{1}t\right)-\frac{i\delta }{2{\mathsf{\Omega }}_1}sin\left({\mathsf{\Omega }}_{1}t\right).$$

(44)

On the other hand, the solution (25) to the corresponding Ermakov equation can be constructed either with ${\phi }_1\left(t\right)=cos\left({\mathsf{\Omega }}_{1}t\right)$ or with ${\phi }_1\left(t\right)=sin\left({\mathsf{\Omega }}_{1}t\right)$. After imposing the required initial conditions, we get

$${\mu }^2\left(t\right)={cos}^2\left({\mathsf{\Omega }}_{1}t\right)+{\kappa }^2{sin}^2\left({\mathsf{\Omega }}_{1}t\right),\kappa ={\mathsf{\Omega }}_0/{\mathsf{\Omega }}_1.$$

(45)

The corresponding driving field can be readily obtained

$$R\left(t\right)=\frac{-i\overline{g}{e}^{i\delta \eta \left(t\right)}}{{cos}^2\left({\mathsf{\Omega }}_{1}t\right)+{\kappa }^2{sin}^2\left({\mathsf{\Omega }}_{1}t\right)}$$

(46)

with

$$\eta \left(t\right)={\int }_0^t\frac{ds}{{cos}^2\left({\mathsf{\Omega }}_{1}s\right)+{\kappa }^2{sin}^2\left({\mathsf{\Omega }}_{1}s\right)}.$$

(47)

The interaction term (46) has the form of a precessing field with an oscillating amplitude. Note that a circularly polarized field is a particular case of our driving fields. Indeed, taking $\kappa =1$, we have ${\mu }^2\left(t\right)=1$ and hence $\eta \left(t\right)=t$. Therefore, $R\left(t\right)=-i\overline{g}{e}^{i\delta t}$, which is the field discussed in Section 4.

On the other hand, note that the function (47) is well-defined in the interval $[0,\infty )$ as ${\mu }^{-2}$ is continuous and hence Riemann integrable. In the Appendix A, we discuss the possibility of writing this integral in terms of elementary functions and also show that $\eta (\pi /{\mathsf{\Omega }}_1)=\pi /{\mathsf{\Omega }}_0$. This last result is useful to determine the conditions of periodicity of V. In fact, the period of the function $\mu$ is $\tau =\pi /{\mathsf{\Omega }}_1$ and, according to Equation (31), for $p\in {\mathbb{Z}}^{+}$, we must impose the condition that

$$\nu =\frac{\mathsf{\Delta }}{{\mathsf{\Omega }}_1}+\frac{p\delta }{{\mathsf{\Omega }}_0}$$

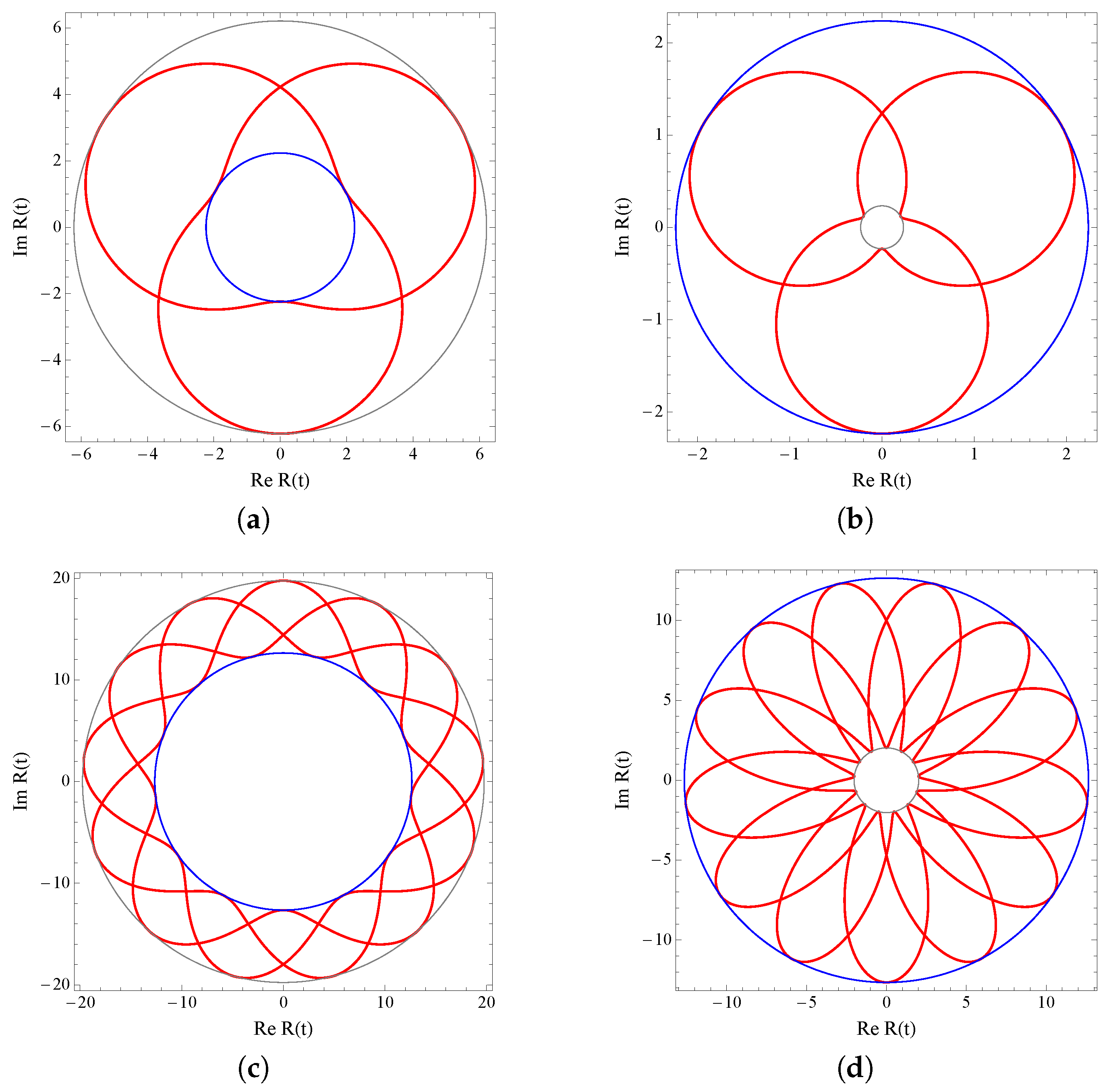
is an even integer number in order to get a periodic driving field of period ${\tau }_p=p\tau$, p being the minimum natural number for which the former condition holds. Remark that, in this case, if $\mathsf{\Delta }=2{\mathsf{\Omega }}_1$, the periodicity of V also assures the periodicity of R. Some plots of the corresponding functions R are shown in Figure 3 for several values of $\delta$, $\mathsf{\Delta }$ and g for which the periodicity condition holds. These describe a flower-like pattern which inscribes (circumscribes) a circle of radius $\left|g\right|$ when $\kappa <1$ ($\kappa >1$). Additionally, an outer (inner) circle of radius $\left|g\right|/{\kappa }^2$ bounds the oscillations amplitude. In both cases, the number p is related to the number of ‘petals’ of the field, that is to say, the number of times the function R reaches its maximum and minimum values in one period ${\tau }_p$. On the other hand, in Figure 4, we have chosen the parameters so that the periodicity condition is not fulfilled, giving rise to open curves in the complex plane.

Now, we can determine the evolution operator. Indeed, after some calculations, we find that the factorizing functions $\alpha$, f and $\beta$ take the form

$$\alpha \left(t\right)=\frac{-2igsin\left({\mathsf{\Omega }}_{1}t\right)e^{-i\mathsf{\Delta }t-i\delta \eta \left(t\right)}}{2{\mathsf{\Omega }}_{1}cos\left({\mathsf{\Omega }}_{1}t\right)-i\delta sin\left({\mathsf{\Omega }}_{1}t\right)},\beta \left(t\right)=\frac{-2i\overline{g}sin\left({\mathsf{\Omega }}_{1}t\right)}{2{\mathsf{\Omega }}_{1}cos\left({\mathsf{\Omega }}_{1}t\right)-i\delta sin\left({\mathsf{\Omega }}_{1}t\right)},$$

(48)

$$\mathsf{\Delta }f\left(t\right)=ln\left[\frac{{\mu }^2\left(t\right)}{{\phi }^2\left(t\right)}\right]-i\delta \eta \left(t\right)-i\mathsf{\Delta }t,$$

(49)

where the functions $\phi$, $\mu$ and $\eta$ are given in Equations (44), (45), and (47), respectively. Again, if the initial state is $\left|\psi \right(0)\rangle =|p\rangle$, the state of the system at an arbitrary time is

$${\displaystyle |\psi \left(t\right)\rangle =\frac{e^{-i\mathsf{\Delta }t/2-i\eta \left(t\right)/2}}{\mu \left(t\right)}\left[cos\left({\mathsf{\Omega }}_{1}t\right)+\frac{i\delta }{2{\mathsf{\Omega }}_1}sin\left({\mathsf{\Omega }}_{1}t\right)\right]|p\rangle -\frac{i\overline{g}{e}^{-i\mathsf{\Delta }t/2-i\eta \left(t\right)/2}}{\mu \left(t\right)}\frac{sin\left({\mathsf{\Omega }}_{1}t\right)}{{\mathsf{\Omega }}_1}|q\rangle .}$$

(50)

The population inversion as function of time can also be computed yielding

$$P\left(t\right)=\frac{4{\mathsf{\Omega }}_1^2{cos}^2\left({\mathsf{\Omega }}_{1}t\right)+({\delta }^2-{4\left|g\right|}^2){sin}^2\left({\mathsf{\Omega }}_{1}t\right)}{4{\mathsf{\Omega }}_1^2[{cos}^2\left({\mathsf{\Omega }}_{1}t\right)+{\kappa }^2{sin}^2\left({\mathsf{\Omega }}_{1}t\right)]},$$

(51)

which is a periodic function of time with period $\tau =\pi /{\mathsf{\Omega }}_1=\pi \kappa /{\mathsf{\Omega }}_0$. Remark that, for $\kappa =1$, the former expression retrieves the conventional expression (36) for the population inversion of a single qubit driven by a circularly polarized field. One can also note that regardless the value of $\kappa$, the population invertion (51) has local minima

$$P_{\min }=\frac{{\delta }^2-4{\left|g\right|}^2}{{\delta }^2+4{\left|g\right|}^2},$$

(52)

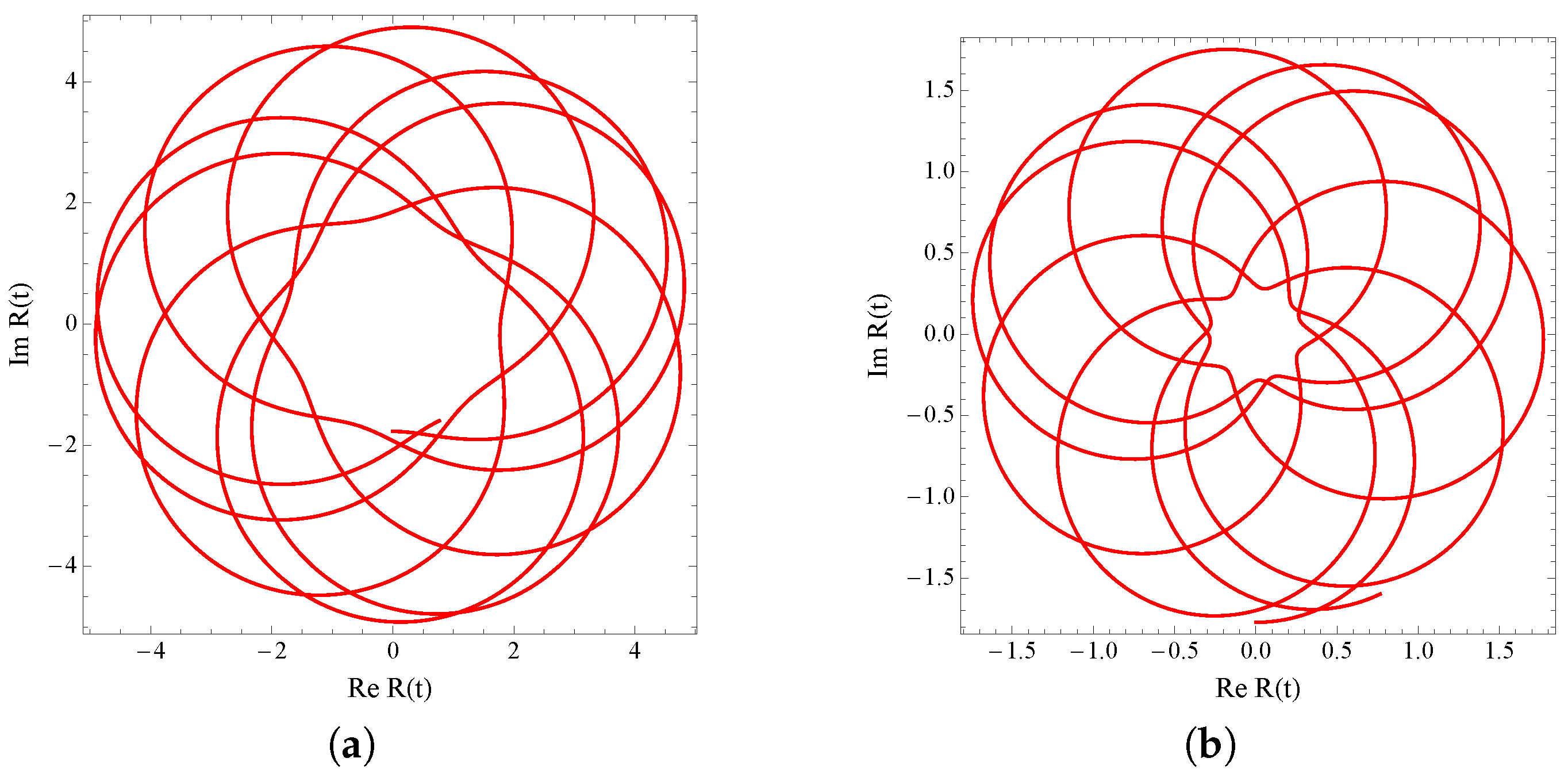
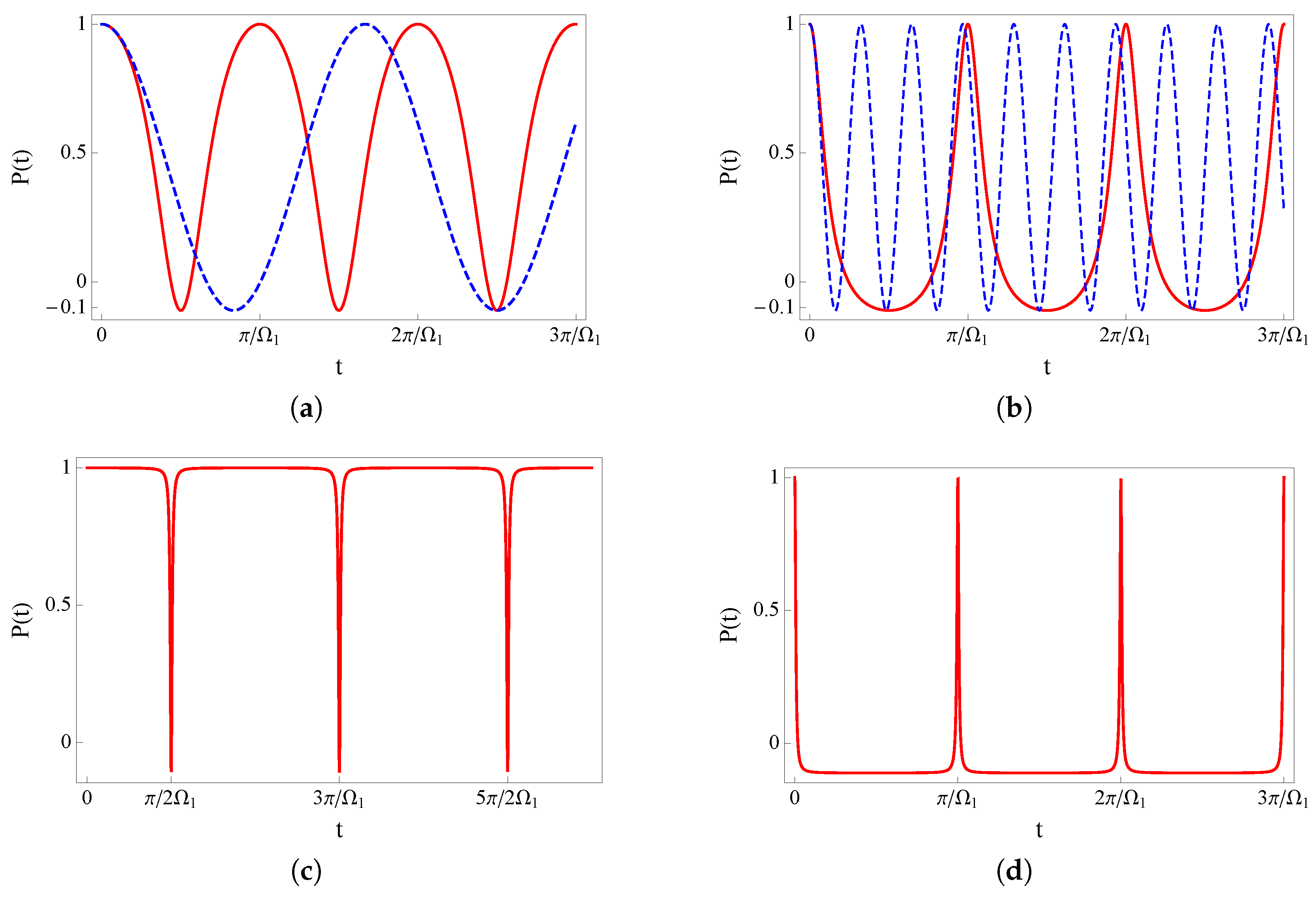
which are achieved at times $t_n=n\pi /2{\mathsf{\Omega }}_1$, with $n\in {\mathbb{Z}}^{+}$. In Figure 5, it is depicted the population inversion for several values of g and $\delta$ as well as for different values of $\kappa$. The blue-dashed curve corresponds to the case of a qubit interacting with a circularly polarized field ($\kappa =1$). It can be also seen that the period of oscillation for $\kappa <1$ is shortened with respect to the case $\kappa =1$ while it is enlarged for $\kappa >1$. On the other hand, in the limits $\kappa \approx 0$ and $\kappa \gg 0$, the oscillations become more defined giving rise to a collapse-and-revival-like behaviour. This can be noted if one compares the shape of the oscillations shown in the plots (a) and (b) with those depicted in (c) and (d) of Figure 5, where we have set the value of $\kappa$ according to the limits mentioned before. Finally, the parameters g and $\delta$ can be used to manipulate both the amplitude and shape of the oscillations on demand, as it is shown in Figure 6.

5.3. Case $\mathsf{\Omega }\left(t\right)=i{\mathsf{\Omega }}_1$: A Precessing Decaying Driving Field

We now consider a pure imaginary constant frequency such that $\mathsf{\Omega }\left(t\right)=i{\mathsf{\Omega }}_1$, with ${\mathsf{\Omega }}_1\in \mathbb{R}$. In this case, the solutions to both the parametric oscillator-like Equation (13) and the Ermakov Equation (21) are given in terms of hyperbolic sine and cosine functions. This can be immediately seen from the fact that Equation (13) reduces to ${\phi }^{″}\left(t\right)-{\mathsf{\Omega }}_1^2\phi \left(t\right)=0$. The corresponding driving fields have analogous forms to those obtained in the previous case once the trigonometric functions in Equations (46) and (47) are interchanged by the corresponding hyperbolic ones. Accordingly, such control fields are no longer oscillating as they give rise to a decaying behavior in the atomic population inversion. A detailed analysis of this case will be reported elsewhere.

6. Conclusions

We have proposed a procedure to generate exactly solvable families of single qubit driving fields. Requiring that the corresponding time-evolution operator is written as a product of exponential operators, we find analytical solutions to the dynamical law using an inverse approach. The control fields are determined by means of the solutions of an Ermakov equation, which is obtained once the time-dependent frequency of the related parametric-oscillator equation is specified. The connection between these equations can be straightforwardly stated if such frequency is either a real-valued or a pure imaginary function of time. The dynamics of a qubit interacting with the so-obtained driving fields strongly depend on the form and the parameters of such a function. We have provided some examples of non-periodic and periodic control fields, as well as decaying fields for the case of a constant frequency. These results may shed some light in the problem of qubit control and the development of quantum gates. Some results on the construction of new solutions for the general case of a complex-valued frequency are in progress.