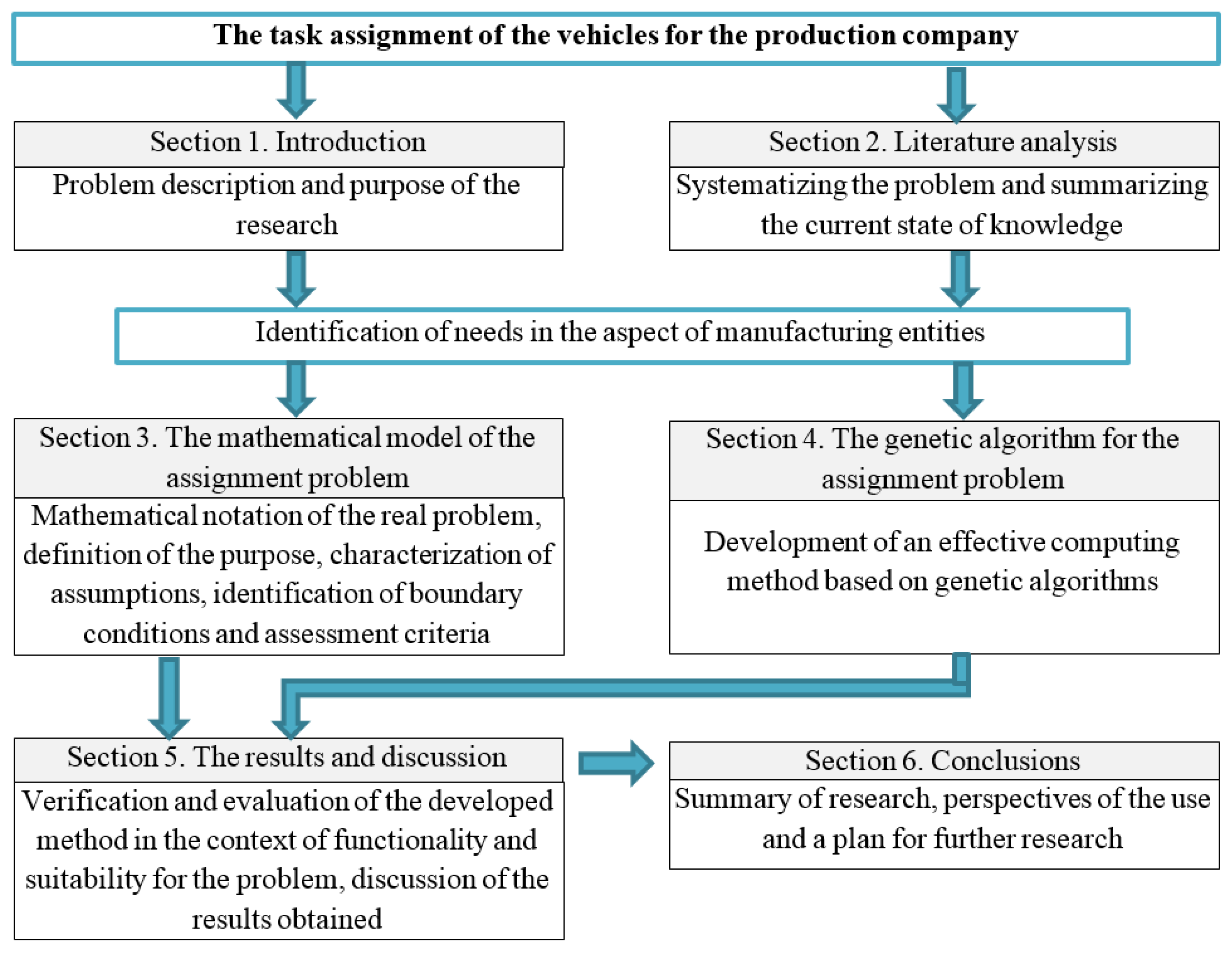
The Task Assignment of Vehicles for a Production Company
Abstract
1. Introduction
2. Literature Analysis
3. The Mathematical Model of the Assignment Problem
- -
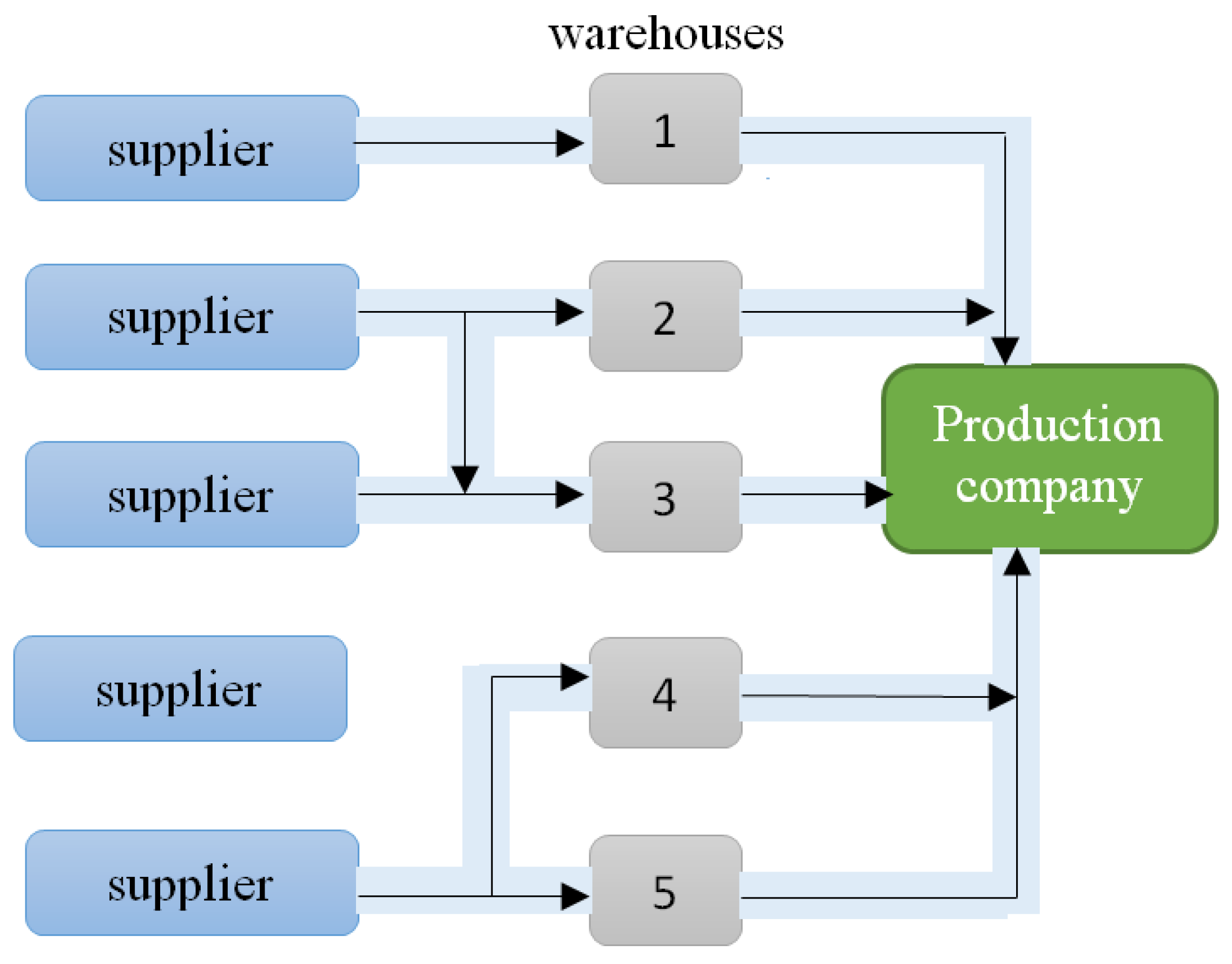
- The production company starts the production process in the case when all the cargo has been gathered in the warehouses. It means that the cargo is transported from the warehouses to the production company. The relation: suppliers and a production company does not exist. All the cargo which is necessary for the production must be stored in the warehouses. This situation is to ensure the continuity of the production process.
- -
- The amount of the cargo which is offered by all the suppliers is bigger than the demand of the production company.
- -
- The organization of transport is on the side of the productize the total costs which result from transporting the on company. The aim of the production company is to minimalicargo from the suppliers to the production company.
- -
- The model assumes that the distances between the suppliers and the warehouses and the warehouses and the production company are the same as between the warehouses and the suppliers, and the production company and the warehouses.
- -
- The warehouses belong only to the production company. This situation lets the production company know the capacity of the warehouses.
4. The Genetic Algorithm for the Assignment Problem
4.1. Main Assumptions
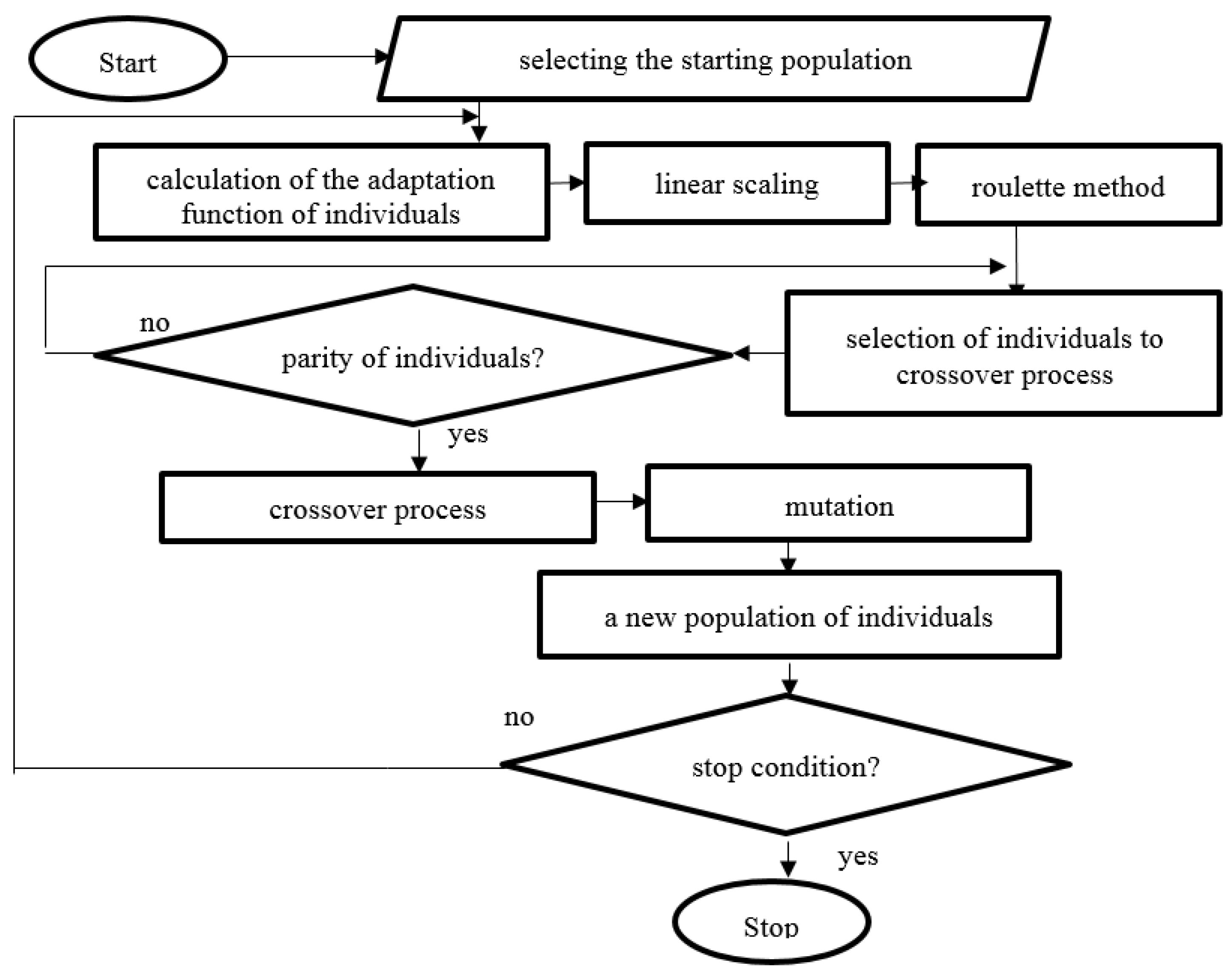
4.2. The Structure of the Genetic Algorithm
- -
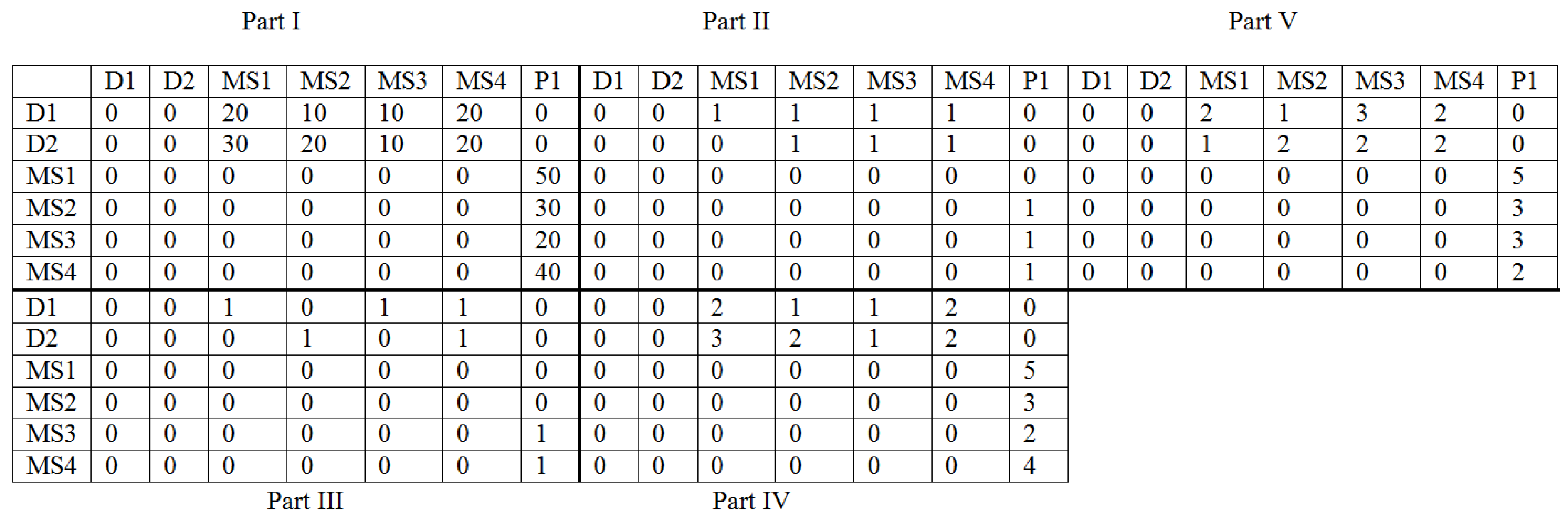
- Step 1: Setting the values of all the cells of the matrix to 0. This value determines, e.g., the connections for which it is not possible to transport the cargo, e.g., among the suppliers.
- -
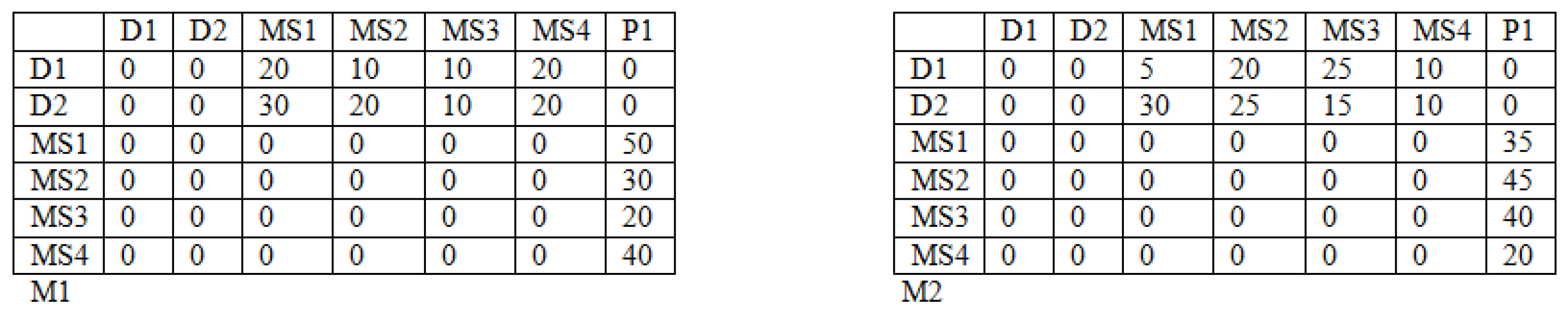
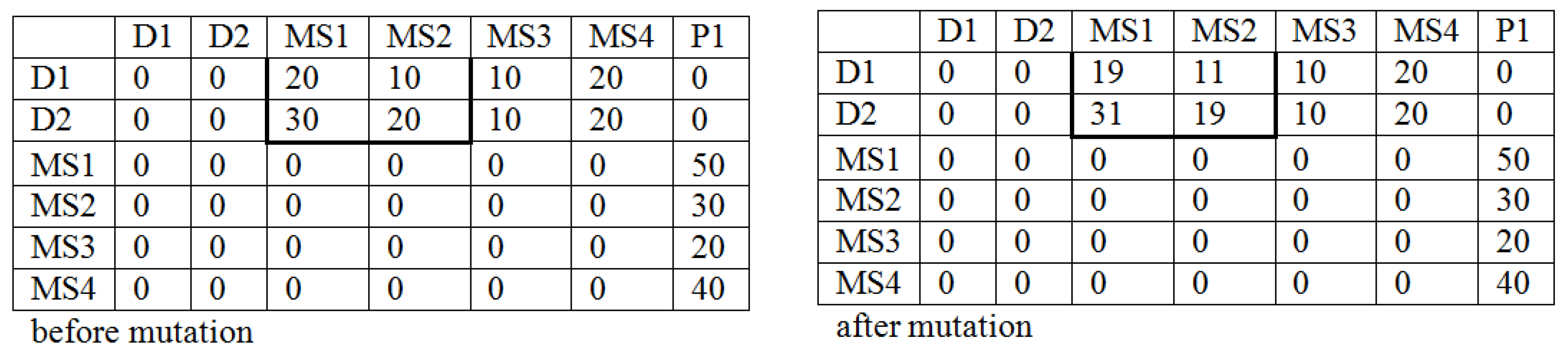
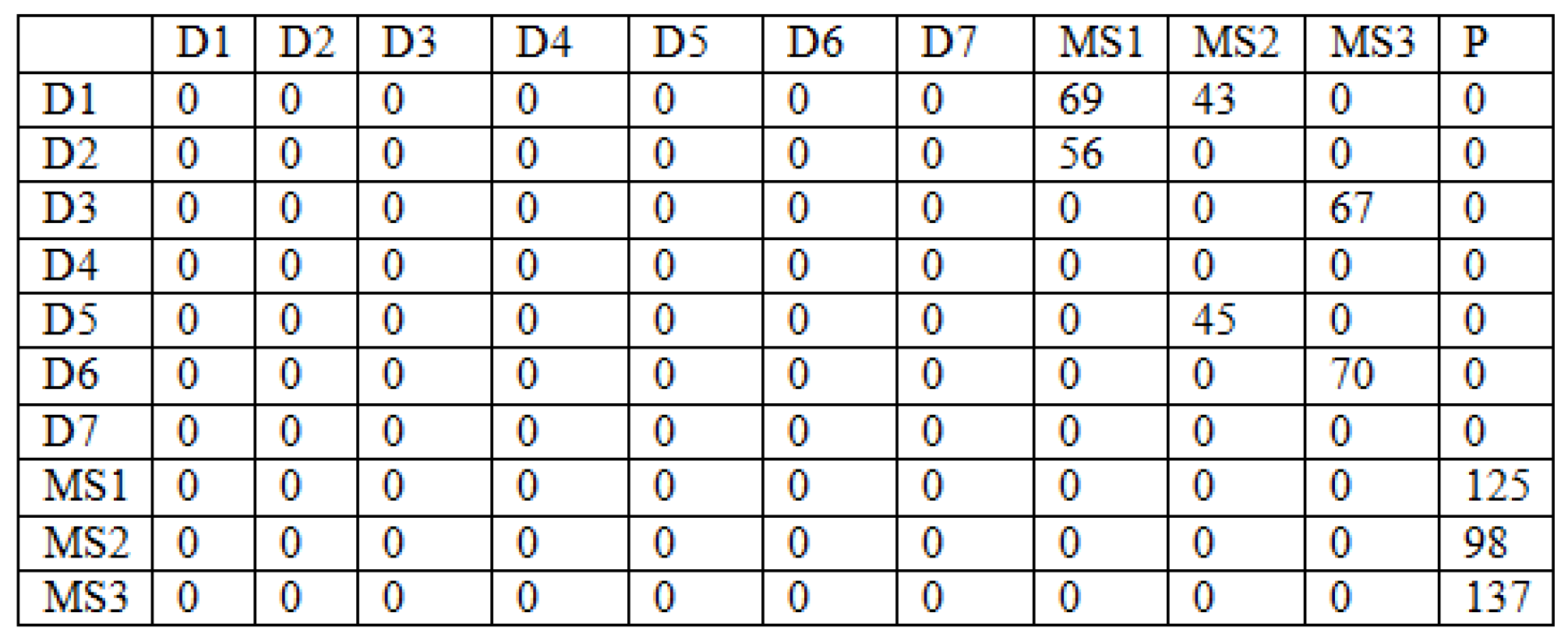
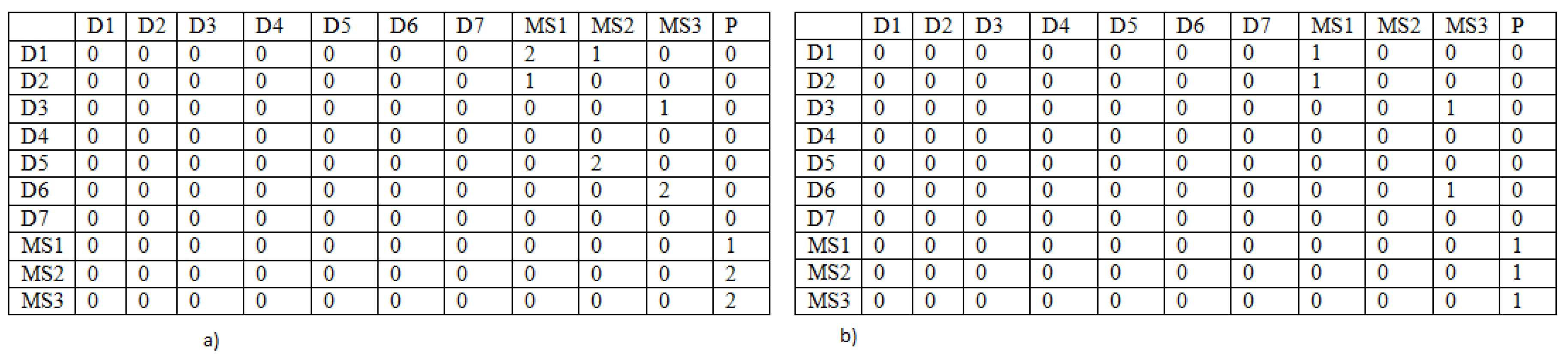
- Step 2: Setting the cells of the structure (Part I): D1, MS1—D2, MS4 in a random way (the relation: the suppliers—the warehouses). The values in these cells must meet the limits: the production capacity of the suppliers (7), the warehouse capacity (9), the minimal stream of the cargo flowing into the warehouses (11). It should be underlined that the sum of the cargo flowing out from the suppliers must be equal the demand of the production company. The cells which do not meet these limits take the value 0. In the case when the demand of the production company is met, other cells which were not designated take the value 0 as well. In the case when the demand is not fulfilled and all the cells from D1, MS1—D2, MS4 are designated, the cells are selected in a random way and their values are increased until the moment when the demand is met.
- -
- Step 3: Setting the cells of the matrix: MS1, P1—MS4, P1. It should be remembered that the cargo flowing out from the warehouse is equal to the cargo flowing into the warehouse (10) and the recipients’ demands must be met (8).
- -
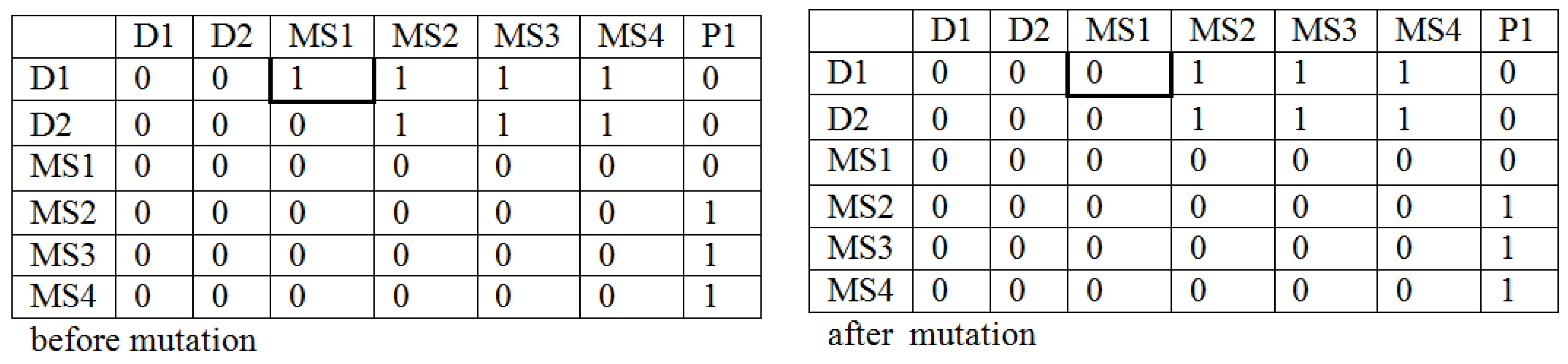
- Step 4: Setting the cells of the matrix in the Part II and III. In the presented matrix two types of the vehicles were considered (the first type of the vehicles—Part II and the second type of the vehicles—Part III). These cells are designated in a random way and take the value 1 or 0. 1—a given type of vehicles is used on the connection, 0—otherwise. In this step the limits: many types of the vehicles can exist on a given relation (12), (13) must be met.
- -
- Step 5: Setting the cells of the matrix in the Part IV and V in a random way. It should be remembered that the number of the vehicles must be met (14).
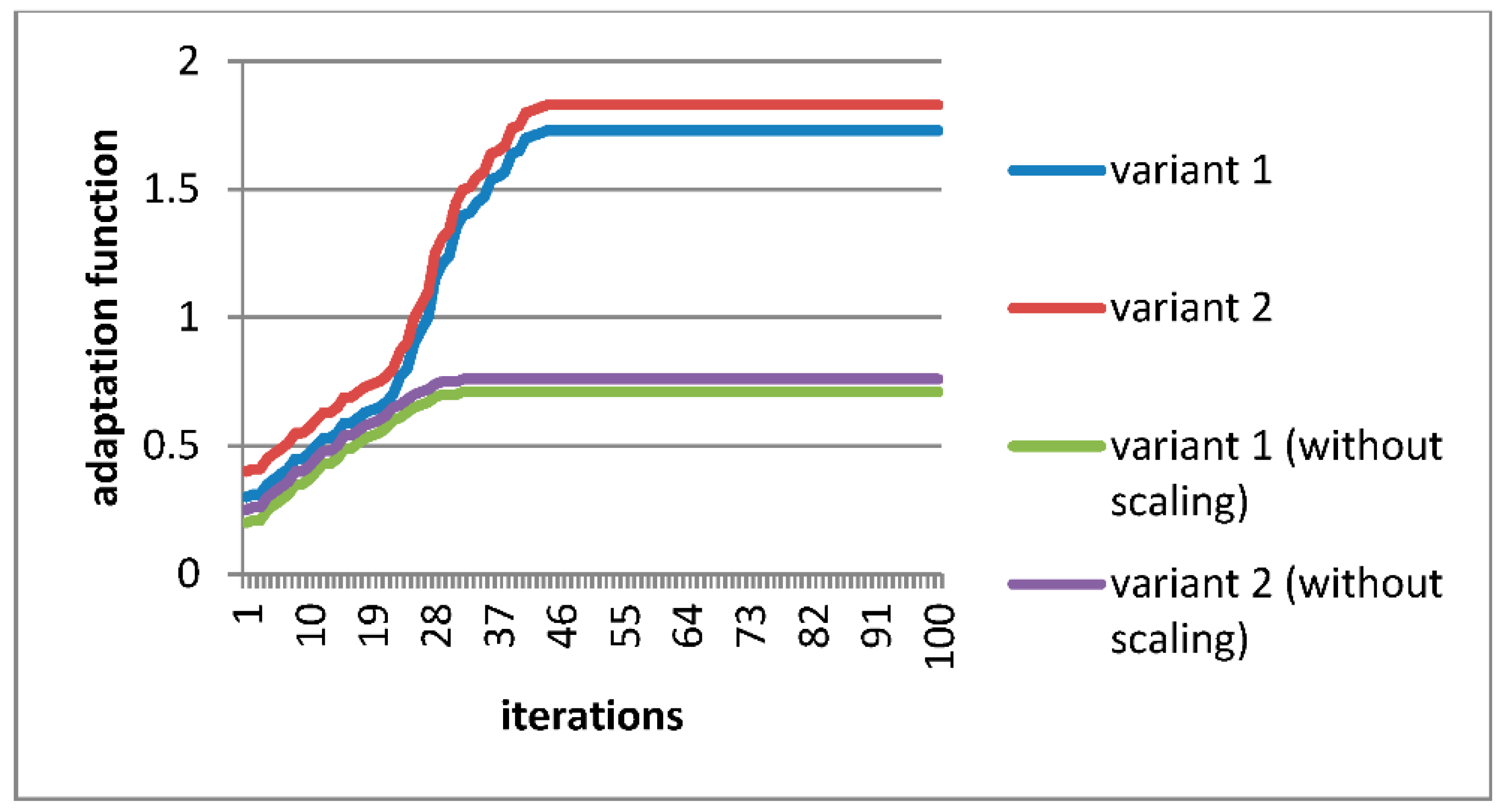
4.3. The Adaptation Function
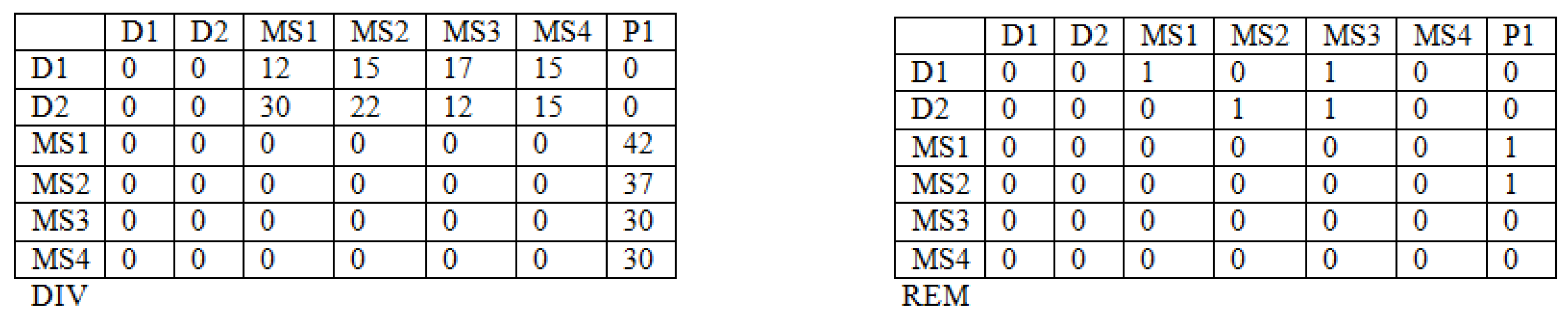
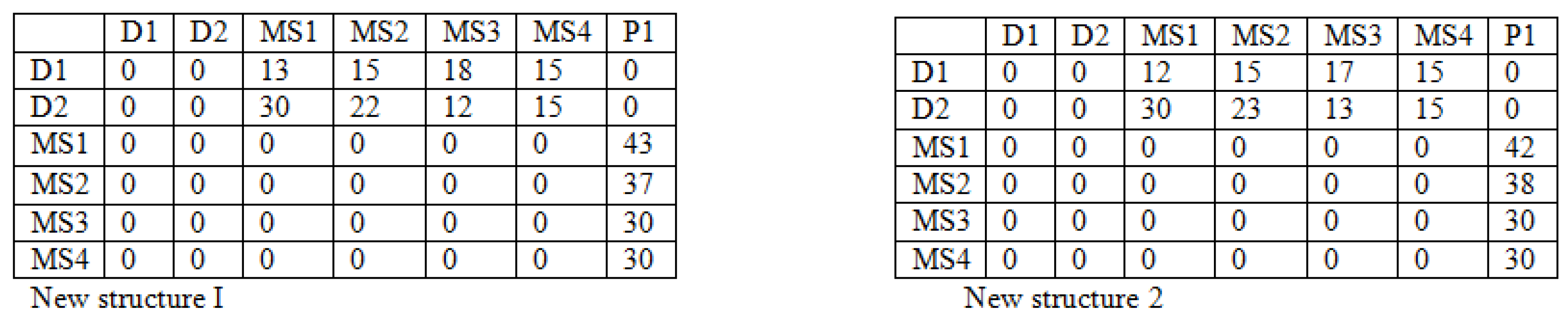
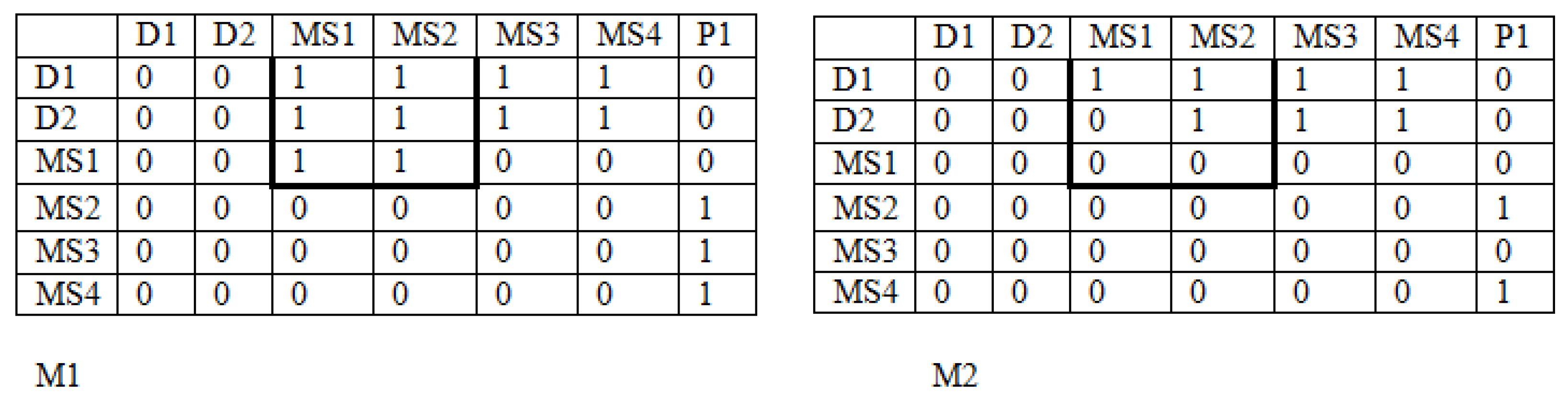
4.4. The Crossover Process
4.5. The Mutation Process
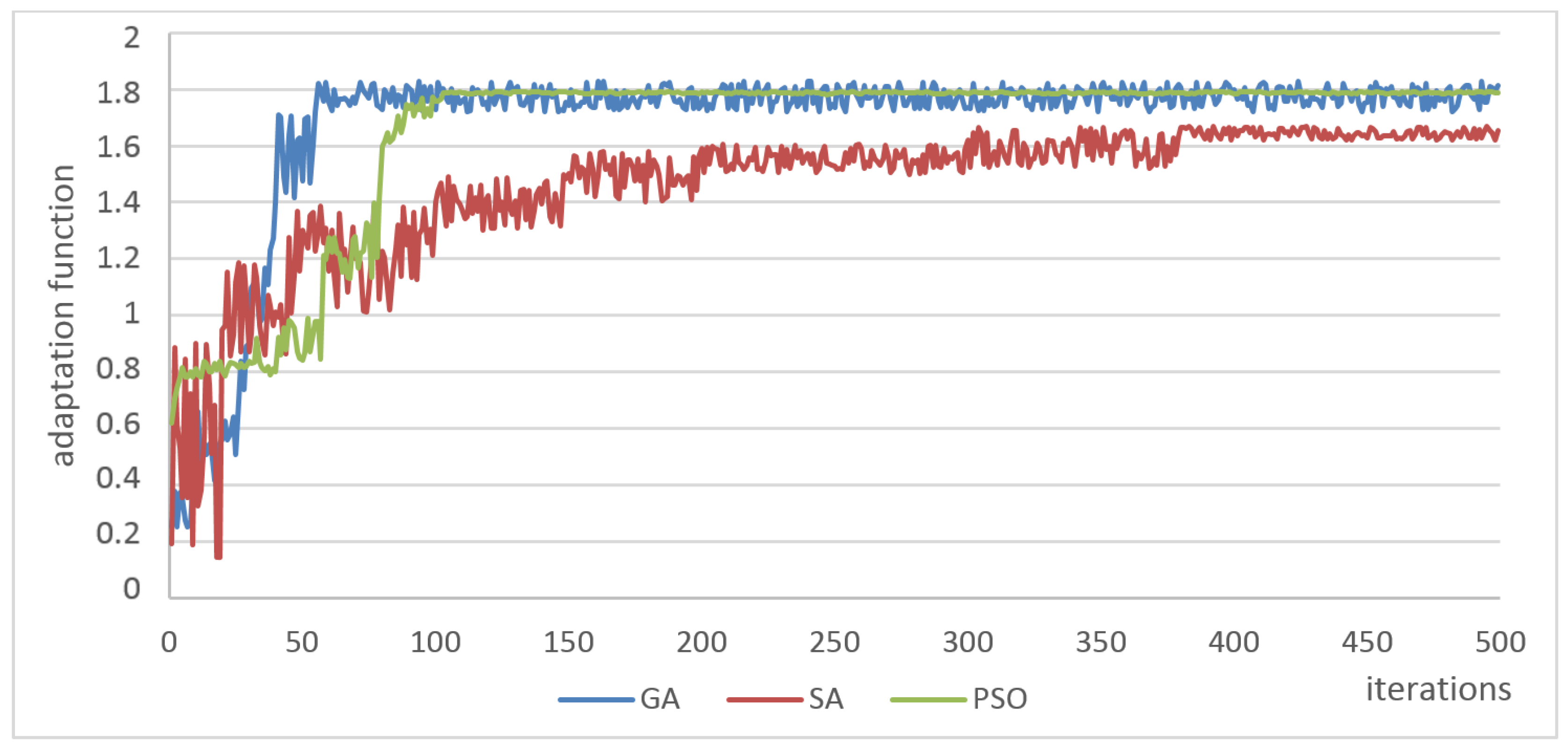
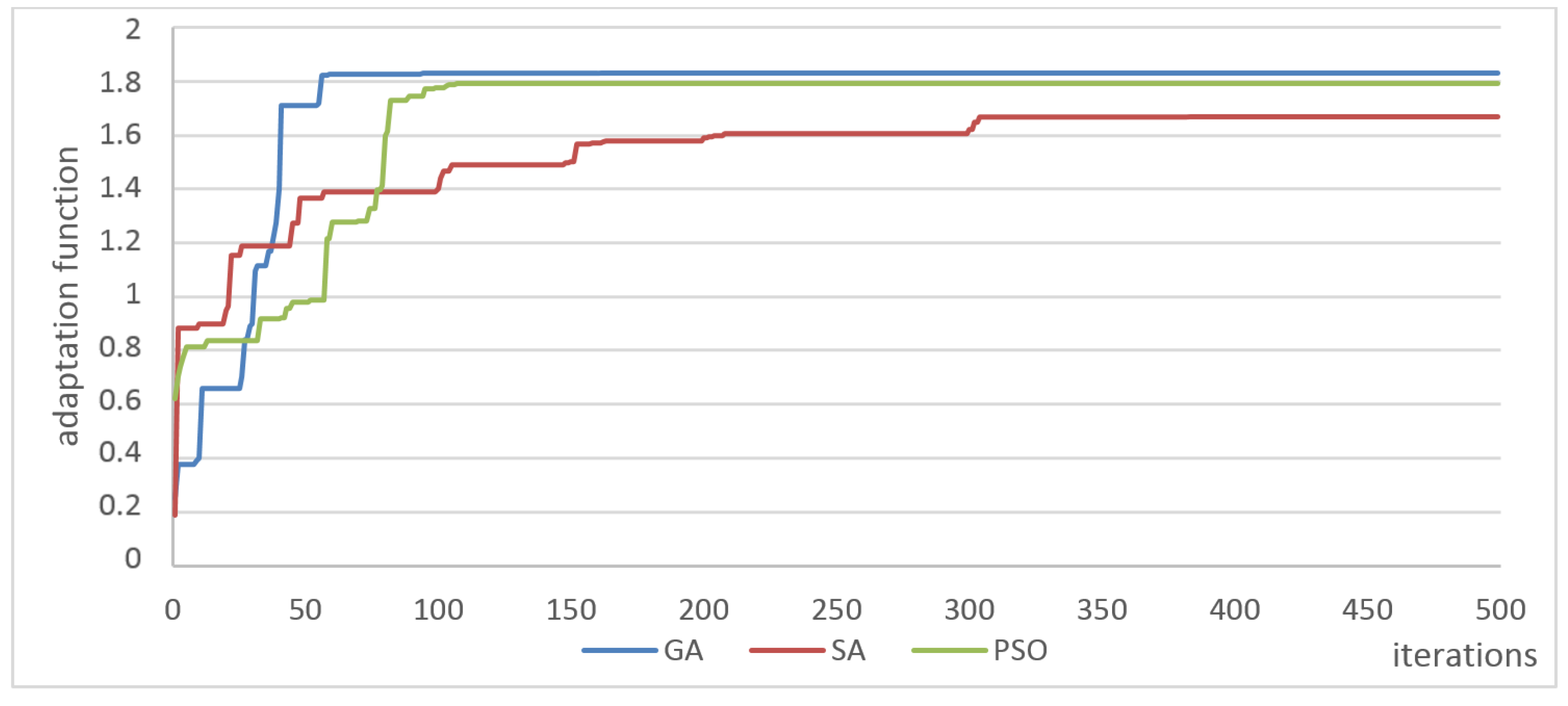
5. The Results and Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ehrgott, M. Multicriteria Optimization; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Brezočnik, L.; Fister, I.; Podgorelec, V. Scrum Task Allocation Based on Particle Swarm Optimization. In Proceedings of the International Conference on Bioinspired Methods and Their Applications, Paris, France, 16–18 May 2018; Springer: Cham, Switzerland, 2018; pp. 38–49. [Google Scholar]
- Ombuki, B. Multi-Objective Genetic Algorithms for Vehicle Routing Problem with Time Windows. Appl. Intell. 2006, 24, 17–30. [Google Scholar] [CrossRef]
- Shuguang, L. A hybrid population heuristic for the heterogeneous vehicle routing problems. Transp. Res. Part E Logist. Transp. Rev. 2013, 54, 67–78. [Google Scholar] [CrossRef]
- Bollobas, B. Modern graph theory. In Graduate Texts in Mathematics; Springer: New York, NY, USA, 1998. [Google Scholar]
- Bondy, J.A.; Murty, U.S.R. Graph Theory with Applications; Elsevier Science Ltd.: North-Holland, The Netherlands, 1976. [Google Scholar]
- Burkhard, R.; Dell’Amico, M.; Marttelo, S. Assignment Problems; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2009. [Google Scholar]
- Harper, P.R.; Senna, V.; Vieria, I.T.; Shahani, A.K. A genetic algorithm for the project assignment problem. Comput. Oper. Res. 2005, 32, 1225–1265. [Google Scholar] [CrossRef]
- Hertz, A.; Lahrichi, N. A patient assignment algorithm for home care services. J. Oper. Res. Soc. 2009, 60, 481–495. [Google Scholar] [CrossRef]
- Holder, A. Navy personnel planning and the optimal partition. Oper. Res. 2005, 53, 77–89. [Google Scholar] [CrossRef]
- Volgenant, A.T. A note on the assignment problem with seniority and job priority constraints. Eur. J. Oper. Res. 2004, 154, 330–335. [Google Scholar] [CrossRef]
- Büther, M. Reducing the elastic generalized assignment problem to the standard generalized assignment problem. J. Oper. Res. Soc. 2010, 61, 1582–1595. [Google Scholar] [CrossRef]
- Cambell, G.M.; Diaby, M. Development and evaluation of an assignment heuristic for allocating cross-trained workers. Eur. J. Oper. Res. 2002, 138, 9–22. [Google Scholar] [CrossRef]
- Cattrysse, D.G.; Van Wassenhove, L.N. A survey of algorithms for the generalized assignmen problem. Eur. J. Oper. Res. 1992, 60, 260–272. [Google Scholar] [CrossRef]
- Nauss, R.M. The elastic generalized assignment problem. J. Oper. Res. Soc. 2004, 55, 1333–1341. [Google Scholar] [CrossRef]
- Wu, T.-H.; Yeh, J.-Y.; Syau, Y.-R. A tabbu search approach to the generalized assignment problem. J. Chin. Inst. Ind. Eng. 2004, 21, 301–311. [Google Scholar] [CrossRef]
- Wilson, J.M. A genetic algorithm for the generalised assignment problem. J. Oper. Res. Soc. 1997, 48, 804–809. [Google Scholar] [CrossRef]
- Błażewicz, J.; Ecker, K.; Pesch, E.; Schmidt, G.; Węglarz, J. Handbook on Scheduling, from Theory to Applications; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Bruckner, P. Scheduling Algorithms, 5th ed.; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Carraresi, P.; Gallo, G. A multi-level bottleneck assignment approach to the bus drivers’ rostering problem. Eur. J. Oper. Res. 1984, 16, 163–173. [Google Scholar] [CrossRef]
- Lourenço, H.R.; Paixão, J.P.; Portugal, R. Multiobjective Metaheuristics for the Bus Driver Scheduling Problem. Transp. Sci. 2001, 35, 331–343. [Google Scholar] [CrossRef]
- Zhang, W.; Xu, W. Simulation-based robust optimization for the schedule of single-direction bus transit route: The design of experiment. Transp. Res. Part E Logist. Transp. Rev. 2017, 106, 203–230. [Google Scholar] [CrossRef]
- Freling, R.; Wagelmans, A.P.M.; Pinto Paixão, J.M. An overview of models and technics for integrating of vehicle and crew scheduling. In Computer-Aided Transit Scheduling; Springer: Berlin/Heidelberg, Germany, 1999; pp. 441–460. [Google Scholar]
- Etschmaier, M.M.; Mathaisel, D.F.X. Airline Scheduling: An Overview. Transp. Sci. 1985, 19, 127–138. [Google Scholar] [CrossRef]
- Klincewicz, J.G.; Rosenwein, M.B. The Airline Exception Scheduling Problem. Transp. Sci. 1995, 29, 4–16. [Google Scholar] [CrossRef]
- Lohatepanont, M.; Barnhart, C. Airline Schedule Planning: Integrated Models and Algorithms for Schedule Design and Fleet Assignment. Transp. Sci. 2004, 38, 19–32. [Google Scholar] [CrossRef]
- Rexing, B.; Barnhart, C.; Kniker, T.; Jarrah, A.; Krishnamurthy, N. Airline Fleet Assignment with Time Windows. Transp. Sci. 2000, 34, 1–20. [Google Scholar] [CrossRef]
- Schaefer, A.J.; Johnson, E.L.; Kleywegt, A.J.; Nemhause, G.L. Airline Crew Scheduling Under Uncertainty. Transp. Sci. 2005, 39, 340–348. [Google Scholar] [CrossRef]
- Yen, J.W.; Birge, J.R. A Stochastic Programming Approach to the Airline Crew Scheduling Problem. Transp. Sci. 2006, 40, 3–14. [Google Scholar] [CrossRef]
- Fischetti, M.; Lodi, A.; Martello, S.; Toth, P. A polyhedral approach to simplified crew scheduling and vehicle scheduling problems. Manag. Sci. 2001, 47, 833–850. [Google Scholar] [CrossRef]
- Freling, R.; Huisman, D.; Wagelmans, A.P.M. Models and Algorithms for Integration of Vehicle and Crew Scheduling. J. Oper. Res. 1989, 37, 63–85. [Google Scholar] [CrossRef]
- Haase, K.; Desaulniers, G.; Desrosiers, J. Simultaneous Vehicle and Crew Scheduling in Urban Mass Transit Systems. Transp. Sci. 2001, 35, 286–303. [Google Scholar] [CrossRef]
- Huisman, D.; Freling, R.; Wagelmans, A. Multiple-Depot Integrated Vehicle and Crew Scheduling. Transp. Sci. 2005, 39, 491–502. [Google Scholar] [CrossRef]
- Jacyna-Gołda, I.; Izdebski, M.; Podviezko, A. Assessment of efficiency of assignment of vehicles to tasks in supply chains: A case study of a municipal company. Transport 2017, 32, 243–251. [Google Scholar] [CrossRef]
- Jiabin, L.; Yue, W. Modelling of dual-cycle strategy for container storage and vehicle scheduling problems at automated container terminals. Transp. Res. Part E Logist. Transp. Rev. 2015, 79, 49–64. [Google Scholar] [CrossRef]
- Petersen, L.; Larsen, A.; Madsen, B.G.; Petersen, B.; Ropke, S. The Simultaneous Vehicle Scheduling and Passenger Service Problem. Transp. Sci. 2013, 47, 603–616. [Google Scholar] [CrossRef]
- Chmielewski, A.; Naujoks, B.; Janas, M.; Clausen, U. Optimizing the Door Assignment in LTL-Terminals. Transp. Sci. 2009, 43, 198–210. [Google Scholar] [CrossRef]
- Aickelin, U.; Dowsland, K.A. An indirect Genetic Algorithm for a nurse-scheduling problem. Comput. Oper. Res. 2004, 31, 761–778. [Google Scholar] [CrossRef]
- Wang, Y.Z. An application of genetic algorithm methods for teacher assignment problems. Expert Syst. Appl. 2002, 22, 295–302. [Google Scholar] [CrossRef]
- Yu, E.; Sung, K.S. A genetic algorithm for a university weekly courses timetabling problem. Int. Trans. Oper. Res. 2002, 9, 703–717. [Google Scholar] [CrossRef]
- Ambroziak, T.; Tkaczyk, S. The selection of transportation means for technological processes. Arch. Transp. 2015, 36, 7–20. [Google Scholar] [CrossRef]
- Akgül, M. A genuinely polynomial primal simplex algorithm for the assignment problem. Discret. Appl. Math. 1993, 45, 93–115. [Google Scholar] [CrossRef]
- Jonker, R.; Volgenant, A.T. Improving the Hungarian assignment algorithm. Oper. Res. Lett. 1986, 5, 171–175. [Google Scholar] [CrossRef]
- Wasiak, M.; Jacyna, M.; Lewczuk, K.; Szczepański, E. The method for evaluation of efficiency of the concept of centrally managed distribution in cities. Transport 2017, 32, 348–357. [Google Scholar] [CrossRef]
- Abraham, P.P.; Aneja, Y.P. A Tabu Search Algorithm for the Resource-Constrained Assignment Problem. J. Oper. Res. Soc. 1995, 46, 214–220. [Google Scholar] [CrossRef]
- Kuo-Jen, H. Fuzzy goal programming technique for solving flexible assignment problem in PCB assembly line. J. Inf. Optim. Sci. 2017, 38, 423–442. [Google Scholar] [CrossRef]
- Mukesh, K.M.; Santosh, K. A goal programming approach for a multi-objective multi-choice assignment problem. Optimization 2014, 63, 1549–1563. [Google Scholar] [CrossRef]
- Pentico, D.W. Assignment problems: A golden anniversary survey. Eur. J. Oper. Res. 2007, 176, 774–793. [Google Scholar] [CrossRef]
- Goldberg, D.E. Genetic Algorithms in Search, Optimization, and Machine Learning, 1st ed.; Addison-Wesley Professional: Boston, MA, USA, 1989. [Google Scholar]
- Michalewicz, Z. Genetic Algorithms + Data Structure = Evolutionary Programs; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Dorigo, M.; Gambardela, L.M. Ant Colonies for the Travelling Salesman Problem. BioSystems 1997, 43, 73–81. [Google Scholar] [CrossRef]
- Bräysy, O.; Gendreau, M. Vehicle Routing Problem with Time Windows, Part II: Metaheuristics. Transp. Sci. 2005, 39, 119–139. [Google Scholar] [CrossRef]
- Szczepański, E.; Jacyna-Gołda, I.; Murawski, J. Genetic algorithms based approach for transhipment hub location in urban areas. Arch. Transp. 2014, 31, 73–82. [Google Scholar] [CrossRef]
- Viotti, P.; Polettini, A.; Pomi, R.; Innocenti, C. Genetic algorithms as a promising tool for optimisation of the MSW collection routes. Waste Manag. Res. 2003, 21, 292–298. [Google Scholar] [CrossRef] [PubMed]
- Ai, T.J.; Kachitvichyanukul, V. Particle swarm optimization and two solution representations for solving the capacitated vehicle routing problem. Comput. Ind. Eng. 2009, 56, 380–387. [Google Scholar] [CrossRef]
- Kuo, Y. Using simulated annealing to minimize fuel consumption for the time-dependent vehicle routing problem. Comput. Ind. Eng. 2010, 59, 157–165. [Google Scholar] [CrossRef]
- Asih, A.M.S.; Sopha, B.M.; Kriptaniadewa, G. Comparison study of metaheuristics: Empirical application of delivery problems. Int. J. Eng. Bus. Manag. 2017, 9. [Google Scholar] [CrossRef]
- Qiu, J.; Wang, T.; Yin, S.; Gao, H. Data-based optimal control for networked double-layer industrial processes. IEEE Trans. Ind. Electron. 2017, 64, 4179–4186. [Google Scholar] [CrossRef]
- Qiu, J.; Wei, Y.; Karimi, H.R.; Gao, H. Reliable control of discrete-time piecewise-affine time-delay systems via output feedback. IEEE Trans. Reliab. 2018, 67, 79–91. [Google Scholar] [CrossRef]
- Jacyna-Gołda, I.; Izdebski, M.; Szczepański, E.; Gołda, P. The assessment of supply chain effectiveness. Arch. Transp. 2018, 45, 43–52. [Google Scholar] [CrossRef]
- Wasiak, M. Vehicle selection model with respect to economic order quantity. Arch. Transp. 2016, 40, 77–85. [Google Scholar] [CrossRef]

| Data | Warehouses [km/km/min/min] | - | |||
|---|---|---|---|---|---|
| 1 | 2 | 3 | Q1 Pallet/KB | ||
| Suppliers [km/km/min/min] | 1 | 50/70/130/90 | 40/25/70/40 | 20/30/30/40 | 300/25 |
| 2 | 60/40/100/60 | 15/20/40/45 | 10/15/20/40 | 250/30 | |
| 3 | 40/55/70/70 | 20/23/35/30 | 10/30/20/40 | 350/15 | |
| 4 | 20/40/40/70 | 80/40/100/60 | 22/15/35/25/ | 150/35 | |
| 5 | 10/30/20/40 | 40/60/50/70 | 10/20/30/35 | 200/40 | |
| 6 | 30/40/50/60 | 10/40/20/60 | 30/20/40/30 | 150/10 | |
| 7 | 10/20 /40/30 | 70/50/90/70 | 20/10/30/20 | 100/15 | |
| Company [km/km/min/min] | - | 25/35/40/50 | 20/30/30/40 | 40/50/60/70 | - |
| Q2 pallet | - | - | - | - | 360 |
| CAP pallet | - | 200 | 150 | 200 | - |
| UMZ pallet | - | 30 | 30 | 30 | - |
| KZ PLN/ pallet | - | 12 | 10 | 11 | - |
| Test | pcross | pmut | Test | pcross | pmut | Test | pcross | pmut |
|---|---|---|---|---|---|---|---|---|
| 1 | 0.2 | 0.01 | 6 | 0.2 | 0.03 | 11 | 0.2 | 0.05 |
| 2 | 0.4 | 0.01 | 7 | 0.4 | 0.03 | 12 | 0.4 | 0.05 |
| 3 | 0.6 | 0.01 | 8 | 0.6 | 0.03 | 13 | 0.6 | 0.05 |
| 4 | 0.8 | 0.01 | 9 | 0.8 | 0.03 | 14 | 0.8 | 0.05 |
| 5 | 1 | 0.01 | 10 | 1 | 0.03 | 15 | 1 | 0.05 |
| Test | The Best Value of Population | Test | The Best Value of Population | Test | The Best Value of the Structure of Population |
|---|---|---|---|---|---|
| 1 | 0.53/0.49 | 6 | 0.57/0.41 | 11 | 0.42/0.3 |
| 2 | 1.3/1.2 | 7 | 1.4/1.0 | 12 | 1.3/1.22 |
| 3 | 1.43/1.39 | 8 | 1.52/1.2 | 13 | 1.6/1.5 |
| 4 | 1.6/1.55 | 9 | 1.73/1.81 | 14 | 1.5/1.77 |
| 5 | 1.7/1.75 | 10 | 1.63/1.7 | 15 | 1.55/1.63 |
| Number of Iterations | GA | SA | PSO | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Adaptation Function | Average Computation Time (s) | Adaptation Function | Average Computation Time (s) | Adaptation Function | Average Computation Time (s) | ||||
| Max | Average | Max | Average | Max | Average | ||||
| 20 | 0.740 | 0.690 | 131.867 | 1.204 | 1.100 | 0.501 | 0.890 | 0.810 | 34.209 |
| 50 | 1.814 | 1.801 | 371.762 | 1.330 | 1.272 | 1.020 | 1.020 | 1.012 | 62.127 |
| 500 | 1.831 | 1.829 | 6259.782 | 1.673 | 1.632 | 14.560 | 1.807 | 1.805 | 651.020 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jacyna, M.; Izdebski, M.; Szczepański, E.; Gołda, P. The Task Assignment of Vehicles for a Production Company. Symmetry 2018, 10, 551. https://doi.org/10.3390/sym10110551
Jacyna M, Izdebski M, Szczepański E, Gołda P. The Task Assignment of Vehicles for a Production Company. Symmetry. 2018; 10(11):551. https://doi.org/10.3390/sym10110551
Chicago/Turabian StyleJacyna, Marianna, Mariusz Izdebski, Emilian Szczepański, and Paweł Gołda. 2018. "The Task Assignment of Vehicles for a Production Company" Symmetry 10, no. 11: 551. https://doi.org/10.3390/sym10110551
APA StyleJacyna, M., Izdebski, M., Szczepański, E., & Gołda, P. (2018). The Task Assignment of Vehicles for a Production Company. Symmetry, 10(11), 551. https://doi.org/10.3390/sym10110551






