Modeling of Free-Form Complex Curves Using SG-Bézier Curves with Constraints of Geometric Continuities

Abstract

The modeling of free-form engineering complex curves is an important subject in product modeling, graphics, and computer aided design/computer aided manufacturing (CAD/CAM). In this paper, we propose a novel method to construct free-form complex curves using shape-adjustable generalized Bézier (or SG-Bézier, for short) curves with constraints of geometric continuities. In order to overcome the difficulty that most of the composite curves in engineering cannot often be constructed by using only a single curve, we propose the necessary and sufficient conditions for G¹ and G² continuity between two adjacent SG-Bézier curves. Furthermore, the detailed steps of smooth continuity for two SG-Bézier curves, and the influence rules of shape parameters on the composite curves, are studied. We also give some important applications of SG-Bézier curves. The modeling examples show that our methods in this paper are very effective, can easily be performed, and can provide an alternative powerful strategy for the design of complex curves.

1. Introduction

As a useful tool for shape designs and geometric representations of different kinds of products, parametric curves and surfaces have become an important research subject in CAD/CAM. Traditional Bézier curves and surfaces, which hold simple definitions and enjoy many excellent properties, are obtained by using the Bernstein basis functions. Due to this superiority, the traditional Bézier curves and surfaces have been becoming an important way to represent curves and surfaces in the CAD/CAM field. However, the Bézier method still has some shortcomings which are manifested mainly in the following two aspects: ① the shapes of the Bézier model are only determined by their control points; ② conic curves and surfaces cannot be represented by the Bézier method accurately. So, in order to overcome the former defect, rational Bézier curves and surfaces have been proposed in recent years whose shapes can be modified by adjusting their weight factors while keeping the control points unchanged. However, some other problems, such as complex calculations, cumbersome integrals, and repetitive differentiation [1,2] will be caused by the introduction of rational fractions. In addition, using the spline method can also realize shape control in constructing complex curves; many theories about splines can be found in [3]. Another relevant class of literature that gives more degrees of freedom for shape control relates to the degree elevation and degree reduction; see [4,5].

For the past few years, scholars have proposed various Bézier curves with shape parameters [6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22] so as to keep the advantages and increase the shape adjustability of the traditional Bézier curves. Oruc et al. [6] constructed a new kind of q-Bernstein basis function and gave the definition of q-Bézier curves. Wang et al. [7] used a selected initial function and combined it with an integral to propose some types of Bézier curves with shape parameters. To introduce one shape parameter into Bézier curves, Yan et al. [8] extended quadratic Bernstein basis functions to quartic Bernstein-like basis functions, and then utilized the De Casteljau elevation algorithm and recursive method; a class of high-degree generalized Bézier curves were obtained. In 2014, Chu [9] used Beta functions to construct a kind of Beta–Bézier basis function, and thereby give the corresponding definition of the Beta–Bézier curve with one shape parameter. Furthermore, Farin et al. [10] and Cao et al. [11] gave two different kinds of high-degree Bézier curves with single shape parameters, respectively. As only one shape parameter is contained in curves in the literature [6,7,8,9,10,11], its value can be modified to make this type of curve merely simply swing from one or two sides of classical Bézier curves. This leads to the limitation of the local shape adjustability.

Scholars have carried out some studies of integrating several shape parameters into high-degree Bézier curves (see [12,13,14,15,16,17,18,19,20,21,22]) in order to improve their local shape adjustability further. The curves in [12,13,14,15,16,17,18,19,20,21,22] had something in common: ① these curves inherited the most beneficial properties of classical Bézier curves; ② these curves possessed multiple local shape parameters, which could be easily utilized to modify the local shapes of these curves once the control points were given. However, as shown in [12,13,14,15,16,17,18,19,20,21,22], these curves have no global shape parameters, which results in the inconvenience of global shape adjustability for the curves.

To sum up, the local shape adjustments of the curves and surfaces in [6,7,8,9,10,11] are difficult and caused by the absence of a local shape parameter, while the global shapes adjustment in [12,13,14,15,16,17,18,19,20,21,22] are inconvenient as a result of the lack of a global shape parameter. In practical engineering applications, the local or global shapes of curves or surfaces often need to be modified under the condition of the control points remaining the same. Therefore, the research on how to construct a kind of special curve and surfaces that holds shape adjustability becomes an important topic with great value. Hu et al. introduced certain polynomial curves and surfaces called SG-Bézier curves, which can be regarded as an extension of classic Bézier curves; their global and local shape can be adjusted by altering the global and local shape parameters under the condition of keeping the control points unchanged, respectively [23]. The theoretical analysis shows that the proposed SG-Bézier curves hold most of the advantages of the classical Bézier model, as well as overcomes the disadvantages of the Bézier model [6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22].

In practical engineering applications, complex curves are often constructed by using the piecewise method. In order to make the final composite curves have overall smoothness, the adjacent curves should meet some specific continuity conditions. As an important current research topic in CAD/CAM systems, the smooth continuity technology between two parametric curves has an impact on the construction of complex curves. At present, two types of standards have been established for measuring the smoothness joining between two adjacent parametric curves [24,25]: ① parametric continuity (usually called Cⁿ continuity); and ② geometric continuity (namely, Gⁿ continuity). Compared with the traditional Bézier curves, the SG-Bézier curves in [23] have more advantages and play a key role in representing complex curves. Nonetheless, the expressions of SG-Bézier curves are polynomials, and one will also be facing the issue of smooth joining to construct composite curves. According to the basis functions and terminal properties of SG-Bézier curves, we give the geometric continuity conditions between two SG-Bézier curves in this paper. The modeling examples show that the shape adjustability of the composite curves are more flexible, which lends itself to the wide application of the SG-Bézier curves.

The outline of this paper is as follows. The definition and properties of SG-Bézier curves are described in Section 2. In Section 3, we give the G¹ and G² continuity conditions for SG-Bézier curves. In Section 4, we then investigate the steps of smooth joining for SG-Bézier curves and give some examples. In Section 5, we analyze the shape adjustment of piecewise SG-Bézier curves. Finally, some practical applications are shown in Section 6. At the end of the paper, we give a short conclusion in Section 7.

2. The family of SG-Bézier Curves

2.1. SG-Bernstein Basis Functions of Degree n

Definition 1.

For$n\ge 2$,$n\in {\mathit{N}}^{+}$and any$t\in [0,1]$, we call the functions with respect to t following:

$$\{\begin{array}{l}{l}_{j,n}(t;{\lambda }_j,{\lambda }_{j+1},\omega )=\left[\left(\begin{array}{l}n\\ j\end{array}\right)+\left(\left(\begin{array}{c}n+1\\ j\end{array}\right)-\left(\begin{array}{l}n\\ j\end{array}\right)-{\lambda }_j\right)\omega +\left({\lambda }_j+{\lambda }_{j+1}-\left(\begin{array}{c}n+1\\ j\end{array}\right)\right)\omega t\right]t^i{(1-t)}^{n-i}\\ l_{n-j,n}(t;{\mu }_j,{\mu }_{j+1},\omega )=\left[\left(\begin{array}{c}n\\ j\end{array}\right)+\left({\mu }_{j+1}-\left(\begin{array}{c}n\\ j\end{array}\right)\right)\omega -\left({\mu }_j+{\mu }_{j+1}-\left(\begin{array}{c}n+1\\ j\end{array}\right)\right)\omega t\right]t^{n-i}{(1-t)}^i\end{array}$$

(1)

the nth-degree shape-adjustable generalized Bernstein (or SG-Bernstein, for short) basis functions with shape parameters [23], where $j=0,1,\cdots ,[n/2]$,$0\le \omega \le 1$, and${\lambda }_0={\mu }_0=0,$$0\le {\lambda }_j,{\mu }_j\le \left(\begin{array}{c}n+1\\ j\end{array}\right)(j=1,2,\cdots ,[n/2]+1)$are shape parameters.

Remark 1.

It can be seen that the values of the shape parameters${\lambda }_j,{\mu }_j$in Equation (1) meet the following constraint conditions:

(a) if n is even,

$${\lambda }_{[n/2]+1}=\left(\begin{array}{c}n+1\\ [n/2]\end{array}\right)-{\mu }_{[n/2]},{\mu }_{[n/2]+1}=\left(\begin{array}{c}n+1\\ [n/2]\end{array}\right)-{\lambda }_{[n/2]};$$

(b) ifnis odd,

$${\lambda }_{[n/2]+1}=\left(\begin{array}{c}n+1\\ [n/2]+1\end{array}\right)-{\mu }_{[n/2]+1}$$

From the definition above, we can know that the SG-Bernstein basis functions in Equation (1) have n + 1 polynomials, each of which is of the degree n + 1. The basis functions defined by Equation (1) have n + 1 different shape parameters, which are $\omega ,{\lambda }_j,{\mu }_j$, respectively. Specially, if n is even, the numbers of ${\lambda }_j$ and ${\mu }_j$ are equal to n/2, respectively; while if n is odd, the number of ${\lambda }_j$ is equal to (n + 1)/2, and the number of ${\mu }_j$ is equal to (n − 1)/2.

It can be verified that the SG-Bernstein basis functions $l_{j,n}(t)(j=0,1,\cdots ,n)$ defined by Equation (1) possess most of the properties that are similar to those of the nth-degree traditional Bernstein basis functions such as:

(1) Degeneracy: If the shape parameter $\omega =0$, the nth-degree SG-Bernstein basis functions are just the traditional Bernstein basis functions.

(2) Non-negativity: For arbitrary $\omega ,{\lambda }_j,{\mu }_j$, we have $l_{j,n}(t)\ge 0(j=0,1,\cdots ,n;n\ge 2)$.

(3) Partition of unity: That is, we have ${\displaystyle \sum _{j=0}^n}{l}_{j,n}(t)=1$.

(4) Symmetry: If shape parameters ${\lambda }_j={\mu }_j$, we have $l_{n-j,n}(t)=l_{j,n}(1-t)(j=1,2,\dots ,[n/2])$.

(5) Linear independence: For any $\omega ,{\lambda }_j,{\mu }_j$, the SG-Bernstein basis functions $l_{j,n}(t)$ $(j=0,1,\dots ,n)$ satisfy the condition of linear independence.

Figure 1 shows the third-degree SG-Bernstein basis functions with different shape parameters, where the blue lines, red dotted lines, cyan dashed lines, and magenta imaginary lines correspond to the four SG-Bernstein basis functions $l_{0,3}(t),l_{1,3}(t),l_{2,3}(t)$ and $l_{3,3}(t)$, respectively. We can see from Figure 1 that the different shape parameters can produce various shapes for the SG-Bernstein basis functions. Similar to the traditional Bernstein basis, the SG-Bernstein basis also has the property of symmetry. Figure 1a,b shows this feature, respectively (while the curves in Figure 1c,d) do not).

2.2. SG-Bézier Curves of Degree n

Definition 2.

For any given set of the control points${\mathit{P}}_j\in {\mathit{R}}^d(d=2,3;j=0,1,\dots ,n)$, a family ofparametric curves$\left\{{\widehat{\prod }}_{t,n}\right\}$can be defined as follows:

$$\left\{{\widehat{\prod }}_{t,n}\right\}:{\mathit{L}}_n(t;{\lambda }_j,{\mu }_j,\omega )={\displaystyle \sum _{j=0}^n}{\mathit{P}}_j{l}_{j,n}(t),(t\in [0,1]),$$

(2)

where$0\le \omega \le 1$and$0\le {\lambda }_j,{\mu }_j\le \left(\begin{array}{c}n+1\\ j\end{array}\right)(j=0,1,\cdots ,[n/2]+1)$are the global and local shape parameters of curves$\left\{{\widehat{\prod }}_{t,n}\right\}$, respectively. Recall that${\{l_{j,n}(t)\}}_{j=0}^n$are thenth-degree SG-Bernstein basis functions (1). Therefore, the polynomial curves defined by Equation (2) are called SG-Bézier curves of degreen[23].

Given n + 1 control points ${\mathit{P}}_j(j=0,1,\cdots ,n)$, they might produce a set of SG-Bézier curves with various shapes when the shape parameters are changing with the values taken over the corresponding ranges. On the basis of the properties of SG-Bernstein basis functions, it is not difficult to prove that the SG-Bézier curves that were defined in Equation (2) inherit a lot of properties of the classical Bézier curves, as follows:

(1) Degeneracy: If shape parameter $\omega =0$, the SG-Bézier curve of degree n degenerates to the classical Bézier curve of degree n.

(2) Symmetry: For any of the given control points ${\mathit{P}}_0,{\mathit{P}}_1,\cdots ,{\mathit{P}}_n$ and ${\mathit{P}}_0^{*},{\mathit{P}}_1^{*},\cdots ,{\mathit{P}}_n^{*}$, if they satisfy the condition ${\mathit{P}}_0^{*}={\mathit{P}}_n,{\mathit{P}}_1^{*}={\mathit{P}}_{n-1},\cdots ,{\mathit{P}}_n^{*}={\mathit{P}}_0$, then the two groups of control points define a common SG-Bézier curve, and they only have the reverse directions. That is:

$${\mathit{L}}_n(t;{\lambda }_j,{\mu }_j,\omega ;{\mathit{P}}_0,{\mathit{P}}_1,\cdots ,{\mathit{P}}_n)={\mathit{L}}_n(1-t;{\mu }_j,{\lambda }_j,\omega ;{\mathit{P}}_0^{*},{\mathit{P}}_1^{*},\cdots ,{\mathit{P}}_n^{*}).$$

(3) Convex hull property: The SG-Bézier curve is contained in the convex hull of its defining control points.

(4) Affine invariance: Rotations, translations, and scalings are applied to an SG-Bézier curve by applying them to its control points, that is:

$$\{\begin{array}{l}{\mathit{L}}_n(t;{\lambda }_j,{\mu }_j,\omega ;{\mathit{P}}_0+\mathit{Q},{\mathit{P}}_1+\mathit{Q},\cdots ,{\mathit{P}}_n+\mathit{Q})={\mathit{L}}_n(t;{\lambda }_j,{\mu }_j,\omega ;{\mathit{P}}_0,{\mathit{P}}_1,\cdots ,{\mathit{P}}_n)+\mathit{Q}\\ {\mathit{L}}_n(t;{\lambda }_j,{\mu }_j,\omega ;\mathit{M}{\mathit{P}}_0,\mathit{M}{\mathit{P}}_1,\cdots ,\mathit{M}{\mathit{P}}_n)=\mathit{M}{\mathit{L}}_n(t;{\lambda }_j,{\mu }_j,\omega ;{\mathit{P}}_0,{\mathit{P}}_1,\cdots ,{\mathit{P}}_n)\end{array},$$

where $\mathit{Q}$ is an arbitrary constant vector in R² or R³, and M $\in$ R^k×k (k = 2 or 3) is an arbitrary constant matrix.

Figure 2 shows the SG-Bézier curves of degree 3. We know that SG-Bézier curves have local and global shape parameters by Definition 2. Figure 2a,b thus show the shape adjustment by modifying the global and local shape parameters, respectively. In Figure 2a, the global shape parameters are $\omega =0,0.5,1$ from outside to inside; while in Figure 2b, the local shape parameters are ${\lambda }_1={\mu }_1={\lambda }_2=1,2,3$ from outside to inside.

Theorem 1.

The nth-degree SG-Bézier curve${\mathit{L}}_n(t;{\lambda }_j,{\mu }_j,\omega )$holds some terminal properties as follows:

$$\{\begin{array}{l}{\mathit{L}}_n(0;{\lambda }_j,{\mu }_j,\omega )={\mathit{P}}_0,\hfill \\ {\mathit{L}}_n(1;{\lambda }_j,{\mu }_j,\omega )={\mathit{P}}_n,\hfill \\ {L^{\prime }}_n(0;{\lambda }_j,{\mu }_j,\omega )=[n+\omega -\omega {\lambda }_1]({\mathit{P}}_1-{\mathit{P}}_0),\hfill \\ {L^{\prime }}_n(1;{\lambda }_j,{\mu }_j,\omega )=[n+\omega -\omega {\mu }_1]({\mathit{P}}_n-{\mathit{P}}_{n-1}),\hfill \\ \begin{array}{ll}{L^{″}}_n(0;{\lambda }_j,{\mu }_j,\omega )& =[n(n-1)+2n\omega -2n\omega {\lambda }_1]{\mathit{P}}_0-[2n(n-1)+4n\omega -2n\omega {\lambda }_1-2\omega {\lambda }_2]{\mathit{P}}_1\\ & +[n(n-1)+2n\omega -2\omega {\lambda }_2]{\mathit{P}}_2,\end{array}\hfill \\ \begin{array}{ll}{L^{″}}_n(1;{\lambda }_j,{\mu }_j,\omega )& =[n(n-1)+2n\omega -2n\omega {\mu }_1]{\mathit{P}}_n-[2n(n-1)+4n\omega -2n\omega {\mu }_1-2\omega {\mu }_2]{\mathit{P}}_{n-1}\\ & +[n(n-1)+2n\omega -2\omega {\mu }_2]{\mathit{P}}_{n-2}.\end{array}\hfill \end{array}$$

(3)

Proof. 

On the basis of the definition and properties of the nth-degree SG-Bernstein basis functions ${\{l_{j,n}(t)\}}_{j=0}^n$, we can obtain the following terminal properties:

$$l_{j,n}(0)=\{\begin{array}{c}1\begin{array}{cc},& (j=0)\end{array}\\ 0\begin{array}{cc},& (j\ne 0)\end{array}\end{array}$$

(4)

$$l_{j,n}(1)=\{\begin{array}{c}1\begin{array}{cc},& (j=n)\end{array}\\ 0\begin{array}{cc},& (j\ne n)\end{array}\end{array}$$

(5)

$${l^{\prime }}_{j,n}(0)=\{\begin{array}{ll}-(n+\omega -\omega {\lambda }_1),\hfill & (j=0)\hfill \\ n+\omega -\omega {\lambda }_1,\hfill & (j=1)\hfill \\ 0,\hfill & (j=2,3,\cdots ,n)\hfill \end{array}$$

(6)

$${l^{\prime }}_{j,n}(1)=\{\begin{array}{ll}-(n+\omega -\omega {\mu }_1),\hfill & (j=n-1)\hfill \\ n+\omega -\omega {\mu }_1,\hfill & (j=n)\hfill \\ 0,\hfill & (j=0,1,\cdots ,n-2)\hfill \end{array}$$

(7)

$${l^{″}}_{j,n}(0)=\{\begin{array}{ll}n(n-1)+2n\omega -2n\omega {\lambda }_1,\hfill & (j=0)\hfill \\ -[2n(n-1)+4n\omega -2n\omega {\lambda }_1-2\omega {\lambda }_2],\hfill & (j=1)\hfill \\ n(n-1)+2n\omega -2\omega {\lambda }_2,\hfill & (j=2)\hfill \\ 0,\hfill & (j=3,4,\cdots ,n)\hfill \end{array}$$

(8)

$${l^{″}}_{j,n}(1)=\{\begin{array}{ll}n(n-1)+2n\omega -2n\omega {\mu }_1,\hfill & (j=n)\hfill \\ -[2n(n-1)+4n\omega -2n\omega {\mu }_1-2\omega {\mu }_2],\hfill & (j=n-1)\hfill \\ n(n-1)+2n\omega -2\omega {\mu }_2,\hfill & (j=n-2)\hfill \\ 0.\hfill & (j=0,1,\cdots ,n-3)\hfill \end{array}$$

(9)

The terminal properties of the SG-Bézier curves shown in Equation (3) can be obtained by combining Equations (4)–(9) with the definition of the SG-Bézier curves. This completes the proof of Theorem 1. □

2.3. The Influence of Shape Parameters on the Shapes of SG-Bézier Curves

Besides the above properties, the most outstanding characteristic of the SG-Bézier curve is that it contains n + 1 different shape parameters. We can modify the local and global shape of the curve conveniently by changing its n + 1 shape parameters under the condition that the control points are kept unchanged. Therefore, it is of great important practical significance to study the influence rules of shape parameters on the SG-Bézier curves.

The geometric meaning of the shape parameters $\omega ,{\lambda }_j,{\mu }_j$: ① According to the definitions of the SG-Bernstein basis functions in Equation (1), each basis function has the shape parameter $\omega$. Thence, the change of shape parameter $\omega$ would affect the value of each basis function, which in turn gives rise to the change of approximation degree of the SG-Bézier curve and each control point. This finally makes the change of the global shape for the SG-Bézier curve. So, we call $\omega$ the global shape parameter. ② Since the shape parameters ${\lambda }_j(j=1,2,\cdots ,[n/2]+1)$ are merely contained in the adjacent basis functions $l_{j-1,n}(t)$ and $l_{j,n}(t)$, the change of ${\lambda }_j$ will greatly affect the local shape of the curve nearby ${\mathit{P}}_{j-1}$ and ${\mathit{P}}_j$. In other words, the curve will approach the control point ${\mathit{P}}_{j-1}$ and be far away from the control point ${\mathit{P}}_j$ when increasing the values of ${\lambda }_j$. Similarly, the change of ${\mu }_j$ will greatly affect the local shape of the curve nearby ${\mathit{P}}_{n-j}$ and ${\mathit{P}}_{n+1-j}$, which means that the curve will approach the control point ${\mathit{P}}_{n+1-j}$ and be far away from the control point ${\mathit{P}}_{n-j}$ when increasing the values of ${\mu }_j$. So, the shape parameters ${\lambda }_j$ and ${\mu }_j$ are all called the local shape parameters.

Figure 3 shows the SG-Bézier curves of degree 3 with different shape parameters. The corresponding shape parameters for the curves from the top to the bottom in Figure 3a are $\omega =0,0.3,0.6,1$, respectively, where the shape parameters ${\lambda }_1,{\lambda }_2$ and ${\mu }_1$ are fixed. Fixing the shape parameters $\omega ,{\lambda }_2$ and ${\lambda }_1$, the other shape parameters for the curves from the top to the bottom in Figure 3b are ${\lambda }_1=1,2,3,4$, respectively. In Figure 3c, the shape parameters $\omega ,{\lambda }_2$ and ${\lambda }_1$ are fixed, and the other shape parameters for the curves from the top to the bottom are ${\mu }_1=1,2,3,4$, respectively. In Figure 3d, the corresponding shape parameters for the curves from the right to the left are ${\lambda }_2=0,2,4,6$, while the other shape parameters $\omega ,{\lambda }_1$ and ${\lambda }_1$ are fixed.

As shown in Figure 3, the global shape of the SG-Bézier curve can be adjusted by altering the global shape parameter $\omega$. In this way, the local shape of the SG-Bézier curve also can be modified by changing other local shape parameters. The effects of all of the shape parameters on the shape of the curve satisfy the above description of geometric significance.

3. Smooth Continuity Conditions of SG-Bézier Curves

In practical applications, we usually encounter some complex curves that cannot be constructed by a single curve. Using the method of piecewise to construct this kind of curve, the first problem is to discuss the continuity conditions between adjacent curves. The continuity conditions for SG-Bézier curves are shown as the following theorem form:

3.1. G¹ Smooth Continuity Conditions of SG-Bézier Curves

Theorem 2.

Suppose that any two given adjacent SG-Bézier curves${\mathit{L}}_n(t;{\lambda }_{j,1},{\mu }_{j,1},{\omega }_1)$and${\mathit{L}}_m(t;{\lambda }_{\tilde{j},2},{\mu }_{\tilde{j},2},{\omega }_2)$with the control points${\mathit{P}}_j^1(j=0,1,\dots ,n)$and${\mathit{P}}_{\tilde{j}}^2(\tilde{j}=0,1,\dots ,m)$reach G¹smooth continuity at the common joint; then, they match the necessary and sufficient conditions as follows:

$$\{\begin{array}{l}{\mathit{P}}_0^2={\mathit{P}}_n^1,\\ {\mathit{P}}_1^2=[1+\frac{n+{\omega }_1-{\omega }_1{\mu }_{1,1}}{\zeta (m+{\omega }_2-{\omega }_2{\lambda }_{1,2})}]{\mathit{P}}_n^1-\frac{n+{\omega }_1-{\omega }_1{\mu }_{1,1}}{\zeta (m+{\omega }_2-{\omega }_2{\lambda }_{1,2})}{\mathit{P}}_{n-1}^1.\end{array}$$

(10)

where$\zeta >0$is a constant, and${\omega }_1,{\lambda }_{j,1},{\mu }_{j,1}(j=1,2,\cdots ,[n/2]+1)$and${\omega }_2,{\lambda }_{\tilde{j},2},{\mu }_{\tilde{j},2}(\tilde{j}=1,2,\cdots ,[m/2]+1)$are the shape parameters of the curves${\mathit{L}}_n(t)$and${\mathit{L}}_m(t)$, satisfying that$m+{\omega }_2-{\omega }_2{\lambda }_{1,2}\ne 0$.

Proof. 

According to Equation (2), we suppose the two splicing SG-Bézier curves that need to be smooth joining are defined as follows:

$${\mathit{L}}_n(t;{\lambda }_{j,1},{\mu }_{j,1},{\omega }_1)={\displaystyle \sum _{j=0}^n}{\mathit{P}}_j^1{l}_{j,n}(t),(j=0,1,\cdots ,n,n\ge 2),$$

(11)

$${\mathit{L}}_m(t;{\lambda }_{\tilde{j},2},{\mu }_{\tilde{j},2},{\omega }_2)={\displaystyle \sum _{\tilde{j}=0}^m}{\mathit{P}}_{\tilde{j}}^2{l}_{\tilde{j},m}(t),(\tilde{j}=0,1,\cdots ,m,m\ge 2).$$

(12)

If the SG-Bézier curves ${\mathit{L}}_n(t;{\lambda }_{j,1},{\mu }_{j,1},{\omega }_1)$ and ${\mathit{L}}_m(t;{\lambda }_{\tilde{j},2},{\mu }_{\tilde{j},2},{\omega }_2)$ need to achieve G¹ continuity, they are required to achieve G⁰ continuity at a common joint in the first place. This signifies that one needs to combine the end of ${\mathit{L}}_n(t;{\lambda }_{j,1},{\mu }_{j,1},{\omega }_1)$ with the beginning of ${\mathit{L}}_m(t;{\lambda }_{\tilde{j},2},{\mu }_{\tilde{j},2},{\omega }_2)$, that is:

$${\mathit{L}}_n(1;{\lambda }_{j,1},{\mu }_{j,1},{\omega }_1)={\mathit{L}}_m(0;{\lambda }_{\tilde{j},2},{\mu }_{\tilde{j},2},{\omega }_2).$$

(13)

Equation (13) above can be simplified to Equation (14) as follows in terms of the terminal properties of Equation (3):

$${\mathit{P}}_n^1={\mathit{P}}_0^2.$$

(14)

Equation (14) shows that the two curves reach G⁰ continuity at a common joint firstly.

Furthermore, for the two splicing SG-Bézier curves, the second condition of the same tangent direction at the joint should be satisfied, that is:

$${L^{\prime }}_n(1;{\lambda }_{j,1},{\mu }_{j,1},{\omega }_1)=\zeta {L^{\prime }}_m(0;{\lambda }_{\tilde{j},2},{\mu }_{\tilde{j},2},{\omega }_2),(\zeta >0).$$

(15)

Equation (15) above can be simplified to Equation (16) as follows on the basis of the terminal properties of the SG-Bézier curve in Theorem 1:

$$\{\begin{array}{l}{L^{\prime }}_n(1;{\lambda }_{j,1},{\mu }_{j,1},{\omega }_1)=(n+{\omega }_1-{\omega }_1{\mu }_{1,1})({\mathit{P}}_n^1-{\mathit{P}}_{n-1}^1),\hfill \\ {L^{\prime }}_m(0;{\lambda }_{\tilde{j},2},{\mu }_{\tilde{j},2},{\omega }_2)=(m+{\omega }_2-{\omega }_2{\lambda }_{1,2})({\mathit{P}}_1^2-{\mathit{P}}_0^2).\hfill \end{array}$$

(16)

Plugging Equation (16) into Equation (15), we have:

$${\mathit{P}}_1^2=[1+\frac{n+{\omega }_1-{\omega }_1{\mu }_{1,1}}{\zeta (m+{\omega }_2-{\omega }_2{\lambda }_{1,2})}]{\mathit{P}}_n^1-\frac{n+{\omega }_1-{\omega }_1{\mu }_{1,1}}{\zeta (m+{\omega }_2-{\omega }_2{\lambda }_{1,2})}{\mathit{P}}_{n-1}^1.$$

(17)

Here, $\zeta >0$ is a constant, and $m+{\omega }_2-{\omega }_2{\lambda }_{1,2}\ne 0$.

In summary, if these two curves satisfy Equations (14) and (17) simultaneously, then they reach G¹ smooth continuity at the common joint, and hence Theorem 2 is proved. □

Specifically, let us set $\alpha =1$. Then, (10) is equal to:

$$\{\begin{array}{l}{\mathit{P}}_0^2={\mathit{P}}_n^1,\\ {\mathit{P}}_1^2=[1+\frac{n+{\omega }_1-{\omega }_1{\mu }_{1,1}}{m+{\omega }_2-{\omega }_2{\lambda }_{1,2}}]{\mathit{P}}_n^1-\frac{n+{\omega }_1-{\omega }_1{\mu }_{1,1}}{m+{\omega }_2-{\omega }_2{\lambda }_{1,2}}{\mathit{P}}_{n-1}^1.\end{array}$$

(18)

That is, the G¹ continuity conditions will degenerate into the C¹ continuity conditions when we set $\alpha =1$, and the signs in Equation (18) are the same as that in Equation (10).

3.2. G² Smooth Continuity Conditions of SG-Bézier Curves

Theorem 3.

For any two splicing SG-Bézier curves${\mathit{L}}_n(t;{\lambda }_{j,1},{\mu }_{j,1},{\omega }_1)$and${\mathit{L}}_m(t;{\lambda }_{\tilde{j},2},{\mu }_{\tilde{j},2},{\omega }_2)$with the control points${\mathit{P}}_j^1(j=0,1,\dots ,n)$and${\mathit{P}}_{\tilde{j}}^2(\tilde{j}=0,1,\dots ,m)$, respectively, they meet the G²smooth continuity if and only if:

$$\{\begin{array}{l}{\mathit{P}}_0^2={\mathit{P}}_n^1,\\ {\mathit{P}}_1^2=[1+\frac{n+{\omega }_1-{\omega }_1{\mu }_{1,1}}{\zeta (m+{\omega }_2-{\omega }_2{\lambda }_{1,2})}]{\mathit{P}}_n^1-\frac{n+{\omega }_1-{\omega }_1{\mu }_{1,1}}{\zeta (m+{\omega }_2-{\omega }_2{\lambda }_{1,2})}{\mathit{P}}_{n-1}^1,\\ {\mathit{P}}_2^2=\frac{1}{c}\{[n(n-1)+2n{\omega }_1-2n{\omega }_1{\mu }_{1,1}]-{\zeta }^2[m(m-1)+2m{\omega }_2-2m{\omega }_2{\lambda }_{1,2}]\\ \hspace{1em}\hspace{1em}+\psi (m+{\omega }_2-{\omega }_2{\lambda }_{1,2})-b(1+a)\}{P}_n^1-\frac{1}{c}[2n(n-1)+4n{\omega }_1-2n{\omega }_1{\mu }_{1,1}-2{\omega }_1{\mu }_{2,1}-ab]{\mathit{P}}_{n-1}^1\\ \hspace{1em}\hspace{1em}+\frac{1}{c}[n(n-1)+2n{\omega }_1-2{\omega }_1{\mu }_{2,1}]{\mathit{P}}_{n-2}^1.\end{array}$$

(19)

where$\zeta >0$is a constant,$\psi$is an arbitrary constant, and$m+{\omega }_2-{\omega }_2{\lambda }_{1,2}\ne 0$.

Here,$a=\frac{n+{\omega }_1-{\omega }_1{\mu }_{1,1}}{\zeta (m+{\omega }_2-{\omega }_2{\lambda }_{1,2})},$$c={\zeta }^2[m(m-1)+2m{\omega }_2-2{\omega }_2{\lambda }_{2,2}]$, and$b=\psi (m+{\omega }_2-{\omega }_2{\lambda }_{1,2})-{\zeta }^2[2m(m-1)+4m{\omega }_2-2m{\omega }_2{\lambda }_{1,2}-2{\omega }_2{\lambda }_{2,2}]$.

Proof. 

If the SG-Bézier curves ${\mathit{L}}_n$ and ${\mathit{L}}_m$ achieve G² continuity, they are required to achieve G¹ continuity at a common joint in the first place, which satisfies:

$$\{\begin{array}{l}{\mathit{P}}_n^1={\mathit{L}}_n(1;{\lambda }_{j,1},{\mu }_{j,1},{\omega }_1)={\mathit{L}}_m(0;{\lambda }_{\tilde{j},2},{\mu }_{\tilde{j},2},{\omega }_2)={\mathit{P}}_0^2,\hfill \\ {L^{\prime }}_n(1;{\lambda }_{j,1},{\mu }_{j,1},{\omega }_1)=\zeta {L^{\prime }}_m(0;{\lambda }_{\tilde{j},2},{\mu }_{\tilde{j},2},{\omega }_2).(\zeta >0)\hfill \end{array}$$

(20)

Assuming the vice-normal vector is ${\mathit{H}}_1$ for ${\mathit{L}}_n$ at $t=1$ and ${\mathit{H}}_2$ for ${\mathit{L}}_m$ at $t=0$, then we have:

$$\{\begin{array}{l}{\mathit{H}}_1={L^{\prime }}_n(1;{\lambda }_{j,1},{\mu }_{j,1},{\omega }_1)\times {L^{″}}_n(1;{\lambda }_{j,1},{\mu }_{j,1},{\omega }_1),\hfill \\ {\mathit{H}}_2={L^{\prime }}_m(0;{\lambda }_{\tilde{j},2},{\mu }_{\tilde{j},2},{\omega }_2)\times {L^{″}}_m(0;{\lambda }_{\tilde{j},2},{\mu }_{\tilde{j},2},{\omega }_2).\hfill \end{array}$$

(21)

Then, the G² continuity requires that the vice-normal vector ${\mathit{L}}_n$ has the same direction at the joint as ${\mathit{L}}_m$. According to Equations (16) and (20), we can obtain the four vectors ${L^{\prime }}_n(1;{\lambda }_{j,1},{\mu }_{j,1},{\omega }_1)$, ${L^{″}}_n(1;{\lambda }_{j,1},{\mu }_{j,1},{\omega }_1)$, ${L^{\prime }}_m(0;{\lambda }_{\tilde{j},2},{\mu }_{\tilde{j},2},{\omega }_2)$, and ${L^{″}}_m(0;{\lambda }_{\tilde{j},2},{\mu }_{\tilde{j},2},{\omega }_2)$, which are coplanar. Thus, using Equation (20), we have:

$${L^{″}}_n(1;{\lambda }_{j,1},{\mu }_{j,1},{\omega }_1)=\beta {L^{″}}_m(0;{\lambda }_{\tilde{j},2},{\mu }_{\tilde{j},2},{\omega }_2)+\psi {L^{\prime }}_m(0;{\lambda }_{\tilde{j},2},{\mu }_{\tilde{j},2},{\omega }_2),$$

(22)

where $\beta >0$ is an arbitrary constant.

Suppose that the curvatures of the curves ${\mathit{L}}_n$ and ${\mathit{L}}_m$ are ${\kappa }_1(1)$ and ${\kappa }_2(0)$, respectively, we obtain:

$$\{\begin{array}{c}{\kappa }_1(1)=\frac{\left|{L^{\prime }}_n(1;{\lambda }_{j,1},{\mu }_{j,1},{\omega }_1)\times {L^{″}}_n(1;{\lambda }_{j,1},{\mu }_{j,1},{\omega }_1)\right|}{{\left|{L^{\prime }}_n(1;{\lambda }_{j,1},{\mu }_{j,1},{\omega }_1)\right|}^3},\\ {\kappa }_2(0)=\frac{\left|{L^{\prime }}_m(0;{\lambda }_{\tilde{j},2},{\mu }_{\tilde{j},2},{\omega }_2)\times {L^{″}}_m(0;{\lambda }_{\tilde{j},2},{\mu }_{\tilde{j},2},{\omega }_2)\right|}{{\left|{L^{\prime }}_m(0;{\lambda }_{\tilde{j},2},{\mu }_{\tilde{j},2},{\omega }_2)\right|}^3}.\end{array}$$

(23)

According to the Equations (20), (22), and (23), the curvature ${\kappa }_2(0)$ is equal to:

$$\begin{array}{ll}{\kappa }_2(0)& =\frac{\left|{L^{\prime }}_m(0;{\lambda }_{\tilde{j},2},{\mu }_{\tilde{j},2},{\omega }_2)\times {L^{″}}_m(0;{\lambda }_{\tilde{j},2},{\mu }_{\tilde{j},2},{\omega }_2)\right|}{{\left|{L^{\prime }}_m(0;{\lambda }_{\tilde{j},2},{\mu }_{\tilde{j},2},{\omega }_2)\right|}^3}\\ & =\frac{\left|\frac{1}{\zeta }{L^{\prime }}_n(1;{\lambda }_{j,1},{\mu }_{j,1},{\omega }_1)\times [\frac{1}{\beta }{L^{″}}_n(1;{\lambda }_{j,1},{\mu }_{j,1},{\omega }_1)-\frac{\psi }{\beta \zeta }{L^{\prime }}_n(1;{\lambda }_{j,1},{\mu }_{j,1},{\omega }_1)]\right|}{\frac{1}{{\zeta }^3}{\left|{L^{\prime }}_n(1;{\lambda }_{j,1},{\mu }_{j,1},{\omega }_1)\right|}^3}\\ & =\frac{{\zeta }^2\left|{L^{\prime }}_n(1;{\lambda }_{j,1},{\mu }_{j,1},{\omega }_1)\times {L^{″}}_n(1;{\lambda }_{j,1},{\mu }_{j,1},{\omega }_1)\right|}{\beta {\left|{L^{\prime }}_n(1;{\lambda }_{j,1},{\mu }_{j,1},{\omega }_1)\right|}^3}.\end{array}$$

(24)

As G² continuity requires that the value of the curvatures ${\kappa }_1(1)$ is equal to the value of ${\kappa }_2(0)$, i.e., ${\kappa }_1(1)={\kappa }_2(0)$. Combining with Equations (23) and (24), we see that $\beta ={\zeta }^2$. Substituting $\beta$ into Equation (22), we have:

$${L^{″}}_n(1;{\lambda }_{j,1},{\mu }_{j,1},{\omega }_1)={\zeta }^2{L^{″}}_m(0;{\lambda }_{\tilde{j},2},{\mu }_{\tilde{j},2},{\omega }_2)+\psi {L^{\prime }}_m(0;{\lambda }_{\tilde{j},2},{\mu }_{\tilde{j},2},{\omega }_2).$$

(25)

The tangent vectors of ${\mathit{L}}_n$ and ${\mathit{L}}_m$ can be computed easily on the basis of the terminal properties of the SG-Bézier curve given in Theorem 1; substituting them into Equation (25) yields:

$$\begin{array}{ll}{\mathit{P}}_2^2& =\frac{1}{c}\{[n(n-1)+2n{\omega }_1-2n{\omega }_1{\mu }_{1,1}]-{\zeta }^2[m(m-1)+2m{\omega }_2-2m{\omega }_2{\lambda }_{1,2}]\\ & +\psi (m+{\omega }_2-{\omega }_2{\lambda }_{1,2})-b(1+a)\}{\mathit{P}}_n^1-\frac{1}{c}[2n(n-1)+4n{\omega }_1-2n{\omega }_1{\mu }_{1,1}-2{\omega }_1{\mu }_{2,1}-ab]{\mathit{P}}_{n-1}^1\\ & +\frac{1}{c}[n(n-1)+2n{\omega }_1-2{\omega }_1{\mu }_{2,1}]{\mathit{P}}_{n-2}^1,\end{array}$$

(26)

where $a=\frac{n+{\omega }_1-{\omega }_1{\mu }_{1,1}}{\zeta (m+{\omega }_2-{\omega }_2{\lambda }_{1,2})}$, $c={\zeta }^2[m(m-1)+2m{\omega }_2-2{\omega }_2{\lambda }_{2,2}]$, and $b=\psi (m+{\omega }_2-{\omega }_2{\lambda }_{1,2})-{\zeta }^2[2m(m-1)+4m{\omega }_2-2m{\omega }_2{\lambda }_{1,2}-2{\omega }_2{\lambda }_{2,2}]$.

To sum up, the two splicing SG-Bézier curves reach G² smooth continuity at a common joint if they meet Equations (20) and (26) simultaneously, thus proving Theorem 3. □

In particular, let $\zeta =1,\psi =0$ in (19). We see that Equation (19) becomes:

$$\{\begin{array}{ll}{\mathit{P}}_0^2& ={\mathit{P}}_n^1,\\ {\mathit{P}}_1^2& =[1+\frac{n+{\omega }_1-{\omega }_1{\mu }_{1,1}}{m+{\omega }_2-{\omega }_2{\lambda }_{1,2}}]{\mathit{P}}_n^1-\frac{n+{\omega }_1-{\omega }_1{\mu }_{1,1}}{m+{\omega }_2-{\omega }_2{\lambda }_{1,2}}{\mathit{P}}_{n-1}^1,\\ {\mathit{P}}_2^2& =\frac{1}{\tilde{c}}\{[n(n-1)+2n{\omega }_1-2n{\omega }_1{\mu }_{1,1}]-[m(m-1)+2m{\omega }_2-2m{\omega }_2{\lambda }_{1,2}]\\ & -\tilde{b}(1+\tilde{a})\}{P}_n^1-\frac{1}{\tilde{c}}[2n(n-1)+4n{\omega }_1-2n{\omega }_1{\mu }_{1,1}-2{\omega }_1{\mu }_{2,1}-\tilde{a}\tilde{b}]{\mathit{P}}_{n-1}^1\\ & +\frac{1}{\tilde{c}}[n(n-1)+2n{\omega }_1-2{\omega }_1{\mu }_{2,1}]{\mathit{P}}_{n-2}^1.\end{array}$$

(27)

where $\tilde{a}=\frac{n+{\omega }_1-{\omega }_1{\mu }_{1,1}}{m+{\omega }_2-{\omega }_2{\lambda }_{1,2}}$, $\tilde{b}=-[2m(m-1)+4m{\omega }_2-2m{\omega }_2{\lambda }_{1,2}-2{\omega }_2{\lambda }_{2,2}]$, $\tilde{c}=m(m-1)+2m{\omega }_2-2{\omega }_2{\lambda }_{2,2}$.

Obviously, when $\zeta =1,\psi =0$, the G² continuity conditions in Equation (19) will degenerate to the corresponding C² continuity conditions in Equation (27).

4. Steps and Examples of Smooth Continuity for SG-Bézier Curves

4.1. The Concrete Steps of Smooth Joining between Two SG-Bézier Curves

According to the smooth continuity conditions between two splicing SG-Bézier curves discussed above, and combining with the shape adjustability of the SG-Bézier curves, now we will give the concrete steps of G² smooth joining between SG-Bézier curves. Meanwhile, other smooth continuity conditions can be carried out similarly.

The concrete steps for G² smooth continuity between two splicing SG-Bézier curves can be given as follows in terms of Theorem 2:

Step 1. For any degree n, we give the initial curve ${\mathit{L}}_n(t;{\lambda }_{j,1},{\mu }_{j,1},{\omega }_1)$ with the shape parameters ${\omega }_1,{\lambda }_{j,1},{\mu }_{j,1}(j=1,2,\cdots ,[n/2]+1)$ and the control points ${\mathit{P}}_j^1(j=0,1,\cdots ,n)$.

Step 2. Set ${\mathit{P}}_0^2={\mathit{P}}_n^1$, so that ${\mathit{L}}_n(t;{\lambda }_{j,1},{\mu }_{j,1},{\omega }_1)$ and ${\mathit{L}}_m(t;{\lambda }_{\tilde{j},2},{\mu }_{\tilde{j},2},{\omega }_2)$ achieve the G⁰ continuity at their common joint.

Step 3. For any given degree m, shape parameters ${\omega }_2$, ${\lambda }_{1，2}$ of ${\mathit{L}}_m(t;{\lambda }_{\tilde{j},2},{\mu }_{\tilde{j},2},{\omega }_2)$ and constant $\zeta >0$, they should satisfy the equation $m+{\omega }_2-{\omega }_2{\lambda }_{1,2}\ne 0$. Based on the second equation in Equation (19), we can compute the second control point ${\mathit{P}}_1^2$ of ${\mathit{L}}_m(t;{\lambda }_{\tilde{j},2},{\mu }_{\tilde{j},2},{\omega }_2)$.

Step 4. Based on steps (2) and (3), we can compute the third control point ${\mathit{P}}_2^2$ of ${\mathit{L}}_m(t;{\lambda }_{\tilde{j},2},{\mu }_{\tilde{j},2},{\omega }_2)$ by using the third equation in Equation (19), once we give an arbitrary constant $\psi$ and shape parameter ${\lambda }_{2，2}$.

Step 5. Finally, the G² smooth continuity between two splicing SG-Bézier curves can be achieved if we freely give the remaining m-2 shape parameters and control points of ${\mathit{L}}_m(t;{\lambda }_{\tilde{j},2},{\mu }_{\tilde{j},2},{\omega }_2)$.

Apparently, a complex SG-Bézier curve with G² smooth continuity can be obtained by repeating the steps above.

4.2. Examples of C¹, G¹ Smooth Continuity between SG-Bézier Curves

Figure 4 shows an example of ‘flower’ modeling, which is constructed by multiple third-degree SG-Bézier curves with C¹ smooth continuity. Given the initial blue SG-Bézier curve of degree 3, the red SG-Bézier curve of degree 3 is constructed by the continuity conditions in Equation (18), with the blue curve reaching C¹ smooth continuity. The shape parameters for these two SG-Bézier curves of degree 3 are ${\lambda }_{1,1}={\mu }_{1,1}={\lambda }_{1,2}={\mu }_{1,2}=2$, ${\lambda }_{2,1}={\lambda }_{2,2}=3$ and ${\omega }_1={\omega }_2=0.5$, with the scale factor $\zeta =1$. Note that the control polygons and control points of each SG-Bézier curve are denoted as broken lines and circular points, respectively; and similarly hereinafter.

Figure 5 shows an example of ‘fish’ modeling, where the main structure is composed of the cubic and quartic SG-Bézier curves reaching G¹ smooth continuity. Given the initial blue SG-Bézier curve of degree 3, the red SG-Bézier curve of degree 4 is constructed by the G¹ continuity conditions in Equation (10), with the blue curves reaching G¹ smooth continuity. The local and global shape parameters for the cubic and quartic SG-Bézier curves are ${\lambda }_{1,2}={\mu }_{1,2}=5$, ${\lambda }_{1,1}={\mu }_{1,1}={\lambda }_{2,1}=4$, ${\lambda }_{2,2}={\mu }_{2,2}=8$, and ${\omega }_1={\omega }_2=0.5$, with the scale factor $\zeta =1/2$. We can see from Figure 5 that the overall modeling of the ‘fish’ are smooth and natural.

4.3. Examples of C², G² Smooth Continuity between SG-Bézier Curves

Figure 6 shows an example of ‘cetacean’ modeling, which was constructed by the cubic and quartic SG-Bézier curves. Given the initial blue SG-Bézier curve of degree 3, the red SG-Bézier curve of degree 4 is constructed by the C² continuity conditions in Equation (27) with the blue curves reaching C² smooth continuity. The shape parameters for these two SG-Bézier curves are ${\omega }_1={\omega }_2=0.5$, ${\lambda }_{1,1}={\mu }_{1,1}=3$, ${\lambda }_{1,2}={\mu }_{1,2}=4$, and ${\lambda }_{2,1}=5,{\lambda }_{2,2}={\mu }_{2,2}=8$, with the scale factors $\zeta =1,\psi =0$.

Figure 7 shows an example of ‘mouse’ modeling, which was constructed by two cubic SG-Bézier curves. The red curve is the given initial SG-Bézier curve of degree 3, and the blue SG-Bézier curve of degree 3 is constructed by G² continuity conditions in Equation (19), with the red curve reaching G² smooth continuity. The shape parameters for these two cubic SG-Bézier curves are ${\lambda }_{1,1}={\lambda }_{1,2}={\mu }_{1,1}={\mu }_{1,2}=3$, ${\lambda }_{2,1}={\lambda }_{2,2}=5$, and ${\omega }_1={\omega }_2=0.5$, with the scale factors $\zeta =1$, $\psi =1/2$. In addition, the line of curvature corresponding to Figure 7 plotted in Figure A1 visually supports the claim on G² continuity (see Appendix A).

Figure 8 shows the influence of two scale factors on the shapes of the curves based on Figure 7b. The blue one is the curve before the scale factors are ready to make a modification, while the green one is the curve after each change in the values of the scale factors. The shape parameters in Figure 8 are the same as that in Figure 7b. As seen from Equation (10) and Figure 8a, for the second curve in the splicing curve, on the basis of the other control points and G² smooth continuity of the splicing curve remaining unchanged, the value of the scale factor $\zeta$ will change the position of the second and third control points. Similarly, Figure 8b shows the change of the third control point of the second curve in the splicing curve by altering the scale factor $\psi$. Analogously, the broken lines and circular points in Figure 8 represent the control polygons and control points of each SG-Bézier curve, respectively. Notice that the asterisks labeled on the control polygon denote the altered control points.

5. Shape Adjustment of the Composite SG-Bézier Curves with Smooth Continuity

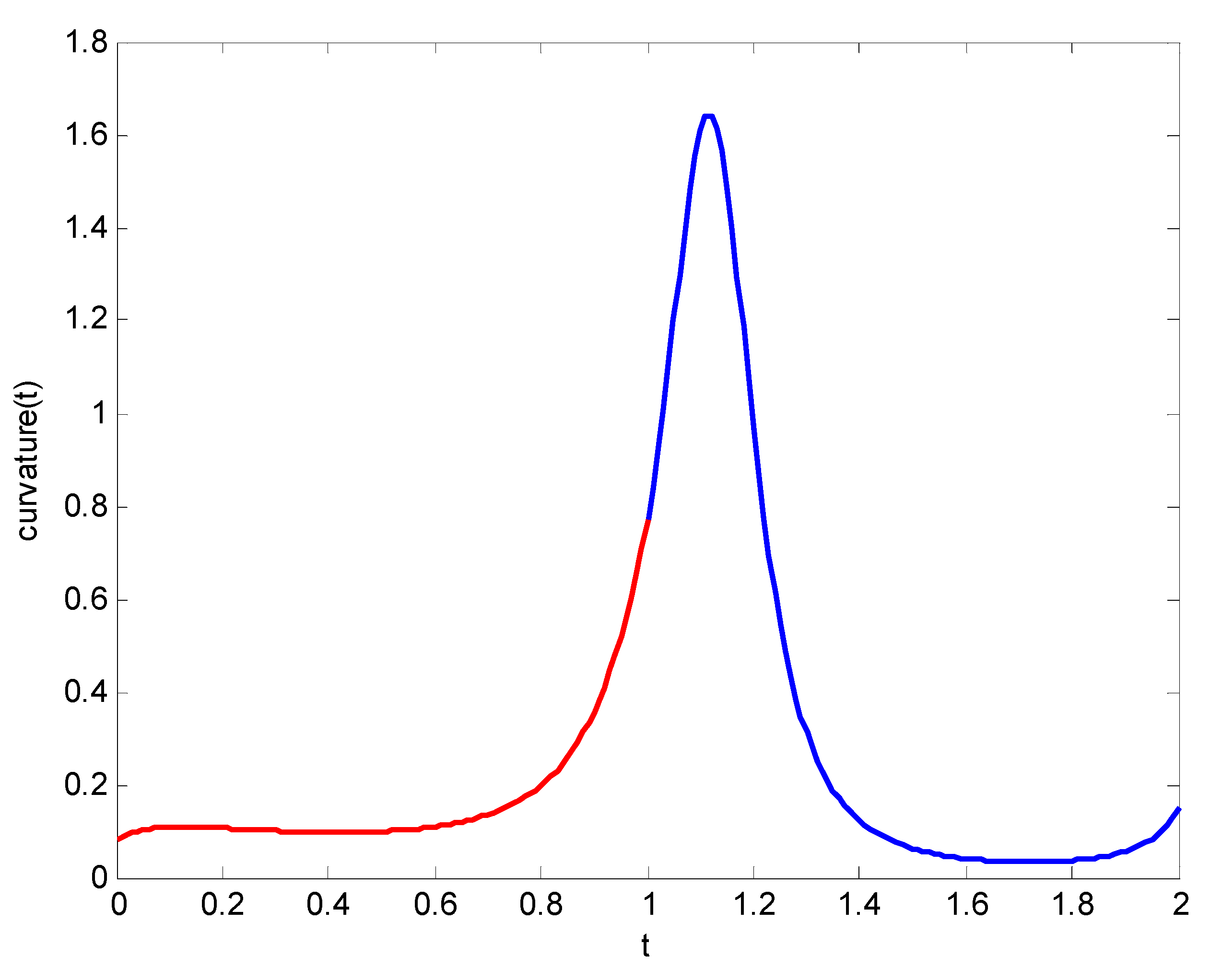
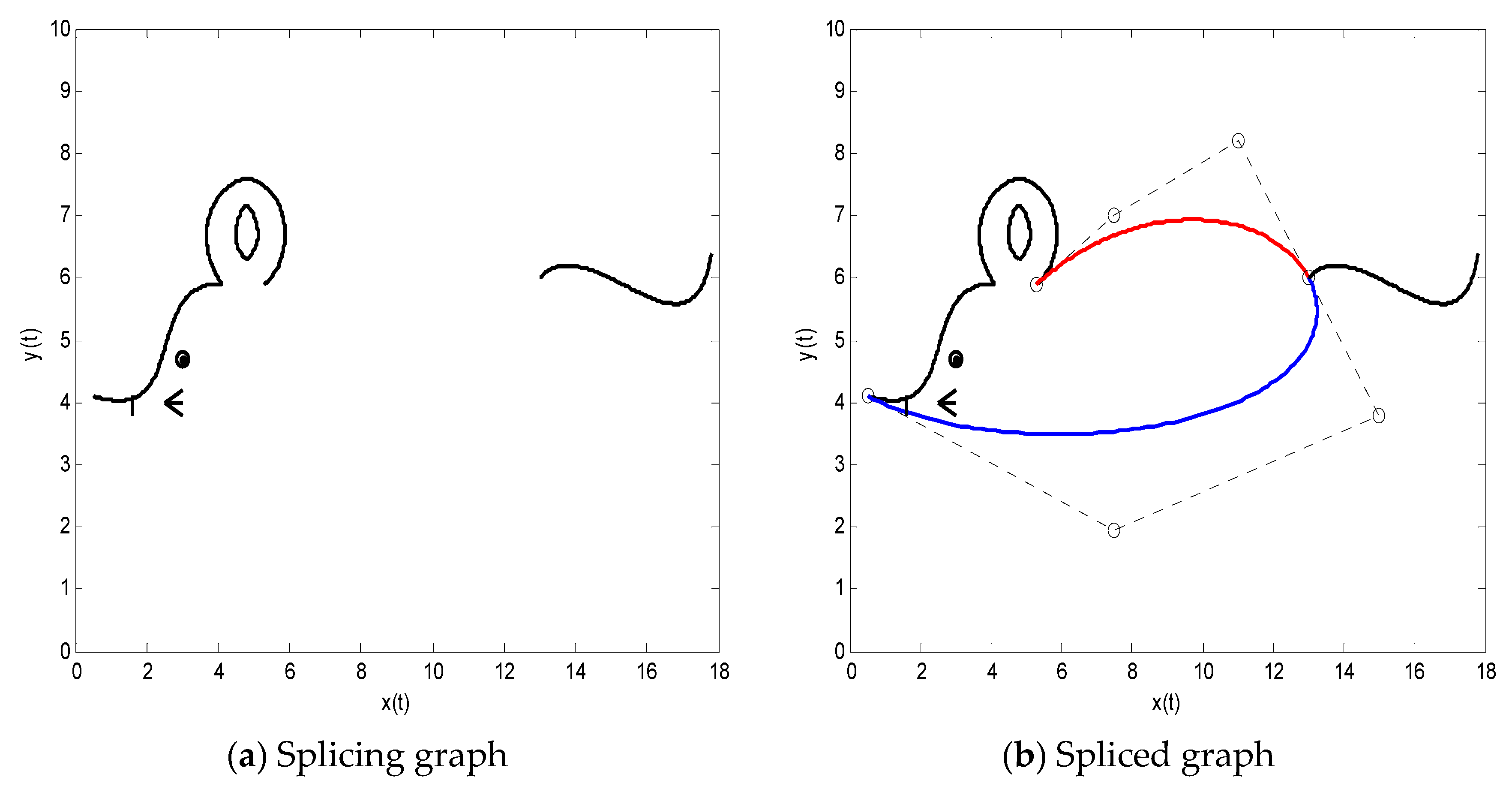
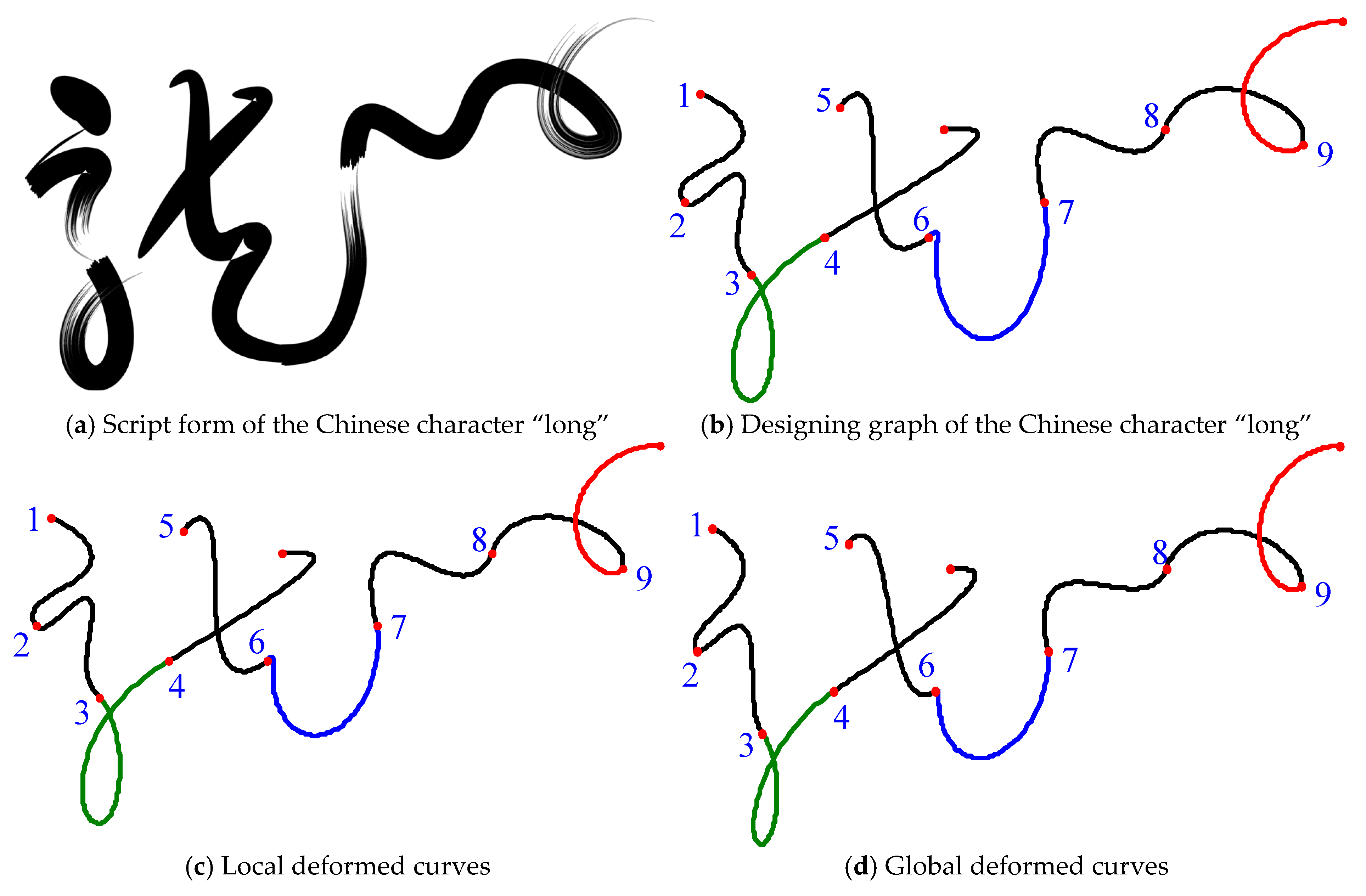
According to the definition of the SG-Bézier curve, an SG-Bézier curve has one global and multiple local shape parameters. In view of this, we can modify the local or global shape under the precondition that the G¹, G² and C¹, C² smooth continuity of the composite curves remain unchanged. In what follows, we shall discuss the shape adjustability of the composite SG-Bézier curves with G¹, G² and C¹, C² continuity, which were constructed by two SG-Bézier curves. Moreover, a similar discussion can be carried out on the multiple curves case.

5.1. Shape Adjustment of the Composite SG-Bézier Curves with C¹ or G¹ Smooth Continuity

Proposition 1.

For a composite SG-Bézier curve with C¹smooth continuity, some significant conclusions can be obtained when keeping its control points and C¹smooth continuity unchanged.

(1) We can adjust the local shape of the composite curve by altering${\lambda }_{j,1}(j=1,2,\cdots ,[n/2]+1),$${\mu }_{j,1}(j=2,3,\cdots ,[n/2]+1)$(or${\lambda }_{\tilde{j},2}(\tilde{j}=2,3,\cdots ,[m/2]+1$),${\mu }_{\tilde{j},2}(\tilde{j}=1,2,\cdots ,[m/2]+1)$).

(2) We can modify the global shape of a composite curve by altering${\omega }_1,{\mu }_{1,1}$and${\omega }_2,{\lambda }_{1,2}$(or the parameters${\lambda }_{j,1}(j=1,2,\cdots ,[n/2]+1),$${\mu }_{j,1}(j=2,3,\cdots ,[n/2]+1)$, and${\lambda }_{\tilde{j},2}(\tilde{j}=2,3,\cdots ,[m/2]+1),$${\mu }_{\tilde{j},2}(\tilde{j}=1,2,\cdots ,[m/2]+1)$) to achieve the global shape adjustment of the splicing curve. Here, at least one of the shape parameters${\omega }_1,{\mu }_{1,1}$(respectively${\omega }_2,{\lambda }_{1,2}$) should be changed.

Proof. 

As the C¹ continuity conditions of Equation (18) just involve the shape parameters ${\omega }_1,{\mu }_{1,1}$ and ${\omega }_2,{\lambda }_{1,2}$, then we can modify the local shape by altering the shape parameters that are not contained in Equation (18). Thus, conclusion (1) is proved. On the other hand, if we change at least one of the shape parameters ${\omega }_1,{\mu }_{1,1}$, then at least one of the shape parameters ${\omega }_2,{\lambda }_{1,2}$ should be changed to ensure that the C¹ smooth continuity is maintained unchanged for the splicing curve (to modify the shape parameters in terms of the second equation in Equation (18)). Therefore, the global shape adjustment of the splicing curve can be achieved by changing the values of the shape parameters:${\mu }_{j,1}(j=2,3,\dots ,[n/2]+1)$, ${\lambda }_{j,1}(j=1,2,\dots ,[n/2]+1),$ and ${\lambda }_{\tilde{j},2}(\tilde{j}=2,3,\dots ,[m/2]+1),$ ${\mu }_{\tilde{j},2}(\tilde{j}=1,2,\cdots ,[m/2]+1)$. This completes the proof of Proposition 1. □

Proposition 2.

Keeping the G¹smooth continuity between splicing curves unchanged, we have:

(1) We can modify the local shape of the composite curve by altering the shape parameters${\omega }_1,{\lambda }_{j,1},{\mu }_{j,1}(j=1,2,\dots ,[n/2]+1)$or${\omega }_2,{\lambda }_{\tilde{j},2},{\mu }_{\tilde{j},2}(\tilde{j}=1,2,\dots ,[m/2]+1)$.

(2) We can modify the global shape of the composite curve by altering the shape parameters${\omega }_1,{\lambda }_{j,1},{\mu }_{j,1}(j=1,2,\dots ,[n/2]+1)$and${\omega }_2,{\lambda }_{\tilde{j},2},{\mu }_{\tilde{j},2}(\tilde{j}=1,2,\dots ,[m/2]+1)$at the same time.

Proof. 

According to equations (15) and (3), G¹ continuity merely requires that the tangent directions at the common joint of the two splicing SG-Bézier curves are the same, that is:

$$(n+{\omega }_1-{\omega }_1{\mu }_{1,1})({\mathit{P}}_n^1-{\mathit{P}}_{n-1}^1)=\zeta (m+{\omega }_2-{\omega }_2{\lambda }_{1,2})({\mathit{P}}_1^2-{\mathit{P}}_0^2)(\zeta >0).$$

(28)

This shows that altering any of the shape parameters of part of the curves simply exerts an influence on the size of the tangent vector without changing its direction. So, the global or local shape can be adjusted once we change the shape parameters of part of the curves while keeping the control points and G¹ smooth continuity the same. Thus, Proposition 2 is proven. □

5.2. Modeling Examples of Shape Adjustment for the Composite SG-Bézier Curves with C¹ or G¹ Smooth Continuity

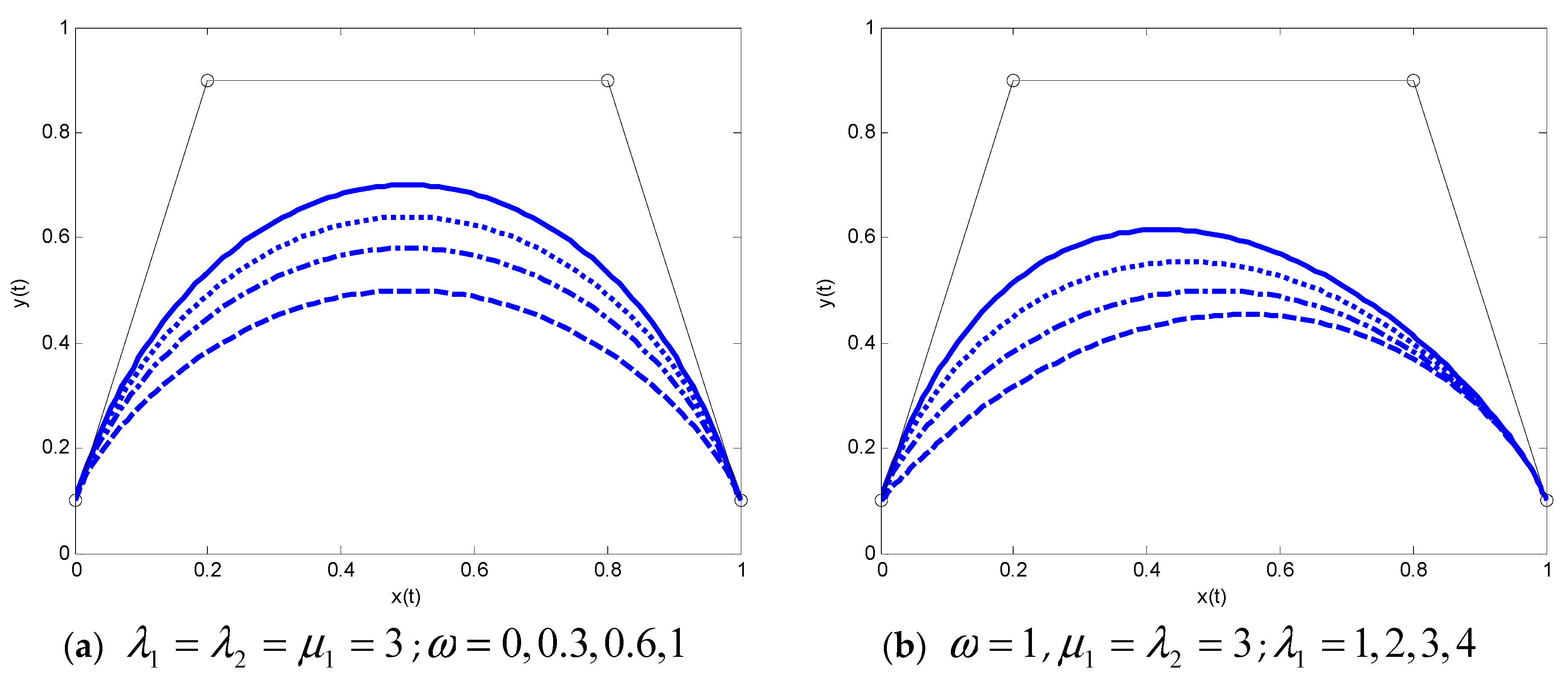
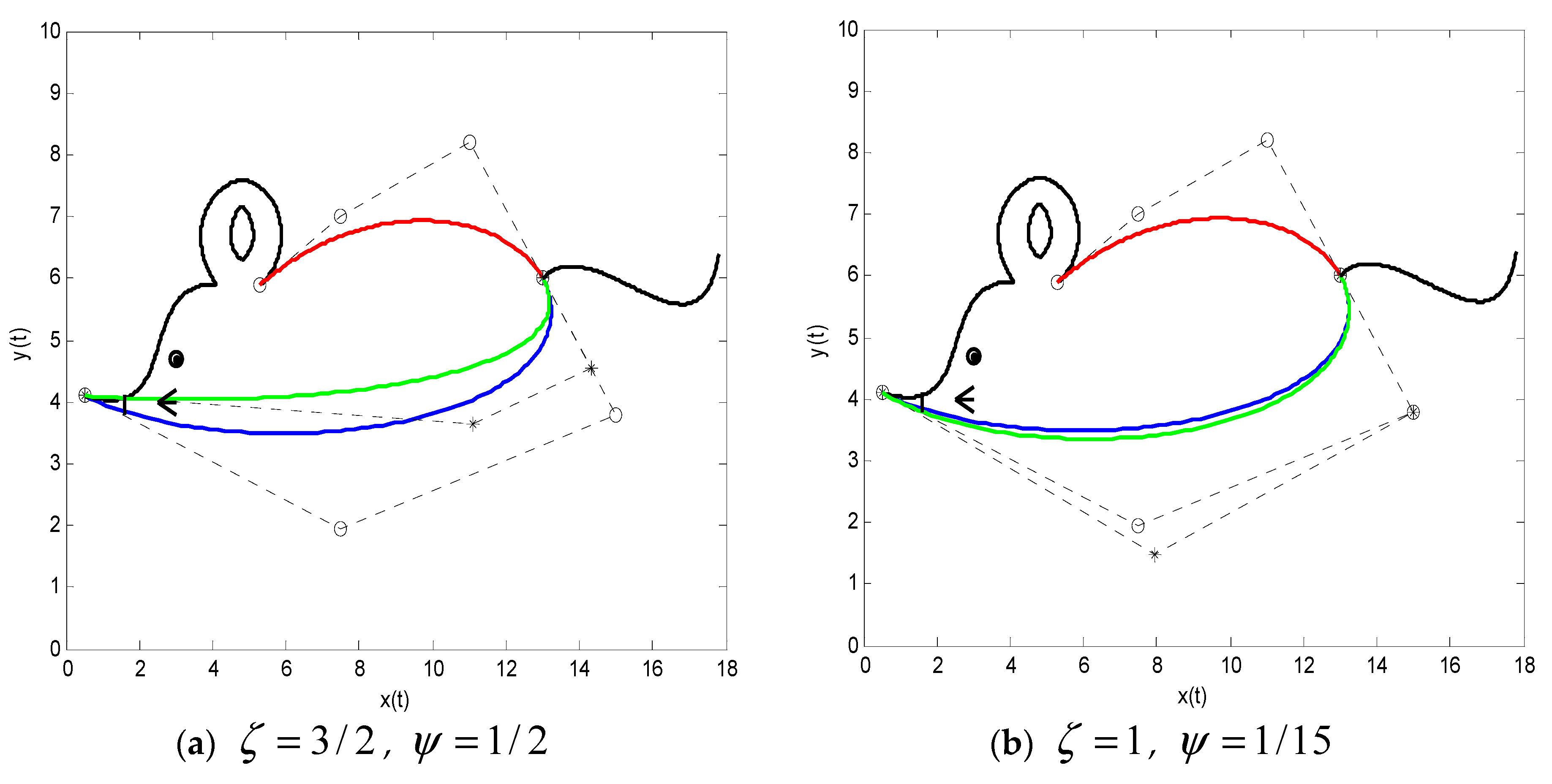
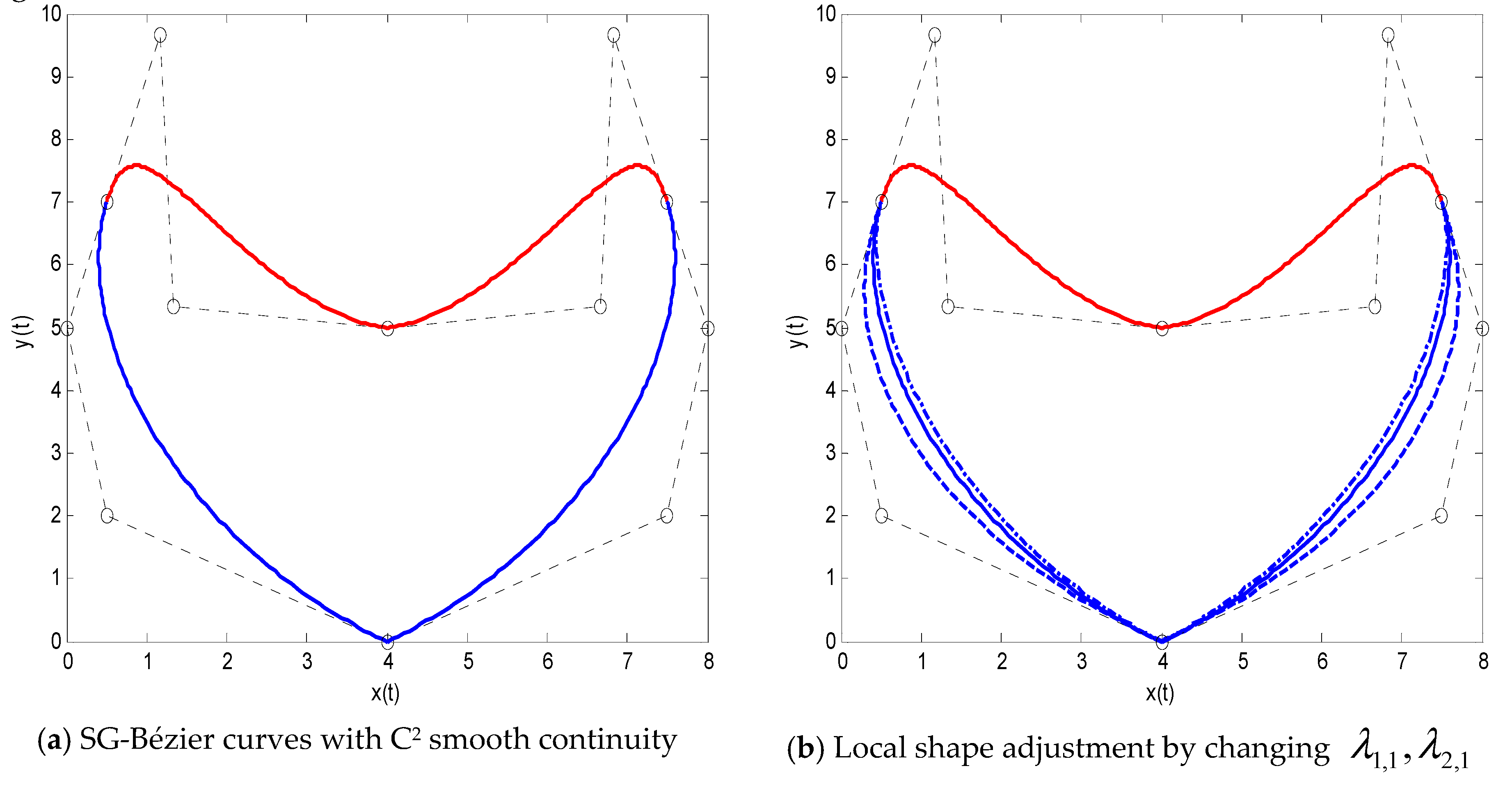
Figure 9 shows the C¹ smooth continuity of two SG-Bézier curves. In Figure 9, the blue curve is the pre-given SG-Bézier curve, and the red SG-Bézier curve is now constructed by the continuity conditions in Equation (18). The shape parameters are ${\lambda }_{1,1}={\mu }_{1,1}={\lambda }_{1,2}={\mu }_{1,2}=2$, ${\lambda }_{2,1}={\lambda }_{2,2}=3$ and ${\omega }_1={\omega }_2=1$. Figure 9b shows the local shape adjustment of the composite curve just by modifying one shape parameter ${\lambda }_{1,1}$. The upper part of the splicing curve is now modified, where the shape parameters of solid lines, dashed lines, and dotted lines are ${\lambda }_{1,1}=3,1.5,0$, respectively. 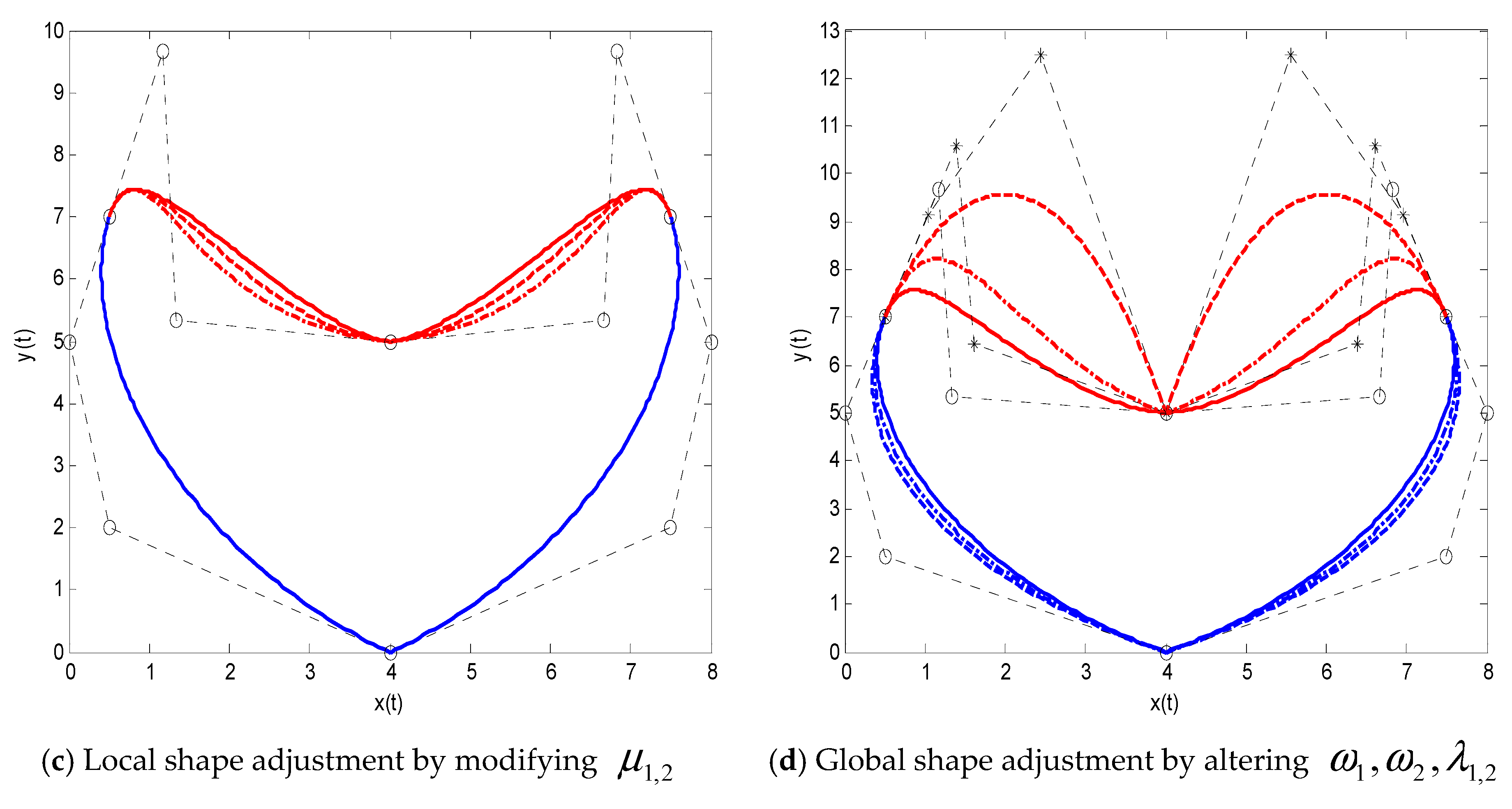Figure 9c shows the local shape adjustment by altering the shape parameters ${\mu }_{1,2}$, and now, the lower part of the splicing curve is modified, with the shape parameters ${\mu }_{1,2}=3$ (solid lines), ${\mu }_{1,2}=1.5$ (dashed lines), and ${\mu }_{1,2}=0$ (dotted lines). We see that the global shape adjustment can be achieved in Figure 9d by changing the shape parameters ${\omega }_1,{\omega }_2$ and ${\mu }_{1,1},{\mu }_{1,2}$, with the shape parameters ${\omega }_1={\omega }_2=1,{\mu }_{1,1},{\mu }_{1,2}=3$ (solid lines), ${\omega }_1={\omega }_2=0.8,{\mu }_{1,1},{\mu }_{1,2}=2$ (dashed lines), and ${\omega }_1={\omega }_2=0.1,{\mu }_{1,1},{\mu }_{1,2}=2$ (dotted lines). The rest of the shape parameters are equal to those in Figure 9a, expect that they are modified in the other three figures.

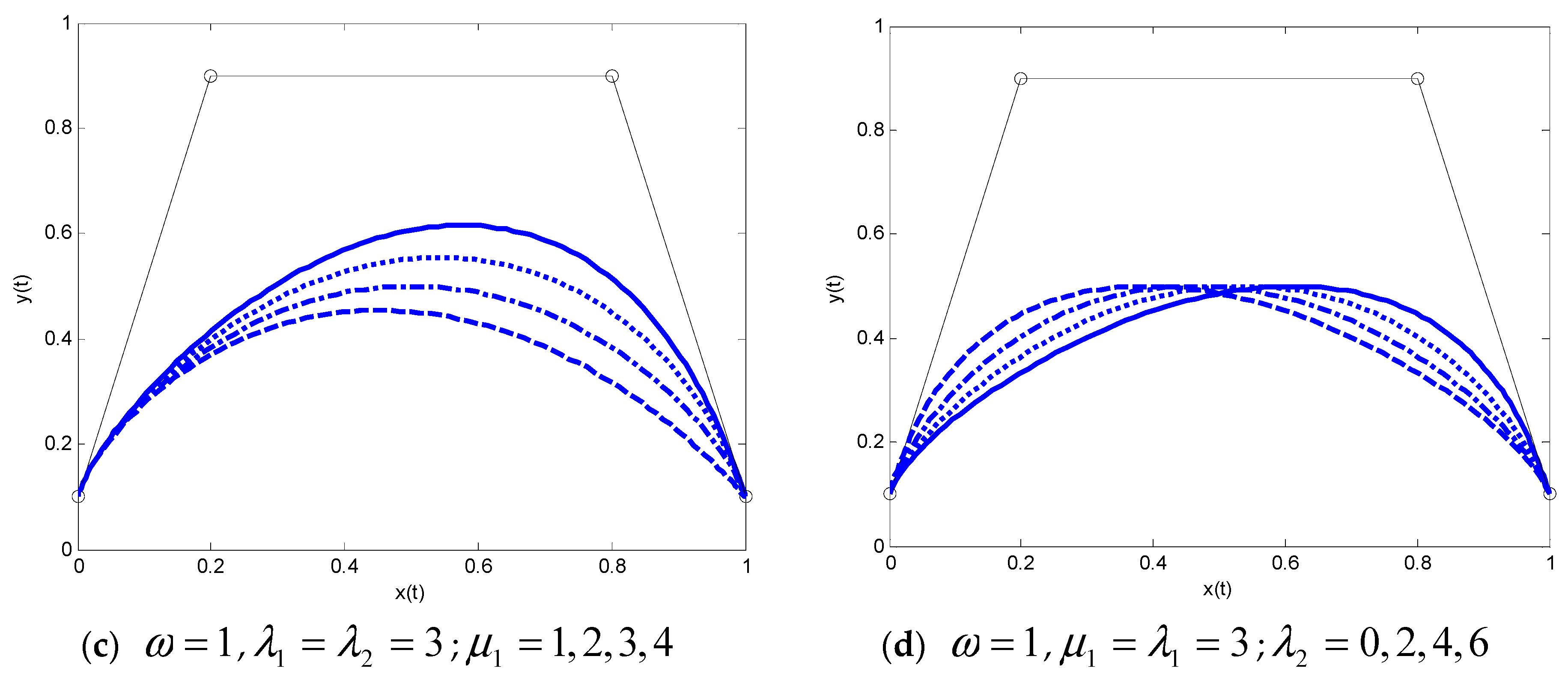
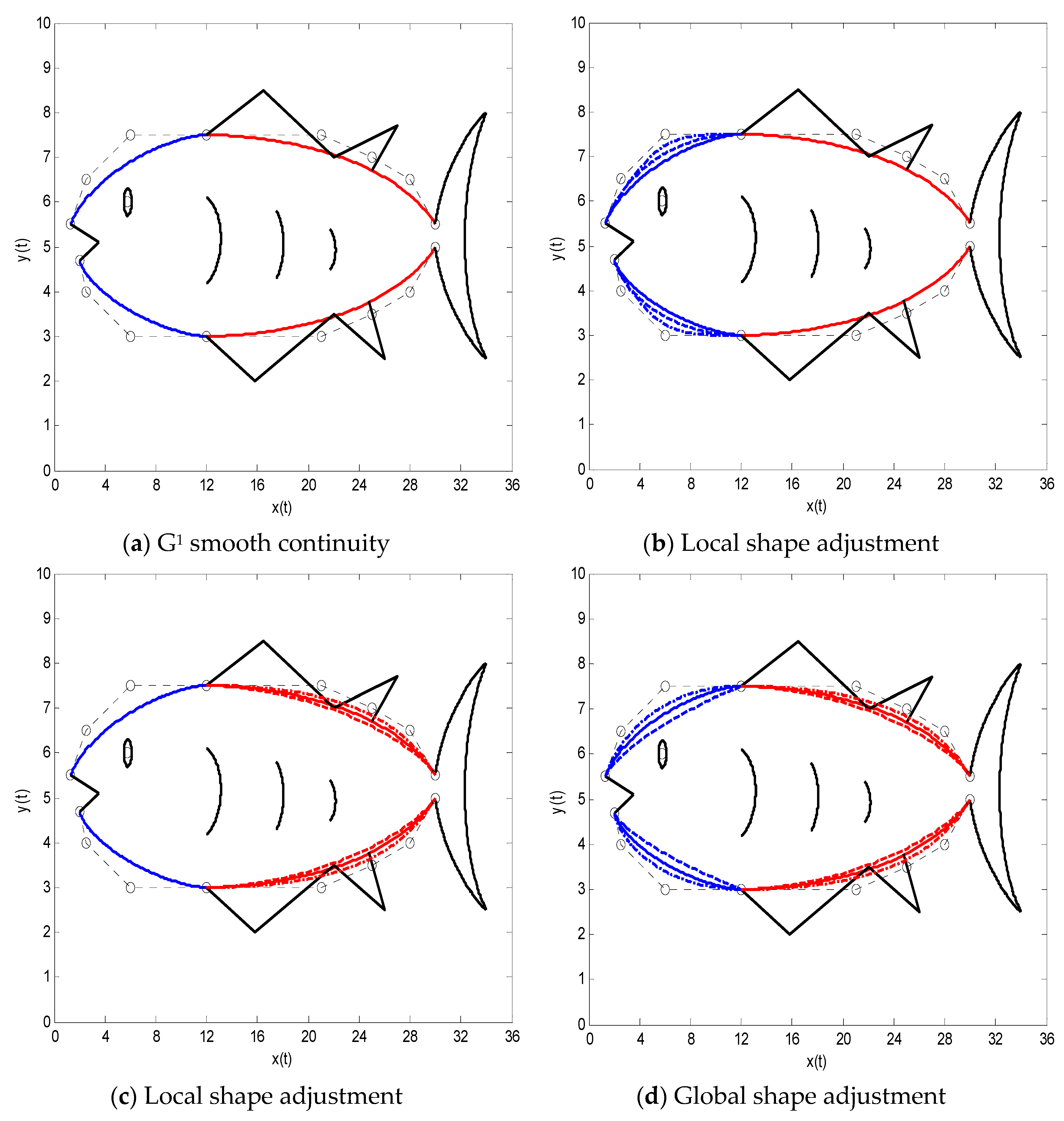
Figure 10 shows the local and global shape adjustment of the composite SG-Bézier curves with G¹ smooth continuity. In Figure 10a, the G¹ smooth continuity and the shape parameters are the same as that in Figure 5b. Figure 10b shows the global shape adjustment by altering the shape parameters ${\omega }_1,{\lambda }_{1,1},{\mu }_{1,1},{\lambda }_{2,1}$. Now, we only adjust the left part of the splicing curve with the shape parameters ${\omega }_1=0.5,{\lambda }_{1,1}=4,{\mu }_{1,1}=4,{\lambda }_{2,1}=4$ (solid lines), ${\omega }_1=0.2,{\lambda }_{1,1}=2,{\mu }_{1,1}=2,{\lambda }_{2,1}=2$ (dashed lines), and ${\omega }_1=1,{\lambda }_{1,1}=1,{\mu }_{1,1}=0,{\lambda }_{2,1}=0$ (dotted lines). Figure 10c shows the graph of the local adjustment for the splicing curve by modifying shape parameters ${\omega }_2,{\lambda }_{1,2},{\mu }_{1,2},{\lambda }_{2,2},{\mu }_{2,2}$, where we only make a adjustment for the right part of the splicing curve with the shape parameters ${\mu }_{1,2}=5,{\lambda }_{2,2}=8,{\mu }_{2,2}=8$ (solid lines), ${\omega }_2=1,{\lambda }_{1,2}=4.5,{\mu }_{1,2}=5,{\lambda }_{2,2}=10,{\mu }_{2,2}=10$ (dashed lines), and ${\omega }_2=0,{\lambda }_{1,2}=0.5,{\mu }_{1,2}=0.5,{\lambda }_{2,2}=0.5,{\mu }_{2,2}=0.5$ (dotted lines). Figure 10d shows the graph of the global adjustment by changing the shape parameters ${\omega }_1,{\lambda }_{1,1},{\mu }_{1,1},{\lambda }_{2,1},{\omega }_2,{\lambda }_{1,2},{\mu }_{1,2},{\lambda }_{2,2},{\mu }_{2,2}$, with the shape parameters ${\omega }_1=0.5,{\lambda }_{1,1}=4,{\mu }_{1,1}=4,{\lambda }_{2,1}=4,{\omega }_2=0.5,{\lambda }_{1,2}=5,{\mu }_{1,2}=5,{\lambda }_{2,2}=8,$ ${\mu }_{2,2}=8$ (solid lines), ${\omega }_1=1,{\lambda }_{1,1}=4,{\mu }_{1,1}=4,{\lambda }_{2,1}=6,{\omega }_2=1,{\lambda }_{1,2}=4.5,{\mu }_{2,2}=10,{\mu }_{1,2}=5,{\lambda }_{2,2}=10$ (dashed lines), and ${\omega }_1=0,{\lambda }_{1,1}=1,{\mu }_{1,1}=1,{\lambda }_{2,1}=0,{\omega }_2=0,{\lambda }_{1,2}=1,{\mu }_{1,2}=1,{\lambda }_{2,2}=1,{\mu }_{2,2}=1$ (dotted lines). The rest of the shape parameters are the same as those in Figure 10a, expect for those that are modified in Figure 10.

5.3. Shape Adjustment of the Composite SG-Bézier Curves with C² or G² Smooth Continuity

Proposition 3.

Suppose that the control points and C²smooth continuity for the splicing curve remain unchanged, we have the following conclusions:

(1) We can alter the local shape of a composite curve by adjusting shape parameters${\lambda }_{j,1}(j=1,$$2,\dots ,[n/2]+1),{\mu }_{j,1}(j=3,4,\dots ,[n/2]+1)$or${\lambda }_{\tilde{j},2}(\tilde{j}=3,4,\dots ,[m/2]+1),{\mu }_{\tilde{j},2}(\tilde{j}=1,2,\dots ,[m/2]+1)$.

(2) We can alter the global shape of a composite curve by changing the parameters${\lambda }_{j,1}(j=1,2,\cdots ,[n/2]+1)$(or${\mu }_{j,1}(j=3,4,\cdots ,[n/2]+1)$) and${\lambda }_{\tilde{j},2}(\tilde{j}=3,4,\cdots ,[m/2]+1)$(or${\mu }_{\tilde{j},2}(\tilde{j}=1,2,\cdots ,[m/2]+1)$) simultaneously. In addition, in the sole situation where the C²smooth continuity is kept unchanged, the global shape of the composite curve can also be adjusted by modifying the following shape parameters and control points:

① By changing the two shape parameters${\omega }_1$and${\omega }_2$, as well as two control points${\mathit{P}}_1^2$and${\mathit{P}}_2^2$.

② By modifying the shape parameters${\omega }_1$,${\omega }_2$,${\mu }_{1,1}$(or${\mu }_{1,1}$,${\mu }_{2,1}$) and the control points${\mathit{P}}_1^2$,${\mathit{P}}_2^2$; or altering the shape parameters${\omega }_1$,${\omega }_2$,${\lambda }_{1,2}$(or${\lambda }_{1,2}$,${\lambda }_{2,2}$) and the control points${\mathit{P}}_1^2$,${\mathit{P}}_2^2$; or changing the shape parameters${\omega }_1$,${\omega }_2$,${\mu }_{1,1}$(or${\mu }_{1,1}$,${\mu }_{2,1}$) and${\lambda }_{1,2}$(or${\lambda }_{1,2}$,${\lambda }_{2,2}$), and the control points${\mathit{P}}_1^2$,${\mathit{P}}_2^2$.

③ By altering the shape parameters${\omega }_1,{\lambda }_{j,1},{\mu }_{j,1}(j=1,2,\cdots ,[n/2]+1)$and${\omega }_2,{\lambda }_{\tilde{j},2},{\mu }_{\tilde{j},2}$$(\tilde{j}=1,$$2,\dots ,[m/2]+1)$and the control points${\mathit{P}}_1^2$and${\mathit{P}}_2^2$.

Here, we can calculate the control points${\mathit{P}}_1^2$and${\mathit{P}}_2^2$according to the second and third equation in Equation (27).

Proof. 

According to the C² continuity conditions in Equation (27), if the control points and C² smooth continuity remain unchanged, we can alter the local shape of the composite curve by changing these shape parameters, which are not included in the conditions in Equation (27). Thus, conclusion (1) is proved. □

As the conditions in Equation (27) involve the global shape parameters ${\omega }_1$, ${\omega }_2$ and local shape parameters ${\mu }_{1,1}$, ${\mu }_{2,1}$, ${\lambda }_{1,2}$, ${\lambda }_{2,2}$, we merely change these shape parameters (apparently these parameters are not included in smooth continuity conditions) to adjust the shape of the composite curve while keeping the control points and C² smooth continuity the same. Now, we only adjust the local shape of the composite curve. So, we cannot modify the global shape only by altering the shape parameters. As ${\omega }_1$ and ${\omega }_2$ are the global shape parameters, we might alter the two control points $P_1^2$ and $P_2^2$ simultaneously to ensure that C² smooth continuity is unchanged once we adjust the global shape by changing ${\omega }_1$ and ${\omega }_2$. Similarly, as the C² smooth continuity conditions involve the parameters ${\omega }_1$, ${\omega }_2$, ${\mu }_{1,1}$, ${\mu }_{2,1}$, ${\lambda }_{1,2}$ and ${\lambda }_{2,2}$, we can adjust the global shape of the two parts that go beyond the splicing curve by modifying the shape parameters ${\omega }_1$, ${\mu }_{1,1}$, ${\mu }_{2,1}$ and ${\omega }_2$, ${\lambda }_{1,2}$, ${\lambda }_{2,2}$, as well as the two control points $P_1^2$ and $P_2^2$ to ensure that the C² smooth continuity is unchanged. Obviously, the global shape adjustment can be achieved by modifying the shape parameters ${\omega }_1,{\lambda }_{j,1},{\mu }_{j,1}(j=1,2,\cdots ,[n/2]+1)$, ${\omega }_2,{\lambda }_{\tilde{j},2},{\mu }_{\tilde{j},2}(\tilde{j}=1,2,\cdots ,[m/2]+1)$, and the control points $P_1^2$ and $P_2^2$. Thus, conclusion (2) is proved. This completes the proof of Proposition 3.

Proposition 4.

For a composite SG-Bézier curve with G²smooth continuity, some significant conclusions can be obtained when keeping its control points and G²smooth continuity unchanged.

(1) We can modify the local shape of the composite curve by changing the shape parameters${\lambda }_{j,1}(j=1,2,\cdots ,[n/2]+1),{\mu }_{j,1}(j=3,4,\cdots ,[n/2]+1)$or${\lambda }_{\tilde{j},2}(\tilde{j}=3,4,\cdots ,[m/2]+1),$${\mu }_{\tilde{j},2}(\tilde{j}=1,2,\cdots ,$$[m/2]+1)$.

(2) The global shape of a composite curve can be altered by changing the parameters${\lambda }_{j,1}(j=1,2,\cdots ,[n/2]+1)$(or${\mu }_{j,1}(j=3,4,\cdots ,[n/2]+1)$) and${\lambda }_{\tilde{j},2}(\tilde{j}=3,4,\cdots ,[m/2]+1)$(or${\mu }_{\tilde{j},2}(\tilde{j}=1,2,\cdots ,[m/2]+1)$) simultaneously. Moreover, if only the G²smooth continuity remains unchanged, we can modify the global shape of the composite curve by altering the following shape parameters and control points:

① By altering the shape parameters${\omega }_1$and${\omega }_2$, as well as the control points${\mathit{P}}_1^2$and${\mathit{P}}_2^2$.

② By modifying shape parameters${\omega }_1$,${\omega }_2$,${\mu }_{1,1}$(or${\mu }_{1,1}$,${\mu }_{2,1}$) and the control points${\mathit{P}}_1^2$and${\mathit{P}}_2^2$; or modifying shape parameters${\omega }_1$,${\omega }_2$,${\lambda }_{1,2}$(or${\lambda }_{1,2}$,${\lambda }_{2,2}$) and the control points${\mathit{P}}_1^2$and${\mathit{P}}_2^2$; or modifying shape parameters${\omega }_1$,${\omega }_2$,${\mu }_{1,1}$(or${\mu }_{1,1}$,${\mu }_{2,1}$),${\lambda }_{1,2}$(or${\lambda }_{1,2}$,${\lambda }_{2,2}$) and the control points${\mathit{P}}_1^2$and${\mathit{P}}_2^2$;

③ By modifying the shape parameters${\omega }_1,{\lambda }_{j,1},{\mu }_{j,1}(j=1,2,\cdots ,[n/2]+1)$and${\omega }_2,{\lambda }_{\tilde{j},2},{\mu }_{\tilde{j},2}(\tilde{j}=1,$$2,\cdots ,[m/2]+1)$, as well as two control points${\mathit{P}}_1^2$and${\mathit{P}}_2^2$.

Here, we can calculate the control points${\mathit{P}}_1^2$and${\mathit{P}}_2^2$according to the second and third equation in Equation (19).

Proof. 

Proposition 4 can follow by the similar argument in Proposition 3. Thus, we omit the proof. □

5.4. Examples of Shape Adjustment between SG-Bézier Curves with C² and G² Smooth Continuity

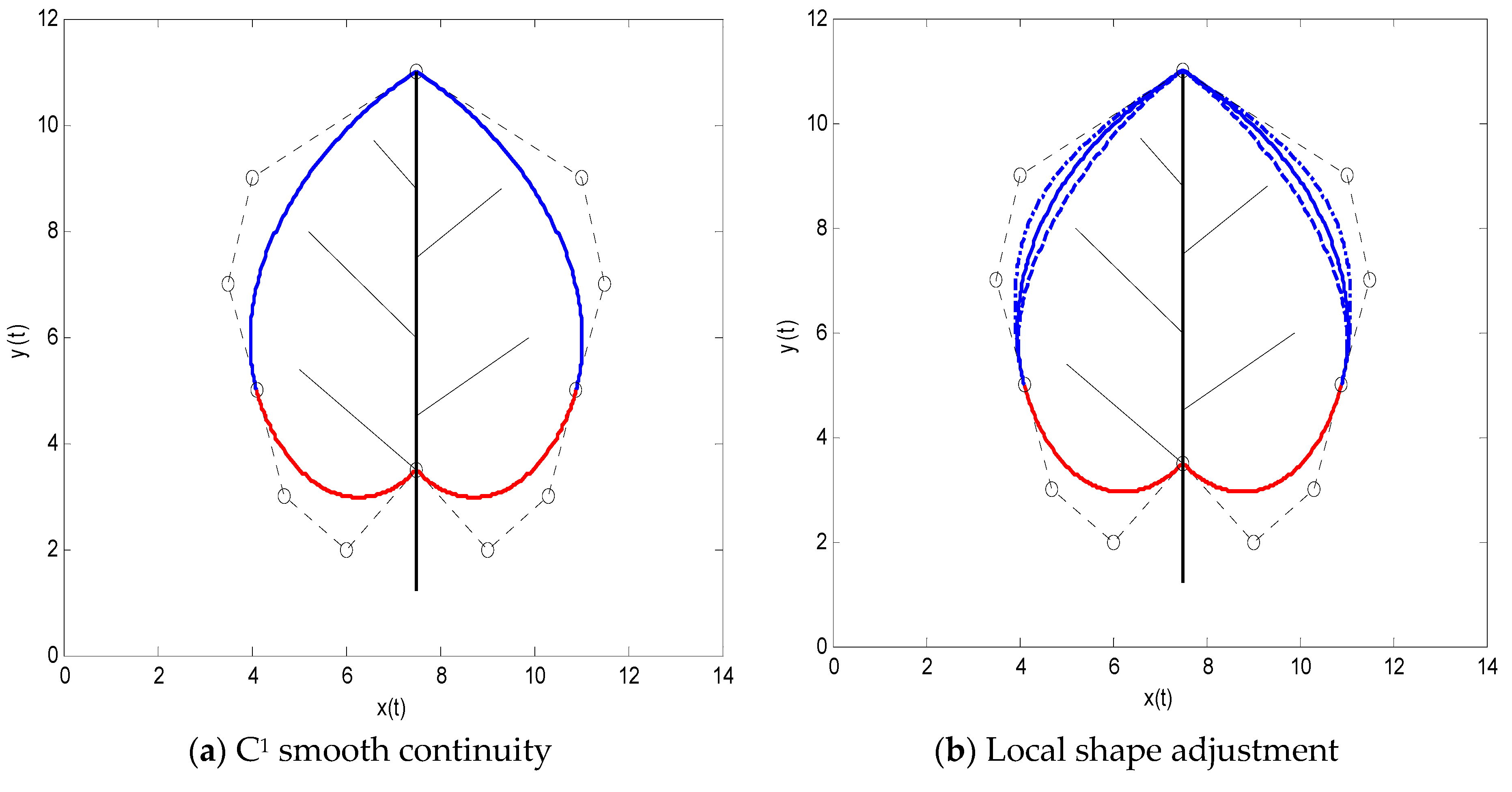
Figure 11 gives an example to show the C² smooth continuity between two SG-Bézier curves of degree 3. In this figure, the blue curve is the given SG-Bézier curve, and the red curve is constructed by the continuity conditions in Equation (27), which together with the blue curve reaches C² smooth continuity. The solid lines denote the curves before adjustment, while the dashed lines and dotted lines denote the curves after the adjustment of the shape parameters. The circular points denote the points before adjustment, and the asterisks indicate the modified control points. The shape parameters in Figure 11a are ${\omega }_1=1,{\lambda }_{1,1}=2,{\mu }_{1,1}=2,{\lambda }_{2,1}=3$ and ${\omega }_2=0.5,{\lambda }_{1,2}=4,{\mu }_{1,2}=4,{\lambda }_{2,2}=3$. 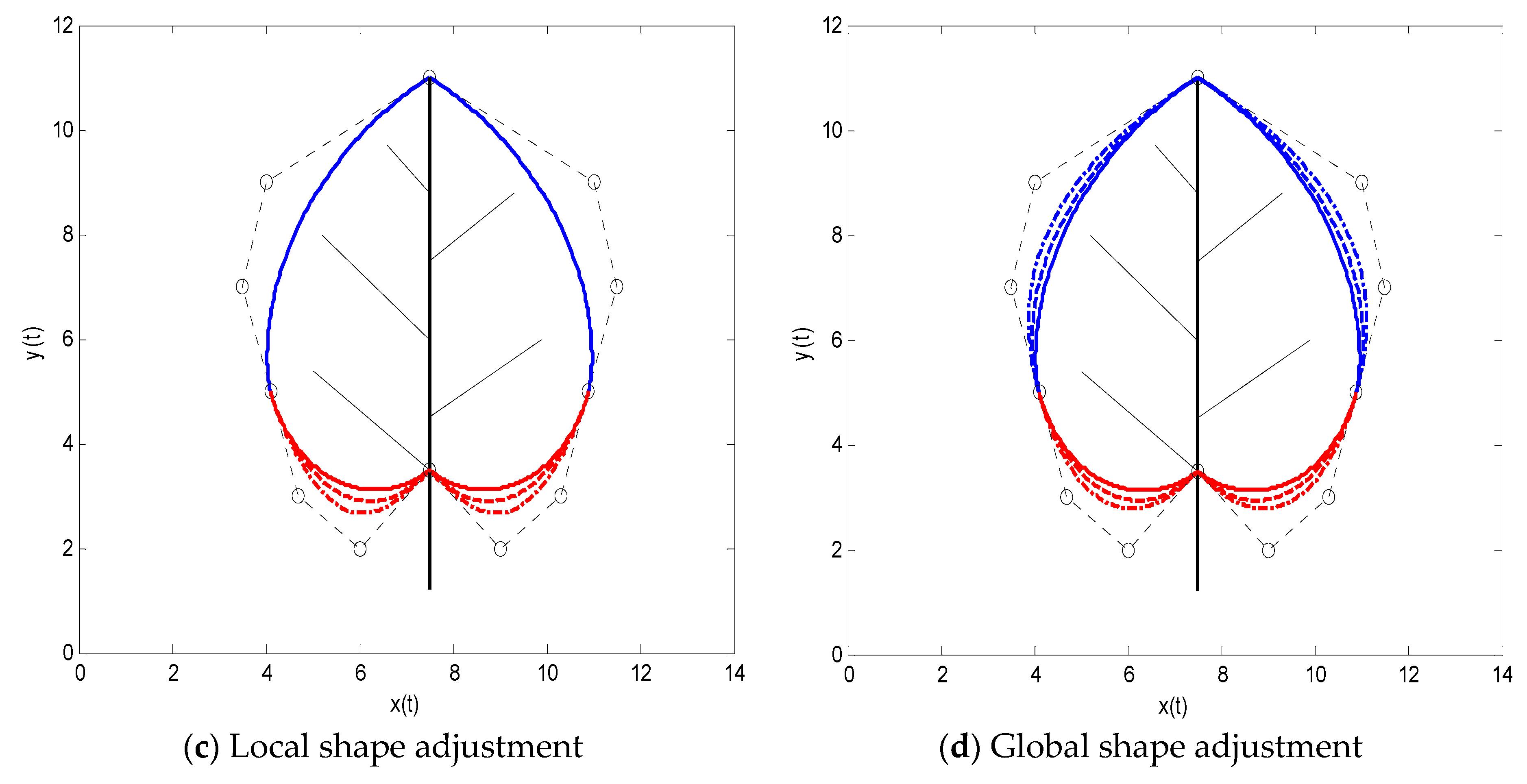Figure 11b displays the global shape adjustment of the composite curve by altering the shape parameters ${\lambda }_{1,1},{\lambda }_{2,1}$, where the shape parameters for the solid lines, dashed lines, and dotted lines are ${\lambda }_{1,1}=2,{\lambda }_{2,1}=3$, ${\lambda }_{1,1}=0,{\lambda }_{2,1}=0$, and ${\lambda }_{1,1}=4,{\lambda }_{2,1}=6$, respectively. Figure 11c displays the local shape adjustment by using a single shape parameter ${\mu }_{1,2}$, where the shape parameters are ${\mu }_{1,2}=4$ (solid lines), ${\mu }_{1,2}=2$ (dashed lines), and ${\mu }_{1,2}=0$ (dotted lines), respectively. Based on Figure 11a, Figure 11d illustrates the global shape adjustment by modifying the shape parameters ${\omega }_1,{\omega }_2,{\lambda }_{1,2}$. From the figure, we realize the global shape adjustment for the dashed lines merely using the shape parameters ${\omega }_1,{\omega }_2$ (with ${\omega }_1={\omega }_2=0.1$), and the dotted lines by changing shape parameters ${\omega }_1,{\omega }_2,{\lambda }_{1,2}$ (with ${\omega }_1=0.5,{\omega }_2=0.8,{\lambda }_{1,2}=3$) . The rest of the shape parameters are equal to those in Figure 11a expect for the ones that are modified in the other three figures.

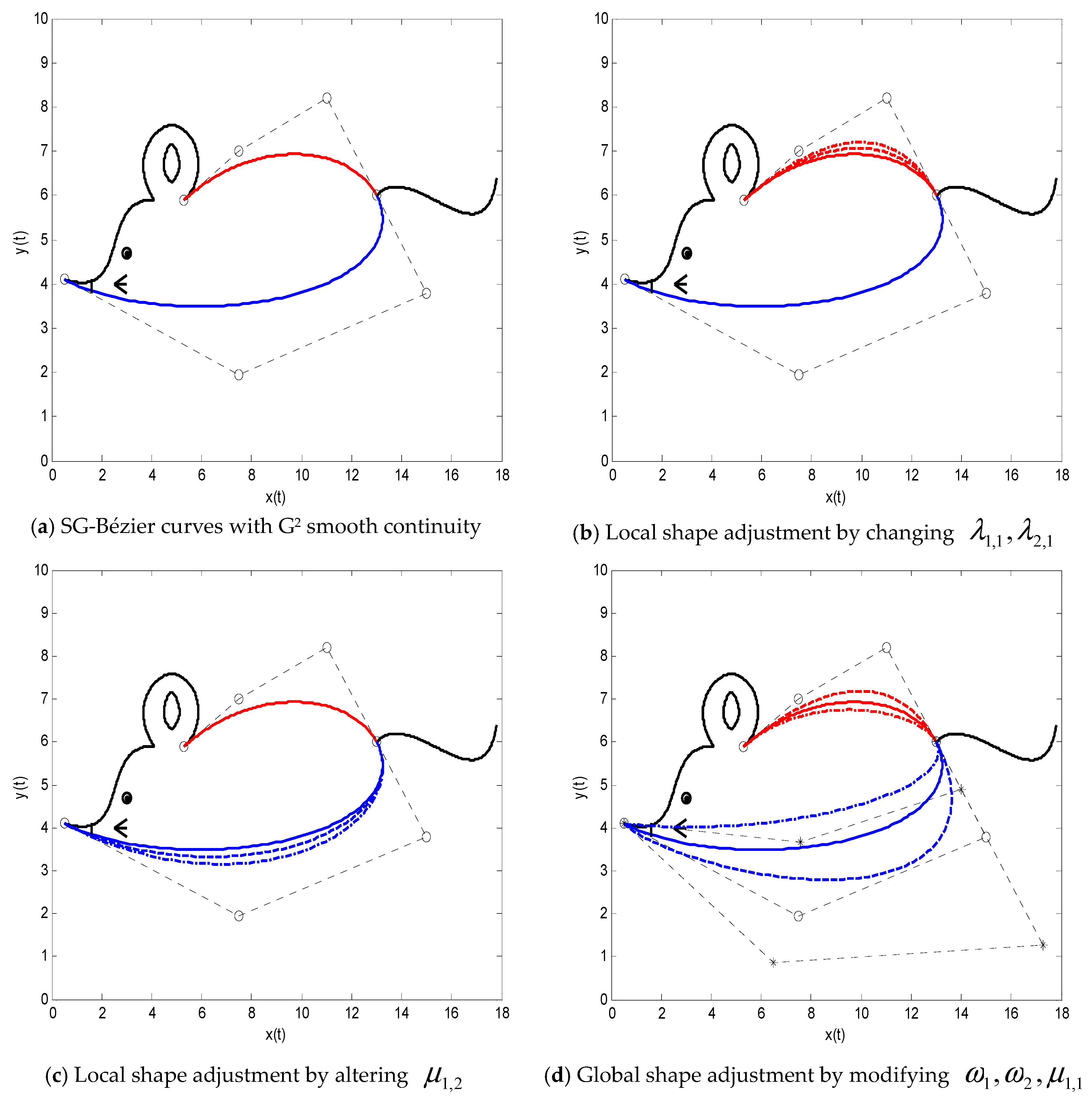
Figure 12 shows the shape adjustment of G² smooth continuity between the two SG-Bézier curves of degree 3. The shape parameters in Figure 12a are the same as those in Figure 7b. As argued in the paragraph above, the solid line means the curves before adjustment, while the dotted lines and dashed lines are the curves after the shape parameters are changed. The circular points in Figure 12 denote the control points before adjustment, and the asterisks marked on the control polygon are the modified control points. Figure 12b displays the local shape adjustment by changing the shape parameters ${\lambda }_{1,1},{\lambda }_{2,1}$, with the shape parameters ${\lambda }_{1,1}=3,{\lambda }_{2,1}=5$ (solid lines), ${\lambda }_{1,1}=2,{\lambda }_{2,1}=2$ (dashed lines), and ${\lambda }_{1,1}=0,{\lambda }_{2,1}=0$ (dotted lines). Figure 12c illustrates the local shape adjustment by using a single shape parameter ${\mu }_{1,2}$, with the shape parameter ${\mu }_{1,2}=3$ (solid lines), ${\mu }_{1,2}=1.5$ (dashed lines) and ${\mu }_{1,2}=0$ (dotted lines). Figure 12d gives an example showing the global shape adjustment by modifying the shape parameters ${\omega }_1,{\omega }_2,{\mu }_{1,1}$. The dashed lines achieve the global shape adjustment merely by using the shape parameters ${\omega }_1,{\omega }_2$ (with ${\omega }_1=0.8,{\omega }_2=0.1$). The dotted lines realize the global shape adjustment in Figure 12d by altering the shape parameters ${\omega }_1,{\omega }_2,{\mu }_{1,1}$ (with ${\omega }_1=0.2,$ ${\omega }_2=0.8,{\mu }_{1,1}=1$). The rest of the shape parameters are all equal to those in Figure 12a expect for the ones that are modified in the other three figures.

6. Applications

In the field of the development of CAD/CAM application software, the SG-Bézier curves provide a new powerful tool in mathematical theory as an extension of the traditional Bézier curves, which play a key role in many areas such as computer animation, computer vision, computer graphics, the manufacturing industry, and multimedia technology. In CAD/CAM, if the apparent surface of a product is a complex composite curve, the curve needs to be treated as a piecewise curve composed of multiple ones.

In order to demonstrate the approaches that can be applied to complex curve design, we will give two practical applications in this section. In computer graphics, the generation technology for different types of Chinese fonts has always been an important research topic. Figure 13 gives an example to design the curves for the script form of the Chinese character “long”, which means Chinese dragon. Figure 13a is a copy of the Chinese script of “long” drawn using the drawing software INKSCAPE. In Figure 13b, the graph of the Chinese character “long” is composed of nine SG-Bézier curves. Figure 13c,d shows the local and global deformation of the graph in Figure 13b by changing the shape parameters, respectively.

Figure 14 displays an example to design the curve graph of a goose by using SG-Bézier curves. In this figure, the shape curves are composed of 13 SG-Bézier curves with different shape parameters.

7. Conclusions

In order to resolve the problem that complex curves can not be constructed by a single curve, we give the C¹, C² and G¹, G² smooth continuity conditions for two adjacent nth-degree SG-Bézier curves, and study the effect of shape parameters on the shapes of the composite curves. Moreover, we give the concrete steps of G² smooth continuity between SG-Bézier curves. Furthermore, we utilize some practical examples to verify the validity of the proposed continuity conditions. The theoretical analysis and modeling examples show that our proposed continuity conditions between two SG-Bézier curves are not only easy to carry out, they also make the shapes of the curves adjusted more conveniently under these conditions. This paper provides an effective scheme for the shape design and construction of complex curves in the engineering that encode the value in the future applications. Notice that the introduction of shape parameters not only brings an advantage to the shape modification of composite SG-Bézier curves, it also provides optimized parameters for the shape optimization design of the SG-Bézier ones. Therefore, the research on how to utilize the genetic algorithm [26] to solve the model of curve shape optimization, which takes the shape parameters as the optimization variables, will be addressed in our future work.