Complexity Effective Sampling Frequency Offset Estimation Method for OFDM-Based HomePlug Green PHY Systems
Abstract
:1. Introduction
2. Signal Model
3. Conventional SFO Estimation Scheme
3.1. Conventional Scheme A
3.2. Conventional Scheme B
3.3. Conventional Scheme C
4. Proposed SFO Estimation Scheme
4.1. Estimation Algorithm
4.2. MSE Analysis
4.3. Complexity
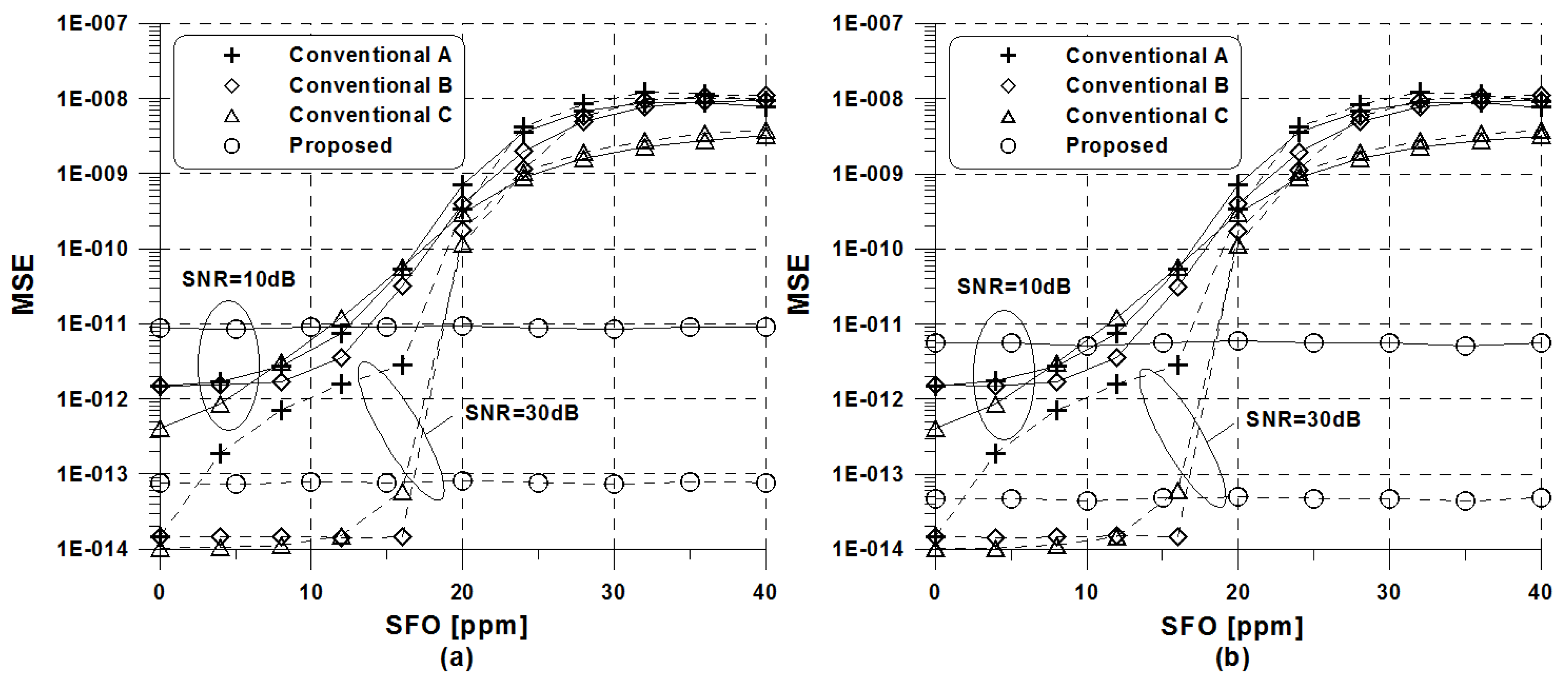
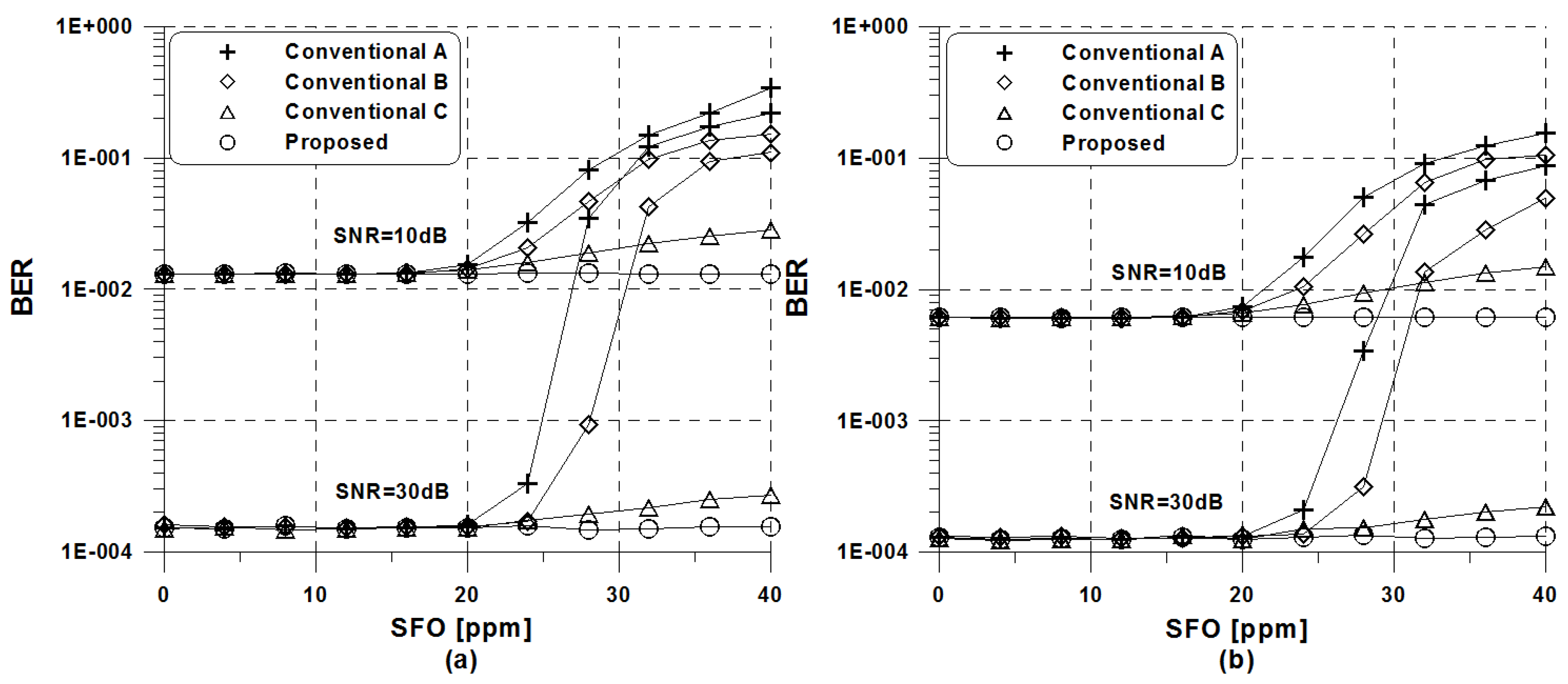
5. Simulation Results and Discussions
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ferreira, H.C.; Lampe, L.; Newbury, J.; Swart, T.G. Power Line Communications: Theory and Applications for Narrowband and Broadband Communications Over Power Lines; Wiley: Chichester, UK, 2010. [Google Scholar]
- Galli, S.; Scaglione, A.; Wang, Z. For the grid and through the grid: The role of power line communications in the smart grid. Proc. IEEE 2011, 6, 998–1027. [Google Scholar] [CrossRef]
- Lampe, L.; Tonello, A.M.; Swart, T.G. Power Line Communications: Principles, Standards and Applications from Multimedia to Smart Grid; Wiley: Chichester, UK, 2016. [Google Scholar]
- Katayama, M.; Yamazato, T.; Okada, H. A mathematical model of noise in narrowband power line communication systems. IEEE J. Sel. Areas Commun. 2006, 7, 1267–1276. [Google Scholar] [CrossRef]
- Marrocco, G.; Statovci, D.; Trautmann, S. A PLC broadband channel simulator for indoor communications. In Proceedings of the IEEE International Symposium on Power Line Communications and Its Applications, Johannesburg, South Africa, 24–27 March 2013; pp. 321–326. [Google Scholar]
- Taherinejad, N.; Rosales, R.; Lampe, L.; Mirabbasi, S. Channel characterization for power line communication in a hybrid electric vehicle. In Proceedings of the IEEE International Symposium on Power Line Communications and Its Applications, Beijing, China, 27–30 March 2012; pp. 328–333. [Google Scholar]
- Amrani, O.; Rubin, A. Contention detection and resolution for multiple-access power-line communications. IEEE Trans. Veh. Technol. 2007, 6, 3879–3887. [Google Scholar] [CrossRef]
- The HD-PLC Alliance Home Page. Available online: http://www.hd-plc.org (accessed on 1 June 2018).
- The HomePlug Powerline Alliance Home Page. Available online: http://www.homeplug.org (accessed on 1 June 2018).
- The Universal Powerline Association Home Page. Available online: http://www.upaplc.org (accessed on 1 June 2018).
- HomePlug Powerline Alliance, Inc. Homeplug Green PHY Specification Release Version 1.1.1; HomePlug Alliance: Portland, OR, USA, 2013. [Google Scholar]
- Sharma, K.; Saini, L.M. Power-line communications for smart grid: Progress, challenges, opportunities and status. Renew. Sustain. Energy Rev. 2017, 67, 704–751. [Google Scholar] [CrossRef]
- Cortés, J.; Díez, L.; Cañete, F.; Sánchez-Martínez, J.; Entrambasaguas, J. Performance analysis of OFDM modulation on indoor broadband PLC channels. EURASIP J. Adv. Signal Process. 2011, 78, 1–2. [Google Scholar] [CrossRef]
- Speth, M.; Fechtel, S.A.; Fock, G.; Meyr, H. Optimum receiver design for wireless broad-band systems using OFDM-Part I. IEEE Trans. Commun. 1999, 11, 1668–1677. [Google Scholar] [CrossRef]
- Chin, W.L. ML estimation of timing and frequency offsets using distinctive correlation characteristics of OFDM signals over dispersive fading channels. IEEE Trans. Veh. Technol. 2011, 2, 444–456. [Google Scholar] [CrossRef]
- Speth, M.; Fechtel, S.A.; Fock, G.; Meyr, H. Optimum receiver design for OFDM-based broadband transmission-Part II: A case study. IEEE Trans. Commun. 2001, 49, 571–578. [Google Scholar] [CrossRef]
- Oberli, C. ML-based tracking algorithms for MIMO-OFDM. IEEE Trans. Wirel. Commun. 2007, 7, 2630–2639. [Google Scholar] [CrossRef]
- Yuan, J.; Torlak, M. Joint CFO and SFO estimator for OFDM receiver using common reference frequenc. IEEE Trans. Broadcast. 2016, 62, 141–149. [Google Scholar] [CrossRef]
- Kim, Y.; Lee, J. Joint maximum likelihood estimation of carrier and sampling frequency offsets for OFDM systems. IEEE Trans. Broadcast. 2013, 57, 277–283. [Google Scholar]
- Tsai, P.Y.; Kang, H.Y.; Chiueh, T.D. Joint weighted least-squares estimation of carrier-frequency offset and timing offset for OFDM systems over multipath fading channels. IEEE Trans. Veh. Technol. 2005, 1, 211–223. [Google Scholar] [CrossRef]
- Chiang, P.; Lin, D.; Li, H.; Stuber, G.L. Joint estimation of carrier-frequency and sampling-frequency offsets for SC-FDE systems on multipath fading channels. IEEE Trans. Commun. 2008, 56, 1231–1235. [Google Scholar] [CrossRef]
- Morelli, M.; Moretti, M. Fine carrier and sampling frequency synchronization in OFDM systems. IEEE Trans. Wirel. Commun. 2010, 4, 1514–1524. [Google Scholar] [CrossRef]
- Shi, K.; Serpedin, E.; Ciblat, P. Decision-directed fine synchronization in OFDM systems. IEEE Trans. Commun. 2005, 3, 408–412. [Google Scholar] [CrossRef]
- Lin, Y.; Chen, S. A blind fine synchronization scheme for SC-FDE systems. IEEE Trans. Commun. 2014, 62, 293–301. [Google Scholar] [CrossRef]
- Lalos, A.; Vgenis, A.; Gioulekas, F.; Birbas, M. Pilot-less time synchronization for OFDM systems: Application to power line receivers. Int. J. Distrib. Sens. Netw. 2016, 12, 1–12. [Google Scholar] [CrossRef]
- Kim, Y.H.; Lee, J.H. Comparison of passband and baseband transmission schemes for power-line communication OFDM systems. IEEE Trans. Power Deliv. 2011, 4, 2466–2475. [Google Scholar] [CrossRef]
- Fowler, M. Phase-based frequency estimation: A review. Digit. Signal Process. 2002, 4, 590–615. [Google Scholar] [CrossRef]
- Golub, G.H.; Vanloan, C.F. Matrix Computations; The Johns Hopkins University Press: Baltimore, MA, USA, 1996. [Google Scholar]
- Tonello, A.M.; D’Alessandro, S.; Lampe, L. Cyclic prefix design and allocation in bit-loaded OFDM over power line communication channels. IEEE Trans. Commun. 2010, 58, 3265–3276. [Google Scholar] [CrossRef]

| Mode | PHY Rate | # Repeat Copies |
|---|---|---|
| Mini ROBO | 3.8 Mbps | 5 |
| Standard ROBO | 4.9 Mbps | 4 |
| High-speed ROBO | 9.8 Mbps | 2 |
| Parameter | Value |
|---|---|
| Sampling rate | MHz |
| FFT size | |
| CP size | |
| Number of subcarriers | |
| Number of non-masked subcarriers | |
| Modulation | QPSK |
| Index m | Standard ROBO | High-Speed ROBO | ||
|---|---|---|---|---|
| Subcarrier Distance | # of Subcarrier | Subcarrier Distance | # of Subcarrier | |
| 1 | 676 | 54 | 816 | 54 |
| 2 | 648 | 41 | 788 | 47 |
| 3 | 674 | 6 | 777 | 13 |
| 4 | 663 | 13 | 789 | 44 |
| 5 | 396 | 44 | 769 | 71 |
| 6 | 376 | 58 | 261 | 36 |
| 7 | 388 | 13 | 251 | 66 |
| 8 | 654 | 36 | 263 | 84 |
| 9 | 644 | 79 | 241 | 24 |
| 10 | 403 | 71 | 267 | 19 |
| 11 | 381 | 43 | - | - |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jung, Y.-A.; You, Y.-H. Complexity Effective Sampling Frequency Offset Estimation Method for OFDM-Based HomePlug Green PHY Systems. Symmetry 2018, 10, 544. https://doi.org/10.3390/sym10110544
Jung Y-A, You Y-H. Complexity Effective Sampling Frequency Offset Estimation Method for OFDM-Based HomePlug Green PHY Systems. Symmetry. 2018; 10(11):544. https://doi.org/10.3390/sym10110544
Chicago/Turabian StyleJung, Yong-An, and Young-Hwan You. 2018. "Complexity Effective Sampling Frequency Offset Estimation Method for OFDM-Based HomePlug Green PHY Systems" Symmetry 10, no. 11: 544. https://doi.org/10.3390/sym10110544
APA StyleJung, Y.-A., & You, Y.-H. (2018). Complexity Effective Sampling Frequency Offset Estimation Method for OFDM-Based HomePlug Green PHY Systems. Symmetry, 10(11), 544. https://doi.org/10.3390/sym10110544




