1. Introduction
Jack polynomials have many applications in physics, especially in statistical physics and quantum physics due to their relation to the many-body problem. In particular, fractional quantum Hall (FQH) states of particles in the lowest Landau levels are described by such polynomials [
1,
2,
3]. In that context, some properties, called clustering properties, are highly relevant. A clustering property can occur for some negative rational parameters of a Jack polynomial and means that the Jack polynomial vanishes when distinct clusters of equal variables are formed. Using tools of algebraic geometry, Berkesch-Zamaere et al. [
4] proved several clustering properties including some special cases conjectured by Bervenig and Haldane [
1]. Coming from theoretical physics, the study of these properties raises very interesting problems in combinatorics and representation theory of the affine Hecke algebra. More precisely, the problem is studied in the realm of Macdonald polynomials which form a
-deformation of the Jack polynomials related to the double affine Hecke algebra and the results are recovered by making degenerate the parameters
q and
t. Recently, a very similar technique has been used in [
5] to prove general formulas for perturbative correlators in basic matrix models that can be interpreted as the Schur-preservation property of Gaussian measures. In this case, the substitution of Schur functions by Macdonald polynomials defines a deformation of the matrix model. For our case, instead of stating the results in terms of clustering properties, we prefer to state them in terms of factorizations. Indeed, clustering properties are shown to be equivalent to very elegant formulas involving factorizations of Macdonald polynomials. For instance, many such factorizations have already been investigated in [
6,
7,
8,
9]. In particular, this paper is the sequel of [
9] in which two of the authors proved factorizations for rectangular Macdonald polynomials. In this paper, we investigate factorizations for more general partitions, called quasistaircase partitions.
The paper is organized as follows. In
Section 2, we recall essential prerequisites on Macdonald polynomials. In
Section 3, we give a brief account on the physics motivations coming from the FQH effect theory. In
Section 4, we investigate some factorizations involved for generic values of
.
Section 5 is devoted to the special cases of specializations of the type
and, in particular, to the consequences on spectral vectors. In
Section 6, we deduce factorizations from the results of Feigen et al. [
10] and, in
Section 7, we prove more general results which are consequences of the highest weight (HW) condition of some Macdonald polynomials indexed by quasistaircase partitions proved in [
11].
Section 8 is devoted to illustrate our results by proving a conjecture stated by Bernevig and Haldane [
2] and also we show many other examples of factorizations that do not follow from our formulas.
2. Background
This paper is focused on the study of four variants of the Macdonald polynomials: symmetric, nonsymmetric, shifted symmetric and shifted nonsymmetric. Before getting into the results, we introduce these polynomials as well as some useful notation. All the results contained in this section are well known results showed in several papers (see, e.g., [
12,
13,
14,
15,
16,
17,
18,
19,
20]). The results of [
21,
22,
23] are extensively used throughout our paper.
2.1. Partitions and Vectors
A partition of n is a weakly decreasing sequence of nonnegative integers such that . The length of a partition is the number of nonzero parts, . We denote by the number of parts of lower or equal to i, and by the multiplicity of the maximal part in .
We consider a dominance order on the partitions: Let and be partitions, we say that if and only if, for all i, .
We also consider vectors, denoting by a vector of length and with nonnegative entries. We denote by the sum of the entries of v. For each vector v, there is a unique partition, , which is a permutation of v. The dominance order defined on partitions extends to vectors with the same definition. In addition, we define another order: For u and v vectors, we say that if and only if either or and . Initially, this order is only defined for vectors such that , and we extend it straightforwardly for any vectors by adding the condition when .
We define the standardization of v, , as the vector obtained by labeling with the integers from 0 to the positions in v from the smallest entries to the largest one and from right to left. Moreover, we define the reciprocal vector of v as , and the reciprocal sum of v as . If there is ambiguity, the indices q and t are added. Note that in the particular case of considering a partition , .
For example, consider the vector of length 6. Then, , , and .
2.2. Affine Hecke Algebra
We present a brief introduction to the affine Hecke algebra
and the Demazure–Lusztig operators
. For more details, see [
24,
25,
26,
27].
Let
be an integer,
q and
t be two independent parameters, and
be a set of formal variables. We consider the right operators
, for
, acting on Laurent polynomials in the variables
by
where
is the elementary transposition permuting the variables
and
. For instance,
and
. In fact, the operators
are the unique operators that commute with multiplication by symmetric functions in
and
satisfying these last two equations. Consider also the
affine operator defined by
The operators
satisfy the relations of the Hecke algebra of the symmetric group:
Then, together with the multiplication by variables
and the affine operator
, they generate the
affine Hecke algebra of the symmetric group:
2.3. Symmetric Functions and Virtual Alphabets
For the sake of simplicity, we use
-ring notation for specializations of symmetric polynomials (see [
22]). A
finite alphabet is a finite set of formal variables and we denote it by
or
. By
specialization, we mean a morphism of algebras and, since we manipulate only finite alphabets, specializing an alphabet is equivalent to sending each letter to a value. Notice that this is no longer the case for infinite alphabets for which the theory is more complicated.
More precisely, we adopt the following convention stated in terms of the basis of power sums symmetric polynomials. For any variable
x, alphabets
and
and scalar
, we set
We set also the following notation:
and
, for
. For two alphabets
and
, the
resultant of and is defined as
which is a symmetric polynomial in
and
separately (but not in
). Hence,
Throughout this paper, the following notation is relevant and very useful. Let and be two polynomials in with coefficients in q and t. We say that if the equality holds up to a scalar factor consisting of powers of q and t.
2.4. Macdonald Polynomials and Variants
In this section, we set up the definitions and the notation for the different variants of Jack and Macdonald polynomials that appear in this paper. For that, we define several vectors and the basis of eigenfunctions associated. First, we define the two variants of nonsymmetric Macdonald polynomials, indexed by vectors.
Definition 1. The -version of the Cherednik operators are the operators defined by The nonsymmetric Macdonald polynomials are the unique basis of simultaneous eigenfunctions of the -version of the Cherednik operators such that . The corresponding vector of eigenvalues is called spectral vector and its ith entry is .
We consider also the following variant of the operators.
Definition 2. The Knop–Cherednik operators are defined by The nonsymmetric shifted Macdonald polynomials are the unique basis of simultaneous eigenfunctions of the Knop–Cherednik operators such that .
As in the case of the nonsymmetric Macdonald polynomials, the eigenvalues make up the spectral vector .
Note that the polynomial
can be recovered as a limit from
:
which follows from the relation
.
Now, we define both variants for symmetric Macdonald polynomials, indexed by partitions, by considering the sum of the operators defined above.
The Debiard–Sekiguchi–Macdonald operator is the operator defined as . The symmetric Macdonald polynomials, , are defined as the eigenfunctions of . Similarly, we can consider the operator and the symmetric shifted Macdonald polynomials, , are defined as the eigenfunctions of . In both cases, the eigenvalues are .
We define the symmetric Jack polynomials, , as the limit of the Macdonald polynomials, , with and . The other versions of Jack polynomials can be also defined as a limit, but we focus our attention on the symmetric variant.
Two families of polynomials are relevant for our study and rely on the difference of the operators presented above. The differences of the Cherednik operators and the Knop–Cherednik operators are known as the Dunkl operators, . We say that a polynomial is singular if it is in the kernel of , for all i. We say that a polynomial is a HW polynomial if it is in the kernel of .
2.5. Computing Macdonald Polynomials Using the Yang–Baxter Graph
In [
21], Lascoux described how to compute the nonsymmetric shifted Macdonald polynomials
using the
Yang–Baxter graph. This computation is based on the following result.
Proposition 1. Let v be a vector.
If , , where is the vector obtained from v by exchanging the values and .
, where . We refer to this step as affine step.
This result provides a method to compute the polynomials
following the Yang–Baxter graph associated to the vector
v, starting with the zero vector
and
. We illustrate how to do it for the nonsymmetric shifted Macdonald polynomials with an example. On the one side, we have the following sequence for the vectors:
Notice that we simplify the notation by writing for the vector . Since our examples do not contain numbers larger than nine, there is no misunderstanding.
The sequence above corresponds to the following sequence on the polynomials:
The nonsymmetric Macdonald polynomials are obtained following an almost similar algorithm where the affine action is substituted by
. For instance, using the same sequence as before,
The symmetric variants of the Macdonald polynomials are hence obtained by applying the symmetrizing operator , where if is a shortest decomposition of in elementary transpositions, to the polynomials labeled by a decreasing vector. In addition, Jack polynomials are obtained following a Yang–Baxter graph with degenerated intertwining operators.
2.6. Vanishing Properties
The shifted variants for Jack and Macdonald polynomials can be defined alternatively by interpolation. Indeed, one shows with the help of the Yang–Baxter graph that the shifted nonsymmetric Macdonald polynomials are characterized up to a global coefficient by the equations , for any vector u satisfying and . That is, by specializing the variables of to the entries of the vector in the nonsymmetric Macdonald polynomial .
By symmetrization, the shifted symmetric Macdonald polynomials are characterized up to a global coefficient by , for any partition satisfying and .
In addition, vanishing properties of shifted symmetric and nonsymmetric Jack polynomials are obtained by making the equations above degenerate.
3. Clustering Properties of Jack Polynomials and the Quantum Hall Effect
3.1. A Gentle History of the Quantum Hall Effect
The quantum Hall effect is a phenomenon involving a collection of electrons restricted to move in a two-dimensional space and subject to a strong magnetic field.
The classical Hall effect was discovered by Edwin Hall in 1879 [
28] and is a direct consequence of the motion of electrons in a magnetic field. More precisely, it comes from the fact that the magnetic field causes electrons to move in circles. Let us recall quickly the calculation. This phenomena is known under the name cyclotron effect and is deduced from the equations of the motion for a particle of mass
m and charge
in a
z-directed magnetic field of intensity
B:
The general solution,
and
, describes a circle. The parameters
,
,
r and
are chosen arbitrary, while
is a linear function of
B and is called the cyclotron frequency. Taking into account an electric field
generating the current together with a linear friction term modeled by the scattering time
, the motion equations become
This model is known under the name of Drude model [
29,
30] and consists in considering the electrons as classical balls. Assuming that the velocity is constant, it can be written as:
The current density
is related to the velocity by the equality
, where
n denotes the number of charged particles. Hence,
where
denotes the conductivity.
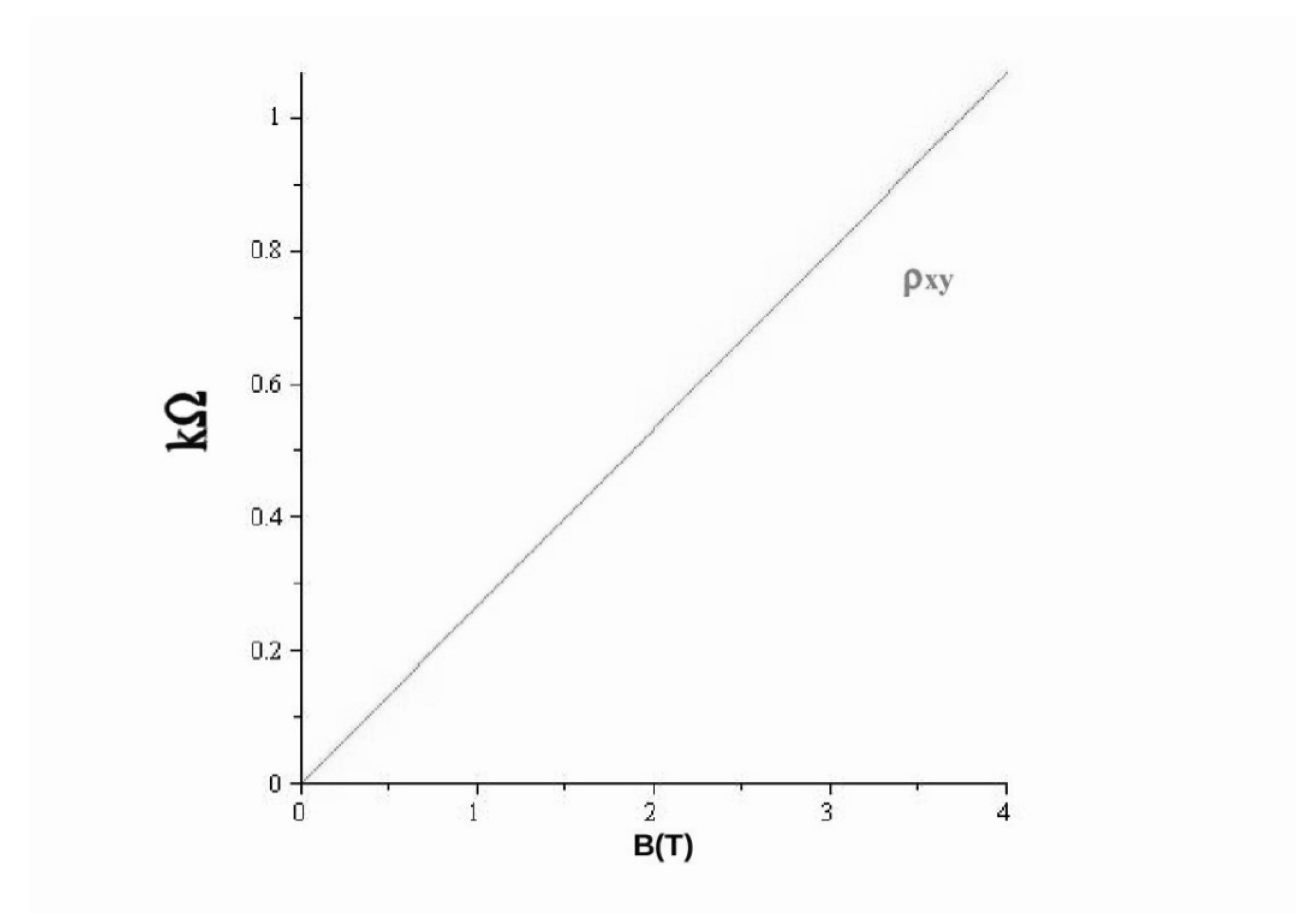
We see that there are two components to the resistivity: the off-diagonal component (Hall resistivity, see
Figure 1)
, which does not depend on
but is linear in
B, and the diagonal component (longitudinal resistivity)
, which does not depend on
B and tends to 0 when the scattering time
tends to
∞.
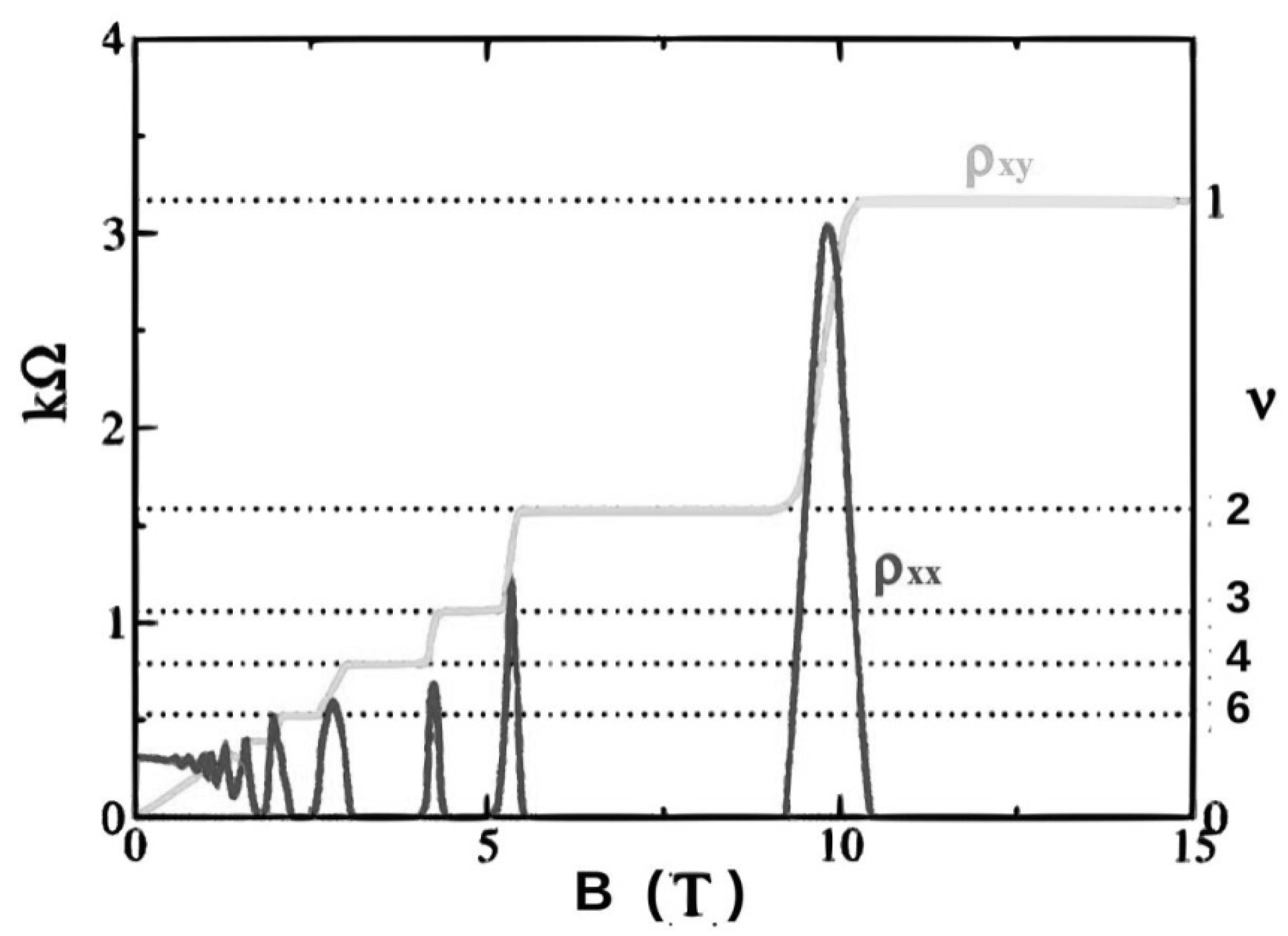
In 1980, Von Klitzing et al. [
31] realized measurements of the Hall voltage of a two-dimensional electron gas with a silicon metal-oxide-semiconductor field-effect transistor and showed the Hall resistivity has fixed values. The exhibited phenomenon is called the integer quantum Hall effect, see
Figure 2 (This figure was obtained by replacing the vertical scale
by
in [
32] (Figure 4.1, Section 4.4) and it is under
Creative Commons Attribution-Noncommercial-Share Alike 3.0 Generic License).
Both the Hall resistivity and longitudinal resistivity have a behavior which highlights a quantum phenomena at the mesoscopic scale. The Hall resistivity is no longer a linear function of B but sits on a plateau for a range of magnetic field before jumping to the next one. These plateaux are centered on values , where is the quantum resistivity, depending on a parameter and the Hall resistivity takes the value . The longitudinal resistivity vanishes when sits on a plateau and spikes when jumps to the next one.
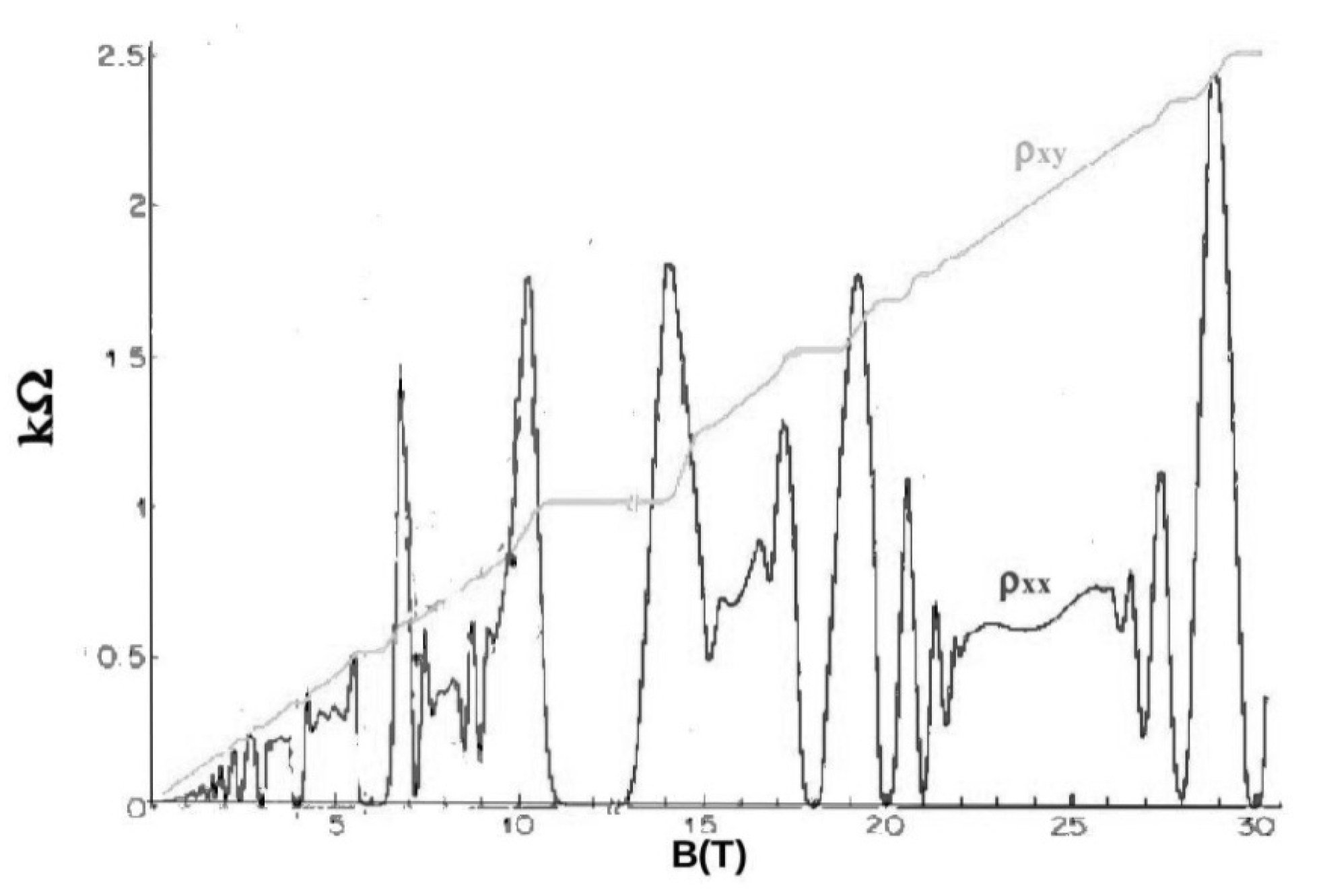
The FQH effect was discovered by Tsui et al. [
33]. They observed that, as the disorder is decreased, the integer Hall plateaux become less prominent and other plateaux emerge for fractional values of
, see
Figure 3 (This figure was drawn by modifying a picture from [
34]).
The difference between the integer quantum Hall effect and the FQH effect is that, to explain the second, physicists need to take into account the interactions between the particles. The interaction between the electrons make the problem interesting from a mathematical point of view. The theoretical approach was pioneered by Laughlin [
35] for
. Since the Hamiltonian is very difficult to diagonalize, he proposed directly a wave function fulfilling several properties motivated by physical insight. The Laughlin wave function overlaps more than
with the true ground state. From the observations of Tsui et al. and the work of Laughlin, more than 80 plateaux have been observed for various filling fractions. The description of the wave functions is one of the challenges of the study. It is in this context that Jack polynomials appear.
3.2. Quantum Hall Wave Functions
The FQH effect appears in many configurations of the gas. Indeed, the Hall voltage can be generated by the motion of the particles but also by quasi-particles or quasi-holes. Quasi-particles and quasi-holes are virtual particles that occur when matter behaves as if it contains different weakly interacting particles. The charges of these virtual particles are fractions of the electron charge and their masses are also different. However, in all cases, for fermion gases, the wave function must take the form
where
is a symmetric polynomial, and
is the magnetic length, which is a characteristic length scale governing quantum phenomena in a magnetic field (see, e.g., [
36] for details). This expression is obtained assuming that the system is in the lowest Landau level, where the single particle wave functions take the form
, and that all the particles play the same role. This last condition is a quite puzzling point. Indeed, since the particles are placed in a finite portion of the plane, they cannot play the same role because the interactions must take into account the distance between the particles and the sides of the sample. Hence, the symmetry comes from an approximation when assuming that the number of particles tends to infinity. The Haldane approach [
37] for this theory consists in placing the particles on a sphere. The position of a particle is specified by spinor coordinates
and
. When the radius tends to infinity the two approaches coincide and the wave functions in the spherical geometry are used to compute approximation for the plane geometry via stereographic projection. All operators and wave function introduced by Haldane have been translated by this way in the plane geometry. In the following, we consider the Haldane point of view after stereographic projection.
The Laughlin wave function [
35] models the simplest FQH states which occurs for
. This wave function is given by
Notice that
can be seen as the stereographic projection of Haldane wave function stated in terms of spinor coordinates by
In the Laughlin states no quasi-particle or quasi-hole is involved. From a mathematical point of view, the absence of quasi-particle and quasi-hole is interpreted in terms of differential operators as follows: We consider the operators and we set and where . The parameter is interpreted in the spherical geometry by the fact that the sphere surrounds a monopole with charge . The absence of quasi-particle is characterized by (HW condition) while the absence of quasi-hole is characterized by (lowest weight (LW) condition). Noticing that , we find that if P is a polynomial satisfying the HW and LW conditions then , that is P is an homogeneous polynomial. The HW condition means that the polynomial is invariant by translations. A fast computation shows that is both a HW and a LW state.
Other interesting wave functions have been exhibited. For instance, the Moore–Read (Pfaffian) state [
38] is
where
denotes the Pfaffian. Surprisingly, it describes the FQH for
. To understand the difference with the integer quantum Hall effect, physicists introduced two values
k and
r such that
. The parameter
k means that the function vanishes for
particles together but not for
k and the parameter
r is the order of the zeros. For instance, in the Laughlin state, we have
and
, while for the Moore–Read state we have
and
. In [
1,
2], Bernevig and Haldane showed how to associate to each Hall state an occupation number configuration. The occupation number configuration is a vector
such that
is the number of particles in the
ith lowest Landau level orbital (
). For a Laughlin state
, we have
. For the Moore–Read state, we have
. The number
is the greatest integer
i such that
. Instead of using the occupation number configuration, we use a decreasing partition
such that the multiplicity of the part
i in
equals
. For instance
and
(
N needs to be even for Moore–Read states). We see that
is the biggest part in
.
Reader interested by FQH effect theory can refer to [
36] for a complete picture on the topic.
3.3. FQHT and Jack Polynomials
Some of the trial wave functions proposed to describe the FQHE are Jack functions. This is the case of the simplest one,
This was first noticed by Bernevig and Haldane [
1]. They obtained this equality by proving that
is an eigenstate of the Laplace–Beltrami operator
It is particularly interesting to remark that the main argument of the proof comes from clustering properties. Indeed, the idea is that the Laughlin wave function, considered as a polynomial in for some , has a multiplicity root at for any . Therefore, it vanishes under the action of the operator where . Since is in the kernel of , it is an eigenfunction of . Hence, is identified with by considering its dominant monomial.
In the same paper [
1], a similar (but a little more complicated) reasoning is used to study the Moore–Read state
described in [
38]. They proved that
Other examples are treated in [
1]. For instance, a generalization of the previous example is given by the
parafermionic states
where
and
denotes the symmetrizing operator. This example is a special case of a Read–Rezayi state for
[
39]. A more complicated example is involved at
and refereed to as “Gaffnian” [
40]. This wave function is also proved to be a Jack polynomial [
1]
with
.
In the aim to provide tools for the understanding of FQH states, Bernevig and Haldane investigated clustering properties of Jack polynomials, [
2]. In particular, they exhibited a family of HW Jack polynomials in
N variables that vanish when
s distinct clusters of
particles are formed. The corresponding partitions are
with
and
. Notice that, in this case, the flux (i.e., the maximal degree in each variable) equals
Bernevig and Haldane investigated three kinds of clustering properties that occur when and are coprime:
First clustering property: clusters of particles and one cluster of k particles, with the remaining particles free.
This situation is formalized by setting
,
,⋯,
, and
. Then, the Jack polynomial
behaves as
when each
, with
, tends to
. For instance, we have
Second clustering property: A cluster of particles.
To formalize this situation, we set
. Then, the Jack polynomial
behaves as
, when each
tends to
Z. More specifically, for HW Jack polynomials,
Third clustering property: clusters of particles.
By setting
sets of variables as follows:
,…,
, the HW Jack
satisfies
The aim of our paper is to show how the material described in [
9] can help in this context. In particular, we focus on the second clustering property for HW polynomials. Although the wave functions are not all Jack polynomials, many of them can be obtained from Jack polynomials by acting by an operator modeling the adding of a quasi-particle or a quasi-hole (see, e.g., [
3]).
3.4. The Interest of Shifted Macdonald Polynomials
In [
1], Bernevig and Haldane looked at the case
and proved the clustering properties on HW Jack polynomials using a result of B. Feigin et al. [
41] together with Lassalle binomial formulas for Jack polynomials [
42]. Lassalle binomial formula are used to describe the action of the operator
on a Jack polynomial. When
, the partitions do not fulfill some admissibility conditions of B. Feigin et al. [
41], and so, the equations are just conjectured from extensive numerical computations.
For the purpose of manipulating these identities properly, we must leave the framework of homogeneous Jack polynomials. One reason is because clustering properties deal with vanishing properties. Therefore, shifted Jack polynomials should be more appropriate for these problems. Nevertheless, the multiplicities of the roots of the polynomials are difficult to manage. Therefore, the idea consists in
-deforming these identities in such a way that they involve products of distinct factors. For instance, a factor
should become
. With such a deformation, it is also easier to manipulate the eigenspaces which are smaller (see [
7] for the example related to
). Consequently, we follow the strategy initiated in [
9], which consists to manipulate shifted Macdonald polynomials in the aim to prove the identities. The recipe, which could be used for other problems, is as follows:
- Step 1:
Find a Macdonald version of the conjecture and we state it in terms of vanishing properties.
- Step 2:
Prove that the Macdonald polynomial involved is a HW polynomial (i.e., in the kernel of a q-deformation of ).
This property might come from [
10] (Macdonald version of [
41]), or by applying the results of [
11], which are based on the Lassalle binomial formula for Macdonald polynomials [
42].
- Step 3:
In the last case of Step 2, the shifted Macdonald polynomial equals the homogeneous Macdonald polynomials.
- Step 4:
Consequently, we deduce the equality from vanishing properties of the shifted Macdonald polynomial and we recover the identity on Jack by setting and q to 1.
Notice that, in [
11], one of the authors with Thierry Jolicoeur found some families of polynomials which have not been considered in [
2]. Indeed, Bernevig and Haldane missed that the family
can be extended by adding a parameter corresponding to the multiplicity of the largest part which can be smaller than
k. In addition, some other Macdonald polynomials do not specialize to a Jack for the considered specialization of
. This is explained in the next sections.
4. Factorizations for Generic Parameters
In this section, we study several factorizations of Macdonald polynomials for different partitions and specializations of the variables, keeping q and t as generic parameters.
4.1. Saturated Partitions
We start by looking at the partitions ending with zeros. From the partitions perspective, adding zeros at the end of a partition does not make a big difference. From the Yang–Baxter graph, the starting vector is longer and the computation might require extra steps permuting entries. Let us see how this relates to the Macdonald polynomials by starting with the definition.
Definition 3. Fix an integer . We say that a partition is saturated if .
The following result shows a general factorization for the Macdonald polynomials indexed by saturated partitions.
Proposition 2. If is saturated, then:
.
.
Proof. We prove both statements at the same time. Recall the affine step for nonsymmetric Macdonald polynomials (respectively, Shifted Macdonald polynomials) from Proposition 1
If we apply this step
N times, we obtain
Hence, if we apply the affine step
N times again, we obtain
By induction, starting with
and applying the affine step
times, one finds
Since the polynomials and are symmetric, they commute with the action of the symmetrizing operator and the result is obtained by applying to and . □
The first result is classical. Indeed, following the Yang–Baxter graph and applying the affine step several times, we have that for any vector
v with
:
Moreover, is obtained from , where , by applying the symmetrization operator . Since is symmetric, it commutes with . Therefore, is proportional to and we deduce our result from the fact that the dominant coefficient of is 1. Furthermore, it is the simultaneous eigenfunction for the Cherednik operators , whose spectral vector is , and it is also an eigenfunction for the operator with eigenvalues .
For the second result, there is an alternative proof based on the examination of the vanishing properties of
Let
, with
. If
, by the vanishing properties of
,
If
, then this means that
. Then, the factor
in (
2) vanishes for
. This proves that the two polynomials have the same vanishing properties and so, that they are equal.
4.2. Standard Specializations for the Variables
Apart from considering partitions ending with at least one zero, we consider now a particular specialization for the variables.
Definition 4. For a partition with , the λ-standard specialization consists in setting , for .
The -standard specialization provides another interesting factorization.
Proof. This polynomial vanishes for , for any . Moreover, , since . Therefore, has the same vanishing properties as . This proves the first equality and, as a direct consequence of Proposition 2, we get the second equality. □
Example 1. We illustrate the principle of the proof with . By its vanishing properties, vanishes for the following values of : , , , , , , , , , and .
Since is a degree 5 symmetric polynomial in two variables, these vanishing properties completely characterize it up to a global factor. Indeed, there are exactly 12 independent symmetric functions of degree at most 5 in 2 variables. The basis of the space spanned by these functions is generated by the polynomials , , , …, . The polynomial is symmetric and so is a linear combination of the 12 polynomials above. It follows that a series of 11 vanishing properties is sufficient to produce a system of linear equations characterizing the coefficients of this combination.
The following table compares the vanishing properties characterizing by listing the partitions μ of length with , together with their reciprocal vector: | | |
| | × |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
We deduce that the polynomials and are proportional. Since these two polynomials have low degree, they are easy to compute with the help of the Yang–Baxter graph: Proof. We prove the property by induction on
. First, we consider the case
. By Proposition 2, we have
Setting
, we have
and, by induction:
Using that
,
as expected.
If
, then we set
, with
, and, by Proposition 3, we obtain
We conclude the proof by induction and applying (
3) since
. □
We conclude this section with an example.
Example 2. Consider ; we alternatively use Propositions 2 and 3 for computing . In each step, the expression we obtain is the product of a polynomial in the alphabet with coefficients in and a symmetric shifted Macdonald polynomial indexed by a smaller partition. The process finishes when is described as a polynomial in the alphabet with coefficients in , up to some coefficient of the form . As expected, the last polynomial is proportional to .
5. Specializations of the Type and Quasistaircase Partitions
In this section, we focus in the quasistaircase partitions for a concrete specialization of the parameters q and t.
Definition 5. Consider the integers , , and , such that is an integer. We define the quasistaircase partition
as the following partition 5.1. Admissible Specializations
We start defining the specialization that we consider as in [
10].
Definition 6. A -admissible specialization is one of the form where and is a primitive gth root of the unity.
From now on in this section, and unless specifying otherwise, these parameters defining the quasistaircase partition satisfy the conditions stated below and the parameters q and t are specialized.
Example 3. Let us illustrate the notion of -admissible specialization by giving a few examples and counter-examples.
is -admissible.
and are -admissible.
is -admissible while is not -admissible.
and are -admissible but is not.
and are -admissible, while and are not -admissible.
We finish this subsection with the following result that highlights the relevance of .
Lemma 1. Suppose , , and , with . Then, and , for some .
Proof. By hypothesis . From , it follows that and , for some . Thus, and , for some , because is a primitive gth root of unity. Hence, and . □
5.2. On the Reciprocal Sum
In this section, we prove that the intersection of the eigenspace of , with eigenvalue , and the space generated by , with , has dimension 1.
We start with the following technical lemma.
Lemma 2. Let λ be the partition , where α is an integer such that . Consider another partition such that there exists i satisfying . Then, and λ and μ have the same k first entries, i.e., , for .
Proof. First, we notice that
, which means that
lies on the line
and that
. Since
,
and, so,
.
If
, then
and the point
lies on or below the line
That is, and, so, .
Now, suppose that
. In this case,
and, from Equation (
4), we obtain
Then, i is strictly greater than the size of , which is impossible.
The only remaining possibility is , and so . Since , we deduce also that , …, . □
Example 4. In Figure 4, we illustrate the proof of Lemma 2 for the parameters , , , and . The shaded area illustrates the inequality in Equation (
6)
, which is defined by the lines in Equations (
4)
(top) and (
5)
(bottom). Below it, we include the partition λ. The following result shows that the reciprocal sum characterizes the quasistaircase partitions.
Proposition 4. Consider a partition μ such that and . Then, .
Proof. Denote by the quasistaircase partition, . Then, there exists i such that . Otherwise, is completely contained in and is impossible.
By Lemma 2, and , for . Now, define two new partitions and as the partitions obtained by deleting the first k entries of and , respectively. That is, and , for . Then, either , and the above argument is applied to and , or else , where is defined in the statement of Lemma 2, and therefore . The proof is complete by noticing that the process must stop because has only finitely many steps. □
Example 5. The following table contains all the reciprocal sums ⟅
μ⟆
associated to the partitions :| ⟅420⟆ | ⟅320⟆ | ⟅220⟆ | ⟅110⟆ |
| | | |
| ⟅410⟆ | ⟅310⟆ | ⟅210⟆ | ⟅100⟆ |
| | | |
| ⟅400⟆ | ⟅300⟆ | ⟅200⟆ | ⟅000⟆ |
| | | |
Under the -admissible specialization , the table becomes:| ⟅420⟆ | ⟅320⟆ | ⟅220⟆ | ⟅110⟆ |
| | | |
| ⟅410⟆ | ⟅310⟆ | ⟅210⟆ | ⟅100⟆ |
| | | |
| ⟅400⟆ | ⟅300⟆ | ⟅200⟆ | ⟅000⟆ |
| | | |
We observe that the only partition whose reciprocal sum equals is .
Notice that Proposition 4 can be alternatively stated as follows.
Corollary 2. Suppose that is a partition such that is a permutation of . Then,
,
The intersection of the eigenspace of ξ with eigenvalue , and the space generated by , with , has dimension 1.
The intersection of the eigenspace of Ξ with eigenvalue , and the space generated by , with , has dimension 1.
Proof. It is easy to see that for a specialization of type the following four assertions are equivalent: is a permutation of , is a permutation of , , and . Proposition 4 allows us to complete the proof. □
5.3. On the Reciprocal Vector
In this section, we prove that, under a -admissible specialization, all the entries of are distinct. For simplicity, we denote by and the specialization by .
Define the utility function , so that, for a partition , . Define also a decreasing sequence as , with ; , for ; and . Notice this sequence splits the interval into pieces.
If , for , then and . If , and .
Let
such that
and
. Then,
Here is an example showing that the utility function h alone does not suffice to separate the values.
Example 6. Let . Then, , , and the relation implies that and . This corresponds to the quasistaircase partition , for which the values of the sequence are , and . Then, the vector of values of is There are two pairs of equal entries, however the corresponding entries of are different. For the value 0, , where . In addition, for the value , .
Proposition 5. The entries of are pairwise distinct.
Proof. Take two indices and and assume without lost of generality that . We check that the values of and are distinct. For that, it is enough to check that or . Let us analyze the differences by looking at the indices in the division of the interval given by the sequence .
If , then . Thus, . The same happens if since .
Now, suppose
, then (
7) shows that
Thus, if , then .
Consider the case ; then, and . There are two different arguments depending on whether .
If , suppose that . By Lemma 1, , for some , but and , which is a contradiction.
If
, or equivalently
, then
. If
, then
and
. In the case
, with
, it follows that
This implies , since . The similar argument applies when .
Suppose
and
. By (
7), and the fact that
,
If , then and . Otherwise, suppose and . Then, , which is impossible for □
7. Beyond the Wheel Condition
First, we recall that, for some specializations of
, the quasistaircase polynomials satisfy the HW condition, [
11]. Using an argument of dimension of eigenspaces, we show that the shifted Macdonald are homogeneous.
Theorem 3 ([
11])
. For β, s, r, k, , with , consider and the specializationwhere and is a rth root of the unity such that is a gth primitive root of the unity. The polynomial is in the kernel of when is an integer. The shifted symmetric polynomial is an eigenfunction of having the same eigenvalue as . However, from Corollary 2, the corresponding eigenspace has dimension 1, which proves the following result.
Corollary 3. Moreover, this implies that is homogeneous.
Applying Proposition 3, we obtain
Again, by Corollary 3,
is an homogeneous polynomial, and then,
Theorem 2 completes the proof of the following theorem.
Let us show this result with an example.
Example 10. For , 8. Conclusions and Perspectives
In this last section, we explore the second clustering property conjectured by Bernevig and Haldane and we present some examples that illustrate future work that can be done in this direction.
8.1. The Second Clustering Property
Most of the different variants of Macdonald polynomials presented in this paper specialize to Jack polynomials by sending
u to 1 when
and
are coprime, which corresponds to setting
and sending
to 1. Moreover, this implies also that
divides
r. In that context, Proposition 7 gives that
The fact that
divides the polynomial
is a special case of a result of [
4] [Theorem 1.1]. The following table contrasts Bernevig and Haldane notation (B-H notation) with our notation in order to transcribe the second clustering property into our notation.
| Our notation | B-H notation |
| ℓ | k |
| k | 0 |
| s | r |
| s |
| |
| |
| |
| |
| |
| y | |
We recover the equality in Equation (
1) by setting
in Equation (
9). This proves the second clustering property conjectured by Bernevig and Haldane [
2]. Furthermore, Equation (
8) is more general than those conjectured in [
2] for two reasons. First, we consider quasistaircase partitions
, with
, while only the case
was investigated in [
1,
2]. It should be interesting to know if some of these polynomials can be interpreted as wave functions in FQHT. In addition, when
, the Macdonald polynomial does not degenerate to a Jack polynomial when
u tends to 1.
More generally, the following equality is obtained from Theorem 4:
We finish this subsection by presenting more general identities involving partitions which are not quasistaircase for the considered specialization. For instance,
This formula is in fact a specialization of
Notice that this polynomial does not satisfy the HW condition. This suggests that there exists a Macdonald version of the result of [
4], Theorem 1.1.
8.2. Other Clustering and Factorizations Properties
The first and third clustering conjectures suggest that there exist many ways to factorize HW Macdonald polynomials by specializing the variables involved. Let us illustrate this remark by giving an example.
For a partition , consider the alphabet . Let be the operator that adds 2 to the ith entry of if, after this operation, the resulting vector is still a partition. We set also .
Starting with
, and by
, one obtains
The next step is more interesting because there are two kinds of specializations that provide nice factorizations:
Continuing, we get other new nice factorizations:
The computation can be graphically represented as in
Figure 5.
Using vanishing properties, it is not too difficult to show that, when
,
factorizes nicely, and that, if
is well defined, one has
This kind of formula takes place in a wider picture which will be investigated in a future paper.
8.3. More Factorizations of Nonsymmetric Macdonald Polynomials
In the preparation of this paper, the authors used experiments with symbolic computation with Maple [
43] to develop conjectures, for which the proofs presented in this paper are constructed with mathematical rigor and do not depend on computers. The experiments also resulted in some fascinating examples which as yet have not led to any guesses at possible underlying structure.
We finish this paper presenting some specializations of nonsymmetric Macdonald polynomials that factorize nicely and that are not included in the results presented.
Notice that the last example is not singular and we have
However, it is deduced from the singular polynomial , by applying the affine step twice.
Some other examples involving vectors which are not partitions are more interesting. For instance, the polynomial
is singular and we have
More general formulas for quasistaircases are also observed. For instance,
Numerical evidence suggests that one has a formula very close to those of Theorem 4 but for a specialization under the form
where
and
is a
gth primitive root of the unity.
In addition, as in
Section 8.2, we observe factorizations for other specializations of the variables
’s. For instance
The precise statements, proofs, and connection with the factorizations of symmetric Macdonald polynomials remain to be investigated.