Invariant Graph Partition Comparison Measures
Abstract
:1. Introduction
- Partition is mapped to the structurally equivalent partition .
- Partition is mapped to the identical partition .
- Because and are structurally equivalent, the RI should be one (as for Cases 1, 2 and 3) instead of .
- Comparisons of structurally different different partitions (Cases 4 and 5) and comparisons of structurally equivalent partitions (Case 6) should not result in the same value.
2. Graphs, Permutation Groups and Graph Automorphisms
- Closure:
- Unit element: The identity function acts as the neutral element:
- Inverse element: For any g in H, the inverse permutation function is the inverse of g:
- Associativity: The associative law holds:
3. Graph Partition Comparison Measures Are Not Invariant
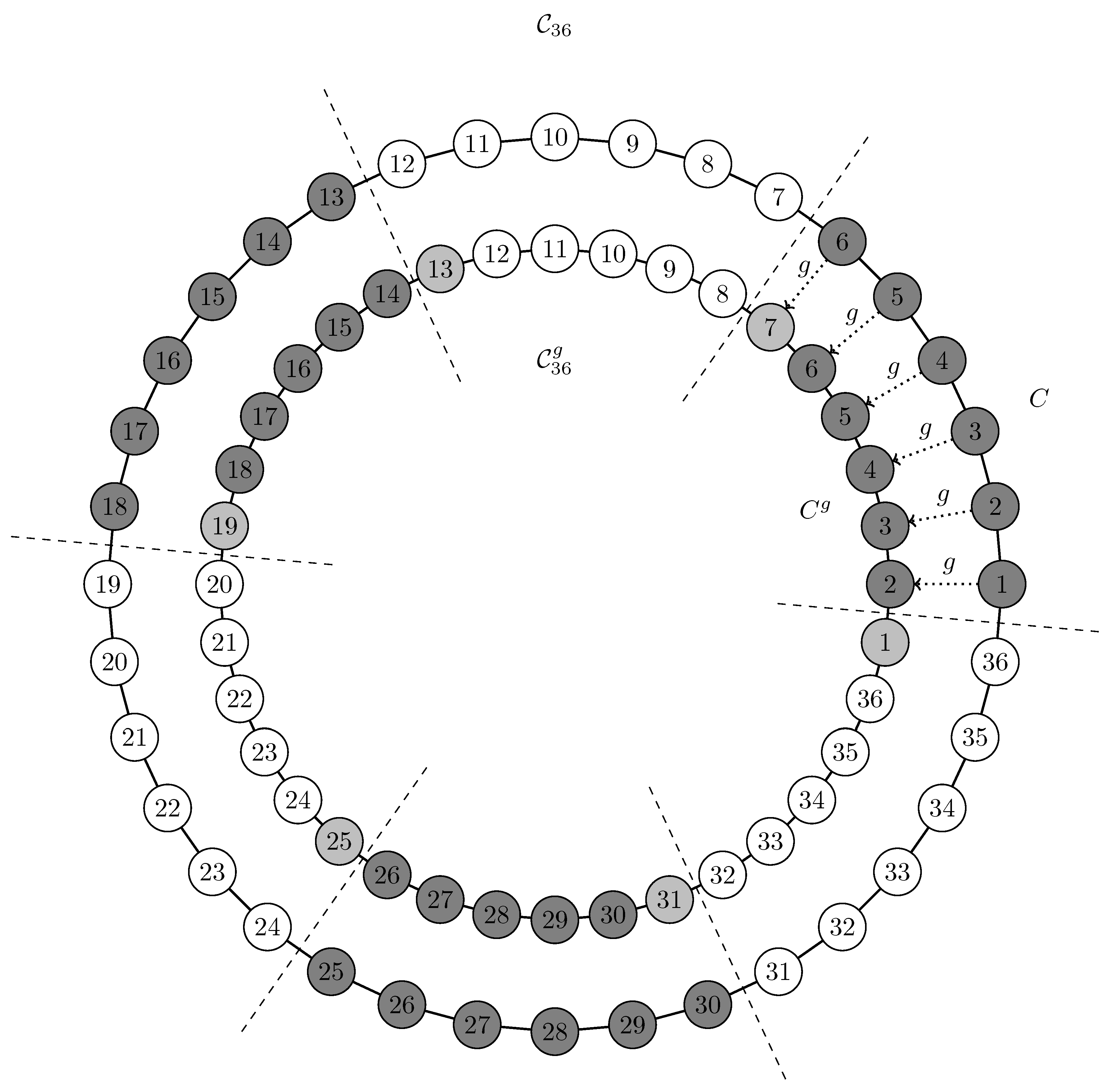
3.1. Variant 1: Construction of a Counterexample
3.2. Variant 2: Inconsistency of the Identity and the Invariance Axiom
- Since is nontrivial, a nontrivial orbit with at least two different partitions, namely and , exists because . It follows from the invariance axiom that .
- The identity axiom implies that it follows from that .
- This contradicts the assumption that and are different.
4. The Construction of Invariant Measures for Finite Permutation Groups
- We construct a pseudometric space from the images of the actions of on partitions in (Definition 1).
- We extend the metrics for partition comparison by constructing invariant metrics on the pseudo-metric space of partitions.
4.1. The Construction of the Pseudometric Space of Equivalence Classes of Graph Partitions
- Symmetry: .
- Identity: if and only if .
- Triangle inequality: .
- is a metric space with and with the function .
- is a metric space with and the function : . We construct three variants of in Section 4.2.
- is the pseudometric space with and with the metric . The partitions in S are mapped to arguments of by the transformation , which is defined as .
4.2. The Construction of Left-Invariant and Additive Measures on the Pseudometric Space of Equivalence Classes of Graph Partitions
- For , we have:by switching the reference systems. In the next sequence of equations, we establish that taking the minimum over all reference systems is equivalent to finding the minimum for one arbitrarily fixed reference system.
- For the proof of for we substitute max for min in the proof of .
- Identity: , if .
- Invariance: , for all and , .
- Symmetry: .
- Triangle inequality:
- Identity holds because of the definition of the distance between two elements in an equivalence class of the pseudometric space .
- Invariance of , and is proven by Theorems 4 and 5.
- Symmetry holds, because d is symmetric, and min, max and the average do not depend on the order of their respective arguments.
- To proof the triangular inequality, we make use of Theorems 4 and 5 and of the fact that d is a metric for which the triangular inequality holds:
- (a)
- For follows:
- (b)
- For the proof of the triangular inequality for , we substitute max for min and for in the proof of the triangular inequality for .
- (c)
- For , it follows:
5. Decomposition of Partition Comparison Measures
- In Case 1, we compare two partitions from nontrivial equivalence classes: the difference of between and indicates that the potential maximal automorphism effect is larger than the lower measure. In addition, it is also smaller (by ) than the automorphism effect in each of the equivalence classes. That is zero for the lower measure implies that the pair is a pair with the minimal distance between the equivalence classes. The fact that is the mid-point between the lower and upper measures indicates a symmetric distribution of the distances between the equivalence classes.
- That is zero for the upper measure in Case 2 means that we have found a pair with the maximal distance between the equivalence classes.
- In Case 3, we have also found a pair with maximal distance between the equivalence classes. However, the maximal potential automorphism effect is smaller than for Cases 1 and 2. In addition, the distribution of distances between the equivalence classes is asymmetric.
- Case 4 shows the comparison of a partition from a trivial with a partition from a non-trivial equivalence class. Note, that in this case, all three invariant measures, as well as coincide and that no automorphism effect exists.
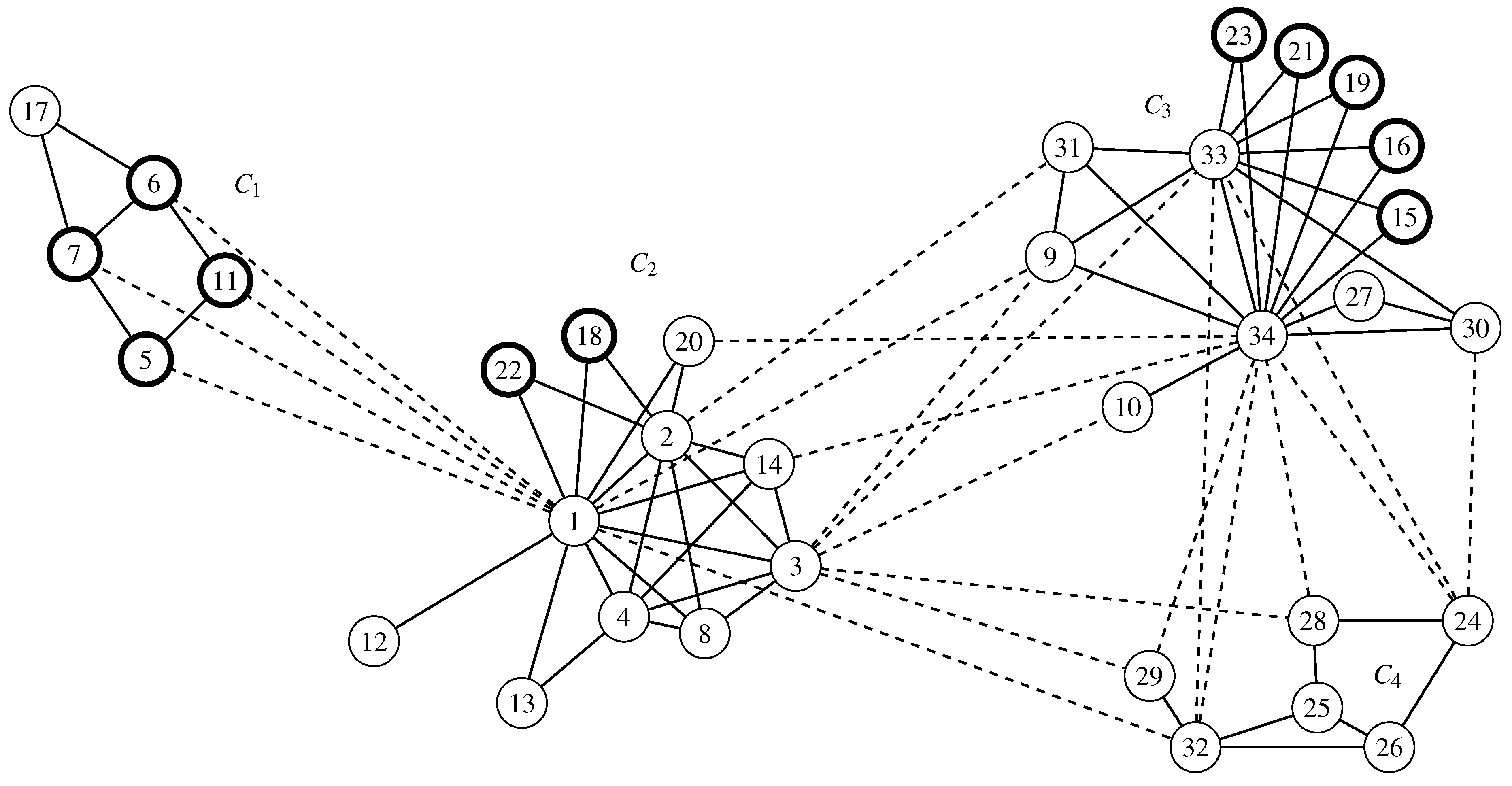
6. Invariant Measures for the Karate Graph
7. Discussion, Conclusions and Outlook
- A formal definition of partition stability, namely is stable iff .
- A proof of the non-invariance of all partition comparison measures if the automorphism group is nontrivial ().
- The construction of a pseudometric space of equivalence classes of graph partitions for three classes of invariant measures concerning finite permutation groups of graph automorphisms.
- The proof that the measures are invariant and that for these measures (after the transformation to a distance), the axioms of a metric space hold.
- The space of partitions is equipped with a metric (the original partition comparison measure) and a pseudometric (the invariant partition comparison measure).
- The decomposition of the value of a partition comparison measure into a structural part and a remainder that measures the effect of group actions.
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Modularity
Appendix B. Measures for Comparing Partitions
- Pair-counting measures.
- Set-based comparison measures.
- Information theory based measures.
Appendix B.1. Pair-Counting Measures
| Abbr. | Measure | Formula | |
|---|---|---|---|
| RI | Rand [43] | ||
| ARI | Hubert and Arabie [44] | ||
| H | Hamann [45] | ||
| CZ | Czekanowski [46] | ||
| K | Kulczynski [47] | ||
| MC | McConnaughey [48] | ||
| P | Peirce [49] | ||
| WI | Wallace [50] | ||
| WII | Wallace [50] | ||
| FM | Fowlkes and Mallows [51] | ||
| Yule [52] | |||
| SS1 | Sokal and Sneath [53] | ||
| B1 | Baulieu [54] | ||
| GL | Gower and Legendre [55] | ||
| SS2 | Sokal and Sneath [53] | ||
| SS3 | Sokal and Sneath [53] | ||
| RT | Rogers and Tanimoto [56] | ||
| GK | Goodman and Kruskal [57] | ||
| J | Jaccard [3] | ||
| RV | Robert and Escoufier [58] |
Appendix B.2. Set-Based Comparison Measures
| Abbr. | Measure | Formula | |
|---|---|---|---|
| LA | Larsen and Aone [65] | ||
| Meilǎ and Heckerman [66] | |||
| D | van Dongen [67] |
Appendix B.3. Information Theory-Based Measures
Appendix B.4. Summary
References
- Melnykov, V.; Maitra, R. CARP: Software for fishing out good clustering algorithms. J. Mach. Learn. Res. 2011, 12, 69–73. [Google Scholar]
- Bader, D.A.; Meyerhenke, H.; Sanders, P.; Wagner, D. (Eds.) 10th DIMACS Implementation Challenge—Graph Partitioning and Graph Clustering; Rutgers University, DIMACS (Center for Discrete Mathematics and Theoretical Computer Science): Piscataway, NJ, USA, 2012. [Google Scholar]
- Jaccard, P. Nouvelles recherches sur la distribution florale. Bull. Soc. Vaud. Sci. Nat. 1908, 44, 223–270. [Google Scholar]
- Horta, D.; Campello, R.J.G.B. Comparing hard and overlapping clusterings. J. Mach. Learn. Res. 2015, 16, 2949–2997. [Google Scholar]
- Romano, S.; Vinh, N.X.; Bailey, J.; Verspoor, K. Adjusting for chance clustering comparison measures. J. Mach. Learn. Res. 2016, 17, 1–32. [Google Scholar]
- Von Luxburg, U.; Williamson, R.C.; Guyon, I. Clustering: Science or art? JMLR Workshop Conf. Proc. 2011, 27, 65–79. [Google Scholar]
- Hennig, C. What are the true clusters? Pattern Recognit. Lett. 2015, 64, 53–62. [Google Scholar] [CrossRef]
- Van Craenendonck, T.; Blockeel, H. Using Internal Validity Measures to Compare Clustering Algorithms; Benelearn 2015 Poster Presentations (Online); Benelearn: Delft, The Netherlands, 2015; pp. 1–8. [Google Scholar]
- Filchenkov, A.; Muravyov, S.; Parfenov, V. Towards cluster validity index evaluation and selection. In Proceedings of the 2016 IEEE Artificial Intelligence and Natural Language Conference, St. Petersburg, Russia, 10–12 November 2016; pp. 1–8. [Google Scholar]
- MacArthur, B.D.; Sánchez-García, R.J.; Anderson, J.W. Symmetry in complex networks. Discret. Appl. Math. 2008, 156, 3525–3531. [Google Scholar] [CrossRef] [Green Version]
- Darga, P.T.; Sakallah, K.A.; Markov, I.L. Faster Symmetry Discovery Using Sparsity of Symmetries. In Proceedings of the 2008 45th ACM/IEEE Design Automation Conference, Anaheim, CA, USA, 8–13 June 2008; pp. 149–154. [Google Scholar]
- Katebi, H.; Sakallah, K.A.; Markov, I.L. Graph Symmetry Detection and Canonical Labeling: Differences and Synergies. In Turing-100. The Alan Turing Centenary; EPiC Series in Computing; Voronkov, A., Ed.; EasyChair: Manchester, UK, 2012; Volume 10, pp. 181–195. [Google Scholar]
- Ball, F.; Geyer-Schulz, A. How symmetric are real-world graphs? A large-scale study. Symmetry 2018, 10, 29. [Google Scholar] [CrossRef]
- Newman, M.E.J.; Girvan, M. Finding and evaluating community structure in networks. Phys. Rev. E 2004, 69, 026113. [Google Scholar] [CrossRef] [PubMed]
- Ovelgönne, M.; Geyer-Schulz, A. An Ensemble Learning Strategy for Graph Clustering. In Graph Partitioning and Graph Clustering; Bader, D.A., Meyerhenke, H., Sanders, P., Wagner, D., Eds.; American Mathematical Society: Providence, RI, USA, 2013; Volume 588, pp. 187–205. [Google Scholar]
- Wielandt, H. Finite Permutation Groups; Academic Press: New York, NY, USA, 1964. [Google Scholar]
- James, G.; Kerber, A. The Representation Theory of the Symmetric Group. In Encyclopedia of Mathematics and Its Applications; Addison-Wesley: Reading, MA, USA, 1981; Volume 16. [Google Scholar]
- Coxeter, H.; Moser, W. Generators and Relations for Discrete Groups. In Ergebnisse der Mathematik und ihrer Grenzgebiete; Springer: Berlin, Germany, 1965; Volume 14. [Google Scholar]
- Dixon, J.D.; Mortimer, B. Permutation Groups. In Graduate Texts in Mathematics; Springer: New York, NY, USA, 1996; Volume 163. [Google Scholar]
- Beth, T.; Jungnickel, D.; Lenz, H. Design Theory; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Erdős, P.; Rényi, A.; Sós, V.T. On a problem of graph theory. Stud. Sci. Math. Hung. 1966, 1, 215–235. [Google Scholar]
- Burr, S.A.; Erdős, P.; Spencer, J.H. Ramsey theorems for multiple copies of graphs. Trans. Am. Math. Soc. 1975, 209, 87–99. [Google Scholar] [CrossRef]
- Ball, F.; Geyer-Schulz, A. R Package Partition Comparison; Technical Report 1-2017, Information Services and Electronic Markets, Institute of Information Systems and Marketing; KIT: Karlsruhe, Germany, 2017. [Google Scholar]
- Doob, J.L. Measure Theory. In Graduate Texts in Mathematics; Springer: New York, NY, USA, 1994. [Google Scholar]
- Hausdorff, F. Set Theory, 2nd ed.; Chelsea Publishing Company: New York, NY, USA, 1962. [Google Scholar]
- Kuratowski, K. Topology Volume I; Academic Press: New York, NY, USA, 1966; Volume 1. [Google Scholar]
- Von Neumann, J. Construction of Haar’s invariant measure in groups by approximately equidistributed finite point sets and explicit evaluations of approximations. In Invariant Measures; American Mathematical Society: Providence, RI, USA, 1999; Chapter 6; pp. 87–134. [Google Scholar]
- Ball, F.; Geyer-Schulz, A. Weak invariants of actions of the automorphism group of a graph. Arch. Data Sci. Ser. A 2017, 2, 1–22. [Google Scholar]
- Zachary, W.W. An information flow model for conflict and fission in small groups. J. Anthropol. Res. 1977, 33, 452–473. [Google Scholar] [CrossRef]
- Bock, H.H. Automatische Klassifikation: Theoretische und praktische Methoden zur Gruppierung und Strukturierung von Daten; Vandenhoeck und Ruprecht: Göttingen, Germany, 1974. [Google Scholar]
- Rossi, R.; Fahmy, S.; Talukder, N. A Multi-level Approach for Evaluating Internet Topology Generators. In Proceedings of the 2013 IFIP Networking Conference, Trondheim, Norway, 2–4 June 2013; pp. 1–9. [Google Scholar]
- Rossi, R.A.; Ahmed, N.K. The Network Data Repository with Interactive Graph Analytics and Visualization. In Proceedings of the Twenty-Ninth AAAI Conference on Artificial Intelligence, Austin, TX, USA, 25–30 January 2015. [Google Scholar]
- Furst, M.; Hopcroft, J.; Luks, E. Polynomial-time Algorithms for Permutation Groups. In Proceedings of the 21st Annual Symposium on Foundations of Computer Science, Syracuse, NY, USA, 13–15 October 1980; pp. 36–41. [Google Scholar]
- McKay, B.D.; Piperno, A. Practical graph isomorphism, II. J. Symb. Comput. 2014, 60, 94–112. [Google Scholar] [CrossRef] [Green Version]
- Babai, L. Graph isomorphism in quasipolynomial time. arXiv, 2015; arXiv:1512.03547. [Google Scholar]
- Fortunato, S.; Barthélemy, M. Resolution limit in community detection. Proc. Natl. Acad. Sci. USA 2007, 104, 36–41. [Google Scholar] [CrossRef] [PubMed]
- Lancichinetti, A.; Fortunato, S. Limits of modularity maximization in community detection. Phys. Rev. E 2011, 84, 66122. [Google Scholar] [CrossRef] [PubMed]
- Geyer-Schulz, A.; Ovelgönne, M.; Stein, M. Modified randomized modularity clustering: Adapting the resolution limit. In Algorithms from and for Nature and Life; Lausen, B., Van den Poel, D., Ultsch, A., Eds.; Studies in Classification, Data Analysis, and Knowledge Organization; Springer International Publishing: Heidelberg, Germany, 2013; pp. 355–363. [Google Scholar]
- Meilǎ, M. Comparing clusterings—An information based distance. J. Multivar. Anal. 2007, 98, 873–895. [Google Scholar] [CrossRef]
- Youness, G.; Saporta, G. Some measures of agreement between close partitions. Student 2004, 51, 1–12. [Google Scholar]
- Denœud, L.; Guénoche, A. Comparison of distance indices between partitions. In Data Science and Classification; Batagelj, V., Bock, H.H., Ferligoj, A., Žiberna, A., Eds.; Studies in Classification, Data Analysis, and Knowledge Organization; Springer: Berlin/Heidelberg, Germany, 2006; pp. 21–28. [Google Scholar]
- Albatineh, A.N.; Niewiadomska-Bugaj, M.; Mihalko, D. On similarity indices and correction for chance agreement. J. Classif. 2006, 23, 301–313. [Google Scholar] [CrossRef]
- Rand, W.M. Objective criteria for the evaluation of clustering algorithms. J. Am. Stat. Assoc. 1971, 66, 846–850. [Google Scholar] [CrossRef]
- Hubert, L.; Arabie, P. Comparing partitions. J. Classif. 1985, 2, 193–218. [Google Scholar] [CrossRef]
- Hamann, U. Merkmalsbestand und Verwandtschaftsbeziehungen der Farinosae: Ein Beitrag zum System der Monokotyledonen. Willdenowia 1961, 2, 639–768. [Google Scholar]
- Czekanowski, J. “Coefficient of Racial Likeness” und “Durchschnittliche Differenz”. Anthropol. Anz. 1932, 9, 227–249. [Google Scholar]
- Kulczynski, S. Zespoly roslin w Pieninach. Bull. Int. Acad. Pol. Sci. Lett. 1927, 2, 57–203. [Google Scholar]
- McConnaughey, B.H. The determination and analysis of plankton communities. Mar. Res. 1964, 1, 1–40. [Google Scholar]
- Peirce, C.S. The numerical measure of the success of predictions. Science 1884, 4, 453–454. [Google Scholar] [CrossRef] [PubMed]
- Wallace, D.L. A method for comparing two hierarchical clusterings: Comment. J. Am. Stat. Assoc. 1983, 78, 569–576. [Google Scholar] [CrossRef]
- Fowlkes, E.B.; Mallows, C.L. A method for comparing two hierarchical clusterings. J. Am. Stat. Assoc. 1983, 78, 553–569. [Google Scholar] [CrossRef]
- Yule, G.U. On the association of attributes in statistics: With illustrations from the material of the childhood society. Philos. Trans. R. Soc. A 1900, 194, 257–319. [Google Scholar] [CrossRef]
- Sokal, R.R.; Sneath, P.H.A. Principles of Numerical Taxonomy; W. H. Freeman: San Francisco, CA, USA; London, UK, 1963. [Google Scholar]
- Baulieu, F.B. A classification of presence/absence based dissimilarity coefficients. J. Classif. 1989, 6, 233–246. [Google Scholar] [CrossRef]
- Gower, J.C.; Legendre, P. Metric and euclidean properties of dissimilarity coefficients. J. Classif. 1986, 3, 5–48. [Google Scholar] [CrossRef]
- Rogers, D.J.; Tanimoto, T.T. A computer program for classifying plants. Science 1960, 132, 1115–1118. [Google Scholar] [CrossRef] [PubMed]
- Goodman, L.A.; Kruskal, W.H. Measures of association for cross classifications. J. Am. Stat. Assoc. 1954, 49, 732–764. [Google Scholar]
- Robert, P.; Escoufier, Y. A unifying tool for linear multivariate statistical methods: The RV-coefficient. J. R. Stat. Soc. Ser. C 1976, 25, 257–265. [Google Scholar] [CrossRef]
- Russel, P.F.; Rao, T.R. On habitat and association of species of anopheline larvae in south-eastern madras. J. Malar. Inst. India 1940, 3, 153–178. [Google Scholar]
- Mirkin, B.G.; Chernyi, L.B. Measurement of the distance between partitions of a finite set of objects. Autom. Remote Control 1970, 31, 786–792. [Google Scholar]
- Hilbert, D. Gesammelte Abhandlungen von Hermann Minkowski, Zweiter Band; Number 2; B. G. Teubner: Leipzig, UK; Berlin, Germany, 1911. [Google Scholar]
- Pearson, K. On the coefficient of racial likeness. Biometrika 1926, 18, 105–117. [Google Scholar] [CrossRef]
- Lerman, I.C. Comparing Partitions (Mathematical and Statistical Aspects). In Classification and Related Methods of Data Analysis; Bock, H.H., Ed.; North-Holland: Amsterdam, The Netherlands, 1988; pp. 121–132. [Google Scholar]
- Fager, E.W.; McGowan, J.A. Zooplankton species groups in the north pacific co-occurrences of species can be used to derive groups whose members react similarly to water-mass types. Science 1963, 140, 453–460. [Google Scholar] [CrossRef] [PubMed]
- Larsen, B.; Aone, C. Fast and Effective Text Mining Using Linear-time Document Clustering. In Proceedings of the Fifth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Diego, CA, USA, 15–18 August 1999; ACM: New York, NY, USA, 1999; pp. 16–22. [Google Scholar]
- Meilǎ, M.; Heckerman, D. An experimental comparison of model-based clustering methods. Mach. Learn. 2001, 42, 9–29. [Google Scholar] [CrossRef]
- Van Dongen, S. Performance Criteria for Graph Clustering and Markov Cluster Experiments; Technical Report INS-R 0012; CWI (Centre for Mathematics and Computer Science): Amsterdam, The Netherlands, 2000. [Google Scholar]
- Vinh, N.X.; Epps, J.; Bailey, J. Information theoretic measures for clusterings comparison: Variants, properties, normalization and correction for chance. J. Mach. Learn. Res. 2010, 11, 2837–2854. [Google Scholar]
- Meilǎ, M. Comparing clusterings by the variation of information. In Learning Theory and Kernel Machines; Schölkopf, B., Warmuth, M.K., Eds.; Number 2777 in Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2003; pp. 173–187. [Google Scholar]
- Danon, L.; Díaz-Guilera, A.; Duch, J.; Arenas, A. Comparing community structure identification. J. Stat. Mech. Theory Exp. 2005, 2005, P09008. [Google Scholar] [CrossRef]
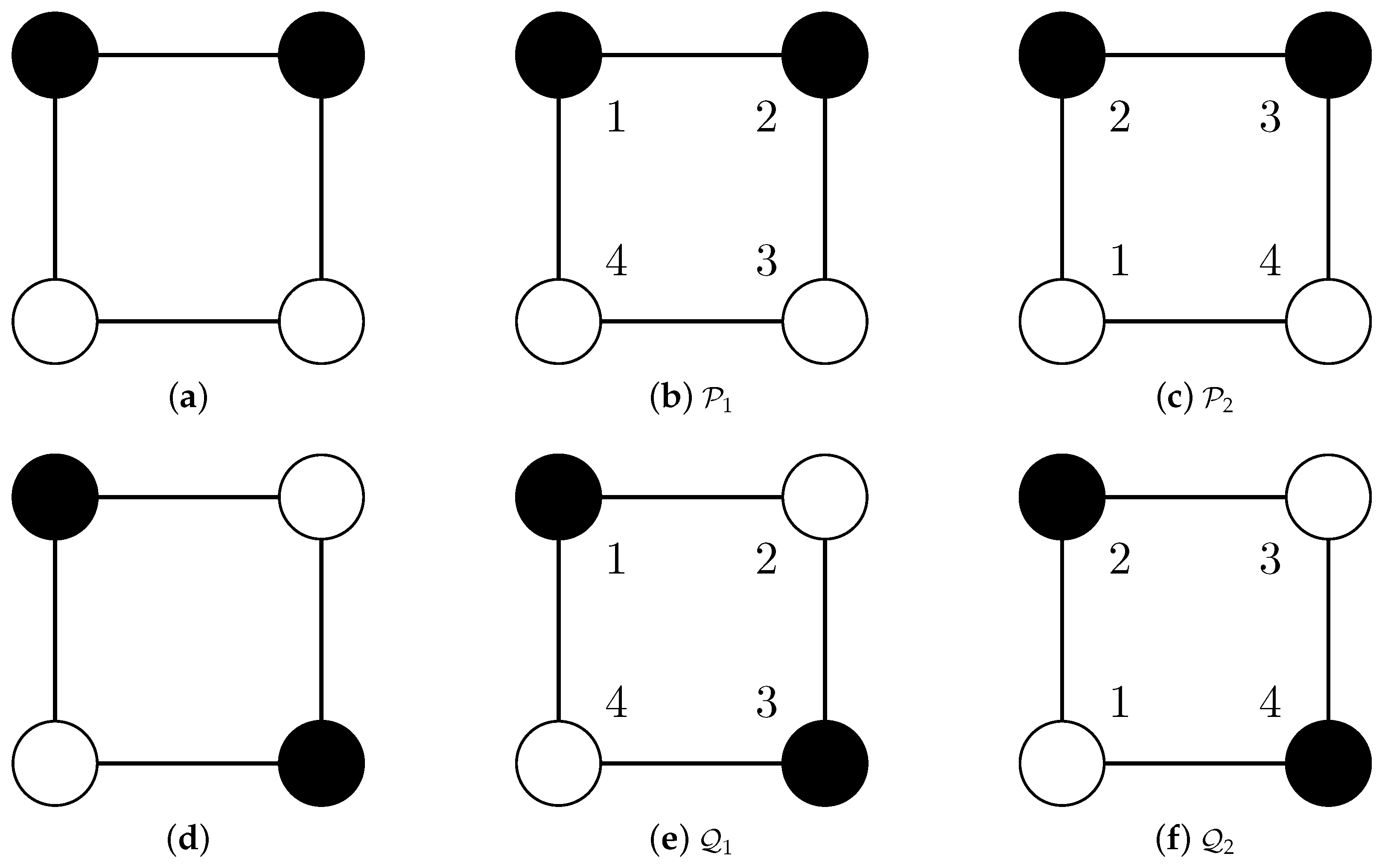
| Case | Compared Partitions | Relation | RI | ||||
|---|---|---|---|---|---|---|---|
| 1 | = | 2 | 0 | 0 | 4 | 1 | |
| 2 | = | 2 | 0 | 0 | 4 | 1 | |
| 3 | or or | = | 2 | 0 | 0 | 4 | 1 |
| 4 | or | ≠ | 0 | 2 | 2 | 2 | |
| 5 | or | ≠ | 0 | 2 | 2 | 2 | |
| 6 | ∼ | 0 | 2 | 2 | 2 |
| Permutation | |||
|---|---|---|---|
| Measure | with for k: | |||||
|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | |
| Pair counting measures (; see Table A1 and Table A2) | ||||||
| RI | ||||||
| ARI | ||||||
| H | ||||||
| CZ | ||||||
| K | ||||||
| MC | ||||||
| P | ||||||
| WI | ||||||
| WII | ||||||
| FM | ||||||
| SS1 | ||||||
| B1 | ||||||
| GL | ||||||
| SS2 | ||||||
| SS3 | ||||||
| RT | ||||||
| GK | ||||||
| J | ||||||
| RV | ||||||
| RR | ||||||
| M | 12 | 19 | 21 | 19 | 12 | |
| Mi | ||||||
| Pe | ||||||
| B2 | ||||||
| LI | 2 | 1 | 1 | |||
| NLI | ||||||
| FMG | ||||||
| Set-based comparison measures (see Table A3) | ||||||
| LA | ||||||
| D | 1 | 2 | 3 | 2 | 1 | |
| Information theory-based measures (see Table A4) | ||||||
| MI | ||||||
| NMI (max) | ||||||
| NMI (min) | ||||||
| NMI () | ||||||
| VI | ||||||
| Q | |||
|---|---|---|---|
| Partition type , , | |||
| Partition type , , | |||
| Partition type , | |||
| 0 | |||
| Partition type , , | |||
| 0 | |||
| Partition type , , | |||
| Partition type , , | |||
| Partition type , , | |||
| 0 |
| Case | ||||||
|---|---|---|---|---|---|---|
| 1 | 0.3 | 0.3 | 0.0 | |||
| 0.3 | 0.5 | −0.2 | ||||
| 0.3 | 0.7 | −0.4 | ||||
| 2 | 0.6 | 0.2 | 0.4 | |||
| 0.6 | 0.4 | 0.2 | ||||
| 0.6 | 0.6 | 0.0 | ||||
| 3 | 0.3 | 0.1 | 0.2 | |||
| 0.3 | 0.25 | 0.05 | ||||
| 0.3 | 0.3 | 0.0 | ||||
| 4 | 0.3 | 0.3 | 0.0 | |||
| 0.3 | 0.3 | 0.0 | ||||
| (, stable) | 0.3 | 0.3 | 0.0 |
| 1 | 20 | 20 | |
| stable? | yes | no | no |
| Measure | |||
|---|---|---|---|
| d | |||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ball, F.; Geyer-Schulz, A. Invariant Graph Partition Comparison Measures. Symmetry 2018, 10, 504. https://doi.org/10.3390/sym10100504
Ball F, Geyer-Schulz A. Invariant Graph Partition Comparison Measures. Symmetry. 2018; 10(10):504. https://doi.org/10.3390/sym10100504
Chicago/Turabian StyleBall, Fabian, and Andreas Geyer-Schulz. 2018. "Invariant Graph Partition Comparison Measures" Symmetry 10, no. 10: 504. https://doi.org/10.3390/sym10100504




