Solution of Fractional Differential Equation Systems and Computation of Matrix Mittag–Leffler Functions
Abstract
:1. Introduction
2. Solutions of System of Fractional Differential Equations of Commensurate Orders
3. The System of Fractional Differential Equations of Incommensurate Orders
4. Computation of Matrix Mittag–Leffler Functions
4.1. Method by the Jordan Canonical Matrix
4.2. Method by the Minimal Polynomial or Eigenpolynomial
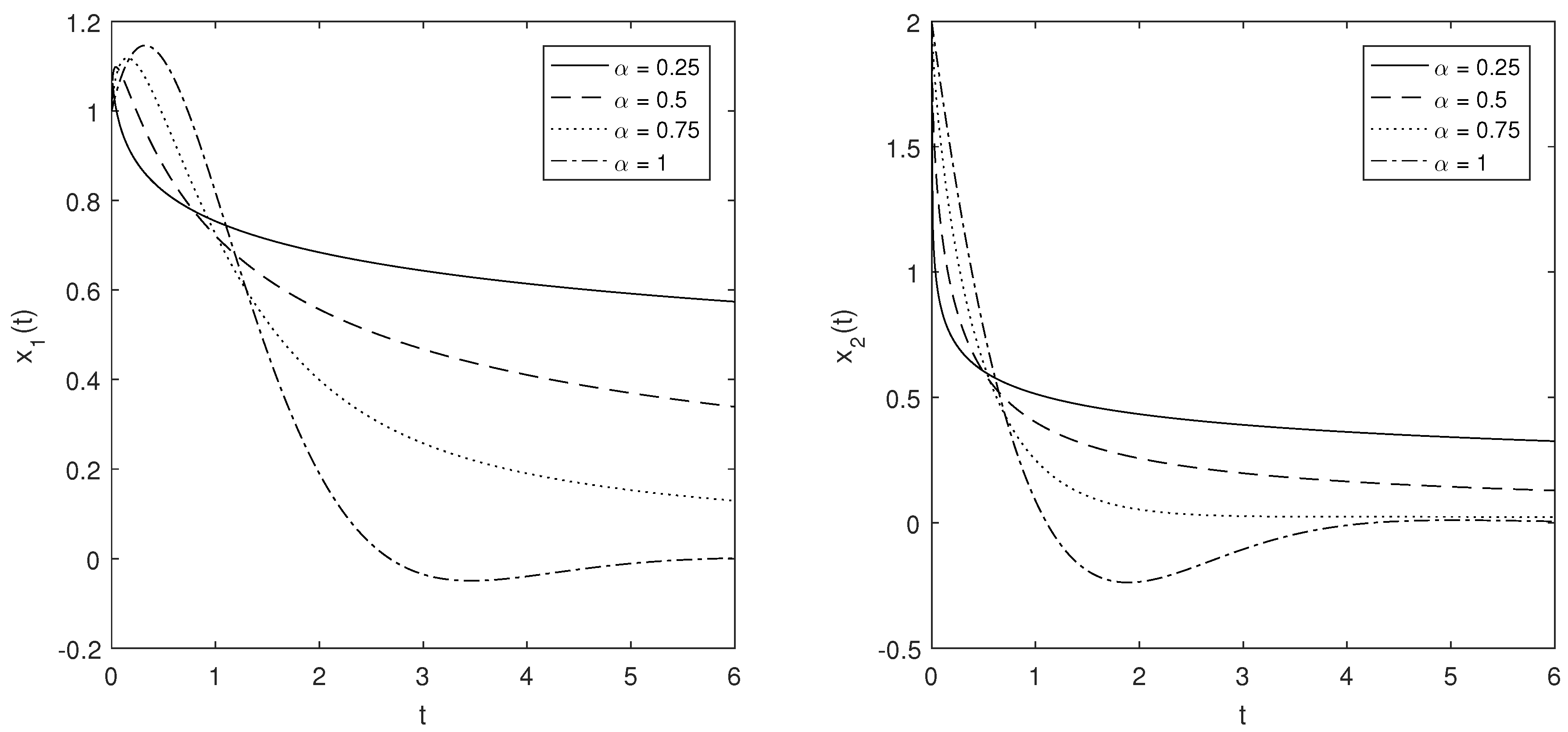
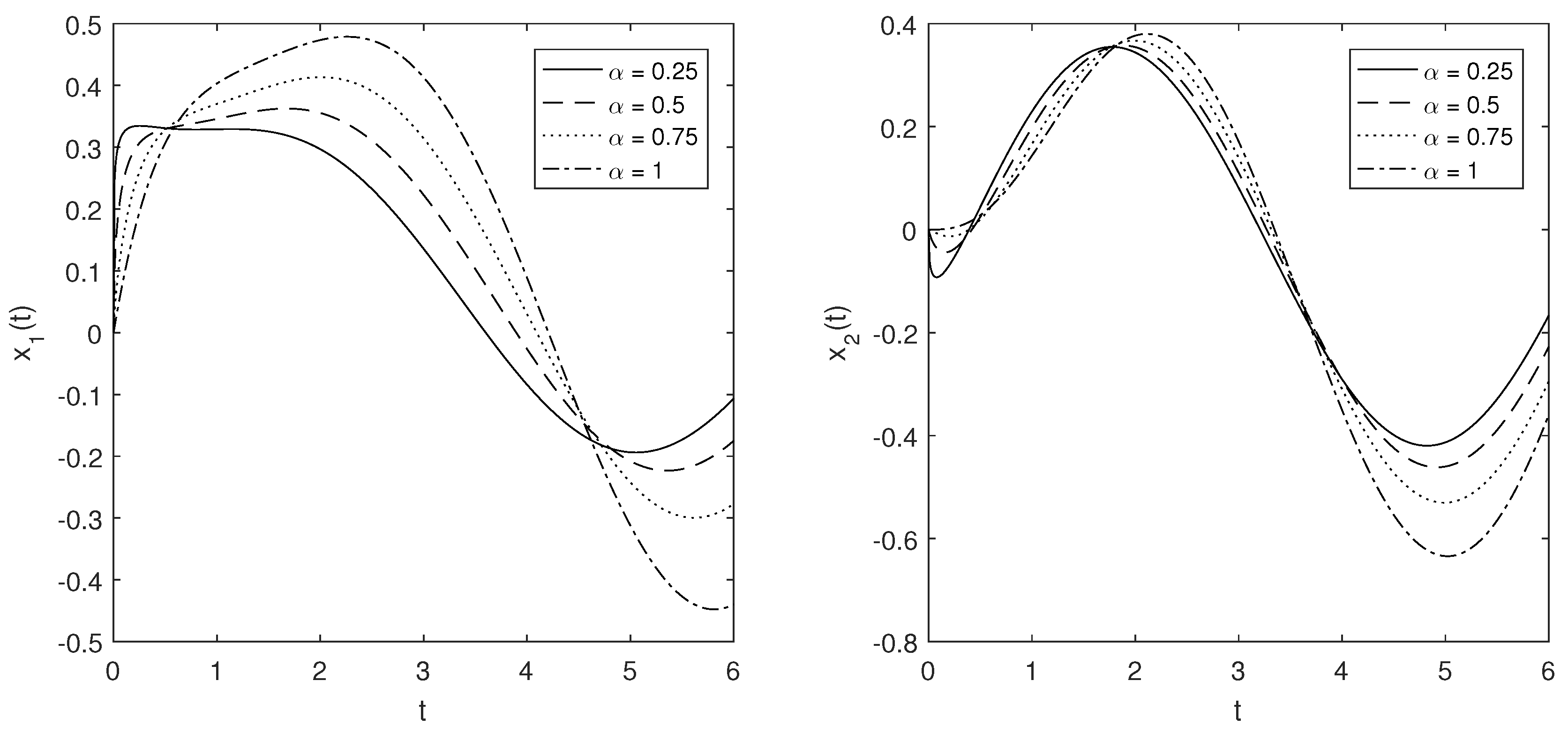
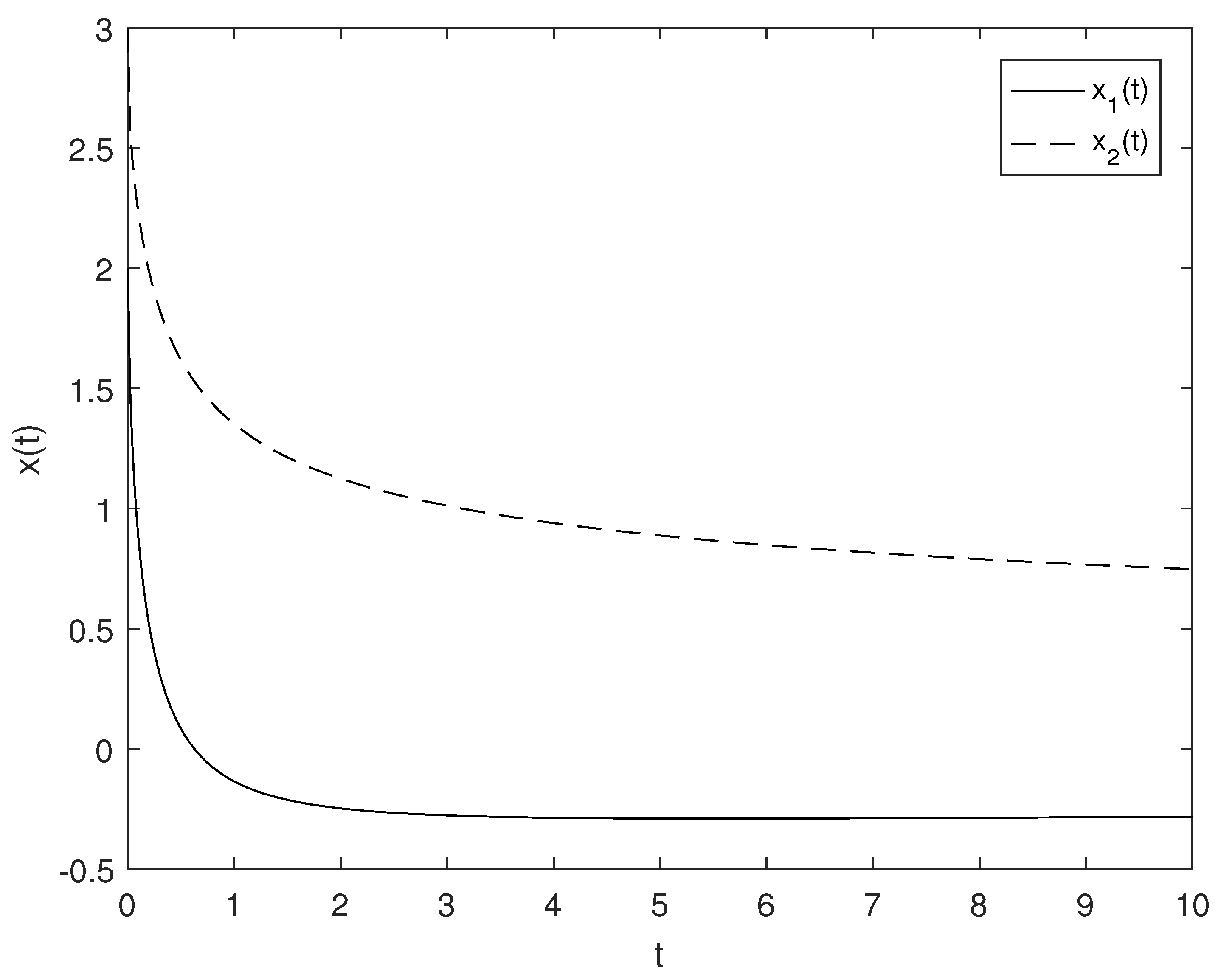
5. Numerical Examples
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Oldham, K.B.; Spanier, J. The Fractional Calculus; Academic: New York, NY, USA, 1974. [Google Scholar]
- Ross, B. (Ed.) Fractional Calculus and Its Applications (Lecture Notes in Mathematics 457); Springer: Berlin, UK, 1975. [Google Scholar]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; Wiley: New York, NY, USA, 1993. [Google Scholar]
- Carpinteri, A.; Mainardi, F. (Eds.) Fractals and Fractional Calculus in Continuum Mechanics; Springer: Wien, Austria; New York, NY, USA, 1997. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic: San Diego, CA, USA, 1999. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Diethelm, K. The Analysis of Fractional Differential Equations; Springer: Berlin, UK, 2010. [Google Scholar]
- Mainardi, F. Fractional Calculus and Waves in Linear Viscoelasticity; Imperial College: London, UK, 2010. [Google Scholar]
- Mainardi, F.; Spada, G. Creep, relaxation and viscosity properties for basic fractional models in rheology. Eur. Phys. J. Spec. Top. 2011, 193, 133–160. [Google Scholar] [CrossRef] [Green Version]
- Li, M. Three classes of fractional oscillators. Symmetry 2018, 10, 40. [Google Scholar] [CrossRef]
- Mainardi, F. Fractional relaxation-oscillation and fractional diffusion-wave phenomena. Chaos Solitons Fractals 1996, 7, 1461–1477. [Google Scholar] [CrossRef]
- Metzler, R.; Klafter, J. The random walk’s guide to anomalous diffusion: A fractional dynamics approach. Phys. Rep. 2000, 339, 1–77. [Google Scholar] [CrossRef]
- Duan, J.S. Time- and space-fractional partial differential equations. J. Math. Phys. 2005, 46, 13504–13511. [Google Scholar] [CrossRef]
- Wu, G.C.; Baleanu, D.; Zeng, S.D.; Deng, Z.G. Discrete fractional diffusion equation. Nonlinear Dyn. 2015, 80, 281–286. [Google Scholar] [CrossRef]
- Monje, C.A.; Chen, Y.Q.; Vinagre, B.M.; Xue, D.; Feliu, V. Fractional-Order Systems and Controls, Fundamentals and Applications; Springer: London, UK, 2010. [Google Scholar]
- Wu, G.C.; Baleanu, D.; Xie, H.P.; Chen, F.L. Chaos synchronization of fractional chaotic maps based on the stability condition. Physica A 2016, 460, 374–383. [Google Scholar] [CrossRef]
- Cao, W.; Xu, Y.; Zheng, Z. Existence results for a class of generalized fractional boundary value problems. Adv. Differ. Equ. 2017, 2017, 348. [Google Scholar] [CrossRef]
- Băleanu, D.; Diethelm, K.; Scalas, E.; Trujillo, J.J. Fractional Calculus Models and Numerical Methods; Series on Complexity, Nonlinearity and Chaos; World Scientific: Boston, UK, 2012. [Google Scholar]
- Li, M.; Lim, S.C.; Chen, S. Exact solution of impulse response to a class of fractional oscillators and its stability. Math. Probl. Eng. 2011, 2011, 657839. [Google Scholar] [CrossRef]
- Li, C.; Zeng, F. Numerical Methods for Fractional Calculus; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Jafari, H.; Khalique, C.M.; Ramezani, M.; Tajadodi, H. Numerical solution of fractional differential equations by using fractional B-spline. Cent. Eur. J. Phys. 2013, 11, 1372–1376. [Google Scholar] [CrossRef] [Green Version]
- Mainardi, F.; Gorenflo, R. On Mittag–Leffler-type functions in fractional evolution processes. J. Comput. Appl. Math. 2000, 118, 283–299. [Google Scholar] [CrossRef]
- Garra, R.; Gorenflo, R.; Polito, F.; Tomovski, Ž. Hilfer-Prabhakar derivatives and some applications. Appl. Math. Comput. 2014, 242, 576–589. [Google Scholar] [CrossRef]
- Garrappa, R.; Mainardi, F.; Guido, M. Models of dielectric relaxation based on completely monotone functions. Frac. Calc. Appl. Anal. 2016, 19, 1105–1160. [Google Scholar] [CrossRef]
- Fernandez, A.; Baleanu, D.; Srivastava, H.M. Series representations for fractional-calculus operators involving generalised Mittag–Leffler functions. Commun. Nonlinear Sci. Numer. Simul. 2019, 67, 517–527. [Google Scholar] [CrossRef]
- Srivastava, H.M. Some families of Mittag–Leffler type functions and associated operators of fractional calculus. TWMS J. Pure Appl. Math. 2016, 7, 123–145. [Google Scholar]
- Tomovski, Z.; Hilfer, R.; Srivastava, H.M. Fractional and operational calculus with generalized fractional derivative operators and Mittag–Leffler type functions. Integral Transform. Spec. Funct. 2010, 21, 797–814. [Google Scholar] [CrossRef]
- Atanackovic, T.M.; Stankovic, B. On a system of differential equations with fractional derivatives arising in rod theory. J. Phys. A 2004, 37, 1241–1250. [Google Scholar] [CrossRef]
- Garrappa, R. Exponential integrators for time-fractional partial differential equations. Eur. Phys. J. Spec. Top. 2013, 222, 1915–1927. [Google Scholar] [CrossRef]
- Daftardar-Gejji, V.; Babakhani, A. Analysis of a system of fractional differential equations. J. Math. Anal. Appl. 2004, 293, 511–522. [Google Scholar] [CrossRef]
- Deng, W.; Li, C.; Lü, J. Stability analysis of linear fractional differential system with multiple time delays. Nonlinear Dyn. 2007, 48, 409–416. [Google Scholar] [CrossRef]
- Charef, A.; Boucherma, D. Analytical solution of the linear fractional system of commensurate order. Comput. Math. Appl. 2011, 62, 4415–4428. [Google Scholar] [CrossRef]
- Duan, J.S.; Fu, S.Z.; Wang, Z. Solution of linear system of fractional differential equations. Pac. J. Appl. Math. 2013, 5, 93–106. [Google Scholar]
- Daftardar-Gejji, V.; Jafari, H. Adomian decomposition: A tool for solving a system of fractional differential equations. J. Math. Anal. Appl. 2005, 301, 508–518. [Google Scholar] [CrossRef]
- Duan, J. A generalization of the Mittag–Leffler function and solution of system of fractional differential equations. Adv. Differ. Equ. 2018, 2018, 239. [Google Scholar] [CrossRef]
- Garrappa, R.; Moret, I.; Popolizio, M. On the time-fractional Schrödinger equation: Theoretical analysis and numerical solution by matrix Mittag–Leffler functions. Comput. Math. Appl. 2017, 74, 977–992. [Google Scholar] [CrossRef]
- Moret, I.; Novati, P. On the convergence of Krylov subspace methods for matrix Mittag–Leffler functions. SIAM J. Numer. Anal. 2011, 49, 2144–2164. [Google Scholar] [CrossRef]
- Matychyn, I.; Onyshchenko, V. Matrix Mittag–Leffler function in fractional systems and its computation. Bull. Pol. Acad. Sci. Tech. Sci. 2018, 66, 495–500. [Google Scholar]
- Garrappa, R.; Popolizio, M. Computing the matrix Mittag–Leffler function with applications to fractional calculus. J. Sci. Comput. 2018, 77, 129–153. [Google Scholar] [CrossRef]
- Garrappa, R. Numerical evaluation of two and three parameter Mittag–Leffler functions. SIAM J. Numer. Anal. 2015, 53, 1350–1369. [Google Scholar] [CrossRef]
- Garrappa, R.; Popolizio, M. Generalized exponential time differencing methods for fractional order problems. Comput. Math. Appl. 2011, 62, 876–890. [Google Scholar] [CrossRef]
- Popolizio, M. Numerical solution of multiterm fractional differential equations using the matrix Mittag–Leffler functions. Mathematics 2018, 6, 7. [Google Scholar] [CrossRef]
- Horn, R.A.; Johnson, C.R. Matrix Analysis, 2nd ed.; Cambridge University: New York, NY, USA, 2013. [Google Scholar]
- Podlubny, I. Mittag–Leffler function; Calculates the Mittag–Leffler function with desired accuracy. MATLAB Central/File Exchange (Updated September 2012), version 1.2.0.0; Available online: https://www.mathworks.com/matlabcentral/fileexchange/8738-mittag-leffler-function (accessed on 14 October 2018).
- Garrappa, R. The Mittag–Leffler function; Evaluation of the Mittag–Leffler function with 1, 2 or 3 parameters. MATLAB Central/File Exchange (Updated December 2015), version 1.3.0.0; Available online: https://au.mathworks.com/matlabcentral/fileexchange/48154-the-mittag-leffler-function (accessed on 14 October 2018).
- Higham, N.J. Functions of Matrices: Theory and Computation; SIAM: Philadephia, PA, USA, 2008. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duan, J.; Chen, L. Solution of Fractional Differential Equation Systems and Computation of Matrix Mittag–Leffler Functions. Symmetry 2018, 10, 503. https://doi.org/10.3390/sym10100503
Duan J, Chen L. Solution of Fractional Differential Equation Systems and Computation of Matrix Mittag–Leffler Functions. Symmetry. 2018; 10(10):503. https://doi.org/10.3390/sym10100503
Chicago/Turabian StyleDuan, Junsheng, and Lian Chen. 2018. "Solution of Fractional Differential Equation Systems and Computation of Matrix Mittag–Leffler Functions" Symmetry 10, no. 10: 503. https://doi.org/10.3390/sym10100503
APA StyleDuan, J., & Chen, L. (2018). Solution of Fractional Differential Equation Systems and Computation of Matrix Mittag–Leffler Functions. Symmetry, 10(10), 503. https://doi.org/10.3390/sym10100503





