Topological Characterizations and Index-Analysis of New Degree-Based Descriptors of Honeycomb Networks

Abstract

Topological indices and connectivity polynomials are invariants of molecular graphs. These invariants have the tendency of predicting the properties of the molecular structures. The honeycomb network structure is an important type of benzene network. In the present article, new topological characterizations of honeycomb networks are given in the form of degree-based descriptors. In particular, we compute Zagreb and Forgotten polynomials and some topological indices such as the hyper-Zagreb index, first and second multiple Zagreb indices and the Forgotten index, F. We, for the first time, determine some regularity indices such as the Albert index, Bell index and $IRM(G)$ index, as well as the F-index of the complement of the honeycomb network and several co-indices related to this network without considering the graph of its complement or even the line graph. These indices are useful for correlating the physio-chemical properties of the honeycomb network. We also give a graph theoretic analysis of some indices against the dimension of this network.

1. Introduction

Chemical graph theory relates the topology of hydrogen-depleted molecular graphs of chemical structures with physio-chemical properties. Some basic tools used so far are characteristic polynomials of different matrices relating to these graphs, topological indices and connectivity polynomials. There has been an urge to find a general polynomial that can capture almost complete information about the properties of a structure. The first attempt was carried out by Weiner when he defined the pass number to determine properties such as boiling point, heats of formation, chromatic retention time and strain energy [1]. In 1971, Hosoya proposed the Hosoya index and also redefined the pass number W of Wiener by using the distance matrix [2]. Although Wiener’s original definition was applicable only to acyclic graphs and did not draw the attention of chemists at all, Hosoya’s paper shone a spotlight on it. Further, in 1988, Hosoya wrote another paper to elaborate the definition of W by proposing the Wiener polynomial, which, however, is now known as the Hosoya polynomial according to Gutman [3]. The next addition is the M-polynomial, which plays the same role in parallel with the Hosoya polynomial. This polynomial determines degree-based indices easily after applying differential and integral operators [4]. The authors in [5,6,7,8,9,10] computed the M-polynomial and related topological indices of nanostar dendrimers, titania and polyhex nanotubes, V-phenylenic nanotubes and nanotori, hex-derived networks and zigzag and rhombic benzenoid systems. This polynomial is considered as the most general polynomial developed till now and is rich in determining degree-based indices of molecular graphs.

Let us denote a simple, connected graph by $G=(V,E)$ with vertex set $V(G)$ and edge set $E(G)$. Graph $G=(V,E)$ is said to be connected if there is a connection between any pair of vertices in G. The number of vertices in a graph represents its order, the number of edges its size and the number of edges connected to a single vertex the degree of that vertex. The topological index is an invariant of the molecular graph, which preserves the topological properties of the structure. The degree-based topological index usually encodes important topological properties of the structure, which play a significant role in determining the physio-chemical properties of the molecules under discussion. These indices are also effectively utilized in quantitative structure-activity relationships (QSARs) and has many applications in risk assessment, toxicity prediction, regularity decisions, drug discovery and lead optimization [2,11,12,13]. Networks as special kind of graphs are used in drug design, computer networking and the representation of chemical structures. In the present article, new topological characterizations of the honeycomb network are given in the form of degree-based descriptors.

1.1. Connectivity Polynomials and Degree-Based Descriptors

Here, we give brief overview of some connectivity polynomials and degree-based descriptors. We reserve $d(t)$ for the degree of vertex t and $M_1$, $M_2$ for the first and second Zagreb indices. The authors in [14] introduced the concept of first and second Zagreb polynomials as:

$$M_1(G,x)={\sum }_{xyϵE(G)}{x}^{[d(x)+d(y)]},$$

$$M_2(G,x)={\sum }_{xyϵE(G)}{x}^{[d(x)\times d(y)]}$$

.

In fact, these polynomials are used to determine Zagreb indices. In 2015, Forgotten index $F(G)$ and Forgotten polynomial $F(G,x)$ were re-introduced by Furtula and Gutman [15] as:

$$F(G)={\sum }_{xyϵE(G)}[d{(x)}^2+d{(y)}^2],$$

$$F(G,x)={\sum }_{xyϵE(G)}{x}^{[d{(x)}^2+d{(y)}^2]}.$$

These indices are also correlated with some chemical properties relating to the energies of molecular graphs. The authors in [16] proved that $M_1+cF$ generates a relatively more accurate model of the chemical properties of alkanes. In 2013, Shirdel et al. introduced a new degree-based Zagreb index named the hyper-Zagreb index $HM(G)$ [17], defined as:

$$HM(G)={\sum }_{xyϵE(G)}{[d(x)+d(y)]}^2,$$

The first and second multiple Zagreb indices $P{M}_1(G)$, $P{M}_2(G)$ were introduced by Ghorbani et al. in 2012 [18] as:

$$P{M}_1(G)={\prod }_{xyϵE(G)}[d(x)+d(y)],$$

$$P{M}_2(G)={\prod }_{xyϵE(G)}[d(x)\times d(y)]$$

.

The hyper-Zagreb index, first multiple Zagreb index, second multiple Zagreb index and Zagreb polynomials are applied to predict the bioactivity of a nano-structure [19]. The authors in [20] introduced Albertson index $A(G)$ to determine the irregularity of a graph as:

$$A(G)={\sum }_{xyϵE(G)}|d(x)-d(y)|,$$

and the Bell index $B(G)$ [21],

$$B(G)={\sum }_{xϵV(G)}{(d(x)-\frac{2m}{n})}^2,$$

where m is the size and n the order of G.

$IRM(G)$ is defined as:

$$IRM(G)={\sum }_{xyϵE(G)}{[d(x)-d(y)]}^2.$$

Albertson, Bell and $IRM$ indices measure the irregularities of the graph. The reformulated Zagreb index was introduced by Milicevic et al. in 2004 [22] as:

$$M_1(L(G))={\sum }_{xyϵE(G)}{[d(x)+d(y)-2]}^2$$

.

This index is actually the ordinary first Zagreb index of the line graph of G. Line graphs have useful applications in chemistry. Heilbronner et al. proved that the eigen values relating to line graph of the hydrogen-filled molecular graph are linearly related to the s-electron energy levels of the corresponding saturated hydrocarbon [23,24].

In 2006, Doslic [25] gave the concept of the first and second Zagreb co-indices, which are defined as:

$$\overline{M_1}(G)={\sum }_{xy\neg ϵE(G)}[d(x)+d(y)],$$

$$\overline{M_2}(G)={\sum }_{xy\neg ϵE(G)}d(x)d(y),$$

In [16], the authors gave some results related to first and second Zagreb co-indices given as:

$$\overline{M_1}(G)=2m(n-1)-M_1(G),$$

$$\overline{M_2}(G)=2m^2-\frac{1}{2}{M}_1(G)-M_2(G),$$

The F-coindex is defined as:

$$\overline{F}(G)={\sum }_{xy\neg ϵE(G)}[d{(x)}^2+d{(y)}^2],$$

In [16], the author computed some results related to the F-coindex, which are given as:

$$F(\overline{G})=n{(n-1)}^3-6m{(n-1)}^2+3(n-1)M_1(G)-F(G),$$

$$\overline{F}(G)=(n-1)M_1(G)-F(G),$$

$$\overline{F}(\overline{G})=2m{(n-1)}^2-2(n-1)M_1(G)+F(G).$$

1.2. Honeycomb Network, $H{C}_n$ for $n>1$

In the present article, we focus on the degree-based indices and co-indices of the honeycomb network, $H{C}_n$ for $n>1$. $H{C}_n$ is a subclass of the benzenoid network. These networks are formed with the benzene units sharing common edges in a particular symmetric pattern. Figure 1 contains four different networks of such a type.

On the top right is a triangular benzenoid, whereas on the top left, we have the hourglass benzenoid obtained by two copies of triangular benzenoids. At the bottom left, we have rectangular benzenoid. A honeycomb network $H{C}_n,n>1,$ is a network having $6n^2$ vertices and $9n^2-3n$ edges. $H{C}_n$ contains vertices of degree two and three, as shown in the figures below.

A honeycomb network of dimension one is simply a benzene; see Figure 2.

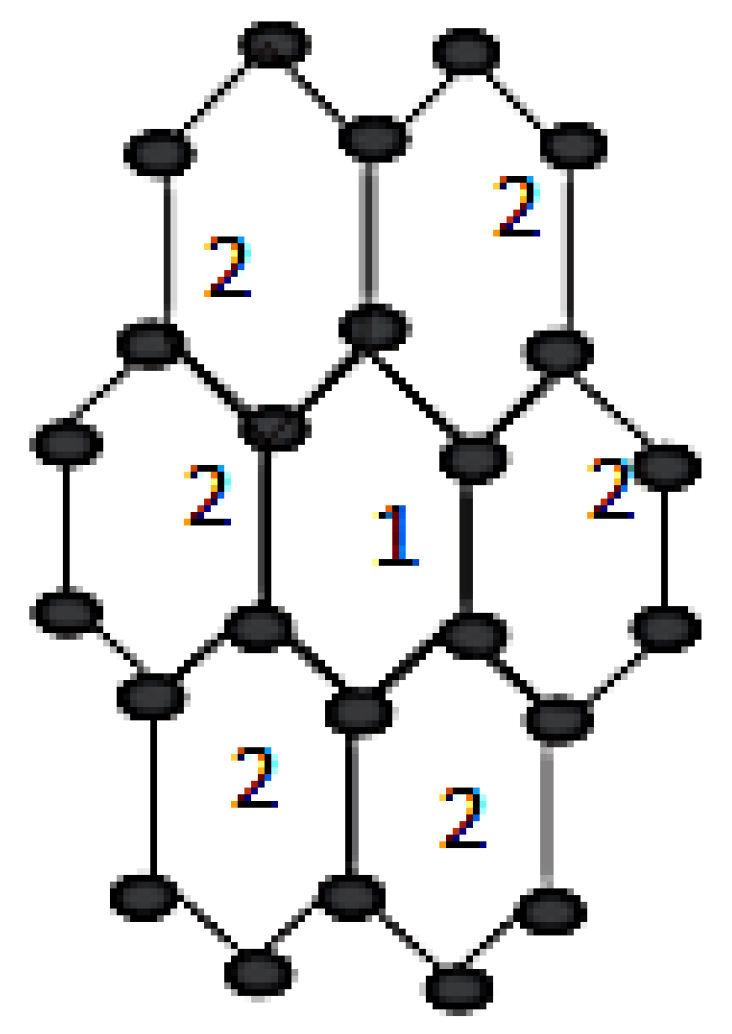
Figure 3 and Figure 4 are the honeycomb network of dimension two and three, respectively.

$H{C}_n$ networks are extensively studied in mathematics because of their extreme importance in chemistry and computer science [26,27,28]. In [29], the authors computed some degree-based indices of line graphs of the subdivision of honeycomb graphs. Paul et al. computed the minimum metric dimension of the honeycomb network [27]. The authors discussed the conditional resolvability of honeycomb and hexagonal networks in [28]. In [30], the authors computed the Zagreb and Randic index of honeycomb networks. In this article, we compute for the first time Zagreb and Forgotten polynomials and some topological indices such as the hyper-Zagreb index, first and second multiple Zagreb indices and Forgotten index. We also determine closed forms of the Albert index, Bell index and $IRM(G)$ indices. We also compute the F-index of the complement of the honeycomb network and several co-indices related to this network. These indices and polynomials are different from those computed in [29,30]. It is important to remark that we compute these above-mentioned co-indices of the honeycomb network without computing the complement and line graph of the honeycomb network. Moreover, index analysis is also given at the end.

2. Main Results

The first theorem contains some results for the connectivity polynomials of honeycomb networks.

Theorem 1.

Let $(H{C}_n)$ be a honeycomb network, then:

a. $M_1(H{C}_n;x,y)=6x^4+12(n-1)x^5+(9n^2-15n+6)x^6,$

b. $M_2(H{C}_n;x)=6x^4+12(n-1)x^6+(9n^2-15n+6)x^9$,

c. $F(H{C}_n;x)=6x^8+12(n-1)x^{13}+(9n^2-15n+6)x^{18}$.

Proof. 

We already discussed that $H{C}_n,n>1$ has only vertices of degree two or three. Then, the partition of vertex sets of $H{C}_n$ can be written as:

$V_{\left\{2\right\}}=\left\{vϵV(G)\right|d_v=2\}\to \left|V_{\left\{2\right\}}\right|=6n,$

$V_{\left\{3\right\}}=\left\{vϵV(G)\right|d_v=3\}\to \left|V_{\left\{3\right\}}\right|=6n^2-6n$.

Now, the edge partitions of $(H{C}_n)$ are:

$E_{\{2,2\}}=\{e=uvϵE(H{C}_n)|d_u=2,d_v=2\}\to \left|E_{\{2,2\}}\right|=6,$

$E_{\{2,3\}}=\{e=uvϵE(H{C}_n)|d_u=2,d_v=3\}\to \left|E_{\{2,3\}}\right|=12(n-1),$

$E_{\{3,3\}}=\{e=uvϵE(H{C}_n)|d_u=3,d_v=3\}\to \left|E_{\{3,3\}}\right|=9n^2-15n+6.$

a. $M_1(H{C}_n,x)={\sum }_{uvϵE(H{C}_n)}{x}^{[d_u+d_v]}$,

$={\sum }_{uvϵE_1(H{C}_n)}{x}^{[d_u+d_v]}+{\sum }_{uvϵE_2(H{C}_n)}{x}^{[d_u+d_v]}+{\sum }_{uvϵE_3(H{C}_n)}{x}^{[d_u+d_v]}$

$=|E_1(H{C}_n)|x^4+|E_2(H{C}_n)|x^5+\left|E_3(H{C}_n)\right|x^6$,

$=6x^4+12(n-1)x^5+(9n^2-15n+6)x^6$.

b. $M_2(H{C}_n,x)={\sum }_{uvϵE(H{C}_n)}{x}^{[d_u\times d_v]}$,

$={\sum }_{uvϵE_1(H{C}_n)}{x}^{[d_u\times d_v]}+{\sum }_{uvϵE_2(H{C}_n)}{x}^{[d_u\times d_v]}+{\sum }_{uvϵE_3(H{C}_n)}{x}^{[d_u\times d_v]}$,

$=|E_1(H{C}_n)|x^4+|E_2(H{C}_n)|x^6+\left|E_3(H{C}_n)\right|x^9$

$=6x^4+12(n-1)x^6+(9n^2-15n+6)x^9$.

c. $F(H{C}_n;x)={\sum }_{uvϵE(H{C}_n)}{x}^{[d_u^2+d_v^2]}$,

$={\sum }_{uvϵE_1(H{C}_n)}{x}^{[d_u^2+d_v^2]}+{\sum }_{uvϵE_2(H{C}_n)}{x}^{[d_u^2+d_v^2]}+{\sum }_{uvϵE_3(H{C}_n)}{x}^{[d_u^2+d_v^2]}$,

$=|E_1(H{C}_n)|x^8+|E_2(H{C}_n)|x^{13}+\left|E_3(H{C}_n)\right|x^{18}$,

$=6x^8+12(n-1)x^{13}+(9n^2-15n+6)x^{18}$. ☐

Proposition 1.

For $H{C}_n$, we have:

a. $HM(H{C}_n)=12(27n^2-20n+1)$,

b. $P{M}_1(H{C}_n)=2^{12}\times 5^{12(n-1)}\times 3^{2(9n^2-15n+6)}$,

c. $P{M}_2(H{C}_n)=2^{12n}\times 3^{18n(n-1)}$,

d. $F(H{C}_n)=162n^2-114n$.

Proof. 

a. By the definition of the hyper-Zagreb index:

$HM(H{C}_n)={\sum }_{uvϵE(H{C}_n)}{[d_u+d_v]}^2$,

$={\sum }_{uvϵE_1(H{C}_n)}{[d_u+d_v]}^2+{\sum }_{uvϵE_2(H{C}_n)}{[d_u+d_v]}^2+{\sum }_{uvϵE_3(H{C}_n)}{[d_u+d_v]}^2$,

$=16|E_1(H{C}_n)|+25|E_2(H{C}_n)|+36|E_3(H{C}_n)|+$,

$=12(27n^2-20n+1)$.

b. Recalling the definition of $P{M}_1(H{C}_n)$ as:

$P{M}_1(H{C}_n)={\prod }_{uvϵE(H{C}_n)}[d_u+d_v],$

$={\prod }_{uvϵE_1(H{C}_n)}[d_u+d_v]+{\prod }_{uvϵE_2(H{C}_n)}[d_u+d_v]+{\prod }_{uvϵE_3(H{C}_n)}[d_u+d_v],$

$=4^{|E_1(H{C}_n)|}\times 5^{|E_2(H{C}_n)|}\times 9^{|E_3(H{C}_n)|},$

$=2^{12}\times 5^{12(n-1)}\times 3^{2(9n^2-15n+6)}.$

c. $P{M}_2(H{C}_n)={\prod }_{uvϵE(H{C}_n)}[d_u\times d_v],$

$={\prod }_{uvϵE_1(H{C}_n)}[d_u\times d_v]\times {\prod }_{uvϵE_2(H{C}_n)}[d_u\times d_v]\times {\prod }_{uvϵE_3(H{C}_n)}[d_u\times d_v],$

$=4^{|E_1(H{c}_n)|}\times 6^{|E_2(H{C}_n)|}\times 9^{|E_3(H{C}_n)|},$

$=2^{12n}\times 3^{18n(n-1)}.$

d. $F(H{C}_n)={\sum }_{uvϵE(H{C}_n)}[d_u^2+d_v^2],$

$={\sum }_{uvϵE_1(H{C}_n)}[d_u^2+d_v^2]+{\sum }_{uvϵE_2(H{C}_n)}[d_u^2+d_v^2]+{\sum }_{uvϵE_3(H{C}_n)}[d_u^2+d_v^2],$

$=8|E_1(H{C}_n)|+13|E_2(H{C}_n)|+18|E_3(H{C}_n)|,$

$=162n^2-114n.$ ☐

Theorem 2.

Let $H{C}_n$ be a honeycomb network, then:

a. $A(H{C}_n)=12(n-1)$,

b. $B(H{C}_n)=\frac{1}{n^2}(6n^3-12n^2+18n-12),$

c. $IRM(H{C}_n)=12(n-1),$

d.$M_1(L(H{C}_n))=144n^2-132n+12.$

Proof. 

Let $H{C}_n$ be a honeycomb network having order $6n^2$ and size $9n^2-3n$. From the figure, we come to know that the honeycomb network $(H{C}_n)$ has only vertices of degree two and three.Let $V_1$ and $V_2$ represent vertices of degree two and three, respectively, where $|V_1|=6n$ and $|V_2|=6n^2-6n$. The edge partitions of $(H{C}_n)$ are:

$E_{\{2,2\}}=e=uvϵE(H{C}_n)/d_u=2,d_v=2\to \left|E_{\{2,2\}}\right|=6,$

$E_{\{2,3\}}=e=uvϵE(H{C}_n)/d_u=2,d_v=3\to \left|E_{\{2,3\}}\right|=12(n-1),$

$E_{\{3,3\}}=e=uvϵE(H{C}_n)/d_u=3,d_v=3\to \left|E_{\{3,3\}}\right|=9n^2-15n+6.$

a. Albertson index:

$A(H{C}_n)={\sum }_{xyϵE(H{C}_n)}|d(x)-d(y)|,$

$={\sum }_{xyϵE_1(H{C}_n)}|d(x)-d(y)|+{\sum }_{xyϵE_2(H{C}_n)}|d(x)-d(y)|+{\sum }_{xyϵE_3(H{C}_n)}|d(x)-d(y)|,$

$=|E_1(H{C}_n)\left|\right|2-2|+|E_2(H{C}_n)\left|\right|2-3|+|E_3(H{C}_n)\left|\right|3-3|,$

$=(6)(0)+(12n-12)(1)+(9n^2-15n+6)(0),$

$=12(n-1).$

b. Bell index:

$B(H{C}_n)={\sum }_{xϵV(H{C}_n)}{(d(x)-\frac{2m}{n})}^2,$

$={\sum }_{xϵV_1(H{C}_n)}{(d(x)-\frac{2m}{n})}^2+{\sum }_{xϵV_2(H{C}_n)}{(d(x)-\frac{2m}{n})}^2,$

$=|V_1(H{C}_n)|{(2-\frac{2(9n^2-3n)}{6n^2})}^2+\left|V_2(O{X}_n)\right|{(3-\frac{2(9n^2-3n)}{6n^2})}^2,$

$=6n{(2-\frac{2(9n^2-3n)}{6n^2})}^2+(12(n-1)){(3-\frac{2(9n^2-3n)}{6n^2})}^2,$

$=\frac{1}{n^2}(6n^3-12n^2+18n-12).$

c. $\mathit{IRM}(\mathit{G})$:

$IRM(H{C}_n)={\sum }_{xyϵE(H{C}_n)}{[d(x)-d(y)]}^2,$

$={\sum }_{xyϵE_1(H{C}_n)}{[d(x)-d(y)]}^2+{\sum }_{xyϵE_2(H{C}_n)}{[d(x)-d(y)]}^2+{\sum }_{xyϵE_3(H{C}_n)}{[d(x)-d(y)]}^2,$

$=|E_1(H{C}_n)|{[2-2]}^2+|E_2(H{C}_n)|{[2-3]}^2+\left|E_3(H{C}_n)\right|{[3-3]}^2,$

$=12(n-1).$

d. ${\mathit{M}}_{\mathbf{1}}(\mathit{L}(\mathit{G}))$:

$M_1(L(G))={\sum }_{xyϵE(G)}{[d(x)+d(y)-2]}^2,$

$M_1(L(H{C}_n))={\sum }_{xyϵE_1(H{C}_n)}{[d(x)+d(y)-2]}^2+{\sum }_{xyϵE_2(H{C}_n)}{[d(x)+d(y)-2]}^2+{\sum }_{xyϵE_3(H{C}_n)}{[d(x)+d(y)-2]}^2,$

$=|E_1(H{C}_n)|{[2+2-2]}^2+|E_2(H{C}_n)|{[2+3-2]}^2+\left|E_3(H{C}_n)\right|{[3+3-2]}^2,$

$=(6){(2)}^2+(12n-12){(3)}^2+(9n^2-15n+6){(4)}^2,$

$=144n^2-132n+12.$ ☐

Theorem 3.

For honeycomb network $(H{C}_n)$, we have:

a. $\overline{M_1}(G)=36n(3n^3-n^2-2n+1),$

b. $\overline{M_2}(G)=6(27n^4-18n^3-15n^2+13n-1).$

Proof. 

Let honeycomb network $H{C}_n$ have order $6n^2$ and size $9n^2-3n$. The first Zagreb index $M_1(H{C}_n)$ is $54n^2-30n$, and the second Zagreb index $M_2(H{C}_n)$ is $81n^2-63n+6$. Then:

a. $\overline{{\mathit{M}}_{\mathbf{1}}}(\mathit{G})$,

$\overline{M_1}(G)=2m(n-1)-M_1(G),$

$\overline{M_1}(H{C}_n)=2(9n^2-3n)(6n^2-1)-(54n^2-30n),$

$=36n(3n^3-n^2-2n+1).$

b. $\overline{{\mathit{M}}_{\mathbf{2}}}(\mathit{G})$:

$\overline{M_2}(G)=2m^2-\frac{1}{2}{M}_1(G)-M_2(G),$

$\overline{M_2}(H{C}_n)=2{(9n^2-3n)}^2-\frac{1}{2}(54n^2-30n)-(81n^2-63n+6),$

$=6(27n^4-18n^3-15n^2+13n-1).$ ☐

Theorem 4.

For honeycomb network $H{C}_n$, we have:

a. $F(\overline{H{C}_n})=1296n^8-2592n^6+648n^5+1728n^4-756n^3-384n^2+132n,$

b. $\overline{F}(H{C}_n)=324n^4-108n^3-216n^2+144n,$

c. $\overline{F}(\overline{H{C}_n})=648n^6-216n^5-864n^4+432n^3-36n^2-120n.$

Proof. 

Let honeycomb network $(H{C}_n)$ have order $6n^2$ and size $9n^2-3n$, with first Zagreb index $M_1(H{C}_n)=54n^2-30n$ and the Forgotten index $F(H{C}_n)=162n^2-144n$, then,

a. $\mathit{F}(\overline{{\mathit{HC}}_{\mathit{n}}})$:

$F(\overline{G})=n{(n-1)}^3-6m{(n-1)}^2+3(n-1)M_1(G)-F(G),$

$F(\overline{H{C}_n})=6n^2{(6n^2-1)}^3-6(9n^2-3n){(6n^2-1)}^2+3(6n^2-1)(54n^2-30n)-(162n^2-144n),$

$F(\overline{H{C}_n})=1296n^8-2592n^6+648n^5+1728n^4-756n^3-384n^2+132n.$

b. $\overline{\mathit{F}}({\mathit{HC}}_{\mathit{n}})$:

$\overline{F}(G)=(n-1)M_1(G)-F(G),$

$\overline{F}(H{C}_n)=(6n^2-1)(54n^2-30n)-(162n^2-144n),$

$\overline{F}(H{C}_n)=648n^6-216n^5-864n^4+432n^3-36n^2-120n.$

c. $\overline{\mathit{F}}(\overline{{\mathit{HC}}_{\mathit{n}}})$:

$\overline{F}(\overline{G})=2m{(n-1)}^2-2(n-1)M_1(G)+F(G),$

$\overline{F}(\overline{H{C}_n})=2(9n^2-3n){(6n^2-1)}^2-2(6n^2-1)(54n^2-30n)+(162n^2-144n),$

$\overline{F}(\overline{H{C}_n})=648n^6-216n^5-864n^4+432n^3-36n^2-120n.$ ☐

3. Index Analysis of Honeycomb Networks

In this section, we draw graphs of key features that determine the properties of the honeycomb network relating to parameter n. It has been established that many properties of the materials are related to topological indices. These indices depend on the dimension of the honeycomb network in many different ways. In turn, we can establish that the properties of honeycomb networks are controlled by the dimension n. The following graphs (Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10) show the trends of this controllability. The first graph, Figure 5, includes the graph of the connectivity polynomials of $H{C}_2$. Different properties such as $\pi$-electron energy, heat of formation and the strain energy of the honeycomb network can be predicted using these polynomials.

The following Figure 6 shows the dependencies of $HM$, in n. The graph of $HM$ keeps on increasing with the increase in n. The properties depending on these indices are directly related to n.

The graphs of $P{M}_1$ and $P{M}_2$ show the same behavior. The following Figure 7 shows that the Forgotten index varies directly with the change in n.

The following graphs, Figure 8, show that the Alberton and Bell indices increase linearly with the increase in the dimension n.

The following graphs, Figure 9 and Figure 10, can also be helpful in the computation of the dependencies of the relevant index with the change in n. Almost all indices show an upward trend with the increase in the dimension of honeycomb networks. The figures can be easily understood on the basis of the analysis they depict; however, the graph of $IRM$ shows a constant behavior.

4. Conclusions

In the present article, we computed degree-based indices and co-indices of $H{C}_n$. We also computed degree-based connectivity polynomials such as Zagreb polynomials and the Forgotten polynomial of this network. We also gave index analysis of these network, which shows the dependency on and relation of indices to the dimension of the network n. Almost all indices increase sharply with the increase in n, except the case of the Alberton and Bell indices, which increase linearly. These facts may be useful for people working in computer science and chemistry who encounter honeycomb networks. An optimum level of any particular index can be obtained by putting a restriction on n.