General (α,2)-Path Sum-Connectivirty Indices of One Important Class of Polycyclic Aromatic Hydrocarbons
Abstract
:1. Introduction
1.1. Application Background
1.2. Definitions and Notations
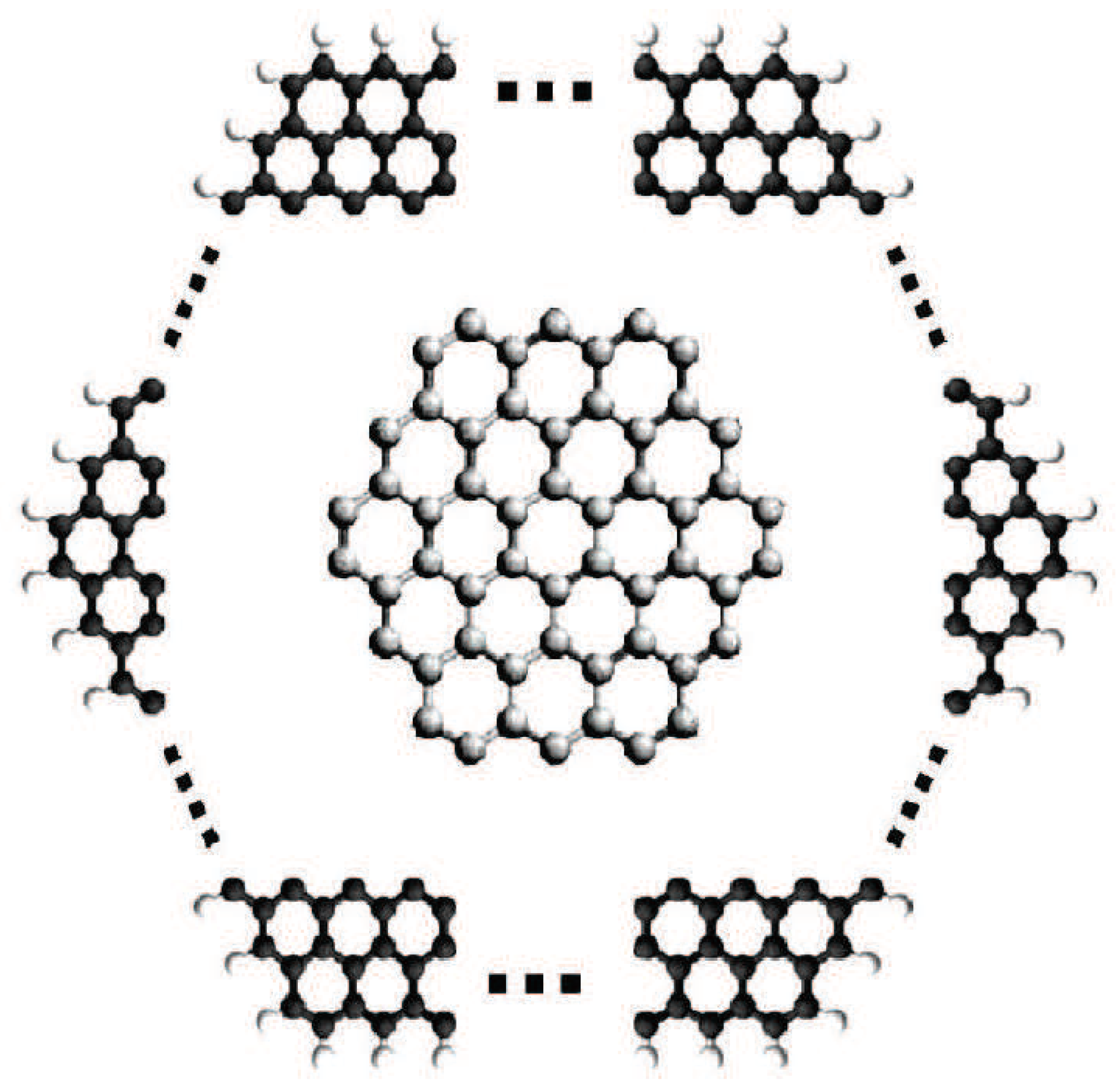
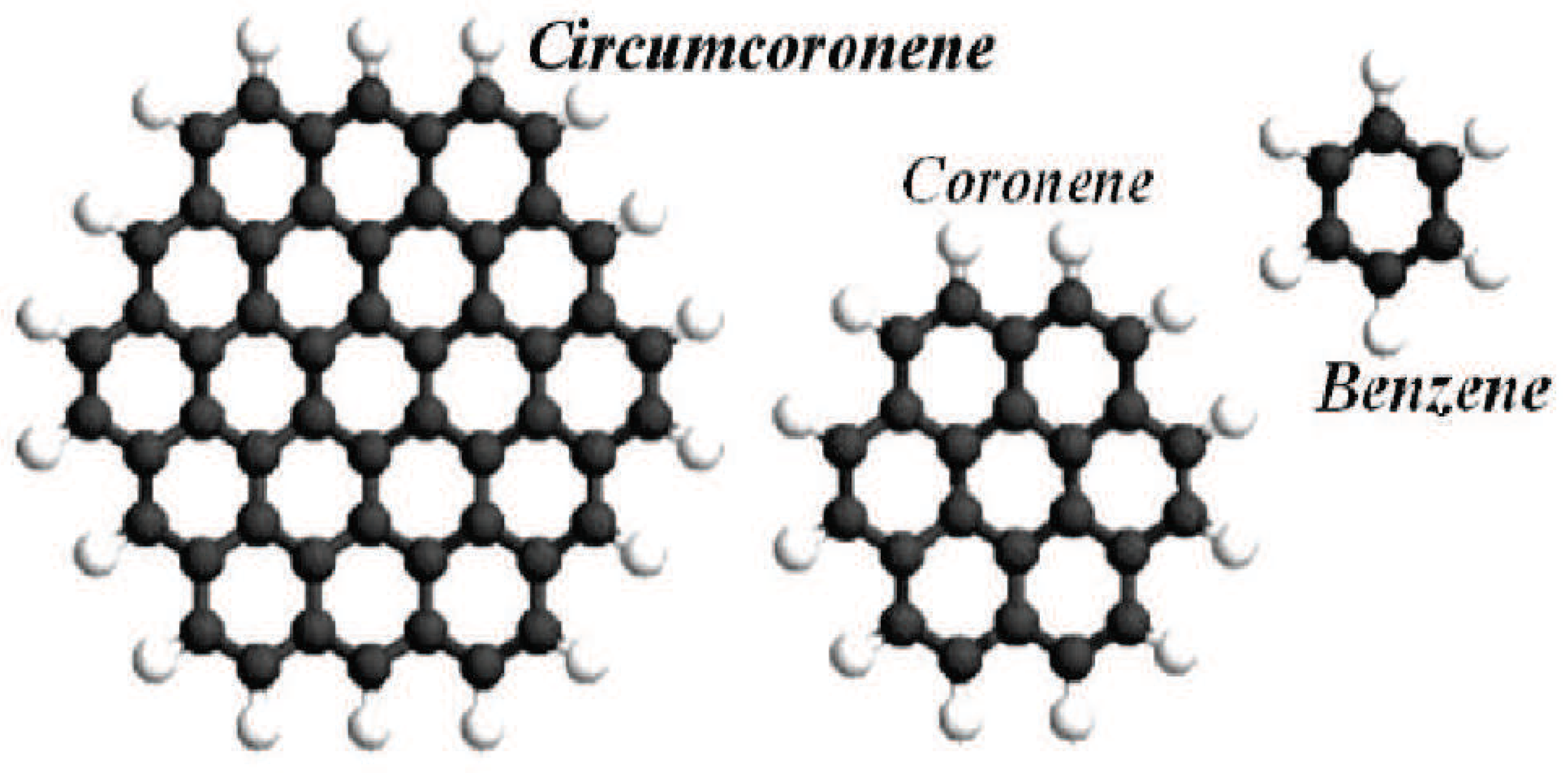
2. Polycyclic Aromatic Hydrocarbons
3. Main Results on the General -Path Sum-Connectivity Indices of
4. The Monotonicity and the Extremal Values of
- For any real number α, we have is strictly increasing with respect to all positive integers n.
- The smallest general -path sum-connectivity index of Polycyclic aromatic hydrocarbons iswhen and only when . Of course, is benzene (see Figure 1).
5. Conclusions
6. Further Research
Funding
Acknowledgments
Conflicts of Interest
References
- Randić, M. On characterization of molecular branching. J. Am. Chem. Soc. 1975, 97, 6609–6615. [Google Scholar] [CrossRef]
- Lu, M.; Zhang, L.; Tian, F. On the Randić index of cacti. MATCH Commun. Math. Comput. Chem. 2006, 56, 551–556. [Google Scholar]
- Wang, S.; Wei, B. Sharp bounds of multiplicative Zagreb indices of k-Trees. Discret. Appl. Math. 2015, 180, 168–175. [Google Scholar] [CrossRef]
- Kier, L.B.; Hall, L.H. Medicinal Chemistry: Molecular Connectivity in Chemistry and Drug Research; Academic Press: New York, NY, USA, 1976. [Google Scholar]
- Kier, L.B.; Hall, L.H.; Murray, W.J.; Randić, M. Molecular connectivity V: The connectivity concept applied to density. J. Pharm. Sci. 1976, 65, 1226–1227. [Google Scholar] [CrossRef] [PubMed]
- Kier, L.B.; Hall, L.H. Molecular Connectivity in Structure-Activity Analysis; Wiley: New York, NY, USA, 1986. [Google Scholar]
- Zanni, R.; Galvez-Liompart, M.; García-Domenech, R.; Galvez, J. Latest advances in molecular topology applications for drug discovery. Expert Opin. Drug Discov. 2015, 9, 945–957. [Google Scholar] [CrossRef] [PubMed]
- Estrada, E.; Patlewicz, G.; Uriarte, E. From molecular graphs to drugs: A review on the use of topological indices in drug design and discovery. Indian J. Chem. 2003, 42, 1315–1329. [Google Scholar]
- Gutman, I. Advances in the theory of Benzenoid hydrocarbons II. In Topics in Current Chemistry; Springer: Berlin, Germany, 1992. [Google Scholar]
- Gutman, I. Extremal hexagonal chains. J. Math. Chem. 1993, 12, 197–210. [Google Scholar] [CrossRef]
- Gutman, I.; Cyvin, S.J. Introduction to the Theory of Benzenoid Hydrocarbons; Springer: Berlin, Germany, 1989. [Google Scholar]
- Gutman, I.; Cyvin, S.J. Advances in the theory of Benzenoid hydrocarbons. In Topics in Current Chemistry; Springer: Berlin, Germany, 1990. [Google Scholar]
- Bondy, J.A.; Murty, U.S.R. Graph Theory with Applications; MacMillan: New York, NY, USA, 1976. [Google Scholar]
- Devillers, J.; Balaban, A.T. Topological Indices and Related Descriptors in QSAR and QSPR; Gordon and Breach Science Publishers: New York, NY, USA, 1999. [Google Scholar]
- Gutman, I.; Trinajesti, N. Graph theory and molecular orbitals. III. Total φ-electron energy of alternant hydrocarbons. Chem. Phys. Lett. 1972, 17, 535–538. [Google Scholar] [CrossRef]
- Gutman, I.; Das, K.C. The first Zagreb index 30 years after. MATCH Commun. Math. Comput. Chem. 2004, 50, 83–92. [Google Scholar]
- Zhou, B.; Trinajesti, N. On a novel connectivity index. J. Math. Chem. 2009, 46, 1252–1270. [Google Scholar] [CrossRef]
- Gupta, S.P. QSAR studies on local anesthetics. Chem. Rev. 1991, 91, 1109–1119. [Google Scholar] [CrossRef]
- Wiersum, U.E.; Jenneskens, L.W. Jenneskens in Gas Phase Reactions in Organic Synthesis; Gordon and Breach Science Publishers: Amsterdam, The Netherlands, 1997; pp. 143–194. [Google Scholar]
- Berresheim, A.J.; Muller, M.; Mollen, K. Polyphenylene nanostructures. Chem. Rev. 1999, 99, 1747–1785. [Google Scholar] [CrossRef] [PubMed]
- Bauschlicher, C.W.; Bakes, E.L.O. Infrared spectra of polycyclic aromatic hydrocarbons. Chem. Phys. 2000, 262, 285–291. [Google Scholar] [CrossRef]
- Anthony, J.E. Functionalized acenes and heteroacenes for organic electronics. Chem. Rev. 2006, 106, 5028–5048. [Google Scholar] [CrossRef] [PubMed]
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H. General (α,2)-Path Sum-Connectivirty Indices of One Important Class of Polycyclic Aromatic Hydrocarbons. Symmetry 2018, 10, 426. https://doi.org/10.3390/sym10100426
Wang H. General (α,2)-Path Sum-Connectivirty Indices of One Important Class of Polycyclic Aromatic Hydrocarbons. Symmetry. 2018; 10(10):426. https://doi.org/10.3390/sym10100426
Chicago/Turabian StyleWang, Haiying. 2018. "General (α,2)-Path Sum-Connectivirty Indices of One Important Class of Polycyclic Aromatic Hydrocarbons" Symmetry 10, no. 10: 426. https://doi.org/10.3390/sym10100426




