On the Classification of Bol-Moufang Type of Some Varieties of Quasi Neutrosophic Triplet Loop (Fenyves BCI-Algebras)

Abstract

In this paper, Bol-Moufang types of a particular quasi neutrosophic triplet loop (BCI-algebra), chritened Fenyves BCI-algebras are introduced and studied. 60 Fenyves BCI-algebras are introduced and classified. Amongst these 60 classes of algebras, 46 are found to be associative and 14 are found to be non-associative. The 46 associative algebras are shown to be Boolean groups. Moreover, necessary and sufficient conditions for 13 non-associative algebras to be associative are also obtained: p-semisimplicity is found to be necessary and sufficient for a $F_3$, $F_5$, $F_{42}$ and $F_{55}$ algebras to be associative while quasi-associativity is found to be necessary and sufficient for $F_{19}$, $F_{52}$, $F_{56}$ and $F_{59}$ algebras to be associative. Two pairs of the 14 non-associative algebras are found to be equivalent to associativity ($F_{52}$ and $F_{55}$, and $F_{55}$ and $F_{59}$). Every BCI-algebra is naturally an $F_{54}$ BCI-algebra. The work is concluded with recommendations based on comparison between the behaviour of identities of Bol-Moufang (Fenyves’ identities) in quasigroups and loops and their behaviour in BCI-algebra. It is concluded that results of this work are an initiation into the study of the classification of finite Fenyves’ quasi neutrosophic triplet loops (FQNTLs) just like various types of finite loops have been classified. This research work has opened a new area of research finding in BCI-algebras, vis-a-vis the emergence of 540 varieties of Bol-Moufang type quasi neutrosophic triplet loops. A ‘Cycle of Algebraic Structures’ which portrays this fact is provided.

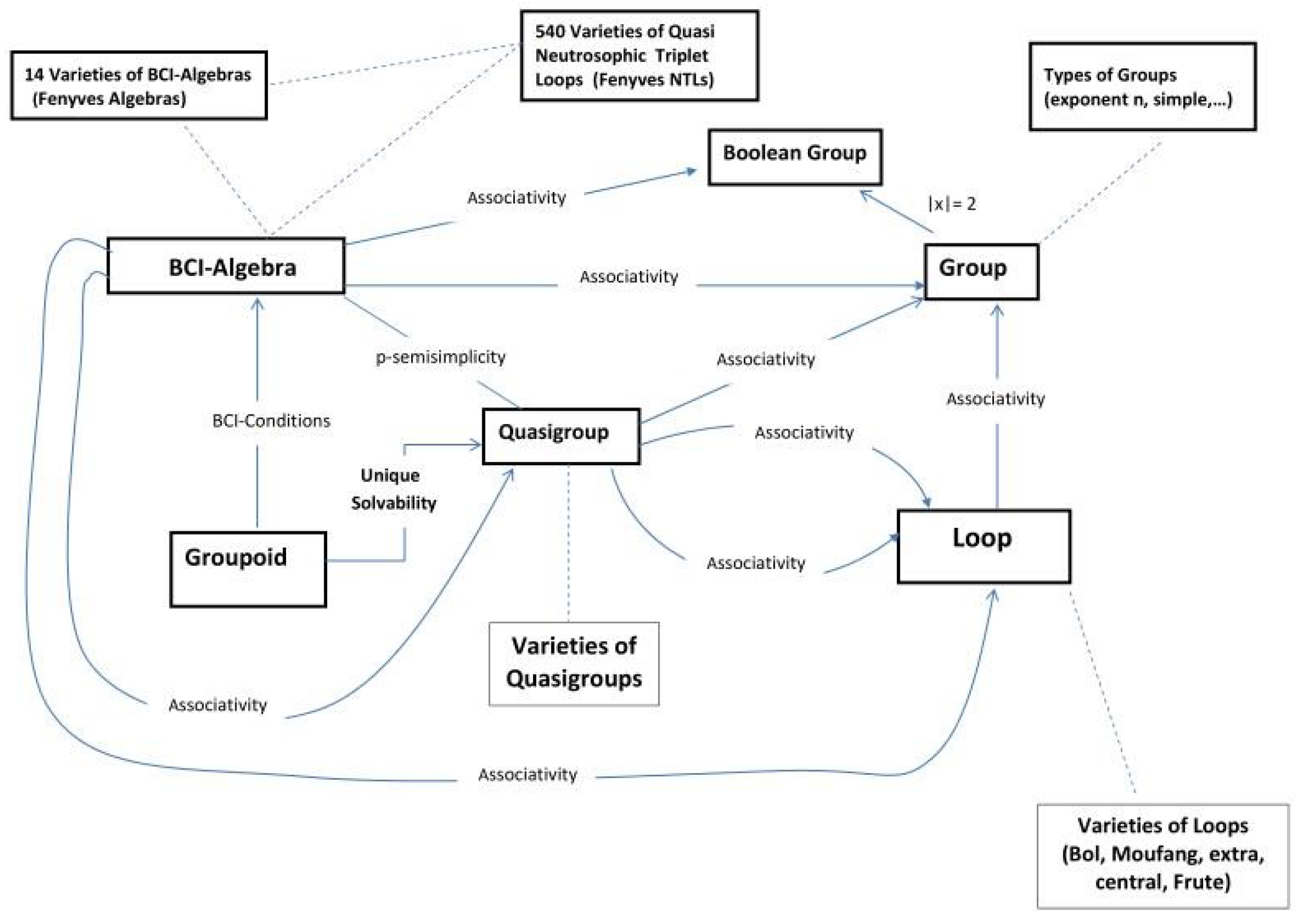
1. Introduction

BCK-algebras and BCI-algebras are abbreviated as two B-algebras. The former was raised in 1966 by Imai and Iseki [1], Japanese mathematicians, and the latter was put forward in the same year by Iseki [2]. The two algebras originated from two different sources: set theory and propositional calculi.

There are some systems which contain the only implicational functor among logical functors, such as the system of weak positive implicational calculus, BCK-system and BCI-system. Undoubtedly, there are common properties among those systems. We know that there are close relationships between the notions of the set difference in set theory and the implication functor in logical systems. For example, we have the following simple inclusion relations in set theory:

$$(A-B)-(A-C)\subseteq C-B,A-(A-B)\subseteq B.$$

These are similar to the propositional formulas in propositional calculi:

$$(p\to q)\to \left(\right(q\to r)\to (p\to r\left)\right),p\to \left(\right(p\to q)\to q),$$

which raise the following questions: What are the most essential and fundamental properties of these relationships? Can we formulate a general algebra from the above consideration? How will we find an axiom system to establish a good theory of general algebras? Answering these questions, K.Iseki formulated the notions of two B-algebras in which BCI-algebras are a wider class than BCK-algebras. Their names are taken from BCK and BCI systems in combinatory logic.

BCI-Algebras are very interesting algebraic structures that have generated wide interest among pure mathematicians.

1.1. BCI-algebra, Quasigroups, Loops and the Fenyves Identities

We start with some definitions and examples of some varieties of quasi neutrosophic triplet loop.

Definition 1.

A triple $(X,*,0)$ is called a BCI-algebra if the following conditions are satisfied for any $x,y,z\in X$:

1. 

$\left(\right(x*y)*(x*z\left)\right)*(z*y)=0$;

2. 

$x*0=x$;

3. 

$x*y=0$ and $y*x=0$ ⟹ $x=y$.

We call the binary operation * on X the multiplication on X, and the constant 0 in X the zero element of X. We often write X instead of $(X,*,0)$ for a BCI-algebra in brevity. Juxtaposition $xy$ will at times be used for $x*y$ and will have preference over * i.e., $xy*z=(x*y)*z$.

Example 1.

Let S be a set. Let $2^S$ be the power set of S, − the set difference and ∅ the empty set. Then $\left(2^S,-,\mathsf{\varnothing }\right)$ is a BCI-algebra.

Example 2.

Suppose $(G,·,e)$ is an abelian group with e as the identity element. Define a binary operation * on G by putting $x*y=x{y}^{-1}$. Then $(G,*,e)$ is a BCI-algebra.

Example 3.

$(\mathbb{Z},-,0)$ and $(\mathbb{R}-\{0\},÷,1)$ are BCI-algebras.

Example 4.

Let S be a set. Let $2^S$ be the power set of S, Δ the symmetric difference and ∅ the empty set. Then $\left(2^S,\Delta ,\mathsf{\varnothing }\right)$ is a BCI-algebra.

The following theorems give necessary and sufficient conditions for the existence of a BCI-algebra.

Theorem 1.

(Yisheng [3])

Let X be a non-empty set, * a binary operation on X and 0 a constant element of X. Then $(X,*,0)$ is a BCI-algebra if and only if the following conditions hold:

1. 

$\left(\right(x*y)*(x*z\left)\right)*(z*y)=0$;

2. 

$(x*(x*y\left)\right)*y=0$;

3. 

$x*x=0$;

4. 

$x*y=0$ and $y*x=0$ imply $x=y$.

Definition 2.

A BCI-algebra $(X,*,0)$ is called a BCK-algebra if $0*x=0$ for all $x\in X$.

Definition 3.

A BCI-algebra $(X,*,0)$ is called a Fenyves BCI-algebra if it satisfies any of the identities of Bol-Moufang type.

The identities of Bol-Moufang type are given below:

$F_1$: $xy*zx=(xy*z)x$ $F_2$: $xy*zx=(x*yz)x$ (Moufang identity) $F_3$: $xy*zx=x(y*zx)$ $F_4$: $xy*zx=x(yz*x)$ (Moufang identity) $F_5$: $(xy*z)x=(x*yz)x$ $F_6$: $(xy*z)x=x(y*zx)$ (extra identity) $F_7$: $(xy*z)x=x(yz*x)$ $F_8$: $(x*yz)x=x(y*zx)$ $F_9$: $(x*yz)x=x(yz*x)$ $F_{10}$: $x(y*zx)=x(yz*x)$ $F_{11}$: $xy·xz=(xy*x)z$ $F_{12}$: $xy*xz=(x*yx)z$ $F_{13}$: $xy*xz=x(yx*z)$ (extra identity) $F_{14}$: $xy*xz=x(y*xz)$ $F_{15}$: $(xy*x)z=(x*yx)z$ $F_{16}$: $(xy*x)z=x(yx*z)$ $F_{17}$: $(xy*x)z=x(y*xz)$ (Moufang identity) $F_{18}$: $(x*yx)z=x(yx*z)$ $F_{19}$: $(x*yx)z=x(y*xz)$ (left Bol identity) $F_{20}$: $x(yx*z)=x(y*xz)$ $F_{21}$: $yx*zx=(yx*z)x$ $F_{22}$: $yx*zx=(y*xz)x$ (extra identity) $F_{23}$: $yx*zx=y(xz*x)$ $F_{24}$: $yx*zx=y(x*zx)$ $F_{25}$: $(yx*z)x=(y*xz)x$ $F_{26}$: $(yx*z)x=y(xz*x)$ (right Bol identity) $F_{27}$: $(yx*z)x=y(x*zx)$ (Moufang identity) $F_{28}$: $(y*xz)x=y(xz*x)$ $F_{29}$: $(y*xz)x=y(x*zx)$ $F_{30}$: $y(xz*x)=y(x*zx)$

$F_{31}$: $yx*xz=(yx*x)z$ $F_{32}$: $yx*xz=(y*xx)z$ $F_{33}$: $yx*xz=y(xx*z)$ $F_{34}$: $yx*xz=y(x*xz)$ $F_{35}$: $(yx*x)z=(y*xx)z$ $F_{36}$: $(yx*x)z=y(xx*z)$ (RC identity) $F_{37}$: $(yx*x)z=y(x*xz)$ (C identity) $F_{38}$: $(y*xx)z=y(xx*z)$ $F_{39}$: $(y*xx)z=y(x*xz)$ (LC identity) $F_{40}$: $y(xx*z)=y(x*xz)$ $F_{41}$: $xx*yz=(x*xy)z$ (LC identity) $F_{42}$: $xx*yz=(xx*y)z$ $F_{43}$: $xx*yz=x(x*yz)$ $F_{44}$: $xx*yz=x(xy*z)$ $F_{45}$: $(x*xy)z=(xx*y)z$ $F_{46}$: $(x*xy)z=x(x*yz)$ (LC identity) $F_{47}$: $(x*xy)z=x(xy*z)$ $F_{48}$: $(xx*y)z=x(x*yz)$ (LC identity) $F_{49}$: $(xx*y)z=x(xy*z)$ $F_{50}$: $x(x*yz)=x(xy*z)$ $F_{51}$: $yz*xx=(yz*x)x$ $F_{52}$: $yz*xx=(y*zx)x$ $F_{53}$: $yz*xx=y(zx*x)$ (RC identity) $F_{54}$: $yz*xx=y(z*xx)$ $F_{55}$: $(yz*x)x=(y*zx)x$ $F_{56}$: $(yz*x)x=y(zx*x)$ (RC identity) $F_{57}$: $(yz*x)x=y(z*xx)$ (RC identity) $F_{58}$: $(y*zx)x=y(zx*x)$ $F_{59}$: $(y*zx)x=y(z*xx)$ $F_{60}$: $y(zx*x)=y(z*xx)$

Consequent upon this definition, there are 60 varieties of Fenyves BCI-algebras. Here are some examples of Fenyves’ BCI-algebras:

Example 5.

Let us assume the BCI-algebra $(G,*,e)$ in Example 2. Then $(G,*,e)$ is an $F_8$-algebra, $F_{19}$-algebra, $F_{29}$-algebra, $F_{39}$-algebra, $F_{46}$-algebra, $F_{52}$-algebra, $F_{54}$-algebra, $F_{59}$-algebra.

Example 6.

Let us assume the BCI-algebra $\left(2^S,-,\mathsf{\varnothing }\right)$ in Example 1. Then $(2^S,-,\mathsf{\varnothing })$ is an $F_3$-algebra, $F_5$-algebra, $F_{21}$-algebra, $F_{29}$-algebra, $F_{42}$-algebra, $F_{46}$-algebra, $F_{54}$-algebra and $F_{55}$-algebra.

Example 7.

The BCI-algebra $(2^S,\Delta ,\mathsf{\varnothing })$ in Example 4 is associative.

Example 8.

By considering the direct product of the BCI-algebras $(G,*,e)$ and $\left(2^S,-,\mathsf{\varnothing }\right)$ of Example 2 and Example 1 respectively, we have a BCI-algebra $\left(G\times 2^S,(*,-),(e,\mathsf{\varnothing })\right)$ which is a $F_{29}$-algebra and a $F_{46}$-algebra.

Remark 1.

Direct products of sets of BCI-algebras will result in BCI-algebras which are $F_i$-algebra for distinct i’s.

Definition 4.

A BCI-algebra $(X,*,0)$ is called associative if $(x*y)*z=x*(y*z)$ for all $x,y,z\in X$.

Definition 5.

A BCI-algebra $(X,*,0)$ is called p-semisimple if $0*(0*x)=x$ for all $x\in X$ .

Theorem 2.

(Yisheng [3]) Suppose that $(X,*,0)$ is a BCI-algebra. Define a binary relation ⩽ on X by which $x⩽y$ if and only if $x*y=0$ for any $x,y\in X$. Then $(X,⩽)$ is a partially ordered set with 0 as a minimal element (meaning that $x⩽0$ implies $x=0$ for any $x\in X$).

Definition 6.

A BCI-algebra $(X,*,0)$ is called quasi-associative if $(x*y)*z\le x*(y*z)$ for all $x,y,z\in X$.

The following theorems give equivalent conditions for associativity, quasi-associativity and p-semisimplicity in a BCI-algebra:

Theorem 3.

(Yisheng [3])

Given a BCI-algebra X, the following are equivalent $x,y,z\in X$:

1. 

X is associative.

2. 

$0*x=x$.

3. 

$x*y=y*x\forall x,y\in X$.

Theorem 4.

(Yisheng [3])

Let X be a BCI-algebra. Then the following conditions are equivalent for any $x,y,z,u\in X$:

1. 

X is p-semisimple

2. 

$(x*y)*(z*u)=(x*z)*(y*u)$.

3. 

$0*(y*x)=x*y$.

4. 

$(x*y)*(x*z)=z*y$.

5. 

$z*x=z*y$ implies $x=y$. (the left cancellation law i.e., LCL)

6. 

$x*y=0$ implies $x=y$.

Theorem 5.

(Yisheng [3])

Given a BCI-algebra X, the following are equivalent for all $x,y\in X$:

1. 

X is quasi-associative.

2. 

$x*(0*y)=0$ implies $x*y=0$.

3. 

$0*x=0*(0*x)$.

4. 

$(0*x)*x=0$.

Theorem 6.

(Yisheng [3])

A triple $(X,*,0)$ is a BCI-algebra if and only if there is a partial ordering ⩽ on X such that the following conditions hold for any $x,y,z\in X$:

1. 

$(x*y)*(x*z)⩽z*y$;

2. 

$x*(x*y)⩽y$;

3. 

$x*y=0$ if and only if $x⩽y$.

Theorem 7.

(Yisheng [3])

Let X be a BCI-algebra. X is p-semisimple if and only if one of the following conditions holds for any $x,y,z\in X$:

1. 

$x*z=y*z$ implies $x=y$. (the right cancellation law i.e., RCL)

2. 

$(y*x)*(z*x)=y*z$.

3. 

$(x*y)*(x*z)=0*(y*z)$.

Theorem 8.

(Yisheng [3])

Let X be a BCI-algebra. X is p-semisimple if and only if one of the following conditions holds for any $x,y\in X$:

1. 

$x*(0*y)=y$.

2. 

$0*x=0\Rightarrow x=0$.

Theorem 9.

(Yisheng [3]) Suppose that $(X,*,0)$ is a BCI-algebra. X is associative if and only if X is p-semisimple and X is quasi-associative.

Theorem 10.

(Yisheng [3]) Suppose that $(X,*,0)$ is a BCI-algebra. Then $(x*y)*z=(x*z)*y$ for all $x,y,z\in X$.

Remark 2.

In Theorem 9, quasi-associativity in BCI-algebra plays a similar role to that which weak associativity (i.e., the $F_i$ identities) plays in quasigroup and loop theory.

We now move on to quasigroups and loops.

Definition 7.

Let L be a non-empty set. Define a binary operation (·) on L . If $x·y\in L$ for all $x,y\in L$, $(L,·)$ is called a groupoid. If in a groupoid $(L,·)$, the equations:

$$a·x=bandy·a=b$$

have unique solutions for x and y respectively, then $(L,·)$ is called a quasigroup. If in a quasigroup $(L,·)$, there exists a unique element e called the identity element such that for all $x\in L$, $x·e=e·x=x$, $(L,·)$ is called a loop.

Definition 8.

Let $(L,·)$ be a groupoid.

The left nucleus of L is the set $N_{\lambda }(L,·)=N_{\lambda }\left(L\right)=\{a\in L:ax·y=a·xy\forall x,y\in L\}$.

The right nucleus of L is the set $N_{\rho }(L,·)=N_{\rho }\left(L\right)=\{a\in L:y·xa=yx·a\forall x,y\in L\}$.

The middle nucleus of L is the set $N_{\mu }(L,·)=N_{\mu }\left(L\right)=\{a\in L:ya·x=y·ax\forall x,y\in L\}$.

The nucleus of L is the set $N(L,·)=N\left(L\right)=N_{\lambda }(L,·)\cap N_{\rho }(L,·)\cap N_{\mu }(L,·)$.

The centrum of L is the set $C(L,·)=C\left(L\right)=\{a\in L:ax=xa\forall x\in L\}$.

The center of L is the set $Z(L,·)=Z\left(L\right)=N(L,·)\cap C(L,·)$.

In the recent past, and up to now, identities of Bol-Moufang type have been studied on the platform of quasigroups and loops by Fenyves [4], Phillips and Vojtechovsky [5], Jaiyeola [6,7,8], Robinson [9], Burn [10,11,12], Kinyon and Kunen [13] as well as several other authors.

Since the late 1970s, BCI and BCK algebras have been given a lot of attention. In particular, the participation in the research of polish mathematicians Tadeusz Traczyk and Andrzej Wronski as well as Australian mathematician William H. Cornish, in addition to others, is causing this branch of algebra to develop rapidly. Many interesting and important results are constantly discovered. Now, the theory of BCI-algebras has been widely spread to areas such as general theory which include congruences, quotient algebras, BCI-Homomorphisms, direct sums and direct products, commutative BCK-algebras, positive implicative and implicative BCK-algebras, derivations of BCI-algebras, and ideal theory of BCI-algebras ([1,14,15,16,17]).

1.2. BCI-Algebras as a Quasi Neutrosophic Triplet Loop

Consider the following definition.

Definition 9.

(Quasi Neutrosophic Triplet Loops (QNTL), Zhang et al. [18])

Let $(X,*)$ be a groupoid.

1. 

If there exist $b,c\in X$ such that $a*b=a$ and $a*c=b$, then a is called an NT-element with (r-r)-property. If every $a\in X$ is an NT-element with (r-r)-property, then, $(X,*)$ is called a (r-r)-quasi NTL.

2. 

If there exist $b,c\in X$ such that $a*b=a$ and $c*a=b$, then a is called an NT-element with (r-l)-property. If every $a\in X$ is an NT-element with (r-l)-property, then, $(X,*)$ is called a (r-l)-quasi NTL.

3. 

If there exist $b,c\in X$ such that $b*a=a$ and $c*a=b$, then a is called an NT-element with (l-l)-property. If every $a\in X$ is an NT-element with (l-l)-property, then, $(X,*)$ is called a (l-l)-quasi NTL.

4. 

If there exist $b,c\in X$ such that $b*a=a$ and $a*c=b$, then a is called an NT-element with (l-r)-property. If every $a\in X$ is an NT-element with (l-r)-property, then, $(X,*)$ is called a (l-r)-quasi NTL.

5. 

If there exist $b,c\in X$ such that $a*b=b*a=a$ and $a*c=b$, then a is called an NT-element with (lr-r)-property. If every $a\in X$ is an NT-element with (lr-r)-property, then, $(X,*)$ is called a (lr-r)-quasi NTL.

6. 

If there exist $b,c\in X$ such that $a*b=b*a=a$ and $c*a=b$, then a is called an NT-element with (lr-l)-property. If every $a\in X$ is an NT-element with (lr-l)-property, then, $(X,*)$ is called a (lr-l)-quasi NTL.

7. 

If there exist $b,c\in X$ such that $a*b=a$ and $a*c=c*a=b$, then a is called an NT-element with (r-lr)-property. If every $a\in X$ is an NT-element with (r-lr)- property, then, $(X,*)$ is called a (r-lr)-quasi NTL.

8. 

If there exist $b,c\in X$ such that $b*a=a$ and $a*c=c*a=b$, then a is called an NT-element with (l-lr)-property. If every $a\in X$ is an NT-element with (l-lr)-property, then, $(X,*)$ is called a (l-lr)-quasi NTL.

9. 

If there exist $b,c\in X$ such that $a*b=b*a=a$ and $a*c=c*a=b$, then a is called an NT-element with (lr-lr)-property. If every $a\in X$ is an NT-element with (lr-lr)-property, then, $(X,*)$ is called a (lr-lr)-quasi NTL.

Consequent upon Definition 9 and the 60 Fenyves identities $F_i,1\le i\le 60$, there are 60 varieties of Fenyves quasi neutrosophic triplet loops (FQNTLs) for each of the nine varieties of QNTLs in Definition 9. Thereby making it 540 varieties of Fenyves quasi neutrosophic triplet loops (FQNTLs) in all. A BCI-algebra is a (r-r)-QNT, (r-l)-QNTL and (r-lr)-QNTL. Thus, any $F_i$ BCI-algebra, $1\le i\le 60$ belongs to at least one of the following varieties of Fenyves quasi neutrosophic triplet loops: (r-r)-QNTL, (r-l)-QNTL and (r-lr)-QNTL which we refer to as (r-r)-FQNTL, (r-l)-FQNTL and (r-lr)-FQNTL respectively. Any associative QNTL will be called quasi neutrosophic triplet group (QNTG).

The variety of quasi neutrosophic triplet loop is a generalization of neutrosophic triplet group (NTG) which was originally introduced by Smarandache and Ali [19]. Neutrosophic triplet set (NTS) is the foundation of neutrosophic triplet group. New results and developments on neutrosophic triplet groups and neutrosophic triplet loop have been reported by Zhang et al. [18,20,21], and Smarandache and Jaiyéọlá [22,23].

It must be noted that triplets are not connected at all with intuitionistic fuzzy set. Neutrosophic set [24] is a generalization of intuitionistic fuzzy set (a generalization of fuzzy set). In Intuitionistic fuzzy set, an element has a degree of membership and a degree of non-membership, and the deduction of the sum of these two from 1 is considered the hesitant degree of the element. These intuitionistic fuzzy set components are dependent (viz. [25,26,27,28]). In the neutrosophic set, an element has three independent degrees: membership (truth-t), indeterminacy (i), and non-membership (falsity-f), and their sum is up to 3. However, the current paper utilizes the neutrosophic triplets, which are not defined in intuitionistic fuzzy set, since there is no neutral element in intuitionistic fuzzy sets. In a neutrosophic triplet set $(X,*)$, for each element $x\in X$ there exists a neutral element denoted $neut\left(x\right)\in X$ such that $x*neut\left(x\right)=neut\left(x\right)*x=x$, and an opposite of x denoted $anti\left(x\right)\in X$ such that $anti\left(x\right)*x=x*anti\left(x\right)=neut\left(x\right)$. Thus, the triple $(x,neut(x),anti(x\left)\right)$ is called a neutrosophic triplet which in the philosophy of ‘neutrosophy’, can be algebraically harmonized with $(t,i,f)$ in neutrosophic set and then extended for neutrosophic hesitant fuzzy [29] set as proposed for $(t,i,f)$-neutrosophic structures [30]. Unfortunately, such harmonization is not readily defined in intuitionistic fuzzy sets.

Theorem 11.

(Zhang et al. [18]) A (r-lr)-QNTG or (l-lr)-QNTG is a NTG.

This present study looks at Fenyves identities on the platform of BCI-algebras. The main objective of this study is to classify the Fenyves BCI-algebras into associative and non-associative types. It will also be shown that some Fenyves identities play the roles of quasi-associativity and p-semisimplicity , vis-a-vis Theorem 9 in BCI-algebras.

2. Main Results

We shall first clarify the relationship between a BCI-algebra, a quasigroup and a loop.

Theorem 12.

1. 

A BCI algebra X is a quasigroup if and only if it is p-semisimple.

2. 

A BCI algebra X is a loop if and only if it is associative.

3. 

An associative BCI algebra X is a Boolean group.

Proof. 

We use Theorem 3, Theorem 7 and Theorem 4.

• From Theorem 7 and Theorem 4, p-semisimplicity is equivalent to the left and right cancellation laws, which consequently implies that X is a quasigroup if and only if it is p-semisimple.
• One of the axioms that a BCI-algebra satisfies is $x*0=x$ for all $x\in X$. So, 0 is already the right identity element. Now, from Theorem 3, associativity is equivalent to $0*x=x$ for all $x\in X$. So, 0 is also the left identity element of X. The conclusion follows.
• In a BCI-algebra, $x*x=0$ for all $x\in X$. And 0 is the identity element of X. Hence, every element is the inverse of itself.

☐

Lemma 1.

Let $(X,*,0)$ be a BCI-algebra.

1. 

$0\in N_{\rho }\left(X\right)$.

2. 

$0\in N_{\lambda }\left(X\right),N_{\mu }\left(X\right)$ implies X is quasi-associative.

3. 

If $0\in N_{\lambda }\left(X\right)$, then the following are equivalent:

(a) 

X is p-semisimple.

(b) 

$xy=0y·x$ for all $x,y\in L$.

(c) 

$xy=0x·y$ for all $x,y\in L$.

4. 

If $0\in N_{\lambda }\left(X\right)$ or $0\in N_{\mu }\left(X\right)$, then X is p-semisimple if and only if X is associative.

5. 

If $0\in N\left(X\right)$, then X is p-semisimple if and only if X is associative.

6. 

If $(X,*,0)$ is a BCK-algebra, then

(a) 

$0\in N_{\lambda }\left(X\right)$.

(b) 

$0\in N_{\mu }\left(X\right)$ implies X is a trivial BCK-algebra.

7. 

The following are equivalent:

(a) 

X is associative.

(b) 

$x\in N_{\lambda }\left(X\right)$ for all $x\in X$.

(c) 

$x\in N_{\rho }\left(X\right)$ for all $x\in X$.

(d) 

$x\in N_{\mu }\left(X\right)$ for all $x\in X$.

(e) 

$0\in C\left(X\right)$.

(f) 

$x\in C\left(X\right)$ for all $x\in X$.

(g) 

$x\in Z\left(X\right)$ for all $x\in X$.

(h) 

$0\in Z\left(X\right)$.

(i) 

X is a (lr-r)-QNTL.

(j) 

X is a (lr-l)-QNTL.

(k) 

X is a (lr-lr)-QNTL

8. 

If $(X,*,0)$ is a BCK-algebra and $0\in C\left(X\right)$, then X is a trivial BCK-algebra.

Proof. 

This is routine by simply using the definitions of nuclei, centrum, center of a BCI-algebra and QNTL alongside Theorems 3–10 appropriately. ☐

Remark 3.

Based on Theorem 11, since an associative BCI-algebra is a (r-lr)-QNTG, then, an associative BCI-algebra is a NTG. This corroborates the importance of the study of non-associative BCI-algebra i.e., weak associative laws ($F_i$-identities) in BCI-algebra, as mentioned earlier in the objective of this work.

Theorem 13.

Let $(X,*,0)$ be a BCI-algebra. If X is any of the following Fenyves BCI-algebras, then X is associative.

1.  $F_1$-algebra 2.  $F_2$-algebra 3.  $F_4$-algebra 4.  $F_6$-algebra 5.  $F_7$-algebra 6.  $F_9$-algebra 7.  $F_{10}$-algebra 8.  $F_{11}$-algebra 9.  $F_{12}$-algebra 10.  $F_{13}$-algebra	11.  $F_{14}$-algebra 12.  $F_{15}$-algebra 13.  $F_{16}$-algebra 14.  $F_{17}$-algebra 15.  $F_{18}$-algebra 16.  $F_{20}$-algebra 17.  $F_{22}$-algebra 18.  $F_{23}$-algebra 19.  $F_{24}$-algebra 20.  $F_{25}$-algebra	21.  $F_{26}$-algebra 22.  $F_{27}$-algebra 23.  $F_{28}$-algebra 24.  $F_{30}$-algebra 25.  $F_{31}$-algebra 26.  $F_{32}$-algebra 27.  $F_{33}$-algebra 28.  $F_{34}$-algebra 29.  $F_{35}$-algebra 30.  $F_{36}$-algebra	31.  $F_{37}$-algebra 32.  $F_{38}$-algebra 33.  $F_{40}$-algebra 34.  $F_{41}$-algebra 35.  $F_{43}$-algebra 36.  $F_{44}$-algebra 37.  $F_{45}$-algebra 38.  $F_{47}$-algebra 39.  $F_{48}$-algebra 40.  $F_{49}$-algebra	41.  $F_{50}$-algebra
				42.  $F_{51}$-algebra
				43.  $F_{53}$-algebra
				44.  $F_{57}$-algebra
				45.  $F_{58}$-algebra
				46.  $F_{60}$-algebra

Proof. 

• Let X be an $F_1$-algebra. Then $xy*zx=(xy*z)x$. With $z=y$, we have $xy*yx=(xy*y)x$ which implies $xy*yx=(xy*x)y=(xx*y)y=(0*y)y=0*(y*y)$ (since $0\in N_{\lambda }\left(X\right)$; this is achieved by putting $y=x$ in the $F_1$ identity) $=0*0=0$. This implies $xy*yx=0$. Now replacing x with y, and y with x in the last equation gives $yx*xy=0$ implying that $x*y=y*x$ as required.
• Let X be an $F_2$-algebra. Then $xy*zx=(x*yz)x$. With $y=z$, we have $xz*zx=(x*zz)x=(x*0)*x=x*x=0$ implying that $xz*zx=0$. Now replacing x with z, and z with x in the last equation gives $zx*xz=0$ implying that $x*z=z*x$ as required.
• Let X be a $F_4$-algebra. Then, $xy*zx=x(yz*x)$. Put $y=x$ and $z=0$, then you get $0*0x=x$ which means X is p-semisimple. Put $x=0$ and $y=0$ to get $0z=0*0z$ which implies that X is quasi-associative (Theorem 5). Thus, by Theorem 9, X is associative.
• Let X be an $F_6$-algebra. Then, $(xy*z)x=x(y*zx)$. Put $x=y=0$ to get $0z=0*0z$ which implies that X is quasi-associative (Theorem 5). Put $y=0$ and $z=x$, then we have $0*x=x$. Thus, X is associative.
• Let X be an $F_7$-algebra. Then $(xy*z)x=x(yz*x)$. With $z=0$, we have $xy*x=x(y*x)$. Put $y=x$ in the last equation to get $xx*x=(x*xx)$ implying $0*x=x$.
• Let X be an $F_9$-algebra. Then $(x*yz)x=x(yz*x)$. With $z=0$, we have $(x*y)*x=x(y*x)$. Put $y=x$ in the last equation to get $(x*x)x=x(x*x)$ implying $0*x=x$.
• Let X be an $F_{10}$-algebra. Then, $x(y*zx)=x(yz*x)$. Put $y=x=z$, then we have $x*0x=0$. So, $0x=0\Rightarrow x=0$. which means that X is p-semisimple (Theorem 8(2)). Hence, X has the LCL by Theorem 4. Thence, the $F_{10}$ identity $x(y*zx)=x(yz*x)\Rightarrow y*zx=yz*x$ which means that X is associative.
• Let X be an $F_{11}$-algebra. Then $xy*xz=(xy*x)z$. With $y=0$, we have $x*xz=xx*z$. Put $z=x$ in the last equation to get $x=0*x$ as required.
• Let X be an $F_{12}$-algebra. Then $xy*xz=(x*yx)z$. With $z=0$, we have $xy*x=x*yx$. Put $y=x$ in the last equation to get $xx*x=x*xx$ implying $0*x=x$ as required.
• Let X be an $F_{13}$-algebra. Then $xy*xz=x(yx*z)$. With $z=0$, we have $(x*y)x=x*yx$ which implies $(x*x)y=x*yx$ which implies $0*y=x*yx$. Put $y=x$ in the last equation to get $0*x=x$ as required.
• Let X be an $F_{14}$-algebra. Then $xy*xz=x(y*xz)$. With $z=0$, we have $xy*x=x*yx$. Put $y=x$ in the last equation to get $0*x=x$ as required.
• Let X be an $F_{15}$-algebra. Then $(xy*x)z=(x*yx)z$. With $z=0$, we have $(xy*x)=(x*yx)$. Put $y=x$ in the last equation to get $0*x=x$ as required.
• Let X be an $F_{16}$-algebra. Then $(xy*x)z=x(yx*z)$. With $z=0$, we have $(xy*x)=(x*yx)$. Put $y=x$ in the last equation to get $0*x=x$ as required.
• Let X be an $F_{17}$-algebra. Then $(xy*x)z=x(y*xz)$. With $z=0$, we have $(xy*x)=x(y*x)$. Put $y=x$ in the last equation to get $0*x=x$ as required.
• Let X be an $F_{18}$-algebra. Then $(x*yx)z=x(yx*z)$. With $y=0$, we have $(x*0x)z=x(0x*z)$. Since $0\in N_{\lambda }\left(X\right)$ and $0\in N_{\mu }\left(X\right)$, (these are obtained by putting $x=0$ and $x=y$ respectively in the $F_{18}$-identity), the last equation becomes $(x0*x)z=x(0*xz)=x0*xz=x*xz$ which implies $0*z=x*xz$. Put $x=z$ in the last equation to get $0*z=z$ as required.
• This is similar to the proof for $F_{10}$-algebra.
• Let X be an $F_{22}$-algebra. Then $yx*zx=(y*xz)x$. Put $y=x,z=0$, then $0x=0*0x$ which implies that X is quasi-associative. By Theorem 10, the $F_{22}$ identity implies that $yx*zx=yx*xz$. Substitute $x=0$ to get $yz=y*0z$. Now, put $y=z$ in this to get $z*0z=0$. So, $0z=0\Rightarrow z=0$. Hence, X is p-semisimple (Theorem 8(2)). Thus, by Theorem 9, X is associative.
• Let X be an $F_{23}$-algebra. Then $yx*zx=y(xz*x)$. With $z=0$, we have $yx*0x=y(x*x)$ which implies $yx*0x=y$. Since $0\in N_{\mu }\left(X\right)$, (this is obtained by putting $z=x$ in the $F_{23}$-identity), the last equation becomes $(yx*0)*x=y$ which implies $(yx*x)=y$. Put $x=y$ in the last equation to get $0*y=y$ as required.
• Let X be an $F_{24}$-algebra. Then $yx*zx=y(x*zx)$. With $z=0$, we have $yx*0x=y(x*0x)$. Since $0\in N_{\mu }\left(X\right)$,(this is obtained by putting $x=0$ in the $F_{24}$-identity), the last equation becomes $\left(\right(yx)0*x)=y(x0*x)$ which implies $yx*x=y$. Put $y=x$ in the last equation to get $0*y=y$ as required.
• Let X be an $F_{25}$-algebra. Then $(yx*z)x=(y*xz)x$. Put $x=0$, then $yz=y*0z$. Substitute $z=y$, then $y*0y=0$. So, $0y=0\Rightarrow y=0$. Hence, X is p-semisimple (Theorem 8(2)). Hence, X has the RCL by Theorem 7. Thence, the $F_{25}$ identity $(yx*z)x=(y*xz)x$ implies $yx*z=y*xz$. Thus, X is associative.
• Let X be an $F_{26}$-algebra. Then $(yx*z)x=y(xz*x)$. With $z=0$, we have $yx*x=y$. Put $x=y$ in the last equation to get $0*y=y$ as required.
• Let X be an $F_{27}$-algebra. Then $(yx*z)x=y(x*zx)$. Put $z=x=y$, then $0x*x=0$ which implies X is quasi-associative. Put $x=0$ and $y=z$ to get $z*0z=0$. So, $0z=0\Rightarrow z=0$. Hence, X is p-semisimple (Theorem 8(2)). Thus, by Theorem 9, X is associative.
• Let X be an $F_{28}$-algebra. Then $(y*xz)x=y(xz*x)$. With $z=0$, we have $yx*x=y$. Put $x=y$ in the last equation to get $0*y=y$ as required.
• The proof of this is similar to the proof for $F_{10}$-algebra.
• Let X be an $F_{31}$-algebra. Then $yx*xz=(yx*x)z$. By Theorem 10, the $F_{31}$ identity becomes $F_{25}$ identity which implies that X is associative.
• Let X be an $F_{32}$-algebra. Then $yx*xz=(y*xx)z$. With $z=0$, we have $yx*x=y$. Put $x=y$ in the last equation to get $0*y=y$ as required.
• Let X be an $F_{33}$-algebra. Then $yx*xz=y(xx*z)$. With $z=0$, we have $yx*x=y$. Put $x=y$ in the last equation to get $0*y=y$ as required.
• Let X be an $F_{34}$-algebra. Then $yx*xz=y(x*xz)$. With $z=0$, we have $yx*x=y$. Put $x=y$ in the last equation to get $0*y=y$ as required.
• Let X be an $F_{35}$-algebra. Then $(yx*x)z=(y*xx)z$. With $z=0$, we have $yx*x=y$. Put $x=y$ in the last equation to get $0*y=y$ as required.
• Let X be an $F_{36}$-algebra. Then $(yx*x)z=y(xx*z)$. With $z=0$, we have $yx*x=y$. Put $x=y$ in the last equation to get $0*y=y$ as required.
• Let X be an $F_{37}$-algebra. Then $(yx*x)z=y(x*xz)$. With $z=0$, we have $yx*x=y$. Put $x=y$ in the last equation to get $0*y=y$ as required.
• Let X be an $F_{38}$-algebra. Then, $yz=y*0z$. Put $z=y$, then $y*0y=0$. So, $0y=0\Rightarrow y=0$. Hence, X is p-semisimple (Theorem 8(2)). Now, put $y=x$, then $xz=x*0z$. Now, substitute $x=0$ to get $0z=0*0z$ which means that X is quasi-associative. Thus, by Theorem 9, X is associative.
• Let X be an $F_{40}$-algebra. By the $F_{40}$ identity, $y*0z=y(x*xz)$. Put $z=x=y$ to get $0*0x=0$. So, $0x=0\Rightarrow x=0$. Hence, X is p-semisimple (Theorem 8(2)). Thus, X has the LCL by Theorem 4. Thence, the $F_{40}$ identity $y(xx*z)=y(x*xz)$ becomes $0*z=x*xz$. Substituting $z=x$, we get $0x=x$ which means that X is associative.
• Let X be an $F_{41}$-algebra. Then $xx*yz=(x*xy)z$. With $z=0$, we have $0*y=x*xy$. Put $y=x$ in the last equation to get $0*x=x$ as required.
• Let X be an $F_{43}$-algebra. Then $xx*yz=x(x*yz)$. With $z=0$, we have $0*y=x(x*y)$. Put $x=y$ in the last equation to get $0*y=y$ as required.
• Let X be an $F_{44}$-algebra. Then $xx*yz=x(xy*z)$. With $z=0$, we have $0*y=x(x*y)$. Put $x=y$ in the last equation to get $0*y=y$ as required.
• Let X be an $F_{45}$-algebra. Then $(x*xy)z=(xx*y)z$. With $z=0$, we have $x*xy=0*y$. Put $x=y$ in the last equation to get $0*y=y$ as required.
• Let X be an $F_{47}$-algebra. Then $(x*xy)z=x(xy*z)$. With $y=0$, we have $0*z=x(x*z)$. Put $x=z$ in the last equation to get $0*z=z$ as required.
• Let X be an $F_{48}$-algebra. Then $(xx*y)z=x(x*yz)$. With $z=0$, we have $0*y=x*xy$. Put $x=y$ in the last equation to get $0*y=y$ as required.
• Let X be an $F_{49}$-algebra. Then $(xx*y)z=x(xy*z)$. With $y=0$, we have $0*z=x*xz$. Put $x=z$ in the last equation to get $0*z=z$ as required.
• This is similar to the proof for $F_{10}$-algebra.
• Let X be an $F_{51}$-algebra. Then $yz*xx=(yz*x)x$. With $z=0$, we have $y=(y*x)x$. Put $x=y$ in the last equation to get $0*y=y$ as required.
• Let X be an $F_{53}$-algebra. Then $yz*xx=y(zx*x)$ which becomes $yz=y(zx*x)$. Put $z=x$ to get $yx=y*0x$. Substituting $y=x$, we get $x*0x=0$. So, $0x=0\Rightarrow x=0$, which means that X is p-semisimple (Theorem 8(2)). Now, put $y=0$ in $yx=y*0x$ to get $0x=0*0x$. Hence, X is quasi-associative. Thus, X is associative.
• Let X be an $F_{57}$-algebra. Then $(yz*x)x=y(z*xx)$. With $z=0$, we have $yx*x=y$. Put $x=y$ in the last equation to get $0*y=y$ as required.
• Let X be an $F_{58}$-algebra. Then $(y*zx)x=y(zx*x)$. Put $y=x=z$ to get $x*0x=0$. So, $0x=0\Rightarrow x=0$, which means that X is p-semisimple (Theorem 8(2)). Now, put $z=x,y=0$ to get $0x=0*0x$. Hence, X is quasi-associative. Thus, X is associative.
• Let X be an $F_{60}$-algebra. Then $y(zx*x)=y(z*xx)$. Put $y=x=z$ to get $x*0x=0$. So, $0x=0\Rightarrow x=0$, which means that X is p-semisimple (Theorem 8(2)). Hence, X has the LCL by Theorem 4. Thence, the $F_{10}$ identity becomes $zx*x=z*xx$. Now, substitute $z=x$ to get $0x=x$. Thus, X is associative.

 ☐

Corollary 1.

Let $(X,*,0)$ be a BCI-algebra. If X is any of the following Fenyves’ BCI-algebras, then $(X,*)$ is a Boolean group.

1.  $F_1$-algebra 2.  $F_2$-algebra 3.  $F_4$-algebra 4.  $F_6$-algebra 5.  $F_7$-algebra 6.  $F_9$-algebra 7.  $F_{10}$-algebra 8.  $F_{11}$-algebra 9.  $F_{12}$-algebra 10.  $F_{13}$-algebra	11.  $F_{14}$-algebra 12.  $F_{15}$-algebra 13.  $F_{16}$-algebra 14.  $F_{17}$-algebra 15.  $F_{18}$-algebra 16.  $F_{20}$-algebra 17.  $F_{22}$-algebra 18.  $F_{23}$-algebra 19.  $F_{24}$-algebra 20.  $F_{25}$-algebra	21.  $F_{26}$-algebra 22.  $F_{27}$-algebra 23.  $F_{28}$-algebra 24.  $F_{30}$-algebra 25.  $F_{31}$-algebra 26.  $F_{32}$-algebra 27.  $F_{33}$-algebra 28.  $F_{34}$-algebra 29.  $F_{35}$-algebra 30.  $F_{36}$-algebra	31.  $F_{37}$-algebra 32.  $F_{38}$-algebra 33.  $F_{40}$-algebra 34.  $F_{41}$-algebra 35.  $F_{43}$-algebra 36.  $F_{44}$-algebra 37.  $F_{45}$-algebra 38.  $F_{47}$-algebra 39.  $F_{48}$-algebra 40.  $F_{49}$-algebra	41.  $F_{50}$-algebra
				42.  $F_{51}$-algebra
				43.  $F_{53}$-algebra
				44.  $F_{57}$-algebra
				45.  $F_{58}$-algebra
				46.  $F_{60}$-algebra

Proof. 

This follows from Theorems 12 and 13. ☐

Theorem 14.

Let $(X,*,0)$ be a BCI-algebra.

1. 

Let X be an $F_3$-algebra. X is associative if and only if $x(x*zx)=xz$ if and only if X is p-semisimple.

2. 

Let X be an $F_5$-algebra. X is associative if and only if $(xy*x)x=yx$.

3. 

Let X be an $F_{21}$-algebra. X is associative if and only if $(yx*x)x=x*y$.

4. 

Let X be an $F_{42}$-algebra. X is associative if and only if X is p-semisimple.

5. 

Let X be an $F_{55}$-algebra. X is associative if and only if $\left[\right(y*x)*x]*x=x*y$.

6. 

(a) 

X is an $F_5$-algebra and p-semisimple if and only if X is associative.

(b) 

Let X be an $F_8$-algebra. X is associative if and only if $x(y*zx)=yz$.

7. 

Let X be an $F_{19}$-algebra. X is associative if and only if quasi-associative.

8. 

X is an $F_{39}$-algebra and obeys $y(x*xz)=zy$ if and only if X is associative.

9. 

Let X be a $F_{46}$-algebra. X is associative if and only if $0(0*0x)=x$.

10. 

(a) 

X is an $F_{52}$-algebra and $F_{55}$-algebra if and only if X is associative.

(b) 

X is an $F_{52}$-algebra and obeys $(y*zx)x=zy$ if and only if X is associative.

(c) 

X is an $F_{55}$-algebra and p-semisimple if and only if X is associative.

(d) 

Let X be an $F_{52}$-algebra. X is associative if and only if X is quasi-associative.

11. 

(a) 

X is an $F_{59}$-algebra and $F_{55}$-algebra if and only if X is associative.

(b) 

X is an $F_{52}$-algebra and obeys $(y*zx)x=zy$ if and only if X is associative.

(c) 

Let X be a $F_{56}$-algebra. X is associative if and only if X is quasi-associative.

(d) 

Let X be an $F_{59}$-algebra. X is associative if and only if X is quasi-associative.

Proof. 

• Suppose X is a $F_3$-algebra. Then, $xy*zx=x(y*zx)$. Put $y=x$ to get $0*zx=x(x*zx)$. Substituting $x=0$, we have $0z=0*0z$ which means X is quasi-associative. Going by Theorem 9, X is associative if and only if X is p-semisimple. Furthermore, by Theorem 4(3) and $0*zx=x(x*zx)$, an $F_3$-algebra X is associative if and only if $xy=x(x*zx)$.
• Suppose X is associative. Then $0*x=x$. X is $F_5$ implies $(xy*z)x=(x*yz)x$. With $z=x$, we have $(xy*x)x=(x*yx)x\Rightarrow (xy*x)x=(x*x)yx\Rightarrow (xy*x)x=0*yx\Rightarrow (xy*x)x=yx$ as required. Conversely, suppose $(xy*x)x=yx$. Put $z=x$ in $(xy*z)x=(x*yz)x$ to get $(xy*x)x=(x*yx)x\Rightarrow (xy*x)x=(x*x)yx\Rightarrow (xy*x)x=0*yx\Rightarrow yx=0*yx$ (since $(xy*x)x=yx$). So, X is associative.
• Suppose X is associative. Then $x*y=y*x$. X is $F_{21}$ implies $yx*zx=(yx*z)x$. With $z=x$, we have $(yx*x)x=y*x=x*y$ as required. Conversely, suppose $(yx*x)x=x*y$. Put $z=x$ in $F_{21}$ to get $(yx*x)x=y*x$. So, $x*y=y*x$ as required.
• Suppose X is associative. Then $0*z=z$. X is $F_{42}$ implies $xx*yz=(xx*y)z$. With $y=0$, we have $0*0z=0*z=z$ as required. Conversely, suppose $0*0z=z$. Put $y=0$ in $F_{42}$ to get $0*0z=0*z$. So, $0*z=z$ as required.
• Suppose X is associative. Then $x*y=y*x$. X is $F_{55}$ implies $\left[\right(y*z)*x]*x=[y*(z*x\left)\right]*x$. With $z=x$, we have $\left[\right(y*x)*x]*x=y*x=x*y$ as required. Conversely, suppose $\left[\right(y*x)*x]*x=x*y$. Put $z=x$ in $F_{55}$ to get $y*x=\left[\right(y*x)*x]*x=x*y$. So, $y*x=x*y$ as required.

The proofs of 6 to 11 follow by using the concerned $F_i$ and $F_j$ identities (plus p-simplicity by Theorem 12 in some cases) to get an $F_k$ which is equivalent to associativity by Theorem 13 or which is not equivalent to associativity by 1 to 5 of Theorem 14. ☐

3. Summary, Conclusions and Recommendations

In this work, we have been able to construct examples of Fenyves’ BCI-algebras. We have also obtained the basic algebraic properties of Fenyves’ BCI-algebras. Furthermore, we have categorized the Fenyves’ BCI-algebras into a 46 member associative class (as captured in Theorem 13). Members of this class include $F_1$, $F_2$, $F_4$, $F_6$, $F_7$, $F_9$, $F_{10}$, $F_{11}$, $F_{12}$, $F_{13}$, $F_{14}$, $F_{15},$$F_{16}$, $F_{17}$, $F_{18}$, $F_{20}$, $F_{22}$, $F_{23}$, $F_{24}$, $F_{25}$, $F_{26}$, $F_{27}$, $F_{28}$, $F_{30}$, $F_{31}$, $F_{32}$, $F_{33}$, $F_{34}$, $F_{35}$, $F_{36}$, $F_{37}$, $F_{38}$, $F_{40}$, $F_{41}$, $F_{43}$, $F_{44}$, $F_{45}$, $F_{47}$, $F_{48}$, $F_{49}$, $F_{50}$, $F_{51}$, $F_{53}$, $F_{57}$, $F_{58}$, $F_{60}$-algebras; and a 14 member non-associative class. Those Fenyves identities that are equivalent to associativity in BCI-algebras are denoted by ✓ in the fifth column of

Table 1. Characterization of Fenyves Identities in Quasigroups, Loops and BCI-Algebras by Associativity.

Fenyves	${\mathit{F}}_{\mathit{i}}\equiv \mathit{ASS}$	${\mathit{F}}_{\mathit{i}}\not\equiv \mathit{ASS}$	Quassigroup	${\mathit{F}}_{\mathit{i}}+\mathit{BCI}$
Identity	Inaloop	Inaloop	⇒ Loop	⇒ ASS
$F_1$	✓		✓	✓
$F_2$		✓	✓	✓
$F_3$	✓		✓	‡
$F_4$		✓		✓
$F_5$	✓			‡
$F_6$		✓	✓	✓
$F_7$	✓			✓
$F_8$	✓			‡
$F_9$		✓		✓
$F_{10}$	✓			✓
$F_{11}$	✓		✓	✓
$F_{12}$	✓		✓	✓
$F_{13}$		✓	✓	✓
$F_{14}$	✓			✓
$F_{15}$		✓		✓
$F_{16}$	✓			✓
$F_{17}$		✓	✓	✓
$F_{18}$	✓		✓	✓
$F_{19}$		✓		‡
$F_{20}$	✓			✓
$F_{21}$	✓		✓	‡
$F_{22}$		✓	✓	✓
$F_{23}$	✓			✓
$F_{24}$	✓			✓
$F_{25}$	✓			✓
$F_{26}$		✓		✓
$F_{27}$		✓	✓	✓
$F_{28}$	✓		✓	✓
$F_{29}$	✓			‡
$F_{30}$		✓		✓
$F_{31}$	✓		✓	✓
$F_{32}$	✓		✓	✓
$F_{33}$	✓			✓
$F_{34}$	✓			✓
$F_{35}$		✓		✓
$F_{36}$		✓		✓
$F_{37}$		✓		✓
$F_{38}$		✓	✓	✓
$F_{39}$		✓		‡
$F_{40}$		✓		✓
$F_{41}$		✓	✓	✓
$F_{42}$		✓		‡
$F_{43}$		✓		✓
$F_{44}$	✓			✓
$F_{45}$		✓		✓
$F_{46}$		✓		‡
$F_{47}$	✓		✓	✓
$F_{48}$		✓		✓
$F_{49}$	✓			✓
$F_{50}$	✓			✓
$F_{51}$		✓		✓
$F_{52}$	✓			‡
$F_{53}$		✓	✓	✓
$F_{54}$		✓		‡
$F_{55}$	✓			‡
$F_{56}$		✓		‡
$F_{57}$		✓		✓
$F_{58}$	✓		✓	✓
$F_{59}$	✓			‡
$F_{60}$		✓		✓

. For those that belong to the non-associative class, we have been able to obtain conditions under which they would be associative (as reflected in Theorem 14). This class includes $F_3$, $F_5$, $F_8$, $F_{19}$, $F_{21}$,$F_{29}$, $F_{39}$ , $F_{42}$, $F_{46}$, $F_{52}$, $F_{54}$, $F_{55}$, $F_{56}$, $F_{59}$-algebras. In Table 1 which summarizes the results, members of this class are identified by the symbol ‘‡’.

Other researchers who have studied Fenyves’ identities on the platform of loops, namely Phillips and Vojtechovsky [5], Jaiyeola [6], Kinyon and Kunen (2004) found Moufang ($F_2$, $F_4$, $F_{17}$, $F_{27}$), extra ($F_6$, $F_{13}$, $F_{22}$), $F_9$, $F_{15}$, left Bol ($F_{19}$), right Bol ($F_{26}$), Moufang ($F_4$, $F_{27}$), $F_{30}$, $F_{35}$, $F_{36}$, C ($F_{37}$), $F_{38}$, $F_{39}$, $F_{40}$, LC ($F_{39}$, $F_{41}$, $F_{46}$, $F_{48}$), $F_{42}$, $F_{43}$, $F_{45}$, $F_{51}$, RC ($F_{36}$, $F_{53}$, $F_{56}$, $F_{57}$), $F_{54}$, and $F_{60}$ Fenyves’ identities not to be equivalent to associativity in loops. Interestingly, in our study, some of these identities, particularly the extra identity ($F_6$, $F_{13}$, $F_{22}$), $F_7$, $F_9$, $F_{15}$, $F_{17}$, right Bol ($F_{26}$), Moufang ($F_4$, $F_{27}$), $F_{30}$, $F_{35}$, $F_{38}$, $F_{40}$, RC($F_{36}$, $F_{53}$, $F_{57}$), C ($F_{37}$), LC ($F_{41}$, $F_{48}$), $F_{43}$, $F_{45}$, $F_{51}$ and $F_{60}$ have been found to be equivalent to associativity in BCI-algebras. In addition, the aforementioned researchers found $F_1$, $F_3$, $F_5$, $F_7$, $F_8$, $F_{10}$, $F_{11}$, $F_{12}$, $F_{14}$, $F_{16}$, $F_{18}$, $F_{20}$, $F_{21}$, $F_{23}$, $F_{24}$, $F_{25}$, $F_{28}$, $F_{29}$, $F_{31}$, $F_{32}$, $F_{33}$, $F_{34}$, $F_{44}$, $F_{47}$, $F_{49}$, $F_{50}$, $F_{52}$, $F_{55}$, $F_{58}$ and $F_{59}$ identities to be equivalent to associativity in loops. We have also found some ($F_7$, $F_{10}$, $F_{11}$, $F_{12}$, $F_{14}$, $F_{16}$, $F_{18}$,$F_{20}$, $F_{23}$, $F_{24}$, $F_{25}$, $F_{28}$, $F_{31}$, $F_{32}$, $F_{33}$, $F_{44}$, $F_{47}$, $F_{49}$, $F_{50}$, $F_{58}$) of these identities to be equivalent to associativity in BCI-algebras while some others ($F_3$, $F_5$, $F_8$, $F_{20}$, $F_{21}$, $F_{29}$,$F_{55}$, $F_{59}$) were not equivalent to associativity in BCI-algebras.

In loop theory, it is well known that:

• A loop is an extra loop if and only if the loop is both a Moufang loop and a C-loop.
• A loop is a Moufang loop if and only if the loop is both a right Bol loop and a left Bol-loop.
• A loop is a C-loop if and only if the loop is both a RC-loop and a LC-loop.

In this work, we have been able to establish (as stated below) somewhat similar results for a few of the Fenyves’ identities in a BCI-algebra X:

• X is an $F_i$-algebra and $F_j$-algebra if and only if X is associative, for the pairs: $i=52,j=55$, $i=59,j=55$.

Fenyves [31], and Phillips and Vojtěchovský [32,33] found some of the 60 $F_i$ identities to be equivalent to associativity in quasigroups and loops (i.e., groups), and others to describe weak associative laws such as extra, Bol, Moufang, central, flexible laws in quasigroups and loops. Their results are summarised in the second, third and fourth columns of Table 1 with the use of ✓. In this paper, we went further to establish that 46 Fenyves’ identities are equivalent to associativity in BCI-algebras while 14 Fenyves’ identities are not equivalent to associativity in BCI-algebras. These two categories are denoted by ✓ and ‡ in the fifth column of Table 1.

After the works of [31,32,33], the authors in [34,35,36,37,38] did an extension by investigating and classifying various generalized forms of the identities of Bol-Moufang types in quasigroups and one sided/two sided loops into associative and non-associative categories. This answered a question originally posed in [39] and also led to the study of one of the newly discovered generalized Bol-Moufang types of loop in Jaiyéọlá et al. [40]. While all the earlier mentioned research works on Bol-Moufang type identities focused on quasigroups and loop, this paper focused on the study of Bol-Moufang type identities (Fenyves’ identities) in special types of groupoids (BCI-algebra and quasi neutrosophic triplet loops) which are not necessarily quasigroups or loops (as proved in Theorem 12). Examples of such well known varieties of groupoids were constructed by Ilojide et al. [41], e.g., Abel-Grassmann’s groupoid.

The results of this work are an initiation into the study of the classification of finite Fenyves’ quasi neutrosophic triplet loops (FQNTLs) just like various types of finite loops have been classified (e.g., Bol loops, Moufang loops and FRUTE loops). In fact, a library of finite Moufang loops of small order is available in the GAPS-LOOPS package [42]. It will be intriguing to have such a library of FQNTLs.

Overall, this research work (especially for the non-associative $F_i$’s) has opened a new area of research findings in BCI-algebras and Bol-Moufang type quasi neutrosophic triplet loops as shown in Figure 1.