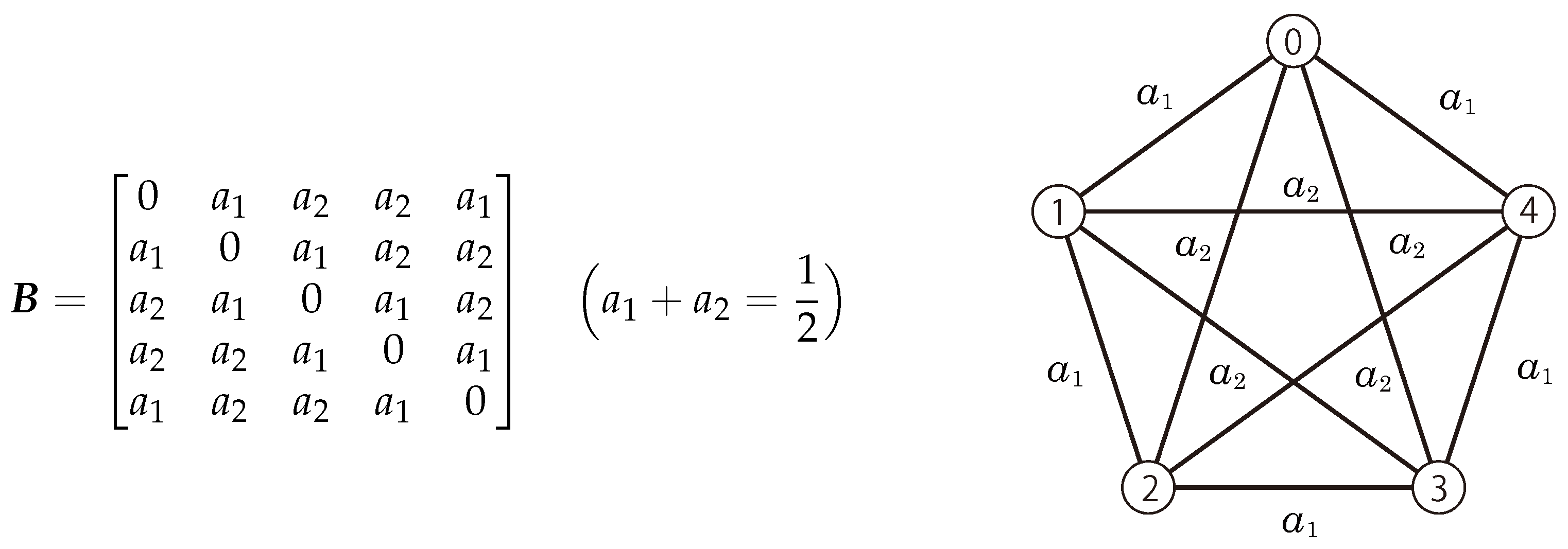A Hierarchical Structure for the Sharp Constants of Discrete Sobolev Inequalities on a Weighted Complete Graph

Abstract

This paper clarifies the hierarchical structure of the sharp constants for the discrete Sobolev inequality on a weighted complete graph. To this end, we introduce a generalized-graph Laplacian $\mathit{A}=\mathit{I}-\mathit{B}$ on the graph, and investigate two types of discrete Sobolev inequalities. The sharp constants $C_0(N;a)$ and $C_0\left(N\right)$ were calculated through the Green matrix $\mathit{G}\left(a\right)={(\mathit{A}+a\mathit{I})}^{-1}(0<a<\infty )$ and the pseudo-Green matrix ${\mathit{G}}_{\ast }={\mathit{A}}^{†}$. The sharp constants are expressed in terms of the expansion coefficients of the characteristic polynomial of A. Based on this new discovery, we provide the first proof that each set of the sharp constants ${\left\{C_0(n;a)\right\}}_{n=2}^N$ and ${\left\{C_0\left(n\right)\right\}}_{n=2}^N$ satisfies a certain hierarchical structure.

1. Introduction

The sharp (smallest) constant and a family of best functions for the Sobolev inequality,

$$\begin{array}{cc}\hfill & {\parallel u\parallel }_{L^q\left({\mathbb{R}}^n\right)}\le C{\parallel \nabla u\parallel }_{L^p\left({\mathbb{R}}^n\right)}{}^{\forall }u\in W^{1,p}\left({\mathbb{R}}^n\right)=\{u\in L^q\left({\mathbb{R}}^n\right),\nabla u\in L^p\left({\mathbb{R}}^n\right)\},\hfill \end{array}$$

(1)

were independently discovered by Aubin [1] and Talenti [2] in the case $1<p<n$, $q=np/(n-p)$. They computed the sharp constant using a symmetric rearrangement and found the family of best functions that satisfy the equality in (1). In our study, we mainly investigate the case $p\le 2$, $q=\infty$ and compute the sharp constants for the Sobolev inequalities using the Green functions corresponding to various boundary value problems. This is a unique approach that remarkably differs from symmetric rearrangement. The Green functions are reproducing kernels for suitable sets of Hilbert space and an inner product. As a relevant application, the sharp constant for the corresponding Sobolev inequality is expressed as the maximum value of the Green function’s diagonal [3]. The obtained Sobolev inequalities are applicable to beam deflection problems [4], electric circuits [5] and a range of other practical problems.

Recently, research works of inequalities were performed on various kinds of graphs (see Chung [6], for example). Similarly to continuous cases, the discrete version of Laplacian A and corresponding Green matrices G play crucial roles. We focused our attention on fundamental and symmetric graphs such as complete graphs, cycles, platonic solids, truncated regular tetrahedrons, hexahedrons, octahedra and Toeplitz graphs [7]. We investigated a graph Laplacian and corresponding discrete Sobolev inequalities in a detailed manner.

The purpose of this paper is to extend the results on a complete graph by Yamagishi et al. [8] to a weighted graph. In the same way as the previous research, we first introduce generalized graph Laplacian A on a graph and investigate its eigenvalues and Green and pseudo-Green matrices [9]. In particular, we derive two types of discrete Sobolev inequalities and obtain their sharp constants $C_0(N;a)$ and $C_0\left(N\right)$ by investigating the reproducing properties of the Green and pseudo-Green matrices. One of the interesting results of this paper is that these sharp constants satisfy suitable hierarchical structures with respect to the graph order N. The sharp constant $C_0(N;a)$ is monotone decreasing with respect to N, whereas the other one $C_0\left(N\right)$ is monotone increasing.

The rest of the paper is organized as follows. Section 2 defines the generalized graph Laplacian on a weighted complete graph, and Section 3 presents the discrete Sobolev inequalities. In Section 4, we compute the diagonal values of the Green matrices, which are the sharp constants of the discrete Sobolev inequalities. Section 5 is devoted to the proofs of our main theorems concerning hierarchical structures of sharp constants. In Section 6, explicit forms of specific sharp constants in two special cases are given for small N.

2. Graph Laplacian

For $N=2,3,\cdots$, we introduce the generalized graph Laplacian on a complete graph.

Let G be a weighted complete graph with a vertex set $V=\{0,1,\cdots ,N-1\}$ and an edge set:

$$\begin{array}{c}\hfill E=\left\{\right[i,j\left]\right|i\ne j,i,j\in V\}.\end{array}$$

In this research, we assume that the complete graphs G are always connected and undirected with no self-loops or multiple edges. We use the conventional construct $\left|V\right(G\left)\right|=N$ and $\left|E\right(G\left)\right|=M$, i.e., G is a weighted complete graph with N vertices and M edges.

Definition 1.

Let $G=K_N$ with a vertex set $V=\{0,1,\cdots ,N-1\}$. The generalized graph Laplacian of G is then defined as the $N\times N$ matrix:

$$\begin{array}{c}\hfill \mathit{A}=\mathit{I}-\mathit{B},\end{array}$$

where I is the identity matrix and B is the adjacency matrix of G (see Figure 1).

$$\begin{array}{c}\hfill \mathit{B}=\left[b(i,j)\right],b(i,j)=\left\{\begin{array}{cc}{a}_{m\left(\right|i-j\left|\right)}\hfill & [i,j]\in E,\hfill \\ 0\hfill & otherwise,\hfill \end{array}\right.\end{array}$$

Here, $a_i>0(1\le i\le [N/2])$ and:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{a}_1=1\hfill & (N=2),\hfill \\ {\displaystyle 2\sum _{i=1}^{n-1}{a}_i+a_n=1}\hfill & (N=2n),\hfill \\ {\displaystyle 2\sum _{i=1}^n{a}_i=1}\hfill & (N=2n+1),\hfill \end{array}\right.(n\in \mathbb{N}\backslash \left\{1\right\}).\end{array}$$

The function $m\left(j\right)$ is defined as $min\{j,N-j\}$.

The matrix B is a symmetric stochastic matrix, expressed as follows [10]:

$$\begin{array}{c}\hfill \mathit{B}=\sum _{j=1}^{N-1}{a}_{m\left(j\right)}({\mathit{F}}^j+{}^t{\mathit{F}}^j),\end{array}$$

(2)

where:

$$\begin{array}{c}\hfill \mathit{F}=\left[\begin{array}{ccccc}0& & & & \mathbf{0}\\ 1& 0& & & \\ & \ddots & \ddots & & \\ \mathbf{0}& & & 1& 0\end{array}\right]=\left[\begin{array}{cc}{\mathbf{0}}_{1,N-1}& 0\\ {\mathit{I}}_{N-1}& \mathbf{0}\end{array}\right].\end{array}$$

A can also be expressed in terms of the $N\times N$ permutation matrix ${\mathit{C}}_N={\mathit{F}}^{N-1}+{}^t\mathit{F}$ as follows:

$$\begin{array}{cc}\hfill \mathit{A}& =\left\{\begin{array}{cc}{\displaystyle {\mathit{I}}_{2n}-\sum _{j=1}^{n-1}{a}_j({\mathit{C}}_{2n}^j+{\mathit{C}}_{2n}^{-j})-a_n{\mathit{C}}_{2n}^n}\hfill & N=2n,\hfill \\ {\displaystyle {\mathit{I}}_{2n+1}-\sum _{j=1}^n{a}_j({\mathit{C}}_{2n+1}^j+{\mathit{C}}_{2n+1}^{-j})}\hfill & N=2n+1,\hfill \end{array}\right.(n\in \mathbb{N}).\hfill \end{array}$$

(3)

The following proposition is a direct consequence of A defined in (3).

Proposition 1.

Let $G=K_N$ with a vertex set, $V=\{0,1,\cdots ,N-1\}$. Subsequently, the generalized graph Laplacian A on G has the following eigenvalues:

($N=2$):

$$\begin{array}{c}\hfill {\lambda }_0=0,{\lambda }_1=2,\end{array}$$

($N\ge 3$):

$$\begin{array}{c}{\lambda }_i=\left\{\begin{array}{cc}{\displaystyle \{1+{(-1)}^{i+1}\}{a}_n+4\sum _{j=1}^{n-1}{a}_j{sin}^2\left(\frac{ij\pi }{2n}\right)}\hfill & N=2n,\hfill \\ {\displaystyle 4\sum _{j=1}^n{a}_j{sin}^2\left(\frac{ij\pi }{2n+1}\right)}\hfill & N=2n+1,\hfill \end{array}\right.(0\le i\le N-1,n\in \mathbb{N}).\hfill \end{array}$$

From Proposition 1, all eigenvalues are distributed as follows:

$$\begin{array}{c}\hfill 0={\lambda }_0<{\lambda }_i\le 2(1\le i\le N-1).\end{array}$$

Let $P_N\left(x\right)$ be the characteristic polynomial for A:

$$\begin{array}{c}\hfill P_N\left(x\right)=\prod _{j=0}^{N-1}(x-{\lambda }_j)=\sum _{j=0}^N{(-1)}^j{d}_{N,j}{x}^{N-j},\end{array}$$

where:

$$\begin{array}{c}\hfill d_{N,0}=1,d_{N,j}=\sum _{0\le i_1<\cdots <i_j\le N-1}\prod _{k=1}^j{\lambda }_{i_k}(j=1,2,\cdots ,N).\end{array}$$

3. Discrete Sobolev Inequalities

Let $G=(V,E)$ be the weighted complete graph in Definition 1. For each vertex $i\in V$, we attach a complex number, $u\left(i\right)$. For the vector $\mathit{u}={}^t[u\left(0\right)u\left(1\right)\cdots u(N-1)]\in {\mathbb{C}}^{\left|V\right|}$, we define two types of Sobolev energies (i.e., potential energies) using the generalized graph Laplacian:

$$\begin{array}{c}{E}_N\left(\mathit{u}\right)=\frac{1}{2}\sum _{[i,j]\in E}{a}_{m\left(\right|i-j\left|\right)}{|u\left(i\right)-u\left(j\right)|}^2={\mathit{u}}^{\ast }\mathit{A}\mathit{u},\hfill \\ E_N(a;\mathit{u})=E_N\left(\mathit{u}\right)+a\sum _{j\in V}{\left|u\left(j\right)\right|}^2={\mathit{u}}^{\ast }(\mathit{A}+a\mathit{I})\mathit{u},\hfill \end{array}$$

where a is a positive dumping constant.

To explain our conclusion, we assume that $\mathit{G}\left(a\right)={(\mathit{A}+a\mathit{I})}^{-1}(0<a<\infty )$ and that ${\mathit{G}}_{\ast }$ is a Penrose–Moore generalized inverse ${\mathit{A}}^{†}$ of A. In particular, ${\mathit{G}}_{\ast }$ satisfies:

$$\begin{array}{c}\hfill \mathit{A}{\mathit{G}}_{\ast }={\mathit{G}}_{\ast }\mathit{A}=\mathit{I}-{\mathit{E}}_0,{\mathit{G}}_{\ast }{\mathit{E}}_0={\mathit{E}}_0{\mathit{G}}_{\ast }=\mathit{O}.\end{array}$$

(4)

${\mathit{E}}_0=(1/N)\mathbf{1}{}^{\mathbf{t}}\mathbf{1}$ is the orthogonal projection matrix to the eigenspace corresponding to the eigenvalue ${\lambda }_0=0$ of A. Hereafter, we refer to ${\mathit{G}}_{\ast }$ as the pseudo-Green matrix.

To prove the relation (4), we derive spectral decompositions of $\mathit{G}\left(a\right)$ and ${\mathit{G}}_{\ast }$. Since the generalized graph Laplacian A is an $N\times N$ real symmetric matrix, A is diagonalized as $\widehat{\mathit{A}}={\mathit{Q}}^{\ast }\mathit{A}\mathit{Q}=\mathrm{diag}\{{\lambda }_0,\cdots ,{\lambda }_{N-1}\}$ using the unitary matrix $\mathit{Q}=\left[q_j\left(i\right)\right](0\le i,j\le N-1)$. Vectors ${\mathit{q}}_j$ are eigenvectors corresponding to eigenvalues ${\lambda }_j$ of A. Furthermore, vectors ${\mathit{q}}_j$ are chosen such that they satisfy the relation ${\mathit{q}}_i^{\ast }{\mathit{q}}_j={\delta }_{ij}$, where ${\delta }_{ij}$ is the Kronecker delta. The orthogonal projection matrices defined by ${\mathit{E}}_k={\mathit{q}}_k{\mathit{q}}_k^{\ast }(0\le k\le N-1)$ satisfy:

$$\begin{array}{c}\hfill {\mathit{E}}_k^{\ast }={\mathit{E}}_k,{\mathit{E}}_k{\mathit{E}}_l={\delta }_{kl}{\mathit{E}}_k(0\le k,l\le N-1).\end{array}$$

Using the projection matrices, the generalized graph Laplacian A and the identity matrix I have the following symmetric eigenvalue decompositions:

$$\begin{array}{c}\hfill \mathit{A}=\mathit{Q}\widehat{\mathit{A}}{\mathit{Q}}^{\ast }=\sum _{k=0}^{N-1}{\lambda }_k{\mathit{E}}_k=\sum _{k=1}^{N-1}{\lambda }_k{\mathit{E}}_k,\mathit{I}=\mathit{Q}{\mathit{Q}}^{\ast }=\sum _{k=0}^{N-1}{\mathit{E}}_k.\end{array}$$

(5)

Thus, we have:

$$\begin{array}{c}\hfill \mathit{A}+a\mathit{I}=\sum _{k=0}^{N-1}({\lambda }_k+a){\mathit{E}}_k.\end{array}$$

(6)

From the above discussions, the spectral decompositions of $\mathit{G}\left(a\right)$ and ${\mathit{G}}_{\ast }$ are expressed as follows:

$$\begin{array}{cc}\hfill \mathit{G}\left(a\right)& =\sum _{k=0}^{N-1}{({\lambda }_k+a)}^{-1}{\mathit{E}}_k,\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill {\mathit{G}}_{\ast }& =\sum _{k=1}^{N-1}{\lambda }_k^{-1}{\mathit{E}}_k.\hfill \end{array}$$

(8)

From (5) and (8), we obtain (4). Additionally, we note that the relation:

$$\begin{array}{c}\hfill {\mathit{G}}_{\ast }=\underset{a\downarrow 0}{lim}(\mathit{G}\left(a\right)-a^{-1}{\mathit{E}}_0)\end{array}$$

(9)

holds between $\mathit{G}\left(a\right)$ and ${\mathit{G}}_{\ast }$.

Thus, we arrive at the following theorems.

Theorem 1.

Let $N=2,3,\cdots$ and $V=\{0,1,\cdots ,N-1\}$. For any $\mathit{u}\in {\mathbb{C}}^{\left|V\right|}$, there exists a positive constant C, independent of u, such that the discrete Sobolev inequality:

$$\begin{array}{c}\hfill {\left(\underset{j\in V}{max}\left|u\left(j\right)\right|\right)}^2\le C{E}_N(a;\mathit{u})\end{array}$$

(10)

holds. Among the set of Cs, the sharp constant $C_0\left(a\right)$ is expressed as follows:

$$\begin{array}{cc}\hfill C_0\left(a\right)& =C_0(N;a)={\displaystyle \frac{1}{\left|V\right|}}\sum _{j=0}^{N-1}{({\lambda }_j+a)}^{-1}.\hfill \end{array}$$

(11)

If C in the above inequality is replaced by $C_0(N;a)$, the inequality becomes an equality for any column vector u of $\mathit{G}\left(a\right)$.

Theorem 2.

Let $N=2,3,\cdots$ and $V=\{0,1,\cdots ,N-1\}$. For any $\mathit{u}\in {\mathbb{C}}^{\left|V\right|}$ satisfying ${}^t\mathbf{1}\mathit{u}=0$, there exists a positive constant C that is independent of u, such that the discrete Sobolev inequality:

$$\begin{array}{c}\hfill {\left(\underset{j\in V}{max}\left|u\left(j\right)\right|\right)}^2\le C{E}_N\left(\mathit{u}\right)\end{array}$$

(12)

holds. Among the set of Cs, the sharp constant $C_0$ is expressed as follows:

$$\begin{array}{c}\hfill C_0=C_0\left(N\right)={\displaystyle \frac{1}{\left|V\right|}}\sum _{j=1}^{N-1}{\lambda }_j^{-1}.\end{array}$$

(13)

If C is replaced by $C_0\left(N\right)$ in the above inequality, the equality holds for any column vector u of ${\mathit{G}}_{\ast }$.

We now explain the physical meaning of Theorems 1 and 2. A real-valued $u\left(i\right)$ represents a deviation from the steady state. In each discrete Sobolev inequality, the square of the maximum deviation $\left|u\right(i\left)\right|$ is estimated by a constant multiple of the potential energy, $E_N(a;\mathit{u})$ or $E_N\left(\mathit{u}\right)$. Hence, the sharp constant is expected to represent the rigidity of the mechanical model corresponding to the weighted complete graph.

From (11), it follows that $C\left(a\right)$ is a monotonically-decreasing function of a. From the monotonicity with respect to a, Equations (9), (11) and (13), we obtain the following theorem:

Theorem 3.

The following relation holds:

$$\begin{array}{c}\hfill C_0=\underset{a\downarrow 0}{lim}\{C\left(a\right)-{\left(Na\right)}^{-1}\}.\end{array}$$

Since the proofs of the main Theorems 1–3 are essentially equivalent to those given in [11], we omit them.

4. Sharp Constants

In this section, we compute the entries on the main diagonals of the Green matrices, which are the sharp constants of the discrete Sobolev inequalities.

For $0\le j\le N-1$, we introduce the j-th unit vector as:

$$\begin{array}{c}\hfill {\mathbf{\delta }}_j={}^t{[\cdots {\delta }_{jk}\cdots ]}_{0\le k\le N-1},\end{array}$$

which is essential for deriving our conclusion.

Proposition 2.

For any $0\le j_0\le N-1$, we have:

$$\begin{array}{c}\hfill C_0(N;a)={}^t{\mathbf{\delta }}_{j_0}\mathit{G}\left(a\right){\mathbf{\delta }}_{j_0}={\displaystyle \frac{1}{\left|V\right|}}\sum _{k=0}^{N-1}{({\lambda }_k+a)}^{-1}.\end{array}$$

$C_0$ can also be expressed in terms of the expansion coefficients of the characteristic polynomial as follows:

$$\begin{array}{c}\hfill C_0(N;a)={\displaystyle \frac{{\displaystyle \sum _{j=0}^{N-1}(N-j)d_{N,j}{a}^{N-j-1}}}{{\displaystyle N\sum _{j=0}^N{d}_{N,j}{a}^{N-j}}}}.\end{array}$$

(14)

Proof of Proposition 2.

As G is a Toeplitz matrix, for any $0\le j_0\le N-1$, we obtain:

$$\begin{array}{cc}\hfill C_0(N;a)& ={}^t{\mathbf{\delta }}_{j_0}\mathit{G}\left(a\right){\mathbf{\delta }}_{j_0}={\displaystyle \frac{1}{\left|V\right|}}\sum _{j=0}^{N-1}{}^t{\mathbf{\delta }}_j\mathit{G}\left(a\right){\mathbf{\delta }}_j={\displaystyle \frac{1}{\left|V\right|}}\sum _{k=0}^{N-1}{({\lambda }_k+a)}^{-1}\sum _{j=0}^{N-1}{}^t{\mathbf{\delta }}_j{\mathit{E}}_k{\mathbf{\delta }}_j\hfill \\ & ={\displaystyle \frac{1}{\left|V\right|}}\sum _{k=0}^{N-1}{({\lambda }_k+a)}^{-1}\sum _{j=0}^{N-1}\parallel {\mathit{q}}_k^{\ast }{\mathbf{\delta }}_j{\parallel }^2={\displaystyle \frac{1}{\left|V\right|}}\sum _{k=0}^{N-1}{({\lambda }_k+a)}^{-1}{\parallel {\mathit{q}}_k\parallel }^2\hfill \\ & ={\displaystyle \frac{1}{\left|V\right|}}\sum _{k=0}^{N-1}{({\lambda }_k+a)}^{-1}.\hfill \end{array}$$

Here, we have used Equation (7). Furthermore, after reducing this expression to a common denominator, we obtain the following expression using the expansion coefficients of the characteristic polynomial:

$$\begin{array}{cc}\hfill C_0(N;a)& ={\displaystyle \frac{1}{N}}\sum _{k=0}^{N-1}{\displaystyle \frac{1}{{\lambda }_k+a}}={\displaystyle \frac{{\displaystyle \sum _{0\le i_1<\cdots <i_{N-1}\le N-1}\prod _{k=1}^{N-1}({\lambda }_{i_k}+a)}}{{\displaystyle N\prod _{k=0}^{N-1}({\lambda }_k+a)}}}\hfill \\ & ={\displaystyle \frac{{\displaystyle N{a}^{N-1}+\sum _{j=1}^{N-1}(N-j)\left(\sum _{0\le i_1<\cdots <i_j\le N-1}\prod _{k=1}^j{\lambda }_{i_k}\right)a^{N-j-1}}}{{\displaystyle N\left\{a^N+\sum _{j=1}^N\left(\sum _{0\le i_1<\cdots <i_j\le N-1}\prod _{k=1}^j{\lambda }_{i_k}\right)a^{N-j}\right\}}}}\hfill \\ & ={\displaystyle \frac{{\displaystyle N{a}^{N-1}+\sum _{j=1}^{N-1}(N-j)d_{N,j}{a}^{N-j-1}}}{{\displaystyle N\left(a^N+\sum _{j=1}^N{d}_{N,j}{a}^{N-j}\right)}}}={\displaystyle \frac{{\displaystyle \sum _{j=0}^{N-1}(N-j)d_{N,j}{a}^{N-j-1}}}{{\displaystyle N\sum _{j=0}^N{d}_{N,j}{a}^{N-j}}}}.\hfill \end{array}$$

The proof of Proposition 2 is now complete. ☐

Proposition 3.

For any $0\le j_0\le N-1$, we have:

$$\begin{array}{c}\hfill C_0\left(N\right)={}^t{\mathbf{\delta }}_{j_0}{\mathit{G}}_{\ast }{\mathbf{\delta }}_{j_0}={\displaystyle \frac{1}{\left|V\right|}}\sum _{k=1}^{N-1}{\lambda }_k^{-1}.\end{array}$$

$C_0\left(N\right)$ can also be expressed in terms of the expansion coefficients of the characteristic polynomial as follows:

$$\begin{array}{c}\hfill C_0\left(N\right)={\displaystyle \frac{d_{N,N-2}}{N{d}_{N,N-1}}}.\end{array}$$

(15)

Proof of Proposition 3.

Since ${\mathit{G}}_{\ast }$ is a Toeplitz matrix, for any $0\le j_0\le N-1$, we therefore obtain:

$$\begin{array}{cc}\hfill C_0\left(N\right)& ={}^t{\mathbf{\delta }}_{j_0}{\mathit{G}}_{\ast }{\mathbf{\delta }}_{j_0}={\displaystyle \frac{1}{\left|V\right|}}\sum _{j=0}^{N-1}{}^t{\mathbf{\delta }}_j{\mathit{G}}_{\ast }{\mathbf{\delta }}_j={\displaystyle \frac{1}{\left|V\right|}}\sum _{k=1}^{N-1}{\lambda }_k^{-1}\sum _{j=0}^{N-1}{}^t{\mathbf{\delta }}_j{\mathit{E}}_k{\mathbf{\delta }}_j\hfill \\ & ={\displaystyle \frac{1}{\left|V\right|}}\sum _{k=1}^{N-1}{\lambda }_k^{-1}\sum _{j=0}^{N-1}\parallel {\mathit{q}}_k^{\ast }{\mathbf{\delta }}_j{\parallel }^2={\displaystyle \frac{1}{\left|V\right|}}\sum _{k=1}^{N-1}{\lambda }_k^{-1}{\parallel {\mathit{q}}_k\parallel }^2\hfill \\ & ={\displaystyle \frac{1}{\left|V\right|}}\sum _{k=1}^{N-1}{\lambda }_k^{-1}.\hfill \end{array}$$

Here, we have used Equation (8). Again reducing $C_0\left(N\right)$ to a common denominator, we obtain the following expressions using the expansion coefficients of the characteristic polynomial:

($N=2$):

$$\begin{array}{c}\hfill C_0\left(2\right)={\displaystyle \frac{1}{2{\lambda }_1}}={\displaystyle \frac{d_{2,0}}{2d_{2,1}}},\end{array}$$

($N\ge 3$):

$$\begin{array}{cc}\hfill C_0\left(N\right)& ={\displaystyle \frac{1}{N}}\sum _{k=1}^{N-1}{\displaystyle \frac{1}{{\lambda }_k}}={\displaystyle \frac{{\displaystyle \sum _{1\le i_1<\cdots <i_{N-2}\le N-1}\prod _{k=1}^{N-2}{\lambda }_{i_k}}}{{\displaystyle N\prod _{k=1}^{N-1}{\lambda }_k}}}={\displaystyle \frac{{\displaystyle \sum _{0\le i_1<\cdots <i_{N-2}\le N-1}\prod _{k=1}^{N-2}{\lambda }_{i_k}}}{{\displaystyle N\sum _{0\le i_1<\cdots <i_{N-1}\le N-1}\prod _{k=1}^{N-1}{\lambda }_{i_k}}}}={\displaystyle \frac{d_{N,N-2}}{N{d}_{N,N-1}}}.\hfill \end{array}$$

The proof of Proposition 3 is now complete. ☐

Note that the sharp constants (14) and (15) satisfy Theorem 3.

5. Conclusions

In this section, we prove that the sharp constants ${\left\{C_0(n;a)\right\}}_{n=2}^N$ and ${\left\{C_0\left(n\right)\right\}}_{n=2}^N$ satisfy certain hierarchical structures.

For $N=3,4,\cdots$, we define the elementary symmetric polynomials on n variables $\{x_1,x_2,\cdots ,x_n\}$ as follows:

$$\begin{array}{cc}\hfill & s_j(x_1,x_2,\cdots ,x_n)=\left\{\begin{array}{cc}1\hfill & (j=0),\hfill \\ {\displaystyle \sum _{1\le i_1<\cdots <i_j\le n}\prod _{k=1}^j{x}_{i_k}}\hfill & (j=1,2,\cdots ,n)\hfill \end{array}\right.(n=2,3,\cdots ,N-1).\hfill \end{array}$$

(16)

We also define the following special value in the elementary symmetric polynomial.

$$\begin{array}{c}\hfill {\sigma }_{n,j}\left(a\right)=s_j({\lambda }_0+a,{\lambda }_1+a,\cdots ,{\lambda }_{n-1}+a).\end{array}$$

(17)

Note that ${\sigma }_{n,j}\left(a\right)$ is positive. The constants ${\sigma }_{n,j}\left(a\right)$ satisfy the following lemmas.

Lemma 1.

For $N=3,4,\cdots$, we have the following inversion formulae:

(i) 

${\displaystyle {\sigma }_{n,i}\left(a\right)=\sum _{j=0}^i\left(\genfrac{}{}{0pt}{}{n-j}{n-i}\right)a^{i-j}{d}_{n,j}(i=0,1,\cdots ,n,n=2,3,\cdots ,N-1),}$

(ii) 

${\displaystyle d_{n,i}=\sum _{j=n-i}^n\left(\genfrac{}{}{0pt}{}{j}{n-i}\right){(-a)}^{i+j-n}{\sigma }_{n,n-j}\left(a\right)(i=0,1,\cdots ,n,n=2,3,\cdots ,N-1).}$

Proof of Lemma 1.

(i) For $n=2,3,\cdots ,N-1$, we introduce the following matrices:

$$\begin{array}{c}{\mathit{P}}_{n+1}\left(a\right)=\left(\begin{array}{c}{p}_{ij}\left(a\right)\end{array}\right),{\mathit{d}}_{n+1}=\left(\begin{array}{c}{d}_{n,0}\\ ⋮\\ d_{n,n}\end{array}\right),{\mathbf{\sigma }}_{n+1}\left(a\right)=\left(\begin{array}{c}{\sigma }_{n,n}\left(a\right)\\ ⋮\\ {\sigma }_{n,0}\left(a\right)\end{array}\right),\hfill \end{array}$$

where:

$$\begin{array}{c}\hfill p_{ij}\left(a\right)=\left\{\begin{array}{cc}{\displaystyle \frac{1}{i!}}{\left({\displaystyle \frac{d}{da}}\right)}^i{a}^{n-j}\hfill & 0\le i+j\le n\hfill \\ 0\hfill & n+1\le i+j\le 2n\hfill \end{array}\right..\end{array}$$

The constants ${\left\{d_{n,j}\right\}}_{j=0}^n$ and ${\left\{{\sigma }_{n,j}\left(a\right)\right\}}_{j=0}^n$ satisfy the following equality:

$$\begin{array}{c}\hfill {\mathit{P}}_{n+1}\left(a\right){\mathit{d}}_{n+1}={\mathbf{\sigma }}_{n+1}\left(a\right).\end{array}$$

From the above equality, we have:

$$\begin{array}{c}\hfill {\sigma }_{n,n-i}\left(a\right)=\sum _{0\le i+j\le n}\left(\genfrac{}{}{0pt}{}{n-j}{i}\right)a^{n-j-i}{d}_{n,j}(i=0,1,\cdots ,n).\end{array}$$

Thus, we have:

$$\begin{array}{c}\hfill {\sigma }_{n,i}\left(a\right)=\sum _{j=0}^i\left(\genfrac{}{}{0pt}{}{n-j}{n-i}\right)a^{i-j}{d}_{n,j}(i=0,1,\cdots ,n).\end{array}$$

(ii) Since the inverse matrix of ${\mathit{P}}_{n+1}\left(a\right)$ is given by:

$$\begin{array}{c}\hfill {\mathit{P}}_{n+1}^{-1}\left(a\right)=\left(\begin{array}{c}{\widehat{p}}_{ij}\left(a\right)\end{array}\right)\end{array}$$

where:

$$\begin{array}{c}\hfill {\hat{p}}_{ij}\left(a\right)=\left\{\begin{array}{cc}0\hfill & 0\le i+j\le n-1\hfill \\ 1\hfill & i+j=n\hfill \\ p_{n-i,n-j}(-a)\hfill & n+1\le i+j\le 2n\hfill \end{array}\right.,\end{array}$$

we have:

$$\begin{array}{cc}\hfill d_{n,i}& ={\sigma }_{n,i}\left(a\right)+\sum _{j=n-i+1}^n{p}_{n-i,n-j}(-a){\sigma }_{n,n-j}\left(a\right)\hfill \\ & =\sum _{j=n-i}^n\left(\genfrac{}{}{0pt}{}{j}{n-i}\right){(-a)}^{i+j-n}{\sigma }_{n,n-j}\left(a\right).\hfill \end{array}$$

The Proof of Lemma 1 is now complete. ☐

Lemma 2.

For $N=3,4,\cdots$, we have:

$$\begin{array}{c}\hfill {\left({\displaystyle \frac{d}{da}}\right)}^k{\sigma }_{n,i}\left(a\right)={\displaystyle \frac{(n-i+k)!}{(n-i)!}}{\sigma }_{n,i-k}\left(a\right)(k=0,1,\cdots ,i,i=0,1,\cdots ,n,n=2,3,\cdots ,N-1).\end{array}$$

Proof of Lemma 2.

From Lemma 1, we have:

$$\begin{array}{cc}\hfill {\left({\displaystyle \frac{d}{da}}\right)}^k{\sigma }_{n,i}\left(a\right)& =\sum _{j=0}^{i-k}\left(\genfrac{}{}{0pt}{}{n-j}{n-i}\right)(i-j)(i-j-1)\cdots (i-j-k+1)a^{i-j-k}{d}_{n,j}\hfill \\ & ={\displaystyle \frac{(n-i+k)!}{(n-i)!}}\sum _{j=0}^{i-k}\left(\genfrac{}{}{0pt}{}{n-j}{n-(i-k)}\right)a^{(i-k)-j}{d}_{n,j}\hfill \\ & ={\displaystyle \frac{(n-i+k)!}{(n-i)!}}{\sigma }_{n,i-k}\left(a\right)\hfill \end{array}$$

The Proof of Lemma 2 is now complete. ☐

We first show that the sharp constants ${\left\{C_0(n;a)\right\}}_{n=2}^N$ satisfy a hierarchical structure.

Theorem 4.

For $N=3,4,\cdots$, if:

$$\begin{array}{c}\hfill \left|\begin{array}{cc}\left(1+\frac{1}{n}\right){\sigma }_{n,n-1}\left(a\right)& {\sigma }_{n+1,n}\left(a\right)\\ {\sigma }_{n,n}\left(a\right)& {\sigma }_{n+1,n+1}\left(a\right)\end{array}\right|>0(n=2,3,\cdots ,N-1),\end{array}$$

the sharp constants ${\left\{C_0(n;a)\right\}}_{n=2}^N$ satisfy the following hierarchical structure:

$$\begin{array}{c}\hfill 0<C_0(n+1;a)<C_0(n;a)\le {\displaystyle \frac{a+1}{a(a+2)}}(n=2,3,\cdots ,N-1).\end{array}$$

Proof of Theorem 4.

Using Equation (17), the sharp constant (11) is given by:

$$\begin{array}{c}\hfill C_0(n;a)={\displaystyle \frac{{\displaystyle \sum _{0\le i_1<\cdots <i_{n-1}\le n-1}\prod _{k=1}^{n-1}({\lambda }_{i_k}+a)}}{{\displaystyle n\prod _{k=0}^{n-1}({\lambda }_k+a)}}}={\displaystyle \frac{{\sigma }_{n,n-1}\left(a\right)}{n{\sigma }_{n,n}\left(a\right)}}.\end{array}$$

(18)

Taking the difference between $C_0(n;a)$ and $C_0(n+1;a)$, the determinant formula is obtained as:

$$\begin{array}{cc}\hfill C_0(n;a)-C_0(n+1;a)& ={\displaystyle \frac{{\sigma }_{n,n-1}\left(a\right)}{n{\sigma }_{n,n}\left(a\right)}}-{\displaystyle \frac{{\sigma }_{n+1,n}\left(a\right)}{(n+1){\sigma }_{n+1,n+1}\left(a\right)}}\hfill \\ & ={\displaystyle \frac{1}{(n+1){\sigma }_{n,n}\left(a\right){\sigma }_{n+1,n+1}\left(a\right)}}\left|\begin{array}{cc}\left(1+\frac{1}{n}\right){\sigma }_{n,n-1}\left(a\right)& {\sigma }_{n+1,n}\left(a\right)\\ {\sigma }_{n,n}\left(a\right)& {\sigma }_{n+1,n+1}\left(a\right)\end{array}\right|.\hfill \end{array}$$

From the assumption, we obtain:

$$\begin{array}{c}\hfill C_0(n;a)-C_0(n+1;a)>0(n=2,3,\cdots ,N-1).\end{array}$$

From the above inequality, the sharp constant $C_0(n;a)$ is a monotonically-decreasing sequence with respect to n. Paying attention to the equality:

$$\begin{array}{c}\hfill C_0(2;a)={\displaystyle \frac{a+1}{a(a+2)}},\end{array}$$

we have obtained the hierarchical structure for the sharp constants ${\left\{C_0(n;a)\right\}}_{n=2}^N$.

The proof of Theorem 4 is now complete. ☐

By using the elementary symmetric polynomials (16), we also define the following special value.

$$\begin{array}{c}\hfill {\sigma }_{n,j}=s_j({\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_n).\end{array}$$

(19)

Note that ${\sigma }_{n,j}$ is positive.

The following theorem shows that the sharp constants ${\left\{C_0\left(n\right)\right\}}_{n=2}^N$ satisfy a hierarchical structure.

Theorem 5.

For $N=3,4,\cdots$, if:

$$\begin{array}{c}\hfill \left|\begin{array}{cc}{\sigma }_{n,n-1}& {\sigma }_{n-1,n-2}\\ \left(1+\frac{1}{n}\right){\sigma }_{n,n}& {\sigma }_{n-1,n-1}\end{array}\right|>0(n=2,3,\cdots ,N-1),\end{array}$$

the sharp constants ${\left\{C_0\left(n\right)\right\}}_{n=2}^N$ satisfy the following hierarchical structure:

$$\begin{array}{c}\hfill {\displaystyle \frac{1}{4}}<C_0\left(n\right)<C_0(n+1)(n=2,3,\cdots ,N-1).\end{array}$$

Proof of Theorem 5.

Using Equation (19), the sharp constant (11) is given by:

$$\begin{array}{c}\hfill C_0\left(n\right)={\displaystyle \frac{{\displaystyle \sum _{1\le i_1<\cdots <i_{n-2}\le n-1}\prod _{k=1}^{n-2}{\lambda }_{i_k}}}{{\displaystyle n\prod _{k=1}^{n-1}{\lambda }_k}}}={\displaystyle \frac{{\sigma }_{n-1,n-2}}{n{\sigma }_{n-1,n-1}}}.\end{array}$$

Taking the difference between $C_0(n+1)$ and $C_0\left(n\right)$, we obtain the determinant formula:

$$\begin{array}{cc}\hfill C_0(n+1)-C_0\left(n\right)& ={\displaystyle \frac{{\sigma }_{n,n-1}}{(n+1){\sigma }_{n,n}}}-{\displaystyle \frac{{\sigma }_{n-1,n-2}}{n{\sigma }_{n-1,n-1}}}\hfill \\ & ={\displaystyle \frac{1}{(n+1){\sigma }_{n-1,n-1}{\sigma }_{n,n}}}\left|\begin{array}{cc}{\sigma }_{n,n-1}& {\sigma }_{n-1,n-2}\\ \left(1+\frac{1}{n}\right){\sigma }_{n,n}& {\sigma }_{n-1,n-1}\end{array}\right|.\hfill \end{array}$$

From the assumption, we obtain:

$$\begin{array}{c}\hfill C_0(n+1)-C_0\left(n\right)>0(n=2,3,\cdots ,N-1).\end{array}$$

According to the above inequality, the sharp constant $C_0\left(n\right)$ is a monotonically-increasing sequence with respect to n. Focusing on the equality:

$$\begin{array}{c}\hfill C_0\left(2\right)={\displaystyle \frac{1}{4}},\end{array}$$

we obtain the following hierarchical structure for the sharp constants ${\left\{C_0\left(n\right)\right\}}_{n=2}^N$.

The proof of Theorem 5 is now complete. ☐

6. Examples

6.1. Example 1 (See [8])

Let G be a weighted complete graph, $K_N$, with a vertex set, $V=\{0,1,\cdots ,N-1\}$. We define the adjacency matrix as follows:

$$\begin{array}{c}\hfill \mathit{B}=\left[b(i,j)\right],b(i,j)=\left\{\begin{array}{cc}{\displaystyle \frac{1}{N-1}}\hfill & [i,j]\in E,\hfill \\ 0\hfill & otherwise.\hfill \end{array}\right.\end{array}$$

Subsequently, for $i\in V$, the generalized graph Laplacian A on G is given by:

$$\begin{array}{c}{\lambda }_0=0,{\lambda }_i=\left\{\begin{array}{cc}{\displaystyle \frac{2n}{2n-1}}\hfill & N=2n,\hfill \\ {\displaystyle \frac{2n+1}{2n}}\hfill & N=2n+1,\hfill \end{array}\right.(1\le i\le N-1,n\in \mathbb{N}).\hfill \end{array}$$

The sharp constant (11) of the Sobolev inequality (10) is then expressed as follows:

$$\begin{array}{c}\hfill C_0(N;a)={\displaystyle \frac{(N-1)a+1}{a\left\{\right(N-1)a+N\}}}=\left\{\begin{array}{cc}{\displaystyle \frac{2an-a+1}{a(2an+2n-a)}}\hfill & N=2n,\hfill \\ {\displaystyle \frac{2an+1}{a(2an+2n+1)}}\hfill & N=2n+1,\hfill \end{array}\right.(n\in \mathbb{N}).\end{array}$$

(20)

Furthermore, the sharp constant (13) of the Sobolev inequality (12) is expressed as follows:

$$\begin{array}{c}\hfill C_0\left(N\right)={\left(1-{\displaystyle \frac{1}{N}}\right)}^2=\left\{\begin{array}{cc}{\displaystyle \frac{{(2n-1)}^2}{4n^2}}\hfill & N=2n,\hfill \\ {\displaystyle \frac{4n^2}{{(2n+1)}^2}}\hfill & N=2n+1,\hfill \end{array}\right.(n\in \mathbb{N}).\end{array}$$

(21)

We obtain the following theorem from Theorems 4 and 5.

Theorem 6.

For $N=3,4,\cdots$, the sharp constants hold the following hierarchical structure:

(i) 

${\displaystyle \frac{1}{a+1}}<C_0(n+1;a)<C_0(n;a)\le {\displaystyle \frac{a+1}{a(a+2)}}(n=2,3,\cdots ,N-1)$,

(ii) 

${\displaystyle \frac{1}{4}}\le C_0\left(n\right)<C_0(n+1)<1(n=2,3,\cdots ,N-1)$.

The proof of Theorem 6 is simple, so we omit it. It is interesting to note that $C_0(n;a)$ and $C_0\left(n\right)$, which are related by Theorem 3, satisfy opposite hierarchical structures.

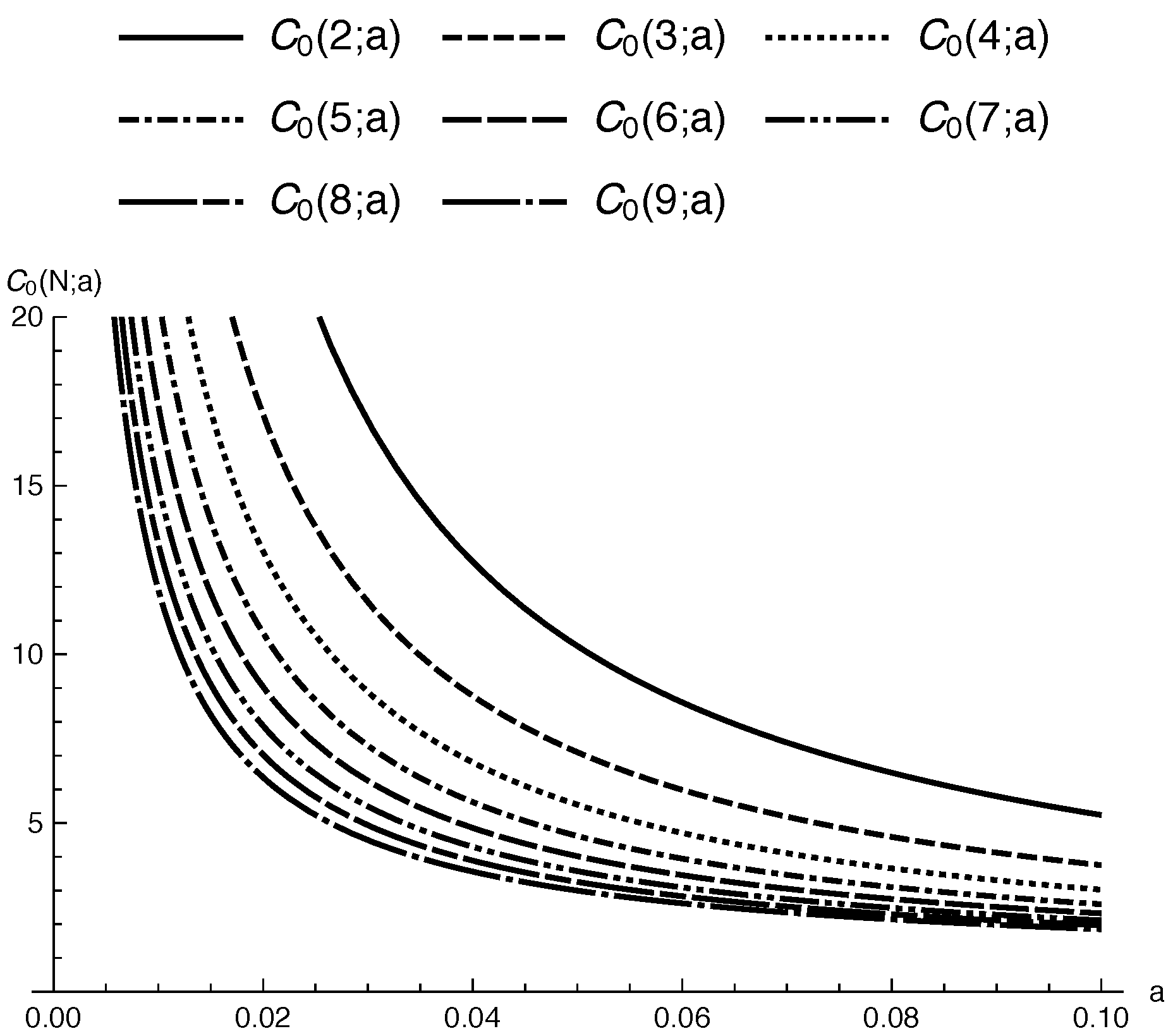
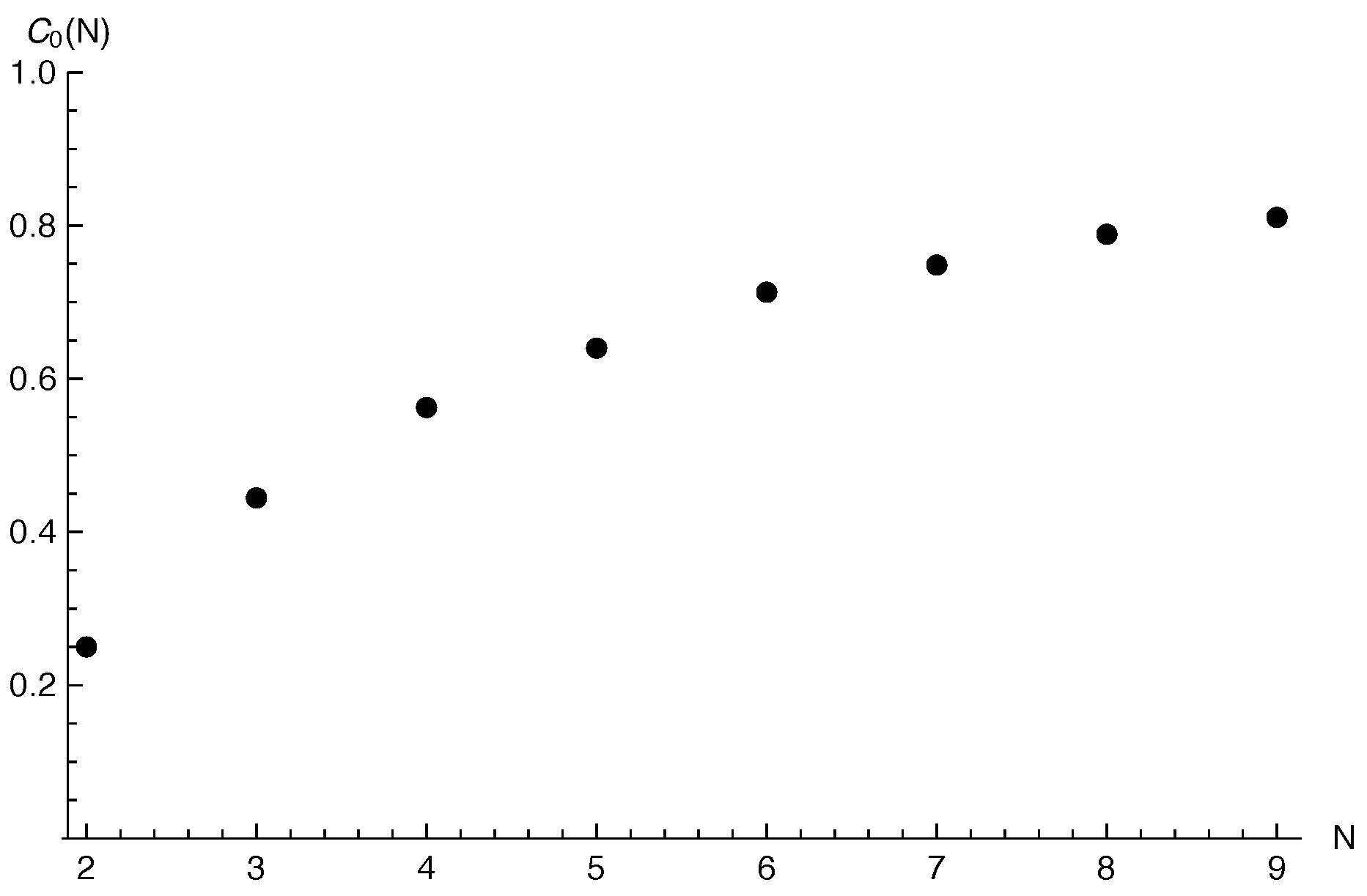
6.2. Example 2

Let G be a weighted complete graph, $K_N$, with a vertex set, $V=\{0,1,\cdots ,N-1\}$. We define the adjacency matrix as follows:

$$\begin{array}{c}\hfill \mathit{B}=\left[b(i,j)\right],b(i,j)=\left\{\begin{array}{cc}{\displaystyle \frac{2m\left(\right|i-j\left|\right)\left(\genfrac{}{}{0pt}{}{\left[\frac{N}{2}\right]}{m\left(\right|i-j\left|\right)}\right)}{\left[\frac{N}{2}\right]\{2^{\left[\frac{N}{2}\right]+1}-1-cos\left(N\pi \right)\}}}\hfill & [i,j]\in E,\hfill \\ 0\hfill & otherwise.\hfill \end{array}\right.\end{array}$$

Subsequently, for $i\in V$, the eigenvalues of the generalized graph Laplacian A on G are given by:

$$\begin{array}{c}{\lambda }_0=0,\hfill \\ {\lambda }_i=\left\{\begin{array}{cc}{\displaystyle \frac{1}{2^n-1}}\left\{{(-1)}^i-1+2^n-2^{n}cos\left({\displaystyle \frac{n+1}{2n}}i\pi \right){cos}^{n-1}\left({\displaystyle \frac{i\pi }{2n}}\right)\right\}\hfill & N=2n,\hfill \\ 1-cos\left({\displaystyle \frac{(n+1)i\pi }{2n+1}}\right){cos}^{n-1}\left({\displaystyle \frac{i\pi }{2n+1}}\right)\hfill & N=2n+1,\hfill \end{array}\right.\hfill \\ (1\le i\le N-1,n\in \mathbb{N}).\hfill \end{array}$$

The concrete forms of the sharp constants (11) of each Sobolev inequality (10) corresponding to N are as follows (see Figure 2):

$$\begin{array}{c}{C}_0(2;a)={\displaystyle \frac{a+1}{a(a+2)}},C_0(3;a)={\displaystyle \frac{2a+1}{a(2a+3)}},C_0(4;a)={\displaystyle \frac{3a+1}{a(3a+4)}},C_0(5;a)={\displaystyle \frac{4a+1}{a(4a+5)}},\hfill \\ C_0(6;a)={\displaystyle \frac{49a^2+56a+9}{a(7a+6)(7a+9)}},\hfill \\ C_0(7;a)={\displaystyle \frac{512a^3+1280a^2+888a+113}{512a(a+1+{cos}^2\frac{\pi }{7}sin\frac{\pi }{14})(a+1-{sin}^2\frac{\pi }{14}sin\frac{3\pi }{14})(a+1+cos\frac{\pi }{7}{sin}^2\frac{3\pi }{14})}},\hfill \\ C_0(8;a)={\displaystyle \frac{10125a^4+35775a^3+43380a^2+19704a+1984}{a(3a+4)(15a+16)(225a^2+480a+248)}},\hfill \\ C_0(9;a)={\displaystyle \frac{65536a^4+229376a^3+273920a^2+121088a+11065}{4096a(16a+15)(a+1+cos\frac{\pi }{9}{cos}^3\frac{2\pi }{9})(a+1+{cos}^3\frac{\pi }{9}sin\frac{\pi }{18})(a+1-cos\frac{2\pi }{9}{sin}^3\frac{\pi }{18})}},\cdots .\hfill \end{array}$$

Explicitly, the sharp constants (13) of each Sobolev inequality (12) are given by (see Figure 3):

$$\begin{array}{c}{C}_0\left(2\right)={\displaystyle \frac{1}{4}},C_0\left(3\right)={\displaystyle \frac{4}{9}},C_0\left(4\right)={\displaystyle \frac{9}{16}},C_0\left(5\right)={\displaystyle \frac{16}{25}},C_0\left(6\right)={\displaystyle \frac{77}{108}},C_0\left(7\right)={\displaystyle \frac{592}{791}},\hfill \\ C_0\left(8\right)={\displaystyle \frac{3129}{3968}},C_0\left(9\right)={\displaystyle \frac{242176}{298755}},\cdots .\hfill \end{array}$$