On the Symmetry of a Zig-Zag and an Armchair Polyhex Carbon Nanotorus

Abstract

A Euclidean graph associated with a molecule is defined by a weighted graph with adjacency matrix M = [d_ij], where for i≠j, d_ij is the Euclidean distance between the nuclei i and j. In this matrix d_ii can be taken as zero if all the nuclei are equivalent. Otherwise, one may introduce different weights for distinct nuclei. The aim of this paper is to compute the automorphism group of the Euclidean graph of a carbon nanotorus. We prove that this group is a semidirect product of a dihedral group by a group of order 2.

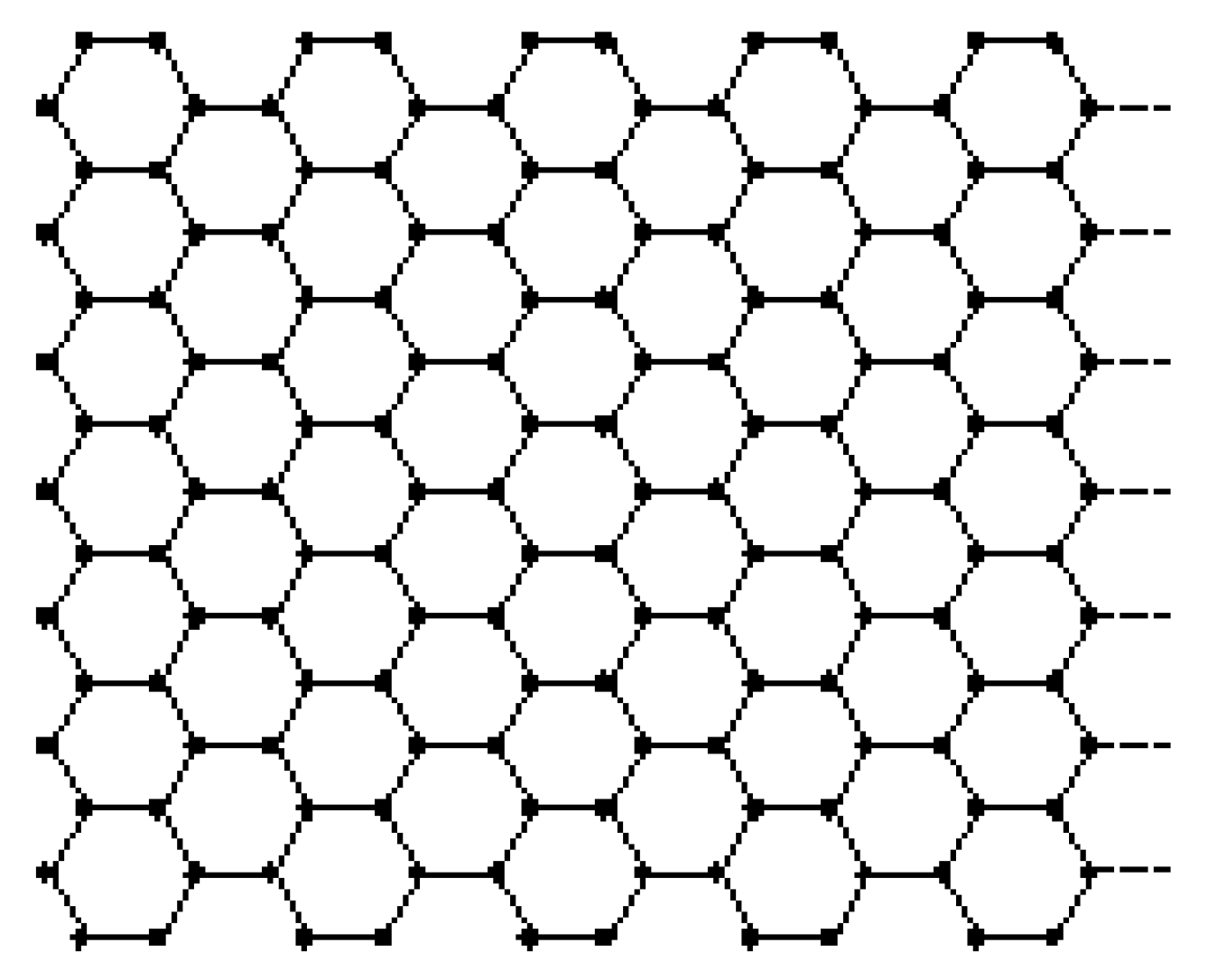
1. Introduction

An object is called symmetrical if some movement or operation leaves the object in a position indistinguishable from its original position. The symmetry of molecules and solids is a very powerful tool for developing and understanding of bonding and physical properties used to predict the nature of molecular orbitals. Chemists and physicists classify molecules in terms of their symmetry. It is of some value to recognize that all molecules that have the same basic “shape” share a number of common properties.

A single-wall carbon nanotube is a quasi one-dimensional high symmetric cylindrical structure, which can be visualized as the structure obtained by rolling a honeycomb lattice such that the endpoints of a rolling-up vector are folded one onto the other. The symmetry group of nanotube depends on this vector and is one of the line groups Lqp22, L2nn/mcm. The line group notations are too technical to include here and we encourage the reader to consult [1,2] and references therein for the main properties of the symmetry group of nanostructures. We only mention that the line groups are the full space groups of one-dimensional systems including translations in addition to the point-group symmetries like rotations or reflections. Many of the physical properties of carbon nanotube such as in generation nuclear spin species, NMR spectra, nuclear spin statistics in molecular spectroscopy, chirality and chemical isomerism are determined by this group.

Throughout this paper T = T[p,q] denotes an arbitrary polyhex nanotorus, Figure 1, in terms of its circumference (q) and its length (p). Our notation is standard and mainly taken from [1,2,3,4]. Our computational method, as described here, is appropriate for all nanotori, but our theoretical proof can be applied just for zig-zag or armchair polyhex nanotube. For properties of nanotori, we encourage the reader to consult papers by Diudea and co-authors [5,6,7].

2. Main Results and Discussion

The aim of this section is to prepare some software program for computing symmetry of nanotorus. We first solve a matrix equation by a MATLAB program [8] and then apply its output in a GAP program [9,10] to compute a generating set for the symmetry group of the nanotorus under consideration.

A Euclidean graph is an edge weighted graph related to a molecule with the adjacency matrix D = [d_ij], where for i ≠ j, d_ij is the Euclidean distance between the nuclei i and j. In this matrix d_ii can be taken as zero if all the nuclei are equivalent. Otherwise, one may introduce different weights for different nuclei. Notice that a Euclidean graph is a complete edge weighted graph. By symmetry we mean the automorphism group symmetry of Euclidean graph of molecule under consideration. Here, an automorphism of a Euclidean graph G is a permutation g of the vertex set of G with the property that for any vertices u and v, d(g(u),g(v)) = d(u,v), where d(-,-) is usual Euclidean meter. The set of all automorphisms of a graph G, with the operation of composition of permutations, is a permutation group on V(G), denoted Aut(G).

Randic [11,12,13] showed that a molecular graph can be depicted in different ways such that its point group symmetry or three-dimensional (3D) perception may differ, but the underlying connectivity symmetry is still the same as characterized by the automorphism group of the graph.

Balasubramanian [14,15,16,17,18,19,20,21] considered the Euclidean matrix of a chemical graph to find its symmetry. He proved that for computing the symmetry of a molecule, it is sufficient to solve the matrix equation P^tEP = E, where E is the adjacency matrix of the molecule under consideration and P varies on the set of all permutation matrices with the same dimension as E. He computed the Euclidean graphs and automorphism group for benzene, eclipsed and staggered forms of ethane and eclipsed and staggered forms of ferrocene. One of the present authors (ARA), in some research papers [22,23,24,25,26,27,28] continued the leading works of Balasubramanian in computing symmetry of molecules.

2.1. Computational Details

The computations of the symmetry properties of molecules we carried out by the aid of GAP [9]. GAP stands for Groups, Algorithms and Programming. The name was chosen to reflect the aim of the system, which is a group theoretical software for solving computational problems in computational group theory. This software was constructed by GAP’s team in Aachen. GAP is a free and extendable software package. The term extendable means that you can write your own programs in the GAP language, and use them in just the same way as the programs which form part of the system (the “library”). More information on the motivation and development of GAP to date can be found on GAP web page on http://www.gap-system.org. GAP contains a large library of functions, which are important for the calculations of this paper. In this paper the GAP functions for computing permutation matrices from permutations and vice versa were crucial for our calculations.

For a permutation σ on n objects, the corresponding permutation matrix is an n × n matrix P_σ given by P_σ = [x_ij], x_ij = 1 if i = σ(j) and 0 otherwise. It is easy to see that P_σP_τ = P_στ, for any two permutations σ and τ on n objects, and so the set of all n × n permutation matrices is a group isomorphic to the symmetric group S_n on n symbols. It is a well-known fact that a permutation σ of the vertices of a graph G belongs to its automorphism group if and only if it satisfies P_σ^tAP_σ = A, where A is the adjacency matrix of G.

Consider the equation (P_σ)^tDP_σ = D, where D is the adjacency matrix of the Euclidean graph G of the nanotorus under consideration. Suppose Aut(G) = {σ₁, σ₂,…, σ_m}. The matrix S_G = [s_ij], where s_ij = σ_i(j) is called a solution matrix for G. Clearly, for computing the automorphism group of G, it is enough to calculate a solution matrix for G.

In mathematics, groups are often used to describe symmetries of objects. This is formalized by the notion of a group action: every element of the group “acts” like a bijective map (or “symmetry”) on some set. To clarify this notion, we assume that G is a group and X is a set. G is said to act on X when there is a map ϕ : G ✕ X → X such that all elements x ∈ X, (i) ϕ(e,x) = x where e is the identity element of G, and, (ii) ϕ(g, ϕ(h,x)) = ϕ(gh,x) for all g,h ∈ G. In this case, G is called a transformation group, X is called a G-set, and ϕ is called the group action. For simplicity we define gx = ϕ(g,x). In a group action, a group permutes the elements of X. The identity does nothing, while a composition of actions corresponds to the action of the composition. For a given X, the set {gx | g ∈ G}, where the group action moves x, is called the group orbit of x. The subgroup which fixes is the isotropy group of x.

Now we discuss techniques that are useful in finding symmetry of molecules. The following theorem is crucial in establishing symmetry of molecules, see [22] for details.

Theorem 1.

Suppose A = [a_ij] and B = [b_ij] are two matrices and P_σ is a permutation matrix. If B = P_σA(P_σ)^t, σ(i) = r and σ(j) = s, then a_rs = b_ij. In particular, if B = A and σ maps i₁ → j₁, i₂ → j₂,…, i_t → j_t. Then we have:

$$\left[\begin{array}{ccccc}{\mathrm{a}}_{{\mathrm{i}}_1{\mathrm{i}}_1}& .& .& .& {\mathrm{a}}_{{\mathrm{i}}_1{\mathrm{i}}_{\mathrm{t}}}\\ .& .& & & .\\ .& & .& & .\\ .& & & .& .\\ {\mathrm{a}}_{{\mathrm{i}}_{\mathrm{t}}{\mathrm{i}}_1}& .& .& .& {\mathrm{a}}_{{\mathrm{i}}_{\mathrm{t}}{\mathrm{i}}_{\mathrm{t}}}\end{array}\right]=\left[\begin{array}{ccccc}{\mathrm{a}}_{{\mathrm{j}}_1{\mathrm{j}}_1}& .& .& .& {\mathrm{a}}_{{\mathrm{j}}_1{\mathrm{j}}_{\mathrm{t}}}\\ .& .& & & .\\ .& & .& & .\\ .& & & .& .\\ {\mathrm{a}}_{{\mathrm{j}}_{\mathrm{t}}{\mathrm{j}}_1}& .& .& .& {\mathrm{a}}_{{\mathrm{j}}_{\mathrm{t}}{\mathrm{j}}_{\mathrm{t}}}\end{array}\right]$$

Let G be the symmetry group of a molecule and X be the set of atoms. One can see that G acts on X. If O₁, O₂, …, O_t are orbits of the action of G on X then for every α ∈ G and every positive integer i, 1 ≤ i ≤ t, α(O_i) ∈ { O₁, O₂, …, O_t O₁, O₂, …, O_t}. We apply this fact and our theorem to prepare the following MATLAB program:

A MATLAB Program for Computing Solution Matrix

function y=permute2(a)

m=length(a);

1:m;

sort(a);

r i=1:m

x=[[];

for j=1:m

if min(b(:,i)==b(:,j))==1

x=[x,j];

end

end

p(i,1:length(x))=x;

end

for i=1:m-2

for j=i+1:m

if max(p(i,:)==j)==1

tt=0;

s=[1:i-1 j];

for r=i+1:m

n=size(s);

w=[[];

for t=1:n(1)

v=p(r,:);

v(v==0)=[[];

k1=1:m;k1(v)=[[];

k=1:m;

k([s(t,:) k1])=[[];

for f=k

if min(a([s(t,:) f],[s(t,:) f])==a(1:r,1:r))==1

w=[w;s(t,:) f];

if r==m

tt=1;

break

end

end

if tt==1

break

end

end

if tt==1

break

end

end

s=w;

end

if length(s)>1

y=[y; s(1,:)];

end

end

end

end

Suppose A is a solution matrix computed by our program. To compute the automorphism group of Euclidean graph of the molecule under consideration, we need a GAP program as follows:

B:=[];

N:=Size(A);

for i in [1,2..N] do

d:=PermListList(A[1],A[i]);

Add(B,d);

od;

G:=AsGroup(B);

GeneratorsOfGroup(G);

Using these programs it is possible to calculate symmetry of every molecules. Using these programs it is possible to compute the symmetry group of nanotorus with at most 2000 carbon atoms. For more than 2000 carbon atoms, our MATLAB program needs a lot of time.

2.2. Theoretical Results

Suppose G is a group and N is a subgroup of G. N is called a normal subgroup, if it is invariant under conjugation; that is, for each element n in N and each g in G, the element gng⁻¹ is still in N. Normal subgroups are important because they can be used to construct quotient groups from a given group. A semidirect product describes a particular way in which a group can be put together from two subgroups, one of which is normal. Let G be a group, N a normal subgroup of G and H a subgroup of G. We say that G is a semidirect product of N and H, or that G splits over N, if every element of G can be written in one and only one way as a product of an element of N and an element of H.

The dihedral group of degree n (denoted by D_n) is the subgroup of S_n generated by the permutations a = (1,2,…,n) and b =(2,n)(3,n-1)(4,n-2)…(n/2,n/2+2) or (2,n)(3,n-1)(4,n-2)…((n+1)/2,(n+3)/2), when n is even or odd, respectively. It is easy to see that D_n is non-abelian, for n ≥ 3, and <a> is a normal subgroup of D_n. It is possible to prove that D_n is actually isomorphic to the group of symmetries of a regular polygon with n-sides. To explain, we consider a regular n-sided polygon P and label it clockwise by numbers 1, 2, …, n. Define the product operation of composition, as follows: for two symmetries f and g, the product fg means “first do f, then do g”. P has exactly n rotational symmetries: these are a, a²(= aa), …, a^n-1 and e = aⁿ, which leaves the polygon fixed. Here a is a function such that a(1) = 2, a(2) = 3, …, a(n-1) = n and a(n) = 1. On the other hand, a^k is rotation about the center of A through an angle 2πk/n. There are also n reflection symmetries: these are reflections in the n lines passing through the center of P and a corner or the midpoint of a side of the polygon. Suppose b is the reflection in the line through 1 and the center of P. Then b =(2,n)(3,n-1)(4,n-2)…(n/2,n/2+2) or (2,n)(3,n-1)(4,n-2)…((n+1)/2,(n+3)/2), when n is even or odd, respectively. Clearly, n reflections of P are b, ab, a²b, …, a^n-1b. Thus all elements of the symmetry group of a polygon P constitute the same group as dihedral group D_n.

Suppose L is the 2-dimensional lattice of a polyhex nanotorus containing p vertical crenels and q rows, Figure 2. It is clear that p is even. Put a = (1,2,…,p/2) and b = (2,p/2)(3,p/2-1)(4,p/2-2)…(p/4,p/4+2) or (2,p/2)(3,p/2-1)(4,p/2-2)…((p/2+1)/2,(p/2+3)/2), when p/2 is even or odd, respectively. Then the group H generated by permutations a and b is a subgroup of the symmetry group of a polyhex carbon nanotorus V. But a vertical plane determines a symmetry element c of V such that c ∉ H. Consider V = <H,c> then V is the symmetry group of the carbon polyhex nanotorus. Since |H| = (1/2)|V| and |H ∩ <c>| = 1, H is a normal subgroup of V and V is a semidirect product of H by a cyclic group of order 2. Therefore, we proved the following theorem:

Theorem 2.

The symmetry group V of armchair and zig-zag polyhex nanotorus is constructed from a dihedral group D_p/2 and a plane symmetry group isomorphic to Z₂, the cyclic group of order 2.

3. Conclusion

The computational methods presented in Section 2.1 are general and can be applied for molecules with the large number of atoms. If the number of atoms are greater than 2000 then our MATLAB program needs a lot of time but our GAP program is efficient. On the other hand, our theoretical method for describing symmetry group of an armchair and zig-zag nanotorus can be applied in a similar way to describe the corresponding nanotubes. Of course, the symmetry of nanotubes is different from nanotorus, but some of the symmetry elements will be the same. Finally, computing a permutation representation for the symmetry group of an arbitrary nanotube or nanotorus is remaining as an open question.