Abstract
We review recent results on how to extend the supersymmetry SUSY formalism in Quantum Mechanics to linear generalizations of the time-dependent Schrödinger equation in (1+1) dimensions. The class of equations we consider contains many known cases, such as the Schrödinger equation for position-dependent mass. By evaluating intertwining relations, we obtain explicit formulas for the interrelations between the supersymmetric partner potentials and their corresponding solutions. We review reality conditions for the partner potentials and show how our SUSY formalism can be extended to the Fokker-Planck and the nonhomogeneous Burgers equation.
1. Introduction
Supersymmetry (SUSY) is a theory that intends to unify the strong, the weak and the electromagnetic interaction. Technically, SUSY assigns a partner (superpartner) to every particle, the spin of which differs by one-half from the spin of its supersymmetric counterpart. For an introduction to SUSY the reader may refer to the book [1]. At first sight, it is therefore somewhat surprising that the SUSY formalism has become very popular in the context of nonrelativistic Quantum Mechanics, a theory that does not take the spin of particles into account. The reason of SUSY’s popularity lies in its computational aspects: while the theoretical framework of SUSY simplifies considerably, the practical assignation of a superpartner to a given system (represented by its Hamiltonian) becomes important. This is so, because in nonrelativistic Quantum Mechanics there are solvable models, the most famous of which being associated to potentials like the harmonic oscillator or the Coulomb potential. Now, to each of such solvable models, the quantum mechanical SUSY formalism generates a new solvable model, namely, the superpartner. In other words, if we have a given solution of a Schrödinger equation for a certain potential, then by means of SUSY we obtain a solution for a Schrödinger equation with a different potential (also called superpartner of the initial potential). Quantum mechanical superpartners are related to each other in many interesting ways, especially in the stationary case. As examples let us mention that superpartners share their energy spectra (isospectrality), and their Green’s functions are interrelated by a very simple trace formula [2,3]. Note that there are many exhaustive reviews on the SUSY formalism for the stationary Schrödinger equation, as examples let us mention [4,5] and [6]. Furthermore, in the references of the latter reviews some recent applications of SUSY for the stationary case can be found. In the present work we will focus on the time-dependent situation, the correspoding SUSY formalism was introduced in [7]. As is well known, there are even less solvable cases of the time-dependent Schrödinger equation (TDSE) than of its stationary counterpart, such that SUSY is one of the very few methods to obtain explicit solutions. It should be pointed out that the mapping that relates solutions of SUSY superpartners to each other, is known as Darboux transformation. This transformation was introduced in a purely mathematical context [8] and only eventually it was found to be equivalent to the mapping that interrelates SUSY superpartners. Darboux transformations do not only exist in the context of Schrödinger equations, but they have been established for many linear and nonlinear equations [9]. Thus, the Darboux transformation can exist independently of SUSY, but within the quantum-mechanical SUSY framework, the Darboux transformation and the SUSY transformation (the mapping between superpartners) coincide. This is true not only for the TDSE, but for a generalized linear version of it, which we will focus on in the present review. For details on the Darboux transformation for generalized TDSEs consult [10]. Our generalized TSDE comprises all known linear special cases - as an example let us mention the TDSE for position-dependent mass - and the SUSY formalism that we will derive here, reduces correctly for each special case. Before we start seeing the generalized TDSE, in section 2 we give a brief review of the conventional SUSY formalism for the TDSE. Section 3 is devoted to the generalized TDSE and the corresponding generalized SUSY formalism. Afterwards we derive a condition for the superpartner potentials to be real-valued (reality condition), as is required in the majority of physical applications, and we verify that our reality condition reduces correctly to the well known case, if our generalized TDSE coincides with a conventional TDSE (section 4). For selected particular cases of the generalized TDSE we then state the corresponding SUSY data (SUSY transformation, explicit form of the superpartners, reality condition) in section 5. We apply our generalized SUSY formalism to a concrete example in section 6 in order to illustrate how a superpartner of a given TDSE can be obtained. Section 7 is devoted to an extension of the SUSY transformation to equations that are different from the TDSE. In particular, we first introduce a concept to generalize the SUSY transformation, and then apply this concept to the Fokker-Planck equation and to the nonhomogeneous Burgers equation. For more details than contained in this review, the reader may refer to the references given above (section 2), to our recent papers [10,11] and references therein (section 3, section 4 and section 5), and to the paper [12] (section 7).
2. Conventional SUSY formalism
In this section we give a brief review of the standard SUSY formalism, as it applies to the TDSE. For details and more information the reader may refer to [13] and references therein.
Preliminaries and the matrix TDSE. Let us start by considering two TDSEs in atomic units (), that is,
where the symbol ∂ denotes the partial derivative, the functions , stand for the respective solutions and the Hamiltonians , are given by
for potentials and . Let us now write the TDSEs (1) and (2) in matrix form:
If we define a matrix Hamiltonian H via diag, together with a matrix solution , then our equation (4) takes the following form:
The components of the vector will turn out to contain the solutions that belong to a supersymmetric pair of Hamiltonians.
The supercharges. As in the stationary case [4], our goal is to construct a superalgebra with three generators, two of which are called supercharge operators or simply supercharges. These are mutually adjoint matrix operators of the following form
where L and its adjoint are linear operators, the purpose of which will be explained below. The supercharges act on two-component solutions of the matrix TDSE (5), in particular we have for that
It is immediate to see that the first component of has been taken into the second component, and the operator L has been applied to it. The supercharge adjoint to Q reverses the above process (7):
Next, let us understand the purpose of introducing the operators L and .
The intertwining relation and its adjoint. Note that is a solution of our matrix TDSE (5), that is, its first and second component and solve the TDSEs (1) and (2), respectively. Now, we want this property to be preserved after application of the supercharges, i.e., and are required to be solutions of the TDSEs (2) and (1), respectively. Consequently, L must be an operator that converts solutions of the first TDSE (1) into solutions of the second TDSE (2), and its adjoint must convert solutions of the second TDSE (2) into solutions of the first TDSE (1). Let us first consider the operator L, which we will determine from the following equation:
This operator equation is called intertwining relation, as it intertwines the two TDSEs (1), (2) by means of the operator L. This is why L is often called an intertwiner. In order to understand how the intertwining relation works, let us assume that we apply both sides of it to a solution of the first TDSE (1). Consequently, the right hand side of (9) vanishes, since we assumed L to be linear, implying . But if the right hand side of equation (9) is zero, so must be its left hand side, which means that is a solution of the second TDSE (2). In order to find the operator L from our intertwining relation (9), assume it to be a linear, first-order differential operator of the form
where the coefficients and are to be determined. After inserting (10) and the Hamiltonians (3) into the intertwining relation (9), we expand the latter and require the coefficients of the respective derivative operators to be the same on both sides. We do not give the calculation here, since it is a special case of a calculation that will be done in full detail for the generalized TDSE. After having evaluated our intertwining relation using (10), we obtain the following results on the and that appear in (10): we have , that is, does not depend on the spatial variable. Furthermore, the function is given by , where u is a solution of the first TDSE (1). If these two conditions are satisfied, then the operator L as given in (10) becomes
Clearly, application to the solution of the first TDSE (1) gives in the form
If in addition and u are linearly independent, then is a nontrivial solution of the second TDSE (2), where the potential is under the following constraint:
where the prime denotes the derivative with respect to t, since does not depend on x. Let us point out here that in the notation the index refers to a derivative of the logarithm and not only to a derivative of its argument. Now, let us make a remark on the solution u of equation (1) that appears in (12). If we want to apply the operator L to a solution of our first TDSE (1), we must provide this solution . Furthemore, we must provide another solution u of the same TDSE (1) in order to determine the operator L. Therefore, the function u is often referred to as auxiliary function or auxiliary solution of the TDSE (1), and throughout the remainder of this note we will adopt that terminology. Let us further point out that in the stationary case the function is often referred to as superpotential. Roughly speaking, this is due to the fact that the stationary Hamiltonians factorize as products of the operators L and . Since this is not true in the present, time-dependent case, we will not use the term superpotential here. Now, the characterization of L as given in (12) is complete and it remains to find its adjoint , which can be done as follows: suppose that the differential operators , , are self-adjoint, and take the adjoint of our intertwining relation (9):
This intertwining relation will be used to find , which is therefore called intertwiner, just as its adjoint L. If we assume to be a linear, first-order differential operator, then we find after substitution into (14) and evaluation that
Application to a solution of the second TDSE (2) gives then is given by
where the function is a solution of the second TDSE (2) and does not depend on the spatial variable. Then, if and u are linearly independent, the function is a nontrivial solution of the first TDSE (1), the potential of which is constrained as
Hence, the characterization of is complete and we can continue with the construction of our superalgebra.
Construction of the superalgebra. We will need to have another generator besides the supercharges, which we obtain as follows. Consider the operators and , defined by
We will now see that is a symmetry operator of the first TDSE (1). To this end, we evaluate the following commutator:
Now we substitute the intertwining relations (9) and (14) in the first and the second term of (16), respectively. This gives
In a similar way one proves that
The vanishing commutators (17) and (18) imply that and are symmetry operators of the TDSEs (1) and (2), respectively. Consequently, diag is a symmetry operator of our matrix TDSE (5). We are now ready to show that the supercharges and the symmetry operator S generate a superalgebra. To this end, we need to evaluate a couple of commutators and anticommutators [13], denoted by ).
This follows from the fact that the supercharge matrices (6) are nilpotent. Next, we have
In the same fashion one shows that
Finally we find
In the same way we find
As in the stationary case [4], our results (19)-(23) imply that the operators and S are the generators of the simplest superalgebra. If the solutions and potentials of our TDSEs (1) and (2) are related by means of (12) and (13), respectively, then the corresponding Hamiltonians and are called supersymmetric partners. This term is also applied to their respective potentials, one says that and are supersymmetric partners. The relation (12) was first introduced in [8] and is known as Darboux transformation, the corresponding operator (11) is called Darboux operator.
3. Generalized SUSY formalism
In this section we develop the SUSY formalism for a generalized form of the TDSE, where we summarize results from [11]. In principle we follow the steps that were taken in the previous section, but this time the intertwining relation and its solution will be studied in detail.
The generalized TDSE. Let us consider the following equation, which we will call generalized TDSE:
Here , , denote arbitrary coefficient functions, is the potential, and stands for the solution. In order to set up the SUSY formalism for equation (24), we first rewrite it in a different form. To this end, let us set
introducing arbitrary functions , and . After insertion of the settings (25) into TDSE (24), the latter obtains the following form:
Note that the settings (25) do not reduce the number of free parameters, the equation is just written in a different form without imposing any restriction.
Generalized matrix TDSE and supercharges. Now let us consider another generalized TDSE, which we will relate to its counterpart (26):
where is the potential and stands for the solution. As in the previous section we will develop a generalized SUSY formalism that relates the TDSEs (26) and (27). The corresponding Hamiltonians we define as
Using these Hamiltonians, the two generalized TDSEs join as components of the following matrix equation:
This equation has exactly the same form as its conventional counterpart (4). If we define a matrix Hamiltonian H via diag, together with a matrix solution , then our equation (29) takes the following form:
Next, we define the supercharge operator and its adjoint as in the conventional case (6):
for two operators L and that are to be determined. It is clear that these supercharges have the properties (7) and (8). The difference between the present and the conventional case lies in the form of the operators L and .
The intertwining relation for . In order to determine L, we require it to convert solutions of the first TDSE (26) into solutions of the second TDSE (27), and its adjoint must convert solutions of the second TDSE (27) into solutions of the first TDSE (26). The intertwining relation involving the operator L is given by (9), where the Hamiltonians are taken from (28):
At this point it is necessary to expand the intertwining relation in order to get conditions for the sought operator L. Let us assume that L is given in the form (10), substitution of which in combination with (28) renders (32) in the form
We will now expand both sides of this intertwining relation and find the coefficients of the derivative operators. The intertwining relation can only be fulfilled if the coefficients of a derivative operator are the same on both sides, which gives conditions on the coefficients. Let us first evaluate the left hand side of the latter intertwining relation:
Next, we process the right hand side of (33) in the same way:
Again, the intertwining relation (33) can only hold if its two sides (34) and (35) are the same. It is easy to see that the terms associated with the derivatives , and are already equal on both sides and therefore cancel in the intertwining relation. Since there are more terms in the coefficients that cancel in the same way, let us now recombine (34) and (35) after simplification, that is, without equal terms that appear on both sides.
As mentioned before, we now collect the coefficients of each derivative operator on both sides of the latter intertwining relation and require the coefficients to be the same.
Resolution of the intertwining relation. Since there are only three different derivative operators left in our intertwining relation (36), namely, , and the multiplication (derivative of order zero), we obtain three equations. These equations have the following form:
We will now solve this system of equations with respect to the coefficients and in our operator L, recall its form as given in (10). Since we are dealing with three equations, we will need a third function as a variable, which we take to be the potential of the TDSE (27). In order to solve the above three equations, we start with (37) and determine :
where is an arbitrary constant of integration. It remains to solve equations (38) and (39) by determining and the potential , which will be done by elimination of the potential difference. In order to do so, we first need to write equations (38) and (39) in a slightly different form:
Now we multiply the first and the second of these equations by and , respectively, such that the right hand sides of these equations become the same. Consequently, the left hand sides must also be the same, and we can equate them to each other. This results in the following equation:
We will now solve this equation with respect to . To this end, we will introduce a new function K defined by . Before we substitute this function into (41), we first evaluate the following expressions, which we will need in the substitution:
where we have used the explicit form (40) of . We use this explicit form and the derivatives (42) in order to rewrite equation (41), where we substitute by . After simplification we arrive at the following equation:
We see that our former equation (41), which depends on and , has been converted to an equation that depends on K only. Unfortunately, we cannot solve (43), as it is an equation of Riccati type for K, which is not integrable in a general case like ours [14]. Still, for practical reasons it makes sense to linearize (43) by means of the following setting:
introducing a new function . Assuming that u is twice continuously differentiable, implying , we substitute (44) in (43) and get after simplification the following equation for the function u:
Clearly, this equation holds if the expression in square brackets does not depend on x. We integrate on both sides and multiply with u:
where is a purely time-dependent constant of integration. Equation (46) is identical to the initial equation (26) for . However, setting C to zero is not a restriction, since solutions to (46) with and differ from each other only by a purely time-dependent factor, which cancels out in (44). Thus, our equation (46) can be taken in the form
The function u is called auxiliary solution of the TDSE (26), as it is needed for determining the function that appears as a coefficient in the operator L. Once a solution u of (47) is known, then the function K can be found from (44), which in turn determines the sought coefficient by means of . Taking into account the explicit form (40) of , we obtain
Thus, with the coefficients and we have determined the sought operator L, as given in (10), completely.
Potential difference and the operator . Before we state the operator L in its explicit form, let us find the potential by solving (38):
This can be specified more by inserting the explicit form of and , as given in (40) and (48), respectively. We obtain
The operator L is given explicitly by
Hence, if is a solution of the first TDSE (26), then is a solution of the second TDSE (27), provided the potential is related to the potential via (50). Let us briefly verify that our expressions for the operator L and the potential reduce correctly to their conventional counterparts that are given in (12) and (13), respectively. To this end, we observe that in the conventional case we have . On substituting this setting into (52), we recover immediately the correct expression (12), if we take . As for the potential , plugging into its explicit form (50), we obtain
which coincides with the desired expression (13) for .
The adjoint operator . The next task is to find the operator in the same way as it was just done for L. The intertwining relation to be used is given by the adjoint of (32):
where the Hamiltonians are of generalized form (28) and we assumed that the operators , , are self-adjoint. The calculation scheme for finding is the same as for L and consists in expanding the two sides of the intertwining relation, collecting the respective coefficients of the derivative operators, and requiring them to be the same on both sides of the intertwining relation. Afterwards, the resulting conditions for have to be resolved. Since the calculations for finding are similar and as tedious as in the case of its counterpart L, we do not present the whole scheme in detailed form. Instead, we state the result, which is the explicit form of the operator :
Let and u be linearly independent solutions of the second TDSE (27), then the function , given by
is a solution of the first TDSE (27), provided the potential is given by
This completes the characterization of the operator .
Construction of the superalgebra. Since the operators L and in the generalized case are now determined, at the same time the supercharges Q and , as given in (31), are determined. As in the coventional case we construct the superalgebra by adding one more generator besides the supercharges, which will be constructed from the following operators and :
This is the same definition as for the conventional case (15). We observe that and are symmetry operators for the TDSEs (26) and (27), respectively, such that diag provides a symmetry operator for the matrix TDSE (30). This can be proved exactly as in the conventional case, see the calculations (16)-(18). Furthermore, the results (19)-(23) transfer to the present, generalized case without change of notation:
This implies that Q, and S generate the simplest superalgebra. As in the conventional case, if the solutions and potentials of our TDSEs (26) and (27) are related by means of (52) and (50), respectively, then the corresponding Hamiltonians and , as given in (28), are called supersymmetric partners (the same can be said about the potentials and ). The operator (51) is called generalized Darboux operator, and its application (52) is called generalized Darboux transformation [10].
4. Reality condition
Throughout this section we continue summarizing results from [11]. In general, the potential and its supersymmetric partner , as given in (50), are allowed to be complex-valued. In fact, even if one of the potentials is real, its supersymmetric partner can still turn out to be non-real. This is sometimes not desirable, as in many applications one is interested in real-valued potentials only. In this section we review a condition on the potential in the second TDSE (27) to be real-valued, provided both the potential of the first TDSE (26), and the parameters f, h are real. This condition is called reality condition, and it is usually fulfilled by choosing the arbitrary function N in (50) accordingly. Since N does not depend on the spatial variable, the reality condition is not guaranteed not have a solution. As a byproduct of our reality condition, we obtain the corresponding condition for the conventional case after setting in the final result. Now, before we start considering the reality condition, we first rewrite the function N in a form that will prove convenient for our purposes. Observe that N can be complex, so let us first find its real and imaginary parts. Write N in polar coordinates as
where the real-valued functions and denote the absolute value and the argument of N, respectively. We obtain
Here the prime stands for the derivative, note that and depend on t only. We are now ready to extract the imaginary part of the potential , as given in (50). After substitution of (55) we obtain the following result for the imaginary part of :
If this expression is zero, then the potential must be real. After regrouping terms, requiring (56) to be zero, and solving with respect to the logarithm containing we arrive at the following condition:
It becomes clear that this equation does not necessarily have a solution for , since its right hand side can depend on both x and t, while the left hand side depends only on t. Furthermore, we do not have any free parameters left except for . Let us rewrite our condition (57):
We will now express the imaginary part on the right hand side of the latter equation in a standard way:
note that the asterisk denotes complex conjugation. We incorporate the latter change into our condition (58) and continue its simplification:
This is the condition for the potential (50) of the second TDSE (27) to be real-valued. It has a solution for if the right hand side does not depend on the spatial variable. If this is so, then we can solve (59) for the function , giving
Let us point out that this is in general not a solution, since the right hand side of (60) can depend on x, while the left hand side cannot. Now let us assume the reality condition (59) to be fulfilled, we will determine the corresponding form of the potential . Substitution of (59) or (60) into the potential as given in (50), gives its real part:
As desired, this expression contains only real-valued terms. Finally, let us verify how the reality condition (59) and the potential of the second TDSE (27) reduce in the conventional case. There we have , which we plug into our reality condition (59):
This allows for a solution if the right hand side does not depend on x, that is, if
which coincides with well known results [13]. Next, we insert into the potential , the explicit form of which is given in (50):
This is precisely the known reality condition for the conventional TDSE [13], if we set the arbitrary phase to zero.
5. SUSY formalism for particular TDSEs
The generalized TDSE (26) does not have an immediate physical meaning. Its importance lies in the fact that it contains many physical equations as special cases, such that for each of these cases the particular SUSY formalism can be easily extracted from the general context. Let us now consider several special cases of the generalized (26) and their corresponding SUSY formalisms, i.e., the explicit form of the SUSY operators L and , the supersymmetric partner potentials and the reality condition. Throughout this section we assume all functions to depend on x and t, unless said otherwise.
5.1. TDSE for position-dependent mass
Position-dependent masses occur in the context of transport phenomena in crystals (e.g. semiconductors), where the electrons are not completely free, but interact with the potential of the lattice. The quantum dynamics of such electrons can then be modeled by an effective mass, the behaviour of which is determined by the band curvature, see [15] for details.
Equation:
Relation to generalized TDSE:
SUSY operators:
Supersymmetric partner potential:
Reality condition:
Supersymmetric partner potential under reality condition:
5.2. TDSE with weighted energy
The following equation carries a nonconstant factor in front of the time derivative. In the stationary case, where the time-derivative is substituted by a multiplication with the energy, the nonconstant factor can be seen as weighting the energy [16], or as generating an energy-dependent potential [17]. For the sake of generality, we consider here the fully time-dependent case.
Equation:
Relation to generalized TDSE:
SUSY operators:
Supersymmetric partner potential:
Reality condition:
Supersymmetric partner potential under reality condition:
5.3. TDSE with minimal coupling
This TDSE resembles a system that is minimally coupled to a vector potential [18]. The form of the coefficients in the TDSE (26) will be a bit more involved than in the other cases. Note that in the following m is a constant.
Equation:
Relation to generalized TDSE:
SUSY operators:
Supersymmetric partner potential:
Reality condition: This condition does not apply here, since the potential as given in (67) is in general not real-valued.
Supersymmetric partner potential under reality condition: This condition does not apply here either.
5.4. Conventional TDSE
Finally, for the sake of completeness let us summarize the SUSY formalism of the conventional TDSE.
Equation:
Relation to generalized TDSE:
SUSY operators:
Supersymmetric partner potential:
Reality condition:
Supersymmetric partner potential under reality condition:
6. Example: TDSE with weighted energy
Before we turn to extensions of the SUSY formalism to equations different from the TDSE, let us now give an example of how our SUSY formalism can be applied. We consider the special case (64), that is, the TDSE for weighted energy:
In this particular application we choose the following weight function h potential :
where and is an arbitrary function that is purely time-dependent. We want to find the supersymmetric partner of the Hamiltonian corresponding to equation (68), or, equivalently, to the potential . To this end, we must apply the operator L, as given in (65), to a solution of the TDSE (68). Furthermore, we need an auxiliary solution u of the same equation, such that and u are linearly independent. These two solutions are chosen as follows:
Clearly, the two solutions (71) and (72) are linearly independent. After substitution of our settings (69) and (70) into the SUSY operator L and the potential difference, as given in (65) and (66), respectively, we get
If we take then imaginary part of the potential becomes zero:
This potential is stationary, as its initial counterpart in (70). If we wanted the potential to be time-dependent, then we would have to satisfy , since the time-dependent terms are in the potential’s imaginary part. Finally, if we wanted the potential , as given in (74), to be time-dependent and real-valued, then we would have to write the arbitrary function N as follows:
introducing a function , which renders the potential (74) in the form
The fact that N has now turned complex does not matter, since it appears only in the solution , as displayed in (73).
7. SUSY formalism beyond the TDSE
The quantum-mechanical SUSY formalism that we developed in section 2 and section 3, is only valid for the conventional and the generalized TDSE, respectively. This concerns especially the construction of the superalgebra by means of the supercharges and the symmetry operator S. However, the computational core of the SUSY formalism can be carried over to different, even nonlinear equations. This is possible, since from a purely mathematical point of view the operator L is nothing else than a transformation between differential equations. This transformation can be used without knowledge of the actual SUSY formalism, such as the supercharges or the superalgebra: it simply maps a solution of a TDSE onto a solution of another TDSE. The principal idea behind extending the transformation operator L to equations different from the TDSE, can be explained by means of the following diagram. In the upper left corner of the diagram, EQ stands for an equation that is related to the TDSE (lower left corner) by means of an invertible transformation P. The TDSE allows application of the operator L, which generates a solution of a different TDSE, called TDSE’ (lower right corner). The latter TDSE can then be mapped back by means of onto an equation called EQ’ (upper right corner). This way, one defines a mapping between the equation EQ and its counterpart EQ’ via
Thus, if for a given equation EQ there is an invertible transformation P that relates the TDSE with EQ, then the operator can be constructed as outlined in figure 1, and it will map solutions of EQ onto solutions of EQ’. We repeat that there is no further restriction on the transformation P, it just needs to be invertible. In the following we will see two applications of the scheme displayed in figure 1.
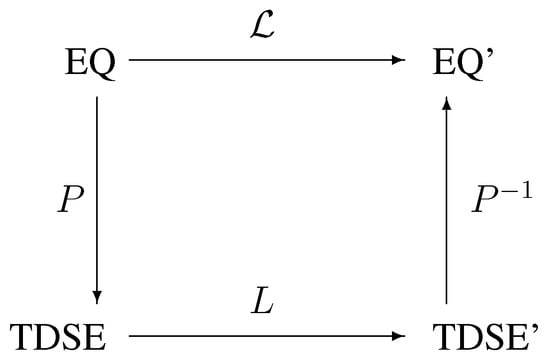
Figure 1.
Extension of the SUSY transformation scheme.
7.1. The Fokker-Planck equation
In the first application we extend the SUSY formalism to the Fokker-Planck equation (FPE) with constant diffusion and stationary drift potential. For more details the reader may consult the underlying work [12]. We first define an appropriate mapping P (see figure 1), and afterwards construct the mapping according to (75).
Statement of the problem. The Fokker-Planck equation (FPE) with constant diffusion and stationary drift has the following form [19]
where denotes its solution and the prime stands for the derivative, note that does depend on x only. We will connect equation (76) with an FPE for a different drift potential by means of the scheme displayed in figure 1. The FPE (76) will be related to the equation
where stands for the solution. We will now show that the first and the second FPE, as given in (76) and (77), can be related by means of an operator as displayed in figure 1, if we identify EQ and EQ’ with the FPEs as given in (76) and (77), respectively.
Mapping the FPE onto the TDSE. Following (75), we first need to find an invertible transformation P that takes solutions of the FPE into solutions of the TDSE. Such a transformation is well known [12]: let f be a solution of the FPE (76), then we define the transformation P as
where E is a constant. The key property of the latter transformation P lies in the fact that the function is a solution of the following ordinary differential equation
and as such does only depend on the spatial variable. Equation (79) is a stationary Schrödinger equation with energy E and potential given by
Equation (79) can be seen as a special case of the conventional TDSE (1), where the derivative with respect to t is left out, simply because the solution does not depend on t. Speaking in terms of our diagram in figure1, equation (79) corresponds to the TDSE in the lower left corner. In the next step we observe that the SUSY operator L in (11) is applicable to equation (79), since it is a special case of (1).
Application of the SUSY formalism. Take the solution and an auxiliary solution u of (79), such that and u are linearly independent. Furthermore, we require the function to solve the Schrödinger equation (79) at energy , note that and u are allowed to be solutions at different energies E. This is due to the fact that the auxiliary function solves (46), where an arbitrary time-dependent function can be included. In the time-dependent case this function cancels out, while in the present stationary case it becomes constant and adds to the energy E in equation (79). This is the reason why the solution and its auxiliary counterpart can be taken at different energies. Now we fix an auxiliary function u at energy, say, , and apply the operator L to the solution of (79) at :
The resulting function , given by (12), is then a solution of the Schrödinger equation (2), in the present case without derivative in t:
where the (here) irrelevant constant has been set to one and the potential has been taken from the general case (13). The Schrödinger equation (81) corresponds to equation TDSE’ of figure 1 in the lower right corner. In the last step we need to apply the inverse of P in order to convert (81) back into an FPE, which then is denoted EQ’ in our diagram. Note that in the present form we cannot go back to the FPE, because the potential in (81) does not have an appropriate form. We will rewrite the potential by means of a function that we introduce by means of the following relation:
Let us solve this equation with respect to :
where a constant of integration has been set to zero. Now we find out which Schrödinger equation is solved by . Evaluation of yields
Thus, by means of the solution we have rewritten our Schrödinger equation (81) in the form (83), which we can now convert into an FPE.
Mapping the TDSE onto the FPE. We introduce the inverse transformation of P as
Note that is not the inverse of P from a mathematical viewpoint, we use this notation here to express that reverses the action of P in a certain sense. Now, substitution of into the Schrödinger equation (83) shows that is a solution of the following FPE for the new drift potential :
which in figure 1 is denoted as EQ’ in the upper right corner. Hence, by means of the scheme displayed in our diagram we have constructed a mapping between two FPEs. This mapping is related to the SUSY operator L as shown in figure 1 and it is given explicitly by (75). We now use this relation to obtain the explicit form of the operator and to express the drift potential through its initial counterpart that appeared in the FPE (76).
Explicit form of the extended SUSY transformation. We start with the drift potential , which we are able to write down after combining our previous findings (80) and (82):
Let us now integrate this expression and substitute the function as given in (78), we get
In the final step we observe that the function u is a solution of the Schrödinger equation (79), whereas we would like it to be expressed through a solution of the FPE (76). To this end, we relate u to a solution v of the NBE by means of the transformation P, as given in (78):
which we now plug into our expression for the solution , as given in (86):
Since appears in the FPE (85) only as a derivative with respect to the spatial variable, the second term on the right hand side of (86) becomes irrelevant. We therefore can write
This is the final form of the drift potential as it enters in the FPE (85), the solution of which we will now construct. To this end, we need to collect our intermediate results on the solutions , and . The corresponding information is contained in (78), (80) and (84). We have
Now we make use of the relation between the drift potentials and that we obtained in (88). Insertion of the latter relation into (89) leads to the following expression:
As before we use (87) to express the auxiliary solution u of the TDSE (79) by an auxiliary solution of the FPE (76). Substitution into (90) gives
This is the solution of the FPE (85) for drift potential as given in (88). Thus, we just finished constructing the mapping that is called in figure 1, and that is given by (75). Suppose a solution for the FPE (76) with drift potential is given, then the relations (91) and (88) state the corresponding solution and drift potential of the FPE (85). In summary, we have extended the SUSY formalism for the TDSE to the FPE. Let us conclude this section with an example.
Example: quadratic drift potential. Let us consider the FPE (76) for the following quadratic drift potential:
where we do not include free parameters, since we want to keep calculations simple. The associated Schrödinger equation (79), that we obtain by means of our mapping P, as defined in (103), transforms the FPE (76) with drift potential (92) into a Schrödinger equation (79), which reads in the present case: :
This equation admits the following set of solutions at energy , respectively:
where stands for the Hermite polynomial of order k. Therefore, by means of our transformation P, as given in (103), we can map the solution set (95) of the Schrödinger equation (79) onto a corresponding solution set of the FPE (76):
Let us now obtain solutions of the FPE (85) with drift potential . To this end, we need to evaluate (91), supplying a solution and an auxiliary solution v of the FPE (76) for drift potential (92). Let us choose
Note that technically the function in (96) should carry an index k, but for the sake of simplicity we omit to set that index. Now, on plugging (96), (97) and from (94) into the explicit form of (91), we obtain
where k is a natural number. The function (99) is a solution of the transformed FPE (85) for the drift potential , which we now determine from its general form (88). Insertion of the drift potential , the auxiliary solution v, and the solution , as given in (92), (97) and (96), respectively, gives
7.2. The Burgers equation
In this section we present a second example of an equation that permits an extension of the SUSY formalism. Note that the only difference between the present and the previous example lies in the mapping P that connects the TDSE with the equation under consideration.
Statement of the problem. We consider the nonhomogeneous Burgers equation (NBE) in the following form [20]
where stands for the solution, denotes the nonhomogeneity and is called viscosity coefficient. We will connect equation (101) with an NBE for a different nonhomogeneity by means of the scheme displayed in figure 1. The NBE (101) will be related to another NBE of the form
where stands for the solution. We will now show that the first and the second NPE, as given in (101) and (102), can be related by means of an operator as displayed in figure 1, if we identify EQ and EQ’ with the NBEs as given in (101) and (102), respectively.
Mapping the NPE onto the TDSE. We must find an invertible mapping P that connects the TDSE with the NBE, as represented by the vertical arrows in figure 1. Such a mapping P is given by the Cole-Hopf transformation:
This transformation linearizes the NBE (101) to a TDSE, corresponding to the equation in the lower left corner of our diagram in figure 1. Consequently, the function is then a solution of the following equation:
where the following abbreviations have been used:
Equation (104) is a TDSE and we can therefore apply the SUSY formalism.
Application of the SUSY formalism. We can transform the solution by means of the operator L, as given in (11):
Recall that the function is arbitrary and that u is an auxiliary solutions of the TDSE (104), such that and u are linearly independent. Now, the function solves the TDSE
where the potential reads
At this point the factor in front of the logarithmic derivative in (109) should be explained, as this factor is not present in the general form of the potential difference (13). However, there is no contradiction if we see the TDSE (104) as a generalized TDSE for position-dependent mass (62). The potential difference generated by the SUSY transformation is then given by (63) and includes precisely the factor that we have in (109), where m must be replaced by . The TDSE (108) corresponds to the TDSE in the lower right corner of our diagram in figure 1. Now, in order to transform the TDSE back into a NBE, we need to apply the inverse Cole-Hopf transformation .
Mapping the TDSE onto an NBE. Inversion of the Cole-Hopf transformation (103) for the solution of (108) yields
We combine this transformation with the settings (105) and
where , and obtain that the function solves the NBE
where the nonhomogeneity is related to the transformed potential by (111). Let us now express the solution of the transformed NBE (112) and its nonhomogeneity through the solution of the initial NBE (101).
Explicit form of the extended SUSY transformation. Let us first take into account that the auxiliary solution u of the TDSE (104) is related to a solution v of the initial NBE (101) via
Now let us first find the explicit relation between the solutions and of the first and the second NBE, as given in (101) and (112), respectively. To this end, we combine our results (107) and (110), which gives
This expression will take its final form, once we substitute the solutions and u of the TDSE (104) by the solutions and v, as given by (103) and (114), respectively:
This is the final form of the relation between the two solutions and of the NBE (101) and (112), respectively. It remains to determine the nonhomogeneity in the NBE (112), which can be extracted from (111):
In the final step we replace the auxiliary solution u of the TDSE (104) by an auxiliary solution v of the NBE (101). The relation between the solutions u and v is given in (114) and will now be substituted into (116):
This is the nonhomogeneity of the FPE (85) in its explicit form. Thus, we have successfully constructed the mapping , as defined in (75), for the NBE: suppose a solution for the NPE (101) with nonhomogeneity is given, then the relations (115) and (117) state the corresponding solution and nonhomogeneity of the BNE (112). In summary, we have extended the SUSY formalism for the TDSE to the NBE. Let us conclude this section by giving an example.
Example: linear nonhomogeneity. We consider the NBE (101) for the following linear nonhomogeneity:
where is an arbitrary, purely time-dependent function. The nonhomogeneity (118) models an external elastic force, where the function k resembles a time-varying string constant [24]. It is well-known that the NBE with nonhomogeneity (118) admits closed-form solutions for many particular choices of k, see for example [21,22,23,24]. We will now take such a solution and apply the extended SUSY formalism to it, given by (115) and (117), respectively. This way we obtain a solution for the NBE (112) for a nonhomogeneity , which will be different from . As for the solution of the NBE (101) with nonhomogeneity (118), we adopt a solution introduced in [23]. Before we state this solution explicitly, let us redefine k in terms of a function c as follows:
Then the solution u of the NBE (101) with nonhomogeneity (118) is given in the following form:
where is a solution of the homogeneous Burgers equation, that is, the NBE (101) for . We choose w to be the regular single-shock solution
where A is a positive constant. This renders the solution (120) in the following explicit form:
Now let us return to the solution and the auxiliary solution v of (101) that we will need for our generalized SUSY formalism. We choose both the auxiliary solution and the solution to be transformed from the general form (122) for and , respectively:
Let us now determine the solution and the corresponding nonhomogeneity of the NBE (112) explicitly. The solution takes the form (115), which in the present case is
It remains to determine the nonhomogeneity , which can be extracted from (117) and reads
where k is defined in (119). In summary, the extended SUSY formalism takes the initial NBE (101) with drift potential as given in (118), into the NBE (112) with solution and drift potential , as given in (115) and (117), respectively.
8. Concluding remarks
In the present work we have reviewed the conventional SUSY formalism for the TDSE and how it extends to the generalized case: the SUSY theory stays essentially the same, while the differences between the standard and the generalized case lie in the computational aspects only (the operators L and ). Furthermore, we have shown how the computational aspect of the SUSY formalism can be applied to equations different from the TDSE and from its generalized counterpart. It should be stressed that that the equations we gave as examples (the Fokker-Planck and the nonhomogeneous Burgers equation) are by far not the only equations that allow a generalized SUSY transformation. The only ingredient for constructing such a transformation is the existence of an invertible mapping P, as displayed in figure 1, that connects the TDSE with another equation, which the generalized SUSY transformation will then be applied to by means of (75). Our diagram in figure 1 even allows replacing the equations denoted TDSE and TDSE’ by generalized equations of the form (26) and (27), such that all equations that can be connected to the generalized TDSEs by means of an invertible mapping P, admit a generalized SUSY transformation. Identification of such equations, the application of our extended SUSY formalism and the classification of physically interesting cases will be subject to future research.
References
- Dine, M. Supersymmetry and String Theory; Cambridge University Press: Cambridge, United Kingdom, 2007. [Google Scholar]
- Samsonov, B.F.; Sukumar, C.V.; Pupasov, A.M. SUSY transformation of the Green function and a trace formula. J. Phys. A 2005, 38, 7557–7565. [Google Scholar] [CrossRef]
- Sukumar, C.V. Green’s functions, sum rules and matrix elements for SUSY partners. J. Phys. A 2004, 37, 10287–10295. [Google Scholar] [CrossRef]
- Cooper, F.; Khare, A.; Sukhatme, U. Supersymmetry and Quantum Mechanics. Phys. Rep. 1995, 251, 267–388. [Google Scholar] [CrossRef]
- de Lima Rodrigues, R. The Quantum Mechanics SUSY algebra: an introductory review. arXiv, arXiv:hep-th/0205017.
- Khare, A. Supersymmetry in Quantum Mechanics. Pramana 1997, 49, 41–64. [Google Scholar] [CrossRef]
- Bagrov, V.G.; Samsonov, B.F. Supersymmetry of a nonstationary Schrödinger equation. Phys. Lett. A 1996, 210, 60–64. [Google Scholar] [CrossRef]
- Darboux, M.G. Sur une proposition relative aux équations linéaires. Comptes Rendus Acad. Sci. Paris 1882, 94, 1456–1459. [Google Scholar]
- Matveev, V.B.; Salle, M.A. Darboux transformations and solitons; Springer: Berlin, Germany, 1991. [Google Scholar]
- Schulze-Halberg, A.; Pozdeeva, E.; Suzko, A.A. Explicit Darboux transformations of arbitrary order for generalized time-dependent Schrödinger equations. J. Phys. A 2009, 42, 115211–115223. [Google Scholar] [CrossRef]
- Suzko, A.A.; Schulze-Halberg, A. Darboux transformations and supersymmetry for the generalized Schrödinger equations in (1+1) dimensions. J. Phys. A 2009, 42, 295203–295217. [Google Scholar] [CrossRef]
- Schulze-Halberg, A.; Morales, J.; Pena Gil, J.J.; Garcia-Ravelo, J.; Roy, P. Exact solutions of the Fokker-Planck equation from an nth order supersymmetric quantum mechanics approach. Phys. Lett. A 2009, 373, 1610–1615. [Google Scholar] [CrossRef]
- Bagrov, V.G.; Samsonov, B.F. Time-dependent supersymmetry in quantum mechanics. In Proceedings of the 7th Lomonosov Conference on Problems of Fundamental Physics, Moscow, Russia, 1997; pp. 54–61. [Google Scholar]
- Kamke, E. Differentialgleichungen - Lösungsmethoden und Lösungen; B.G. Teubner: Stuttgart, Germany, 1983. [Google Scholar]
- Landsberg, G.T. Solid state theory: methods and applications; Wiley-Interscience: London, United Kingdom, 1969. [Google Scholar]
- Suzko, A.A.; Giorgadze, G. Darboux transformations for the generalized Schrödinger equation. Physics of Atomic Nuclei 2007, 70, 607–610. [Google Scholar] [CrossRef]
- Formanek, J.; Lombard, R.J.; Mares, J. Wave equations with energy-dependent potentials. Czech. J. Phys. 2004, 54, 289–316. [Google Scholar] [CrossRef]
- Song, D.Y.; Klauder, J.R. Generalization of the Darboux transformation and generalized harmonic oscillators. J. Phys. A 2003, 36, 8673–8684. [Google Scholar] [CrossRef]
- Risken, H. The Fokker-Planck Equation: Method of solution and Applications; Springer: Berlin, Germany, 1996. [Google Scholar]
- Burgers, J.M. Mathematical examples illustrating relations occurring in the theory of turbulent fluid motion. Kon. Ned. Akad. Wet. Verh. 1939, 17, 1–53. [Google Scholar]
- Xiaqi, D.; Quansen, J.; Cheng, H. On a nonhomogeneous Burgers equation. Science in China Series A: Mathematics 2001, 44, 984–993. [Google Scholar]
- Eule, S.; Friedrich, R. A note on the forced Burgers equation. Phys. Lett. A 2006, 351, 238–241. [Google Scholar] [CrossRef]
- Eule, S.; Friedrich, R. An exact solution for the forced Burgers equation, Progress in Turbulence II. Springer Proceedings in Physics 2007, 109, 37–40. [Google Scholar]
- Moreau, E.; Vallee, O. Connection between the Burgers equation with an elastic forcing term and a stochastic process. Phys. Rev. A 2006, 73, 016112, (4 pages). [Google Scholar] [CrossRef] [PubMed]
© 2009 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license http://creativecommons.org/licenses/by/3.0/.