Applying the RUSLE and ISUM in the Tierra de Barros Vineyards (Extremadura, Spain) to Estimate Soil Mobilisation Rates
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. The Improved Stock Unearthing Method (ISUM)
2.3. The Revised Universal Soil Loss Equation (RUSLE) Model
2.4. Mapping the Current Soil Surface Level for ISUM
3. Results
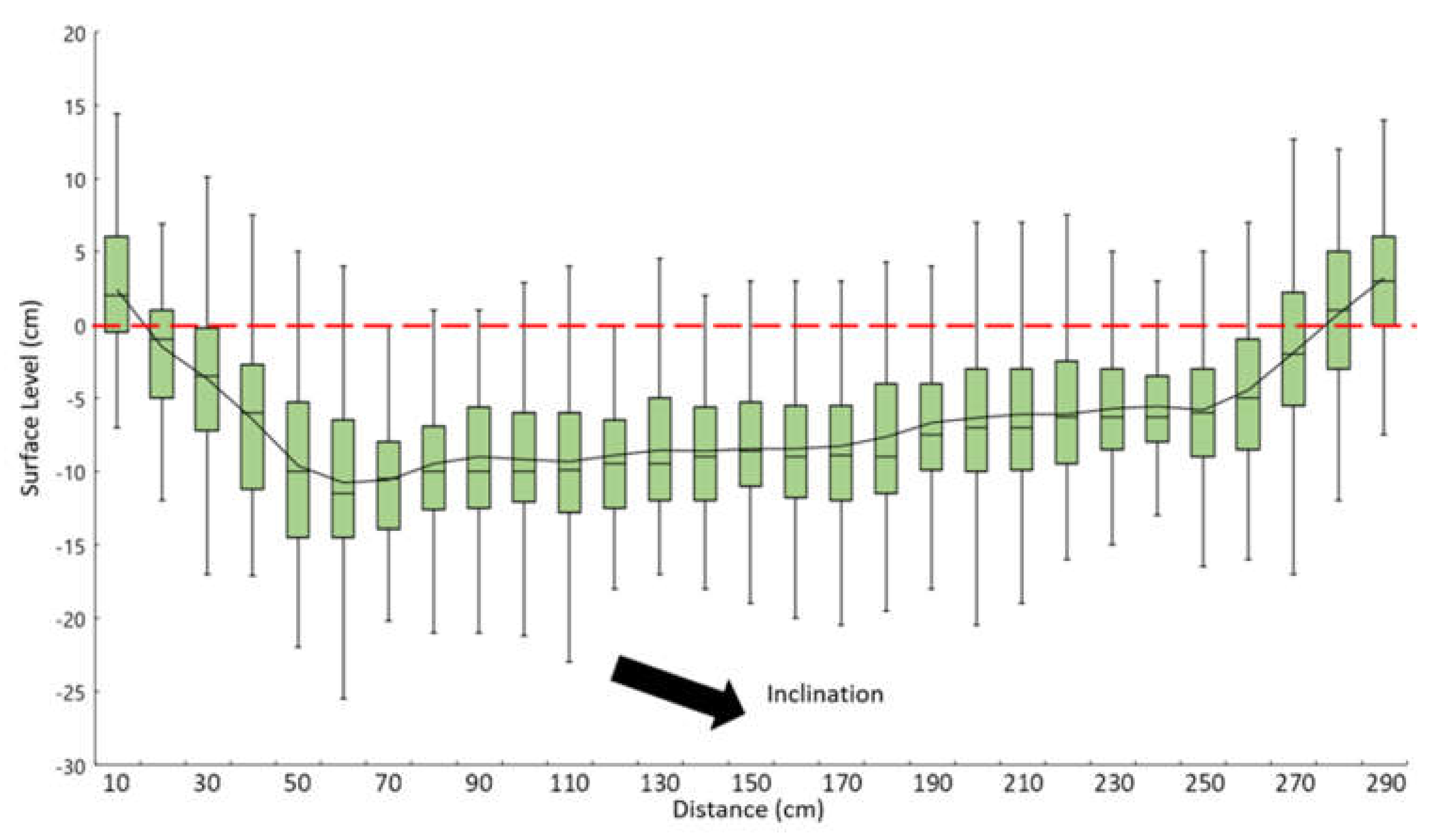
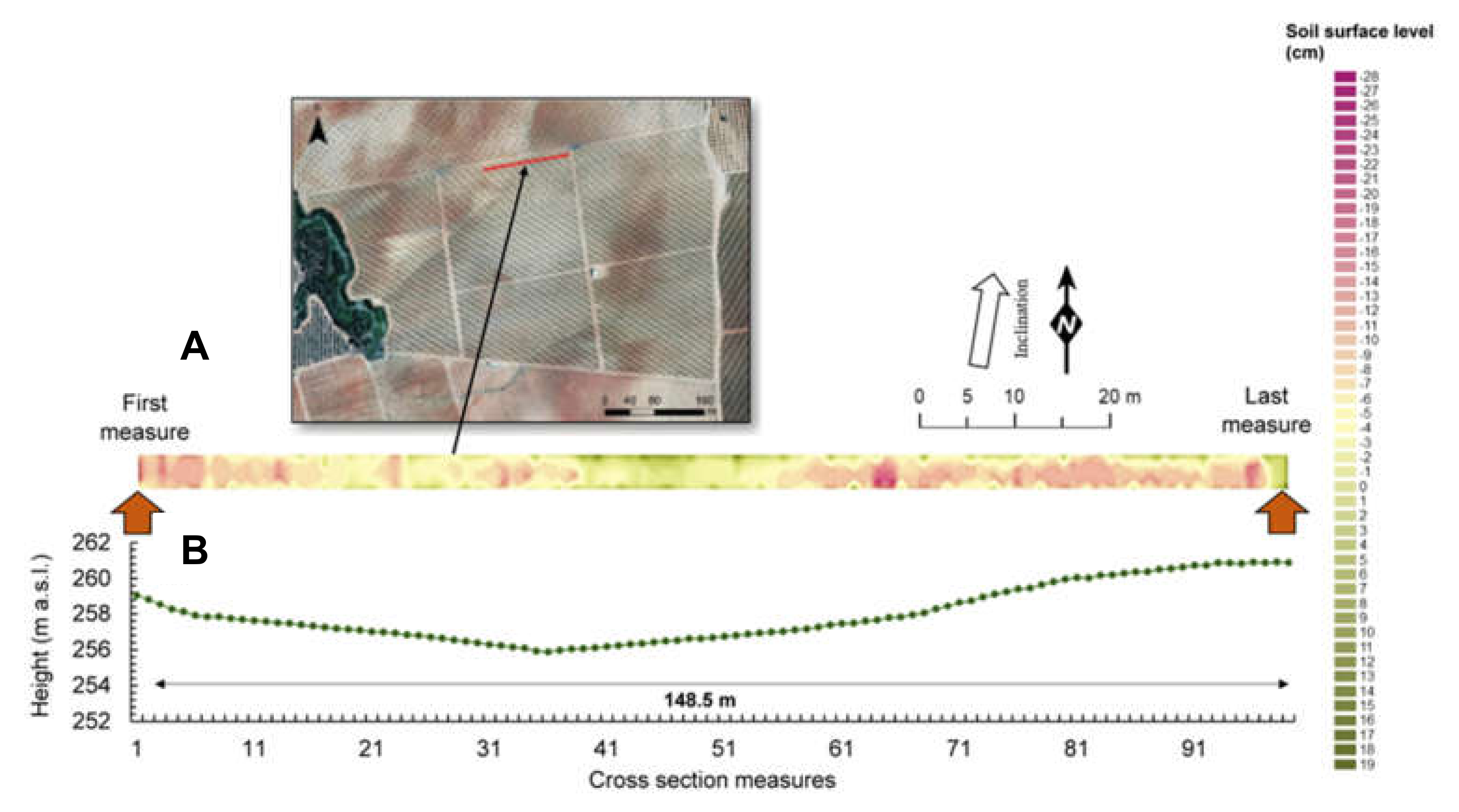
3.1. Current Soil Surface using ISUM
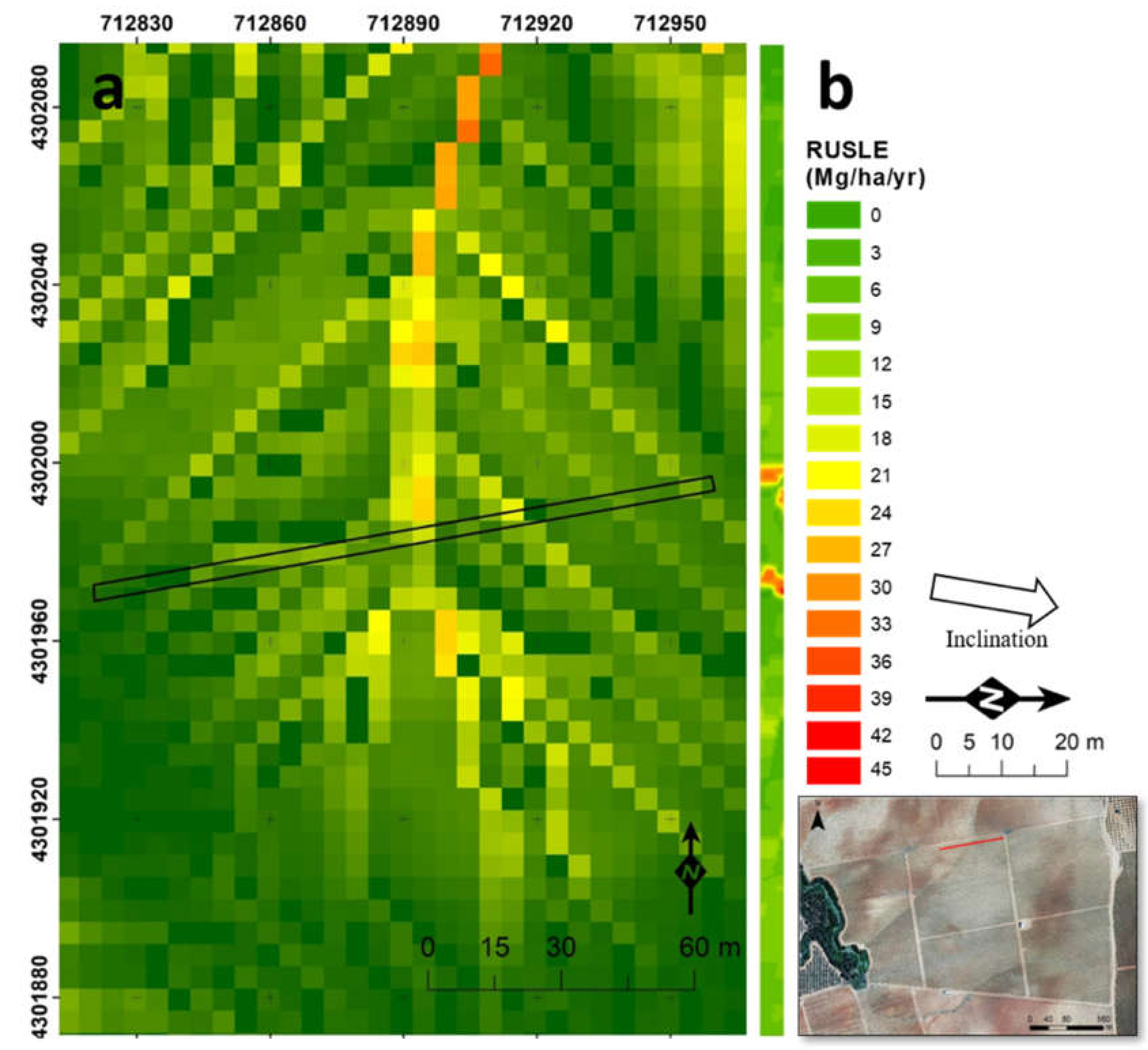
3.2. Soil Erosion Estimates using RUSLE
3.3. Soil Erosion and Mobilisation Rates
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- García-Ruiz, J.M.; Beguería, S.; Nadal-Romero, E.; González-Hidalgo, J.C.; Lana-Renault, N.; Sanjuán, Y. A meta-analysis of soil erosion rates across the world. Geomorphology 2015, 239, 160–173. [Google Scholar] [CrossRef]
- Keesstra, S.; Mol, G.; De Leeuw, J.; Okx, J.; Molenaar, C.; De Cleen, M.; Visser, S. Soil-Related Sustainable Development Goals: Four Concepts to Make Land Degradation Neutrality and Restoration Work. Land 2018, 7, 133. [Google Scholar] [CrossRef]
- Pacheco, F.A.L.; Varandas, S.G.P.; Fernandes, L.S.; Junior, R.V. Soil losses in rural watersheds with environmental land use conflicts. Sci. Total Environ. 2014, 485, 110–120. [Google Scholar] [CrossRef] [PubMed]
- Griggs, D.; Smith, M.S.; Rockström, J.; Öhman, M.C.; Gaffney, O.; Glaser, G.; Kanie, N.; Noble, I.; Steffen, W.; Shyamsundar, P. An integrated framework for sustainable development goals. Ecol. Soc. 2014, 19, 49. [Google Scholar] [CrossRef]
- García-Ruiz, J.M.; Beguería, S.; Lana-Renault, N.; Nadal-Romero, E.; Cerdà, A. Ongoing and Emerging Questions in Water Erosion Studies. Land Degrad. Dev. 2017, 28, 5–21. [Google Scholar] [CrossRef]
- Panagos, P.; Borrelli, P.; Meusburger, K.; Alewell, C.; Lugato, E.; Montanarella, L. Estimating the soil erosion cover-management factor at the European scale. Land Use Policy 2015, 48, 38–50. [Google Scholar] [CrossRef]
- Boellstorff, D.; Benito, G. Impacts of set-aside policy on the risk of soil erosion in central Spain. Agric. Ecosyst. Environ. 2005, 107, 231–243. [Google Scholar] [CrossRef]
- Li, X.H.; Yang, J.; Zhao, C.Y.; Wang, B. Runoff and sediment from orchard terraces in southeastern China. Land Degrad. Dev. 2014, 25, 184–192. [Google Scholar] [CrossRef]
- Taguas, E.V.; Arroyo, C.; Lora, A.; Guzmán, G.; Vanderlinden, K.; Gómez, J.A. Exploring the linkage between spontaneous grass cover biodiversity and soil degradation in two olive orchard microcatchments with contrasting environmental and management conditions. Soil 2015, 1, 651–664. [Google Scholar] [CrossRef]
- Verheijen, F.G.; Jones, R.J.; Rickson, R.J.; Smith, C.J. Tolerable versus actual soil erosion rates in Europe. Earth Sci. Rev. 2009, 94, 23–38. [Google Scholar] [CrossRef]
- Blavet, D.; De Noni, G.; Le Bissonnais, Y.; Leonard, M.; Maillo, L.; Laurent, J.Y.; Asseline, J.; Leprun, J.C.; Arshad, M.A.; Roose, E. Effect of land use and management on the early stages of soil water erosion in French Mediterranean vineyards. Soil Tillage Res. 2009, 106, 124–136. [Google Scholar] [CrossRef]
- Napoli, M.; Cecchi, S.; Orlandini, S.; Mugnai, G.; Zanchi, C.A. Simulation of field-measured soil loss in Mediterranean hilly areas (Chianti, Italy) with RUSLE. Catena 2016, 145, 246–256. [Google Scholar] [CrossRef]
- Pappalardo, S.E.; Gislimberti, L.; Ferrarese, F.; De Marchi, M.; Mozzi, P. Estimation of potential soil erosion in the Prosecco DOCG area (NE Italy), toward a soil footprint of bottled sparkling wine production in different land-management scenarios. PLoS ONE 2019, 14, e0210922. [Google Scholar] [CrossRef] [PubMed]
- Baiamonte, G.; Minacapilli, M.; Novara, A.; Gristina, L. Time Scale Effects and Interactions of Rainfall Erosivity and Cover Management Factors on Vineyard Soil Loss Erosion in the Semi-Arid Area of Southern Sicily. Water 2019, 11, 978. [Google Scholar] [CrossRef]
- Quiquerez, A.; Chevigny, E.; Allemand, P.; Curmi, P.; Petit, C.; Grandjean, P. Assessing the impact of soil surface characteristics on vineyard erosion from very high spatial resolution aerial images (Côte de Beaune, Burgundy, France). Catena 2014, 116, 163–172. [Google Scholar] [CrossRef]
- Rodrigo-Comino, J.; Brings, C.; Iserloh, T.; Casper, M.C.; Seeger, M.; Senciales, J.M.; Brevik, E.C.; Ruiz-Sinoga, J.D.; Ries, J.B. Temporal changes in soil water erosion on sloping vineyards in the Ruwer- Mosel Valley. The impact of age and plantation works in young and old vines. J. Hydrol. Hydromech. 2017, 65, 402. [Google Scholar] [CrossRef]
- Prosdocimi, M.; Cerdà, A.; Tarolli, P. Soil water erosion on Mediterranean vineyards: A review. Catena 2016, 141, 1–21. [Google Scholar] [CrossRef]
- Rodrigo-Comino, J. Five decades of soil erosion research in “terroir”. The State-of-the-Art. Earth Sci. Rev. 2018, 179, 436–447. [Google Scholar] [CrossRef]
- Rodrigo-comino, J.; Martínez-hernández, C.; Iserloh, T.; Cerdà, A. Contrasted Impact of Land Abandonment on Soil Erosion in Mediterranean Agriculture Fields. Pedosphere 2018, 28, 617–631. [Google Scholar] [CrossRef]
- Galati, A.; Gristina, L.; Crescimanno, M.; Barone, E.; Novara, A. Towards more efficient incentives for agri-environment measures in degraded and eroded vineyards. Land Degrad. Dev. 2015, 26, 557–564. [Google Scholar] [CrossRef]
- Martínez-Casasnovas, J.A.; Ramos, M.C.; Cots-Folch, R. Influence of the EU CAP on terrain morphology and vineyard cultivation in the Priorat region of NE Spain. Land Use Policy 2010, 27, 11–21. [Google Scholar] [CrossRef]
- Aranda, A.; Zabalza, I.; Scarpellini, S. Economic and environmental analysis of the wine bottle production in Spain by means of life cycle assessment. Int. J. Agric. Resour. Gov. Ecol. 2005, 4, 178. [Google Scholar] [CrossRef]
- Novara, A.; Stallone, G.; Cerdà, A.; Gristina, L. The Effect of Shallow Tillage on Soil Erosion in a Semi-Arid Vineyard. Agronomy 2019, 9, 257. [Google Scholar] [CrossRef]
- Martínez-Casasnovas, J.A.; Ramos, M.C.; Ribes-Dasi, M. On-site effects of concentrated flow erosion in vineyard fields: Some economic implications. Catena 2005, 60, 129–146. [Google Scholar] [CrossRef]
- Martínez-Casasnovas, J.A.; Ramos, M.C.; Benites, G. Soil and Water Assessment Tool Soil Loss Simulation at the Sub-Basin Scale in the Alt Penedès–Anoia Vineyard Region (Ne Spain) in the 2000s. Land Degrad. Dev. 2016, 27, 160–170. [Google Scholar] [CrossRef]
- Ben-Salem, N.; Álvarez, S.; López-Vicente, M. Soil and Water Conservation in Rainfed Vineyards with Common Sainfoin and Spontaneous Vegetation under Different Ground Conditions. Water 2018, 10, 1058. [Google Scholar] [CrossRef]
- Rodrigo-Comino, J.; Senciales, J.M.; Ramos, M.C.; Martínez-Casasnovas, J.A.; Lasanta, T.; Brevik, E.C.; Ries, J.B.; Sinoga, J.R. Understanding soil erosion processes in Mediterranean sloping vineyards (Montes de Málaga, Spain). Geoderma 2017, 296, 47–59. [Google Scholar] [CrossRef]
- Arnaez, J.; Lasanta, T.; Ruiz-Flaño, P.; Ortigosa, L. Factors affecting runoff and erosion under simulated rainfall in Mediterranean vineyards. Soil Tillage Res. 2007, 93, 324–334. [Google Scholar] [CrossRef]
- Arnáez, J.; Lana-Renault, N.; Lasanta, T.; Ruiz-Flaño, P.; Castroviejo, J. Effects of farming terraces on hydrological and geomorphological processes. A review. Catena 2015, 128, 122–134. [Google Scholar] [CrossRef]
- Prosdocimi, M.; Jordán, A.; Tarolli, P.; Keesstra, S.; Novara, A.; Cerdà, A. The immediate effectiveness of barley straw mulch in reducing soil erodibility and surface runoff generation in Mediterranean vineyards. Sci. Total Environ. 2016, 547, 323–330. [Google Scholar] [CrossRef]
- Martínez-Casasnovas, J.A.; Ramos, M.C. Soil alteration due to erosion, ploughing and levelling of vineyards in north east Spain. Soil Use Manag. 2009, 25, 183–192. [Google Scholar] [CrossRef]
- Capello, G.; Biddoccu, M.; Ferraris, S.; Cavallo, E. Effects of tractor passes on hydrological and soil erosion processes in tilled and grassed vineyards. Water 2019, 11, 2118. [Google Scholar] [CrossRef]
- Rodrigo-Comino, J.; Keesstra, S.; Cerdà, A. Soil erosion as an environmental concern in vineyards: The case study of Celler del Roure, Eastern Spain, by means of rainfall simulation experiments. Beverages 2018, 4, 31. [Google Scholar] [CrossRef]
- Cárdenas Alonso, G.; Nieto Masot, A. Towards Rural Sustainable Development? Contributions of the EAFRD 2007–2013 in Low Demographic Density Territories: The Case of Extremadura (SW Spain). Sustainability 2017, 9, 1173. [Google Scholar] [CrossRef]
- Renard, K.G.; Foster, G.R.; Weesies, G.A.; Porter, J.P. RUSLE: Revised universal soil loss equation. J. Soil Water Conserv. 1991, 46, 30–33. [Google Scholar]
- Rodrigo-Comino, J.; Cerdà, A. Improving stock unearthing method to measure soil erosion rates in vineyards. Ecol. Indic. 2018, 85, 509–517. [Google Scholar] [CrossRef]
- Wischmeier, W.H.; Smith, D.D. Predicting Rainfall Erosion Losses—A Guide to Conservation Planning; U.S. Department of Agriculture: Washington, DC, USA, 1978.
- IUUS-WRB. World Reference Base for Soil Resources 2014: International Soil Classification System for Naming Soils and Creating Legends for Soil Maps—Update 2015; Food & Agriculture Organization: Rome, Italy, 2015; ISBN 978-92-5-108369-7. [Google Scholar]
- Biddoccu, M.; Zecca, O.; Audisio, C.; Godone, F.; Barmaz, A.; Cavallo, E. Assessment of Long-Term Soil Erosion in a Mountain Vineyard, Aosta Valley (NW Italy). Land Degrad. Dev. 2018, 29, 617–629. [Google Scholar] [CrossRef]
- Rodrigo-Comino, J.; Keshavarzi, A.; Zeraatpisheh, M.; Gyasi-Agyei, Y.; Cerdà, A. Determining the best ISUM (Improved stock unearthing Method) sampling point number to model long-term soil transport and micro-topographical changes in vineyards. Comput. Electron. Agric. 2019, 159, 147–156. [Google Scholar] [CrossRef]
- Paroissien, J.-B.; Lagacherie, P.; Le Bissonnais, Y. A regional-scale study of multi-decennial erosion of vineyard fields using vine-stock unearthing–burying measurements. Catena 2010, 82, 159–168. [Google Scholar] [CrossRef]
- ICONA. Agresividad de la Lluvia en España: Valor del Factor R de la Ecuación Universal de Pérdida del Suelo; ICONA: Madrid, Spain, 1998.
- Walkley, A.; Black, I.A. An examination of the Degtjareff method for determining soil organic matter, and a proposed modification of the chromic acid titration method. Soil Sci. 1934, 37, 29–38. [Google Scholar] [CrossRef]
- Busacca, A.J.; Cook, C.A.; Mulla, D.J. Comparing landscape-scale estimation of soil erosion in the palouse using Cs-137 and RUSLE. J. Soil Water Conserv. 1993, 48, 361–367. [Google Scholar]
- Cerdà, A.; Rodrigo-Comino, J. Is the hillslope position relevant for runoff and soil loss activation under high rainfall conditions in vineyards? Ecohydrol. Hydrobiol. 2020, 20, 59–72. [Google Scholar] [CrossRef]
- López Bermúdez, F. Evaluación de la erosión hídrica en las áreas receptoras de los embalses de la Cuenca del Segura. Applicación de la USLE. In Estudios Sobre Geomorfología del Sur de España; University of Murcia: Murcia, Spain, 1986; pp. 93–99. [Google Scholar]
- Soto, B.; Benito, E.; Díaz-Fierros, F. Heat-induced degradation processes in forest soils. Int. J. Wildland Fire 1991, 1, 147–152. [Google Scholar] [CrossRef]
- Bagarello, V.; Ferro, V.; Keesstra, S.; Comino, J.R.; Pulido, M.; Cerdà, A. Testing simple scaling in soil erosion processes at plot scale. Catena 2018, 167, 171–180. [Google Scholar] [CrossRef]
- Jardí, M.; Cabanillas, M.; Ferrando, C.; Peña-Rabadán, J.C. Impacto de las Pistas Forestales en Medios Frágiles Mediterráneos. El Caso del Turó de Burriach (Maresme Barcelona-España); Cadernos do laboratorio xeolóxico de Laxe; Universidad de Barcelona: Barcelona, Spain, 1996; Volume 21, pp. 103–121. [Google Scholar]
- Avellanas, J.M.R.; Velilla, F.J.V.; Villas, D.B.; Martorell, J.A. Efecto del incendio forestal sobre la autosucesión vegetal y erosión, en los montes de Castejón de Valdejasa (Zaragoza). Geórgica: Revista del Espacio Rural 1999, 7, 55–68. [Google Scholar]
- Porta i Casanellas, J.; Ramos Martín, M.C. Erosió hídrica en vinya per a producció de vi d’alta qualitat en zona mediterrània (Anoia-Penedès): Quantificació de les pèrdues de nutrients per erosió del sòl i implicacions. Quad. Agrar. 1993, 16, 5–19. [Google Scholar]
- Ferre-Bueno, E.; Senciales, J.M. Estimaciones de la Erosión por Escorrentía Superficial en la Zona Suroriental de la Provincia de Málaga. Baetica 1991, 13, 19–34. [Google Scholar]
- Edeso, J.M.; Merino, A.; González, M.J.; Marauri, P. Manejo de explotaciones forestales y pérdida de suelo en zonas de elevada pendiente del País Vasco. Cuatern. Geomorfol. 1998, 12, 105–116. [Google Scholar]
- Rodrigo-Comino, J.; Novara, A.; Gyasi-Agyei, Y.; Terol, E.; Cerdà, A. Effects of parent material on soil erosion within Mediterranean new vineyard plantations. Eng. Geol. 2018, 246, 255–261. [Google Scholar] [CrossRef]
- Rodrigo-Comino, J.; Brevik, E.C.; Cerdà, A. The age of vines as a controlling factor of soil erosion processes in Mediterranean vineyards. Sci. Total Environ. 2018, 616, 1163–1173. [Google Scholar] [CrossRef]
- Smetanová, A.; Follain, S.; David, M.; Ciampalini, R.; Raclot, D.; Crabit, A.; Le Bissonnais, Y. Landscaping compromises for land degradation neutrality: The case of soil erosion in a Mediterranean agricultural landscape. J. Environ. Manag. 2019, 235, 282–292. [Google Scholar] [CrossRef] [PubMed]
- Cerdà, A.; Rodrigo-Comino, J.; Giménez-Morera, A.; Novara, A.; Pulido, M.; Kapović-Solomun, M.; Keesstra, S.D. Policies can help to apply successful strategies to control soil and water losses. The case of chipped pruned branches (CPB) in Mediterranean citrus plantations. Land Use Policy 2018, 75, 734–745. [Google Scholar] [CrossRef]
- Rodrigo-Comino, J.; Keesstra, S.D.; Cerdà, A. Connectivity assessment in Mediterranean vineyards using improved stock unearthing method, LiDAR and soil erosion field surveys. Earth Surface Processes and Landforms 2018, 43, 2193–2206. [Google Scholar] [CrossRef]



| Factor | Source | Value |
|---|---|---|
| R (rainfall factor) | ICONA (Instituto para la Conservación de la Naturaleza) [42] | 338 |
| K (soil factor) | Wischmeier and Smith [37] | 0.28 |
| C (cover management) | Panagos et al. [6] | 0.396 |
| P (practice) | Panagos et al. [6] | 0.9293 |
| Method | Mean (cm) | RMSE (cm) | R2 |
|---|---|---|---|
| OK Anisotropy | −0.113 | 2.603 | 0.829 |
| M-Q | −0.097 | 2.627 | 0.826 |
| EBK | −0.104 | 2.647 | 0.823 |
| TPS | −0.064 | 2.709 | 0.820 |
| IM-Q | −0.211 | 2.780 | 0.806 |
| OK Isotropy | −0.154 | 2.854 | 0.798 |
| IDW | −0.210 | 2.856 | 0.798 |
| CRS | −0.180 | 2.865 | 0.796 |
| ST | −0.202 | 2.974 | 0.781 |
| RUSLE Strip | Mg ha yr−1 | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 | 33 | 36 | 39 | 42 | 45 |
| % | 7 | 23.2 | 29.6 | 28.4 | 3.5 | 3.3 | 0.5 | 0.4 | 0.4 | 0.5 | 0.9 | 0.6 | 0.8 | 0.7 | 0.05 | 0.029 |
| In Situ Measures | Possible Error +2 cm | Possible Error –2 cm | |||||||
|---|---|---|---|---|---|---|---|---|---|
| m3 | Mg ha−1 | Mg ha−1 yr−1 | m3 | Mg ha−1 | Mg ha−1 yr−1 | m3 | Mg ha−1 | Mg ha−1 yr−1 | |
| ISUM | 51.03 | 70.93 | 45.69 | 34.95 | 48.58 | 31.30 | 67.11 | 93.28 | 60.09 |
| Row | 5.92 | 8.22 | 5.30 | 0.93 | 1.29 | 0.83 | 10.91 | 15.16 | 9.77 |
| Inter-row | 45.11 | 62.71 | 40.40 | 34.02 | 47.29 | 30.47 | 56.20 | 78.12 | 50.32 |
| RUSLE | 17.39 | ||||||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barrena-González, J.; Rodrigo-Comino, J.; Gyasi-Agyei, Y.; Pulido Fernández, M.; Cerdà, A. Applying the RUSLE and ISUM in the Tierra de Barros Vineyards (Extremadura, Spain) to Estimate Soil Mobilisation Rates. Land 2020, 9, 93. https://doi.org/10.3390/land9030093
Barrena-González J, Rodrigo-Comino J, Gyasi-Agyei Y, Pulido Fernández M, Cerdà A. Applying the RUSLE and ISUM in the Tierra de Barros Vineyards (Extremadura, Spain) to Estimate Soil Mobilisation Rates. Land. 2020; 9(3):93. https://doi.org/10.3390/land9030093
Chicago/Turabian StyleBarrena-González, Jesús, Jesús Rodrigo-Comino, Yeboah Gyasi-Agyei, Manuel Pulido Fernández, and Artemi Cerdà. 2020. "Applying the RUSLE and ISUM in the Tierra de Barros Vineyards (Extremadura, Spain) to Estimate Soil Mobilisation Rates" Land 9, no. 3: 93. https://doi.org/10.3390/land9030093
APA StyleBarrena-González, J., Rodrigo-Comino, J., Gyasi-Agyei, Y., Pulido Fernández, M., & Cerdà, A. (2020). Applying the RUSLE and ISUM in the Tierra de Barros Vineyards (Extremadura, Spain) to Estimate Soil Mobilisation Rates. Land, 9(3), 93. https://doi.org/10.3390/land9030093









