Comparing Quantity, Allocation and Configuration Accuracy of Multiple Land Change Models
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Location
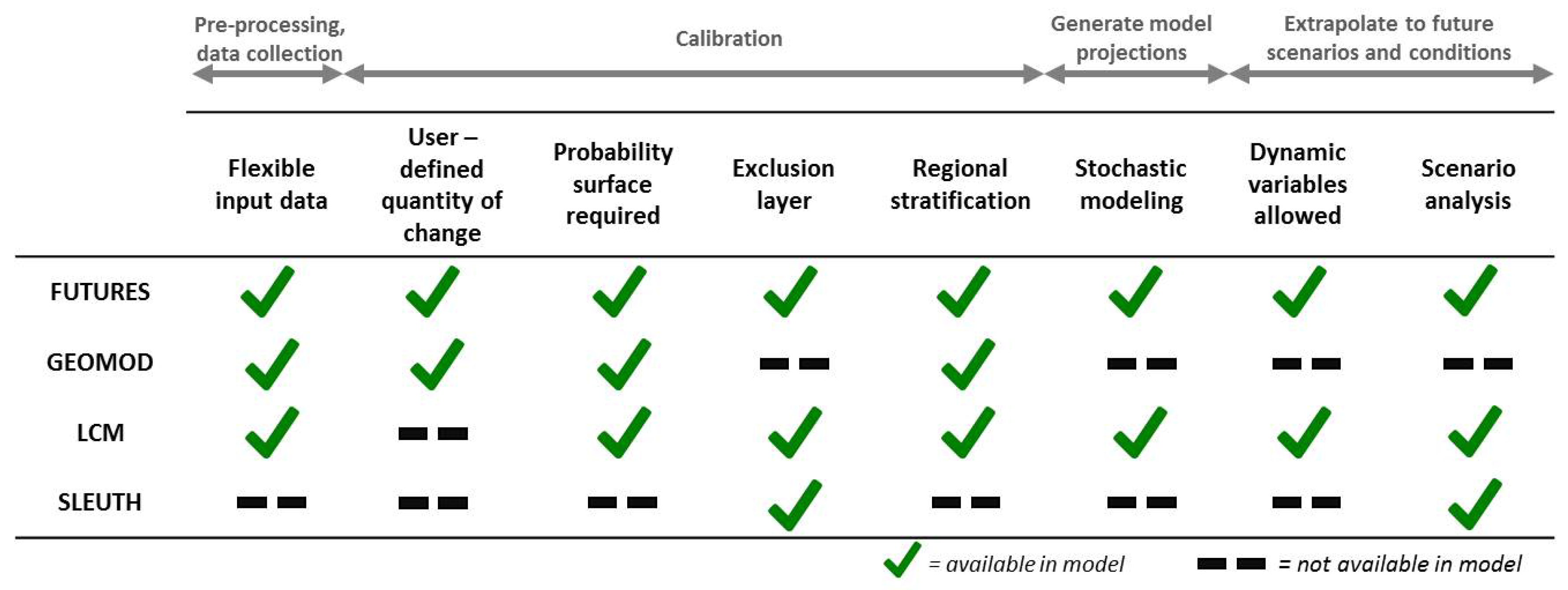
2.2. Land Change Models
2.2.1. GEOMOD
2.2.2. SLEUTH
2.2.3. Land Change Modeler
2.2.4. Future Urban-Regional Environment Simulation
2.3. Input and Validation Data
2.3.1. Remote Sensing of Land Cover
2.3.2. Estimating the Quantity of Urban Development Change
2.3.3. Site Suitability Surface Modeling
2.4. Accuracy Assessment
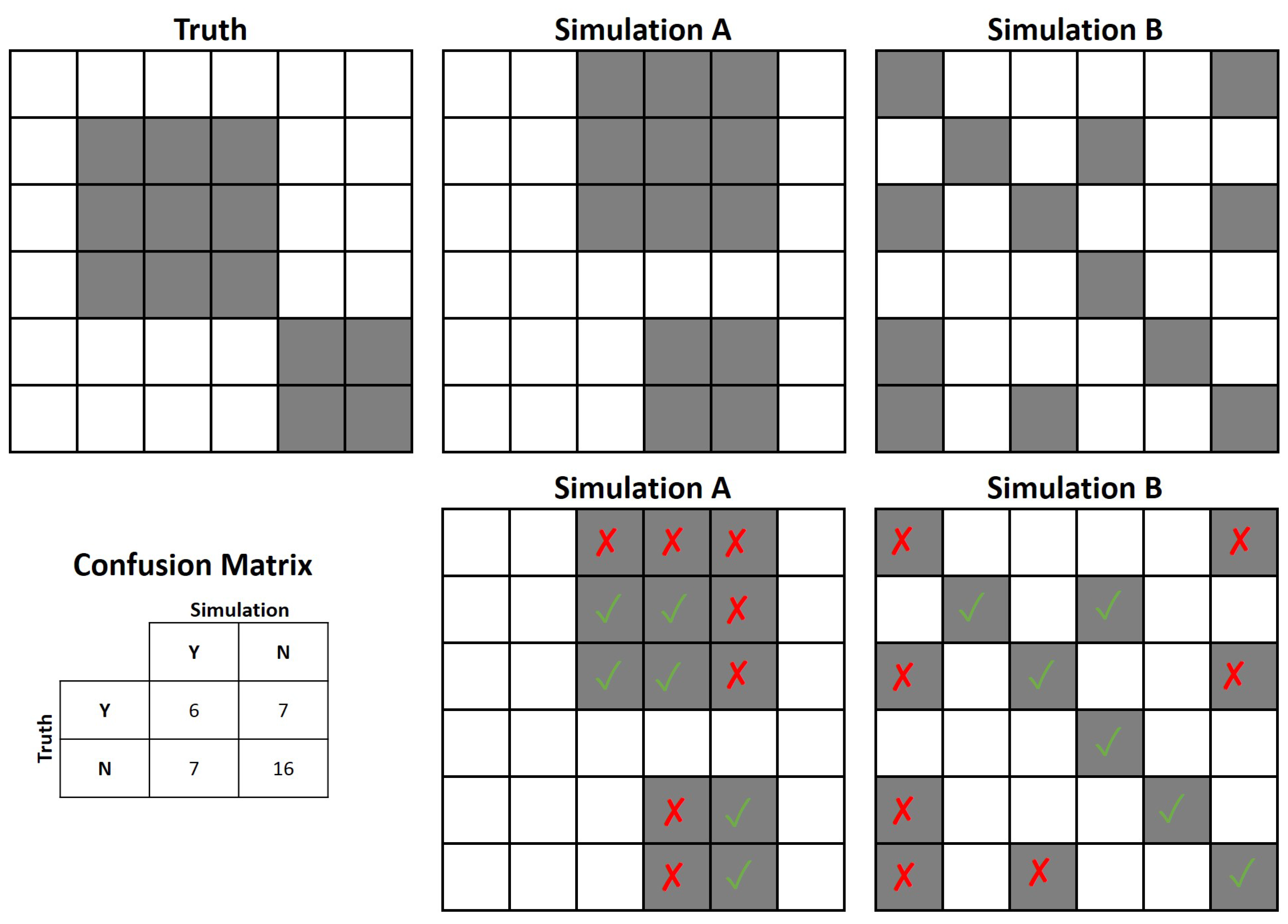
2.4.1. Quantity Disagreement
2.4.2. Allocation Disagreement
2.4.3. Kappa Simulation
2.4.4. Configuration Disagreement
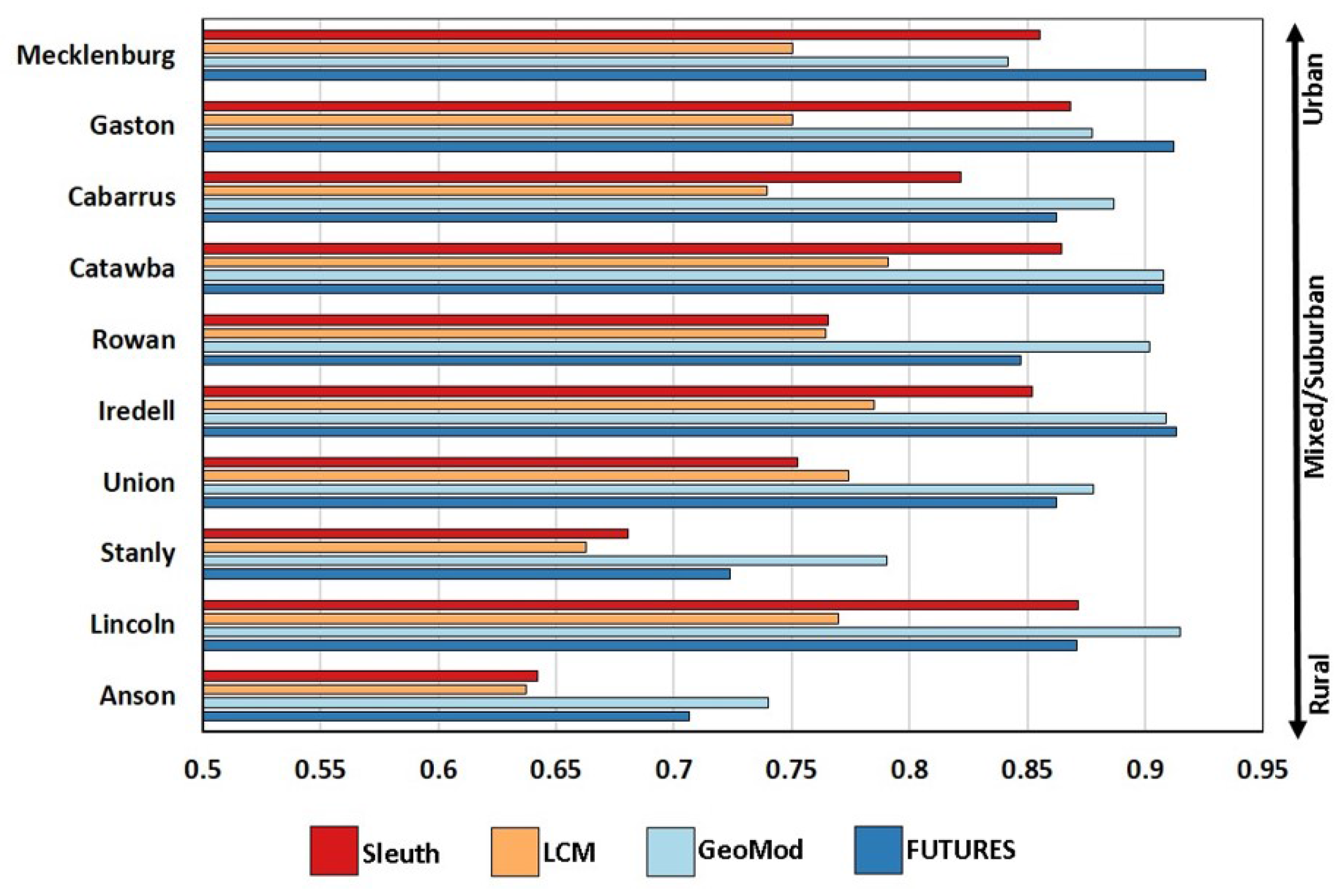
2.4.5. Accuracy Assessments at Multiple Scales
3. Results
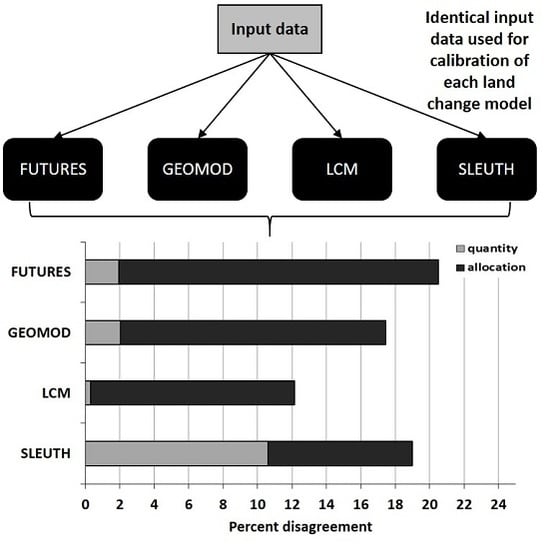
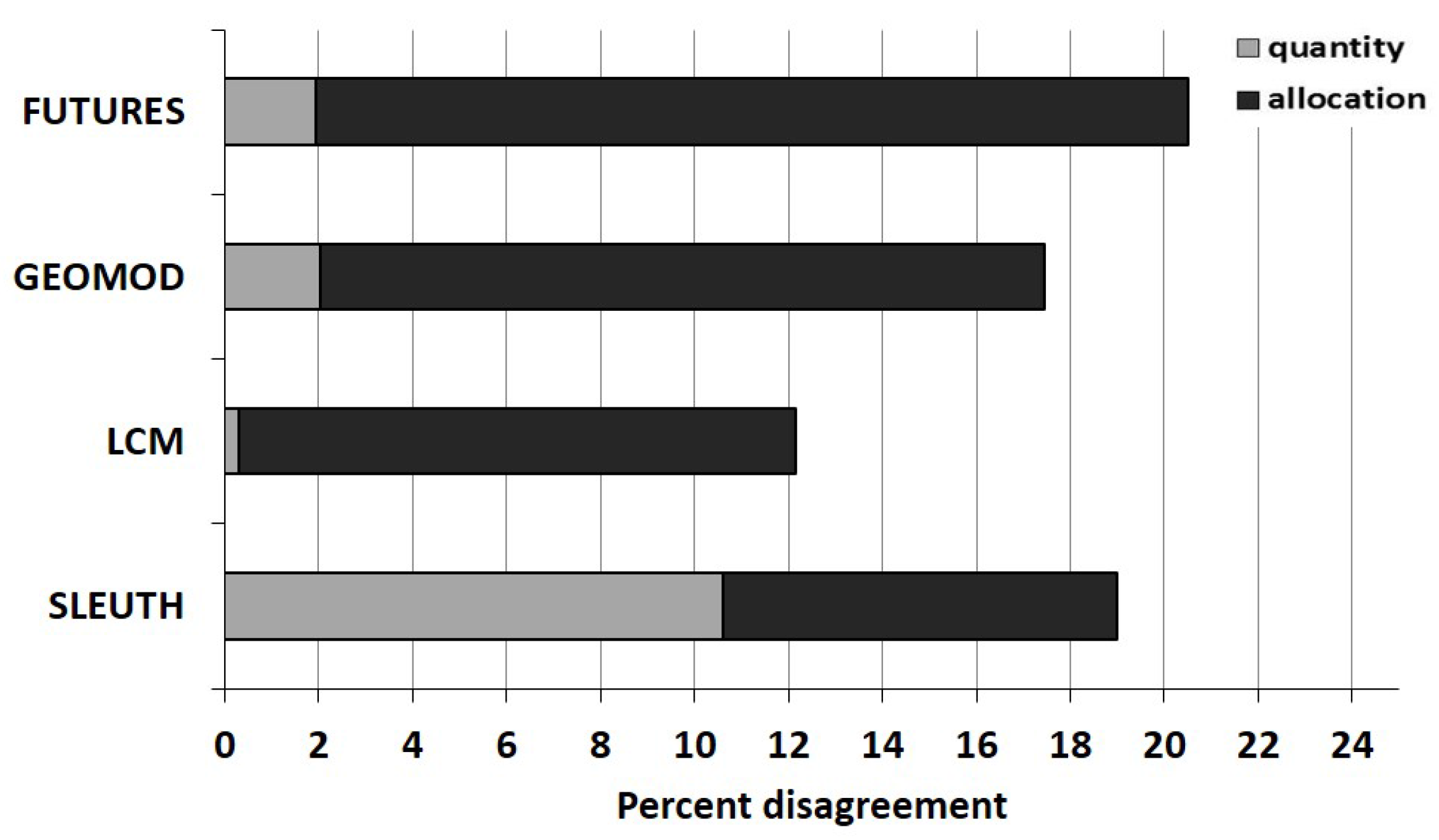
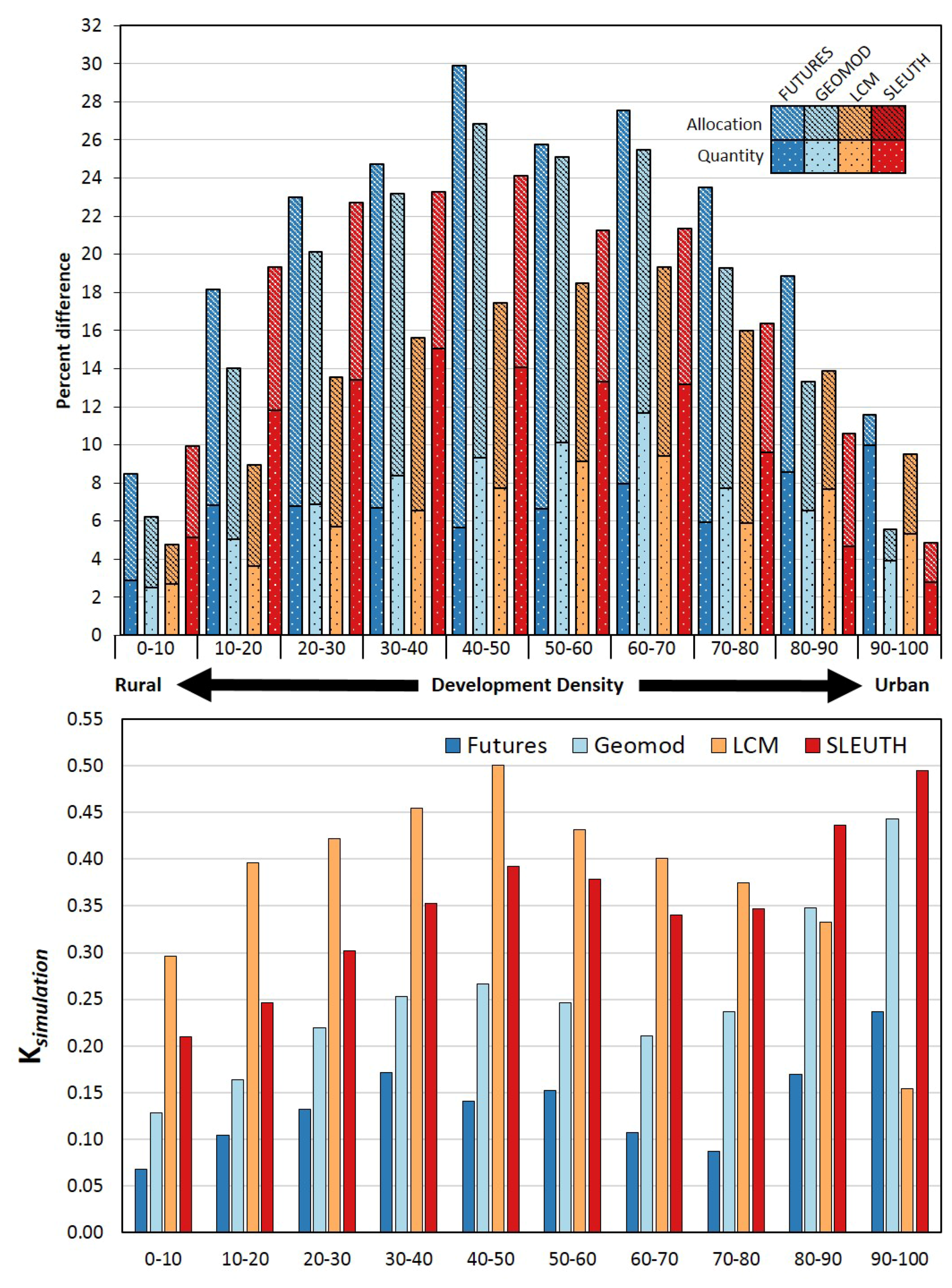
3.1. Quantity Disagreement
3.2. Allocation and Total Disagreement
3.3. K Accuracy
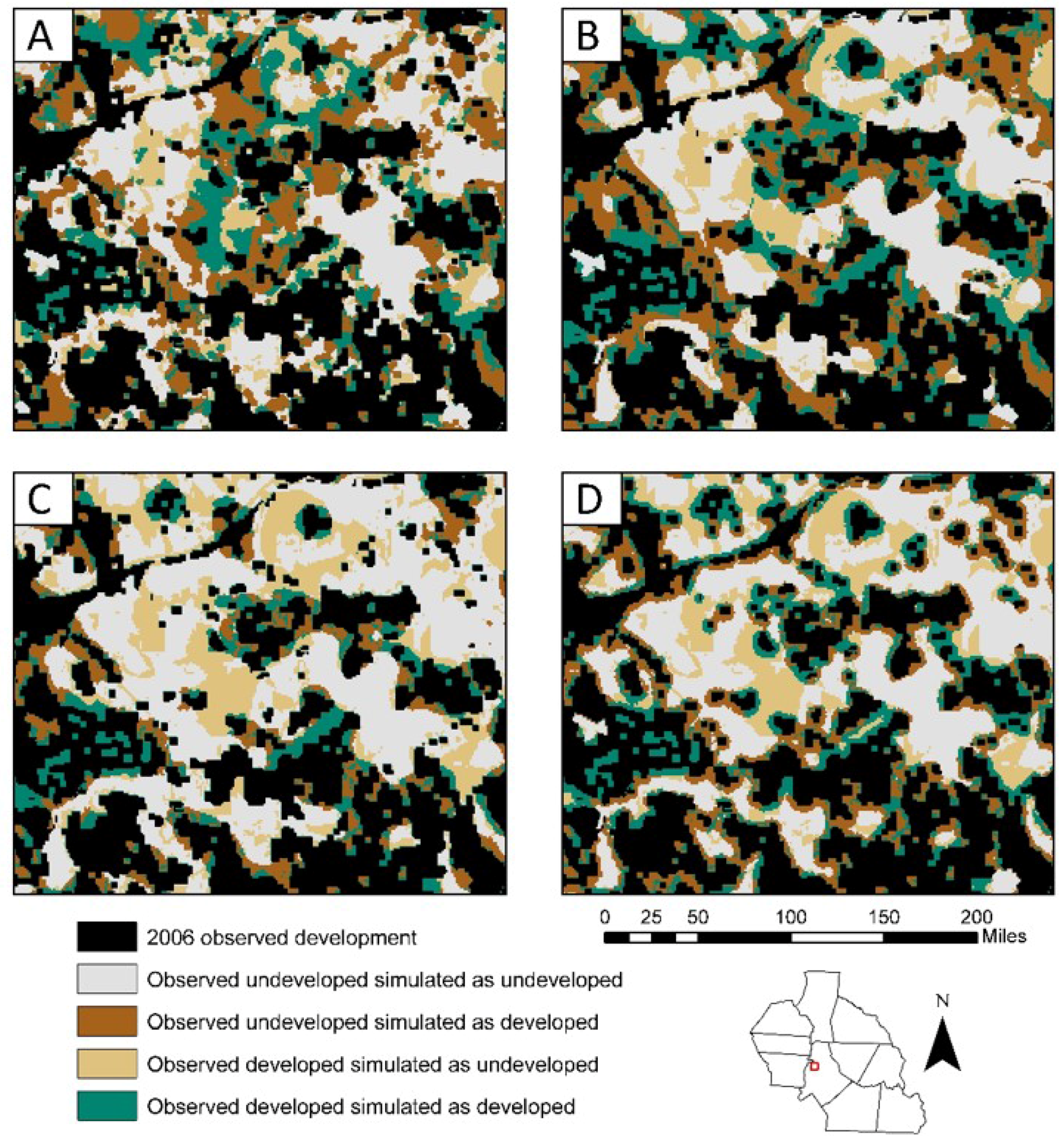
3.4. Configuration Accuracy
4. Discussion
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| CFD | clusters of fractional difference metric used by SLEUTH model |
| DEMAND | submodel that controls the total amount of urban growth allocated in FUTURES |
| ENN_MN | mean Euclidean nearest neighbor distance |
| FUTURES | FUTure Urban-Regional Environment Simulation |
| LCM | Land Change Modeler |
| LPI | largest patch index |
| LSI | Landscape similarity index |
| LULC | Land use land change |
| MSS | Landsat Multispectal Scanner, Landsat 4 |
| NCOSBM | North Carolina Office of State Budget and Management |
| NP | number of urban patches |
| OLI | Operational Land Imager—Landsat 8 |
| PARA_MN | mean perimeter-area ratio |
| PFD | pixel fractional difference metric used by SLEUTH model |
| PGA | stochastic patch growing algorithm submodel of FUTURES |
| POTENTIAL | submodel in FUTURES that contains the site suitability surface for new urban development |
| REDD | Reducing emissions from deforestation and forest degradation projects |
| TM | Thematic Mapper, Landsat 5 |
| VIS | Vegetation-Impervious Surface Soil |
References
- Pontius, R., Jr.; Boersma, W.; Castella, J.C.; Clarke, K.; Nijs, T.; Dietzel, C.; Duan, Z.; Fotsing, E.; Goldstein, N.; Kok, K.; et al. Comparing the input, output, and validation maps for several models of land change. Ann. Reg. Sci. 2008, 42, 11–37. [Google Scholar] [CrossRef]
- Prestel, R.; Alexander, P.; Rounsevell, M.D.A.; Arneth, A.; Calvin, K.; Doelman, J.; Eitelberg, D.A.; Engstrom, K.; Fujumori, S.; Hasegawa, T.; et al. Hotspots of uncertainty in land-use and land cover change projections: A global scale perspective. Glob. Chang. Biol. 2016, 22, 3967–3983. [Google Scholar] [CrossRef] [PubMed]
- Beardsley, K.; Thorne, J.H.; Roth, N.E.; Gao, S.; McCo y, M.C. Assessing the influence of rapid urban growth and regional policies on biological resources. Landsc. Urban Plan. 2009, 93, 172–183. [Google Scholar] [CrossRef]
- Svirejeva-Hopkins, A.; Schellnhuber, H.J.; Pomaz, V.L. Urbanised territories as a specific component of the global carbon cycle. Ecol. Model. 2004, 173, 295–312. [Google Scholar] [CrossRef]
- Bounoua, L.; Zang, P.; Mostovoy, G.; Thome, K.; Masek, J.; Imhoff, M.; Shephard, M.; Quattrochi, D.; Santanello, J.; Silva, J.; et al. Impact of urbanization on US surface climate. Environ. Res. Lett. 2015, 10, 084010. [Google Scholar] [CrossRef]
- Ren, L.; Cui, E.; Sun, H. Temporal and spatial variations in the relationship between urbanization and water quality. Environ. Sci. Pollut. Res. 2014, 21, 13646–13655. [Google Scholar] [CrossRef] [PubMed]
- Feng, H.; Zhao, Z.; Chen, F.; Wu, L. Using land change trajectories to quantify the effects of urbanization on urban heat islands. Adv. Space Res. 2014, 53, 463–473. [Google Scholar] [CrossRef]
- Liu, Z.; He, C.; Wu, J. The relationship between habitat loss and fragmentation during urbanization: An empirical e valuation from 16 world cities. PLoS ONE 2016, 11, e0154613. [Google Scholar] [CrossRef] [PubMed]
- Romano, B.; Zullo, F.; Fiorini, L.; Ciabo, S.; Marucci, A. Sprinkling: An approach to describe urbanization dynamics in Italy. Sustainability 2017, 9, 97. [Google Scholar] [CrossRef]
- Eigenbrod, F.; Bell, V.A.; Davies, H.N.; Heinemeyer, A.; Armsowrth, P.R.; Gaston, K.J. The impact of projected increases in urbanization on ecosystem services. Proc. R. Soc. B 2011, 278, 3201–3208. [Google Scholar] [CrossRef] [PubMed]
- Sohl, T.L.; Wimberly, M.C.; Radeloff, V.C.; Theobald, D.M.; Sleeter, B.M. Divergent projections of future land use in the United States arising from different models and scenarios. Ecol. Model. 2016, 337, 281–297. [Google Scholar] [CrossRef]
- Eastman, J.R.; Solorzano, L.A.; van Fossen, M.E. Transition potential modeling for land-cover change. In GIS, Spatial Analysis, and Modeling; Maguire, D.J., Batty, M., Goodchild, M.F., Eds.; ESRI Press: Redlands, CA, USA, 2005. [Google Scholar]
- Pontius, R., Jr.; Millones, M. Death to kappa: Birth of quantity disagreement and allocation disagreement for accuracy assessment. Int. J. Remote Sens. 2011, 232, 4407–4429. [Google Scholar] [CrossRef]
- Van Vliet, J.; Bregt, A.K.; Hagen-Zanker, A. Revisiting Kappa to account for change in the accuracy assessment of land use change models. Ecol. Model. 2011, 222, 1367–1375. [Google Scholar] [CrossRef]
- Pontius, R., Jr.; Parmentier, B. Recommendations for using the relative operating characteristic (ROC). Landsc. Ecol. 2014, 29, 367–382. [Google Scholar] [CrossRef]
- Pontius, R., Jr.; Si, K. The total operating characteristic to measure diagnostic ability for multiple thresholds. Int. J. Geogr. Inf. Sci. 2014, 28, 570–583. [Google Scholar] [CrossRef]
- Olofsson, P.; Foody, G.M.; Herold, M.; Stehman, S.V.; Woodcock, C.E.; Wulder, M.A. Good practices for estimating area and assessing accuracy of land change. Remote Sens. Environ. 2014, 148, 42–57. [Google Scholar] [CrossRef]
- Pontius, R., Jr.; Malanson, J. Comparison of the structure and accuracy of two land change models. Int. J. Geogr. Inf. Sci. 2005, 19, 243–265. [Google Scholar] [CrossRef]
- Busch, G. Future European agricultural landscapes: What can we learn from existing quantitative land use scenario studies? Agric. Ecosyst. Environ. 2006, 114, 121–140. [Google Scholar] [CrossRef]
- Mas, J.F.; Kolb, M.; Paegelow, M.; Camacho-Olmedo, M.T.; Houet, T. Inductive pattern-based land use/cover change models: A comparison of four software packages. Environ. Model. Softw. 2014, 51, 94–111. [Google Scholar] [CrossRef]
- Congalton, R.G. A review of assessing the accuracy of classifications of remotely sensed data. Remote Sens. Environ. 1991, 46, 35–46. [Google Scholar] [CrossRef]
- Foody, G.M. Status of land cover classification accuracy. Remote Sens. Environ. 2002, 80, 185–201. [Google Scholar] [CrossRef]
- Foody, G.M. Remote sensing of tropical forest environments: Towards the monitoring of environmental resources for sustainable development. Int. J. Remote Sens. 2003, 24, 4035–4046. [Google Scholar] [CrossRef]
- Congalton, R.G. Accuracy assessment of remotely sensed data: Future needs and directions. In Proceedings of the Pecora 12 Land Information from Space-Based Systems; ASRPS: Bethesda, MD, USA, 2006. [Google Scholar]
- Hagen, A. Fuzzy set approach to assessing similarity of categorical maps. Int. J. Geogr. Inf. Sci. 2003, 17, 235–249. [Google Scholar] [CrossRef]
- Kamusoko, C.; Gamba, J. Simulating urban growth using a random forest-cellular automata (RF-CA) model. ISPRS Int. J. Geoinf. 2015, 4, 447–470. [Google Scholar] [CrossRef]
- Weber, A.; Fohrer, N.; Moller, D. Long-term land use changes in a mesoscale watershed due to socio-economic factors—Effects on landscape structures and functions. Ecol. Model. 2001, 140, 125–140. [Google Scholar] [CrossRef]
- Weibull, A.C.; Ostman, O.; Granquist, A. Species richness in agroecosystems: The effect of landscape, habitat and farm management. Biodivers. Conserv. 2003, 140, 1335–1355. [Google Scholar] [CrossRef]
- Seppelt, R.; Voinov, A. Optimizing methodology for land use patters using spatially explicit landscape models. Ecol. Model. 2002, 151, 125–142. [Google Scholar] [CrossRef]
- Kennedy, C.M.; Lonsdorf, E.; Neel, M.C.; Williams, N.M.; Ricketts, T.H.; Winfree, R.; Bommarco, R.; Brittain, C.; Burley, A.L.; et al. A global quantitative synthesis of local and landscape effects on wild bee pollinators in agroecosystems. Ecol. Lett. 2013, 16, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Chaplin-Kramer, R.; Hamel, P.; Sharp, R.; Kowal, V.; Wolny, S.; Sim, S.; Mueller, C. Landscape configuration is the primary driver of impacts on water quality associated with agricultural expansion. Environ. Res. Lett. 2016, 11, 074012. [Google Scholar] [CrossRef]
- Connors, J.P.; Galletti, C.S.; Chow, W.T.L. Landscape configuration and urban heat island effects: Assessing the relationship between landscape characteristics and land surface temperature in Phoenix, Arizona. Landsc. Ecol. 2013, 28, 271–283. [Google Scholar] [CrossRef]
- Van Vliet, J.; Bregt, A.K.; Brown, D.G.; Delden, H.; Heckbert, S.; Verburg, P.H. A review of current calibration and validation practices in land-change modeling. Environ. Model. Softw. 2016, 82, 174–182. [Google Scholar] [CrossRef]
- Heistermann, M.; Muller, C.; Ronneberger, K. Land in sight? Acheivements, deficits, and potentials of continental to global scale land-use modeling. Agric. Ecosyst. Environ. 2006, 114, 141–158. [Google Scholar] [CrossRef]
- Cash, D.W.; Adger, W.N.; Berkes, F.; Garden, P.; Lebel, L.; Olsson, P.; Pritchard, L.; Young, O. Scale and cross-scale dynamics: Governance and information in a multilevel world. Ecol. Soc. 2006, 11, 8. [Google Scholar] [CrossRef]
- Clark, K.C.; Hoppen, S.; Gaydos, L. A self-modifying cellular automation model of historical urbanization in the San Francisco Bay area. Environ. Plan. B Plan. Des. 1997, 24, 247–261. [Google Scholar] [CrossRef]
- Pontius, R., Jr.; Chen, H. GEOMOD Modeling. In Idrisi 15: The Andes; Pontius, R., Jr., Chen, H., Eds.; Clark Labs, Clark University: Worcester, MA, USA, 2006. [Google Scholar]
- Eastman, J.R. IDRISI Taiga Guide to GIS and Image Processing; Clark Labs, Clark University: Worcester, MA, USA, 2009. [Google Scholar]
- Meentemeyer, R.K.; Tang, W.; Dorning, M.A.; Vogler, J.B.; Cunniffe, N.J.; Shoemaker, D.A. FUTURES: Multilevel simulations of emerging urban-rural landscape structure using a stochastic patch-growing algorithm. Ann. Assoc. Am. Geogr. 2013, 103, 785–807. [Google Scholar] [CrossRef]
- Wang, C.; Thill, J.C.; Meentemeyer, R.K. Estimating the demand for public open space: Evidence from North Carolina municipalities. Pap. Reg. Sci. 2012, 91, 219–232. [Google Scholar] [CrossRef]
- Liu, J.; Dietz, T.; Carpenter, S.R.; Alberti, M.; Folke, C.; Moran, E.; Pell, A.N.; Deadman, P.; Kratz, T.; Lubchenco, J.; et al. Complexities of coupled human and natural systems. Science 2007, 317, 1513–1516. [Google Scholar] [CrossRef] [PubMed]
- Hall, C.; Tian, H.; Qi, Y.; Pontius, R., Jr.; Cornell, J. Modelling spatial and temporal patterns of tropical land-use change. J. Biogeogr. 1995, 22, 753–757. [Google Scholar] [CrossRef]
- Hall, C.; Tian, H.; Qi, Y.; Pontius, R., Jr.; Cornell, J.; Uhlig, J. Spatially-Explicit Models of Land-Use Change and Their Application to the Tropics; DOE Research Summary; DOE: Washington, DC, USA, 1995; p. 31.
- Hall, C.; Tian, H.; Qi, Y.; Pontius, R., Jr.; Cornell, J.; Uhlig, J. Modeling land-use change. In CDIAC Communications 21; Oak Ridge National Laboratory: Oak Ridge, TN, USA, 1995. [Google Scholar]
- Jantz, C.A.; Goetz, S.J.; Donator, D.; Clagett, P. Designing and implementing a regional urban modeling system using the SLEUTH cellular urban model. Comput. Environ. Urban Syst. 2010, 34, 1–16. [Google Scholar] [CrossRef]
- Clark, K.C.; Gaydos, L.J. Loose-coupling a cellular automation model and GIS: Long-term urban growth prediction for San Francisco and Washington/Baltimore. Int. J. Geogr. Inf. Sci. 1998, 12, 699–714. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.; Lo, C.P. Modelling urban growth and landscape changes in the Atlanta metropolitan area. Int. J. Geogr. Inf. Sci. 2003, 17, 463–488. [Google Scholar] [CrossRef]
- Silva, E.A.; Clarke, K.C. Calibration of the SLEUTH urban growth model for Libson and Porto, Spain. Comput. Environ. Urban Syst. 2002, 26, 525–553. [Google Scholar] [CrossRef]
- Atkinson, P.M.; Tatnall, A. Introduction of neural networks in remote sensing. Int. J. Remote Sens. 1997, 18, 699–709. [Google Scholar] [CrossRef]
- Kim, O.S. An Assessment of Deforestation Models for Reducing Emissions from Deforestation and Forest Degradation (REDD). Trans. GIS 2010, 14, 631–654. [Google Scholar] [CrossRef]
- Khoi, D.D.; Murayama, Y. Modeling deforestation using a neural network-Markov model. In Spatial Analysis and Modeling in Geographical Transformation Process: GIS-Based Applications; Murayama, Y., Thapa, R.B., Eds.; Springer: New York, NY, USA, 2011. [Google Scholar]
- Sangermano, F.; Toledano, J.; Eastman, J.R. Land cover change in the Bolivian Amazon and its implications for REDD+ and endemic biodiversity. Landsc. Ecol. 2012, 27, 571–584. [Google Scholar] [CrossRef]
- Uddin, K.; Chaudhary, S.; Chettri, N.; Kotru, R.; Murthy, M.; Chaudhary, R.P.; Ning, W.; Shrestha, S.M.; Gautam, S.K. The changing land cover and fragmenting forest on the Roof of the World: A case study in Nepal’s Kailash Sacred Landscape. Landsc. Urban Plan. 2015, 141, 1–10. [Google Scholar] [CrossRef]
- Lein, J.K. Sensing sprawl: Towards the monitoring of urban expansion using Dempster-Shafer theory. Geocarto Int. 2003, 18, 61–70. [Google Scholar] [CrossRef]
- Kityuttachai, K.; Tripathi, N.K.; Tipdecho, T.; Shrestha, R. CA-Markov Analysis of Constrained Coastal Urban Growth Modeling: Hua Hin Seaside City, Thailand. Sustainability 2013, 5, 1480–1500. [Google Scholar] [CrossRef]
- Halmy, M.W.A.; Gessler, P.E.; Hicke, J.A.; Salem, B.B. Land use/land cover change detection and prediction in the north-western coastal desert of Egypt using Markov-CA. Appl. Geogr. 2015, 141, 101–112. [Google Scholar] [CrossRef]
- Petrasova, A.; Petras, V.; van Berkel, D.; Harmon, B.A.; Mitasova, H.; Meentemeyer, R.K. Open source approach to urban growth simulation. Int. Arch. Photogramm. Remote Sesn. Spat. Inf. Sci. 2016, 953–959. [Google Scholar] [CrossRef]
- Dorning, M.A.; Kock, J.; Shoemaker, D.A.; Meentemeyer, R.K. Simulating urbanization scenarios reveals trade-offs between conservation planning strategies. Landscape and Urban Planning. Landsc. Urban Plan. 2015, 136, 28–39. [Google Scholar] [CrossRef]
- Lee, S.; Lathrop, R.G. Sub-pixel estimation of urban land cover components with linear mixture model analysis and Landsat Thematic Mapper imagery. Int. J. Remote Sens. 2005, 26, 4885–4905. [Google Scholar] [CrossRef]
- Gluch, R.M.; Ridd, M.K. The V-I-S model: Quantifying the urban environment. In Remote Sensing of Urban and Suburban Areas; Rashad, T., Jurgens, C., Eds.; Springer: New York, NY, USA, 2010. [Google Scholar]
- Olofsson, P.; Foody, G.M.; Stehman, S.V.; Woodcock, C.E. Making better use of accuracy data in land change studies: Estimating accuracy and area and quantifying uncertainty using stratified estimation. Remote Sens. Environ. 2013, 139, 122–131. [Google Scholar] [CrossRef]
- Lu, D.; Weng, Q. A survey of image classification methods and techniques for improving classification performance. Int. J. Remote Sens. 2007, 28, 823–870. [Google Scholar] [CrossRef]
- North Carolina Office of State Budget and Management. State Demographics Branch. County/State Population Projections. North Carolina Office of State Budget and Management, 2016. Available online: www.obsm.state.nc.us/ncosbm/factsandfigures/socioeconomicdata/populationestimates (accessed on 15 January 2016).
- Gelman, A.; Hill, J. Data Analysis Using Regression and Multilevel/Hierarchical Models; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Holzkamper, A.; Lausch, A.; Seppelt, R. Optimizing landscape configuration to enhance habitat suitability for species with contrasting habitat requirements. Ecol. Model. 2006, 198, 277–292. [Google Scholar] [CrossRef]
- Hins, C.; Ouellet, J.P.; Dussault, C.; St-Laurent, M.H. Habitat selection by forest-dwelling caribou in managed boreal forest of eastern Canada: Evidence of a landscape configuration effect. For. Ecol. Manag. 2009, 257, 636–643. [Google Scholar] [CrossRef]
- Chaplin-Kramer, R.; Sharp, R.P.; Mandle, L.; Sim, S.; Johnson, J.; Butnar, I.; Mila i Canals, L.; Eichelberger, B.A.; Ramler, I.; Mueller, C.; et al. Spatial patterns of agricultural expansion determine impacts on biodiversity and carbon storage. Proc. Natl. Acad. Sci. USA 2015, 112, 7402–7407. [Google Scholar] [CrossRef] [PubMed]
- Xheng, B.; Myint, S.W.; Fan, C. Spatial configuration of anthropogenic land cover impacts on urban warming. Landsc. Urban Plan. 2014, 130, 104–111. [Google Scholar]
- Verhagen, W.; Van Teeffelen, A.J.A.; Compagnucci, A.B.; Poggio, L.; Gimona, A.; Verburg, P.H. Effects of landscape configuration on mapping ecosystem service capacity: A review of evidence and a case study in Scotland. Landsc. Ecol. 2016, 31, 1457–1479. [Google Scholar] [CrossRef]
- Pickard, B.R.; Van Berkel, D.; Petrasova, A.; Meentemeyer, R.K. Forecasts of urbanization scenarios reveal trade-offs between landscape change and ecosystem services. Landsc. Ecol. 2017, 32, 617–634. [Google Scholar] [CrossRef]
- Chen, Y.; Li, X.; Ai, B. Modeling urban land-use dynamics in a fast developing city using the modified logistic cellular automation with a patch-based simulation strategy. Int. J. Geogr. Inf. Sci. 2014, 28, 234–255. [Google Scholar] [CrossRef]
- McGarigal, K.; Cushman, S.A.; Ene, E. FRAGSTATS v4: Spatial Pattern Analysis Program for Categorical and Continuous Maps; Department of Environmental Conservation, University of Massachusetts Amherst: Amherst, MA, USA, 2012. [Google Scholar]
- Brown, D.G.; Page, S.; Riolo, R.; Zellner, M.; Rand, W. Path dependence and the validation of agent-based spatial models of land use. Int. J. Geogr. Inf. Sci. 2005, 19, 153–174. [Google Scholar] [CrossRef]
- Verburg, P.H. Simulating feedbacks in land use and land cover change models. Landsc. Ecol. 2006, 21, 1171–1183. [Google Scholar] [CrossRef]
- Epstein, J.M. Why model? J. Artif. Soc. Soc. Simul. 2008, 11, 12. [Google Scholar]
- Clarke, K.C. A Decade of Cellular Urban Modeling with SLEUTH: Unresolved Issues and Problems, Ch. 3. In Planning Support Systems for Cities and Regions; Brail, R.K., Ed.; Lincoln Institute of Land Policy: Cambridge, MA, USA, 2008. [Google Scholar]
- Burgi, M.; Hersperger, A.M.; Schneeberger, N. Driving forces of landscape change—Current and new directions. Landsc. Ecol. 2004, 19, 857–868. [Google Scholar] [CrossRef]
- Brown, D.G.; Verburg, P.H.; Pontius, R., Jr.; Lange, M.D. Opportunities to improve impact, integration, and evaluation of land change models. Curr. Opin. Environ. Sustain. 2013, 5, 452–457. [Google Scholar] [CrossRef]
- Verburg, P.H. The representation of human-environment interactions in land change research and modelling. In Understanding Society and Natural Resources: Forging New Strands of Integration Across the Social Sciences; Springer: New York, NY, USA, 2014. [Google Scholar]
- Garcia, A.M.; Sante, I.; Boullon, M.; Crecente, R. A comparative analysis of cellular automata models for simulation of small urban areas in Galicia, NW Spain. Comput. Environ. Urban Syst. 2013, 36, 291–301. [Google Scholar] [CrossRef]
- Parker, D.C.; Manson, S.M.; Janssen, M.A.; Hoffman, M.; Deadman, P. Multi-agent systems for the simulation of land-use and land-cover change: A review. Ann. Assoc. Am. Geogr. 2003, 93, 314–337. [Google Scholar] [CrossRef]
- Overmars, K.P.; Verburg, P.H.; Veldkamp, T.A. Comparison of a deductive and an inductive approach to specify land suitability in a spatially explicit land use model. Land Use Policy 2007, 24, 584–599. [Google Scholar] [CrossRef]
| Parameter | Description | Base Data | Year(s) | Data Source |
|---|---|---|---|---|
| Landcover | Lands designated as developed and undeveloped | Landsat MSS and TM imagery | 1976, 1985, 1996, 2006, 2015 | United States Geological Survey |
| Roads | Road networks, proximity to roads, distance to interchanges | Primary and secondary road networks | 1976, 1985, 1996, 2006 | North Carolina Department of Transportation |
| Topography | Slope, elevation, and aspect | National Elevation Dataset | 2006 | United States Geological Survey |
| Population | Observed population | State demographic data | 1976, 1985, 1996–2015 | State Demographics Branch of the North Carolina Office of State and Budget Management |
| Hydrograpy | Proximity to water bodies | Rivers, lakes, and reservoirs | 2006 | National Hydrography Dataset |
| Municipal Centers | Proximity to municipalities | Locations of cities, towns, and counties | 2006 | United States Census |
| Quantity Disagreement | Allocation Disagreement | K | Configuration Difference | |
|---|---|---|---|---|
| FUTURES | 1.93 (0.01) * | 18.56 (0.03) | 0.20 (0.00) | 0.14 (0.00) |
| GEOMOD | 2.03 (0.00) | 15.42 (0.00) | 0.33 (0.00) | 0.16 (0.00) |
| LCM | 0.30 (0.01) | 11.87 (0.02) | 0.51 (0.00) | 0.24 (0.00) |
| SLEUTH | 10.60 (0.00) | 8.40 (0.00) | 0.40 (0.00) | 0.20 (0.00) |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pickard, B.; Gray, J.; Meentemeyer, R. Comparing Quantity, Allocation and Configuration Accuracy of Multiple Land Change Models. Land 2017, 6, 52. https://doi.org/10.3390/land6030052
Pickard B, Gray J, Meentemeyer R. Comparing Quantity, Allocation and Configuration Accuracy of Multiple Land Change Models. Land. 2017; 6(3):52. https://doi.org/10.3390/land6030052
Chicago/Turabian StylePickard, Brian, Joshua Gray, and Ross Meentemeyer. 2017. "Comparing Quantity, Allocation and Configuration Accuracy of Multiple Land Change Models" Land 6, no. 3: 52. https://doi.org/10.3390/land6030052
APA StylePickard, B., Gray, J., & Meentemeyer, R. (2017). Comparing Quantity, Allocation and Configuration Accuracy of Multiple Land Change Models. Land, 6(3), 52. https://doi.org/10.3390/land6030052