Exploring the Association Between Street Scaling Structure and POI Distributions: Evidence from Shenzhen, China

Abstract

Urban space exhibits marked heterogeneity in both form and function, yet how urban functions align with multilevel street structures remains insufficiently understood. This study investigates the coupling between street hierarchy and urban functions in Shenzhen through two complementary representations: (1) the relationship between street connectivity and POIs located near each street, and (2) the relationship between street nodes and POIs contained within street-node-based hotspots. Both datasets were hierarchically partitioned using head/tail breaks to reveal intrinsic scaling structures. Power-law detection shows that natural streets and hotspot clusters follow heavy-tailed distributions, forming nested living structures. The exponents for node- and POI-based clusters fall within the typical range of 2.0–2.2, whereas exponents for street connectivity and street-based POIs are higher, indicating stronger heterogeneity. Correlation analyses reveal consistent positive associations between POIs and street connectivity across all levels, with the strongest relationships in mid- to upper-level substructures. Toward finer levels, correlations weaken and become increasingly nonlinear, reflecting growing spatial irregularity. These findings demonstrate that Shenzhen’s urban functions are coherently organized along its street hierarchy, highlighting the fundamental role of multilevel street configurations in shaping functional spatial patterns.

1. Introduction

Urban space exhibits intrinsic heterogeneity in both physical structure and functional activities, which often follow scaling laws and can be characterized by power-law or other heavy-tailed distributions [1,2,3,4]. To investigate the scaling structure within a single city, a topology-based representation is essential [2]. Natural streets are constructed from continuous street segments, and they can be ranked and subdivided into hierarchical levels, typically revealing that far more short or weakly connected streets exist than long or highly connected ones [5,6,7]. A city is not a tree, as claimed by Christopher Alexander (1965), the street network forms the morphological backbone of the city, shaping both its physical form and the dynamics of urban life [8]. Huang et al. later extended this idea across multiple cities and demonstrated that street configuration fundamentally shapes urban vitality, accessibility, and social interaction [9].

Similarly, city hotspots can be delineated and stratified into nested spatial hierarchies guided by Jiang’s wholeness perspective [10]. Urban hotspots represent concentrations of human activities or built-environment elements such as POIs, population density, or nighttime lights [11,12,13,14]. Detecting these hotspots from large geospatial datasets allows researchers to capture the city’s underlying living structure, characterized by far more small centers than large ones [15,16,17]. From the wholeness perspective, these hotspots are not isolated entities but interconnected centers that interact across multiple spatial scales [18,19]. Together, they constitute a coherent whole in which the relationships among centers, rather than their individual attributes, define the city’s overall complexity and vitality.

Prior studies have shown that urban mobility exhibits Lévy-flight-like heavy-tailed patterns [20,21], and that human movement flows are closely linked to the scaling properties of street networks [7,22]. However, few studies have examined how these structural hierarchies relate to the spatial distribution of urban functions across scales. Points of Interest (POIs), reflecting aggregated commercial, public service, and other urban functions, provide a direct proxy for localized activity patterns. Ai et al. used POI data to classify urban functional agglomerations at the block level [23], while Li et al. monitored the evolution of urban functional zones using multi-source POI data [24]. Yet, limited work has integrated urban form and function into a unified multi-scale framework to examine their coupling effects.

A fractal or scaling perspective, which captures the self-similarity and complexity of nested spatial structures, offers new insight into how physical form relates to functional distribution. Identifying and comparing hierarchical street and hotspot clusters helps reveal how structural layers co-organize POI locations and urban activities. Derudder et al. identified polycentric structures and emphasized the importance of accurate identification of dominant centers [25], and Ren et al. showed that such structures can be further decomposed into nested intra-urban cores [26].

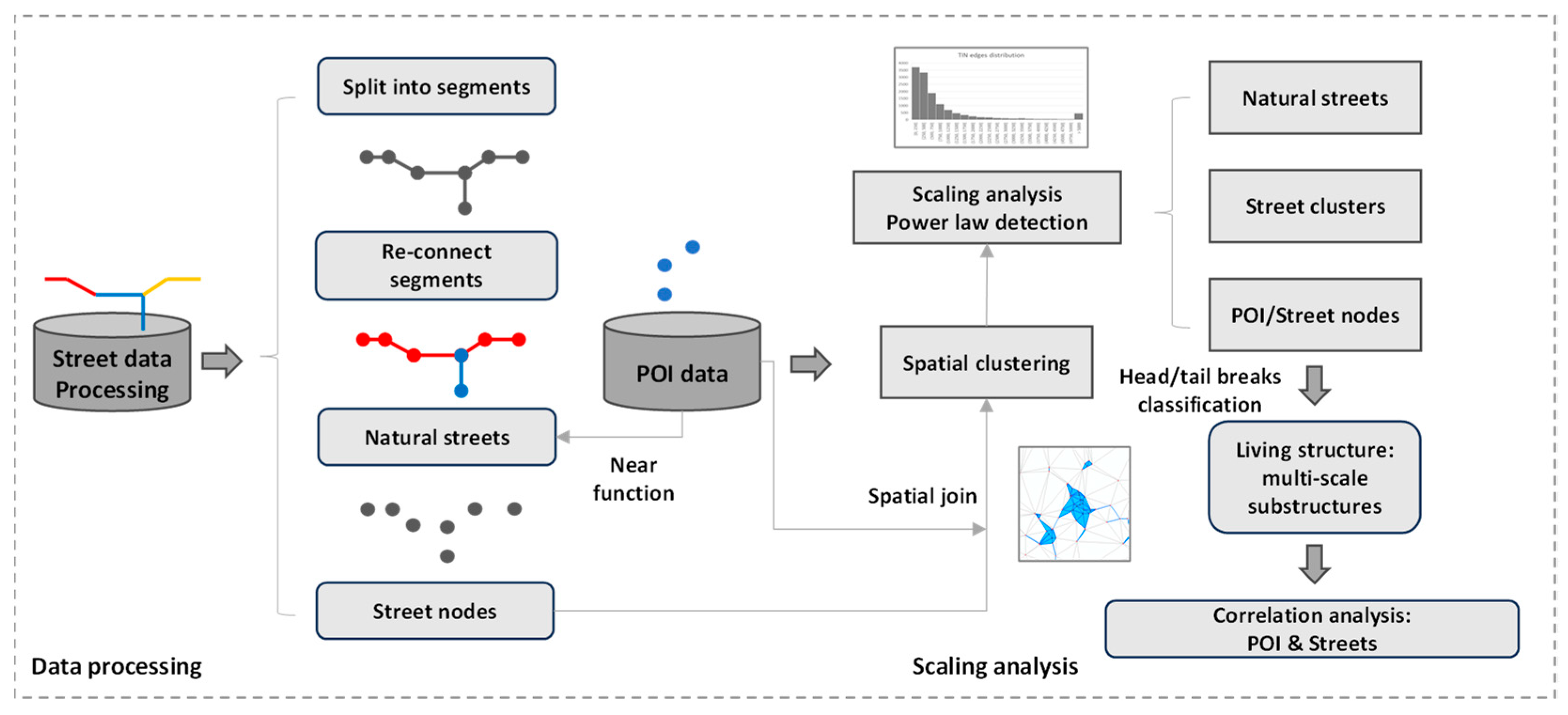
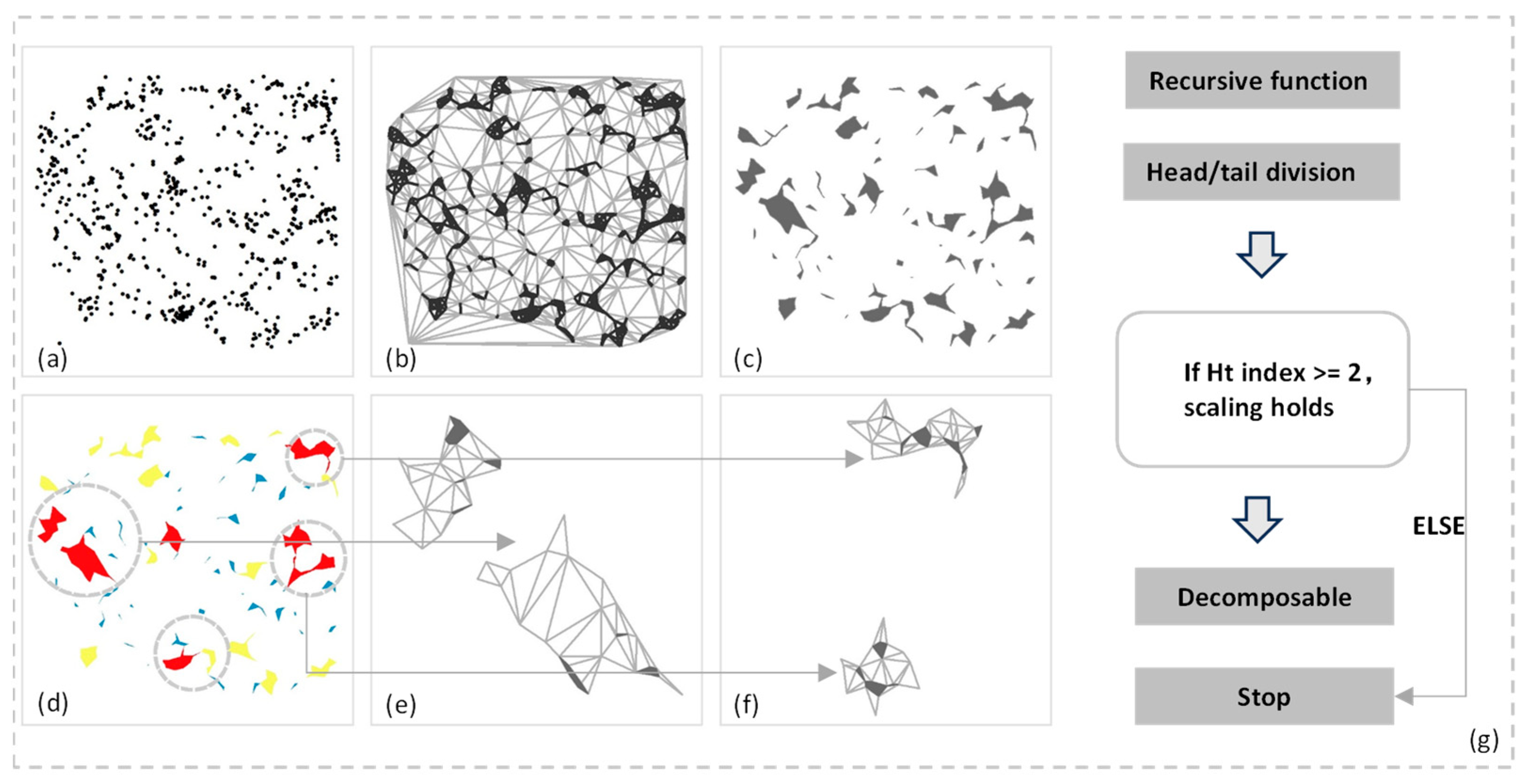
Accordingly, this study examines whether and how the hierarchical scaling of streets corresponds to the spatial distribution of POIs within a single city. Accordingly, this study examines whether and how the hierarchical scaling of streets corresponds to the spatial distribution of POIs within a single city. We generated natural streets and extracted street nodes for hotspots, which were then hierarchically classified using head/tail breaks based on street connectivity and number of street nodes. Unlike previous studies that identify hotspots only once or at a single scale, we recursively generated hotspots using street nodes to capture the inner heterogeneity of spatial distribution, allowing finer-scale structures to emerge through multiple recursions [16,17]. POI data were spatially linked to streets by nearest distance and assigned to corresponding hotspot levels.

From the street perspective, we conducted multilevel correlation analyses between street connectivity and the number of nearby POIs across hierarchical street levels. From the hotspot perspective, we evaluated correlations between the number of street nodes and POIs within each recursively derived hotspot. Our results show that POI locations are not randomly dispersed but are shaped and constrained by the multilevel street configuration. Highly connected streets and dense node clusters act as spatial anchors for POI concentration, reflecting a nonlinear and dynamic coupling between urban form and function.

This study makes three key contributions. First, it integrates street networks and TIN-based hotspots into a unified multiscale analytical framework that jointly models morphological hierarchies (from natural streets and street-node hotspots) and functional hierarchies (from POI distributions). Second, it provides theoretical insight by demonstrating that POI locations are shaped and constrained by the multilevel configuration of the street network. Third, it offers empirical evidence that street-based and hotspot-based hierarchies exhibit similar scaling patterns and that the strength of form–function coupling varies systematically across levels. These findings reveal that Shenzhen’s structural and functional complexity co-evolves through consistent multilevel organization, offering a new analytical lens for understanding urban systems.

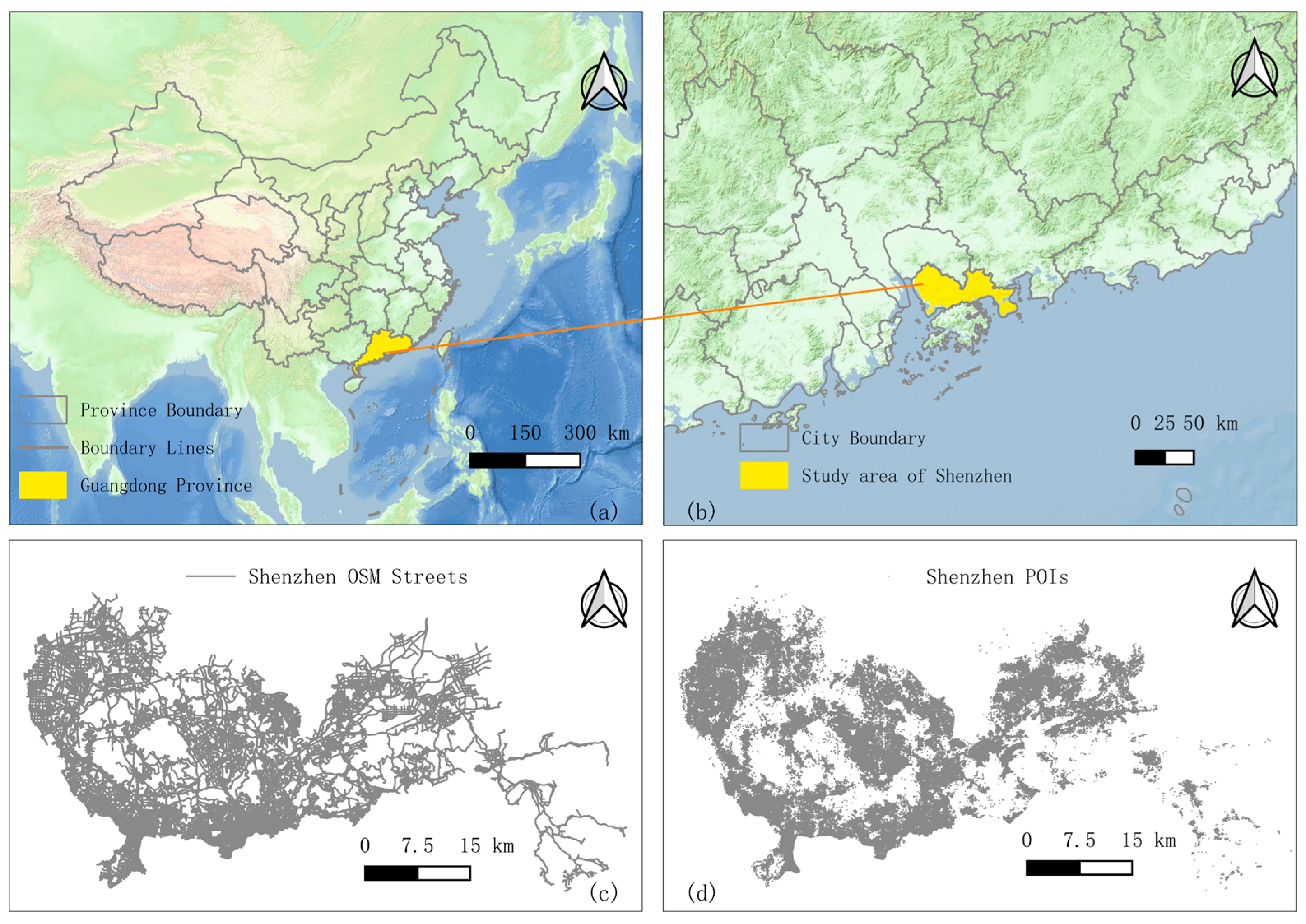
The content of this paper is structured as follows. Section 2 introduces the study area, describes the datasets used, and details the procedures for deriving natural streets, street nodes, and POI clusters, followed by the methodological framework for hierarchical scaling analysis. Section 3 presents the empirical results, including the power-law characterization of street and POI hierarchies and the multi-scale correlation analysis between street connectivity and POI distribution. Section 4 discusses the implications of the observed structural–functional coupling from the perspective of living structure theory and highlights how hierarchical form–function alignment informs our understanding of urban complexity. Section 5 concludes the study by summarizing major findings, outlining contributions, and proposing future research directions.

2. Materials and Methods

2.1. Study Area, Data Sources and Preprocessing

The study focuses on Shenzhen, the largest and most rapidly developing city within the Guangdong-Hong Kong-Macao Greater Bay Area (GBA) in southern China. Located on the eastern shore of the Pearl River Estuary, Shenzhen covers an area of approximately 2000 square kilometers and serves as a key node linking mainland China with Hong Kong. From a spatial perspective, Shenzhen exhibits a highly complex and dynamic urban morphology, shaped by continuous expansion, redevelopment, and the integration of multiple sub-centers such as Luohu, Futian, Nanshan, and Bao’an. These districts form a polycentric urban structure, connected by a dense street network and supported by a diverse range of functional activities represented by points of interest (POIs) including commercial hubs, parks, educational institutions, and residential communities (Figure 1).

To ensure transparency and reproducibility, all datasets used in this study were accompanied by explicit metadata and standardized preprocessing procedures (

Table 1. Metadata and preprocessing of datasets used in this study.

Data Type	Source & Access	Acquisition Time	Raw Attributes	Cleaning & Preprocessing	Final Dataset
Street network	OpenStreetMap (OSM), downloaded via Geofabrik API	August 2025	Street geometry, road class, name	Removed incomplete segments; split into segments	16,497 natural streets; 43,658 street nodes
POIs	Amap (Gaode) API	August 2025	20 POI categories (e.g., commercial, industrial, residential, education, transport)	Duplicates removed; non-Shenzhen POIs removed	681,987 cleaned POIs linked to nearest natural street
Urban boundary	http://www.resdc.cn/	March 2022	Shapefile	Re-projected	Administrative boundary of Shenzhen
Basemap	Tianditu (National Map Service)	-	WMTS tiles	-	-

). The street network data were downloaded from OpenStreetMap (OSM) in August 2025 via the Geofabrik website (https://www.geofabrik.de/). The dataset includes street geometries, road hierarchy, name tags, and topological attributes [27]. After removing incomplete or duplicated segments, the raw streets were split into primitive segments and subsequently merged into natural streets based on geometric continuity using Axwoman 6.3, an extension of ArcGIS 10.2 designed for street-based spatial analysis [7]. This merging process follows human perception of continuous movement along a street, rather than relying solely on street names or administrative definitions. In total, 16,497 natural streets were derived. They capture the morphological continuity of urban streets, preserving both their geometric and functional coherence across the network.

Street nodes—representing intersections and ends between natural streets—were extracted automatically using the NaturalCitiesModel tool [28]. A total of 43,658 nodes were identified, forming the topological backbone necessary for examining street connectivity and scaling structure. POI data were retrieved from Amap (Gaode) API in August 2025, covering 20 categories. The raw dataset was cleaned by removing duplicates, entries outside Shenzhen, and records with missing coordinates. POIs were then aggregated into eight standardized functional groups. In total, 681,987 POIs remained and were linked to their nearest natural streets for form–function coupling analysis. The administrative boundary of Shenzhen was obtained from the Chinese Academy of Sciences (2022 edition) and reprojected (EPSG:2362) to ensure consistency across datasets. Table 1 summarizes the metadata and preprocessing steps.

2.2. Methods

The objective of this study is to reveal how urban form and function—represented, respectively, by streets and POIs—are organized across multiple spatial scales and how they interact to shape Shenzhen’s urban complexity. Figure 2 outlines the complete workflow, beginning with street derivation, hotspot extraction, scaling analysis, and finally form–function coupling assessment.

By constructing nested clusters of streets, the framework enables the identification of multi-level living structures, where larger clusters contain smaller ones in a recursive manner. This hierarchical representation captures the city’s inherent order and complexity, aligning with the concept of living structure proposed by Alexander [15] and further developed by Jiang [10]. Finally, correlation analysis between street connectivity, street hotspots and POI distribution quantifies the degree of coupling between urban morphology and function across scales.

2.2.1. Scaling Analysis of Streets and Node-Based Hotspots

To capture multi-scale hierarchical structures, we employed the head/tail breaks method [29] and its associated ht-index to quantify the depth of hierarchy within street connectivity, street-node density, and POI intensity [30]. Head/tail breaks recursively divide a heavy-tailed dataset into a “head” (values above the mean) and a “tail” (values below the mean), continuing the process while the head remains a minority (typically less than 40%). Each recursive division reveals one additional hierarchical level in the scaling structure. The number of valid recursive partitions is denoted by m, and the ht-index is defined as:

$$\mathrm{h}\mathrm{t}=\mathrm{m}+1$$

(1)

The ht-index therefore represents the number of hierarchical levels inherent in the data, reflecting the degree of complexity or livingness of the spatial pattern. In this study, the ht-index was used to measure the hierarchical complexity of street connectivity, street nodes, and POI distributions, thereby enabling a comparative assessment of how urban form and function evolve across multiple spatial scales.

To examine whether the distributions of urban morphological and functional indicators follow a scaling law, we performed a power-law detection analysis on the variables of street connectivity, street nodes, and POI counts. A power-law distribution implies that the probability p(x) of observing a value x scales as:

$$\mathrm{p}\left(\mathrm{x}\right)\propto X^{-\alpha }$$

(2)

where α is the scaling exponent that quantifies the degree of heterogeneity in the data. In such a distribution, a small number of elements possess very large values (e.g., highly connected streets or dense clusters of POIs), while the majority have relatively small values. All variables were log-transformed and sorted to derive the complementary cumulative distribution function (CCDF), which provides a linear relationship in logarithmic space for data following a power law.

We then estimated the scaling exponent α using maximum likelihood estimation (MLE) [31]. MLE estimates the power-law exponent, α, using smallest data value Xmin from where the data is power-law distributed. The exponent α is described as in Equation (3):

$$\mathsf{\alpha }=1+\mathrm{n}{\left[\sum _{i=1}^n\ln {\displaystyle \frac{X_i}{X_{min}}}\right]}^{-1}$$

(3)

Exponent values in power-law distributions typically range between 1 and 3, with larger exponents indicating greater heterogeneity. The Kolmogorov–Smirnov (KS) statistic was used to assess goodness of fit, following the procedure outlined by Clauset et al. [4]. The p-value, calculated as the proportion of synthetic datasets with larger KS statistics than the empirical one, indicates the plausibility of a power-law fit; values above 0.05 suggest statistical consistency with the power-law hypothesis. A special case, Zipf’s law [32], states that the size of a city or element is inversely proportional to its rank.

In real-world urban systems, empirical data do not always pass the strict p-value threshold for a perfect power-law fit. However, even when the goodness-of-fit test is not fully satisfied, the scaling exponent (α) still meaningfully reflects the degree of heterogeneity and the underlying “far more small things than large ones” tendency. Therefore, α is used in this study primarily to characterize the scaling trend rather than to claim an ideal power-law distribution.

2.2.2. Living Structure and Recursive Generation of Hotspots

Christopher Alexander’s concept of living structure [15] provides a theoretical foundation for understanding multi-level spatial coherence. Living structures are characterized by nested centers that reinforce each other, leading to far more small centers than large ones. This perspective has been formalized in computational geography through the ht-index and power-law scaling [18,19,30]. In the context of urban systems, a living structure reflects how cities evolve through self-organization, where spatial forms (streets, buildings, and nodes) and human activities (POIs, mobility patterns) together generate multi-level spatial order [33]. Urban environments with higher livingness exhibit both functional diversity and morphological coherence, contributing to their adaptability and vitality.

To delineate intra-urban substructures, we developed an algorithm based on triangulated irregular network (TIN) modeling of point data (Figure 3). Previous studies have demonstrated that both urban boundaries and internal hotspots can be effectively extracted from massive point datasets through TIN construction [13,14,16,17]. First, a triangulated irregular network was constructed using all street nodes; shorter TIN edges represent denser spatial configurations. By applying the head/tail division rule to edge lengths, short edges were polygonized to derive hotspot boundaries. This process was recursively repeated within each hotspot, continuing until the ht-index dropped below 2, indicating insufficient heterogeneity. The result is a hierarchical set of spatial clusters reflecting Shenzhen’s living structure.

2.2.3. Correlation Analysis Across Scales

To quantify the coupling between urban form and function, we performed multi-scale correlation analyses using both Pearson’s r and Spearman’s ρ [34]. Pearson’s r captures linear association, whereas Spearman’s ρ—based on ranked values—is more appropriate for heavy-tailed datasets where relationships may be monotonic but nonlinear. For natural streets, we measured correlations between street connectivity and the number of POIs linked to each street. For recursively generated hotspots, we assessed the relationship between the number of street nodes and the number of POIs inside each hotspot. Both analyses were conducted across multiple hierarchical levels derived from head/tail breaks, enabling a scale-dependent comparison of form–function interactions. The Pearson correlation coefficient was computed as:

$$\mathrm{r}={\displaystyle \frac{{\sum }_{i=1}^n(x_i-\overline{x})(y_i-\overline{y})}{\sqrt{{\sum }_{i=1}^n{(x_i-\overline{x})}^2{\sum }_{i=1}^n{(y_i-\overline{y})}^2}}}$$

(4)

where x_i and y_i represent the values of street connectivity and POI counts in the i-th nearest street, respectively. The resulting r values range from −1 to +1, where positive value indicates that highly connected streets are generally associated with dense POI distributions, while negative values suggest the opposite. We also calculated the coefficient of determination (R²) derived from the linear fit between these two variables. The R² value indicates the proportion of variance in POI density that can be statistically explained by variations in street connectivity. Because the distributions of connectivity and POI counts are heavy-tailed and potentially nonlinear, we also used Spearman’s ρ, a rank-based nonparametric measure of monotonic association, given by:

$$\rho =1-{\displaystyle \frac{6\sum d_i^2}{n\left(n^2-1\right)}}$$

(5)

where dᵢ is the difference between the paired ranks and n is the number of observations. In this study, we report both Pearson’s correlation coefficient (r) and Spearman’s rank correlation (ρ). Pearson’s r and the associated R² values are derived from simple linear regression on the original variables, whereas Spearman’s ρ is computed from their ranked values to capture monotonic relationships in heavy-tailed data. To avoid confusion, R² is interpreted only in relation to Pearson’s r, and Spearman’s ρ is presented separately as a nonparametric measure of hierarchical consistency. By performing the correlation across multiple hierarchical levels, we examined whether the relationship between urban form and function remains consistent across scales, thereby revealing the degree of form function coherence.

3. Experiments and Findings

3.1. The Scaling Structure of Natural Streets and Street Junctions

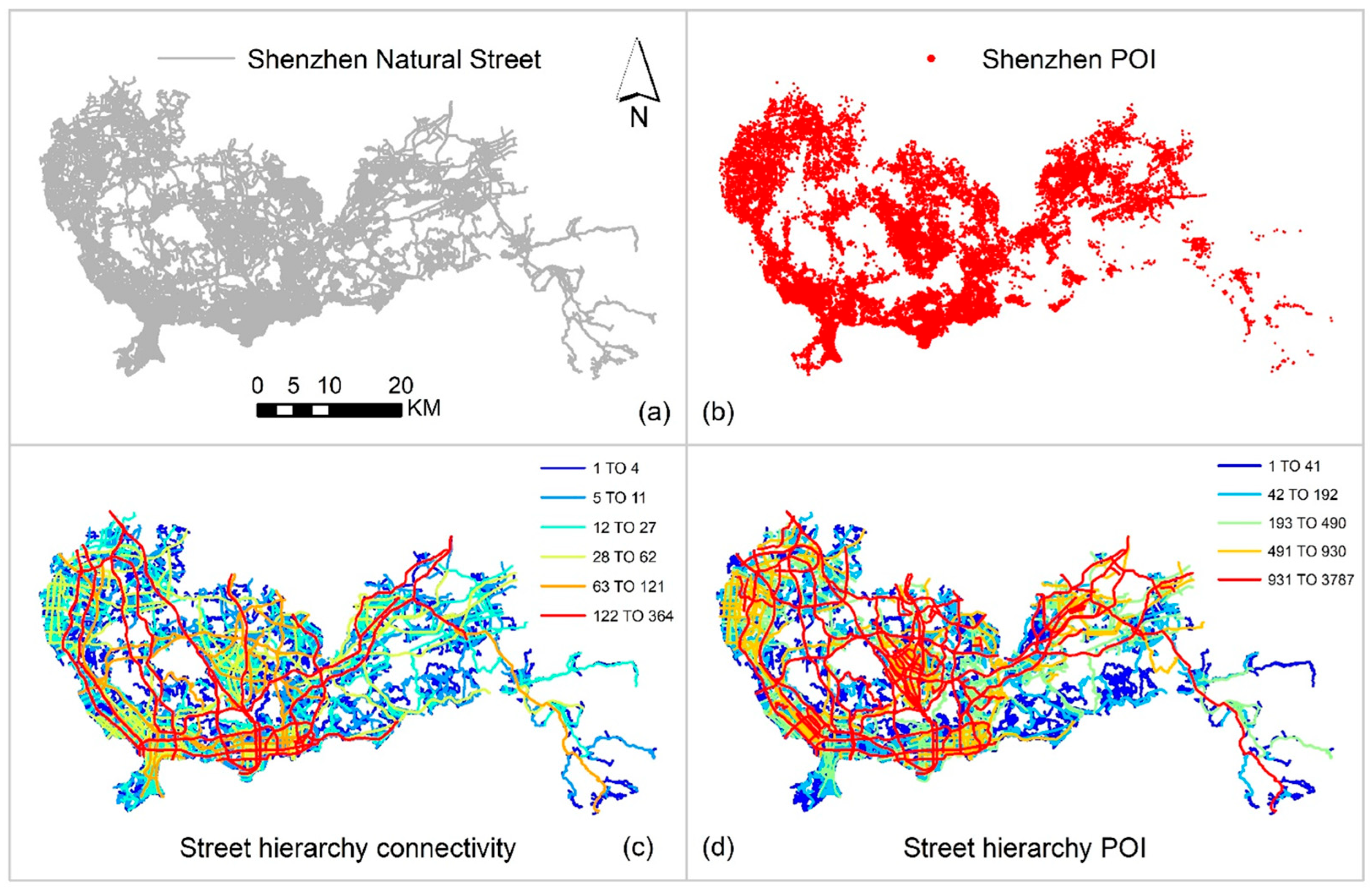
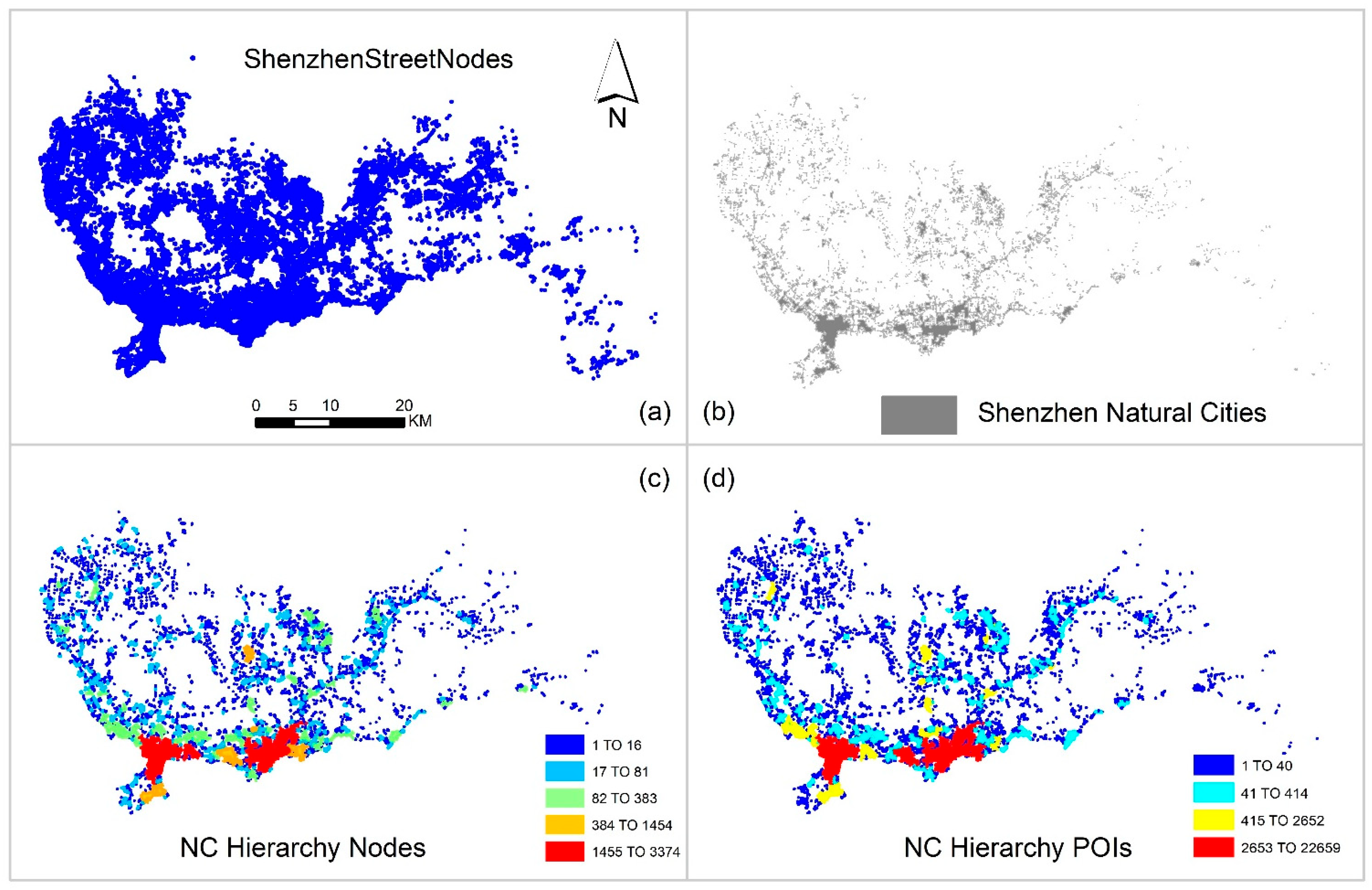
The hierarchical scaling analysis of the Shenzhen streets reveals that both the street structure and its associated node and POI distributions exhibit a clear multi-level organization consistent with living structure theory. As shown in Figure 4, the natural streets derived from OpenStreetMap data form a continuous spatial hierarchy with an ht-index of 6, indicating that the distribution of street connectivity spans six hierarchical levels. This relatively high ht-index suggests a deeply nested structure in which a few long, highly connected streets act as the primary backbone of the city, while the majority consist of progressively smaller and less connected streets. The color-coded hierarchy maps demonstrate that these major streets primarily run through the central and western parts of Shenzhen, forming the main structural skeleton that supports urban movement and accessibility.

When the analysis is extended to POI-based street hierarchies, the results show a slightly lower ht-index of 5, reflecting that the distribution of functional density (POI count) also follows a heavy-tailed pattern but with one less hierarchical level than the topologic street network. This indicates that while the morphological complexity of the street system reaches six levels, the functional and topological hierarchies (as reflected by POIs and nodes) are marginally simpler, suggesting a strong coupling but not a perfect alignment between urban form and function. The consistent scaling between the two confirms that both physical and functional aspects of the city conform to the principle of “far more small things than large ones,” reinforcing the living structure nature of the urban system.

As shown in Figure 5, the analysis of street-node clusters and intra-urban hotspots reveals ht-indices of 5 and 4, respectively. The street-node clusters (ht = 5) exhibit a hierarchical nesting pattern similar to that of the street network, where dense clusters of intersections emerge around the city’s main structural axes. In contrast, the intra-urban hotspots from street nodes (ht = 4), joined from the distribution of POIs, display a slightly shallower hierarchy, suggesting that urban functions are concentrated in fewer dominant centers. This implies that Shenzhen’s functional hotspots are more centralized compared to the more evenly scaled geometric and topological structures. Collectively, these findings illustrate that Shenzhen’s Street and node hierarchies are deeply structured and spatially coherent, while its functional hierarchy, although still scaling, is more concentrated, reflecting the interaction between urban form, connectivity, and functional intensity across multiple spatial scales.

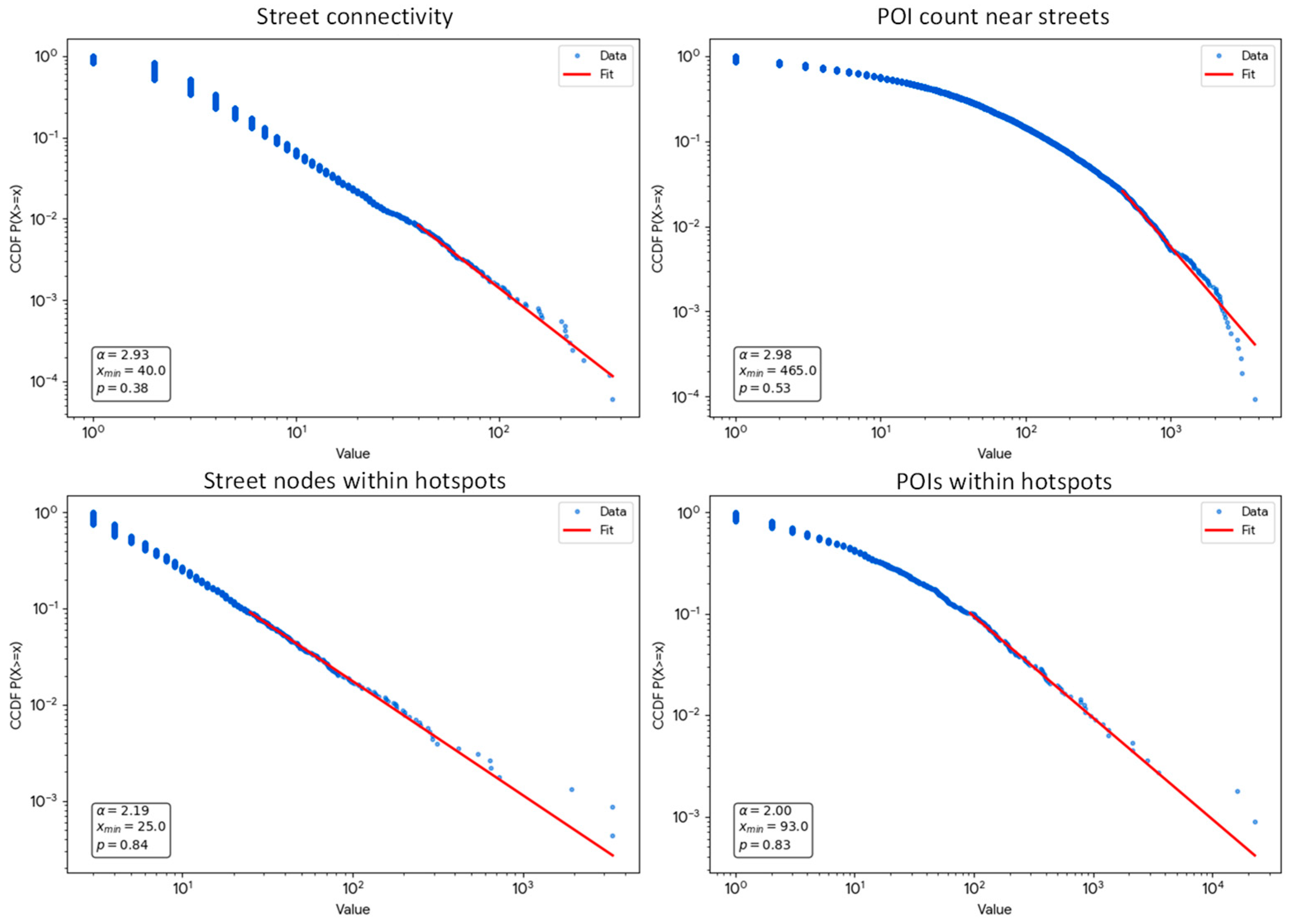
The power-law analysis reveals consistent scaling behavior across both the street network and node-based hotspot systems in Shenzhen, underscoring their hierarchical and self-organizing nature (

Table 2. Power law statistics of street-based and cluster-based metrics.

Name	Count	α	xmin	p
Street connectivity	16,497	2.93	40	0.38
Street POIs	10,729	2.98	465	0.53
Cluster nodes	2282	2.19	25	0.84
Cluster POIs	1114	2.00	93	0.83

, Figure 6). For the street network, street connectivity exhibits a power-law exponent of 2.93 (α = 2.93) and a lower bound of x_min = 40. It indicates a scale-free structure in the tail, although the relatively high exponent implies a steeper hierarchy where super-connected streets are somewhat rarer than in systems with lower scaling parameters. Similarly, street-based POIs follow a power-law distribution with α = 2.98, suggesting that functional activities are more unevenly distributed, concentrating along a small number of major streets.

For the node-based clusters, both structural and functional properties also demonstrate clear scaling regularities. The cluster node size has an exponent of α = 2.19, while the cluster POI count yields α = 2.00. The scaling exponent of node clusters is close to the critical value of 2.0, align well with empirical findings in complex urban systems and indicate that many small clusters coexist with a few dominant centers, forming a nested and hierarchical configuration. Overall, these results confirm that both the physical street structure and the functional activity distribution in Shenzhen follow power-law scaling, reflecting the city’s underlying living structure of high hierarchies.

When compared with findings from other Chinese cities, the scaling exponents observed in Shenzhen show an interesting duality. The exponents for node- and POI-based clusters fall well within the typical range of α = 2.0–2.2, reported in previous studies on urban street and hotspot systems [7,13,26]. This range is widely interpreted as a signature of critical complexity, a balance between complete disorder and rigid uniformity. In contrast, the exponents for street connectivity and street-based POIs are higher than the typical range. This may suggest that while the functional “living structure” of clusters evolved towards a robust bottom-up hierarchy, the physical street network exhibits a stronger decay in the tail, likely consistent with Shenzhen’s rapid, top-down urban expansion which limits the formation of extremely high-connectivity hubs compared to organic evolution.

3.2. Multi-Scale Correlation Analysis for Streets and Hotspots

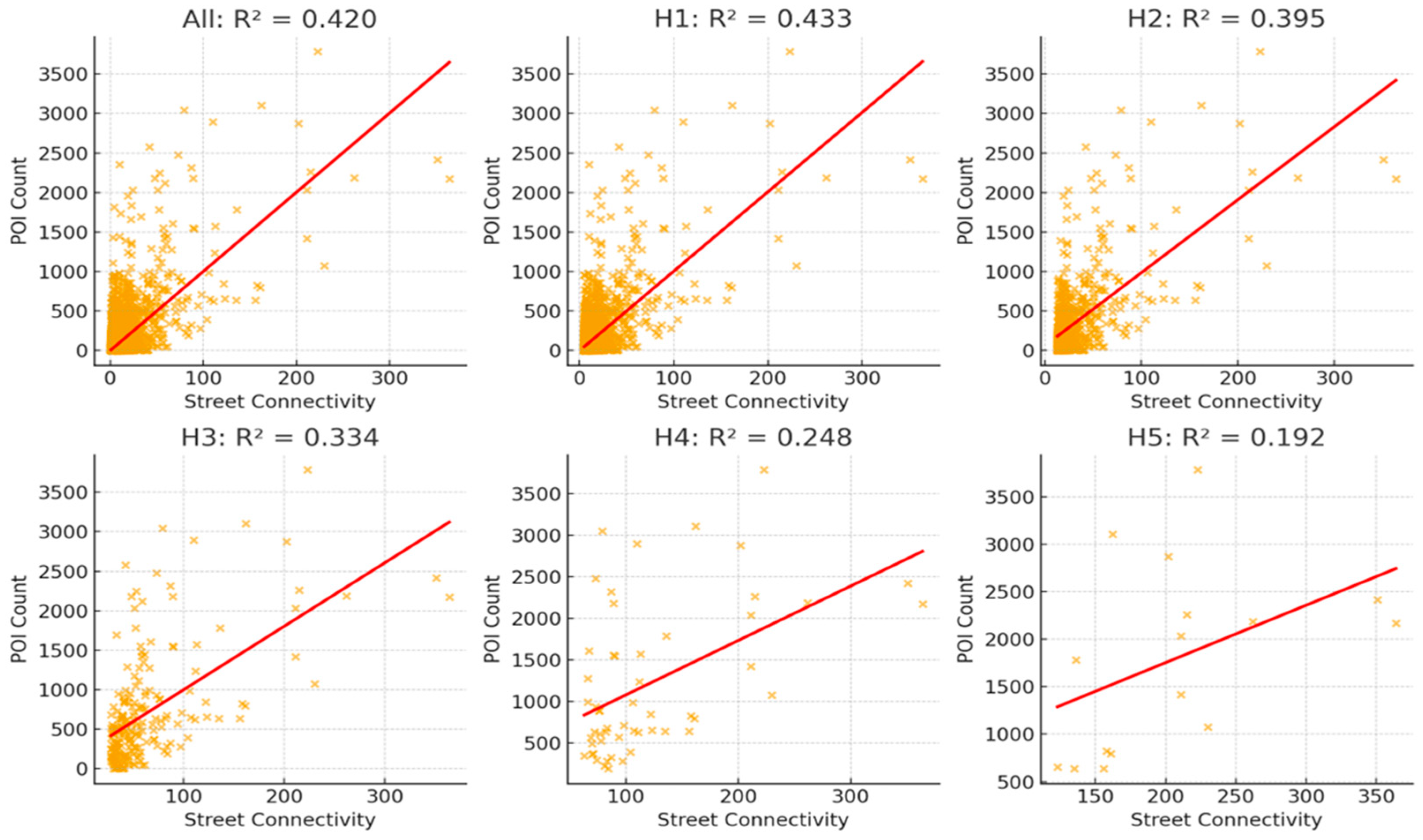
In this study, we conducted correlation analyses at multiple scales induced by head/tail breaks on the street connectivity and number of POIs within hotspots as shown in Figure 7. The streets are divided into five levels, and we conducted correlation at four largest levels. For the spatial cluster or hotspots, we recursively divided hotspots at four recursions. The correlations between number of nodes and POIs were calculated. The multi-scale correlation analysis reveals a statistically significant association between street connectivity and the density of nearby Points of Interest (POIs) across hierarchical levels of the street network (

Table 3. Correlations between connectivity and nodes at each level of streets.

Group	Pearson’s r	R2 (Linear Fit)	Spearman ρ
All	0.65	0.42	0.27
H1	0.66	0.43	0.40
H2	0.63	0.40	0.53
H3	0.57	0.33	0.55

).

For the overall dataset, a moderate positive correlation is observed (Spearman r = 0.27, p < 0.001) with a linear fit of R² = 0.42, indicating that streets with higher topological connectivity generally host denser concentrations of POIs. This result supports the hypothesis that urban form and function are interrelated, where well-connected streets tend to attract more urban activities due to their structural accessibility and spatial prominence.

Across the hierarchical levels derived from head/tail breaks, the strength of correlation varies systematically (Figure 8). The correlation increases from H1 (r = 0.40) to H2 (r = 0.53) and peaks at H3 (r = 0.55), while slightly declining at H4 (r = 0.45). Correspondingly, the R² values range between 0.25 and 0.43, suggesting that although the linear relationship remains consistent, the explanatory power differs among scales. The stronger association at intermediate levels (H2–H3) implies that these scales represent the most functionally active and structurally coherent components of the urban network, where street connectivity most strongly governs the spatial distribution of POIs.

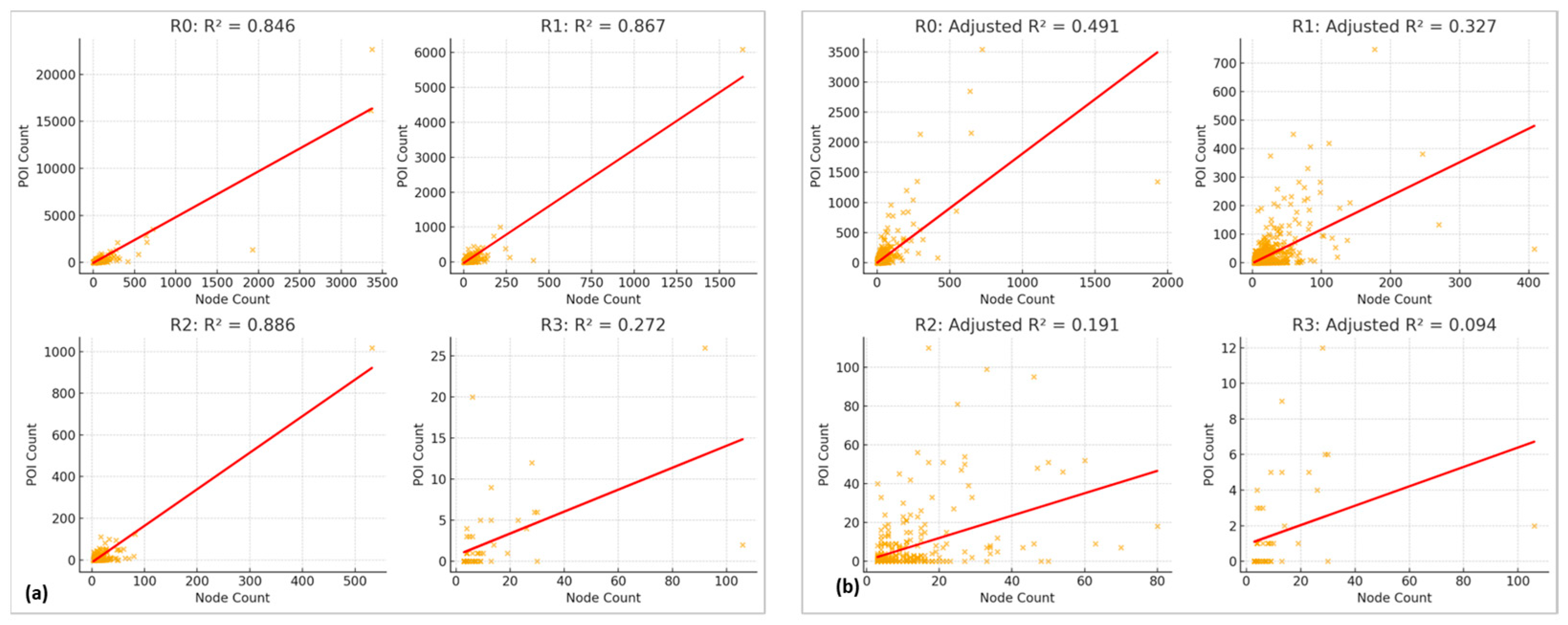
For the correlations within hotspots, the statistical analysis revealed a consistent and meaningful relationship between street-node density and POI (Point of Interest) density across the four regional levels (R0–R3) (Figure 9). The results of both Spearman’s rank correlation and linear regression analysis confirm that areas with denser street networks tend to host a higher concentration of functional activities (

Table 4. Correlations between POIs and nodes at each recursion of clusters.

Group	Pearson’s r	R2 (Linear Fit)	Adjusted R2	Spearman ρ
R0	0.92	0.85	0.49	0.47
R1	0.93	0.87	0.33	0.53
R2	0.94	0.89	0.19	0.47
R3	0.52	0.27	0.094	0.55

).

Spearman’s coefficients (r = 0.47–0.55, p < 0.001) indicate a moderate to strong monotonic relationship across all groups, suggesting that the association between urban form and function remains robust even after removing extreme outliers. This consistency implies that the spatial coupling between structural and functional hierarchies is an intrinsic property of the city rather than an artifact of extreme values.

The linear fit results show that the coefficient of determination (R²) and adjusted R² values decrease progressively from R0 (0.85, 0.49) to R3 (0.27, 0.094), indicating that the strength of the linear relationship weakens toward peripheral or higher-level subregions. The central regions (R0–R1) display strong linear form–function coupling, where street-node density explains a substantial proportion of POI variation, while outer regions (R2–R3) exhibit more complex, nonlinear spatial patterns. Taken together, these results suggest that Shenzhen’s urban system exhibits hierarchical scaling behavior, where the correlation between urban form and function is strongest in core areas and becomes more irregular yet remains monotonic toward the periphery.

We noted that the correlation decreases at the finest hierarchical levels for both the street hierarchy and the hotspot hierarchy. At these local scales, spatial patterns become more evenly distributed and heterogeneous, and functional differences between small units are less pronounced. This increased spatial randomness weakens the monotonic relationship between connectivity and POI intensity. The reduction in correlation therefore reflects the expected transition from strong structural organization at higher levels to more context-dependent and irregular patterns at local scales.

Overall, the findings highlight the scale-dependent coupling between urban form and function, emphasizing that the relationship between connectivity and functional intensity varies along the structural hierarchy rather than being uniform. Mid-level streets appear to play a crucial bridging role, linking the global arterial framework with localized street networks and facilitating the transition between large-scale structural organization and small-scale functional diversity. This scale-sensitive behavior demonstrates the hierarchical nature of urban systems and underscores the importance of multi-level analysis in understanding urban complexity. By capturing how the interaction between street structure and activity distribution strengthens or weakens across scales, the results provide empirical evidence for the living structure of Shenzhen, in which order and adaptability coexist through nested spatial hierarchies.

4. Discussion

This study demonstrates that Shenzhen’s urban form and function are jointly structured by multilevel scaling hierarchies, revealing a coherent living structure that manifests across the street network, street nodes, and the spatial distribution of POIs. The results show that natural streets, street-node clusters, and POI hotspots all follow heavy-tailed distributions, with ht-index values between 4 and 6, demonstrating that each component of the urban system is highly hierarchical and deeply heterogeneous. These findings align with the core tenets of living structure theory proposed by Alexander [15] and formalized by Jiang [18,19,30], namely that cities evolve through nested, mutually reinforcing centers rather than uniform or randomly distributed spatial elements.

The strong correlations observed at higher and intermediate hierarchical levels reinforce this interpretation. More connected streets and denser street-node clusters consistently coincide with higher concentrations of POIs, demonstrating that the functional layout of the city is fundamentally conditioned by its underlying morphological hierarchy. These results echo earlier findings that street configuration shapes human activities and urban vitality [7,9,22,26]. In Shenzhen, major streets act as spatial anchors that structure not only movement but also functional agglomerations. This spatial anchoring effect reflects the principle of “far more small things than large ones,” manifested as many small local centers embedded within a few dominant large centers.

These findings empirically support Alexander’s concept of living structure by showing that hierarchical centers emerge not only in the physical street system but also in functional spatial distribution. Natural streets and POIs each generate nested centers that reinforce one another across scales, revealing a shared spatial logic. This multiscale alignment extends earlier mobility-based research by demonstrating that stationary economic and service functions follow similar structural constraints. It also bridges network-based and hotspot-based perspectives, illustrating that both linear routes and point clusters contribute to the city’s recursive spatial order. The street network, urban hotspots, and the living structure together form the essential morphological and functional framework of a city.

The method of this study resonates strongly with Lynch’s (1984) notion of “good city form” which emphasizes legibility, vitality, and a sense of place as key dimensions of urban quality [35]. The living structure perspective extends this idea by suggesting that the degree of legibility and vitality in a city arises naturally from its underlying scaling hierarchy—a configuration in which a few large, well-connected centers coexist with many smaller, supporting ones. Thus, a “good city” is not merely one that is visually ordered or functionally efficient, but one whose street network and hotspots are arranged in a living, coherent hierarchy that fosters both accessibility and emotional attachment. Integrating Lynch’s qualitative vision with quantitative measures of living structure offers a promising pathway toward cities that are not only efficient and sustainable but also psychologically and aesthetically whole.

An additional noteworthy insight emerging from this study is the bidirectional perspective between form and function. While much of urban analysis traditionally evaluates how street form shapes functional patterns, our results show that functional clusters derived solely from POI distributions can themselves serve as an effective lens for revealing the underlying urban form. The hierarchical structure of POI-based hotspots mirrors, to a remarkable degree, the hierarchical morphology of the street network. This suggests that urban function is not merely an outcome of form, but also a powerful indicator of form—particularly in dense, rapidly evolving cities like Shenzhen.

5. Conclusions

This study demonstrates that Shenzhen’s urban form and function are jointly structured by nested scaling hierarchies, providing clear evidence that the spatial organization of POIs is closely linked to the city’s street configuration. Both natural streets and POI clusters follow heavy-tailed distributions, reflecting a living structure composed of multiple hierarchical levels. Although the street network exhibits a deeper hierarchy than the POI system, their overall scaling consistency indicates that major streets and dense street-node clusters serve as structural anchors for functional aggregation. Correlation analyses further reveal that highly connected streets consistently attract more POIs, with the strongest associations observed in mid- and upper-level structural layers. At finer scales, the coupling becomes weaker and more nonlinear, reflecting more diverse and context-specific functional patterns in peripheral or weakly connected areas.

In summary, this study makes three key contributions. First, it develops a unified multiscale analytical framework integrating natural streets, street nodes, head/tail breaks, and TIN-based clustering to jointly model morphological and functional hierarchies. Second, it provides theoretical evidence that POI distributions are strongly conditioned by the underlying street hierarchy. Third, it shows that both streets and hotspots exhibit consistent scaling behaviors and that the strength of form–function coupling varies systematically across hierarchical levels. These findings suggest that Shenzhen’s morphological and functional systems co-evolve as parallel living structures, offering important implications for planning strategies that seek to align spatial configuration with functional needs.

Future research should expand beyond morphology to incorporate socioeconomic, environmental, and behavioral dimensions. Integrating spatial network metrics with data on income, mobility, land use, or well-being could deepen understanding of how urban form shapes accessibility and opportunity. Additionally, the use of AI-based and generative models may enable dynamic simulations of how changes in street configuration or hotspot distribution influence urban evolution over time.