Comprehensive MCDM Approach in the Process of Land Consolidation Project Choice

Abstract

Multi-criteria decision-making models are very useful tools for use in the process of land consolidation project choice. However, they can lead to wrong or suboptimal choices. Under limited budgetary conditions (where the available budget does not cover all project candidates’ requirements for their realization), it is necessary to make a proper choice regarding financial asset distribution. This process should lead to the best possible budget distribution, i.e., to the choice of land consolidation projects that promises the maximal return on the assets invested. In this research, the authors have conducted theoretical research based on real data to determine the sensitivity of the choice of land consolidation projects with regard to the influence of the chosen criteria for decision-making. The utilized data were obtained via four multi-criteria decision-making (MCDM) methods (AHP, VIKOR, SAW and TOPSIS). The method used for investigating the influence of certain criteria on decision-making was based on a multidimensional linear regression method where the rank of a land consolidation project is a dependent variable, while the values of criteria are independent variables.

1. Introduction

Multi-criteria decision-making (MCDM) is one of the main decision-making problems used to determine the best alternative option, doing so by considering more than one criterion in the selection process [1]. In cases where the choice of best alternative is highly complex, multi-criteria decision-making methods provide the possibility of determining the structure and solution by involving multiple criteria [2]. The use of multi-criteria decision-making methods has increased significantly in different applications [3]. One problem with MCDM methods is their uniqueness, which results the development of a vast number of theories, which while solving one specific problem always leaves unanswered questions [4]. This statement, if it is true, implies that there is no best solution and that MCDM methods, even though they are very useful, still suffer from imperfections. To draw further conclusions, it is possible to state that every solution obtained via MCDM methods must be analyzed in detail to check their validity or to avoid drawing inaccurate conclusions. Another approach is to use the same method proposed for separating multiattribute utility theory (MAUT) models into two groups: riskless and risky choices [5]. The other specific approach is to utilize multiattribute value theory (MAVT) models, which are a family of multi-criteria decision analysis methods that include stakeholders’ values in decision-making [6]. Multiattribute decision-making (MADM) is cognitive process for evaluating data under various attributes to find the best option in terms of the preferences of the decision maker [7]. The above-mentioned methods MAUT, MAVT and MADM are considered to be specific cases of general MCDM approaches, but of their differences have not been explained in detail.

Multi-criteria decision-making problems are mostly solved by two approaches: the first one is based on a priori information collection regarding decision makers’ preferences and second one is based on obtaining information in a stepwise manner [8]. Multiattribute problems are related to several conflicting attributes, and the stochastic dominance relationship could be applied solving for this type of problem [9].

Bearing in mind that decision-making is a complex mental process that is considered to result in the most desirable option considering different aspects, Taherdoost and Madanchian, 2023 [1] imply that further research should be conducted to investigate certain situations in which a decision should be made. Analyzing the afore-mentioned statement, it is noticeable that two terms are important, namely “decision making is complex mental process” and “most desirable option”. Those two terms are quite indefinite and could be significantly dependent on the subjective preferences of the decision maker. This statement is valid even though the decision maker fulfilled the requirement defined by Nowak, 2007 [8] because the decision maker will never have all the relevant information or obtain information in a stepwise manner. Another problem in the decision-making process is related to the situation when a group of decision makers have different preferences about alternatives. In that case, it is possible to state that the majority’s preferences should be accepted [10]. According to Tang and Lin, Arrow’s impossibility theorem is “one of the landmark results in social choice theory” [11]. This theoretical approach is researched with regard to the incompleteness of social preference and, by introducing the concept of minimal comparability, makes it possible to generate the complete social preference [12]. Furthermore, other conditions become consistent with the hypothesis that the set of individuals is infinite [13]. Of course, in practice, it is impossible to provide an infinite number of decision makers, but including a higher number of stakeholders in the process of decision-making should lead to a more acceptable solution. The problem of impossibility is recognized as very important, and there are other impossibility theorems such as those of Sen and Muller–Satterthwaite and Tang and Lin, 2009 [11]. Some approaches used for researching impossibility theorems include the absence of collective rationality [14], the absence of the Pareto principle [15], and the existence of many agents and invisible dictators [16]. Arrow’s theorem of impossibility could be explained using Boolean algebra [17]. To solve the problem of impossibility, different approaches were utilized such as the model of the greatest common decision maker [18] and the concept of fuzzy preference for a set of alternatives [19]. Based on afore-mentioned references, it is obvious that the dominant approach used in dealing with Arrow’s impossibility theorem is based on the mathematical approach. Strictly speaking, Arrow’s theorem is valid except under specific conditions, especially when the differences in the preferences of decision makers are not insurmountable. Even if the preferences are insurmountable, the dominant preferences should be accepted in the decision-making process. Solving the problem of impossibility in the decision-making process (decision-making) implies that the differences between decision makers must be surmounted by different actions, including minimizing them and increasing the number of decision makers. According to the presented results for the comprehensive decision-making approaches, it follows that conducting careful research and directing decision makers to involve make reasonable effort to obtain the best possible solution are necessary steps. The term ‘reasonable effort’ means that the number of decision makers and decision-making approaches (MCDM methods) should both be increased. This increase should occur at a scale that does not affect the efficiency of decision-making.

Starting from the assumption that the mental process and the applied methods of MCDM are complex, it follows that entire decision-making process should be carefully questioned. Some important questions are “Are the aspects properly chosen?”, “Are the aspects properly valuated?”, “Was the process of decision making conducted properly?”, and, finally, “Are obtained results really in concordance with desires which were considered at the start of decision-making process?” Considering the above statements, suggesting that the MCDM methods are imperfect, further questions also appear. These questions can be answered by considering the decision-making process in a linear manner, i.e., considering the goal of the decision maker (person or investor), defining the environment in which that goal should be achieved, evaluating different aspects, applying the proper MCDM method, and checking the results. The steps in the multi-criteria decision-making process are shown in Figure 1.

Despite the claim that multi-criteria decision-making (or multi-criteria decision analysis) is one of the most accurate decision-making methods [1], the authors of this paper have been critically questioning every step in the decision-making process, trying to identify both every possible risk of making the wrong decision wrong and how to reduce that risk. We can state with a high level of certainty that every step in the decision-making process has the possibility of being inadequately carried out, and, consequently, the results obtained by decision makers may significantly differ from the desired goal. Moreover, the evaluation of the criteria could be affected by uncertainties. Furthermore, preferences represent the subjective opinions of decision makers. This attribute of MCDM models implies that augmenting uncertainties could lead to suboptimal decision-making, even in the case that the chosen model is created properly. Another problem that could occur is an incorrect level of concordance between the utilized MCDM model and the situation in which it is applied. Moreover, the final problem is determining how to understand the obtained results (ranks) and compare them with the desired results.

In this research, all the above-mentioned steps will be considered and discussed carefully, especially the results of the decision-making process. In our case, the result of the applied MCDM method is the ranking of land consolidation projects, which was the initial issue of interest.

Desire can be defined very easily. For example, local authorities may want to choose the group of cadastral municipalities in which their goals are maximized. This legitimate desire is general and could be questioned from different aspects: Which goals do we want to achieve? How can we prioritize goals? Is there a set of goals acceptable for all stakeholders? A further problem is that different goals could be achieved if they are not defined precisely in advance. For example, are the goals predominantly related to agricultural production maximization or sustainable agricultural production? This simple example shows that general desire could be ambiguous and, if not precisely clarified in advance, the decision maker could not state if the decision-making process led to the best solution. On the other hand, when the goals are not clearly defined, opposite statements could be made. This situation is of extreme importance when there are numerous stakeholders competing for resources and interested in results of a decision-making process that considers their own interests. In the case of sensitive decision-making, the category where land consolidation projects belong, the precise definition of goals and their acceptance by all participants is of crucial importance. In that case, the goals must be the defined at a level of generalization acceptable for all participants and not be burdened by details that exclude the realization of a land consolidation process. The proper choice of goals can influence further decision-making, and mistakes made in this stage will affect the remaining process.

The decision maker should be aware of the environment in which land consolidation is realized. The environment is predominantly related to limitations, including a limited budget, legal limitations, the topographic characteristics of the area, available land and its distribution and participants’ interests. In the process of limitation determination, it is possible that some factors could be underestimated or overestimated and, consequently, certain errors in model could be introduced.

Aspects or criteria values for determination also could produce results with errors or that deviate from their true values. For example, some costs in the land consolidation process could be hidden or overlooked, some important aspects could be neglected and others of less importance could be overestimated, some characteristics of cadastral municipalities could be determined with less or more uncertainty, etc. Furthermore, the preferences of decision makers could differ significantly in the criteria (aspects) evaluation process. This step could lead to the overestimation of some criteria that objectively are not important for achieving goals and underestimate other, really important ones. This fact underlines the subjectivity component of the decision-making process.

Choosing the best MCDM method is also not easy because of the vast number of existing methods and their specificity. It could be assumed that different MCDM methods will generate results with different ranks for alternatives and that different decision makers will prioritize the criteria in different ways. This assumption implies that the application of different ranking determination methods depends on the number of decision makers involved and the number of MCDM methods applied.

In general, it is possible to define the classification of MCDM methods based on the number of decision makers involved and MCDM methods utilized. The possibilities are shown in

Table 1. The classification of the decision-making process depends on the number of decision makers involved and the number of MCDM methods applied.

		Number of decision makers
		One	Multiple
Number of MCDM methods	One	One decision maker and one MCDM method: this approach is simple and can be applied quickly but suffers from a lack of control	Multiple decision makers use one MCDM method. This approach engages multiple decision makers and underlines the subjectivity of decision makers. Deviations in the results stress the influence of subjective valuation of decision makers’ preferences.
	Multiple	Decision makers use multiple MCDM methods to check the validity of its priorities. This approach requires more time and additional analyses but increases the reliability of the decisions made.	Multiple decision makers use multiple MCDM methods. This approach engages multiple decision makers and employs multiple MCDM methods. Deviations in the results stress the influence of subjective valuation of multiple decision makers’ preferences.

.

The analytical matrix based on the afore-mentioned assumption is determined based on the number of decision makers involved (one or multiple) and the number of MCDM methods applied (one or multiple). This approach results in four possibilities: one decision maker and one MCDM method are applied (which means that the subjective views of one decision maker and one MCDM method are applied); one decision maker utilizes multiple MCDM methods (actually checking the differences between MCDM methods); multiple decision makers use one MCDM method (which means that potentially different preferences regarding criteria result in different ranks); multiple decision makers utilize different MCDM methods (which could lead to different ranks but represents the diversity of decision makers’ approaches to an issue). The process could also be complicated if different decision makers use different MCDM methods, but in this research, it is assumed that every decision maker will use the same set of MCDM methods.

The final step in the proposed approach is to check the results for obtained ranks. Results checking is based on evaluating the influence of the criteria on each rank. In this research, the evaluation of the criteria’s influence on the rank is based on performing multidimensional linear regression on the obtained rank results.

Analyzing the decision-making process, we can state that it is dependent on the situation in which decision is made. If one decision maker is free to choose the criteria and to weight them according to their preferences, the decision-making process is relatively simple: the decision maker can vary the weights and decide whether to apply one or more MCDM methods. In a situation when there are multiple decision makers, there is a high probability that every one of them will weight the criteria differently.

In this research, the authors have investigated the ranks of land consolidation projects by considering a case where multiple MCDM methods (AHP, TOPSIS, VIKOR and SAW) and multiple decision makers are included. Every decision maker is free to choose their own preferences, i.e., to weight criteria in their own way. The differences between rankings are treated as randomly distributed results [20] because it is impossible to predict the preferences of all included decision makers. Furthermore, it is assumed that decision makers can be consistent, quasi-consistent and inconsistent [21]. This approach produces the three different sets of data analyzed and explained in detail [21].

Bearing in mind the importance of making the best possible decision (especially for budget distribution), the complexity of the decision-making process and its imperfections, we simulated the decision-making process for multiple decision makers and multiple MCDM methods. This approach has been adopted and implemented for the dataset related to land consolidation project ranking and based on real data for the municipality of Bela Crkva, Serbia.

Theoretical Background

The vast number of MCDM methods and their variations suggests that no perfect MCDM method exists, and an implicit consequence of this fact is that it is very difficult (if even possible) to state that one method is superior to others. In further discussion, the authors try to elaborate the main characteristics of the utilized methods. In fact, the MCDM methods could be considered hybrid methods because the decision maker chooses the criteria, algorithm (method) and weights, while only the data are fixed [21]. The hybridity of model is valid before these choices have been made—when those choices are made, it is possible to state that rank of alternatives is determined, even though the decision maker still does not know this before the rank is calculated. The only way to change the result is to change the initial choice. Consequently, for one dataset, the rankings of alternatives are always the same. This hybridity of one model (one model combines the subjective expert’s preferences regarding the alternatives and the choice of MCDM method, paired with objective data and an objective mathematical MCDM method) should not be confused with the hybrid approach resulting from the combination of MCDM methods. The first one should be considered to represent hybridity in the “narrow” sense, and other should be considered to represent hybridity in a “broader” sense.

The analytic hierarchy process (AHP) method among the most popular decision-making methods [22]. The analytical hierarchy process was initially developed by Thomas L. Saaty and expanded into different domains of human activity by Hartwich, 1999 [23]. The analytical hierarchy process is considered to be a means of applying exact methods in the decision-making process [24]. This statement is valid, but this does not mean that the decision-making process will result in the best decision. It only means that the decision-making process, only as defined and for the adopted dataset, will result in identical ranks, regardless of the number of repeated calculations. The analytical hierarchy process is explained in detail in Saaty, 1980 and 2005 [25,26]. According to Saaty, everything one does consciously or unconsciously leads to some decision, and even though our judgment may be inconsistent, it is necessary to measure inconsistency and to improve the judgement [27]. This is an important statement that underlines the imperfections of judgment as a complex and imperfect process, while highlighting that it is not an obstacle to improvement.

Although the AHP is popular and widely used in decision-making, research has presented critical opinions. In their book, Munier and Hontoria, 2021 [28] analyzed the 30 subjects that highlight shortcomings and drawbacks in the AHP. Another criticism is that the AHP is very likely to provide a ranking of options that would not be acceptable to a rational person [29]. Another problem with utilizing the AHP is that analysts may encounter a lack of data, deficient databases, defective information or, more importantly, a lack of specialists with adequate expertise [30]. The sensitivity of consistency coefficient determined via the AHP is also an object of discussion: to be consistent, this measure should be less than 0.1, but the manipulation of objective weights indicates that if all objective weights are of near-equal importance, the consistency measure will require relatively consistent rankings of all objectives; otherwise, if one objective is much more important than the others, very little consistency is needed among the other objective ratings to pass the test limit [31]. This paper underlines the sensitivity of the AHP method in terms of expressing the significance of the consistency coefficient near its value of delimitation, considering both consistent and inconsistent results. This issue could be termed as “consistency on a certain level” [21]. This term refers to the situation when the decision maker does not care about rules proposed vis the AHP method for weighting alternatives and instead conducts the process intuitively or randomly accepts the values of weights.

Despite criticism, the AHP method is widely used for decision-making in different domains, often combined with SWAT (strength, weakness, opportunity, threat) analysis [32], and it is considered the optimal choice for decision-making in forest management (despite its weaknesses) [33]. Furthermore, the analytic hierarchy process should receive more attention than it has up to now and could be of great use in decision-making [34]. In conclusion, we can state that, despite criticism, the AHP has a place both in theoretical research and practical application.

The Technique for Order Preference by Similarity to Ideal Solution (TOPSIS) is one of the most widely used multi-criteria decision-making methods, and it has various improved versions [35]. The TOPSIS is numerical method, broadly applicable and simple in the mathematical sense [36]. The TOPSIS is based on the idea that the best alternative is placed at the shortest distance from the positive ideal solution and the greatest distance from the negative one [37]. The greatest distance from the most negative solution could be questionable, and another approach might be based on the distance from the veto threshold set by the decision makers [38]. The influence of weights on the alternative ranking obtained via the TOPSIS showed that it is not noticeably more accurate than direct weighting methods; what is more, it is quite similar in accuracy except when equal weights are applied, leading to the conclusion that the most favorable aspect of the TOPSIS is that it determines accurate weights [39]. Some noted imperfections of the TOPSIS resulted in its improvement. Starting from the basic idea of the TOPSIS, i.e., that it uses a pair of a positive and negative ideal solutions as two reference points to rank a set of alternatives and that, in some situations, those two distances may not be meaningful, one study proposed introducing a third middle reference point [40]. A significant aspect of the development of the TOPSIS is its use of fuzzy logic [41,42,43]; and many another studies). Regarding the utilization of the TOPSIS for ranking algorithms under evaluation (which the classical TOPSIS cannot do), the development of new algorithm was required [44]. This case illustrates the adaptability and usability of the TOPSIS under contemporary conditions.

A literature review of a significant number of articles conducted over a decade showed that the TOPSIS continues to work satisfactorily across different application areas [45]. This finding highlights that the TOPSIS is viable and reliable method for application in of decision-making process, even though it is still under development.

The MCDM method VIKOR (Serbian: Više Kriterijumska Optimizacija i Kompromisno Rešenje), meaning multi-criteria optimization and compromise solution, was developed in 1998 by Serafim Opricovic to solve decision problems with conflicting criteria and has attracted much attention for coping with complex problems with conflict factors [46] (other authors state that the VIKOR method was proposed by Opricovic in 1979 [47]). The VIKOR method is a widely used method, and, in 2009, the corresponding paper by Opricovic and Tzeng, 2004 [47] became the most cited paper in the field of economics [48]. The afore-mentioned authors questioned why this approach is empirically successful even though the model is very complicated and unintuitive, and they found one straightforward and one sophisticated justification by conducting detailed mathematical analyses [48]. Another study conducted a systematic literature review of papers related to the VIKOR method published from 2004 to 2015 in high-ranking journals, most of which were related to operational research, management sciences, decision-making, sustainability and renewable energy, highlighting the usability of the VIKOR method in various theoretical and practical implementations [49]. The VIKOR method can be used for material selection [50], as well as for customer satisfaction-related thorough sentiment analysis schemes that simultaneously consider maximum group utility and individual regret [51]. The spherical fuzzy VIKOR method is utilized for validating the complex spherical fuzzy model because of its adequacy for dealing with two-dimensional data [52].

Depending on the specific decision problem, six variants of the VIKOR method have been subsequently developed, including comprehensive VIKOR, fuzzy VIKOR, regret theory-based VIKOR, modified VIKOR and interval VIKOR [53]. All rankings obtained via different variants of VIKOR have produced different results, except the original and fuzzy VIKOR variants. Furthermore, VIKOR and other MCDM methods have been applied on an equal set of alternatives and criteria results with different rankings of alternatives. Utilizing PROMETHEE and VIKOR for choosing energy supply systems for space heating in residential buildings resulted in different sources of energy being used [54]. One possible improvement in VIKOR is based on achieving distance improvement by implementing generalized weighted Mahalanobis distance, Euclidian distance and Canberra distance [55]. Other improvements to VIKOR were made by including CRiteria Through Intercriteria Correlation (CRITIC) in the modified VIKOR technique to reduce the impact of expert preference [56] and by integrating entropy and fuzzy VIKOR models [57].

It is difficult to find research on the disadvantages of VIKOR in the literature. One of the disadvantages of VIKOR is that its subjective initial weighting is challenging to validate [58], while other references stress improvements in this area [59]. Among the advantages of fuzzy VIKOR (F-VIKOR) are simplicity, rational, comprehensibility and good computational efficiency, with the ability to measure the relative performances of alternatives in a simple mathematical form [60]. The advantages of the original VIKOR method include handling both quantitative and qualitative data, providing a compromise solution that balances conflicting criteria and usability for problems with difficulties in expressing preferences, etc., while its disadvantages are related to sensitivity regarding changes in weights and thresholds, increased complexity with the number of criteria and alternatives, and requirement differences between initial weights, [61]. The main disadvantage of VIKOR is its search compromise ranking order between expected and pessimistic solutions, which implies that changing weights can impact rankings (although this issue is considered a merit by some authors because it could identify the influence of weights on the alternatives’ rankings) [62]. Summarizing the literature on VIKOR, most studies have been conducted with regard to its improvement and adaptation rather than stressing its disadvantages and shortcomings. Furthermore, the original VIKOR was not criticized when released, and its usability was not questioned seriously. These arguments recommend utilizing VIKOR method in this research.

Simple Additive Weighting (SAW) is known as weighted direct mix technique with a very simple mathematical model [63]. SAW produces results very efficiently and easily, even when testing different cases [64]. Comprehensive advantages and disadvantages of SAW encompass six cases in which efficiency is a major advantage and the following disadvantages: it may be applied when all variables are maximizing (but this requirement is solvable via normalization by converting minimizing variables into maximizing ones) and positive, and its results may not be logical [65].

Summarizing the advantages and disadvantages of SAW, it is fair to include it in this research because of its simplicity and efficiency, as well as its widespread presence in contemporary research.

A further justification for authors utilizing multiple decision makers and MCDM methods in the process of choosing land consolidation projects is that a vast number of investigations are devoted to comparison rankings obtained via different MCDM methods applied on the same data, alternatives and criteria. Studying the utilization of the TOPSIS and VIKOR for ranking European countries based on aspects of the sustainable development goals (SDGs) has resulted in different rankings [66]. Utilizing three MCDM methods, the TOPSIS, VIKOR and COPRAS (Complex Proportional Assessment), for COVID-19 showed that closest result to that of the Deep Knowledge Group consortium report was obtained using COPRAS and the most dissimilar result was obtained via VIKOR [67]. Another interesting approach is utilizing a hybrid model (in this sense, “hybrid” denotes the utilization of two or more MCDM methods for making decisions). A review of 55 papers published from 1994 to 2019 indicated that a hybrid model combination of two or more MCDM methods is the most applied technique for material selection [68]. Recently developed MCDM method combinations such as COPRAS and WASPAS (Weighted Aggregated Sum Product Assessment) are also utilized for material selection [69]. A comprehensive literature review of papers published in 2008–2018 concluded that conducting further research on the creation of hybrid models could upgrade the existing MCDM methods [70]. Another approach integrated FUCOM with the rough COPRAS method and utilized a rough Dombi aggregator, combining the positive aspects of the utilized MCDM methods to determine the stability of the best solution [71]. The Hybrid MCDM (HMCDM) method, which combines multiple MCDM methods, could increase confidence in the obtained solution among single decision makers or groups of decision makers, especially in cases of increasing variety and complexity, as well as when facing more challenging problems [72]. The main explanation for utilizing MCDM method combinations (hybrid MCDMs) is that different users (decision makers) will obtain different results by utilizing the same method since their backgrounds, expertise and experience differ [73]. Even though every user (decision maker) of the MCDM method could have their own preferences, choice of alternatives and criteria evaluation approach, there still are some universal criteria for estimating the reliability of MCDM methods [74]. The most important issue, i.e., whether different MCDM methods are benchmarkable, has been investigated and presented in the contemporary literature. Some research showed similarity with the final rankings obtained via different MCDM methods [75], while other research showed that some applied MCDM methods (two) were determined to be more suitable methods than another five popular methods [76].

Summarizing the literature that deals with the imperfections and/or limitations of utilizing one MCDM method and solving their imperfections/limitations with a hybrid approach, we can conclude that utilizing a hybrid approach has become imperative under contemporary conditions. Furthermore, every step in the decision-making process should be questioned seriously, and every MCDM method should be tested consciously to reduce the risk of possible mistakes.

These logical conclusions direct our research on ranking land consolidation projects. In this research, we adopt the following description of land consolidation (LC): LC represents a comprehensive reallocation procedure for a rural area consisting of fragmented agricultural or forest holdings or their parts, aiming to improve land division and to promote the appropriate use of the local real estate [77]. Other points of view define LC as readjusting land parcels shapes, relocating land rights to minimize the farmland fragmentation, optimizing agricultural output, and generating optimal living and working conditions in rural areas [78]. Land consolidation could provide multifunctional possibilities, including promoting rural revitalization, revitalizing the countryside, multi-objective and multifunctional transformation, and social, economic and ecological benefits, but its potential risks cannot be ignored [79]. The latest justification for land consolidation seems to be the most comprehensive, because it encompasses the consequences of land consolidation projects, i.e., both benefits and potential risks. This approach is suitable for decision-making because it requires serious consideration, especially considering the budget needed for realizing land consolidation projects. It should be stressed that there were investigations that considered the application of different MCDM methods in land consolidation project prioritization. The suitability of cadastral municipality ranking based on information by applying three different multi-criteria methods is suitable for national agricultural or other spatial planning purposes [80]. An integrated assessment methodology for land consolidation projects was proposed for the improving decision-making process [81].

Without further developing the LC in detail, we can state that LC projects are quite complex, and the main limitation hindering their realization is a limited budget. In that case, it is necessary to determine which LC projects among all competitive options should be realized within the available budget. Considering the significance of realizing LC projects, it is of crucial importance to provide the most accurate ranking among competitive projects to determine the best budget distribution.

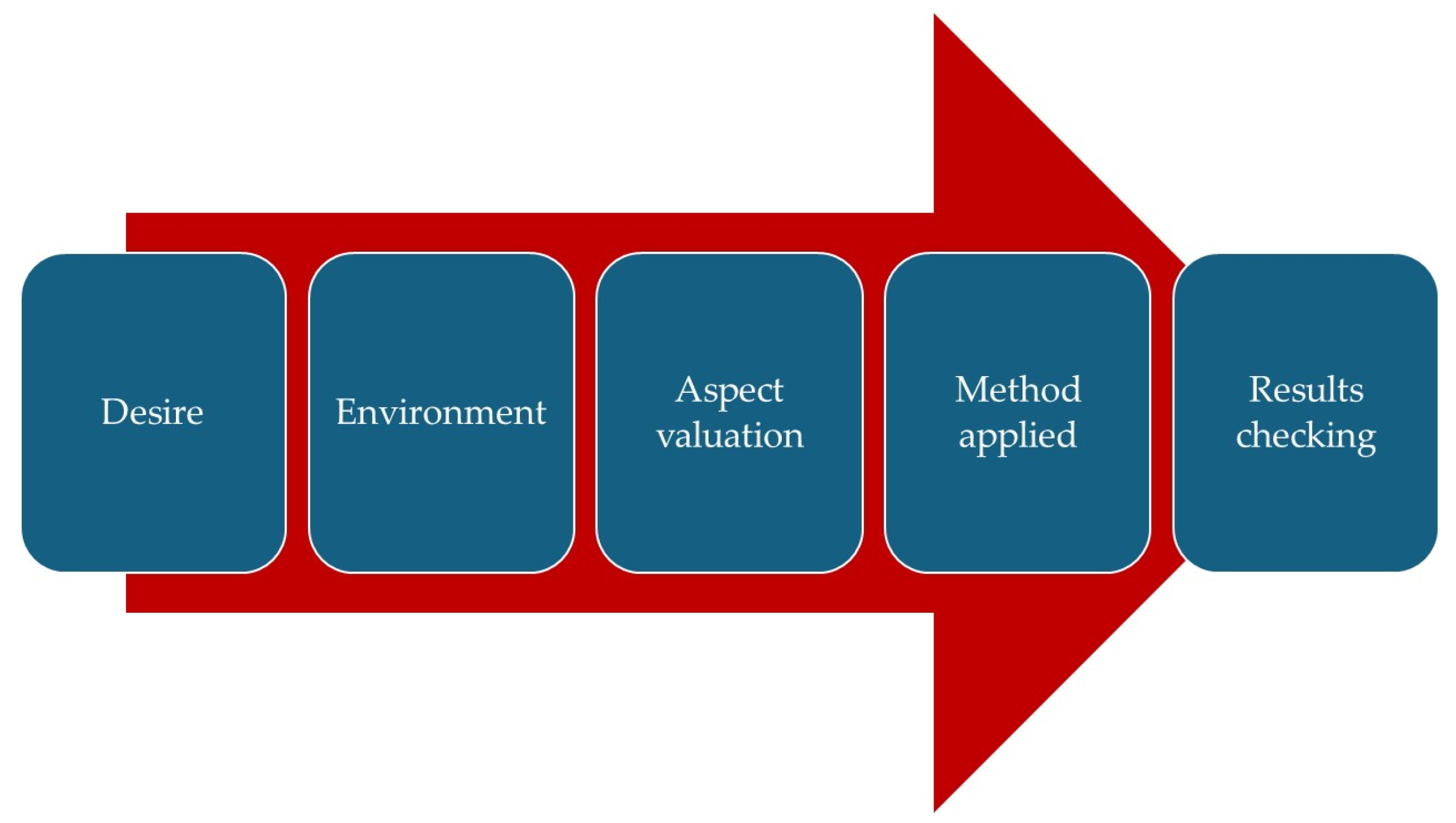
The research should answer a fundamental set of questions derived from the above-proposed decision-making process (Figure 1):

-

Are the criteria that describe land consolidation projects well chosen (is the goal well reflected in the criteria)?;

-

How does the environment (limitation values of criteria and alternatives) affect the choice of land consolidation project?;

-

Do the different approaches for weighting criteria affect the rank of land consolidation projects (is the environment understood well?)?;

-

How does the applied method impact the rank of land consolidation projects?

-

Are the results of different MCDM method-based land consolidation project rankings mutually consistent?

Due to the complexity of the questions formulated, it is not possible to cover and present all of them in this paper; thus, the authors focused only the question “does the application of multiple decision makers and multiple MCDM methods lead to a more consistent choice of land consolidation project?” Consistency in this context means that the choice will be more reflective of the real situation. The measure of consistency is obtained using the decrease in standard deviation between rankings of the same project and the difference between them. This question seems to be neglected in the analyzed literature. In this research, four methods were used: AHP, the TOPSIS, VIKOR and SAW; they were applied to land consolidation projects for the Bela Crkva (Republic of Serbia, Vojvodina) municipality.

2. Materials and Methods

The materials used for this research are based on the chosen criteria for fifteen land consolidation projects that compete for the limited budget of the Bela Crkva municipality, Serbia. Figure 2 presents the position of Bela Crkva municipality in the Vojvodina region (Republic of Serbia). The approximate coordinates are ϕ = 445,438, λ = 212,445 (source: Google Earth).

Each LC project represents one cadastral municipality with their own values (characteristics).

The criteria have the following meanings:

• (f₁) The share of agricultural land in the total area of the land consolidation area;
• (f₂) The average surface area of cadastral parcels for each land consolidation area;
• (f₃) The average number of cadastral parcels per participant for each land consolidation area;
• (f₄) The average surface area of the participants’ property for each land consolidation area;
• (f₅) The percentage of farmers owning property larger than 5 ha;
• (f₆) The share of state property out of the total agricultural land;
• (f₇) The active agricultural population;
• (f₈) The land consolidation cost per hectare;
• (f₉) The estimated return periods for assets invested into land consolidation;
• (f₁₀) An estimation of the profitability of agricultural production due to land consolidation in the adopted period.

The data are presented in

Table 2. The alternatives, the criteria and their values for each land consolidation project.

Criterion	f1	f2	f3	f4	f5	f6	f7	f8	f9	f10
Unit	%	ha/parc	parc	ha	%	%	%	€/ha	year	Un. N
Goal	max	min	max	max	max	max	max	min	min	max
Alternative
800317	25.54	0.49	10.12	4.93	10.99	53.53	74.45	142.0	9.6	0.52
800660	75.82	0.56	6.09	3.39	16.42	21.98	75.23	159.1	3.6	1.38
800333	74.39	1.30	3.22	4.19	2.44	29.66	5.65	133.5	3.1	1.61
800643	60.71	0.43	5.47	2.35	9.71	25.18	51.36	160.5	4.6	1.09
800732	77.03	0.60	3.18	1.91	5.41	38.16	51.36	228.9	5.1	0.97
800449	57.25	0.46	5.44	2.53	10.97	23.23	89.35	162.3	4.9	1.02
800678	84.04	0.92	7.02	6.48	16.35	48.00	89.17	132.1	2.7	1.84
800392	53.70	0.41	7.21	2.94	13.89	24.08	81.17	171.6	5.5	0.90
800465	79.43	0.43	5.51	2.39	10.88	15.69	36.75	133.3	2.9	1.72
800473	11.76	0.80	4.44	3.57	2.88	75.24	89.14	211.4	31.1	0.16
800481	68.56	0.47	13.86	6.24	24.52	23.89	80.56	173.1	4.4	1.14
800503	87.27	0.36	9.43	3.43	13.48	9.54	55.34	133.4	2.6	1.89
800708	76.39	0.32	6.17	2.01	8.71	16.05	45.02	139.9	3.2	1.54
800724	64.79	0.42	17.17	7.28	5.13	59.86	45.02	204.9	5.5	0.91
800341	78.94	0.50	5.61	2.78	8.23	19.22	28.45	141.1	3.1	1.62

.

As mentioned in the Introduction and justified by contemporary trends in the relevant literature review, approaches that include multiple decision makers and multiple methods were applied in this research. The further development of the proposed approach included questioning its each step. The first step was to check if desire (intention) was properly defined and whether it was properly decomposed into criteria.

Table 3. The cases of the definition and decomposition of desire.

		Definition of desire
		Proper	Improper
Desire decomposition	Proper	Ideal case: The desire is properly (clearly) defined and is decomposed properly. This situation promises that the initial stage is based correctly.	Incorrect case: The desire is not defined properly but is decomposed properly. This case could lead to the wrong goals being achieved.
	Improper	Questionable case: The desire is properly defined but is decomposed improperly. This case could lead to deviations from the original goal.	Wrong case: The desire is not defined properly and is decomposed improperly. The chances of achieving the desired goals are negligible.

shows the case, which will be further discussed in detail.

Desire is analyzed in two dimensions: its definition and its decomposition into the measurable criteria. Defining desire in the case of land consolidation could be a very sensitive process. For example, if LC projects are planned only with the goal of reallocating fragmented real estate ownership for regrouping parcels, they could neglect the principles of sustainable development or other possibilities to achieve other common goals. Furthermore, if desire is related to sustainable development but, in the process of its decomposition, any important principle of sustainable development is not included, it immediately follows that the decomposition of desire was not proper. Considering those possibilities, further discussion is immediately required. The first case is ideal: the desire is properly defined, and it is properly decomposed into criteria. The second case relates to the situation when the desire is defined improperly but its decomposition is provided in strict way. This case is named incorrect. The third case is when the desire is correctly defined, but its decomposition is provided improperly. This case is denoted as questionable. The fourth case is wrong: desire is improperly defined, and its decomposition is improperly provided. The aim of explaining the derivation of desire in this research is to determine which land consolidation projects are most suitable for existing budget distributions. In the investigated case, the fifteen land consolidation projects compete for the limited budget. Decision makers should decide which land consolidation projects are the most deserving of realization. In conclusion, regarding knowledge of land consolidation and its benefits, it could be stated that the position of land consolidation belongs to the first quadrant, known as “ideal case”. This statement is justified by the decision to distribute the budget to fund land consolidation projects that improve agricultural production and bring other benefits to rural communities, because each cadastral municipality represents one land consolidation project.

A further step in the proposed approach is denoted as “Environment”, and it is analyzed from the perspective of environment friendship and environment assessment.

Table 4. The cases of using environment assessment and environmental friendship for achieving goals.

		Environment assessment
		Proper	Improper
Environment friendship	High	Ideal case: The environment (the values of the criteria and limitation factors) is assessed properly, and their suitability for achieving goals is high.	Incorrect case: The environment for achieving goals is assessed improperly. This case could lead to wrong decisions: either missed chances or difficulties in achieving goals.
	Low	Questionable case: The environment is assessed properly, but its friendship is low. In this case, a lot of risks are present, even though the values of the criteria that represent the environment are well-assessed at the moment of decision making. Risks are related to the possibility of changing criteria values.	Wrong case: The environment is not properly assessed and the environmental friendship is low. The values of the criteria were assessed under the required threshold for accuracy and there is a risk of significant changes.

shows this case, and it will be further discussed in detail.

Environmental assessment is very important, but it should be considered from at least two perspectives: its environmental friendship to the land consolidation project and proper assessment of criteria values. The first case is ideal since environment assessment is proper and environment friendship is high. This means that the data are accurate and are stable in the time required for land consolidation project realization. The second case is denoted as “incorrect” because the environment assessment is not proper, even though the environment friendship is high. The third case is questionable because the proper assessment of the environment is conducted under low environment friendship conditions. The fourth case is denoted as wrong because the environment is not assessed properly in the environmental friendship is low. The position of land consolidation projects could be also defined in the “ideal position” because the environment is friendliness-orientated (each landowner is interested in improving quality of their land) and the situation does not change faster than the land consolidation project takes be realized.

A further step in the proposed approach is related to aspect evaluation and their relevance for decision-making. The aspect evaluation process is divided into two dimensions: their relevance and their valuation. Those two dimensions are in the domain of decision makers’ preferences. One decision maker could view one set of aspects as relevant, while another will view another set of aspects as relevant. Furthermore, one decision maker may evaluate the aspects differently to another one.

Table 5. The cases of aspect valuation and aspect relevance.

		Aspect valuation
		Accurate	Inaccurate
Relevance of included aspects	High	Ideal case: Accurate aspects and relevant aspects are included in the model. This situation promises that the initial stage is based correctly.	Incorrect case: The relevance of the included aspects is high, but their valuation is incorrect. This case could lead to deviations from the desired goal.
	Low	Questionable case: The relevance of the included aspects is low, but their valuation is accurate. This case could lead to deviations from the original goal.	Wrong case: The relevance of the included aspects is low and their valuation is inaccurate. The chances of achieving the desired goals are negligible.

shows the case, and it will be further discussed in detail.

From that point of view, the first case is ideal because the relevance of the aspects included in the process of decision-making is high and their evaluation is accurate. The second case occurs when the aspects are highly relevant and their evaluation is inaccurate. This case is denoted as “Incorrect”. The third case appears when the relevance of aspects is low but they are accurately determined. This case is denoted as “questionable” because it requires aspects of higher relevance. The fourth case is denoted as “wrong” because both the evaluation of aspects is inaccurate and their relevance are low. The relevance of the included aspects (chosen criteria) and their accuracy should be assessed, as they belong to the “ideal” or “questionable” quadrants. This could be explained in the following way: the data are obtained from official sources, and they are hardly inaccurate (or they are as accurate as possible, and the relevance of the included aspects may belong to a set of high or low relevance). This is a consequence of the quite subjective preferences of decision makers regarding which criteria are included in decision-making process.

The next step in the decision-making process is related to the choice of MCDM method. As discussed before, there is no ideal choice of MCDM method. Consequently, it is possible to apply a MCDM method that is not suitable for problems that one wants to solve. Furthermore, one could make mistakes if using certain MCDM methods improperly.

Table 6. MCDM method choice and use.

		MCDM method use
		Properly	Improperly
Applied MCDM method suitability	High	Ideal case: The method is used properly and is suitable for the kind of problem to be solved. This situation promises that the results will be obtained correctly.	Incorrect case: The MCDM is used improperly but is highly suitable for the considered problem. This case could lead to the wrong goals being achieved.
	Low	Questionable case: The method is used properly but has low suitability for the considered problem. This case could lead to deviations from the original goal.	Wrong case: The MCDM method is used improperly and is not suitable for the considered problem. The chance of achieving the desired goals is negligible.

illustrates those possibilities.

The analysis of the MCDM method applied is divided into two dimensions: its suitability for solving the problem and its proper utilization. The first case is ideal: the applied MCDM method is highly suitable for problem solving and it is used properly. The second case is denoted as incorrect: a highly suitable MCDM method is used improperly. The third case is denoted as questionable because a low-suitability MCDM method is used properly. The fourth case is denoted as wrong: a low-suitability MCDM method is used improperly. The choice of MCDM method is a subjective decision and should be based on the experience and knowledge of the decision maker. Consequently, in this step, all possible variants could occur. In the worst-case scenario, the decision maker would choose an inappropriate MCDM method and utilize it in the wrong way without being aware of the mistakes made. Using a hybrid (in the broader sense) approach could reduce the risk of applying the “wrong” case, but the risk of omitting the “ideal” case could be considered high. Consequently, this step deserves careful consideration.

The final step in the decision-making process is checking the results (consistency). This step is also related to the decision maker’s knowledge and their ability to note if there were any mistakes in the decision-making process when utilizing MCDM methods. This case is shown in

Table 7. Results checking step.

		Results difference from expectations
		Acceptable	Unacceptable
Results differ from expectations	Possible	Ideal case: The decision maker should decide if additional efforts are needed to reduce the differences between the desired and obtained results.	Incorrect case: The decision maker should decide whether there are possibilities for reducing the differences and if such additional efforts are acceptable.
	Impossible	Questionable case: The differences are acceptable, but reductions are impossible. The decision maker should decide whether they should investigate possible hidden solutions.	Wrong case: The differences are unacceptable, and reductions are impossible. The decision maker should investigate the entire decision making process and determine where they went wrong.

.

Results checking is considered from two dimensions: the difference from expert’s expectations and the possibility of differences between obtained and expected reductions. The first case represents the ideal situation when the differences are acceptable and their reduction is possible. The decision maker, in this case, may decide to accept the obtained results or to make further improvements. The second case is denoted as incorrect: a reduction in differences is possible, but the differences are still unacceptable, and the decision maker should decide whether to reduce the differences or to examine the complete decision-making process. The third case is denoted as questionable because a reduction in differences is impossible, but the differences are acceptable. The fourth case is denoted as wrong: the differences are not acceptable and their reduction is impossible. This step is also quite subjective, and it should be discussed between all participants (stakeholders) included in the process of land consolidation project choice. In this research, a statistical analysis is proposed for analyzing the differences between the ranks of land consolidation projects (cadastral municipalities) and for analyzing the influences of each criterion on the land consolidation project rankings. The model is described in the below text.

Before starting to analyze a certain set of potential choices, it is necessary to separate the common and concrete goals. Common goals should encompass the general intentions for the wider region, while concrete goals, which should be realized in certain land consolidation projects, must be in concordance with common goals. In that sense, we can state that local land consolidation projects are only part of a wider strategy.

Considering this premise, it could be stated that chosen projects already fulfil the common goals and could be concretized. This could explain the chosen criteria for land consolidation project ranking (explained at beginning of this section and shown in Table 2) due to the assumption that the municipality of Bela Crkva already fulfills the common criteria. The chosen criteria regarded locally leads to conclusion that the main goal of land consolidation projects is to regroup and defragment land ownership in the area considered. Consequently, desire is transformed into the goal of regrouping and defragmenting landownership by utilizing consolidation projects. This intention could be considered the ideal case, in the sense that it is the first step in the process of choice, since the desire is properly decomposed and its definition is clear.

A further step considers environment friendship and the accuracy of environments. In this case, we can state that environment is friendliness-orientated, and its assessment is proper. The increase in land ownership value and its benefits regarding the sustainability of agricultural production obtained through land consolidation guarantee long-term stability and increase food security. On the other hand, the chosen aspects (criteria) are relevant since they cover the main question connected to land ownership issues connected to agricultural production.

Aspects’ (criteria) relevance and evaluation checking are very important steps in the decision-making process. Aspects of inadequate relevance could lead to decision-making that differs from the desired goals. Moreover, the inaccuracy of the data utilized could lead to deviation from the optimal ranking.

This situation is described as follows:

$$C_c\subseteq C_R+C_I$$

(1)

where the following definitions are used:

-

$C_c$—set of chosen criteria;

-

$C_R$—set of relevant criteria;

-

$C_I$—set of irrelevant criteria.

It might be stated that the decision maker can never be certain if they have chosen the criteria that only belong to the set of relevant criteria.

The decision maker has been modeled as “absolutely consistent” (Marinković et al., 2024 [21]), which means that every decision maker is modeled via random function for choice of weights for each criteria:

$$w_{ij}=rand\left(f_{ij}\right)$$

(2)

where $w_{ij}$ is the value of certain weights obtained randomly for each criterion and by each decision maker.

The mathematical model for estimating the significance of each criterion and combination of criteria for land consolidation project ranking is based on multidimensional linear regression. The model is described as follows [82]:

$$Y_i={\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_2+\cdots +{\theta }_n{x}_n+{\epsilon }_i; i=1,m$$

(3)

where the following definitions are used:

-

$Y$—dependent variable (rank of land consolidation project);

-

$\theta$—coefficients;

-

$x_j=F_j; j=1,n$—independent variables (values of criteria);

-

${\epsilon }_i$—free term.

The values of coefficients are obtained using the means of the least squares method. In this case, according to Table 2, $n$ = 10 and $m$ = 15, which means that there are only four degrees of freedom in the model of multidimensional linear regression.

3. Results

As explained before, for each method, the final average ranks of land consolidation projects obtained by a hundred decision makers were determined as follows:

$${\overline{r}}_{i,j}={\displaystyle \frac{1}{100}}\sum _{i=1}^{100}{r}_{i,j}$$

(4)

where $r_i$ is the rank obtained by $i$-th decision maker and $j$ is the land consolidation project ($j=1~15$). Formula (4) was utilized for each method applied (AHP, TOPSIS, VIKOR and SAW).

The mean root square deviation for each rank was calculated as follows:

$$m_{r_{i,j}}=\sqrt{{\displaystyle \frac{1}{99}}\sum _{i=1}^{100}{\left(r_{i,j}-{\overline{r}}_{i,j}\right)}^2}$$

(5)

The mean root square deviation of average rank was determined as follows:

$$m_{{\overline{r}}_{i,j}}={\displaystyle \frac{m_{r_{i,j}}}{\sqrt{100}}}={\displaystyle \frac{m_{r_{i,j}}}{10}}$$

(6)

The results of land consolidation project ranking and their standards for each multi-criteria decision-making method are given in Table 2 while their final ranks obtained as the average of all methods and their standards are given in

Table 8. Ranks of land consolidation projects.

	AHP		TOPSIS		VIKOR		SAW		Overall
Project ID	Rank	Standard	Rank	Standard	Rank	Standard	Rank	Standard	Avg	Standard
800317	5.25	1.28	7.2	3.46	6.97	2.69	9.52	2.6	7.23	1.16
800660	5.67	0.53	4.72	1.1	5.05	0.87	5.2	1.07	5.16	0.39
800333	12.73	1.59	13.54	1.63	13.16	1.32	12.61	1.61	13.01	0.42
800643	12.4	0.49	10.87	1.2	11.85	0.64	11.88	0.69	11.75	0.64
800732	13.85	0.52	12.75	1.63	13.77	0.58	13.99	0.5	13.59	0.57
800449	9.85	1.19	9.27	1.8	9.5	1.58	9.86	1.57	9.62	0.29
800678	1.71	0.76	2.12	0.99	1.48	0.67	1.11	0.35	1.61	0.42
800392	9.07	1.74	6.99	1.64	8.5	1.47	9.0	1.29	8.39	0.97
800465	8.06	1.2	8.33	1.92	7.73	1.54	6.45	1.44	7.64	0.86
800473	14.68	0.78	14.43	1.88	14.74	0.8	14.6	1.03	14.61	0.13
800481	1.86	0.73	1.91	0.91	1.78	0.63	2.39	0.67	1.97	0.31
800503	4.12	0.69	4.84	1.71	3.58	0.97	2.77	0.81	3.83	0.87
800708	9.99	1.07	9.31	1.65	8.52	1.55	6.66	1.62	8.62	1.44
800724	2.63	1.03	7.83	2.56	4.4	2.23	4.76	1.8	3.81	0.96
800741	8.13	1.32	10.45	1.94	9.66	1.39	9.21	1.54	9.36	0.97

.

Table 9. Final rank, standards and confidence interval.

Final Ranks
Project ID	Average	Standard	${\overline{\mathit{r}}}_{\mathit{m}\mathit{i}\mathit{n}}$	${\overline{\mathit{r}}}_{\mathit{m}\mathit{a}\mathit{x}}$
800678	1.61	0.42	0.93	2.28
800481	1.93	0.31	1.43	2.43
800724	3.81	0.96	2.28	5.33
800503	3.83	0.87	2.44	5.22
800660	5.16	0.39	4.53	5.79
800317	7.23	1.76	4.43	10.02
800465	7.49	0.86	6.12	8.87
800392	8.39	0.97	6.85	9.93
800708	8.62	1.44	6.33	10.91
800341	9.36	0.97	7.82	10.90
800449	9.62	0.29	9.16	10.08
800643	11.75	0.64	10.73	12.77
800333	13.01	0.42	12.33	13.69
800732	13.59	0.57	12.69	14.49
800473	14.61	0.13	14.40	14.83

presents the influence of each criterion on the rank.

Statistical testing of the hypothesis was carried out to determine if some competing projects are equally ranked in a statistical sense. The statistics for hypothesis testing read as follows:

$$t={\displaystyle \frac{{\overline{r}}_k-{\overline{r}}_l}{\sqrt{\frac{{m_{{\overline{r}}_k}}^2}{100}+\frac{{m_{{\overline{r}}_l}}^2}{100}}}}~t_{f, 1-\alpha };k=1,n;l=1,n;k\ne l$$

(7)

where the following definitions are used:

-

$t$—Student’s statistics;

-

${\overline{r}}_k$—average rank of the $k$^th land consolidation project obtained via one MCDM method ($k=1,n$);

-

${\overline{r}}_l$—average rank of the $l$^th land consolidation project obtained via one MCDM method ($k=1,n$);

-

$t_{f, 1-\alpha }$—Student’s distribution for the degrees of freedom $f$ (in this case, $f=$100) and for the level of significance $\alpha$ (in this case, $\alpha =$0.05)

Considering that

$$t_{\mathrm{99,0.95}}=1.9842$$

it immediately follows that for every $t$ statistic when $t<t_{\mathrm{99,0.95}}=1.9842$, there are no reasons for rejecting hypothesis $H_0$ that state that the compared ranks are equal.

The ranks obtained by each of the hundred decision makers were included in the average rank calculation, and the standard deviation of each rank is given in Table 8. Accordingly, the interval of confidence for the average ranking was obtained via the following formula:

$${\overline{r}}_i\in ({\overline{r}}_i-1.9842\times {\displaystyle \frac{m_{r_{i,j}}}{10}},{\overline{r}}_i+1.9842\times {\displaystyle \frac{m_{r_{i,j}}}{10}})$$

(8)

By analyzing the average ranks obtained by different decision makers and utilizing different methods, it immediately follows that some differences in ranking exist and that different methods resulted in different ranks for each land consolidation project, with the standard deviation of each rank varying within several rank positions. However, considering the standard deviation of the average rank (dividing each standard deviation by 10), it immediately follows that ranks are within one or two positions. This implies that average ranks are determined with a high level of reliability.

Further analysis is based on averaging the ranks of land consolidation projects obtained via different MCDM methods. These data are given in Table 9.

By analyzing the average ranks obtained via different methods, it is possible to state that the average ranks of land consolidation projects have relatively small standard deviations and that the standard deviation of the average rank should be obtained via the following formula:

$$m_{{\overline{r}}_{i,j}}={\displaystyle \frac{m_{r_{i,j}}}{\sqrt{4}}}={\displaystyle \frac{m_{r_{i,j}}}{2}}$$

(9)

The interval of confidence for average ranks then reads as follows:

$${\overline{r}}_i\in ({\overline{r}}_i-3.1824\times {\displaystyle \frac{m_{r_i}}{2}}={\overline{r}}_{min},{\overline{r}}_i+3.1824\times {\displaystyle \frac{m_{r_i}}{2}}={\overline{r}}_{max})$$

(10)

However, considering the standard deviation of the average rank (dividing each standard deviation by 2), it immediately follows that ranks are mostly within one or two positions, except for some which exceed this interval, including land consolidation project 800708, which exceeds more than four positions (its interval span is 4.58). This implies that average ranks are determined based on the high level of reliability, respecting the preferences of multiple decision makers and the results obtained via four MCDM methods.

The wider quantile of Student’s distribution caused by three degrees of freedom (due to only four MCDM methods being applied) is compensated via the reduction in standard deviation by ten times (a standard deviation of average rank value for each land consolidation project).

Further research relates to the influence of each criterion on the rank of land consolidation project. Applying the multidimensional linear regression (MDLR) given by Formula (2), it is possible to determine the contribution of each criterion to the rank. The results of MDLR showed that a high level of rank explanation by the chosen criteria was determined via R² at a level of 0.82; this result justifies the applied criteria but implies that there is room for model improvement. The results for each criterion (given in

Table 10. The influence of each criterion obtained via MDLR.

Criterion	${\mathit{\theta }}_{\mathit{j}}$
f1	−0.17
f2	−50.17
f3	−4.30
f4	14.70
f5	−1.27
f6	−0.75
f7	−0.02
f8	0.14
f9	0.75
f10	7.65

) require further discussion.

At first look at the obtained results, it could be stated that the criteria f₂ (average surface area of cadastral parcels for each land consolidation area), f₃ (average number of cadastral parcels per participant for each land consolidation area), f₄ (average surface area of the participants’ property for each land consolidation area) and f₁₀ (estimation of profitability of agricultural production due to land consolidation in the adopted period) have the biggest influence on the land consolidation project ranking. Moreover, it should be noted that criteria f₂ and f₃ decrease the rank of a land consolidation project, while the criterions f₄ and f₁₀ increase the rank of a land consolidation project when their initial values increase. It is necessary to consider that their initial values do not vary significantly but could cause ranking sensitivity if the data for those criteria are not accurate. The negative value of ${\theta }_j$ indicates that the ranks of certain land consolidation projects decrease when the initial value is greater, and in contrast, the rank of the land consolidation project increases when its value is smaller. Consequently, when value ${\theta }_j$ is negative, its smaller (in the absolute sense) value increases the probability of a land consolidation project being chosen compared to a land consolidation project with a greater value (in the absolute sense).

4. Discussion

The proposed method applied to land consolidation project ranking for the municipality of Bela Crkva resulted in the final ranks of projects and gave a basis for further analysis. It could be stated that the average rank obtained via each method, as well as the final ranking, have relatively small standard deviations. This fact implies that there are relatively small deviations between different decision makers and that they could be actively included in decision-making in land consolidation project ranking. Furthermore, the more decision makers are involved in the land consolidation project ranking process, the more objectivity can be expected.

Considering the efficiency of algorithms used for applying the hybrid MCDM models, a model’s increased employment should not increase the costs of the decision-making process. This argument could be used to enable further investigation by including larger hybrid models (in broader sense) and variations in criteria regarding the different sets of criteria applied.

Further investigation should encompass different MCDM models and increase the number of decision makers participating in the decision-making process, considering the weights of their preferences and the sensitivity analysis of each ranking obtained. Moreover, the influence of accuracy of the initial data of criteria should be analyzed in detail. Those noticed possibilities should be included in further investigation of proposed model, including unified decision-making for ranking consolidation projects for different regions.

The R² value at the level of 0.82 implies that there are some possibilities for model improvement by including other criteria and/or excluding some of the applied ones. For example, in the study of Tomić [80], the three MCDM methods and seven criteria were applied, and the conclusion was that the ranking results were more dependent on the indicator weights than the choice of MCDM method. In this research, 4 MCDM methods and 10 criteria were applied, and the results showed that with the increases in the number of MCDM methods and decision makers used, the ranking tended to gravitate towards a certain value (the standard deviation of the ranks decreased).

Analyzing the confidence interval is also important if the ranks of land consolidation projects are statistically equal. According to the analyzed references and the findings of the research conducted in this domain, we can state that efforts in this direction should be continued. This research showed that even though significant efforts have been made, there is still room for further investigation. The analysis of decision makers’ preferences and the accuracy of the criteria’s influence should be explored in cases with a greater number of competing land consolidation projects and, if possible, with real decision makers or landowners and officials. This could be beneficial because it is possible that specific social groups might have similar preferences and, consequently, could cause some biases in mathematical models. This could be a direction for further investigation in the domain of land consolidation project ranking.

5. Conclusions

The proposed multi-criteria decision-making method based on the use of multiple decision makers and multiple MCDM methods provides the possibility of dispersing preferences in decision-making and increasing the objectivity of land consolidation project ranking. The proposed method based on the averaging of land consolidation project rankings and the determination of their standard deviations provides the possibility of estimating the rank of the land consolidation project in a broader sense and in a more objective way. Utilizing multidimensional linear regression provides the possibility of identifying the most influential factor influencing land consolidation project rankings. In this case, the coefficient R² was obtained at the level of 0.82, which means, on the one hand, that the chosen model is properly formed, while on the other hand, there is still room for further research. Further development of the proposed model should consider the sensitivity analysis of ranks regarding the accuracy of the initial data for each criterion and the adequacy of the chosen set of criteria.