Analysis of Carbon Storage Changes in the Chengdu–Chongqing Region Based on the PLUS-InVEST-MGWR Model
Abstract
1. Introduction
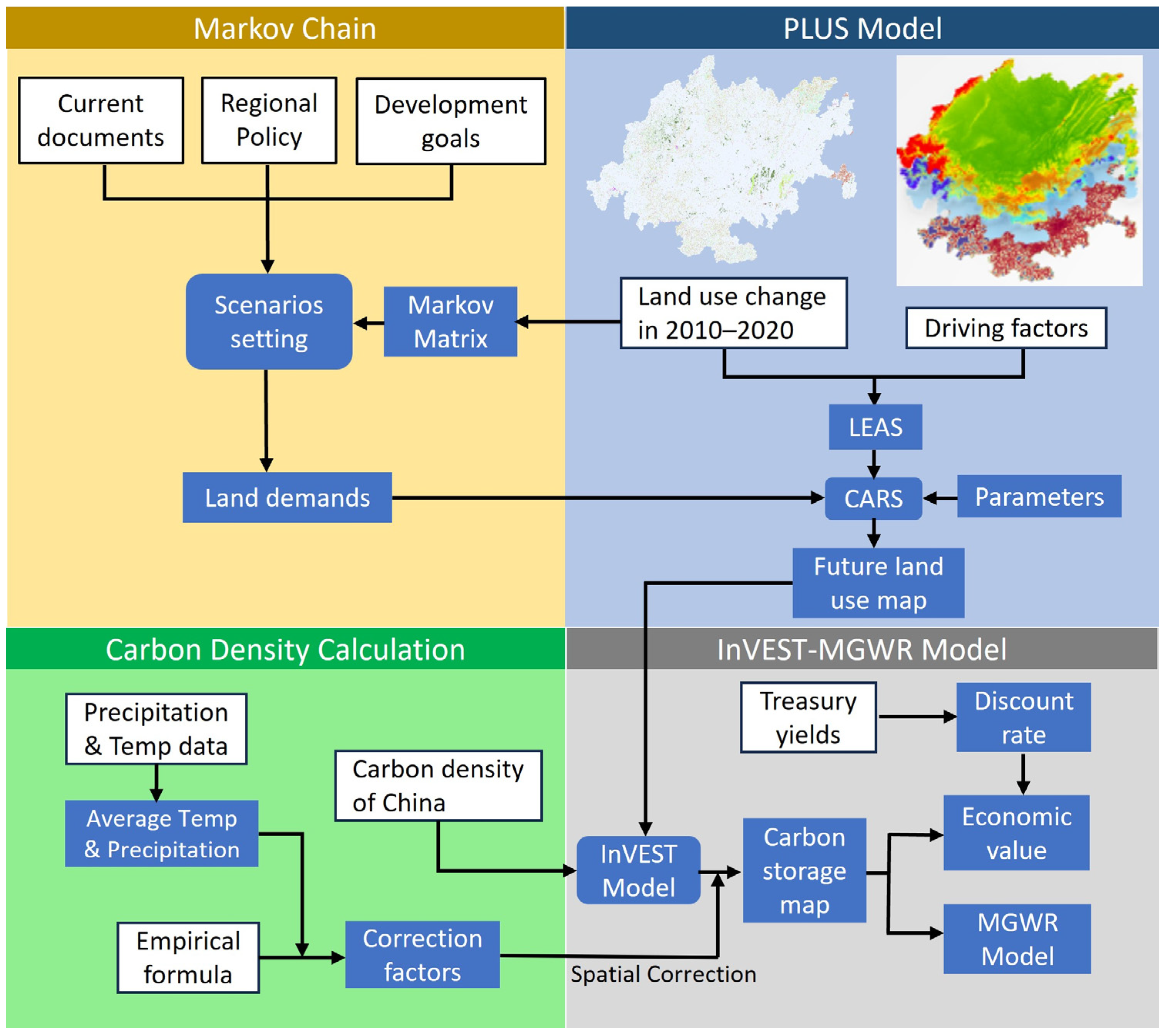
2. Materials and Methods
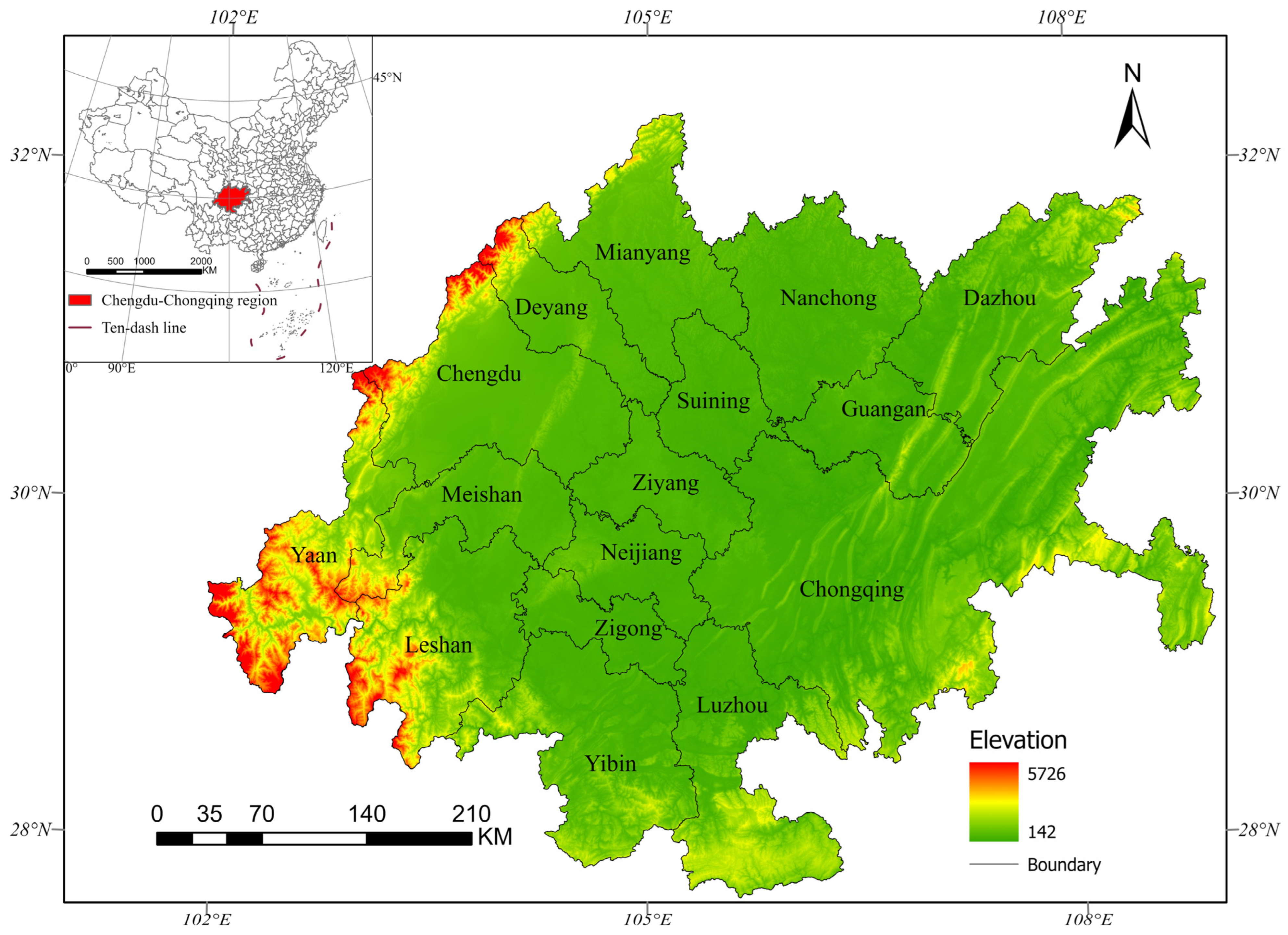
2.1. Study Area
2.2. Data Sources and Processing
2.3. Methods
2.3.1. PLUS Model
2.3.2. Markov Chain
2.3.3. Scenarios and Parameters
- (1)
- Land demand
- (2)
- Transition matrix
- (3)
- Neighborhood weights
2.3.4. Kappa Test
2.3.5. Carbon Storage Assessment
2.3.6. Assessment of Economic Value of Carbon Storage
2.3.7. Multiscale Geographically Weighted Regression
3. Results
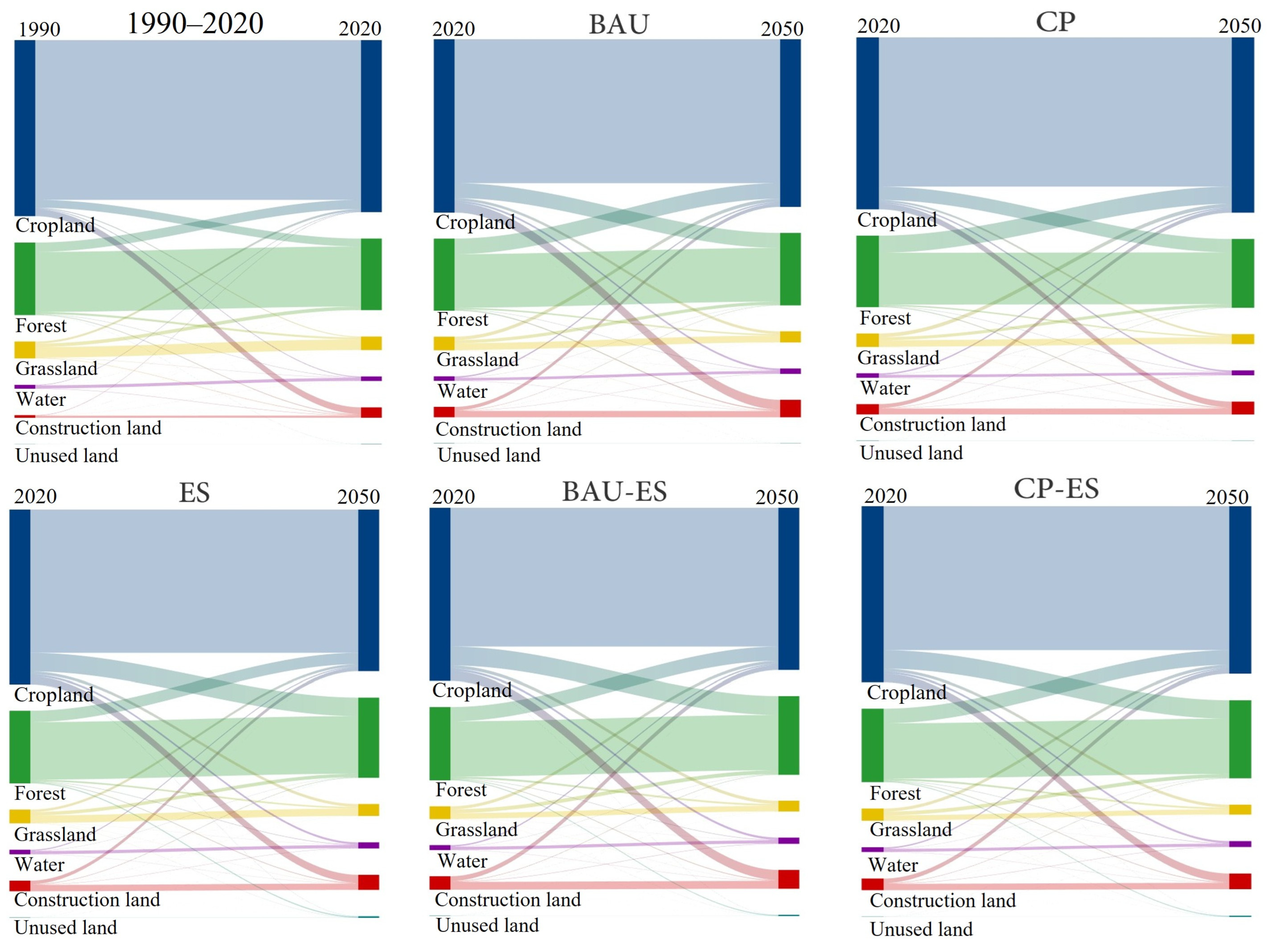
3.1. Multi-Scenario Simulation Results
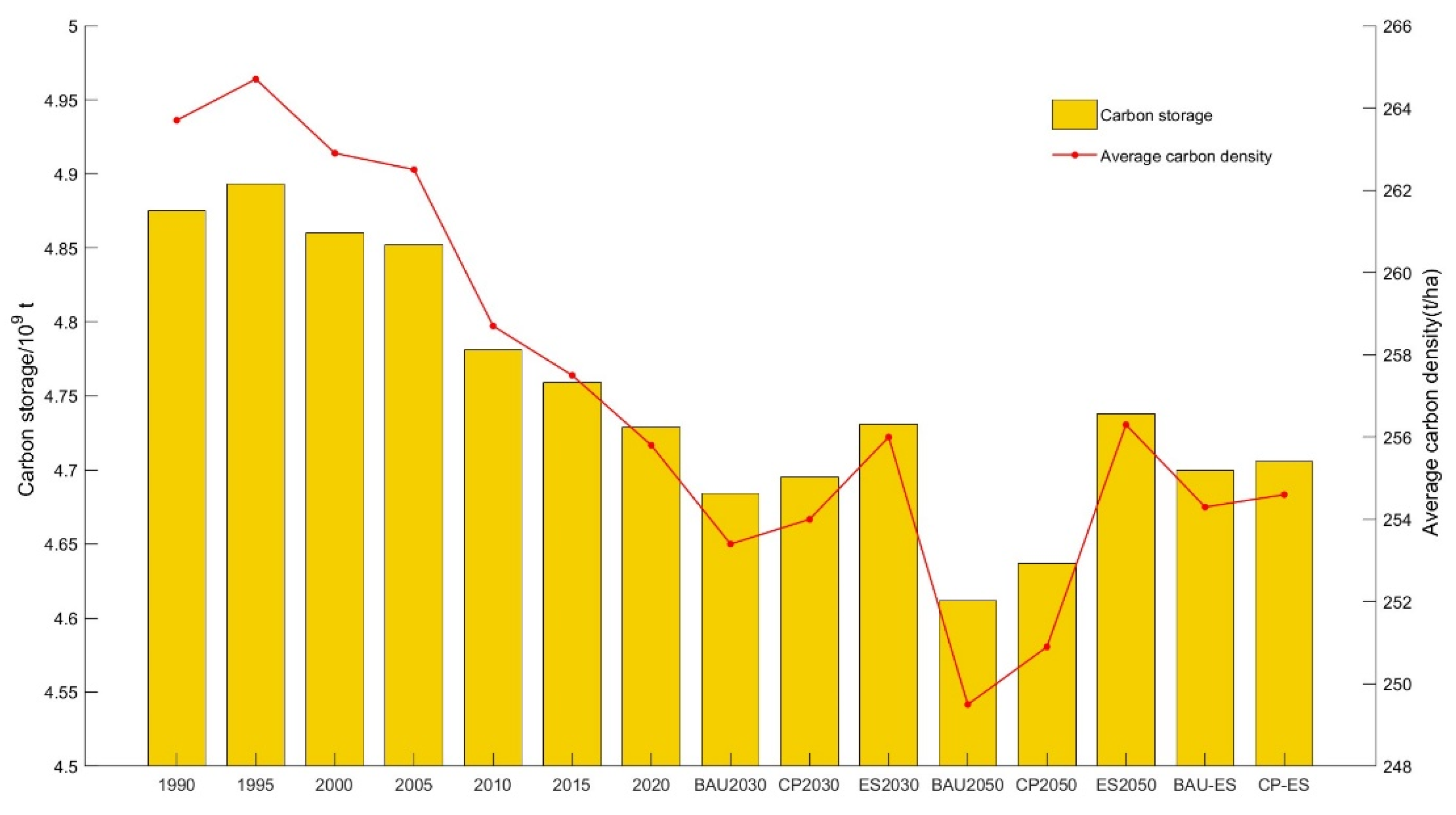
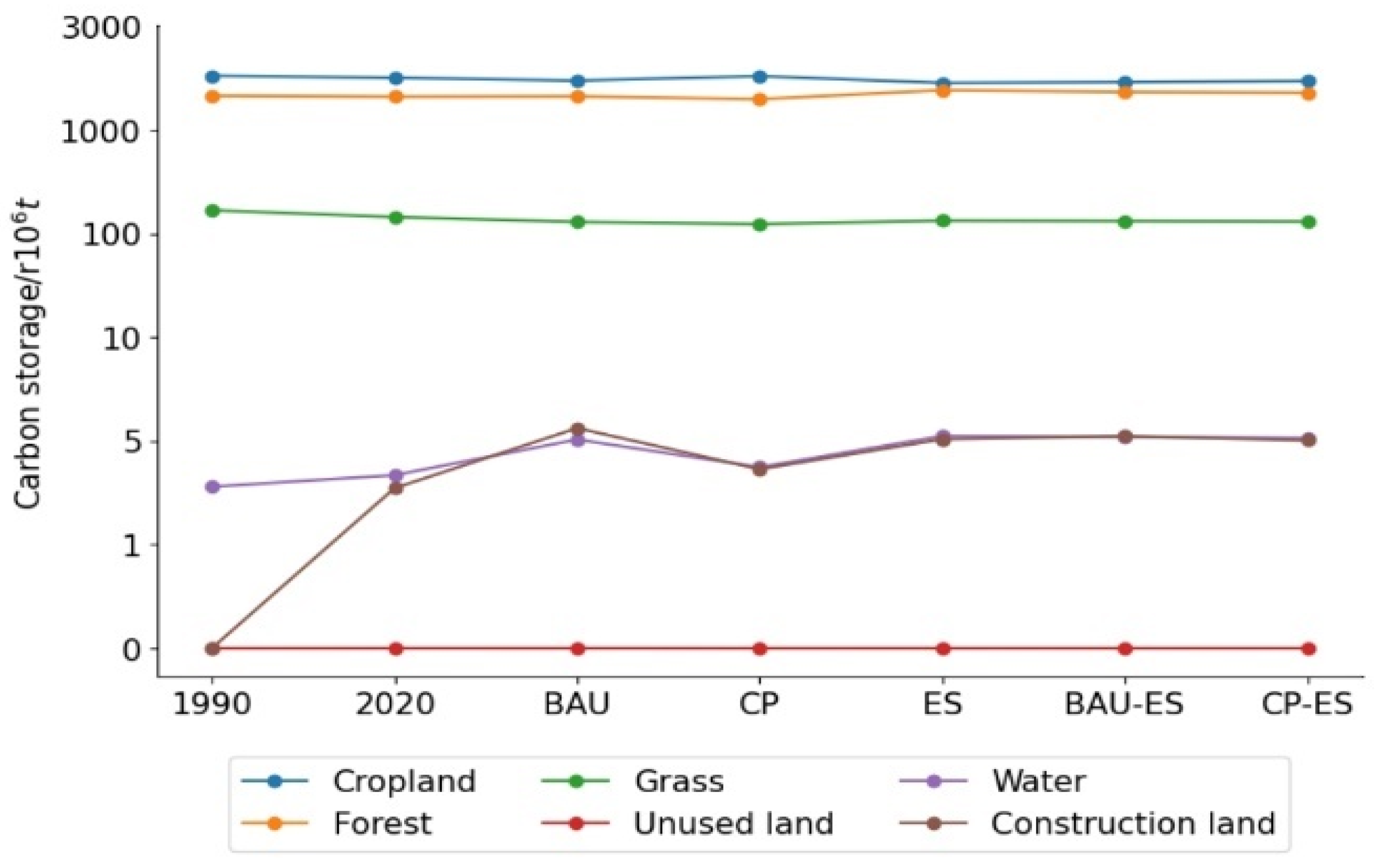
3.2. Changes in Carbon Storage
3.3. Impacts of Urban Expansion on Carbon Storage
3.4. Economic Value of Carbon Storage
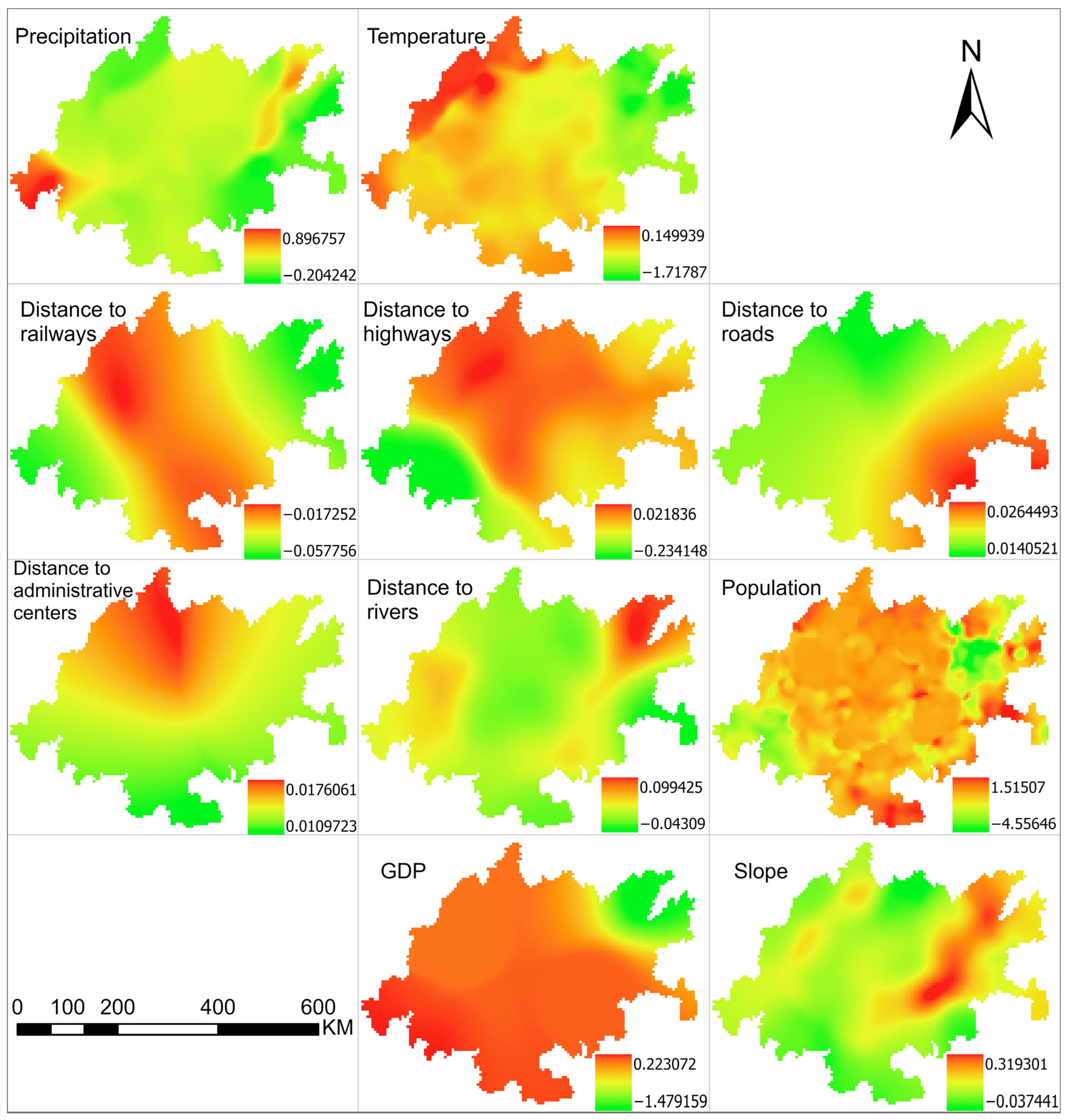
3.5. Analysis of MGWR
4. Discussion
4.1. Correlation Between Factors and Carbon Storage
4.2. The Critical Role of Spatial Corrections to Heterogeneity
4.3. Policy Recommendations
4.4. Limitations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SCC | Social cost of carbon |
| EVCS | Economic value of carbon storage |
| LUCC | Land Use and Land Cover Change |
| IGBP | International Geosphere-Biosphere Program |
| IHDP | International Human Dimensions Program on Global Environmental Change |
| RF | Random Forest |
| MGWR | Multiscale geographically weighted regression |
| LEAS | Land Expansion Analysis Strategy |
| CA | Cellular automata |
| CARS | Multiple Random Seeds |
| AICc | Akaike Information Criterion with correction |
| BAU | Business as usual |
| CP | Cropland protection |
| ES | Ecological security |
| OA | Overall accuracy |
| GWR | Geographically weighted regression |
| OLS | Ordinary least squares |
| CR | Contribution rate of urban to carbon loss |
| ENP | Effective Number of Parameters |
| DoD | Degree of Spatial Dependency |
References
- Xu, W.; Song, J.; Long, Y.; Mao, R.; Tang, B.; Li, B. Analysis and simulation of the driving mechanism and ecological effects of land cover change in the Weihe River basin, China. J. Environ. Manag. 2023, 344, 118320. [Google Scholar] [CrossRef]
- Li, K.; Wang, X.; Zhao, F.; An, B.; Li, P. Land use modeling and carbon storage projections of the Bosten Lake Basin in China from 1990 to 2050 across multiple scenarios. Nature 2024, 14, 27136. [Google Scholar] [CrossRef]
- Xu, L.; Li, Y.; Ye, W.; Zhang, X. Terrestrial organic carbon storage modes based on relationship between soil and lake carbon, China. J. Environ. Manag. 2019, 250, 109483. [Google Scholar] [CrossRef]
- Piao, S.; He, Y.; Wang, X.; Chen, F. Estimation of China’s terrestrial ecosystem carbon sink: Methods, progress and prospects. Sci. China Earth Sci. 2022, 65, 641–651. [Google Scholar] [CrossRef]
- United Nations. Millennium Ecosystem Assessment: Ecosystems and Human Well-Being: Synthesis; Island Press: Washington, DC, USA, 2005. [Google Scholar]
- Wang, R.Y.; Cai, H.A.; Chen, L.K.; Li, T.H. Spatiotemporal evolution and multi-scenario prediction of carbon storage in the GBA based on PLUS-InVEST models. Sustainability 2023, 15, 8421. [Google Scholar] [CrossRef]
- Chu, X.; Zhan, J.Y.; Li, Z.H.; Zhang, F.; Qi, W. Assessment on forest carbon sequestration in the three-north Shelterbelt Program region, China. J. Clean. Prod. 2019, 215, 382–389. [Google Scholar] [CrossRef]
- Lahiji, R.N.; Dinan, N.M.; Liaghati, H.; Ghaffarzadeh, H.; Vafaeinejad, A. Scenario-based estimation of catchment carbon storage: Linking multi-objective land allocation with InVEST model in a mixed agriculture-forest landscape. Front. Earth Sci. 2020, 14, 637–646. [Google Scholar] [CrossRef]
- Jiang, W.; Deng, Y.; Tang, Z.; Lei, X.; Chen, Z. Modelling the potential impacts of urban ecosystem changes on carbon storage under different scenarios by linking the CLUE-S and the InVEST models. Ecol. Model. 2017, 345, 30–40. [Google Scholar] [CrossRef]
- Wu, Q.; Wang, L.; Wang, T.; Ruan, Z.; Du, P. Spatial-temporal evolution analysis of multi-scenario land use and carbon storage based on PLUS-InVEST model: A case study in Dalian, China. Ecol. Indic. 2024, 166, 112448. [Google Scholar] [CrossRef]
- Kalnay, E.; Cai, M. Impact of urbanization and land-use change on climate. Nature 2003, 423, 528. [Google Scholar] [CrossRef] [PubMed]
- Foley, J.A.; DeFries, R.; Asner, G.P.; Barford, C.; Bonan, G.; Carpenter, S.R.; Chapin, F.S.; Coe, M.T.; Daily, G.C.; Gibbs, H.K.; et al. Global consequences of land use. Science 2005, 309, 570–574. [Google Scholar] [CrossRef]
- Nie, Q.; Wu, G.; Li, L.; Man, W.; Ma, J.; Bao, Z.; Luo, L.; Li, H. Exploring scaling differences and spatial heterogeneity in drivers of carbon storage changes: A comprehensive geographic analysis framework. Ecol. Indic. 2024, 165, 112193. [Google Scholar] [CrossRef]
- Lai, L.; Huang, X.; Yang, H.; Chuai, X.; Zhang, M.; Zhong, T.; Chen, Z.; Chen, Y.; Wang, X.; Thompson, J.R.; et al. Carbon emissions from land-use change and management in China between 1990 and 2010. Sci. Adv. 2016, 2, e1601063. [Google Scholar] [CrossRef]
- Nie, X.; Lu, B.; Chen, Z.; Yang, Y.; Chen, S.; Chen, Z.; Wang, H. Increase or decrease? Integrating the CLUMondo and InVEST models to assess the impact of the implementation of the Major Function Oriented Zone planning on carbon storage. Ecol. Indic. 2020, 118, 106708. [Google Scholar] [CrossRef]
- Hu, Y.; Batunacun; Zhen, L.; Zhuang, D. Assessment of land-use and land-cover change in Guangxi, China. Nature 2019, 9, 2189. [Google Scholar] [CrossRef]
- Ling, M.; Feng, Z.; Chen, Z.; Lan, Y.; Li, X.; You, H.; Han, X.; Chen, J. Evaluation of driving effects of carbon storage change in the source of the Yellow River: A perspective with CMIP6 future development scenarios. Ecol. Inform. 2024, 83, 102790. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, Z.; Chen, Y.; Wei, W. Evaluating the corresponding relationship between the characteristics of resource utilization and the level of urbanization: A case study in Chengdu-Chongqing Economic Circle, China. Environ. Sci. Pollut. Res. 2022, 29, 55816–55829. [Google Scholar] [CrossRef]
- National Development and Reform Commission; Ministry of Construction. Methods and Parameters for Economic Evaluation of Construction Projects, 3rd ed.; China Planning Press: Beijing, China, 2006.
- Sang, L.; Zhang, C.; Yang, J.; Zhu, D.; Yun, W. Simulation of land use spatial pattern of towns and villages based on CA-Markov model. Math. Comput. Model. 2011, 54, 938–943. [Google Scholar] [CrossRef]
- Koomen, E.; Stillwell, J.; Bakema, A.; Scholten, H.J. (Eds.) Modelling land-use change. In The GeoJournal Library; Springer: Dordrecht, The Netherlands, 2007; Volume 90, pp. 1–22. [Google Scholar] [CrossRef]
- Gollnow, F.; Göpel, J.; Hissa, L.D.V.; Schaldach, R.; Lakes, T. Scenarios of land-use change in a deforestation corridor in the Brazilian Amazon: Combining two scales of analysis. Reg. Environ. Change 2018, 18, 143–159. [Google Scholar] [CrossRef]
- Baker, W.L. A review of models of landscape change. Landsc. Ecol. 1989, 2, 111–133. [Google Scholar] [CrossRef]
- Yang, Y.; Lu, Z.; Yang, M.; Yan, Y.; Wei, Y. Impact of land use changes on uncertainty in ecosystem services under different future scenarios: A case study of Zhang-Cheng area, China. J. Clean. Prod. 2024, 434, 139881. [Google Scholar] [CrossRef]
- Guan, D.; Zhao, Z.; Tan, J. Dynamic simulation of land use change based on logistic-CA-Markov and WLC-CA-Markov models: A case study in three gorges reservoir area of Chongqing, China. Environ. Sci. Pollut. Res. 2019, 26, 20669–20688. [Google Scholar] [CrossRef]
- Yang, X.; Chen, R.; Zheng, X.Q. Simulating land use change by integrating ANN-CA model and landscape pattern indices. Geomat. Nat. Hazards Risk 2015, 7, 918–932. [Google Scholar] [CrossRef]
- Verburg, P.H.; Soepboer, W.; Veldkamp, A.; Limpiada, R.; Espaldon, V.; Mastura, S.S.A. Modeling the spatial dynamics of regional land use: The CLUE-S model. Environ. Manag. 2002, 30, 391–405. [Google Scholar] [CrossRef] [PubMed]
- Verburg, P.H.; Kok, K.; Pontius, R.G.; Veldkamp, A. Modeling land-use and land-cover change. In Land-Use and Land-Cover Change: Local Processes and Global Impacts; Lambin, E.F., Geist, H., Eds.; Springer: Berlin/Heidelberg, Germany, 2006; pp. 117–135. [Google Scholar] [CrossRef]
- Verburg, P.H.; Overmars, K.P. Combining top-down and bottom-up dynamics in land use modeling: Exploring the future of abandoned farmlands in Europe with the Dyna-CLUE model. Landsc. Ecol. 2009, 24, 1167–1181. [Google Scholar] [CrossRef]
- Van Asselen, S.; Verburg, P.H. Land cover change or land-use intensification: Simulating land system change with a global-scale land change model. Glob. Change Biol. 2013, 19, 3648–3667. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Liang, X.; Li, X.; Xu, X.; Ou, J.; Chen, Y.; Li, S.; Wang, S.; Pei, F. A future land use simulation model (FLUS) for simulating multiple land use scenarios by coupling human and natural effects. Landsc. Urban Plan. 2017, 168, 94–116. [Google Scholar] [CrossRef]
- Liang, X.; Guan, Q.; Clarke, K.C.; Liu, S.; Wang, B.; Yao, Y. Understanding the drivers of sustainable land expansion using a patch-generating land use simulation (PLUS) model: A case study in Wuhan, China. Comput. Environ. Urban Syst. 2021, 85, 101569. [Google Scholar] [CrossRef]
- Li, C.; Wu, Y.; Gao, B.; Zheng, K.; Wu, Y.; Li, C. Multi-scenario simulation of ecosystem service value for optimization of land use in the Sichuan-Yunnan ecological barrier, China. Ecol. Indic. 2021, 132, 108328. [Google Scholar] [CrossRef]
- Zhai, H.; Lv, C.; Liu, W.; Yang, C.; Fan, D.; Wang, Z.; Guan, Q. Understanding spatio-temporal patterns of land use/land cover change under urbanization in Wuhan, China, 2000–2019. Remote Sens. 2021, 13, 3331. [Google Scholar] [CrossRef]
- Barau, A.; Maconachie, R.; Ludin, A.; Abdulhamid, A. Urban morphology dynamics and environmental change in Kano, Nigeria. Land Use Policy 2015, 42, 307–317. [Google Scholar] [CrossRef]
- Cairns, G.; Goodwin, P.; Wright, G. A decision-analysis-based framework for analysing stakeholder behaviour in scenario planning. Eur. J. Oper. Res. 2016, 249, 1050–1062. [Google Scholar] [CrossRef]
- Dorning, M.A.; Koch, J.; Shoemaker, D.A.; Meentemeyer, R.K. Simulating urbanization scenarios reveals tradeoffs between conservation planning strategies. Landsc. Urban Plan. 2015, 136, 28–39. [Google Scholar] [CrossRef]
- Wu, J. Urban sustainability: An inevitable goal of landscape research. Landsc. Ecol. 2010, 25, 1–4. [Google Scholar] [CrossRef]
- Li, C.; Li, J.; Wu, J. Quantifying the speed, growth modes, and landscape pattern changes of urbanization: A hierarchical patch dynamics approach. Landsc. Ecol. 2013, 28, 1875–1888. [Google Scholar] [CrossRef]
- Li, J.; Li, C.; Zhu, F.; Song, C.; Wu, J. Spatiotemporal pattern of urbanization in Shanghai, China between 1989 and 2005. Landsc. Ecol. 2013, 28, 1545–1565. [Google Scholar] [CrossRef]
- Hang, J.; Sandberg, M.; Li, Y. Effect of urban morphology on wind condition in idealized city models. Atmos. Environ. 2009, 43, 869–878. [Google Scholar] [CrossRef]
- Luo, X.; Le, F.; Zhang, Y.; Zhang, H.; Zhai, J.; Luo, Y. Multi-scenario analysis and optimization strategy of ecological security pattern in the Weihe river basin. J. Environ. Manag. 2024, 66, 121813. [Google Scholar] [CrossRef]
- Chen, L.; Yao, Y.; Xiang, K.; Dai, X.; Li, W.; Dai, H.; Lu, K.; Li, W.; Lu, H.; Zhang, Y.; et al. Spatial-temporal pattern of ecosystem services and sustainable development in representative mountainous cities: A case study of Chengdu-Chongqing Urban Agglomeration. J. Environ. Manag. 2024, 368, 122261. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Li, H.; Qian, C. Analysis of the implementation effects of ecological restoration projects based on carbon storage and eco-environmental quality: A case study of the Yellow River Delta, China. J. Environ. Manag. 2023, 340, 117929. [Google Scholar] [CrossRef] [PubMed]
- Ye, X.; Chuai, X. Carbon sinks/sources’ spatiotemporal evolution in China and its response to built-up land expansion. J. Environ. Manag. 2022, 321, 115863. [Google Scholar] [CrossRef]
- Mendoza-Ponce, A.; Corona-Núñez, R.; Kraxner, F.; Leduc, S.; Patrizio, P. Identifying effects of land use cover changes and climate change on terrestrial ecosystems and carbon stocks in Mexico. Glob. Environ. Change 2018, 53, 12–23. [Google Scholar] [CrossRef]
- Peng, Y.; Cheng, W.; Xu, X.; Song, H. Analysis and prediction of the spatiotemporal characteristics of land-use ecological risk and carbon storage in Wuhan metropolitan area. Ecol. Indic. 2024, 158, 111432. [Google Scholar] [CrossRef]
- Xiang, H.; Shen, Z.; Tan, L.; Gao, C.; Wu, G.; Wang, J. Community identification and carbon storage monitoring of Heritiera littoralis with UAV hyperspectral imaging. Ecol. Indic. 2024, 167, 112653. [Google Scholar] [CrossRef]
- Song, M.; Huang, Z.; Chen, C.; Li, X.; Mao, F.; Huang, L.; Zhao, Y.; Lv, L.; Yu, J.; Du, H. Multi-scale geographically weighted regression estimation of carbon storage on coniferous forests considering residual distribution using remote sensing data. Ecol. Indic. 2024, 166, 112495. [Google Scholar] [CrossRef]
- Qiu, W.; Guo, R.; Jia, D.; Wu, M.; Wang, Z.; Zhang, L.; Jiang, L.; Li, M.; Hu, X. Spatio-temporal dynamics of global forest-urban carbon balance and its driving patterns during 1985–2020. J. Clean. Prod. 2025, 519, 145060. [Google Scholar] [CrossRef]
- Yang, S.; Peng, S.; Li, X.; Wei, X.; Pan, Y.; Jiao, Y. Spatial heterogeneity and interacting intensity of drivers for trade-offs and synergies between carbon sequestration and biodiversity. Glob. Ecol. Conserv. 2024, 56, e03256. [Google Scholar] [CrossRef]
- Luo, D.; Zhou, Z.; Zhang, L.; Chen, Q.; Huang, D.; Feng, Q.; Wu, T.; Wu, L. Evolution and driver analysis of forest carbon stocks in karst mountainous areas of southwest China in the context of rocky desertification management. CATENA 2024, 246, 108335. [Google Scholar] [CrossRef]
- Ji, W.; Wang, Z.; Zhang, H.; Zhang, B.; Yang, F.; Yu, Z.; Li, H.; He, M.; Lv, H.; Feng, Z. Carbon storage change, driving mechanism, and scenario prediction in Beijing-Tianjin-Hebei region for regional carbon neutral target: From history to future. Sci. Total Environ. 2025, 993, 180028. [Google Scholar] [CrossRef]
- Lai, J.; Qi, S.; Chen, J.; Guo, J.; Wu, H.; Chen, Y. Exploring the spatiotemporal variation of carbon storage on Hainan Island and its driving factors: Insights from InVEST, FLUS models, and machine learning. Ecol. Indic. 2025, 172, 113236. [Google Scholar] [CrossRef]
- Tang, J.; Peng, W. Spatiotemporal dynamics and influencing factors of land carbon stock in Chengdu Plain using an integrated model. Sci. Rep. 2025, 15, 11248. [Google Scholar] [CrossRef]
- Jia, X.; Han, H.; Feng, Y.; Song, P.; He, R.; Liu, Y.; Wang, P.; Zhang, K.; Du, C. Shidong Ge, Guohang Tian, Scale-dependent and driving relationships between spatial features and carbon storage and sequestration in an urban park of Zhengzhou, China. Sci. Total Environ. 2023, 894, 164916. [Google Scholar] [CrossRef]
- Wei, Y.; Zhou, P.; Zhang, L.; Zhang, Y. Spatio-temporal evolution analysis of land use change and landscape ecological risks in rapidly urbanizing areas based on Multi-Situation simulation—A case study of Chengdu Plain. Ecol. Indic. 2024, 166, 112245. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, L.; Wang, J.; Dong, G.; Wei, Y. Quantitative analysis of NDVI driving factors based on the geographical detector model in the Chengdu-Chongqing region, China. Ecol. Indic. 2023, 155, 110978. [Google Scholar] [CrossRef]
- Wei, Y.; Li, Y.; Wang, S.; Wang, J.; Zhu, Y. Research on the Spatial Expansion Characteristics and Industrial and Policy Driving Forces of Chengdu–Chongqing Urban Agglomeration Based on NPP-VIIRS Night Light Remote Sensing Data. Sustainability 2023, 15, 2188. [Google Scholar] [CrossRef]
- Ding, Y.X.; Peng, S.Z. Spatiotemporal trends and attribution of drought across China from 1901–2100. Sustainability 2020, 12, 477. [Google Scholar] [CrossRef]
- Xiao, J.; Dai, J.; Fang, X.; Li, L.; Chen, G. Simulation of ecosystem service value scene in Xuzhou city based on PLUS model. Land Sci. China 2024, 38, 125–134. [Google Scholar]
- Yang, Y.; Yang, M.; Zhao, B.; Lu, Z.; Sun, X.; Zhang, Z. Spatially explicit carbon emissions from land use change: Dynamics and scenario simulation in the Beijing-Tianjin-Hebei urban agglomeration. Land Use Policy 2025, 150, 107473. [Google Scholar] [CrossRef]
- Fischer, G.; Sun, L. Model based analysis of future land-use development in China. Agric. Ecosyst. Environ. 2001, 85, 163–176. [Google Scholar] [CrossRef]
- López, E.; Bocco, G.; Mendoza, M.; Duhau, E. Predicting land-cover and land-use change in the urban fringe: A case in Morelia city, Mexico. Landsc. Urban Plan. 2001, 55, 271–285. [Google Scholar] [CrossRef]
- Masetti, G.; Robol, L. Computing performability measures in Markov chains by means of matrix functions. J. Comput. Appl. Math. 2020, 368, 112534. [Google Scholar] [CrossRef]
- Guan, D.; Li, H.; Inohae, T.; Su, W.; Nagaie, T.; Hokao, K. Modeling urban land use change by the integration of cellular automaton and Markov model. Ecol. Model. 2011, 222, 3761–3772. [Google Scholar] [CrossRef]
- Myint, S.W.; Wang, L. Multicriteria decision approach for land use land cover change using Markov chain analysis and a cellular automata approach. Can. J. Remote Sens. 2006, 32, 390–404. [Google Scholar] [CrossRef]
- Jenerette, G.D.; Wu, J. Analysis and simulation of land-use change in the central Arizona–Phoenix region, USA. Landsc. Ecol. 2001, 16, 611–626. [Google Scholar] [CrossRef]
- Su, D.; Cao, Y.; Fang, X.; Wang, J.; Cao, Y. Regional integration, agricultural production, and their heterogeneous interaction in the classic urban agglomeration of China. J. Clean. Prod. 2024, 464, 142806. [Google Scholar] [CrossRef]
- Yang, Y.; Bao, W.; Liu, Y. Scenario simulation of land system change in the Beijing-Tianjin-Hebei region. Land Use Policy 2020, 96, 104677. [Google Scholar] [CrossRef]
- Gong, J.; Hu, Z.; Chen, W.; Liu, Y.; Wang, J. Urban expansion dynamics and modes in metropolitan Guangzhou, China. Land Use Policy 2018, 72, 100–109. [Google Scholar] [CrossRef]
- He, J.; Li, Z.; Zhang, X.; Wang, H.; Dong, W.; Du, E.; Chang, S.; Ou, X.; Guo, S.; Tian, Z.; et al. Towards carbon neutrality: A study on China’s long-term low-carbon transition pathways and strategies. Environ. Sci. Ecotechnology 2022, 9, 100134. [Google Scholar] [CrossRef] [PubMed]
- Guo, W.; Teng, Y.; Yan, Y.; Zhao, C.; Zhang, W.; Ji, X. Simulation of land use and carbon storage evolution in multi-scenario: A case study in Beijing-Tianjin-Hebei urban agglomeration, China. Sustainability 2022, 14, 13436. [Google Scholar] [CrossRef]
- Cohen, J. A Coefficient of Agreement for Nominal Scales. Educ. Psychol. Meas. 1960, 20, 37–46. [Google Scholar] [CrossRef]
- Foody, G.M. Status of land cover accuracy assessment. Remote Sens. Environ. 2002, 80, 185–201. [Google Scholar] [CrossRef]
- Wilkinson, G.G. Results and implications of a study of fifteen years of satellite image classification experiments. IEEE Trans. Geosci. Remote Sens. 2005, 43, 433–440. [Google Scholar] [CrossRef]
- Monserud, R.A.; Leemans, R. Comparing global vegetation maps with the Kappa statistic. Ecol. Model. 1992, 62, 275–293. [Google Scholar] [CrossRef]
- Hagen-Zanker, A.; Lajoie, G. Neutral models of landscape change as benchmarks in the assessment of model performance. Landsc. Urban Plan. 2008, 86, 284–296. [Google Scholar] [CrossRef]
- Wang, Z.; Zeng, J.; Chen, W. Impact of urban expansion on carbon storage under multi-scenario simulations in Wuhan, China. Environ. Sci. Pollut. Res. 2022, 29, 45507–45526. [Google Scholar] [CrossRef]
- van Vliet, J.; Bregt, A.K.; Hagen-Zanker, A. Revisiting Kappa to account for change in the accuracy assessment of land-use change models. Ecol. Model. 2011, 222, 1367–1375. [Google Scholar] [CrossRef]
- Landis, J.R.; Koch, G.G. The Measurement of Observer Agreement for Categorical Data. Biometrics 1977, 33, 159–174. [Google Scholar] [CrossRef] [PubMed]
- McHugh, M.L. Interrater reliability: The kappa statistic. Biochem. Medica 2012, 22, 276–282. [Google Scholar] [CrossRef]
- Chuai, X.; Huang, X.; Lai, L.; Wang, W.; Peng, J.; Zhao, R. Land use structure optimization based on carbon storage in several regional terrestrial ecosystems across China. Environ. Sci. Policy 2013, 25, 50–61. [Google Scholar] [CrossRef]
- Fu, Q.; Xu, L.; Zheng, H.; Chen, J. Spatiotemporal dynamics of carbon storage in response to urbanization: A case study in the Su-Xi-Chang Region, China. Processes 2019, 7, 836. [Google Scholar] [CrossRef]
- Raich, J.; Nadelhoffer, K. Belowground Carbon Allocation in Forest Ecosystems: Global Trends. Ecology 1989, 70, 1346–1354. [Google Scholar] [CrossRef]
- Alam, S.A.; Starr, M.; Clark, B.J.F. Tree biomass and soil organic carbon densities across the Sudanese woodland savannah: A regional carbon sequestration study. J. Arid. Environ. 2017, 89, 67–76. [Google Scholar] [CrossRef]
- Giardina, C.P.; Ryan, M.G. Evidence that decomposition rates of organic carbon in mineral soil do not vary with temperature. Nature 2000, 404, 858–861. [Google Scholar] [CrossRef] [PubMed]
- Wu, F.; Wang, Z. Assessing the impact of urban land expansion on ecosystem carbon storage: A case study of the Changzhutan metropolitan area, China. Ecol. Indic. 2023, 154, 110688. [Google Scholar] [CrossRef]
- Tian, L.; Ye, Q.; Zhen, Z. A new assessment model of social cost of carbon and its situation analysis in China. J. Clean. Prod. 2019, 211, 1434–1443. [Google Scholar] [CrossRef]
- Kim, J.; Nicholls, S. Using geographically weighted regression to explore the equity of public open space distributions. J. Leis. Res. 2016, 48, 105–133. [Google Scholar] [CrossRef]
- Yang, Q.; Han, B. Analysis of the yield curve of China’s treasury bonds. Huabei Financ. 2013, 9, 42–45. (In Chinese) [Google Scholar]
- Lloyd, C.; Shuttleworth, I. Analysing commuting using local regression techniques: Scale, sensitivity, and geographical patterning. Environ. Plan. A 2005, 37, 81–103. [Google Scholar] [CrossRef]
- Zhou, X.; Wang, Y.C. Dynamics of land surface temperature in response to landuse/cover change. Geogr. Res. 2011, 49, 23–36. [Google Scholar] [CrossRef]
- Jiang, W.; Wang, Y.; Dou, M.; Liu, S.; Shao, S.; Liu, H. Solving competitive location problems with social media data based on customers’ local sensitivities. ISPRS Int. J. Geo-Inf. 2019, 8, 202. [Google Scholar] [CrossRef]
- Yu, S.; Hu, X.; Sheng, Y.; Zhao, C. Similarity and geographically weighted regression considering spatial scales of features space. Spat. Stat. 2025, 67, 100897. [Google Scholar] [CrossRef]
- Gan, L.; Halik, U.; Shi, L.; Welp, M. Multi-scenario dynamic prediction of ecological risk assessment in an arid area of northwest China. Ecol. Indic. 2023, 154, 110727. [Google Scholar] [CrossRef]
- Zhao, M.M.; He, Z.B.; Du, J.; Chen, L.F.; Lin, P.F.; Fang, S. Assessing the effects of ecological engineering on carbon storage by linking the CA-Markov and InVEST models. Ecol. Indic. 2019, 98, 29–38. [Google Scholar] [CrossRef]
- Garrigues, S.; Allard, D.; Baret, F.; Weiss, M. Influence of landscape spatial heterogeneity on the non-linear estimation of leaf area index from moderate spatial resolution remote sensing data. Remote Sens. Environ. 2006, 105, 286–298. [Google Scholar] [CrossRef]
- Wang, L.; Li, Y.; Gan, Y.; Zhao, L.; Fan, L.; Qin, W.; Ding, L. Reconstructing high-resolution gridded precipitation data in the southwest China highland canyon area using an improved (MGWR) downscaling method. Sci. Total Environ. 2024, 948, 174866. [Google Scholar] [CrossRef]
- Luan, C.; Liu, R.; Li, Y.; Zhang, Q. Comparison of various models for multi-scenario simulation of land use/land cover to predict ecosystem service value: A case study of Harbin-Changchun Urban Agglomeration, China. J. Clean. Prod. 2024, 478, 144012. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, J.; Chen, Y.; Huang, S.; Liang, B. Spatiotemporal variation and prediction of NPP in Beijing-Tianjin-Hebei region by coupling PLUS and CASA models. Ecol. Inform. 2024, 81, 102620. [Google Scholar] [CrossRef]
- Zhang, C.; Jia, Q.; Liu, Y.; Zheng, Z.; Gao, Y.; Li, K. Evaluation and multi scenario simulation of ecosystem service value in Zhengzhou Metropolitan Area based on PLUS model. Meas. Sens. 2024, 32, 101079. [Google Scholar] [CrossRef]

| Type | Name | Source | Time |
|---|---|---|---|
| Basic geographic information | Elevation | European Space Agency (https://panda.copernicus.eu) Accessed on 15 June 2024 | 2022 |
| Slope | Generate based on elevation | 2022 | |
| Annual precipitation | Geographic Data Sharing Infrastructure, global resources data cloud (www.gis5g.com) Accessed on 15 July 2024 | 1990–2020 | |
| Annual average temperature | National Tibetan Plateau Science Data Center (https://data.tpdc.ac.cn) Accessed on 13 July 2024 | 1990–2020 | |
| Distance to rivers | OpenStreetMap (https://www.openstreetmap.org) Accessed on 16 July 2024 | 2020 | |
| Socioeconomic information | Population density | Resource and Environmental Science Data Platform (https://www.resdc.cn) Accessed on 30 May 2024 | 2020 |
| GDP density | |||
| Distance to railways | OpenStreetMap (https://www.openstreetmap.org) Accessed on 16 July 2024 | 2020 | |
| Distance to highways | |||
| Distance to roads | |||
| Distance to administrative centers | National Bureau of Statistics (https://www.stats.gov.cn) Accessed on 30 May 2024 | 2021 | |
| Land use | LUCC | Resource and Environmental Science Data Platform (https://www.resdc.cn) Accessed on 15 April 2024 | 1990–2020 |
| Cropland | 0.57 | 8.07 | 10.84 | 2.73 |
| Forest | 4.24 | 11.59 | 23.69 | 5.3 |
| Grassland | 3.53 | 8.65 | 9.99 | 3.06 |
| Water | 0.25 | 0 | 7.8 | 0 |
| Construction land | 0.3 | 0 | 0 | 0 |
| Unused land | 0.36 | 0.92 | 0.99 | 0.85 |
| 1990–2020 | 2020–2050 BAU | 2020–2050 CP | 2020–2050 ES | 2020–2050 BAU-ES | 2020–2050 CP-ES | |
|---|---|---|---|---|---|---|
| Urban expansion (ha) | 520,380 | 473,175 | 172,665 | 272,088 | 329,508 | 250,461 |
| Carbon loss due to urban expansion (106 t) | 117.86 | 109.47 | 64.18 | 56.97 | 74.34 | 78.31 |
| Urban decrease (ha) | 37,953 | 66,123 | 62,028 | 5931 | 23,580 | 50,247 |
| Carbon rise due to urban decrease (106 t) | 2.76 | 2.51 | 0.92 | 1.44 | 1.75 | 1.33 |
| Carbon loss due to urban (106 t) | 115.1 | 106.96 | 63.26 | 55.53 | 72.59 | 76.98 |
| Total carbon change (106 t) | −144.42 | −113.42 | −88.95 | 11.71 | −24.49 | −19.66 |
| Contribution rate of urban to carbon loss | 79.7% | 94.3% | 71.1% | - | 296.4% | 391.6% |
| Total Value (CNY 109) | Cropland (CNY 109) | Forest (CNY 109) | Grassland (CNY 109) | Water (CNY 109) | Construction Land (CNY 109) | Unused Land (CNY 109) | |
|---|---|---|---|---|---|---|---|
| 2015 | 289.516 | 153.685 | 118.12 | 17.23 | 0.253 | 0.181 | 0.046 |
| 2020 | 287.656 | 152.346 | 119.035 | 15.739 | 0.264 | 0.226 | 0.045 |
| BAU2030 | 284.93 | 150.275 | 119.495 | 14.546 | 0.282 | 0.287 | 0.044 |
| CP2030 | 285.578 | 153.451 | 117.552 | 14.013 | 0.273 | 0.248 | 0.042 |
| ES2030 | 287.815 | 148.764 | 123.607 | 14.85 | 0.29 | 0.262 | 0.041 |
| BAU2050 | 280.551 | 147.374 | 119.606 | 12.837 | 0.312 | 0.379 | 0.043 |
| CP2050 | 282.098 | 155.3 | 114.586 | 11.605 | 0.288 | 0.282 | 0.037 |
| ES2050 | 288.196 | 143.28 | 130.674 | 13.559 | 0.332 | 0.314 | 0.037 |
| BAU-ES | 285.926 | 144.518 | 127.367 | 13.343 | 0.328 | 0.332 | 0.038 |
| CP-ES | 286.294 | 146.687 | 125.933 | 13.01 | 0.32 | 0.307 | 0.037 |
| Variable | Estimation | p | t | VIF |
|---|---|---|---|---|
| Intercept | 0 | 0 | −6.509 | - |
| Temperature | 0.018 | 0.599 | 0.526 | 15.014 |
| Distance to administrative centers | 0.143 | 0.000 | 13.248 | 1.436 |
| Elevation | 0.188 | 0.000 | 5.158 | 16.419 |
| GDP | 0.044 | 0.041 | 2.046 | 5.823 |
| Distance to highways | −0.71 | 0.000 | −6.061 | 1.681 |
| Population | −0.116 | 0.000 | −5.166 | 6.194 |
| Precipitation | 0.314 | 0.000 | 32.725 | 1.140 |
| Distance to railways | 0.001 | 0.908 | 0.116 | 1.457 |
| Distance to rivers | −0.008 | 0.439 | −0.774 | 1.382 |
| Distance to roads | 0.100 | 0.000 | 8.924 | 1.544 |
| Slope | 0.274 | 0.000 | 20.872 | 2.127 |
| Variable | OLS Est | Mean | Median | p | t | Adj t-val (95%) |
|---|---|---|---|---|---|---|
| Intercept | −0.000 | 0.082 | −0.037 | 1.000 | −0.000 | 2.855 |
| Temperature | −0.146 | −0.683 | −0.648 | 0.000 | −10.290 | 3.355 |
| Distance to administrative centers | 0.130 | 0.014 | 0.014 | 0.000 | 12.374 | 2.053 |
| GDP | 0.050 | −0.109 | 0.030 | 0.021 | 2.305 | 2.430 |
| Distance to highways | −0.062 | −0.067 | −0.048 | 0.000 | −5.397 | 2.809 |
| Population | −0.121 | −0.445 | −0.171 | 0.000 | −5.417 | 3.802 |
| Precipitation | 0.313 | 0.196 | 0.203 | 0.000 | 32.607 | 3.147 |
| Distance to railways | 0.005 | −0.034 | −0.031 | 0.619 | 0.497 | 2.307 |
| Distance to rivers | −0.005 | 0.014 | 0.008 | 0.656 | −0.445 | 2.912 |
| Distance to roads | 0.101 | 0.019 | 0.019 | 0.000 | 9.025 | 2.199 |
| Slope | 0.294 | 0.112 | 0.104 | 0.000 | 23.545 | 3.159 |
| Uncorrected | Corrected | |||||
|---|---|---|---|---|---|---|
| Bandwidth | Coefficient Range | Scale | Bandwidth | Coefficient Range | Scale | |
| Intercept | 294 | [−0.827, 1.012] | b | 513 | [−0.773, 1.217] | b |
| Temperature | 198 | [−1.208, 0.198] | b | 194 | [−1.718, 0.150] | b |
| Distance to administrative centers | 102 | [−0.330, 0.724] | a | 7387 | [0.011, 0.018] | d |
| GDP | 443 | [−0.293, 3.644] | b | 1188 | [−1.479, 0.223] | c |
| Distance to highways | 1370 | [−0.149, 0.015] | c | 1129 | [−0.234, 0.022] | c |
| Population | 47 | [−8.848, 4.908] | a | 47 | [−4.556, 1.515] | a |
| Precipitation | 102 | [−0.526, 2.212] | a | 294 | [−0.204, 0.897] | b |
| Distance to railways | 7387 | [−0.039, −0.034] | d | 3575 | [−0.058, −0.017] | d |
| Distance to rivers | 1560 | [−0.054, 0.038] | c | 1239 | [−0.043, 0.099] | c |
| Distance to roads | 2126 | [−0.029, 0.064] | d | 7127 | [0.014, 0.026] | d |
| Slope | 423 | [−0.110, 0.359] | b | 443 | [−0.037, 0.319] | b |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, K.; Li, R.; Liu, M.; Cao, Y.; Yang, J.; Wei, Y. Analysis of Carbon Storage Changes in the Chengdu–Chongqing Region Based on the PLUS-InVEST-MGWR Model. Land 2025, 14, 1651. https://doi.org/10.3390/land14081651
Xu K, Li R, Liu M, Cao Y, Yang J, Wei Y. Analysis of Carbon Storage Changes in the Chengdu–Chongqing Region Based on the PLUS-InVEST-MGWR Model. Land. 2025; 14(8):1651. https://doi.org/10.3390/land14081651
Chicago/Turabian StyleXu, Kuiyuan, Ruhan Li, Mengnan Liu, Yajie Cao, Jinwen Yang, and Yali Wei. 2025. "Analysis of Carbon Storage Changes in the Chengdu–Chongqing Region Based on the PLUS-InVEST-MGWR Model" Land 14, no. 8: 1651. https://doi.org/10.3390/land14081651
APA StyleXu, K., Li, R., Liu, M., Cao, Y., Yang, J., & Wei, Y. (2025). Analysis of Carbon Storage Changes in the Chengdu–Chongqing Region Based on the PLUS-InVEST-MGWR Model. Land, 14(8), 1651. https://doi.org/10.3390/land14081651







