Abstract
As global urbanization accelerates amidst compounding risks, comprehensive urban resilience assessment has emerged as a pivotal issue in optimizing risk governance pathways. Grounded in the Pressure–State–Response (PSR) theoretical framework, this study constructs a multidimensional evaluation system for comprehensive urban resilience. Through the integration of a combined weighting method and the TOPSIS model, we systematically measure resilience levels across 13 prefecture-level cities in Jiangsu Province, with the obstacle degree model employed to identify critical resilience constraints. The findings reveal significant spatial heterogeneity in regional resilience patterns. High-resilience cities establish positive feedback mechanisms through economic foundations, innovation-driven strategies, and institutional coordination. Conversely, low-resilience cities face multidimensional constraints, including industrial structure imbalance, inadequate social security systems, and infrastructure deficiencies. The resilience disparity stems from the coupling effects of systemic multidimensional elements, with three core obstacles identified: energy consumption and population pressure in the Pressure dimension, medical resource scarcity and innovation deficit in the State dimension, and fiscal expenditure inefficiency in the Response dimension. The study proposes strategic interventions, including fiscal structure optimization, cross-regional resource coordination enhancement, and innovation–translation mechanism improvement, to facilitate urban systems’ transformation from passive resistance to proactive adaptation. This research provides novel perspectives for analyzing complex system resilience evolution and offers scientific grounds for urban agglomeration risk prevention and sustainable development.
1. Introduction
1.1. Research Context
Amid accelerating global urbanization and intensifying uncertainties ranging from climate change to public health crises, urban systems are confronting increasingly complex and compounded pressures [1]. Resilience, defined as the core capacity of urban systems to withstand disturbances, adapt to changes, and achieve sustainable development, has emerged as a frontier research focus in urban planning and governance. The research focus of urban resilience assessment has shifted from emphasizing single-disaster responses—such as static analyses of engineering resilience or the recovery capacity of specific systems—toward comprehensive investigations into how multidimensional social, economic, institutional, and other subsystems dynamically synergize to generate adaptability and transformative capacities. This evolution centers on urban areas as complex adaptive systems confronting compound pressures arising from intertwined economic fluctuations, social disruptions, and environmental hazards. Fostering socioeconomic system resilience and its synergistic interactions with ecological and infrastructural dimensions constitutes the conceptual cornerstone for understanding comprehensive urban resilience [2]. Jiangsu Province, an economically advanced coastal region in eastern China, has maintained its position as the nation’s leading province in per capita GDP for 13 consecutive years [3]. According to 2024 statistics from China’s National Bureau of Statistics, its urbanization rate exceeds 75.5% [4]. However, this rapid development masks systemic risks, including population over-concentration, industrial structure imbalance, and declining environmental carrying capacity. First, significant development disparities exist between Northern and Southern Jiangsu [5]. The Southern Jiangsu region, occupying less than 30% of the province’s land area, contributes 62% of the provincial GDP, while the per capita fiscal revenue in the five cities of Northern Jiangsu remains below half that of Southern Jiangsu’s level [6]. Second, rapid urbanization has intensified resource constraints, leading to the continuous compression of natural and social spaces coupled with diminished self-recovery capacity [7]. Extreme climate events in 2016 caused flooding that affected 299,000 residents across eight Jiangsu cities [8]. In 2023, industrial chain disruptions in Southern Jiangsu revealed regional economic vulnerability through the widespread corporate debt defaults [9]. These developments underscore both the paradigmatic value and urgency of comprehensive urban resilience research in Jiangsu, providing critical implications for advancing high-quality urban construction and sustainable development.
The concept of resilience originated in mechanical engineering and was initially defined as “a system’s capacity to return to its original state after external disturbances” [10]. In 1973, Holling introduced this idea of resilience into ecology, proposing a concept of ecological resilience that emphasizes systems’ transformative capacity between multiple stable states [11]. Since the 21st century, evolutionary resilience theory has revolutionized conventional frameworks by conceptualizing cities as complex adaptive systems whose resilience extends beyond passive recovery. It emphasizes systems’ dynamic adaptation processes—achieved through continuous learning and proactive innovation—for enabling structural transformation [12,13]. Scholarly consensus now crystallizes around three core dimensions of resilience: Robustness, Recovery, and Adaptation [14]. The complexity of resilience emerges from intricate couplings across social, economic, ecological, and infrastructural subsystems, alongside their interactions across multiple spatial scales (e.g., city clusters) [15]. Consequently, assessing comprehensive urban resilience cannot be confined to singular dimensions. Regarding assessment methodologies, early studies predominantly employed vulnerability inverse indicators for indirect measurement [16]. With theoretical advancements, direct assessment has become mainstream, manifesting three developmental trends: (1) Dimensional expansion from singular economic/engineering metrics to social–ecological–economic–infrastructure quadripartite frameworks [17]; (2) Dynamic quantification, which is widely applied in infrastructure resilience assessment and exemplified by Bruneau’s resilience triangle model that evaluates system recovery efficiency through functionality loss curves [18]; (3) Spatial correlation analysis, as demonstrated by Xiu Chunliang’s research team, who revealed complex relationships between urban form compactness and disaster recovery capacity through their “scale–density–morphology” tripartite framework [19]. However, the existing research presents notable limitations: (1) Existing assessments predominantly concentrate on ecological or infrastructural dimensions, with insufficient analysis of dynamic socioeconomic interlinkages; (2) Overreliance on subjective weighting persists despite the limited application of data-driven methodologies; (3) Indicator redundancy and collinearity remain poorly addressed; (4) Diagnostic mechanisms for identifying resilience constraining factors are critically lacking.
As a pioneering region in China’s new urbanization, Jiangsu Province’s resilient-city-development experience holds significant referential value for comparable regions [20,21]. The significance of this study lies in its integration of socioeconomic dynamic pressures, systemic stability states, and policy response efficacy within Jiangsu’s city clusters under the Pressure–State–Response (PSR) framework. Employing a comprehensive weighting approach that synthesizes subjective and objective weights, we utilize the TOPSIS model coupled with diagnostic identification of obstacle factors to elucidate the mechanisms underlying this regional heterogeneity. This methodology aims to provide scientific foundations for optimizing resilience governance pathways. The research innovations manifest in three aspects: First, by establishing a tri-level “Pressure–State–Response” indicator system that addresses traditional studies’ limitations in analyzing system dynamics and risk-response synergies. Second, by developing an innovative composite weighting approach that balances expert judgment with objective data contributions. Third, by identifying critical resilience barrier factors to guide context-specific policy formulation across regions. This research deepens the theoretical understanding of resilience through complex system perspectives while providing decision support for risk prevention in the Yangtze River Delta urban agglomeration.
1.2. Framework of the PSR Theoretical Model
In urban resilience research, scholars typically conceptualize cities as complex adaptive systems [22], with the evaluation and analysis predominantly grounded in systems theory [23]. Major analytical perspectives encompass urban systems, climate change and disaster-risk management, energy systems, and geographical dimensions, as detailed in Table 1:

Table 1.
Representative institutions and perspectives in urban resilience research.
The geographical perspective, exemplified by Xiu et al. (2021), focuses on urban scale, population density, and spatial morphology. Urban systems scholarship—spanning Foster (2012), the Rockefeller Foundation (2014), Sharifi and Yamagata (2014), and Kusumastuti et al. (2014)—encompasses economic, social, and infrastructural dimensions. Climate change and disaster-risk research synthesizes contributions from the International Development Association (2007), the Rockefeller Foundation (2011), Osaka University (2014), UNDRR (2014), and Li et al. (2024), which center on governance frameworks and risk-mitigation mechanisms. However, existing studies predominantly focus on homogeneous dimension evaluations or static indicators, which inadequate address the dynamic feedback mechanisms and synergistic interactions among components in urban composite systems when confronting external shocks. This limitation thus necessitates the introduction of the PSR theoretical framework. The Pressure–State–Response (PSR) model serves as a pivotal theoretical framework for analyzing the resilience of complex urban systems [34]. Originally conceptualized in the late 1970s by Canadian statisticians Rapport and Friend [35], the model underwent systematic integration and expansion through the Organisation for Economic Co-operation and Development (OECD) and the United Nations Environment Programme (UNEP) [36]. The PSR model elucidates the interaction mechanisms between human activities and ecological environments [37]. Distinct from traditional ecological resilience studies that emphasize simple factor aggregation, the PSR framework prioritizes synergistic effects among institutional design, capital flows, and human capital under comprehensive factor-interaction perspectives [38]. Within the Pressure dimension, socioeconomic stressors require systematic assessment [39]. The State dimension mandates the integration of macroeconomic operational indicators, while the Response dimension necessitates the performance prediction of policy instruments and innovation strategies through observable metrics [40]. Comprehensive urban resilience is not only constrained by the natural-resource carrying capacity, but it is also challenged by systemic risks, including industrial homogenization competition [41], local government debt accumulation, and the public service supply–demand imbalance [42]. Implementing the PSR model incorporates both “hard power” indicators (e.g., per capita infrastructure stock) and “soft power” elements (e.g., social organization mobilization efficiency, information dissemination velocity) [43], thereby establishing theoretical justification for subsequent multi-criteria decision-making using the TOPSIS methodology. The PSR framework, through its “Pressure–State–Response” causal chain, enables multidimensional synergy analysis for Jiangsu’s city clusters. At the pressure level, it quantifies socioeconomic stressors, including the population’s social carrying capacity; at the state level, it assesses system stability indicators such as foundational and innovation resource reserves; at the response level, it measures fiscal resource allocation efficiency—delivering a systematic analytical pathway for city-cluster resilience governance [44].
As depicted in Figure 1, when urban systems encounter external disturbances, the PSR theoretical framework enables a systematic analysis of internal impact mechanisms during dynamic evolutionary processes across different phases and components [45]. When composite urban systems face external perturbations, evolutionary trajectories diverge due to divergent socioeconomic resilience levels. The resilience response process can be decomposed into three sequential phases: the resistance phase (pre-disturbance), the adaptation phase (mid-disturbance), and the response–innovation phase (post-disturbance), which correspond, respectively, to the system Pressure dimension, system State dimension, and system Response dimension [46]. For low-resilience cities, during the pre-disturbance phase, systems confront external shocks from Pressure-dimension factors such as corporate debt ratios and population–resource pressures. The State dimension’s inherent defense mechanisms sustain basic operations. When disturbances exceed critical thresholds in intensive impact phases, even though preliminary resistance persists through State-dimension elements, constrained resilience capacity and innovation deficiency in the Response dimension may trap systems in low-adaptation states (Path i), which ultimately lead to a failure to surpass innovation thresholds with prolonged suboptimal functionality [47]. Moderate-resilience cities demonstrate transitional characteristics. When faced with Pressure-dimension disturbances, these systems leverage stabilization capacities from the State and Response dimensions to achieve functional restoration through inherent recovery mechanisms [48], ultimately attaining new dynamic equilibria (Path ii). High-resilience systems exhibit superior performance. When confronting pressure impacts, synergistic effects between the State dimension’s robust risk resistance and the Response dimension’s innovation-driven momentum propel structural transitions [49]. Such systems not only rapidly recover to new equilibrium states but also achieve superior sustainable development through experiential learning and transformative innovation (Path iii) [50], demonstrating enhanced self-adaptive capacities.
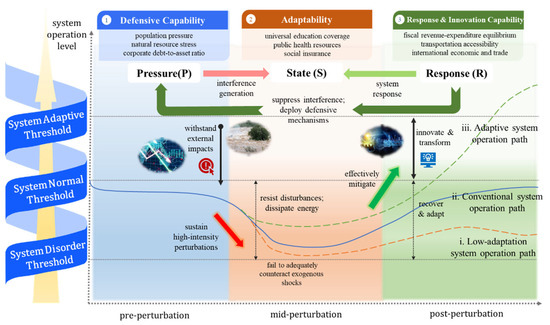
Figure 1.
Resilience model framework of the PSR theory.
2. Materials and Methods
2.1. Study Area
Jiangsu Province is situated in the central eastern coastal region of China, occupying the lower reaches of the Yangtze and Huai River basins. Its geographical coordinates span 116°18′ E to 121°57′ E longitude and 30°45′ N to 35°20′ N latitude. Bordered by the Yellow Sea to the east, Shandong Province to the north, Anhui Province to the west, and Shanghai/Zhejiang Province to the southeast, Jiangsu constitutes a vital component of the Yangtze River Delta. The provincial topography is predominantly composed of plains with low-lying terrain, featuring extensive water surfaces and an intricate river network. The Yangtze River traverses the province east–west, while the Beijing–Hangzhou Grand Canal crosses north–south, forming a dense hydrological system. Jiangsu remains China’s only province that integrates fluvial (rivers), lacustrine (lakes), and coastal geographical characteristics and is endowed with diverse natural conditions and abundant resources [51]. The climate exhibits transitional characteristics from temperate to subtropical zones, marked by distinct seasons and synchronized precipitation–thermal patterns [52]. The geographical profile of Jiangsu Province is illustrated in Figure 2.
Figure 2.
Geographical profile of Jiangsu Province.
Jiangsu stands as one of China’s most rapidly urbanizing regions and is characterized by a robust real economy and highly developed urban agglomerations [53]. In 2023, Jiangsu Province’s resident population reached 85.26 million, with a population density of 796 persons per square kilometer. The provincial gross regional product totaled CNY 12,822.22 billion, representing a 5.8% year-on-year growth in constant prices. Specifically, the value-added of the primary sector amounted to CNY 507.58 billion, up 3.5% year-on-year; the secondary sector contributed CNY 5690.97 billion, rising 6.7%; while the tertiary sector generated CNY 6623.67 billion, representing an increase of 5.1%. As a cradle of modern national industries, the province was early in establishing comprehensive industrial systems and open economic patterns, accumulating substantial experience in urban modernization [54]. In 2023, the output value of strategic emerging industries and high-tech industries within Jiangsu Province’s industrial enterprises above designated size accounted for 41.3% and 49.9% of the total above-designated-size industrial output value, respectively. In infrastructure and public services, Jiangsu boasts advanced transportation networks, with expressway and high-speed-rail densities ranking among the highest nationally, complemented by abundant port resources [55]. However, regional economic development exhibits pronounced gradient disparities, which are correspondingly reflected in the urban resilience differentials [56]. The geographical demarcation of Southern Jiangsu and Northern Jiangsu is illustrated in Figure 3. Southern Jiangsu, leveraging the Yangtze River’s golden waterway and Shanghai’s economic radiation, clusters high-end manufacturing and modern service industries with outstanding innovation capacity. Central Jiangsu specializes in industrial transfer reception and characteristic industrial clusters. Northern Jiangsu, which is predominantly reliant on agriculture and traditional industries, experiences relatively lagged development [57]. Simultaneously, infrastructure distribution imbalances persist across Jiangsu’s regions, which are manifested in transportation accessibility and medical–educational resource disparities [58]. Recent years have witnessed provincial efforts to optimize industrial structures, with emerging industries and digital economies achieving rapid growth. Nevertheless, some cities continue grappling with the dual pressures of traditional industry transformation and modern financial risks [59]. Ecologically, Jiangsu’s industrial expansion has generated severe environmental carrying pressures and land resource pollution, highlighting how imperative it is to enhance synergy between ecological security and urban development—a critical constraint on urban resilience [60].
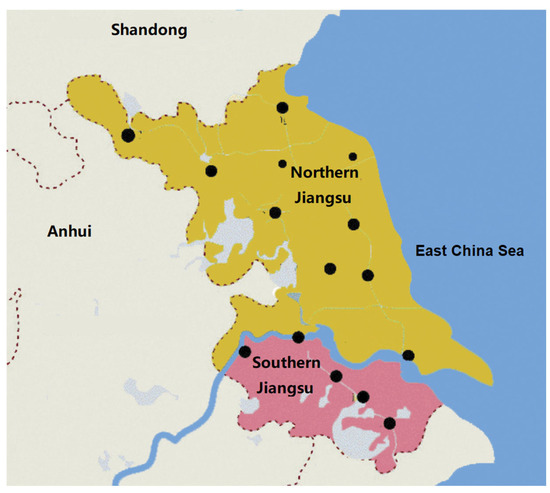
Figure 3.
Regional demarcation map of Southern and Northern Jiangsu.
As the strategic confluence point of the Belt and Road Initiative and a pivotal node in Yangtze River Delta integration, Jiangsu Province occupies a pivotal position in China’s national strategic framework [61]. While endowed with favorable policy support and resource endowments, the province faces novel governance challenges in their urban agglomeration systems’ capacity to withstand external shocks. The comprehensive development status of Jiangsu’s cities across the areas of population mobility, industrial collaboration, and ecological conservation constitutes a critical determinant shaping its overall regional resilience levels. Therefore, resilience evaluation research targeting Jiangsu’s cities encompasses both a theoretical need and paradigmatic significance.
2.2. Data Sources
Jiangsu Province comprises thirteen prefecture-level cities (administering districts): Nanjing, Wuxi, Xuzhou, Changzhou, Suzhou, Nantong, Lianyungang, Huai’an, Yancheng, Yangzhou, Zhenjiang, Taizhou, and Suqian. Among these, Nanjing serves as the provincial capital. Figure 4 illustrates the spatial distribution of the thirteen cities within Jiangsu Province.
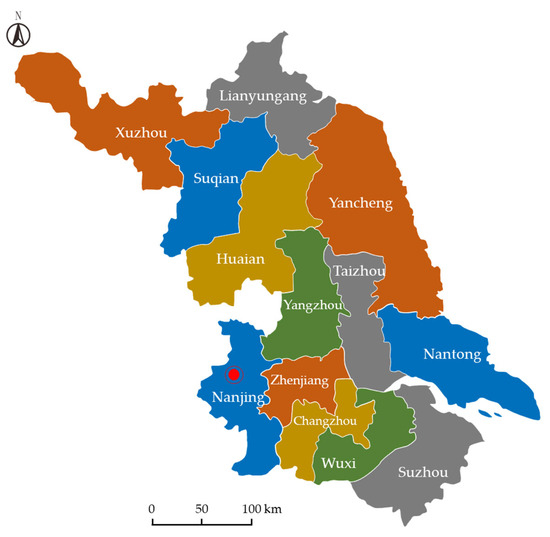
Figure 4.
Geographical distribution of the 13 prefecture-level cities in Jiangsu Province.
To ensure data integrity, accuracy, consistency, and timeliness, the indicator data were sourced from authoritative publications including the China Urban Construction Statistical Yearbook 2024, the China Regional Economic Statistical Yearbook 2024, the Jiangsu Statistical Yearbook 2024, the Jiangsu Provincial Government Work Report 2024, and statistical yearbooks/socioeconomic development bulletins from all 13 prefecture-level cities. Where data were missing for specific cities or indicators, we implemented rigorous processing through the SPSS 27.0 software, employing mean imputation or linear interpolation methods after a comprehensive evaluation of the data-missing mechanisms.
2.3. Construction of the Indicator System
Building upon the theoretical framework, the criterion layers are structured into three dimensions: the Pressure layer, the State layer, and the Response layer. Each criterion layer contains multiple indicators, collectively forming the comprehensive urban resilience evaluation system. The indicator screening process followed a rigorous methodological protocol: First, preliminary selection of 34 candidate indicators was conducted through bibliometric analysis, considering regional characteristics and data availability, supplemented by derivations from raw datasets. Where there were missing data from specific cities, differentiated imputation approaches were implemented based on the data characteristics. Using the SPSS 27.0 software, linear interpolation was applied to indicators with missing completely at random (MCAR) patterns. For missing not at random (MNAR) indicators, multiple imputations combining an Expectation–Maximization (EM) algorithm with industry averages was performed to ensure data integrity and unbiased estimation.
This study employs Pearson correlation coefficients to systematically examine indicator redundancy within each criterion layer, thereby mitigating multicollinearity interference among the indicators. The Pearson correlation coefficient is calculated as
where xi and yi represent the observed values of any two indicators under the same criterion layer, and denote their respective means, and n indicates the number of city samples. Indicators demonstrating absolute correlation coefficients exceeding 0.9 are identified as exhibiting high collinearity and subsequently removed in accordance with data integrity principles.
In the correlation analysis of Pressure-dimension indicators, the absolute correlation coefficients between “commercial housing sales area density” and “population density”/“resident-to-registered population ratio” were 0.918 and 0.902, respectively. Given the strong influence of population scale and urbanization progress on commercial housing transactions, this indicator was therefore eliminated. Regarding State-dimension indicators, “per capita disposable income” exhibited absolute correlation coefficients of 0.946, 0.941, and 0.963 with “per capita GDP”, “patent application density”, and “basic pension insurance coverage rate”, respectively. Considering the direct driving effects of regional economic aggregates, social security, and innovation capacity on resident income, this indicator was removed. After two rounds of rigorous screening, a three-tier evaluation system comprising 32 indicators was finalized. All the variance inflation factors (VIFs) across dimensions remained below 5, satisfying model construction requirements.
Following indicator screening, the Pressure dimension (P) incorporates ten indicators: population density, built-up area ratio, resident population proportion, motor vehicle ownership per capita, per capita electricity consumption, industrial electricity consumption per unit output value, agricultural machinery power intensity, secondary–tertiary industry output ratio, and per capita residential floor area. These metrics collectively reflect population agglomeration pressures, industrial structure risks, and energy consumption challenges during urbanization [62].
The State dimension (S) comprises eleven indicators: per capita GDP, GDP index, tertiary sector contribution to GDP, Engel coefficient, student–teacher ratio in primary/secondary schools, per capita hospital beds, per capita licensed physicians, per capita public library collections, patent application density, per capita deposit balance, and basic pension insurance coverage rate. This cluster evaluates urban systems’ inherent risk-resistance capacity and stability maintenance during disturbances [63].
The Response dimension (R) includes eleven indicators: fiscal revenue–expenditure ratio to GDP, tax revenue to GDP ratio, total retail sales of consumer goods to GDP ratio, import–export volume to GDP ratio, per capita grain output, industrial enterprise operating profit margin, loan-to-deposit ratio, highway network density, and per capita passenger/freight volume. These parameters assess urban systems’ potential to achieve functional recovery and structural optimization through policy interventions, infrastructure development, and resource allocation. Detailed indicators are presented in Table 2 [64]. The positive or negative impact of each indicator on resilience is marked in the table.

Table 2.
Comprehensive urban resilience evaluation indicator system.
2.4. Determination of Indicator Weights
2.4.1. Data Standardization
To eliminate dimensional heterogeneity interference in multi-indicator evaluation systems, this study employs Min-Max linear transformation for data standardization. Let the original data matrix be X = (xij)m×n, where m = 13 represents the 13 prefecture-level city samples in Jiangsu Province, and n = 32 denotes the screened three-level PSR indicator system.
For positive indicators (where higher values indicate enhanced system resilience), the standardization formula is defined as follows:
For negative indicators (where higher values reflect reduced system resilience), the standardization formula is
where
- xij = original observed value of city i for indicator j;
- max(xj) and min(xj) = maximum and minimum values of indicator j across the 13 cities.
The standardized data preserve essential mathematical properties: order preservation, comparability, and boundedness. Through this processing, the Pressure–State–Response indicators are transformed into positive, dimensionless values within the [0, 1] interval.
2.4.2. Subjective Weight Determination via the Analytic Hierarchy Process (AHP)
The Analytic Hierarchy Process (AHP) was employed to ascertain subjective indicator weights. Initially proposed by American operations researcher Thomas L. Saaty in the 1970s, this method addresses multi-criteria weight allocation challenges in complex decision-making. Through expert judgments, the relative importance of hierarchical indicators can be quantified numerically. In a 1985 study on U.S. urban livability rankings, Saaty employed a six-expert panel comprising university professors, corporate executives, students, and other stakeholders. Through weighted geometric means of integrated judgment matrices, he demonstrated that multi-expert independent evaluations effectively counteracted subjective biases [65]. In a 1994 review article, Saaty further emphasized that when expert participation reaches ≥5 individuals, the geometric mean matrix of group judgments significantly reduces individual random errors while maintaining the consistency ratio (CR) below critical thresholds [66].
Considering the interdisciplinary research focus, eight experts specializing in urban planning and public policy were invited, all holding associate senior or higher professional titles with over a decade of practical experience, ensuring judgment professionalism and authority. Following Saaty’s 1–9 scale method, experts conducted pairwise importance comparisons among same-level indicators to construct judgment matrices. The scaling rules are defined as: 1 (equally important), 3 (moderately more important), 5 (strongly more important), 7 (very strongly more important), 9 (extremely more important), with even values representing intermediate judgments. The judgment matrix configuration is presented in Table 3.

Table 3.
Definition and interpretation of comparative scale values.
To mitigate extreme value interference, this study adopts the geometric mean method to aggregate individual expert judgment matrices into a group consensus matrix. Based on the group judgment matrix, the eigenvector method is employed to derive the weight vectors of the criteria, concurrently calculating the maximum eigenvalue λmax (computational procedures detailed in Appendix A.1).
To verify the judgment matrix’s logical consistency, the Consistency Index (CI) and Consistency Ratio (CR) were computed:
where RI denotes the Random Index, whose values depend on the matrix order k (see Table 4). A CR value below 0.1 indicates an acceptable consistency; otherwise, the expert scoring requires recalibration. In this study, all three criterion-layer judgment matrices passed the CR threshold.

Table 4.
Random Consistency Index (RI) values.
2.4.3. Objective Weight Determination via the Entropy Weight Method
The Entropy Weight Method (EWM), grounded in information entropy theory, serves as an objective weighting approach that quantifies the data dispersion degrees to determine the indicator weights, thereby circumventing subjective judgment biases. This study independently applies the EWM to the Pressure (P), State (S), and Response (R) dimensions to calculate objective weights, ensuring intra-dimensional weight allocation independence while preventing cross-dimensional interference. Let standardized data matrices for each criterion layer be defined as
where x′∗,ij ∈ [0, 1] denotes standardized values, with subscript i representing cities (i = 1, 2, …, 13) and j indicating the indicator sequence within each dimension.
Weight calculation proceeds via a three-stage process: initially, the information entropy value of each criterion is computed, followed by derivation of the divergence coefficients to quantify discrete variations among the indicators and concluding with normalization to obtain the final weights. The complete computational workflow is detailed in Appendix A.2.
2.4.4. Combined Weighting Method
In multi-criteria decision-making research, subjective weighting methods relying on expert knowledge can capture the theoretical importance of indicators but remain susceptible to cognitive biases. Conversely, objective weighting methods based on data statistics circumvent human interference but may overlook practical significance. To synthesize their respective strengths, this study adopts a combined weighting approach.
For weight vectors generated by AHP and Entropy methods within the same criterion layer, a coefficient α ∈ [0, 1] is introduced to calculate comprehensive indicator weights through
where
- WΛ,j = combined weight of indicator j in dimension Λ (Λ ∈ {P, S, R}, representing the Pressure, State, and Response dimensions);
- wAHPΛ,j = subjective weight from the Analytic Hierarchy Process;
- wEntropyΛ,j = objective weight from the Entropy Weight Method.
This study equalizes methodological contributions by setting α = 0.5.
Assuming equilibrium contributions of Pressure (P), State (S), and Response (R) dimensions to urban resilience, the global weight vector integrating all criterion layers is formulated as
where ⊕ denotes the vector concatenation operation.
2.5. TOPSIS Comprehensive Evaluation Model
This study employs the Technique for Order Preference by Similarity to Ideal Solution (TOPSIS) method for urban resilience assessment. Originally proposed by Hwang and Yoon in 1981, TOPSIS is a multi-attribute decision-making technique based on distance measurement that ranks evaluation objects by calculating their relative closeness to idealized positive and negative benchmark solutions [67]. Compared with conventional evaluation methods, TOPSIS effectively handles complex indicator systems with multiple dimensions and measurement units while intuitively demonstrating the evaluation objects’ deviation from optimal and inferior states. The method demonstrates strong compatibility with multi-dimensional information integration scenarios. Aligned with the comprehensive and hierarchical characteristics of urban resilience assessment, this research constructs a PSR-framework-based TOPSIS model.
First, Hierarchical Weighted Matrices are constructed. For the standardized matrix X′ = (x′ij)13×32, where the Pressure (P), State (S), and Response (R) dimensions contain 10, 11, and 11 indicators, respectively, hierarchical weighted matrices are defined via the Hadamard product for each dimension Λ ∈ {P, S, R}, with the combined weight vectors WΛ satisfying ∑j∈ΛWΛ,j = 1:
Next, the Ideal Solutions per Dimension is determined. For each dimension Λ, positive and negative ideal solutions VΛ+ and VΛ− are defined based on the indicator directionality:
Then, weighted Euclidean distances between cities and ideal solutions are computed for dimension Λ:
The dimension-level closeness coefficient for city i is calculated:
Global closeness coefficients are then synthesized considering equal resilience contributions from the P-S-R dimensions as defined in the weight analysis:
2.6. Obstacle Degree Calculation Model
This study introduces an obstacle degree model to identify critical indicators constraining urban resilience enhancement. The model quantifies the indicators’ deviation from ideal states and calculates their contribution to systemic obstacles through integrated weights. For the standardized matrix X′ = (x′ij)13×32, the deviation degree Oij is defined as the gap between actual values and the full ideal state (x′ij = 1):
Using the combined weights Wj from the integrated weighting method, the obstacle factor Fij is formulated as the product of the weight and the deviation. Higher values indicate more pronounced shortboard effects:
To eliminate inter-city total obstacle variations, the obstacle percentage Obstacleij is defined as indicator j’s contribution ratio to city i’s total obstacles:
Finally, ranking Obstacle values per city identifies and facilitates in-depth analysis of critical resilience-constraining factors.
3. Results
3.1. Indicator Weights
Integrating subjective weights from the Analytic Hierarchy Process (AHP) and objective weights from the Entropy Weight Method (EWM), Table 5 presents the weight allocation of indicators across the Pressure, State, and Response dimensions. All three criterion layers exhibit Consistency Ratio (CR) values below 0.1, confirming that the judgment matrices satisfy consistency requirements. This validates the high reliability of the weighting results.

Table 5.
Calculation results of indicator weights.
In the Pressure dimension, indicators such as the “Secondary–Tertiary Industry Output Ratio”, “Resident-to-Registered Population Ratio”, and “Industrial Electricity Intensity” demonstrate relatively higher weights. Accelerated urbanization drives transformation in traditional industrial structures. Excessive industrialization may exacerbate resource and ecological pressures, potentially constraining urban resilience. The significant weight of the resident population proportion indicates that demographic pressures and mobility patterns impact governmental social integration capacities, intensifying resource allocation challenges. The prominence of energy consumption metrics underscores resource constraints’ critical role in system disturbance resistance, where suboptimal resource utilization efficiency could induce systemic pressure risks, jeopardizing sustainable development.
Within the State dimension, “Patent Application Density”, “Licensed Physicians per 10,000 Residents”, and “Per Capita GDP” exhibit substantial weights. Patent application density reflects urban innovation vitality, where enhanced technological accumulation capacity and innovation-driven mechanisms facilitate systemic adaptation and upgrading. Medical resource availability directly determines crisis-responsive capacities during public health emergencies. As a core economic foundation metric, per capita GDP significantly influences resilience levels.
Regarding the Response dimension, high-weight indicators encompass the “Fiscal Expenditure/GDP Ratio”, “Fiscal Revenue/GDP Ratio”, and “Retail Sales/GDP Ratio”. Fiscal expenditure manifests the governmental capacity for social investment, which is essential for maintaining public goods provision during risk-mitigation processes. Fiscal revenue ensures the continuity of regulatory interventions. Retail sales volume, which is intrinsically linked to public welfare, mirrors resident consumption confidence and market resilience. During systemic crises, urban populations’ self-sufficiency capacities constitute vital stabilizing factors for social systems.
3.2. Comprehensive Resilience Levels of 13 Prefecture-Level Cities in Jiangsu Province
Based on the TOPSIS-derived resilience evaluation results, the calculated Consistency Index (CI) values were classified into five tiers: Very Low (I), Relatively Low (II), Moderate (III), Relatively High (IV), and Very High (V). The urban resilience performance across different criterion layers was then categorized accordingly, as detailed in Table 6.

Table 6.
Tier classification of urban resilience levels.
In the model robustness verification, Monte Carlo simulation was implemented to perturb weights within a ±10% variation. Generating 300 randomized weight sets wj′ = wj⋅(1 + δ) with δ∼U(−0.1, 0.1), the coefficient of variation (CV) for the cities’ closeness coefficients was computed:
The results demonstrated the maximum CV value remained below 5%, indicating that the model exhibits low sensitivity to parametric perturbations, substantiating the data credibility and evaluation reliability.
Table 7 presents the key parameters and resilience tier classifications for the 13 prefecture-level cities in Jiangsu Province under the Pressure dimension, calculated via the TOPSIS model. Figure 5 visually presents the spatial distribution of the resilience tiers, where darker colors indicate higher resilience tiers. Cities such as Yangzhou, Zhenjiang, Xuzhou, Huaian, Nantong, Taizhou, Nanjing, and Suqian demonstrate Very High (Tier V) resilience levels in the Pressure dimension, followed by Lianyungang, Yancheng, and Changzhou at Relatively High (Tier IV) levels, while Wuxi and Suzhou exhibit Moderate (Tier III) resilience performance.

Table 7.
Urban resilience ranking in the Pressure dimension.
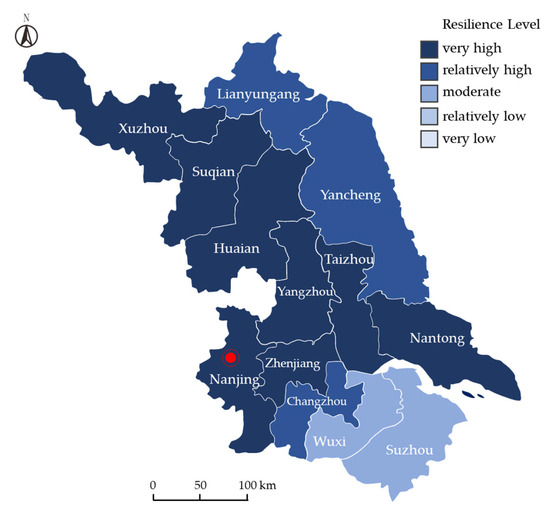
Figure 5.
Resilience tiers in the Pressure dimension.
Table 8 presents the key parameters and resilience tier classifications for the 13 prefecture-level cities in Jiangsu Province under the State dimension, calculated via the TOPSIS model. Figure 6 visually illustrates the spatial distribution of the resilience tiers, where darker colors indicate higher resilience tiers. Nanjing, Suzhou, Wuxi, and Changzhou demonstrate Very High (Tier V) resilience levels in the State dimension. Nantong and Yangzhou exhibit Moderate (Tier III) resilience performance, while Taizhou, Zhenjiang, Huaian, and Yancheng are classified as Relatively Low (Tier II). Xuzhou, Lianyungang, and Suqian register Very Low (Tier I) resilience levels.

Table 8.
Urban resilience ranking in the State dimension.
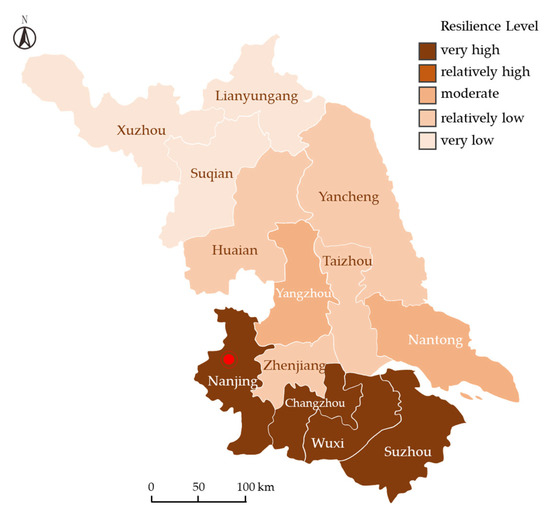
Figure 6.
Resilience tiers in the State dimension.
Table 9 presents the key parameters and resilience tier classifications for the 13 prefecture-level cities in Jiangsu Province under the Response dimension, calculated via the TOPSIS model. Figure 7 visually illustrates the spatial distribution of the resilience tiers, where darker colors indicate higher resilience tiers. Only Suzhou and Nanjing demonstrate Very High (Tier V) resilience levels in the Response dimension. Yancheng, Huaian, and Lianyungang follow closely with Relatively High (Tier IV) performance. Suqian and Xuzhou exhibit Moderate (Tier III) resilience levels. Taizhou, Wuxi, Zhenjiang, and Changzhou are classified as Relatively Low (Tier II), while Xuzhou, Lianyungang, and Suqian register Very Low (Tier I) resilience capacity in their response capabilities.

Table 9.
Urban resilience ranking in the Response dimension.
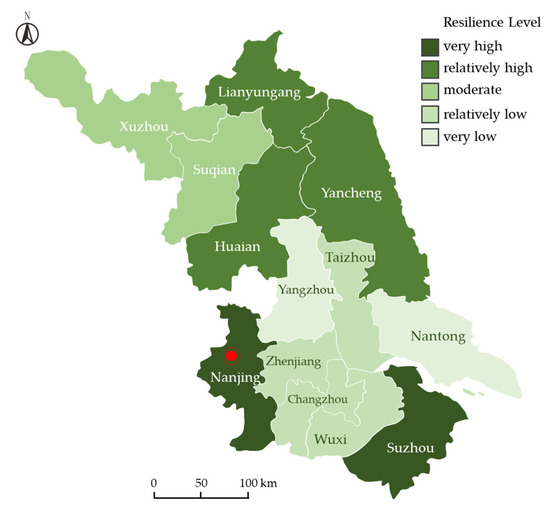
Figure 7.
Resilience tiers in the Response dimension.
Through the aforementioned computational results, we comprehensively evaluated the resilience of cities in Jiangsu Province under multi-dimensional influences. As shown in Table 10, the parameters and resilience tier classifications for all 13 cities across all criterion layers were calculated via the TOPSIS model. Figure 8 visually demonstrates the spatial distribution of the comprehensive resilience tiers, where darker hues indicate higher overall resilience tiers. Nanjing and Suzhou exhibit Very High (Tier V) comprehensive resilience levels. Wuxi and Huaian demonstrate Relatively High (Tier IV) resilience performance. Multiple cities—including Taizhou, Yancheng, Changzhou, Yangzhou, Zhenjiang, Xuzhou, Nantong, and Lianyungang—are classified as Moderate (Tier III). Suqian shows marginally lower resilience (Tier II), while no cities register Very Low (Tier I) resilience levels.

Table 10.
Comprehensive resilience rankings of cities in Jiangsu Province.
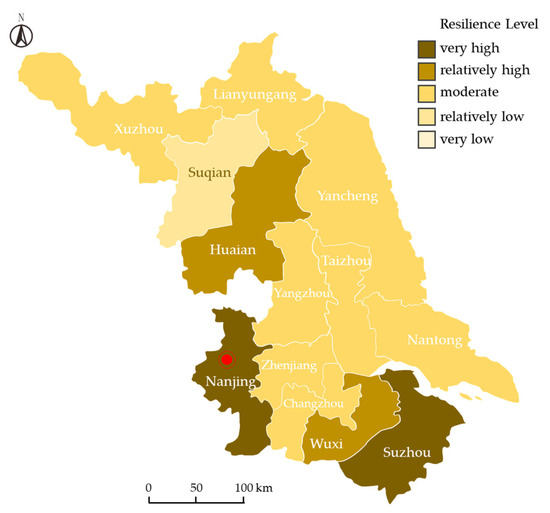
Figure 8.
Comprehensive resilience tiers of cities in Jiangsu Province.
3.3. Results of Obstacle Degree for Urban Resilience in Jiangsu Province
The obstacle degree model was employed to diagnose factors that are potentially hindering urban systems’ disturbance resistance capacity and constraining comprehensive resilience development across the 13 prefecture-level cities in Jiangsu Province (2023). First, by analyzing obstacle degrees of individual indicators, the average obstacle degree for each indicator across all the cities was calculated (see Figure 9). Second, the top six indicators with the highest obstacle degrees were identified by ranking, representing the critical constraints affecting most cities’ comprehensive resilience (see Table 11).
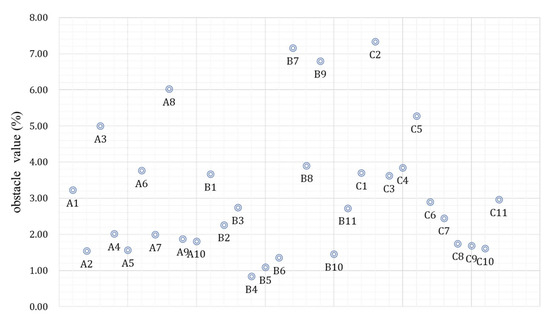
Figure 9.
Average obstacle degrees of urban resilience indicators in Jiangsu Province.

Table 11.
Key obstacle factors constraining urban resilience.
As evidenced in Table 11, the top six factors constraining comprehensive urban resilience in Jiangsu Province are the Fiscal Expenditure/GDP Ratio (C2), Licensed Physicians per 10,000 Residents (B7), Patent Application Density (B9), Secondary–Tertiary Industry Output Ratio (A8), Import–Export Volume/GDP Ratio (C5), and Resident-to-Registered Population Ratio (A3). For each city, the three most impactful obstacle factors were identified (see Table 12), with factor labels corresponding to elements in the indicator system. Cities are ordered by their comprehensive resilience levels in the table, facilitating a comparative analysis of commonalities and city-specific particularities.

Table 12.
Top three obstacle factors for urban resilience in Jiangsu cities.
4. Discussion
4.1. Regional Development Disparities Inducing Spatial Resilience Heterogeneity
Jiangsu Province exhibits pronounced north–south gradient differences in comprehensive urban resilience across its spatial distribution. Southern Jiangsu cities, including Nanjing, Suzhou, and Wuxi, consistently rank highest in comprehensive resilience (CI > 0.45), while northern counterparts like Suqian, Lianyungang, and Xuzhou demonstrate moderate to low resilience levels. The economic foundation plays a pivotal role in underpinning urban resilience, with this gradient fundamentally rooted in regional economic development disparities across Jiangsu Province. Within the PSR analytical framework, most constraining factors originate from the State and Response dimensions. Taking Nanjing as an example, the provincial capital demonstrates robust infrastructure development and resource retention capacities [68]. In the State dimension, medical resource availability and patent output metrics excel, supported by concentrated higher education institutions and advanced medical facilities that establish solid foundations for risk resilience [69].
Southern Jiangsu cities’ superior resilience predominantly stems from their diversified industrial structures and well-established public service systems. Nanjing leverages dense scientific research clusters and premium healthcare resources to enhance public health emergency responsiveness. Suzhou achieves risk dispersion through manufacturing–service integration and industrial chain synergy effects [70]. Conversely, the northern cities reveal vulnerabilities in State-dimension indicators like per capita GDP and pension insurance coverage rates, exposing economic fragility and social security deficiencies that undermine systemic risk resistance. Response-dimension deficiencies manifest in subpar infrastructure metrics like highway network density and freight volume per capita, indicating inadequate post-disaster resource allocation efficiency.
Central Jiangsu cities (Yangzhou, Taizhou) exhibit strong Pressure-dimension performances with minimal stress indicators yet show only moderate comprehensive resilience (CI ≈ 0.42). This paradox stems from imbalances between their stress mitigation and adaptive capacity development [71]. Yangzhou, despite low demographic pressures and corporate debt levels, suffers from insufficient endogenous growth momentum due to policy biases that favor the southern regions (fiscal expenditure barrier intensity: 9.16%). Systemic weaknesses persist in the State dimension of patent application density (e.g., Taizhou B9 barrier: 8.19%) and in Response-dimension fiscal expenditure ratios across the central–northern cities, highlighting that mere stress reduction cannot enhance resilience without strengthening institutional learning and innovation-driven transformation capacities.
4.2. Mechanistic Pathways of Core Barrier Factors
Based on the obstacle degree analysis, the Fiscal Expenditure/GDP Ratio (C2 avg: 7.33%), Licensed Physicians per 10,000 Residents (B7 avg: 7.16%), and Patent Application Density (B9 avg: 6.79%) emerged as the three primary constraints on urban resilience enhancement in Jiangsu. The obstacle effect of fiscal expenditure ratios paradoxically intensifies in economically robust cities like Nanjing and Wuxi. Local governments likely face trade-offs between public service investments and industrial/trade expenditures. Nanjing’s fiscal expenditure obstacle degree peaks at 13.08%, necessitating scrutiny of this high-input–low-efficiency model. Unresolved, this imbalance may compress the fiscal flexibility in maintaining public welfare during crises, eroding governmental credibility.
Healthcare resource scarcity manifests more acutely in Northern Jiangsu cities. Xuzhou and Suqian’s low physician-to-population ratios (e.g., Xuzhou B7 barrier: 6.82%) suggest diminished healthcare system resilience thresholds during pandemics or disasters [72]. The disproportionate concentration of premium medical resources (e.g., tertiary hospitals, specialists) in Nanjing and Suzhou contrasts starkly with Northern Jiangsu’s resource deficits despite higher population densities [73]. Grassroots medical institutions further suffer from insufficient general practitioners and subpar service quality, weakening primary healthcare services at the community level and allowing risks to escalate unchecked [74].
Innovation capacity deficits rank third among the resilience constraints. While Suzhou and Nanjing lead nationally in patent applications, critical gaps persist in the technology transfer efficiency and SME innovation initiative. Suzhou Industrial Park’s agglomeration of high-tech enterprises coexists with peripheral counties’ heavy reliance on traditional manufacturing (e.g., textiles, machinery), constrained by workforce skill barriers and transient talent inflows [75]. This core–periphery innovation disparity severely limits knowledge spillovers [76]. For cities like Huai’an and Yancheng, fiscal constraints, limited academic institutions, low R&D investment, and “brain drain” hinder systemic functional upgrading through technological innovation.
4.3. Dynamic System Analysis of Pressure–State–Response Interactions
The PSR framework reveals coupling characteristics in urban resilience evolution. High-resilience cities achieve systemic stability through positive feedback loops between the Pressure and Response dimensions, with adaptive capacities potentially enhancing post-shock recovery. Take Suzhou as an example: In its Pressure dimension, prioritizing tertiary industry development over industrialization alleviates industrial pollution and energy consumption impacts [77]. The Response dimension leverages export-oriented economies to attract international capital, financing technological innovation and establishing a virtuous cycle [78]. At the macro level, Suzhou demonstrates agility in trade structure adjustments amid global supply chain and financial volatilities, mitigating an overreliance on singular markets.
Moderate-resilience cities exhibit systemic interaction imbalances. Nantong exemplifies this: While demonstrating strong “household savings capacity” in the State dimension, its Response dimension suffers from inefficient financial resource conversion. Despite abundant household deposits, limited corporate financing channels trap capital within banking systems, failing to mobilize market mechanisms for risk-resilient investments [79]. Conservative credit policies and immature SME credit evaluation systems further constrain the financial market vitality [80]. Institutional innovations like optimized credit incentives and risk-sharing funds are imperative to activate dormant resources.
Low-resilience cities face compounded vulnerabilities from intersecting obstacles. Suqian’s fragility arises when Pressure-dimension corporate debt ratios escalate alongside State-dimension social security deficiencies, creating resonance effects that amplify crisis risks. Exogenous economic shocks triggering profit declines may force workforce reductions. Incomplete unemployment insurance coverage could leave displaced workers without basic safeguards, escalating social tensions and prolonging risk-recovery cycles [81]. Thus, constructing comprehensive multi-tiered social safety nets urgently necessitates policy prioritization for low-resilience cities.
5. Conclusions and Recommendations
As a developed coastal province in eastern China, Jiangsu exhibits pronounced north–south gradient disparities in comprehensive urban resilience, with Southern Jiangsu cities demonstrating markedly higher resilience levels than their northern counterparts. Through the PSR-TOPSIS modeling framework, these disparities emerge from dynamic interactions across the Pressure–State–Response dimensions. High-resilience cities such as Nanjing, Suzhou, and Wuxi in Southern Jiangsu exhibit superior performance in the State and Response dimensions, leveraging robust economic foundations, innovation capacities, and fiscal resources to construct effective risk-resistant mechanisms. The crux lies in establishing a virtuous cycle that simultaneously alleviates pressures and fortifies responsive capacities. Conversely, Northern Jiangsu cities like Suqian and Xuzhou face systemic fragility due to mono-industrial structures, insufficient social security, and infrastructure deficiencies.
Evolutionary pathways for risk resistance diverge across resilience tiers. High-resilience cities can establish positive feedback mechanisms through stress mitigation and response enhancement, enabling transitions to higher-order stability. Medium-resilience cities exhibit constrained capacity for transforming accumulated strengths into systemic resilience due to internal coordination deficits. Low-resilience cities struggle to alleviate severe shocks due to compounded vulnerabilities from multi-factor negative synergies.
From the perspective of the Pressure dimension, industrial structure imbalances, demographic pressures, and energy consumption intensity constitute primary stressors constraining urban resilience. Southern Jiangsu alleviates resource–environmental pressures through tertiary-industry-led structural optimization, while Northern Jiangsu’s reliance on traditional industrial models undermines its systemic disturbance resistance. In the State dimension, medical resource shortages and innovation capacity deficits represent province-wide systemic vulnerabilities. Inadequate investments in public health and technological innovation exacerbate these weaknesses. In the Response dimension, inefficient fiscal expenditure allocation and insufficient open-economy resilience emerge as critical bottlenecks. Even cities with substantial fiscal inputs fail to convert resources into effective risk-countering capacities due to suboptimal allocation strategies.
The obstacle degree model identifies fiscal expenditure efficiency, medical resource allocation, and innovation-driven capacities as three core constraints. Research confirms that single-dimensional advantages cannot sustain systemic resilience, necessitating functional upgrading through cross-element synergy. For instance, Nanjing’s substantial fiscal investments yield limited responsiveness due to inefficient utilization. Suzhou and Wuxi’s innovation capacities are structurally constrained by technology transfer inefficiencies and insufficient regional synergy, thus failing to fully harness innovation dividends, while pervasive knowledge silos impede technological diffusion; concurrently, cities in Northern Jiangsu exhibit a significant developmental lag in public service equalization.
Methodologically, integrated weighting effectively balances subjective–objective deviations, while TOPSIS modeling and obstacle diagnostics enhance the analytical rigor. These findings provide empirical foundations for resilience governance in the Yangtze River Delta urban agglomeration, revealing structural contradictions in current urban management practices. The study offers actionable insights for cross-regional collaborative governance, innovation-driven development, and risk-mitigation strategies. We propose the following actionable strategies:
- Optimize the Fiscal Expenditure Structure
Refine fiscal fund performance evaluation systems by incorporating resilience enhancement metrics into government budget assessments. For cities like Nanjing and Suzhou with high fiscal expenditure ratios yet low efficiency, prioritize funding allocations to resilience-critical sectors, including public health and emergency infrastructure, within defined thresholds while reducing inefficient administrative expenditures. Northern Jiangsu cities should focus on strengthening medical and transportation infrastructure deficiencies.
- Promote Regional Medical Resource Equalization
In cities with subpar medical resources like Xuzhou and Suqian, enhance grassroot service capacities through tiered support systems in which provincial tertiary hospitals partner with township clinics, complemented by telemedicine coverage. Incentivize south-to-north medical resource flows by offering professional title evaluation bonuses and housing subsidies for physicians practicing in the northern regions.
- Strengthen Industrial Innovation Synergy Mechanisms
Establish technology transfer centers in innovation hubs to diffuse patented technologies to underperforming regions. Provide tax incentives and innovation subsidies for SMEs in Northern Jiangsu. Support coastal port cities like Yancheng and Lianyungang in developing marine economy pilot zones and port-adjacent industrial innovation clusters.
- Develop an Adaptive Management Framework for Population Mobility
For cities with low demographic pressures like Yangzhou and Taizhou, enhance migrant integration through affordable housing provision and vocational skills training. In cities experiencing resident-registered population imbalances like Wuxi and Changzhou, incorporate resilience-building metrics (e.g., community emergency training participation) into points-based household registration systems.
- Enhance Open-Economy Risk Resilience
Establish a Yangtze River Delta import–export risk monitoring platform to intensify the supply chain surveillance for export-dependent cities like Suzhou and Nantong. Improve enterprise credit insurance mechanisms to mitigate exchange-rate volatility impacts on SMEs. Support Yancheng and Lianyungang in diversifying export markets to reduce single-market dependency risks.
- Accelerate Green Energy Transition
Implement tiered energy-saving retrofit programs for high-consumption industries in Xuzhou and Zhenjiang, recognizing compliant enterprises as low-carbon exemplars. Establish pilot carbon quota trading systems in steel and chemical sectors, allocating saved quotas to fund enterprise resilience infrastructure.
This study’s methodological framework exhibits significant potential for international dissemination. The PSR framework accommodates complex system analyses across diverse scales; through flexible indicator system adjustments, it can be adapted to ecological resilience assessments or climate adaptation research in global cities ranging from European–American to Southeast Asian contexts. The distance measurement approach of the TOPSIS model—being independent of region-specific statistical standards—enables cross-regional comparative analyses of urban resilience after appropriate calibration. For instance, applications for African cities could employ TOPSIS and barrier diagnosis models to identify critical constraints within water scarcity and urbanization processes, thereby providing evidence-based analytical toolkits for global urban resilience governance.
This study acknowledges several limitations warranting further research. First, the reliance on static statistical yearbook data may inadequately capture dynamic socioeconomic transitions, with real-time impacts of industrial restructuring insufficiently reflected. Second, the Pressure–State–Response model’s assumption of equal dimensional weighting potentially obscures nonlinear feedback mechanisms within systems, limiting its explanatory power for cities with institutional misalignments. Third, risk factors such as natural disasters and industrial accidents remain underrepresented in the indicator system. Future research should extend the temporal dimensions by integrating real-time monitoring data to enhance timeliness, develop dynamic weighting models to accommodate resilience evolution patterns across development stages, and refine the assessment framework through ecological safety and public security indicators. Cross-provincial comparative validation of the model’s generalizability and an analysis of residents’ collective behavioral impacts on systemic resilience constitute additional critical avenues.
Author Contributions
Conceptualization, Z.Z. and Y.R.; methodology, Z.Z. and C.L.; software, Z.Z.; validation, W.C. and Y.R.; formal analysis, C.L.; investigation, Z.Z., C.L., W.C. and Y.R.; resources, Z.Z.; data curation, Z.Z.; writing—original draft, Z.Z.; writing—review and editing, C.L., W.C. and Y.R.; visualization, W.C.; supervision, Y.R.; project administration, Z.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Horizontal Projects of Local Research Institutes: Comprehensive Evaluation of Environmental and Economic Impact of Urban Renewable Water Use in Jiangsu Province and Research on Collaborative Countermeasures (grant number 823149816); the Fundamental Research Funds for the Central Universities: Research on Organizational Coordination of Flood Disaster Management in Jiangsu Province under the Framework of “Great Security” (grant number B240207048); and the General Research Projects of Philosophy and Social Sciences in Jiangsu Universities: Research on the Internal Mechanism and Regulation Countermeasures of the Evolution and Upgrading of Urban Innovation Chain in the Yangtze River Delta Driven by Digital Economy (grant number 2023SJYB0042).
Institutional Review Board Statement
The local Ethics Committee of Hohai University approved the consent form.
Informed Consent Statement
Not applicable.
Data Availability Statement
The evaluation data selected in this article are all derived from the following authoritative publications: the China Urban Construction Statistical Yearbook 2024, the China Regional Economic Statistical Yearbook 2024, the Jiangsu Statistical Yearbook 2024, and the Jiangsu Provincial Government Work Report 2024, along with statistical yearbooks and socioeconomic development bulletins from all 13 prefecture-level cities in Jiangsu Province. These data are accessible through official publications or open government reports, and researchers can apply through formal channels for their utilization.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
Appendix A.1. Details of the Construction of AHP Group Judgment Matrices and the Weight Calculation
Let a criterion layer contain k indicators. For expert e (e = 1, 2, …, 8), the constructed judgment matrix is denoted as Ae = (aeij)k×k, satisfying the positive reciprocity property aeij = 1/aeji with diagonal elements aeii = 1. To mitigate extreme value interference in the group consensus, we aggregated individual judgment matrices using the geometric mean method to form the group judgment matrix A = (aij)k×k, whose elements are calculated as
The logarithmic transformation of this method yields
The geometric mean method preserves the positive reciprocity of judgment matrices while demonstrating lower sensitivity to outliers compared with arithmetic mean approaches.
Next, the eigenvector method was employed to derive the weight vector from the group judgment matrix A. This involves calculating the matrix’s maximum eigenvalue λmax and its corresponding normalized eigenvector WAHP = (w1, w2, …, wk)T, such that the following is satisfied:
Numerical solutions were computed via the Power Iteration method. First, initialize a random positive vector W(0) = (1/k, 1/k, …, 1/k)T, with a convergence threshold set at ϵ = 10−6. Iteratively compute W(t+1) = AW(t)/∥AW(t)∥1 until ∥W(t+1) − W(t)∥2 < ϵ. Finally, calculate the maximum eigenvalue:
Appendix A.2. Details of the Weight Calculation Using the Entropy Weight Method
For each indicator j in the Pressure dimension, compute its information entropy EP,j:
where the probability distribution pP,ij is defined as
Calculate the divergence coefficients to measure the indicator dispersion:
Through normalization, the relative importance of indicators within the dimension is reflected, yielding entropy weights for the Pressure-dimension indicator j:
Analogously, the State- and Response-dimension weights are computed as
References
- Jabareen, Y. Planning the resilient city: Concepts and strategies for coping with climate change and environmental risk. Cities 2013, 31, 220–229. [Google Scholar]
- Zhang, X.; Tian, C. Measurement and Influencing Factors of Regional Economic Resilience in China. Sustainability 2024, 16, 3338. [Google Scholar] [CrossRef]
- Ding, Z.; Wang, G.; Liu, Z.; Long, R. Research on differences in the factors influencing the energy-saving behavior of urban and rural residents in China–A case study of Jiangsu Province. Energy Policy 2017, 100, 252–259. [Google Scholar]
- He, W.; Li, X.; Yang, J.; Ni, H.; Sang, X. How land use functions evolve in the process of rapid urbanization: Evidence from Jiangsu Province, China. J. Clean. Prod. 2022, 380, 134877. [Google Scholar]
- Li, H.; Liu, Z.; James, N.; Li, X.; Hu, Z.; Shi, H.; Sun, L.; Lu, Y.; Jia, X. Agricultural transformations and their influential factors revealed by archaeobotanical evidence in Holocene Jiangsu Province, eastern China. Front. Earth Sci. 2021, 9, 661684. [Google Scholar]
- Peng, B.; Li, Y.; Elahi, E.; Wei, G. Dynamic evolution of ecological carrying capacity based on the ecological footprint theory: A case study of Jiangsu province. Ecol. Indic. 2019, 99, 19–26. [Google Scholar]
- Wei, Y.D.; Wu, Y.; Liao, F.H.; Zhang, L. Regional inequality, spatial polarization and place mobility in provincial China: A case study of Jiangsu province. Appl. Geogr. 2020, 124, 102296. [Google Scholar]
- Yang, L.; Shen, F.; Zhang, L.; Cai, Y.; Yi, F.; Zhou, C. Quantifying influences of natural and anthropogenic factors on vegetation changes using structural equation modeling: A case study in Jiangsu Province, China. J. Clean. Prod. 2021, 280, 124330. [Google Scholar]
- Zang, Y.; Yang, Y.; Liu, Y. Understanding rural system with a social-ecological framework: Evaluating sustainability of rural evolution in Jiangsu province, South China. J. Rural Stud. 2021, 86, 171–180. [Google Scholar]
- Gulyas, B.Z.; Edmondson, J.L. Increasing city resilience through urban agriculture: Challenges and solutions in the Global North. Sustainability 2021, 13, 1465. [Google Scholar] [CrossRef]
- Holling, C.S. Resilience and stability of ecological systems. Annu. Rev. Ecol. Syst. 1973, 4, 1–23. [Google Scholar]
- Apostu, S.A.; Vasile, V.; Vasile, R.; Rosak-Szyrocka, J. Do smart cities represent the key to urban resilience? Rethinking urban resilience. Int. J. Environ. Res. Public Health 2022, 19, 15410. [Google Scholar] [PubMed]
- Gimenez, R.; Labaka, L.; Hernantes, J. A maturity model for the involvement of stakeholders in the city resilience building process. Technol. Forecast. Soc. Change 2017, 121, 7–16. [Google Scholar]
- Leitner, H.; Sheppard, E.; Webber, S.; Colven, E. Globalizing urban resilience. Urban Geogr. 2018, 39, 1276–1284. [Google Scholar]
- Marana, P.; Eden, C.; Eriksson, H.; Grimes, C.; Hernantes, J.; Howick, S.; Labaka, L.; Latinos, V.; Lindner, R.; Majchrzak, T.A. Towards a resilience management guideline—Cities as a starting point for societal resilience. Sustain. Cities Soc. 2019, 48, 101531. [Google Scholar]
- Shamsuddin, S. Resilience resistance: The challenges and implications of urban resilience implementation. Cities 2020, 103, 102763. [Google Scholar]
- Wang, J.; Wang, J.; Zhang, J. Spatial distribution characteristics of natural ecological resilience in China. J. Environ. Manag. 2023, 342, 118133. [Google Scholar]
- Bruneau, M.; Chang, S.E.; Eguchi, R.T.; Lee, G.C.; O’Rourke, T.D.; Reinhorn, A.M.; Shinozuka, M.; Tierney, K.; Wallace, W.A.; Von Winterfeldt, D. A framework to quantitatively assess and enhance the seismic resilience of communities. Earthq. Spectra 2003, 19, 733–752. [Google Scholar]
- Feng, X.; Xiu, C.; Bai, L.; Zhong, Y.; Wei, Y. Comprehensive evaluation of urban resilience based on the perspective of landscape pattern: A case study of Shenyang city. Cities 2020, 104, 102722. [Google Scholar]
- Chen, H.; Li, G.; Li, M.; Lyu, L.; Zhang, T. A cross-sectional study on nurse turnover intention and influencing factors in Jiangsu Province, China. Int. J. Nurs. Sci. 2018, 5, 396–402. [Google Scholar]
- Jing, X.; Tian, G.; He, Y.; Wang, M. Spatial and temporal differentiation and coupling analysis of land use change and ecosystem service value in Jiangsu Province. Ecol. Indic. 2024, 163, 112076. [Google Scholar]
- Büyüközkan, G.; Ilıcak, Ö.; Feyzioğlu, O. A review of urban resilience literature. Sustain. Cities Soc. 2022, 77, 103579. [Google Scholar]
- Hatuka, T.; Rosen-Zvi, I.; Birnhack, M.; Toch, E.; Zur, H. The political premises of contemporary urban concepts: The global city, the sustainable city, the resilient city, the creative city, and the smart city. Plan. Theory Pract. 2018, 19, 160–179. [Google Scholar]
- Feng, X.; Xiu, C.; Li, J.; Zhong, Y. Measuring the evolution of urban resilience based on the Exposure–Connectedness–Potential (ECP) approach: A case study of shenyang city, china. Land 2021, 10, 1305. [Google Scholar]
- Foster, K.A.; Barnes, W.R. Reframing regional governance for research and practice. Urban Aff. Rev. 2012, 48, 272–283. [Google Scholar]
- The Rockefeller Foundation and ARUP. City Resilience Framework; The Rockefeller Foundation and ARUP: New York, NY, USA, 2014; p. 928. [Google Scholar]
- Sharifi, A.; Yamagata, Y. Resilience-oriented urban planning. In Resilience-Oriented Urban Planning: Theoretical and empirical insights; Springer: Berlin/Heidelberg, Germany, 2018; pp. 3–27. [Google Scholar]
- Kusumastuti, R.D.; Husodo, Z.A.; Suardi, L.; Danarsari, D.N. Developing a resilience index towards natural disasters in Indonesia. Int. J. Disaster Risk Reduct. 2014, 10, 327–340. [Google Scholar]
- Plummer, R.; Armitage, D. A resilience-based framework for evaluating adaptive co-management: Linking ecology, economics and society in a complex world. Ecol. Econ. 2007, 61, 62–74. [Google Scholar]
- Shaw, R.; Sharma, A. Climate and Disaster Resilience in Cities; Emerald Group Publishing: Leeds, UK, 2011. [Google Scholar]
- Ebisudani, M.; Tokai, A. Resilience: Ecological and Engineering Perspectives Present Status and Future Consideration Referring on Two Case Studies in US. In Proceedings of the 2014 SRA Japan Conference, Kyoto, Japan, 28–30 November 2014; Society for Risk Analysis Japan, Kyoto University: Kyoto, Japan. [Google Scholar]
- Bonati, S. Resilientscapes: Perception and resilience to reduce vulnerability in the island of Madeira. Procedia Econ. Financ. 2014, 18, 513–520. [Google Scholar]
- Li, H.; Wang, Y.; Zhang, H.; Yin, R.; Liu, C.; Wang, Z.; Fu, F.; Zhao, J. The spatial-temporal evolution and driving mechanism of Urban resilience in the Yellow River Basin cities. J. Clean. Prod. 2024, 447, 141614. [Google Scholar]
- Cook, G.S.; Fletcher, P.J.; Kelble, C.R. Towards marine ecosystem based management in South Florida: Investigating the connections among ecosystem pressures, states, and services in a complex coastal system. Ecol. Indic. 2014, 44, 26–39. [Google Scholar]
- Rapport, D.J.; Singh, A. An ecohealth-based framework for state of environment reporting. Ecol. Indic. 2006, 6, 409–428. [Google Scholar]
- Bai, X.; Tang, J. Ecological security assessment of Tianjin by PSR model. Procedia Environ. Sci. 2010, 2, 881–887. [Google Scholar]
- Boelee, E.; Geerling, G.; van der Zaan, B.; Blauw, A.; Vethaak, A.D. Water and health: From environmental pressures to integrated responses. Acta Trop. 2019, 193, 217–226. [Google Scholar] [PubMed]
- Chen, X.; Rong, F.; Li, S. Driving force–pressure–state–impact–response-based evaluation of rural human settlements’ resilience and their influencing factors: Evidence from Guangdong, China. Sustainability 2024, 16, 813. [Google Scholar]
- Zhou, Q.; Zhu, M.; Qiao, Y.; Zhang, X.; Chen, J. Achieving resilience through smart cities? Evidence from China. Habitat Int. 2021, 111, 102348. [Google Scholar]
- Cheng, H.; Zhu, L.; Meng, J. Fuzzy evaluation of the ecological security of land resources in mainland China based on the Pressure-State-Response framework. Sci. Total Environ. 2022, 804, 150053. [Google Scholar]
- Meyer, N.; Auriacombe, C. Good urban governance and city resilience: An afrocentric approach to sustainable development. Sustainability 2019, 11, 5514. [Google Scholar] [CrossRef]
- Sekovski, I.; Newton, A.; Dennison, W.C. Megacities in the coastal zone: Using a driver-pressure-state-impact-response framework to address complex environmental problems. Estuar. Coast. Shelf Sci. 2012, 96, 48–59. [Google Scholar]
- Yin, S.; Zhang, N.; Ullah, K.; Gao, S. Enhancing digital innovation for the sustainable transformation of manufacturing industry: A pressure-state-response system framework to perceptions of digital green innovation and its performance for green and intelligent manufacturing. Systems 2022, 10, 72. [Google Scholar]
- Chelleri, L. From the «Resilient City» to Urban Resilience. A review essay on understanding and integrating the resilience perspective for urban systems. Doc. D’anàlisi Geogràfica 2012, 58, 287–306. [Google Scholar]
- Liu, D.; Hao, S. Ecosystem health assessment at county-scale using the pressure-state-response framework on the Loess Plateau, China. Int. J. Environ. Res. Public Health 2017, 14, 2. [Google Scholar]
- Amirzadeh, M.; Sobhaninia, S.; Sharifi, A. Urban resilience: A vague or an evolutionary concept? Sustain. Cities Soc. 2022, 81, 103853. [Google Scholar]
- Debnath, R.; Pettit, C.; Leao, S.Z. Geodesign approaches to city resilience planning: A systematic review. Sustainability 2022, 14, 938. [Google Scholar] [CrossRef]
- Huang, G.; Li, D.; Zhu, X.; Zhu, J. Influencing factors and their influencing mechanisms on urban resilience in China. Sustain. Cities Soc. 2021, 74, 103210. [Google Scholar]
- Li, D.; Yang, W.; Huang, R. The multidimensional differences and driving forces of ecological environment resilience in China. Environ. Impact Assess. Rev. 2023, 98, 106954. [Google Scholar]
- Wang, H.; Liu, Z.; Zhou, Y. Assessing urban resilience in China from the perspective of socioeconomic and ecological sustainability. Environ. Impact Assess. Rev. 2023, 102, 107163. [Google Scholar]
- Dong, F.; Pan, Y.; Zhang, X.; Sun, Z. How to evaluate provincial ecological civilization construction? The case of Jiangsu province, China. Int. J. Environ. Res. Public Health 2020, 17, 5334. [Google Scholar]
- Kong, Y.; He, W.; Shen, J.; Yuan, L.; Gao, X.; Ramsey, T.S.; Peng, Q.; Degefu, D.M.; Sun, F. Adaptability analysis of water pollution and advanced industrial structure in Jiangsu Province, China. Ecol. Model. 2023, 481, 110365. [Google Scholar]
- Lyu, H.; Dong, Z.; Roobavannan, M.; Kandasamy, J.; Pande, S. Rural unemployment pushes migrants to urban areas in Jiangsu Province, China. Palgrave Commun. 2019, 5, 92. [Google Scholar]
- Shi, G.; Ye, P.; Ding, L.; Quinones, A.; Li, Y.; Jiang, N. Spatio-temporal patterns of land use and cover change from 1990 to 2010: A case study of Jiangsu Province, China. Int. J. Environ. Res. Public Health 2019, 16, 907. [Google Scholar]
- Tang, S.; Lee, H.F.; Huang, X.; Zhou, J. Poverty Stories of rural households in China: The case of North Jiangsu. J. Rural Stud. 2022, 91, 1–9. [Google Scholar]
- Wu, C.; Chen, B.; Huang, X.; Wei, Y.D. Effect of land-use change and optimization on the ecosystem service values of Jiangsu province, China. Ecol. Indic. 2020, 117, 106507. [Google Scholar]
- Yi, X.; Jue, W.; Huan, H. Does economic development bring more livability? Evidence from Jiangsu Province, China. J. Clean. Prod. 2021, 293, 126187. [Google Scholar]
- Zhang, L.; Wu, Y. Market segmentation and willingness to pay for green electricity among urban residents in China: The case of Jiangsu Province. Energy Policy 2012, 51, 514–523. [Google Scholar]
- Zhang, M.; Wang, W. Decouple indicators on the CO2 emission-economic growth linkage: The Jiangsu Province case. Ecol. Indic. 2013, 32, 239–244. [Google Scholar]
- De Falco, S.; Angelidou, M.; Addie, J.-P.D. From the “smart city” to the “smart metropolis”? Building resilience in the urban periphery. Eur. Urban Reg. Stud. 2019, 26, 205–223. [Google Scholar]
- Fu, Y.; Zhou, T.; Yao, Y.; Qiu, A.; Wei, F.; Liu, J.; Liu, T. Evaluating efficiency and order of urban land use structure: An empirical study of cities in Jiangsu, China. J. Clean. Prod. 2021, 283, 124638. [Google Scholar]
- Croese, S.; Green, C.; Morgan, G. Localizing the sustainable development goals through the lens of urban resilience: Lessons and learnings from 100 resilient cities and cape town. Sustainability 2020, 12, 550. [Google Scholar] [CrossRef]
- Feng, Y.; Lee, C.-C.; Peng, D. Does regional integration improve economic resilience? Evidence from urban agglomerations in China. Sustain. Cities Soc. 2023, 88, 104273. [Google Scholar]
- Glaeser, E.L. Urban resilience. Urban Stud. 2022, 59, 3–35. [Google Scholar]
- Saaty, T.L. Absolute and relative measurement with the AHP. The most livable cities in the United States. Socio-Econ. Plan. Sci. 1986, 20, 327–331. [Google Scholar]
- Saaty, T.L. Highlights and critical points in the theory and application of the analytic hierarchy process. Eur. J. Oper. Res. 1994, 74, 426–447. [Google Scholar]
- Hwang, C.-L.; Yoon, K.; Hwang, C.-L.; Yoon, K. Methods for multiple attribute decision making. In Multiple Attribute Decision Making: Methods and Applications a State-of-the-Art Survey; Springer: Berlin/Heidelberg, Germany, 1981; pp. 58–191. [Google Scholar]
- Li, Q.; Wei, J.; Jiang, F.; Zhou, G.; Jiang, R.; Chen, M.; Zhang, X.; Hu, W. Equity and efficiency of health care resource allocation in Jiangsu Province, China. Int. J. Equity Health 2020, 19, 211. [Google Scholar] [PubMed]
- Liu, Y.; Wang, J.; Long, H. Analysis of arable land loss and its impact on rural sustainability in Southern Jiangsu Province of China. J. Environ. Manag. 2010, 91, 646–653. [Google Scholar]
- Lu, X.; Shi, Y.; Chen, C.; Yu, M. Monitoring cropland transition and its impact on ecosystem services value in developed regions of China: A case study of Jiangsu Province. Land Use Policy 2017, 69, 25–40. [Google Scholar]
- Wang, L.; Liu, Y.; Sun, C.; Liu, Y. Accessibility impact of the present and future high-speed rail network: A case study of Jiangsu Province, China. J. Transp. Geogr. 2016, 54, 161–172. [Google Scholar]
- You, X.; Sun, Y.; Liu, J. Evolution and analysis of urban resilience and its influencing factors: A case study of Jiangsu Province, China. Nat. Hazards 2022, 113, 1751–1782. [Google Scholar]
- Zhang, M.; Song, Y.; Li, P.; Li, H. Study on affecting factors of residential energy consumption in urban and rural Jiangsu. Renew. Sustain. Energy Rev. 2016, 53, 330–337. [Google Scholar]
- Cadogan, C.A.; Hughes, C.M. On the frontline against COVID-19: Community pharmacists’ contribution during a public health crisis. Res. Soc. Adm. Pharm. 2021, 17, 2032–2035. [Google Scholar]
- Zhang, M.; Zhang, K.; Hu, W.; Zhu, B.; Wang, P.; Wei, Y.-M. Exploring the climatic impacts on residential electricity consumption in Jiangsu, China. Energy Policy 2020, 140, 111398. [Google Scholar]
- Khatibi, H.; Wilkinson, S.; Eriwata, G.; Sweya, L.N.; Baghersad, M.; Dianat, H.; Ghaedi, K.; Javanmardi, A. An integrated framework for assessment of smart city resilience. Environ. Plan. B Urban Anal. City Sci. 2022, 49, 1556–1577. [Google Scholar]
- Li, H.-B.; Zhang, X.-L.; Wu, Q.-Y.; Wang, Y.-H. Characteristics and mechanism of rural settlements spatial reconstruction in developed areas—A case study of southern Jiangsu. J. Nat. Resour. 2015, 30, 591–603. [Google Scholar]
- Li, X.; Fang, B.; Yin, R.-M.; Rong, H.-F. Spatial-temporal change and collaboration/trade-off relationship of” production-living-ecological” functions in county area of Jiangsu province. J. Nat. Resour. 2019, 34, 2363–2377. [Google Scholar]
- Xiao, S.; Wu, W.; Guo, J.; Ou, M.; Pueppke, S.G.; Ou, W.; Tao, Y. An evaluation framework for designing ecological security patterns and prioritizing ecological corridors: Application in Jiangsu Province, China. Landsc. Ecol. 2020, 35, 2517–2534. [Google Scholar]
- Huang, J.; Geng, H. Investigating of Spatiotemporal Correlation between Urban Spatial Form and Urban Ecological Resilience: A Case Study of the City Cluster in the Yangzi River Midstream, China. Buildings 2024, 14, 274. [Google Scholar] [CrossRef]
- Zhu, S.; Li, D.; Feng, H. Is smart city resilient? Evidence from China. Sustain. Cities Soc. 2019, 50, 101636. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).