Abstract
Land-use fragmentation is an important issue for land management and rural development. For the last few decades, the relationship between mankind and land has become more dynamic though the traditional cadastral system has been slow in responding to the changing needs of society. Associated with land-use fragmentation, there are different sizes of land parcels with different biophysical characteristics that will dictate different land management decisions, and, in many countries, it is a problem that constitutes a challenge for correct land management. This article proposes a compromise programming approach for determining the biophysical potential of land parcels. This approach was implemented in Loulé municipality, Portugal, in more than 50,000 parcels. Results were promising since the approach was able to build a ranking of parcels that have different biophysical conditions, proving that this approach is relevant and interesting for land management.
1. Introduction
The land register is a parcel-based land information database that integrates the rights, restrictions and responsibilities existing within the territory [1]. National agencies who are responsible for conducting these surveys are in a good position to manage the development of the landscape [2]. In recent years, the relationship between society and land has become dynamic and interconnected. Nevertheless, the cadastral system is slow in answering the needs of governments, companies and society [3]. Understanding the concepts of land parcel boundaries implies knowing land descriptions [1,4]. Therefore, land register is a multipurpose tool that helps efficient land markets, protects land rights, supports long-term land management [5] and is a crucial component of land administration [1].
Land is a scarce resource, subject to different interests and objectives [2]. Therefore, land administration is regarded as a component of the infrastructure that allows the interaction of society with land, aiming for sustainable development of the territory. Land administration integrates the efficiency of land markets, land valuation and taxation with different uses of land [2]. Therefore, studying the biophysical potential of each of the land parcels is an important issue that is related to understanding its impact in land fragmentation. This is crucial in Portugal, namely, in areas where the cadastral registry was recently carried out, as is the case of Loulé municipality, which is an area where there are very conflicting uses (namely, agriculture and urbanism), and the potential of each land parcel should be carefully analyzed to understand land fragmentation and better managing the territory considering the conflicting activities. In this municipality, the biophysical potential needs to be defined for agricultural and forest uses. Usual biophysical suitability maps constructed using the additive weighted sum of biophysical scores [6,7,8] are limited because they do not prevent the fact that there may be several criteria with low values masked by one with a considerable high value. Considering the most balanced situation is an interesting proposal, since it allows respecting minimum requirements for several biophysical criteria, overpassing the limitations identified.
Moreover, different criteria may have different relevance for building biophysical suitability maps, and the opinion of stakeholders and experts may need to be integrated. Finally, the statistical relations among land parcel size and biophysical indexes need to be analyzed.
Therefore, the following research problems were formulated: (1) to develop a suitability biophysical map method that, considering land uses, should be able to integrate not only the best aggregated solution of suitability but also to provide information on the most balanced one; (2) to integrate stakeholders’ and managers’ preferences; (3) to establish a relation among land register parcel size and biophysical suitability; and (4) to define the typologies of biophysical suitability conditions.
Geographical Information Systems (GISs) are increasingly recognized as valuable tools for land-use identification and the creation of biophysical suitability maps. GIS platforms facilitate the retrieval, processing and manipulation of data to analyze and visualize various quality indices relevant to land suitability [9]. Land-use suitability tries to identify the correct spatial pattern for future land uses considering requirements and preferences for the activities to be developed within the territory [10,11]. The GIS suitability analysis has been implemented in a wide variety of problems, which include the ecology, geological favorability, and suitability of land for agricultural activities [11].
Multi-criteria decision analysis (MCDA) has been widely employed in numerous research endeavors and decision-making contexts. Fundamentally, a multi-criteria decision problem involves a set of alternatives that are assessed against various criteria based on the decision-maker’s preferences [12]. Spatial raster GIS models can effectively integrate diverse criteria to generate maps that support informed decision making [13], offering a standardized framework for evaluating multiple management options.
In the context of MCDA, several approaches allow weighting criteria. Pairwise comparison is a commonly used and relevant approach for defining the relative importance of several criteria [14]. One of the most widely applied pairwise comparison techniques is the AHP (analytical hierarchy process), which is based on the human ability to estimate magnitudes using pairwise comparisons of criteria. In more recent studies, the authors of [14] introduced an extended goal programming (EGP) approach for aggregating pairwise comparison matrices. This methodology has subsequently been applied by the studies of [15,16,17]. Regarding the aggregation of criteria, various approaches exist [18], ranging from simple methods like weighted averages to more complex techniques. One interesting technique is compromise programming, which has been implemented in several studies for sustainability analysis [19,20,21,22]. Notably, compromise programming [19,20,21,22] has not been previously applied to the assessment of biophysical land parcel suitability. Forest and agricultural, biophysical land suitability should consider not only the best aggregate but also the distribution and equilibrium among the several indicators considered. Therefore, compromise programming offers several operational advantages, since it considers the ‘‘maximum aggregate biophysical potential’’ (an engineering solution) and the ‘‘most balanced biophysical potential’’ (a balanced solution), besides allowing us to identify several intermediate solutions.
Furthermore, the authors of [21,22] proposed an entropy-based approach, incorporating the information index, to enhance the outcomes of their research. However, the authors did not explore the information index as a standalone criterion for selecting the most balanced solution. The information index, originating in the field of physics, was introduced by Shannon in information science as a function to quantify uncertainty. Additionally, the simultaneous consideration of both the most balanced solution and the information index could potentially yield valuable insights. These authors also proposed simultaneously solving the compromise programming model for dealing with about 300 units, but the considerable number of biophysical units that involves the biophysical suitability maps still poses a challenge for implementing a compromise programming model in biophysical suitability analysis.
To analyze the relations between land parcels and the resulting biophysical suitability scores for agricultural and forest uses, and, if they are statistically significant, methods such as bivariate correlations and statistical tests may be used. Moreover, clustering techniques may be used to classify the territory considering its biophysical characteristics. Clustering is a fundamental task within the field of data mining, employed to identify distinct groups or patterns within a dataset. Clustering algorithms partition data into subsets based on similarity or dissimilarity measures, such that elements within a cluster exhibit a greater degree of similarity to one another compared to elements belonging to different clusters [23].
This paper proposes a novel approach that uses MCDA to build biophysical maps, in combination with statistical techniques, namely, multivariate and statistical analysis (bivariate correlation and ANOVA—Analysis of Variance) in a GIS environment that presents several innovations regarding previous studies [19,20,21,22]. A new compromise programming approach is presented and implemented, using as a case study the biophysical suitability of the rural cadastral registry parcels of Loulé municipality, providing results that not only allow us to account the best aggregated suitability but also the most balanced one. The most balanced suitability is analyzed using both the maximum deviation and the information index, resulting from an entropy function. Intermediate results from the three solutions may also be obtained as well as a trade-off among them. Therefore, this approach has several operational upgrades regarding the existing indexes [19,20,21,22] as it allows dealing with a considerable amount of data using compromise programming, and it introduces cluster analysis and statistical tests to better analyze the results.
Therefore, the main objectives of this work are as follows: (1) to create clusters of parcels according to their biophysical characteristics; (2) to analyze the biophysical suitability of parcels for agricultural uses by means of a compromise programming approach; (3) to identify possible relations between the biophysical suitability indexes and the parcel size; and (4) to test if the biophysical clusters have influence in the biophysical suitability indexes created and if the difference in the clusters indexes are statistically significative.
2. Materials and Methods
2.1. Previous Studies
The GIS-based techniques to analyze land suitability have their origins in the early 20th century in the applications of hand-drawn overlay techniques by landscape architects [11]. The development of GIS-based methodologies for land-use suitability analysis has significantly advanced over the past three decades, evolving from traditional map overlay modeling to more sophisticated MCDA techniques and hybrid approaches. Numerous case studies demonstrate the effective combination of these methods. For example, multi-criteria evaluation techniques can be synergistically employed with artificial intelligence techniques. The classical overlay mapping approach remains a widely used technique for land-use suitability analysis within the GIS environment [11]. Malczewski [24]’s comprehensive review of GIS-MCDA approaches in the literature, examining 319 papers, reveals that 47.6% of the studies focused on raster data-based research, while 47.0% explored vector-based analyses. More recent studies approach specific problems. Fathi et al. [25] reviewed the GIS-MCDA suitability mapping methods to manage aquifer recharge located in semi-arid regions. Villacreses et al. [26] reviewed GIS-MCDA methods to consider the installation of photovoltaic solar farms. Aazagreyir et al. [27] presented a review and critical assessment of studies on GIS-based fuzzy MCDA in the last decade. Despite these developments, and, as already pointed out by Malczewski [11], in his review of GIS-based land-use suitability, a significant limitation of these techniques is the lack of mechanisms to effectively incorporate subjective value judgments into the GIS.
To solve this problem, Malczewski [24] mentioned that there are several GIS-MCDA approaches that allow the definition of weights. The analytical hierarchy process (AHP) is one of these approaches. It can be used to define the weights associated with map layers, and the weights can be combined to construct a multi-attribute map. Finally, the AHP can be used to aggregate the priority for all levels of the hierarchy to represent the alternatives.
The analytical network process (ANP) has also been used in several studies [28,29,30], and one promising technique still not used to its full extent in a GIS analysis is the extended goal programming (EGP) approach for the aggregation of “pairwise” comparison matrices, developed by González-Pachón and Romero [14] and implemented by Diaz-Balteiro et al. [15] and Nordström et al. [16]. The method allows dealing with situations without satisfactory conditions regarding reciprocity and consistence [14,15].
Several studies across diverse research domains have integrated GIS-MCDA approaches to conduct suitability analysis and site selection. Graymore [31] developed a GIS-based decision support system to assess sustainability in Victoria, Australia. De Feo et al. [32] proposed a methodology combining MCDA with geographical information to evaluate the suitability of solid waste facility locations, introducing a preliminary screening phase to identify potentially suitable areas based on various plant types. Jaiswal et al. [33] applied Saaty’s AHP to prioritize vulnerable areas within a watershed. Kidd et al. [34] created suitability maps to identify potential areas for expanding or diversifying crop enterprises. Wordley et al. [35] utilized habitat suitability models (HSMs) for bat habitats in the Western Ghats of India. Demesouka et al. [36] presented a map-based, interactive Spatial UTA (UTilités Additive)-or S-UTA for ranking candidate sites for wastewater treatment. El Baroudy [9] developed a GIS-based spatial model for assessing land suitability for wheat cultivation. Danvi et al. [37] adopted the FAO parameter method and guidelines for land evaluation, implementing a GIS-based approach to evaluate and integrate biophysical factors such as climate, hydrology, soil, and landscape. Massei et al. [38] proposed an MCDA-GIS integration, incorporating several MCDA techniques into an extension of GRASS GIS 6.4, facilitating the application of suitability analysis. Khodakarami [39] conducted a study on sustainability assessments at the neighborhood scale in Isfahan Metropolitan, utilizing an integrated framework of spatial modeling and MCDA. Akpoti et al. [40] reviewed the agricultural land suitability analysis (ALSA) approaches for crop production. Matos et al. [8] proposed a GIS-MDA for identifying the most suitable compressed air energy storage reservoirs, where the aggregation was performed using the simple additive weighting (SAW) method. Wijesinghe and Withanage [41] studied the land suitability for crop production in Thalawa DSD, Sri Lanka, using GIS combined with analytical hierarchy process (AHP). Fadafan et al. [42] used GIS-MCDA to study the mountain tourism and a weighted linear aggregation for combining the criteria. Shi et al. [43] used a combination of spatial analysis and machine learning to assess crop yield stability over a 20-year period. The goal is to maximize biogas yield from agricultural byproducts. Rojas-Briceño et al. [44] used the analytic hierarchy process (AHP), maximum entropy (MaxEnt), and a combined AHP-MaxEnt approach to rank and to create a model showing areas suitable for sustainable cocoa production. Nungula et al. [45] combined the AHP and GIS to create crop suitability distribution maps for bean and cassava production. The weighted sum was used to aggregate the criteria and create the suitability maps. del Mar Esponda-Bernal et al. [7] identified the potential of crops integrating fuzzy suitability functions and aptitude criteria weighting, drawing on the analytical hierarchical process. Final aggregation of criteria was performed using a weighted sum.
Regarding compromise programming (CP) to build ranks, there are quite fewer studies. Diaz-Balteiro et al. [19] proposed a CP approach for constructing a sustainability ranking of the paper industry in several EU countries. Diaz-Balteiro et al. [20] applied the same methodology to circular economy and considered three different decision rules: average achievement, balanced achievement in terms of proximity to the ideal, and balanced achievement in terms of distance to the anti-ideal. Costa-Freitas et al. [21] also implemented a CP approach to the analysis of sustainable water use in Portugal. They introduced an entropy approach for improving the results of the ranking. Xavier et al. [22] used a compromise programming approach for studying the agricultural sustainability of Portuguese municipalities in the last decade, which was improved using an entropy approach.
Fragmentation of rural property can hinder efficient land management because it prevents economies of scale in the use of resources. Regarding land fragmentation indices, Heider et al. [46] introduced the Fragmentation Index for Drip Irrigation and Distance Assessment (FIDIDA) utilizing GIS. Ciaian et al. [47] investigated the impact of land fragmentation on production diversification in rural Albania, employing the Simpson index to analyze fragmentation. Austin et al. [48] quantified land-use fragmentation and its effects on food production, based on data from 125 families distributed across 12 communities in Umuahia, Nigeria. Wei et al. [49] developed a quantitative and intuitive index approach to analyze the characteristics of land fragmentation for construction purposes in urban areas of China. Demetriou et al. [50] proposed a novel ‘global land fragmentation index’ that integrates a multi-attribute decision-making method with a GIS. Liang and Zhou [51] used a case study in China for analyzing land fragmentation and its factors. Zhao and Feng [52] analyzed land fragmentation in Shaanxi province, China. They used the entropy weight method (EWM) to construct a comprehensive fragmentation index of cultivated land (CLFI). Su et al. [53] studied the driving factors of land fragmentation using as a case study a Chinese province. They introduced the cultivated land fragmentation index (CLFI) to analyze land fragmentation.
2.2. The Methodological Approach
The methodological approach considers the previous studies [19,20,21,22]. Also, several GIS-MCDA studies were considered, mainly [31,32,35,36,38,39,44]. For the statistical methods, ref. [54] was considered as reference. Figure 1 presents the methodological approach designed for this study.
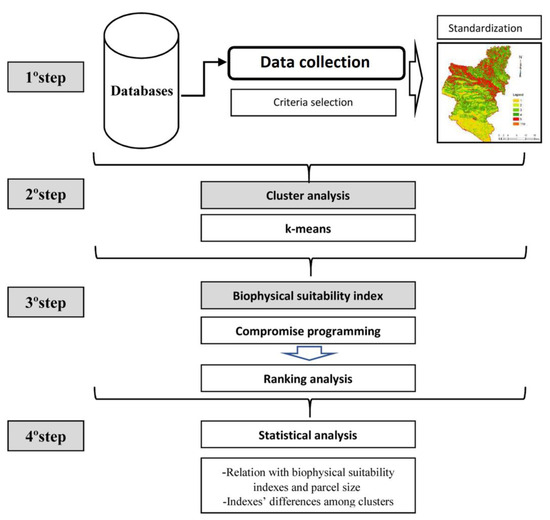
Figure 1.
The methodological approach.
The proposed approach is divided in several steps:
- (1)
- In the first step, a database screening of the available information was carried out. Then, according to the available information, the most relevant criteria for studying the biophysical suitability of parcels were selected. Their values were divided in 5 classes, which were then normalized according to the potential. The normalization determines values between 1 and 5, in which 5 represents the most suitable conditions for agriculture and forest development and 1 the least suitable.
- (2)
- In the second step, a cluster analysis was carried out regarding the different biophysical conditions, using the normalized data. A K-means clustering method was chosen due to its simplicity and objectives of this study.
- (3)
- In the third step, the weights of each indicator were defined, and a ranking analysis was implemented. The indicators were normalized using a MIN-MAX procedure for ranging between 0 and 1. A compromise programming approach considering simultaneously the best aggregated solution and the most balanced one accounting for the minimum maximum deviation and the information index was implemented.
- (4)
- In the fourth step, the statistical methods were carried out. A correlation matrix between the indexes and the size of the parcels was presented. A one-way ANOVA allowed us to analyze the influences of the clusters in the average indexes and if the average among clusters were statistically significant.
The model formulation is as follows:
- (1)
- The criteria selection follows a qualitative valuation by experts, which defined 5 classes of potential and associated them with the codification from 1 to 5, where 1 means a low suitability and 5 a very good suitability. Several relevant bibliographic references were also consulted.
- (2)
- Cluster analysis
The main objective of the cluster analysis is to “group objects into clusters such that objects within one cluster share more in common with one another than they do with the objects of other clusters” [55], as the objects were arranged into relatively homogeneous groups [55].
In this study, a non-hierarchical clustering method will be used. The non-hierarchical clustering methods are intended for grouping objects in a specific number of clusters defined by the analyst [54]. K-means clustering is an unsupervised machine learning algorithm that partitions a dataset into distinct clusters. The parameter ‘K’ represents the desired number of clusters. The algorithm categorizes data points into K groups of similar characteristics. Euclidean distance is commonly employed as a metric to measure the similarity between data points.
- (3)
- Ranking analysis definition
The ranking analysis definition will be performed using a compromise programming approach.
After defining the preferential weights, now, we have c territorial units and i indicators, which will allow for the evaluation of these units. Since the indicators are measured in very different units, a normalization of each indicator Ric regarding each criterion i and unit c must be carried out, which will be performed using a MIN-MAX approach [18,19]:
where is the optimum value of the ith indicator and is the worst value achieved by the ith indicator; elements are the individual normalized indicators i for each unit c.
According to [19], using the normalized indicators , a binary compromise programming approach may be implemented, which imply an iterative solution of the model providing individually the selection of each unit c according to its position in the ranking.
Thus, a linear binary-weighted compromise model may be formulated corresponding to metric p = 1. By solving the model, the ‘most suitable’ system was obtained in terms of aggregate biophysical suitability [19,20]. Solving the model to the metric p = ∞, the ‘most balanced’ system was obtained in terms of balanced biophysical suitability [56]. To overcome this problem, we may join both compromise programming models into one [19]. This is a binary compromise programming approach, considering the trade-off among metrics L1 and L∞, which allows iteratively ranking construction. The model will run n times corresponding to the c geographical units considered, which carries out serious limitations when dealing with thousands of units. Therefore, an approach that allows simultaneously solving the problem must be used [21,57]. Finally, the results may be improved using an entropy approach [21,22]. The entropy may also be used as a criterion for the most balanced distribution, using as reference the information index.
The best aggregated solution, the minimization of the maximum deviation and the information index offer (for the entropy measure) three different measures that we may take the utmost advantage. Several authors offer solutions to integrate three criteria. Diaz-Balteiro et al. [58] proposed a model for EGP and Diaz-Balteiro et al. [20], an extended compromise programming model for ranking analysis. Our approach adapts, therefore, several studies [18,19,20,21,58], as follows:
where CIc is the objective function representing a composite indicator of biophysical suitability, which indicates the position in the ranking of territorial unit c; is the maximum deviation for the i criteria in territorial unit c; and are the control parameters and αic are the weights of the i criteria in territorial unit c.
Equations (2) and (3) allow the minimization of the aggregate objective function that minimizes the unwanted deviation variables (highest aggregated suitability), the maximum deviation (D) or the minimization of the information index (ID). Equation (4) allows calculating the maximum deviation D for each unit c. Please note that IDc was calculated previously before this model. Final ordering of the ranking was defined using simple Microsoft Excel functions [57].
When equals one, the best aggregated solution is obtained; when equals one and equals 0, the most balanced/uniform distribution according to the concept of the information index is obtained; and, when equals zero and equals one, the solution, which minimizes the maximum deviation regarding the ideal, is obtained. For values of the control parameters and such that ∈ [0,1] compromises between the above three solutions, if they exist, are obtained [58].
- (4)
- Statistical analyses
To identify the correlation among biophysical suitability indexes and the size of the parcels, a correlation matrix was constructed using the Pearson correlation coefficient with a statistical significance test.
For analyzing the influence of clusters in the average suitability indexes and if the differences among them are statistically significant, a one-way ANOVA was implemented. The ANOVA assumes that all groups share a common standard deviation (or variance) even when their means are different. If your groups have unequal variances, your results can be incorrect if you use the classic test. The test to be used will be the Welch’s ANOVA, which is not sensitive to unequal variances.
3. Empirical Implementation
3.1. The Study Area
The municipality of Loulé, in the district of Faro, is located in the Algarve (NUT II and NUT III), Portugal. It is bordered to the west by Silves and Albufeira, to the east by S. Brás de Alportel, Alcoutim and Tavira, to the north by Almodôvar, and to the south by Faro and the Atlantic Ocean. It occupies an area of 765 km2, which is distributed across 11 parishes: Almancil, Alte, Ameixial, Boliqueime, Quarteira, Querença, Salir, São Clemente, São Sebastião, Benafim and Tôr. Figure 2 presents the municipality of Loulé and its parishes.
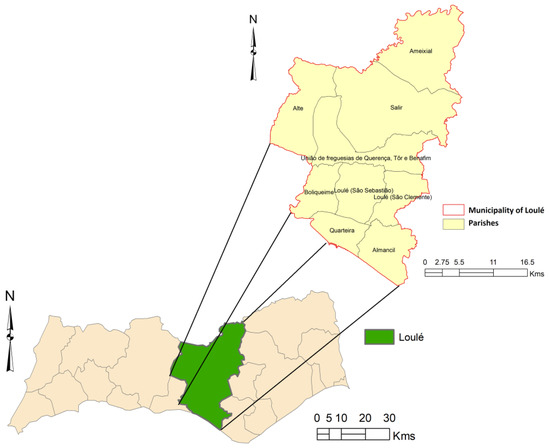
Figure 2.
The study area.
The parcels considered in the study area are presented in Figure 3. A total of 73,252 parcels (including urban and rural) were identified, with a total area of 56,554.79 hectares. In the municipality, the parcel average area is 0.77 ha, and the median is 0.19 ha. Our study will focus on the rural parcels. These include a total of 51,365, with a total area of 51,631 ha. The average area is 1.01 hectares, and the median 0.31 hectares.
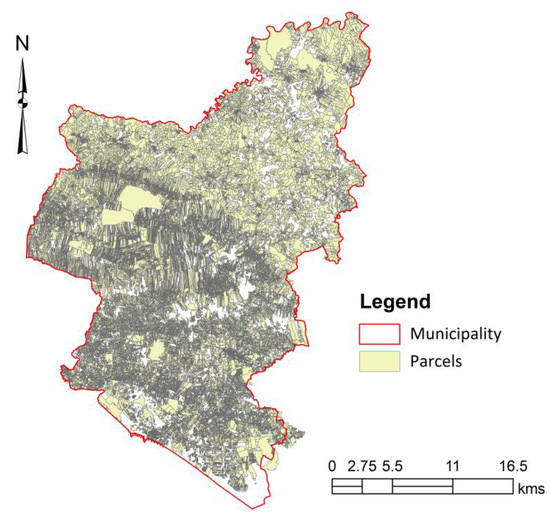
Figure 3.
The parcels of the land registry (Source: General Direction of the Territory).
3.2. Data Collection
One key aspect of this study was the data collection and its quality, since it will determine the results obtained. Regarding the land register data of Loulé municipality, these are high-resolution data that constitute the official limits of the territorial properties and have legal effects. Nevertheless, the biophysical data used have a more limited resolution, and are restricted to existent official data.
The biophysical data were selected to represent the biophysical suitability for agriculture and forests and may be adapted to other studies and problems. The data were selected according to experts’ opinions and several bibliographic references for land management and biophysical suitability. After, a careful screening of the existent databases was compiled.
To build the model, several layers of data were considered, and different databases were consulted. The criteria for defining biophysical suitability potential were selected according to experts’ analysis.
The hypsometry, aspect and slope maps have a pixel of 25 m2 and regard to a scale of 1:25,000. The soil capacity map (1:25,000) was obtained by digital analog conversion of the Land-Use Capacity Map. The hoar frost map is more limited (1:1,000,000), and it is obtained using a 30-year series of data. Regarding the climate data, the resolution is low, but this is limited to the low number of meteorological stations in the Algarve Region, which do not allow more detailed extrapolations. Local topography should also be considered, as it influences these occurrences at the local level. Table 1 presents the sources of information consulted for building the biophysical suitability index.

Table 1.
The sources of the criteria.
Nevertheless, the combination of different data layers will allow a guideline for territorial management at the municipality level. A detailed analysis at a more local level will imply field data collection and a further analysis of the biophysical characteristics of the territory.
3.3. Data Analysis
After collection, data were classified according to the potential for agriculture and forest development using a scale from 1 to 5 (Table 2). These suitability classes were defined considering expert and researcher opinions as well as several previous research [59]. These normalized data were then used in the cluster analysis.

Table 2.
The classification limits for each biophysical suitability criteria.
There are several clustering techniques, which generally are classified as partition-based clustering, hierarchical clustering and density-based clustering. These techniques have different cluster analysis approaches, and the most suitable for a given dataset is difficult to predict. Nevertheless, Euclidian distance and K-means are the most frequent clustering techniques used in social science studies [60]. The K-means is a simple technique that can split the dataset into K distinct non-overlapping clusters [61]. For implementing this technique, we decided the number of clusters to retain by an experts’ analysis.
These results were then normalized according to Equation (1), from 0 to 1 for implementing the compromise programming approach. Figure 4 presents the maps that were constructed using these normalized indexes. These indexes will be then used in the compromise programming approach.
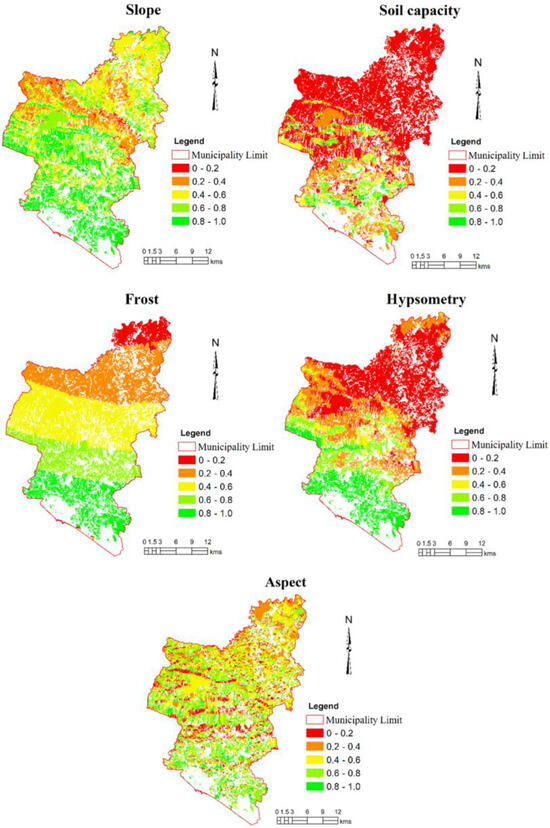
Figure 4.
The spatial distribution of the normalized indexes used in the compromise programming approach.
To define the preferential weights for the criteria, we assume that all indicators are equally important.
The K-means cluster analysis was implemented using the SPSS software (v.22), the compromise programming approach was implemented using the General Algebraic Modeling System (GAMS) and the Microsoft Excel Software. Finally, all the other statistical analyses were implemented using the SPSS software. The maps and spatial analysis were done using QGIS and ARCGIS by ESRI.
4. Results
4.1. The Cluster Analysis
The final clusters’ centers regarding the land register are presented in Table 3. The definition of each cluster (i.e., its main characteristics) is the following:

Table 3.
The final clusters’ centers.
- Cluster 1—Parcels with a medium-high biophysical suitability regarding Slope and Hoar frost, satisfactory for Hypsometry but a low suitability regarding Soil capacity and Aspect.
- Cluster 2—Parcels that present a good suitability potential for the following criteria: Slope, Soil capacity and Hoar frost but tend to present a low suitability for the Aspect criteria.
- Cluster 3—Parcels that tend to present a low to very low potential in almost all criteria, namely, in Soil capacity and Hypsometry.
- Cluster 4—Parcels that tend to present a very good Slope biophysical capacity and a good suitability regarding the other criteria, except for Hypsometry.
- Cluster 5—Parcels that tend to present satisfactory suitability regarding Slope and Hoar Frost but present low levels for Soil capacity and Hypsometry.
- Cluster 6—Parcels that tend to present very good suitability results regarding Slope and Hoar frost but also regarding Hypsometry, Aspect and Soil capacity.
Cluster 1 presents its highest mean values for Slope and Hoar frost. Cluster 2 presents the highest mean value for Slope, Soil capacity and Hoar frost. Cluster 3 tends to have the lowest mean values of all clusters, as the best means are always lower than 3 and are registered in Slope, Hoar frost and Aspect. Cluster 4 presents the highest mean score for Slope with 4.583. Cluster 5 presents the highest mean for Slope (3.797), Hoar frost (3.224) and Aspect (3.835). Cluster 6 presents the highest mean for Slope (4.765) and Hoar frost (4.896).
According to the one-way ANOVA in Table 4, the dimension that allows better differentiation of the clusters is Soil capacity (F = 25,338.704), followed by Hypsometry (F = 23,279.059) and Hoar frost (F = 22,038.702) (Table 4).

Table 4.
The one-way ANOVA.
The number of parcels by cluster is presented in Figure 5. The three clusters with a larger number of parcels are cluster 6 (11,462), cluster 5 (11,189) and cluster 3 (10,570). The total area of each cluster is presented in Figure 6. The clusters with more area are cluster 3 and cluster 5.
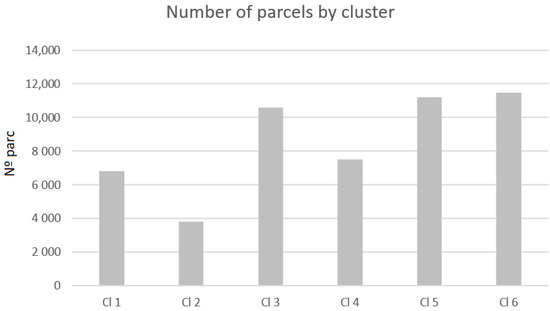
Figure 5.
The number of parcels by cluster.
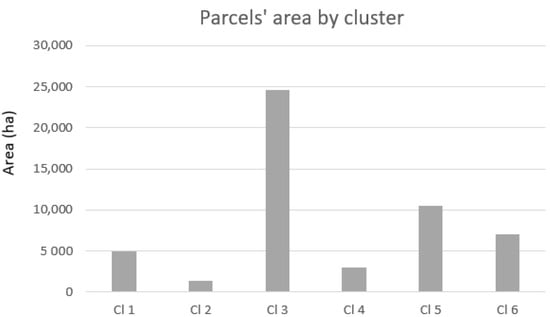
Figure 6.
The parcels’ area by cluster.
Figure 7 presents the spatial distribution of the clusters created. The analysis of the clusters’ spatial distribution shows that cluster 3 is dominant in the interior of the municipality, while cluster 6 is dominant at the south of the municipality, near the littoral.
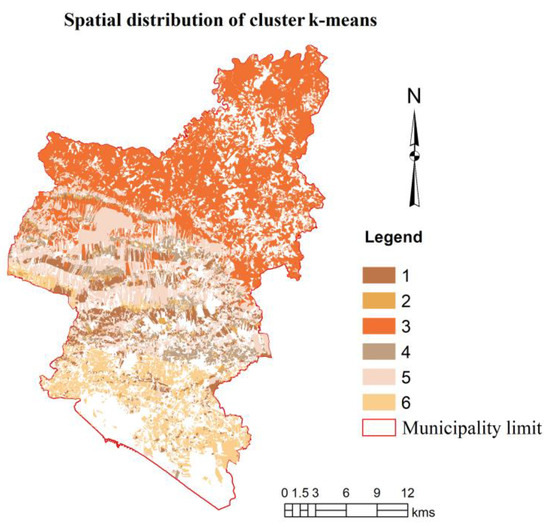
Figure 7.
Spatial distribution of the clusters resulting from the K-means analysis.
4.2. Ranking Analysis
As stated in the methodology, the suitability indexes were calculated using compromise programming to calculate the deviations from the ideal and were then ordered to define the respective rankings.
Table 5 presents the 10th best positioned parcels using the proposed approach. Several parcels occupy the first place in the ranking, since all the deviations are 0 regarding the ideal. However, if we analyze the 10th worst positions in the ranking (Table 6), we may identify several changes. In the last position, it is always the parcel 105881, except for = 0, = 0 and 1 − − = 1; for = 0, = 0.5 and 1 − − = 0.5; and, for = 0.25, = 0.25 and 1 − − = 0.5, where it is the parcel 84,679.

Table 5.
The 10 first parcels in the ranking.

Table 6.
The 10 last parcels in the ranking.
Figure 8 represents examples of the spatial distribution of the rankings, which were grouped in several classes. Class 1 groups parcels ranked from 1 to 10,000, i.e., the most 10,000 suitable parcels. Class 5 groups parcels ranked with a value higher than 40,000 in the ranking, the least suitable parcels. The rankings obtained in the best aggregated solution (1 − = 1) reveal that the best positioned parcels, for which the compromise between Slope, Soil capacity, Hoar frost, Hypsometry and Aspect is the best possible, tend to be in the areas near the littoral, while the worst positioned are in the municipality inland. Intermediate positions in the rankings occur in the center of the municipality.
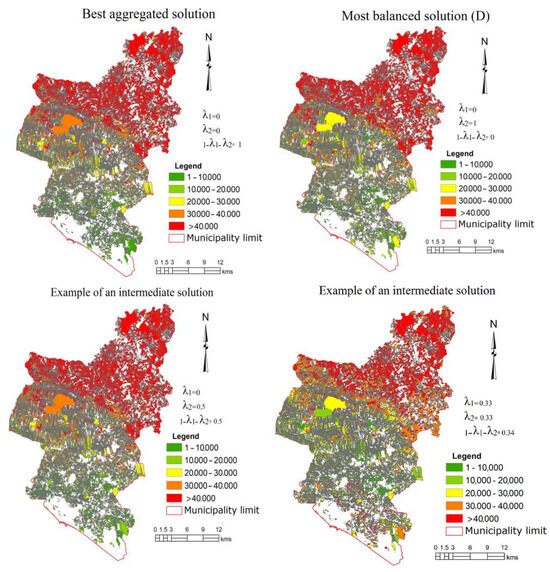
Figure 8.
Examples of the spatial distribution of the rankings.
Regarding the most balance solution, i.e., the one that valorizes the minimization of the maximum deviation D ( = 1), the spatial distribution has some similarities. The lowest ranking positions are in the municipality inland. Intermediate ranking positions are located at the littoral and at the center of the municipality, while the best positions in the ranking are located also at littoral and center of the municipality. Several changes are identified in areas that are in middle-ranking positions.
Finally, the last two figures represent intermediate solutions. A clear tendency of the location of the areas with lowest positions in the ranking in the interior north of the municipality is identified.
4.3. Statistical Analysis
The descriptive statistics were made for the indexes calculated with the compromise programming approach. Its results are presented, as an example, in Table 7, for the following solutions: aggregate suitability index ( = 0, = 0 and 1 − = 1) and the information index (ID) ( = 1, = 0 and 1 − − = 0). According to the analysis, we may conclude that the aggregate suitability index (λ1 = 0, = 0 and 1 − − = 1) presents an average mean of 0.444. The ID ( = 1, = 0 and 1 − − = 0), which represents the most balanced solution according to the entropy concept, presents an average score of 0.224, better than the aggregate ( = 0, λ2 = 0 and 1 − − = 1). Nevertheless, when considering the standard deviation and the respective coefficient of variation, we conclude that the aggregate presents one of 48% ( = 0, = 0 and 1 − − = 1), while the ID (λ1 = 1, = 0 and 1 − − = 0) presents 113%.

Table 7.
Descriptive statistics.
For assessing normality, the skewness and kurtosis were used. Skewness measures the degree of asymmetry in a distribution, with a skewed distribution exhibiting an elongated tail to the right or left. A skewness value within the range of −1 to +1 is generally considered excellent for assessing normality, although values between −2 and +2 are also deemed acceptable [62]. Kurtosis quantifies the peakness or flatness of a distribution relative to a normal distribution. A positive kurtosis indicates a more peaked distribution, while a negative kurtosis suggests a flatter shape. Kurtosis values between −2 and +2 are typically accepted as indicators of normality [62].
The skewness and kurtosis are presented in Table 8 for all aggregated clusters. Since the skewness and kurtosis values are between −2 and 2, we may conclude that the data are normally distributed, except for the normalized area of the parcels, because of the high contrast among the size of the parcels.

Table 8.
The skewness and kurtosis.
A correlation analysis was carried out with a statistical significance test. Results are presented in Table 9, showing that the correlations among the parcel size and the biophysical potential indexes are quite low. There is a positive correlation of 0.108 between the parcels and the best aggregated solution (p = 0.01) and between the parcels and the most balanced solution ID of −0.070. There is a negative one between the parcels and the information index ID of −0.070 (p = 0.01).

Table 9.
The correlation matrix.
A one-way ANOVA was performed to identify if the differences in the index scores are significant among clusters. The descriptive statistics regarding the clusters are presented as follows for each of the solutions (Table 10 and Table 11).

Table 10.
Descriptive statistics—best aggregated solution.

Table 11.
Descriptive statistics—information index.
Table 12 presents the skewness and kurtosis values. According to the limits presented previously, we may conclude that the data are normally distributed, in both cases. Concerning the information index, cluster 3 presents values of kurtosis higher than 2, which are still accepted due to the large sample size.

Table 12.
The skewness and kurtosis for each cluster.
Table 13 presents the results of the Welch ANOVA. In all models, we reject the null hypothesis (p < 0.01) of equality of means and accept the alternative hypothesis of existing differences among groups; i.e., there is a statistically significant difference in mean biophysical suitability condition scores between at least two groups in all models. Therefore, there is an effect of the clusters created in the biophysical scores: aggregated [F(5, 18,750) = 73,274.41; p = 0.00]; D [F(5, 16,874) = 24,021.79; p = 0.00] and ID [F(5, 16,875) = 13,060.12; p = 0.00].

Table 13.
Results of the one-way Welch’s ANOVA.
5. Discussion
This paper presented a novel compromise programming approach for analyzing the biophysical suitability of land-use parcels. Nevertheless, there are some issues to be discussed.
Selecting suitable biophysical parcels is a complex process because it needs a multidisciplinary approach that incorporates natural, physical-social sciences, politics, and ethics. Therefore, the selection of the criteria used was carried out by several experts and related to the agricultural and forestry land uses. Nevertheless, these criteria were limited by the available data and the spatial resolution. Also, when dealing with several criteria and several agricultural and forest activities, we should consider that some of them have suitability criteria that are different from the general ones. Therefore, these must be understood as general criteria for the development of agricultural and forestry activities since activities with specific criteria may exist.
Another issue is land-use fragmentation. Binns [63] identified the following land fragmentation typologies: “(1) that is unavoidable by reason of natural conditions, (2) that arises from physical conditions from human activities not connected with agriculture, (3) that is agricultural rational and (4) that, not falling within the first two categories, is agriculturally irrational” [63]. Thus, not all land fragmentation can be addressed and solved easily. Although this research did not address land-use fragmentation, the biophysical potential and the related biophysical conditions may be an explaining factor of land-use fragmentation. This study will require a complete set of data identifying the parcels by owner. This is special important, since an analysis of the most recent agricultural census suggests that not only is the farm’s average area increasing but also the number of parcels that it includes. Therefore, there may be an increase in land-use fragmentation. Moreover, our study also suggests that the parcels with larger sizes tend to be in areas with lower biophysical conditions. This is especially true in the interior of Loulé municipality.
Land-use allocation problems are complex planning problems. Often, a large number of different stakeholders is involved in the planning process. A key issue will be to integrate these preferences of experts and stakeholders in land management. In our case, we assumed that the criteria would have equal weights, but it would be of great value to use group decision methods such as Extended Goal Programming [15]. Therefore, the decisions made with respect to land use must be clear and transparent to these stakeholders [49].
Various methods have been developed to support suitability or land allocation issues; however, they concentrate almost entirely on size, location, and the number of land units. The analyses of topological relationships that are the results of the biophysical/environmental and socio-economic processes should be further analyzed [64].
Another aspect to be discussed regards the compromise programming method used. The approach allows integrating the best aggregated solution, the most balanced/uniform distribution according to the concept of normalized entropy and the most balanced solution that minimizes the maximum deviation regarding the ideal. This approach is novel in the way that it allows a more complete set of information. However, it must be highlighted that there will be an added complexity to the approach, which recommends a careful analysis of the several solutions’ trade-off before the implementation of this approach.
One crucial aspect will be the interpretation of the resulting indexes. These are deviations regarding the optimal conditions, except for the entropy analysis (although an information index of 0 will mean a total balanced distribution). Having this in mind, a careful analysis of the indexes needs to be carried out.
Sensitivity analysis allows us to understand how changes in inputs affect the model output [65]. Since MCDA problems often use data that can change [8], sensitivity analysis may be an interesting final step. Nevertheless, our model allows obtaining a considerable amount of data regarding the best aggregated solution, the most balanced ones and intermediate solutions. Trade-off curves could be obtained, but we analyzed the patterns in each solution and compared them to the municipality reality to identify changes and limitations.
6. Concluding Remarks
This research proposed an alternative approach using compromise programming for aggregating the criteria of land-use suitability. This approach allows considering not only the best aggregated solution but also the most balanced one and intermediate solutions among them. It has, therefore, several operational advantages: (1) it allows adding a complete set of information for the manager; (2) its formulation allows an easy implementation for a considerable number of units; (3) the preferences of the stakeholders can be added to the analysis; and (4) it allows dealing with a considerable amount of data to draw information in a more complete way than the common biophysical suitability maps.
Regarding the previous approaches that use compromise programming, we must highlight the consideration of the best aggregated solution, the most balanced one regarding the minimization of the maximum deviation and the most balanced one according to the concept of entropy, in the calculation of suitability indexes applied to land management.
The approach presented in this paper also takes a step further in compromise programming, proving its ability to deal with a very large amount of data.
The use of cluster analysis allowed creating typologies regarding the biophysical conditions, and the differences were analyzed by means of an ANOVA analysis, where we accept the alternative hypothesis of existing differences among groups; i.e., there is a statistically significant difference in mean biophysical suitability conditions score between at least two groups in all models.
Therefore, the approach has a relevant practical application, since it will allow not only creating rankings but also indexes considering aggregated and balanced solutions; additionally, it combines MCDA, statistical approaches and GIS, building an integrated framework for analyzing the territory. For policy implementation, it will allow a better territorial allocation of activities and to understand the existent ones. Nevertheless, although the analysis of the property fragmentation results is critical and related to the biophysical characteristics and cultural capabilities of the territory, it should also be highlighted that, without knowing the land tenure structure and which are, in fact, the land management units that make decisions over the territory, planning instruments will always risk being biased.
This study has, however, some limitations that must be addressed in further studies.
One main limitation is the resolution of the data used. The biophysical data have a less detailed geographical scale than the land register. This is especially relevant when considering climate date. Further studies must conduct surveys and local analysis mainly to identify climatic risks.
This study presents an illustrative example of this methodology considering land register data and the biophysical suitability for agricultural and forest land uses. Future research should focus each use individually (e.g., for each type of forest or each crop).
Furthermore, the research conducted in this paper assumes equal weights among biophysical criteria. An interesting upgrade would be to use different weights according to the importance of the biophysical criteria. This may be performed using experts’ opinions, pairwise comparisons and an analytical hierarchy process [24] or using extended goal programming [14,15].
Finally, one limitation regards the analysis of the relation among land fragmentation and the biophysical conditions as the available land register data did not allow the identification of the landowner’s parcels.
Therefore, three future research lines may be identified.
The first one regards the integration of weights in each biophysical criteria to better reflect the biophysical suitability of the territory using different methods, such as EGP. This will imply a careful data collection from researchers, managers, and other relevant stakeholders. A sensibility analysis should be carried out using different sets of weights.
The second research line will be to implement this approach using detailed data for specific forest and agricultural uses. This will imply the selection of temporary crops, permanent crops or forest uses to be analyzed individually.
Finally, a third research line is related to the implementation of the proposed approach in other geographical areas of the Portuguese territory or in other selected geographical locations in other countries. We believe that the approach is flexible and has potential to address different situations and contexts.
Author Contributions
Conceptualization, A.X. and M.d.B.C.F.; methodology, A.X., M.d.B.C.F. and C.A.; software, A.X.; validation, A.X., M.d.B.C.F. and C.A.; formal analysis, A.X., M.d.B.C.F. and C.A.; investigation, A.X., M.d.B.C.F. and C.A.; resources, A.X. and M.d.B.C.F.; data curation, A.X., M.d.B.C.F. and C.A.; writing—original draft preparation, A.X., M.d.B.C.F. and C.A.; writing—review and editing, A.X., M.d.B.C.F. and C.A.; visualization, A.X., M.d.B.C.F. and C.A.; supervision, A.X., M.d.B.C.F. and C.A.; funding acquisition, M.d.B.C.F. and C.A. All authors have read and agreed to the published version of the manuscript.
Funding
The authors acknowledge support from the project “Valorização e aproveitamento da floresta Mediterrânica: o caso do concelho de Loulé”, ALG-05-3928-FEDER-000044.
Data Availability Statement
Data for the land register are available at https://dados.gov.pt/pt/datasets/cadastro-predial/. Creative Commons Attribution 4.0-CC BY 4.0. Accessed last time 15 January 2025.
Acknowledgments
The authors thank the General Direction of the Territory for the land register data provided to the Algarve University to be used in the project: “Valorização e aproveitamento da floresta Mediterrânica: o caso do concelho de Loulé”, ALG-05-3928-FEDER-000044. The authors also acknowledge CEFAGE (https://doi.org/10.54499/UIDB/04007/2020), MED (https://doi.org/10.54499/UIDB/05183/2020) and CHANGE (https://doi.org/10.54499/LA/P/0121/2020).
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of this study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Getie, A.M.; Birhanu, T.A.; Dadi, T.F. Developing a framework for assessing the efficacy of rural cadastral system in the Amhara region, Ethiopia. Surv. Rev. 2023, 55, 147–168. [Google Scholar] [CrossRef]
- Hämäläinen, E.; Krigsholm, P. Exploring the strategy goals and strategy drivers of national mapping, cadastral, and land registry authorities. ISPRS Int. J. Geo-Inf. 2022, 11, 164. [Google Scholar] [CrossRef]
- Steudler, D.; Williamson, I.P.; Rajabifard, A.; Enemark, S. Good practices in land administration and cadastre: The Cadastral Template Project. In Proceedings of the FIG Working Week 2004, Athens, Greece, 22–27 May 2004. [Google Scholar]
- Cole, M.G.; Wilson, A.D. Land Tenure, Boundary Surveys, and Cadastral Systems; Taylor & Francis Group: Boca Raton, FL, USA, 2017. [Google Scholar]
- Enemark, S. From cadastre to land governance. In Proceedings of the Cadastral Surveyor-Paving the Way to the Future 2nd European Conference on Cadastre, Bucharest, Romania, 6–7 May 2010. [Google Scholar]
- Sass, C.K.; Andrew Lodder, R.; Lee, B.D. Combining biophysical and socioeconomic suitability models for urban forest planning. Urban For. Urban Green. 2019, 38, 371–382. [Google Scholar] [CrossRef]
- del Mar Esponda-Bernal, M.; Echeverri-Sanchez, A.F.; Aguirre-Gonzalez, E.F.; Andrade, R.S. A biophysical suitability model to identify best areas for the cultivation of potential cash crops: The case of basil in Valle del Cauca. Agric. Syst. 2024, 216, 103909. [Google Scholar] [CrossRef]
- Matos, C.R.; Carneiro, J.F.; Pereira da Silva, P.; Henriques, C.O. A GIS-MCDA Approach Addressing Economic-Social-Environmental Concerns for Selecting the Most Suitable Compressed Air Energy Storage Reservoirs. Energies 2021, 14, 6793. [Google Scholar] [CrossRef]
- El Baroudy, A.A. Mapping and evaluating land suitability using a GIS-based model. Catena 2016, 140, 96–104. [Google Scholar] [CrossRef]
- Collins, M.G.; Steiner, F.R.; Rushman, M.J. Land-use suitability analysis in the United States: Historical development and promising technological achievements. Environ. Manag. 2001, 28, 611–621. [Google Scholar] [CrossRef]
- Malczewski, J. GIS-based land-use suitability analysis: A critical overview. Prog. Plan. 2004, 62, 3–65. [Google Scholar] [CrossRef]
- Malczewski, J.; Rinner, C. Multicriteria Decision Analysis in Geographic Information Science; Springer: New York, NY, USA, 2015. [Google Scholar]
- McCoy, J.; Johnston, K. Using ArcGIS Spatial Analyst; Environmental Systems Research Institute (ESRI): Redlands, CA, USA, 2001. [Google Scholar]
- González-Pachón, J.; Romero, C. Inferring consensus weights from pairwise comparison matrices without suitable properties. Ann. Oper. Res. 2007, 154, 123–132. [Google Scholar] [CrossRef]
- Diaz-Balteiro, L.; González-Pachón, J.; Romero, C. Forest management with multiple criteria and multiple stakeholders: An application to two public forests in Spain. Scand. J. For. Res. 2009, 24, 87–93. [Google Scholar] [CrossRef]
- Nordström, E.; Romero, C.; Eriksson, L.; Öhman, L. Aggregation of Preferences in Participatory Forest Planning with Multiple Criteria: An Application to the Urban Forest in Lycksele, Sweden. Can. J. For. Res. 2009, 39, 1979–1992. [Google Scholar] [CrossRef]
- Xavier, A.; Costa Freitas, M.B.; Antunes, C.R. The water surfaces’ ecosystem services and the opinion of different stakeholders: An approach based on goal programming. Int. J. Manag. Decis. Mak. 2016, 15, 184–204. [Google Scholar] [CrossRef]
- OECD (Organization for Economic Co-operation and Development; JRC, Joint Research Centre). Handbook on Constructing Composite Indicators. Methodology and User Guide; OECD: Paris, France, 2008. [Google Scholar]
- Diaz-Balteiro, L.; Voces González, R.; Romero, C. Making sustainability rankings using compromise programming. An application to European paper industry. Silva Fenn. 2011, 45, 761–773. [Google Scholar] [CrossRef]
- Diaz-Balteiro, L.; Romero, C.; García de Jalón, S. An analysis of the degree of circularity of the wood products industry in Europe. J. Ind. Ecol. 2022, 26, 1350–1363. [Google Scholar] [CrossRef]
- Costa Freitas, M.D.B.C.; Xavier, A.; Fragoso, R.; Antunes, C. A composite indicator to measure sustainable water use in Portugal: A compromise programming approach. J. Environ. Manag. 2022, 311, 114791. [Google Scholar] [CrossRef] [PubMed]
- Xavier, A.; Costa Freitas, M.D.B.; Fragoso, R.; Rosário, M.D.S. Analysing the Recent Dynamics of Agricultural Sustainability in Portugal Using a Compromise Programming Approach. Sustainability 2022, 14, 12512. [Google Scholar] [CrossRef]
- Blashfield, R.K.; Aldenderfer, M.S. The literature on cluster analysis. Multivar. Behav. Res. 1978, 13, 271–295. [Google Scholar] [CrossRef]
- Malczewski, J. GIS-based multicriteria decision analysis: A survey of the literature. Int. J. Geogr. Inf. Sci. 2006, 20, 703–726. [Google Scholar] [CrossRef]
- Fathi, S.; Hagen, J.S.; Matanó, A.; Nogueira, G.E. Review of GIS multi-criteria decision analysis for managed aquifer recharge in semi-arid regions. In Groundwater Resources Development and Planning in the Semi-Arid Region; Pande, C.B., Moharir, K.N., Eds.; Springer International Publishing: Cham, Switzerland, 2021; pp. 154–196. [Google Scholar] [CrossRef]
- Villacreses, G.; Martínez-Gómez, J.; Jijón, D.; Cordovez, M. Geolocation of photovoltaic farms using Geographic Information Systems (GIS) with Multiple-criteria decision-making (MCDM) methods: Case of the Ecuadorian energy regulation. Energy Rep. 2022, 8, 3526–3548. [Google Scholar] [CrossRef]
- Aazagreyir, P.; Appiahene, P.; Appiah, O.; Boateng, S. GIS-based fuzzy multi-criteria decision making methods: A systematic review and meta-analysis. J. Theor. Appl. Inf. Technol. 2022, 100, 5119–5133. [Google Scholar]
- Pourebrahim, S.; Hadipour, M.; Mokhtar, M.B.; Mohamed, M.I.H. Analytic network process for criteria selection in sustainable coastal land use planning. Ocean Coast. Manag. 2010, 53, 544–551. [Google Scholar] [CrossRef]
- Jaafari, A.; Najafi, A.; Melón, M.G. Decision-making for the selection of a best wood extraction method: An analytic network process approach. For. Policy Econ. 2015, 50, 200–209. [Google Scholar] [CrossRef]
- Ferretti, V. A multicriteria spatial decision support system development for siting a landfill in the province of Torino (Italy). J. Multi-Criteria Decis. Anal. 2011, 18, 231–252. [Google Scholar] [CrossRef]
- Graymore, M.L.; Wallis, A.M.; Richards, A.J. An Index of Regional Sustainability: A GIS-based multiple criteria analysis decision support system for progressing sustainability. Ecol. Complex. 2009, 6, 453–462. [Google Scholar] [CrossRef]
- De Feo, G.; De Gisi, S. Using MCDA and GIS for hazardous waste landfill siting considering land scarcity for waste disposal. Waste Manag. 2014, 34, 2225–2238. [Google Scholar] [CrossRef]
- Jaiswal, R.K.; Ghosh, N.C.; Galkate, R.V.; Thomas, T. Multi criteria decision analysis (MCDA) for watershed prioritization. Aquat. Procedia 2015, 4, 1553–1560. [Google Scholar] [CrossRef]
- Kidd, D.; Webb, M.; Malone, B.; Minasny, B.; McBratney, A. Digital soil assessment of agricultural suitability, versatility and capital in Tasmania, Australia. Geoderma Reg. 2015, 6, 7–21. [Google Scholar] [CrossRef]
- Wordley, C.F.; Sankaran, M.; Mudappa, D.; Altringham, J.D. Landscape scale habitat suitability modelling of bats in the Western Ghats of India: Bats like something in their tea. Biol. Conserv. 2015, 191, 529–536. [Google Scholar] [CrossRef]
- Demesouka, O.E.; Vavatsikos, A.P.; Anagnostopoulos, K.P. Spatial UTA (S-UTA)–A new approach for raster-based GIS multicriteria suitability analysis and its use in implementing natural systems for wastewater treatment. J. Environ. Manag. 2013, 125, 41–54. [Google Scholar] [CrossRef]
- Danvi, A.; Jütten, T.; Giertz, S.; Zwart, S.J.; Diekkrüger, B. A spatially explicit approach to assess the suitability for rice cultivation in an inland valley in central Benin. Agric. Water Manag. 2016, 177, 95–106. [Google Scholar] [CrossRef]
- Massei, G.; Rocchi, L.; Paolotti, L.; Greco, S.; Boggia, A. Decision Support Systems for environmental management: A case study on wastewater from agriculture. J. Environ. Manag. 2014, 146, 491–504. [Google Scholar] [CrossRef]
- Khodakarami, L.; Pourmanafi, S.; Mokhtari, Z.; Soffianian, A.R.; Lotfi, A. Urban sustainability assessment at the neighborhood scale: Integrating spatial modellings and multi-criteria decision making approaches. Sustain. Cities Soc. 2023, 97, 104725. [Google Scholar] [CrossRef]
- Akpoti, K.; Kabo-bah, A.T.; Zwart, S.J. Agricultural land suitability analysis: State-of-the-art and outlooks for integration of climate change analysis. Agric. Syst. 2019, 173, 172–208. [Google Scholar] [CrossRef]
- Wijesinghe, W.M.D.C.; Withanage, N.C. Application of the GIS-MCDA to identify land suitability for legume crops cultivation: An empirical investigation based on Thalawa DSD, Sri Lanka. Int. J. Spat. Temporal Multimed. Inf. Syst. 2022, in press. [Google Scholar] [CrossRef]
- Fadafan, F.K.; Soffianian, A.; Pourmanafi, S.; Morgan, M. Assessing eco-tourism in a mountainous landscape using GIS–MCDA approaches. Appl. Geogr. 2022, 147, 102743. [Google Scholar] [CrossRef]
- Shi, Z.; Marinello, F.; Ai, P.; Pezzuolo, A. Assessment of bioenergy plant locations using a GIS-MCDA approach based on spatio-temporal stability maps of agricultural and livestock byproducts: A case study. Sci. Total Environ. 2024, 947, 174665. [Google Scholar] [CrossRef]
- Rojas-Briceño, N.B.; García, L.; Cotrina-Sánchez, A.; Goñas, M.; Salas López, R.; Silva López, J.O.; Oliva-Cruz, M. Land Suitability for Cocoa Cultivation in Peru: AHP and MaxEnt Modeling in a GIS Environment. Agronomy 2022, 12, 2930. [Google Scholar] [CrossRef]
- Nungula, E.Z.; Massawe, B.J.; Chappa, L.R.; Nhunda, D.M.; Seleiman, M.F.; Ali, N.; Gitari, H.I. Multicriteria land suitability assessment for cassava and bean production using integration of GIS and AHP. Cogent Food Agric. 2024, 10, 2333316. [Google Scholar] [CrossRef]
- Heider, K.; Lopez, J.M.R.; Avilés, J.M.G.; Balbo, A.L. Land fragmentation index for drip-irrigated field systems in the Mediterranean: A case study from Ricote (Murcia, SE Spain). Agric. Syst. 2018, 166, 48–56. [Google Scholar] [CrossRef]
- Ciaian, P.; Guri, F.; Rajcaniova, M.; Drabik, D.; Paloma, S.G. Land fragmentation and production diversification: A case study from rural Albania. Land Use Policy 2018, 76, 589–599. [Google Scholar] [CrossRef]
- Austin, O.C.; Ulunma, A.C.; Sulaiman, J. Exploring the link between land fragmentation and agricultural productivity. Int. J. Agric. For. 2012, 2, 30–34. [Google Scholar] [CrossRef]
- Wei, Y.; Zhang, Z. Assessing the fragmentation of construction land in urban areas: An index method and case study in Shunde, China. Land Use Policy 2012, 29, 417–428. [Google Scholar] [CrossRef]
- Demetriou, D.; Stillwell, J.; See, L. A new methodology for measuring land fragmentation. Comput. Environ. Urban Syst. 2013, 39, 71–80. [Google Scholar] [CrossRef]
- Liang, J.; Zhou, T. Cultivated Land Fragmentation and Its Influencing Factors Detection: A Case Study in Huaihe River Basin, China. Int. J. Environ. Res. Public Health 2022, 19, 138. [Google Scholar] [CrossRef]
- Zhao, Y.; Feng, Q. Identifying spatial and temporal dynamics and driving factors of cultivated land fragmentation in Shaanxi province. Agric. Syst. 2024, 217, 103948. [Google Scholar] [CrossRef]
- Su, M.; Sun, K.; Deng, B.; Cheng, N.; Cao, Y. Quantification and Driving Factors of Cultivated Land Fragmentation in Rapidly Urbanizing Area: A Case Study in Guang-dong Province. Remote Sens. 2024, 16, 2633. [Google Scholar] [CrossRef]
- Marôco, J. Análise Estatística Com o SPSS Statistics; Report Number: Lisbon, Portugal, 2014. [Google Scholar]
- Gore, P.A. 11-Cluster Analysis. In Handbook of Applied Multivariate Statistics and Mathematical Modeling; Tinsley, H., Brown, S.D., Eds.; Academic Press: Cambridge, MA, USA, 2000; pp. 297–321. [Google Scholar] [CrossRef]
- Diaz-Balteiro, L.; Romero, C. Sustainability of forest management plans: A discrete goal programming approach. J. Environ. Manag. 2004, 71, 351–359. [Google Scholar] [CrossRef]
- Xavier, A.; Freitas, M.B.C.; Fragoso, R.; Rosário, M.S. A regional composite indicator for analysing agricultural sustainability in Portugal: A goal programming approach. Ecol. Indic. 2018, 89, 84–100. [Google Scholar] [CrossRef]
- Diaz-Balteiro, L.; Alfranca, O.; González-Pachón, J.; Romero, C. Ranking of industrial forest plantations in terms of sustainability: A multicriteria approach. J. Environ. Manag. 2016, 180, 123–132. [Google Scholar] [CrossRef]
- Xavier, A. Um Modelo Bioeconómico para a Gestão Sustentável das Florestas Mediterrâneas. Ph.D. Thesis, University of Algarve, Faro, Portugal, 2014. [Google Scholar]
- Fragoso, R.; Vieira, A. Efficiency analysis of the Portuguese wine industry using accounting and operational metrics. Results Eng. 2022, 14, 100389. [Google Scholar] [CrossRef]
- Troccoli, E.B.; Cerqueira, A.G.; Lemos, J.B.; Holz, M. K-means clustering using principal component analysis to automate label organization in multi-attribute seismic facies analysis. J. Appl. Geophys 2022, 198, 104555. [Google Scholar] [CrossRef]
- Hair, J.F.; Hult, G.T.M.; Ringle, C.M.; Sarstedt, M. A Primer on Partial Least Squares Structural Equation Modeling (PLS-SEM), 3rd ed.; Sage: Thousand Oaks, CA, USA, 2022. [Google Scholar]
- Binns, B.; Skovgaard, K. The consolidation of fragmented agricultural holdings. In Agricultural and Food Sciences; Conference Proceedings; Food and Agriculture Organization of the United Nations: Rome, Italy, 1950. [Google Scholar]
- Carsjens, G.J.; Van Der Knaap, W. Strategic land-use allocation: Dealing with spatial relationships and fragmentation of agriculture. Landsc. Urban Plan. 2002, 58, 171–179. [Google Scholar] [CrossRef]
- Saltelli, A.; Tarantola, S.; Chan, K. A Role for Sensitivity Analysis in Presenting the Results from MCDA Studies to Decision Makers. J. Multi-Criteria Decis. Anal. 1999, 8, 139–145. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).