Machine Learning-Based Prediction of Ecosystem-Scale CO2 Flux Measurements
Abstract
1. Introduction
- A wide-ranging comparison of many common machine learning methods for predicting tower-based FCO2;
- The discovery of a generalizable machine learning-based model that can predict FCO2 to within 1.81 μmolm−2s−1 of tower-based measurements;
- An open-source gap-filled FCO2 dataset covering 44 unique sites for free use by other researchers in the climate science community;
- An open-source code repository for reproducibility and wider implementation.
2. Background Information
2.1. The AmeriFlux Network
2.2. Natural Climate Solutions
3. Literature Review
4. Methods
4.1. Data
- Agricultural (AG);
- Deciduous Broadleaf (DB);
- Evergreen Broadleaf (EB);
- Evergreen Needleleaf (EN);
- Grassland (GR);
- Shrub (SH);
- Tundra (TN).
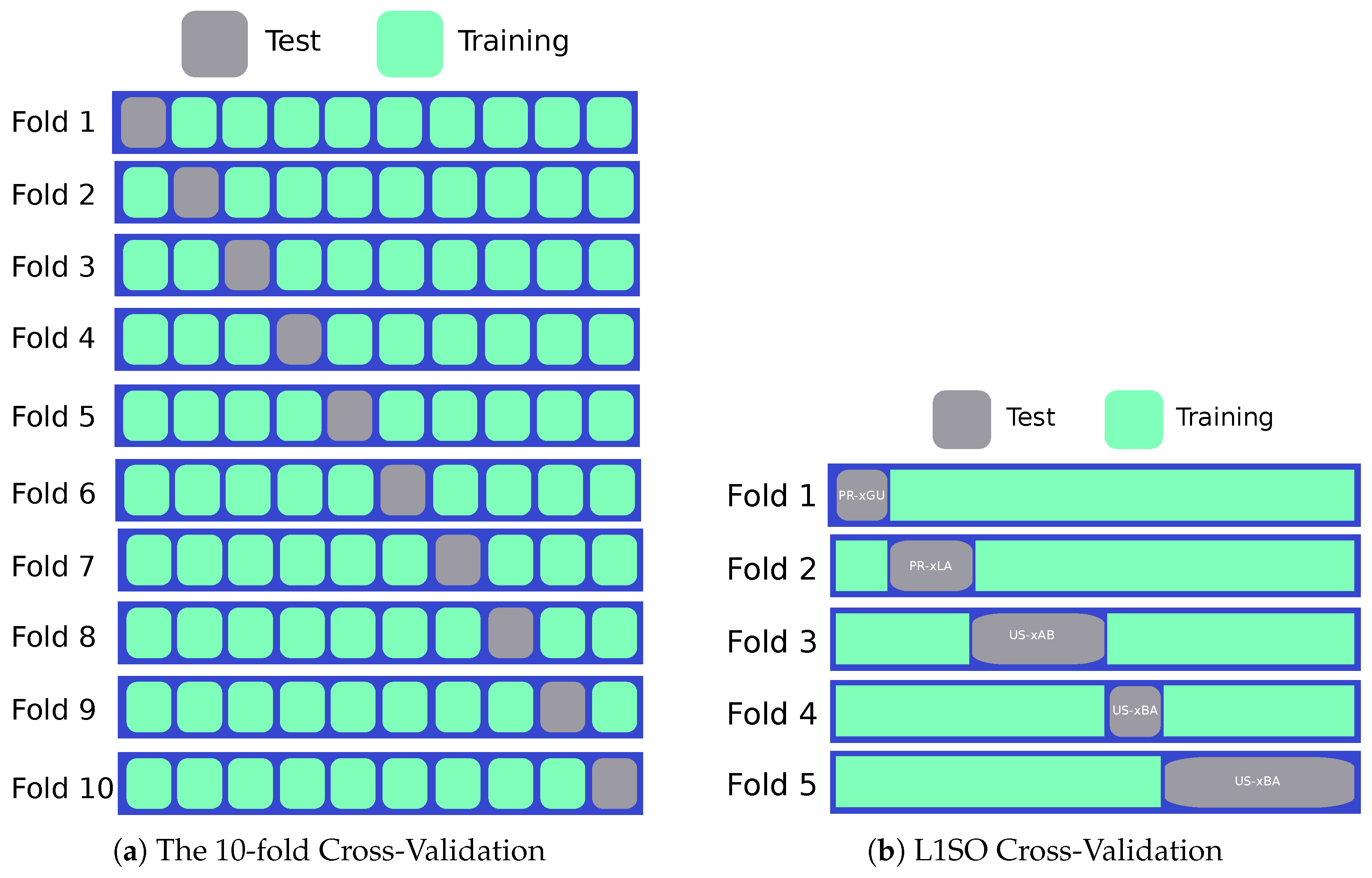
4.2. Experimental Design
4.3. Machine Learning Models
- Linear Regression (all predictors): This is a linear model including all of the variables using the maximum likelihood estimates for the coefficients. Linear regression assumes a linear relationship between the predictors and the response variable, which is unlikely in complex modeling problems, but does provide a baseline for the comparison of the performance of other models.
- Stepwise Linear Regression: This model began by testing for the most significant single variable in a linear regression model, and then iteratively added variables and tested for greatest improvement. A threshold number of selection variables was set to 15 for this forward selection technique. In this way, we simplify the basic linear regression model to find feature variables with greater importance for linear prediction.
- Decision Tree: A decision tree is a model based on recursively splitting the data on values of variables to maximize the difference between observations. Decision trees are most effective on problems where there is a non-linear relationship between the predictors and response variable [46,47]. The optimal tree depth was found to be 10, which was found through cross-validation.
- Random Forest: A random forest model [48] is a bagged ensemble of decision trees. The algorithm creates an uncorrelated forest of decision trees by using random subsets of features in each tree. When predicting a regression variable with a random forest model, the overall prediction is the average of the results of each of its constituent trees.
- Extreme Gradient Boosting (XGBoost): The XGBoost model [49] is a boosted ensemble of n underfit decision tree models. In practice, a decision tree is fit the to data and the errors in prediction are measured. Next, a second decision tree is used to fit the errors of the first tree. Then, a third decision tree is fit to the errors of the second tree, and we continue until we have n trees in our ensemble. The optimal number of trees in our ensemble was found to be 2000. We also set the number of rounds for early stopping to be 50, and we used a learning rate of 0.05, a max depth of 10, a subsample ratio of 0.5, and a subsample ratio of columns for each node of 0.45. Finally, we used the histogram-optimized approximate greedy algorithm for tree construction to optimize our XGBoost model. All hyperparameters were optimized through 10-fold cross-validation using an exhaustive grid search.
- Neural Network (single layer): A neural network is the sum of weighted non-linear functions of the predictor variables. This model is a single-layer neural network, with 256 neurons in the hidden layer, and uses a feed-forward architecture with ReLU activation. Early stopping was implemented to prevent model over-fitting, and training was performed with a data loader with a batch size of 128. The learning rate was set to 0.0003, and the best performance was achieved with no weight decay using the Adam optimizer. For more information on the mathematics of neural networks, see [50,51].
- Deep Neural Network: The model uses the same mathematical structure as the single-layer neural network, but increases the number of hidden layers to 3, each consisting of 256 neurons. Compared to the single-layer neural network, the increased depth of the model increases the number of parameters to learn, meaning the model is capable of modeling more complex relationships, but also takes longer to learn from the data.
5. Results
5.1. Results of 10-Fold Cross-Validation
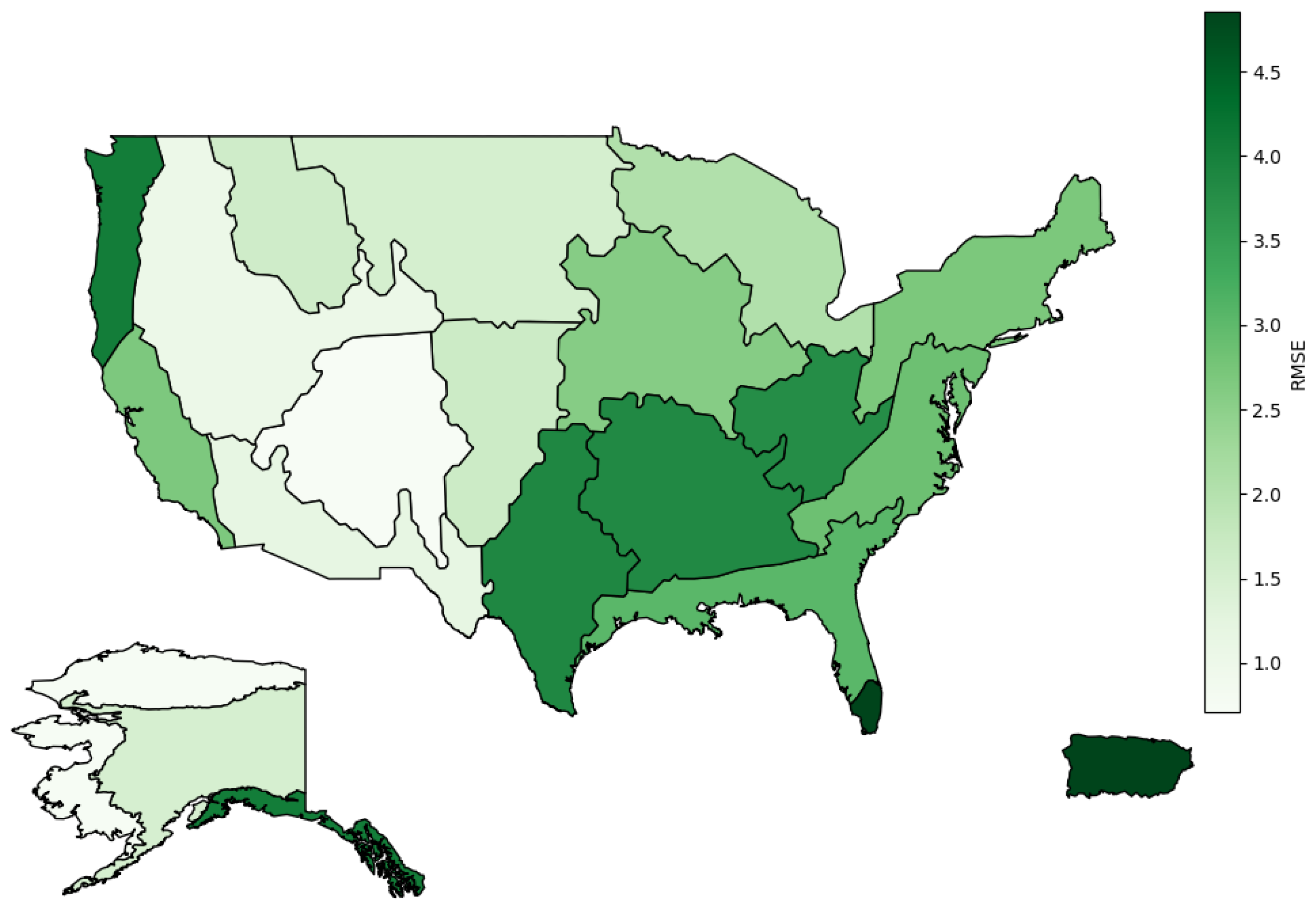
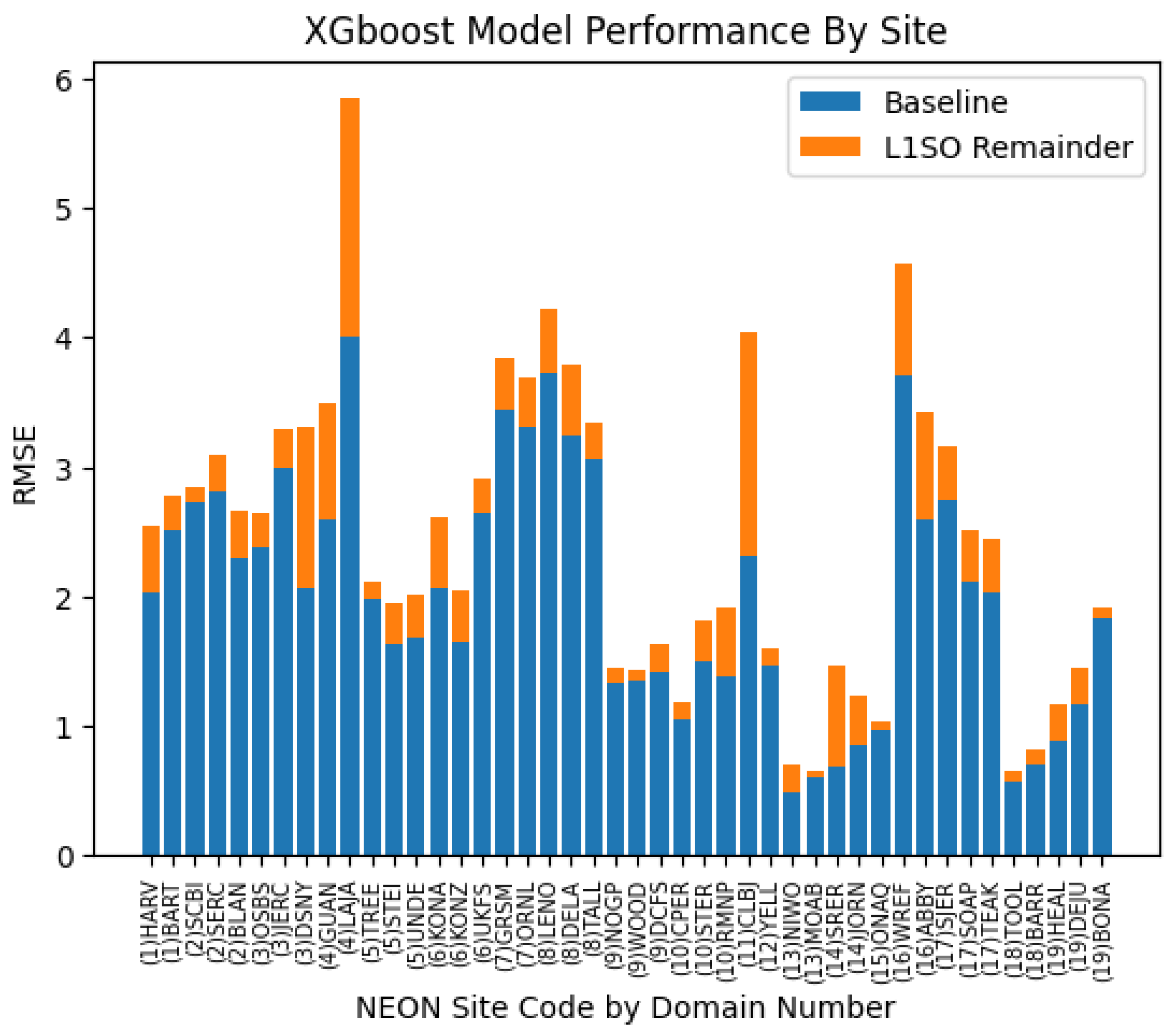
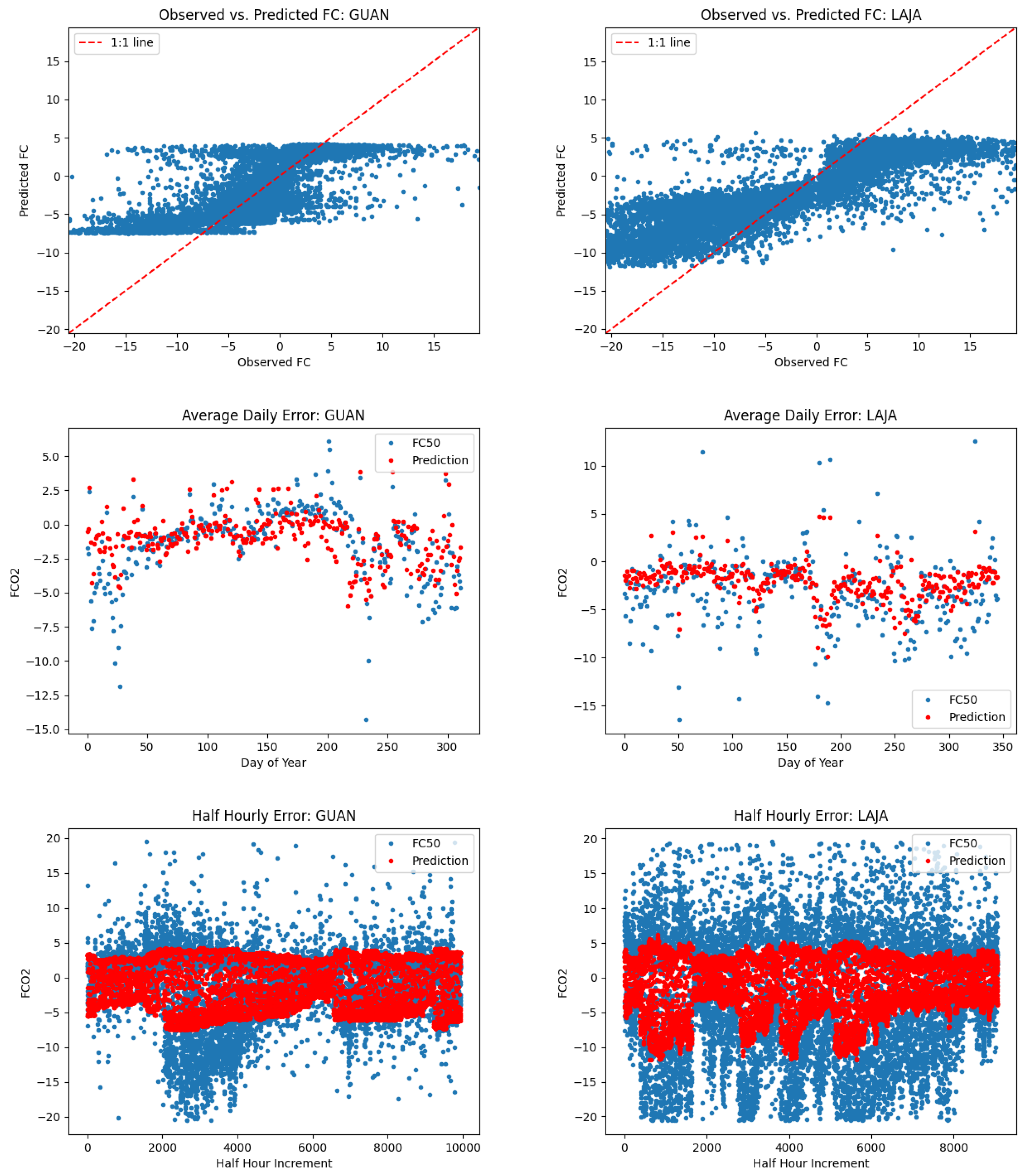
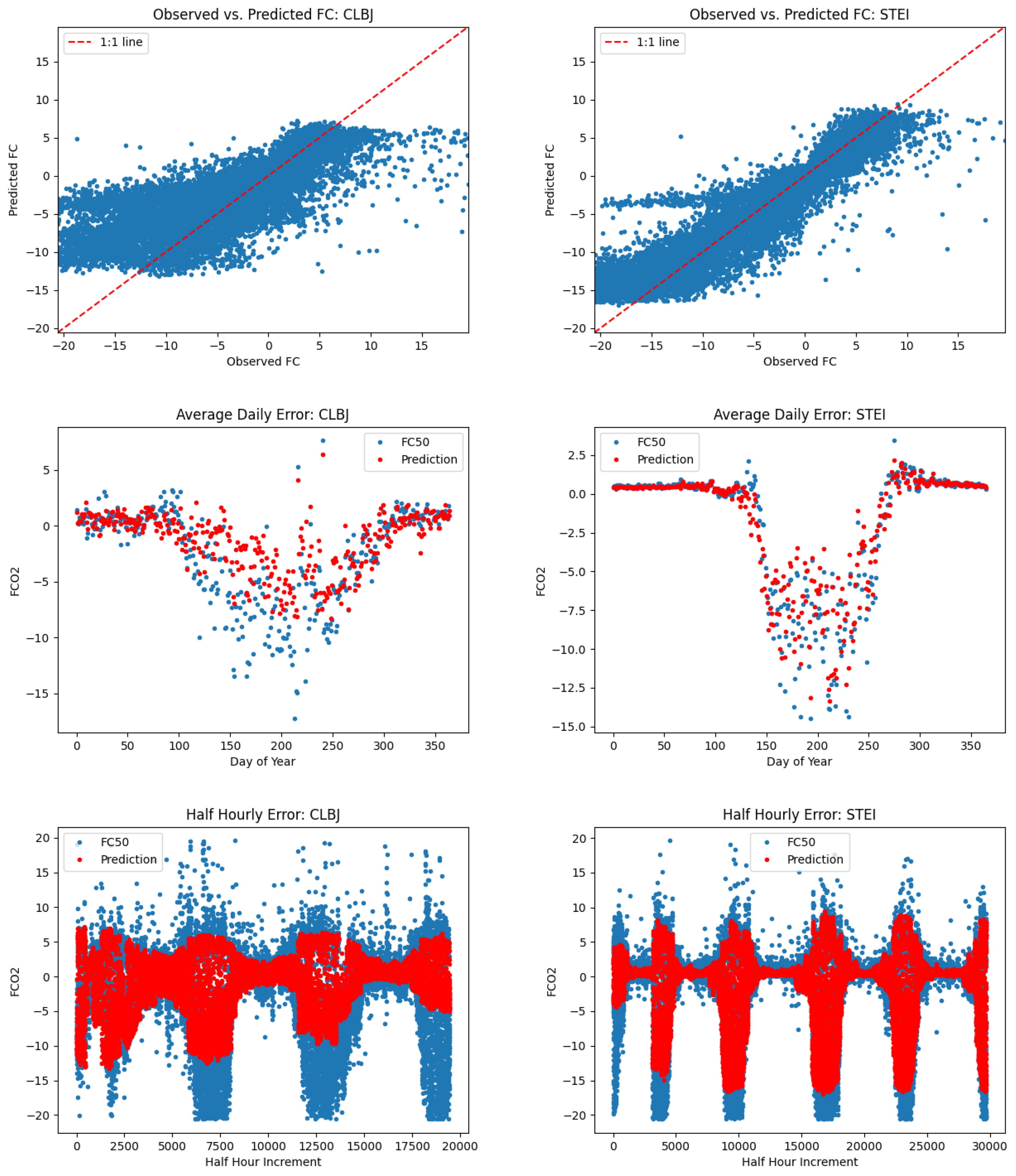
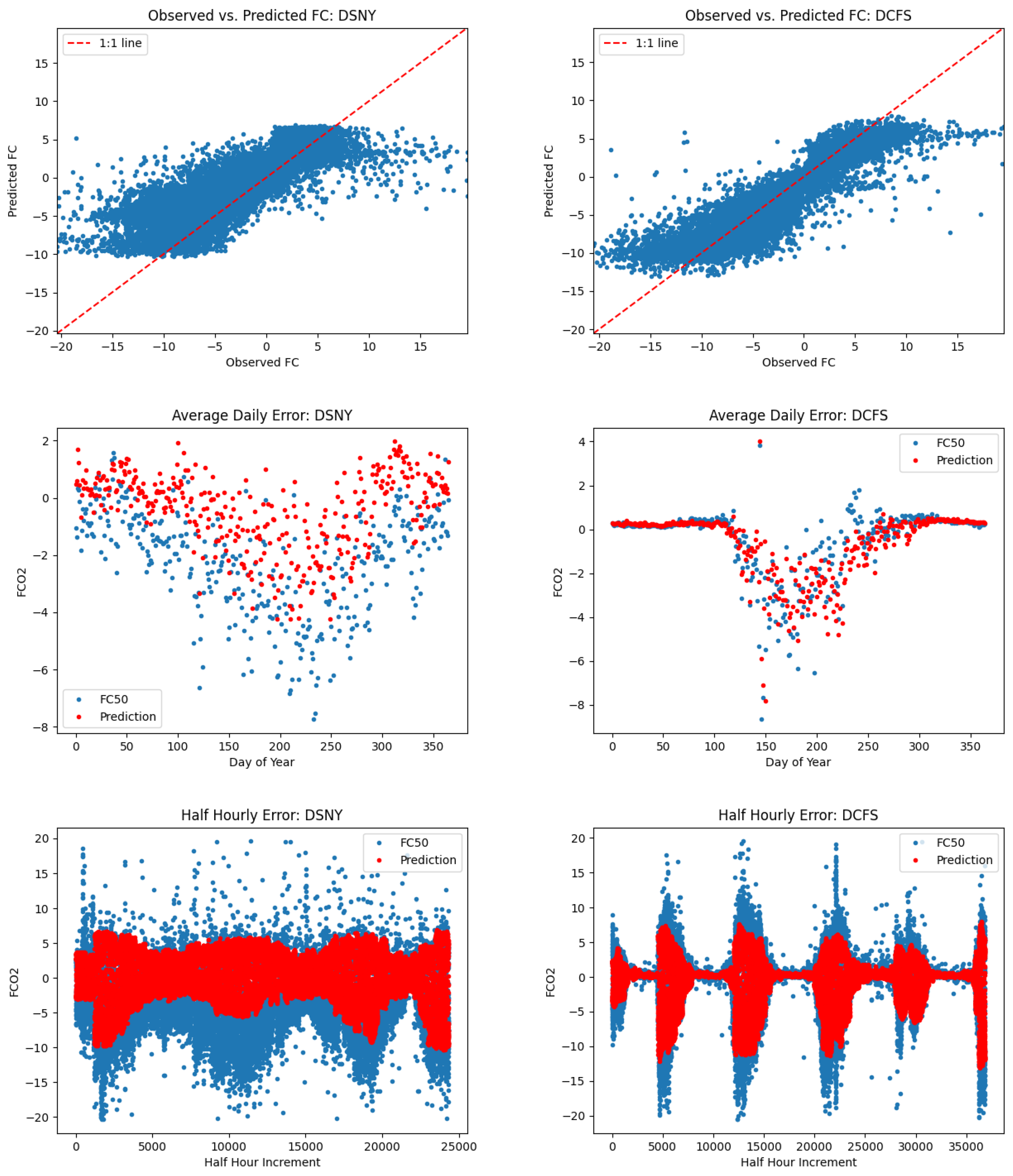
5.2. L1SO Cross-Validation Results
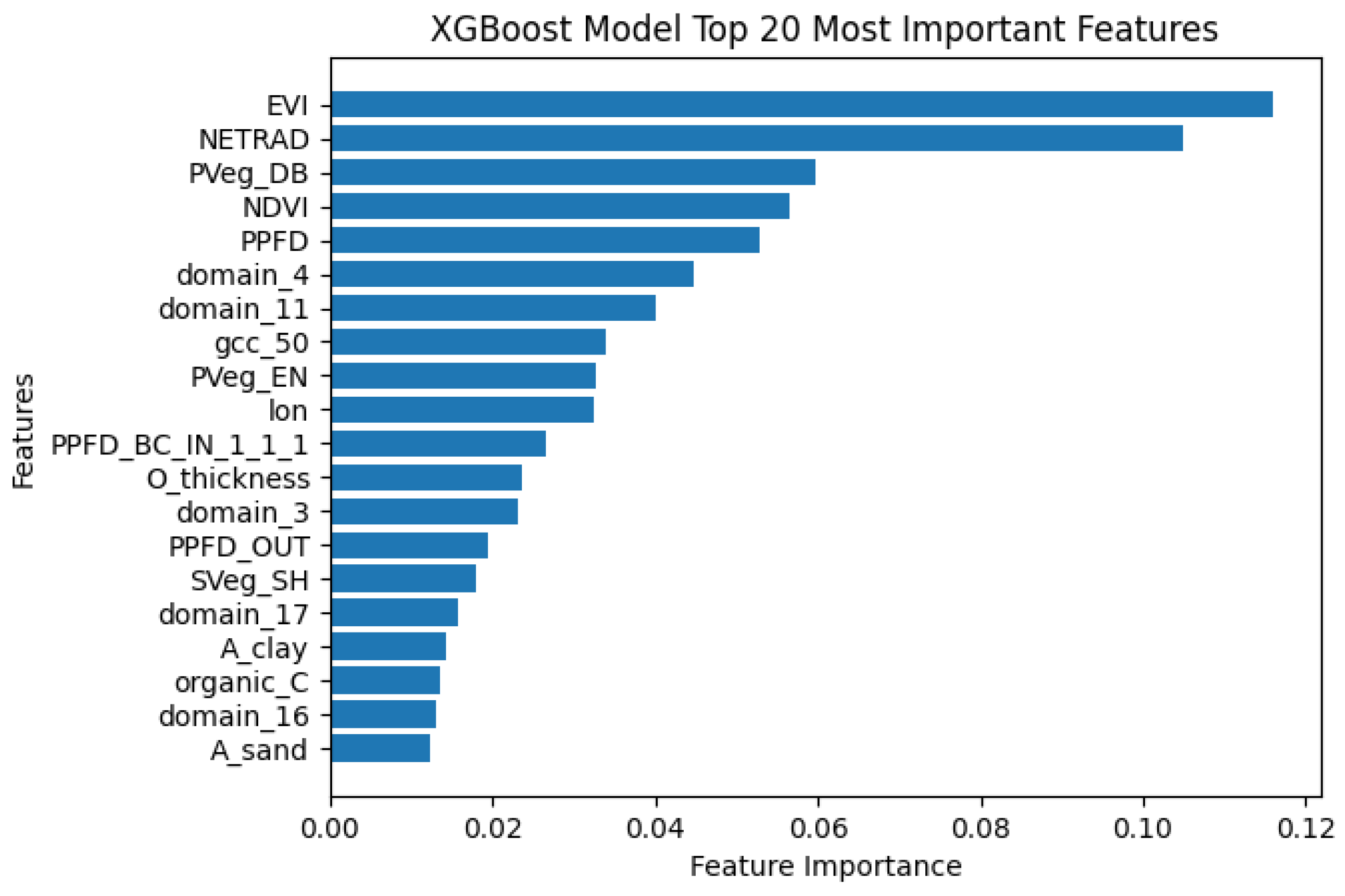
5.3. XGBoost Feature Importance
6. Discussion
6.1. Comparison of 10-Fold and L1SO Experimental Results
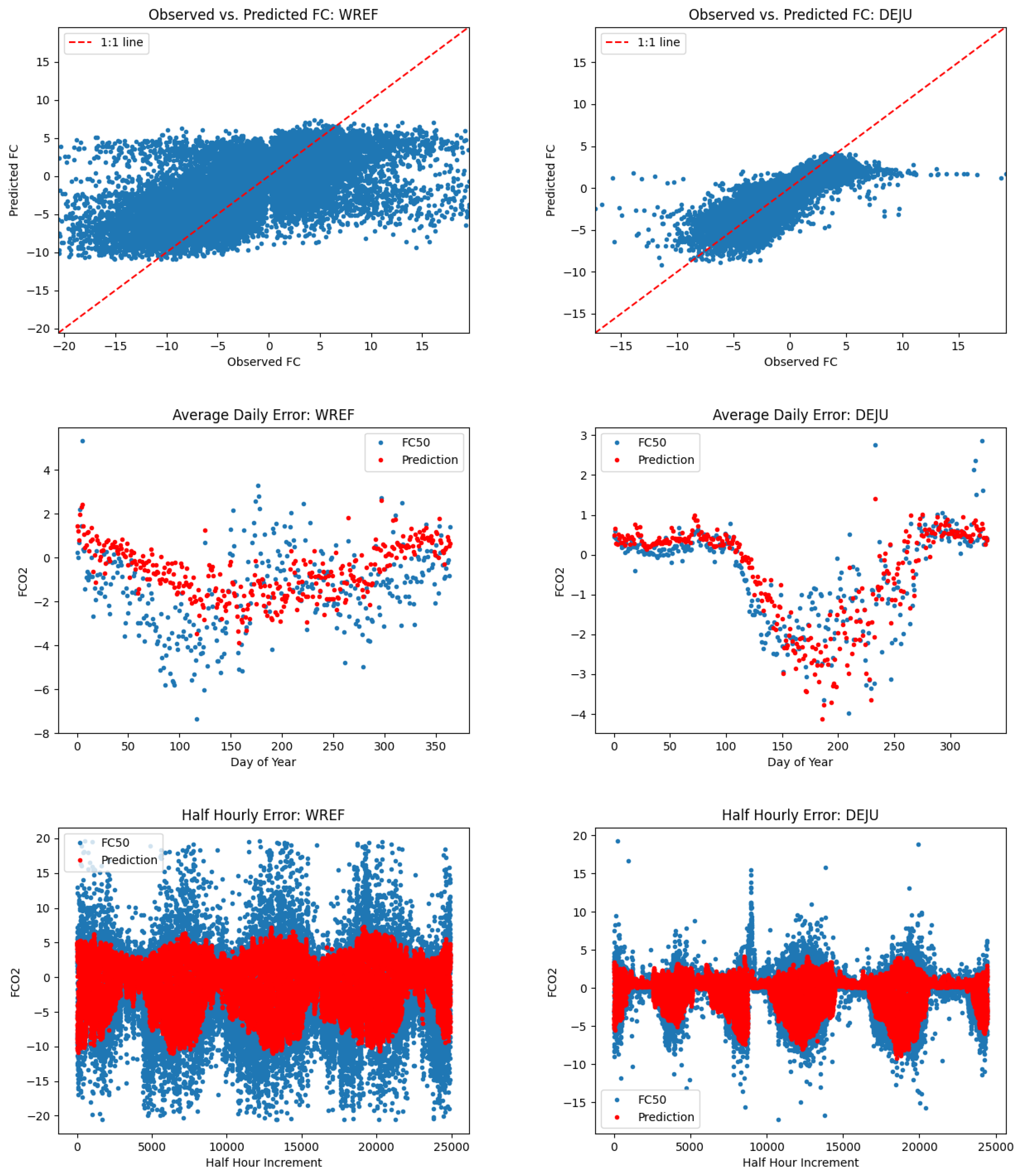
6.2. Relevance of L1SO Predictions for Unseen Sites
6.3. Leveraging Site-Level Data When Standardized Model Inputs Are Not Available
6.4. Annual Carbon Sums
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Baldocchi, D.D. How eddy covariance flux measurements have contributed to our understanding of Global Change Biology. Glob. Change Biol. 2020, 26, 242–260. [Google Scholar] [CrossRef] [PubMed]
- Novick, K.A.; Biederman, J.; Desai, A.; Litvak, M.; Moore, D.J.; Scott, R.; Torn, M. The AmeriFlux network: A coalition of the willing. Agric. For. Meteorol. 2018, 249, 444–456. [Google Scholar] [CrossRef]
- Chu, H.; Christianson, D.S.; Cheah, Y.W.; Pastorello, G.; O’Brien, F.; Geden, J.; Ngo, S.T.; Hollowgrass, R.; Leibowitz, K.; Beekwilder, N.F.; et al. AmeriFlux BASE data pipeline to support network growth and data sharing. Sci. Data 2023, 10, 614. [Google Scholar] [CrossRef] [PubMed]
- Wolpert, D. The Lack of A Priori Distinctions Between Learning Algorithms. Neural Comput. 1996, 8, 1341–1390. [Google Scholar] [CrossRef]
- Hino, M.; Benami, E.; Brooks, N. Machine learning for environmental monitoring. Nat. Sustain. 2018, 1, 583–588. [Google Scholar] [CrossRef]
- United States Department of Energy. AmeriFlux Management Project. 2023. Available online: https://ameriflux.lbl.gov/ (accessed on 1 June 2023).
- Dietze, M.C.; Vargas, R.; Richardson, A.D.; Stoy, P.C.; Barr, A.G.; Anderson, R.S.; Arain, M.A.; Baker, I.T.; Black, T.A.; Chen, J.M.; et al. Characterizing the performance of ecosystem models across time scales: A spectral analysis of the North American Carbon Program site-level synthesis. J. Geophys. Res. Biogeosciences 2011, 116. [Google Scholar] [CrossRef]
- Schwalm, C.R.; Williams, C.A.; Schaefer, K.; Anderson, R.; Arain, M.A.; Baker, I.; Barr, A.; Black, T.A.; Chen, G.; Chen, J.M.; et al. A model-data intercomparison of CO2 exchange across North America: Results from the North American Carbon Program site synthesis. J. Geophys. Res. Biogeosci. 2010, 115. [Google Scholar] [CrossRef]
- Keenan, T.; Baker, I.; Barr, A.; Ciais, P.; Davis, K.; Dietze, M.; Dragoni, D.; Gough, C.M.; Grant, R.; Hollinger, D.; et al. Terrestrial biosphere model performance for inter-annual variability of land-atmosphere CO2 exchange. Glob. Change Biol. 2012, 18, 1971–1987. [Google Scholar] [CrossRef]
- Richardson, A.D.; Anderson, R.S.; Arain, M.A.; Barr, A.G.; Bohrer, G.; Chen, G.; Chen, J.M.; Ciais, P.; Davis, K.J.; Desai, A.R.; et al. Terrestrial biosphere models need better representation of vegetation phenology: Results from the N orth A merican C arbon P rogram S ite S ynthesis. Glob. Change Biol. 2012, 18, 566–584. [Google Scholar] [CrossRef]
- Schaefer, K.; Schwalm, C.R.; Williams, C.; Arain, M.A.; Barr, A.; Chen, J.M.; Davis, K.J.; Dimitrov, D.; Hilton, T.W.; Hollinger, D.Y.; et al. A model-data comparison of gross primary productivity: Results from the North American Carbon Program site synthesis. J. Geophys. Res. Biogeosci. 2012, 117. [Google Scholar] [CrossRef]
- Papale, D.; Valentini, R. A new assessment of European forests carbon exchanges by eddy fluxes and artificial neural network spatialization. Glob. Change Biol. 2003, 9, 525–535. [Google Scholar] [CrossRef]
- Xiao, J.; Zhuang, Q.; Baldocchi, D.D.; Law, B.E.; Richardson, A.D.; Chen, J.; Oren, R.; Starr, G.; Noormets, A.; Ma, S.; et al. Estimation of net ecosystem carbon exchange for the conterminous United States by combining MODIS and AmeriFlux data. Agric. For. Meteorol. 2008, 148, 1827–1847. [Google Scholar] [CrossRef]
- Kang, Y.; Gaber, M.; Bassiouni, M.; Lu, X.; Keenan, T. CEDAR-GPP: Spatiotemporally upscaled estimates of gross primary productivity incorporating CO2 fertilization. Earth Syst. Sci. Data Discuss. 2023, 2023, 1–51. [Google Scholar]
- Jung, M.; Schwalm, C.; Migliavacca, M.; Walther, S.; Camps-Valls, G.; Koirala, S.; Anthoni, P.; Besnard, S.; Bodesheim, P.; Carvalhais, N.; et al. Scaling carbon fluxes from eddy covariance sites to globe: Synthesis and evaluation of the FLUXCOM approach. Biogeosciences 2020, 17, 1343–1365. [Google Scholar] [CrossRef]
- Battelle. National Science Foundation’s National Ecological Observatory Network (NEON). 2024. Available online: https://www.neonscience.org/ (accessed on 1 June 2023).
- Fer, I.; Kelly, R.; Moorcroft, P.R.; Richardson, A.D.; Cowdery, E.M.; Dietze, M.C. Linking big models to big data: Efficient ecosystem model calibration through Bayesian model emulation. Biogeosciences 2018, 15, 5801–5830. [Google Scholar] [CrossRef]
- Hemes, K.S.; Runkle, B.R.; Novick, K.A.; Baldocchi, D.D.; Field, C.B. An ecosystem-scale flux measurement strategy to assess natural climate solutions. Environ. Sci. Technol. 2021, 55, 3494–3504. [Google Scholar] [CrossRef]
- Hollinger, D.; Davidson, E.; Fraver, S.; Hughes, H.; Lee, J.; Richardson, A.; Savage, K.; Sihi, D.; Teets, A. Multi-decadal carbon cycle measurements indicate resistance to external drivers of change at the Howland forest AmeriFlux site. J. Geophys. Res. Biogeosciences 2021, 126, e2021JG006276. [Google Scholar] [CrossRef]
- Wofsy, S.C.; Harris, R.C. The North American Carbon Program 2002. Technical Report, The Global Carbon Project. 2002. Available online: https://www.globalcarbonproject.org/global/pdf/thenorthamericancprogram2002.pdf (accessed on 1 June 2023).
- Schimel, D.S.; House, J.I.; Hibbard, K.A.; Bousquet, P.; Ciais, P.; Peylin, P.; Braswell, B.H.; Apps, M.J.; Baker, D.; Bondeau, A.; et al. Recent patterns and mechanisms of carbon exchange by terrestrial ecosystems. Nature 2001, 414, 169–172. [Google Scholar] [CrossRef]
- Griscom, B.W.; Adams, J.; Ellis, P.W.; Houghton, R.A.; Lomax, G.; Miteva, D.A.; Schlesinger, W.H.; Shoch, D.; Siikamäki, J.V.; Smith, P.; et al. Natural climate solutions. Proc. Natl. Acad. Sci. USA 2017, 114, 11645–11650. [Google Scholar] [CrossRef]
- Fargione, J.E.; Bassett, S.; Boucher, T.; Bridgham, S.D.; Conant, R.T.; Cook-Patton, S.C.; Ellis, P.W.; Falcucci, A.; Fourqurean, J.W.; Gopalakrishna, T.; et al. Natural climate solutions for the United States. Sci. Adv. 2018, 4, eaat1869. [Google Scholar] [CrossRef]
- Bossio, D.; Cook-Patton, S.; Ellis, P.; Fargione, J.; Sanderman, J.; Smith, P.; Wood, S.; Zomer, R.; Von Unger, M.; Emmer, I.; et al. The role of soil carbon in natural climate solutions. Nat. Sustain. 2020, 3, 391–398. [Google Scholar] [CrossRef]
- Ellis, P.W.; Page, A.M.; Wood, S.; Fargione, J.; Masuda, Y.J.; Carrasco Denney, V.; Moore, C.; Kroeger, T.; Griscom, B.; Sanderman, J.; et al. The principles of natural climate solutions. Nat. Commun. 2024, 15, 547. [Google Scholar] [CrossRef] [PubMed]
- Lee, H.; Calvin, K.; Dasgupta, D.; Krinner, G.; Mukherji, A.; Thorne, P.; Trisos, C.; Romero, J.; Aldunce, P.; Barret, K.; et al. IPCC, 2023: Climate Change 2023: Synthesis Report, Summary for Policymakers. Contribution of Working Groups I, II and III to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Core Writing Team, Lee, H., Romero, J., Eds.; Technical report; Intergovernmental Panel on Climate Change (IPCC): Geneva, Switzerland, 2023. [Google Scholar]
- AlOmar, M.K.; Hameed, M.M.; Al-Ansari, N.; Razali, S.F.M.; AlSaadi, M.A. Short-, medium-, and long-term prediction of carbon dioxide emissions using wavelet-enhanced extreme learning machine. Civ. Eng. J. 2023, 9, 815–834. [Google Scholar] [CrossRef]
- Hou, Y.; Liu, S. Predictive Modeling and Validation of Carbon Emissions from China’s Coastal Construction Industry: A BO-XGBoost Ensemble Approach. Sustainability 2024, 16, 4215. [Google Scholar] [CrossRef]
- Fang, D.; Zhang, X.; Yu, Q.; Jin, T.C.; Tian, L. A novel method for carbon dioxide emission forecasting based on improved Gaussian processes regression. J. Clean. Prod. 2018, 173, 143–150. [Google Scholar] [CrossRef]
- Mardani, A.; Liao, H.; Nilashi, M.; Alrasheedi, M.; Cavallaro, F. A multi-stage method to predict carbon dioxide emissions using dimensionality reduction, clustering, and machine learning techniques. J. Clean. Prod. 2020, 275, 122942. [Google Scholar] [CrossRef]
- Zhang, Y.; Fu, B. Impact of China’s establishment of ecological civilization pilot zones on carbon dioxide emissions. J. Environ. Manag. 2023, 325, 116652. [Google Scholar] [CrossRef]
- Baareh, A.K. Solving the Carbon Dioxide Emission Estimation Problem: An Artificial Neural Network Model. J. Softw. Eng. Appl. 2013, 6, 338–342. [Google Scholar] [CrossRef][Green Version]
- Hamrani, A.; Akbarzadeh, A.; Madramootoo, C.A. Machine learning for predicting greenhouse gas emissions from agricultural soils. Sci. Total Environ. 2020, 741, 140338. [Google Scholar] [CrossRef]
- Durmanov, A.; Saidaxmedova, N.; Mamatkulov, M.; Rakhimova, K.; Askarov, N.; Khamrayeva, S.; Mukhtorov, A.; Khodjimukhamedova, S.; Madumarov, T.; Kurbanova, K. Sustainable growth of greenhouses: Investigating key enablers and impacts. Emerg. Sci. J. 2023, 7, 1674–1690. [Google Scholar] [CrossRef]
- Tramontana, G.; Jung, M.; Schwalm, C.R.; Ichii, K.; Camps-Valls, G.; Ráduly, B.; Reichstein, M.; Arain, M.A.; Cescatti, A.; Kiely, G.; et al. Predicting carbon dioxide and energy fluxes across global FLUXNET sites with regression algorithms. Biogeosciences 2016, 13, 4291–4313. [Google Scholar] [CrossRef]
- Dou, X.; Yang, Y.; Luo, J. Estimating forest carbon fluxes using machine learning techniques based on eddy covariance measurements. Sustainability 2018, 10, 203. [Google Scholar] [CrossRef]
- Vais, A.; Mikhaylov, P.; Popova, V.; Nepovinnykh, A.; Nemich, V.; Andronova, A.; Mamedova, S. Carbon sequestration dynamics in urban-adjacent forests: A 50-year analysis. Civ. Eng. J. 2023, 9, 2205–2220. [Google Scholar] [CrossRef]
- Zhao, J.; Lange, H.; Meissner, H. Estimating Carbon Sink Strength of Norway Spruce Forests Using Machine Learning. Forests 2022, 13, 1721. [Google Scholar] [CrossRef]
- Safaei-Farouji, M.; Thanh, H.V.; Dai, Z.; Mehbodniya, A.; Rahimi, M.; Ashraf, U.; Radwan, A.E. Exploring the power of machine learning to predict carbon dioxide trapping efficiency in saline aquifers for carbon geological storage project. J. Clean. Prod. 2022, 372, 133778. [Google Scholar] [CrossRef]
- Zhu, S.; Clement, R.; McCalmont, J.; Davies, C.A.; Hill, T. Stable gap-filling for longer eddy covariance data gaps: A globally validated machine-learning approach for carbon dioxide, water, and energy fluxes. Agric. For. Meteorol. 2022, 314, 108777. [Google Scholar] [CrossRef]
- Madan, T.; Sagar, S.; Virmani, D. Air Quality Prediction using Machine Learning Algorithms –A Review. In Proceedings of the 2020 2nd International Conference on Advances in Computing, Communication Control and Networking, Greater Noida, India, 18–19 December 2020; pp. 140–145. [Google Scholar]
- National Ecological Observatory Network (NEON). Bundled Data Products—Eddy Covariance (DP4.00200.001). 2024. Available online: https://data.neonscience.org/data-products/DP4.00200.001 (accessed on 1 June 2023).
- Richardson, A.D.; Hufkens, K.; Milliman, T.; Aubrecht, D.M.; Chen, M.; Gray, J.M.; Johnston, M.R.; Keenan, T.F.; Klosterman, S.T.; Kosmala, M.; et al. Tracking vegetation phenology across diverse North American biomes using PhenoCam imagery. Sci. Data 2018, 5, 1–24. [Google Scholar] [CrossRef]
- Seyednasrollah, B.; Young, A.M.; Hufkens, K.; Milliman, T.; Friedl, M.A.; Frolking, S.; Richardson, A.D. Tracking vegetation phenology across diverse biomes using Version 2.0 of the PhenoCam Dataset. Sci. Data 2019, 6, 222. [Google Scholar]
- Rodriguez, J.D.; Perez, A.; Lozano, J.A. Sensitivity analysis of k-fold cross validation in prediction error estimation. IEEE Trans. Pattern Anal. Mach. Intell. 2009, 32, 569–575. [Google Scholar] [CrossRef]
- Nie, F.; Zhu, W.; Li, X. Decision Tree SVM: An extension of linear SVM for non-linear classification. Neurocomputing 2020, 401, 153–159. [Google Scholar] [CrossRef]
- Vanli, N.D.; Sayin, M.O.; Mohaghegh, M.; Ozkan, H.; Kozat, S.S. Nonlinear regression via incremental decision trees. Pattern Recognit. 2019, 86, 1–13. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM Sigkdd International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning: With Applications in R, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- Mahabbati, A.; Beringer, J.; Leopold, M.; McHugh, I.; Cleverly, J.; Isaac, P.; Izady, A. A comparison of gap-filling algorithms for eddy covariance fluxes and their drivers. Geosci. Instrum. Methods Data Syst. 2021, 10, 123–140. [Google Scholar] [CrossRef]
- Stoy, P.C.; Dietze, M.C.; Richardson, A.D.; Vargas, R.; Barr, A.G.; Anderson, R.S.; Arain, M.A.; Baker, I.T.; Black, T.A.; Chen, J.M.; et al. Evaluating the agreement between measurements and models of net ecosystem exchange at different times and timescales using wavelet coherence: An example using data from the North American Carbon Program Site-Level Interim Synthesis. Biogeosciences 2013, 10, 6893–6909. [Google Scholar] [CrossRef]
- Richardson, A.D.; Aubinet, M.; Barr, A.G.; Hollinger, D.Y.; Ibrom, A.; Lasslop, G.; Reichstein, M. Uncertainty Quantification. In Eddy Covariance: A Practical Guide to Measurement and Data Analysis; Aubinet, M., Vesala, T., Papale, D., Eds.; Springer: Dordrecht, The Netherlands, 2012; pp. 173–209. [Google Scholar]
- Braswell, B.H.; Sacks, W.J.; Linder, E.; Schimel, D.S. Estimating diurnal to annual ecosystem parameters by synthesis of a carbon flux model with eddy covariance net ecosystem exchange observations. Glob. Change Biol. 2005, 11, 335–355. [Google Scholar] [CrossRef]
- Siqueira, M.; Katul, G.G.; Sampson, D.; Stoy, P.C.; Juang, J.Y.; McCarthy, H.R.; Oren, R. Multiscale model intercomparisons of CO2 and H2O exchange rates in a maturing southeastern US pine forest. Glob. Change Biol. 2006, 12, 1189–1207. [Google Scholar] [CrossRef]
- Ricciuto, D.M.; Davis, K.J.; Keller, K. A Bayesian calibration of a simple carbon cycle model: The role of observations in estimating and reducing uncertainty. Glob. Biogeochem. Cycles 2008, 22. [Google Scholar] [CrossRef]
- Lucas, B.; Pelletier, C.; Schmidt, D.; Webb, G.I.; Petitjean, F. Unsupervised Domain Adaptation Techniques for Classification of Satellite Image Time Series. In Proceedings of the IGARSS 2020—2020 IEEE International Geoscience and Remote Sensing Symposium, Virtual Event, 26 September–2 October 2020; pp. 1074–1077. [Google Scholar]
- Lucas, B.; Pelletier, C.; Inglada, J.; Schmidt, D.; Webb, G.; Petitjean, F. Exploring data quantity requirements for Domain Adaptation in the classification of satellite image time series. In Proceedings of the MultiTemp 2019, 10th International Workshop on the Analysis of Multitemporal Remote Sensing Images, Shanghai, China, 5–7 August 2019; Bovolo, F., Liu, S., Eds.; IEEE, Institute of Electrical and Electronics Engineers: Piscataway Township, NJ, USA, 2019. [Google Scholar]
- Ou, Y.; Zheng, J.; Liang, Y.; Bao, Z. When green transportation backfires: High-speed rail’s impact on transport-sector carbon emissions from 315 Chinese cities. Sustain. Cities Soc. 2024, 114, 105770. [Google Scholar] [CrossRef]
- Ou, Y.; Bao, Z.; Ng, S.T.; Song, W.; Chen, K. Land-use carbon emissions and built environment characteristics: A city-level quantitative analysis in emerging economies. Land Use Policy 2024, 137, 107019. [Google Scholar] [CrossRef]
- Huang, C.; Xu, N. Quantifying urban expansion from 1985 to 2018 in large cities worldwide. Geocarto Int. 2022, 37, 18356–18371. [Google Scholar] [CrossRef]
- Friedlingstein, P.; O’Sullivan, M.; Jones, M.W.; Andrew, R.M.; Hauck, J.; Landschützer, P.; Le Quéré, C.; Li, H.; Luijkx, I.T.; Olsen, A.; et al. Global Carbon Budget 2024. Earth Syst. Sci. Data 2024, 2024, 1–133. [Google Scholar] [CrossRef]
- Friedlingstein, P.; O’Sullivan, M.; Jones, M.W.; Andrew, R.M.; Bakker, D.C.E.; Hauck, J.; Landschützer, P.; Le Quéré, C.; Luijkx, I.T.; Peters, G.P.; et al. Global Carbon Budget 2023. Earth Syst. Sci. Data 2023, 15, 5301–5369. [Google Scholar] [CrossRef]
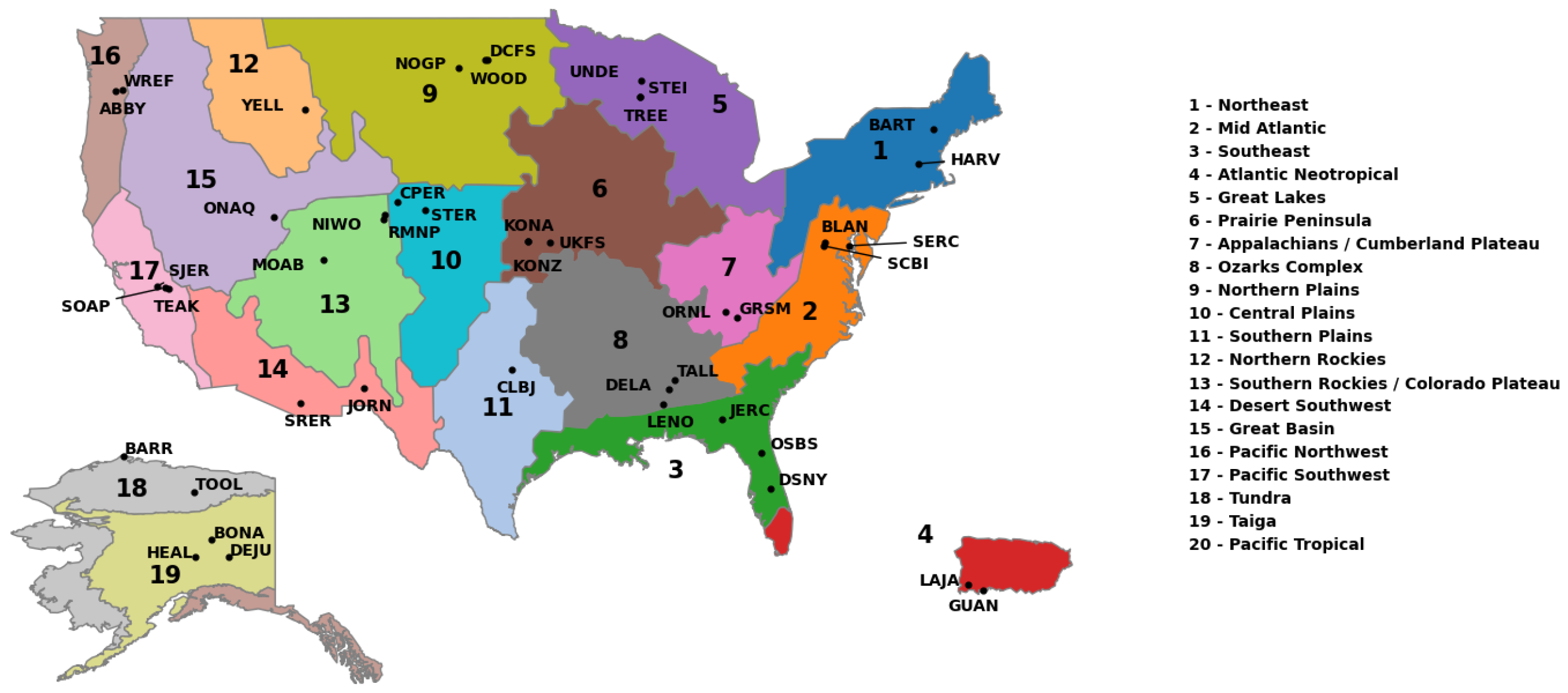
| Variable | Description (Units) | Source |
|---|---|---|
| DOY | Day of Year (as percentage of a year) | AmeriFlux/NEON |
| HOUR | Hour Of Day (as percentage of a day) | AmeriFlux/NEON |
| TS_1_1_1 | Soil Temperature Depth 1 (degrees C) | AmeriFlux/NEON |
| TS_1_2_1 | Soil Temperature Depth 2 (degrees C) | AmeriFlux/NEON |
| PPFD | Photosynthetic Photon Flux Density (μmolPhoton m−2 s−1) | AmeriFlux/NEON |
| TAIR | Air Temperature (degrees C) | AmeriFlux/NEON |
| VPD | Vapor Pressure Deficit (hPa) | AmeriFlux/NEON |
| SWC_1_1_1 | Soil Water Content (as percentage of volume) | AmeriFlux/NEON |
| PPFD_OUT | Photosynthetic Photon Flux Density, Outgoing (μmolPhoton m−2 s−1) | AmeriFlux/NEON |
| PPFD_BC_IN_1_1_1 | Photosynthetic Photon Flux Density, Below Canopy Incoming (μmolPhoton m−2 s−1) | AmeriFlux/NEON |
| RH | Relative Humidity (percentage) | AmeriFlux/NEON |
| NETRAD | Net Radiation (W m−2) | AmeriFlux/NEON |
| USTAR | Friction velocity (ms−1) | AmeriFlux/NEON |
| GCC_50 | Green Chromatic Coordinate, median (dimensionless) | Phenocam |
| RCC_50 | Red Chromatic Coordinate, median (dimensionless) | Phenocam |
| MAT_DAYMET | Mean Annual Temperature (degree C) | DAYMET |
| MAP_DAYMET | Mean Annual Precipitation (mm) | DAYMET |
| PVEG | Primary Vegetation Type (categorical) | Phenocam |
| SVEG | Secondary Vegetation Type (categorical) | Phenocam |
| LW_OUT | Longwave Radiation, Outgoing (W m−2) | AmeriFlux/NEON |
| DAILY PRECIPITATION | Daily Precipitation (mm) | AmeriFlux/NEON |
| PRCP1WEEK | Cummulative Precipitation 1 Week (mm) | AmeriFlux/NEON |
| PRCP2WEEK | Cumulative Precipitation 2 Week (mm) | AmeriFlux/NEON |
| NDVI | Normalized Difference Vegetation Index (dimensionless) | MODIS |
| EVI | Enhanced Vegetation Index (dimensionless) | MODIS |
| LAT | Latitude (decimal degrees) | Phenocam |
| LON | Longitude (decimal degrees) | Phenocam |
| ELEV | Elevation (meters) | Phenocam |
| DOMAIN | NEON Field Site Domain (categorical) | Phenocam |
| organic_C | Total Organic Carbon Stock in Soil Profile (g C m−2) | AmeriFlux/NEON |
| total_N | Total Nitrogen Stock in Soil Profile (g C m−2) | AmeriFlux/NEON |
| O_thickness | Total Thickness of Organic Horizon (cm) | AmeriFlux/NEON |
| A_pH | pH of A Horizon (dimensionless) | AmeriFlux/NEON |
| A_sand | Texture of A Horizon (% Sand) | AmeriFlux/NEON |
| A_silt | Texture of A Horizon (% Silt) | AmeriFlux/NEON |
| A_clay | Texture of A Horizon (% Clay) | AmeriFlux/NEON |
| A_BD | Bulk Density of A Horizon (g cm−3) | AmeriFlux/NEON |
| Linear Reg | Stepwise | Decision Tree | Random Forest | XGB | NN 1-Layer | NN Deeper | |
|---|---|---|---|---|---|---|---|
| RMSE | 3.49 | 3.58 | 2.39 | 2.26 | 1.81 | 2.06 | 1.91 |
| R2 | 0.48 | 0.46 | 0.76 | 0.77 | 0.86 | 0.82 | 0.85 |
| Test Set | Site Code | Site Name | Primary Veg Type | Linear Reg | Stepwise | Decision Tree | Random Forest | XGB | NN 1-Layer | NN Deeper |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | PR-xGU | Guanica Forest (GUAN) | EB | 4.83 | 4.47 | 5.83 | 5.32 | 3.49 | 5.95 | 6.48 |
| 2 | PR-xLA | Lajas Experimental Station (LAJA) | EB | 7.52 | 6.99 | 7.60 | 6.68 | 6.22 | 6.02 | 6.60 |
| 3 | US-xAB | Abby Road (ABBY) | EN | 7.25 | 4.45 | 4.72 | 3.86 | 3.43 | 3.55 | 3.66 |
| 4 | US-xBA | Barrow Environmental Observatory (BARR) | TN | 135.35 | 1.30 | 1.51 | 1.49 | 0.86 | 2.91 | 0.89 |
| 5 | US-xBL | Blandy Experimental Farm (BLAN) | DB | 4.10 | 3.96 | 2.77 | 2.69 | 2.62 | 2.89 | 2.98 |
| 6 | US-xBN | Caribou Creek—Poker Flats Watershed (BONA) | EN | 14.61 | 2.41 | 2.12 | 2.01 | 1.93 | 2.70 | 1.92 |
| 7 | US-xBR | Bartlett Experimental Forest (BART) | DB | 5.21 | 4.41 | 3.33 | 3.06 | 2.77 | 3.13 | 3.06 |
| 8 | US-xCL | LBJ National Grassland (CLBJ) | DB | 5.19 | 4.17 | 4.38 | 4.16 | 3.88 | 4.11 | 3.31 |
| 9 | US-xCP | Central Plains Experimental Range (CPER) | GR | 4.24 | 2.47 | 1.38 | 1.29 | 1.22 | 1.60 | 1.48 |
| 10 | US-xDC | Dakota Coteau Field School (DCFS) | GR | 20.35 | 2.70 | 1.79 | 1.70 | 1.61 | 1.64 | 1.74 |
| 11 | US-xDJ | Delta Junction (DEJU) | EN | 5.52 | 2.28 | 2.05 | 1.64 | 1.44 | 1.56 | 1.44 |
| 12 | US-xDL | Dead Lake (DELA) | DB | 9.86 | 5.29 | 4.36 | 4.21 | 3.84 | 4.23 | 4.26 |
| 13 | US-xDS | Disney Wilderness Preserve (DSNY) | GR | 10.21 | 3.03 | 3.64 | 3.25 | 3.33 | 2.67 | 3.35 |
| 14 | US-xGR | Great Smoky Mountains National Park, Twin Creeks (GRSM) | DB | 6.51 | 6.06 | 4.21 | 3.99 | 3.87 | 4.12 | 3.94 |
| 15 | US-xHA | Harvard Forest (HARV) | DB | 5.24 | 4.50 | 3.05 | 2.91 | 2.60 | 2.73 | 2.92 |
| 16 | US-xHE | Healy (HEAL) | TN | 5.03 | 1.72 | 2.00 | 1.65 | 1.15 | 1.77 | 1.17 |
| 17 | US-xJE | Jones Ecological Research Center (JERC) | DB | 6.07 | 4.37 | 3.75 | 3.46 | 3.19 | 3.43 | 3.41 |
| 18 | US-xJR | Jornada LTER (JORN) | GR | 2.56 | 1.79 | 1.25 | 1.23 | 1.17 | 1.76 | 1.26 |
| 19 | US-xKA | Konza Prairie Biological Station - Relocatable (KONA) | AG | 6.57 | 3.64 | 3.02 | 2.95 | 2.61 | 3.05 | 3.56 |
| 20 | US-xKZ | Konza Prairie Biological Station (KONZ) | GR | 6.88 | 3.57 | 2.60 | 2.23 | 2.21 | 2.06 | 2.16 |
| 21 | US-xLE | Lenoir Landing (LENO) | DB | 6.83 | 5.27 | 4.92 | 4.53 | 4.32 | 4.25 | 4.19 |
| 22 | US-xMB | Moab (MOAB) | GR | 8.63 | 1.86 | 0.73 | 0.71 | 0.68 | 1.54 | 0.68 |
| 23 | US-xNG | Northern Great Plains Research Laboratory (NOGP) | GR | 5.07 | 2.29 | 1.67 | 1.59 | 1.46 | 1.55 | 1.96 |
| 24 | US-xNQ | Onaqui-Ault (ONAQ) | SH | 4.01 | 1.73 | 1.17 | 1.11 | 1.05 | 1.90 | 1.21 |
| 25 | US-xNW | Niwot Ridge Mountain Research Station (NIWO) | TN | 9.63 | 1.46 | 0.85 | 0.80 | 0.74 | 1.86 | 1.76 |
| 26 | US-xRM | Rocky Mountain National Park, CASTNET (RMNP) | EN | 8.49 | 3.18 | 2.70 | 2.31 | 1.92 | 2.45 | 1.94 |
| 27 | US-xRN | Oak Ridge National Lab (ORNL) | DB | 5.75 | 5.11 | 4.43 | 4.22 | 3.68 | 3.92 | 3.61 |
| 28 | US-xSB | Ordway-Swisher Biological Station (OSBS) | EN | 7.77 | 3.40 | 3.06 | 2.78 | 2.63 | 3.17 | 3.08 |
| 29 | US-xSC | Smithsonian Conservation Biology Institute (SCBI) | DB | 4.53 | 4.11 | 3.36 | 3.00 | 2.86 | 3.12 | 2.98 |
| 30 | US-xSE | Smithsonian Environmental Research Center (SERC) | DB | 6.79 | 4.62 | 3.40 | 3.21 | 3.08 | 3.35 | 3.32 |
| 31 | US-xSJ | San Joaquin Experimental Range (SJER) | EN | 5.13 | 4.23 | 3.23 | 3.11 | 3.02 | 3.23 | 3.81 |
| 32 | US-xSL | North Sterling, CO (STER) | AG | 6.10 | 2.40 | 2.00 | 1.93 | 1.83 | 1.90 | 2.08 |
| 33 | US-xSP | Soaproot Saddle (SOAP) | EN | 3.57 | 3.58 | 4.16 | 3.86 | 2.50 | 2.78 | 2.67 |
| 34 | US-xSR | Santa Rita Experimental Range (SRER) | SH | 3.22 | 2.19 | 4.23 | 3.63 | 1.18 | 2.42 | 1.12 |
| 35 | US-xST | Steigerwaldt Land Services (STEI) | DB | 3.96 | 4.06 | 2.44 | 2.10 | 1.91 | 2.34 | 1.78 |
| 36 | US-xTA | Talladega National Forest (TALL) | EN | 5.36 | 5.16 | 4.53 | 4.33 | 3.34 | 3.77 | 3.98 |
| 37 | US-xTE | Lower Teakettle (TEAK) | EN | 6.11 | 3.07 | 2.99 | 2.93 | 2.53 | 2.48 | 2.95 |
| 38 | US-xTL | Toolik (TOOL) | TN | 134.54 | 1.44 | 1.24 | 0.79 | 0.66 | 2.12 | 0.96 |
| 39 | US-xTR | Treehaven (TREE) | DB | 5.13 | 3.89 | 2.41 | 2.35 | 2.12 | 2.61 | 2.21 |
| 40 | US-xUK | The University of Kansas Field Station (UKFS) | DB | 5.16 | 4.12 | 3.20 | 3.06 | 2.92 | 3.56 | 2.92 |
| 41 | US-xUN | University of Notre Dame Environmental Research Center (UNDE) | DB | 3.79 | 3.81 | 2.51 | 2.47 | 2.11 | 2.53 | 1.92 |
| 42 | US-xWD | Woodworth (WOOD) | GR | 5.16 | 2.21 | 1.77 | 1.61 | 1.49 | 1.52 | 1.70 |
| 43 | US-xWR | Wind River Experimental Forest (WREF) | EN | 7.53 | 5.31 | 5.89 | 5.82 | 4.67 | 4.92 | 4.68 |
| 44 | US-xYE | Yellowstone Northern Range (Frog Rock) (YELL) | EN | 5.05 | 2.49 | 2.10 | 2.05 | 1.61 | 1.71 | 1.74 |
| AVERAGE | 12.28 | 3.51 | 3.05 | 2.82 | 2.45 | 2.88 | 2.70 |
| Test Set | Site Code | Site Name | Primary Veg Type | Linear Reg | Stepwise | Decision Tree | Random Forest | XGBoost | NN (1-Layer) | NN (Deep) |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | PR-xGU | Guanica Forest (GUAN) | EB | 0.07 | 0.21 | −0.35 | −0.12 | 0.52 | −0.40 | −0.67 |
| 2 | PR-xLA | Lajas Experimental Station (LAJA) | EB | 0.31 | 0.40 | 0.29 | 0.45 | 0.53 | 0.56 | 0.47 |
| 3 | US-xAB | Abby Road (ABBY) | EN | −0.37 | 0.48 | 0.42 | 0.61 | 0.69 | 0.67 | 0.65 |
| 4 | US-xBA | Barrow Environmental Observatory (BARR) | TN | −16,320.00 | −0.51 | −1.03 | −0.97 | 0.34 | −6.54 | 0.29 |
| 5 | US-xBL | Blandy Experimental Farm (BLAN) | DB | 0.54 | 0.57 | 0.79 | 0.80 | 0.81 | 0.77 | 0.76 |
| 6 | US-xBN | Caribou Creek—Poker Flats Watershed (BONA) | EN | −33.28 | 0.07 | 0.28 | 0.35 | 0.40 | −0.17 | 0.41 |
| 7 | US-xBR | Bartlett Experimental Forest (BART) | DB | 0.34 | 0.53 | 0.73 | 0.77 | 0.81 | 0.76 | 0.77 |
| 8 | US-xCL | LBJ National Grassland (CLBJ) | DB | 0.35 | 0.58 | 0.54 | 0.58 | 0.64 | 0.59 | 0.74 |
| 9 | US-xCP | Central Plains Experimental Range (CPER) | GR | −4.44 | −0.85 | 0.42 | 0.50 | 0.55 | 0.22 | 0.33 |
| 10 | US-xDC | Dakota Coteau Field School (DCFS) | GR | −28.15 | 0.49 | 0.78 | 0.80 | 0.82 | 0.81 | 0.79 |
| 11 | US-xDJ | Delta Junction (DEJU) | EN | −3.89 | 0.17 | 0.32 | 0.57 | 0.67 | 0.61 | 0.67 |
| 12 | US-xDL | Dead Lake (DELA) | DB | −0.89 | 0.46 | 0.63 | 0.66 | 0.71 | 0.65 | 0.65 |
| 13 | US-xDS | Disney Wilderness Preserve (DSNY) | GR | −3.07 | 0.64 | 0.48 | 0.59 | 0.57 | 0.72 | 0.56 |
| 14 | US-xGR | Great Smoky Mountains National Park, Twin Creeks (GRSM) | DB | 0.39 | 0.48 | 0.75 | 0.77 | 0.79 | 0.76 | 0.78 |
| 15 | US-xHA | Harvard Forest (HARV) | DB | 0.31 | 0.49 | 0.77 | 0.79 | 0.83 | 0.81 | 0.79 |
| 16 | US-xHE | Healy (HEAL) | TN | −4.45 | 0.36 | 0.14 | 0.41 | 0.72 | 0.33 | 0.71 |
| 17 | US-xJE | Jones Ecological Research Center (JERC) | DB | 0.19 | 0.58 | 0.69 | 0.74 | 0.78 | 0.74 | 0.75 |
| 18 | US-xJR | Jornada LTER (JORN) | GR | −2.75 | −0.85 | 0.11 | 0.13 | 0.21 | −0.77 | 0.09 |
| 19 | US-xKA | Konza Prairie Biological Station - Relocatable (KONA) | AG | −1.33 | 0.28 | 0.51 | 0.53 | 0.63 | 0.50 | 0.31 |
| 20 | US-xKZ | Konza Prairie Biological Station (KONZ) | GR | −0.85 | 0.50 | 0.74 | 0.81 | 0.81 | 0.83 | 0.82 |
| 21 | US-xLE | Lenoir Landing (LENO) | DB | 0.19 | 0.52 | 0.58 | 0.64 | 0.67 | 0.69 | 0.69 |
| 22 | US-xMB | Moab (MOAB) | GR | −145.46 | −5.79 | −0.05 | 0.01 | 0.09 | −3.66 | 0.09 |
| 23 | US-xNG | Northern Great Plains Research Laboratory (NOGP) | GR | −2.17 | 0.36 | 0.66 | 0.69 | 0.74 | 0.71 | 0.52 |
| 24 | US-xNQ | Onaqui-Ault (ONAQ) | SH | −7.30 | −0.54 | 0.29 | 0.37 | 0.43 | −0.87 | 0.25 |
| 25 | US-xNW | Niwot Ridge Mountain Research Station (NIWO) | TN | −120.13 | −1.77 | 0.05 | 0.17 | 0.28 | −3.53 | −3.04 |
| 26 | US-xRM | Rocky Mountain National Park, CASTNET (RMNP) | EN | −5.45 | 0.09 | 0.35 | 0.52 | 0.67 | 0.46 | 0.66 |
| 27 | US-xRN | Oak Ridge National Lab (ORNL) | DB | 0.25 | 0.41 | 0.56 | 0.60 | 0.69 | 0.65 | 0.71 |
| 28 | US-xSB | Ordway-Swisher Biological Station (OSBS) | EN | −1.39 | 0.54 | 0.63 | 0.69 | 0.73 | 0.60 | 0.62 |
| 29 | US-xSC | Smithsonian Conservation Biology Institute (SCBI) | DB | 0.42 | 0.52 | 0.68 | 0.74 | 0.77 | 0.72 | 0.75 |
| 30 | US-xSE | Smithsonian Environmental Research Center (SERC) | DB | −0.01 | 0.53 | 0.75 | 0.77 | 0.79 | 0.75 | 0.76 |
| 31 | US-xSJ | San Joaquin Experimental Range (SJER) | EN | −0.51 | −0.03 | 0.40 | 0.44 | 0.47 | 0.40 | 0.17 |
| 32 | US-xSL | North Sterling, CO (STER) | AG | −4.83 | 0.10 | 0.38 | 0.42 | 0.47 | 0.44 | 0.32 |
| 33 | US-xSP | Soaproot Saddle (SOAP) | EN | −0.98 | −0.98 | −1.68 | −1.31 | 0.03 | −0.19 | −0.10 |
| 34 | US-xSR | Santa Rita Experimental Range (SRER) | SH | −7.73 | −3.04 | −14.04 | −10.11 | −0.18 | −3.93 | −0.06 |
| 35 | US-xST | Steigerwaldt Land Services (STEI) | DB | 0.53 | 0.50 | 0.82 | 0.87 | 0.89 | 0.83 | 0.90 |
| 36 | US-xTA | Talladega National Forest (TALL) | EN | 0.39 | 0.44 | 0.57 | 0.60 | 0.76 | 0.70 | 0.66 |
| 37 | US-xTE | Lower Teakettle (TEAK) | EN | −2.27 | 0.17 | 0.22 | 0.25 | 0.44 | 0.46 | 0.24 |
| 38 | US-xTL | Toolik (TOOL) | TN | −12181.30 | −0.40 | −0.03 | 0.58 | 0.71 | −2.01 | 0.38 |
| 39 | US-xTR | Treehaven (TREE) | DB | 0.24 | 0.57 | 0.83 | 0.84 | 0.87 | 0.80 | 0.86 |
| 40 | US-xUK | The University of Kansas Field Station (UKFS) | DB | 0.24 | 0.52 | 0.71 | 0.73 | 0.76 | 0.64 | 0.76 |
| 41 | US-xUN | University of Notre Dame Environmental Research Center (UNDE) | DB | 0.56 | 0.55 | 0.81 | 0.81 | 0.86 | 0.80 | 0.89 |
| 42 | US-xWD | Woodworth (WOOD) | GR | −2.01 | 0.45 | 0.65 | 0.71 | 0.75 | 0.74 | 0.67 |
| 43 | US-xWR | Wind River Experimental Forest (WREF) | EN | −0.65 | 0.18 | −0.01 | 0.02 | 0.37 | 0.30 | 0.36 |
| 44 | US-xYE | Yellowstone Northern Range (Frog Rock) (YELL) | EN | −2.28 | 0.20 | 0.43 | 0.46 | 0.67 | 0.62 | 0.61 |
| AVERAGE | −656.42 | −0.02 | 0.06 | 0.23 | 0.60 | −0.01 | 0.44 |
| Primary Vegetation | Site | Mean Bias | R |
|---|---|---|---|
| AG | US-xSL | −15.80 | 0.58 |
| US-xKA | 4.73 | 0.22 | |
| AVERAGE | −5.53 ± 10.27 | 0.40 ± 0.18 | |
| DB | US-xSC | −60.82 | |
| US-xLE | 134.12 | ||
| US-xJE | 76.42 | 0.68 | |
| US-xHA | −46.71 | 0.32 | |
| US-xGR | 20.46 | 0.05 | |
| US-xRN | −67.14 | 0.82 | |
| US-xDL | 55.57 | −0.56 | |
| US-xST | 21.37 | 0.75 | |
| US-xSE | 17.43 | −0.36 | |
| US-xCL | 170.94 | −0.78 | |
| US-xBR | 114.38 | 0.85 | |
| US-xTR | −3.15 | 0.96 | |
| US-xBL | 135.44 | 0.019 | |
| US-xUK | 1.47 | 0.98 | |
| US-xUN | 4.95 | −0.44 | |
| AVERAGE | 38.32 ± 71.72 | 0.25 ± 0.64 | |
| EB | PR-xLA | 140.70 | |
| PR-xGU | 31.93 | ||
| AVERAGE | 86.32 ± 54.38 | ||
| EN | US-xSB | 121.02 | −0.20 |
| US-xSP | −44.92 | 0.48 | |
| US-xTA | −68.90 | 0.32 | |
| US-xTE | 47.40 | −0.35 | |
| US-xSJ | −15.44 | −0.65 | |
| US-xRM | −48.55 | −0.67 | |
| US-xYE | 4.31 | 0.57 | |
| US-xDJ | 20.68 | 0.24 | |
| US-xWR | −10.31 | −0.92 | |
| US-xAB | 52.29 | 0.09 | |
| US-xBN | −18.25 | 0.55 | |
| AVERAGE | 3.57 ± 51.99 | −0.05 ± 0.51 | |
| GR | US-xWD | −5.97 | 0.62 |
| US-xCP | −9.58 | 0.52 | |
| US-xDC | 21.99 | 0.88 | |
| US-xMB | 17.88 | 0.98 | |
| US-xDS | 230.26 | −0.90 | |
| US-xJR | 28.82 | 0.63 | |
| US-xKZ | 19.34 | −0.62 | |
| US-xNG | 34.74 | 0.85 | |
| AVERAGE | 42.18 ± 72.57 | 0.37 ± 0.67 | |
| SH | US-xSR | −61.37 | 0.99 |
| US-xNQ | 63.5 | 0.99 | |
| AVERAGE | 1.07 ± 62.44 | 0.99 ± 0.01 | |
| TN | US-xNW | −28.12 | 0.95 |
| US-xHE | −12.39 | 0.76 | |
| US-xTL | −22.12 | 0.54 | |
| US-xBA | −29.72 | 0.81 | |
| AVERAGE | −23.09 ± 6.80 | 0.77 ± 0.15 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Uyekawa, J.; Leland, J.; Bergl, D.; Liu, Y.; Richardson, A.D.; Lucas, B. Machine Learning-Based Prediction of Ecosystem-Scale CO2 Flux Measurements. Land 2025, 14, 124. https://doi.org/10.3390/land14010124
Uyekawa J, Leland J, Bergl D, Liu Y, Richardson AD, Lucas B. Machine Learning-Based Prediction of Ecosystem-Scale CO2 Flux Measurements. Land. 2025; 14(1):124. https://doi.org/10.3390/land14010124
Chicago/Turabian StyleUyekawa, Jeffrey, John Leland, Darby Bergl, Yujie Liu, Andrew D. Richardson, and Benjamin Lucas. 2025. "Machine Learning-Based Prediction of Ecosystem-Scale CO2 Flux Measurements" Land 14, no. 1: 124. https://doi.org/10.3390/land14010124
APA StyleUyekawa, J., Leland, J., Bergl, D., Liu, Y., Richardson, A. D., & Lucas, B. (2025). Machine Learning-Based Prediction of Ecosystem-Scale CO2 Flux Measurements. Land, 14(1), 124. https://doi.org/10.3390/land14010124





