A Multicriteria Decision Analysis Model for Optimal Land Uses: Guiding Farmers under the New European Union’s Common Agricultural Policy (2023–2027)

Abstract

Focusing on sustainability, the new Common Agricultural Policy (2023–2027) sets ambitious goals for water management, as reducing irrigation water use is a vital issue. Cooperation among farmers, relevant authorities, and researchers plays a significant role in achieving these objectives. Therefore, this study applies a multicriteria mathematical programming model to optimize land use, considering water use, profit, labor, and cost. The model was applied to three farmer groups located in Greece and proved to be valuable in the implementation of irrigation water use. Using the same methodology, two additional cases of farmer groups that utilize drylands are presented in complementary ways to investigate how the new CAP affects non-irrigated land uses. Regarding the irrigated case, reducing water usage involves decreasing the land dedicated to crops characterized by high water demand, such as rice, corn, vetch, and clover. This adjustment stems from the necessity to replace irrigated land with non-irrigated land because climate change demands low water consumption for crops and underscores the importance of the new policy framework to promote sustainable agriculture. As for the non-irrigated case, achieving optimal farm planning entails reducing the cultivated areas of vetch, grassland, and sunflower. This result is driven by the need to increase crops receiving primary subsidies, highlighting the necessity for non-irrigated farms to enhance their profitability through the benefits provided by the Common Agricultural Policy. Lastly, it is important to note that this study significantly contributes to guiding decision-makers in achieving alternative agricultural land uses and farm plans while also aiding in the comprehension of the new cross-compliance rules.

1. Introduction

The study of proper water management is considered crucial due to environmental, social, and economic challenges such as climate change, globalization, population growth, wasting water, and dietary habits changes [1,2,3,4], which put pressure on water resources [5]. Additionally, drought [6], water pollution [7,8], and poor water resource management [9] threaten the agricultural sector’s sustainability. Certainly, it has been widely recognized for some time now that the natural resources (soil and water) employed in agricultural practices are no longer viewed as abundant and infinite reserves [10].

The Common Agricultural Policy (CAP) of the European Union has undergone significant reforms over time, adapting to the new challenges and needs of agriculture, markets, and environmental protection [11]. To be more precise, the current policy (2023–2027) focuses on enhancing the sustainability, resilience, and competitiveness of the EU agricultural sector by supporting environmental sensitivity (green architecture and environmental criteria), social justice (redistribution of subsidies and support for young farmers) and increasing competitiveness (digitization and access to markets) [12]. Regarding sustainability enhancement, the new CAP sets ambitious goals for water management, such as reducing the use of irrigation water [13], which is a critical issue. To achieve this goal, the adoption of sustainable irrigation practices, water reuse, and monitoring and management of water resources are promoted [13]. Cooperation among farmers, relevant authorities, and researchers [14,15] is a significant factor in the successful implementation of the aforementioned measures.

Therefore, this paper is developed within the framework of the “Measure 16: Cooperation” project and applies a multicriteria mathematical programming model that contributes to rational water use—through useful land use changes—while considering the main goals of farmers, such as profit maximization, total labor minimization and more. The “Measure 16: Cooperation” of the Greek Rural Development Program (RDP) aims to develop partnerships between stakeholders in the Greek agri-food sector and promote innovation, sustainable development, and competitiveness [16]. Measure 16 comprises two sub-measures. The first one concerns the establishment and operation of business groups for agricultural productivity and sustainability, while the second one focuses on collaboration for environmental projects, practices, and actions addressing climate change. To be precise, through Measure 16, collaborating entities undertake projects such as the same production and marketing of agricultural products, adoption of environmentally friendly practices, development of new technologies, and promotion of research and innovation [16]. All the above demonstrates the significance of “Measure 16: Cooperation“ within the Common Agricultural Policy (CAP) framework. This measure can act as a catalyst for fostering a spirit of collaboration in the agri-food sector, contributing to enhancing the competitiveness of Greek food and agricultural products and promoting sustainable development [16].

The model was applied to three farmer groups located in Greece and proved to be valuable in the implementation of irrigation water use policies and in the achievement of sustainable resource management goals. Using the same methodology, two additional cases of farmer groups that utilize non-irrigated lands are presented. This additional analysis was chosen to be conducted to investigate how the new CAP policy affects the land use of farms that do not use irrigated farming techniques. The five producer groups analyzed in this study were defined by the coordinating body of the project “Measure 16: Cooperation”. Developing a decision support model (DSM) aiming to adapt to cross-compliance rules and achieve optimal economic efficiency in farms represents a plan with a consistent implementation process. Data collection was initially conducted through a questionnaire for the model’s development. Subsequently, the decision support model was developed, considering the new CAP rules regarding proper water management, as well as other economic, environmental, and social parameters, along with the producers’ real aims (e.g., gross profit maximization). Finally, the multi-criteria analysis method was applied to extract the new land uses [17,18] for each of the five farmer groups.

The multi-criteria analysis method has been applied extensively in the context of agriculture and a research project. Precisely, through a brief literature review [19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45], it emerges that the method is widely used by researchers, demonstrating how to achieve better policy-making procedures and simulate realistic decision-making processes [17]. This method has been used for many years, as various scientists have used it to study the impacts of periodic reforms of the Common Agricultural Policy [46]. A relevant study is that of Bournaris et al. [17], where they examined the “Setting up Young Farmers” measure of the Common Agricultural Policy (CAP). Through this study, the role of the measure in encouraging young and educated farmers to engage more actively in agriculture was essentially highlighted, while a multicriteria mathematical model revealed land uses that can result in better economic results. It is worth mentioning that the European Union’s Rural Development Plan Setting Up Young Farmers measure has also engaged other Greek researchers from time to time [47,48]. Furthermore, Bournaris et al. [49] have developed a multicriteria mathematical programming model to support decision-making in water and land management in Kozani (Greece). The model incorporates vulnerability maps and helps protect water resources from excessive fertilizer use [49]. Additionally, the relevant literature reviews centers on multicriteria analysis as a tool for evaluating agricultural policies [50] and discussing agri-environment schemes [51,52,53]. While the literature on applying the multi-criteria decision analysis method in agriculture is extensive, its practical use among many farmer groups in various Greek rural areas, especially under the conditions of the latest CAP, seems limited.

The article is structured into six sections. Section 2 introduces the study area and details the farmer groups involved. It then closely examines the research methodology, describing the questionnaire design and the chosen analysis method. Section 3 presents the study’s findings, followed by a detailed discussion (Section 4) that interprets the results. Finally, Section 5 concludes the article by explaining the research’s limitations and originality.

2. Materials and Methods

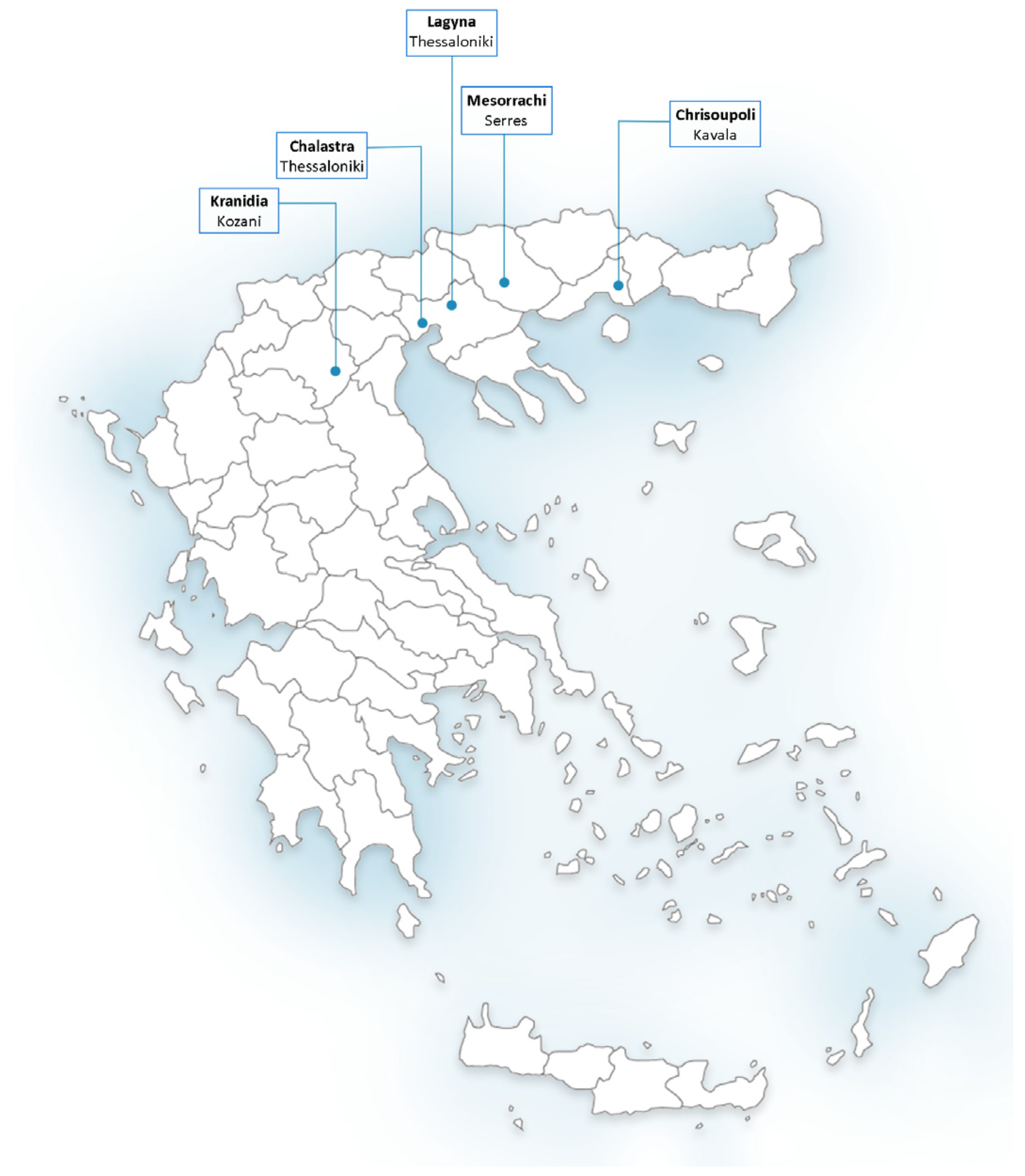
2.1. Study Area and Farmer Groups

The research involves a total of five farmer groups operating in the field of crop production, as they specialize in the production of animal feed, cotton, rice, and grains. The groups are located in the regions of Thessaloniki, Kavala, Kozani, and Serres (Northern Greece) (Figure 1).

The first of the five farmer groups consists of rice farmers and is based in Chalastra, located on the western side of the Regional Unit of Thessaloniki. The next farmer group consists of dried forage and animal feed and is in Lagyna (Regional Unit of Thessaloniki). The third one is located in Chrysoupoli and consists of fodder crops for animal feed producers. Chrisoupoli is an agricultural area located in the Regional Unit of Kavala. The fourth group consists of farmers who are based in Kranidia and are engaged in the production of animal feed. Kranidia is an area that belongs to the Regional Unit of Kozani. Lastly, the fifth group comprises cereal producers based in Mesorachi, within the Regional Unit of Serres. It is widely accepted that agricultural production in the above-mentioned areas plays a significant role in the economy, contributing to the supply of the market and livestock units.

2.2. Questionnaire Design and Data Collection Temporal Structure

To develop the model, data were initially collected using a questionnaire based on the scientific literature [17,18,49]. The questionnaire analysis consists of three sections. The initial section focuses on the demographic details of the farmers involved in the research process. The second one concerns the existent crop plans, which were acquired through the survey of cultivated land. Finally, the third section includes questions regarding the technical and economic data of the production sectors for each of the farmer groups [17,49].

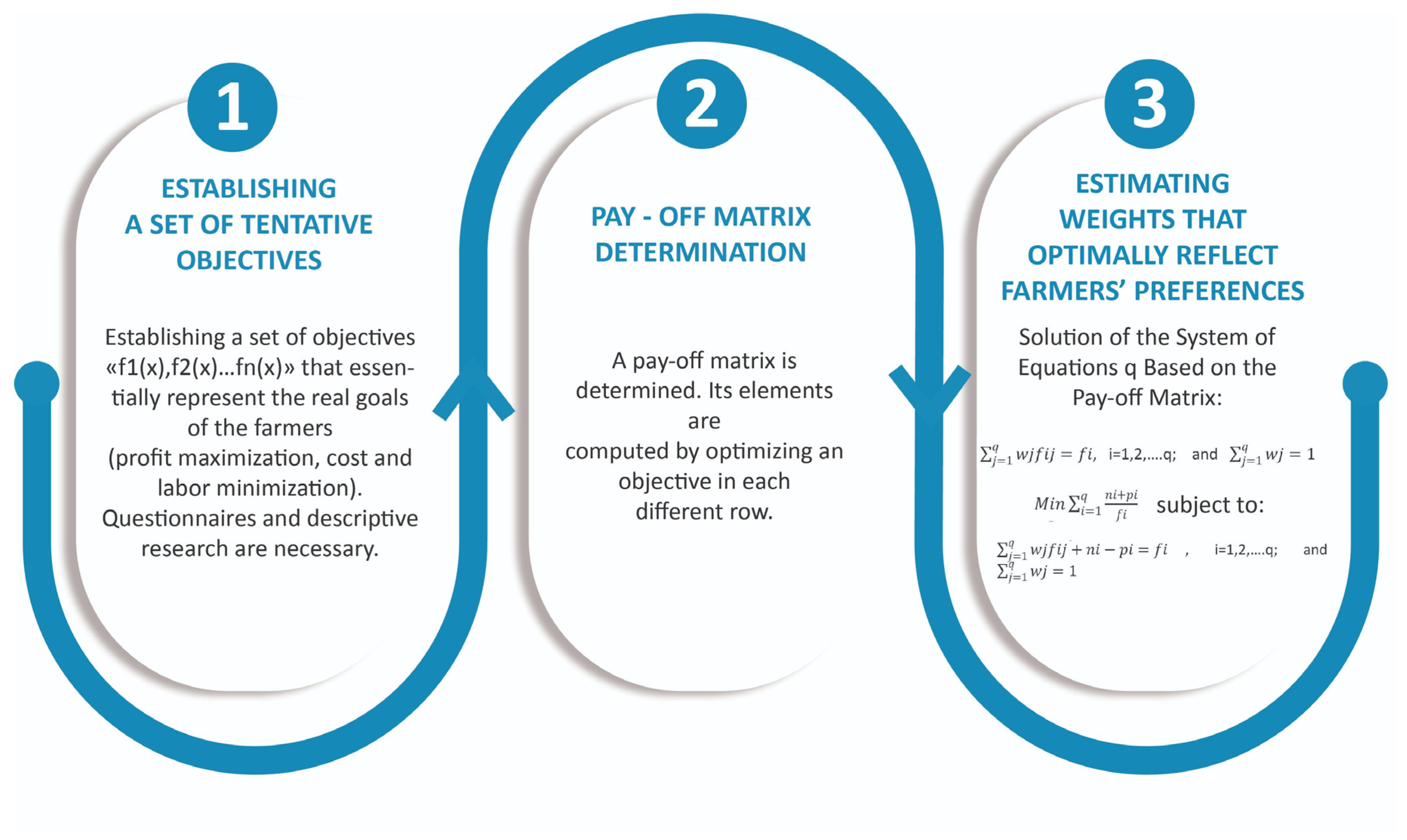
2.3. Methodology—Weighting Goal Programming

According to Moulogianni [54], mathematical programming serves as a mathematical framework that is specially designed for the optimization of the allocation of limited resources through planning or design processes. In this case, multicriteria analysis was chosen as the main tool to promote the rational use of irrigation water through land use changes. This decision is grounded in the capability of a multicriteria decision analysis (MCDA) model to combine various criteria for a utility function while ensuring compliance with policy constraints. Moreover, it considers the available resources, such as land, labor, and capital, making it an important approach for decision-making [17]. The MCDA model considers the multi-functionality of agriculture, which includes variables relating to economic, social, and environmental issues [55]. Considering the farmer and their preferences, the MCDA model emerges as the best choice for the current analysis since it takes into consideration the variety of criteria farmers evaluate when planning their crop plans, hence expanding the traditional concept of profit maximization [17,49].

Multi-criteria mathematical programming has been applied over time to find constructive land use changes and discover optimal farm plans based on the aforementioned criteria. This is something that is proved by reviewing a wide range of the relative literature [17,18,49,56]. Sumpsi et al. (1993, 1997) [57,58] and Amador et al. (1998) [59] developed methodologies for simulating agricultural systems using multi-criteria techniques. Specifically, they propose weighted goal programming as a methodology for decision-making analysis [57,58,59]. In general, this methodology has been used for farm planning [60,61,62,63,64], decoupling [46], environmental management [65] and water agricultural policy evaluation [66,67]. The final case deals with this study’s question regarding land use changes and rational water use within the context of the new CAP (2023–2027).

In the context of this study, this methodology essentially aims to estimate an objective utility function, allowing the decision-making processes of farmers to be simulated. This reduces irrigation water use while maximizing profit and achieving other objectives. The implementation of this methodology consists of three main parts [17]. Firstly, it begins by identifying a preliminary set of objectives likely to hold the highest importance for farmers. This task can be effectively accomplished through questionnaires and descriptive methods, which provide valuable insights into farmers’ priorities. Following this, it establishes a pay-off matrix corresponding to the set of objectives. Lastly, using this matrix, a set of weights is computed to capture and reflect farmers’ preferences accurately [17,49].

The first part involves establishing a set of objectives «f1(x), f2(x)…fn(x)» that essentially represent the real goals of the farmers [59] such as profit maximization, cost, and labor minimization [17]. Once the objectives are set, the analysis proceeds to the second part, where a pay-off matrix is determined [18]. The elements of this matrix are computed by optimizing an objective in each different row [49]. Once the pay-off matrix is obtained, the analysis proceeds to the third step, where the following system of equations q is solved [17,18,49]:

$${\sum }_{j=1}^q{w}_j{f}_{ij}=f_i, \mathrm{i}=1, 2, \dots .\mathrm{q}; \mathrm{and} {\sum }_{j=1}^q{w}_j=1$$

(1)

where:

• w_j: The weights attached to each objective represent the actual behavior of the farmer.
• f_ij: The pay-off matrix elements.
• f_i: Τhe outcome obtained for the i-th objective based on the observed crop distribution.

Τhe system described above typically does not produce a specific set of weights. Therefore, the search for the optimal solution involves minimizing the sum of deviational variables that most align with the closest set of weights [17]. To achieve this, a weighted goal program can be formulated using percentage deviation variables [68]. The solution will be derived by solving the following linear programming (LP) model [17]:

$$Min{\sum }_{i=1}^q\frac{n_i+p_i}{f_i} \mathrm{subject} \mathrm{to}: {\sum }_{j=1}^q{w}_j{f}_{ij}+n_i-p_i=f_i, \mathrm{i}=1, 2, \dots .\mathrm{q}; \mathrm{and} {\sum }_{j=1}^q{w}_j=1$$

(2)

where:

• p_i: The positive deviational variable, measuring the degree of over-achievement for the i-th objective concerning a given target.
• n_i: The negative deviational variable that assesses the variance between the actual value and the modeled solution for the i-th objective.

The following figure provides a visual representation of the aforementioned process (Figure 2).

2.4. Model Specification

In the case of this project, the MCDA model comprises the following elements:

2.4.1. Variables

Each farmer group has a set of variables Xi representing its crops. These variables are called “decision variables” and take values that belong to the feasible set. The corresponding values were derived from the research, as described in the previous section, and relate to the production year 2023.

2.4.2. Objectives

Four objectives were identified as part of the farmers’ decision-making process [17,56,69]. These are:

• Profit maximization: MaxGM = Σ GMi × Xi
  The term “profit maximization” is equivalent to maximizing gross profit, which is obtained by subtracting the variable cost from the gross output.
• Variable cost minimization: MinGC = Σ GCii × Xi
  This kind of cost arises from the total expenses on fertilizers, pesticides, fuel, irrigation fees, hired machinery work, and other consumables.
• Labor minimization: MinLAB = Σ LABi × Xi
  This term refers to the total agricultural activities expressed in hours of the human family and “hired” labor.
• Water use minimization: MinWAT = Σ WATi × Xi
  This term refers to the total volume of irrigation water per cultivation.

Other goals are simultaneously satisfied by achieving the above-mentioned objec-tives, such as providing a direct answer to the farmers’ question of “what to cultivate”.

2.4.3. Constraints

The model’s execution required the definition of specific constraints [17,56,69]. Such as:

• Total cultivation land: Up to 100 acres per farmer group.
• Common Agricultural Policy: According to the new CAP (2023–2027) rules, it is stated that all farms with arable land must adopt environmental practices. This implies that farms’ arable land should be converted into an ecological focus area [13]. Therefore, it is essential to consider the constraints arising from the new CAP, such as the set-aside land, which affects most cultivated species.
• Irrigation: Additionally, it is also important to consider the CAP’s constraints regarding the rational use of irrigation water [13]. Specifically, it has been estimated in advance that potential irrigation water savings are considered necessary during the production process [13]. The first three farmer groups (Chalastra, Lagyna, and Chrisoupoli) primarily utilize irrigation techniques. The irrigated crops are cotton, alfalfa, alfalfa hay, clover, vetch, sunflower, corn, corn silage, and rice.
  Non-irrigated crops are: Soft wheat, dryland alfalfa, fallow (SA) land, chopped alfalfa, and grassland. Regarding the two remaining farmer groups (Kranidia and Mesorrachi), their land is exclusively utilized for dry farming. The crops cultivated by these farmer groups are: Alfalfa seed production, alfalfa hay, dryland alfalfa, clover, vetch, corn, grassland, hard and soft wheat, rapeseed, sunflower, barley, and fallow (SA) land.
• Market constraints and other constraints: They were determined according to market constraints. Some crops are not subject to the specific constraints of the CAP, but market constraints impose an upper limit on short-term variations.

After the model was developed, it was executed through the software RStudio v3.6 [70], allowing the corresponding land use changes to be extracted. These results will be analyzed in more detail in the next section.

3. Results

The essential data for the five farmer groups were initially collected for the present analysis. These data were then analyzed, revealing the existing crop plans and useful technical and economic information such as costs, labor hours, etc. The multi-criteria decision analysis was then applied to generate the model’s crop plans, which can be adopted by each farmer group. This section presents the existing and optimal crop plans for each of the five farmer groups.

3.1. Chalastra’s Farmer Group—Existing Crop Plan

Chalastra’s farmer group has a total of 1900.7 acres under cultivation. As illustrated in Figure 3, rice cultivation constitutes most of the existing crop plan at 73.9%, followed by cotton at 25.9%, and corn at 0.2%.

3.1.1. Optimal Land Change of Chalastra’s Farmer Group

The MCDA model implementation recommends improvements to the agricultural land of Chalastra’s farmer group. These land changes entail a revised crop plan deemed optimal for the farmers.

Table 1. Existing and optimum production plan of Chalastra’s farmer group.

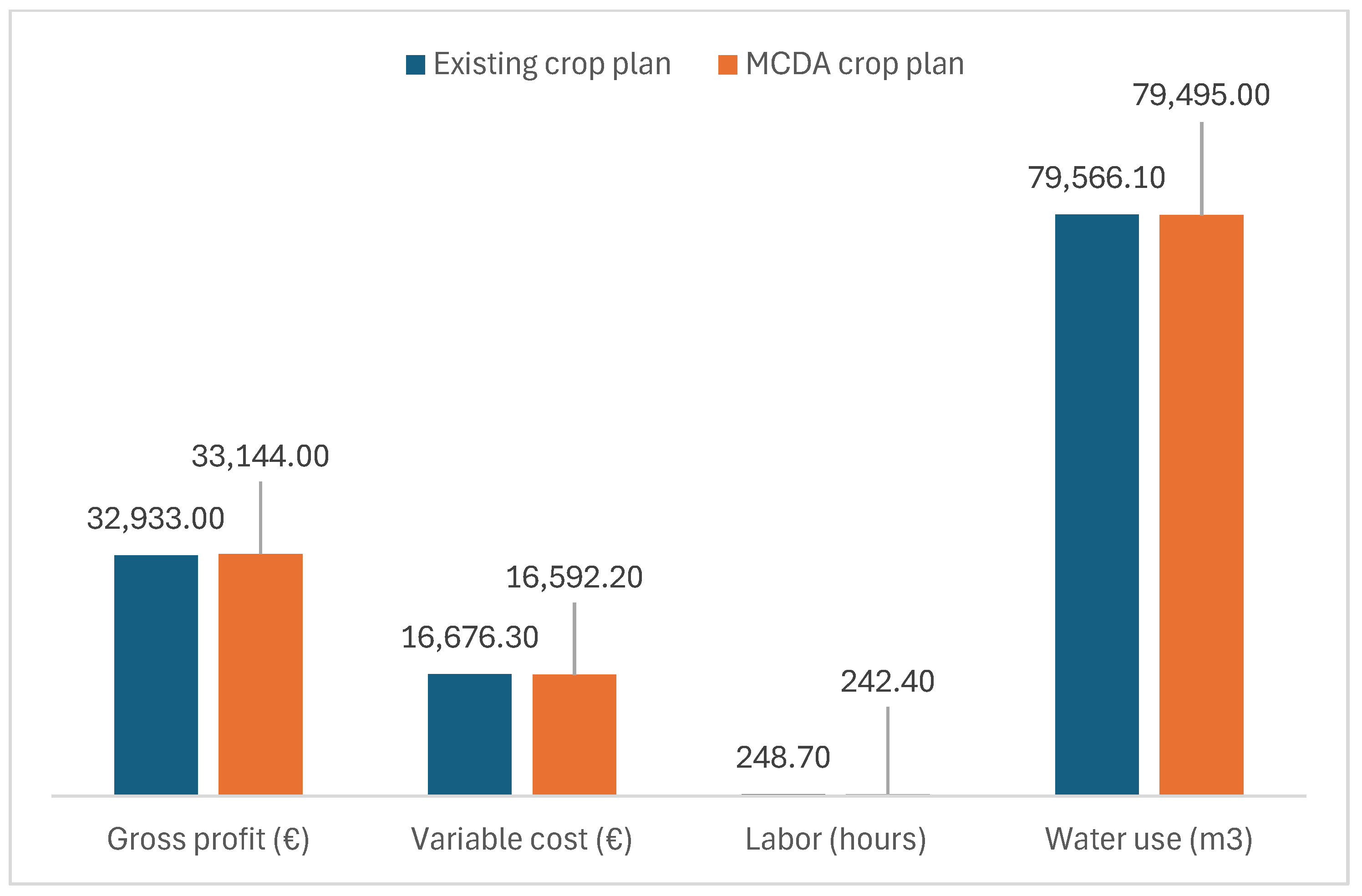
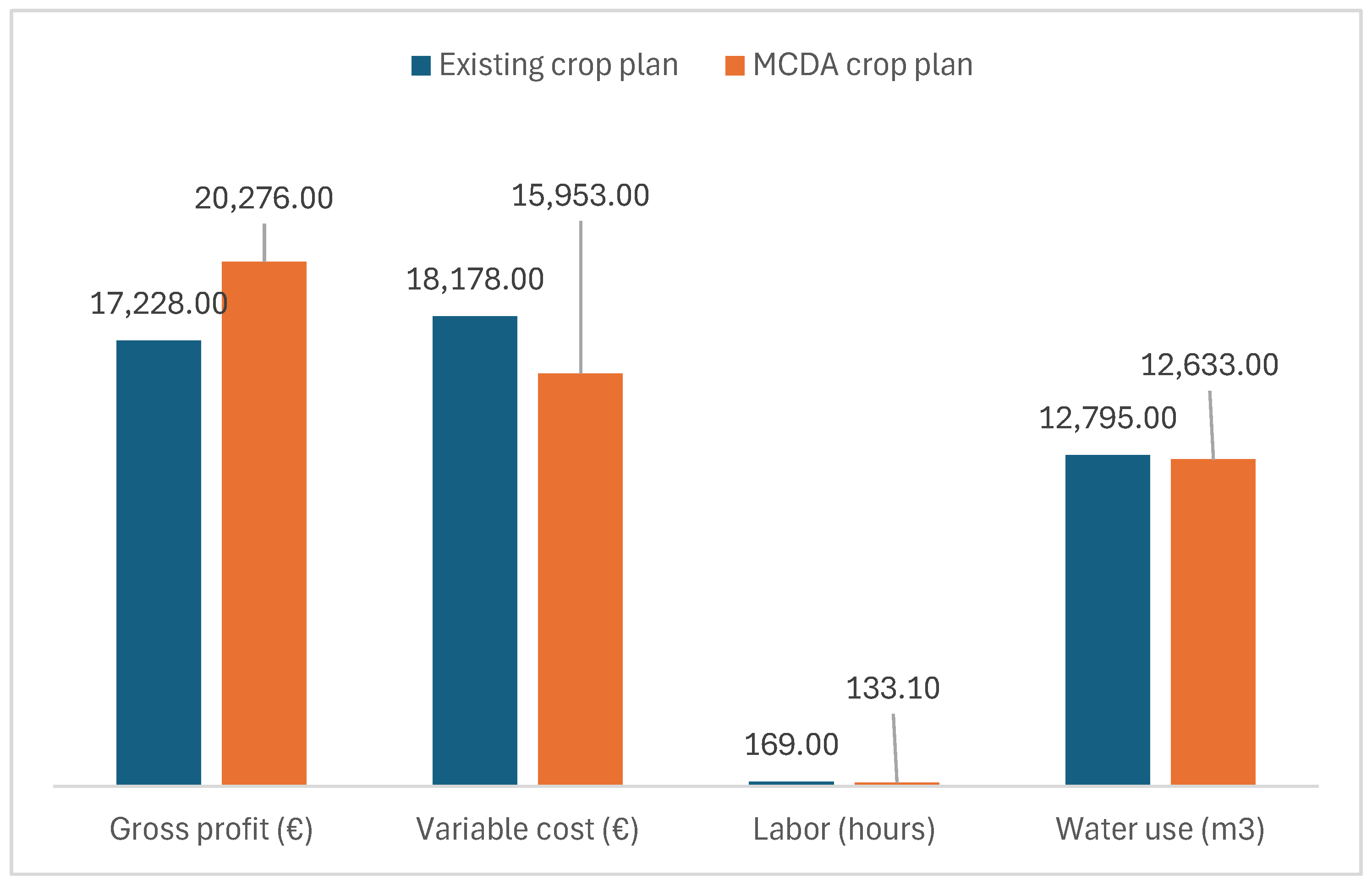
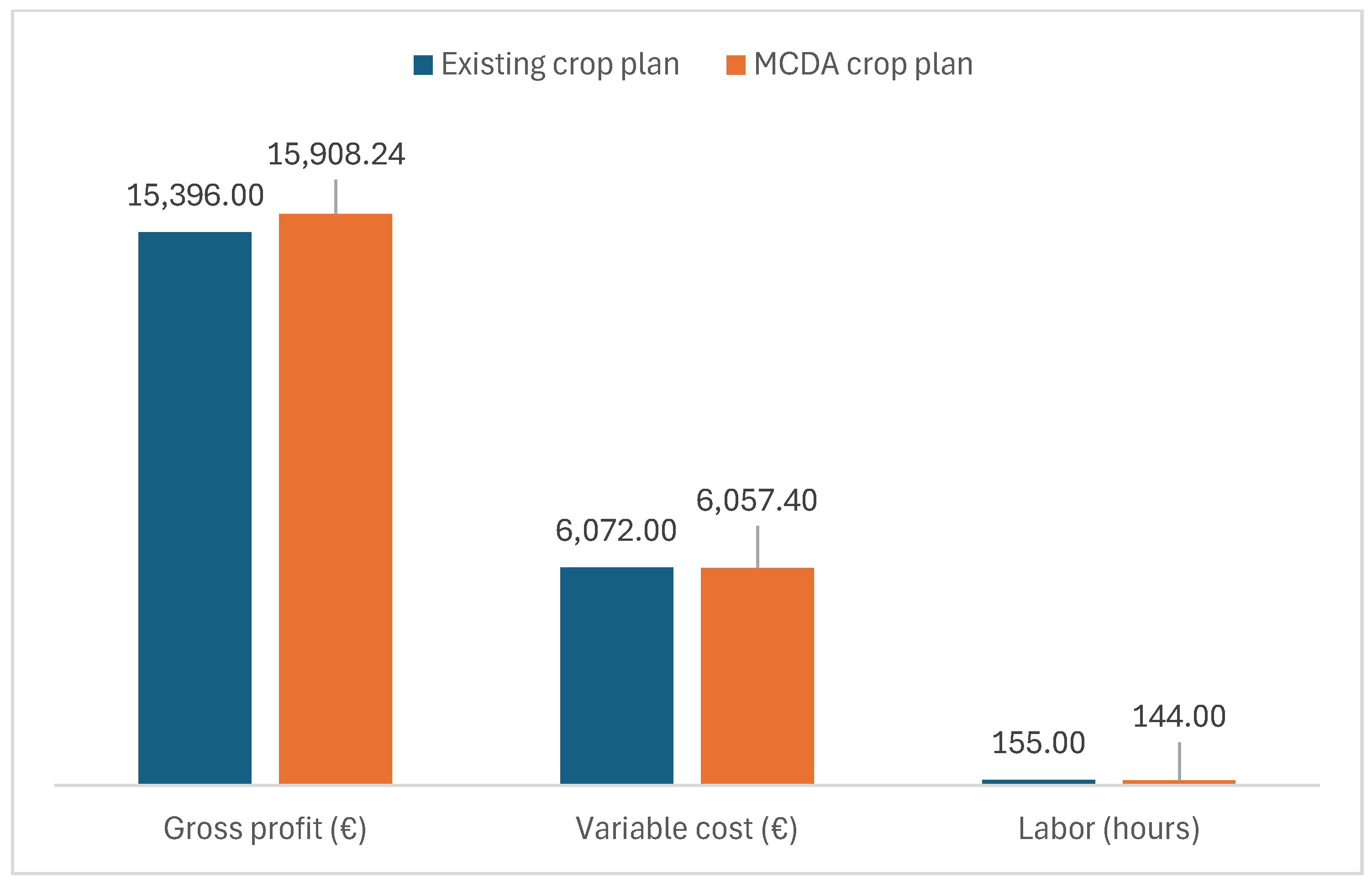
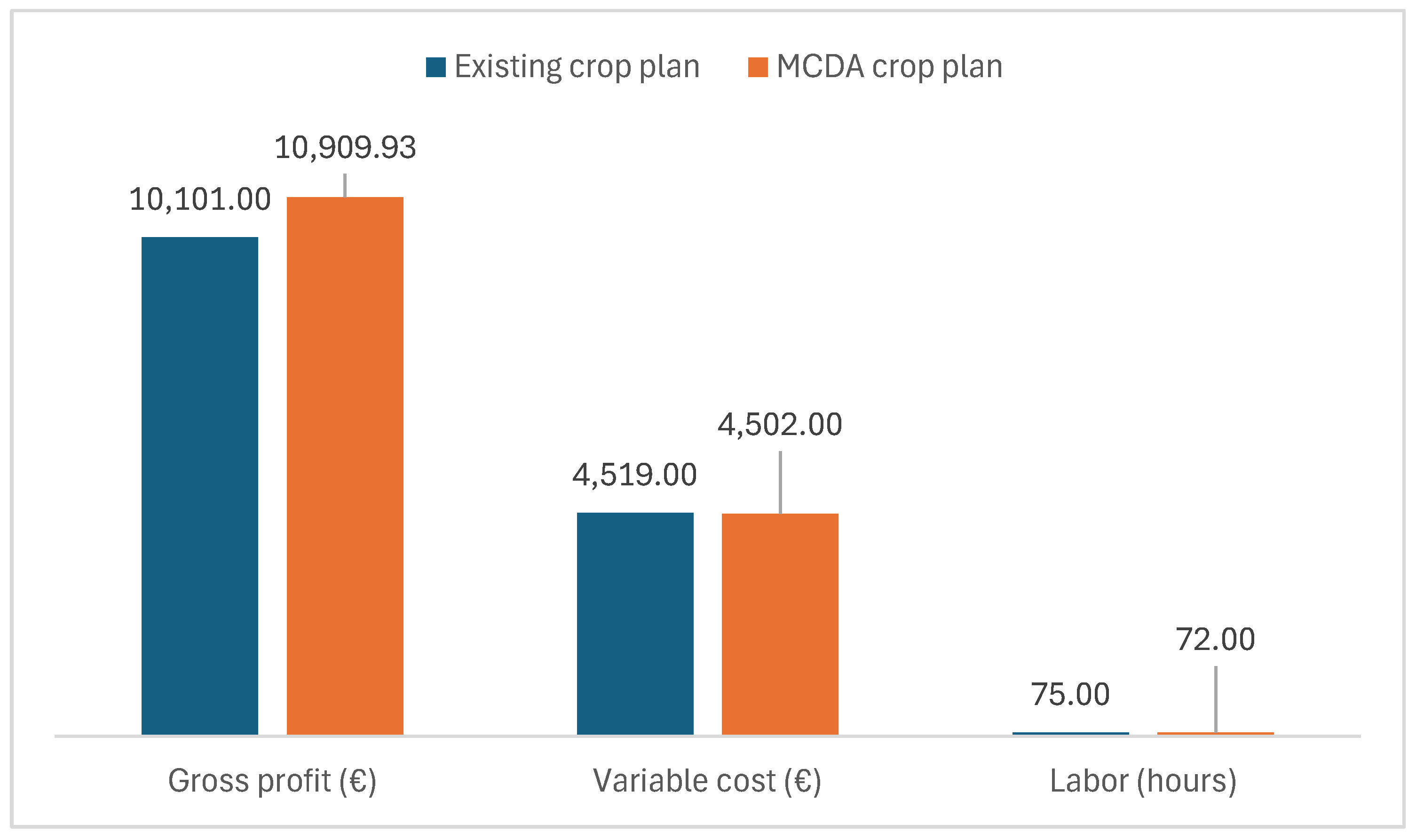
Crop	Acres	Existing Plan %	MCDA %	Deviation %
Cotton	492	25.90	30.91	19.34
Rice	1405	73.90	68.93	−6.73
Corn	4	0.20	0.16	−20.00
Total	1901	100.00	100.00

presents the suggested new land changes in the crop plan. According to the model, the suggested crops for this farmer group include rice, cotton, and corn. The optimal scenario implies expanding cotton cultivation by 19.34%. Reductions are proposed for rice by 6.73% and corn by 20.0%, aiming to achieve the model’s objectives of increasing profits, lowering production costs, minimizing labor, and reducing water use.

In the next figure, Figure 4, the above-mentioned information is summarized, illustrating noticeable differences compared to the existing crop plan. In the next section, the results of achieving the objectives are presented after the implementation of the MCDA model.

3.1.2. Objectives Analysis of Chalastra’s Farmer Group

Table 2. Objectives achievement of Chalastra’s farmer group model.

	Existing Plan	MCDA Model
		Value	Deviation (%)
Gross profit (€)	17,078.00	17,405.00	1.91
Variable cost (€)	21,279.00	21,108.44	−0.80
Labor (hours)	271.00	265.00	−2.21
Water use (m3)	108,754.00	105,697.19	−2.81

shows the changes in the four objectives of gross profit, cost, labor, and water use. In the existing crop plan, gross profit is equal to EUR 17,078.00s, while in the optimum farm plan achieved by the MCDA model, it is equal to EUR 17,405.00, showing an increase of 1.91%. The cost in the existing crop plan is EUR 21,279.00, while in the optimum plan it decreases to EUR 21,108.44 (−0.80%). Labor is equal to 271.00 h, while in the optimum farm plan achieved by the MCDA model, it is equal to 265.00 h, showing a decrease of 2.21%. Lastly, the water use equals to 108,754.00 m³, while in the optimum plan it decreases to 105,697.19 m³ (−2.81%).

Above, Figure 5 shows the deviations in gross profit variable cost, labor, and water use between the existing and model crop plans.

3.2. Lagyna’s Farmer Group—Existing Crop Plan

Lagyna’s farmer group cultivates a total of 1923 acres. Specifically, as depicted below (Figure 5), most of the acres are occupied by alfalfa, constituting 45.76%, followed by vetch at 20.19%. Next, silage corn is the established crop at 18.32%, followed by soft wheat (10.02%), dryland alfalfa (4.47%), and clover (1.24%) (Figure 6).

3.2.1. Agricultural Land Change of Lagyna’s Farmer Group

The MCDA model implementation proposes adjustments to the agricultural land of Lagyna’s farmer group.

Table 3. Existing and optimum production plan of Lagyna’s farmer group.

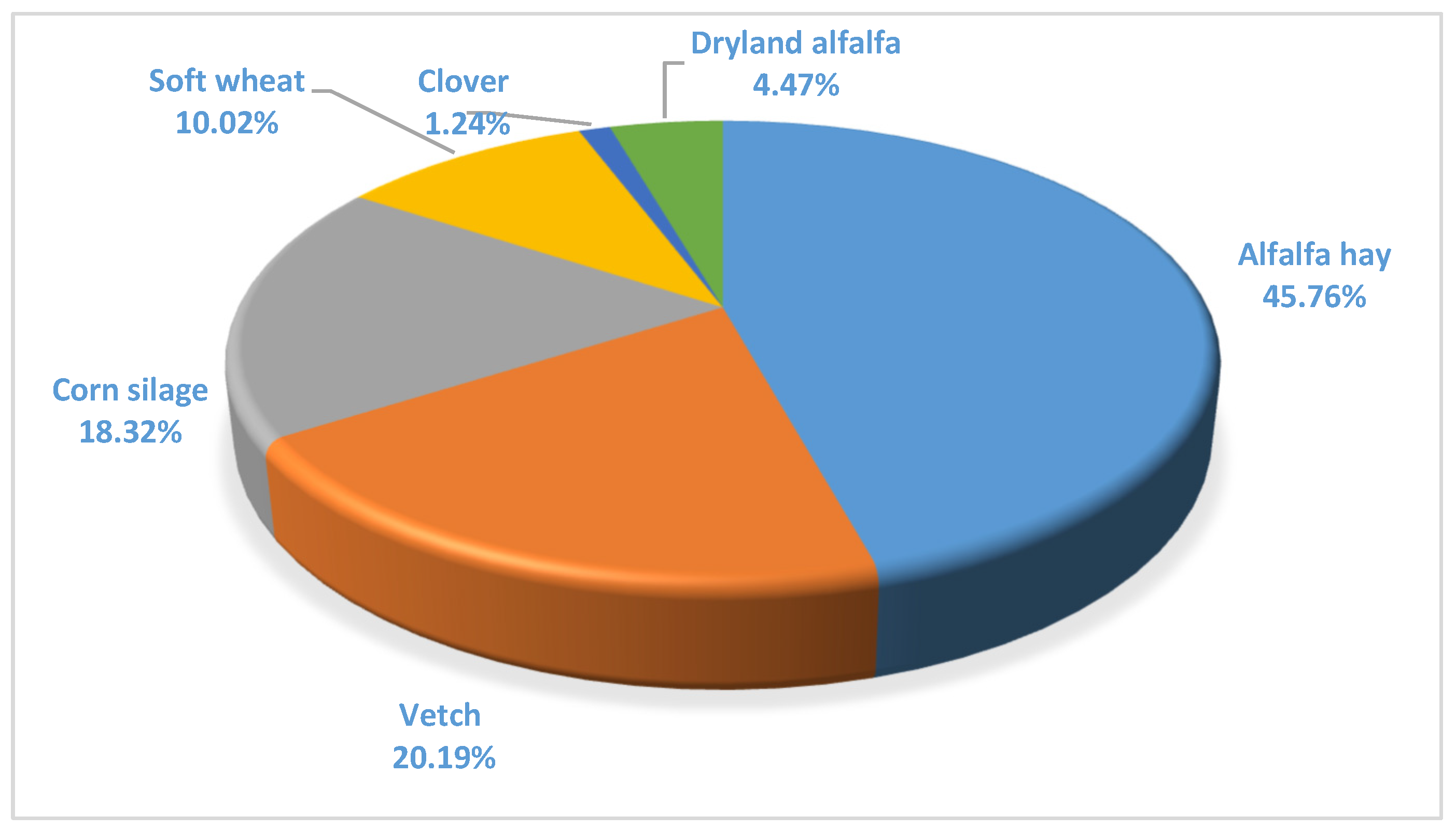
Crop	Acres	Existing Plan %	MCDA %	Deviation %
Alfalfa hay	880	45.76	48.96	6.90
Vetch	388	20.19	13.30	−34.16
Corn silage	352	18.32	20.34	11.15
Soft wheat	193	10.02	11.70	17.00
Clover	24	1.24	1.00	−16.67
Dryland alfalfa	86	4.47	4.70	4.44
Total	1923	100.00	100.00

shows the suggested new land changes in the crop plan. For this particular farmer group, the recommended crops are alfalfa hay, vetch, silage corn, corn, soft wheat, clover, and dryland alfalfa. For optimal conditions, an increase of 6.9% for alfalfa hay, 11.15% for silage corn, 17.00% for soft wheat, and 4.44% for dryland alfalfa is proposed. To satisfy the model’s objectives, significant decreases of 34.16% and 16.67% are proposed for vetch and clover, respectively.

The above-mentioned information is summarized in Figure 7, illustrating noticeable differences compared to the existing crop plan.

3.2.2. Objectives Analysis of Lagyna’s Farmer Group

In the existing crop plan, gross profit is equal to EUR 32,933.00, while in the optimum farm plan achieved by the MCDA model, it is equal to EUR 33,144.00, showing an increase of 0.64%. Regarding the cost of the existing crop plan, this is EUR 16,676.30s, while in the optimum plan it decreases to EUR 16,592.20 (−0.50%). Labor is equal to 248.70 h, while in the optimum farm plan achieved by the MCDA model, it is equal to 242.40 h, showing a decrease of 2.53%. Lastly, the water use is equal to 79,566.10 m³ while in the optimum plan it decreases to 79,495.00 m³ (−0.09%) (

Table 4. Objectives achievement of Lagyna’s farmer group model.

	Existing Plan	MCDA Model
		Value	Deviation (%)
Gross profit (€)	32,933.00	33,144.00	0.64
Variable cost (€)	16,676.30	16,592.20	−0.50
Labor (hours)	248.70	242.40	−2.53
Water use (m3)	79,566.10	79,495.00	−0.09

).

The deviations between the existing and model’s crop plan become evident in the following figure (Figure 8).

3.3. Chrisoupoli’s Farmer Group—Existing Crop Plan

Regarding this group of livestock feed farmers, a total of 2296 acres are cultivated. Below is a presentation (Figure 9) of the structure of the existing crop plan. The cultivation of dryland alfalfa exceeds that of the others (36.81%), followed by chopped alfalfa (17.19%), corn (7.77%), rice (5%), and finally alfalfa hay (2.05%). Additionally, grassland and fallow (SA) land account for 28.28% and 2.90%, respectively, of the total acres.

3.3.1. Agricultural Land Change of Chrisoupoli’s Farmer Group

The MCDA model implementation recommends changes to the agricultural land of Chrisoupoli’s farmer group. These land changes entail a revised crop plan that is deemed optimal for the farmers.

Table 5. Existing and optimum production plan of Chrisoupoli’s farmer group.

Crop	Acres	Existing Plan %	MCDA %	Deviation %
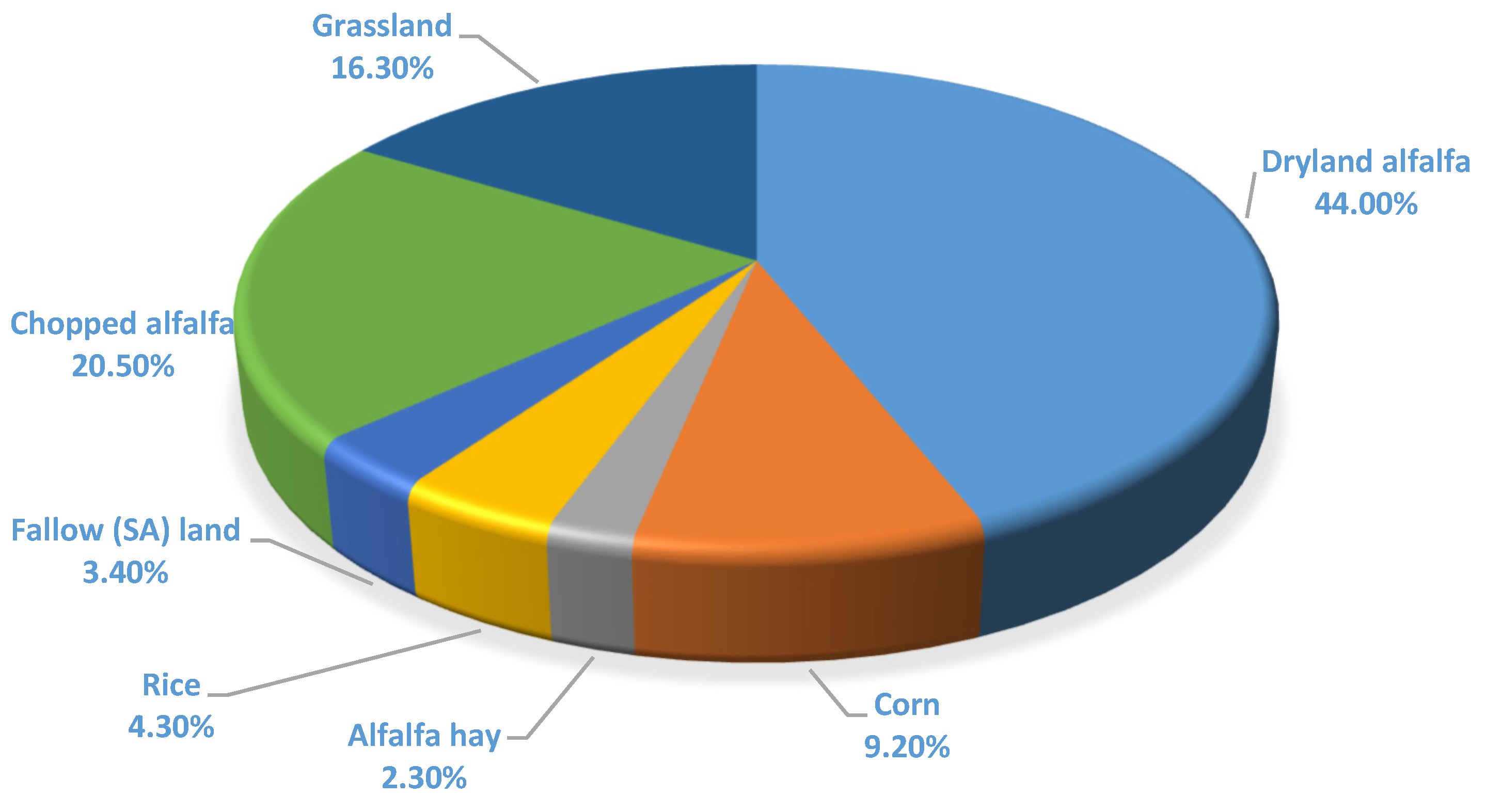
Dryland alfalfa	845	36.81	44.00	19.57
Corn	178	7.77	9.20	17.95
Alfalfa hay	47	2.05	2.30	15.00
Rice	115	5.00	4.30	−14.00
Fallow (SA) land	67	2.90	3.40	17.24
Chopped alfalfa	395	17.19	20.50	19.19
Grassland	649	28.28	16.30	−42.40
Total	2296	100.00	100.00

presents the suggested new land changes in the crop plan. For the optimal condition, an increase is specifically recommended for all crops except rice and grassland, which are proposed to decrease by 14.00% and 42.40%, respectively.

The next figure (Figure 10) summarizes the above-mentioned information, illustrating noticeable differences compared to the existing crop plan.

3.3.2. Objectives Analysis of Chrisoupoli’s Farmer Group

Table 6. Objectives achievement of Chrisoupoli’s farmer group.

	Existing Plan	MCDA Model
		Value	Deviation (%)
Gross profit (€)	17,228.00	20,276.00	17.69
Variable cost (€)	18,178.00	15,953.00	−12.24
Labor (hours)	169.00	133.10	−21.24
Water use (m3)	12,795.00	12,633.00	−1.27

shows the changes in the four objectives of gross profit, cost, labor, and water use. In the existing crop plan, gross profit is equal to EUR 17,228.00, while in the optimum farm plan, it is equal to EUR 20,276.00, showing an increase of 17.69%. Regarding the variable cost in the existing crop plan, this is EUR 18,178.00, while in the optimum plan it decreases to EUR 15,953.00 (−12.24%). Labor is equal to 169.00 h, while in the optimum farm plan achieved by the MCDA model, it is equal to 133.10 h, showing a decrease of 21.24%. Lastly, the water use is equal to 12,795.00 m³ while in the optimum plan it decreases to 12,633.00 m³ (−1.27%).

The deviations between the existing and model’s crop plan become evident in the following figure (Figure 11).

As mentioned in the introduction section, using the same methodology, two additional cases of farmer groups that utilize drylands are presented. This additional analysis was chosen to investigate how the new CAP affects the land uses of farms that do not use irrigated farming techniques. Both of these farmer groups are located in Kranidia (Kozani) and Mesorrachi (Serres), respectively. Their results will be presented in the following sections.

3.4. Kranidia’s Farmer Group—Existing Crop Plan

Regarding this group of animal feed producers, a total of 1688.7 acres are cultivated. The existing crop plan is presented below (Figure 12). The cultivation of alfalfa seed production predominates over the others, occupying 58.24% of the existing crop plan. This is followed by the cultivation of organic vetch (12.00%), conventional alfalfa hay (6.88%), organic alfalfa hay (5.21%), and organic (2.90%) and conventional clover (1.67%). Additionally, corn (1.41%) and conventional vetch (1.39%) are cultivated. Finally, grassland occupies 10.30% of the total cultivated acres.

3.4.1. Agricultural Land Change of Kranidia’s Farmer Group

The MCDA model implementation recommends changes to the agricultural land of Kranidia’s farmer group.

Table 7. Existing and optimum production plan of Kranidia’s farmer group.

Crop	Acres	Existing Plan %	MCDA %	Deviation %
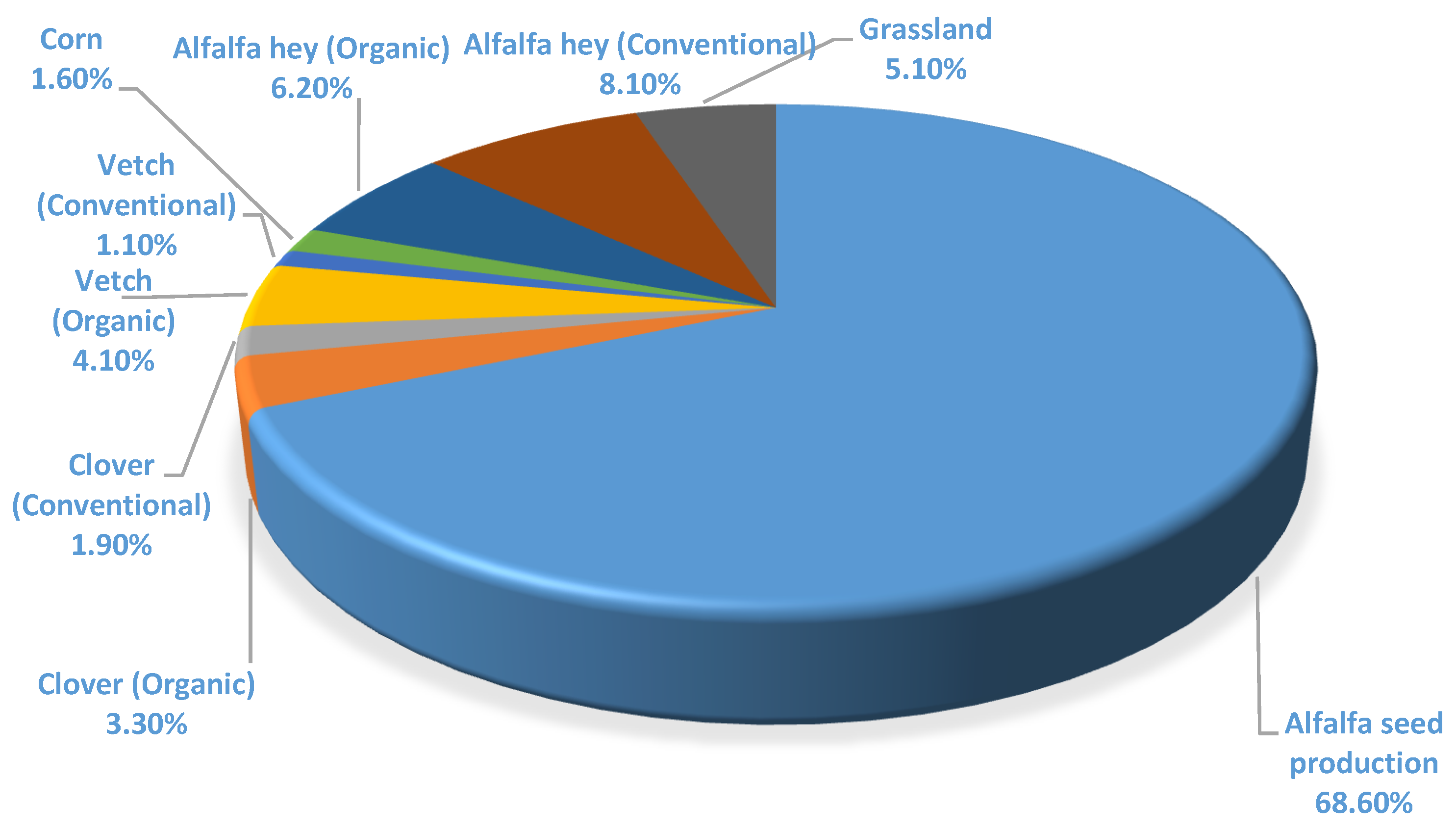
Alfalfa seed production	983	58.23	68.60	17.87
Clover (Organic)	49	2.90	3.30	13.79
Clover (Conventional)	28	1.67	1.90	11.76
Vetch (Organic)	203	12.00	4.10	−65.83
Vetch (Conventional)	23	1.39	1.10	−21.43
Corn	24	1.41	1.60	14.29
Alfalfa hay (Organic)	88	5.21	6.20	19.23
Alfalfa hay (Conventional)	116	6.88	8.10	17.39
Grassland	174	10.30	5.10	−50.48
Total	1688	100.00	100.00

presents the suggested new land changes in the crop plan. For an optimal condition, an increase in all crops is proposed, except for organic vetch (decreased by 65.83%), conventional vetch (decreased by 21.43%), and grassland (decreased by 50.48%), to meet the model’s objectives for increasing profit, reducing production costs, and minimizing labor.

In the next figure (Figure 13), the above-mentioned information is summarized, illustrating noticeable differences compared to the existing crop plan.

3.4.2. Objectives Analysis of Kranidia’s Farmer Group

Considering the non-use of water, in the existing crop plan, the gross profit is equal to EUR 15,396.00, while in the optimum farm plan, it is equal to EUR 15,908.24, showing an increase of 3.33%. The variable cost in the existing crop plan is EUR 6072.00, while in the optimum plan it decreases to EUR 6057.40 (−0.24%). Labor is equal to 155.00 h, while in the optimum farm plan achieved by the MCDA model, it equals to 144.00 h, showing a decrease of 3.87% (

Table 8. Objectives achievement of Kranidia’s farmer group.

	Existing Plan	MCDA Model
		Value	Deviation (%)
Gross profit (€)	15,396.00	15,908.24	3.33
Variable cost (€)	6072.00	6057.40	−0.24
Labor (hours)	155.00	144.00	−3.87

).

The deviations between the existing and model’s crop plan become evident in the following figure (Figure 14).

3.5. Mesorrachi’s Farmer Group—Existing Crop Plan

A total of 6354.0 acres are cultivated by this group of cereal producers. The figure (Figure 15) below presents the distribution of the existing crop plan. Hard wheat, dry-land alfalfa, and rapeseed crops are the most cultivated, accounting for 43.78%, 19.25%, and 15.47%, respectively. This is followed by sunflower (14.40%), soft wheat (3.84%), barley (1.69%), and fallow (SA) land (1.57%).

3.5.1. Agricultural Land Change of Mesorrachi’s Farmer Group

The MCDA model implementation recommends changes to the agricultural land of the Mesorrachi’s farmer group. These land changes entail a revised crop plan that is deemed optimal for the farmers.

Table 9. Existing and optimum production plan of Mesorrachi’s farmer group.

Crop	Acres	Existing Plan %	MCDA %	Deviation %
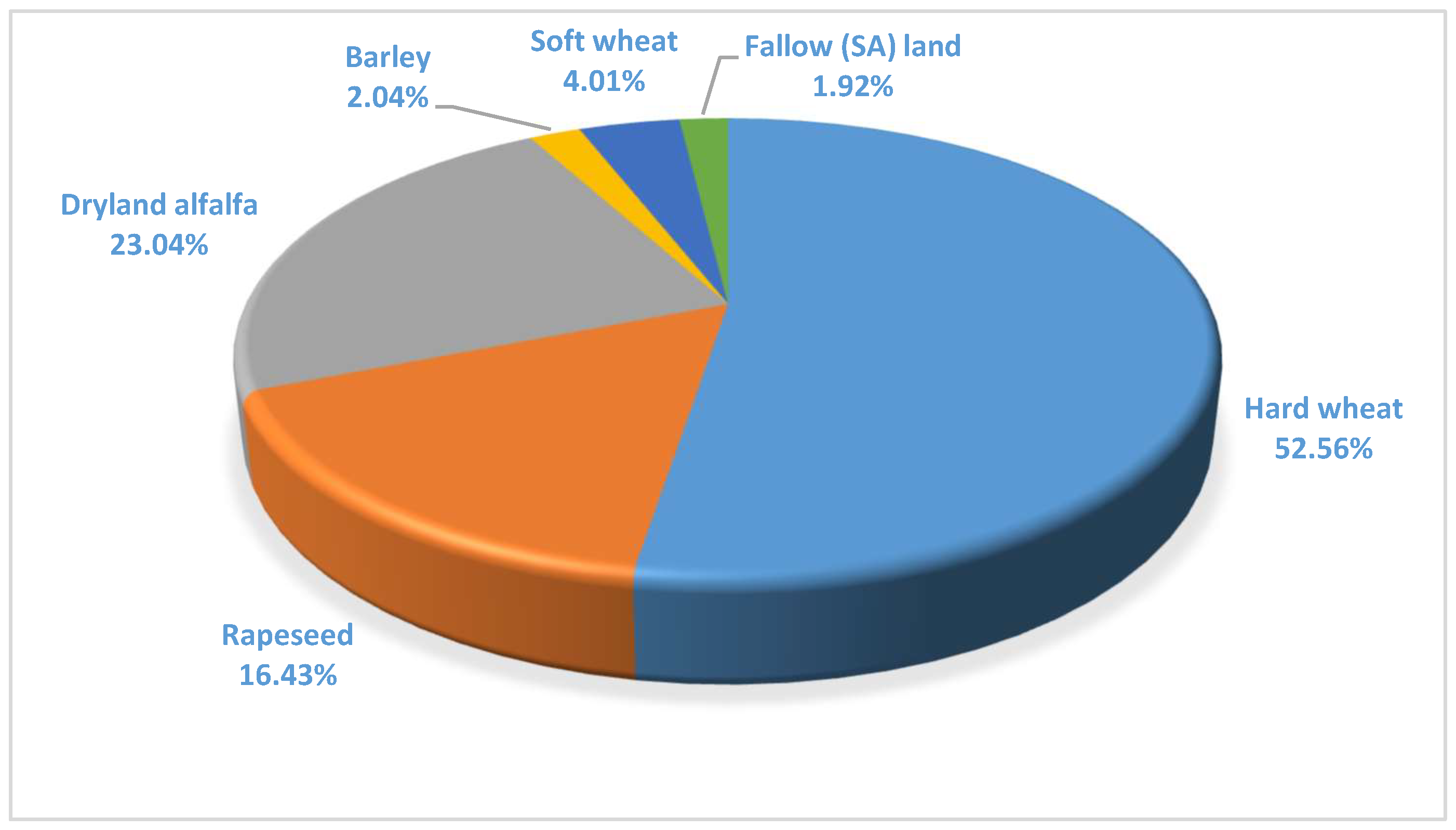
Hard wheat	2782	43.79	52.56	20.00
Rapeseed	983	15.47	16.43	6.00
Dryland alfalfa	1223	19.25	23.04	20.00
Sunflower	915	14.40	0.00	−100.00
Barley	107	1.69	2.04	20.00
Soft wheat	244	3.84	4.01	5.53
Fallow (SA) land	100	1.57	1.92	20.00
Total	6354	100.00	100.00

presents the suggested new land changes in the crop plan. For this particular group, the model suggests as eligible crops: hard wheat at 52.5%, rapeseed at 16.43%, dryland alfalfa at 23.04%, barley at 2.04%, soft wheat at 4.01%, and fallow (SA) land at 1.92%. An increase is proposed in all crops except for sunflower, which is recommended for export to meet the model’s objectives for increasing profit, reducing production costs, and minimizing labor (Table 9).

In the next figure (Figure 16), the above-mentioned information is summarized, illus-trating noticeable differences compared to the existing crop plan.

3.5.2. Objectives Analysis of Mesorrachi’s Farmer Group

Table 10. Objectives achievement of Mesorrachi’s farmer group.

	Existing Plan	MCDA Model
		Value	Deviation (%)
Gross profit (€)	10,101.00	10,909.93	8.01
Variable cost (€)	4519.00	4502.00	−0.38
Labor (hours)	75.00	72.00	−4.00

shows the changes in the three objectives of gross profit, variable cost, and working labor. In the existing crop plan, gross profit is equal to EUR 10,101.00, while in the optimum farm plan, it is equal to EUR 10,909.93, showing an increase of 8.01%. The variable cost in the existing crop plan is EUR 4519.00, while in the optimum plan it decreases to EUR 4502.00 (−0.38%). Labor is equal to 75.00 h, while in the optimum farm plan, it is equal to 72.00 h, showing a decrease of 4.00% (Table 10).

The deviations between the existing and the model’s crop plan become evident in the following figure (Figure 17).

4. Discussion

A multi-criteria decision analysis model was developed for optimizing land use within the framework of the new CAP for five farmer groups based in Greece. This model was used as part of the ”Measure 16: Cooperation” initiative, aiming to improve agricultural practices and promote sustainable development. More specifically, this study focused on determining the best land use practices to ensure effective water management, while also exploring how the new CAP could influence additional land use strategies in farms that do not rely on irrigation techniques. Additionally, an attempt was made to address sustainable agriculture on farms, considering water conservation, economic sustainability, and farmers’ optimal decision-making. This approach is not unique to this study but can be observed in much of the associated literature, since prior studies tried to attain similar aims, with an emphasis on proper water management [49] and sustainable resource management [54,69].

Regarding the three farmer groups (Chalastra, Lagyna, and Chrisoupoli), which primarily use irrigation techniques, it has been shown that they should reduce the water use by decreasing the land dedicated to crops with high water requirements such as rice, corn, vetch, and clover. This finding is similar to that of other studies [17,18,56]. Contrary to the expectations, other irrigated crops with high water requirements, such as cotton, alfalfa hay, corn (in case of the third farmers’ group), and corn silage, may be increasing. The same finding does not apply to many studies [17,18,54,56], but it could be explained by the reduction in the cultivated land uses [17,18,56] and the fact that these specific crops hold substantial economic value for the areas (Northern Greece) where the farmer groups are located [71]. Most of the non-irrigated land appear to be increasing, which points to the fact that the desire to reduce water use due to climate change implies lower water consumption for crops. This means that irrigated crops are substituted with non-irrigated crops or those requiring less irrigation [56].

The increase−reduction in the above-cultivated land indicates the achievement of additional goals, principally connected to the farmers’ actual demands as well as objectives of profit maximization, and cost and labor minimization [17,18,49,56,69,72]. According to the proposed land use, the first farmer group (in Chalastra) might reduce the gap between profit and cost, while the other two farmer groups (in Lagyna and Chrysoupoli) could be more profitable and less labor-intensive. Regarding the two farmer groups (Kranidia and Mesorrachi) who do not utilize irrigation techniques, it has been demonstrated that they can achieve profitable farm planning by reducing the cultivated areas of vetch, grassland, and sunflower due to their lower profitability and high cultivation costs, which limit their contribution to the overall economic sustainability of the farms. This result implies that greater emphasis should be placed on land use related to the remaining crops such as soft and hard wheat, barley, corn, rapeseed, alfalfa, clover, and fallow (SA) land. This conclusion is consistent with the findings of other studies [17,49,54,56] and may be explained by the fact that several of these cropping options, including soft and hard wheat, barley, alfalfa, clover, and corn, receive not only direct payments but also coupled payments from the CAP [12,13]. It is also important to note that rapeseed can receive support for organic farming methods if the farmers choose this direction [13].

Mesorrachi’s farmer group’s 100% sunflower abandonment is notable but not surprising, given that similar results have been reported for cotton [54], sugar beet [54,69], soft wheat, and barley [49,54], either due to low profitability, high costs, or unfavorable production conditions for these crops, or because the conditions required by the model were not met.

In the case of 100% sunflower abandonment, it can be conjectured that this specific crop was entirely excluded from the optimal crop plan because there is a lack of extra coupled payments from the CAP [69] since the profits were very low due to the high production costs. In this case, the findings support previous research on the general impact of CAP subsidies on crop choice [73,74,75,76,77]. This is evident from other studies on the impact of economic policies and financial incentives on decision-makers’ behavior [76]. Increasing or decreasing all the above-mentioned cultivated lands achieves the objectives of the model (profit maximization, cost minimization, labor minimization). As a result of the suggested land uses, the two farmer groups (in Kranidia and Mesorrachi) are more profitable and require less labor [17,18,49,56,69].

5. Conclusions

The study of proper water management in agriculture is considered crucial as drought, pollution, and poor water resource management threaten the sustainability of the agricultural sector. Focusing on sustainability, the new Common Agricultural Policy (2023–2027) sets ambitious goals for water management, as reducing irrigation water use is a critical issue. Therefore, this paper is developed within the framework of the ”Measure 16: Cooperation” initiative and applies a multicriteria mathematical programming model that contributes to optimal land uses. Also, it considers the rational water use and the main goals of farmers, such as profit maximization, and cost and labor minimization. The model was applied to three farmer groups located in Greece. Using the same methodology, two additional cases of farmer groups that utilize drylands are presented complementarily to investigate how the new CAP policy affects land uses of farms that do not use irrigated farming techniques.

From the present analysis, several conclusions can be drawn. Multi-criteria decision analysis can be considered a valuable tool in implementing water use policies, as it can indicate optimal land uses and achieve more effective irrigation management practices. This is evidenced by the results of the analysis, as the reduction in land dedicated to crops such as rice, corn, alfalfa, and vetch (Thessaloniki, Lagyna, and Chrisoupoli) implies potential water savings, allowing farmers to retain or even enhance their profitability. In addition, it turned out that this methodology is valuable since it can combine economic and environmental factors. This is explained by the fact that this study considered both economic sustainability (profit, cost, labor) and environmental sustainability (water use) when making land-use decisions in agriculture.

The present multicriteria decision analysis (MCDA) model, focusing on crop diversity, promotes economic and environmental sustainability. This is evident because the current model investigates alternative crops with low water demand and greater economic benefits, informing farmer groups about how they should operate. Farmers can thus be helped and, in the future, adapt to conditions related to environmental protection and market demands. This approach contributes to the effective management of agricultural activities, with a focus on environmental protection and the rural areas’ long-term sustainability assurance.

Farmers generally prefer less labor-intensive practices or prioritize achieving higher profits even if it requires more working hours. In this case, the results of the multicriteria decision analysis (MCDA) model can inform farmers about profitability and labor intensity and guide them to make special decisions by following different land use strategies. Last but not least, it is worth mentioning that through the implementation of this study, the significant impact of the Common Agricultural Policy on land use decisions is highlighted. This refers to the well-known subsidies that play a significant role in farmers’ cultivation choices and land management.

This study offers valuable insights into optimizing land use for water management and profitability in Greek agriculture. However, certain limitations need to be addressed for future research directions. The study focuses on three irrigated and two non-irrigated groups of farmers in Northern Greece. Extending the model’s application to more farmer groups and other Greek regions with varying climates, soil types, and crop selections would strengthen the conclusions about the new Common Agricultural Policy (CAP). For this reason, it is essential to expand the sample size in future studies, both in terms of the number of farmers involved and the geographical scope. The model emphasizes only water use, profit, cost, and labor. Future iterations could incorporate additional sustainability indicators such as soil health, biodiversity, and greenhouse gas emissions to provide a more holistic picture. Acknowledging the limitations of using data from a single year, this study also aimed to provide a snapshot of the current situation and demonstrate the implementation of the MCDA model within a specific timeframe. However, incorporating longer-term averages for crop yields and prices can be valuable and aligns with a more comprehensive analysis. This consideration can be incorporated into future iterations of this research to enhance the reliability of the current findings.

Furthermore, the study includes information regarding local crops, aiming at the integrated management of agricultural areas. Data collection, model development, understanding, and compliance with the multiple CAP rules by farmers are critical steps that ensure not only the success of this model but also the maximum possible subsidy allocation according to each farmer’s capabilities. It is also believed that the overall process will encourage producers—through the understanding of the new cross-compliance rules—to choose more efficient crops while maintaining existing ones, always to increase their profitability. It is also important to note that the success of this model depends on the adoption of new land uses, which will be confirmed through the conduct of a future study.