Optimizing Non-Point Source Pollution Management: Evaluating Cost-Effective Strategies in a Small Watershed within the Three Gorges Reservoir Area, China
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. SWAT Model Set Up
2.3. SWAT Model Calibration and Validation
2.4. Geographic Detector
2.5. BMP Implementation Setup and Efficiency Evaluation
2.6. Entropy Weight Method
- (i)
- Constructing the BMPs’ attribute decision matrix, A:where aij represents the jth evaluation factor of the ith BMPs, and n and m are the number of BMPs and evaluation factors, respectively.
- (ii)
- Decision matrix standardization:
- (iii)
- Decision matrix normalization, R:
- (iv)
- Information entropy, Ej, for each evaluation factor:where when .
- (v)
- Weight vector, w, of each evaluation factor:
- (vi)
- Comprehensive evaluation index, z, for each BMP:
3. Results
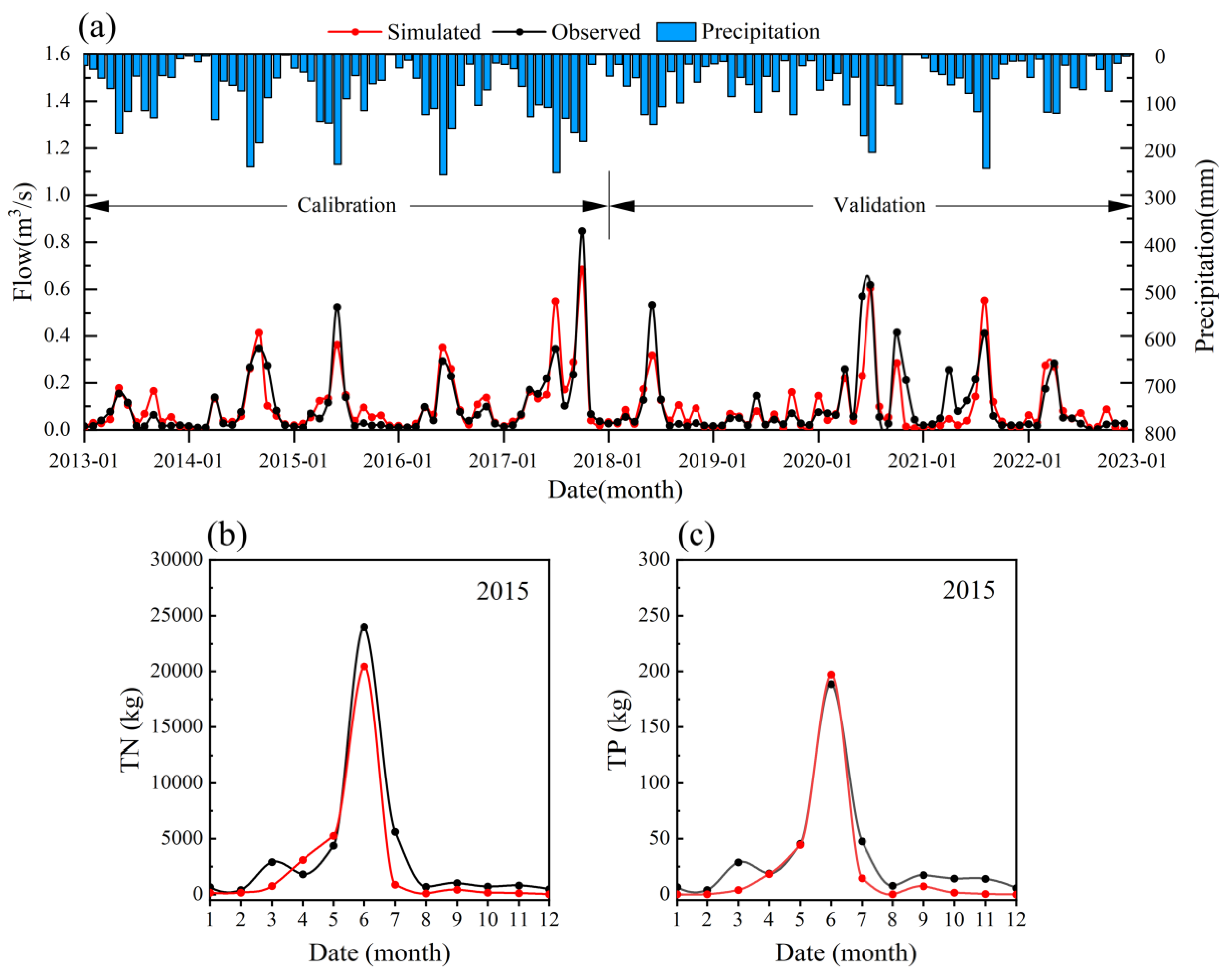
3.1. Model Performance in Simulating Flow and TN/TP Loads
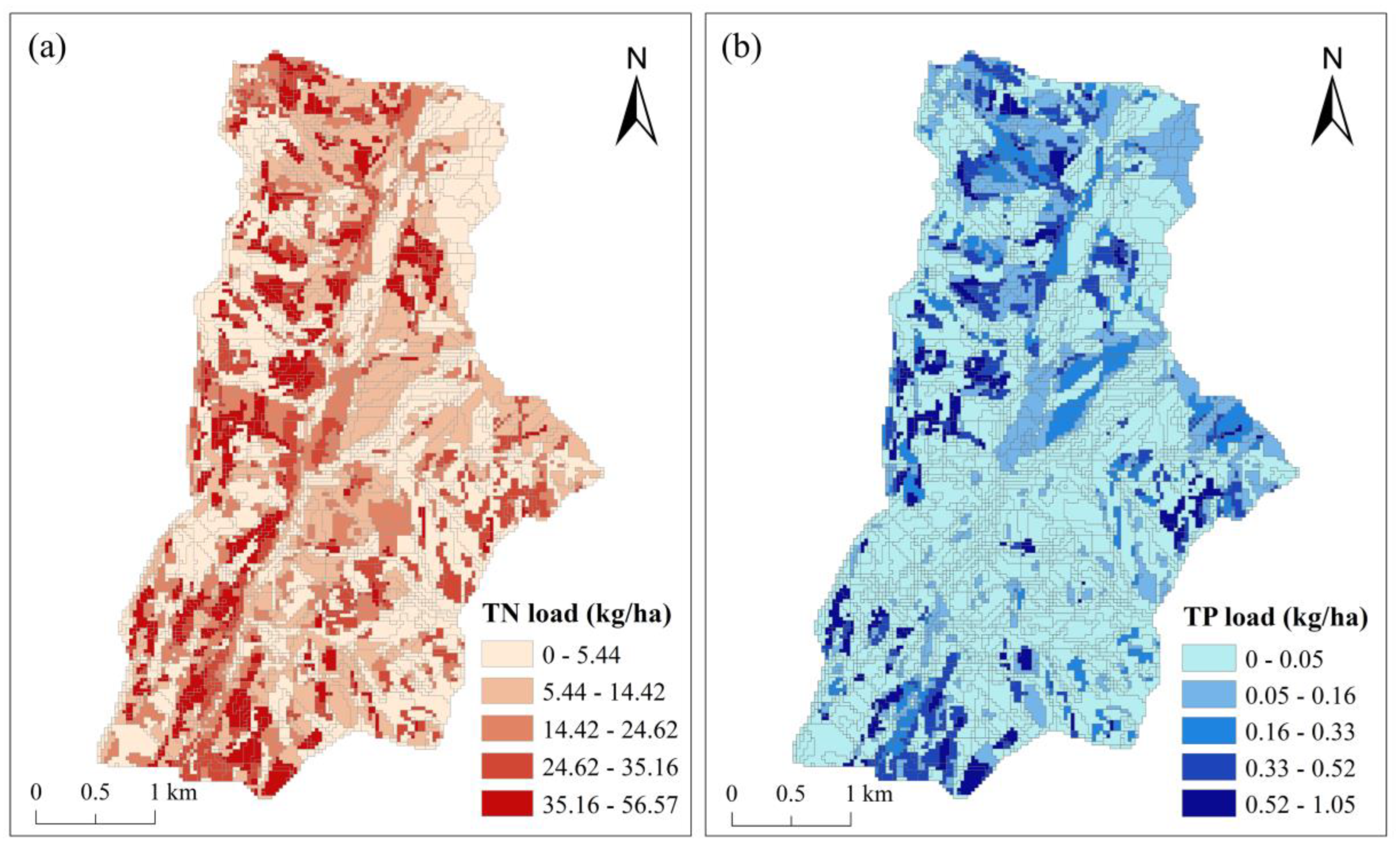
3.2. Distribution Characteristics and Drivers of TN/TP Loads in the Watershed
3.2.1. Distribution Characteristics
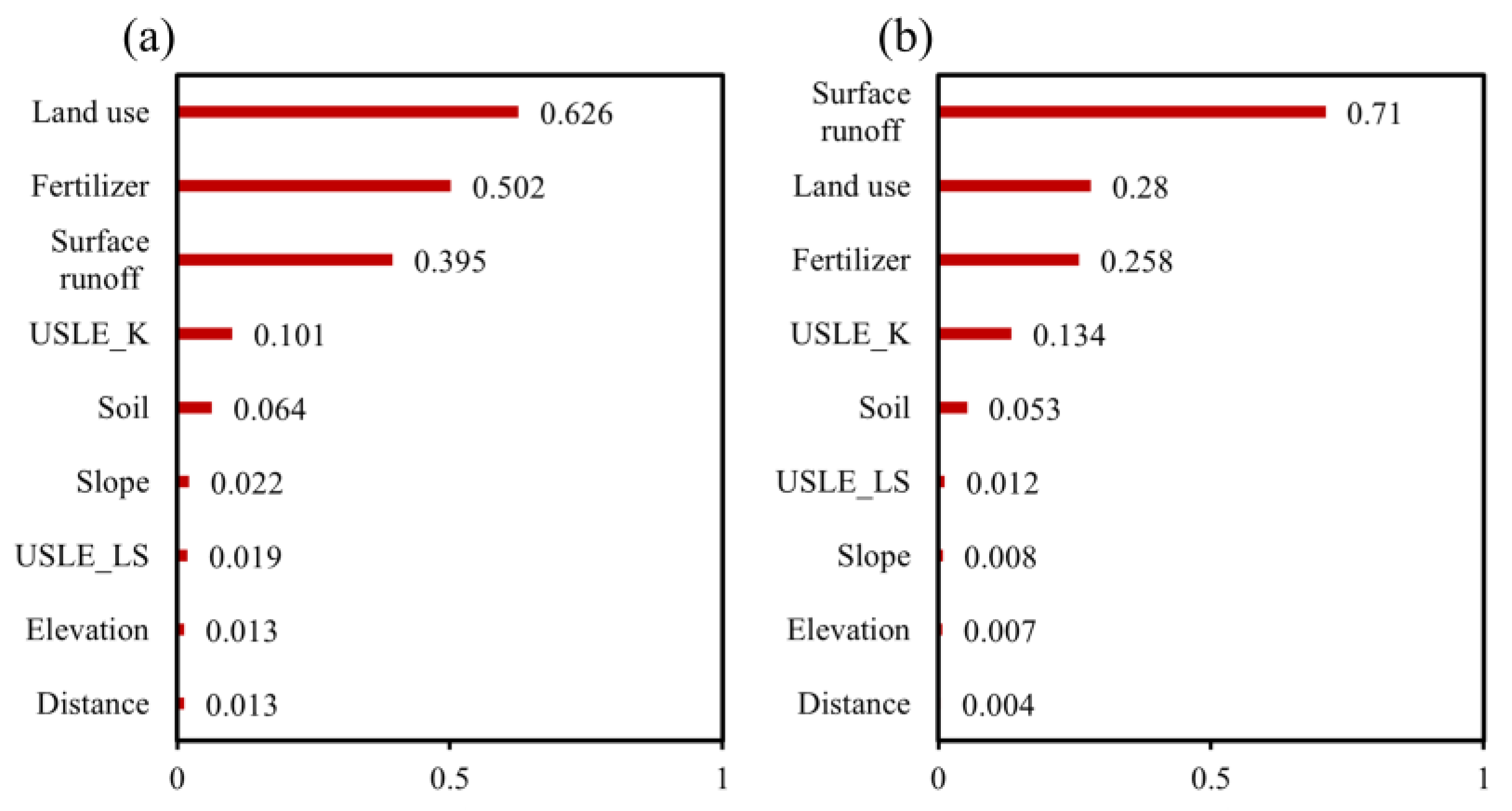
3.2.2. Driving Factors
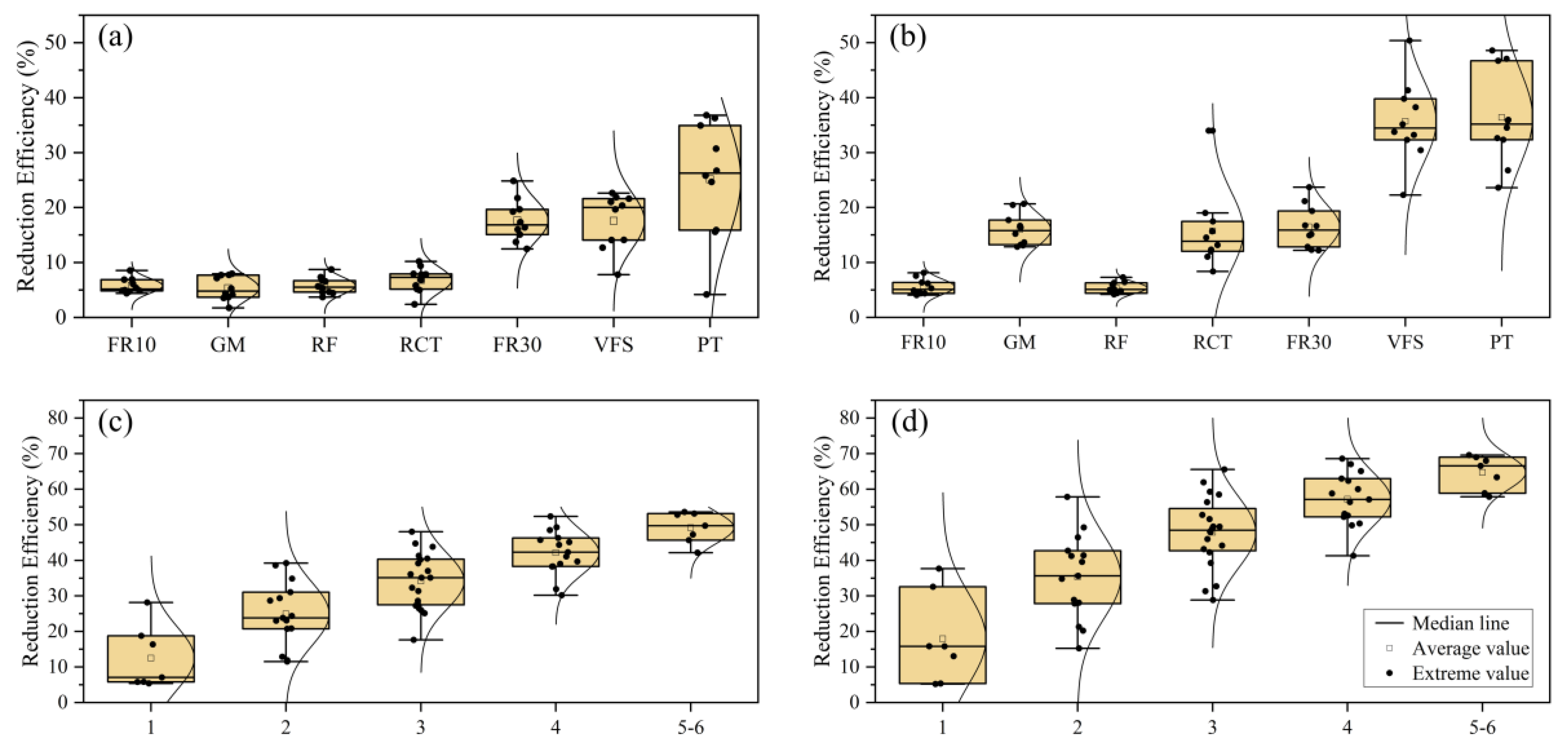
3.3. Efficiencies and Cost-Effectiveness of BMP Scenarios in Reducing NPS Pollution Loads
3.3.1. Efficiencies of BMP Scenarios
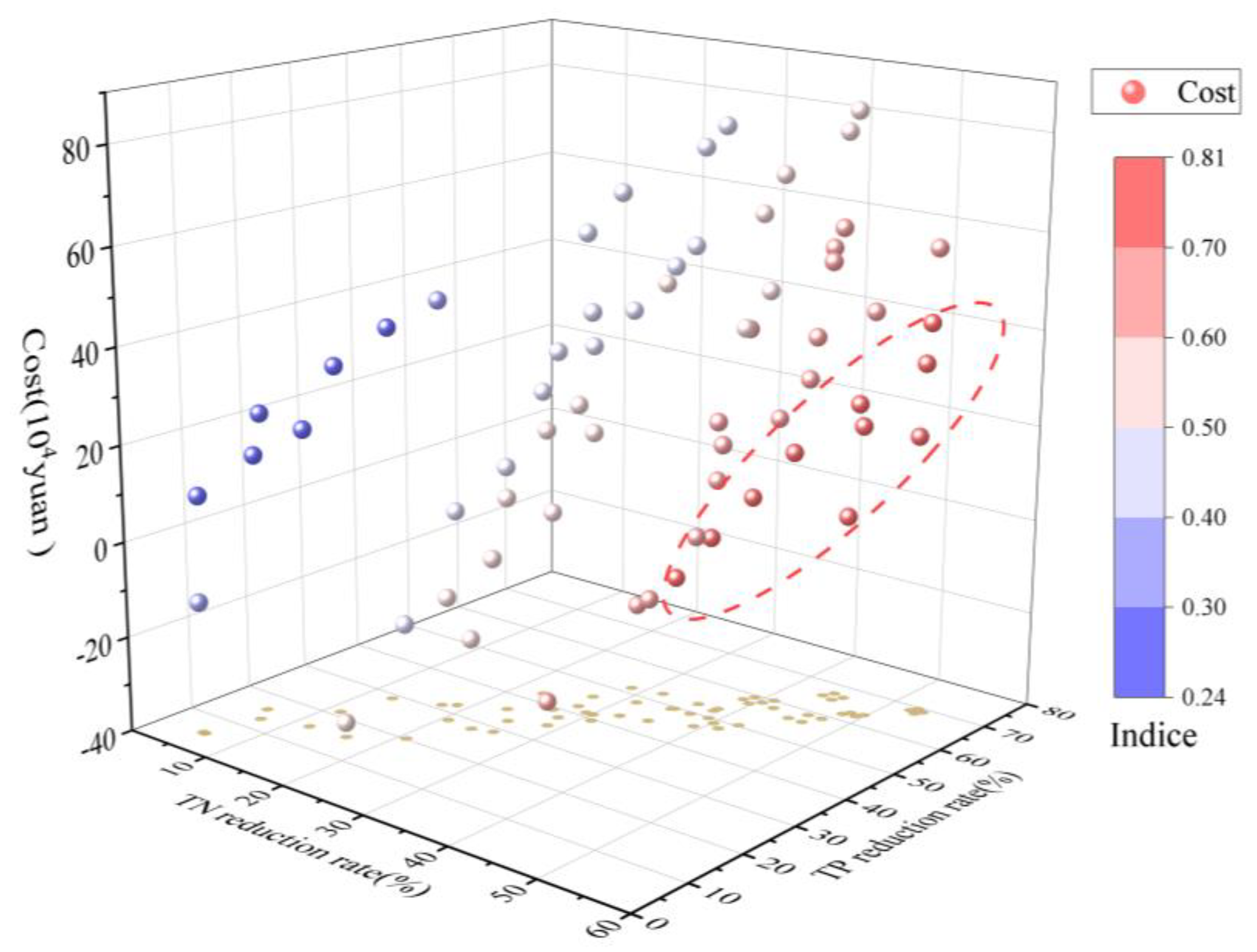
3.3.2. Cost-Effectiveness of BMP Scenarios
4. Discussion
4.1. Analysis of Driving Factors for N and P Loss
4.2. Analysis of Reduction Efficiency of Watershed BMPs
4.3. Analysis of Cost-Effectiveness of Watershed BMPs
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Acuña-Alonso, C.; Fernandes, A.C.P.; Alvarez, X.; Valero, E.; Pacheco, F.A.L.; Varandas, S.D.P.; Terêncio, D.P.S.; Fernandes, L.F.S. Water security and watershed management assessed through the modelling of hydrology and ecological integrity: A study in the Galicia-Costa (NW Spain). Sci. Total Environ. 2021, 759, 143905. [Google Scholar] [CrossRef] [PubMed]
- Casquin, A.; Gu, S.; Dupas, R.; Petitjean, P.; Gruau, G.; Durand, P. River network alteration of C-N-P dynamics in a mesoscale agricultural catchment. Sci. Total Environ. 2020, 749, 141551. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.Y.; Wang, H.; Deng, Y.Q.; Liang, D.F.; Li, Y.P.; Gu, Q.H. Applying water environment capacity to assess the non-point source pollution risks in watersheds. Water Res. 2023, 240, 120092. [Google Scholar] [CrossRef] [PubMed]
- Conley, D.J.; Paerl, H.W.; Howarth, R.W.; Boesch, D.F.; Seitzinger, S.P.; Havens, K.E.; Lancelot, C.; Likens, G.E. Controlling Eutrophication: Nitrogen and Phosphorus. Science 2009, 323, 1014–1015. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Zhang, L.; Wu, H.L.; Wang, Y.F.; Zhang, Y.L.; Xu, J.Y.; Wei, D.Y.; Zhang, R.; Yu, Y.; Wu, D.S.; et al. Strategy for cost-effective BMPs of non-point source pollution in the small agricultural watershed of Poyang Lake: A case study of the Zhuxi River. Chemosphere 2023, 333, 138949. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Feng, L.; Hou, X.J. Algal Blooms in Lakes in China Over the Past Two Decades: Patterns, Trends, and Drivers. Water Resour. Res. 2023, 59, e2022WR033340. [Google Scholar] [CrossRef]
- Xue, B.L.; Zhang, H.W.; Wang, G.Q.; Sun, W.C. Evaluating the risks of spatial and temporal changes in nonpoint source pollution in a Chinese river basin. Sci. Total Environ. 2022, 807, 151726. [Google Scholar] [CrossRef] [PubMed]
- Wang, R.J.; Wang, Q.B.; Dong, L.S.; Zhang, J.F. Cleaner agricultural production in drinking-water source areas for the control of non-point source pollution in China. J. Environ. Manag. 2021, 285, 112096. [Google Scholar] [CrossRef] [PubMed]
- Wang, T.; Xiao, W.F.; Huang, Z.L.; Zeng, L.X. Interflow pattern govern nitrogen loss from tea orchard slopes in response to rainfall pattern in Three Gorges Reservoir Area. Agric. Water Manag. 2022, 269, 107684. [Google Scholar] [CrossRef]
- Zhang, T.; Yang, Y.H.; Ni, J.P.; Xie, D.T. Construction of an integrated technology system for control agricultural non-point source pollution in the Three Gorges Reservoir Areas. Agric. Ecosyst. Environ. 2020, 295, 106919. [Google Scholar] [CrossRef]
- Zhong, S.Q.; Chen, F.X.; Xie, D.T.; Shao, J.A.; Yong, Y.; Zhang, S.; Zhang, Q.W.; Wei, C.F.; Yang, Q.Y.; Ni, J.P. A three-dimensional and multi-source integrated technology system for controlling rural non-point source pollution in the Three Gorges Reservoir Area, China. J. Clean. Prod. 2020, 272, 122579. [Google Scholar] [CrossRef]
- Wang, M.H.; Wang, Y.; Li, Y.; Liu, X.L.; Liu, J.; Wu, J.S. Natural and anthropogenic determinants of riverine phosphorus concentration and loading variability in subtropical agricultural catchments. Agric. Ecosyst. Environ. 2020, 287, 106713. [Google Scholar] [CrossRef]
- Li, L.; Gou, M.M.; Wang, N.; Ma, W.; Xiao, W.F.; Liu, C.F.; La, L.M. Landscape configuration mediates hydrology and nonpoint source pollution under climate change and agricultural expansion. Ecol. Indic. 2021, 129, 107959. [Google Scholar] [CrossRef]
- Xue, J.Y.; Wang, Q.R.; Zhang, M.H. A review of non-point source water pollution modeling for the urban-rural transitional areas of China: Research status and prospect. Sci. Total Environ. 2022, 826, 154146. [Google Scholar] [CrossRef] [PubMed]
- Deng, X.J. Correlations between water quality and the structure and connectivity of the river network in the Southern Jiangsu Plain, Eastern China. Sci. Total Environ. 2019, 664, 583–594. [Google Scholar] [CrossRef] [PubMed]
- Mao, Y.P.; Zhang, H.; Cheng, Y.H.; Zhao, J.W.; Huang, Z.W. The characteristics of nitrogen and phosphorus output in China’s highly urbanized Pearl River Delta region. J. Environ. Manag. 2023, 325, 116543. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.Z.; Chen, L.; Shen, Z.Y. Dynamic export coefficient model for evaluating the effects of environmental changes on non-point source pollution. Sci. Total Environ. 2020, 747, 141164. [Google Scholar] [CrossRef] [PubMed]
- Tan, S.J.; Xie, D.T.; Ni, J.P.; Chen, L.; Ni, C.S.; Ye, W.; Zhao, G.Y.; Shao, J.A.; Chen, F.X. Output characteristics and driving factors of non-point source nitrogen (N) and phosphorus (P) in the Three Gorges reservoir area (TGRA) based on migration process: 1995-2020. Sci. Total Environ. 2023, 875, 162543. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.E.; Wang, Y.X.; Zhang, K.; Hu, M.; Weng, Q.; Zhang, H.C. Spatial heterogeneity modeling of water quality based on random forest regression and model interpretation. Environ. Res. 2021, 202, 111660. [Google Scholar] [CrossRef]
- Feng, Q.Y.; Flanagan, D.C.; Engel, B.A.; Yang, L.; Chen, L.D. GeoAPEXOL, a web GIS interface for the Agricultural Policy Environmental eXtender (APEX) model enabling both field and small watershed simulation. Environ. Model. Softw. 2020, 123, 104569. [Google Scholar] [CrossRef]
- Wang, S.H.; Wang, Y.Q.; Wang, Y.J.; Wang, Z. Assessment of influencing factors on non-point source pollution critical source areas in an agricultural watershed. Ecol. Indic. 2022, 141, 109084. [Google Scholar] [CrossRef]
- Xie, H.; Dong, J.W.; Shen, Z.Y.; Chen, L.; Lai, X.J.; Qiu, J.L.; Wei, G.Y.; Peng, Y.X.; Chen, X.Q. Intra- and inter-event characteristics and controlling factors of agricultural nonpoint source pollution under different types of rainfall-runoff events. Catena 2019, 182, 104105. [Google Scholar] [CrossRef]
- Guo, T.; Cibin, R.; Chaubey, I.; Gitau, M.; Arnold, J.G.; Srinivasan, R.; Kiniry, J.R.; Engel, B.A. Evaluation of bioenergy crop growth and the impacts of bioenergy crops on streamflow, tile drain flow and nutrient losses in an extensively tile-drained watershed using SWAT. Sci. Total Environ. 2018, 613, 724–735. [Google Scholar] [CrossRef]
- Huang, J.; Liu, R.M.; Wang, Q.R.; Gao, X.; Han, Z.Y.; Gao, J.M.; Gao, H.; Zhang, S.B.; Wang, J.F.; Zhang, L.; et al. Climate factors affect N2O emissions by influencing the migration and transformation of nonpoint source nitrogen in an agricultural watershed. Water Res. 2022, 223, 119028. [Google Scholar] [CrossRef] [PubMed]
- Luo, Z.Y.; Zhang, H.L.; Pang, J.Z.; Yang, J.; Li, M. Coupling of SWAT and EPIC Models to Investigate the Mutual Feedback Relationship between Vegetation and Soil Erosion, a Case Study in the Huangfuchuan Watershed, China. Forests 2023, 14, 844. [Google Scholar] [CrossRef]
- Huang, J.J.; Lin, X.J.; Wang, J.H.; Wang, H. The precipitation driven correlation based mapping method (PCM) for identifying the critical source areas of non-point source pollution. J. Hydrol. 2015, 524, 100–110. [Google Scholar] [CrossRef]
- Deng, J.; Zhou, Y.W.; Chu, L.; Wei, Y.J.; Li, Z.X.; Wang, T.W.; Dai, C.T. Spatiotemporal variations and determinants of stream nitrogen and phosphorus concentrations from a watershed in the Three Gorges Reservoir Area, China. Int. Soil Water Conserv. Res. 2023, 11, 507–517. [Google Scholar] [CrossRef]
- Sun, S.Y.; Zhang, J.F.; Cai, C.J.; Cai, Z.Y.; Li, X.G.; Wang, R.J. Coupling of non-point source pollution and soil characteristics covered by Phyllostachys edulis stands in hilly water source area. J. Environ. Manag. 2020, 268, 110657. [Google Scholar] [CrossRef]
- Yan, Z.Y.; Wang, Y.Q.; Wang, Z.; Zhang, C.R.; Wang, Y.J.; Li, Y.M. Spatiotemporal Analysis of Landscape Ecological Risk and Driving Factors: A Case Study in the Three Gorges Reservoir Area, China. Trans. ASABE 2023, 15, 4884. [Google Scholar] [CrossRef]
- Fei, X.F.; Lou, Z.H.; Xiao, R.; Ren, Z.Q.; Lv, X.N. Contamination assessment and source apportionment of heavy metals in agricultural soil through the synthesis of PMF and GeogDetector models. Sci. Total Environ. 2020, 747, 141293. [Google Scholar] [CrossRef]
- Shen, Z.L.; Zhang, W.S.; Peng, H.; Xu, G.H.; Chen, X.M.; Zhang, X.; Zhao, Y.X. Spatial characteristics of nutrient budget on town scale in the Three Gorges Reservoir area, China. Sci. Total Environ. 2022, 819, 152677. [Google Scholar] [CrossRef] [PubMed]
- Sun, H.H.; Tian, Y.; Li, L.P.; Zhuang, Y.; Zhou, X.; Zhang, H.R.; Zhan, W.; Zuo, W.; Luan, C.Y.; Huang, K.M. Unraveling spatial patterns and source attribution of nutrient transport: Towards optimal best management practices in complex river basin. Sci. Total Environ. 2024, 906, 167686. [Google Scholar] [CrossRef] [PubMed]
- López-Ballesteros, A.; Trolle, D.; Srinivasan, R.; Senent-Aparicio, J. Assessing the effectiveness of potential best management practices for science-informed decision support at the watershed scale: The case of the Mar Menor coastal lagoon, Spain. Sci. Total Environ. 2023, 859, 160144. [Google Scholar] [CrossRef] [PubMed]
- Leh, M.D.K.; Sharpley, A.N.; Singh, G.; Matlock, M.D. Assessing the impact of the MRBI program in a data limited Arkansas watershed using the SWAT model. Agric. Water Manag. 2018, 202, 202–219. [Google Scholar] [CrossRef]
- Lee, S.; McCarty, G.W.; Moglen, G.E.; Li, X.; Wallace, C.W. Assessing the effectiveness of riparian buffers for reducing organic nitrogen loads in the Coastal Plain of the Chesapeake Bay watershed using a watershed model. J. Hydrol. 2020, 585, 124779. [Google Scholar] [CrossRef]
- Geng, R.Z.; Sharpley, A.N. A novel spatial optimization model for achieve the trad-offs placement of best management practices for agricultural non-point source pollution control at multi-spatial scales. J. Clean. Prod. 2019, 234, 1023–1032. [Google Scholar] [CrossRef]
- Gassman, P.W.; Reyes, M.R.; Green, C.H.; Arnold, J.G. The soil and water assessment tool: Historical development, applications, and future research directions. Trans. ASABE 2007, 50, 1211–1250. [Google Scholar] [CrossRef]
- Wallace, C.W.; Flanagan, D.C.; Engel, B.A. Quantifying the effects of conservation practice implementation on predicted runoff and chemical losses under climate change. Agric. Water Manag. 2017, 186, 51–65. [Google Scholar] [CrossRef]
- Risal, A.; Parajuli, P.B. Evaluation of the Impact of Best Management Practices on Streamflow, Sediment and Nutrient Yield at Field and Watershed Scales. Water Resour. Manag. 2022, 36, 1093–1105. [Google Scholar] [CrossRef]
- Yuan, Y.P.; Koropeckyj-Cox, L. SWAT model application for evaluating agricultural conservation practice effectiveness in reducing phosphorous loss from the Western Lake Erie Basin. J. Environ. Manag. 2022, 302, 114000. [Google Scholar] [CrossRef]
- Liu, Y.Z.; Guo, T.; Wang, R.Y.; Engel, B.A.; Flanagan, D.C.; Li, S.Y.; Pijanowski, B.C.; Collingsworth, P.D.; Lee, J.G.; Wallace, C.W. A SWAT-based optimization tool for obtaining cost-effective strategies for agricultural conservation practice implementation at watershed scales. Sci. Total Environ. 2019, 691, 685–696. [Google Scholar] [CrossRef] [PubMed]
- Wu, L.; Liu, X.; Chen, J.L.; Li, J.F.; Yu, Y.; Ma, X.Y. Efficiency assessment of best management practices in sediment reduction by investigating cost-effective tradeoffs. Agric. Water Manag. 2022, 265, 107546. [Google Scholar] [CrossRef]
- Cheng, W.J.; Xi, H.Y.; Sindikubwabo, C.; Si, J.H.; Zhao, C.G.; Yu, T.F.; Li, A.L.; Wu, T.R. Ecosystem health assessment of desert nature reserve with entropy weight and fuzzy mathematics methods: A case study of Badain Jaran Desert. Ecol. Indic. 2020, 119, 106843. [Google Scholar] [CrossRef]
- Xiang, R.; Wang, L.J.; Li, H.; Tian, Z.B.; Zheng, B.H. Water quality variation in tributaries of the Three Gorges Reservoir from 2000 to 2015. Water Res. 2021, 195, 116993. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.W.; Li, Z.X.; Wang, T.W.; Wang, J.; Deng, J.; Du, Y.N.; Dai, C.T.; Zhang, X.M.; Zhao, S.J. Divergent hydrological responses to intensive production under different rainfall regimes: Evidence from long-term field observations. J. Hydrol. 2023, 617, 128918. [Google Scholar] [CrossRef]
- Garosi, Y.; Sheklabadi, M.; Conoscenti, C.; Pourghasemi, H.R.; Van Oost, K. Assessing the performance of GIS-based machine learning models with different accuracy measures for determining susceptibility to gully erosion. Sci. Total Environ. 2019, 664, 1117–1132. [Google Scholar] [CrossRef] [PubMed]
- Ding, W.L.; Xia, J.; She, D.X.; Zhang, X.Y.; Chen, T.; Huang, S.; Zheng, H.S.Y. Assessing multivariate effect of best management practices on non-point source pollution management using the coupled Copula-SWAT model. Ecol. Indic. 2023, 153, 110393. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Woo, S.Y.; Kim, S.J.; Lee, J.W.; Kim, S.H.; Kim, Y.W. Evaluating the impact of interbasin water transfer on water quality in the recipient river basin with SWAT. Sci. Total Environ. 2021, 776, 145984. [Google Scholar] [CrossRef]
- Wang, J.F.; Hu, Y. Environmental health risk detection with GeogDetector. Environ. Model. Softw. 2012, 33, 114–115. [Google Scholar] [CrossRef]
- Alnahit, A.O.; Mishra, A.K.; Khan, A.A. Stream water quality prediction using boosted regression tree and random forest models. Stoch. Environ. Res. Risk Assess. 2022, 36, 2661–2680. [Google Scholar] [CrossRef]
- Arabi, M.; Frankenberger, J.R.; Enge, B.A.; Arnold, J.G. Representation of agricultural conservation practices with SWAT. Hydrol. Process. 2008, 22, 3042–3055. [Google Scholar] [CrossRef]
- Shi, J.H.; Jin, R.; Zhu, W.H. Quantification of Effects of Natural Geographical Factors and Landscape Patterns on Non-point Source Pollution in Watershed Based on Geodetector: Burhatong River Basin, Northeast China as An Example. Chin. Geogr. Sci. 2022, 32, 707–723. [Google Scholar] [CrossRef]
- Li, T.Y.; Zhang, Y.; He, B.H.; Wu, X.Y.; Du, Y.N. Nitrate loss by runoff in response to rainfall amount category and different combinations of fertilization and cultivation in sloping croplands. Agric. Water Manag. 2022, 273, 107916. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, S.Y.; Huang, Y.R.; Chen, M.H.; Huang, L. Modeling of rainfall induced phosphorus transport from soil to runoff with consideration of phosphorus-sediment interactions. J. Hydrol. 2022, 609, 127732. [Google Scholar] [CrossRef]
- Xin, Y.; Liu, G.; Xie, Y.; Gao, Y.; Liu, B.Y.; Shen, B. Effects of soil conservation practices on soil losses from slope farmland in northeastern China using runoff plot data. Catena 2019, 174, 417–424. [Google Scholar] [CrossRef]
- Shen, Z.Y.; Chen, L.; Ding, X.W.; Hong, Q.; Liu, R.M. Long-term variation (1960-2003) and causal factors of non-point-source nitrogen and phosphorus in the upper reach of the Yangtze River. J. Hazard. Mater. 2013, 252, 45–56. [Google Scholar] [CrossRef] [PubMed]
- Liu, R.M.; Zhang, P.P.; Wang, X.J.; Chen, Y.X.; Shen, Z.Y. Assessment of effects of best management practices on agricultural non-point source pollution in Xiangxi River watershed. Agric. Water Manag. 2013, 117, 9–18. [Google Scholar] [CrossRef]
- Wang, K.; Wang, P.X.; Zhang, R.D.; Lin, Z.B. Determination of spatiotemporal characteristics of agricultural non-point source pollution of river basins using the dynamic time warping distance. J. Hydrol. 2020, 583, 124303. [Google Scholar] [CrossRef]
- Shen, Z.Y.; Qiu, J.L.; Hong, Q.; Chen, L. Simulation of spatial and temporal distributions of non-point source pollution load in the Three Gorges Reservoir Region. Sci. Total Environ. 2014, 493, 138–146. [Google Scholar] [CrossRef]
- Srinivas, R.; Singh, A.P.; Dhadse, K.; Garg, C. An evidence based integrated watershed modelling system to assess the impact of non-point source pollution in the riverine ecosystem. J. Clean. Prod. 2020, 246, 118963. [Google Scholar] [CrossRef]
- Bu, H.M.; Zhang, Y.; Meng, W.; Song, X.F. Effects of land-use patterns on in-stream nitrogen in a highly-polluted river basin in Northeast China. Sci. Total Environ. 2016, 553, 232–242. [Google Scholar] [CrossRef] [PubMed]
- Fang, S.B.; Deitch, M.J.; Gebremicael, T.G.; Angelini, C.; Ortals, C.J. Identifying critical source areas of non-point source pollution to enhance water quality: Integrated SWAT modeling and multi-variable statistical analysis to reveal key variables and thresholds. Water Res. 2024, 253, 121286. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.Y.; Liu, Q.; Fu, G.T.; He, Y.; Luo, X.Z.; Zheng, Z. Spatiotemporal patterns and source attribution of nitrogen load in a river basin with complex pollution sources. Water Res. 2016, 94, 187–199. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Chen, S.B.; Li, S.; Shen, Z.Y. Temporal and spatial scaling effects of parameter sensitivity in relation to non-point source pollution simulation. J. Hydrol. 2019, 571, 36–49. [Google Scholar] [CrossRef]
- Zhu, Y.X.; Chen, L.; Wang, K.; Wang, W.Z.; Wang, C.C.; Shen, Z.Y. Evaluating the spatial scaling effect of baseflow and baseflow nonpoint source pollution in a nested watershed. J. Hydrol. 2019, 579, 124221. [Google Scholar] [CrossRef]
- Huang, C.B.; Huang, X.; Peng, C.H.; Zhou, Z.X.; Teng, M.J.; Wang, P.C. Land use/cover change in the Three Gorges Reservoir area, China: Reconciling the land use conflicts between development and protection. Catena 2019, 175, 388–399. [Google Scholar] [CrossRef]
- Teshager, A.D.; Gassman, P.W.; Secchi, S.; Schoof, J.T. Simulation of targeted pollutant-mitigation-strategies to reduce nitrate and sediment hotspots in agricultural watershed. Sci. Total Environ. 2017, 607, 1188–1200. [Google Scholar] [CrossRef]
- Mtibaa, S.; Hotta, N.; Irie, M. Analysis of the efficacy and cost-effectiveness of best management practices for controlling sediment yield: A case study of the Joumine watershed, Tunisia. Sci. Total Environ. 2018, 616, 1–16. [Google Scholar] [CrossRef]
- Uniyal, B.; Jha, M.K.; Verma, A.K.; Anebagilu, P.K. Identification of critical areas and evaluation of best management practices using SWAT for sustainable watershed management. Sci. Total Environ. 2020, 744, 140737. [Google Scholar] [CrossRef]
- Zhang, Z.S.; Montas, H.; Shirmohammadi, A.; Leisnham, P.; Negahban-Azar, M. Effectiveness of BMP plans in different land covers, with random, targeted, and optimized allocation. Sci. Total Environ. 2023, 892, 164428. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.Z.; Wang, R.Y.; Guo, T.; Engel, B.A.; Flanagan, D.C.; Lee, J.G.; Li, S.Y.; Pijanowski, B.C.; Collingsworth, P.D.; Wallace, C.W. Evaluating efficiencies and cost-effectiveness of best management practices in improving agricultural water quality using integrated SWAT and cost evaluation tool. J. Hydrol. 2019, 577, 123965. [Google Scholar] [CrossRef]
- Liu, Y.Z.; Bralts, V.F.; Engel, B.A. Evaluating the effectiveness of management practices on hydrology and water quality at watershed scale with a rainfall-runoff model. Sci. Total Environ. 2015, 511, 298–308. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.Y.; Xia, J.; Shao, Q.X.; Zhai, X.Y. Water quantity and quality simulation by improved SWAT in highly regulated Huai River Basin of China. Stoch. Environ. Res. Risk Assess. 2013, 27, 11–27. [Google Scholar] [CrossRef]
- Kalcic, M.M.; Kirchhoff, C.; Bosch, N.; Muenich, R.L.; Murray, M.; Gardner, J.G.; Scavia, D. Engaging Stakeholders To Define Feasible and Desirable Agricultural Conservation in Western Lake Erie Watersheds. Environ. Sci. Technol. 2016, 50, 8135–8145. [Google Scholar] [CrossRef] [PubMed]
- Dong, F.F.; Li, J.C.; Dai, C.; Niu, J.; Chen, Y.; Huang, J.C.; Liu, Y. Understanding robustness in multiscale nutrient abatement: Probabilistic simulation-optimization using Bayesian network emulators. J. Clean. Prod. 2022, 378, 134394. [Google Scholar] [CrossRef]
- Li, W.Q.; Zinda, J.A.; Zhang, Z.M. Does the “Returning Farmland to Forest Program” Drive Community-Level Changes in Landscape Patterns in China? Forests 2019, 10, 933. [Google Scholar] [CrossRef]
- Yang, L.; Pang, S.J.; Wang, X.Y.; Du, Y.; Huang, J.Y.; Melching, C.S. Optimal allocation of best management practices based on receiving water capacity constraints. Agric. Water Manag. 2021, 258, 107179. [Google Scholar] [CrossRef]
- Zhang, X.; Li, P.; Bin Li, Z.; Yu, G.Q. Effects of grass strips distribution on soil erosion and its optimal configuration on hillslopes. Catena 2024, 238, 107882. [Google Scholar] [CrossRef]
- Wang, N.A.; Luo, J.; He, S.Q.; Li, T.X.; Zhao, Y.H.; Zhang, X.Z.; Wang, Y.D.; Huang, H.G.; Yu, H.Y.; Ye, D.H.; et al. Characterizing the rill erosion process from eroded morphology and sediment connectivity on purple soil slope with upslope earthen dike terraces. Sci. Total Environ. 2023, 860, 160486. [Google Scholar] [CrossRef]
- Han, J.X.; Xin, Z.H.; Han, F.; Xu, B.; Wang, L.F.; Zhang, C.; Zheng, Y. Source contribution analysis of nutrient pollution in a P-rich watershed: Implications for integrated water quality management. Environ. Pollut. 2021, 279, 116885. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Wang, Y.Q.; Ding, X.K.; Wang, Y.J.; Yan, Z.Y.; Wang, S.H. Evaluation of net anthropogenic nitrogen inputs in the Three Gorges Reservoir Area. Ecol. Indic. 2022, 139, 108922. [Google Scholar] [CrossRef]



| Data | Data Type | Source | Resolution | Period |
|---|---|---|---|---|
| Geographic data | Digital elevation model | Geospatial Data Cloud (http://www.gscloud.cn, accessed on 20 January 2024) | 30 m × 30 m | - |
| Land use | Zigui Water Conservancy Bureau | 30 m × 30 m | 2017 | |
| Soil types and soil properties | Zigui Water Conservancy Bureau | 30 m × 30 m | - | |
| Meteorological data | Precipitation Temperature Relative humidity Wind speed Solar radiation | Wangjiaqiao Gauge Station National Meteorological Station | Daily | 2012–2022 |
| Evaluation data | Discharge | Wangjiaqiao Gauge Station | Daily | 2012–2022 |
| TN concentration TP concentration | Wangjiaqiao Gauge Station | Monthly | 2015 | |
| Agricultural practices | Application of fertilizer Dates of farming practices Crop rotations | Field investigations, Hubei statistical yearbooks | Yearly | 2012–2022 |
| Variable | Parameter | Description | Range | Method | Rank | Value |
|---|---|---|---|---|---|---|
| Flow | CN2 | SCS runoff curve number | 35–98 | r | 2 | −0.154 |
| ALPHA_BF | Baseflow alpha factor (days) | 0–1 | v | 10 | 0.499 | |
| GW_DELAY | Groundwater delay (days) | 0–500 | v | 5 | 3.331 | |
| GWQMN | The threshold depth of water in the shallow aquifer required for return flow to occur (mm) | 0–5000 | v | 1 | 2526.301 | |
| SOL_BD | Moist bulk density | 0.9–2.5 | r | 4 | −0.139 | |
| ESCO | Soil evaporation compensation factor | 0–1 | v | 11 | 0.465 | |
| CANMX | Maximum canopy storage (mm H2O) | 0–100 | v | 12 | 2.776 | |
| SOL_K | Saturated hydraulic conductivity | 0–2000 | r | 9 | −0.431 | |
| SOL_AWC | Available water capacity of the soil layer | 0–1 | r | 6 | −0.579 | |
| CH_N2 | Manning’s “n” value for the main channel | −0.01–0.3 | v | 8 | 0.038 | |
| GW_REVAP | Groundwater “revap” coefficient | 0.02–0.2 | v | 3 | 0.071 | |
| EPCO | Plant uptake compensation factor | 0–1 | v | 7 | 0.635 | |
| TN | BIOMIX | Biological mixing efficiency | 0–1 | v | 2 | 0.27 |
| N_UPDIS | Nitrogen uptake distribution parameter | 0–100 | v | 4 | 81 | |
| NPERCO | Nitrogen percolation coefficient | 0–1 | v | 3 | 0.37 | |
| ERORGN | Organic N enrichment ratio | 0–5 | v | 1 | 2.65 | |
| TP | P_UPDIS | Phosphorus uptake distribution parameter | 0–100 | v | 2 | 31.625 |
| PHOSKD | Phosphorus soil partitioning coefficient | 100–200 | v | 4 | 196.625 | |
| PPERCO | Phosphorus percolation coefficient | 10–17.5 | v | 3 | 10.03 | |
| ERORGP | Organic P enrichment ratio. | 0–5 | v | 1 | 0.023 |
| Performance Rating | R2 | NSE | PBIAS (%) | |
|---|---|---|---|---|
| Streamflow | N, P | |||
| Very good | 0.75 < R2 ≤ 1.00 | 0.75 < NSE ≤ 1.00 | PBIAS < ±10 | PBIAS < ±25 |
| Good | 0.65 < R2 ≤ 0.75 | 0.65 < NSE ≤ 0.75 | ±10 < PBIAS < ±15 | ±25 < PBIAS < ±40 |
| Satisfactory | 0.50 < R2 ≤ 0.65 | 0.75 < NSE ≤ 0.65 | ±15 < PBIAS < ±25 | ±40 < PBIAS < ±70 |
| Unsatisfactory | R2 ≤ 0.50 | NSE ≤ 0.50 | PBIAS ≥ ±25 | PBIAS ≥ ±70 |
| Land Use | Sloping Field | Orchard | Terrace | Paddy Field | Residential Area | Forest | Brush | Others | Entire Watershed |
|---|---|---|---|---|---|---|---|---|---|
| Area, ha | 27.46 | 467.51 | 69.14 | 83.45 | 47.08 | 683.57 | 148.54 | 3.96 | 1530.71 |
| TN loads | 39.06 | 22.44 | 21.98 | 29.46 | 29.08 | 3.72 | 5.56 | 1.33 | 13.25 |
| Organic N loads | 35.12 | 13.78 | 17.04 | 24.63 | 26.93 | 3.69 | 5.5 | 1.31 | 9.96 |
| Nitrate N loads | 3.94 | 8.66 | 4.94 | 4.83 | 2.15 | 0.03 | 0.06 | 0.02 | 3.29 |
| TP loads | 0.32 | 0.18 | 0.11 | 0.34 | 0.07 | 0.03 | 0.06 | 0.05 | 0.11 |
| Organic P loads | 0.08 | 0.01 | 0.02 | 0.04 | 0.04 | 0.01 | 0.02 | 0.01 | 0.02 |
| Sediment P loads | 0.2 | 0.09 | 0.06 | 0.19 | 0.02 | 0.02 | 0.04 | 0.03 | 0.06 |
| Dissolved P loads | 0.04 | 0.07 | 0.02 | 0.11 | 0.02 | 0.01 | 0 | 0 | 0.03 |
| Category | BMPs | Annual Costs, 104 CNY | TN Reduction Rate, % | TP Reduction Rate, % | Comprehensive Evaluation Indices |
|---|---|---|---|---|---|
| Structural measures | VFSs | 2.1 | 18.75 | 32.53 | 0.47 |
| PTs | 37.39 | 28.12 | 37.69 | 0.45 | |
| Non-structural measures | FR10 | −12.3 | 5.38 | 5.35 | 0.31 |
| FR30 | −36.91 | 16.34 | 15.77 | 0.51 | |
| RCT | 16.2 | 7.06 | 13.03 | 0.26 | |
| GM | 23.38 | 5.79 | 15.81 | 0.24 | |
| Landscape management measure | RF | 10.19 | 5.81 | 5.21 | 0.24 |
| Rank | BMPs in Series | Annual Costs, 104 CNY | TN Reduction Rate (%) | TP Reduction Rate (%) | Comprehensive Evaluation Indices |
|---|---|---|---|---|---|
| 1 | VFS_PT_RCT_FR30 | 18.79 | 52.37 | 68.58 | 0.81 |
| 2 | VFS_PT_FR30 | 2.58 | 48.05 | 61.95 | 0.8 |
| 3 | VFS_PT_RF_RCT_FR30 | 34.43 | 53.15 | 67.97 | 0.76 |
| 4 | VFS_PT_RF_FR30 | 21.9 | 49.3 | 62.35 | 0.75 |
| 5 | VFS_PT_RCT_GM_FR30 | 42.16 | 52.81 | 69.59 | 0.74 |
| 6 | VFS_PT_GM_FR30 | 25.96 | 48.49 | 62.96 | 0.74 |
| 7 | VFS_RCT_GM_FR30 | 4.77 | 39.68 | 57.11 | 0.71 |
| 8 | PT_RCT_FR30 | 16.68 | 44.75 | 56.37 | 0.71 |
| 9 | VFS_GM_FR30 | −11.43 | 35.11 | 49.51 | 0.7 |
| 10 | VFS_RF_RCT_FR30 | −1.19 | 39.02 | 49.84 | 0.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, R.; Wang, Y.; Liu, H.; Wang, Z.; Ma, L.; Zhang, J.; Li, J.; Yan, Z.; Zhang, Y.; Li, D. Optimizing Non-Point Source Pollution Management: Evaluating Cost-Effective Strategies in a Small Watershed within the Three Gorges Reservoir Area, China. Land 2024, 13, 742. https://doi.org/10.3390/land13060742
Chang R, Wang Y, Liu H, Wang Z, Ma L, Zhang J, Li J, Yan Z, Zhang Y, Li D. Optimizing Non-Point Source Pollution Management: Evaluating Cost-Effective Strategies in a Small Watershed within the Three Gorges Reservoir Area, China. Land. 2024; 13(6):742. https://doi.org/10.3390/land13060742
Chicago/Turabian StyleChang, Renfang, Yunqi Wang, Huifang Liu, Zhen Wang, Lei Ma, Jiancong Zhang, Junjie Li, Zhiyi Yan, Yihui Zhang, and Danqing Li. 2024. "Optimizing Non-Point Source Pollution Management: Evaluating Cost-Effective Strategies in a Small Watershed within the Three Gorges Reservoir Area, China" Land 13, no. 6: 742. https://doi.org/10.3390/land13060742
APA StyleChang, R., Wang, Y., Liu, H., Wang, Z., Ma, L., Zhang, J., Li, J., Yan, Z., Zhang, Y., & Li, D. (2024). Optimizing Non-Point Source Pollution Management: Evaluating Cost-Effective Strategies in a Small Watershed within the Three Gorges Reservoir Area, China. Land, 13(6), 742. https://doi.org/10.3390/land13060742





