Highlights
- The implementation of a Digital Soil Mapping (DSM) approach for the prediction of top soil SOC and soil texture via Sentinel-2 satellite imagery data and AI architectures.
- Innovative integration of Artificial Intelligence into the RUSLE model for the generation of finer spatial resolution maps.
- Utilization of the Soil Data Cube self-hosted custom tool to process and handle a large volume of EO data.
Abstract
The existing digital soil maps are mainly characterized by coarse spatial resolution and are not up to date; thus, they are unable to support the physical process-based models for improved predictions. The overarching objective of this work is oriented toward a data-driven approach and datacube-based tools (Soil Data Cube), leveraging Sentinel-2 imagery data, open access databases, ground truth soil data and Artificial Intelligence (AI) architectures to provide enhanced geospatial layers into the Revised Universal Soil Loss Equation (RUSLE) model, improving both the reliability and the spatial resolution of the final map. The proposed methodology was implemented in the agricultural area of the Imathia Regional Unit (northern Greece), which consists of both mountainous areas and lowlands. Enhanced soil maps of Soil Organic Carbon (SOC) and soil texture were generated at 10 m resolution through a time-series analysis of satellite data and an XGBoost (eXtrene Gradinent Boosting) model. The model was trained by 84 ground truth soil samples (collected from agricultural fields) taking into account also additional environmental covariates (including the digital elevation model and climatic data) and following a Digital Soil Mapping (DSM) approach. The enhanced layers were introduced into the RUSLE’s soil erodibility factor (K-factor), producing a soil erosion layer with high spatial resolution. Notable prediction accuracy was achieved by the AI model with 0.61 for SOC and 0.73, 0.67 and 0.63 for clay, sand, and silt, respectively. The average annual soil loss of the unit was found to be 1.76 ton/ha/yr with 6% of the total agricultural area suffering from severe erosion (>11 ton/ha/yr), which was mainly found in the mountainous border regions, showing the strong influence of the mountains in the agricultural fields. The overall methodology could strongly support regional decision making and planning and environmental policies such as the European Common Agricultural Policy (CAP) and the Sustainable Development Goals (SDGs).
1. Introduction
In the European Union (EU) alone, 70% of the soils are estimated to be at an unhealthy condition with carbon loss, erosion, land take and contamination being the major threats [1]. Soils are integral in the functioning of the Earth’s systems by enabling the provision of vital ecosystem services [2] while soil erosion, a critical global environmental issue, poses substantial challenges to sustainable land management, agricultural productivity, and ecosystem health [3,4]. Agricultural fields suffer by soil erosion with nutrient loss, increased runoff and decreased water availability to plants [5]. Thus, the quantification and spatial characterization of soil erosion rates play a pivotal role in understanding and mitigating its far-reaching socio-environmental impacts [6,7]. Traditional methods involving field-based assessments and empirical models, while informative, often encounter limitations in providing comprehensive and spatially explicit erosion estimations across diverse landscapes. To address these challenges, the integration of Earth Observation (EO) technologies and remote sensing methodologies has emerged as a promising approach, facilitating a more comprehensive, dynamic, and spatially explicit assessment of soil erosion patterns [8].
The Revised Universal Soil Loss Equation (RUSLE), a widely acclaimed empirical model, serves as a foundational tool in the field of soil erosion modeling [9]. Originally developed by Wischmeier and Smith in the late 20th century, RUSLE calculates soil loss rates by factoring in key variables encompassing rainfall erosivity, soil erodibility, slope length and steepness, vegetation cover, and conservation practices, and it is the most popular soil erosion prediction model [10]. RUSLE has been applied across diverse landscapes and terrain types, including watersheds [11,12] and lakes [13,14], mountainous [15] or hilly areas [16], and agricultural lands [17]. While RUSLE has been instrumental in estimating soil erosion rates at regional scales, its application in conjunction with EO data and remote sensing techniques offers a transformative potential to enhance its spatial resolution, accuracy, and applicability across diverse geographic and land-use settings [18,19].
The integration of EO data and remote sensing techniques with RUSLE presents an innovative pathway to overcome the limitations inherent in traditional soil erosion modeling methods. Remote sensing platforms, including satellite imagery and aerial photography, offer an unprecedented ability to capture Earth’s surface dynamics [20], allowing for the derivation of crucial input parameters for RUSLE. Variables such as land cover, topography, vegetation indices, and rainfall patterns derived from EO data empower the enhancement of RUSLE’s predictive capabilities, enabling high-resolution and spatially explicit soil erosion mapping at various scales. Most of the studies employ remote sensing products to estimate RUSLE’s C and LS-factors, which describe the crop cover and management and slope length and steepness, respectively [8]. A key factor in RUSLE is also the soil erodibility, known as the K-factor, which characterizes a soil’s inherent susceptibility to erosion caused by rainfall and runoff; different soil types display varying levels of vulnerability to water-induced erosion. This erosion susceptibility is influenced by a broad range of physical and chemical properties of the soil, including primary particle size distribution, organic matter content, soil structure, and permeability. Most studies use traditional sampling and either calculate the K-factor per each soil type in the area [11,21] or use simple geostatistics (e.g., ordinary kriging [22,23,24]) to generate maps of these properties.
In Digital Soil Mapping (DSM), multiple covariates are used to predict the soil properties, and they may be broadly categorized as follows according to the SCORPAN model [25]: soil (other or previously measured properties at a given point), climate, organisms (including land cover and natural vegetation), relief or topography, parent material, age, and space (spatial or geographic position). Relief, organisms, and climate are the three most frequently used environmental covariates with SOC and texture being amongst the most well-researched soil properties [26]. DSM has been applied at various spatial scales across the globe [27] with varying levels of accuracy and with limited studies to use this approach to improve the K-factor [28,29,30,31].
In this paper, the goal is to improve the spatial resolution of the final erosion map by providing highly detailed soil maps of SOC and soil texture, into the K-factor, using the DSM approach and by specifically relying on high-resolution Sentinel-2 EO data. In essence, two different flows are implemented where the first flow generates enhanced geospatial maps of SOC content and soil texture, while the second flow will introduce these maps as enhanced layers into the RUSLE providing improved soil loss predictions. All the aforementioned indicators have already been recognized from various official European documentation reports [32] as critical indicators for soil health as well as for their importance in several policies such as the European Green Deal, EU Common Agriculture Policy (CAP) and Sustainable Development Goals (SDGs).
2. Materials and Methods
2.1. Proposed Architecture Pipeline
The goal of the proposed architecture pipeline is to create an end-to-end framework that will generate a final soil erosion layer with high spatial resolution (10 m). For the convenience of the reader, Figure 1 illustrates the proposed pipeline separated into two different flows.
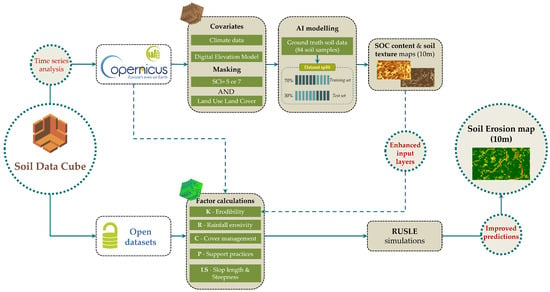
Figure 1.
The Soil Data Cube pipeline flow diagram for the generation of the soil erosion map.
To efficiently generate all the necessary layers as well as to handle and to process the large volume of EO data needed, the Soil Data Cube (SDC) was utilized. It is a self-hosted custom tool, powered by the Open Data Cube [33]; further details of the system may be found in [34,35]. Concerning the soil erosion process, the RUSLE formula was chosen, as it is among the most commonly used predictive erosion models and aligns perfectly with the objectives of this study. However, this formula has demanding input requirements. Considering the limitations of existing digital soil maps, which have a relatively coarse grid resolution and lack up-to-date data, incorporating enhanced soil spatial layers as input datasets could significantly enhance the spatial resolution and reliability of the final soil erosion simulations. Keeping this in mind, and recognizing that SOC and soil texture are primary indicators of soil health, we leveraged Sentinel-2 imagery data and AI to initially generate SOC and soil texture maps with a pixel-based spatial resolution of 10 m. Subsequently, these maps were integrated into the RUSLE model to enhance soil erosion predictions.
It should also be noted that in both processes, various datasets, primarily from open-access sources, are utilized to generate layers and calculate factors. Detailed descriptions of these processes will be provided in the following sections.
2.2. Study Area
The study area is located in the Region of Central Macedonia in northern Greece and more specifically focuses on the Regional Unit of Imathia (according to EU Nomenclature of Territorial Units for Statistics). Its central coordinates are 40°36′24.77″ N and 22°11′59.05″ E, while it encompasses a total area of 1702 km2. In general, the Regional Unit of Imathia is rich in natural resources, especially in surface water bodies, with one of the largest rivers in the country, namely the Aliakmonas River, crossing it. It has large and fertile agricultural areas of high productivity with an emphasis in intensive crops (fruit, beet, cotton, horticulture, etc.) as well as livestock.
According to the Köppen climate classification, the area is classified as Csa (hot-summer Mediterranean climate), which is also known as “typical Mediterranean climate”. Although the coastal area of the Unit is small, the proximity of the sea has a strong influence, while the mountainous areas in the west significantly contribute to the differentiation of the Unit’s meteorological and climatic characteristics in relation to the lowland part (agricultural area) in the east. The average temperature most of the year (January–September) exceeds 20 °C, but during the winter season in the mountains, the temperature often drops down to 0 °C, while in summer, the temperature reaches around 34 °C (generally the temperature varies from −11 to 30 °C). The annual amount of rain varies between 400 and 600 mm in the lowlands, while in the mountains, it is around 830 mm. The topography of the area is equally divided with the eastern side having a low altitude while the western side is dominated by mountainous areas with a maximum altitude of 2040 m (Figure 2a). Moreover, according to the FAO (Food and Agriculture Organization of the United Nations) soil classification, the four predominant soil classes are the Lithosols (I) covering 31% of the total area and the substratum of the mountainous area, while the classes of Calcaric Fluvisols (Jc) with 25%, Chromic Luvisols (Lc) with 38% and Calcaric Regosols (Rc) with 6% cover mainly the agricultural area of the Unit (Figure 2b). Furthermore and based on the Corine 2018 classification, the area is covered by croplands (56.3%), forest (27.7%), grasslands (13.30%), urban (1.74%) and industrial (0.89%) (Figure 2c), while almost the same class coverage was validated by the WorldCover classification, which is an annual product with 10 m of spatial resolution provided by the European Space Agency (ESA).
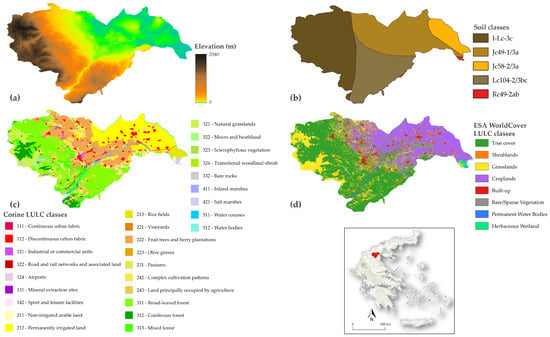
Figure 2.
Maps of the study area presenting (a) is the EU-DEM, (b) the soil classes according to FAO, (c) Corine LULC, and (d) LULC by ESA WorldCover.
2.3. Datasets
In this study, several datasets were used, including satellite imagery data, topographic data, meteorological data, land use land management data as well as ground truth soil data. The datasets will be described in detail in this section while they are referring to both modeling flows (AI and erosion).
2.3.1. Satellite Imagery Data
As far as the optical data are concerned, 427 L2A Sentinel-2 images were ingested in the SDC from 2019 to 2021 across 4 tiles and using a cloud filter percentage of <20%. The cloud coverage filter is responsible for the variance in the file counts per year. For each pixel, the following statistical moments were calculated per each of the 10 Sentinel-2 bands (i.e., without B09 and B10 that correspond to water vapour and cirrus, respectively) across the multi-temporal data: the minimum, maximum, mean, and standard deviation. Moreover, the same moments were calculated for NDVI as an additional vegetation index.
2.3.2. Topographic Data
The EU-DEM (Digital Elevation Model over Europe) was used in this study, which is a product produced by the Copernicus programme with 30m of spatial resolution. It is a hybrid product based on SRTM (Shuttle Radar Topography Mission) and ASTER GDEM data that are fused by a weighted averaging approach.
2.3.3. Meteorological Data
ERA5-Land, a product of the European Centre for Medium-Range Weather Forecasts (ECMWF), constitutes a comprehensive dataset offering insights into surface-level water and energy cycles from 1950 onward [36]. Within the ERA5-Land monthly averaged data subset, two significant variables which are instrumental in understanding atmospheric conditions and hydrological processes were extracted. These are the temperature and total precipitation. The temperature represents the air temperature at a height of 2 ms above land, sea, or inland waters. Meanwhile, total precipitation encompasses the cumulative liquid and frozen water, including rain and snow, reaching the Earth’s surface. The ERA5-Land dataset employs a temporal resolution of 1 h and originally features a spatial resolution of 9 km on a reduced Gaussian grid, which is subsequently calculated with a horizontal resolution of 0.1° × 0.1° (corresponding to native resolution of 9 km) within the Copernicus Climate Data Store. After downloading the monthly averaged data for 2007–2021, the same statistical moments (i.e., the minimum, maximum, mean, and standard deviation) were extracted for each pixel value, to represent annual trends, seasonality, and extreme values.
2.3.4. Land Use Land Cover data
The Land Use Land Cover (LULC) data utilized in this study were derived from the CORINE (Coordination of Information on the Environment) Land Cover dataset via the Copernicus Land Monitoring Service portfolio (https://land.copernicus.eu/en/products/corine-land-cover, accessed on 10 October 2023). This dataset was mainly used for the AI flow in order to filter out LULC classes that do not correspond to agricultural areas.
2.3.5. Ground Truth Soil Data
A soil sampling campaign was carried out during the year of 2020, and a total of 84 soil samples were collected. All samples were taken from agricultural fields, covering to a satisfactory extent the entire agricultural area of the Unit. Figure 3 presents the soil sample distribution in the cropland area. After the field collection, the samples were carefully stored and transferred to a chemical laboratory.
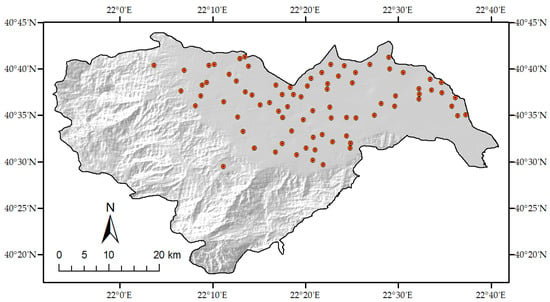
Figure 3.
The 84 soil samples distribution in the Imathia Regional Unit agricultural area.
Regarding the sample preparation and chemical analysis, possible non-soil particles such as vegetation, roots, stones, etc. were carefully removed from the original soil sample and air-dried. Furthermore, each of the samples was crushed and passed through a 2 mm sieve, and then the final chemical analysis followed. It should be highlighted that all the samples were analyzed in the same chemical laboratory under the same measurement methods and protocols in order to construct a homogenized reference dataset. Specifically, the SOC content was measured with the Walkley–Black method [37], and the soil texture was determined using the Bouyoucos hydrometer method [38].
2.4. Methodological Approach
2.4.1. Generation of SOC and Soil Texture Maps Using Artificial Intelligence Techniques
To generate the maps of SOC content and soil texture through DSM, we employed an AI-based approach [39]. As input to the model, we used data from multiple sources (Section 2.3): specifically, (i) multi-temporal Sentinel-2 satellite imagery, (ii) climate data from ERA5, and (iii) terrain data from the EU–DEM.
To ensure that the analysis was focused solely on croplands, the collected data were carefully processed by masking it with the Corine Land Cover data and with Sentinel-2’s Scene Classification Layer (SCL). Specifically, we included from Corine all classes under “2. Agricultural areas” except 2.3.1. (Pastures) and 2.4.4. (Agro-forestry areas). With respect to SCL, we included values 4 (Vegetation), 5 (Not-vegetated), and 7 (Unclassified). This masking procedure facilitated the extraction of the relevant data pertaining specifically to cropland areas, eliminating irrelevant regions from the dataset and enhancing the accuracy of subsequent analyses.
Following this step, at the specific soil sample locations, the required data for modeling SOC and texture were extracted, i.e., the values from the three aforementioned data sources. The collected datasets were meticulously organized to form a comprehensive dataset for modeling purposes. To train and evaluate the predictive models, we randomly split the data into training (70%) and independent test sets (30%). Moreover, the XGBoost algorithm [40] was employed for modeling, utilizing a 5-fold cross-validation strategy to optimize the hyperparameters of the model. We specifically developed models for SOC, clay, and sand content; silt content was calculated as the difference between 100% and the predicted values for clay and sand in order to ensure that the particle size distribution added up to 100%. Clay and sand content were chosen because these two are the most commonly modeled from EO data, and they are in the two extremes of the distribution.
XGBoost, an abbreviation for eXtreme Gradient Boosting, is a powerful machine learning algorithm widely used for regression tasks due to its exceptional performance and efficiency. It operates on the principle of boosting, sequentially combining weak learners, usually decision trees, to form a robust and accurate predictive model. One of the key strengths of XGBoost lies in its ability to handle complex relationships within data while mitigating overfitting through regularization techniques. To optimize the model, the focus was placed on three important hyperparameters:
- Learning Rate (or ): This hyperparameter controls the contribution of each tree to the final prediction. A lower learning rate makes the model more robust by shrinking the contribution of each individual tree, potentially improving generalization but requiring more trees in the ensemble. The grid space used was .
- Maximum Depth: Determines the maximum depth of each tree in the boosting process. A deeper tree can capture more complex patterns in the data but can also lead to overfitting if not properly controlled. The optimal value was selected from .
- Subsampling: The fraction of samples that are randomly selected to build each tree in the ensemble. It controls the sampling of the training dataset to prevent overfitting and improve the model’s generalization ability and was selected from .
Finally, to ascribe feature importance scores to each of the input features used and to thus identify how the input–output association is modeled, the importance metric based on gain was chosen. This represents the average gain of the feature when it is used in trees and is calculated by measuring the improvement to the model’s accuracy brought by a particular feature to each split. High values of this metric indicate that the given feature is more important for generating a prediction.
2.4.2. Generation of Soil Erosion Map Using RUSLE Formula
This section provides the methodological framework to produce the soil erosion layer based on the enhanced soil layers generated through AI architectures, open access EO data and the RUSLE formula. Figure 4 illustrates at a high level the key factors for RUSLE as well as the sources from which the necessary information were extracted and also the final inputs used on the model.
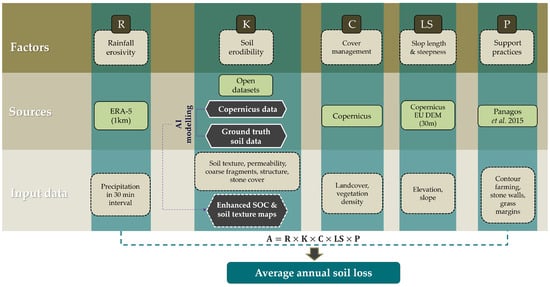
Figure 4.
RUSLE formula pipeline [41].
The annual soil loss was estimated following the RUSLE model [9]:
where A is the average annual soil loss (ton/ha/yr), R is the rainfall erosivity factor (MJ mm/ha/h/yr), K is the soil erodibility factor [(t ha h)/(ha MJ mm)], LS is the topographic factor, C is the vegetation cover factor and P is the soil conservation protection factor (dimensionless).
The following steps explain in detail the process, formulas and sources used in this study to calculate each of the RUSLE factors.
- R-factor—RainfallThe erosive force of a specific rainfall in particular location could be measured by the rainfall erosivity factor (R), and it depends on the amount and the intensity of rainfall [42,43].For the R-factor, the ERA-5 dataset was used, which offers data with 1 km of spatial resolution. As already mentioned, meteorological data from 2007 to 2021 were downloaded and the equation of Wichmeier and Smith (1978) [44] was used:where Pm is the monthly precipitation in mm and Pa is the annual precipitation in mm.
- K-factor—Soil erodibilityThe soil erodibility factor (K) is perhaps the most critical factor governing soil erosion, and it expresses the susceptibility of soils toward erosion and measures the contribution of soil types [45]. At this point, it should be highlighted that the K-factor (soil erodibility) is related mainly to soil texture and SOC (see also Equation (3)). By using a time-series analysis of Sentinel-2 imagery data and ground truth point estimations from a soil survey, an AI approach was implemented (Section 2.4.1) to generate the soil spatial explicit indicators of SOC and soil texture with higher spatial resolution than the existing soil digital soil maps. These enhanced products are used as inputs to calculate the K-factor based on the equation described in [46]:where Sand, Silt, Clay and OC are the percentage contents of sand, silt, clay and organic carbon, while SN equates to 1 − Sand/100.
- C-factor—Crop cover and managementGenerally, various formulas exist in the literature for calculating the C-factor, which often involve the use of vegetation indices derived from satellite imagery data. In this study, the C-factor is determined by taking the median value of the NDVI index, which is calculated using bands B4 and B8 from multi-temporal Sentinel-2 imagery with a spatial resolution of 10 m. This approach is applied in accordance with the equation described by van Der Knijff et al. (1999) [47], who suggest that employing this scaling approach yields better outputs compared to assuming a linear relationship:where and b are unitless parameters that determine the shape of the curve relating to the values of the NDVI and C factors.
- LS-factor—Slope length and steepnessThe RUSLE topographic factor (LS) in general is defined by the combination of the slope length factor (L) and slope steepness factor (S), describing the effect of topography and terrain morphology on the complicated soil erosion processes [48]. The aforementioned factors in most cases can be calculated by using the DEM, which was generated either from topographic maps or from satellite data [49,50], while the reliability and accuracy factors depend on the topographic dataset precision [51,52,53].In this study, the required input data in order to calculate the LS-factor are the slope values extracted from the Copernicus DEM (30 m) and the flow accumulation, downloaded from https://github.com/davidbrochart/flow_acc_3s, accessed on 18 November 2023, which is a 3 s flow accumulation derived form HydroSHEDS. After that, the equation proposed by [54] was used:where L is the slope length factor; S is the slope steepness factor; is the horizontal projected slope length (based on flow accumulation); m is a variable length-slope exponent; is a factor that varies with slope gradient; and is the slope angle.
- P-factor—Support practicesAccording to Panagos et al. (2015) [41], p-values can be derived either from image classifications using remote sensing data from previous studies or expert knowledge. As this study focuses on an agricultural area inside Europe, we decided to utilize the estimated P-factor data developed by [41] for all arable lands in Europe, which is based on the Common Agricultural Policy (CAP) implementation. This dataset has a spatial resolution of 1 km and was downloaded from the European Soil Data Centre (ESDAC) official platform (https://esdac.jrc.ec.europa.eu/themes/support-practices-factor, accessed on 2 February 2023).
2.4.3. Artificial Intelligence Model Performance Metrics
The models were validated on the independent test set using the following metrics:
- The coefficient of determination , quantifying the degree of any linear correlation between the observed and the model predicted output; it usually ranges from 0 to 1 (higher is better) and is calculated as:with being the prediction for the i-th pattern, being its ground truth value, and being the mean ground truth value across all N patterns.
- The root mean squared error (RMSE) which is calculated via:
- The ratio of performance to interquartile range (RPIQ) which takes both the prediction error and the variation of observed values into account without making assumptions about the distribution of the observed values. It is defined as the interquartile range of the observed values divided by the RMSE of prediction [55]:where is the lower quartile or the 25th percentile of the data, whereas is the upper quartile which corresponds to the 75th percentile.
3. Results
3.1. SOC and Soil Texture Analysis in the Laboratory
Table 1 provides the summary statistics of the SOC and soil texture measurements from the 84 collected soil samples. The SOC content (in g C/kg) exhibits a rather low mean value of 9.32 g C/kg and a standard deviation of 1.28, indicating that the agricultural soils of the region have low SOC concentrations. The distribution of SOC content displays a very slight positive skewness, which is indicated by the rightward shift of the mean relative to the median () and the lower quartile (), suggesting a small tail extending toward higher values.

Table 1.
Summary statistics of SOC content and soil texture measurements from the collected soil samples in the region.
Conversely, the clay content (in g/kg) indicates a mean of 244.08 g/kg with a standard deviation of 61.2. The clay content statistics portray a different distribution with a less pronounced skewness. The values of the particle size distribution suggest a soil texture that ranges from loamy soils to clayey soils. Specifically, the higher clay content within the observed range indicates a soil texture tending toward clayey, potentially influencing soil properties such as water retention and nutrient availability in the agricultural setting under consideration.
The sand content, however, is skewed to the left and has a large left tail. The bulk of the values is concentrated between 346 and 383 g/kg with the minimum standing at over three standard deviations to the left of the mean value.
3.2. AI Model Performance; Predicting SOC and Soil Texture from EO Data
3.2.1. Model Accuracy
The model accuracy of XGBoost for both soil properties in the independent test set is provided in Figure 5. The RMSE for SOC is at 0.68 g C/kg, with an of 0.61 and an RPIQ of 1.58, with the two samples that have higher SOC content being underpredicted. With respect to the clay content, the RMSE stands at 27.48 g/kg, while the is 0.73 and the RPIQ is 3.24, indicating that the model could predict this property with higher precision. Among the three soil separates (i.e., clay, silt, and sand), the results for clay are the most precise.
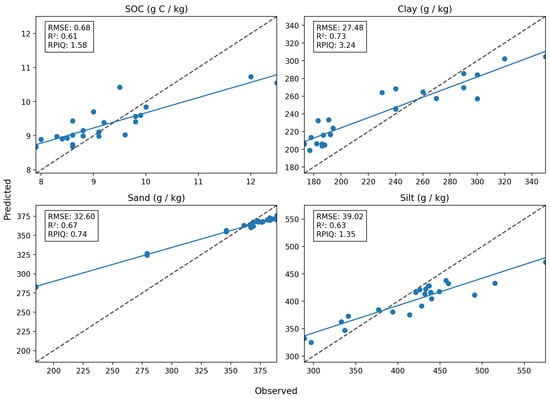
Figure 5.
Scatter plot between observed and predicted values in the independent test set for the SOC, clay and sand content using the developed AI models. The predictions for silt content are derived using a mathematical expression from the predicted sand and clay values in order for the particle size distribution to sum up to 100%. The dashed line is the 1:1 line, while the straight line is the least squares fit.
3.2.2. Feature Importance
The ascribed feature importances, calculated by considering the contribution of each feature across all trees in the model, are shown in Figure 6. Depicted are the normalized values of the importance calculated using the gain, i.e., based on the training error reduced by each split in all trees. Interestingly, the standard deviation of NDVI is considered important for both soil properties, while the climate data tend to have higher importance for clay content estimations. Conversely, the height parameter (as extracted from DEM) appears to have a limited effect on the model. All in all, the Sentinel-2 data appear to be the most important source of information.
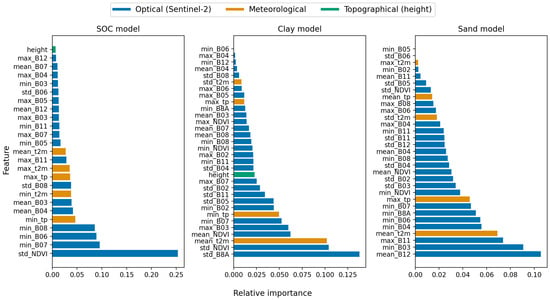
Figure 6.
Feature importance for the SOC, clay, and sand content models using the developed AI models.
3.2.3. Generating Enhanced Geospatial Layers
The geospatial layers of SOC content and soil texture were generated utilizing remote sensing data from Sentinel-2 and an AI model trained with ground truth soil data. Figure 7 presents the resulting maps of SOC and clay content, showcasing local variations in these indicators with a spatial resolution of 10 m, covering the agricultural area of the Imathia Regional Unit. The maps reveal higher SOC and clay values predominantly in the northern agricultural part of the Unit, while lower values for both indicators are observed in the western part, which is associated with the mountainous area. Moreover, it should be highlighted that areas with flat topography, corresponding to Calcaric Fluvisol soil types, exhibit higher indicator values, whereas lower values are found in regions near the mountains, which are characterized mainly by Chromic Luvisols soils.
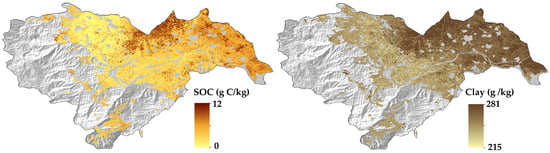
Figure 7.
Spatial distribution of SOC and clay content in the agricultural area of the Imathia Regional Unit.
3.3. Soil Erosion Assessment
3.3.1. Spatial Layers of RUSLE Factors
In the current study, the six RUSLE factors were generated through various methods, combining remote sensing data and other open datasets as well as input layers produced through AI architecture.
The C-factor was generated based on Sentinel-2 imagery data, the NDVI index and the Corine LULC dataset. The factor ranges from 0.19 to 0.31 with the highest values in the mountainous areas and lower values in the flat topography (Figure 8a).
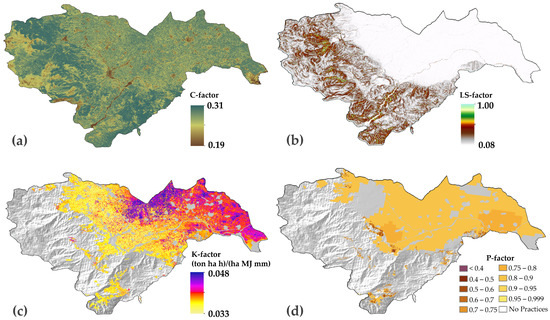
Figure 8.
Spatial distribution of the produced RUSLE factors: (a) C-factor, (b) LS-factor, (c) K-factor and (d) P-factor.
The LS-factor represented in Figure 8b describes the influence of the topographic characteristics of the area on soil erosion. The LS-factor varies from 0.08 to 1. Low LS-factor values prevailed in the region with flat topography, increasing significantly near the river borders and in the areas with high elevation.
The generated rasterized layer of the K-factor (Figure 8c) varies from 0.033 to 0.048 with a mean value of 0.038. As the soil erodibility is influenced by the soil texture, the highest values are spatially correlated with the high values of SOC and clay content corresponded mainly to Calcaric Fluvisols (Jc) soil types.
The used P-factor value shows values ranging from 0.36 to 1 (Figure 8d). The effectiveness of the technique for reducing soil erosion increases with a decreasing P-factor value. The map reveals that the highest P-factor values were in the main agricultural areas of the Unit with 0.88 being the mean value of the area.
3.3.2. Map of Average Annual Soil Erosion in the Unit
The SDC was used to produce the map of the average annual soil loss, corresponding to 2021, in the agricultural area of the Imathia Regional Unit at 10 m resolution by multiplying the six RUSLE factors. Figure 9 portrays the estimated average annual soil erosion for the Unit, and in order to provide a more comprehensive map, we utilized the erosion classification as proposed by [56] where soil erosion values are classified into low (<2), moderate (2–5), high (5–8), very high (8–11) and extremely high (>11) with the unit of ton/ha/yr for all values, while we followed the accepted limit of more than 11 ton/ha/yr in arable lands considered as severe erosion (threshold set by the Organisation for Economic Co-operation and Development) as previous studies [57,58].
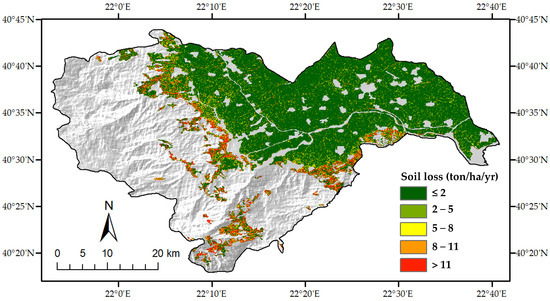
Figure 9.
Average annual soil erosion for agricultural area in Imathia Regional Unit for 2021.
The Unit has a mean average annual soil loss of about 1.76 ton/ha/yr with a range of 0 to 58 ton/ha/yr. Figure 10 illustrates the portions of the total agricultural area per erosion class (from low to extremely high). More than 80% of the total agricultural area classified as low erosion, covering 8942 km2. 6% of the total agricultural area, suffers from severe erosion. These fields are particularly located in the mountainous border areas, showing the significant influence of the mountains in the total soil loss of the Unit. Low to moderate soil loss values mainly prevail in the flat topography areas of the Unit with some exceptions across the river side banks where there are higher values (>5 ton/ha/yr) compared to the rest of the flat area.
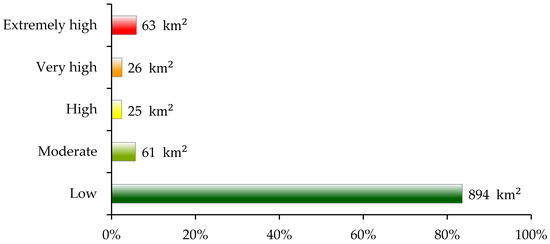
Figure 10.
Portions of total agricultural area per erosion class (from low to extremely high).
Figure 11 provides a close-up view of two distinct areas within the Unit, depicting SOC and clay content, the K-factor, and the final soil erosion map. The resolution achieved at 10 m enables discrimination even at the field level, offering a more detailed spatial distribution of the indicators.
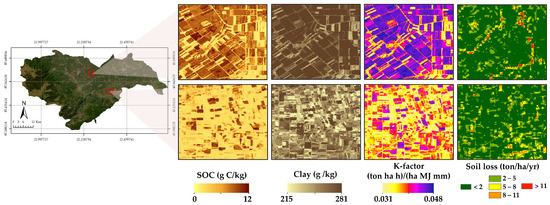
Figure 11.
SOC, clay content, K-factor and soil erosion in two different demonstration areas in the Unit.
4. Discussion
4.1. Generation of the Enhanced Soil Property Layers
4.1.1. Accuracy of the AI Models
Three separate models were developed to predict the SOC, clay, and sand content in the croplands of the Imathia region from the EO data which covered optical data from Sentinel-2, meteorological data, and topography, following the DSM approach. Silt content was estimated from the prediction values of the other two soil separates. The accuracy results were acceptable (Figure 5) with SOC content noting the lowest performance with an 0.61, while soil texture was predicted more robustly ( of 0.73, 0.67, and 0.63 for clay, sand, and silt, respectively).
Compared to other studies in the literature, it can be noted that the performance for both SOC and soil texture is similar. In a recent review on EO data-driven cropland soil monitoring that included only studies that focused on the detection of bare soil [59], it was noted that at a regional scale, the median for SOC was 0.67, while for clay, it was 0.39. Extending the comparison with other DSM studies, i.e., papers which include other covariates like in the present study, it should be highlighted that most make use of terrain variables with multiple studies using also machine learning models [60,61]. With respect to the accuracy of SOC, the value in landscape-scale assessments in Tanzania was reported as 0.60 for the 0–30 cm topsoil [62]. A value of 0.57 was noted in China for the first layer (0–5 cm) [63], while a mean of 0.58 was reported in a study of Central Nova Scotia, Canada [64]; all these values are slightly higher than the median value noted in the review of Chen et al., which was 0.49 [26]. In the same review, DSM studies focusing on topsoil texture have a median of about 0.50 with notable variance. For example, at the 0–5 cm depth in China, a performance of 0.45 for clay, 0.49 for sand, and 0.48 for silt were noted [65]. Higher values ( of 0.74, 0.69, and 0.37 for clay, sand, and silt, respectively) were reported for Brazil [66].
4.1.2. Relative Feature Importance Results
The relative feature importance scores across the three models (Figure 6) indicate that the optical and meteorological data are the most important sources of information across all soil properties, while, interestingly, the topographical parameters are ascribed low importance scores. In a 2022 review that analyzed papers employing DSM techniques to map SOC in agricultural lands at regional or broader scales, it was ascertained that across the studies, the parameters that were categorized as “influential” or “very influential” are (in order): precipitation, temperature, elevation, slope, NDVI or other vegetation indices [67]. The lower importance of the topography noted in our models, despite the excellent 30 m resolution of EU-DEM, may be due to the small differences in topography in the examined area (Figure 3), which covers the mostly flat part of the Imathia region that contains the agricultural land. This is potentially offset with the models relying more on the optical data to infer the soil properties, giving rise to higher feature importance scores to the Sentinel-2 data.
It is also noteworthy to highlight that the SOC model focuses mainly on the deviation of NDVI, which may be used to potentially identify correlations between SOC and crop type (including permanent versus perennial crops) and on the infrared portion of the spectrum using the minimum values, which may be directly correlated with SOC from bare soil signatures or indirectly noted from vegetated areas. The mean soil color is also noted as important, albeit a bit less, which is known to be correlated with SOC [68]. With respect to soil texture, the use of bands in the SWIR which is correlated with the presence of clay minerals and the increased importance of climate variables is noted. The latter are significant due to their influence on the soil formation processes, affecting the rate of weathering, decomposition of organic matter, and mineral transformations, thereby shaping soil texture composition.
Considering the drivers of SOC storage, in a meta-analysis of the strength and direction of changes in SOC stocks caused by irrigated agriculture, it was determined that climate (and in particular aridity), the irrigation method, and soil texture were strong predictors of change in SOC in irrigated agricultural systems; while the average annual precipitation and temperature, elevation, crop type, and other management practices had no or only minor importance [69]. Moreover, conservation agriculture practices such as minimum tillage, the use of cover crops in perennial systems, and direct drilling has been found to facilitate the increase of organic matter and carbon sequestration in Mediterranean rainfed agro-ecosystems [70,71]. In this study, the agronomic management practices and the type of irrigation were not recorded; considering also that data from the Land Parcel Information System are not publicly available, examining the estimation accuracy and variation of SOC within such groups was not feasible.
4.2. Spatial Distribution of the Soil Erosion
Soil erosion is one of the most important land processes with many hot spots of soil erosion (rates > 20 ton/ha/y) in the Mediterranean region [72]. Moreover, Greece is among the EU countries (including Slovenia, Italy, Austria and Spain) that suffer from severe erosion in cultivated areas (11.6% eroded) [57] and present high P-factor values, which is also considered the most uncertain RUSLE factor [73]. The importance of the K-factor in the RUSLE is indisputable, and this work offers an approach to improve the spatial resolution and the reliability of this layer through DSM techniques and ground truth soil data. To our knowledge, a limited number of studies have used remote sensing and DSM approaches to spatially predict the K-factor. Thomas et al. in 2018 [28] implemented DSM processes using a Random Forest (RF) model trained by 356 in situ soil samples, covering three different catchments in Australia, and generated a K-factor map with 90 m resolution. Taghizadeh et al. (2019) [30] produced a K-factor layer with 30 m resolution, at the watershed scale in the West Corn Belt (WCB) in the USA, by using DSM techniques. An Artificial Neural Network (ANN) was trained with 200 K-factor soil samples, achieving an value of 0.71. Recently, Jahandideh et al. (2021) [31] used Landsat-8 satellite imagery data and several environmental covariates to produce a K-factor map with 30 m resolution in two adjacent sites in the Behbahan region in Iran. Here, 150 soil samples were used to train two models: RF and ANN. Both models resulted in good and unbiased K-factor estimates.
Based on our results, our case study area is generally characterized by low to moderate erosion levels. Nevertheless, it serves as an excellent example as it encompasses both flat and mountainous terrain simultaneously, highlighting the substantial impact of elevated lands on agricultural fields. The areas with lower erosion align with regions where SOC and soil texture exhibit higher values along with corresponding K-factor values.
Due to the lack of soil erosion ground truth measurements, we examined the correlation with existing generated results from a previous study that was based on, to some extent, a similar approach that is considerable reliable and is freely available. Thus, our mean value for the area (1.76 ton/ha/yr) approaches, but falls short, of the mean value of 1.18 ton/ha/yr provided by the erosion product from Panagos et al. (2015) [74] (available upon request via the https://esdac.jrc.ec.europa.eu/content/soil-erosion-water-rusle2015, accessed 20 October 2023). The difference between the two products can be considered reasonable for a variety of reasons: (i) the products refer to different simulation years (2016 and 2021), (ii) the use of different ground truth soil data for organic carbon and soil texture (LUCAS, study’s sampling campaign), (iii) the use of different formulas and methods to calculate the six different RUSLE factors as well as (iv) the uncertainties included on the methods. Also, again, according to Panagos et al. (2015) [74] for the study area, the percentage difference in soil erosion from 2010 to 2016 was estimated to be between 3 and 5%, verifying in this way the findings of this research for increasing erosion in the Unit.
In addition, having in mind that the main difference of our soil erosion map with other products is the spatial resolution, the ready to use product by [74] was re-selected, and an additional simulation was carried out using the MODIS satellite data for comparison. The produced soil erosion product by [74] has 100 m resolution and used all the available LUCAS points in order to calculate the K-factor, while for the new simulation, we used the SOC and soil texture layers from the SoilGrids (https://soilgrids.org/, accessed on 11 October 2023) platform with 250 m resolution. Figure 12 presents the three different products following the same classification criteria (from low to extremely high). As presented, there is a correlation regarding the soil erosion values (with differences for various reasons, mentioned above); however, subsequent differences occurred in the spatial distribution of the soil layer and in the maps’ spatial resolution. All three products present advantages and disadvantages; however, regarding the spatial resolution of the layers and considering also that about two-thirds (63.8%) of the EU’s agricultural area consists of parcels less than 5 ha in size, it is a necessity to improve the spatial resolution of the maps [35], and the current work findings offer an alternative approach to this dimension.
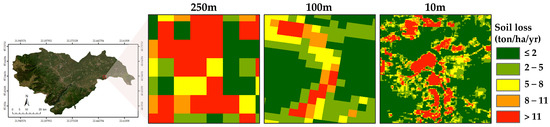
Figure 12.
Soil erosion maps produced with different spatial resolution.
4.3. Limitations and Future Perspectives
Significant results were obtained during the current work; however, there are certain limitations that should be addressed. This research focused only on agricultural areas excluding the permanent vegetated classes such as forests, grasslands, etc. Further research could focus on using DSM approaches for the generation of improved soil layers (e.g., SOC and clay content) for the areas with permanent vegetation as well as exploring alternative formulas for the K-factor calculation. Moreover, it should be pointed out that except for the K-factor, which was produced with 10 m resolution, the other input data in the RUSLE have a resolution of more than 30 m, creating a future need to use improved spatial products for these data as well. Additionally, while this research provides pixel-level results for soil erosion, the European Integrated Administration and Control System (IACS) could be also used in future research to provide parcel-level estimations, supporting in that way policies that demand this resolution such as the CAP. Furthermore, inevitably, the AI soil products of SOC and soil texture, and soil erosion as well, are vulnerable to uncertainties for various reasons; therefore, the overall estimation of the uncertainty level should be investigated and estimated in the future. Also, due to the recognized importance of the soil health indicators SOC, texture, and erosion, a potential combination of them to construct a land degradation index could also be explored [75], while the overall methodology at the end could be integrated as part of a wider soil digital twin framework [76]. It should be also highlighted that the current work did not make an in-depth analysis per the RUSLE factor, as the pros and cons of the model has already been described in previous studies [18,77].
5. Conclusions
This study delved into the crucial realm of soil erosion assessment, emphasizing the significance of finer spatial resolution and the innovative integration of Artificial Intelligence within the RUSLE. We successfully generated a soil erosion map for the Imathia Regional Unit in northern Greece with special focus on the agricultural area. A significant novelty of this work lies in the utilization of SOC and texture maps at an unprecedented 10 m resolution, which influences the K-factor. These were derived through a DSM approach incorporating DEM, climate data, and Sentinel-2 imagery through the Soil Data Cube. Specifically, the learning algorithm was XGBoost, which indicated a fair accuracy, with the generated high-resolution maps providing a detailed spatial distribution of soil erosion indicators. The resulting maps were rigorously compared with existing products, showcasing the effectiveness and innovation brought forth by the integration of fine-resolution SOC and texture data into the soil erosion modeling process. Moreover, our findings indicate that the complexity of the topography in the study area highlights the limitations of coarse spatial resolution products in identifying the spatial distribution of soil loss in sensitive and vulnerable areas, such as near stream networks where eroded soils are present.
As we navigate an era of heightened environmental awareness and the imperative for sustainable land use practices, our work underscores the pivotal role of advanced technologies in shaping the future of soil erosion research. The integration of finer spatial resolution products and the spatially explicit nature of our AI-driven RUSLE enables stakeholders to prioritize intervention strategies, allocate resources judiciously, and implement sustainable land management practices with unprecedented accuracy.
Author Contributions
Conceptualization, N.S. and E.K.; methodology, N.S. and N.L.T.; software, N.S. and N.L.T.; validation, E.K. and G.C.Z.; formal analysis, E.K.; investigation, N.S. and N.L.T.; data curation, N.S. and N.L.T.; writing—original draft preparation, N.S.; writing—review and editing, N.S., N.L.T. and E.K.; visualization, N.S. and N.L.T.; supervision, G.C.Z.; project administration, G.C.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This paper is supported by the European Union’s Caroline Herschel Framework Partnership Agreement on Copernicus User Uptake under grant agreement contract No. 8-SI2.829837 and the development of applications for users supporting the sector information system in the field of Climate Change Service under the partnership framework agreement of the Caroline Hershel Program (acronym: FP CUP Downstream Applications).
Data Availability Statement
Data are available in publicly accessible repositories from the links provided in the paper.
Acknowledgments
The authors would like to thank the European Commission and specifically the European Soil Data Centre (ESDAC) and Joint Research Centre (JRC) who made available the soil erosion map (100 m resolution) in order to draw conclusions.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AI | Artificial Intelligence |
| CAP | Common Agricultural Policy |
| DSM | Digital Soil Mapping |
| EO | Earth Observation |
| EU | European Union |
| FAO | Food and Agriculture Organization of the United Nations |
| LUCAS | Land Use and Coverage Frame Survey |
| LULC | Land Use Land Cover |
| IACS | Integrated Administration and Control System |
| ODC | Open Data Cube |
| NDVI | Normalized Difference Vegetation Index |
| RF | Random Forest |
| RPIQ | Ratio of Performance to Interquartile Range |
| RMSE | Root Mean Square Error |
| RUSLE | Revised Universal Soil Loss Equation |
| SCL | Scene Classification |
| SDC | Soil Data Cube |
| SOC | Soil Organic Carbon |
| SWIR | Shortwave Infrared |
| XGBoost | eXtreme Gradient Boosting |
References
- Panagos, P.; Montanarella, L.; Barbero, M.; Schneegans, A.; Aguglia, L.; Jones, A. Soil priorities in the European Union. Geoderma Reg. 2022, 29, e00510. [Google Scholar] [CrossRef]
- Keesstra, S.D.; Bouma, J.; Wallinga, J.; Tittonell, P.; Smith, P.; Cerdà, A.; Montanarella, L.; Quinton, J.N.; Pachepsky, Y.; van der Putten, W.H.; et al. The significance of soils and soil science towards realization of the United Nations Sustainable Development Goals. Soil 2016, 2, 111–128. [Google Scholar] [CrossRef]
- Poesen, J. Soil erosion in the Anthropocene: Research needs. Earth Surf. Process. Landforms 2017, 43, 64–84. [Google Scholar] [CrossRef]
- Wuepper, D.; Borrelli, P.; Finger, R. Countries and the global rate of soil erosion. Nat. Sustain. 2019, 3, 51–55. [Google Scholar] [CrossRef]
- Ganasri, B.; Ramesh, H. Assessment of soil erosion by RUSLE model using remote sensing and GIS—A case study of Nethravathi Basin. Geosci. Front. 2016, 7, 953–961. [Google Scholar] [CrossRef]
- Pimentel, D.; Burgess, M. Soil Erosion Threatens Food Production. Agriculture 2013, 3, 443–463. [Google Scholar] [CrossRef]
- Amundson, R.; Berhe, A.A.; Hopmans, J.W.; Olson, C.; Sztein, A.E.; Sparks, D.L. Soil and human security in the 21st century. Science 2015, 348, 1261071. [Google Scholar] [CrossRef] [PubMed]
- Phinzi, K.; Ngetar, N.S. The assessment of water-borne erosion at catchment level using GIS-based RUSLE and remote sensing: A review. Int. Soil Water Conserv. Res. 2019, 7, 27–46. [Google Scholar] [CrossRef]
- Renard, K.G.; Foster, G.R.; Weesies, G.A.; McCool, D.; Yoder, D. Predicting Soil Erosion by Water: A Guide to Conservation Planning with the Revised Universal Soil Loss Equation (RUSLE); Agriculture Handbook No. 537; US Department of Agriculture, Agricultural Research Service: Washington, DC, USA, 1997.
- Borrelli, P.; Alewell, C.; Alvarez, P.; Anache, J.A.A.; Baartman, J.; Ballabio, C.; Bezak, N.; Biddoccu, M.; Cerdà, A.; Chalise, D.; et al. Soil erosion modelling: A global review and statistical analysis. Sci. Total Environ. 2021, 780, 146494. [Google Scholar] [CrossRef] [PubMed]
- Weslati, O.; Serbaji, M.M. Spatial assessment of soil erosion by water using RUSLE model, remote sensing and GIS: A case study of Mellegue Watershed, Algeria–Tunisia. Environ. Monit. Assess. 2023, 196, 14. [Google Scholar] [CrossRef] [PubMed]
- Hagos, Y.G.; Andualem, T.G.; Sebhat, M.Y.; Bedaso, Z.K.; Teshome, F.T.; Bayabil, H.K.; Kebede, E.A.; Demeke, G.G.; Mitiku, A.B.; Ayele, W.T.; et al. Soil erosion estimation and erosion risk area prioritization using GIS-based RUSLE model and identification of conservation strategies in Jejebe watershed, Southwestern Ethiopia. Environ. Monit. Assess. 2023, 195, 1501. [Google Scholar] [CrossRef]
- Behera, D.K.; Jamal, S.; Ahmad, W.S.; Taqi, M.; Kumar, R. Estimation of Soil Erosion Using RUSLE Model and GIS Tools: A Study of Chilika Lake, Odisha. J. Geol. Soc. India 2023, 99, 406–414. [Google Scholar] [CrossRef]
- Ejaz, N.; Elhag, M.; Bahrawi, J.; Zhang, L.; Gabriel, H.F.; Rahman, K.U. Soil Erosion Modelling and Accumulation Using RUSLE and Remote Sensing Techniques: Case Study Wadi Baysh, Kingdom of Saudi Arabia. Sustainability 2023, 15, 3218. [Google Scholar] [CrossRef]
- Romshoo, S.A.; Yousuf, A.; Altaf, S.; Amin, M. Evaluation of Various DEMs for Quantifying Soil Erosion Under Changing Land Use and Land Cover in the Himalaya. Front. Earth Sci. 2021, 9, 782128. [Google Scholar] [CrossRef]
- Al Shoumik, B.A.; Khan, M.Z.; Islam, M.S. Soil erosion estimation by RUSLE model using GIS and remote sensing techniques: A case study of the tertiary hilly regions in Bangladesh from 2017 to 2021. Environ. Monit. Assess. 2023, 195, 1096. [Google Scholar] [CrossRef] [PubMed]
- Abdi, B.; Kolo, K.; Shahabi, H. Soil erosion and degradation assessment integrating multi-parametric methods of RUSLE model, RS, and GIS in the Shaqlawa agricultural area, Kurdistan Region, Iraq. Environ. Monit. Assess. 2023, 195, 1149. [Google Scholar] [CrossRef] [PubMed]
- Benavidez, R.; Jackson, B.; Maxwell, D.; Norton, K. A review of the (Revised) Universal Soil Loss Equation ((R)USLE): With a view to increasing its global applicability and improving soil loss estimates. Hydrol. Earth Syst. Sci. 2018, 22, 6059–6086. [Google Scholar] [CrossRef]
- Ustin, S.L.; Middleton, E.M. Current and near-term advances in Earth observation for ecological applications. Ecol. Process. 2021, 10, 1. [Google Scholar] [CrossRef]
- Di, L.; Yu, E. Remote Sensing. In Remote Sensing Big Data; Springer International Publishing: Berlin/Heidelberg, Germany, 2023; pp. 17–43. [Google Scholar] [CrossRef]
- Jodhani, K.H.; Patel, D.; Madhavan, N.; Singh, S.K. Soil Erosion Assessment by RUSLE, Google Earth Engine, and Geospatial Techniques over Rel River Watershed, Gujarat, India. Water Conserv. Sci. Eng. 2023, 8, 49. [Google Scholar] [CrossRef]
- Ferreira, V.; Panagopoulos, T. Seasonality of Soil Erosion Under Mediterranean Conditions at the Alqueva Dam Watershed. Environ. Manag. 2014, 54, 67–83. [Google Scholar] [CrossRef] [PubMed]
- Othmani, O.; Khanchoul, K.; Boubehziz, S.; Bouguerra, H.; Benslama, A.; Navarro-Pedreño, J. Spatial Variability of Soil Erodibility at the Rhirane Catchment Using Geostatistical Analysis. Soil Syst. 2023, 7, 32. [Google Scholar] [CrossRef]
- Lin, B.S.; Chen, C.K.; Thomas, K.; Hsu, C.K.; Ho, H.C. Improvement of the K-Factor of USLE and Soil Erosion Estimation in Shihmen Reservoir Watershed. Sustainability 2019, 11, 355. [Google Scholar] [CrossRef]
- McBratney, A.; Mendonça Santos, M.; Minasny, B. On digital soil mapping. Geoderma 2003, 117, 3–52. [Google Scholar] [CrossRef]
- Chen, S.; Arrouays, D.; Mulder, V.L.; Poggio, L.; Minasny, B.; Roudier, P.; Libohova, Z.; Lagacherie, P.; Shi, Z.; Hannam, J.; et al. Digital mapping of GlobalSoilMap soil properties at a broad scale: A review. Geoderma 2022, 409, 115567. [Google Scholar] [CrossRef]
- Arrouays, D.; Lagacherie, P.; Hartemink, A.E. Digital soil mapping across the globe. Geoderma Reg. 2017, 9, 1–4. [Google Scholar] [CrossRef]
- Thomas, M.; Brough, D.; Bui, E.; Harms, B.; Hill, J.; Holmes, K.; Morrison, D.; Philip, S.; Searle, R.; Smolinski, H.; et al. Soil erodibility DSM data of the Fitzroy catchment WA, Darwin catchments and Mitchell catchment Qld generated by the Northern Australia Water Resource Assessment. CSIRO Data Collection 2018. [Google Scholar] [CrossRef]
- Yang, X.; Gray, J.; Chapman, G.; Zhu, Q.; Tulau, M.; McInnes-Clarke, S. Digital mapping of soil erodibility for water erosion in New South Wales, Australia. Soil Res. 2018, 56, 158. [Google Scholar] [CrossRef]
- Taghizadeh-Mehrjardi, R.; Bawa, A.; Kumar, S.; Zeraatpisheh, M.; Amirian-Chakan, A.; Akbarzadeh, A. Soil Erosion Spatial Prediction using Digital Soil Mapping and RUSLE methods for Big Sioux River Watershed. Soil Syst. 2019, 3, 43. [Google Scholar] [CrossRef]
- Jahandideh, M.; Amirian-Chakan, A.; Faraji, M.; Jafarizadeh, M. Soil Erodibility and its Spatial Variation in Areas under Erosion Control Measures in Behbahan Region. Appl. Soil Res. 2021, 9, 73–88. [Google Scholar]
- European Environment Agency. Soil Monitoring in Europe—Indicators and Thresholds for Soil Health Assessments. 2023. Available online: https://www.eea.europa.eu/publications/soil-monitoring-in-europe (accessed on 15 October 2023).
- Killough, B. Overview of the Open Data Cube Initiative. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 8629–8632. [Google Scholar] [CrossRef]
- Kalopesa, E.; Tsakiridis, N.L.; Boletos, G.; Tziolas, N.; Zalidis, G.C. The Greek Soil Data Cube in support of generating soil-related Analysis Ready Data. In Proceedings of the IGARSS 2023–2023 IEEE International Geoscience and Remote Sensing Symposium, Pasadena, CA, USA, 16–21 July 2023; pp. 5363–5366. [Google Scholar]
- Samarinas, N.; Tsakiridis, N.L.; Kokkas, S.; Kalopesa, E.; Zalidis, G.C. Soil Data Cube and Artificial Intelligence Techniques for Generating National-Scale Topsoil Thematic Maps: A Case Study in Lithuanian Croplands. Remote Sens. 2023, 15, 5304. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Walkley, A.; Black, I.A. An Examination of the Degtjareff Method for Determining Soil Organic Matter, and a Proposed Modification of the Chromic Acid Titration Method. Soil Sci. 1934, 37, 29–38. [Google Scholar] [CrossRef]
- Bouyoucos, G.J. Hydrometer Method Improved for Making Particle Size Analyses of Soils1. Agron. J. 1962, 54, 464–465. [Google Scholar] [CrossRef]
- Wadoux, A.M.C.; Minasny, B.; McBratney, A.B. Machine learning for digital soil mapping: Applications, challenges and suggested solutions. Earth-Sci. Rev. 2020, 210, 103359. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the KDD’16: Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Panagos, P.; Borrelli, P.; Meusburger, K.; van der Zanden, E.H.; Poesen, J.; Alewell, C. Modelling the effect of support practices (P-factor) on the reduction of soil erosion by water at European scale. Environ. Sci. Policy 2015, 51, 23–34. [Google Scholar] [CrossRef]
- Lee, J.; Lee, S.; Hong, J.; Lee, D.; Bae, J.H.; Yang, J.E.; Kim, J.; Lim, K.J. Evaluation of Rainfall Erosivity Factor Estimation Using Machine and Deep Learning Models. Water 2021, 13, 382. [Google Scholar] [CrossRef]
- Li, H.; Chen, J.; Jiang, L. Elevated critical micelle concentration in soil–water system and its implication on PAH removal and surfactant selecting. Environ. Earth Sci. 2013, 71, 3991–3998. [Google Scholar] [CrossRef]
- Wischmeier, W.H.; Smith, D.D. Predicting Rainfall Erosion Losses a Guide to Conservation Planning; Agriculture Handbook No. 537; US Department of Agriculture: Washington, DC, USA, 1978.
- Sharma, A. Integrating terrain and vegetation indices for identifying potential soil erosion risk area. Geo-Spat. Inf. Sci. 2010, 13, 201–209. [Google Scholar] [CrossRef]
- Sharply, A.N.; Williams, J.R. EPIC—Erosion/Productivity Impact Calculator 1. Model Documentation; United 257 States Department of Agriculture Technical Bulletin Number 1768, 258 USDA-ARS; US Department of Agriculture: Washington, DC, USA, 1990.
- Van der Knijff, J.; Jones, R.; Montanarella, L. Soil Erosion Risk: Assessment in Europe. 2000. Available online: https://esdac.jrc.ec.europa.eu/ESDB_Archive/pesera/pesera_cd/pdf/ereurnew2.pdf (accessed on 18 November 2023).
- Lu, S.; Liu, B.; Hu, Y.; Fu, S.; Cao, Q.; Shi, Y.; Huang, T. Soil erosion topographic factor (LS): Accuracy calculated from different data sources. CATENA 2020, 187, 104334. [Google Scholar] [CrossRef]
- Hickey, R. Slope Angle and Slope Length Solutions for GIS. Cartography 2000, 29, 1–8. [Google Scholar] [CrossRef]
- Van Remortel, R.; Maichle, R.; Hickey, R. Computing the LS factor for the Revised Universal Soil Loss Equation through array-based slope processing of digital elevation data using a C++ executable. Comput. Geosci. 2004, 30, 1043–1053. [Google Scholar] [CrossRef]
- Wang, C.; Yang, Q.; Guo, W.; Liu, H.; Jupp, D.; Li, R.; Zhang, H. Influence of resolution on slope in areas with different topographic characteristics. Comput. Geosci. 2012, 41, 156–168. [Google Scholar] [CrossRef]
- Wolock, D.M.; McCabe, G.J. Differences in topographic characteristics computed from 100- and 1000-m resolution digital elevation model data. Hydrol. Process. 2000, 14, 987–1002. [Google Scholar] [CrossRef]
- Wu, S.; Li, J.; Huang, G. An evaluation of grid size uncertainty in empirical soil loss modeling with digital elevation models. Environ. Model. Assess. 2005, 10, 33–42. [Google Scholar] [CrossRef]
- McCool, D.K.; Brown, L.C.; Foster, G.R.; Mutchler, C.K.; Meyer, L.D. Revised Slope Steepness Factor for the Universal Soil Loss Equation. Trans. ASAE 1987, 30, 1387–1396. [Google Scholar] [CrossRef]
- Bellon-Maurel, V.; Fernandez-Ahumada, E.; Palagos, B.; Roger, J.M.; McBratney, A. Critical review of chemometric indicators commonly used for assessing the quality of the prediction of soil attributes by NIR spectroscopy. TrAC Trends Anal. Chem. 2010, 29, 1073–1081. [Google Scholar] [CrossRef]
- Parris, K. Environmental indicators for agriculture: Overview in OECD countries. In Environmental Indicators and Agricultural Policy; CABI: Oxford, UK, 1999. [Google Scholar]
- Panagos, P.; Ballabio, C.; Poesen, J.; Lugato, E.; Scarpa, S.; Montanarella, L.; Borrelli, P. A Soil Erosion Indicator for Supporting Agricultural, Environmental and Climate Policies in the European Union. Remote Sens. 2020, 12, 1365. [Google Scholar] [CrossRef]
- Schmaltz, E.M.; Krammer, C.; Dersch, G.; Weinberger, C.; Kuderna, M.; Strauss, P. The effectiveness of soil erosion measures for cropland in the Austrian Agri-environmental Programme: A national approach using local data. Agric. Ecosyst. Environ. 2023, 355, 108590. [Google Scholar] [CrossRef]
- Tziolas, N.; Tsakiridis, N.; Chabrillat, S.; Demattê, J.A.M.; Ben-Dor, E.; Gholizadeh, A.; Zalidis, G.; van Wesemael, B. Earth Observation Data-Driven Cropland Soil Monitoring: A Review. Remote Sens. 2021, 13, 4439. [Google Scholar] [CrossRef]
- Pouladi, N.; Gholizadeh, A.; Khosravi, V.; Borůvka, L. Digital mapping of soil organic carbon using remote sensing data: A systematic review. CATENA 2023, 232, 107409. [Google Scholar] [CrossRef]
- Folorunso, O.; Ojo, O.; Busari, M.; Adebayo, M.; Joshua, A.; Folorunso, D.; Ugwunna, C.O.; Olabanjo, O.; Olabanjo, O. Exploring Machine Learning Models for Soil Nutrient Properties Prediction: A Systematic Review. Big Data Cogn. Comput. 2023, 7, 113. [Google Scholar] [CrossRef]
- Kempen, B.; Dalsgaard, S.; Kaaya, A.K.; Chamuya, N.; Ruipérez-González, M.; Pekkarinen, A.; Walsh, M.G. Mapping topsoil organic carbon concentrations and stocks for Tanzania. Geoderma 2019, 337, 164–180. [Google Scholar] [CrossRef]
- Song, X.D.; Wu, H.Y.; Ju, B.; Liu, F.; Yang, F.; Li, D.C.; Zhao, Y.G.; Yang, J.L.; Zhang, G.L. Pedoclimatic zone-based three-dimensional soil organic carbon mapping in China. Geoderma 2020, 363, 114145. [Google Scholar] [CrossRef]
- Paul, S.S.; Heung, B.; Lynch, D.H. Modeling of total and active organic carbon dynamics in agricultural soil using digital soil mapping: A case study from Central Nova Scotia. Can. J. Soil Sci. 2023, 103, 64–80. [Google Scholar] [CrossRef]
- Liu, F.; Zhang, G.L.; Song, X.; Li, D.; Zhao, Y.; Yang, J.; Wu, H.; Yang, F. High-resolution and three-dimensional mapping of soil texture of China. Geoderma 2020, 361, 114061. [Google Scholar] [CrossRef]
- Safanelli, J.L.; Demattê, J.A.; Chabrillat, S.; Poppiel, R.R.; Rizzo, R.; Dotto, A.C.; Silvero, N.E.; de S. Mendes, W.; Bonfatti, B.R.; Ruiz, L.F.; et al. Leveraging the application of Earth observation data for mapping cropland soils in Brazil. Geoderma 2021, 396, 115042. [Google Scholar] [CrossRef]
- Xia, Y.; McSweeney, K.; Wander, M.M. Digital Mapping of Agricultural Soil Organic Carbon Using Soil Forming Factors: A Review of Current Efforts at the Regional and National Scales. Front. Soil Sci. 2022, 2, 890437. [Google Scholar] [CrossRef]
- Angelopoulou, T.; Tziolas, N.; Balafoutis, A.; Zalidis, G.; Bochtis, D. Remote Sensing Techniques for Soil Organic Carbon Estimation: A Review. Remote Sens. 2019, 11, 676. [Google Scholar] [CrossRef]
- Emde, D.; Hannam, K.D.; Most, I.; Nelson, L.M.; Jones, M.D. Soil organic carbon in irrigated agricultural systems: A meta-analysis. Glob. Chang. Biol. 2021, 27, 3898–3910. [Google Scholar] [CrossRef] [PubMed]
- García-Tejero, I.F.; Carbonell, R.; Ordoñez, R.; Torres, F.P.; Durán Zuazo, V.H. Conservation Agriculture Practices to Improve the Soil Water Management and Soil Carbon Storage in Mediterranean Rainfed Agro-Ecosystems. In Soil Health Restoration and Management; Springer: Singapore, 2019; pp. 203–230. [Google Scholar] [CrossRef]
- Francaviglia, R.; Almagro, M.; Vicente-Vicente, J.L. Conservation Agriculture and Soil Organic Carbon: Principles, Processes, Practices and Policy Options. Soil Syst. 2023, 7, 17. [Google Scholar] [CrossRef]
- Borrelli, P.; Robinson, D.A.; Fleischer, L.R.; Lugato, E.; Ballabio, C.; Alewell, C.; Meusburger, K.; Modugno, S.; Schütt, B.; Ferro, V.; et al. An assessment of the global impact of 21st century land use change on soil erosion. Nat. Commun. 2017, 8, 2013. [Google Scholar] [CrossRef] [PubMed]
- Morgan, R.P.C. Soil Erosion and Conservation; Longman: London, UK; New York, NY, USA, 1995. [Google Scholar]
- Panagos, P.; Borrelli, P.; Poesen, J.; Ballabio, C.; Lugato, E.; Meusburger, K.; Montanarella, L.; Alewell, C. The new assessment of soil loss by water erosion in Europe. Environ. Sci. Policy 2015, 54, 438–447. [Google Scholar] [CrossRef]
- Samarinas, N.; Tziolas, N.; Zalidis, G. Assess land degradation status based on Earth Observation driven proxy indicator. In Proceedings of the Copernicus Meetings EGU General Assembly 2023, Vienna, Austria, 24–28 April 2023. [Google Scholar] [CrossRef]
- Tsakiridis, N.L.; Samarinas, N.; Kalopesa, E.; Zalidis, G.C. Cognitive Soil Digital Twin for Monitoring the Soil Ecosystem: A Conceptual Framework. Soil Syst. 2023, 7, 88. [Google Scholar] [CrossRef]
- Alewell, C.; Borrelli, P.; Meusburger, K.; Panagos, P. Using the USLE: Chances, challenges and limitations of soil erosion modelling. Int. Soil Water Conserv. Res. 2019, 7, 203–225. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).