1. Introduction
As a crucial factor contributing to global change, researchers have extensively studied Land Use and Land Cover Change (LUCC) in terms of its development and evolution, driving mechanisms, distribution patterns, and simulation and reconstruction [
1,
2,
3]. Recent advancements in remote sensing satellites have yielded a plethora of high-precision data for LUCC research [
4,
5,
6,
7]. However, these satellite observations are limited in terms of the monitoring period. To overcome the scarcity of remote sensing data for long-term land use studies, the model simulation method emerges as a crucial approach [
8]. For instance, scholars have utilized various models, including PBM, CLUE, and REVEALS, to reconstruct historical land use patterns [
9,
10,
11]. Additionally, researchers have been adapting classical models by adjusting parameters and variables to develop region-specific land use models [
12,
13,
14]. Recently, some scholars have incorporated rules that capture human land use behavior into cellular automata models, resulting in more precise reconstructions of past land use distributions [
15,
16].
Compared to the models mentioned above, the Binary Logistic Regression (BLR) model, known for its simplicity and fewer parameter constraints, has been extensively employed in land use reconstruction. Peppler et al. employed the BLR model to simulate land use in northern Hesse, Germany, incorporating physical factors and highlighting their role in determining the distribution pattern of land use in this region [
17]. Similarly, Matasov et al. utilized socioeconomic statistics, historical maps, satellite images, and the BLR model to reconstruct the land use cover of the province of Ryazen, Russia, from 1770 to 2010 [
18]. In China, Bai et al. utilized a BLR model to generate a probability map depicting the distribution of various land types in Dulbert Autonomous County of Inner Mongolia over the past century [
19]. Their study considered both natural and socio-economic factors. In a similar manner, Chen et al. employed the same model to reconstruct the distribution of cultivated land during the late Neolithic period in the North China Plain using factors such as elevation, slope, soil, rivers, and proximity to residential areas [
20]. Moreover, Yang et al. achieved a more precise reconstruction of the distribution of cultivated land in the Lower Mississippi Alluvial Valley from 1850 to 2018 [
21]. This study showed that using machine learning algorithms and county-level census data has higher accuracy than relying solely on state-level population data.
Most prehistoric or historic cultivated reconstructions obeyed the following steps [
22,
23]: Firstly, a model is used to establish a quantitative relationship between modern populations and land use, ensuring high prediction accuracy. Next, the model parameters are also applied in conjunction with spatial analysis tools such as GIS to recreate the spatial and temporal distribution patterns of cultivated land in previous periods. In China, most studies on this topic have validated the model using land use data from the 1980s. The accuracy of predicting the distribution of cultivated land in the 1980s is frequently regarded as a significant criterion for assessing their suitability in predicting prehistoric or historic periods. However, when we attempted to apply the same method to simulate the year 1985′s cultivated land in the Yulin region of northern China, we encountered a low accuracy rate with the model. Peppler argued that data quality, parameter selection, and random errors can affect the predictive accuracy of a logistic regression model. Additionally, the absence of human factors may contribute to the poor predictive accuracy of land use simulations over the past 2000 years. However, there are limited studies analyzing the factors influencing the prediction accuracy of the model.
Additionally, previous research on cultivated land reconstruction in China has mainly focused on traditional farming areas in the east, with less attention given to the farming–pastoral transitional zone. Archaeological evidence suggests that advanced agriculture was already present in the local area during the Yangshao period (ca. 5000-4900 BCE) [
24]. The Longshan culture (ca. 3000-2000/1900 BCE) developed a diversified subsistence strategy, with agriculture as the main focus and animal husbandry as a supplement [
25]. Farmland is the foundation and product of agricultural activities; however, there is currently no clear understanding of the distribution pattern of cultivated land in the region. This ecotone exhibits stronger heterogeneity in various natural factors compared to the plain area in eastern China. At the same time, the landscape pattern of the farming–pastoral ecotone is highly sensitive to both natural and human-induced changes. Some scholars argued that climatic fluctuations, such as precipitation, directly impact the development of arable land in the region [
26]. However, other studies suggested that population pressure, policies, and technological advancements are the main drivers behind the recurrent expansion and contraction of arable land [
27]. In reality, the spatial and temporal changes in the agricultural and pastoral landscape pattern in the region were a combined response to climate change and human activities [
28,
29,
30]. Therefore, this study aims to collect relevant physical and social factors as independent variables to build a BLR model. And the potential distribution of arable land in the Yulin area for the time period of 1985 was reconstructed. This reconstructed result was compared with the actual land use data to explore the factors that may affect the prediction accuracy of the model at a certain scale. In order to minimize the influence of human activity on validating farmland data, this paper presents a method for batch-modifying raster data values to improve the accuracy of prediction evaluation. The findings of this research will serve as a reference for accurately simulating and predicting the spatial distribution patterns of cultivated land in this region, whether historical or prehistoric, in future studies.
2. Study Area
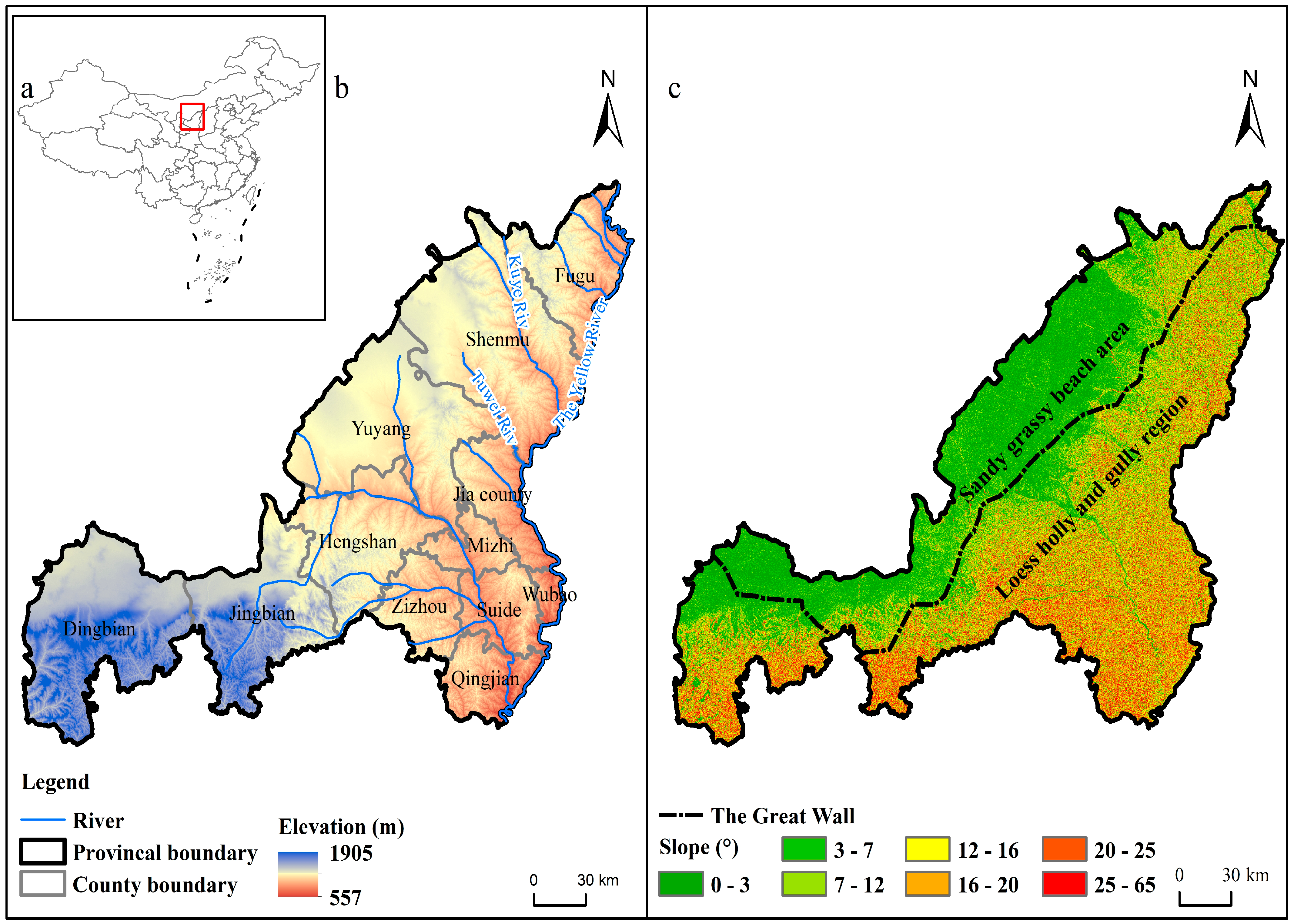
Yulin is located in the north of Shaanxi Province, China (36°57′~39°34′ N, 107°28′~111°15′ E), with a total land area of 4.292 × 10
4 km
2 (
Figure 1). In terms of the climate type, the region belongs to the transition zone from a temperate monsoon climate to temperate continental climate, from northwest to southeast, with an annual temperature of 7–9 °C. The frost-free period is short, and the precipitation ranges from 300 to 500 mm, mainly in the summer. Taking the Ming Great Wall as the boundary, the topography and geomorphology of the study area show great differences. Beyond the Great Wall lies an expanse of sandy and grassland terrain, encompassing 42% of the total area. This region features a gentle and undulating topography, characterized by a continuous distribution of sand dunes as well as scattered beaches and lakes. Within the Great Wall, there is a significant expanse of loess hills and gullies, encompassing 58% of the total area. This region can be further classified into the eastern loess hills and gullies, as well as the western low mountain hills area. The eastern loess hilly and gully area is characterized by an alternating distribution of hills and ridges. The surface in this area is fragmented due to the impact of flowing water erosion, resulting in significant fluctuations in the terrain. On the other hand, the western low mountain and hilly area has a higher elevation. The tableland in this area is wide and the slope is relatively gentle. In conclusion, the terrain in this region is higher in the west and lower in the east. Influenced by the topography, most rivers flow from northwest to southeast. Major rivers, including Kuye River, Tuwei River, and Wuding River, all directly discharge into the Yellow River.
3. Materials and Methods
3.1. Parameter Factor Selection
Based on previous research and combined with the development process of cultivated land in the region from Ming-Qing (1368-1911CE) to the present [
31,
32,
33,
34], this article identified the variables that affect the spatial distribution pattern of the cultivated land. Natural variables such as the slope, altitude, soil type, and proximity to rivers have been found to play a crucial role in determining the formation of arable land. Previous studies have also highlighted the significant influence of precipitation and temperature on the development of arable land [
30,
35,
36]. Moreover, the amount of cultivated land is influenced by population density, as it is a result of human activities. Furthermore, the spatial distribution of cultivated land is closely associated with the distance from the residential area [
37]. The research area exhibits a rugged and uneven surface, which means that the visible distance (Euclidean distance) may not accurately reflect the actual distance required to reach a specific location. In order to address this problem, this study focused on calculating the time it takes to walk 1 m under different slope conditions and applied the results for a Cost–Distance Analysis. Additionally, eight factors were selected as driving factors that influence cultivated land development: elevation, slope, soil type (ST), annual average temperature (AAT), annual average precipitation (AAP), distance from rivers (DR), distance from settlements (DS), and population density (PD).
3.2. Data Sources
The land use data for Yulin in 1985 were extracted from the dataset by Yang et al. [
38], with a spatial resolution of 30 m. Digital Elevation Model (DEM) data were downloaded from the Geographic Spatial Data Cloud (
http://www.gscloud.cn, accessed on 5 July 2023) with a spatial resolution of 30 m, and slope data were calculated from the DEM data using ArcGIS 10.2 software. Soil data were obtained from the Resource and Environment Science Data Center of the Chinese Academy of Sciences (
http://www.resdc.cn, accessed on 5 July 2023). These data were digitized based on the “1:10,000,000 soil map of the People’s Republic of China (PRC)”, which was compiled and published by the National Soil Census Office in 1995, according to the traditional “Soil Occurrence Classification System” (SOCS). The STs were divided into 12 soil orders, 61 soil classes, and 227 subclasses, with a spatial resolution of 1 km. AAT and AP data were derived from the WorldClim project (
http://worldclim.org, accessed on 6 July 2023). The temporal coverage spans from 1970 to 2000, with a spatial resolution of 1 km. PD data are derived from the 1 Kilometer Grid Population Spatial Distribution Dataset of China [
39]. This study utilized population density data from 1990, which is also the year closest to the distribution of cultivated land to be reconstructed. The vector boundaries, river, and settlement point data for the study area were downloaded from the National Geographical Information Resource Catalog Service System (
http://www.webmap.cn, accessed on 6 July 2023). The scale of the latter two datasets is 1:250,000.
3.3. Data Processing
The land use data of 1985 were reclassified in ArcGIS. Cultivated land was separated into one category, while all other land use types were grouped into another category. The distance to rivers raster data were created using the Euclidean Distance tool in ArcGIS 10.2, based on river vector data. Similarly, the distance to settlement points raster data were generated using the Cost–Distance tool. A previous study identified a relationship between walking time and slope, which is as follows [
40]:
In the equation, Y represents the time (second) required to walk 1 m, and x represents the slope.
Using the Raster Calculator tool in ArcGIS 10.2, the slope–time raster was derived and used as the cost raster data. This raster, combined with settlement point data, generated the distance to settlement points raster. Combining the soil organic matter content and the “barren land” type in the land use data of 1985, the ST data were reclassified into 5 levels using ArcGIS 10.2. They included the most unsuitable type and the other four types based on organic matter content from low to high. To ensure comparability of contribution rates for each variable, it is essential to standardize the variables due to their non-uniform units and significant differences in numerical values. The processing formula is as follows [
41]:
represents the grid number, is the maximum value of each independent variable, is the value of each independent variable, is the standardized value of the independent variable for grid , with a range of [0, 1].
The spatial scope of the research area determined that the simulated reconstruction of cultivated land in this study has a resolution of 250 m. Additionally, resampling was conducted on each grid dataset to ensure that the number and resolution of each variable grid can be overlaid and analyzed.
3.4. Model Configuration
The BLR model is an equation model that predicts a binary dependent variable (0 or 1, yes or no) based on continuous or categorical independent variables. It calculates separate coefficients for each explanatory variable and determines the probability of the dependent variable occurring through weighted calculations. In this study, we considered the distribution of cultivated land in 1985 as the dependent variable and took eight natural and social factors that influence cultivated land distribution as independent variables. A BLR model was built to calculate the weights of each independent variable. Finally, the Raster Calculator tool in ArcGIS 10.2 was utilized to derive the spatial probability distribution of cultivated land in 1985. The formula of the BLR model is the following [
42]:
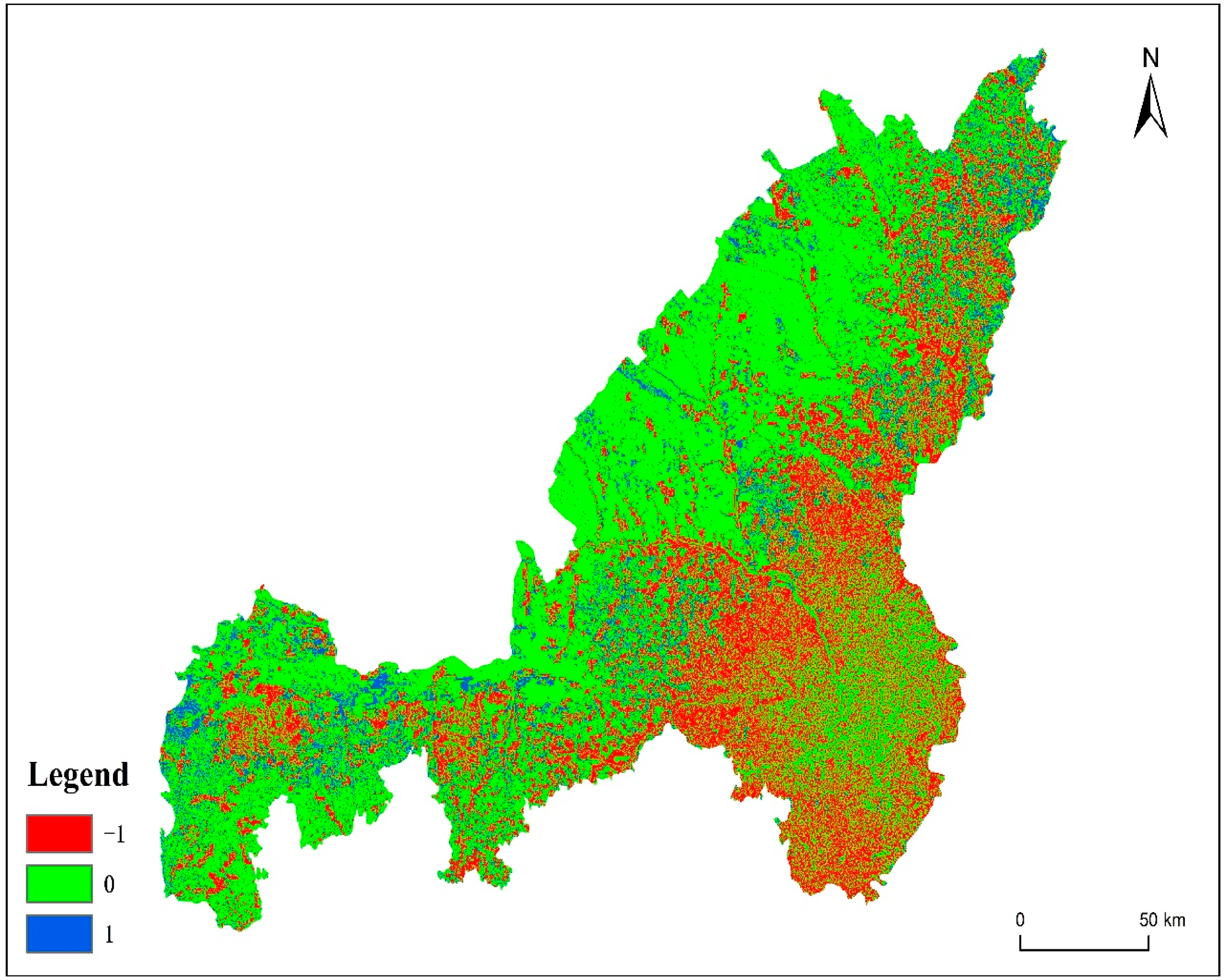
represents the raster number, is the probability of raster becoming cultivated land or non-cultivated land, α is the constant term, is the variable value, β is the regression coefficient, and is the number of independent variables. For the analysis of the model’s independent variables, a p-value of less than 0.05 indicates that the selected factors have reached a significant level and are variables that influence the probability of cultivated land distribution. This article assumed p ≤ 0.5 for arable land and p > 0.5 for non-arable land. Comparing the predicted results with the actual land use data, the higher the prediction accuracy, the more reasonable the model construction is considered as.
To determine the parameters of the BLR model, 50,000 grids were randomly selected from a total of 686,541 grids in the study area for cultivated land and non-cultivated land, respectively. Label points were then used to extract the corresponding values of each independent variable. The extracted data were exported and loaded into Excel. The calculation of the model’s paraments was conducted using IBM SPSS Statistics 22.
3.5. Precision Evaluation
This paper uses the Kappa coefficient to evaluate the model’s prediction accuracy. The formula for calculating the Kappa coefficient is as follows:
is the proportion of correctly simulated data and
is the proportion of expected correct simulated data under a random situation. When the
P0 is greater than the
, the Kappa value is positive, and a larger Kappa value indicates better consistency. When the predicted results are entirely consistent with the actual data, the Kappa coefficient equals 1. Detailed classifying criteria can be found in
Table 1 [
43].