Assessment and Forecast of Shoreline Change Using Geo-Spatial Techniques in the Gulf of California
Abstract
1. Introduction
2. Data and Methods
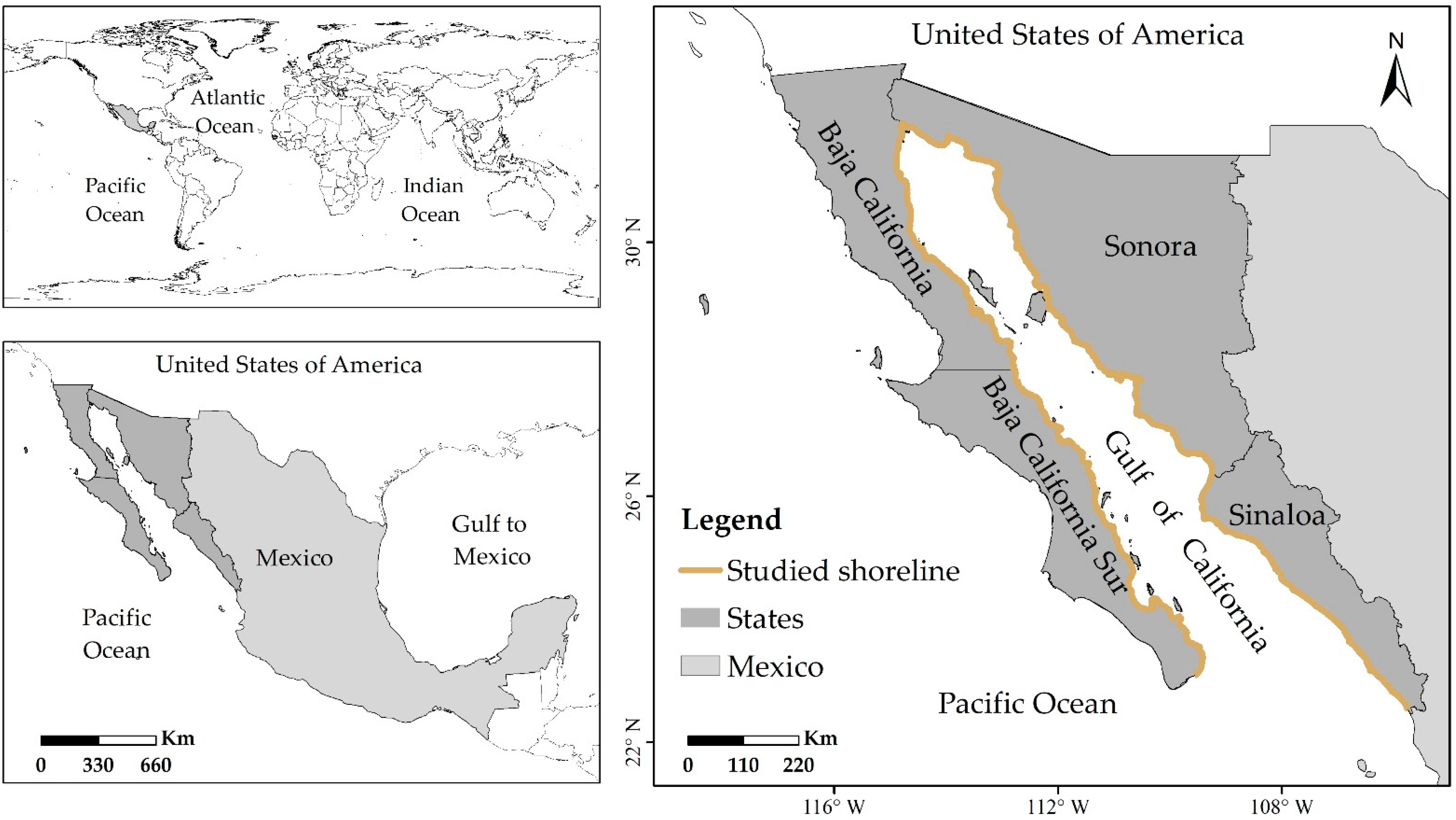
2.1. Study Area
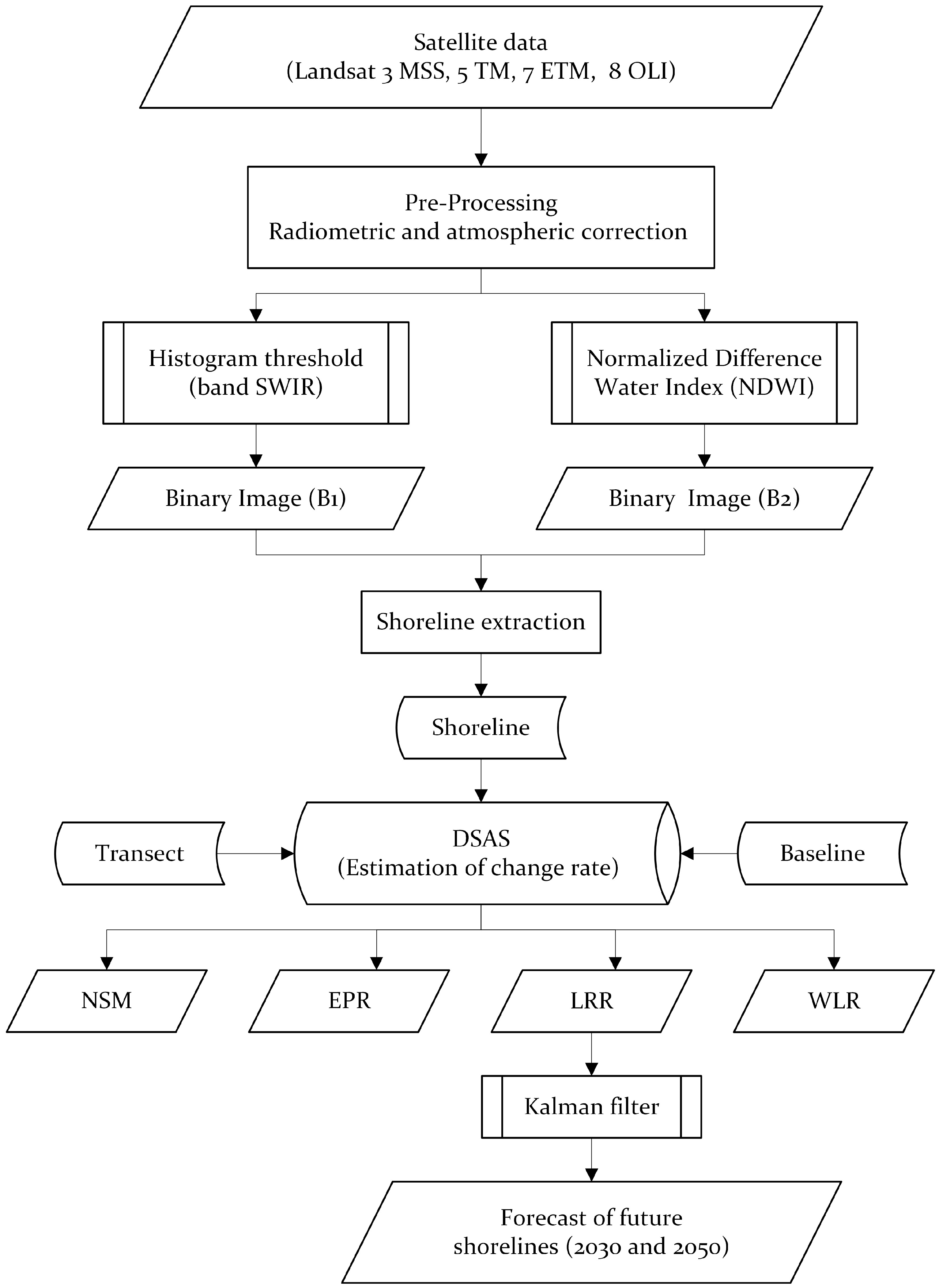
2.2. Methodology
2.3. Remote Sensing Image Preprocessing
2.4. Shoreline Extraction
2.5. Digital Shoreline Analysis System
- (1)
- Creating a geodatabase within a Geographic Information System environment.
- (2)
- Extracting the shorelines stated in Section 2.4.
- (3)
- (4)
- Generating transects perpendicular to the baseline. Creating 33,225 transects at 100 m intervals and a smoothing distance of 3000 m for Sonora and 2000 m for the rest of the states (Figure 3).
- (5)
- Calculating the rates of change of the shoreline for which DSAS runs statistical models based on different measures between the historical positions of the shorelines for each of the transects, and generating different rates of change depending on the selected statistical methods [21].
- Net Shoreline Movement (NSM) is the distance between the first and last shoreline. A statistical parameter calculated for each transect launched perpendicularly to the coast, [28] and represented by the following equation, where is the distance in meters:
- Linear Regression Rate (LRR) comprises fitting the fewest squares regression line to multiple shoreline position points for a specific transect [28]. It is calculated by plotting the points where the coasts are intercepted by transects and calculating the linear regression, an equation:where Y is the distance in meters from the baseline, x is the coastal date interval in years, and b is the slope of the fitted line (m/year), i.e., the rate of change of the LRR shoreline, and as is the intersection. LRR is the line slope suitable for the long-term analysis of the shoreline change [51,52] and is based on accepted statistical concepts with satisfactory accuracy [38]. The next positions of the shoreline change were forecasted using this method [53].
- Weighted Linear Regression (WLR) determines a line of a better fit than the LRR, as it gives more weight to reliable data with a 95% confidence interval [54]. According to [54], the weight is defined as a function of the variance in the measurement uncertainty , and the weighting value ω is linked to the shore data before examining its rate of change [21].
- WLR considers ambiguity at each shoreline position when calculating a trend line. The weight assigned to each shore position is the inverse of the squared positional uncertainty. Therefore, the shorelines with higher uncertainty have less influence on the trend line than data points with higher uncertainty [38].
Uncertainty Estimation
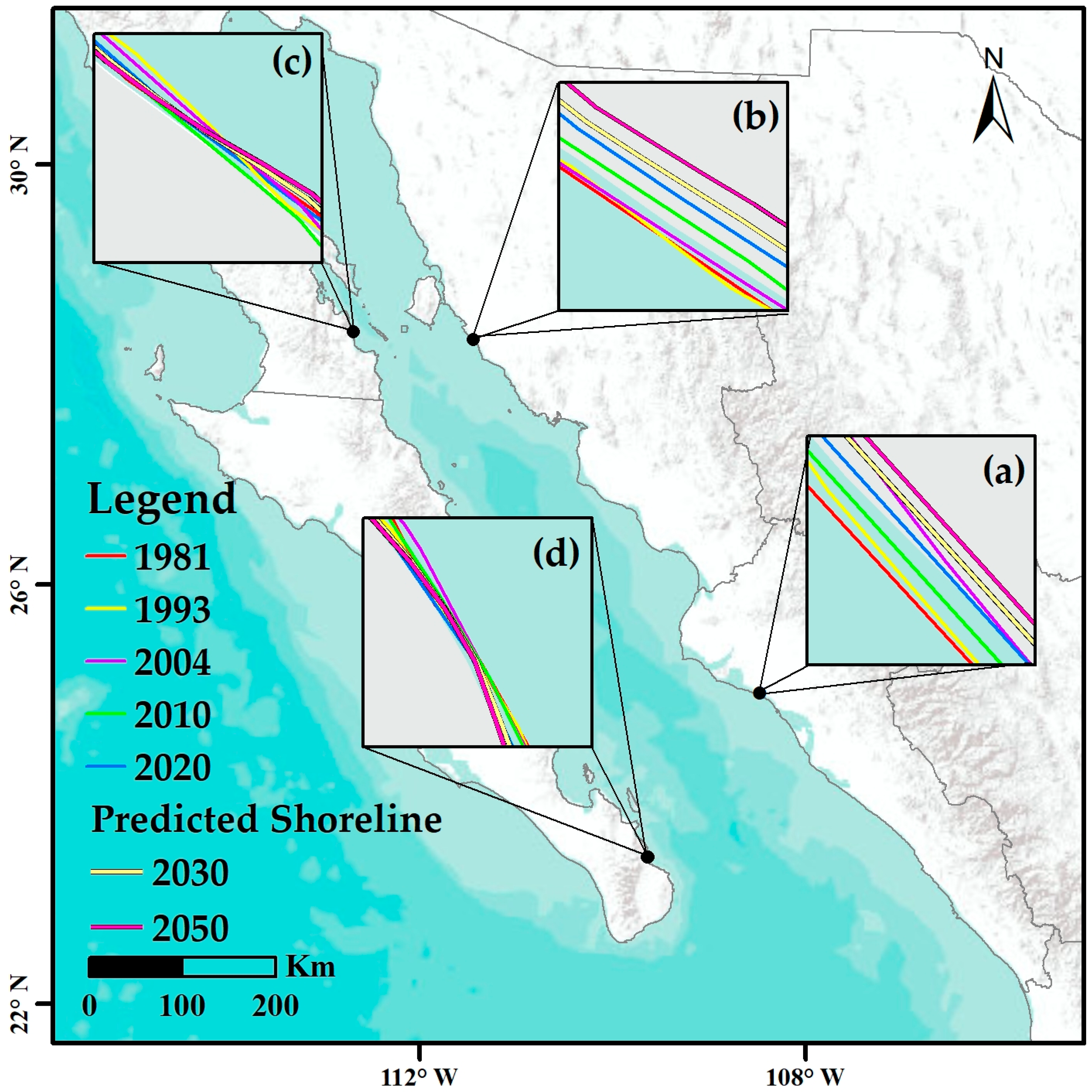
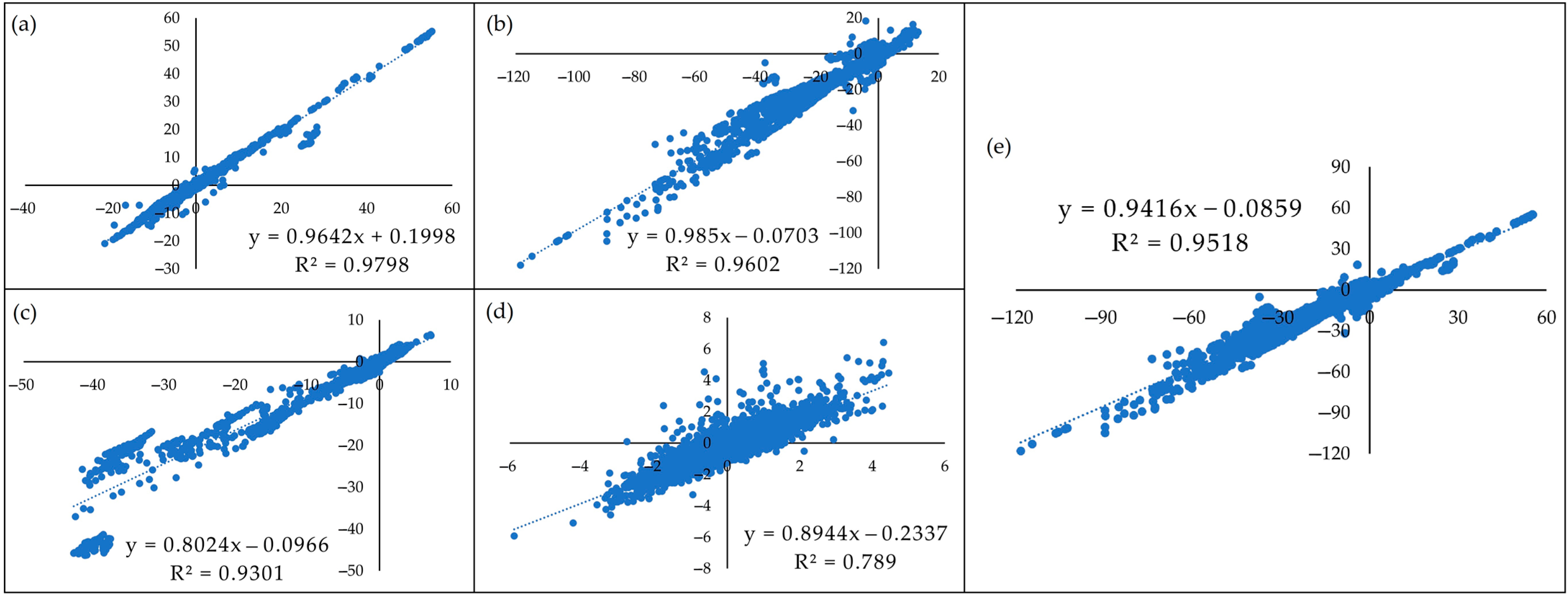
2.6. Shoreline Forecast (2030, 2050) and Model Validation
3. Results and Discussions
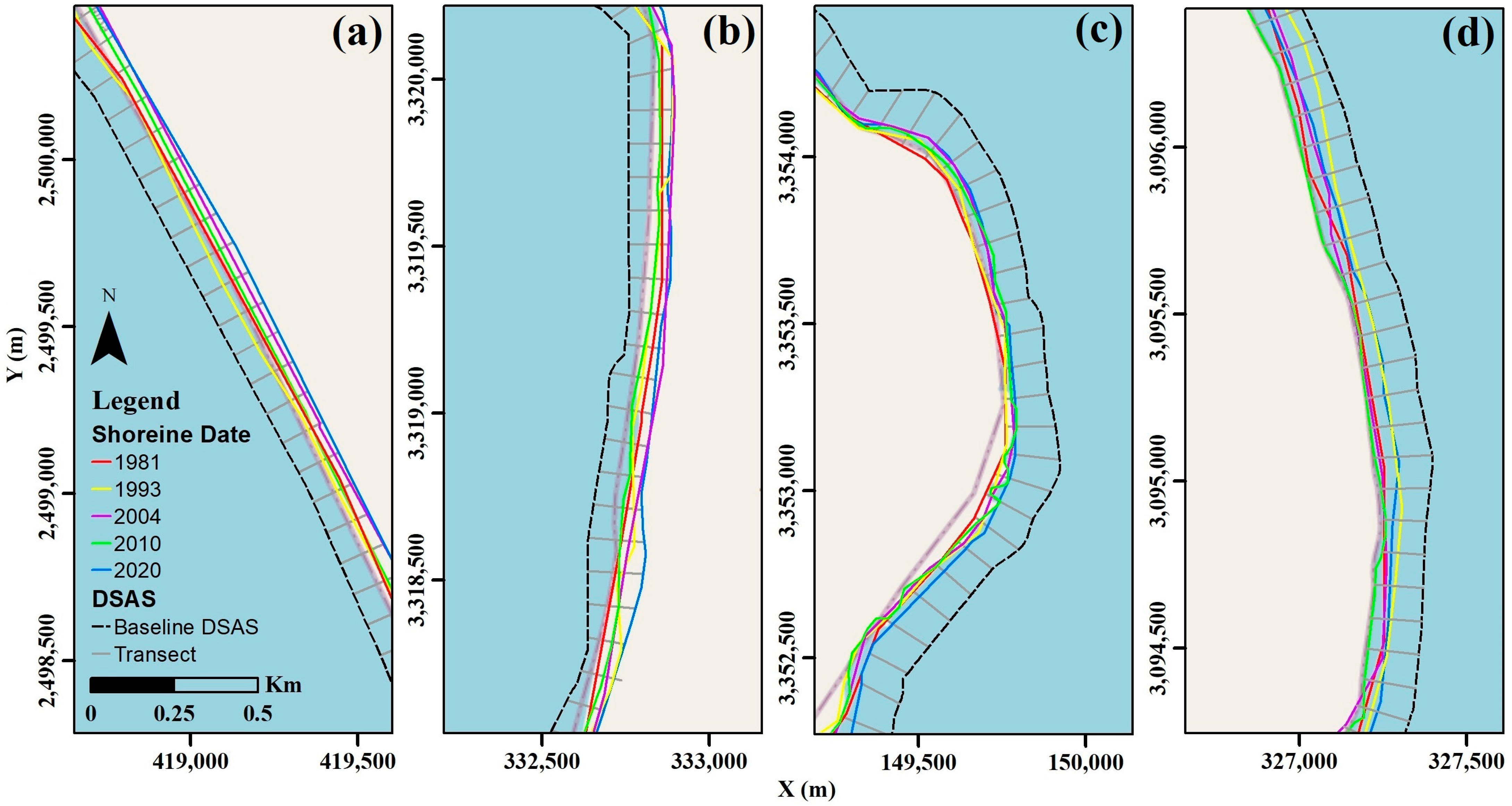
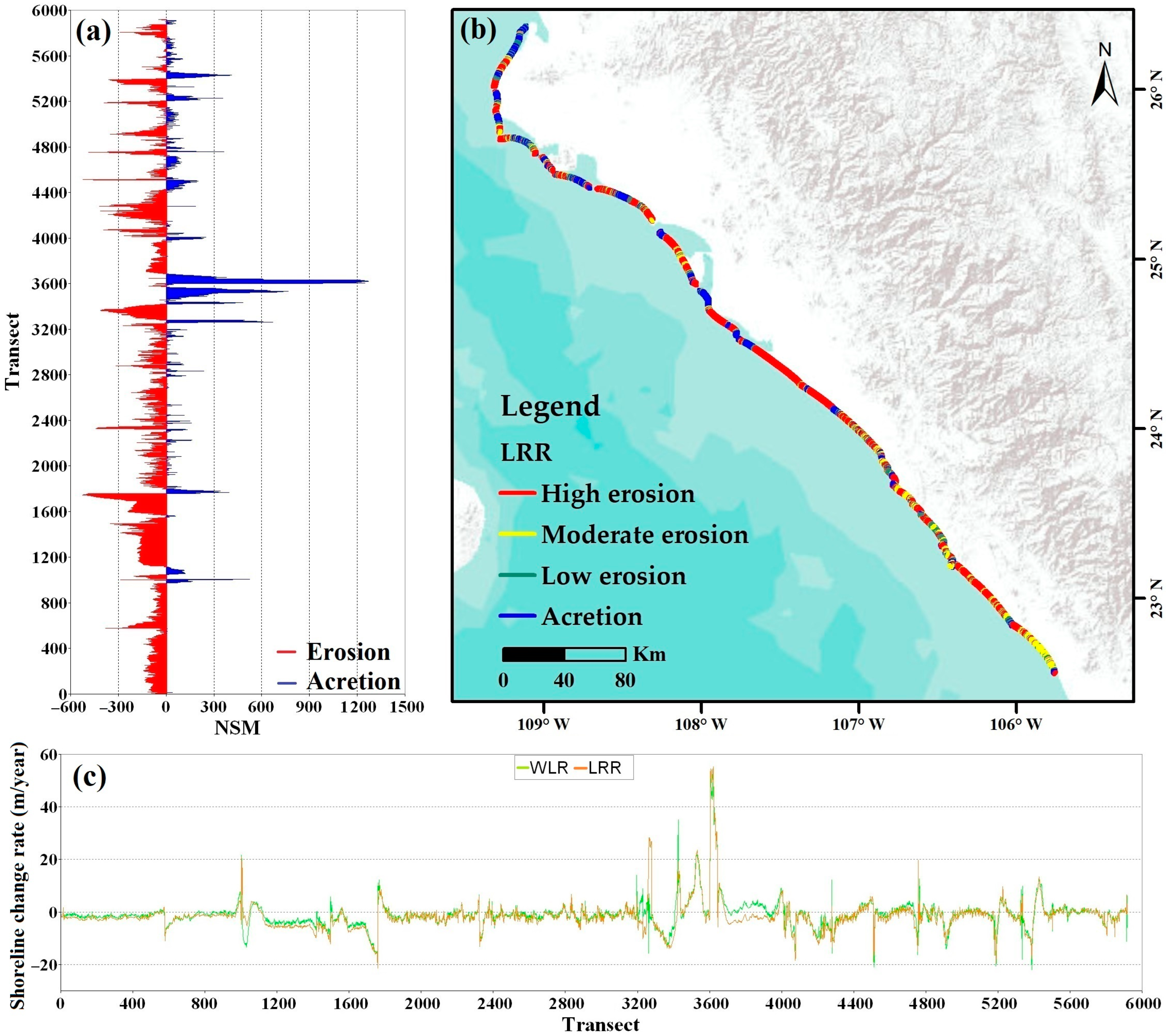
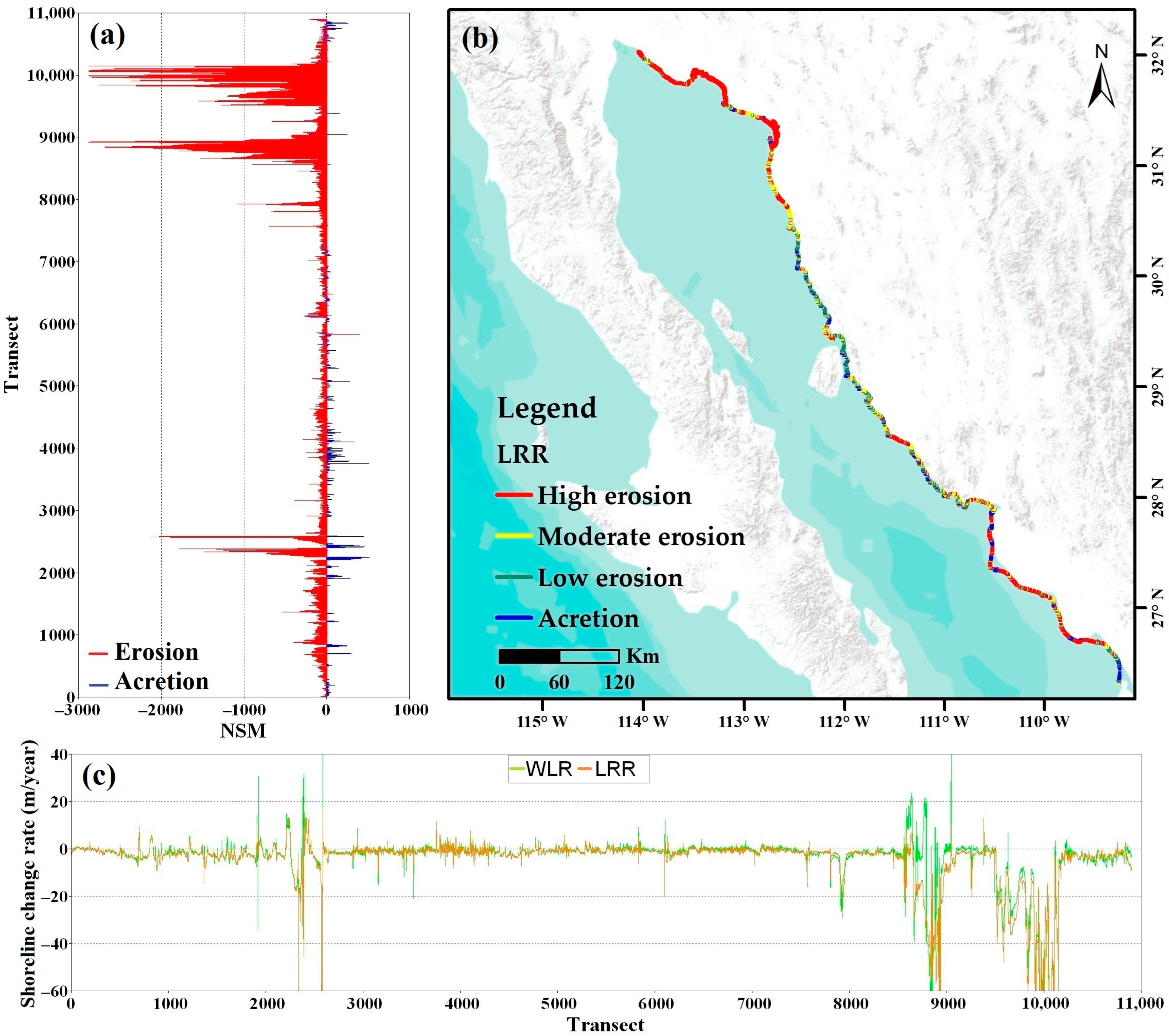
3.1. Shoreline Change Analysis between 1981 and 2020
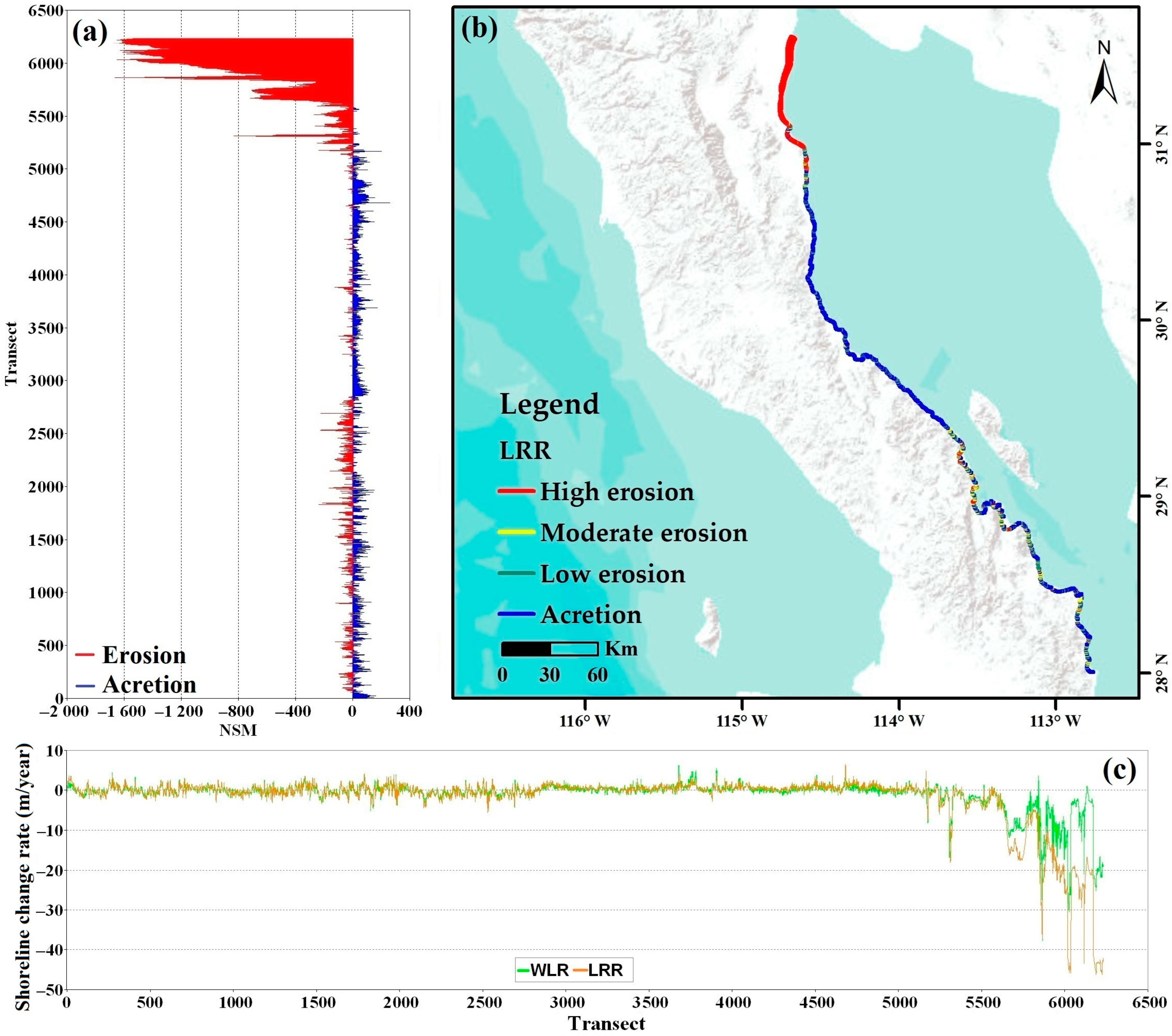
3.2. Analysis by State
3.3. Future Shoreline Forecast and Model Validation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Boak, E.H.; Turner, I.L. Shoreline Definition and Detection: A Review. J. Coast. Res. 2005, 214, 688–703. [Google Scholar] [CrossRef]
- Sevilla, N.P.M.; Adeath, I.A.; Le Bail, M.; Ruiz, A.C. Coastal Development: Construction of a Public Policy for the Shores and Seas of Mexico. In Coastal Management: Global Challenges and Innovations; Academic Press: Cambridge, MA, USA, 2018; pp. 21–38. [Google Scholar] [CrossRef]
- National Commission for the Knowledge and Use of Biodiversity. Cartography of the Mexican Littoral Fundamental for Decision Making on Coastal Natural Resources. Available online: https://www.gob.mx/conabio/prensa/conabio-genera-nueva-cartografia-de-la-linea-de-costa-de-mexico?idiom=es (accessed on 26 November 2022).
- Franco-Ochoa, C.; Zambrano-Medina, Y.; Plata-Rocha, W.; Monjardín-Armenta, S.; Rodríguez-Cueto, Y.; Escudero, M.; Mendoza, E. Long-Term Analysis of Wave Climate and Shoreline Change along the Gulf of California. Appl. Sci. 2020, 10, 8719. [Google Scholar] [CrossRef]
- Piazza Forgiarini, A.P.; Amaral de Figueiredo, S.; Calliari, L.J.; Goulart, E.S.; Marques, W.; Trombetta, T.B.; Oleinik, P.H.; Guimarães, R.C.; Arigony-Neto, J.; Cabral Salame, C. Quantifying the Geomorphologic and Urbanization Influence on Coastal Retreat under Sea Level Rise. Estuar. Coast. Shelf Sci. 2019, 230, 106437. [Google Scholar] [CrossRef]
- Özpolat, E.; Demir, T. The Spatiotemporal Shoreline Dynamics of a Delta under Natural and Anthropogenic Conditions from 1950 to 2018: A Dramatic Case from the Eastern Mediterranean. Ocean Coast. Manag. 2019, 180, 104910. [Google Scholar] [CrossRef]
- Hamid, A.I.A.; Din, A.H.M.; Abdullah, N.M.; Yusof, N.; Hamid, M.R.A.; Shah, A.M. Exploring Space Geodetic Technology for Physical Coastal Vulnerability Index and Management Strategies: A Review. Ocean Coast. Manag. 2021, 214, 105916. [Google Scholar] [CrossRef]
- Parthasarathy, K.S.S.; Deka, P.C. Remote Sensing and GIS Application in Assessment of Coastal Vulnerability and Shoreline Changes: A Review. ISH J. Hydraul. Eng. 2019, 27, 588–600. [Google Scholar] [CrossRef]
- Roy, S.; Mahapatra, M.; Chakraborty, A. Shoreline Change Detection along the Coast of Odisha, India Using Digital Shoreline Analysis System. Spat. Inf. Res. 2018, 26, 563–571. [Google Scholar] [CrossRef]
- Yan, D.; Yao, X.; Li, J.; Qi, L.; Luan, Z. Shoreline Change Detection and Forecast along the Yancheng Coast Using a Digital Shoreline Analysis System. Wetlands 2021, 41, 47. [Google Scholar] [CrossRef]
- Williams, S.J. Sea-Level Rise Implications for Coastal Regions. J. Coast. Res. 2013, 63, 184–196. [Google Scholar] [CrossRef]
- Chen, C.; Bu, J.; Zhang, Y.; Zhuang, Y.; Chu, Y.; Hu, J.; Guo, B. The Application of the Tasseled Cap Transformation and Feature Knowledge for the Extraction of Coastline Information from Remote Sensing Images. Adv. Space Res. 2019, 64, 1780–1791. [Google Scholar] [CrossRef]
- Charles, W.F.; Makowski, C. Encyclopedia of Coastal Science; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar] [CrossRef]
- Daud, S.; Milow, P.; Rozainah; Zakaria, M. Analysis of Shoreline Change Trends and Adaptation of Selangor Coastline, Using Landsat Satellite Data. J. Indian Soc. Remote Sens. 2021, 49, 1869–1878. [Google Scholar] [CrossRef]
- Zhang, Y.; Xie, J.; Liu, L. Investigating Sea-Level Change and Its Impact on Hong Kong’s Coastal Environment. Ann. GIS 2011, 17, 105–112. [Google Scholar] [CrossRef]
- Mujabar, P.S.; Chandrasekar, N. Shoreline Change Analysis along the Coast between Kanyakumari and Tuticorin of India Using Remote Sensing and GIS. Arab. J. Geosci. 2013, 6, 647–664. [Google Scholar] [CrossRef]
- Appeaning Addo, K.; Jayson-Quashigah, P.N.; Kufogbe, K.S. Quantitative Analysis of Shoreline Change Using Medium Resolution Satellite Imagery in Keta, Ghana. Mar. Sci. 2012, 1, 1–9. [Google Scholar] [CrossRef]
- Mutagi, S.; Yadav, A.; Hiremath, C.G. Shoreline Change Model: A Review. Lect. Notes Civ. Eng. 2022, 162, 1019–1031. [Google Scholar] [CrossRef]
- Hossain, S.A.; Mondal, I.; Thakur, S.; Linh, N.T.T.; Anh, D.T. Assessing the Multi-Decadal Shoreline Dynamics along the Purba Medinipur-Balasore Coastal Stretch, India by Integrating Remote Sensing and Statistical Methods. Acta Geophys. 2022, 70, 1701–1715. [Google Scholar] [CrossRef]
- Alesheikh, A.A.; Ghorbanali, A.; Nouri, N. Coastline Change Detection Using Remote Sensing. Int. J. Environ. Sci. Technol. 2007, 4, 61–66. [Google Scholar] [CrossRef]
- Godwyn-Paulson, P.; Jonathan, M.P.; Roy, P.D.; Rodríguez-Espinosa, P.F.; Muthusankar, G.; Muñoz-Sevilla, N.P.; Lakshumanan, C. Evolution of Southern Mexican Pacific Coastline: Responses to Meteo-Oceanographic and Physiographic Conditions. Reg. Stud. Mar. Sci. 2021, 47, 101914. [Google Scholar] [CrossRef]
- Williams, D.L.; Goward, S.; Arvidson, T. Landsat: Yesterday, Today, and Tomorrow. Photogramm. Eng. Remote Sens. 2006, 72, 1171–1178. [Google Scholar] [CrossRef]
- Masria, A.; Nadaoka, K.; Negm, A.; Iskander, M. Detection of Shoreline and Land Cover Changes around Rosetta Promontory, Egypt, Based on Remote Sensing Analysis. Land 2015, 4, 216–230. [Google Scholar] [CrossRef]
- Turner, I.L.; Harley, M.D.; Almar, R.; Bergsma, E.W.J. Satellite Optical Imagery in Coastal Engineering. Coast. Eng. 2021, 167, 103919. [Google Scholar] [CrossRef]
- Randazzo, G.; Barreca, G.; Cascio, M.; Crupi, A.; Fontana, M.; Gregorio, F.; Lanza, S.; Muzirafuti, A. Analysis of Very High Spatial Resolution Images for Automatic Shoreline Extraction and Satellite-Derived Bathymetry Mapping. Geosciences 2020, 10, 172. [Google Scholar] [CrossRef]
- Abdul Maulud, K.N.; Selamat, S.N.; Mohd, F.A.; Md Noor, N.; Wan Mohd Jaafar, W.S.; Kamarudin, M.K.A.; Ariffin, E.H.; Adnan, N.A.; Ahmad, A. Assessment of Shoreline Changes for the Selangor Coast, Malaysia, Using the Digital Shoreline Analysis System Technique. Urban Sci. 2022, 6, 71. [Google Scholar] [CrossRef]
- Vallarino Castillo, R.; Negro Valdecantos, V.; Moreno Blasco, L. Shoreline Change Analysis Using Historical Multispectral Landsat Images of the Pacific Coast of Panama. J. Mar. Sci. Eng. 2022, 10, 1801. [Google Scholar] [CrossRef]
- Himmelstoss, E.A.; Henderson, R.E.; Kratzmann, M.G.; Farris, A.S. Digital Shoreline Analysis System (DSAS) Version 5.1 User Guide; Open-File Report 2021-1091; USGS Publication Warehouse: Reston, VI, USA, 2021. [Google Scholar] [CrossRef]
- Zambrano-medina, Y. Shoreline Analysis and Erosion Risk Assessment of a Coastal Strip Subjected to High Anthropogenic Pressure. Tecnol. Cienc. Agua 2022, 13, 249–300. [Google Scholar] [CrossRef]
- Hakkou, M.; Maanan, M.; Belrhaba, T.; El khalidi, K.; El Ouai, D.; Benmohammadi, A. Multi-Decadal Assessment of Shoreline Changes Using Geospatial Tools and Automatic Computation in Kenitra Coast, Morocco. Ocean Coast. Manag. 2018, 163, 232–239. [Google Scholar] [CrossRef]
- Dewidar, K.; Bayoumi, S. Forecasting Shoreline Changes along the Egyptian Nile Delta Coast Using Landsat Image Series and Geographic Information System. Environ. Monit. Assess. 2021, 193, 429. [Google Scholar] [CrossRef]
- SEMARNAT Gulf of California: 1126 km of Imposing Beauty and Prodigal Biodiversity. Available online: https://www.gob.mx/semarnat/articulos/golfo-de-california-mil-126-km-de-imponente-belleza-y-prodiga-biodiversidad-150945 (accessed on 15 August 2022).
- Jiménez-Illescas, Á.R.; Zayas-Esquer, M.M.; Espinosa-Carreón, T.L. Integral Management of the Coastal Zone to Solve the Problems of Erosion in Las Glorias Beach, Guasave, Sinaloa, Mexico. In Coastal Management; Krishnamurthy, R.R., Jonathan, M.P., Srinivasalu, S., Glaeser, B., Eds.; Academic Press: Cambridge, MA, USA, 2019; pp. 141–163. ISBN 9780128104736. [Google Scholar]
- Liu, D.; Xu, Y.; Faghihinia, M.; Kay, P.; Chan, F.K.S.; Wu, N. Evolving Framework of Studies on Global Gulf Ecosystems with Sustainable Development Goals. Environ. Sci. Pollut. Res. 2022, 29, 18385–18397. [Google Scholar] [CrossRef]
- Vellanoweth, R.L.; Porcayo-Michelini, A.; Guttenberg, R.B.; Hayden, W.; Ainis, A.F.; Hernández-Estrada, R.L. Spring Tides, Storm Surges, and the Destruction of Coastal Middens: A Case Study from the Upper Gulf of California, México. J. Isl. Coast. Archaeol. 2020, 17, 420–431. [Google Scholar] [CrossRef]
- Ledesma-Vázquez, J.; Johnson, M.E.; Gonzalez-Yajimovich, O.; Santamaría-del-Angel, E. Gulf of California Geography, Geological Origins, Oceanography, and Sedimentation Patterns. In Atlas of Coastal Ecosystems in the Western Gulf of California; The University of Arizona Press: Tucson, AZ, USA, 2009; pp. 1–10. [Google Scholar]
- Nava-Sánchez, E.H.; Martínez-Flores, G.; Murillo-Jiménez, J.M. Factors That Cause Beach Erosion in Baja California Sur, Mexico; University of El Salvador: San Salvador, El Salvador, 2018; Volume 4. [Google Scholar]
- Baig, M.R.I.; Ahmad, I.A.; Shahfahad; Tayyab, M.; Rahman, A. Analysis of Shoreline Changes in Vishakhapatnam Coastal Tract of Andhra Pradesh, India: An Application of Digital Shoreline Analysis System (DSAS). Ann. GIS 2020, 26, 361–376. [Google Scholar] [CrossRef]
- Zed, A.A.A.; Soliman, M.R.; Yassin, A.A. Evaluation of Using Satellite Image in Detecting Long Term Shoreline Change along El-Arish Coastal Zone, Egypt. Alex. Eng. J. 2018, 57, 2687–2702. [Google Scholar] [CrossRef]
- Sekovski, I.; Stecchi, F.; Mancini, F.; Del Rio, L. Image Classification Methods Applied to Shoreline Extraction on Very High-Resolution Multispectral Imagery. Int. J. Remote Sens. 2014, 35, 3556–3578. [Google Scholar] [CrossRef]
- Tsai, Y.L.S. Monitoring 23-Year of Shoreline Changes of the Zengwun Estuary in Southern Taiwan Using Time-Series Landsat Data and Edge Detection Techniques. Sci. Total Environ. 2022, 839, 156310. [Google Scholar] [CrossRef] [PubMed]
- Kankara, R.S.; Selvan, S.C.; Markose, V.J.; Rajan, B.; Arockiaraj, S. Estimation of Long and Short Term Shoreline Changes along Andhra Pradesh Coast Using Remote Sensing and GIS Techniques. Procedia Eng. 2015, 116, 855–862. [Google Scholar] [CrossRef]
- Jalaludin, M.; Setiawan, C.; Zid, M.; Utomo, R.T. Analysis of Shoreline Changes before and after the Tsunami at Tanjung Lesung Beach, Banten Province of Indonesia. IOP Conf. Ser. Earth Environ. Sci. 2020, 412, 012004. [Google Scholar] [CrossRef]
- Kermani, S.; Boutiba, M.; Guendouz, M.; Guettouche, M.S.; Khelfani, D. Detection and Analysis of Shoreline Changes Using Geospatial Tools and Automatic Computation: Case of Jijelian Sandy Coast (East Algeria). Ocean Coast. Manag. 2016, 132, 46–58. [Google Scholar] [CrossRef]
- Barbaro, G.; Bombino, G.; Foti, G.; Borrello, M.M.; Puntorieri, P. Shoreline Evolution near River Mouth: Case Study of Petrace River (Calabria, Italy). Reg. Stud. Mar. Sci. 2019, 29, 100619. [Google Scholar] [CrossRef]
- McFeeters, S.K. The Use of the Normalized Difference Water Index (NDWI) in the Delineation of Open Water Features. Int. J. Remote Sens. 1996, 17, 1425–1432. [Google Scholar] [CrossRef]
- Mondejar, J.P.; Tongco, A.F. Near Infrared Band of Landsat 8 as Water Index: A Case Study around Cordova and Lapu-Lapu City, Cebu, Philippines. Sustain. Environ. Res. 2019, 29, 16. [Google Scholar] [CrossRef]
- Ashtekar, A.S.; Mohammed-Aslam, M.A.; Moosvi, A.R. Utility of Normalized Difference Water Index and GIS for Mapping Surface Water Dynamics in Sub-Upper Krishna Basin. J. Indian Soc. Remote Sens. 2019, 47, 1431–1442. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, X.; Ling, F.; Xu, S.; Wang, C. Analysis of Coastline Extraction from Landsat-8 OLI Imagery. Water 2017, 9, 816. [Google Scholar] [CrossRef]
- Crowell, M.; Leatherman, S.P.; Buckley, M.K. Historical Shoreline Change: Error Analysis and Mapping Accuracy. J. Coast. Res. 1991, 7, 839–852. [Google Scholar]
- Kumar Das, S.; Sajan, B.; Ojha, C.; Soren, S. Shoreline Change Behavior Study of Jambudwip Island of Indian Sundarban Using DSAS Model. Egypt. J. Remote Sens. Space Sci. 2021, 24, 961–970. [Google Scholar] [CrossRef]
- Kuleli, T.; Guneroglu, A.; Karsli, F.; Dihkan, M. Automatic Detection of Shoreline Change on Coastal Ramsar Wetlands of Turkey. Ocean Eng. 2011, 38, 1141–1149. [Google Scholar] [CrossRef]
- Douglas, B.C.; Crowell, M. Long-Term Shoreline Position Prediction and Error Propagation. J. Coast. Res. 2000, 16, 145–152. [Google Scholar]
- Genz, A.S.; Fletcher, C.H.; Dunn, R.A.; Frazer, L.N.; Rooney, J.J. The Predictive Accuracy of Shoreline Change Rate Methods and Alongshore Beach Variation on Maui, Hawaii. J. Coast. Res. 2007, 23, 87–105. [Google Scholar] [CrossRef]
- Coca, O.; Ricaurte-Villota, C. Regional Patterns of Coastal Erosion and Sedimentation Derived from Spatial Autocorrelation Analysis: Pacific and Colombian Caribbean. Coasts 2022, 2, 125–151. [Google Scholar] [CrossRef]
- Dar, I.A.; Dar, M.A. Prediction of Shoreline Recession Using Geospatial Technology: A Case Study of Chennai Coast, Tamil Nadu, India. J. Coast. Res. 2009, 25, 1276–1286. [Google Scholar] [CrossRef]
- Vu, M.T.; Lacroix, Y.; Than, V.V.; Nguyen, V.T. Prediction of Shoreline Changes in Almanarre Beach Using Geospatial Techniques. Indian J. Geo Mar. Sci. 2020, 49, 207–2017. [Google Scholar]
- Kalman, R.E. A New Approach to Linear Filtering and Prediction Problems. J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef]
- Long, J.W.; Plant, N.G. Extended Kalman Filter Framework for Fore-Casting Shoreline Evolution. Geophys. Res. Lett. 2012, 39, 13603. [Google Scholar] [CrossRef]
- Molina, R.; Anfuso, G.; Manno, G.; Prieto, F.J.G. The Mediterranean Coast of Andalusia (Spain): Medium-Term Evolution and Impacts of Coastal Structures. Sustainability 2019, 11, 3539. [Google Scholar] [CrossRef]
- Jiménez-Illescas, A.R.; Ma Magdalena, Z.E.; Leticia, E.C.T. Integral Management of the Coastal Zone to Solve the Problems of Erosion in Las Glorias Beach, Guasave, Sinaloa, Mexico. Coast. Manag. Glob. Chall. Innov. 2018, 141–163. [Google Scholar] [CrossRef]
- Laksono, F.A.T.; Borzì, L.; Distefano, S.; Di Stefano, A.; Kovács, J. Shoreline Prediction Modelling as a Base Tool for Coastal Management: The Catania Plain Case Study (Italy). J. Mar. Sci. Eng. 2022, 10, 1988. [Google Scholar] [CrossRef]
- Oyedotun, T.D.T.; Ruiz-Luna, A.; Navarro-Hernández, A.G. Contemporary Shoreline Changes and Consequences at a Tropical Coastal Domain. Geol. Ecol. Landsc. 2018, 2, 104–114. [Google Scholar] [CrossRef]
- Montaño-Ley, Y.; Carbajal, N.; Páez-Osuna, F. Bed Load Transport of Sediments and Morphodynamics in the Topolobampo Coastal Lagoon System, Mexico. J. Coast. Conserv. 2014, 18, 55–67. [Google Scholar] [CrossRef]
- Hernández Azcúnaga, L. Sediment Transport Dynamics as Bottom Load in the Upper Gulf of California; Potosino Institute of Scientific and Technological Research: San Luis, Mexico, 2005. [Google Scholar]
- Carriquiry, J.D.; Sánchez, A. Sedimentation in the Colorado River Delta and Upper Gulf of California after Nearly a Century of Discharge Loss. Mar. Geol. 1999, 158, 125–145. [Google Scholar] [CrossRef]
- Carriquiry, J.D.; Sánchez, A.; Camacho-Ibar, V.F. Sedimentation in the Northern Gulf of California after Cessation of the Colorado River Discharge. Sediment. Geol. 2001, 144, 37–62. [Google Scholar] [CrossRef]
- Lizarraga, O. Impacts of US Residential Tourism in Northwest Mexican Coastal Destinations: The Cases of Mazatlán, Sinaloa; Cabo San Lucas, Baja California Sur and Puerto Peñasco, Sonora. Rev. Lat.-Am. Tur. 2019, 5, 1–14. [Google Scholar] [CrossRef]
- Lluch-Cota, S.E.; Aragón-Noriega, E.A.; Arreguín-Sánchez, F.; Aurioles-Gamboa, D.; Jesús Bautista-Romero, J.; Brusca, R.C.; Cervantes-Duarte, R.; Cortés-Altamirano, R.; Del-Monte-Luna, P.; Esquivel-Herrera, A.; et al. The Gulf of California: Review of Ecosystem Status and Sustainability Challenges. Prog. Oceanogr. 2007, 73, 1–26. [Google Scholar] [CrossRef]
- Castillo, M.; Muñoz-Salinas, E.; Sanderson, D.C.W.; Cresswell, A. Landscape Evolution of Punta Arena Sand Spit (SE Baja California Peninsula, NW Mexico): Implications of ENSO on Landscape Erosion Rates. Catena 2020, 193, 104601. [Google Scholar] [CrossRef]
- Johnson, M.E.; Johnson, E.M.; Guardado-France, R.; Ledesma-Vázquez, J. Holocene Hurricane Deposits Eroded as Coastal Barriers from Andesite Sea Cliffs at Puerto Escondido (Baja California Sur, Mexico). J. Mar. Sci. Eng. 2020, 8, 75. [Google Scholar] [CrossRef]

| Satellite Data/Sensor | Year of Acquisition | Spatial Resolution (m) |
|---|---|---|
| Landsat 3-Multi-Spectral Scanner | 1981 | 60 |
| Landsat 5-Multi Spectral Scanner and Thematic Mapper | 1993 | 30 |
| Landsat 5-Multi Spectral Scanner and Thematic Mapper | 2004 | 30 |
| Landsat 7-Enhanced Thematic Mapper | 2010 | 30 |
| Landsat 8-Operational Land imager and Thermal Infrared Sensor | 2020 | 30 |
| Statistics | Sinaloa | Sonora | BC | BCS | GC |
|---|---|---|---|---|---|
| Number of transects | 5937 | 10,906 | 6293 | 10,089 | 33,225 |
| Average distance (m) | −39.61 | −176.9 | −105.46 | −4.32 | −81.57 |
| Number of transects with a negative distance | 4417 | 9558 | 2749 | 5571 | 22,295 |
| Maximum negative distance (m) | −515.90 | −2880.39 | −1650.21 | −176.94 | −2880.39 |
| Average of all negative distances (m) | −105.48 | −210.54 | −281.73 | −30.95 | −157.17 |
| Number of transects with a negative distance | 1520 | 1348 | 3544 | 4518 | 10,930 |
| Maximum positive distance (m) | 1325.71 | 747.76 | 278.6 | 318.92 | 1325.71 |
| Average of all positive distances (m) | 116.424 | 65.2 | 37.64 | 29 | 62.06 |
| Statistics | Sinaloa | Sonora | BC | BCS | GC |
|---|---|---|---|---|---|
| Average rate (m/year) | −1.32 | −4.56 | −2.69 | −0.09 | 2.16 |
| Maximum value erosion (m/year) | −26.54 | −118.36 | −42.83 | −29.93 | −118.36 |
| Average of all erosional rates (m/year) | −3.23 | −5.44 | −7.39 | −0.76 | −4.20 |
| Maximum value accretion (m/year) | 66.09 | 40.25 | 7.21 | 16.58 | 66.09 |
| Average of all accretion rates (m/year) | 4.24 | 1.63 | 0.97 | 0.74 | 1.89 |
| Statistics | Sinaloa | Sonora | BC | BCS | GC |
|---|---|---|---|---|---|
| Average rate (m/year) | −1.58 | −4.57 | −2.35 | −0.31 | −2.20 |
| Percent of all transects that are erosional (%) | 78.64 | 88.05 | 47.83 | 66.14 | 72.19 |
| Percent of all transects that have statistically significant erosion (%) | 33.54 | 36.36 | 3.91 | 10.14 | 21.91 |
| Maximum value erosion (m/year) | −20.87 | −118.02 | −46.27 | −5.92 | −118.02 |
| Average of all erosional rates (m/year) | −3.33 | −5.42 | −5.88 | −0.83 | −3.86 |
| Percent of all transects that are accretion (%) | 21.36 | 11.95 | 51.17 | 33.86 | 27.62 |
| Percent of all transects that have statistically significant accretion (%) | 5.12 | 1.84 | 5.13 | 3.14 | 3.46 |
| Maximum value accretion (m/year) | 55.21 | 18.34 | 6.54 | 6.43 | 55.21 |
| Average of all accretion rates (m/year) | 4.89 | 1.75 | 0.89 | 0.7 | 2.05 |
| Statistics | Sinaloa | Sonora | BC | BCS | GC |
|---|---|---|---|---|---|
| Average rate (m/year) | −1.12 | −3.69 | −1.89 | −0.45 | 1.78 |
| Percent of all transects that are erosional (%) | 68.87 | 77.84 | 53.54 | 69.38 | 69.06 |
| Percent of all transects that have statistically significant erosion (%) | 18.41 | 22.14 | 1.57 | 7.54 | 13.21 |
| Maximum value erosion (m/year) | −32.27 | −130.32 | −37.74 | −28.1 | −130.32 |
| Average of all erosional rates (m/year) | −2.91 | −5.32 | −2.77 | −1.02 | −3.00 |
| Percent of all transects that are accretion (%) | 31.13 | 22.16 | 46.46 | 30.62 | 30.93 |
| Percent of all transects that have statistically significant accretion (%) | 5.51 | 1.12 | 2.19 | 1.71 | 2.32 |
| Maximum value accretion (m/year) | 64.04 | 60.61 | 6.20 | 36.13 | 64.04 |
| Average of all accretion rates (m/year) | 3.74 | 2.06 | 0.82 | 0.82 | 1.86 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zambrano-Medina, Y.G.; Plata-Rocha, W.; Monjardin-Armenta, S.A.; Franco-Ochoa, C. Assessment and Forecast of Shoreline Change Using Geo-Spatial Techniques in the Gulf of California. Land 2023, 12, 782. https://doi.org/10.3390/land12040782
Zambrano-Medina YG, Plata-Rocha W, Monjardin-Armenta SA, Franco-Ochoa C. Assessment and Forecast of Shoreline Change Using Geo-Spatial Techniques in the Gulf of California. Land. 2023; 12(4):782. https://doi.org/10.3390/land12040782
Chicago/Turabian StyleZambrano-Medina, Yedid Guadalupe, Wenseslao Plata-Rocha, Sergio Alberto Monjardin-Armenta, and Cuauhtémoc Franco-Ochoa. 2023. "Assessment and Forecast of Shoreline Change Using Geo-Spatial Techniques in the Gulf of California" Land 12, no. 4: 782. https://doi.org/10.3390/land12040782
APA StyleZambrano-Medina, Y. G., Plata-Rocha, W., Monjardin-Armenta, S. A., & Franco-Ochoa, C. (2023). Assessment and Forecast of Shoreline Change Using Geo-Spatial Techniques in the Gulf of California. Land, 12(4), 782. https://doi.org/10.3390/land12040782










